Abstract
Coronavirus 2019 (COVID-19) is an extreme acute respiratory syndrome. Early diagnosis and accurate assessment of COVID-19 are not available, resulting in ineffective therapeutic therapy. This study designs an effective intelligence framework to early recognition and discrimination of COVID-19 severity from the perspective of coagulation indexes. The framework is proposed by integrating an enhanced new stochastic optimizer, a brain storm optimizing algorithm (EBSO), with an evolutionary machine learning algorithm called EBSO-SVM. Fast convergence and low risk of the local stagnant can be guaranteed for EBSO with added by Harris hawks optimization (HHO), and its property is verified on 23 benchmarks. Then, the EBSO is utilized to perform parameter optimization and feature selection simultaneously for support vector machine (SVM), and the presented EBSO-SVM early recognition and discrimination of COVID-19 severity in terms of coagulation indexes using COVID-19 clinical data. The classification performance of the EBSO-SVM is very promising, reaching 91.9195% accuracy, 90.529% Matthews correlation coefficient, 90.9912% Sensitivity and 88.5705% Specificity on COVID-19. Compared with other existing state-of-the-art methods, the EBSO-SVM in this paper still shows obvious advantages in multiple metrics. The statistical results demonstrate that the proposed EBSO-SVM shows predictive properties for all metrics and higher stability, which can be treated as a computer-aided technique for analysis of COVID-19 severity from the perspective of coagulation.
Keywords: Coronavirus Disease 2019, Coagulation index, Brain Storm optimization algorithm, Support vector machine, Harris hawks optimization
1. Introduction
In December 2019, a serious coronavirus first emerged in Wuhan, China, and later spread rapidly across the world in a short period of time (Li et al., 2020, Hu et al., 2021, Li et al., 2021, Singh et al., 2020). On January 30, 2020, the World Health Organization (WHO) declared that the novel coronavirus outbreaks a Public Health Emergency of International Concern (PHIC) (World Health Organization, 2020). According to the recommendations by the WHO, the novel coronavirus was named coronavirus disease (COVID-19) in February 2020 (World Health Organization, 2020). As of May 23, 2020, there have been a total of 5,103,006 confirmed cases of COVID-19 worldwide with 333401 fatal cases (World Health Organization, 2020). Despite governments worldwide having put great effortsthere is still a lack of effective strategies to control the spread of the disease. The rising number of COVID-19 patients can lead to a shortage of health care resources and increase the workload of medical staff. Once the medical capacity of the hospital is overloaded, it may increase the risk of COVID-19 patient mortality. A recent study has found that if the novel coronavirus is not effectively controlled, it could collapse the entire health care system in a short time (Pourhomayoun and Shakibi, 2020). Therefore, it is urgently required to develop a new prediction model for early recognition and classify the severity of COVID-19. Developing an effective prediction model can help medical institutions decide whether the patient needs to get attention first, whether the patient has a higher priority for hospitalization, whether the patient can get a greater level of monitoring and treatment, and thereby rationally and effectively allocate medical resources and reduce the healthcare burden.
In recent years, machine learning and optimization approaches (or a hybrid of them) have become highly critical in the field of medicine (Jordan and Mitchell, 2015, Rajkomar et al., 2019). Machine learning methods for diagnosing different diseases were widely used, predictive model creation helped clinical decision making, and significant risk factors related to the disease were identified (Obermeyer and Emanuel, 2016, Bhagyashree et al., 2018). Optimization is a root idea in not only development of e-healthcare systems but also areas such as fault diagnosis of rolling bearings (Deng, 2020, Zhao et al., 2019), scheduling problems (Pang et al., 2018, Zhou et al., 2018), bankruptcy prediction (Cai et al., 2019, Yu et al., 2021, Zhang et al., 2020), wind speed prediction (Chen et al., 2019), image segmentation (Zhao et al., 2020, Zhao et al., 2020), engineering design problems (Ba et al., 2020, Gupta et al., 2019, Liang et al., 2020, Zhang et al., 2020). The exploration and exploitation competencies of these stochastic search methods can play a significant role in dealing with medical data classification (Lufeng et al., 2017, Huang et al., 2019, Li et al., 2018, Zhao et al., 2019), PID optimization control (Zeng et al., 2015, Zeng et al., 2014, Zeng et al., 2019), feature selection (Hu et al., 2021, Li et al., 2017, Liu et al., 2015, Zhang et al., 2020, Zhang et al., 2020), hard maximum satisfiability problem (Zeng et al., 2011, Zeng et al., 2012), parameter optimization (Heidari et al., 2019, Shen et al., 2016, Wang and Chen, 2020, Wang et al., 2017), gate resource allocation (Deng et al., 2020, Deng et al., 2020), detection of foreign fiber in cotton (Zhao et al., 2015, Zhao et al., 2014), and prediction cases in educational concerns (Lin et al., 2019, Jixia et al., 2019, Wei et al., 2020, Wei et al., 2017, Zhu et al., 2020). In particular, the machine learning technique may contribute to improving the diagnostic quality, reducing the workload of radiologists, anatomical pathologists, and the accuracy of diagnoses in diseases (Obermeyer and Emanuel, 2016), to minimize error and missed diagnosis incidence. Machine learning techniques have now become an important tool in clinical work. During the COVID-19 outbreak, machine learning methods were developed and used to identify, track and manage COVID-19, COVID-19 epidemic. In recent years, the use of artificial intelligence (AI) is popular in many fields of life sciences (De-Kuang Hwang et al., 2019, Alam et al., 2019). In the field of ophthalmology, for example, AI has achieved the level of a specialist in the distinction of diseases (Kermany et al., 2018). AI can help radiologists to diagnose benign and malignant thyroid nodules in radiology in qualitative terms (Wang et al., 2019). With the rapid growth of AI, AI machine learning technologies have been widely used for disease diagnosis; predictive models have been created to support clinical decision making in medical fields, and key factors related to illness have been quickly established (Obermeyer and Emanuel, 2016, Bhagyashree et al., 2018, Lee et al., 2014). As a result, AI technology based on machine learning is increasingly important in the medical field in computing technology. Machine-based AI technology has also been used for diagnosis of disease (Albahri et al., 2020). Computer tomography (CT) or X-ray image recognition (Kang et al., 2020, Albahli, 2021), disease epidemic, surveillance,and control (Yang et al., 2020, Zheng et al., 2020) in the course of the COVID-19 outbreak. By using classical and ensemble machine learning algorithms, Khanday et al. (2020) categorized textual clinical reports in four groups. Effect design has been carried out using frequency term/inverse document frequency (TF/IDF), word bag, and report length. Term frequency/inverse document length was used. These features have been given to classifying conventional and ensemble machines. Booth et al. (2021) designed a prognostic model for mortality in COVID-19 infection using machine learning. Prakash et al. (2020) used machine learning algorithms to analysis, prediction and evaluation of covid-19 datasets. Erraissi and Banane (2020) used a machine learning model to predict the number of cases contaminated by COVID-19, and the results showed the possibility of achieving better scores prediction after using the proposed method. Many documents show that machine learning algorithms have shown great potential in solving new coronary covid-19-related problems.
This study is first developed from the point of view of the coagulation indexes, an evolutionary SVM to diagnose COVID-19. However, in SVM, penalty factor C and the value can change the accuracy and efficiency of the learning process, and it is sensitive to these values. Both core operators are employing this proposed method (EBSO-SVM) to improve and re-establish the search capacity for the brain storm optimization algorithm (BSO) (Shi, 2011), abstracted from the Harris hawks optimization, that can ensure substantial convergence and spring potential of the local stagnant. Though, a large number of evolutionary algorithms has been designed such as monarch butterfly optimization (MBO) (Wang et al., 2019), slime mould algorithm (SMA) (Li et al., 2020), moth search algorithm (MSA) (Wang, 2018) and Harris hawks optimization (HHO) (Algorithm and applications, 2019). Typical BSO collects a group of specialists with various backgrounds, expertise, and skills to find a solution to the problem. Due to the effective learning and utilization of the samples sampled in the optimization process and its ease of implementation. The proposed EBSO algorithm is verified on 23 benchmarks, composed of 7 unimodal benchmark functions, six multimodal benchmark functions, and ten fixed-dimension multimodal benchmark functions. Finally, COVID-19 clinical data were used for EBSO-SVM and other SVM competitors based on other optimization algorithms, along with coagulation indexes. The EBSO core compensation is validated by evaluating the experimental findings, and different performance evaluation indexes can establish a strong EBSO-SVM for determining COVID-19 status from the perspective of the coagulation index. The results of the test showed that the EBSO-SVM proposed was seemingly beneficial.
The key contributions in this study are as follows:
-
•
The two core operators have taken the opportunity to improve the brain storm optimizing algorithm, EBSO, from harris hawks optimization.
-
•
The proposed EBSO algorithm is verified on 23 benchmarks composed of 7 unimodal benchmark functions, six multimodal benchmark functions, and ten fixed-dimension multimodal benchmark functions.
-
•
The EBSO has successfully solved the optimization of SVM’S parameters and feature selection at the same time.
-
•
An efficient EBSO-SVM technique is used to assist COVID-19 diagnosis from the coagulation index perspective.
The paper was organized according to next arrange. The materials and processes are reported in paragraph 2. The proposed EBSO algorithm is defined in Section 3. Section 4 describes the proposed EBSO-SVM model. Section 5 describes the designs of the tests. The results of EBSO-SVM on COVID-19 data set-simulations are described in Section 6, and the results of EBSO on 23 benchmarks are also exhibited in this section. The findings are discussed in Section 7. Section 8 shows the conclusion and path of the future.
2. Materials and methods
2.1. Data collection
The participants in our study were from the Wenzhou Rural retrospective study. The Ethics Committee of the Affiliated Yueqing Hospital of Wenzhou Medical University (approval No. 202000002) approved the present study. A total of 51 participants aged between 18 to 93 years were recruited from the Affiliated Yueqing Hospital of Wenzhou Medical University over the period between January 21 and March 20, 2020. The following general clinical information was collected for each participant: gender, age, and coagulation function indexes. Coagulation functions were measured using an automated blood coagulation analyzer (Sysmex CA-7000 analyzer, Kobe, Japan).
In our study, the diagnosis of COVID-19 was carried out and guided according to the criteria issued by the National Health Commission of the People’s Republic of China. The etiological criteria for diagnosing COVID-19 are at least one of the following: (i) severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) confirmed by positive real-time reverse transcriptase-polymerase chain reaction (RT-PCR) on the nasopharyngeal swab, sputum, or stool samples; (ii) to sequence the virus genome, which is highly homologous to the genome of SARS-CoV-2. According to clinical characteristics, COVID-19 patients are classified into four categories: mild, general, severe, and critically ill patients. Mild patients with the following characteristics: (i) patient has no symptoms or mild symptoms; (ii) patient has no lung involvement. General patients with the following characteristics: (i) the clinical manifestations of COVID-19 patients were fever, dry cough, fatigue, nose congestion, runny nose, myalgia, sore throat, diarrhea, and so on; (ii) the lungs affected by SARS-CoV-2. Severe patients with at least one of the following characteristics: (i) patient present with dyspnea and respiratory rate (RR) greater than 30 breaths/min; (ii) patient blood oxygen saturation lower than ; (iii) patient oxygenation index (arterial partial pressure of oxygen to fraction inspired oxygen) below 300 mmHg (1 mmHg = 0.133 kPa). Critical ill patients with at least one of the following characteristics: (i) patient required intubation and mechanical ventilation because of acute respiratory failure; (ii) patient present with shock; (iii) patient present with multiple organ failure. On admission, initial COVID-19 severity was assessed by sixth revised trial version of the Novel Coronavirus Pneumonia Diagnosis and Treatment Guidance (El-Solh et al., 2020, Cheung et al., 2021). Cases meeting any of the following criteria were defined as severe cases: (1) RR greater than 30 breaths/min; (2) patient blood oxygen saturation lower than 93%; (3) patient oxygenation index below 300 mmHg; (4) patients with respiratory failure needing mechanical ventilation, septic shock, and/or multiple organ dysfunction. Taken together, depending on the clinical symptoms and clinical guidelines, the confirmed COVID-19 cases were further classified into two categories: mild and general cases were categorized as the non-severe group, severe and critical cases were categorized as the severe group (Szklanna et al., 2021, Suvarna et al., 2021).
2.1.1. Statistical analysis
Statistical analysis was performed with SPSS, version 21 (IBM, Somers, NY, USA). The differences in coagulation function indicators and age between the non-severe COVID-19 and severe COVID-19 groups were analyzed by an independent sample t-test. The data are expressed as the mean standard deviation ( SD). P-values less than 0.05 (P < 0.05) were considered significant. A total of 9 parameters were used as illustrated in Table 1 . A detailed description of statistical analyses is described in Table 2 .
Table 1.
List of the features used in this study and their definitions.
| No. | Feature | Abbreviation |
|---|---|---|
| F1 | Gender | Gender |
| F2 | Age | Age |
| F3 | Prothrombin time | PT |
| F4 | International normalized ratio | INR |
| F5 | Prothrombin time activity | PTA |
| F6 | Fibrinogen | FIB |
| F7 | Activated partial thromboplastin time | APTT |
| F8 | Thrombin time | TT |
| F9 | D-dimer | D-D |
Table 2.
Coagulation function indicators clinical parameter in severe group and non-severe group.
| Index | Non-severe (n = 30) | Severe (n = 21) | p-value |
|---|---|---|---|
| Age(years) | 42.300 ± 11.530 | 61.43 ± 17.64 | 0.000 |
| PT (s) | 13.030 ± 0.780 | 14.930 ± 3.050 | 0.011 |
| INR | 1.030 ± 0.060 | 1.090 ± 0.070 | 0.003 |
| PTA (%) | 95.880 ± 7.350 | 88.280 ± 8.400 | 0.001 |
| FIB (g/l) | 4.170 ± 0.870 | 4.970 ± 1.650 | 0.053 |
| APTT (s) | 38.480 ± 4.310 | 43.650 ± 8.780 | 0.019 |
| TT (s) | 16.210 ± 0.740 | 16.520 ± 0.820 | 0.171 |
| D-D(mg/l) | 0.480 ± 0.260 | 1.990 ± 3.750 | 0.032 |
2.2. Brief introduction of support vector machine (SVM)
The SVM is the most frequently utilized machine learning model developed based on some mathematical concepts on risk prevention and the idea of the VC dimension. In this model, we intend that reach an excellent compromise between decreasing the error of the output signals in the training domain and optimizing the margin to attain the best generalization capacity and prevent the overfitting concern. In some cases, the SVM was used (Shen et al., 2016, Chen et al., 2011, Chen et al., 2014) to deal with some small sample data sets in particular because of it adequate velocity rate and good classification accuracy.
When we set a suitable w and b for tests, the SVM model is able to distinguish the undecided samples according to the utilization of the hyperplanes with acceptable classification rates. SVM can also tackle non-linear classification problems if we apply kernel-based methods during the modeling. The non-linear feature of concern is modeled as follows:
| (1) |
where is the kernel function and is Gaussian kernel. For more details, readers refer to work by Shen et al. (2016). In SVM, penalty factor C and the parameter of the kernel can change the accuracy and efficiency of the learning process, and it is sensitive to these values. C can show us how much the SVM can generalize. can show us how much the model is fitting.
2.3. Brain storm optimization (BSO)
The brain storm optimization (BSO) algorithm has been appeared in 2011 (Shi, 2011). That is a promising and early swarm intelligence algorithm. Moreover, it is focused on the human being’s collective actions, that is, brainstorming. Speciation is a natural selection process, which means the population is differentiated into individual species. BSO solutions also diverge into many clusters. The new solutions are based on the mutation of one particle or two. The basic BSO algorithm is conceptually simple and easy to be programmed. The original algorithm consists of four steps: Initialization, Clustering, New particles’ generation, and Selection. Randomly generate n potential solutions (particles), and evaluate the n particles, Cluster n particles into m clusters by a clustering model, and then randomly select one or two cluster(s) to generate new particle, finally execute the selection operator. The detailed procedure of the BSO can be seen in Algorithm 1. The n is the population size, T is the maximum number of iteration, is the current best position, is current best fitness value, means the population, and are pre-determined probability.
| Algorithm 1: The pseudo-code of original BSO | ||
 |
||
2.4. Core operators to be introduced
By imitating the cooperation conduct of hawks to catch the prey, the Harris Hawks Optimizer (HHO) is built (Algorithm and applications, 2019). The hawks are one of nature’s cleverest birds. First, the Hawks seek in a number of neighborhood sites for rabbits (bearers) and then hunt rabbits (victim). The rabbits also demonstrate escape behavior by pursuing different methods, thereby increasing their survival chances. The typical HHO imitates these chasing-escaping actions and reactions in order to identify the best answers to a single objective problem of optimization. The main part of HHO is composed of exploration phase, transition phase and exploitation phase. For exploring the search area, the search algorithms are mathematically represented as follows:
| (2) |
where are the search agent vector of respectively, is location of target preyrabbit, , , , , and are all interval of random values (0,1), the lower and the upper limits of choice variables, represents the selected swarm hawk’s random position, and is the mean swarm state for the iteration and mean hawk condition is determined as . The rabbit’s energy is utilised to make the transformation as , where symbolizes the rabbit’s escape energy, is the initial state of its strength and is the maximum number of iterations utilized for the traditional HHO stop criteria, which as transition phase.
The exploitation phase is composed of soft besiege with progressive rapid dives. It is supposed that hawks may evaluate their next step with the following formula, to conduct a soft besiege:
| (3) |
| (4) |
where shows the problem dimension, and represents a random size vector and is the random vector distributed by levy-flight and can be determined as follows:
| (5) |
where , means random interval values (0,1), is fixed as 1.5 as constant. Hard besiege with PRD and this strategy models the mechanism utilized as follows:
| (6) |
3. Proposed EBSO
In this study, the two core operators from harris hawks optimization to further enhance and improve the search ability of the original BSO, EBSO is designed. To the best of our knowledge, this is the first time the BSO has been effectively integrated with several efficient operators from harris hawks optimization. The designed algorithm EBSO can be divided into two parts. The first part is to execute each step of the original BSO; the second is to complete the execution of the introduced operators derived from harris hawks optimization. The detailed pseudo-code of the presented EBSO can refer to Algorithm 2.
| Algorithm 2: The pseudocode of designed EBSO | ||
 |
||
4. Proposed EBSO-SVM model
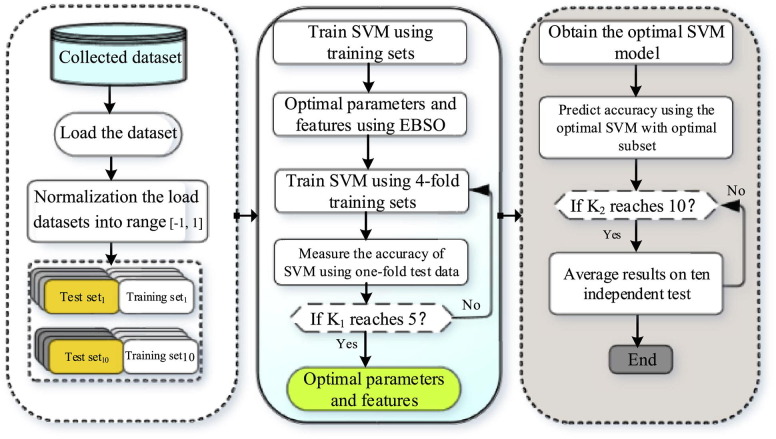
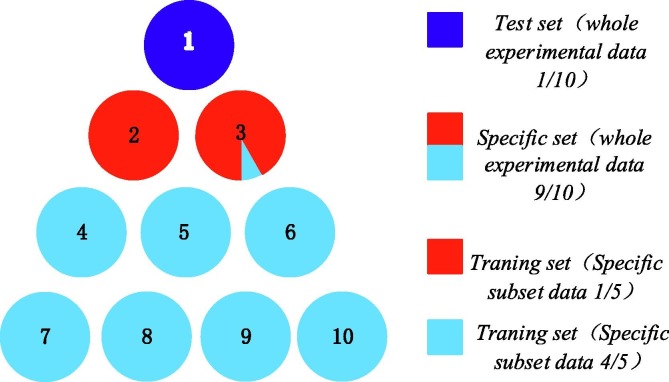
In this study, an evolutionary support vector machine-driven enhanced brain storm optimization algorithm for analysis of COVID-19 from the perspective of coagulation index is designed (EBSO-SVM). The framework of the EBSO-SVM is exhibited in Fig. 1 . From this Figure, we see that the Cross-validation mechanism is utilized as the internal 5- and external 10-fold process, respectively, which means the and in this paper. The detailed data segmentation diagram is shown in Fig. 2. It shows us that it is divided into 10 equal parts, the blue part indicates that the test sample is one-tenth of all data sets, the 9/10 data set is called a special set whose colors are red and light blue. It is worth noting that the red part of the special data set is one-fifth of the special data set, which is used as training data. In addition, the encoding of the enhanced BSO can be seen as Fig. 3 , and encoding is divided into two parts, the first part is used as the key parameter of the support vector machine, and the remaining part is used as the attribute of the tested data.
Fig. 1.
The Flowchart of the proposed EBSO-SVM.
Fig. 2.
Data segmentation diagram.
Fig. 3.

Encoding form.
SVM is regarded as the core zone of the proposed model; in terms of the input domain, the radial basis function (RBF) kernel has been utilized to map the aggregate info into a kind of hidden layer domain. The procedure of the method deals with the main factors C and width , and n features subset, the first C represents the harmony among fitting error minimization and complexity of the model, the second kernel bandwidth denotes the non-linear mapping action from the input domain to higher-dimensional spaces. Also, the EBSO technique considers these main parameters and the optimal feature subset at the same time. If we report more details, the continuous space has been converted using the sigmoid function into a binary domain. To this aim, the feature is selected if it be less than 0.5; otherwise, the details or gens can be deleted as exposed in Fig. 3. Finally, the optimized SVM by EBSO can give us an accurate early diagnosis of COVID-19 from the perspective of the coagulation index. In addition, the classification accuracy is set as the fitness function as Eq. 7, where average ACC refers to average test classification accuracy ratio using the SVM and the internal 5-fold CV and K is the number of folds.
| (7) |
5. Experimental designs
There are two components to the experimental phase of this analysis. The first phase will be the efficacy investigation of the proposed EBSO, and the second will use the proposed EBSO-SVM algorithm to diagnose the COVID-19 from the perspective of the coagulation index. First of all, the efficiency of the proposed EBSO is extensively verified and carried out in comparison with other algorithms on 23 benchmarks (Ballester et al., 2005), which is composed of 7 unimodal benchmark functions as shown Table 3 , 6 multimodal benchmark functions as shown in Table 4 , and 10 fixed-dimension multimodal benchmark functions as shown in Table 5 and also strictly perforce the balance and diversity analyzes of the improved EBSO and its original BSO. Several other algorithms, including BSO, DE (Price, 2013), PSO (Marini and Walczak, 2015), GSA (Rashedi et al., 2009), and MFO (Mirjalili, 2015), were involved as competitors on the common benchmark. The parameters of these peers are tested based on the original papers.
Table 3.
Unimodal benchmark functions.
| Function | Dim | Range | fmin |
|---|---|---|---|
| 50 | [−100, 100] | 0 | |
| 50 | [−10, 10] | 0 | |
| 50 | [−100, 100] | 0 | |
| 50 | [−100, 100] | 0 | |
| 50 | [−30, 30] | 0 | |
| 50 | [−100, 100] | 0 | |
| 50 | [−1.28, 1.28] | 0 |
Table 4.
Multimodal benchmark functions.
| Function | Dim | Range | fmin |
|---|---|---|---|
| 50 | [−500,500] | −2094.9145 | |
| 50 | [−5.12, 5.12] | 0 | |
| 50 | [−32,32] | 0 | |
| 50 | [−600,600] | 0 | |
| 50 | [−50,50] | 0 | |
| 50 | [−50,50] | 0 |
Table 5.
Fixed-dimension multimodal benchmark functions.
| Function | Dim | Range | fmin |
|---|---|---|---|
| 2 | [−65,65] | 1 | |
| 4 | [−5, 5] | 0.0003 | |
| 2 | [−5,5] | −1.0316 | |
| 2 | [−5,5] | 0.398 | |
| 2 | [−2,2] | 3 | |
| 3 | [1,3] | −3.86 | |
| 6 | [0,1] | −3.32 | |
| 4 | [0,10] | −10.1532 | |
| 4 | [0,10] | −10.4028 | |
| 4 | [0,10] | −10.5363 |
The experimental results EBSO-SVM, employed for a diagnosis of coagulation indices in COVID-19 in the field of data collection, was extensively reviewed by the proposed EBSO method for optimizing the combination of the best parameter and SVM sub-subset function. Several typical learning procedures, including original SVM, GWO-SVM, MFO-SVM, PSO-SVM, ELM, and KNN, were also compared in the case of EBSO-SVM. The two main parameters of and , respectively, have been specified in the original SVM. In order to avoid the uncertainty in tests due to the large datasets, all info has been scaled into the interval of [-1, 1].
The MATLAB tests has been performed with the Xeon CPU E5-2660 v3 (2.60 GHz) and 16 GB of RAM on a Windows Server 2018 R2 operating machine. A Cross-Validation 10-fold (CV) is used to assess classifying findings in an unbiased and objective manner. In addition, the EBSO-SVM performance assessment was carried out using four normal parameters comprising specificity, sensitivity, classification accuracy (ACC), and a Matthews (MCC). The detailed definition of the formula can refer to Wang and Chen (2020).
6. Experimental and analytical results
6.1. Results of benchmark functions
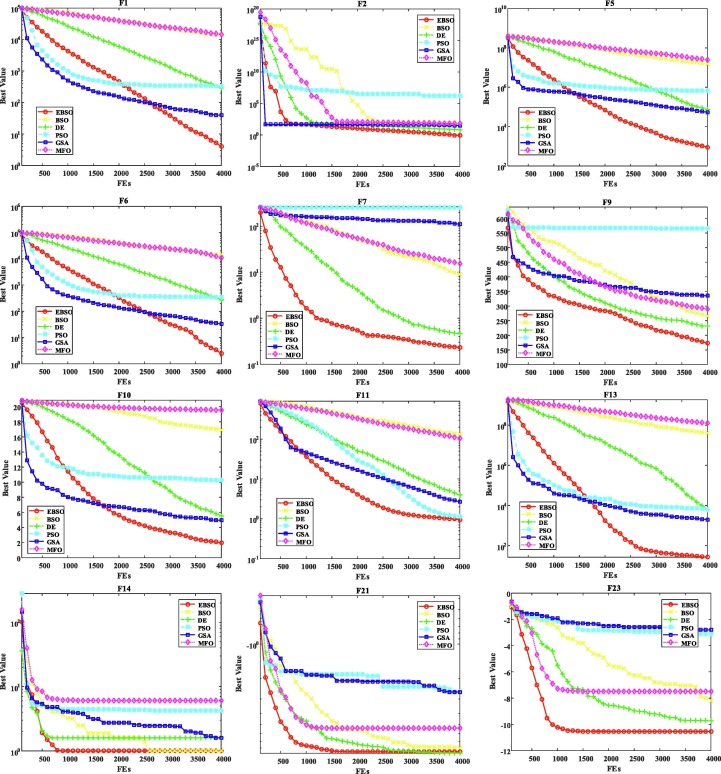
In this part, the 23 benchmarks have been utilized to evaluate EBSO’s efficiency, and these cases have always been applied in multiple projects using fair comparison rules (Wang et al., 2020, Weng et al., 2021, Qiang et al., 2020, Yang et al., 2018, Zhao et al., 2020, Zou et al., 2019). Furthermore, 30 experiments were performed independently to limit the impact of random variables. The EBSO is compared to the BSO, DE, PSO, GSA und MFO algorithms in this investigation. Thirty individual executions carried out all of these ways to these benchmark standards.
In the Table 6 , detailed experimental results are demonstrated by the average and standard deviationSTDvalues. It can be seen that the EBSO have the best property of not only average values but also STD, though it may perform not well on some cases Moreover, the EBSO is substantially higher than the other couples in the most relevant test criteria in the Wilcoxon test. Table 7 presents Friedman EBSO test results against all other rivals. The EBSO shows the first best results of these benchmarks, with the poorest findings being BSO, MFO, GSA, PSO, and DE, in line with the average ranking of the algorithms in question. One cause for this may be the major aspects of the existing movement strategies abstracted from optimizing harris hawks. In this analysis, the original BSO can be enhanced between exploration and mining.
Table 6.
The statistical experiment results and the comparison algorithms on the test benchmarks.
| Algorithms | F1 | F2 | F3 | F4 | F5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| mean | STD | mean | STD | mean | STD | mean | STD | mean | STD | |
| EBSO | 4.0409869 | 4.565512 | 0.848937 | 0.32468 | 5308.9514 | 1916.3288 | 7.577523 | 2.163198 | 909.548 | 672.3266 |
| BSO | 14216.69366 | 1936.4153 | 73.042895 | 5.8637549 | 70294.044 | 10991.059 | 70.005317 | 4.7751876 | 14888839 | 5430531.7 |
| DE | 286.5318805 | 80.04938 | 6.7574347 | 0.6717474 | 85066.864 | 8903.3004 | 59.555309 | 3.056055 | 72392.185 | 18945.928 |
| PSO | 331.5727461 | 37.50266 | 1661020.4 | 4334397.6 | 4836.1655 | 1315.6191 | 10.840428 | 1.829634 | 681313.26 | 166072.15 |
| GSA | 40.21357786 | 12.449257 | 30.790421 | 7.9833557 | 3082.485 | 1262.17 | 18.862995 | 2.798129 | 53327.901 | 28552.84 |
| MFO | 14353.41746 | 8511.954 | 63.966444 | 19.574595 | 62399.277 | 13471.362 | 82.965428 | 4.3295102 | 24824531 | 25784078 |
| Algorithms | F6 | F7 | F8 | F9 | F10 | |||||
| mean | STD | mean | STD | mean | STD | mean | STD | mean | STD | |
| EBSO | 2.4478589 | 0.942465 | 0.229856 | 0.10233 | −11173.4 | 718.747 | 172.6646 | 17.44842 | 1.989142 | 0.515402 |
| BSO | 14572.66347 | 2369.2804 | 9.0611144 | 2.8662241 | −8879.693 | 666.81149 | 266.02169 | 15.214212 | 16.952533 | 0.508035 |
| DE | 273.4697128 | 64.452586 | 0.4612938 | 0.1143467 | −8907.786 | 363.95443 | 231.08217 | 11.055591 | 5.5215554 | 0.4519889 |
| PSO | 339.425991 | 36.361857 | 254.76347 | 37.413359 | −7155.622 | 1294.4444 | 566.25084 | 34.593948 | 10.276171 | 0.3276113 |
| GSA | 32.75943606 | 5.2913592 | 110.65906 | 16.96339 | −3077.189 | 664.71759 | 335.0435 | 13.968292 | 4.9673752 | 0.3732885 |
| MFO | 11176.15861 | 4626.9133 | 15.377483 | 14.019924 | −10395.76 | 1185.279 | 289.99885 | 44.965597 | 19.565532 | 0.3733107 |
| Algorithms | F11 | F12 | F13 | F14 | F15 | |||||
| mean | STD | mean | STD | mean | STD | mean | STD | mean | STD | |
| EBSO | 0.9543863 | 0.121121 | 7.0724065 | 3.7750497 | 26.51097 | 11.10599 | 0.998004 | 1.96E-16 | 0.0043187 | 0.0084562 |
| BSO | 133.7178699 | 14.668046 | 13245314 | 6397676.3 | 41034266 | 19312164 | 0.9980038 | 1.877E-11 | 0.0015329 | 0.0009859 |
| DE | 3.975427709 | 1.0276143 | 28.112923 | 13.85836 | 6299.2424 | 9589.2105 | 1.5904907 | 1.5560234 | 0.001011 | 0.000272 |
| PSO | 1.15537423 | 0.0262132 | 12.926533 | 2.8005088 | 6343.4568 | 8514.9991 | 4.2516365 | 2.5355863 | 0.0016576 | 0.0007102 |
| GSA | 2.694441032 | 1.1526546 | 6.366073 | 2.89656 | 2004.7167 | 3433.8448 | 1.6061734 | 0.6890466 | 0.0052248 | 0.0027588 |
| MFO | 105.8181227 | 61.608213 | 19925243 | 13625159 | 125560603 | 172385521 | 6.090624 | 4.2799447 | 0.0024782 | 0.0031255 |
| Algorithms | F16 | F17 | F18 | F19 | F20 | |||||
| mean | STD | mean | STD | mean | STD | mean | STD | mean | STD | |
| EBSO | −1.03162845 | 9.735E-16 | 0.397887 | 0 | 3 | 1.39E-15 | −3.86278 | 6.94E-16 | -3.286327 | 0.0574308 |
| BSO | −1.0316284 | 3.13E-07 | 0.3978874 | 5.085E-10 | 3 | 2.94E-09 | −3.86278 | 1.56E-08 | -3.301074 | 0.0356608 |
| DE | −1.03162845 | 1.958E-16 | 0.3978874 | 0 | 3 | 1.92E-15 | −3.86278 | 7.83E-16 | −3.32183 | 0.000367 |
| PSO | −1.02490226 | 0.0053364 | 0.4117694 | 0.0142042 | 3.6032981 | 0.8927914 | -3.808387 | 0.0557767 | -2.643092 | 0.1640719 |
| GSA | −0.99227955 | 0.0216461 | 0.408267 | 0.0101211 | 3.3711742 | 0.3749822 | -3.838708 | 0.0146349 | -2.802657 | 0.2136215 |
| MFO | −1.03162845 | 1.282E-16 | 0.3978874 | 0 | 3 | 2.5E-15 | −3.86278 | 8.24E-16 | -3.237214 | 0.0770919 |
| Algorithms | F21 | F22 | F23 | |||||||
| mean | STD | mean | STD | mean | STD | |||||
| EBSO | −8.6538929 | 3.16084 | −8.443763 | 3.2038506 | −10.5364 | 3.14E-12 | ||||
| BSO | −7.99693838 | 2.7755981 | −8.72163 | 1.61663 | −8.203202 | 2.4544712 | ||||
| DE | −8.3009019 | 2.0025497 | −10.16796 | 0.5866285 | −9.74481 | 2.1880623 | ||||
| PSO | −2.58648777 | 1.2965977 | −2.450181 | 1.0838472 | −3.096436 | 1.4694115 | ||||
| GSA | −2.61413202 | 0.5856597 | −2.532658 | 1.0300769 | −2.80029 | 0.7462128 | ||||
| MFO | −5.39182791 | 3.4275629 | −7.147333 | 3.520498 | −7.47797 | 3.9669906 | ||||
Table 7.
The results of Friedman’s test.
| EBSO | BSO | DE | PSO | GSA | MFO | ||
|---|---|---|---|---|---|---|---|
| mean level | 1.4236 | 5.4251 | 3.3625 | 3.5489 | 4.3549 | 4.5219 |
Fig. 4 shows the convergence curves of these algorithms for several selected benchmarks to verify the performance of the designed EBSO. From this viewpoint, the planned EBSO indicates the quick capacity of the conference and the apparent superiority to all other competitors in this benchmark. Furthermore, the developed EBSO contains rapid convergence searches, such F7, F21, and F23, which ensure it achieves an optimal theoretical value in no time. In addition, the same convergence tendency is found as regards other benchmarks. In short, it can be concluded that the property of the original BSO can be significantly enhanced.
Fig. 4.
Convergence curves of selected benchmark functions.
6.2. Application in the diagnosis of COVID-19 from the perspective of coagulation index
In this part, the proposed algorithm EBSO-SVM for diagnosis of COVID-19 from the perspective of coagulation index is evaluated deeply. Table 8 records the detailed statistical results of the collected COVID-19 coagulation index data set. The 91.9195% classification accuracy of the ESMA-SVM can be seen from this Table 8, 90.529% of Matthew correlation coefficient, 90.9912% of sensitivity, 88.5705% of specificity, and their variance is 0.049967, 0.039574, 0.050529 and 0.060838 respectively. In addition, the suggested EBSO-SVM can acquire the optimum SVM model configuration automatically, largely due to the upgraded EBSO, which can effectively detect optimum parameters settings and feature subset.
Table 8.
The results of EBSO-SVM on collected data.
| Fold | ACC | MCC | Sensitivity | Specificity |
|---|---|---|---|---|
| #1 | 0.88759 | 0.85847 | 0.95214 | 0.80251 |
| #2 | 0.88952 | 0.89568 | 0.89687 | 0.87548 |
| #3 | 0.97521 | 0.96324 | 0.96252 | 0.87549 |
| #4 | 0.97635 | 0.84356 | 0.88573 | 0.85321 |
| #5 | 0.98521 | 0.88821 | 0.96595 | 0.97584 |
| #6 | 0.88521 | 0.95321 | 0.89654 | 0.93251 |
| #7 | 0.88597 | 0.89524 | 0.90251 | 0.96524 |
| #8 | 0.96874 | 0.88754 | 0.80521 | 0.81258 |
| #9 | 0.87584 | 0.93254 | 0.95624 | 0.84265 |
| #10 | 0.86231 | 0.93521 | 0.87541 | 0.92154 |
| Mean | 0.919195 | 0.90529 | 0.909912 | 0.885705 |
| STD | 0.049967 | 0.039574 | 0.050529 | 0.060838 |
Furthermore, the EBSO-SVM approach is comparable with the original SVM and other evolutionary SVM computational methods (including BSO-SVM, Original SVM, GWO-SVM, MFO-SVM, PSO-SVM, and two popular ELM and KNN algorithms). A complete statistical experiment in Table 9 shows comparisons of the accuracy, Matthew’s correlation coefficients, susceptibility, specificity, and standard deviation. The result can be overlooked that in quatre assessment methodologies such as ACC, MCC, sensibility, and specificity, the EBSO-SVM algorithm is higher than other competition and its related standard difference between all models is also less relevant. The EBSO-SVM is more efficient and stable compared to the traditional CBSO-based SVM. It should be noted that the original SVM, original ELM, and KNN all demonstrate their worst diagnosis performance of COVID-19 from the coagulation index perspective, which can preliminarily be shown to improve the SVM model selection ability and the ability to solve the precise diagnosis of COVID-19 from the capacity perspective from the algorithm suggested in this article. We can observe in this experiment that EBSO SVM can automatically obtain the best property among all these competing designs, mainly thanks to the upgraded EBSO, which automatically identifies the best SVM parameters and the perfect sub-features.
Table 9.
The statistical experiment results of comparison in terms of the four metrics.
| Algorithms | ACC | MCC | Sensitivity | Specificity |
|---|---|---|---|---|
| EBSO-SVM | 0.91919 ± 0.04996 | 0.90529 ± 0.03957 | 0.90991 ± 0.05052 | 0.88570 ± 0.06083 |
| BSO-SVM | 0.88574 ± 0.07541 | 0.86354 ± 0.06584 | 0.88579 ± 0.07584 | 0.83595 ± 0.09658 |
| SVM | 0.79254 ± 0.08025 | 0.77854 ± 0.08547 | 0.79587 ± 0.09521 | 0.70124 ± 0.16254 |
| GWO-SVM | 0.85362 ± 0.06524 | 0.83569 ± 0.06854 | 0.87623 ± 0.07215 | 0.86598 ± 0.14584 |
| MFO-SVM | 0.84325 ± 0.06758 | 0.83758 ± 0.06851 | 0.88215 ± 0.07219 | 0.85784 ± 0.09236 |
| PSO-SVM | 0.81587 ± 0.06741 | 0.85812 ± 0.06954 | 0.87259 ± 0.07359 | 0.86325 ± 0.10594 |
| ELM | 0.80563 ± 0.08652 | 0.76325 ± 0.08812 | 0.78851 ± 0.10584 | 0.71265 ± 0.13625 |
| KNN | 0.78954 ± 0.08547 | 0.80145 ± 0.10258 | 0.78852 ± 0.11263 | 0.73541 ± 0.14587 |
In addition, the developed EBSO will be used to simultaneously optimize parameters and choose functions for SVM to diagnose COVID-19 from the coagulation index perspective. The 10-fold CV approach during function selection is used in this work. Table 10 shows the detailed number of features, and statistical values picked for each 10-fold cycle. Regarding statistics, AGE, INR, PTA, and D-D features were selected respectively by the EBSO-SVM with values 9, 8, 9, and 9 while comparing the other features with the features with fewer ones. The EBSO-SVM is superior to other competitors. But other opponents did not fulfill these characteristics. It can thus be concluded that those characteristics that typically seem present can recognize COVID-19 early and discriminate against other low-frequency characteristics. In practice, more consideration for these features AGE, INR, PTA, and D-D should therefore be given in relation to the underlying information in these frequency characteristics.
Table 10.
The numbers of selected feature.
| Index |
Algorithms |
||||
|---|---|---|---|---|---|
| EBSO-SVM | BSO-SVM | GWO-ELM | MFO-ELM | PSO-ELM | |
| F1 | 0 | 0 | 0 | 2 | 3 |
| F2 | 9 | 6 | 7 | 7 | 8 |
| F3 | 2 | 2 | 1 | 4 | 3 |
| F4 | 8 | 8 | 7 | 8 | 7 |
| F5 | 9 | 8 | 7 | 7 | 8 |
| F6 | 1 | 3 | 6 | 2 | 4 |
| F7 | 0 | 2 | 2 | 3 | 1 |
| F8 | 1 | 2 | 1 | 1 | 2 |
| F9 | 9 | 8 | 8 | 7 | 9 |
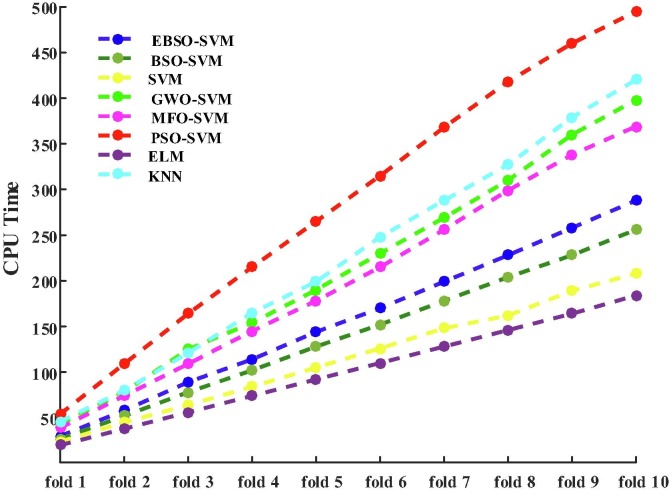
In addition, the comparison results among these methods regarding CPU time consuming via 10-fold CV is shown in Fig. 5 . It can be observed that the original ELM has the least CPU time whose speed is the fastest among these algorithms, the original SVM has the second least time. An explicit argument is that a lot of execution time will be saved without the aid of search algorithms compared to models. However, the unintended outcome is a considerably decreased algorithm classification performance. It can also be observed that the presented EBSO-SVM performs only the fourth-least time consuming, which has more time than the original BSO-SVM, and it illustrates that the add operator increases the algorithm’s execution time. The time-consuming of KNN and GWO-SVM is very similar and, the PSO-SVM has the most time-consuming. Finally, although the proposed EBSO-SVM has good classification performance, its performance increase is at the cost of time consumption, and this also directs us towards the future path of study using acceptable parallel programming to reduce the duration for ECPA-KELM CPU use.
Fig. 5.
Comparison results among these methods in terms of CPU time via 10-fold CV.
7. Discussion
Early recognition and discrimination of COVID-19 severity from a coagulation index standpoint were studied using EBSO to optimize the parameter and select SVM features simultaneously. Important aspects such as Age, INR, PTA, and D-D have been found. Through the coagulation index, an EBSO-SVM model was subsequently designed to diagnose COVID-19 accurately. We believe that the EBSO-SVM model could contribute to informing the clinical decision-making process.
Several studies have shown that age plays a key role in developing Severe Acute Respiratory Syndrome (SARS) and Middle East Respiratory Syndrome (MERS). Meanwhile, researchers confirm that advanced age was associated as a strong independent risk predictor of SARS and MERS (Majumder et al., 2015, Choi et al., 2003). Similarly, investigators have demonstrated that age plays a critical role in the progression of the COVID-19 disease in this outbreak. Chen and colleagues revealed that age was positive association with the degree of radiographic severity in patients with COVID-19 (Chen et al., 2020). Many researchers have found that older patients are more vulnerable to COVID-19 infections and that they are more prone to develop severe COVID-19 complications (Wang et al., 2020). Wang et al. reported that adults are more vulnerable and susceptible to COVID-19 than children and the adult’s condition was severe than that in children (Wang et al., 2020). Wang et al. also found that these elderly persons, once infected with SARS-CoV-2, are prone to death (Wang et al., 2020). One of the possible reasons is that with aging, the cellular and humoral immune function of the body gradually declines, resulting in an increased risk of infection (Weiskopf et al., 2009, Opal et al., 2005). Another possible reason is that elderly patients with numerous comorbidities, including hypertension, diabetes, chronic lung diseases, may be more prone to acute respiratory failure and have a poor prognosis (Liu et al., 2020, Zhou and Liu, 2020). Consistent with previous studies, we also found the average age of the severe COVID-19 group was 61.43 ± 17.64 years, and that of the non-severe COVID-19 group was 42.30 ± 11.53 years, suggesting age is an important factor affecting rehabilitation. To summarize, age may be a promising indicator for predicting the prognosis of patients with COVID-19.
Severe infection and inflammation lead to activation of coagulation. Research findings reveal that coagulation function abnormalities are commonly found in patients with sepsis. Fibrinogen levels of C-reactive protein were closely correlated to the sepsis, suggesting the level of fibrinogen can reflect the inflammatory state of the body(Kim et al., 2007). D-dimer is a fibrin degradation product of the crosslinked fibrin polymer under the fibrinolytic system (Bai et al., 2017). D-dimer is the smallest fragment of fibrin degradation products and serves as an important molecular marker for fibrinolytic system hyperactivity and hypercoagulable state in vivo (Baboolall et al., 2019). The level of D-dimer in normal human serum is less than 280 ng/mL, and the concentration is difficult to detect in normal situations (Li et al., 2018). D-dimer plays an important role in inflammation. When the body is infected, a variety of inflammatory factors may damage vascular endothelial cells, leading to activation of blood coagulation and consume mass clotting factors inducing hyper coagulability (Duarte et al., 2015). Guneysel et al. found that plasma D-dimer levels are positively correlated with the degree of community-acquired pneumonia (CAP). Moreover, patients with severe CAP had significantly higher plasma D-dimer levels than those with a non-severe CAP suggesting D-dimer may be a promising prognostic indicator in CAP (Guneysel et al., 2004). It has been reported that various vasoactive substances were increased in patients with CAP or mechanical ventilation occurs more easily when plasma D-dimer levels increase (Li et al., 2018). Recently, a population-based study of more than 300 CAP patients showed that plasma D-dimer levels are measured before the use of antibiotics, suggesting plasma D-dimer levels are positively associated with the acute physiology and chronic health evaluation II (APACHE II) and pneumonia severity index (PSI) scoring system. Moreover, the D-dimer levels in the non-survival CAP patients were significantly higher than in the survival CAP group (Querol-Ribelles et al., 2004). In line with these findings, Han et al. found that the levels of plasma D-dimer in patients with severe COVID-19 were significantly higher than those in the non-severe COVID-19 group, and monitoring plasma D-dimer levels are helpful for the early diagnosis, management of severe/critically ill patients (Han et al., 2020). In addition, among COVID-19 patients, high levels of D-dimer were closely related to the poor prognosis of patients with COVID-19 (Tang et al., 2020). Similar to their findings, in this study, we revealed that plasma D-dimer levels were 4.14-fold higher in the severe COVID-19 group compared with the non-severe COVID-19 group (P = 0.032), suggesting that plasma D-dimer levels may be regarded as a promising indicator of clinical outcome in COVID-19 patients.
Similar to D-dimer, PT is a sensitive screening test for the extrinsic coagulation pathway and a vital monitoring indicator in clinical anticoagulation therapy (Liu et al., 2018). Meanwhile, PT is also an important prognostic index for patients with severe hepatitis. PTA has the same significance as PT. Coagulation function indicators are believed to be correlated with the clinical course or prognosis of sepsis. PT, APTT, FIB, and D-dimer are widely used for detecting sepsis (Hoshino et al., 2017). A previous study has revealed that PT was prolonged in patients with sepsis, at the same time, proving PT was positively related to illness severity and poor prognosis in sepsis patients (Walsh et al., 2010). Vasques and colleagues reported that coagulation disorder has a great influence on sepsis, especially septic shock. The prognosis became worse with the increase of PT (Macrae et al., 2014). Therefore, PT can be served as a valuable prognostic indicator in sepsis and septic shock. Additionally, a population-based study of 113 deceased COVID-19 patients also suggested that all fatal cases had sepsis complications, suggesting sepsis is the most common and serious complication of exacerbation of covid-19 (Chen et al., 2020). In terms of PT, PTA, Liu et al. observed a very significant difference between severe COVID-19 and non-severe COVID-19 patients (Liu et al., 2020). In our study, we found that the average PT of the severe COVID-19 group was 14.93 ± 3.05 s, and that of the non-severe COVID-19 group was 13.03 ± 0.78 s, and the average PTA was 88.28 ± 8.40 % in the severe COVID-19 group and 95.88 ± 7.35 % in the non-severe COVID-19 group. This finding was similar to the results from previous studies (Wang et al., 2020, Liu et al., 2020). In short, a close and important relationship exists between COVID-19, sepsis, and coagulation disorder. There are very few reports in the literature describing coagulation function indexes and clinical parameters to predict the severity and prognosis of the infectious disease jointly. As far as we know, this is the first attempt at combining age, PT, PTA, and D-dimer for predicting COVID-19 severity using the machine learning method.
Based on the finding of this research on the performance of the proposed hybrid support vector machine, we can propose its application to more variety of complex problems, such as active surveillance (Pei et al., 2020), evaluation of human lower limb motions (Qiu et al., 2016), prediction (Xu et al., 2020), medical diagnosis (Chen et al., 2020, Fei et al., 2020, Hu et al., 2021, Saber et al., 2021). Also, it can be utilized to evaluate the service ecosystem (Xue et al., 2020, Xue et al., 2019), optimal e-healthcare systems (Zhang et al., 2020), optimal performance design (Meng et al., 2018), edge computing (Sheng et al., 2021, Zhiang et al., 2020), drug discovery (Zhuo et al., 2020), optimal control (Luo et al., 2020, Qian et al., 2021, Ye et al., 2020, Zhao et al., 2021), and image and video processing (Mai et al., 2018, Zhou et al., 2021). Another potential is to develop the binary variant of the optimizer for dealing with wrapper-based feature selection (Fan and Zhang, 2021, Zhang et al., 2020, Zhang et al., 2015).
However, the present study has some limitations. Currently, our data set came from a retrospective design and single-center data, and the sample size is not big enough. Larger study samples and prospective studies are needed in order to further improve and optimize our model. Second, independent/ external datasets will still be required to train the EBSO-SVM model in the future so as to make the model more reliable. Third, we recommend including more indicators of hematological parameters such as blood routine, liver function indicators, kidney function indicators, immune index, inflammatory indicators, and blood gas indexes in future studies. In addition, the proposed EBSO-SVM may still have some room to improve. The performance of the algorithm proposed is obtained at the expense of some computational costs. For this, in the future, we will consider paralleling (Zhiang et al., 2017) the implementation of the algorithm to reduce the consumption of computational time. In addition, the algorithm proposed EBSO-SVM should seek more medical application scenarios and try to solve more medical classification problems.
8. Conclusion and future Work
The work uses clinical data of the affiliated Yueqing Hospital of Wenzhou Medical University to develop an effective EBSO-SVM approach to identify and discriminate COVID-19 severity early on (Yueqing, China). The fundamental novelty in the proposed methodology is the incorporation of the new strategy by the present EBSO to improve and restore search capabilities to the original BSO. The efficiency of EBSO was thoroughly controlled with the 23 benchmark tests compared to many other competitors. The experimental findings showed that the proposed EBSO is significantly better able than other partners to achieve this feature optimization. In addition, the recommended EBSO was utilized to develop synchronized optimal SVM parameters and features; the resulting EBSO-SVM was successfully applied to early identification and discern its severity with the COVID-19. An EBSO-SVM analysis with other competitive algorithms has also been carried out. Moreover, the findings demonstrated EBSO-SVM to forecast the more stable attribute more accurately.
A number of concerns must be examined in more detail for future study. In order to lessen the computing burden in the application phase, more variables and coefficients are introduced, and the following parallel processing should be highlighted. Readers can also collect additional data samples to construct a safer and more effective system. In order to extend the application of this technique, EBSO-SVM can also be utilized for prejudging other conditions like the clustering and splitting of the picture into CT.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Beibei Shi, Hua Ye contributed equally to this paper and are co-first authors. Huiling Chen, Peiliang Wu also contributed equally to this work and are co-corresponding authors. Taif University Researchers Supporting Project Number (TURSP-2020/125), Taif University, Taif, Saudi Arabia.
References
- Qun Li, Xuhua Guan, Peng Wu, Xiaoye Wang, Lei Zhou, Yeqing Tong, Ruiqi Ren, Kathy SM Leung, Eric HY Lau, Jessica Y Wong, et al., 2020. Early transmission dynamics in wuhan, china, of novel coronavirus–infected pneumonia. New England journal of medicine. [DOI] [PMC free article] [PubMed]
- Tao Hu, Siqin Wang, Bing She, Mengxi Zhang, Xiao Huang, Yunhe Cui, Jacob Khuri, Yaxin Hu, Xiaokang Fu, Xiaoyue Wang, 2021. Human mobility data in the covid-19 pandemic: Characteristics, applications, and challenges. Applications, and Challenges (May 24, 2021).
- Li Xiang, Dong Zhi-Qiang, Peng Yu., Wang Lian-Ping, Niu Xiao-Dong, Yamaguchi Hiroshi, Li De-Cai. Effect of self-assembly on fluorescence in magnetic multiphase flows and its application on the novel detection for covid-19. Phys. Fluids. 2021;33(4) doi: 10.1063/5.0048123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh Dilbag, Kumar Vijay, Kaur Manjit, et al. Classification of covid-19 patients from chest ct images using multi-objective differential evolution–based convolutional neural networks. Eur. J. Clin. Microbiol. Infectious Dis. 2020;39(7):1379–1389. doi: 10.1007/s10096-020-03901-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization et al. 2020. Novel coronavirus (2019-ncov): situation report, 3.
- Pourhomayoun Mohammad, Shakibi Mahdi. Predicting mortality risk in patients with covid-19 using artificial intelligence to help medical decision-making. MedRxiv. 2020 doi: 10.1016/j.smhl.2020.100178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan Michael I., Mitchell Tom M. Machine learning: trends, perspectives, and prospects. Science. 2015;349(6245):255–260. doi: 10.1126/science.aaa8415. [DOI] [PubMed] [Google Scholar]
- Rajkomar Alvin, Dean Jeffrey, Kohane Isaac. Machine learning in medicine. N. Engl. J. Med. 2019;380(14):1347–1358. doi: 10.1056/NEJMra1814259. [DOI] [PubMed] [Google Scholar]
- Obermeyer Ziad, Emanuel Ezekiel J. Predicting the future–big data machine learning and clinical medicine. New England J. Med. 2016;375(13):1216. doi: 10.1056/NEJMp1606181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhagyashree Sheshadri Iyengar Raghavan, Nagaraj Kiran, Prince Martin, Fall Caroline H.D., Krishna Murali. Diagnosis of dementia by machine learning methods in epidemiological studies: a pilot exploratory study from south india. Soc. Psychiatry Psychiatric Epidemiol. 2018;53(1):77–86. doi: 10.1007/s00127-017-1410-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Wu, Liu Hailong, Xu Junjie, Zhao Huimin. Yingjie on Instrumentation Song, and Measurement. An improved quantum-inspired differential evolution algorithm for deep belief network. IEEE Trans. Instrum. Meas. 2020 doi: 10.1109/TIM.2020.2983233. [DOI] [Google Scholar]
- Zhao Huimin, Liu Haodong, Xu Junjie, Deng Wu. Performance prediction using high-order differential mathematical morphology gradient spectrum entropy and extreme learning machine. IEEE Trans. Instrum. Meas. 2019 doi: 10.1109/TIM.2019.2948414. [DOI] [Google Scholar]
- Pang Jihong, Zhou Hongming, Tsai Ya-Chih, Chou Fuh-Der. A scatter simulated annealing algorithm for the bi-objective scheduling problem for the wet station of semiconductor manufacturing. Comput. Ind. Eng. 2018;123:54–66. [Google Scholar]
- Zhou Hongming, Pang Jihong, Chen Ping-Kuo, Chou Fuh-Der. A modified particle swarm optimization algorithm for a batch-processing machine scheduling problem with arbitrary release times and non-identical job sizes. Comput. Ind. Eng. 2018;123:67–81. [Google Scholar]
- Cai Zhennao, Jianhua Gu., Luo Jie, Zhang Qian, Chen Huiling, Pan Zhifang, Li Yuping, Li Chengye. Evolving an optimal kernel extreme learning machine by using an enhanced grey wolf optimization strategy. Expert Syst. Appl. 2019;138 [Google Scholar]
- Caiyang Yu, Mengxiang Chen, Kai Cheng, Xuehua Zhao, Chao Ma, Fangjun Kuang, and Huiling Chen. Sgoa: annealing-behaved grasshopper optimizer for global tasks. Engineering with Computers, pages 2021, 10.1007/s00366-020-01234-1.
- Yanan Zhang, Renjing Liu, Ali Asghar Heidari, Xin Wang, Ying Chen, Mingjing Wang, and Huiling Chen. Towards augmented kernel extreme learning models for bankruptcy prediction: Algorithmic behavior and comprehensive analysis. Neurocomputing, page 2020, doi: 10.1016/j.neucom.2020.10.038.
- Chen M., Zeng G., Lu K., Weng J. A two-layer nonlinear combination method for short-term wind speed prediction based on elm, enn, and lstm. IEEE Internet Things J. 2019;6(4):6997–7010. [Google Scholar]
- Dong Zhao, Lei Liu, Fanhua Yu, Ali Asghar Heidari, Mingjing Wang, Diego Oliva, Khan Muhammad, and Huiling Chen, 2020. Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation. Expert Systems with Applications, page 114122 (https://doi.org/10.1016/j.eswa.2020.114122).
- Dong Zhao, Lei Liu, Fanhua Yu, Ali Asghar Heidari, Mingjing Wang, Guoxi Liang, Khan Muhammad, and Huiling Chen, 2020. Chaotic random spare ant colony optimization for multi-threshold image segmentation of 2d kapur entropy. Knowledge-Based Systems, page 106510 (https://doi.org/10.1016/j.knosys.2020.106510).
- Abdoul Fatakhou Ba, Hui Huang, Mingjing Wang, Xiaojia Ye, Zhiyang Gu, Huiling Chen, and Xueding Cai, 2020. Levy-based antlion-inspired optimizers with orthogonal learning scheme. Engineering with Computers, pages 1–22.
- Shubham Gupta, Kusum Deep, Ali Asghar Heidari, Hossein Moayedi, Huiling Chen, 2019. Harmonized salp chain-built optimization. Engineering with Computers, pages 1–31.
- Xi Liang, Zhennao Cai, Mingjing Wang, Xuehua Zhao, Huiling Chen, and Chengye Li, 2020. Chaotic oppositional sine-cosine method for solving global optimization problems. Engineering with Computers, pages 1–17.
- Hongliang Zhang, Zhennao Cai, Xiaojia Ye, Mingjing Wang, Fangjun Kuang, Huiling Chen, Chengye Li, and Yuping Li, 2020. A multi-strategy enhanced salp swarm algorithm for global optimization. Engineering with Computers, pages 1–27.
- Lufeng Hu, Li Huaizhong, Cai Zhennao, Lin Feiyan, Hong Guangliang, Chen Huiling, Zhongqiu Lu. A new machine-learning method to prognosticate paraquat poisoned patients by combining coagulation, liver, and kidney indices. Plos One. 2017;12(10) doi: 10.1371/journal.pone.0186427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Hui, Zhou Suying, Jiang Jionghui, Chen Huiling, Li Yuping, Li Chengye. A new fruit fly optimization algorithm enhanced support vector machine for diagnosis of breast cancer based on high-level features. BMC Bioinform. 2019;20(8):1–14. doi: 10.1186/s12859-019-2771-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Chengye, Hou Lingxian, Sharma Bishundat Yanesh, Li Huaizhong, Chen ChengShui, Li Yuping, Zhao Xuehua, Huang Hui, Cai Zhennao, Chen Huiling. Developing a new intelligent system for the diagnosis of tuberculous pleural effusion. Comput. Methods Programs Biomed. 2018;153:211–225. doi: 10.1016/j.cmpb.2017.10.022. [DOI] [PubMed] [Google Scholar]
- Zhao Xuehua, Zhang Xiang, Cai Zhennao, Tian Xin, Wang Xianqin, Huang Ying, Chen Huiling, Lufeng Hu. Chaos enhanced grey wolf optimization wrapped elm for diagnosis of paraquat-poisoned patients. Computat. Biol. Chem. 2019;78:481–490. doi: 10.1016/j.compbiolchem.2018.11.017. [DOI] [PubMed] [Google Scholar]
- Zeng Guo-Qiang, Chen Jie, Dai Yu-Xing, Li Li-Min, Zheng Chong-Wei, Min-Rong Design of fractional order pid controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing. 2015;160:173–184. [Google Scholar]
- Guo-Qiang Zeng, Kang-Di Lu, Yu-Xing Dai, Zheng-Jiang Zhang, Min-Rong Chen, Chong-Wei Zheng, Di Wu, Wen-Wen, 2014. Binary-coded extremal optimization for the design of pid controllers. Neurocomputing, 138:180–188.
- Zeng Guo-Qiang, Xie Xiao-Qing, Chen Min-Rong, Weng Jian. Adaptive population extremal optimization-based pid neural network for multivariable nonlinear control systems. Swarm Evolut. Comput. 2019;44:320–334. [Google Scholar]
- Jiao Hu, Huiling Chen, Ali Asghar Heidari, Mingjing Wang, Xiaoqin Zhang, Ying Chen, and Zhifang Pan, 2021. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowledge-Based Syst., 213:106684.
- Li Qiang, Chen Huiling, Huang Hui, Zhao Xuehua, Cai ZhenNao, Tong Changfei, Liu Wenbin, Tian Xin. An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Comput. Math. Methods Med. 2017;2017 doi: 10.1155/2017/9512741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Tong, Liang Hu, Ma Chao, Wang Zhi-Yan, Chen Hui-Ling. A fast approach for detection of erythemato-squamous diseases based on extreme learning machine with maximum relevance minimum redundancy feature selection. Int. J. Syst. Sci. 2015;46(5):919–931. [Google Scholar]
- Zhang Xiang, Xu Yueting, Yu Caiyang, Heidari Ali Asghar, Li Shimin, Chen Huiling, Li Chengye. Gaussian mutational chaotic fruit fly-built optimization and feature selection. Expert Syst. Appl. 2020;141 [Google Scholar]
- Yanan Zhang, Renjing Liu, Xin Wang, Huiling Chen, Chengye Li, 2020. Boosted binary harris hawks optimizer and feature selection. Eng. Comput., pages 1–30.
- Zeng Guo-qiang, Yong-zai Lu., Mao Wei-Jie. Modified extremal optimization for the hard maximum satisfiability problem. J. Zhejiang Univ. SCIENCE C. 2011;12(7):589–596. [Google Scholar]
- Zeng Guoqiang, Lu Yongzai, Dai Yuxing, Wu Zhengguang, Mao Weijie, Zhang Zhengjiang, Chongwei Backbone guided extremal optimization for the hard maximum satisfiability problem. Int. J. Innov. Comput. Inform. Control. 2012;8(12):8355–8366. [Google Scholar]
- Heidari Ali Asghar, Abbaspour Rahim Ali, Chen Huiling. Efficient boosted grey wolf optimizers for global search and kernel extreme learning machine training. Appl. Soft Comput. 2019;81 [Google Scholar]
- Shen Liming, Chen Huiling, Zhe Yu., Kang Wenchang, Zhang Bingyu, Li Huaizhong, Yang Bo, Liu Dayou. Evolving support vector machines using fruit fly optimization for medical data classification. Knowl.-Based Syst. 2016;96:61–75. [Google Scholar]
- Wang Mingjing, Chen Huiling. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020;88 [Google Scholar]
- Wang Mingjing, Chen Huiling, Yang Bo, Zhao Xuehua, Lufeng Hu, Cai ZhenNao, Huang Hui, Tong Changfei. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing. 2017;267:69–84. [Google Scholar]
- Deng W., Xu J., Zhao H., Song Y. A novel gate resource allocation method using improved pso-based qea. IEEE Trans. Intell. Transp. Syst. 2020 doi: 10.1109/TITS.2020.3025796. [DOI] [Google Scholar]
- Deng W., Xu J.J., Song Y.J., Zhao H.M. An effective improved co-evolution ant colony optimization algorithm with multi-strategies and its application. Int. J. Bio-Inspired Comput. 2020;16(3):158–170. [Google Scholar]
- Zhao Xuehua, Li Daoliang, Yang Bo, Chen Huiling, Yang Xinbin, Chenglong Yu., Liu Shuangyin. A two-stage feature selection method with its application. Comput. Electr. Eng. 2015;47:114–125. [Google Scholar]
- Zhao Xuehua, Li Daoliang, Yang Bo, Ma Chao, Zhu Yungang, Chen Huiling. Feature selection based on improved ant colony optimization for online detection of foreign fiber in cotton. Appl. Soft Comput. 2014;24:585–596. [Google Scholar]
- Aiju Lin, Quanquan Wu, Ali Asghar Heidari, Yueting Xu, Huiling Chen, Wujun Geng, and Chengye Li, 2019. Predicting intentions of students for master programs using a chaos-induced sine cosine-based fuzzy k-nearest neighbor classifier. IEEE Access, 7:67235–67248.
- Jixia Tu., Lin Aiju, Chen Huiling, Li Yuping, Li Chengye. Predict the entrepreneurial intention of fresh graduate students based on an adaptive support vector machine framework. Math. Probl. Eng. 2019;1–16:2019. [Google Scholar]
- Yan Wei, Huijing Lv, Mengxiang Chen, Mingjing Wang, Ali Asghar Heidari, Huiling Chen, and Chengye Li, 2020. Predicting entrepreneurial intention of students: An extreme learning machine with gaussian barebone harris hawks optimizer. IEEE Access, 8:76841–76855.
- Wei Yan, Ni Ni, Liu Dayou, Chen Huiling, Wang Mingjing, Li Qiang, Cui Xiaojun, Ye Haipeng. An improved grey wolf optimization strategy enhanced svm and its application in predicting the second major. Math. Probl. Eng. 2017;1–12:2017. [Google Scholar]
- Wei Zhu, Chao Ma, Xuehua Zhao, Mingjing Wang, Ali Asghar Heidari, Huiling Chen, and Chengye Li, 2020. Evaluation of sino foreign cooperative education project using orthogonal sine cosine optimized kernel extreme learning machine. IEEE Access, 8:61107–61123.
- De-Kuang Hwang, Chih-Chien Hsu, Kao-Jung Chang, Daniel Chao, Chuan-Hu Sun, Ying-Chun Jheng, Aliaksandr A Yarmishyn, Jau-Ching Wu, Ching-Yao Tsai, Mong-Lien Wang, et al., 2019. Artificial intelligence-based decision-making for age-related macular degeneration. Theranostics, 9(1):232. [DOI] [PMC free article] [PubMed]
- Minhaj Alam, David Le, Jennifer I Lim, Robison VP Chan, and Xincheng Yao, 2019. Supervised machine learning based multi-task artificial intelligence classification of retinopathies. Journal of clinical medicine, 8(6):872. [DOI] [PMC free article] [PubMed]
- Daniel S Kermany, Michael Goldbaum, Wenjia Cai, Carolina CS Valentim, Huiying Liang, Sally L Baxter, Alex McKeown, Ge Yang, Xiaokang Wu, Fangbing Yan, et al., 2018. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell, 172(5), 1122–1131. [DOI] [PubMed]
- Wang Lei, Yang Shujian, Yang Shan, Zhao Cheng, Tian Guangye, Gao Yuxiu, Chen Yongjian, Yun Lu. Automatic thyroid nodule recognition and diagnosis in ultrasound imaging with the yolov2 neural network. World J. Surg. Oncol. 2019;17(1):1–9. doi: 10.1186/s12957-019-1558-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Soo-Kyoung, Son Youn-Jung, Kim Jeongeun, Kim Hong-Gee, Lee Jae-Il, Kang Bo-Yeong, Cho Hyeon-Sung, Lee Sungin. Prediction model for health-related quality of life of elderly with chronic diseases using machine learning techniques. Healthcare Inform. Res. 2014;20(2):125. doi: 10.4258/hir.2014.20.2.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albahri A.S., Hamid Rula A., Alwan Jwan K., Al-Qays Z.T., Zaidan A.A., Zaidan B.B., Albahri A.O.S., AlAmoodi A.H., Khlaf Jamal Mawlood, Almahdi E.M., et al. Role of biological data mining and machine learning techniques in detecting and diagnosing the novel coronavirus (covid-19): a systematic review. J. Med. Syst. 2020;44:1–11. doi: 10.1007/s10916-020-01582-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang Hengyuan, Xia Liming, Yan Fu.hua., Wan Zhibin, Shi Feng, Yuan Huan, Jiang Huiting, Dijia Wu, Sui He, Zhang Changqing, et al. Diagnosis of coronavirus disease 2019 (covid-19) with structured latent multi-view representation learning. IEEE Trans. Med. Imaging. 2020;39(8):2606–2614. doi: 10.1109/TMI.2020.2992546. [DOI] [PubMed] [Google Scholar]
- Albahli Saleh. A deep neural network to distinguish covid-19 from other chest diseases using x-ray images. Curr. Med. Imaging. 2021;17(1):109–119. doi: 10.2174/1573405616666200604163954. [DOI] [PubMed] [Google Scholar]
- Yang Zifeng, Zeng Zhiqi, Wang Ke, Wong Sook-San, Liang Wenhua, Zanin Mark, Liu Peng, Cao Xudong, Gao Zhongqiang, Mai Zhitong, et al. Modified seir and ai prediction of the epidemics trend of covid-19 in china under public health interventions. J. Thoracic Disease. 2020;12(3):165. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Nanning, Shaoyi Du., Wang Jianji, Zhang He, Cui Wenting, Kang Zijian, Yang Tao, Lou Bin, Chi Yuting, Long Hong, et al. Predicting covid-19 in china using hybrid ai model. IEEE Trans. Cybern. 2020;50(7):2891–2904. doi: 10.1109/TCYB.2020.2990162. [DOI] [PubMed] [Google Scholar]
- Akib Mohi Ud Din Khanday, Syed Tanzeel Rabani, Qamar Rayees Khan, Nusrat Rouf, and Masarat Mohi Ud Din, 2020. Machine learning based approaches for detecting covid-19 using clinical text data. International Journal of Information Technology, 12(3):731–739. [DOI] [PMC free article] [PubMed]
- Booth Adam L., Abels Elizabeth, McCaffrey Peter. Development of a prognostic model for mortality in covid-19 infection using machine learning. Mod. Pathol. 2021;34(3):522–531. doi: 10.1038/s41379-020-00700-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolla Bhanu Prakash, S. Sagar Imambi, Mohammed Ismail, T. Pavan Kumar, and Y.N. Pawan, 2020. Analysis, prediction and evaluation of covid-19 datasets using machine learning algorithms. International Journal, 8(5).
- Erraissi Allae, Banane Mouad. Machine learning model to predict the number of cases contaminated by covid-19. Int. J. Comput. Dig. Syst. 2020;9:1–11. [Google Scholar]
- Shi Yuhui. International conference in swarm intelligence. Springer; 2011. Brain storm optimization algorithm; pp. 303–309. [Google Scholar]
- Wang Gai-Ge, Deb Suash, Cui Zhihua. Monarch butterfly optimization. Neural Comput. Appl. 2019;31(7):1995–2014. [Google Scholar]
- Li Shimin, Chen Huiling, Wang Mingjing, Heidari Ali Asghar, Mirjalili Seyedali. Slime mould algorithm: a new method for stochastic optimization. Future Gener. Comput. Syst. 2020;111:300–323. [Google Scholar]
- Wang Gai-Ge. Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018;10(2):151–164. [Google Scholar]
- Ali Asghar Heidari, Seyedali Mirjalili, Hossam Faris, Ibrahim Aljarah, Majdi Mafarja, and Huiling Chen, 2019. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst., 97:849–872.
- Ali A El-Solh, Yolanda Lawson, Michael Carter, Daniel A. El-Solh, and Kari A. Mergenhagen, 2020. Comparison of in-hospital mortality risk prediction models from covid-19. PloS one, 15(12):e0244629. [DOI] [PMC free article] [PubMed]
- Chun Chau Lawrence Cheung, Denise Goh, Xinru Lim, Tracy Zhijun Tien, Jeffrey Chun Tatt Lim, Justina Nadia Lee, Benedict Tan, Zhi En Amos Tay, Wei Yee Wan, Eileen Xueqin Chen, et al., 2021. Residual sars-cov-2 viral antigens detected in gi and hepatic tissues from five recovered patients with covid-19. Gut. [DOI] [PubMed]
- Paulina B. Szklanna, Haidar Altaie, Shane P. Comer, Sarah Cullivan, Sarah Kelliher, Luisa Weiss, John Curran, Emmet Dowling, Katherine M.A. O’Reilly, Aoife G. Cotter, et al., 2021. Routine hematological parameters may be predictors of covid-19 severity. Front. Med., 8. [DOI] [PMC free article] [PubMed]
- Kruthi Suvarna, Deeptarup Biswas, Medha Gayathri J Pai, Arup Acharjee, Renuka Bankar, Viswanthram Palanivel, Akanksha Salkar, Ayushi Verma, Amrita Mukherjee, Manisha Choudhury, et al., 2021. Proteomics and machine learning approaches reveal a set of prognostic markers for covid-19 severity with drug repurposing potential. Front. Physiol., 12:432. [DOI] [PMC free article] [PubMed]
- Shen Liming, Chen Huiling, Zhe Yu, Kang Wenchang, Zhang Bingyu, Li Huaizhong, Yang Bo, Liu Dayou. Evolving support vector machines using fruit fly optimization for medical data classification. Knowl.-Based Syst. 2016;96:61–75. [Google Scholar]
- Chen Hui-Ling, Liu Da-You, Yang Bo, Liu Jie, Wang Gang. A new hybrid method based on local fisher discriminant analysis and support vector machines for hepatitis disease diagnosis. Expert Syst. Appl. 2011;38(9):11796–11803. [Google Scholar]
- Hui ling Chen, Bo Yang, Su jing Wang, Gang Wang, Huai zhong Li, Wen bin Liu, et al., 2014. Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy. Applied Mathematics and Computation, 239:180–197.
- Pedro J. Ballester, John Stephenson, Jonathan N Carter, and Kerry Gallagher, 2005. Real-parameter optimization performance study on the cec-2005 benchmark with spc-pnx. In 2005 IEEE Congress on Evolutionary Computation, volume 1, pages 498–505. IEEE.
- Price Kenneth V. Handbook of optimization. Springer; 2013. Differential evolution; pp. 187–214. [Google Scholar]
- Marini Federico, Walczak Beata. Particle swarm optimization (pso). a tutorial. Chemometrics and Intelligent Laboratory Systems. 2015;149:153–165. [Google Scholar]
- Rashedi Esmat, Nezamabadi-Pour Hossein, Saryazdi Saeid. Gsa: a gravitational search algorithm. Inform. Sci. 2009;179(13):2232–2248. [Google Scholar]
- Mirjalili Seyedali. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl.-based Syst. 2015;89:228–249. [Google Scholar]
- Wang Mingjing, Chen Huiling. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020;88 [Google Scholar]
- Wang Xian-Fang, Gao Peng, Liu Yi-Feng, Li Hong-Fei, Fan Lu. Predicting thermophilic proteins by machine learning. Curr. Bioinform. 2020;15(5):493–502. [Google Scholar]
- Weng Lintianran, He Yuan, Peng Jianhua, Zheng Jianchao, Li Xinyu. Deep cascading network architecture for robust automatic modulation classification. Neurocomputing. 2021;455:308–324. [Google Scholar]
- Qiang Xu., Zeng Yu., Tang Wenjun, Peng Wei, Xia Tingwei, Li Zongrun, Teng Fei, Li Weihong, Guo Jinhong. Multi-task joint learning model for segmenting and classifying tongue images using a deep neural network. IEEE J. Biomed. Health Inform. 2020;24(9):2481–2489. doi: 10.1109/JBHI.2020.2986376. [DOI] [PubMed] [Google Scholar]
- Yang Ren, Mai Xu, Liu Tie, Wang Zulin, Guan Zhenyu. Enhancing quality for hevc compressed videos. IEEE Trans. Circuits Syst. Video Technol. 2018;29(7):2039–2054. [Google Scholar]
- Zhao Can, Zhong Shouming, Zhang Xiaojun, Zhong Qishui, Shi Kaibo. Novel results on nonfragile sampled-data exponential synchronization for delayed complex dynamical networks. Int. J. Robust Nonlinear Control. 2020;30(10):4022–4042. [Google Scholar]
- Zou Quan, Xing Pengwei, Wei Leyi, Liu Bin. Gene2vec: gene subsequence embedding for prediction of mammalian n6-methyladenosine sites from mrna. Rna. 2019;25(2):205–218. doi: 10.1261/rna.069112.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maimuna S. Majumder, Sheryl A. Kluberg, Sumiko R. Mekaru, and John S. Brownstein, 2015. Mortality risk factors for middle east respiratory syndrome outbreak, south korea, 2015. Emerging infectious diseases, 21(11):2088. [DOI] [PMC free article] [PubMed]
- Kin Wing Choi, Tai Nin Chau, Owen Tsang, Eugene Tso, Ming Chee Chiu, Wing Lok Tong, Po Oi Lee, Tak Keung Ng, Wai Fu Ng, Kam Cheong Lee, et al., 2003. Outcomes and prognostic factors in 267 patients with severe acute respiratory syndrome in hong kong. Annals of internal medicine, 139(9):715–723. [DOI] [PubMed]
- Chen Nanshan, Zhou Min, Dong Xuan, Jieming Qu., Gong Fengyun, Han Yang, Qiu Yang, Wang Jingli, Liu Ying, Wei Yuan, et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in wuhan, china: a descriptive study. Lancet. 2020;395(10223):507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Dawei, Hu Bo, Hu Chang, Zhu Fangfang, Liu Xing, Zhang Jing, Wang Binbin, Xiang Hui, Cheng Zhenshun, Xiong Yong, et al. Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus–infected pneumonia in wuhan, china. Jama. 2020;323(11):1061–1069. doi: 10.1001/jama.2020.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.F., Yuan J., Zheng Y.J., Chen J., Bao Y.M., Wang Y.R., Wang L.F., Li H., Zeng J.X., Zhang Y.H., et al. Retracted: Clinical and epidemiological characteristics of 34 children with 2019 novel coronavirus infection in shenzhen. Zhonghua er ke za zhi. Chinese journal of pediatrics. 2020;58:E008. doi: 10.3760/cma.j.issn.0578-1310.2020.0008. [DOI] [PubMed] [Google Scholar]
- Wang Weier, Tang Jianming, Wei Fangqiang. Updated understanding of the outbreak of 2019 novel coronavirus (2019-ncov) in wuhan, china. J. Med. Virol. 2020;92(4):441–447. doi: 10.1002/jmv.25689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiskopf Daniela, Weinberger Birgit, Grubeck-Loebenstein Beatrix. The aging of the immune system. Transplant Int. 2009;22(11):1041–1050. doi: 10.1111/j.1432-2277.2009.00927.x. [DOI] [PubMed] [Google Scholar]
- Steven M. Opal, Timothy D. Girard, and E. Wesley Ely, 2005. The immunopathogenesis of sepsis in elderly patients. Clinical infectious diseases, 41(Supplement_7):S504–S512. [DOI] [PubMed]
- Kui Liu, Yuan-Yuan Fang, Yan Deng, Wei Liu, Mei-Fang Wang, Jing-Ping Ma, Wei Xiao, Ying-Nan Wang, Min-Hua Zhong, Cheng-Hong Li, et al., 2020. Clinical characteristics of novel coronavirus cases in tertiary hospitals in hubei province. Chin. Med. J. [DOI] [PMC free article] [PubMed]
- Zhou L., Liu H.G. Early detection and disease assessment of patients with novel coronavirus pneumonia. Zhonghua jie he he hu xi za zhi= Zhonghua Jiehe he Huxi Zazhi= Chin. J. Tubercul. Respirat. Dis. 2020;43:E003. doi: 10.3760/cma.j.issn.1001-0939.2020.0003. [DOI] [PubMed] [Google Scholar]
- Gee Young Kim, Su Yon Park, Hwi Joong Yoon, Jin Tae Suh, So Young Kang, and Woo In Lee, 2007. Investigation of hemostatic changes in patients with sepsis. The Korean journal of laboratory medicine, 27(3):157–161. [DOI] [PubMed]
- Bai Zhuxiao, Huang Yurong, Song Chenghua, Liu Huimin, Chen Yihui, Zhang Haitao, Xinhong Lu., Song Yingbo, Zhang Xin. Clinical application of the innovance d-dimer assay in the diagnosis of acute pulmonary thromboembolism. Exp. Therapeutic Med. 2017;13(6):3543–3548. doi: 10.3892/etm.2017.4400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uttam Baboolall, Ying Zha, Xun Gong, Dong Rui Deng, Fuyuan Qiao, and Haiyi Liu, 2019. Variations of plasma d-dimer level at various points of normal pregnancy and its trends in complicated pregnancies: A retrospective observational cohort study. Medicine, 98(23). [DOI] [PMC free article] [PubMed]
- Li Ning, Duan Qingcheng, Zhang Weidan. Risk factors and coping strategies of severe community-acquired pneumonia in chemotherapy induction period of acute leukemia. Oncol. Lett. 2018;15(3):3566–3571. doi: 10.3892/ol.2018.7731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joana Clemente Duarte, Ana Tavares, Raquel Silva, Lurdes Correia, Adélia Simão, Armando Carvalho, et al., 2015. Prognostic value of plasma d-dimer level in adults with community-acquired pneumonia: A prospective study. Revista portuguesa de pneumologia, 21(4):218–219. [DOI] [PubMed]
- Guneysel O., Pirmit Serpil, Karakurt Sait. Plasma d-dimer levels increase with the severity of community acquired pneumonia. Tuberk Toraks. 2004;52(4):341–347. [PubMed] [Google Scholar]
- Jose M. Querol-Ribelles, Jose M. Tenias, Enric Grau, Jose M. Querol-Borras, Jose L. Climent, Emilio Gomez, and Isidoro Martinez, 2004. Plasma d-dimer levels correlate with outcomes in patients with community-acquired pneumonia. Chest, 126(4), 1087–1092. [DOI] [PubMed]
- Huan Han, Lan Yang, Rui Liu, Fang Liu, Kai-lang Wu, Jie Li, Xing-hui Liu, and Cheng-liang Zhu, 2020. Prominent changes in blood coagulation of patients with sars-cov-2 infection. Clinical Chemistry and Laboratory Medicine (CCLM), 1(ahead-of-print). [DOI] [PubMed]
- Tang Ning, Li Dengju, Wang Xiong, Sun Ziyong. Abnormal coagulation parameters are associated with poor prognosis in patients with novel coronavirus pneumonia. J. Thrombosis Haemostasis. 2020;18(4):844–847. doi: 10.1111/jth.14768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Xue, Wang Shuyao, Cao Sujian, He Xiaoxi, Qin Ling, He Meijia, Yang Yajing, Hao Jiejie, Mao Wenjun. Structural characteristics and anticoagulant property in vitro and in vivo of a seaweed sulfated rhamnan. Marine drugs. 2018;16(7):243. doi: 10.3390/md16070243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshino Kota, Kitamura Taisuke, Nakamura Yoshihiko, Irie Yuhei, Matsumoto Norihiko, Kawano Yasumasa, Ishikura Hiroyasu. Usefulness of plasminogen activator inhibitor-1 as a predictive marker of mortality in sepsis. J. Intensive Care. 2017;5(1):1–8. doi: 10.1186/s40560-017-0238-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh Timothy S., Stanworth Simon J., Prescott Robin J., Lee Robert J., Watson Douglas M., Wyncoll Duncan, et al. Prevalence, management, and outcomes of critically ill patients with prothrombin time prolongation in united kingdom intensive care units. Crit. Care Med. 2010;38(10):1939–1946. doi: 10.1097/CCM.0b013e3181eb9d2b. [DOI] [PubMed] [Google Scholar]
- Macrae Duncan, Tasker Robert C, Elbourne Diana. A trial of hyperglycemic control in pediatric intensive care. New England J. Med. 2014;370(14):1355–1356. doi: 10.1056/NEJMc1401343. [DOI] [PubMed] [Google Scholar]
- Tao Chen, DI Wu, Huilong Chen, Weiming Yan, Danlei Yang, Guang Chen, Ke Ma, Dong Xu, Haijing Yu, Hongwu Wang, et al., 2020. Clinical characteristics of 113 deceased patients with coronavirus disease 2019: retrospective study. bmj, 368. [DOI] [PMC free article] [PubMed]
- H. Pei, B. Yang, J. Liu, and K. Chang. Active surveillance via group sparse bayesian learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, page 2020, DOI: 10.1109/TPAMI.2020.3023092. [DOI] [PubMed]
- Qiu Sen, Wang Zhelong, Zhao Hongyu, Huosheng Hu. Using distributed wearable sensors to measure and evaluate human lower limb motions. IEEE Trans. Instrum. Meas. 2016;65(4):939–950. [Google Scholar]
- Lei Xu, Shanshan Jiang, and Quan Zou, 2020. An in silico approach to identification, categorization and prediction of nucleic acid binding proteins. bioRxiv. [DOI] [PubMed]
- Chen C., Qi Wu., Li Z., Xiao Lei, Hu Zhong Yi. Diagnosis of alzheimer’s disease based on deeply-fused nets. Combinatorial Chemistry & High Throughput Screening. 2020 doi: 10.2174/1386207323666200825092649. [DOI] [PubMed] [Google Scholar]
- Fei Xiaoyan, Wang Jun, Ying Shihui, Zhongyi Hu, Shi Jun. Projective parameter transfer based sparse multiple empirical kernel learning machine for diagnosis of brain disease. Neurocomputing. 2020;413:271–283. [Google Scholar]
- Zhongyi Hu, Jun Wang, Chunxiang Zhang, Zhenzhen Luo, Xiaoqing Luo, Lei Xiao, and Jun Shi, 2021. Uncertainty modeling for multi center autism spectrum disorder classification using takagi-sugeno-kang fuzzy systems. IEEE Transactions on Cognitive and Developmental Systems.
- Saber A., Sakr M., Abo-Seida O.M., Keshk A., Chen H. A novel deep-learning model for automatic detection and classification of breast cancer using the transfer-learning technique. IEEE Access. 2021;9:71194–71209. [Google Scholar]
- Xue X., Chen Z., Wang S., Feng Z., Duan Y., Zhou Z. Value entropy: A systematic evaluation model of service ecosystem evolution. IEEE Trans. Serv. Comput. 2020 doi: 10.1109/TSC.2020.3016660. [DOI] [Google Scholar]
- Xue X., Wang S.F., Zhan L.J., Feng Z.Y., Guo Y.D. Social learning evolution (sle): Computational experiment-based modeling framework of social manufacturing. IEEE Trans. Ind. Inform. 2019;15(6):3343–3355. [Google Scholar]
- Mingwu Zhang, Yu Chen, and Willy Susilo, 2020. Ppo-cpq: a privacy-preserving optimization of clinical pathway query for e-healthcare systems. IEEE Internet Things J., 7(10):10660–10672.
- Meng Fanwei, Pang Aiping, Dong Xuefei, Han Chang, Sha Xiaopeng. H8 optimal performance design of an unstable plant under bode integral constraint. Complexity. 2018;2018:4942906. [Google Scholar]
- Sheng H., Wang S., Zhang Y., Yu D., Cheng X., Lyu W., Xiong Z. Near-online tracking with co-occurrence constraints in blockchain-based edge computing. IEEE Internet Things J. 2021;8(4):2193–2207. [Google Scholar]
- Zhiang Wu., Li Changsheng, Cao Jie, Ge Yong. On scalability of association-rule-based recommendation: a unified distributed-computing framework. ACM Transactions on the Web (TWEB) 2020;14(3):1–21. [Google Scholar]
- Zhuo Zhenjian, Wan Youyang, Guan Daogang, Ni Shuaijian, Wang Luyao, Zhang Zongkang, Liu Jin, Liang Chao, Yuanyuan Yu., Aiping Lu. A loop-based and ago-incorporated virtual screening model targeting ago-mediated mirna-mrna interactions for drug discovery to rescue bone phenotype in genetically modified mice. Adv. Sci. 2020;7(13):1903451. doi: 10.1002/advs.201903451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Jinnan, Li Mengling, Liu Xinzhi, Tian Wenhong, Zhong Shouming, Shi Kaibo. Stabilization analysis for fuzzy systems with a switched sampled-data control. J. Franklin Inst. 2020;357(1):39–58. [Google Scholar]
- Qian Xu., Wang Kang, Zou Zhenwei, Zhong Liqiong, Akkurt Nevzat, Feng Junxiao, Xiong Yaxuan, Han Jingxiao, Wang Jiulong, Yanping Du. A new type of two-supply, one-return, triple pipe-structured heat loss model based on a low temperature district heating system. Energy. 2021;218 [Google Scholar]
- Ye Run, Liu Peng, Shi Kaibo, Yan Bin. State damping control: a novel simple method of rotor uav with high performance. IEEE Access. 2020;8:214346–214357. [Google Scholar]
- Zhao Can, Liu Xinzhi, Zhong Shouming, Shi Kaibo, Liao Daixi, Zhong Qishui. Secure consensus of multi-agent systems with redundant signal and communication interference via distributed dynamic event-triggered control. ISA Trans. 2021;112:89–98. doi: 10.1016/j.isatra.2020.11.030. [DOI] [PubMed] [Google Scholar]
- Mai Xu., Li Chen, Chen Zhenzhong, Wang Zulin, Guan Zhenyu. Assessing visual quality of omnidirectional videos. IEEE Trans. Circuits Syst. Video Technol. 2018;29(12):3516–3530. [Google Scholar]
- Zhou W., Lv Y., Lei J., Yu L. Global and local-contrast guides content-aware fusion for rgb-d saliency prediction. IEEE Trans. Syst., Man, Cybern.: Syst. 2021;51(6):3641–3649. [Google Scholar]
- Fan Mingyu, Zhang Xiaoqin, Hu Jie, Gu Nannan, Tao Dacheng. Adaptive data structure regularized multiclass discriminative feature selection. IEEE Trans. Neural Networks Learn. Syst. 2021 doi: 10.1109/TNNLS.2021.3071603. [DOI] [PubMed] [Google Scholar]
- Zhang Xiaoqin, Fan Mingyu, Wang Di, Zhou Peng, Tao Dacheng. Top-k feature selection framework using robust 0–1 integer programming. IEEE Trans. Neural Networks Learn. Syst. 2020 doi: 10.1109/TNNLS.2020.3009209. [DOI] [PubMed] [Google Scholar]
- Zhang Xiaoqin, Li Wei, Ye Xiuzi, Maybank Stephen. Robust hand tracking via novel multi-cue integration. Neurocomputing. 2015;157:296–305. [Google Scholar]
- Zhiang Wu., Song Aibo, Cao Jie, Luo Junzhou, Zhang Lu. Efficiently translating complex sql query to mapreduce jobflow on cloud. IEEE Trans. Cloud Comput. 2017;8(2):508–517. [Google Scholar]