Review of Statistical Methods for Evaluating the Performance of Survival or Other Time-to-Event Prediction Models (from Conventional to Deep Learning Approaches)

Abstract

The recent introduction of various high-dimensional modeling methods, such as radiomics and deep learning, has created a much greater diversity in modeling approaches for survival prediction (or, more generally, time-to-event prediction). The newness of the recent modeling approaches and unfamiliarity with the model outputs may confuse some researchers and practitioners about the evaluation of the performance of such models. Methodological literacy to critically appraise the performance evaluation of the models and, ideally, the ability to conduct such an evaluation would be needed for those who want to develop models or apply them in practice. This article intends to provide intuitive, conceptual, and practical explanations of the statistical methods for evaluating the performance of survival prediction models with minimal usage of mathematical descriptions. It covers from conventional to deep learning methods, and emphasis has been placed on recent modeling approaches. This review article includes straightforward explanations of C indices (Harrell's C index, etc.), time-dependent receiver operating characteristic curve analysis, calibration plot, other methods for evaluating the calibration performance, and Brier score.

INTRODUCTION

Time-to-event analysis refers to the analysis of the length of time until the occurrence of the event of interest. Time-to-event analysis is often colloquially referred to as survival analysis, although survival analysis in a narrow sense specifically deals with survival versus death. Survival prediction (or, more accurately, time-to-event prediction) involves predicting the occurrence of events of interest that develop as time elapses. Various modeling methods are available for the prediction, ranging from conventional statistical approaches to deep learning [1]. Survival prediction is different from the diagnosis/prediction of static binary outcomes, such as the diagnosis of cancerous and benign lung nodules on chest radiographs [2]. For survival prediction, the follow-up length is considered. The same patient can be in a state of no events or have already had an event depending on the time of analysis, and the patients can be censored (explained later). Therefore, statistical methods to evaluate the performance of survival prediction models are different from those used for evaluating the performance of models for static diagnosis/prediction.

The recent introduction of various high-dimensional modeling approaches, such as radiomics and deep learning [3,4,5,6,7], in medical research has resulted in greater diversity in recent studies on survival prediction modeling compared with previous studies. The novelty of the modeling approaches and the unfamiliarity of researchers and practitioners with the model outputs may cause some confusion related to the evaluation of the performance of such models. This article intends to provide intuitive, conceptual, and practical explanations of the statistical methods for evaluating the performance of survival prediction models, with minimal usage of mathematical descriptions. It covers from conventional to deep learning methods, with a greater emphasis on recent modeling approaches. In line with this, this article addresses methods frequently appearing in medical research papers instead of reviewing an extensive list of related methods. To effectively explain the fundamental methodological concepts, we use a simplified division of survival (no events) and death (event), and we intentionally do not consider the detailed definitions of the events related to various oncologic survival endpoints [8]. The methodological concepts explained in this article generally apply to other time-to-event predictions.

Basics of Survival Data and Survival Curve

Readers who are familiar with the concepts of censoring, survival probability, and the Kaplan-Meier curve may skip this section without loss of continuity. Table 1 shows the imaginary survival data obtained from 20 patients with malignancy, and Figure 1 shows the corresponding Kaplan-Meier curve. The follow-up time was calculated from time zero, which is not a specified calendar date, but the time when each patient was admitted for observations after a certain diagnosis or treatment required for the study. In the hypothetical data, patient follow-ups were conducted for up to 200 days. Six patients died, and the time of death is known. The 14 patients who did not die were either those who were alive at the end of the study or those who were lost to follow-up at some time points. In either case, these 14 patients are called censored subjects. Censoring poses a difficulty that is unique to survival analysis because exact survival times are unknown in censored patients, unlike in patients who have died [9]. Although we do not know what happened to the censored patients after the censored time, we know that the patients were alive at the time of censoring. Therefore, they still contribute useful information that should be included when analyzing survival. Ignoring the censored subjects would result in a loss of information when estimating the survival statistics.

Table 1. Imaginary Survival Data in 20 Patients with a Malignancy.

Patient ID	Follow-Up Time (Day)	Outcome (1 = Death; 0 = Censored)	Survival Probability by the Kaplan-Meier Method	Cumulative Incidence of Death (1 − Survival Probability)
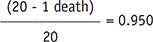
1	22	1		0.050
2	40	0	0.950	0.050
3	63	1		0.103
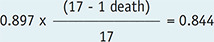
4	75	1		0.156
5	82	0	0.844	0.156
6	105	0	0.844	0.156
7	125	0	0.844	0.156
8	132	0	0.844	0.156
9	140	0	0.844	0.156
10	148	0	0.844	0.156
11, 12	150	1		0.324
13	157	0	0.676	0.324
14	162	0	0.676	0.324
15	165	0	0.676	0.324
16	170	0	0.676	0.324
17	175	1		0.493
18	190	0	0.507	0.493
19	200	0	0.507	0.493
20	200	0	0.507	0.493

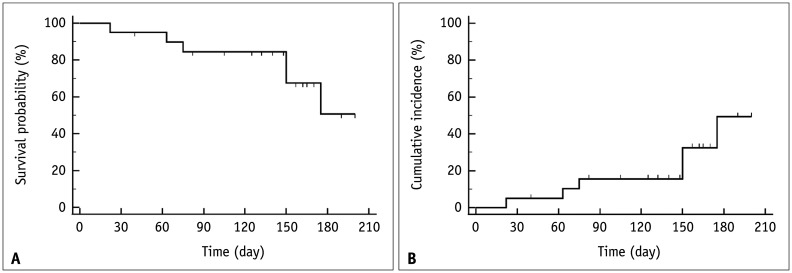
Fig. 1. Kaplan-Meier plots from the data in Table 1.

A. Kaplan-Meier curve showing survival probability, which is the probability that a patient survives until a particular time plotted on the y-axis as a function of the follow-up time on the x-axis. The censored patient is denoted by a downward blip. At the time a patient is censored, the survival curve does not dip down as no one has died. B. Kaplan-Meier curve showing the cumulative incidence of death, which is ‘1 − survival probability,’ on the y-axis as a function of follow-up time on the x-axis. The censored patient is denoted by an upward blip.

A survival curve plots survival probability on the y-axis, also referred to as cumulative survival, which is the probability that a patient survives until a particular time as a function of follow-up time on the x-axis. Among the different methods, the Kaplan-Meier method is the most widely used in the medical field. The Kaplan-Meier method recalculates the survival probability every time a patient dies, which decreases as shown by a downward step in the curve (Fig. 1A). To calculate the survival probability on a particular day t, denoted as S(t), the fraction of patients alive at the end of the day out of the patients who were alive past the immediately previous time (t−1) for survival probability calculation is first obtained. This calculation excludes patients who were censored in between from both the numerator and denominator. For example, on day 63 according to Table 1, 17 patients (‘19 patients who were alive past day 22’ − ‘1 patient who died on day 63’ − ‘1 patient censored on day 40’) divided by 18 patients (‘19 patients who were alive past day 22’ − ‘1 patient censored on day 40’) gives the fraction. Subsequently, the survival probability at the immediately previous time (t-1) is multiplied by the fraction to calculate S(t). For example, for day 63 in Table 1, 0.950 × (19 − 1 death − 1 censored)/(19 − 1 censored) = 0.897. In other words, to calculate the survival probability at time t, the fractions calculated at each time point until time t are successively multiplied.

$$S\left(t\right)=S(t-1)\times \frac{\#\mathrm{\hspace{1em}}\text{alive until}\mathrm{\hspace{1em}}(t-1)\mathrm{\hspace{1em}}-\mathrm{\hspace{1em}}\#\mathrm{\hspace{1em}}\text{died between}\mathrm{\hspace{1em}}(t-1)\mathrm{\hspace{1em}}\text{and}\mathrm{\hspace{1em}}t\mathrm{\hspace{1em}}-\mathrm{\hspace{1em}}\#\mathrm{\hspace{1em}}\text{censored between}\mathrm{\hspace{1em}}(t-1)\mathrm{\hspace{1em}}\text{and}\mathrm{\hspace{1em}}t}{\#\mathrm{\hspace{1em}}\text{alive until}\mathrm{\hspace{1em}}(t-1)\mathrm{\hspace{1em}}-\mathrm{\hspace{1em}}\#\mathrm{\hspace{1em}}\text{censored between}\mathrm{\hspace{1em}}(t-1)\mathrm{\hspace{1em}}\text{and}\mathrm{\hspace{1em}}t}$$

This method is called the product-limit method. The censored subjects are included for the calculations before their censored time; thus, they contribute to the calculation of survival probability, although they are excluded after their censored time. A modified plot, using ‘1 − survival probability’ = cumulative incidence of death, can also be generated (Fig. 1B).

Time-Independent and Time-Dependent Outputs from Survival Prediction Models

The outputs of survival prediction models vary because the modeling methods are diverse [1]. However, the outputs can be categorized into two large types: time-independent and time-dependent. Table 2 shows some typical model outputs and corresponding exemplary modeling methods. The statistical methods used to evaluate the performance of the prediction models are different for the two model output types.

Table 2. Common Outputs from Survival Prediction Models and Examples of Modeling Methods.

Model Output	Time Dependency	Mathematical Notation	Example Modeling Method
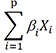
Log-risk score	Time-independent		DeepSurv, Lasso-Cox
Survival probability	Time-dependent	S(t, X)	Nnet-survival
Cumulative hazard	Time-dependent	Λ(t, X)	Random survival forest

The mathematical notations are for a patient who has characteristics X = (X₁, X₂, …, X_p) at time t. Both DeepSurv and Lasso-Cox use Cox proportional hazards model. βs are estimated coefficients in the Cox proportional hazards model. S(t, X) = e^{−Λ(t, X)} in general. In proportional hazards model, $S\left(t,X\right)=S_0{\left(t\right)}^{\text{exp}\left({\sum }_{i=1}^p{\beta }_i{X}_i\right)}$, where S₀(t) is baseline survival function that does not depend on patient characteristics X.

Time-Independent Model Output

The prediction model generates a single value as the output for each patient, regardless of the follow-up time. These outputs are scores that show the overall risk of death in a patient. Typically, patients assigned with greater values (or, conversely, smaller values depending on the specific final form the values are presented) are more likely to die early. Some examples are prediction models that use the log-risk score estimated by the Cox proportional hazards model (which is equivalent to the decision function in machine learning), such as DeepSurv and Lasso-Cox, and risk scores created using the rounded integer values of the regression coefficients (β) divided by the reference value (generally, the smallest β in the regression model) [10,11,12,13,14]. DeepSurv is a deep learning model that uses the log-risk function of the Cox proportional hazards model as the final output function [10]. Lasso-Cox is an L₁-penalized estimation for a Cox model using the least absolute shrinkage and selection operator method and is frequently used for radiomic analysis [11,12].

Time-Dependent Model Output

The prediction model calculates the output value separately for each follow-up time for each patient. Therefore, one patient had multiple model output values, one for each follow-up time. A typical time-dependent output is the survival probability at time t, as explained earlier, denoted as S(t, X), where X = (X₁, X₂, …, X_p) indicates the patient characteristics that are input to the model. For example, Nnet-survival provides the predicted S(t, X) at multiple specified time points as the model output (Table 2) [15]. Another example is the random survival forest, which estimates the cumulative hazard function at time t, denoted as Λ(t, X) (Table 2) [16].

Conversion between the Two Types of Model Outputs

One type of model output can be converted to another under certain circumstances. The time-independent model outputs can be converted into time-dependent results. For example, the survival probability at time t, S(t, X), can be calculated from the log-risk scores if the baseline survival probability at time t is available (Table 2). It should be noted that estimating the baseline survival probability is a separate procedure from the one that obtains the time-independent model outputs. Therefore, the methods of estimating the baseline survival probability (or baseline hazard) need to be explicitly specified when converting time-independent model outputs into time-dependent values for subsequent analyses, such as the conversion of time-independent outputs into survival probability and subsequent evaluation of calibration performance (which will be explained later).

Conversely, multiple time-dependent model outputs per patient may be reduced to a single time-independent value for analytical purposes. For example, the developers of the random survival forest suggested a mathematical method to combine its time-dependent multiple model output values (cumulative hazard) from multiple time points to create a time-independent result [16]. They then evaluated the model performance using Harrell's C index, which is explained later in this article. Kim et al. [17] evaluated the performance of a deep learning model based on Nnet-survival in predicting disease-free survival in patients with lung adenocarcinoma. Nnet-survival predicts survival probability (or, conversely, the cumulative incidence of events as ‘1 − survival probability’) at multiple time points [15]. Among the multiple sets of model output values, the investigators chose the cumulative incidence of the events at day 900 as the value that represented a patient as a whole for the prediction task and assessed the model performance by analyzing it using Harrell's C index. When reducing multiple time-dependent model output values to a single time-independent value, it is important to explain why such a reduction is reasonable mathematically and medically; thus, after the reduction, the reduced value is representative of the prediction task.

Statistical Methods for Evaluating Discrimination Performance of Survival Prediction Models

Discrimination performance refers to the ability of a model to predict patients who will die earlier (or develop an event earlier, more generally) and those who would die later. This is distinguished from the calibration performance (explained later).

Method for Time-Independent Model Outputs: C Index

The C index (or statistic) is the most commonly used method. If a prediction model that assigns each patient a numerical value indicating the risk of death as a single model output is any good, the patient with the higher value should have a shorter time-to-death. The C index is a measure that shows how good a model is in this regard. Suppose that one selects two patients from the study sample and compares their model output values and the time-to-death. If a patient with a higher value has a shorter time-to-death than the other patient, the two patients are called a concordant pair. If a patient with a higher value has a longer time-to-death than the other patient, it creates a discordant pair. If this comparison is performed for all available patient pairs in the study sample, the proportion of concordant pairs out of all possible patient pairs can be obtained. A higher proportion of concordant pairs indicates better model performance. This is the fundamental concept of the C-index.

There are a few different forms of C indices depending on how censored patients (i.e., those who have not died or were lost to follow-up) are considered and the exact definitions of concordant and discordant pairs [18]. Among these, Harrell's C index seems to be the most commonly used in the medical literature (Fig. 2) [19]. Harrell's C index discards the pairs that are incomparable because of censoring when computing the index value [1]. Because censored patients are largely discarded, Harrell's C index is dependent on the study-specific censoring distribution. In comparison, censoring-independent methods such as Uno's C and Efron's C indices have also been proposed [18,20].

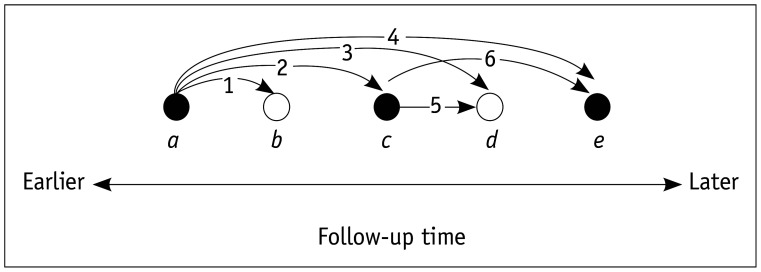
Fig. 2. Depiction of Harrell's C-index.

Black and white circles, labeled as a through e, represent death (event) and censored patients at different follow-up times, respectively. In the example of five patients, 10 patient pairs exist. Among these, only six pairs, labeled 1 through 6, are comparable. When the score indicating the risk of death calculated by a prediction model for patient i is RDi:

• • For pairs 2, 4, and 6, RDa > RDc, RDa > RDe, and RDc > RDe make concordant pairs, and RDa < RDc, RDa < RDe, and RDc < RDe are discordant pairs.
• • For pairs 1, 3, and 5, RDa > RDb, RDa > RDd, and RDc > RDd make concordant pairs, and RDa < RDb, RDa < RDd, and RDc < RDd are discordant pairs.
• • Pairs between b and c or e and between d and e (not marked in the figure) are not considered for computing Harrell's C index, as we do not know for sure whose time-to-death is shorter.
• • The pair between b and d (not marked in the figure) is also not considered for computing Harrell's C index, as we do not know whose time-to-death is shorter.

As the C index is a proportion, it can assume any value from 0 to 1. Values near 1 indicate high performance, and a value of 0.5 indicates that the discrimination performance of the model is the same as a coin flip (random concordance) in predicting which patient will live longer [21]. Values below 0.5 indicate that the model output is worse than a coin flip; therefore, concluding the opposite of what the model output indicates would be better for a more accurate prediction.

Method for Time-Dependent Model Outputs: Time-Dependent Receiver Operating Characteristic Analysis

Time-dependent receiver operating characteristic (ROC) analysis refers to an ROC analysis for any follow-up time point in the time-to-event data. The analysis generates an ROC curve and the area under the curve (AUC), also abbreviated as AUROC, separately for the specific time point(s). Therefore, the ROC curves and their AUC values are provided as a function of time, and hence the analysis is time-dependent. It typically consists of multiple ROC analyses, one performed for one of the various individual time points during the follow-up period (Fig. 3). However, time-dependent analysis can be performed for one particular time point during the follow-up if only that particular time is of interest for research. Time-dependent ROC analysis has two notable differences from the conventional ROC analysis used for the discrimination of static binary outcomes [2,22,23]. First, the outcome state of a patient (i.e., event vs. no event) is not fixed and can change over time. Second, the data include censored subjects for whom the outcome state is unknown. There are multiple approaches to addressing these two issues. Thus, according to a systematic review, there are at least 18 different variations in estimating time-dependent ROC curves [24].

Fig. 3. An example of a set of time-dependent ROC curves.

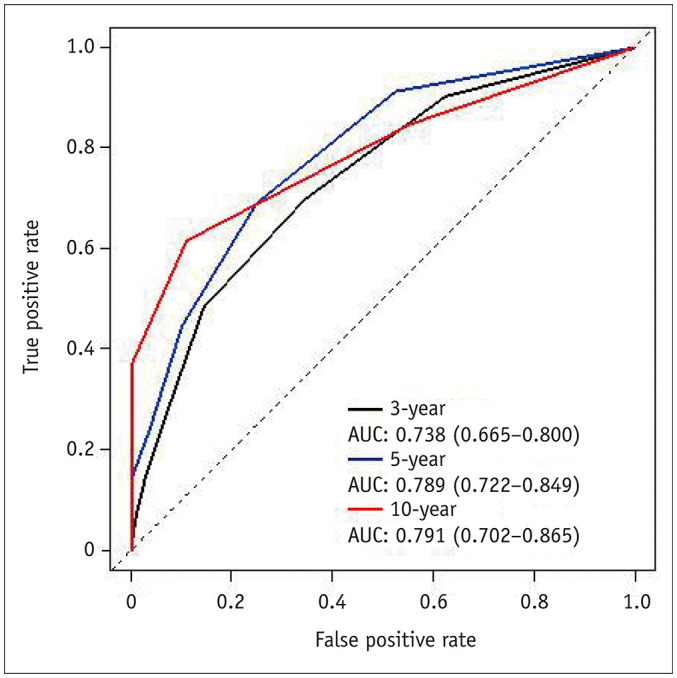
Time-dependent ROC curves for 3-year, 5-year, and 10-year follow-up times are shown. Modified from Park et al. Korean J Radiol 2021;22:213–224 [47]. AUC = area under the curve, ROC = receiver operating characteristic

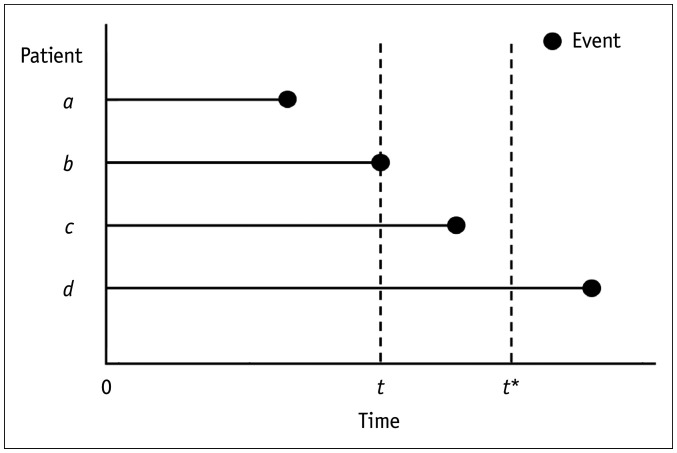
For the definition of event (case) and no events (control) at a particular follow-up time, Heagerty and Zheng [25] proposed three different approaches: 1) cumulative/dynamic (C/D), 2) incident/dynamic (I/D), and 3) incident/static (I/S) definitions. Figure 4 illustrates the differences between the three approaches. C/D defines patients who died (i.e., having the event) between time zero and time t as cases and those who survived (i.e., event-free) at time t as controls for the ROC analysis at time t. I/D defines patients who died at the time of t as cases and those who survived at time t as controls. I/S defines patients who died at the time of t as cases and those who survived at time t and survived further until a pre-specified fixed time (denoted as t^* in Fig. 4) as controls. According to a systematic review [24], the C/D definition was the dominant definition used in the published literature (adopted in 63% of the relevant methodology papers and 83% of the clinical research papers that applied the methodology). The I/S definition is used when a researcher attempts to distinguish between individuals who have an event at time t and those who are event-free after a sufficiently long follow-up time (t^*), who are long-term survivors [24].

Fig. 4. C/D, I/D, and I/S definitions.

For a time-dependent ROC analysis at time t, C/D defines patients a and b, who encountered the event between time zero and time t as cases, and patients c and d, who were event-free at time t as controls. I/D defines patient b, who had the event at time t, as a case, and patients c and d, who were event-free at time t, as controls. I/S defines patient b, who had the event at time t as a case, and patient d, who was event-free at time t and until a pre-specified fixed time (denoted as t^*), as controls. C/D = cumulative/dynamic, I/D = incident/dynamic, I/S = incident/static, ROC = receiver operating characteristic

Censored subjects create another complexity for time-dependent ROC analysis. If censored individuals are ignored, the estimation of sensitivity and specificity may be biased because the information from the individuals before censoring may contribute to the estimation [24]. Multiple methods to deal with censoring have been suggested, of which the details are beyond the scope of this article but can be found elsewhere [24].

As long as the above issues are addressed, the ROC analysis for any follow-up time is similar to the usual ROC analysis for static binary outcomes. An ROC curve can be generated by plotting the sensitivity on the y-axis and the false-positive rate (1 − specificity) on the x-axis while varying the threshold value for the model output for the time point, and its AUC can then be obtained (Fig. 3). The AUC indicates the model's performance for discriminating the binary outcomes, which are death and survival (or event vs. no events, more generally) at a time point, with a value closer to 1 indicating better performance.

The AUC for classifying static binary outcomes (i.e., the conventional ROC analysis) is sometimes referred to as the ‘C index’ in the literature [2,21,26]. It should be noted that the C index in this context does not refer to Harrell's C or other related C indices explained earlier. It refers to static binary discrimination instead of survival prediction. The concept of the C index can be applied to both binary discriminations that involve follow-up time and static binary discrimination. When applied to static binary discrimination, the C index reduces to the proportion of patient pairs in which the case has a higher predicted model output value compared to the control out of all available patient pairs in the study sample. The C index value then becomes identical to the Wilcoxon-Mann-Whitney statistic, an empirical estimator of AUC for the ROC analysis [26]. Therefore, the AUC is referred to as the C index in the context of static binary discrimination, which should not be confused with the C index for evaluating the discrimination performance of survival prediction.

An integrated AUC (iAUC) is a mathematical integration of multiple time-dependent AUC values across the follow-up period, and it can be expressed as follows: iAUC= ∫AUC(t)·w(t)dt, where t = time and w = weight. Heagerty and Zheng [25] suggested that w(t) should be proportional to the marginal density of survival time multiplied by the survival function, which makes the iAUC equivalent to ‘concordance,’ which is the probability that the order of deaths in randomly chosen two patients agrees with the order predicted by the model. In other words, iAUC is a weighted sum or a global average of time-dependent AUC values from time-dependent ROC analyses across the follow-up duration. Slightly different methods of computing iAUC exist, and R packages, such as ‘survAUC’ and ‘risksetROC,’ are available to carry out this analysis [27,28]. ‘survAUC’ uses C/D and I/D definitions, and ‘risksetROC’ uses I/D definition.

Statistical Methods for Evaluating Calibration Performance of Survival Prediction Models

The calibration performance describes the similarity of the probability values predicted by a model and the observed probabilities. Therefore, it applies to a model that specifically presents survival probability. As explained earlier (see the section entitled conversion between the two types of model outputs), not all survival prediction models directly estimate survival probability. Given that the probabilities are calculated separately for individual time points, the calibration performance is time-dependent. Similar to the time-dependent ROC analysis, the calibration performance is evaluated separately for each follow-up time. A good discrimination performance does not always ensure good calibration performance and vice versa.

Calibration Plot

A calibration plot is the primary graphical method for evaluating calibration performance (Fig. 5). In this plot, the x-axis is the probability predicted by the model, and the y-axis is the observed real probability. Because real probability cannot be observed in a single subject (i.e., each subject can only have either the event or no event state), unlike the predicted probability that is assigned to each subject by a model, the subjects are first divided into subgroups by similar predicted probabilities, typically by deciles of the predicted probabilities (i.e., 10 subgroups) [2]. Then, a plot is drawn using the mean predicted probability in each decile as the x-coordinate and the real probability observed in the same decile as the corresponding y-coordinate. A perfect calibration should lie on the 45° line of the plot. The calibration slope and intercept can be obtained [14,29,30,31]. A slope close to 1 and an intercept close to 0 (i.e., the 45° line of the plot) indicates good calibration. If the sample size is small, splitting the subjects into many subgroups becomes difficult because some subgroups may contain only a few subjects. Thus, calibration analysis may not be robust. Therefore, using a large study sample and a sufficient number of subgroups is important for an adequate evaluation of the calibration performance. R packages are available for analysis, such as ‘caret’ and ‘rms’ [32,33].

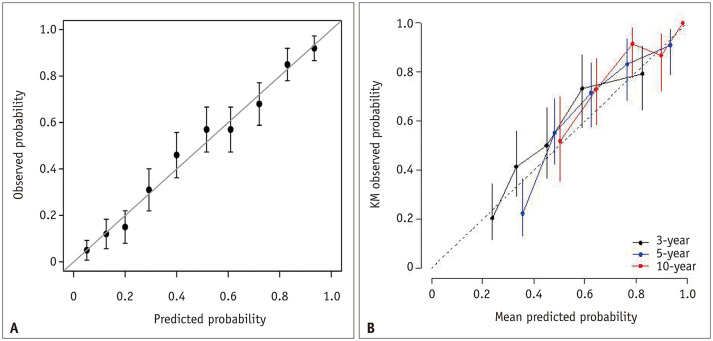
Fig. 5. Examples of calibration plots.

A. A schematic example of the calibration plot. Error bars represent 95% confidence intervals of the mean predicted probabilities. Reprinted from Park and Han. Radiology 2018;286:800–809 [2]. B. Calibration plots in a research study. Modified from Park et al. Korean J Radiol 2021;22:213–224 [47]. Calibration plots for 3-year, 5-year, and 10-year follow-up times are shown. KM = Kaplan-Meier

Statistical Tests and Measures

Various statistical measures and tests can also be used to describe the degree of calibration, in addition to the graphical method. Details on the specific statistical tests and measures are beyond the scope of this article but can be found elsewhere [29]. Statistical testing for calibration, such as the Hosmer-Lemeshow test, has pitfalls. Although an insignificant result of the test (i.e., with a p value ≥ 0.05, if 0.05, is chosen as the criterion for statistical significance) is meant to indicate good calibration because the null hypothesis (H₀) is good calibration, the p value can be ≥ 0.05 merely due to low statistical power caused by a small sample [2,29]. These statistical tests and measures should be accompanied by a calibration plot instead of being presented alone.

Statistical Methods for Evaluating the Overall Performance of Survival Prediction Models

Brier Score

The Brier score is not a measure of either discrimination performance or calibration performance alone, but a measure of overall performance, which incorporates both the discrimination and calibration aspects of a model that predicts binary outcomes [29]. Therefore, it would be more appropriate to present both the Brier score and the calibration plot instead of presenting the Brier score as a substitute for the calibration plot.

The Brier score is calculated as follows:

$$\text{Brier score}=\frac{1}{n}{\sum }_{i=1}^n{(p_i-0_i)}^2$$

where n is the number of subjects, p_i is the probability of event predicted by the model for the ith subject, and o_i is the observed outcome in the ith subject (i.e., 1 for event or 0 for non-event) [34]. Therefore, a score closer to 0 indicates a better predictive performance. The Brier score is calculated separately for each follow-up time point. The mathematical integration of multiple Brier score values obtained at all follow-up times, called the integrated Brier score, can then be calculated as an overall average performance measure for the prediction model for all times, similar to integrating time-dependent AUC values to generate an iAUC [35,36]. The integrated Brier score for a time interval is the average of the score values for the interval, which is the area under a curve that plots the score against the follow-up time divided by the length of the time interval. The R package ‘pec’ is available for analysis [37].

Other Measures

Several other measures exist for assessing the overall performance, such as Royston's D index, the modification of Nagelkerke's R² index by O'Quigley et al., and Kent and O'Quigley measure of dependence [38,39,40,41,42]. These methods also show robustness to censored data. Further details are beyond the scope of this article, and we recommend referring to the more specific literature for more information [38,39,40,41,42].

Statistical Methods for Comparing the Performance of Models

The difference between survival prediction models in the statistical measures discussed above can be tested using the 95% confidence interval (CI) of the difference obtained from the bootstrap samples in most cases [43,44,45]. If the 95% CI of the difference does not include zero, it indicates that the p value is less than 0.05, and the difference is statistically significant. For the C index, a non-parametric method to compare two survival prediction models without having to use bootstrap samples has been developed and implemented in the R package called ‘compareC’ [46].

SUMMARY

In summary, survival prediction (or, more generally, time-to-event prediction) involves the prediction of the development of events of interest over time. The outputs of survival prediction models vary because the modeling methods are diverse, ranging from conventional statistical approaches to deep learning. However, the outputs can be categorized into two types: time-independent and time-dependent. The statistical methods used to evaluate the performance of the prediction models are different for the two model output types. To adequately evaluate the performance of a survival prediction model, both discrimination and calibration performance should be analyzed appropriately if applicable. The typical statistical measures and methods used are summarized in Table 3. For evaluating the discrimination performance, the C index or time-dependent ROC curve can be calculated depending on the time dependency of the model outputs. There are several variations in the C index and multiple methods of time-dependent ROC analysis. The calibration performance of a survival prediction model is visually assessed with a calibration plot and is further described using the calibration slope and intercept. Statistical testing for good calibration is commonly performed to obtain p values, but care should be taken due to its pitfalls. The Brier score is a measure of the overall performance that incorporates both discrimination and calibration. The number of publications on survival prediction models is increasing, and there is an increased interest in the methodology among readers. We believe this review article summarizes the basic statistical concepts for the evaluation of survival prediction models for those who want to develop or critically appraise them.

Table 3. Typical Statistical Measures and Methods for Evaluating the Performance of Survival Prediction Models.

Aspect of Performance	Statistical Measure or Method	Nature of Model Output	Meaning
Discrimination	C index	Time-independent	Agreement between the predicted vs. the observed order of the events
	Time-dependent ROC AUC	Time-dependent	Probability that the model predicts a randomly chosen patient who encountered the event before the specific time point as having higher risk than a randomly chosen patient who did not encounter the event by then
Calibration	Calibration plot (with slope and intercept)	Event probability (time-dependent)	Plot of the event probability values predicted by a model against the observed event probabilities
Overall	Brier score	Time-dependent	Mean squared error of the predicted risks

AUC = area under the curve, ROC = receiver operating characteristic