Emulating Target Trials to Improve Causal Inference From Agent-Based Models

Abstract

Agent-based models are a key tool for investigating the emergent properties of population health settings, such as infectious disease transmission, where the exposure often violates the key “no interference” assumption of traditional causal inference under the potential outcomes framework. Agent-based models and other simulation-based modeling approaches have generally been viewed as a separate knowledge-generating paradigm from the potential outcomes framework, but this can lead to confusion about how to interpret the results of these models in real-world settings. By explicitly incorporating the target trial framework into the development of an agent-based or other simulation model, we can clarify the causal parameters of interest, as well as make explicit the assumptions required for valid causal effect estimation within or between populations. In this paper, we describe the use of the target trial framework for designing agent-based models when the goal is estimation of causal effects in the presence of interference, or spillover.

Abbreviations

ABM

agent-based model

HIV

human immunodeficiency virus

PrEP

preexposure prophylaxis

 

Agent-based models (ABMs) have long been used in infectious disease epidemiology to understand principles of disease transmission and for learning about potential causal relationships via triangulation of model results with observed data under varying model structures and inputs, but until recently there has been little discussion of the use of these models for quantifying causal parameters under a potential outcome framework (1, 2). An important benefit of ABMs over existing causal-effect estimation approaches is the ability to incorporate information about how disease or health behaviors circulate in a population, and to assess potential impacts of spillover (also known as dissemination, or interference). Unfortunately, this very feature makes causal inference more difficult, because a key assumption of the potential outcomes framework is the stable unit value treatment assumption (SUTVA) (3, 4). This assumption is violated, in part, by the presence of dissemination or interference between simulated agents. As a result, with few exceptions (5–7), most of the literature combining causal effect estimation with agent-based modeling has focused on the simplest case of no interference, “spillover,” or interpersonal transmission in the specific exposure of interest by which counterfactuals are indexed (1, 2, 8–10). However, the target trial framework, often employed for causal inference in empirical observational studies, presents a potential solution to understanding causal effects estimated via ABMs in the presence of interference or spillover.

We recently published work in the Journal using this approach to understand the causal effects of preexposure prophylaxis (PrEP) use among men who have sex with men on preventing human immunodeficiency virus (HIV) acquisition (11). Here, we describe how extension of the target trial framework works to clarify causal effect estimation from agent-based simulation models with interference, spillover, and/or transmission by exploiting existing statistical methodology for estimating causal effects in randomized controlled trials of infectious disease and other transmissible conditions.

THE PROBLEM OF INTERFERENCE

Interference describes a situation in which an individual’s exposure status can affect another individual’s outcome status, despite that second individual’s own exposure status (4). The classic example of interference occurs in studies of vaccines: an unvaccinated individual in a community with a high proportion of vaccinated people will have a different probability of becoming infected than the same unvaccinated individual in a community in which no one has been vaccinated. However, interference is not restricted to the domain of infectious diseases. It can also occur in studies of educational or health promotion programs, where one individual may share the information they have learned with another individual. Many social epidemiologic questions can also be framed in a setting of interference (12, 13). Our applied example examines the use of PrEP within sexual networks for the prevention of HIV in men who have sex with men (11). In this study, agents who are assigned to PrEP receive a direct benefit in terms of reduced probability of HIV acquisition, but there is also a benefit to agents who do not themselves take PrEP but whose sexual partners are assigned to PrEP. Understanding the relative benefits of taking PrEP versus being in a sexual network with some frequency of PrEP use can help improve our ability to target intervention strategies to result in the overall greatest reduction in HIV incidence in the population.

A number of causal estimators have been proposed to clarify the causal question of interest in the context of interference (14, 15). The most common of these is to define direct effect and disseminated (i.e., indirect) effects within and across clusters of individuals (14). In this context, a “cluster” represents a distinct group—similar to a network component in network science applications, with some differences in whom individuals can mix with—that consists of a set of individuals who are all possibly connected to and influence each other in some way but who are not connected (or influenced by) any individuals in another cluster/component. Under this framework, the causal effect of an intervention in the presence of interference can be separated into 4 types of effects (Figure 1).

Figure 1.

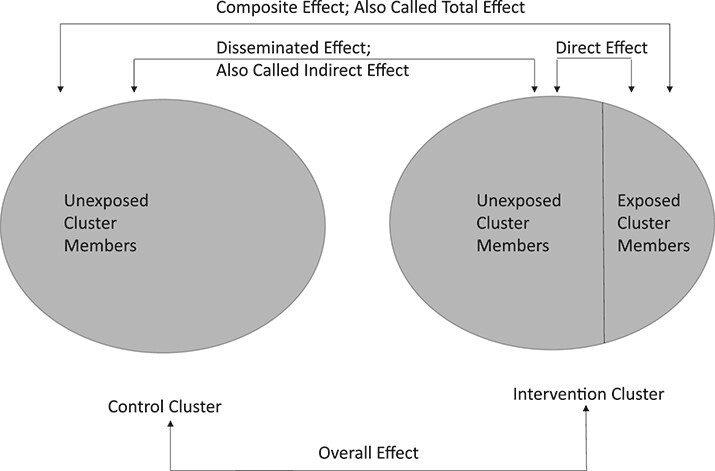
Causal estimands available in a cluster-randomized trial or agent-based model designed to emulate a cluster-randomized trial. Adapted from Halloran and Struchiner (14).

First, the direct effect represents the average causal effect of receiving versus not receiving the intervention while belonging to a cluster where a specified proportion of other individuals receive the intervention. In our applied paper (11), the direct effect measures the additional beneficial effect on reduction of HIV acquisition of being on PrEP versus not being on PrEP beyond that obtained by being part of a sexual network with a fixed PrEP coverage level. Second, the disseminated (or indirect) effect represents the average causal effect of being part of a cluster where other individuals do or do not receive the intervention, while never receiving the intervention oneself. In our applied paper, the disseminated effect measures the beneficial effect on reduction in HIV acquisition of being part of a sexual network where a fixed proportion of individuals take PrEP compared with being part of sexual network where no individuals take PrEP, when an agent is not themselves assigned to PrEP. The total (or composite) effect is the average causal effect of jointly receiving the intervention and being part of a cluster with a specific intervention level compared with jointly not receiving the intervention and being part of a cluster that does not receive the intervention. In our example, this measures the combined effects of being on PrEP oneself and being part of a sexual network with a fixed PrEP coverage. Finally, the overall effect is the average causal effect if everyone is in a control cluster versus if everyone is in an intervention cluster, without regard to the particular status of individuals. In the applied example, this is the beneficial effect on reduction in HIV acquisition among individuals in sexual networks with a fixed level of PrEP coverage compared with networks with no PrEP coverage, averaged over individual PrEP use (14, 16, 17).

We note that the terminology used in the literature to describe these effects may be confusing to epidemiologists more accustomed to working in noncommunicable settings, where “direct” and “indirect” effects have meanings related to causal mediation. However, these meanings can be linked—in fact, when there are only 2 individuals in a cluster, interference can be recast as mediation where the mediator for one individual is the exposure status of the other individual (18). We briefly provide some intuition on these causal effect terms in the 2 contexts. In both settings, the term “total effect” refers to the combined effect of all pathways or mechanisms. The term “direct effect” in the presence of transmission or interference refers to the direct benefit or harm of an exposure to an individual conditional on a specified background setting of exposure for other individuals. This is somewhat akin to (but distinct from) the idea of a “direct effect” in mediation analyses, which is the direct benefit or harm of an exposure to an individual conditional on a specified background setting of mediators for that individual. Similarly, in the presence of transmission or interference, the “indirect effect” refers to the indirect benefit or harm to an individual with a set level of exposure (typically unexposed) via the mechanism of changes to other individuals’ exposures. In the noncommunicable, mediation setting, the “indirect effect” refers to the indirect benefit or harm to an individual of a set level of exposure (either exposed or unexposed) via the mechanism of a change in that individual’s mediator levels.

In the setting of randomized clinical trials, these 4 causal effects can be straightforward to define and estimate (at least for the intention-to-treat effect). Three types of randomized trials are available for estimating these effects: 2-stage randomized trials, where randomization occurs first at the cluster level and then at the individual level within selected intervention clusters; cluster-randomized or network-randomized trials, where randomization occurs at the group level only (17, 19); and ring-vaccination trials, which typically compare immediate intervention with delayed intervention (20, 21). In 2-stage randomized trials, identification of these direct, indirect, and total effects is possible without any further considerations of confounding (15). Similarly, Buchanan et al. (17) have described the extension of these effects to network randomized controlled trials. In a cluster-randomized trial, the clusters or components are randomly assigned to intervention or control. Typically, everyone in the cluster should receive the intervention that their cluster was assigned; however, in some designs or due to noncompliance, a self-selected subset of individuals in the intervention cluster may receive the intervention. Network-randomized trials differ from cluster-randomized trials by specifying particular contact structures among individuals. However, the distinction between these trial designs is not always clear cut (17).

The main concern for interpretability of these effects in the randomized trial setting is transportability or generalizability to settings with different background levels of exposure, including different interference patterns, or different patterns of effect modifiers (22–24). This is a concern with all types of randomized trials but may be particularly challenging for randomized trials with interference due to the complex nature of the relationships between individuals in the trial population, leading to potential outcomes indexed by both an individual’s exposure and as exposures of other individuals in the cluster (sometimes called the “interference set”). In general, transportability depends on the distribution of effect modifiers in the trial population and in the target population for inference. Importantly, some (but not all) drivers of interference in a population may be conceptualized as effect modifiers. This means that generalizing or transporting the results of an ABM may require either parameterizing the model to include drivers of interference or restricting generalization to populations with similar distributions of these interference drivers. To parameterize interference, a model would need to include specification of the types, frequencies, and reasons for contacts between individuals, and/or the correct full contact network (25). In some cases, the patterns of interference may differ in fundamental ways between populations, such that the definition of the potential outcomes (which depends on the interference pattern) no longer applies to the new population. When this happens, effects estimated in one setting may not be applicable in another setting. Methods are being developed to address the challenges of transportability and generalizability in individual-level randomized trials (23, 24, 26, 27) but have generally not yet been extended to the group-level randomized trials we discuss here.

THE TARGET TRIAL FRAMEWORK FOR CAUSAL INFERENCE

Comparison with trial design has been used as a motivation for observational study design for many decades—dating to at least 1953 (28). More recently, the target trial framework for causal inference of observational study designs was formalized to provide clarity about the causal estimand of interest and help reduce bias from common mistakes, such as inappropriate selection of individuals, choice of baseline, or confounding control (29–38). A full description of the target trial framework is beyond the scope of this paper, but briefly, this approach requires the research team to describe the hypothetical randomized trial that would need to be conducted in order to obtain a quantitative estimate of the causal effect of interest, if a trial were feasible.

Before defining a target trial, it is crucial to specify a clear and meaningful causal contrast—in epidemiology, this often means specifying a “well-defined intervention” (39–41). Some researchers have stated that a requisite for a well-defined intervention is that it be humanly feasible. However, others have argued that this understanding of a “well-defined intervention” is limiting in terms of the causal questions that can be evaluated (42) because of its seeming emphasis on interventions or manipulations that are currently humanly feasible and exclusion of those that are not (41, 43, 44). We disagree with both framings of this conflict for 3 reasons. First, in the absence of randomization, a clearly specified causal contrast can add clarity and credibility to the required assumptions for quantitative estimation of a causal effect, whether or not that causal contrast could be brought about via human manipulation. When intervention is currently humanly feasible, the specification of a well-defined intervention that could actually be conducted is sufficient to ensure the causal assumption of consistency is met. In cases where an intervention is not currently humanly feasible, specifying a clear causal contrast can make that fact more readily identifiable to readers and allows them to determine the value of resulting effect estimates for decision-making or further scientific research. Second, when available, a well-defined intervention that is humanly feasible provides clear link to interventions that could be implemented to effect meaningful change and improve population health, even if those interventions would be extremely difficult to implement. Importantly, describing a hypothetical intervention that is not currently humanly feasible may spur innovation and enhance focus on what might be needed for such an intervention to be feasible in the future. Finally, causal contrasts do not necessarily need to be practically or feasibly implemented in the real world to be sufficiently clearly specified but must at minimum represent a meaningful change. A causal contrast that cannot be practically or feasibly implemented can still be of use when all mechanisms by which change in exposure occurs or could occur in the world are believed to have similar impacts on the outcome (45). Importantly, this makes it clear that in general we should not specify causal contrasts that combine multiple mechanisms with conflicting effects, and that we should not specify causal contrasts for which the concept of exposure “change,” however that may be brought about, cannot be meaningfully described. For example, it is likely not meaningful to construct a causal contrast around varying levels of race, but it may be meaningful to construct a causal contrast around varying levels of racism.

In fact, this latter reason is one of the chief benefits of using an ABM for causal effect estimation. Crucially, because an ABM is a simulation, all exposures of interest must be algorithmically specifiable. Therefore, any set of exposures that can be compared in simulations must also be algorithmically specifiable. This algorithmic specification is the core component of what the target trial requires for identification of a clear and meaningful causal contrast. We can thus in theory use an ABM to simulate clear and well-defined causal contrasts even when interventions cannot currently be implemented in the real world—all we need are reasonable assumptions about the model structure and parameter inputs. This is because the target trial framework does not require that we can necessarily obtain our contrasting exposure levels in an actual real-world trial. In addition, because ABMs are simulations, we can randomly assign exposures to agents, regardless of their complexity, equipoise, or ethical concerns.

With this in hand, the first step in this framework is to create a detailed, clear, and explicit specification of the hypothetical, target randomized controlled trial that would allow the researcher to answer the causal question of interest in a world with no ethical, logistical, or financial constraints, and in which the exposure of interest is perfectly manipulable by study investigators, regardless of whether this is actually feasible or ethical in the real world. This target trial represents the ideal study that could be conducted to answer the research question of interest and should include details on the inclusion/exclusion criteria based on the target population of interest, well-defined treatment and comparator strategies and how these could (hypothetically) be delivered (in the context of an ABM, a clearly defined algorithm for simulating the treatment and comparator strategies), outcomes of interest (where applicable with specification of handling of competing events or right-truncation by death), follow-up time (both start and end of follow-up), and causal estimands of interest.

Next, a mapping is made between the available or accessible observational data and the proposed target trial framework such that the observational data collection and analysis are designed to emulate as closely as possible the key features of the target trial. Particularly important is the choice of population, exposures, and time frame to ensure that the observational data is able to provide an estimate of the causal estimand of interest in the population of interest, despite the lack of randomization. This emulation process may require modification of the original target trial design if some features of the trial are intractable in the observational data, and may even lead to the conclusion that observational data cannot be used to answer the causal question at hand (34). Nonetheless, where observational data are sufficiently rich and accurately measured, the target trial emulation approach can help researchers avoid common sources of bias such as immortal time bias, selection bias, confounding, and poorly specified causal questions, as well as bias in interpretation due to a lack of external validity (29, 31–33, 35, 36). The target trial framework provides clarity on external validity in 2 ways—first, by requiring a clear and explicit a priori description of the population of interest in terms of inclusion and exclusion criteria (thus clarifying to whom the estimates directly apply), and second, through the enhanced ability to use methods for transportability or generalizability developed for randomized trials (22, 23).

Note that the challenges of poor quality or limited data exist regardless of whether the target trial framework is employed or not. Rather than solving or creating problems based on data availability, the target trial framework serves to highlight areas where insufficient data are likely to cause problems for drawing causal inferences and forces researchers to explicitly confront potential limitations of their study design before conducting the analysis.

EMULATING TARGET TRIALS WITH AGENT-BASED MODELS

In the absence of interference, individual-level simulation models can be relatively easily extended to estimate causal effects provided that all assumptions required for causal inference are supported for the specific exposure-outcome relationship, population, and model of interest (1). In fact, an individual-level simulation model, when correctly specified in terms of the required causal structure and assumptions, and parameterized entirely from a single data set can be viewed as a form of the parametric g-formula (1). However, even for individual-level simulation models with no interference, parameterizing all required inputs from a single data set can be challenging—indeed many inputs can never be obtained empirically (45). As a consequence of this, individual-level simulation models, and ABMs, are most useful when no single data set exists in which to answer the causal question of interest. These models can be used to synthesize inputs from multiple sources, including experts’ best estimates (8). In addition, ABMs have long been used as a solution to the interference problem, because these models allow explicit simulation of interference, and can allow for different levels of community exposure, but have not been theoretically linked to the estimation of causal effects in the presence of interference or more generally, assuming no interference. As a result, it remains unclear which scenarios are appropriate to assess, and how (or indeed, whether) to interpret the model results as the “effect” of the intervention or an outcome associated with exposure to the intervention.

By explicitly designing the ABM to emulate a target trial protocol, the causal estimands and the interpretation of these causal effects are made clear. Unlike emulation of target trials with observational data, ABMs can be designed to exactly mimic the hypothetical randomized trial of interest, whether a cluster- or network-randomized trial, 2-stage randomized trial, ring-vaccination trial, or an individually randomized trial where participants are socially or biologically connected. The main challenge for emulating randomized trials with ABMs will be obtaining empirical data to parameterize the model inputs, especially those related to transmission of the disease or health behavior of interest, which may not be directly estimable from data (45). However, when a randomized trial exists in a related population, this information could be used to calibrate the inputs of an ABM designed to estimate the effects that would be observed had the trial been conducted in a second population under some slight modifications, such as adding effect modifiers or outcome causes that differ between populations (1, 8). In addition, observational studies designed under the target trial framework can also serve as a source of calibration targets or parameter inputs (1, 8). Importantly, the challenge of obtaining appropriate empirical data to parameterize an ABM exists regardless of whether the target trial framework is used to design the model (45); this framework simply helps to clarify the parameters needed and the likely types of bias that may arise from incorrect or guessed parameters.

In our recently published study, we designed our ABM to simulate the results of a 2-staged randomized trial of PrEP use in sexual networks of men who have sex with men (11). Using this design, we were now able to estimate beneficial direct (individual) and disseminated (indirect) effects of PrEP use within these sexual networks, and we identified a complex interaction between these 2 effects as the level of PrEP coverage within a network component increases. In particular, increasing the proportion of a sexual network component receiving PrEP reduces HIV incidence in those members of the component who had not been randomized to receive PrEP but somewhat diminishes the benefit to any individual of receiving PrEP themselves, particularly among higher coverage levels. This makes intuitive sense—as the level of risk in the network component decreases, the potential additional amount of protection an individual can receive also decreases.

ABMs may also provide a solution to the challenges of generalizability and transportability of group-level randomized trials in the setting of interference. When all effect modifiers are included in the ABM structure, then an estimate of the causal effect in a new population may be obtained by changing the prevalence of those variables to match the new target population of interest. This is similar to the data fusion approach for the randomized trial setting (22), but when combined with the target trial framework could allow for the incorporation of interference into the effect estimates. Importantly, some drivers of interference may be effect modifiers, and those should be considered when creating an ABM designed for transportability. However, other drivers of interference may be more appropriately considered components of the exposure of interest, or may be part of the definition of the potential outcomes. Understanding how to generalize or transport the results thus relies on a detailed understanding of the causal structure, and on the ability to obtain input parameters that describe the relationships between effect modifiers and other components, as well as the contact patterns or other drivers of interference.

Finally, clear parallels exist between individual-level simulation models and the parametric g-formula—a tool for quantitative causal effect estimation using observational or randomized trial data in the presence of time-varying treatment-confounder feedback or informative censoring. The recent development of an auto-g-computation algorithm for observational quantitative causal effect estimation of networks parallels the use of ABMs for settings with interference and provides a clear statistical framework for the use of ABMs in target trial emulation (25).

CONCLUSIONS

Causal inference in the presence of interference, transmission, or spillover is more complicated than in the absence of these conditions, especially when randomization is infeasible due to ethical, financial, logistic, or other constraints. However, by combining knowledge about how to estimate these causal effects in randomized trials with the flexibility of ABMs to allow simulation of transmission and spillover, causal inference under interference becomes more feasible. The target trial framework is designed to improve causal inference from observational studies and help researchers avoid common biases, such as immortal time bias. This framework requires researchers to be explicit about the target population for inference; the interventions, causal question, and estimand of interest; and the time frame for intervention and effect estimation. ABMs and other individual-level simulation models can benefit from the target trial framework, especially the clarification of the causal question and estimand. By explicitly designing ABMs to emulate cluster-randomized trials, ring vaccination trials, or 2-staged randomized trials in populations with network features, the interpretation of the results of simulation models as causal effects is clarified. Our group demonstrated the feasibility and usefulness of this method in a recent publication estimating the intracluster, disseminated, and composite effects of PrEP use among men who have sex with men on HIV infection (11), and we encourage other researchers to adopt this approach to clarifying and improving the interpretability of their ABMs when the goal is estimation of a causal effect under settings of interference.