Abstract
We use simple examples to show how the bias and standard error of an estimator depend in part on the type of estimator chosen from among parametric, nonparametric, and semiparametric candidates. We estimated the cumulative distribution function in the presence of missing data with and without an auxiliary variable. Simulation results mirrored theoretical expectations about the bias and precision of candidate estimators. Specifically, parametric maximum likelihood estimators performed best but must be “omnisciently” correctly specified. An augmented inverse probability–weighted (IPW) semiparametric estimator performed best among candidate estimators that were not omnisciently correct. In one setting, the augmented IPW estimator reduced the standard error by nearly 30%, compared with a standard Horvitz-Thompson IPW estimator; such a standard error reduction is equivalent to doubling the sample size. These results highlight the gains and losses that can be incurred when model assumptions are made in any analysis.
Keywords: bias, estimators, nonparametric estimators, parametric estimators, precision, semiparametric estimators
Abbreviations
- IPW
inverse probability weighted
- MLE
maximum likelihood estimator
- NPF
nonparametric full data
- SPA
semiparametric augmented inverse probability weighted
- SPF
semiparametric full data
- WF
Weibull full data
- WG
Weibull g-computation
Accuracy is a combination of validity (i.e., lack of bias) and precision (i.e., small standard error) (1, pp. 128, 231). Here accuracy tradeoffs are illustrated between parametric maximum likelihood, nonparametric, and semiparametric estimators. A simple yet nontrivial example is used to show how the bias and standard error of an estimator depend on the type of estimator chosen.
Before discussing types of estimators, the target parameter should be carefully defined. All information about some outcome of interest, say  , is captured by the risk function or cumulative distribution function. Therefore, our parameter of interest is the risk function of
, is captured by the risk function or cumulative distribution function. Therefore, our parameter of interest is the risk function of 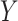 , defined as
, defined as  (2), where the probability
(2), where the probability 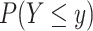 is defined as
is defined as 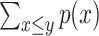 for discrete
for discrete 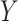 with mass function
with mass function 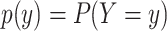 , or as
, or as  for continuous
for continuous 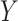 with density function
with density function 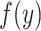 . Many common parameters can be calculated directly from the risk function (e.g., mean, median, or other percentiles). To highlight differences between types of estimators, we will study the (all too common) case where there is missing data for the outcome of interest.
. Many common parameters can be calculated directly from the risk function (e.g., mean, median, or other percentiles). To highlight differences between types of estimators, we will study the (all too common) case where there is missing data for the outcome of interest.
To fix ideas, say we are given 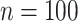 numbers from a positively distributed outcome of interest
numbers from a positively distributed outcome of interest 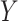 (e.g., biomarker levels, lifetimes). Assume the sample units were independently and randomly drawn from an infinite population.
(e.g., biomarker levels, lifetimes). Assume the sample units were independently and randomly drawn from an infinite population.
Estimators can be classified in many ways. One useful classification entails whether the estimators arise from parametric, nonparametric, or semiparametric models. Parametric models have a finite number of parameters. For example, without covariates, an exponential model for a distribution function has 1 (rate) parameter. On the other hand, nonparametric models (for continuously distributed variables) have an infinite number of parameters. For example, assuming a nonparametric model, we can estimate the risk 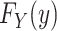 using the Kaplan-Meier estimator (3). For semiparametric models, the parameter space is split into a piece that is finite and a piece that is infinite (4). As a canonical example, the Cox model (5) has a linear predictor, which has a finite number of parameters, and a reference hazard function, which is infinite dimensional.
using the Kaplan-Meier estimator (3). For semiparametric models, the parameter space is split into a piece that is finite and a piece that is infinite (4). As a canonical example, the Cox model (5) has a linear predictor, which has a finite number of parameters, and a reference hazard function, which is infinite dimensional.
Given an observed random sample of size  , at one extreme we make no assumption about the shape of the distribution
, at one extreme we make no assumption about the shape of the distribution 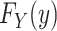 and use a nonparametric maximum likelihood estimator (MLE) (i.e.,
and use a nonparametric maximum likelihood estimator (MLE) (i.e., 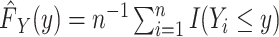 ). This nonparametric MLE places probability mass
). This nonparametric MLE places probability mass  on each of the
on each of the 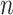 observed values of
observed values of 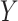 . Using the weak law of large numbers (6, p. 232), this nonparametric MLE is a pointwise asymptotically consistent estimator for any value
. Using the weak law of large numbers (6, p. 232), this nonparametric MLE is a pointwise asymptotically consistent estimator for any value 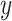 of the distribution, regardless of the shape of the function in the population. But because this nonparametric MLE is unconstrained, it is not optimally precise if the data are generated from a distribution in a particular finite-dimension parametric model. That is, estimators that make constraints based on a correct parametric form, or otherwise leverage auxiliary information, can be more precise than the unconstrained nonparametric MLE.
of the distribution, regardless of the shape of the function in the population. But because this nonparametric MLE is unconstrained, it is not optimally precise if the data are generated from a distribution in a particular finite-dimension parametric model. That is, estimators that make constraints based on a correct parametric form, or otherwise leverage auxiliary information, can be more precise than the unconstrained nonparametric MLE.
In the absence of censored data, the above nonparametric MLE is equivalent to the Kaplan-Meier estimator. But the Kaplan-Meier estimator extends the above nonparametric MLE to allow for independent right censoring of the data Y (as the Turnbull (7) and Aalen-Johansen (8) estimators extend the above nonparametric MLE to allow for arbitrary censoring/truncation and estimation of subdistribution functions for competing events, respectively).
At another extreme, assume the distribution is exponential, formally 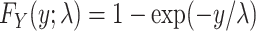 , where
, where 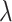 is the mean of
is the mean of 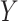 . We often estimate
. We often estimate 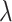 by the MLE, say
by the MLE, say 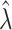 , and then estimate the target (or interest) parameter with
, and then estimate the target (or interest) parameter with 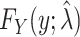 . This MLE is a pointwise asymptotically consistent estimator of
. This MLE is a pointwise asymptotically consistent estimator of 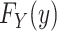 , if
, if  is a member of the family of exponential distributions indexed by
is a member of the family of exponential distributions indexed by 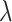 . If the population distribution function
. If the population distribution function 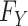 is a member of the exponential distribution, then this MLE attains the Cramér-Rao efficiency bound (6, p. 335) and is therefore maximally precise. To be maximally precise means that the estimator uses all the information relevant to the parameter given by the combination of data and model constraints. The exponential assumption can be relaxed by instead supposing
is a member of the exponential distribution, then this MLE attains the Cramér-Rao efficiency bound (6, p. 335) and is therefore maximally precise. To be maximally precise means that the estimator uses all the information relevant to the parameter given by the combination of data and model constraints. The exponential assumption can be relaxed by instead supposing 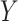 is a mixture of exponentials. In particular, assume the conditional distribution of
is a mixture of exponentials. In particular, assume the conditional distribution of  given covariate
given covariate  is exponential with mean
is exponential with mean  . Auxiliary variables
. Auxiliary variables  are covariates that can help to more accurately estimate the target parameter
are covariates that can help to more accurately estimate the target parameter  when
when 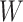 is not independent of
is not independent of  (9). In scenarios with one or more auxiliary variables, the parameter of interest
(9). In scenarios with one or more auxiliary variables, the parameter of interest  might be estimated by first estimating the conditional distribution of
might be estimated by first estimating the conditional distribution of 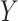 given
given  and the marginal distribution of
and the marginal distribution of 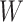 , and then using the relation
, and then using the relation 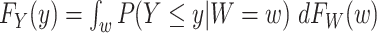 where
where 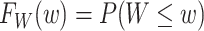 . If
. If 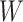 is discrete, this relation can be expressed simply as
is discrete, this relation can be expressed simply as 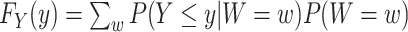 .
.
Alternatively, more flexible parametric MLEs can be entertained, such as the 2-parameter Weibull model, 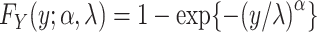 , which can again be estimated using the MLE
, which can again be estimated using the MLE 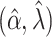 . Or even more flexible parametric models with 3 or more parameters can be considered (10, 11). In turn, these models can be made more flexible yet by adding covariate effects, as above. In at least an informal sense, the limit of this process of relaxing the constraints on parametric models leads toward the infinite-dimensional nonparametric case.
. Or even more flexible parametric models with 3 or more parameters can be considered (10, 11). In turn, these models can be made more flexible yet by adding covariate effects, as above. In at least an informal sense, the limit of this process of relaxing the constraints on parametric models leads toward the infinite-dimensional nonparametric case.
Semiparametric estimators provide a third, or middle, way. Say that we assume a semiparametric Cox proportional hazards model (5) for the association between  and
and  , formally
, formally 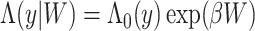 where
where 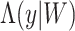 is the cumulative hazard function of
is the cumulative hazard function of 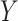 at y given
at y given 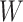 , and
, and 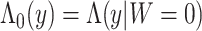 is the cumulative reference hazard function. The set of finite-dimensional parameters
is the cumulative reference hazard function. The set of finite-dimensional parameters 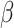 are estimated by the maximum partial likelihood estimator
are estimated by the maximum partial likelihood estimator 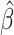 , and, assuming
, and, assuming 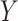 continuous, the infinite-dimensional parameter
continuous, the infinite-dimensional parameter 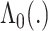 can be estimated using the Breslow estimator
can be estimated using the Breslow estimator 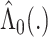 (12). Then a semiparametric estimator of the risk function
(12). Then a semiparametric estimator of the risk function 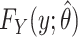 is
is
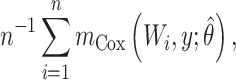 |
(1) |
where 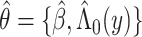 and
and 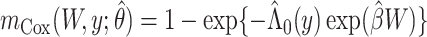 . This estimator, with or without right censoring, provides an estimate of
. This estimator, with or without right censoring, provides an estimate of  by averaging the covariate-conditional estimates over the sample and constrains the
by averaging the covariate-conditional estimates over the sample and constrains the  relationship to follow a proportional hazards model.
relationship to follow a proportional hazards model.
We say that an estimator is valid if it is asymptotically consistent—that is, the estimator converges in probability to the true data generating value as the sample size 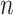 tends toward infinity. For any of the above estimators to be valid in this sense, the population function
tends toward infinity. For any of the above estimators to be valid in this sense, the population function 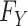 must be a possible value of the limit of the estimator, for all values
must be a possible value of the limit of the estimator, for all values  , as
, as  tends toward infinity. This is always the case for the nonparametric estimators we consider because these estimators remain consistent with no constraints on the shape of the risk function. On the other hand, when the true function
tends toward infinity. This is always the case for the nonparametric estimators we consider because these estimators remain consistent with no constraints on the shape of the risk function. On the other hand, when the true function  does not satisfy the model assumptions of the parametric or semiparametric estimator employed, the best possible member of the family is the member that most closely resembles the actual
does not satisfy the model assumptions of the parametric or semiparametric estimator employed, the best possible member of the family is the member that most closely resembles the actual 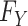 , which is sometimes called the “least false” parameter (13). Choosing to estimate a least-false parameter is like allowing a tolerance for bias. In certain settings, bias might be tolerable in exchange for some benefit, such as precision, speed, or ease.
, which is sometimes called the “least false” parameter (13). Choosing to estimate a least-false parameter is like allowing a tolerance for bias. In certain settings, bias might be tolerable in exchange for some benefit, such as precision, speed, or ease.
Barring extra-data information, for the above estimators to be optimally efficient, they must extract all the information relevant to the parameter available in the data, which consists of  , and
, and 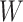 in scenarios with an auxiliary covariate. The parametric MLEs, when constraints are correct, automatically maximally extract information from
in scenarios with an auxiliary covariate. The parametric MLEs, when constraints are correct, automatically maximally extract information from 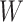 , and the nonparametric estimators we considered ignore the covariate and so extract no information about
, and the nonparametric estimators we considered ignore the covariate and so extract no information about  present in
present in 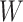 . The semiparametric estimators, even when optimal, achieve the Hájek-Le Cam semiparametric efficiency bound, which is no smaller (and typically larger) than the Cramér-Rao bound for the parametric maximum likelihood model under consideration (4, 14–16). Next, we describe an experiment, simulating data like those described above, to demonstrate the accuracy (i.e., bias and variance) tradeoffs among a set of estimators.
. The semiparametric estimators, even when optimal, achieve the Hájek-Le Cam semiparametric efficiency bound, which is no smaller (and typically larger) than the Cramér-Rao bound for the parametric maximum likelihood model under consideration (4, 14–16). Next, we describe an experiment, simulating data like those described above, to demonstrate the accuracy (i.e., bias and variance) tradeoffs among a set of estimators.
METHODS
We generate 5,000 samples of  and 200 units, indexed by
and 200 units, indexed by 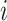 , where
, where 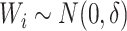 , that is,
, that is,  is mean zero Gaussian with standard deviation
is mean zero Gaussian with standard deviation 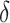 , and
, and  , where
, where 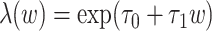 is the scale parameter and
is the scale parameter and 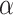 is the Weibull shape parameter, that is,
is the Weibull shape parameter, that is, 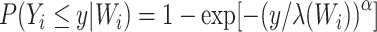 . When
. When  the Weibull coincides with an exponential distribution, which corresponds to a constant hazard. When
the Weibull coincides with an exponential distribution, which corresponds to a constant hazard. When 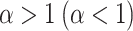 there is an increasing (decreasing) hazard of
there is an increasing (decreasing) hazard of 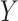 . For all scenarios we set
. For all scenarios we set  and
and 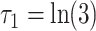 , which corresponds to a strong association between
, which corresponds to a strong association between  and
and 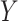 (i.e., a unit increase in
(i.e., a unit increase in 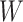 is associated with a 3-fold increase in the hazard of
is associated with a 3-fold increase in the hazard of 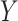 when
when 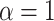 ). Below, for convenience, we focus on the single parameter, the value for the marginal distribution function of
). Below, for convenience, we focus on the single parameter, the value for the marginal distribution function of  at
at 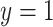 , or
, or  . The pattern of results should hold for any value
. The pattern of results should hold for any value 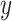 not in the extremity of the distribution of
not in the extremity of the distribution of  .
.
For each scenario, approximately half the 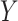 values are missing. To generate missing data for
values are missing. To generate missing data for 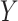 , we draw an indicator of being observed
, we draw an indicator of being observed  , distributed as Bernoulli with expectation
, distributed as Bernoulli with expectation 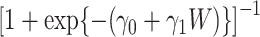 , where
, where 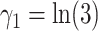 or 0, and
or 0, and  set such that
set such that 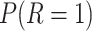 is approximately 1/2.
is approximately 1/2.
We consider 6 scenarios from a factorial experiment varying 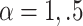 , and the combination of
, and the combination of 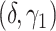 as (0,0), (1,0), and
as (0,0), (1,0), and  . These parameter choices correspond to the following 6 scenarios: 1) exponential with no covariate (i.e., the covariate
. These parameter choices correspond to the following 6 scenarios: 1) exponential with no covariate (i.e., the covariate 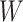 is a constant 0); 2) exponential with a standard normal covariate that causes the outcome but not missingness; 3) exponential with a standard normal covariate that causes the outcome and missingness; 4) Weibull with no covariate; 5) Weibull with a standard normal covariate that causes the outcome but not missingness; and 6) Weibull with a standard normal covariate that causes the outcome and missingness.
is a constant 0); 2) exponential with a standard normal covariate that causes the outcome but not missingness; 3) exponential with a standard normal covariate that causes the outcome and missingness; 4) Weibull with no covariate; 5) Weibull with a standard normal covariate that causes the outcome but not missingness; and 6) Weibull with a standard normal covariate that causes the outcome and missingness.
For each of the 6 scenarios, we fit 14 estimators, as detailed in Table 1. First, we fit 2 nonparametric estimators, which both ignore the auxiliary covariate. The first nonparametric estimator was fitted to the full data (NPF) and the second was fitted to the observed data (NPO), that is, where  . The NPF estimator ought to be approximately unbiased in all scenarios, and the NPO estimator ought to be likewise unbiased in scenarios 1, 2, 4, and 5 where the missingness is completely at random. The NPF and NPO estimators ought to be less precise than the correctly specified parametric models. Throughout, estimators using the full data are provided for reference, as well as to make comparisons between estimators in the absence of missing data.
. The NPF estimator ought to be approximately unbiased in all scenarios, and the NPO estimator ought to be likewise unbiased in scenarios 1, 2, 4, and 5 where the missingness is completely at random. The NPF and NPO estimators ought to be less precise than the correctly specified parametric models. Throughout, estimators using the full data are provided for reference, as well as to make comparisons between estimators in the absence of missing data.
Table 1.
Nonparametric, Semiparametric, and Parametric Estimators
| Estimator, With Abbreviation | Definition a |
|---|---|
| Nonparametric | |
| NPF: full data |
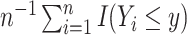
|
| NPO: observed data |

|
| Semiparametric b | |
| SPF: semiparametric full data |
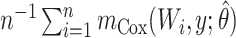
|
| SPO: observed data |
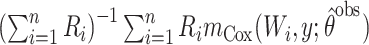
|
| SPI: Horvitz-Thompson IPW |

|
| SPH: Hájek IPW |
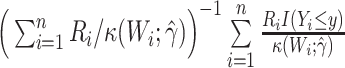
|
| SPG: g-computation |
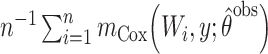
|
| SPA: augmented IP |
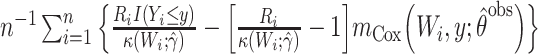
|
| Weibull c | |
| WF: full data |
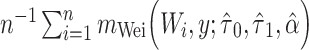
|
| WO: observed data |
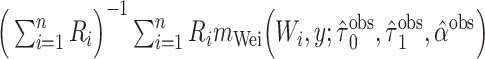
|
| WG: g-computation |

|
| Exponential d | |
| EF: exponential full data |
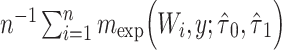
|
| EO: observed data |

|
| EG: g-computation |
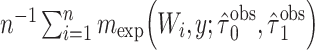
|
Abbreviations: EF, exponential full data; EG, exponential g-computation; EO, exponential observed data; IPW, inverse probability weighted; MLE, maximum likelihood estimator; NPF, nonparametric full data; NPO, nonparametric observed data; SPA, semiparametric augmented inverse probability weighted; SPF, semiparametric full data; SPG, semiparametric g-computation; SPH, semiparametric Hájek inverse probability weighted; SPI, semiparametric Horvitz-Thompson inverse probability weighted; SPO, semiparametric observed data; WF, Weibull full data; WG, Weibull g-computation; WO, Weibull observed data.
a  is the outcome,
is the outcome,  indicates
indicates  is observed, and
is observed, and  is an auxiliary covariate.
is an auxiliary covariate.
b 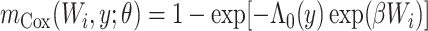 , where
, where 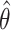 and
and 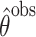 are the MLEs of
are the MLEs of 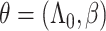 in the full and observed (i.e.,
in the full and observed (i.e.,  ) data, respectively.
) data, respectively.
c  , where
, where 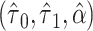 and
and 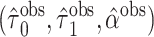 are the MLEs of
are the MLEs of  in the full and observed (i.e.,
in the full and observed (i.e.,  ) data, respectively.
) data, respectively.
d  , where
, where 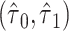 and
and 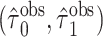 are the MLEs of
are the MLEs of  in the full and observed (i.e.,
in the full and observed (i.e.,  ) data, respectively.
) data, respectively.
Second, we fit 6 semiparametric estimators. The first semiparametric estimator, given as equation 1 above, used the full data (SPF). The remaining 5 semiparametric estimators used the observed data on  when
when  , with or without using observed data on the auxiliary variable
, with or without using observed data on the auxiliary variable 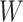 when
when  . The second semiparametric estimator was a simple complete-case estimator fitted on data where
. The second semiparametric estimator was a simple complete-case estimator fitted on data where  (semiparametric observed; SPO) and ignores
(semiparametric observed; SPO) and ignores  when
when  , and so ought to be biased in scenarios 3 and 6. The third, fourth, and fifth semiparametric estimators were Horvitz-Thompson (17) inverse probability weighted (IPW; SPI), Hájek (18) IPW (SPH), and g-computation (SPG) (19) estimators, which use
, and so ought to be biased in scenarios 3 and 6. The third, fourth, and fifth semiparametric estimators were Horvitz-Thompson (17) inverse probability weighted (IPW; SPI), Hájek (18) IPW (SPH), and g-computation (SPG) (19) estimators, which use  when
when  . This Hájek estimator is sometimes referred to as a modified ((20), see technical points 12.1 and 12.2) or “stabilized” IPW estimator, but this stabilization is distinct from that described by Robins et al. (21). These semiparametric estimators ought to be approximately unbiased in every scenario, with the SPG estimator more precise than SPI and SPH. The sixth and last semiparametric estimator was an augmented inverse probability–weighted estimator (SPA), which also ought to be approximately unbiased in all scenarios with precision intermediate between the SPI and SPG (22–24). For estimators using an inverse probability weight (i.e., SPI, SPH, SPA), the model for missingness was a correctly specified logistic regression model fitted by maximum likelihood. For the SPA estimator, we combined information from the semiparametric estimator given above (equation 1) with a finite-dimension parametric logistic regression model for the probability of being observed given
. This Hájek estimator is sometimes referred to as a modified ((20), see technical points 12.1 and 12.2) or “stabilized” IPW estimator, but this stabilization is distinct from that described by Robins et al. (21). These semiparametric estimators ought to be approximately unbiased in every scenario, with the SPG estimator more precise than SPI and SPH. The sixth and last semiparametric estimator was an augmented inverse probability–weighted estimator (SPA), which also ought to be approximately unbiased in all scenarios with precision intermediate between the SPI and SPG (22–24). For estimators using an inverse probability weight (i.e., SPI, SPH, SPA), the model for missingness was a correctly specified logistic regression model fitted by maximum likelihood. For the SPA estimator, we combined information from the semiparametric estimator given above (equation 1) with a finite-dimension parametric logistic regression model for the probability of being observed given 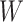 (23). Specifically, the form of the SPA estimator is:
(23). Specifically, the form of the SPA estimator is:
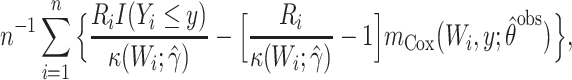 |
(2) |
where  is the maximum partial likelihood estimator of
is the maximum partial likelihood estimator of  and the Breslow estimator of the cumulative baseline hazard function based only on the observed data where
and the Breslow estimator of the cumulative baseline hazard function based only on the observed data where  ,
,  denotes
denotes 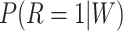 under the assumed logistic regression model with finite-dimensional parameter
under the assumed logistic regression model with finite-dimensional parameter 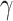 , and
, and 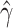 is the MLE of
is the MLE of 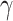 . Notably, this SPA estimator is double robust and therefore consistent if either the model for the outcome
. Notably, this SPA estimator is double robust and therefore consistent if either the model for the outcome 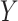 or the missing data mechanism
or the missing data mechanism 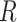 is correct. All 6 semiparametric estimators should be less precise than the correct parametric MLE, and more precise than the nonparametric estimator when an informative auxiliary variable is present.
is correct. All 6 semiparametric estimators should be less precise than the correct parametric MLE, and more precise than the nonparametric estimator when an informative auxiliary variable is present.
Third, we fit 3 parametric Weibull estimators. Each estimator entailed fitting a correctly specified Weibull model for 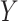 given
given  via maximum likelihood and then marginalizing over
via maximum likelihood and then marginalizing over  to obtain an estimate of the population-average risk. The first Weibull estimator was fitted to the full data (WF) and ought to be approximately unbiased in all scenarios. The second Weibull estimator was fitted to the observed data (WO), where
to obtain an estimate of the population-average risk. The first Weibull estimator was fitted to the full data (WF) and ought to be approximately unbiased in all scenarios. The second Weibull estimator was fitted to the observed data (WO), where  , and ought to be approximately unbiased in scenarios 1, 2, 4, and 5. The third Weibull estimator is a parametric g-computation estimator (WG). The WG estimator ought to be approximately unbiased for all 6 scenarios, most precise in scenarios 4–6, but somewhat inefficient in scenarios 1–3 (compared with the correct exponential submodel estimator).
, and ought to be approximately unbiased in scenarios 1, 2, 4, and 5. The third Weibull estimator is a parametric g-computation estimator (WG). The WG estimator ought to be approximately unbiased for all 6 scenarios, most precise in scenarios 4–6, but somewhat inefficient in scenarios 1–3 (compared with the correct exponential submodel estimator).
Fourth, we fit 3 parametric exponential estimators, which are akin to the Weibull estimators above, with the sole additional constraint that 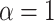 . The first exponential estimator was fitted to the full data (EF), and ought to be approximately unbiased in scenarios 1–3 with maximal precision. The second exponential estimator was fitted to the observed data (EO) and ought to be approximately unbiased in scenarios 1 and 2. The third exponential estimator (EG) is a parametric g-computation estimator. The EG estimator ought to be approximately unbiased for scenarios 1–3.
. The first exponential estimator was fitted to the full data (EF), and ought to be approximately unbiased in scenarios 1–3 with maximal precision. The second exponential estimator was fitted to the observed data (EO) and ought to be approximately unbiased in scenarios 1 and 2. The third exponential estimator (EG) is a parametric g-computation estimator. The EG estimator ought to be approximately unbiased for scenarios 1–3.
We also explored the impact of an unmeasured common cause of the outcome and missingness. Specifically, we added a standard normal covariate with a log(3) coefficient to the linear component of both data-generating models. Therefore, 12 of the 14 estimators ought to be biased due to misspecification, with only the NPF and semiparametric full-data estimators expected to be approximately unbiased.
In addition to bias in the estimate of the risk function, we quantify precision by the standard errors of each estimator, which are approximated by the standard deviation of the 5,000 simulation estimates. Experiments were performed separately using SAS (SAS Institute, Inc., Cary, North Carolina) and R (R Foundation for Statistical Computing, Vienna, Austria).
RESULTS
Figures 1 and 2 group the 14 estimators in 3 panels each; Figure 1 presents results from scenarios 1–3, and Figure 2 presents results from scenarios 4–6. Each scenario highlights specific aspects of semiparametric theory. For example, for scenario 1 (Figure 1A), the outcome data are exponential and there is no covariate. In this scenario, as expected, all estimators are unbiased with precision improving as the estimators become more restrictive. For scenario 2 (Figure 1B), the outcome data are exponential with a standard normal covariate which does not predict missingness, and the results are similar to scenario 1. For scenario 3 (Figure 1C), the outcome data are exponential with a standard normal covariate, which causes the outcome and missingness, and the results illustrate how the observed data estimators are biased due to incorrectly assuming missingness is completely at random.
Figure 1.

Bias and precision of the estimated probability 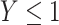 in 5,000 Monte Carlo simulation trials, each of sample size 100. A) Scenario 1: exponential with no covariate; B) scenario 2: exponential with a covariate that causes
in 5,000 Monte Carlo simulation trials, each of sample size 100. A) Scenario 1: exponential with no covariate; B) scenario 2: exponential with a covariate that causes 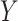 ; C) scenario 3: exponential with a covariate that causes
; C) scenario 3: exponential with a covariate that causes  and missingness. EF, exponential full data; EG, exponential g-computation; EO, exponential observed data; NPF, nonparametric full data; NPO, nonparametric observed data; SPA, semiparametric augmented inverse probability weighted; SPF, semiparametric full data; SPG, semiparametric g-computation; SPH, semiparametric Hájek inverse probability weighted; SPI, semiparametric Horvitz-Thompson inverse probability weighted; SPO, semiparametric observed data; WF, Weibull full data; WG, Weibull g-computation; WO, Weibull observed data.
and missingness. EF, exponential full data; EG, exponential g-computation; EO, exponential observed data; NPF, nonparametric full data; NPO, nonparametric observed data; SPA, semiparametric augmented inverse probability weighted; SPF, semiparametric full data; SPG, semiparametric g-computation; SPH, semiparametric Hájek inverse probability weighted; SPI, semiparametric Horvitz-Thompson inverse probability weighted; SPO, semiparametric observed data; WF, Weibull full data; WG, Weibull g-computation; WO, Weibull observed data.
Figure 2.

Bias and precision of the estimated probability 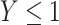 in 5,000 Monte Carlo simulation trials, each of sample size 100. A) Scenario 4: Weibull with no covariate; B) scenario 5: Weibull with a covariate that causes
in 5,000 Monte Carlo simulation trials, each of sample size 100. A) Scenario 4: Weibull with no covariate; B) scenario 5: Weibull with a covariate that causes 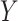 ; C) scenario 6: Weibull with a covariate that causes
; C) scenario 6: Weibull with a covariate that causes 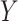 and missingness. EF, exponential full data; EG, exponential g-computation; EO, exponential observed data; NPF, nonparametric full data; NPO, nonparametric observed data; SPA, semiparametric augmented inverse probability weighted; SPF, semiparametric full data; SPG, semiparametric g-computation; SPH, semiparametric Hájek inverse probability weighted; SPI, semiparametric Horvitz-Thompson inverse probability weighted; SPO, semiparametric observed data; WF, Weibull full data; WG, Weibull g-computation; WO, Weibull observed data.
and missingness. EF, exponential full data; EG, exponential g-computation; EO, exponential observed data; NPF, nonparametric full data; NPO, nonparametric observed data; SPA, semiparametric augmented inverse probability weighted; SPF, semiparametric full data; SPG, semiparametric g-computation; SPH, semiparametric Hájek inverse probability weighted; SPI, semiparametric Horvitz-Thompson inverse probability weighted; SPO, semiparametric observed data; WF, Weibull full data; WG, Weibull g-computation; WO, Weibull observed data.
For scenario 4 (Figure 2A), the outcome data are Weibull with no covariate, and results mimic the results for scenario 1, with the exception that the parametric exponential results are biased due to the inappropriate restriction. For scenario 5 (Figure 2B), the outcome data are Weibull with a standard normal covariate that causes only the outcome, and results again mimic the results for scenario 2, apart from the exponential models being biased. Finally, for scenario 6 (Figure 2C), outcome data are Weibull with a standard normal covariate that causes the outcome and missingness, and results illustrate a combination of features seen in the prior scenarios. In scenario 6, all observed data estimators and the parametric exponential estimators are biased. The WG and SPA estimators were unbiased and most precise (with WG more precise than SPA).
Table 2 presents numerical summaries for scenarios 1 through 6. Many patterns are illustrated that are expected based on parametric, nonparametric, and semiparametric theory. For example, when the data are generated as exponential but a (more flexible) Weibull model estimator is used, there is a slight loss of precision due to the estimation of an unnecessary (Weibull shape) parameter. Contrariwise, when the data are generated as Weibull but a more restrictive exponential model estimator is used, the estimator is biased for the parameter of interest. Across estimators, there is precision gained when estimators leverage the presence of the informative auxiliary covariate, because more information from the data is used. In the absence of missing data (i.e., looking only at the 4 estimators based on full data), there is no discernable advantage to the semiparametric estimator. The augmented IPW estimator (which is semiparametric efficient (22)) is shown to improve on the simpler IPW estimators (which are not semiparametric efficient), specifically, compared with the Horvitz-Thompson IPW, the augmented IPW standard error is reduced by 28% in scenario C (1 − 0.062/0.086) and by 22% in scenario F (1 − 0.072/0.092). In the former case, this near 30% reduction in the standard error equates to about a doubling of sample size. The Hájek IPW estimator recovered a sizable portion of the precision loss of the Horvitz-Thompson IPW estimator compared with the augmented IPW estimator. The WG estimator was slightly more precise than the SPA estimator. This is expected because the parametric WG estimator encodes more restrictions than the SPA estimator (i.e., the outcome model is Weibull rather than Cox). These restrictions also make the WG estimator less robust than the SPA estimator, as demonstrated by analogy with the bias of the parametric g-computation estimator (EG) in scenarios 4–6.
Table 2.
Bias and Precision of Estimated Probability  in 5,000 Monte Carlo Simulation Trials With Sample Size 100, Scenarios 1 Through 6, Half Data Missing
in 5,000 Monte Carlo Simulation Trials With Sample Size 100, Scenarios 1 Through 6, Half Data Missing
| Estimator | 1: Exponential With No Covariate | 2: Exponential With Covariate | 3: Exponential With Biasing Covariate | 4: Weibull With No Covariate | 5: Weibull With Covariate | 6: Weibull With Biasing Covariate | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias a | SE | Bias a | SE | Bias a | SE | Bias a | SE | Bias a | SE | Bias a | SE | |
| Nonparametric | ||||||||||||
| Full data | −0.003 | 0.048 | −0.003 | 0.049 | −0.003 | 0.049 | −0.003 | 0.048 | −0.003 | 0.048 | −0.003 | 0.048 |
| Observed data | −0.007 | 0.068 | −0.006 | 0.069 | −0.130 | 0.071 | −0.007 | 0.068 | −0.007 | 0.068 | −0.084 | 0.070 |
| Semiparametric | ||||||||||||
| Full data | −0.003 | 0.048 | −0.003 | 0.048 | −0.003 | 0.048 | −0.003 | 0.048 | −0.003 | 0.047 | −0.003 | 0.048 |
| Observed data | −0.007 | 0.068 | −0.006 | 0.067 | −0.130 | 0.070 | −0.007 | 0.068 | −0.007 | 0.068 | −0.085 | 0.070 |
| HT IPW | −0.001 | 0.068 | 0.000 | 0.064 | −0.003 | 0.086 | −0.001 | 0.069 | −0.001 | 0.067 | −0.001 | 0.092 |
| Hájek IPW | −0.001 | 0.068 | 0.000 | 0.064 | −0.003 | 0.066 | −0.001 | 0.069 | −0.001 | 0.067 | −0.002 | 0.074 |
| G-computation | −0.007 | 0.068 | −0.006 | 0.062 | −0.008 | 0.061 | −0.007 | 0.068 | −0.007 | 0.066 | −0.008 | 0.068 |
| Augmented IPW | −0.001 | 0.068 | 0.000 | 0.063 | 0.000 | 0.062 | −0.001 | 0.069 | −0.001 | 0.067 | 0.000 | 0.072 |
| Weibull | ||||||||||||
| Full data | 0.000 | 0.039 | 0.001 | 0.040 | 0.000 | 0.040 | 0.001 | 0.039 | 0.000 | 0.039 | 0.001 | 0.039 |
| Observed data | 0.000 | 0.056 | 0.001 | 0.057 | −0.126 | 0.059 | 0.001 | 0.056 | 0.001 | 0.056 | −0.078 | 0.058 |
| G-computation | 0.000 | 0.056 | 0.001 | 0.049 | −0.002 | 0.051 | 0.001 | 0.056 | 0.001 | 0.054 | −0.001 | 0.057 |
| Exponential | ||||||||||||
| Full data | 0.002 | 0.036 | 0.003 | 0.038 | 0.002 | 0.038 | −0.228 | 0.067 | −0.175 | 0.060 | −0.174 | 0.062 |
| Observed data | 0.003 | 0.052 | 0.005 | 0.053 | −0.119 | 0.053 | −0.218 | 0.095 | −0.165 | 0.086 | −0.283 | 0.079 |
| G-computation | 0.003 | 0.052 | 0.005 | 0.045 | 0.003 | 0.047 | −0.218 | 0.095 | −0.165 | 0.082 | −0.169 | 0.093 |
Abbreviations: HT, Horvitz-Thompson; IPW, inverse probability weighted; SE, empirical standard error.
a Monte Carlo simulation error for bias < 0.002.
Analogous figures for the scenario with  are provided in the Web material (Web Figures 1 and 2, available at https://doi.org/10.1093/aje/kwab024). The pattern of results is similar in the scenario with
are provided in the Web material (Web Figures 1 and 2, available at https://doi.org/10.1093/aje/kwab024). The pattern of results is similar in the scenario with 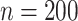 shown here. Also, Figures and tabular results for the scenario with misspecified models (due to an unmeasured common cause of the outcome and missingness) are provided in the Web material (Web Figures 3 and 4, Web Table 1). As expected, only the NPF and semiparametric full-data estimators were unbiased in the misspecified scenario, and the Weibull full-data estimator performed best among misspecified approaches.
shown here. Also, Figures and tabular results for the scenario with misspecified models (due to an unmeasured common cause of the outcome and missingness) are provided in the Web material (Web Figures 3 and 4, Web Table 1). As expected, only the NPF and semiparametric full-data estimators were unbiased in the misspecified scenario, and the Weibull full-data estimator performed best among misspecified approaches.
DISCUSSION
The moral of this story is an old one: It is best to be right. To be most accurate, be an “omniscient” oracle and pick the correct parametric model or rely on chance to accidentally specify the model correctly. Failing omniscience or luck, and at a small loss of precision, have enough foresight to choose a flexible parametric model that incorporates the correct parametric model as a special case. Failing omniscience, luck, and such seemingly impossible foresight, the semiparametric estimator performs best in the limited scenarios explored here. Of course, the parametric component of the semiparametric model needs to be correct for the semiparametric estimator to perform well. This point is reinforced with the results of the misspecified scenario. In our primary setting, the semiparametric model assumed proportional hazards of the outcome for unit changes in the auxiliary variable. Finally, all our estimators assumed data were independent, and there was no measurement error.
In principle, we could specify a nonparametric model for the distribution of 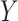 condition on
condition on  and allow our nonparametric estimators to depend on some data-adaptive function of the covariate
and allow our nonparametric estimators to depend on some data-adaptive function of the covariate  (e.g., a data-adaptive restricted quadratic spline), but if
(e.g., a data-adaptive restricted quadratic spline), but if  were more than a single variable, restrictions would be needed to obtain well-functioning data-adaptive nonparametric estimators, and while this is an intriguing frontier, it is beyond the scope of the present work.
were more than a single variable, restrictions would be needed to obtain well-functioning data-adaptive nonparametric estimators, and while this is an intriguing frontier, it is beyond the scope of the present work.
Of course, our results are only guaranteed to hold in scenarios like those explored. This lack of generality is a central limitation of simulations, like those presented here. The scenarios explored were chosen to clearly illustrate theoretical claims about semiparametric statistical theory that might not be within the typical training of epidemiologists. Moreover, our results pertain to the set of estimators explored. We did not explore confidence interval coverage probability or length, which are helpful metrics for epidemiologic practice. Here we concentrated on the estimators themselves, rather than estimates of variability, which are complicated in their own right and are therefore the topic of future work.
In conclusion, we present these experimental results to help epidemiologists and other health data scientists better understand justifications for the use of estimators based on modern semiparametric statistical theory.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, UNC Gillings School of Global Public Health, University of North Carolina, Chapel Hill, Chapel Hill, North Carolina, United States (Stephen R. Cole, Jessie K. Edwards); NoviSci, Durham, North Carolina, United States (Alexander Breskin); and Department of Biostatistics, UNC Gillings School of Global Public Health, University of North Carolina, Chapel Hill, Chapel Hill, North Carolina, United States (Michael G. Hudgens).
This work was supported in part by the National Institute of Allergy and Infectious Diseases (grants R01AI157758—S.R.C, J.K.E, M.G.H.; P30AI50410—S.R.C., M.G.H.; and K01AI125087—J.K.E.).
Thanks to Dr. Alexander P. Keil for expert advice.
Conflicts of interest: none declared.
REFERENCES
- 1.Rothman KJ, Greenland S, Lash T. Modern Epidemiology. 3rd ed. New York, NY: Lippincott-Raven; 2008. [Google Scholar]
- 2.Cole SR, Hudgens MG, Brookhart MA, et al. Risk. Am J Epidemiol. 2015;181(4):246–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. JASA. 1958;53:457–481. [Google Scholar]
- 4.Wellner JA. Semiparametric models: progress and problems. Bull Inst Int Stat. 1985;51:1–23. [Google Scholar]
- 5.Cox DR. Regression models and life tables. J R Statist Soc (B). 1972;34(2):187–220. [Google Scholar]
- 6.Casella G, Berger RL. Statistical Inference. 2nd ed. Pacific Grove, CA: Duxbury Press; 2002. [Google Scholar]
- 7.Turnbull BW. The empirical distribution function with arbitrarily grouped, censored and truncated data. J R Stat Soc B. 1976;38:290–295. [Google Scholar]
- 8.Aalen OO, Johansen S. Empirical transition matrix for non-homogeneous Markov chains based on censored observations. Scand J Stat. 1978;5:141–150. [Google Scholar]
- 9.Godambe VP. Estimation in survey sampling: robustness and optimality. J Am Stat Assoc. 1982;77:393–403. [Google Scholar]
- 10.Cox C, Chu H, Schneider MF, et al. Parametric survival analysis and taxonomy of hazard functions for the generalized gamma distribution. Stat Med. 2007;26(23):4352–4374. [DOI] [PubMed] [Google Scholar]
- 11.Cox C. The generalized F distribution: an umbrella for parametric survival analysis. Stat Med. 2008;27(21):4301–4312. [DOI] [PubMed] [Google Scholar]
- 12.Lin DY. On the Breslow estimator. Lifetime Data Anal. 2007;13(4):471–480. [DOI] [PubMed] [Google Scholar]
- 13.Hjort N. On inference in parametric survival data models. Int Stat Rev. 1992;60:355–387. [Google Scholar]
- 14.Newey WK. Semiparametric efficiency bounds. J Appl Economet. 1990;5:99–135. [Google Scholar]
- 15.Stein C. Efficient nonparametric testing and estimation. In: Neyman J, ed. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability. Berkeley. CA: University of California Press; 1956:187–195. [Google Scholar]
- 16.Begun JM, Hall WJ, Huang W, et al. Information and asymptotic efficiency in parametric-nonparametric models. Ann Stat. 1983;11:432–452. [Google Scholar]
- 17.Horvitz DG, Thompson DJ. A generalization of sampling without replacement from a finite universe. JASA. 1952;47:663–685. [Google Scholar]
- 18.Hájek J. Comment on an Essay by D. Basu. In: Godambe VP, Sprott DA, eds. Foundations of Statistical Inference. Toronto, Canada: Holt, Rinehart, and Winston; 1971:236. [Google Scholar]
- 19.Robins JM. A new approach to causal inference in mortality studies with a sustained exposure period: application to control of the healthy worker survivor effect. Math Model. 1986;7:1393–1512. [Google Scholar]
- 20.Hernán MA, Robins JM. Causal Inference: What If? Boca Raton, FL: Chapman & Hall/CRC Press; 2020. [Google Scholar]
- 21.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 22.Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some regressors are not always observed. JASA. 1994;89:846–846. [Google Scholar]
- 23.Tsiatis AA. Semiparametric Theory and Missing Data. New York, NY: Springer; 2006. [Google Scholar]
- 24.Daniel R. Double robustness. In: StatsRef: Statistics Reference Online. New York, NY: John Wiley & Sons, Ltd; 2018. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


