A Comparison of Quantitative R1 and Cortical Thickness in Identifying Age, Lifespan Dynamics, and Disease States of the Human Cortex

Abstract

Brain development and aging are complex processes that unfold in multiple brain regions simultaneously. Recently, models of brain age prediction have aroused great interest, as these models can potentially help to understand neurological diseases and elucidate basic neurobiological mechanisms. We test whether quantitative magnetic resonance imaging can contribute to such age prediction models. Using R1, the longitudinal rate of relaxation, we explore lifespan dynamics in cortical gray matter. We compare R1 with cortical thickness, a well-established biomarker of brain development and aging. Using 160 healthy individuals (6–81 years old), we found that R1 and cortical thickness predicted age similarly, but the regions contributing to the prediction differed. Next, we characterized R1 development and aging dynamics. Compared with anterior regions, in posterior regions we found an earlier R1 peak but a steeper postpeak decline. We replicate these findings: firstly, we tested a subset (N = 10) of the original dataset for whom we had additional scans at a lower resolution; and second, we verified the results on an independent dataset (N = 34). Finally, we compared the age prediction models on a subset of 10 patients with multiple sclerosis. The patients are predicted older than their chronological age using R1 but not with cortical thickness.

Introduction

Across the lifespan, the human brain changes at both microstructural (i.e., cellular composition) and macrostructural (i.e., geometric organization) spatial scales (Peters 2006). Recently, the prediction of age using such brain-related features has garnered great interest in the neuroscience community (Kaufmann et al. 2019). In these studies, researchers try to predict age by modeling the relationship between a biological measurement and the subjects’ chronological age (i.e., time since birth). Here, we define “chronological age” as distinct from “biological age,” which irrespective of birth year, is based on the level of biological maturation at a given time. Different biological sources may influence age prediction differentially (Jylhävä et al. 2017). Brain-based age prediction is motivated by the fact that different neurological diseases can cause deviations in the predicted age. Therefore, to understand both normal aging and diseases that impact the brain, a useful model of brain-based age prediction is needed, especially one that harnesses cutting-edge imaging techniques.

For predicting age in humans in vivo, we can use magnetic resonance imaging (MRI). MRI allows us to look at both brain macrostructure and microstructure. At the macrostructural level, multiple features extracted from MRI scans have been shown to change with age, both in development and aging. For example, cortical thickness follows a constant decay pattern across the lifespan (Salat et al. 2004). The overall brain volume, on the other hand, varies in an inverted-U fashion: Brain volume increases from childhood to adolescence, then remains constant for about three decades, and finally decreases at later ages (Courchesne et al. 2000).

Brain development and aging also have been linked to changes at the microstructural level. Development processes include increases in axonal packing, myelination, and synaptic pruning (Paolicelli et al. 2011; Lebel and Deoni 2018), while aging has been related to changes in synaptic structures (decreased synaptic density and synaptic terminals), reduced neurogenesis and synaptic plasticity, increase of astrocytes and oligodendrocytes, and a reduction of nerve growth factor concentration (Price and Morris 1999; Peters 2002; LaPoint et al. 2017). Changes in myelin over the lifespan are another well-documented phenomenon (Peters et al. 1996; Peters 2002; Peters and Sethares 2002; Marner et al. 2003; Bartzokis 2004).

Microstructural changes that occur across the lifespan can be measured with MRI metrics. In particular, quantitative MRI (qMRI) can provide accurate information about such biophysical tissue properties (Basser and Pierpaoli 1996; Callaghan et al. 2014; Lorio et al. 2014; Yeatman et al. 2014; Cox et al. 2016; Gracien, Reitz, et al. 2016b; Carey et al. 2018; Filo et al. 2019). For example, qMRI measures have been shown to follow an inverted-U pattern over the lifespan, similar to the aforementioned pattern in overall brain volume, in white matter and brainstem (Yeatman et al. 2014; Arshad et al. 2016; Melie-Garcia et al. 2018; Slater et al. 2019; Bouhrara, Cortina, et al. 2020a; Bouhrara, Rejimon, et al. 2020b). One important qMRI measurement is quantitative R1 (or 1/T1), which represents the longitudinal relaxation rate. R1 is commonly used, is reliable and has served as a proxy for tissue microstructure properties including myelin, lipid content, and iron content (Mottershead et al. 2003; Schmierer et al. 2004; Dick et al. 2012; Sereno et al. 2013; Lorio et al. 2014; Lutti et al. 2014; Stüber et al. 2014; Gomez et al. 2017; Warntjes et al. 2017; Carey et al. 2018; Edwards et al. 2018; Filo et al. 2019).

In brain age prediction, when comparing chronological age with the predicted age as computed by prediction models, researchers can identify mismatches between the two and assess how they potentially relate to brain pathology. Examples include studies on traumatic brain injury (Cole et al. 2015) mild cognitive impairment and Alzheimer's disease (Gaser et al. 2013), HIV infection (Cole, Underwood, et al. 2017b), and schizophrenia (Schnack et al. 2016).

A critical issue in such studies is the selection of a suitable approach to achieve the highest robustness and precision when quantifying the mismatch between chronological and biological age (i.e., the brain-age gap). One important aspect of that is choosing what brain measurement to use as the model’s input. Most previous works employ either structural (e.g., cortical thickness, brain volume) or connectivity measurements (e.g., connectome-wise connectivity or functional connectivity (FC)), or some combination of them (Dosenbach et al. 2010; Franke et al. 2010; Gaser et al. 2013; Franke et al. 2014; Han et al. 2014; Koutsouleris et al. 2014; Cole et al. 2015; Luders et al. 2016; Steffener et al. 2016; Liem et al. 2017; Cole, Ritchie, et al. 2017a; Cole, Underwood, et al. 2017b; Bonifazi et al. 2018; Kaufmann et al. 2019). Crucially, though, none of these studies, has tested whether qMRI measurements can be used to predict brain aging. Indeed, in a recent study of age prediction using nonquantitative structural MRI, (Lewis et al. 2019) argued that qMRI may improve the accuracy of age-prediction models.

Recently, Kaufmann et al. (2019) used structural MRI data from more than 45 000 people for age prediction in both healthy and diseased individuals. When predicting the age of each disease’s subgroup using the model built from the healthy individuals, the researchers found that patients with multiple sclerosis (MS) exhibited one of the largest brain-age gaps. While MS is unfortunately a common neurological disease, its outcome is highly variable, which makes its research more challenging. Indeed, research has found low correlation between clinical impairment and MS disease progression as monitored by MRI (most commonly MRI estimates of the brain lesions’ load, mostly in white matter) (Barkhof 1999). Previous studies have found that qMRI is sensitive to myelination changes in MS (Laule et al. 2004; Schmierer et al. 2004; Vrenken et al. 2006; Manfredonia et al. 2007; Vavasour et al. 2009; Mezer et al. 2013; Enzinger et al. 2015; Gracien, Jurcoane, et al. 2016a; Gracien, Reitz, et al. 2016b; Laule and Moore 2018; Andica et al. 2019; Lommers et al. 2019). Therefore, in this article, we build a cortical-R1-driven age-prediction model and test it on a cohort of MS patients.

In this study, we extend previous work in age prediction models and demonstrate that quantitative measures can predict age similarly to models using cortical thickness, a well-established biomarker for age prediction. By comparing cortical R1 and cortical thickness as age predictors, we are able to highlight the potential differences of macro- and micro-structural contributions to age prediction. Notably, the qMRI model provides additional information when predicting age in MS patients. We provide a description for the differences between cortical thickness and R1, both for their role in the models and for the way in which they manifest in the cortex during underlying biological processes of development and aging. We further study how different cortical regions differ in terms of peak maturation and in the rate of development and aging. Importantly, we replicate our findings in independent datasets.

Methods

Overview

We used qMRI and cortical thickness to measure trends in the tissue properties of 104 major cortical regions in 160 healthy subjects between the ages of 6 and 81 years. We also analyzed an additional dataset of 10 MS patients, who were scanned at two different times with a 2-year gap between scans. The following sections describe in detail the subjects, the MRI protocol, and the data processing. Example code and data are available at github.com/MezerLab/age-pred-r1.

Subjects

The main dataset used for this study comes from aggregating data from three previously published works (Yeatman et al. 2014; Sacchet and Gotlib 2017; Natu et al. 2019), all of which acquired the data using the same scanning protocol using a 3T Discovery 750 MRI system (General Electric). The three dataset all together make N = 209, but after quality control, we end up with a final dataset of N = 160 (67 males) (see Imaging Quality Control). A more detailed description of the dataset is given in Supplementary Table 1. All participants were healthy volunteers recruited from the San Francisco Bay Area based on flyers, advertisements in local papers and school newsletters. All participants were screened for neurological, psychiatric, and cognitive disorders. Additionally, we included a dataset of 10 MS patients (4 males) acquired with the same scan, protocol, and parameters (Mezer et al. 2013) and another dataset of 10 children (3 males) between the ages of 6–8 years, acquired in the same scan but with a different voxel size (Travis et al. 2019).

To test the replicability of our model, we use the dataset of (Filo et al. 2019), acquired on a 3T scanner (Siemens). This dataset consists of 34 subjects (23 males), divided in two groups: 17 young subjects (24–31 years, 10 males) and 17 adult subjects (57–77 years, 10 males).

Quantitative R1 Mapping Protocol

Main dataset

To create the R1 maps, where R1 = 1/T1, we used the T1 relaxation protocol as in Mezer et al. (2016). It was measured from spoiled gradient echo (GE) images acquired at different flip angles (α = 4°, 10°, 20°, and 30°), with TR = 14 ms and TE = 2.4 ms. The scan resolution was 0.93 × 0.93 × 1 mm³. In addition, spin-echo inversion recovery (SEIR) T1 mapping was done with an echo planar imaging (EPI) readout (SEIR-epi), a slab inversion pulse, and spectral spatial fat suppression. For the SEIR-epi acquisition, the TR was 3 s, the TE was set to minimum full, and the inversion times were 50, 400, 1200, and 2400 ms. We used 2 mm² in-plane resolution with a slice thickness of 4 mm. The EPI readout was performed using an acceleration factor of 2 to minimize spatial distortions.

We used the advanced normalization tools software package (Avants et al. 2011) to register the spoiled-GE images with the SEIR-EPI image. The transmit-coil inhomogeneity (B1 excited inhomogeneity map (B1+)) was calculated by combining the unbiased gold-standard SEIR fits with the spoiled-GE data (for more details and algorithm, see Mezer et al. 2013, 2016; Appendix A). We used the estimated B1+ and the multiflip-angle spoiled-GE measurements to derive the maps. The maps were calculated using a nonlinear least-squares fitting procedure to minimize the difference between the data and the spoiled-GE signal equation predictions. In areas where there is good registration between the B1+ and the spoiled GE, the voxel values are interpolated, while values are extrapolated in the areas where the registration is not good enough. Whole-brain R1 maps were generated by calculating the inverse of T1 maps (1/T1). These, together with the bias correction maps of B1+, were computed using the mrQ software (github.com/mezera/mrQ). We note that areas that tend to have extrapolated B1 values (such as the temporal and lower occipital lobes) also did not show an inverted-U trend for R1 across the lifespan, in contrast with other cortical areas. We assume this is an erroneous effect of extrapolated values (see Development and Aging and Fig. 1A).

Figure 1 .

Age-prediction model comparison. (A) Cortical thickness and R1 predict age with similar accuracy using the PCA method. This figure shows the relationship between the mean predicted age (cross-validation: 75% for training set, 25% for testing set, and averaging over 1000 iterations) and the chronological age of each subject. The respective values of MAE for cortical thickness and R1 are 3.40 and 3.64 years for the young group and 10.45 and 9.62  years for the adult group. For the young group, a t-test showed no significant difference between the MAE for cortical thickness and the MAE for R1, and the same was true for the adult group. For the ElasticNet case, see Figure 5A. (B) Contributions of regions to the linear model are different between young/adult groups and R1/cortical thickness. The contribution of the different regions to the model differs both between groups and measures (but not between methods; for the ElasticNet case, see Fig. 5B). For the PCA method, contributions of the regions were calculated by taking the dot product of the explained variance of each feature in each component, and by the contribution (weight) of each component to the linear regression (see Methods section Age Prediction). For visualization purposes, we show the 75th percentile for both the positive and negative values. For the R1 adult group aging model, we found a separation between the cortical regions that contribute positively and negatively to age prediction, which were distributed in anterior and midposterior areas, respectively.

For the 10 MS patients, an additional fluid-attenuated inversion recovery (FLAIR) image was acquired with 0.43 × 0.43 mm² in-plane resolution and 5 mm axial slice thickness. This image was used to identify and remove MS lesions from the data, although these lesions were found mostly in the white matter. For 10 of the children, clinical limitations necessitated a faster scan, which meant that their spoiled-GE images had a lower resolution. For these subjects, the R1 maps were of the resolution 0.9375 × 0.9375 × 1.5 mm³.

Replication dataset

Data were collected for a previously published study (Filo et al. 2019). For the quantitative T1 mapping, 3D spoiled-GE images were acquired with different flip angles (α = 4°, 10°, 20°, and 30°). The TR was 19 ms, and for the TE each image included five equally spaced echoes between 3.34 and 14.02 ms (except for six young subjects for whom the scan included only the shortest TE) and the TR was 19 ms. The scan resolution was 1 mm isotropic. For calibration, SEIR-epi data were acquired, which were done with a slab-inversion pulse and spatial-spectral fat suppression. For SEIR-epi, the TE was 49 ms, the TR was 2920 ms, and the TI were 200, 400, 1200, and 2400 ms. We used 2 mm² in-plane resolution with a slice thickness of 3 mm. The EPI readout was performed using an acceleration factor of 2. R1 maps were generated using the same procedure explained above, voxels in which the B1+ inhomogeneities were extrapolated and not interpolated were removed from the analysis.

Anatomical images were acquired with 3D magnetization-prepared rapid gradient echo (MPRAGE) scans for 24 of 34 subjects (14 of 17 younger subjects, 10 of 17 older subjects). The scan resolution was 1 mm isotropic, the TE was 2.98 ms, and the TR was 2300 ms. Magnetization-prepared 2 rapid acquisition gradient Echoes (MP2RAGE) scans were acquired for the rest of the subjects. The scan resolution was 1 mm isotropic, the TE was 2.98 ms, and the TR was 5000 ms.

Cortical Parcellation

Main dataset

The mrQ pipeline also creates a synthetic T1-weighted image, which we use here as input to perform a whole-brain automatic cortical parcellation with FreeSurfer (Fischl et al. 2002). We used the Destrieux et al. (2010) atlas to parcellate the cortex into 148 cortical gray-matter regions. In each region, we calculate the midcortical layer using FreeSurfer. This calculation interpolates the values between the pial surface and inner white matter for each region to get a mean R1 value per-region. This method allows us to minimize cerebrospinal fluid (CSF) contamination on the measurement. Cortical thickness of each region was also calculated with FreeSurfer. Note that 44 of these regions were discarded from the analysis, since they did not show substantial R1 differences with age (probably due to B1+ inhomogeneities) (Development and Aging and Fig. 1A).

Replication dataset

For subjects who had an MPRAGE scan, we used it as input for FreeSurfer. For the other subjects, the MP2RAGE scan was used. We used a rigid-body alignment to register these anatomical images to the R1 space prior to the parcellation process.

Imaging Quality Control

R1 maps from all subjects in the dataset were visually inspected for ringing and movement artifacts. Before starting the analysis, 49 subjects (47 of them younger than 25 years old) were removed from the main dataset due to movement artifacts. The FreeSurfer output was also visually inspected for errors, but no subjects were removed for a problematic segmentation. After quality control, we had a final dataset of 160 subjects.

For MS patient data, the lesions were first outlined by the white-matter hypointensity maps, which were created by FreeSurfer from the T1w. Next, this automatic segmentation was manually corrected by an expert, using each patient’s FLAIR image that had been registered to T1w space. The correction with the FLAIR was done in order to identify lesions that were not detectable with the white-matter hypointensities in T1w. Only those areas that contained a lesion were removed from the analysis, in order to prevent MS lesions from impacting the prediction model. Most of the visible lesions were located in the white matter and not in the cortex.

Development and Aging

To predict age, we started by dividing the dataset into two subsets, young (6–25 years, N = 87, 37 males) and adults (26–81 years, N = 73, 30 males). This allows to separate the processes of development and aging in R1 into two semilinear processes. In each group, we fit a multiple linear regression model across all 104 cortical regions (see Age Prediction) using the MRI measurement of either cortical thickness or R1. To avoid overfitting (since we have approximately 80 subjects per group, with age as the response variable and 104 regions as the predicting features), we used a principal components analysis (PCA) approach (see Age Prediction) that reduces the data’s dimensionality: We reduced the number of features (i.e., cortical regions) from 104 to the number of principal components (PC) which explain 95% of the variance of the data. These PCs (~30 for R1 and ~40 for cortical thickness in both young and adult groups) were the input variables for the multiple linear regression model (we also tested other regression models; see Age Prediction). This process was performed separately for both young and adult groups and for each one of the measures (cortical thickness and R1). Thus, there were four different dimensionality reductions: young cortical thickness, adult cortical thickness, young-R1 and adult-R1. Additionally, to make sure that our result is not sensitive to the specific method of dimensionality reduction, we replicate the results using an ElasticNet model, similar to Richie-Halford et al. (2019) (for a detailed description, see Age Prediction, where we also describe locally linear embedding, a third, nonlinear dimensionality reduction method).

We chose to separate the two age groups at 25 years old, in order to obtain balanced groups. We tested the sensitivity of the results to the cutoff choice by repeating all analyses with a cutoff at 23, 30, and 45 years (based on maturation peak of R1). To test if the model could benefit from different cutoff strategies, we further tested a multivariate piecewise linear regression method that made unsupervised decisions on the cutoffs. For this analysis, we made use of the “pwlf” Python library. This package allows for a multivariate piecewise linear regression and includes options for selecting the number of segments (we tested for two and three age groups) and degree of the fits (we tested linear and quadratic fits). For extended explanations, results, and discussion regarding the cutting age selection, please see Fig. 1.

To analyze the lifespan dynamics for each region, we fitted linear trends for cortical thickness and quadratic trends for R1 over the whole population in the main dataset (i.e., the dependent variable is cortical thickness or R1, and the independent variable is age). Regions whose R1 trend did not follow the inverted-U-shaped trend over the lifespan were discarded from the analysis (44 of 148 regions 29.7%). As explained in quantitative R1 mapping protocol, these regions are on the edge of our B1+ inhomogeneities correction mask and therefore may be more sensitive to residual bias. The regions, which are specified in Figure 1A, are located in the inferior parts of the brain and mainly show stationary R1 values across the lifespan (and therefore they do not add significant information to the prediction models). Nevertheless, we ran the analysis with all 148 regions, and found no significant difference in the age prediction error in terms of absolute mean error (ME) (Fig. 3).

Figure 3 .

Spatial pattern of development and aging rates is different for R1 and cortical thickness. For R1 in development, anterior cortical regions tend to have higher rates of change, whereas posterior regions have lower rates. In aging, most regions with a strong decline rate are located in the midposterior part of the cortex. This shows an inverse posterior/anterior dynamic for development and aging. For cortical thickness, both development and aging are equal (follows a linear decay dynamic). We also find a pronounced difference on the anterior part with age.

For the fitted linear distribution of cortical thickness, we calculated its slope as the only value for the rate of change, since cortical thickness follows a linear decay trend. We repeated this analysis for each region in turn. For j = 160 subjects and a given cortical region i, let x be a j × 1 vector of predictors (cortical thickness or R1) and y be a j × 1 vector of responses (age). 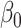is the intercept and is the free parameter. The fitted model for cortical thickness in region i is as follows:

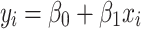For the fitted quadratic distribution of our R1 model, we add a quadratic term to the model since it is well-fitted by a parabola:

For R1, we calculated two rates per region: one from the start to the peak of the quadratic distribution, and one from the peak to the end. The rate of change for maturation is given by the slope between the fitted value at the age of 6 (minimum point of the parabola on the left side) and the fitted value on the peak of the parabola. Similarly, the rate of change for aging is given by the slope between the peak value and the fitted value at the age of 81 (minimum point of the parabola on the right side).

In the replication dataset, we only have young and adult groups. We computed the difference of the mean values per region between the young and adult groups in the replication dataset, with the mean fitted value of the same regions in the main dataset for the correspondent age range (specified in Subjects).

Age Prediction

We modeled age using ScikitLearn (Abraham et al. 2014) to perform multiple linear regression with cross validation (25% of data for testing). For each subset, three different dimensionality reduction approaches were tested:

1. Fitting after PCA:

For the linear fitting, we used as predictors the number of components required to explain at least 95% of the variability in the original data. We used ScikitLearn for the PCA analysis. For the PCA, we use an m × n matrix as input (m subjects and n independent variables, where each independent variable is demeaned before calculating the PCs). We calculate the explained variance per principal component (PC) as a fraction from 0 to 1, and the cumulative explained variance from the first PC to the nth PC. With this information, we select the set of the PCs at which at least 95% of the variance in the data is explained. For R1 modeling, this resulted in 30 components for young subjects and 27 for adult subjects; for cortical thickness modeling, the number of components was 38 and 43, respectively. These PCs are the ones we use to fit the prediction model (see below). For R1 modeling, this resulted in 30 components for young subjects and 27 for adult subjects; for cortical thickness modeling, the number of components was 38 and 43, respectively. The linear model is a multiple linear regression model:

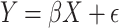where Y is the n × 1 response vector where n is the number of response variables (subjects’ age), X is an n × q with q predictors (q PCs and n subjects). Let ϵ be an n × 1 vector that are independent and identically distributed intercepts, and β be a q × 1 vector of free parameters.

We ran the age prediction model 1000 times, and each time we used cross-validation (75% train, 25% test) to evaluate the model. For each model-fitting iteration, we separated the training and the testing data. The PCA space is created with the training data, and the prediction model is fitted. Then, the testing data are projected to the space of the training data PCs. Finally, we fit the prediction model and we evaluate the testing data against it.

Other fitting approaches were also tested:

• Support vector regression (SVR) is an extension of support vector machines (Cortes and Vapnik 1995) to solve regression problems. We tested the model with the “linear” and “poly” kernels (2°).

• Kernel ridge regression (KRR) combines ridge regression (linear least squares with l2-norm regularization) with the kernel trick (Murphy 2012). It thus learns a linear function in the space induced by the respective kernel and the data. For nonlinear kernels, this corresponds to a nonlinear function in the original space. The form of the model learned by KRR is identical to SVR, though different loss functions are used: KRR uses a squared-error loss while SVR uses epsilon-insensitive loss.

To quantify the contribution of each region to the prediction model, we calculated the dot product of the explained variance in each component by the contribution (weight) of each component to the linear regression. In other words, we first calculated the dot product of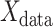and . Here, is an M × N matrix (where M is the number of region and N is the number of subjects) and 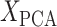is an N × P matrix (where N is the number of coefficients and P is the number of PCs):

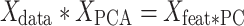The new matrix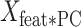is an M × P matrix that contains information about the weight of each of the M features (regions) in each PC. Finally, we calculated the dot product of 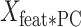with the weights of the linear model for each component (P × 1 vector) and got the contribution of each region to the model (M × 1 vector).

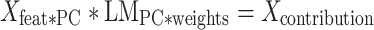• ElasticNet:

  The ElasticNet method is a weighted average of the LASSO and ridge penalties (Zou and Hastie 2005). The LASSO penalty (L1) forces many parameters to have a value of zero which leads to variable selection, while the ridge penalty (L2) helps to ensure that highly correlated variables are selected simultaneously and have similar model weights. We hyperparametrized L1 and L2, so the number of weights used for the linear fitting would match the number of PCs used in the previous approach, with the maximum possible accuracy.

• Fitting after locally linear embedding (LLE):

  LLE (Roweis and Saul 2000) seeks a lower dimensional projection of the data, which preserves distances within local neighborhoods. This approach can be conceptualized as a series of local PCAs, which are globally compared to find the best nonlinear embedding. We used the “LocallyLinearEmbedding” class from ScikitLearn, and defined the “n_components” (number of dimensions of the manifold) as the number of PCs obtained in the PCA analysis.

Model Error Calculation

We calculated the mean absolute error (MAE) and ME to estimate the accuracy of the model. We used the MAE to compare the performance of the models. ME was used in the intragroup comparison between different predicted groups (e.g., healthy vs. MS). MAE was calculated as the absolute difference between the predicted and chronological ages for each subject and then averaged over the whole subgroup (young, adults or MS). ME was calculated as the average (nonabsolute) difference between the predicted and chronological ages. MAE gives a measure of the magnitude of the error with respect to the real value, while ME is informative about the directionality of this error (predicted older or younger). We also evaluated the models with R² (the coefficient of determination, which measures the proportion of the variance in the dependent variable that is predictable from the independent variables).

Results

Age Prediction Using Cortical Thickness Versus R1

Cortical thickness is a widely used brain measurement in age prediction. In this work, we compare it with cortical quantitative R1. Our first observation is that while cortical thickness is estimated from images whose contrast is affected by R1, the two measurements are separable, as evident by the weak linear relationship between them across subjects and brain regions (Fig. 1B [r = −0.28; P = 0]). Furthermore, the two measurements show different dependencies on age: Cortical thickness exhibits a moderate linear change across the lifespan, while R1 shows a quadratic pattern. In development, R1 and cortical thickness have a moderate negative correlation (Fig. 1C) and this effect is reduced in older age. These results support the notion that cortical thickness and R1 differ in their ability to predict age, as well as in the specific regions that drive the age prediction.

Next, we compared age prediction models in the main dataset using either cortical thickness or R1. We found that cortical thickness and R1 each predict age with similar accuracy (Fig. 1A). Mean absolute prediction errors for cortical thickness and R1 are comparable in both age groups: in the young group, 3.40 and 3.64 years for cortical thickness and R1, respectively; and in the adult group, 10.45 and 9.62 years. Note that both for the R1 and cortical thickness models, the error for the young group is smaller than for the adult group, probably since the age range of the input group is also smaller. With respect to the proportion of the variance of age that can be predicted from the independent variables (R² score), in the young group the mean values were 0.45 and 0.39 for cortical thickness and R1; in the adult group, the values are 0.21 and 0.34, respectively (Fig. 4A). For additional information on the variability of the error per subject and age gap across the lifespan, see (Fig. 4B,C). Finally, we tested the effect of sex on the regression. In no case was the effect of sex significant in explaining the variance of age (P > |t|: P = 0.34 for R1 and P = 0.11 for cortical thickness).

Figure 4 .

Replication of aging dynamics on an independent dataset. We plotted the difference of the average R1/cortical thickness values for each region of the brain for the age range limited by the replication dataset. Results are shown for the main dataset (top) and for the replication dataset (bottom). (A) For R1, we find an agreement between both datasets. Different regions have either positive or negative values due to the fact that maturation peaks are different. This is, between the age ranges (young: 24–31 years old; adult: 57–77 years old), some areas are developing and some others are aging. The aging effect is similar for all regions in both datasets (see B)). We find that the replication dataset has a stronger aging effect particularly in posterior regions. (B) Each point in the scatterplot represents one of the 104 regions analyzed. We find a remarkable agreement of R1 between both datasets (r = 0.65). (C) For cortical thickness, since the aging dynamics follows a constant decay in all the regions, we only find positive values (accounting for the reduction from the Young group to the Adult group). We find the greatest thickness reduction to be located in the superior and frontal parts in both datasets. We also find disagreements between the datasets, mostly in the right posterior regions. (D) Similar to B, the points in the scatterplot represent each of the 104 regions analyzed. We find cortical thickness to be less consistent than R1 between the two datasets.

Age Prediction Models Robustness

We replicated the analysis using different methodological approaches and other data-handling procedures. To test the effect of dimensionality reduction algorithms, we compared PCA with two alternative methods, ElasticNet and LLE. We found similar results, suggesting invariance for dimensionality reduction method (Fig. 5A,D).

Figure 5 .

Predicting the MS cohort and identifying differences between the MS and healthy groups. (A) The MS group was evaluated against the trained regression models of healthy adult subjects. While the R1 age prediction model is able to detect cortical differences for MS patients, this effect could not be seen with the cortical thickness model. For both cases, most MS predicted points in the scatter plot are shifted to the right (i.e., MS patients are predicted as being older than their chronological age). The effect of the prediction is clear from the ME, which accounts for the direction of the error. A t-test was performed to test the differences in mean prediction accuracy between healthy adults and MS patients for subjects between the same age ranges. The t-test proved that the prediction has different mean values in accuracy for the case of R1, but not for cortical thickness. An additional t-test was performed without the two outliers for the R1 MS visit #1 (orange dots to the right) and the difference with respect to the healthy group was still significant (P < 0.047). For ElasticNet results, see Figure 10A. (B) We identify differences in groups by subtracting the mean value per region of the healthy subjects from those of the MS patients (healthy patients only from the same age range as the MS patients). First, we identify the regions that show the greatest differences between the patient and control groups. For R1 (1), the regions that show the greatest differences are the parietal and occipital regions, while for cortical thickness (2), the differences are more dispersed, including larger differences in midfrontal regions. For R1 (3) we do see a relationship between the disease-related changes and the weights of the age prediction linear model (LM). Yet, for cortical thickness (4), there is no evidence for a strong relationship between differences in healthy and MS values and the model weights.

We used two different fitting methods, such as KRR and SVR, to test if the multiple linear regression was a suitable approach. None of them showed significant improvement in terms of absolute ME; see Figure 6.

The different nature of the two measurements suggests that combining them within a single model could have a synergy effect and improve age prediction. To test this hypothesis, we combined cortical thickness and R1 features together in a single age prediction model (details in Fig. 7). The results improved slightly compared to using each measurement separately: the absolute ME was 3.24 years for the young group and 8.42 years for the adult group (compared with 3.40 and 10.45 years for cortical thickness alone and 3.64 and 9.62  years for R1 alone, for young and old groups, respectively). In the case of the adult group, a statistically significant improvement was detected for the combination of R1 and cortical thickness compared with cortical thickness alone (P = 0.03). For all other cases, the combination of cortical thickness and R1 improved the original individual predictions but not significantly.

The dependency of R1 with respect to age is parabolic, and therefore we divided the data into two groups (young and old). Indeed, when using the full dataset to predict age (with no groups), cortical thickness performed better than R1 (Fig. 6). We selected the cutoff between the two age groups at 25 years to keep the groups balanced. We also tried other approaches to divide subjects into different age groups using a multivariate piecewise linear regression model. This approach did not outperform our initial approach (Fig. 1A). We also performed the prediction analysis with a separation cutoff of the groups at 23, 30, and 45 years, and the results were similar in terms of absolute ME (Fig. 1B,C). For extended explanations, results, and discussion regarding the cutting age selection, please see Figure 2.

Figure 2 .

Aging pattern differences between cortical thickness and R1. (A) Lifespan trajectories of R1 and cortical thickness for different regions of the brain (right hemisphere, the first entry of panel B enlarged). We find lifespan dynamics that match those described in the literature. Age-dependency differs between R1 and cortical thickness: Cortical thickness follows a linear decay pattern while R1 follows a parabola (peak of the parabola marked with a star). The color code (colorbar in panel B) corresponds to the peak age of each one of the cortical regions. (B) R1 shows spatial differences in peak maturation (described in the colorbar as years). Posterior regions hit maximum maturation between the fourth and fifth decade, while anterior regions will peak later, starting during the sixth decade of life. (C) For different cortical regions, we find a linear relationship between the peak maturation age (x-axis) and the region weight (y-axis) in the adult group’s R1 prediction model (r = 0.68).

Finally, to test the sensitivity of the model to imaging resolution, we used the R1 prediction model of the young subjects on a dataset of 10 young individuals acquired in the same scan of the main dataset with different voxel size (see Methods section Subjects) against the young prediction model. Despite the difference in image resolution, these subjects’ predicted ages gave similar mean accuracy as the subjects from the main dataset (Fig. 8).

Different Regions Contribute to the Cortical Thickness and R1 Models

Because the prediction errors for cortical thickness and R1 are similar, we might expect that these measures are indexing the same underlying phenomena. To test whether the two methods rely on similar cortical regions for predicting age, we plotted the model coefficients on the cortical surface. Figure 1B highlights the cortical regions with large contributions to the models, according to the weights of the multivariate linear regression model. The regions with the largest weights vary between the cortical thickness and R1 models, and also between the young and adult groups. Nevertheless, the identity of these regions does not depend on the method of dimensionality reduction: Both the PCA (Fig. 1B) and ElasticNet (Fig. 5B) models showed similar agreement regarding the regions (r = 0.84), again emphasizing the invariance for dimensionality reduction method (Fig. 5C). Taken together these results suggest that, despite arriving at similar measures of accuracy, the cortical thickness and R1 models rely on different biological sources of information to predict brain age.

Interestingly, for the R1 model for the adult group (Fig. 1B, top right), we find an anatomical separation between the brain regions that contribute positively and negatively to age prediction. While the positively contributing regions are concentrated in the anterior parts of the brain (frontal lobe), the regions contributing negatively are midposterior (parietal lobe). For the R1 model in the young group, the primary motor cortex is the most significant region for predicting age. For the cortical thickness model, we do not find such clear spatial patterns.

Aging Pattern Differences between Cortical Thickness and R1

To better understand the different contributions of each brain region to age prediction models, we further investigated the age pattern of both cortical thickness and R1.

In Figure 2A, we replicate the previous studies that show the inverted-U shape for changes in R1 across the lifespan (Yeatman et al. 2014; Slater et al. 2019). We also replicate the linear decay of cortical thickness across the lifespan, as reported in (Courchesne et al. 2000; Salat et al. 2004; Thambisetty et al. 2010). We find that the patterns of cortical thickness and R1 in cortical regions show different age dependency. Figure 2B describes R1 differences in peak maturation. Interestingly, we find that posterior regions reach maximum R1 values between the fourth and fifth decade, while anterior regions peak from the sixth decade of life onward.

We compared this aging pattern with the age prediction model in the adult group, and found a linear relation between a brain region’s maturation peak age and its model weight (r = 0.66), see Figure 2C.

Next, we compared the two measurements’ rates of change in each cortical region (see Methods section Development and Aging). We found that the spatial pattern of development and aging rates is different for R1 and cortical thickness (Fig. 3).

We observe an inverse posterior/anterior dynamic for development and aging in R1. For development, the R1 in anterior cortical regions (central sulcus and frontal lobe) tends to have higher rates of change, whereas the R1 in posterior regions (occipital and parietal lobe) tends to have lower rates. In aging, most regions with a higher decline rate are located in the posterior part of the cortex (central sulcus and parietal lobe). Strikingly, we find that aging happens more abruptly in the regions that have the earliest maturation peak (r = 0.59; see Fig. 9A). This is, a region with an early peak, starts its descent early and with a steeper slope than the ascent. We also find that regions that have the strongest R1 changes in aging are significant to the age prediction models in the adult group (r = 0.44; see Fig. 9B).

For cortical thickness, we also find a more pronounced age-related difference in the anterior brain regions, specifically in the frontal lobe and part of the temporal lobe. We also find a moderate relationship (r = 0.39) between the rate of aging and the age prediction model weights (Fig. 9C).

Replication of Aging Dynamics on an Independent Dataset

Next, we tested the replicability of aging dynamics using a different dataset acquired in a different scanner (see Subjects in Methods). In this dataset, we have only two age groups, young (24–31 years old) and adult (57–77 years old). To compare between datasets, we first calculated the mean expected values per region from the fitted distribution from the main dataset for these age ranges. For R1, we computed adult minus young in the main dataset, and compared it with adult minus young in the replication dataset. We performed a similar analysis for cortical thickness, though here we used young minus adult in order to get positive values in our result.

In Figure 4A, we plot adult–young differences for R1 for each region in the cortex for the two datasets. We find a remarkable agreement between both datasets (r = 0.65; Fig. 4B) with similar aging patterns. While the aging pattern is similar, we find that the replication dataset has a stronger aging effect, particularly in posterior regions. For cortical thickness (Fig. 4C), we found that the greatest thickness reductions are located in the superior and frontal parts in both datasets, which is in agreement with earlier studies (Thambisetty et al. 2010). We also find discrepancies in the young–adult differences between the datasets, mostly in the right posterior regions. Altogether, we find cortical thickness (r = 0.31; Fig. 4D) to be less consistent than R1 between the two datasets.

R1 is Able to Identify Tissue Alterations

One of the main motivations for performing age prediction is that it can be used for clinical identification of brain diseases (Cole, Ritchie, et al. 2017a). Therefore, we tested the models’ ability to identify MS patients. The MS patients’ data were inputted to the models built only with healthy adult subjects. We found that R1 predicted MS patients to be older than their chronological age, while cortical thickness did not (Fig. 5A; for results with the ElasticNet instead of PCA, see Fig. 10A). For the MS analysis, we removed the visible lesions found in the cortex to avoid predictions driven by visible lesions; however, when we performed the analysis without removing the lesions, the results did not vary (Fig. 10B). We also performed the prediction analysis with a separation cutoff of the groups at 23 and 30 years, and again the MS patients were predicted to be older only for the R1 case (Fig. 1C).

Multiple Sclerosis Differences with Respect to Healthy Cohort

After noting the many differences between the two models of age prediction (R1 and cortical thickness), we tested whether the differences in the data can explain the difference in age predictions of the MS patients. First, we identified the regions that show the greatest differences between the healthy and patient groups in the same age range: For R1, the parietal and occipital regions show the greatest difference (Fig. 5B1), while for cortical thickness the differing regions are located in the midfrontal area (Fig. 5B2). Next, we asked whether there is a per-region relationship between the weights of the age prediction model and the difference in values between the healthy group and the MS group. We found that such a relationship exists for R1 (r = −0.32, P < 0.01) but not for cortical thickness (r = 0.1, P < 0.29; Fig. 5B3,B4). This result explains why R1, but not cortical thickness, can identify the MS group based on age prediction.

Finally, we asked whether we could select features a priori that would show the greatest difference between healthy and MS groups for cortical thickness, and then build an age prediction model from the healthy population data that could identify MS subjects (similar to our R1 model). While manual feature selection may raise a “double dip” concern (Smialowski et al. 2010), we wanted to determine whether we could indeed build such a model.

When we trained an age model with 40 regions that show the largest differences in cortical thickness between MS patients and healthy subjects, we found that MS patients are indeed predicted as older than their chronological age (Fig. 11). We found that cortical thickness can provide a model that predicts age for the healthy group and is able to separate the MS group from the healthy group. Importantly, this is not the model that gave the best performance in terms of age prediction in the healthy subjects.

Discussion

The modeling of healthy brain aging has received considerable interest in recent years. In this study, we showed that cortical thickness (a widely used measurement for age prediction) and quantitative R1 (a quantitative measure of the tissue’s underlying microstructure) have similar accuracy for the prediction of age in healthy patients. Our results reveal that cortical R1 is suitable for age prediction. Importantly, while age prediction accuracy seems comparable for R1 and cortical thickness, we found that the model for each measure relies on different anatomical features both macroscopic and microscopic. To better understand the difference in the structural features between the models, we described lifespan dynamics of cortical thickness and R1 across the cortex. Finally, we showed how the aging process is altered for individuals with MS. For these patients, R1 and cortical thickness provide different age predictions.

Age Prediction Using R1 Versus Cortical Thickness

Several recent studies have addressed age prediction using different MRI modalities, including T1-weighted (T1w) imaging, diffusion weighted imaging, and functional MRI (Dosenbach et al. 2010; Gaser et al. 2013; Liem et al. 2017; Cole, Underwood, et al. 2017b; Bonifazi et al. 2018; Richie-Halford et al. 2019). The use of functional and structural modalities has been widely studied, but there is a critical lack of studies that predict brain age with quantitative estimates of brain structure. Therefore, in this study, we utilize qMRI measures, for which the intensity measures are individually meaningful (Lebel et al. 2012; Lorio et al. 2014; Edwards et al. 2018; Filo et al. 2019). Since R1 is considered an in vivo histological tool (Edwards et al.), R1 age prediction is an important model that links the process of aging to cortical microstructure.

We compared the accuracy of predicting aging in the cortex for R1 with cortical thickness, a robust, widely used, and frequently studied structural measurement of the brain. We showed that both measurements had similar performances when predicting age in terms of MAE, although the ability of the independent variables to explain the variance of age (R²) was significantly different. The error rates in this work are moderately greater than the range of error rates of prediction models that use structural data (Cole, Ritchie, et al. 2017a; Cole, Underwood, et al. 2017b; Dafflon et al. 2020; Franke et al. 2010). Other approaches in the literature build on the combination of morphological and resting-state fMRI correlation (also called FC) features (Liem et al. 2017); FC features alone (Dosenbach et al. 2010); tractography-based connectivity (also called structural connectivity (SC)) features (Han et al. 2014); or a combination of FC and SC features (Bonifazi et al. 2018). However, the objective of our study is not only to maximize the model’s performance, but also to identify the potential benefits of using exclusively quantitative microstructural features as compared with macrostructural or morphological features.

We found that the R1 and cortical thickness models emphasize different sets of brain regions as contributing most to the age prediction (Fig. 1B). This suggests that features contributing to aging in our R1 and cortical thickness models reflect different biological sources. Changes in trends across the lifespan (Fig. 1C) between the different measurements emphasize the difference in the underlying biological sources. It is reasonable to believe that cortical thickness and R1 are weighted by different macrostructural and microstructural aspects, respectively, of cortical organization. Brain regions that contribute to age prediction in cortical thickness have been enumerated previously in the literature, for example in (Khundrakpam et al. 2015). For R1, while myelin is likely to contribute to the age-related R1 differences (Mottershead et al. 2003; Schmierer et al. 2004; Lutti et al. 2014; Stüber et al. 2014; Warntjes et al. 2017), other biological sources also may contribute, including iron, lipids, water fraction, cell and dendritic arborization, and molecular makeup (Gomez et al. 2017; Filo et al. 2019; Natu et al. 2019). Furthermore, these biological sources likely vary in their contribution between development and aging. In the literature, we can find inconsistent results between age-related volume loss derived from imaging techniques and postmortem analyses (Piguet et al. 2009). For example, age-related differences in myelination could differentially affect the GM/WM boundaries, which could affect the apparent cortical thickness as measured by MRI (Westlye et al. 2010; Lorio et al. 2016; Gomez et al. 2017; Natu et al. 2019).

Aging Pattern Differences Between Cortical Thickness and R1

In this study, we found a significant correlation between aging patterns and the weights of the prediction model (Fig. 2C and Fig. 9A). However, this relation is stronger for R1 than for cortical thickness (Fig. 9B,C). In comparing the age dependency of R1 and cortical thickness across the lifespan, we found different age dynamics. The linear decay of cortical thickness across the lifespan has been widely reproduced in the literature (Courchesne et al. 2000; Storsve et al. 2014). We reproduced previous findings of frontal regions having higher rates of thickness loss than other regions (Salat et al. 2004).

For R1, we observe different dynamics for different parts of the brain (Fig. 2A,B) in comparison with cortical thickness, posterior regions peak at a younger age and the decline rate is relatively higher, while the opposite pattern is apparent for frontal and temporal regions (Fig. 3). The pattern of posterior-to-anterior brain myelination process in brain development has been reported in (McArdle et al. 1987; Timmler and Simons 2019). These dynamics agree with previous findings that claim that the brain’s lightly and later myelinated regions are the prefrontal, inferior parietal, and lateral temporal cortex. These cortical areas are the main regions involved in higher brain functions (Collins et al. 2010; Glasser and Essen 2011; Donahue et al. 2018).

Grydeland et al. (2019) argues that well-connected regions such as association cortex, which are highly specialized for multimodal integration and underpin most complex behaviors, need to remain plastic, and consolidate their connections by an extended myelination stage. Our findings support this argument, which is known as the “last in, last out” theory of development, which suggests that regions that develop and peak in later years will also be the ones to decline last. This is in contrast to the “last in, first out” hypothesis (Raz 2000).

R1 is also sensitive to iron, which progressively accumulates with age, particularly in the first three decades, with a heterogeneous distribution in different regions of the adult brain (Drayer et al. 1986). Zhou et al. (2001) reported a higher concentration of iron in the occipital cortex compared with the prefrontal cortex, which could be mediated by the effect of early maturation observed in these regions. Lorio et al. (2014) found correlations between gray-matter volume differences and R2* maps in the prefrontal cortex in aging, which could be interpreted as an effect of iron content on the R1. Furthermore, R1 changes are mediated by both molecular composition and water content (Mezer et al. 2013). Recently, Filo et al. (2019) revealed that aging-related R1 changes in the cortex originate from changes in water content and lipid composition. We also found that the regions around the central sulcus show the highest rates in development and aging (Fig. 3). This finding supports the “gain-predicts-loss” hypothesis that assumes a symmetric rate of development and aging (Yeatman et al. 2014; Grydeland et al. 2019). The regions around the central sulcus peaking around the age of 45 years (approximately the median age of the subject pool) may contribute to an accurate estimation of the rates, since they cover development and aging with a similar number of years, showing the whole dynamic.

R1 is Able to Identify MS Patients

Recently, Kaufmann et al. (2019) found MS to be one of the diseases where age prediction (using T1w images) was off by a significant margin. Therefore, we tested our age prediction model against a group of MS patients. Even when we use only normal-appearing tissue in our model, we report that MS patients are predicted older than their chronological age (Fig. 5A). This effect was evident from the quantitative R1 model, but harder to detect with cortical thickness. Our finding would seem to be in contrast to (Kaufmann et al. 2019), who found a clear age gap in MS using T1w. However, here we used only cortical thickness and not cortical area and volume as well as gray and white-matter features (we also excluded the lesions where the prior studies did not). Importantly, our patient sample is small (N = 10), so our model needs to be further tested with a larger patient dataset. The R1 sensitivity we report in MS patients is in agreement with claims that damage in the cortex (not only in white matter) plays a significant role in MS (Lucchinetti et al. 2011; Absinta et al. 2016).

MS Differences with Respect to a Healthy Cohort

For the MS patient group, we identified an age prediction gap in R1 but not in cortical thickness (Fig. 5A). In the cortex, we found that R1 is able to capture microstructural changes associated with MS, as evident by its effect on age prediction in the patient cohort. To prevent the common lesions in MS from driving the observed effect, we excluded all visible lesions in the patients’ T1w and FLAIR images. Nevertheless, it is well known that cortical and juxtacortical lesions are common and almost invisible in MRI (Futatsuya et al. 2016), unless using specialized sequences such as double inversion recovery (DIR) (Geurts et al. 2005). Therefore, even if we excluded all visible lesions, it is possible that invisible cortical lesions were still present. This strengthens our claim that deviations between the biological and chronological age within the presented framework provide important insight into disease effects in the cortex, which otherwise would be hard to uncover using MRI. Future studies using specialized sequences, such as DIR, could shed light on whether or not cortical lesions are indeed driving the observed effect.

To better understand this difference, we directly compared the MS patients with the healthy population. We found that while MS patients’ brain regions showed deficits (compared with the healthy population) in both R1 and cortical thickness, the regions that had high contributions to the model showed deficits only in R1 (Fig. 5B).

Although our age prediction model for cortical thickness was unable to identify the MS group, differences in cortical thickness for MS patients have been reported previously in the literature (Benedict et al. 2006; Calabrese et al. 2010). Our results (Fig. 5B1) also show differences between the healthy and the MS groups. We used supervised feature selection to build a model to predict MS patient age, and found that this model predicted MS patients to be older than both their chronological age and their healthy counterparts’ predicted age (Fig. 11). However, these regions do not correspond with the ones that contribute to the more accurate age prediction model. This result highlights the fact that optimal age prediction may be suboptimal in detecting diseases.

Limitations of the Study

In this study, we compared age-prediction models of two MRI-based measurements: cortical thickness and R1. We acknowledge that using a linear model to fit part of the lifespan might be limiting our ability to compare the measurements, as each metric follows a different dynamic for the whole lifespan. Another limitation is that we selected a threshold (i.e., 25 years) to split the dataset into two groups, which was based on the criteria of having the groups balanced and describing specific dynamics (development for the young group; plateau and aging for adults). We found that our results are robust with respect to the choice of age threshold: using other thresholds, we did not find differences neither in the general prediction accuracy nor in the MS patients being predicted as older (Fig. 1C). A more balanced distribution of the dataset would have helped to overcome this limitation and could have allowed us to devise a more accurate prediction.

Quantification of magnetic resonance imaging parameters in cortical brain regions can be challenging due to CSF contamination (misidentifying CSF voxels as correct values). We minimized the potential CSF effect by interpolating the values between the pial surface and the inner white matter. This was done by calculating the midcortical layer in FreeSurfer. To support the use of the midlayer analysis, we tested the model on data with a lower resolution (which is more prone to CSF contamination), and found no change in the prediction quality (Fig. 8). Nevertheless, there might still be residual contamination of CSF in our analysis. A better resolution acquisition would be beneficial to solve this issue.

Our results might be sensitive to our methodological choices, which include simple and reliable methods (PCA, multiple linear regression, linear and quadratic fittings) and widely used measurements (cortical thickness and cortical R1). To account for the effect of the methodological choices, we also tested several different methodological approaches (different dimensionality reduction methods and fitting models) among other data handling procedures (using all features, combining different measurements, piecewise regressions). Overall, we obtained similar results, which suggest a robust effect.

The number of subjects used in this study (N = 160) and its distribution limits our ability to fit the prediction models in a manner that is fully robust and resistant to noise. Nevertheless, we report a consistent matching between two independent datasets, especially for R1 as well as between data in different resolutions. This result highlights the added value of using quantitative measures in terms of reliability (Weiskopf et al. 2013; Lévy et al. 2018; Lee et al. 2019; Gracien et al. 2020). The cohort of MS patients is limited in the number of subjects. MS interindividual variability is large, and therefore focusing on the mean difference with respect to healthy subjects might overlook important aspects of the disease. Due to the well-known heterogeneity of this neurological condition, analysis on a larger sample would be helpful in drawing broader conclusions.

Summary

In conclusion, in this study, we describe a novel view on the age prediction paradigm by using quantitative R1 in the cortex, and provide evidence for similar accuracy compared with the commonly used measure of cortical thickness. We explore the nature of these models and the dynamics driving the aging process. For R1, the prediction model and its component weights are able to capture dynamics directly related to aging. The fact that MS patients are predicted older than their chronological age suggests that substantial changes are occurring in regions significant for the prediction model. The model for cortical thickness seems to be driven by other biological processes, and relies on different cortical regions than does the R1 model. Therefore, we also use the age predictors to highlight the importance that the model weights have in disease assessment. We propose that the use of quantitative measures in age prediction models can provide additional utility for the characterization of neurological diseases, and adds novel information to classic measures such as cortical thickness. Future studies may explore the effects of including white-matter and subcortical features to the age prediction models, and of combining quantitative and classic measures within the same model.

Funding

The Edmond and Lily Safra Center for Brain Sciences (to A.E. and A.A.M.) and U.S. Department of Health and Human Services, National Institutes of Health (grant numbers R37-MH101495 and RO1 EY 022318-06); the Basque Government (grant POS_2019_2_0020 to A.E.); National Science Foundation Graduate Research Fellowship Program (NSF GRFP) (grant DGE-1147470 to J.D.Y.); the Stanford Medicine Spectrum’s Stanford Predictives and Diagnostics Accelerator (SPADA); the United States-Israel Binational Science Foundation (BCS1551330 to A.A.M. and J.D.Y.); the Israel Science Foundation (0399306 to A.A.M.). This research was supported by the Israel Science Foundation (grant no. 1169/20) granted to A.A.M.

Notes

The authors wish to thank the Weston Havens Foundation and Wandell’s lab for sharing the data, Drs Brian A. Wandell, Kalanit Grill-Spector, and Jonathan S. Bain for valuable comments and discussion. Conflict of Interest: None declared.