Brain Activity Fluctuations Propagate as Waves Traversing the Cortical Hierarchy

Abstract

The brain exhibits highly organized patterns of spontaneous activity as measured by resting-state functional magnetic resonance imaging (fMRI) fluctuations that are being widely used to assess the brain’s functional connectivity. Some evidence suggests that spatiotemporally coherent waves are a core feature of spontaneous activity that shapes functional connectivity, although this has been difficult to establish using fMRI given the temporal constraints of the hemodynamic signal. Here, we investigated the structure of spontaneous waves in human fMRI and monkey electrocorticography. In both species, we found clear, repeatable, and directionally constrained activity waves coursed along a spatial axis approximately representing cortical hierarchical organization. These cortical propagations were closely associated with activity changes in distinct subcortical structures, particularly those related to arousal regulation, and modulated across different states of vigilance. The findings demonstrate a neural origin of spatiotemporal fMRI wave propagation at rest and link it to the principal gradient of resting-state fMRI connectivity.

Introduction

The human brain represents about only 2% of the total body weight but accounts for approximately 20% of the total energy budget, and a majority (~95%) of brain energy is consumed by intrinsic brain activity at rest (Raichle 2006; Raichle and Mintun 2006). This budget allocation is consistent with a highly organized nature of functional magnetic resonance imaging (fMRI) signals collected in the resting state, which are being widely used for inferring functional brain connectivity in health and disease (Biswal et al. 1995; Fox and Raichle 2007). The study of resting-state fMRI (rsfMRI) dynamics has suggested that the highly structured rsfMRI connectivity, that is, correlations, may arise from transient fMRI coactivations caused by event-like brain activity (Tagliazucchi et al. 2012; Liu and Duyn 2013; Liu et al. 2018; Matsui et al. 2018), which were also to show systematic transitioning patterns (Ma and Zhang 2018; Liu and Zhang 2019). Consistent with these findings, the propagating structures have been found in rsfMRI by using a template-refining approach to extract repeated quasi-periodic patterns (QPP) (Majeed et al. 2011; Thompson et al. 2014; Yousefi et al. 2018) or by decomposing rsfMRI lag structures to recover lag threads (Mitra et al. 2014; Mitra, Snyder, Blazey, et al. 2015a). These propagating structures contribute significantly to rsfMRI connectivity (Mitra, Snyder, Blazey, et al. 2015a; Abbas et al. 2019) and appear sensitive to brain state changes and diseases (Mitra, Snyder, Constantino, et al. 2015b; Mitra, Snyder, Tagliazucchi, et al. 2015c; Mitra et al. 2018), and thus could be the key to understanding the functional role of intrinsic brain activity (Raut et al. 2019).

Nevertheless, to date the neural origin of the rsfMRI propagations remains elusive despite the ample evidence for the neural origin of rsfMRI connectivity (Nir et al. 2008; Hermes et al. 2012; Foster et al. 2015; Hacker et al. 2017). The study of propagating activity using fMRI faces a serious issue due to the spatial heterogeneity of hemodynamic delays (Handwerker et al. 2004). A series of recent studies have shown that a systemic low-frequency oscillation of blood signals, which can be recorded at peripheral sites such as fingertips and toes, induces systematic rsfMRI delays across brain regions that are consistent with the blood transit time through the cerebrovascular tree (Tong and Frederick 2010, 2012; Tong et al. 2012, 2017, 2018), suggesting a potential contribution of hemodynamic delays to apparent rsfMRI propagations. On the other hand, simultaneous fMRI–electrophysiology recordings in rats have provided clear evidence for the co-modulation of neural activity with the rsfMRI propagations (Thompson et al. 2014), which is, however, insufficient to prove the neural origin of the “propagation” per se. In other experimental setups, spatially propagating waves have been observed among neural populations, for example, wide-field optical imaging of voltage-sensitive dye or calcium in mice. However, such waves are difficult to compare with those measured with fMRI, as they are usually local (millimeters) and on a rapid time scale (<1 s) (Mohajerani et al. 2013; Greenberg et al. 2018). Most recently, globally propagating waves on the seconds timescale (~5 s) and the lag structure were observed in mice using calcium imaging and suggested to account for resting-state hemodynamic connectivity (Matsui et al. 2016; Mitra et al. 2018). However, it remains unclear whether similar resting-state infra-slow propagations over the entire cortex are present in neural signals of awake primates, and if so, whether and how are they similar to the propagating activity in human rsfMRI. There is also a lack of a detailed characterization of the infra-slow propagating activity, including its trajectories and subcortical involvements. Furthermore, although the contribution of these slow propagations to rsfMRI connectivity has been demonstrated (Mitra et al. 2014; Mitra, Snyder, Blazey, et al. 2015a; Matsui et al. 2016; Mitra and Raichle 2016; Abbas et al. 2019), it remains unclear whether they can be linked to any specific component of rsfMRI connectivity. Both the major QPP (Majeed et al. 2011) and the latency projection of the lag structure (Mitra et al. 2014; Mitra, Snyder, Blazey, et al. 2015a) showed a distinct contrast between the default-mode network and sensory/motor (SM) regions. This contrast superficially resembles the so-called “principal gradient” (PG) of the brain’s spontaneous activity, which has been derived by embedding the rsfMRI connectivity matrix into a low-dimensional space (Margulies et al. 2016; Huntenburg et al. 2018). This coincidence raises 2 important questions. First, is the direction of spatiotemporal fMRI propagation fundamentally linked to the reported rsfMRI connectivity gradient? And second, do the large-scale propagating waves reflect an underlying pattern of electrophysiological activity following the same trajectory?

To address these questions, this study combines human rsfMRI and monkey electrophysiology to study the infra-slow propagating brain activity. We developed a data-driven method to detect single propagating instances and map their propagating trajectories. The application of this method to high-resolution rsfMRI data of Human Connectome Project (HCP) revealed global propagations mostly in 2 opposite directions along an axis strikingly similar to the PG of rsfMRI connectivity (Margulies et al. 2016). The application of the same method to a large-scale electrocorticography (ECoG) recording from monkeys revealed very similar cross-hierarchy propagations between the lower- and higher-order brain regions, which are present most strongly at the gamma-band (42–95 Hz) power signals. Close inspection of the global rsfMRI propagations suggests local, embedded propagations within sensory modalities proceed in the opposite direction of the global propagation. More importantly, these cortical propagations are accompanied by sequential coactivation/deactivation in specific subcortical structures, particularly those related to arousal regulation. Consistent with this finding, the temporal dynamics of the infra-slow propagating activity are significantly modulated across brain states of distinct vigilance. Taken together, the study demonstrates a characteristic pattern of spontaneous, slowly propagating activity across the cortical hierarchy in humans and nonhuman primates, maps its detailed trajectories and associated subcortical changes, demonstrates its brain-state dependency, and also links it to the PG of the rsfMRI connectivity.

Materials and Methods

HCP Data and Preprocessing

We used the HCP 500-subject data release, including 526 healthy subjects scanned on a 3 T customized Siemens Skyra scanner. We limited our analyses to 460 subjects (age: 22–35 years, 271 females) who completed all four 15-min rsfMRI sessions on 2 separate days (2 sessions per day). The data were collected using multiband echo-planar imaging with an acceleration factor of 8 (Uǧurbil et al. 2013). The temporal and spatial resolutions of the data are 0.72 s and 2-mm isotropic, respectively. Four 15-min scanning sessions of 460 subjects were used in our analysis.

The rsfMRI data were preprocessed based on (Smith et al. 2013) using FSL (Jenkinson et al. 2012), FreeSurfer (Fischl 2012), and HCP workbench (Marcus et al. 2013) and the HCP FIX-ICA denoising pipeline was applied to remove artifacts. The multimodal surface matching registration was used in the HCP dataset to improve intersubject registration (Robinson et al. 2014, 2018). We used both rsfMRI surface and volume data. The rsfMRI cortical surface data were represented in standard HCP fs_LR 32k surface mesh and each hemisphere included 32 492 nodes (59 412 total excluding the noncortical medial wall). We smoothed rsfMRI data both spatially on the fs_LR 32k surface using a Gaussian smoothing kernel (sigma = 2 mm) and temporally using bandpass filtering at 0.001–0.1 Hz and then standardized each vertex’s signal by subtracting the mean and dividing by the standard deviation (SD). For the rsfMRI volume data including both cortical and subcortical areas, we smoothed rsfMRI volume data temporally (0.001–0.1 Hz) and standardized each voxel’s signal by subtracting the mean and dividing by the SD.

ECoG Data and Preprocessing

The monkey electrophysiology dataset was downloaded from the website (http://neurotycho.org) and had been described in a previous publication (Liu et al. 2014). To sum up, all procedures were approved by the RIKEN Ethics Committee. An implanted customized 128-channel ECoG electrode array (Unique Medical) was used to record neural signals (Nagasaka et al. 2011). Each ECoG electrode had a 3-mm diameter platinum disc with a 5-mm interelectrode distance. We used the ECoG data from 4 adult macaque monkeys (monkey K, G, and C Macaca fuscata and monkey S Macaca mulatta). The 128-channel ECoG electrode array was implanted in the left hemisphere covering the majority of cortical regions. The reference and ground electrodes were implanted in the subdural space and the epidural space, respectively. ECoG recordings were conducted with a sampling rate of 1 kHz using the Cerebus data acquisition system. More specific information can be found in (Yanagawa et al. 2013).

The ECoG signals were recorded under 3 brain states: the eyes-open, eyes-closed, and sleep states. Under the eyes-closed waking state and the natural sleep state, the monkeys sat calmly in a dark and quiet environment with eyes covered. During the sleep condition, the slow-wave oscillations were observed intermittently on the ECoG data. Under the eye-open condition, the eye mask was removed. Experiments were conducted on separate days. The ECoG data under the eyes-open and eyes-closed conditions were available in all of the 4 monkeys. The ECoG data under the natural sleep condition were only available in monkey C and monkey G.

The total length of ECoG data under the eyes-closed condition was about 85, 89, 60, and 62 min for monkey C, monkey G, monkey K, and monkey S, respectively. The total length of ECoG data under the eyes-open condition was about 103, 85, 60, and 61 min for monkey C, monkey G, monkey K, and monkey S, respectively. The total length of ECoG data under the sleep condition was about 243 and 157 min for monkey C and monkey G, respectively.

We removed the line noise at the primary frequency (50 Hz) and its harmonics using Chronux (Mitra and Bokil 2009). We excluded 3 channels for monkey G, 1 channel for monkey K, and 1 channel for monkey S from subsequent analyses due to serious artifacts that cannot be removed. We re-referenced the ECoG signals to the mean of all channels. To extract the band-limited power signals, we first calculated spectrograms between 1 and 100 Hz using a multitaper time–frequency transformation with a window length of 1 s, a step of 0.2 s and the number of tapers equal to 5 provided by Chronux (Mitra and Bokil 2009). We then converted the power spectrogram into decibel units using the logarithmic function. Next, we normalized the power spectrogram at each frequency bin by subtracting the temporal mean and dividing by its temporal SD. The normalized spectrogram was averaged within different frequency bands: delta 1–4 Hz; theta 5–8 Hz; alpha 9–15 Hz; beta 17–32 Hz; and gamma 42–95 Hz. The gamma frequency band was defined conservatively as 42–95 Hz, within which the power signals of different frequency bins show similar temporal dynamics. We also extracted the power of the low- (30–80 Hz) and high-gamma (80–150 Hz) bands as defined by a previous study (Ray and Maunsell 2011). Then, the band-limited power signals were smoothed both temporally using a low-pass filter (<0.1 Hz) and spatially using a Gaussian smoothing kernel (sigma = 5 mm), then standardized by removing the mean and dividing by its SD. The effect of temporal filter used here was examined to make sure that it will not produce any phase shifts (Supplementary Fig. S1).

Projecting the rsfMRI Signals Onto the PG Direction

The rsfMRI signals were projected onto the PG (Margulies et al. 2016) direction to generate time–position correlations as follows. The PG was obtained by a previous study with applying the diffusion mapping, a low-dimensional embedding method, to a group averaged connectome matrix (Margulies et al. 2016). First, we reduced the spatial dimension by sorting 59 412 cortical surface vertices according to the PG and then dividing these cortical surface vertices into 70 position bins of equal size. The position bin of 70 was chosen arbitrarily and we examined different number of position bins (Supplementary Fig. S2), for example, 50, 500, 5000. Next, the fMRI signals within each position bin were averaged to generate the time–position graph. Secondly, the time–position graph was cut into time segments based on the troughs of the global mean signal, and a local peak was found for each position bin within each time segment. Thirdly, for each time segment, the Pearson’s correlation was computed between the timing (relative to the global mean peak) and position of local peaks of all the position bins. A strong positive time–position correlation would indicate a propagation of the fMRI signal along the PG direction within this time segment and a strong negative time–position correlation would indicate a propagation opposite the PG direction. The local peak was detected for each position bin as the local maxima with a value larger than zero. If more than 1 local maximum were detected, the one with the largest peak amplitude was regarded as the local peak. The time–position correlation was only computed for time segments whose local peaks were identified in at least 56 (70 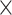 80%) position bins.

To focus our analysis on the time segments with global involvement, we identified time segments with a relatively large global positive peak amplitude by using a threshold derived from a null distribution and then computed time–position correlations of those identified time segments. The null distribution of global positive peak amplitudes was generated by randomly shifting the fMRI signal of different position bins in time and then calculating the global positive peak amplitudes of those randomly shifted signals. The random shifts were uniformly distributed integers between 1 and the total number of time points (1200) in a single scanning session. The time segments with global involvement were defined as those with a global peak amplitude exceeding the 99th percentile of the null distribution, which account for 58.80% of the total segments. We also calculated the delays between the global peak and the local peaks of 70 position bins for time segments of the real fMRI signals and randomly shifted signals.

For the time segments with global involvement, the time–position correlations along 4 other control directions were also computed in the same way as described for the PG. The 4 control directions included the second gradient of rsfMRI connectivity derived by the PG study (Margulies et al. 2016), and 3 artificial directions, that is, anterior-to-posterior direction, dorsal-to-ventral direction, and randomly rotated PG. The anterior-to-posterior direction map was generated by assigning increasing amplitude to vertices from posterior to anterior direction according to the y coordinate. The dorsal-to-ventral direction map was generated by assigning increasing amplitude to vertices from ventral to dorsal direction according to the z coordinate. The randomly rotated PG was generated by rotating the PG map on the spherical fs_LR 32k surface space with random degrees with respect to the x, y, z axes, which preserved the relative topology of the PG.

Principal Propagating Direction in the Human rsfMRI Signals

A principal delay (PD) profile was derived by applying a singular value decomposition (SVD) (Golub and Reinsch 1970) to delay profiles of time segments with global involvement. For any given time segment with global involvement, a delay profile was computed as the relative time delay of the local peak at each cortical surface vertex with respect to the global peak. The local peak was computed for each vertex as the local maxima with a value larger than zero. If more than one local maximum were detected, which were rare, the one with the largest peak amplitude was then regarded as the local peak. We focused on the delay profiles with at least 47 530 (59 412 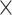80%) local peaks. For those selected delay profiles, if the local peak amplitude was less than zero or no local maxima was detected, then its relative time delay was defined as the mean time delay of its 3 nearest vertices with local peaks larger than zero. Specifically, for each vertex without time delay, the distance on the brain surface between this vertex and other vertices with time delay was calculated and sorted. Then, the averaged time delay of 3 vertices with smallest distance were used to replace the time delay of that vertex. The distance on the brain surface was calculated based on the coordinates of vertices. Next, a delay matrix was formed by concatenating all of the delay profiles, to which we then applied SVD to extract the PD profiles. This delay profile decomposition method shares a similar idea with several previous approaches (Mitra and Pesaran 1999; Aquino et al. 2012; Muller et al. 2014) in utilizing the time delays between brain regions to infer propagating brain activity.

SVD is to reduce high-dimensional data to lower dimensions of uncorrelated components. The delay matrix is an 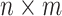matrix, where 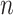is the number of cortical vertices and 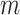is the number of delay profile. The delay matrix was denoted as 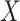. Applying SVD to 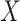generates

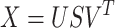(1)

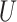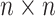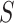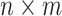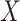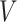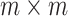where is an orthonormal matrix, whose column represents left singular vector. is an diagonal matrix, whose diagonal entries represent singular values of . is an orthonormal matrix, whose column represents right singular vector. The columns of 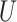were ordered based on the variance explained of 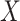. The square of each diagonal singular value in 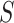denoted the variance of the corresponding vectors. The PD profile is the first column of 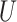, which explains the largest variance of X. It is expected to reflect the major propagating direction.

The rsfMRI time segments with a propagation along the PD profile were defined as described below. The rsfMRI segments with global involvement were projected onto the PD profile direction and the corresponding time–position correlations were then computed. This was done in the same way as the projection of rsfMRI signal onto the PG direction. We repeated the same procedure for the 4 control directions describe above and built a null distribution of time–position correlations by pooling time–position correlations for all the 4 control directions. A positive correlation exceeding the 1.64 SD of the null distribution was regarded as a bottom-up (from SM regions to the default mode network [DMN]) propagation and a negative correlation exceeding 1.64 SD of the null distribution was regarded as a top-down (from the DMN to SM) propagation. The 1.64 SD was used because the critical value for a 90% confidence level with 5% on each side is 1.64. The total time of the top-down or bottom-up propagations was calculated as the total length of all the time segments identified to have a top-down or bottom-up propagation.

The SVD components captured the major propagating directions but in an arbitrary unit rather than in seconds. Therefore, we rescaled the derived PD profile based on the time–position relationship of the time segments with top-down or bottom-up propagations. Specifically, we calculated the regression coefficient of the time–position relationship for each segment with a propagation to estimate the propagating speed with assuming the geodesic distance on the cortical surface between the primary SM regions and the default-mode network is 80 mm (Margulies et al. 2016). We computed the averaged propagating speed across all the time segments with propagations and then utilized it to rescale the PD profiles into the unit of seconds. Applying such rescaling procedure on the synthesized data successfully generated 2 PD profiles that are consistent with the duration of simulated propagating structures (Supplementary Fig. S3).

The z-score maps for averaged bottom-up and top-down propagations were calculated in the surface and volume space as follows. First, the global peaks within the time segments with propagations were located. A time window of 14.4 s (20TR 0.72 s/TR) was defined to contain 10 time points before and 10 time points after each of these global peaks (set as time zero), which the delays of the delay profiles were defined with respect to. The global signal peak was used for aligning the propagation segments also because it showed a sensory-dominant coactivation pattern (Liu et al. 2018) that could be a specific phase of propagations. Second, rsfMRI signals of these time windows were averaged, in both surface and volume spaces, to obtain maps showing averaged propagation, which were then converted to z-score maps according to the formula below:

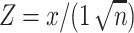(2)

where 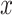is the averaged propagating map value and n is the number of time segments being averaged. Since the rsfMRI signals were standardized in the preprocessing steps and followed the standard Gaussian distribution, their mean across n randomly chosen segments would thus follow a Gaussian distribution of zero mean and 1/n variance. Therefore, the z-score quantifies the significant level at which the computed mean is deviated from zero. The false discovery rate (FDR) is used to correct multiple comparisons. The function ‘fizt_t2p’ from AFNI (Cox 1996) was used to covert the z-score to the P value. The FDR q values were generated by using the 3dFDR program from AFNI (Cox 1996). The associated time–position graphs of the defined time windows with propagations were also averaged.

The cerebrospinal fluid regions were masked out from the averaged top-down and bottom-up propagations in the volume space. The cerebrospinal fluid regions were defined based on the Harvard–Oxford subcortical structural probabilistic atlas (Desikan et al. 2006) using a threshold of 30% probability.

We tested the reproducibility of the PD profile in humans using a split-half analysis. There are 4 sessions of rsfMRI data acquired in 2 different days. For each session of data, we randomly split subjects into 2 equal groups and calculated the PD profile for each group as described above.

The PD profile was also computed on fMRI signals with skipping the temporal filtering and/or spatial filtering, or switching their order (Supplementary Fig. S4). For all these cases, the fMRI signals were also cut into time segments based on the global mean signal calculated using the filtered fMRI signals. Otherwise, we would have time segments with the duration of a few seconds and cannot conduct any meaningful subsequent analyses. The PD profile was also computed on rsfMRI signals after the global signal regression (Supplementary Fig. S5A) or regressing out the physiological signals, that is, the heart rate and respiratory volume (Supplementary Fig. S5B). The heart rate for each session was computed by averaging the time differences of consecutive peaks of the raw cardiac trace in a sliding window of 6.48 s centered at each time point and converting to units of beats-per-minute (Chang et al. 2009). The respiratory volume for each session was computed as the SD of the raw respiratory trace in a sliding window of 6.48 s centered at each time point (Chang et al. 2009). The heart rate and respiratory volume were convolved with the cardiac response function (Chang et al. 2009) and the respiratory response function (Birn et al. 2008), respectively, before regression. The PD profile was computed on fMRI signals from 50 subjects with the lowest head motion (Supplementary Fig. S5C). The head motion was quantified for each subject by the mean framewise displacement (Yoo et al. 2005) over the scanning session. The PD profile of negative local peaks was also computed with cutting rsfMRI signal into time segments based on the positive peaks of the global mean signal and then decomposing the delay profiles defined by local negative peaks within time segments (Supplementary Fig. S6).

Simulation of rsfMRI Signals With Artificial Propagations

To test whether the delay profile decomposition method and the PG method can successfully identify the direction of propagating activity, we simulated fMRI signals on the brain cortical surface containing propagating structures along artificial directions and then applied these 2 methods to the simulated data. The propagating structures were generated by creating a spatial band of high-amplitude signals and then shifting it along the anterior-to-posterior, posterior-to-anterior, or dorsal-to-ventral directions over time on the brain surface. The signal modulation within the activation band along its propagating direction was described as a Gaussian function (sigma = 9 mm). We simulated 6 types of propagating structures that propagated across the whole brain with 2 different speeds in 3 different directions, including those propagating through the whole brain in the anterior–posterior and the opposite directions in 19 and 29 s, respectively, as well as those propagating across the whole brain in the dorsal-to-ventral directions in 11 and 20 s. The simulated propagating structures were convolved with a canonical hemodynamic response function from SPM (https://www.fil.ion.ucl.ac.uk/spm/) and then randomly inserted into background fMRI signals that were modeled as white noise. We randomly inserted 2 of each type of propagating structure along the anterior-to-posterior direction, 1 of each type of propagating structure along the posterior-to-anterior direction, 3 of each type of propagating structure along the dorsal-to-ventral direction into each session of simulated fMRI signals of 1200 time points. The temporal resolution of simulated fMRI signals was assigned as 1 s arbitrarily. The simulated fMRI signals were further spatially smoothed using a Gaussian smoothing kernel (sigma = 2 mm) and temporally filtered using bandpass filtering at 0.001–0.1 Hz. We simulated a total of 50 sessions of fMRI data and then derived their PD profile using the method described above and the PG using the diffusion embedding method (Margulies et al. 2016). For the PG, we computed the functional connectivity matrix of each session and then averaged them across all the 50 sessions. The diffusion embedding method was applied to the averaged connectivity matrix to find its low-dimensional embeddings as the PGs. The code of the diffusion embedding method was provided by the previous study (Margulies et al. 2016). The procedure was repeated for 2 sets of simulated data with different signal-to-noise ratio, which were obtained by setting the peak signal of the activation bands as 2 and 5 times of the SD of background white noise.

Principal Propagating Direction in the Monkey ECoG Data

The delay profile decomposition method described above was also applied to the ECoG data to derive the PD profile for different bandlimited powers. Here we take the gamma-power as an example. The global mean signal was calculated as the averaged ECoG gamma-power across all electrodes. The signals were cut into time segments based on troughs of the global mean signal. Next, the time segments with global involvement were identified if the global peak amplitude exceeded the threshold (the 99th percentile of a null distribution of the global peak amplitudes). The null distribution was created by calculating the global peak amplitudes after randomly shifting the time series of each electrode. The random shifts were uniformly distributed integers between 1 and the number of the time points in the experimental session. The analyses below focused on the time segments with global involvement.

A delay profile was generated for each time segment by computing the relative time delays between the local peak of individual electrodes and the global peak. The local peak of each electrode within each time segment was defined as the local maxima with a value larger than zero. If more than one local peak were detected for a signal segment, the local peak was defined as the one with the largest peak amplitude. We focused on the delay profiles with at least 102 (128 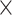 80%) local peaks within a time segment. For those selected delay profiles, if the local peak was less than zero or no local maxima was detected, its relative time delay with respect to the global peak was defined as the mean of its 3 neighboring electrodes. Next, a delay matrix was formed by concatenating all of the delay profiles, to which we then applied SVD to extract the PD profile.

The ECoG gamma-power signals were projected onto the PD profile direction to identify time segments with propagations. The time segments were generated as described above and only those with global involvement, which account for 44.05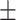 3.59% (mean SD across 4 monkeys) of the total segments, were analyzed. For each time segment, the Pearson’s correlation between the relative timing and position of local peaks across all the electrodes was calculated. To create a threshold for detecting time segments with propagations, we generated a null distribution of time–position correlations along the randomly rotated PD profiles with retaining the relative positions of electrodes, which were obtained by randomly rotating the PD profiles on a coordinate plane with random degrees with respect to the x, y axes. The time segments with a bottom-up (from the SM regions to the high-order regions) propagation along the PD profile were identified if the time–position correlation had a positive value exceeding the threshold (1.64 SD of the null distribution of time–position correlations). The time segments with a top-down (from the high-order regions to the SM regions) propagation along the PD profile were identified if the time–position correlation had a negative value exceeding the threshold (1.64 SD of the null distribution of time–position correlations). The averaged top-down and bottom-up propagation maps were calculated as follows. First, we identified the global peaks for the time segments with propagations. Then, a 12-s time window (60 0.2 s; the temporal resolution of bandlimited power signals is 0.2 s) centering on each of these global peaks was defined to cover 30 time points before and 30 time points after the global peak. Second, we averaged the ECoG bandlimited power signals and associated time–position graphs of these time windows to obtain the averaged propagating maps.

Considering that SVD components captured the major propagating directions in an arbitrary unit, we rescaled the derived PD profile to second unit using the same strategy as we used for human rsfMRI data. Briefly, we calculated the regression coefficient of the position–time relationship for each segment with a propagation to estimate the propagating speed. Then, the averaged propagating speed across all the time segments with propagations was computed and utilized to rescale the PD profiles into the unit of seconds.

We quantified the cross-hierarchy pattern of the PD profile from monkeys by comparing it with the cortical myelination map, which has been suggested to be a good estimation of cortical anatomical hierarchy (Burt et al. 2018). Given that the cortical myelination map was available on the average Yerkes19 macaque surface (Donahue et al. 2016), we manually mapped the location of 128 electrodes of each monkey onto the average Yerkes19 macaque surface (Donahue et al. 2016) based on the gyrus and sulci of the brain (see Supplementary Fig. S7). Next, we extracted a vector of the myelination values at the locations of the 128 electrodes for each monkey. Then, a Pearson’s correlation between the PD profile and this myelination vector was calculated to estimate their spatial similarity, which was used for quantifying the cross-hierarchy pattern of the PD profile.

The PD profile was also calculated from ECoG gamma powers with skipping the temporal filtering and/or spatial filtering or switching their order (Supplementary Fig. S8).

Fine-Scale Propagations Within Sensory Modalities in the rsfMRI Signals

A simple linear regression was applied to examine the relationship between the delay in the PD profile and the hierarchy level across brain regions within each sensory modality. Each vertex was numbered according to the hierarchy level of the brain region to which the vertex belongs. In the simple linear regression model, the hierarchy level of vertices was the predictor variable and the delay value was the response variable. A significant P value of the regression coefficient would indicate whether the propagation is along the hierarchy order in a sensory modality.

The hierarchical level of different visual regions was determined according to (Felleman 2009). The hierarchy of the auditory system was determined according to (Okada et al. 2010; Moerel et al. 2014). The hierarchy of the somatosensory cortex was determined according to (Felleman and Van Essen 1991). The retinotopy map (Benson et al. 2018) was used to identify the peripheral and foveal areas of the V1–V4. Peripheral and foveal areas in the V1–V4 were divided based on a cutoff value of 2.5 in the eccentricity map. The atlas of topographic subareas in the somatosensory–motor strip (Van Essen and Glasser 2018) was used to identify brain regions responsible for face, upper limb, trunk, lower limb, and eye. The HCP’s multimodal cortical parcellation atlas (Glasser et al. 2016) was used to locate different brain regions on the cortical surface. All these atlases can be downloaded from the website (https://balsa.wustl.edu).

Subcortical Coactivations/Deactivations Associated With rsfMRI Propagations

The temporal dynamics of subcortical regions at the top-down and bottom-up propagations were studied mainly based on the z-score maps of the propagations in the volume space, which were obtained as described above. We simply averaged these z-score maps of various time points across voxels within any subcortical region of interests. The location of thalamic nuclei/regions was determined according to Morel Atlas (Krauth et al. 2010). The Harvard ascending arousal network (AAN) atlas was used to locate the brainstem nuclei of the AAN (Edlow et al. 2012). The masks of the substantia nigra (SN), the nucleus accumbens (NAc), and the nucleus basalis (NB) were acquired by taking the overlap between the brain regions showing significant (Z ≤ 7) deactivations at time zero z-score map for the bottom-up propagation and those defined by brain atlases of SN (Keuken and Forstmann 2015), NAc (Desikan et al. 2006), and NB (Liu et al. 2018). The deactivations in SN and NAc appeared to be only in a subsection of atlas-defined structures (Supplementary Fig. S9).

Modulation of Cross-Hierarchy Propagations Across Different Brain States

We quantified and compared the occurrence rate of the top-down and bottom-up propagations across different brain states or sessions that are likely associated with distinct arousal levels. For the human rsfMRI data, we classified fMRI sessions into subgroups with different arousal levels, which were estimated in 2 different ways. First, we adapted a template-matching method (Chang et al. 2016) to estimate the drowsiness level based on a previous study (Gu et al. 2020). Briefly, we calculated the spatial correlation between individual rsfMRI time points and a global coactivation pattern that has been linked to transient arousal events previously (Liu et al. 2018). Then, the drowsiness index was quantified by extracting the envelope amplitude of this spatial correlation time course. The mean drowsiness index over each session is used to estimate the general arousal state of subjects in a specific session. The envelope amplitude was computed as the absolute value of the Hilbert transform. Since the presence of this global coactivation pattern suggests the occurrence of transient arousal events and thus relatively drowsy state, a higher value of this fMRI-based metric was corresponding to a drowsier state. Based on this fMRI-based drowsiness measure, we divided all of the rsfMRI scanning sessions into 3 groups of equal size (N = 613 sessions for each, each session is 15 min in length) with low, medium, and high drowsiness levels and then compared the occurrence rate of the rsfMRI propagations. Secondly, we identified, based on the note of HCP experimenters, a subset of 117 rsfMRI sessions in which the subjects were noted to be sleeping (Glasser et al. 2018). We then compared the occurrence rate of propagations in this subset and all other sessions (N = 1723 sessions). For the ECoG gamma-band powers concatenated from the 4 monkeys, we compared the occurrence rate of the top-down and bottom-up propagations across sessions collected in 3 different conditions: 11 sessions (each session is 25 min in length) for eyes-open state, 10 sessions for eyes-closed state, 15 sessions for sleep state.

Since these propagations are detected only in rsfMRI/ECoG segments with global involvement, and their occurrence rate changes across arousal states might simply reflect a change of the global signal, which has been shown to be closely related to brain arousal level (Kiviniemi et al. 2005; Fukunaga et al. 2006; Licata et al. 2013; Wong et al. 2013, 2016). For this reason, we also calculated and compared the ratio of the top-down propagations to the bottom-up propagations that should be exempted from any potential bias caused by the change of globally averaged signal.

The statistical significance of the difference in the occurrence rate of propagations, as well as its ratio, across different arousal states were determined using permutation test. For each comparison described above, we randomly divided the data into subgroups of the same size, calculated the differences, and repeated the procedure 1 000 000 times to build a null distribution for the differences. Then, we obtained the P values of the observed differences by comparing them with the null distributions.

Results

Infra-Slow Propagations Along the PG of rsfMRI Connectivity

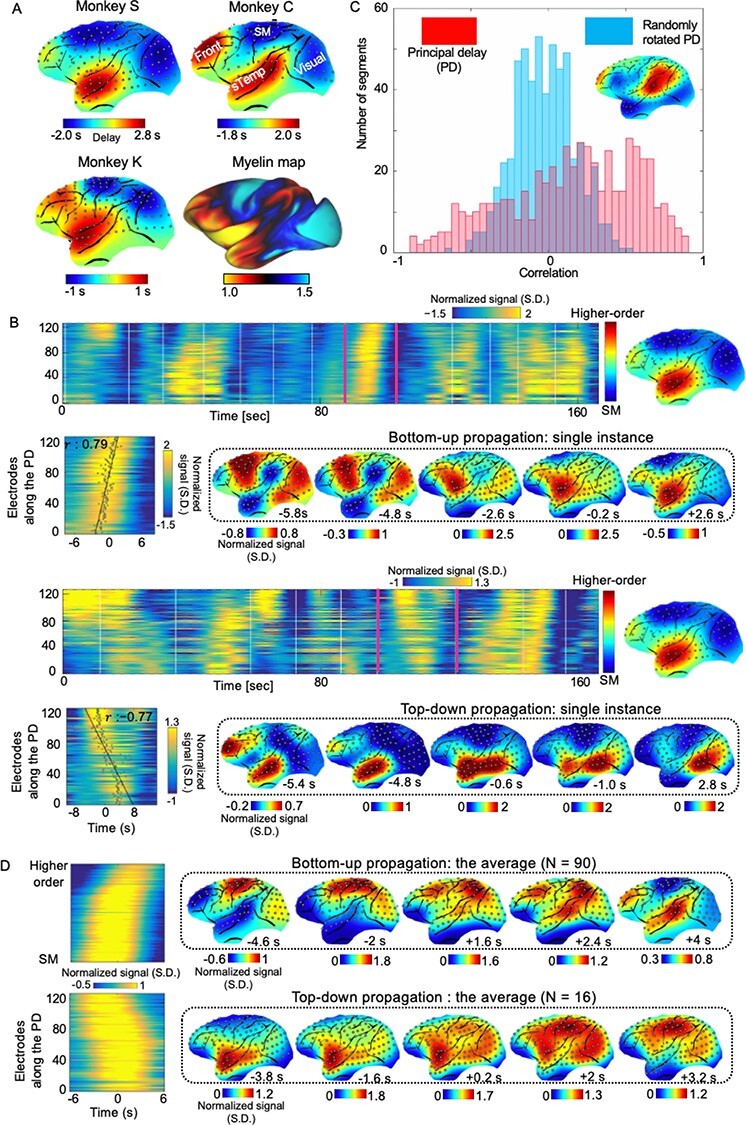
We first examined and characterized infra-slow propagating activity in rsfMRI signals using data from 460 HCP subjects. Simple visual inspection of preprocessed signals suggested clear propagating activity that often coursed from higher-order cognitive areas, mostly the default-mode network, to lower-order SM regions, a direction similar to the PG of rsfMRI connectivity, or in an opposite direction. Following previous work (Margulies et al. 2016), the PG was obtained by decomposing rsfMRI connectivity data using a data-driven method, and it reveals a gradient of functional connections that aligns well with the cortical hierarchy defined both anatomically and functionally (Margulies et al. 2016). To visualize the propagating activity in a 2D representation, we projected the rsfMRI signals onto the PG direction (Fig. 1A) to generate time–position graphs (Fig. 1B). It was immediately noticed that local rsfMRI peaks at various PG positions tended to cluster together in time and form continuous bands, some of which were tilted and propagated either from the SM to the default-mode network or in an opposite direction (Fig. 1B, upper), which we will refer to as the bottom-up and top-down propagations henceforth. In contrast, projecting the same signal onto a few other directions, including one obtained by randomly rotating the PG map on brain surface (Fig. 1B, bottom), revealed straightly vertical bands, suggesting an absence of propagating behavior along these directions. To locate and quantify single propagating instances, we cut the rsfMRI signals into time segments based on troughs of the global mean signal, which successfully separated the bands in the time–position graphs (Fig. 1B). For each segment, we correlated the relative timing of local rsfMRI peaks with their relative position along different directions. A high time–position correlation would suggest a propagation along the corresponding direction (Fig. 1C and Animations 1–2). We then computed and summarized the time–position correlations for all rsfMRI segments showing global involvement (defined as the global signal peak exceeding a threshold established using a null model, see Methods and Supplementary Fig. S10 for the details), which account for 58.80% of the total segments. The time–position correlations of local peaks for the PG direction showed a non-Gaussian, bimodal (P = 0.012, Hartigan’s dip test) distribution with a relatively larger peak for positive correlations, indicating significant propagations along this axis, particularly in the bottom-up direction (Fig. 1D, the left column). In contrast, they showed Gaussian-like, single-mode distributions for the other 4 control directions (Fig. 1D, the right 4 columns), which are significantly different from the PG distribution (P = 0 for all 4 control directions, 2-sample Kolmogorov–Smirnov test). This is even true for the second gradient of rsfMRI connectivity (Margulies et al. 2016) that showed a strong motor-to-visual contrast (Fig. 1D, the second column), suggesting a lack of propagations along this direction in these rsfMRI time segments. All these results suggest the existence of significant rsfMRI propagating activity along the PG direction.

Figure 1 .

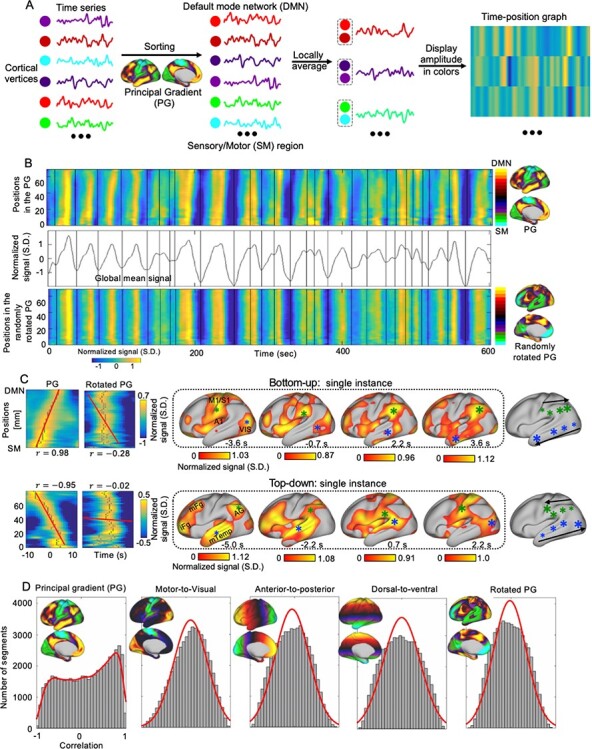
RsfMRI propagations along the PG of rsfMRI connectivity. (A) Illustration of the steps for projecting rsfMRI signals onto a specific direction, for example, the PG, to produce a time–position graph. The PG was computed in a previous study (Margulies et al. 2016) by applying the diffusion mapping to the averaged connectome matrix and indicted a transition across brain hierarchies from the SM regions to the DMN. (B) The time–position graphs for the PG and a control direction from a representative subject show clear bands, which are tilted only in the PG time–position graph. The bands can be well separated by cutting rsfMRI segments according to troughs (black vertical lines) of the global mean signal. The vertical axis of the time–position graph represents the cortical distance from core regions of the DMN to the SM on the PG (Margulies et al. 2016). (C) Two exemplary rsfMRI segments with propagations in 2 opposite directions along the PG, that is, the DMN-to-SM (i.e., top-down) and SM-to-DMN (i.e., bottom-up) propagations. The relative timing of the local rsfMR peaks show a significant correlation with their positions along the PG but not in the control direction (left), and the propagating activity can be viewed on brain surface (right). Gray dots in the time–position graphs indicate the local rsfMRI peaks and the red lines are the regression lines for their time–position relationship. The time is with respect to the global mean peak of the segment. These surface maps at each time point were demeaned and only the values larger than 0 were shown with colors. Note that the propagation patterns are largely mirrored in the 2 hemispheres, so only the left hemisphere results were shown here. The exemplary propagating patterns on both the lateral and medial surface in 2 hemispheres can be found in Supplementary Fig. S29A. Green and blue asterisks mark approximately spatial peaks with a larger size representing a later time point and the timing being denoted by the direction of the black arrows. (D) The distributions of the time–position correlations of rsfMRI segments in 5 different directions. The PG direction is associated with a clear bimodal distribution that is significantly different from those of the motor-to-visual, the anterior-to-posterior, the dorsal-to-ventral, and the rotated PG directions (P = 0 for all 4 control directions, 2-sample Kolmogorov–Smirnov test). Abbreviations: VIS, visual cortex; M1, primary motor cortex; S1, primary somatosensory cortex; iFG, inferior frontal gyrus; mFG, middle frontal gyrus; AG, angular gyrus; mTemp, middle temporal cortex.

The Cortical Hierarchical Axis Is the Dominant Direction of rsfMRI Propagations

We then developed a data-driven method to obtain main trajectories of rsfMRI propagations without setting a priori direction. The existing QPP method was designed to find repeated spatiotemporal patterns that are not necessarily propagations (Thompson et al. 2014), whereas the lag structure/thread method relied on session-based quantification of temporal lags in which the delays caused by antidirection propagations may cancel each other (Mitra et al. 2014; Mitra, Snyder, Blazey, et al. 2015a). We show that the propagations can cause systematic delays of local peaks and thus a significant time–position relationship along the propagating direction (Fig. 1C). To identify the major propagating direction in a data-driven way, we derived a delay profile for each rsfMRI segment by computing the relative delay of local peaks with respect to the global mean peak and then applied an SVD to extract the principal components of all the delay profiles, which are expected to represent main trajectories of propagating activity (Fig. 2A). The application of this method to synthesized data containing simulated propagating structures successfully recovered 2 propagating directions (Fig. 2B). In comparison, the diffusive embedding method, which was employed to derive the PG of rsfMRI connectivity (Margulies et al. 2016), recovered the more frequent propagation but not the other one (Fig. 2B and Supplementary Fig. S3). Decomposing the delay profiles of the rsfMRI segments of global involvement generated a principal delay (PD) profile (Fig. 2C), that is, the first principal component (4.22% of the total variance, see Supplementary Fig. S11 for additional components), that is extremely similar (r = 0.93 across 59 412 vertices, P = 0) to the PG of rsfMRI connectivity (Fig. 2D). In particular, the primary visual cortex (V1) appears to be an outlier for the overall hierarchical arrangements suggested by both maps. This deviation is, however, consistent with our observation that the V1 coactivates with the DMM in the cross-hierarchy propagations (Fig. 1C for a single instance example). This PD profile is highly reproducible across sessions and subject groups (Supplementary Fig. S12) and distinct from the lag map measured through dynamic susceptibility contrast magnetic resonance imaging (MRI) scans (r = 0.0035, P = 0.39; Supplementary Fig. S13) (Tong et al. 2017). We then projected the rsfMRI signals onto this principal propagating direction and identified segments showing a significant (P < 0.05, compared with a pooled null distribution from the 4 control directions) time–position correlation. The top-down propagations (N = 8519) and bottom-up propagations (N = 18 114) were found to account for 9.08% and 19.7% of the total scanning time, respectively, with an average speed of 13.45 ± 7.78 and 13.74 ± 7.51 mm/s (mean ± SD), respectively. We obtained the averaged patterns of these 2 types of propagations in both the time–position graph and brain surface (Fig. 2E), which are consistent with those of single instances (Fig. 1C) and very similar to the average patterns of propagations detected with respect to the PG (Supplementary Fig. S14). While these 2 types of propagations are largely the time-reversed version of each other, certain differences are evident, including the coactivation of the V1 and the DMN in the late phase of the bottom-up propagations was not seen in the top-down propagations (Fig. 2E).

Figure 2 .

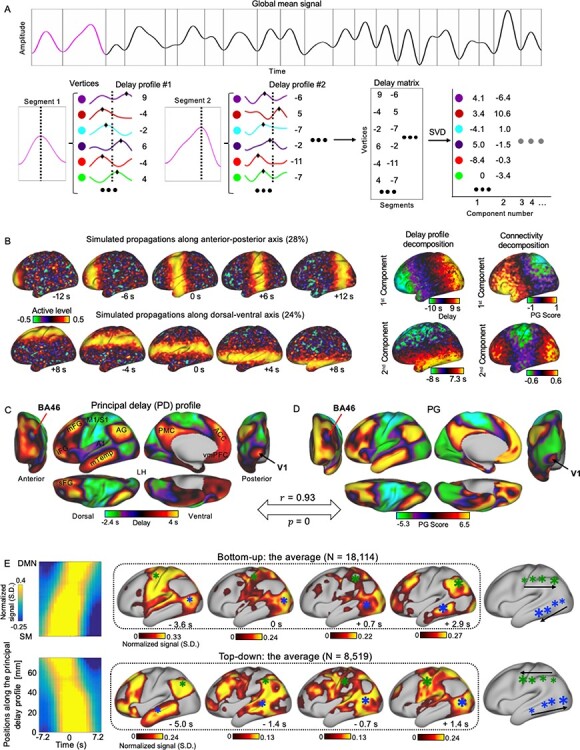
The major propagating direction of rsfMRI signals is highly similar to the PG of rsfMRI connectivity. (A) Illustration of the procedures for deriving the PD profiles that represent the major propagating directions of rsfMRI signals. Specifically, the fMRI signals were cut into time segments based on the troughs of the global mean signal denoted by the gray vertical lines. Next, a delay profile was computed for each segment as the relative time delays of the local peak (black diamonds) at each cortical vertex with respect to the global peak (black dashed line). Finally, an SVD was applied to the delay matrix composed by delay profiles to extract the PD profile. (B) Decomposing delay profiles of synthesized fMRI data (left) using the proposed method recovered the directions of simulated propagating structures (middle). The decomposition of the connectivity matrix of the synthesized signals using the PG method recovered the dominant direction but not the second one (right). (C) The application of the proposed method to real rsfMRI data produced the PD profile representing the principal direction of infra-slow rsfMRI propagations, which is extremely similar (r = 0.93, P = 0) to (D) the PG of rsfMRI connectivity, including detailed features at the V1 and Brodmann area 46 (BA 46). (E) The averaged bottom-up (top, N = 18 114) and top-down (bottom, N = 8519) propagations as presented on the time–position graphs (left) and the brain surface (right). The averaged propagating patterns on both the lateral and medial surface in 2 hemispheres were shown in Supplementary Fig. S29B. Abbreviations: A1, primary auditory cortex; sFG, superior frontal gyrus; PMC, posteromedial cortex; ACC, anterior cingulate cortex; vmPFC, ventromedial prefrontal cotex.

The above analyses were repeated on the rsfMRI signals going through different spatial and temporal filtering procedures. Despite some fine-scale differences at the SM regions, the overall cross-hierarchy contrast remained highly similar with different filtering procedures (Supplementary Fig. S4). Similar PD profiles were also derived after regressing out the global signal or physiological signals or using the sessions with very low head motions (Supplementary Fig. S5). Temporal relationships between the detected propagations (Supplementary Fig. S15) suggested that they occurred mostly as isolated events but did show weak periodicity of approximately 12 s when appearing as clusters. These propagations are also similar to both lag thread (Mitra, Snyder, Blazey, et al. 2015a) and the QPP (Thompson et al. 2014) derived from the same dataset (Supplementary Fig. S16). Altogether, the infra-slow rsfMRI propagations are primarily along a hierarchical axis linking the higher-order and the lower-order brain regions, as represented either by the PG or our PD profile.

Infra-Slow Propagations in Monkey ECoG Signals Follow a Similar Cross-Hierarchy Trajectory

To determine whether similar propagations are present in electrophysiological data free of hemodynamic contributions, we applied the same method to large-scale ECoG recordings from 4 monkeys in an eyes-closed rest condition. Using the same dataset, we have previously identified brain networks highly similar to resting-state connectivity networks based on power signal correlations (Liu et al. 2014). We first focused on the gamma-band (42–95 Hz) power that is known to be tightly linked to fMRI signals (Logothetis et al. 2001). The principal propagating direction (detected as the second component in one of 4 monkey) obtained by decomposing delay profiles of ECoG gamma-power showed a clear cross-hierarchy contrast between the SM areas and the higher-order frontal, anterior temporal, and parietal regions (Fig. 3A). This pattern, which is reproducible in all 4 monkeys (Fig. 3A and Supplementary Fig. S17), is inversely similar (r = −0.71 ± 0.067, P < 10⁻¹⁶, see Supplementary Fig. S7 for electrode mapping on a macaque brain surface; Donahue et al. 2016) to the cortical myelination map that has been suggested to be a good approximation of cortical hierarchy (Burt et al. 2018). To further validate the existence of infra-slow propagations, we projected the ECoG gamma power signals onto this propagating direction in a similar way as the human rsfMRI analysis. The resulting time–position graphs clearly contained tilted bands with significant time–position correlations among local peaks of individual electrodes, which are corresponding to the cross-hierarchy propagating activity on the brain surface (Fig. 3B and Animations 3–4). The time–position correlations for this cross-hierarchy axis showed a heavy tailed distribution that is significantly different (P = 1.65 × 10⁻³⁴, 2-sample Kolmogorov–Smirnov test) from that of control directions (Fig. 3C), which were obtained by rotating the PD profiles at a random angle to preserve the spatial continuity of electrodes (Supplementary Fig. S17). Similar to the human results, the distribution is also asymmetric and characterized by a much larger peak for positive time–position correlations, suggesting more bottom-up propagations. We identified ECoG segments with propagating activity based on the time–position correlations and averaged them to obtain the mean propagating patterns of ECoG gamma power (Fig. 3D), which are similar to those of single instances.

Figure 3 .

Cross-hierarchy propagations in the monkey ECoG signals. (A) The PD profile of the ECoG gamma-band (42–95 Hz) power shows a clear contrast between the SM areas and the higher-order brain regions, including the frontal, anterior temporal, and parietal cortices. This pattern is consistent across monkeys and inversely similar to the cortical myelination map of the monkey, which has been suggested as a good surrogate for estimating the cortical hierarchy (Burt et al. 2018). (B) Single exemplary instances of the top-down (i.e., from the higher-order to the SM regions) and bottom-up (i.e., from the SM to the higher-order regions) propagations as shown in the time–position graphs and on the brain surface. (C) The time–position correlations of the ECoG gamma-power segments for the principal propagating direction show a heavy tailed distribution that is significantly different (P = 1.65 × 10⁻³⁴, 2-sample Kolmogorov–Smirnov test) from the one obtained for control directions. The distributions were obtained by pooling the results from all 4 monkeys. (D) The averaged patterns of the top-down (N = 16) propagations for monkey S and bottom-up (N = 90) propagations for monkey C as shown in the time–position graphs (left) and the brain surface (right). Abbreviations: sTemp, superior temporal cortex; Front, frontal cortex; Visual, visual cortex.

To know whether similar cross-hierarchy propagations are also present in resting-state brain activity of other frequency ranges, we repeated the same analysis for ECoG power signals of 4 other bands, that is, delta (1–4 Hz), theta (5–8 Hz), alpha (9–15 Hz), and beta (17–32 Hz) bands. It appeared that the PD profiles for the powers of the lower-frequency bands are more characterized by a big contrast between the somatosensory/motor areas and the visual regions (Fig. 4A), and their spatial correlation with the cortical myelination map of monkeys is significantly (P < 0.01 for all 4 bands compared with the gamma band) lower than the gamma-band power (Fig. 4B and Supplementary Figs S18–S22). Since it has been suggested that the low (30–80 Hz) and high (80–150 Hz) gamma activity may originate from different sources (Ray and Maunsell 2011), we derived the PD profiles separately for the powers of the low and high gamma bands. Similar infra-slow propagations are present in the powers of these 2 gamma bands (Supplementary Fig. S23). We repeated the same analyses on the ECoG gamma-band power going through different spatial and temporal filtering procedures, and the overall cross-hierarchy contrast of the PD profile remained similar (Supplementary Fig. S8). In summary, the gamma-band power of monkey ECoG signals exhibited infra-slow propagations similar to human rsfMRI in terms of the time scale (~5–10 s) and, more importantly, the dominant propagating direction across the cortical hierarchy.

Figure 4 .

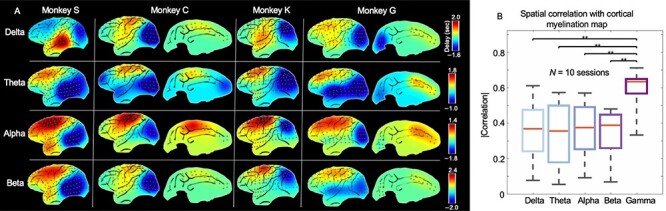
A reproducible cross-hierarchy propagating direction was present most strongly in the gamma-band power of ECoG signals. (A) The PD profiles derived for the ECoG powers of 4 other frequency bands: delta, 1–4 Hz; theta, 5–8 Hz; alpha, 9–15 Hz; beta, 17–32 Hz. (B) The spatial similarity between different PD profiles and the monkey cortical myelination map that has been suggested to be a good approximation of cortical hierarchy (Burt et al. 2018). The PD profiles and associated statistics were derived with respect to ten 25-min eyes-closed sessions from all the monkeys. The error bar represents the standard error of mean. Asterisks represent the level of significance: ^**: 0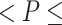.001  0.01.

Fine-Scale Propagations Within Sensory Modalities Are Against the Direction of Global Propagations

The anomalous position of the V1 in the PG and the PD profile (Fig. 2C,D), that is, having similar scores/delays with the DMN, motivated us to examine fine-scale propagations within sensory modalities that are embedded in the global cross-hierarchy propagations. Within the visual system, the PD profile showed the most negative delay values at 3 isolated brain areas, including the MT+ complex, the dorsal stream visual cortex, and the ventral stream visual cortex (Glasser et al. 2016), and increased its value toward the early visual cortex, as well as retinotopically from the periphery toward foveal areas (Fig. 5A). A simple linear regression confirmed a significant relationship between the delay value and the hierarchy level of brain regions (P = 3.3 × 10⁻²⁹⁸ for fV1–fV2–fV3–fV4–V4t–MT–MST–V6–V6A; and P = 0 for pV1–pV2–pV3–pV4–V4t–MT–MST–V6–V6A), which was defined based on a previous study (Felleman 2009) (Fig. 5B). This pattern is consistent with the trajectory of the bottom-up (i.e., SM to DMN) propagations within the visual cortex (Fig. 5C), which is actually from high-hierarchical visual areas to lower low-hierarchical ones. We then had closer inspection of the PD profile within the auditory and somatosensory systems to see whether the similar trend is present. Within the auditory system, the PD profile displayed a clear gradient across hierarchies from the A4, to belt regions, and then to A1 (P = 0) (Fig. 5D,E), which is again consistent with the bottom-up propagation of local rsfMRI peaks (Fig. 5F). Local propagations within somatosensory system (Fig. 5G,H) appeared to follow more closely the somatotopic arrangement and show a strong contrast between limbs areas and eyes, face, and trunk areas (Fig. 5I). Nevertheless, the PD profile indeed showed a gradual and significant (P = 6.1 × 10⁻³¹³) increase of value from the Brodmann area 2 (BA 2), to BA 1, and then to BA 3b and BA 3a (Fig. 5J). Similar analyses were also performed for the PG map, and the weaker but still significant relationships were found between the PG value and the hierarchical level (Fig. 5 and Supplementary Fig. S24). Outside the sensory systems, the very negative delays were also found in the frontal eye field, intraparietal sulcus, and BA 46 (Fig. 5K). Altogether, these regions compose a task-positive network known to have strong negative rsfMRI correlations with the default-mode network (Fox et al. 2005). To summarize, the local propagations within the sensory systems, which are embedded in the global cross-hierarchy propagations, appear to start/end at the sensory association areas and are opposite to the overall direction of the global propagation.

Figure 5 .

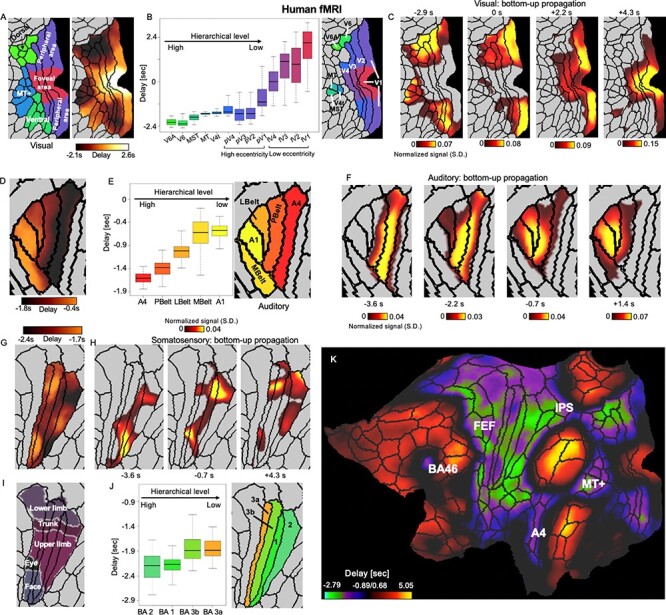
Local embedded propagations within the sensory modalities in human fMRI signals. (A) The local contrast of the PD profile within the 3 visual-related regions defined by a multimodal parcellation atlas (Glasser et al. 2016). (B) The averaged delay values of 13 visual parcels that were arranged according to their hierarchical (Felleman 2009) and retinotopic relationships (Benson et al. 2018). It should be noted that we do not assume any hierarchical relationship between the foveal and peripheral visual parcels. (C) The local trajectory of the bottom-up propagation within the visual system closely follows the PD profile, that is, from the visual association areas to the early peripheral visual areas and then to the early foveal visual regions. (D–F) Results for the auditory system indicated a similar contrast and local propagation between the primary and association auditory areas. (G–I) Results for the somatosensory system show a weaker but still significant relationship between the delay and hierarchical level of 4 somatosensory parcels. The contrast of the PD profile also shows certain correspondence with (J) the somatotopic arrangement (Van Essen and Glasser 2018). (K) The PD profile on a flat brain surface suggests a few other brain regions outside the sensory systems showing large negative delays. Together with the sensory association areas, they compose the task-positive regions that have been shown previously to have strong negative-correlation with the DMN (Fox et al. 2005). Abbreviations: V6A, area V6A; V6, sixth visual area; MT+, MT+ complex; MST, medial superior temporal area; MT/V5, middle temporal area/fifth visual area; V4t, V4 transition zone; V4, fourth visual area (pV4 and fV4 are peripheral and foveal V4, respectively, same thereafter); V3, third visual area; V2, second visual area; V1, primary visual cortex; A4, auditory 4 complex; PBelt, parabelt complex; LBelt, lateral belt complex; MBelt, medial belt complex; BA, Brodmann area; FEF, frontal eye fields; IPS, intraparietal sulcus area.

Subcortical Coactivations/Deactivations Associated With the Cross-Hierarchy Propagations

We then examined subcortical changes associated with these cortical propagations for additional evidence for its neural origin and also for important clues for underlying mechanisms. We averaged, in the volume space, the rsfMRI segments showing the propagations and converted them to Z-scores that represent the significance level of the deviation from the temporal mean. We found that the bottom-up cortical propagation is associated with strong, sequential coactivations/deactivations in specific subcortical regions. At the very early phase (t = −5.0 s, with respect to the global signal peak) of this propagation, the weak coactivations at the SM regions are accompanied by strong deactivations in the default-mode network and extended areas. These cortical changes are associated with strong thalamic deactivations at the anterior nuclei (AN; peak Z: −24.41, mean Z: −12.98) and the dorsal part of the parvocellular division of the mediodorsal nucleus (MDpc; peak Z: −24.43, mean Z: −7.19), and to a less extent at the lateral dorsal (peak Z: −19.56, mean Z: −10.73), the ventral lateral (VL; peak Z: −17.42, mean Z: −8.11), and the central lateral (peak Z: −26.45, mean Z: −8.73) nuclei of the thalamus (Fig. 6A). In contrast, the significant thalamic coactivations are mostly confined at the anterior pulvinar (PuA; peak Z: 8.98, mean Z: 5.05). Starting from this time point, the thalamic coactivations started to spread from the PuA first to the posterior and ventral parts of the thalamus, which include many sensory relay nuclei, such as the ventral posterior medial, the ventral posterior lateral nuclei and other parts of the pulvinar, and later to the AN and MDpc (Fig. 6B–D). Along this process, the cortical and thalamic co(de)activations show striking correspondence consistent with known anatomical connections. For example, the V1 deactivation (t = −5.0 s) is associated with very specific deactivation at the lateral geniculate nucleus (Fig. 6A, the first row), and the maximal A1 coactivation (t = 1.4 s) is also accompanied by the peak coactivation at the medial geniculate nucleus (MGN) (Fig. 6C, left). Outside the thalamus, a number of brainstem regions, including multiple nuclei related to arousal regulation, that is, the dorsal raphé (peak Z: −13.17, mean Z: −6.73), the median raphé (MR; peak Z: −9.07, mean Z: −6.14), the pendunculopontine nucleus (peak Z: −8.46, mean Z: −5.65), the ventral tegmental area (VTA; peak Z: −11.02, mean Z: −6.79), and the locus coeruleus (LC; peak Z: −9.46, mean Z: −6.23) showed significant deactivations at very early phase (t = −6.5 s) of the bottom-up propagation (Fig. 6E), along with the strong cortical deactivations at the precuneus and the cingulate (Fig. 6E, top right). The early deactivation of these brainstem nuclei was followed by a slow and gradual deactivation of 3 subcortical regions of arousal relevance, including the NB, the ventral part of the NAcc at the basal forebrain, and the SN, which reached their peak deactivations around the middle of this propagation (t = 0) with widespread cortical coactivations (Fig. 6F,G). Interestingly, the subcortical dynamics at the top-down propagation does not simply mirror that of the bottom-up propagation (Fig. 6 and Supplementary Fig. S25). Most notably, the strong deactivations are largely absent for the AN/MD and the brainstem nuclei throughout the top-down propagation (Fig. 6 and Supplementary Fig. S25). In summary, the cortical propagations are associated with coactivations and deactivations in corresponding thalamic nuclei as well as the deactivation of subcortical regions of arousal relevance.

Figure 6 .

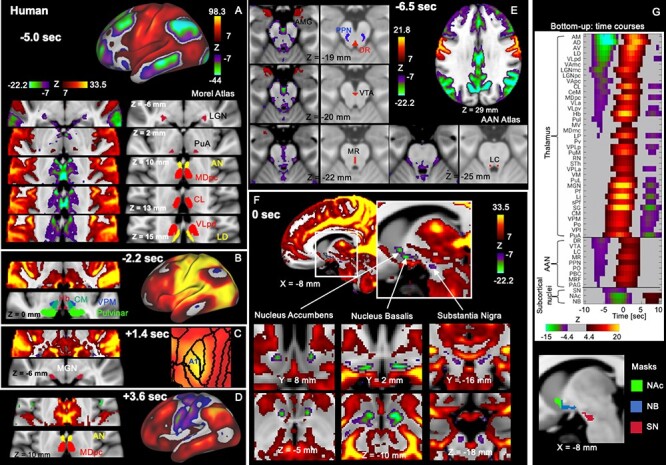
Subcortical co-(de)activations associated with the bottom-up propagation. (A–D) The thalamic coactivations/deactivations at different phases of the bottom-up propagations show a good correspondence with the cortical changes. The thalamic nuclei were located using the Morel Atlas (Krauth et al. 2010). The time is with respect to the global mean peak. (A) The early deactivation of the default-mode network and V1 are associated with the thalamic deactivations in a few higher-order nuclei, particularly the AN and a part of MDpc, as well as the LGN, but the thalamic coactivation is only limited to the PuA. The thalamic coactivations then spread first to the posterior and ventral part of the thalamus (B) and eventually to the AN and MDpc at very late phase (D). (C) The MGN shows specific coactivations with the maximal A1 coactivation. (E) The earliest phase of the bottom-up propagation (t = −6.5 s) involves the deactivations of a few brainstem nuclei of the AAS, which were located using the Harvard AAN Atlas (Edlow et al. 2012). The plots also showed the early coactivation of the AMG in the brainstem. (F) Following the early brainstem deactivations, the NAc at the ventral striatum, the NB at the basal forebrain, and the SN at the brain stem started to slowly deactivate and reach the plateau with the widespread cortical coactivation. (G) The temporal dynamics of the subcortical regions shown in (A–F). The Z-score time courses were averaged within 37 thalamic regions of interest (ROIs) defined by the Morel’s atlas and 9 brainstem ROIs defined by the Harvard AAS atlas, as well as the 3 ROIs (NAc, NB, and SN) we defined by combining our results with corresponding brain atlases (Desikan et al. 2006) (see the bottom for the masks we used). Each group of ROIs were sorted according to their value at t = −5.8 s. The q-value after FDR corresponding to z-score 4.4 and 7 is 10⁻⁵ and 7.4 × 10⁻¹³, respectively. Error bars represent the standard error of the mean (SEM). Asterisks represent the level of significance: ^*: 0.01 P 0.05; ^**: 0.001  P  0.01; ^***: P  0.001. Abbreviations: AMG, amygdala; MDmc, mediodorsal nucleus magnocellular part; MV, medioventral nucleus; CL, central lateral nucleus; CeM, central median nucleus; CM, centre median nucleus; Pv, paraventricular nucleus; Hb, habenular nucleus; Pf, parafascicular nucleus; sPf, subparafascicular nucleus; PuM, medial pulvinar; PuI, inferior pulvinar; PuL, lateral pulvinar; LP, lateral posterior nucleus; SG, suprageniculate nucleus; Li, limitans nucleus; Po, posterior nucleus; LGN, lateral geniculate nucleus; VPLa, ventral posterior lateral nucleus anterior part; VPLp, ventral posterior lateral nucleus posterior part; VPM, ventral posterior medial nucleus; VPI, ventral posterior inferior nucleus; VLa, ventral lateral anterior nucleus; VLpd, ventral lateral posterior nucleus dorsal part; VLpv, ventral lateral posterior nucleus ventral part; VAmc, ventral anterior nucleus magnocellular part; VApc, ventral anterior nucleus parvocellular part; VM, ventral medial nucleus; AD, anterior dorsal nucleus; AM, anterior medial nucleus; AV, anterior ventral nucleus; LD, lateral dorsal nucleus; AN, anterior nucleus; STh, subthalamic nucleus; DR, dorsal raphe; PPN, pedunculopontine nucleus; PO, pontis oralis; PBC, parabrachial complex; MRF, midbrain reticular formation; PAG, periaqueductal gray.

The Modulation of the Cross-Hierarchy Propagations Across Brain States of Vigilance

The deactivations of arousal-related subcortical regions suggested a potential link between the bottom-up propagation and the brain arousal. Consistent with this notion, the rsfMRI lags between different brain regions were found to be completely reversed from wake to sleep in humans (Mitra et al. 2016) and also from wake to anesthesia in mice (Mitra et al. 2018). We thus suspected that the cross-hierarchy propagations in 2 opposite directions are sensitive to changes of brain arousal state. To test this hypothesis, we divided all rsfMRI sessions into 3 groups with the low, medium, and high level of drowsiness according to an adapted fMRI-based drowsiness estimation (Chang et al. 2016; Gu et al. 2020) and then compared their cross-hierarchy propagations. The ratio of the cross-hierarchy propagations in the 2 opposite directions is significantly different (P = 0 low vs. medium; P = 0 high vs. low; permutation test) in the 3 groups with the low drowsiness group having less bottom-up but more top-down propagations (Fig. 7A and Supplementary Fig. S26). The fMRI-based drowsiness estimation involved only a template-matching process that is not expected to introduce any bias toward any propagating directions. To have a more independent estimation of brain arousal level, we also computed this ratio in a subset of the sessions in which subjects were noted by experimenters to be sleeping during rsfMRI scanning. This subset of rsfMRI sessions showed significantly lower (P = 0.021, permutation test) ratio compared with other sessions (Fig. 7B and Supplementary Fig. S26). Consistent with these results, the bottom-up propagations are associated with the larger global signal peaks and higher drowsiness index than the top-down propagations (Supplementary Fig. S27) and also tended to increase over the course of the scanning session (Supplementary Fig. S28), suggesting their close link to drowsy state.

Figure 7 .

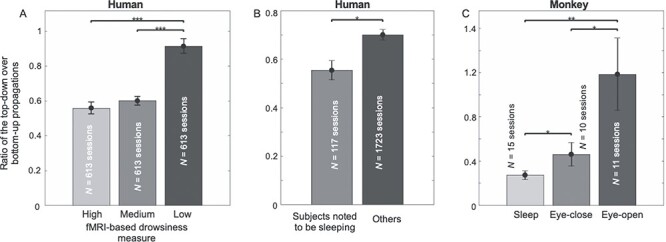
The cross-hierarchy propagating activity is sensitive to brain arousal level. (A) The ratio of the top-down propagation to the bottom-up propagation is significantly different in 3 groups of sessions showing distinct drowsiness levels as measured by an fMRI-based drowsiness index (Gu et al. 2020). (B) The same ratio is also significantly lower in a subset of sessions in which subjects were noted to be sleeping during rsfMRI scanning. (C) The ratio of the top-down propagation to the bottom-up propagation in the monkey EcoG gamma powers shows a similar and significant modulation across the eyes-open, eyes-closed, and sleep sessions. Error bars represent the SEM. Asterisks represent the level of significance: ^*: 0.01 < P  0.05; ^**: 0.001 < P  0.01; ^***: P  0.001.

A similar comparison was made for the cross-hierarchy propagations in monkey ECoG gamma powers across 3 experimental conditions: a more alert eyes-open condition, a more sleep-conducive eyes-closed condition, and the sleep condition. Consistent with the human rsfMRI results, the ratio of the top-down propagations to the bottom-up propagations are significantly different (P = 0.0233 eye-open vs. eye-closed; P = 0.0045 eye-open vs. sleep; P = 0.029 eye-closed vs. sleep; permutation test) across the 3 conditions with the sleep state showing much more bottom-up propagations and less top-down ones (Supplementary Fig. S26). To summarize, both monkey electrophysiology and human rsfMRI data suggest that the state of lower arousal is associated with less top-down but more bottom-up propagating activity.

Discussion

Here, we showed that the resting-state brain activity, measured by fMRI in humans or electrophysiology in monkeys, is characterized by distinctive propagations sweeping the cortex in 2 opposite directions along an axis. This trajectory is extremely similar to, and thus, these spatiotemporal propagations may underlie, the PG of rsfMRI connectivity (Margulies et al. 2016). The cross-hierarchy ECoG propagations are present most strongly in the gamma-band power. The local propagations within the sensory modalities are in a direction opposite to the overall direction of the global propagation, suggesting that these neuronal processes start/end at the sensory association regions. The bottom-up propagation is associated with sequential co-(de)activations at specific subcortical nuclei, including many related to arousal regulation. Consistent with this finding, the cross-hierarchy propagations are significantly modulated by the brain arousal level. Overall, the findings from this study supported the neural origin of the infra-slow rsfMRI propagations, revealed detailed features and behavioral relevance of infra-slow propagating activity, and also linked it to the PG of rsfMRI connectivity.

The study added direct evidence for the neural origin of rsfMRI propagations by showing corresponding electrophysiological propagations on a similar time scale, along a similar direction, and with a similar state dependency. Inferring the propagating activity with fMRI signals could be problematic given the known region-specific hemodynamic delays (Handwerker et al. 2004). This concern became heightened given a series of studies showing that the systematic low-frequency oscillations of blood signals cause rsfMRI signal delays consistent with the blood transition time (Tong and Frederick 2010, 2012; Tong et al. 2012, 2017, 2018). Some indirect evidence has been used to argue against the vascular origin of the infra-slow rsfMRI propagations. For example, the rsfMRI lag structures/threads persist after regressing out the vascular time lags (Amemiya et al. 2016) and are sensitive to brain state, which are not expected from a vascular based propagation (Mitra et al. 2016, 2018). Consistent with the previous findings, we found no similarity (r = 0.0035 and P = 0.39, Supplementary Fig. S13) between the PD profile and the vascular lags as measured by the dynamic susceptibility contrast MRI (Tong et al. 2017), as well as a strong dependency of the cross-hierarchy propagations on brain state (Fig. 7). Moreover, the detailed features of the cross-hierarchy propagations, including the existence of propagating instances in opposite directions (Fig. 1C), their fine-scale trajectories within the sensory systems (Fig. 5), the sequential involvement of specific subcortical nuclei (Fig. 6), good correspondences between cortical and thalamic coactivations/deactivations (Fig. 6) added further evidence against their vascular origin.

The study provided additional details about the infra-slow propagating activity. First, the cross-hierarchy propagations are present much more strongly in the gamma-band power than other bandlimited powers. This explains the previous finding that the long-range ECoG power correlations between the high-order regions can only be found in the gamma band (Liu et al. 2014). Given that the gamma activity is correlated with neuronal firing rates (Ray et al. 2008), the cross-hierarchy propagations of gamma-band power may represent an excursion of cortical excitation sweeping along the hierarchical axis. Although it has been suggested that the evoked low (30–80 Hz) and high (80–150 Hz) gamma powers originate from different sources (Ray and Maunsell 2011), we observed similar cross-hierarchy propagations in these 2 sub-gamma-bands. Either the spontaneous gamma-band activity may not contain 2 separate components, or they both contain similar cross-hierarchy propagations. Secondly, the fine-scale spatiotemporal dynamics were also elucidated within the sensory modalities. Specifically, the cross-hierarchy propagations appear to start/end at the unimodal association areas, rather than the primary areas. Thirdly, the cross-hierarchy propagating activity is conserved across human and monkeys. The fast (<1 s) propagating brain activity has also been studied in mice mostly using the optical imaging and often described as along the anterior–posterior axis (Matsui et al. 2016; Greenberg et al. 2018). Close inspection has suggested that they may indeed follow more specific trajectories between the SM regions and higher-order cortices (Mohajerani et al. 2013; Mitra et al. 2018), and it remains to be determined whether the infra-slow propagating activity in rodents is also aligned with the cortical hierarchical gradient.

The specific subcortical coactivations/deactivations point to the involvement of the ascending arousal system (AAS) in the bottom-up propagation, which might represent a brain process associated with transient arousal modulations. The earliest coactivations at the sensory association areas are accompanied by significant deactivations in multiple brainstem nuclei of the AAS, including the LC, MR, pedunculopontine nucleus, and VTA. The early brainstem deactivation is then followed by a slow and gradual deactivation of 3 other subcortical regions of arousal relevance, that is, the SN, NB, and NAc (Valentino and Volkow 2020). Importantly, the brainstem deactivation is also accompanied, if not triggered, by strong deactivations in a set of cortical and thalamic regions, including the default-mode network, the frontoparietal network, the precuneus, and the anterior and mediodorsal thalamus (Fig. 6E). This exact set of brain regions showed significant reduction in glucose metabolic rate and cerebral blood flow during anesthetic-induced unconsciousness (Akeju et al. 2014), suggesting that the bottom-up propagating activity is associated with transient arousal modulations. Consistent with this hypothesis, the bottom-up propagation was significantly modulated across brain states of distinct arousal levels (Fig. 7) and also associated with a larger amplitude in global signal (Supplementary Fig. S27A). The large global rsfMRI peaks have been linked to a neurophysiological event indicative of arousal modulations (Liu et al. 2018) and may represent an instantaneous phase (at t = 0) of this bottom-up propagation, based on their similar sensory-dominant cortical coactivations and subcortical deactivations (Liu et al. 2018). This potential relationship should not contradict with the minimal effect of the global signal regression on the PD profile (Supplementary Fig. S5A), since the procedure is not expected to effectively remove systematic time delays caused by the quasi-synchronized propagations.

While the subcortical AAS may be involved in the initiation of the cross-hierarchy propagations, the network mechanism underlying its cortical propagation remains elusive. The traveling waves have been extensively investigated using electrophysiology and optical imaging but were mostly observed at subseconds timescale and/or often across small brain regions (Bringuier et al. 1999; Girard et al. 2001; Massimini 2004; Muller et al. 2016, 2018). The fast traveling waves propagate at a speed of 2 ~ 5 m/s (Muller et al. 2016), which is similar to the conduction speed of white matter fibers. However, the cross-hierarchy propagations observed in the present study are unlikely mediated through axonal conduction given its slow speed (~5–25 mm/s). This speed, however, fells into the velocity range (~10–100 mm/s) of spontaneous waves of depolarization observed in the barrel cortex of rodents through optical imaging and whole-cell recordings (Petersen et al. 2003). It has been hypothesized that the recurrent excitation through local synaptic connections in layer 2/3 contributes to those spontaneous propagating waves. The similar mechanisms may also underlie the infra-slow propagations observed in this study. Moreover, the top-down and bottom-up propagations may take distinct routes cross cortical layers that are consistent with the known feedback and feedforward connections (van Kerkoerle et al. 2014; Scheeringa et al. 2016; Scheeringa and Fries 2019). The propagating speed is close to what has been observed for the propagation of epileptic activity (20–100 mm/s) (Chervin et al. 1988; Pinto et al. 2005; Trevelyan et al. 2006, 2007), but it remains unclear whether they share common mechanisms. Multimodal techniques capable of imaging brain activity across distinct spatial and temporal scales are required for a deep understanding of the mechanism underlying the cross-hierarchy propagations in the future.

Cross-hierarchy propagating activity may, in fact, underlie the PG of rsfMRI connectivity (Margulies et al. 2016). We showed an extremely high similarity (r = 0.93) between the principal propagating direction and the principal connectivity gradient, which is unlikely a coincidence. In fact, the propagation is expected to synchronize rsfMRI signals and affect, in a gradual way along its trajectory, rsfMRI correlations, from which the principal connectivity gradient was computed. The propagations, which account for 29% of the total scanning time, are expected to synchronize rsfMRI signals of different regions repeatedly in a rather complicated way. This could profoundly affect the rsfMRI connectivity considering a potential nonlinear relationship between the frequency of synchronization events and linear cross-correlations. Therefore, the PG method could be a different way of recovering the trajectory of the propagating activity. Consistent with this notion, the principal connectivity gradient indeed mapped the direction of major propagation in simulated data (Supplementary Fig. S3). It is also worth noting that we failed to find a trajectory similar to the second motor-to-visual gradient of rsfMRI connectivity using the delay profile method (Supplementary Fig. S11) or observe single instances of such propagation (Fig. 1D, the second column). Such a motor-to-visual contrast, which is also present in the vascular lag map (Supplementary Fig. S13), may be caused by small but significant time delays observed between the motor and visual areas in the cross-hierarchy propagations. The cross-hierarchy propagating activity might also be related to other rsfMRI findings showing features related to the hierarchical axis. For example, converging evidence from rats, monkeys, and humans has suggested that rsfMRI connectivity/dynamics of the higher-order cognitive networks and lower-order SM networks are divergently modulated by anesthesia (Martuzzi et al. 2010; Barttfeld et al. 2014; Liang et al. 2015; Ma et al. 2016).

The overlap between the principal propagating direction and the hierarchical axis of the brain implies the functional significance of the infra-slow propagating activity. A speculation of its functional roles comes from its analogy to “propagations” in artificial neuronal networks (Lecun et al. 2015). The learning of such large-scale, nonlinear models requires efficient algorithms, which often involves iterative propagations of information across hierarchical layers, including a forward propagation of information and, more importantly, a backpropagation of model errors to optimize weights/connections in a successive manner (Rumelhart et al. 1986). Such repetitive, sequential activations across hierarchical stages might be even more important for the modification of real neuronal synapses. The cross-hierarchy propagations would serve this purpose by creating successive excitations across the hierarchical axis of the brain. Consistent with this conjecture, the hippocampal ripples, a neuronal process tightly linked to learning and memory consolidation, have been found to be associated with brain-wide fMRI activations with region-specific delays suggestive of propagating behavior (Logothetis et al. 2012). The hippocampal ripple activity is highly brain state dependent and occurs mostly during rest and sleep (O’Neill et al. 2006; Cheng and Frank 2008). More importantly, it has been found to be comodulated with cortical delta-band power in a slow (~0.1 Hz) rhythm (Sirota et al. 2003), which is consistent with the timescale of the infra-slow propagations and their potential relevance to transient arousal modulations.

The new methods used in this study can be complementary to existing ones for studying propagating activity. The essential rationale of decomposing the delay profiles of signal segments (the current study) is similar to that of decomposing the connectivity matrix (the PG method) (Margulies et al. 2016) and temporal delay matrix (the lag threads method) (Mitra, Snyder, Blazey, et al. 2015a). However, the segment-based quantification is expected to maximally extract and utilize the propagation-induced signal delays, which could be partly canceled out for session-based metrics, such as connectivity metrics and temporal lags, given the existence of propagations in opposite directions (Figs 1C and 2E). Consistent with this notion, our method appeared to outperform the PG method in charactering local propagations within sensory modalities (Fig. 5 and Supplementary Fig. S24) and recovering simulated propagating directions (Fig. 2B and Supplementary Fig. S3). The delay cancellation for the session-based quantifications may also explain the different time scales seen for the lag structure/threads (~1–2 s) and the infra-slow propagating activity (~5–10 s). In addition, the new method could be computationally more efficient for neural signals with a large number of spatial dimensions, such as fMRI, with no need to construct huge connectivity or lag matrices. Compared with the QPP method, which identifies repeated spatiotemporal structures that are not necessarily propagations, the new method is designed to detect the propagations based on a continuous time–position relationship with allowing individual instances to have different speeds. Detailed differences between the various methods remain to be investigated by future studies with a technical focus.

Author Contributions

Conceptualization, Y.G. and X.L.; Methodology, Y.G. and X.L.; Formal Analysis, Y.G. and X.L.; Data Curation, Y.G. and X.L.; Writing -- Original Draft, Y.G., F.H., Y.L., N.Z., X.Z., D.A.L., X.L.; Writing -- Review & Editing, Y.G. and X.L.; Visualization, Y.G., L.E.S., S.K., J.W.W., X.L.; Supervision, X.L.; Funding Acquisition, X.L.

Data and Materials Availability

Both the HCP data and the monkey electrophysiology dataset are public and available from the websites https://www.humanconnectome.org and http://neurotycho.org/anesthesia-and-sleep-task, respectively. The MATLAB code for the analysis and the human PD profile in this study are available at GitHub: https://github.com/YamengGu/the-cross-hierarchy-propagation (Gu and Liu 2020).

Funding

This work was supported by the National Institutes of Health Pathway to Independence Award K99/R00 (5R00NS092996-03), the Brain Initiative Award (1RF1MH123247-01), and the National Institutes of Health R01 Award (1R01NS113889-01A1) to X.L.

Notes

We thank Dr Matthew F. Glasser for sharing the information about subjects’ sleeping state during the scanning and the Computer Vision Laboratory for sharing the Morel thalamus atlas. We also thank Dr Yunjie Tong for sharing the averaged time lag map from dynamic susceptibility contrast. The human data were analyzed using the computing resources provided by the Institute for Computational and Data Sciences at the Pennsylvania State University (https://icds.psu.edu). The human data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University. Conflict of Interest: None declared.