Abstract
Humans use prior knowledge to efficiently solve novel tasks, but how they structure past knowledge during learning to enable such fast generalization is not well understood. We recently proposed that hierarchical state abstraction enabled generalization of simple one-step rules, by inferring context clusters for each rule. However, humans’ daily tasks are often temporally-extended, and necessitate more complex multi-step, hierarchically structured strategies. The options framework in hierarchical reinforcement learning provides a theoretical framework for representing such transferable strategies. Options are abstract multi-step policies, assembled from simpler one-step actions or other options, that can represent meaningful reusable strategies as temporal abstractions. We developed a novel sequential decision making protocol to test if humans learn and transfer multi-step options. In a series of four experiments, we found transfer effects at multiple hierarchical levels of abstraction that could not be explained by flat reinforcement learning models or hierarchical models lacking temporal abstraction. We extended the options framework to develop a quantitative model that blends temporal and state abstractions. Our model captures the transfer effects observed in human participants. Our results provide evidence that humans create and compose hierarchical options, and use them to explore in novel contexts, consequently transferring past knowledge and speeding up learning.
Keywords: Hierarchical Reinforcement Learning, The Options Framework, Transfer Learning
1. Introduction
Reinforcement learning theory (RL, (Sutton & Barto, 2018)) offers a computational level account of how agents can learn to make choices that will maximize their future cumulative rewards. Recent advances have shown that RL can give rise to extremely powerful artificial intelligence (AI) systems (Mnih et al., 2015; Silver et al., 2018). RL modeling has also greatly helped advance our understanding of motivated human behavior in both simple conditioning contexts and much more complex learning environments (Collins & Frank, 2012, 2013; Farashahi, Rowe, Aslami, Lee & Soltani, 2017; Gläscher, Daw, Dayan & O’Doherty, 2010; Leong, Radulescu, Daniel, DeWoskin & Niv, 2017; Niv, 2009). However, despite tremendous recent progress, artificial RL agents are unable to mimic and capture humans’ ability to learn fast, efficiently, as well as transfer and generalize knowledge (Botvinick, Niv & Barto, 2009; Collins, 2019; Diuk, Schapiro et al., 2013; Lake, Ullman, Tenenbaum & Gershman, 2017).
Human behavior and cognition possesses two key features that are essential to humans’ efficient and flexible learning: cognitive representations are hierarchical (Badre, 2008; Koechlin & Jubault, 2006; Koechlin, Ody & Kouneiher, 2003; Solway et al., 2014) and compositional (Lake et al., 2017). Hierarchy has been identified as a crucial element of cognition (Anderson et al., 2004; Taatgen, Lebiere & Anderson, 2006) in multiple domains such as perception (Bill, Pailian, Gershman & Drugowitsch, 2019; Lee & Mumford, 2003; Van Essen & Maunsell, 1983; Wessinger et al., 2001), decision making (Badre, 2008; Badre & D’Esposito, 2007; Badre & D’esposito, 2009; Balleine, Dezfouli, Ito & Doya, 2015; Dezfouli & Balleine, 2012, 2013; Eckstein & Collins, 2019; Krigolson & Holroyd, 2006; Tomov, Yagati, Kumar, Yang & Gershman, 2018; Zarr & Brown, 2016), and learning (Badre & Frank, 2011; Collins, Cavanagh & Frank, 2014; Collins & Frank, 2013; Eckstein & Collins, 2019; Frank & Badre, 2011). Hierarchy in choices is often temporal (Botvinick, 2007; Botvinick & Plaut, 2004): choices may be described at multiple degrees of granularity by breaking them down into more and more basic chunks. For example, the task of making dinner can be broken down to making potatoes and making black beans; making potatoes can be broken down into sub-tasks such as cutting potatoes, boiling, etc. However, hierarchical levels may also represent different degrees of state abstractions at a similar time scale (Badre, 2008; Collins, 2018; Collins & Frank, 2013; Koechlin et al., 2003): for example, you may decide to make dinner (highest, most abstract level), which will consist of a salad, which will specifically be a Cesar salad (lowest, most concrete level).
Human behavior is also compositional: humans are able to compose simpler skills together in novel ways to solve new tasks in real life. For example, we can combine cutting potatoes with different routines to accomplish various tasks including fried potatoes, meshed potatoes, etc. Compositionality goes hand in hand with hierarchy, as it assumes the existence of different levels of skills. It has also been central to the study of human cognition (Biederman, 1987; Franklin & Frank, 2018; Lake, Salakhutdinov & Tenenbaum, 2015) and artificial agents (Andreas, Klein & Levine, 2017; Peng, Chang, Zhang, Abbeel & Levine, 2019; Wingate, Diuk, O’Donnell, Tenenbaum & Gershman, 2013; Xu et al., 2018).
While it is well established that human behavior is hierarchical and compositional, how we learn such representations remains poorly characterized. A theoretical framework of interest is the hierarchical reinforcement learning (HRL) options framework (Sutton, Precup & Singh, 1999), originally proposed in AI, which incorporates aspects of both hierarchy and compositionality in an effort to make learning more flexible and efficient. The options framework augments traditional RL algorithms by allowing agents to select not only simple actions, but also options in different states. Broadly summarized, options are temporally-extended multi-step policies assembled from simple actions or other simpler options to achieve a meaningful subgoal (see (Sutton et al., 1999) for a formal definition). Consider making potatoes as an example option. We can break down the task into sub-options such as cutting potatoes, boiling, etc. (Fig. 1). These sub-options can be further divided into simpler tasks. In the HRL options framework, agents can learn option-specific policies (e.g. how to make potatoes) by using, for example, subgoals as pseudo-rewards that reinforce within-option choices.
Figure 1:
Schematics of how state and temporal abstractions can be used to describe increasingly more complex human cognition. Flat Model. The usual flat RL model learns one-step policies for different vegetables (potatoes and carrots) separately as different states (gray), with potentially multiple actions leading to reward in a given state (e.g. boil or stir fry potatoes). Task-set Model. The task-set model clusters both potatoes and carrots into the same state abstraction, namely, vegetable, thus everything learned about one vegetable will be immediately transferable to all the other vegetables. However, the task-set model only learns one-step policies, and in this non-Markovian task is unable to resolve the optimal action after the vegetable is cut, since it can be either boiled (blue) or stir fried (green). Option Model. The option model learns state abstractions, but also temporal abstractions by combining one-step rules into temporally-extended policies, resolving the action selection after the vegetable is cut by activating a temporal abstraction from the beginning. Now one activates either the option of boiling vegetable (blue) or stir frying vegetable (green) from the start of cutting vegetable. Sequence learning Model. The sequence learning model learns about optimal action sequences starting from the initial state ((cut, boil) for boiling vegetable, i.e. blue; (cut, stir fry) for stir frying vegetable, i.e. green); however, it does not learn full-fledged policies, and thus cannot deal with tasks that require state-dependency (see Experiment 1 design, Fig. 2A for an example) once a sequence is initiated.
Options are referred to as temporal abstractions because selecting an option is a single decision step, but this single decision may trigger a series of decisions constrained by the option (until the option terminates), so that time is compressed in a single decision.
Each option is additionally characterized by an initiation set (the set of states where the option can be initiated), and a termination function that maps each state to the probability of terminating the current option. For example, the initiation set for the option of making potatoes might be kitchen, and the option might terminate when the potatoes are cooked. Agents learn when to select options in the same way they learn to select actions (e.g. make potatoes for breakfast in the US, but not in France) by using normal reinforcement signals. Agents learn the policies determined by an option using pseudo-rewards obtained when reaching the subgoal option.
The options framework provides many theoretical benefits for learning (Botvinick et al., 2009; Botvinick & Weinstein, 2014), assuming that useful options are available. Unlike traditional RL algorithms that only learn step-by-step policies, options help explore more efficiently and plan longer term. For example, when we learn how to cook a new kind of potato, we already know how to cut potatoes. Moreover, we can plan with high-level behavioral modules such as cutting potatoes, instead of planning in terms of reaching, grabbing, and peeling. If non-useful options are available, the options framework predicts that learning can be instead slowed down (Botvinick et al., 2009). The question of how to identify and create useful options has been a topic of active and intense research in AI (Fox, Krishnan, Stoica & Goldberg, 2017; Jayaraman, Ebert, Efros & Levine, 2018; Jiang, Gu, Murphy & Finn, 2019; Marios C Machado, Bellemare & Bowling, 2017; Marlos C Machado et al., 2017; McGovern & Barto, 2001; Menache, Mannor & Shimkin, 2002; Nair & Finn, 2019; Şimşek & Barto, 2004; Xu et al., 2019).
Recent literature (Diuk, Schapiro et al., 2013; Diuk, Tsai, Wallis, Botvinick & Niv, 2013; Ribas-Fernandes, Shahnazian, Holroyd & Botvinick, 2019; Ribas-Fernandes et al., 2011; Schapiro, Rogers, Cordova, Turk-Browne & Botvinick, 2013) shows early evidence that the options framework could be a useful model of human learning and decision making. (Diuk, Schapiro et al., 2013; Schapiro et al., 2013) showed that participants were able to spontaneously identify bottleneck states from transition statistics, which aligned with graph-theoretic objectives for option discovery developed in AI (Menache et al., 2002). In addition, in hierarchical decision-making tasks, (Diuk, Tsai et al., 2013; Ribas-Fernandes et al., 2019; Ribas-Fernandes et al., 2011) showed that human participants signaled reward prediction error (RPE), a key construct for RL algorithms, for both subgoals and overall goals. These results indicate that humans are able to identify meaningful subgoals, and to track sub-task progression, both key features of the options framework. (Botvinick, 2012; Holroyd & Yeung, 2012) have also suggested potential neural correlates for implementing the computations required to use options.
However, the fundamental question of whether and how humans learn and use options during learning remains unanswered (Diuk, Schapiro et al., 2013): there is little work probing the learning dynamics in tasks with a temporal hierarchy, or directly testing the theoretical benefits of options in a behavioral setting. In this paper, we aim to 1) characterize how humans learn representations that support hierarchical and compositional behavior, and 2) investigate whether an expanded options framework can account for it. In particular, do humans create options in such a way that they can flexibly reuse them in new problems? If so, how flexible is this transfer? In order to address these questions, we need to first identify aspects of human learning and transfer that reflect the use of options, but cannot be explained by traditional RL, from a modeling perspective.
Previous research (Collins et al., 2014; Collins & Frank, 2013, 2016) showed evidence for flexible creation and transfer of a simple type of options that operate in non-sequential environments: one-step policies, also called task-sets (Monsell, 2003). While a vanilla flat RL model learns about state-action mappings (policies) as they are, such as cutting, boiling and stir frying potatoes (Fig. 1), RL models that learn task-sets achieve transfer by learning state abstractions. For example, the model, after learning the policy of cutting potatoes, can generalize to cutting other vegetables by clustering the vegetables that it has never encountered before to the context of potatoes. (Collins et al., 2014; Collins & Frank, 2013, 2016) showed that humans can create multiple task-sets over the same state space in a context-dependent manner in a contextual multi-armed bandit task; furthermore, humans can cluster different contexts together if the task-set is successful. This clustering structure provides opportunities for transfer, since anything newly learned for one of the contexts can be immediately generalized to all the others in the same cluster (Fig. 1). Moreover, human participants can identify novel contexts as part of an existing cluster if the cluster-defined strategy proves successful, resulting in more efficient exploration and faster learning.
However, the task-sets framework only supports hierarchy in “state abstraction”, not hierarchical structure in time (also called “temporal abstraction”, Fig. 1), an essential component of the options framework. Since most real world tasks require multiple steps, RL models that only learn one-step task-sets are not sufficient. In particular, note that RL models that only learn task-sets might still get confused about whether it should boil or stir fry after the vegetable is cut. This is due to the non-Markovian (or semi-Markovian (Sutton et al., 1999)) aspect of the environment: for the same observed state (cut vegetable), the optimal action might be different depending on the over-arching goal, that cannot be currently observed. An RL model that further learns temporal abstractions such as options would instead combine one-step task-sets together as one abstract behavioral module. Once a specific option is activated, it resolves the ambiguity regarding the optimal action following cutting vegetable.
Here, we propose that combining state abstraction from task-set transfer (Collins et al., 2014; Collins & Frank, 2013, 2016) and temporal abstraction from the options framework (Sutton et al., 1999) can provide important insights into complex human cognition. The additional temporal hierarchical structure offered by options should enable transfer of prior knowledge at multiple levels of hierarchy, providing rich opportunity for capturing the flexibility of human transfer. For example, in addition of being able to resolve the optimal action in a non-Markovian task (Fig. 1), if humans have learned the simple sub-option of boiling water while learning how to make coffee, they do not need to re-learn it for learning to make tea or steamed potatoes; this sub-option can instead be naturally incorporated into a tea-making option, speeding up learning.
In this paper, we present a new experimental protocol that allows us to characterize how humans develop hierarchical, compositional representations to guide behavior during trial-by-trial learning from reward feedback. In particular, it allows us to test whether humans create options during learning, and whether they use them in new contexts to explore more efficiently and transfer learned skills, at multiple levels of hierarchy. Our new two-stage learning game provides participants opportunities to create and transfer options at multiple levels of complexity.
To characterize how humans learn hierarchical and compositional representations to interact with the world and to test various predictions of learning and transferring temporal abstractions, we conducted a series of four experiments. The structure of the environment in Experiment 1 was non-Markovian, encouraging participants to learn option-like temporally-extended policies, and included test phases in which options could be transferred or re-composed; indeed, we found evidence of participants learning and transferring options at multiple levels. Experiment 2 provided a replication of Experiment 1 and further revealed interesting interaction between option transfer and meta-learning, as well as the complexity of credit assignment in hierarchical tasks. Experiment 3 mimicked Experiment 1, but removed the non-Markovian feature of Experiment 1: because all relevant information was observable, there was no additional benefit to creating options. Thus, Experiment 3 allowed us to test whether participants would spontaneously learn and transfer options even when there was no behavioral benefit to do so. Last, Experiment 4 aimed to test whether participants could compose options learned at different time and different levels. Given that humans can transfer task-sets to novel contexts (Collins et al., 2014; Collins & Frank, 2013, 2016), we hypothesized that humans would learn and transfer options to guide exploration and achieve better learning performance. The results of these four experiments (3 replicated in an independent sample) showed that human participants are able to learn, flexibly transfer and compose option-like temporally-extended policies at multiple levels.
We also present a formal computational RL model that brings together aspects of the classic hierarchical RL options framework with the task-set model’s Bayesian inference mechanisms for clustering and transfer. The model combines the benefits of both frameworks. Specifically, the model relies on HRL-like options at three levels of hierarchy, and uses HRL-like learning mechanisms (using both rewards and pseudo-rewards) to learn policies and option-specific policies, respectively. Furthermore, our model uses Bayesian inference with a non-parametric prior to guide exploration and selection of options, inspired by the task-set model, and in that sense departing from traditional HRL framework. Our model makes specific predictions about learning, transfer, exploration, and error types in the four experiments. Our computational model captured the observed patterns of behavior, supporting the importance of hierarchical representations of choices for flexible, efficient, generalizable learning and exploration. Additionally, we showed that other models, including flat RL models, hierarchical RL models with no temporal abstraction, or sequence-learning models are insufficient in explaining the learning and transfer patterns we observe in human participants. Thus, our new experimental and theoretical framework characterizes how humans learn hierarchical and compositional representations to interact with our environment, and shows how this supports flexible transfer and efficient exploration.
2. Experiment 1
Experiment 1 was designed to test if human participants are able to learn and flexibly transfer options. We designed a sequential 2-step decision-making paradigm (where each step was a contextual 4-armed bandit) to allow participants to learn options at multiple levels of complexities. Options changed between blocks, but the design provided participants with opportunities to practice reusing previously learned options. In two final test blocks, we directly tested creation and transfer of options by changing and/or combining previously learned options in novel ways.
2.1. Methods
2.1.1. Participants
All experiments were approved by the Institutional Review Board of the University of California, Berkeley (UCB). Experiment 1 was administered in-lab to UCB undergraduates who received course credit for their participation. 34 (22 female; age: mean = 20.6, sd = 1.6, min = 18, max = 24) UCB undergraduates participated in Experiment 1, and 9 participants were excluded due to incomplete data or poor learning performance, resulting in 25 participants for data analysis.
For replication purposes, we also recruited participants through Amazon Mechanical Turk (MTurk, (Paolacci, Chandler & Ipeirotis, 2010)) who performed the same experiment online. Participants were compensated a minimum of $3 per hour for their participation, with a bonus depending on their performance to incentivize them. 116 participants (65 female; see age range distribution in Table 3) finished the experiment. 61 participants were further excluded due to poor performance (see Sec 2.1.4 for explanations about the high exclusion rate), resulting in 55 participants for data analysis.
2.1.2. Experiment 1 in-lab Protocol
Experiment 1 consisted of eight 60-trial blocks (Fig. 2A), with optional 20-second breaks in between blocks. In each block, participants used deterministic truthful feedback to learn which of four keys to press for four different shapes. Each trial included two stages; each stage involved participants making choices in response to a single stimulus (Fig. 2A) by pressing one of four keys. Each trial started with one of two possible stimuli, henceforth the first stage stimuli (e.g. circle and square). Participants had 2 seconds to make a choice. Participants only moved on to the second stage of the trial when they pressed the correct key for the first stage stimulus, or after 10 unsuccessful key presses, which enabled them to potentially try all four keys for a given stimulus in a single trial. Specifically, unsuccessful key-presses led to a repeat of the exact same first-stage shape. Successful key press for the first stage of a trial did not result in reward feedback, but triggered a transition to the second stage, where participants saw one of the two other stimuli, henceforth labeled second stage stimuli (e.g. diamond and triangle). To prevent participants from learning action sequences, the second stage stimuli were unpredictable: both first stage stimuli led to both second stage stimuli equally often. Shapes were randomly assigned to either first or second stage across participants. In the second stage, participants also could not move on until they selected the correct choice (or selected wrong 10 times in a row for the same image). Participants received explicit feedback after each second stage choice: the screen indicated 1/0 point for pressing the correct/incorrect key, displayed for 0.5 second (Fig. 2A). After a correct second stage choice, participants saw a fixation cross for 0.5 second, followed by the next trial’s first stage stimulus. Each block contained 60 trials, with each first stage stimulus leading to each second stage stimulus 15 times in a pseudo-randomized sequence of trials.
Figure 2:
Experiment 1 protocol and overall performance. (A) Experiment 1 design. Left: Block and trial structure; Blocks 1–6 were learning blocks, followed by two testing blocks: Blocks 7 and 8. Each block had 60 trials. In each trial, participants needed to select the correct response for the first stage stimulus (e.g. circle) in order to move on to the second stage stimulus (e.g. triangle), where they could win points by selecting the correct response. Right: Stimulus-action assignments; in Blocks 1–6, participants had the opportunity to learn options (temporally-extended policies) at three levels of complexity: high, middle, and low-level options (HO, MO, and LO). In the testing phase, Block 7 tested participants’ ability to reuse MO policies outside of their HO context, potentially eliciting positive transfer (green) of LOs in the second stage, and negative transfer (red) of choices in the first stage. Block 8 tested predicted positive transfer in the first stage, but negative transfer of MO policies in the second stage, by replacing old LOs with new ones. Blocks were color-coded for later result figures: Blocks 1–4 gray; Blocks 5–6 purple; Block 7 rose; Block 8 blue. (B) Average number of key presses in the first and the second stages per block. Chance is 2.5; ceiling is 1 press. (C) Average number of key presses for the first 10 trials of Blocks 5–8 for the first (left) and second stages (right). We use n.s. to indicate p ≥ 0.1; † for p < 0.1; * for p < 0.05; ** for p < 0.01; *** for p < 0.001; and >*** for p < 0.0001. We indicated all statistical significance with these notations in further figures.
Crucially, the correct stimulus-action assignments were designed to create a non-Markovian environment, and thus to encourage the creation of multi-step policies. In particular, second stage correct choices were dependent on what the first stage stimulus was - for example, in Block 1’s second stage, pressing action A2 for a triangle only led to a reward if the first stage stimulus was a circle; if it was a square, participants needed to press action A3 for the triangle to obtain reward (Fig. 2A). This encouraged participants to make temporally-extended choices (potentially options): their second stage strategies needed to depend on the first stage. The contingencies were also designed to test their grouping into sets of policies at multiple levels. Indeed, assignments, illustrated in Fig. 2A, changed across blocks. Blocks 1, 3, 5 shared the same assignments; Blocks 2, 4, 6 shared the same assignments; this encouraged participants to not unlearn policies, but rather discover that they could reuse previously learned multi-level policies as a whole in new blocks.
Assignments in Blocks 7 and 8 intermixed some of the learning blocks assignments with new ones to test (positive and negative) transfer of options at various hierarchy levels. Specifically, the protocol was set up so that participants could learn up to 3 levels of hierarchical task structure (low, mid, and high level policies). More precisely, low-level options (LO) corresponded to second stage policies (a pair of stimulus-action associations, commonly labelled a task-set) (Monsell, 2003). Mid-level options (MO) were policies over both first and second stage stimuli. High-level options (HO) were policies over MOs (a pair of stimulus-MO associations in the first stage, which could be thought of as a task-set over options). As a concrete analogy, in Blocks 1, 3, 5, the participants learned how to make breakfast (HO1), consisting of potatoes (MO1) and eggs (MO2). Making potatoes (MO1) was broken down into cutting potatoes (the first stage) and then roasting (the second stage, LO1). In Blocks 2, 4, 6, participants learned how to make lunch (HO2), consisting of carrots (MO3) and sandwich (MO4). Making carrots (MO3) was broken down into washing carrots (the first stage) and then steaming (the second stage, LO3).
Block 7 tested positive transfer of second stage policies and negative transfer of first stage policies. In particular, we combined the policies for potatoes from breakfast (MO1) and sandwich from lunch (MO4) to form a new policy HO3 (dinner). If participants build three levels of options, we expect positive transfer of mid-level options MO1 and MO4: participants should be unimpaired in making potatoes or a sandwich. However, we expect negative transfer of high-level options HO1 and HO2: participants seeing that making potatoes was rewarded might start making eggs as usual in breakfast (HO1), instead of sandwich as rewarded here.
Block 8 tested positive transfer of first stage policies and negative transfer of second stage policies. In particular, the first stage of Block 8 shared the same assignments as Blocks 1, 3, 5 in the first stage, allowing participants to immediately transfer HO1. However, the second stage policies (LO5 and LO6) were novel, which might potentially result in negative transfer: for example, participants might try to transfer LO1 (roasting) following MO1 (make potatoes), but the second stage policy was changed to LO5 (e.g. frying).
2.1.3. Experiment 1 MTurk Protocol
To replicate our findings, we ran a minimally modified version of Experiment 1 online via MTurk. The task was slightly shortened, due to evidence that in-lab participants reached asymptotic behavior (Fig. S17) early in a block, and to make the experiment more acceptable to online workers. Blocks 1 and 2 had a minimum of 32 and a maximum of 60 trials, but participants moved on to the next block as soon as they reached a criterion of less than 1.5 key presses per second stage trial in the last 10 trials (the 55 Mturk participants included for data analysis on average used 42 (SD = 10, median = 37, min = 32, max = 60) trials in Block 1 and 39 (SD = 10, median = 33, min = 32, max = 60) trials in Block 2). Blocks 3–8 were all shortened to 32 trials, with each first stage stimulus leading to each second stage stimulus 8 times.
2.1.4. Data analysis
We used the number of key presses until correct choice in each stage of a trial as an index of performance. Since the experiment would not progress unless the participants chose the correct action, more key presses indicates worse performance. Ceiling performance was 1 press per stage within a trial. Chance level was 2.5, assuming choosing 1 out of 4 keys randomly, unless indicated otherwise. To probe for any potential transfer effects, we calculated the average number of key presses at the beginning of each block (trials 1–10), before learning has saturated. As a stronger test of option transfer, we also calculated the probability that the first press for a given stimulus at each stage of a trial was correct in different blocks.
To rule out participants who were not engaged in the task, we excluded any participant who did not complete Blocks 5–8 within an allotted amount of time (6 minutes each) - indeed this could only happen if participants often reached the 10 key presses needed to move on to the next stage without the correct answer, a clear sign of no engagement.
We additionally excluded any participant whose average performance in the last 10 trials of either first or second stage in either Block 5 or 6 was at or below chance, since it indicated a lack of learning and engagement in both stages of the task. These exclusion criteria were applied to all experiments, including Mturk participants.
Note that the analysis of the first 10 trials and the last 10 trials served different purposes, since they reflected different stages of learning. The beginning of each block when participants had not yet integrated all the new block information was where we expected to see transfer effects. On the other hand, the last 10 trials of a block showed asymptotic performance and were used to ensure learning had occurred, in particular for exclusion criteria. In short, the performance in the last 10 trials answered the question of how participants made choices after repeated exposure to the same environments for many iterations, while the first 10 focused on learning (and potentially transfer) in a new environment.
Among 116 Mturk participants in Experiment 1, 104 were above chance in the second stage (the more difficult one), but only 55 were above chance in the first stage (the easier one). Thus most participants were excluded due to the first stage performance criterion. The same trend was true for the other two Mturk experiments: most Mturk participants were excluded due to performance in the first stage in Experiment 3 and Experiment 4. We hypothesize that the poor first stage performance in many is due to the task’s incentive structure - participants knew they only earned points (which were converted to monetary bonus for MTurk participants) in the second stage. All second stage results were qualitatively similar to the ones reported in this paper for all experiments when we relaxed the exclusion criterion to include participants at chance in the first stage.
The options framework makes predictions about the specific choices made in response to a stimulus, beyond whether a choice is correct: the nature of the errors made can be informative (Collins & Frank, 2013). We categorized the specific choices participants made into meaningful choice types, to further test our predictions about potential option transfer effects. As the choice types were stage and experiment dependent, we describe the choice type definitions in the result sections where necessary. When performing choice type analysis, we only considered the first key press of the first or second stage in each trial. We also compared reaction time of different choice types to test potential sequence learning effects.
For statistical testing, we used parametric tests (ANOVAs and paired t-test) when normality assumptions held, and non-parametric tests (Kruskall-Wallis and sign test) otherwise.
2.1.5. Computational modeling
To quantitatively formalize our predictions, we designed a computational model for learning and transferring options, inspired by the classic HRL framework as well as other hierarchical RL literature (Collins & Frank, 2013; Sutton et al., 1999). We simulated this model, as well as four other learning models that embody different hypotheses about learning in this task, and compared which model best captures patterns of human learning and transfer. All models were simulated 500 times. We did not fit the model to the trial-by-trial choices of participants because computing the likelihood of the hierarchical models is intractable. In flat reinforcement learning models, state, action and rewards on each trial are fully observed. However, for the main HRL model used in this paper, we assume that participants first select an option, conditioned on which they select a primitive action. Note that we only observed the primitive action from participants’ key presses, not the selection of options. Therefore, in order to calculate the full likelihood, one would have to marginalize the option choices for each trial, resulting in the integration of exponentially many trajectories throughout the experiment. Even if participants only needed to choose between 2 hidden options, participants often made more than 1000 key presses in our experiment, which would require summing over 21000(> 10300) trajectories, rendering the calculation of the likelihood function intractable.
All results presented in the main text figures were simulated with parameters chosen to match participants’ behavioral patterns qualitatively and quantitatively well (Table 1). However, our qualitative predictions are largely independent of specific model parameters: we show in Sec. 9.4 that a single set of parameters (Table 2), consistent across all experiments, makes the same qualitative predictions regarding transfer effects.
2.1.5.1. The Naive Flat Model.
The Naive Flat Model is a classic reinforcement learning model that learns Q-values to guide action selection in response to stimuli. In the first stage, it learns a Q-value table , where F1 and F2 are two first stage stimuli, A1,...,A4 are four possible actions. We use superscript to index stage (1 means first stage, 2 means second stage). The Q-values are initialized to uninformative Q-values , since each of the four actions has an equal probability of resulting in a pseudo-reward of 1 for transitioning into the second stage. On each choice, a first stage policy is computed based on the first stage stimulus, Fi, with the softmax function:
| (1) |
where is the inverse temperature parameter. A first stage action A1, ranging from A1 to A4, is then sampled from this softmax policy. After observing the outcome (moving on to the second stage or not), the Q-values is updated with Q-learning (Sutton & Barto, 2018):
| (2) |
where α1 is the learning rate parameter, and the pseudo-reward r is 1 if A1 is correct and 0 otherwise.
In the second stage, the model similarly learns another Q-value table , where S1 and S2 are two second stage stimuli, with learning rate α2 and inverse temperature . Note that this disregards the non-Markovian nature of the task: it learns the Q-values for the two second stage stimuli without remembering the first stage stimulus. As such, this model is a straw man model that cannot perform the task accurately, but exemplifies the limitations of classic RL in more realistic tasks, and serves as a benchmark.
At the start of a new block, the Naive Flat Model resets all Q-values to , and thus has to re-learn all Q-values from scratch. To better account for human behavior, we also included two forgetting parameters, f1 and f2. After each choice, the model decays all Q-values for the first stage based on f1:
| (3) |
Forgetting in the second stage is implemented similarly.
Participants very quickly learned that the correct second stage action was different from the first stage one (see results). To account for this meta-learning heuristic, we add a free meta-learning parameter, m, that discourages selecting the same action in the second stage as in the first stage. Specifically, if π is the second stage policy as computed from softmax, we set , where A1 is the action chosen in the first stage, and re-normalize:
| (4) |
where is any action other than A1.
Parameters f1, f2 and m, which capture memory mechanisms and heuristics orthogonal to option learning, are included in all models and implemented in the same way. In total, the Naive Flat Model has 7 parameters: α1,β1,f1,α2,β2,f2,m.
2.1.5.2. The Flat Model.
The Flat Model extends the Naive Flat Model with a single addition of first-stage memory, which makes this model able to perform the task well in both stages. Specifically, in the second stage, the Flat Model remembers the first stage stimulus by treating each of the 4 combinations of the first and second stage stimuli as a distinct state and learns Q-values for all 4 combinations. The Flat Model has the same 7 parameters as the Naive Flat Model.
2.1.5.3. The Task-Set Model.
The Task-Set Model is given the capability of transferring previously learned task-sets (one-step policies) with Bayesian inference. In particular, the Task-Set Model uses Chinese Restaurant Process (CRP, (Pitman, 2006)), a nonparametric Bayesian prior, that specifies the probability of transferring one of the previously learned task-sets and the probability of creating a new task-set and learning from scratch. In the first stage, the model tracks the probability P1 of selecting each first stage task-set HOi in different first stage contexts , which encodes the current temporal (block) context (e.g. 8 contexts in the first stage of Experiment 1 due to 8 blocks). The model uses CRP to select HO: if contexts are clustered on , when the model encounters a new context , the prior probability of selecting a new high-level option in this new context is set to:
| (5) |
and the probability of reusing a previously created high-level option is set to:
| (6) |
where is the clustering coefficient for the CRP, is the number of first stage contexts clustered on HOi, and is the normalization constant. The new policy is initialized with uninformative Q-values . The model samples HO based on the conditional distribution over all HOs given the current temporal context. The model also tracks HO-specific policies via Q-learning. Once an HO is selected, a first stage policy is computed based on the HO’s Q-values and the first stage stimulus Fi with softmax:
| (7) |
where is the inverse temperature. A first stage action A1, ranging from A1 to A4, is then sampled from this softmax policy. After observing the outcome (moving on to the second stage or not), the model uses Bayes’ Theorem to update P1:
| (8) |
where the pseudo-reward r is 1 if A1 is correct and 0 otherwise, and if , or if . Then the Q-values of the HO with the highest posterior probability is updated:
| (9) |
where α1 is the learning rate.
The second stage runs a separate CRP with P2, similar to P1 in the first stage, which guides selection of task-sets LO over second stage stimuli. All other aspects are identical to the first stage except that the second stage contexts are determined by both temporal (block) context and the first stage stimulus (e.g. 16 contexts in the second stage of Experiment 1 due to 8 blocks and 2 first stage stimuli). All the equations of CRP, action selection and Q-learning remain the same. The Task-Set Model has 9 parameters: α1, β1, γ1, f1, α2, β2, γ2, f2, m.
2.1.5.4. The Option Model.
The Option Model extends the task-set model to include multi-step decisions (mid-level options MO). The first stage is identical to the Task-Set Model. However, instead of just choosing an action for the first stage, a whole MO is activated. For example, if the circle is observed in Block 1, HO1 may trigger the model to select MO1, which triggers the selection of A1. The selection of MO1 would then make the model likely to select LO1 for the second stage (Fig. 2B). To simplify credit assignment, we make the simplifying assumption - warranted in our task - that there is a one-on-one mapping between first-stage actions and options, allowing us to index MOs by their first-stage action. This is meant as a technical simplification, rather than a theoretical assumption.
The second stage is the same as the Task-Set Model, except that each MO has an MO-specific probability table . In the Task-Set Model, the CRP in the second stage using P2 is independent of the first stage choices. In contrast, in the Option Model, the first stage choice determines which MO is activated, which then determines which probability table, , to use for running the CRP in the second stage to select LOs. This implementation captures the essence of options in the HRL framework, in that selection of MO in the first stage constrains the policy chosen until the end of the second stage (where the option terminates). The Option Model has the same 9 parameters as the Task-Set Model. A full description can be found in the supplement.
Note that in our Option Model, there are two ways in which the option selection is instantiated. (1) One way is to use inference with a CRP prior (Pitman, 2006): instead of estimating the values of different HO’s through incremental Q-learning, we estimated the likelihood of reward after selecting each HO’s using Bayes’ formula. This is inspired from our previous task-set model (Collins & Frank, 2013), and equips our Option Model with a level of flexibility in transfer (by inferring which option is likely to be useful in a new environment), something that traditional HRL options framework cannot achieve. We discuss this departure from classic HRL options framework further in the discussion (Sec. 6.1.2). (2) We also implemented the option value functions by learning the values of different MO’s within each HO’s. Since MO are indexed by their first-stage action, the Q-values that participants learned for actions in the first stage correspond to MO option values. This is in line with the classic option values in the HRL options framework (Sutton et al., 1999).
2.1.5.5. Sequence learning model.
For completeness, and to show that sequence learning cannot account for learning in this experiment, we also simulated a simple sequence learning model. This model stores perfect memories of 2-action sequences, and of their association with a first-stage stimulus when that sequence leads to reward. We assume that the model can perfectly store 2-action sequences associated with each first stage shape in each block. On every trial, the model selects from the 2-action sequences associated with the first stage shape, each with 0.5 chance. For example, in Blocks 1, 3, 5 (Fig. 2A), the model would pick from sequences (A1, A4) and (A1, A2) for the circle in the first stage. However, since the model cannot predict which shape will come up in the second stage, there is 0.5 chance that the selected action sequence would be incorrect, in which case the model would immediately choose the second stage action of the other action sequence in the next attempt. For example, if the model selects sequence (A1, A4) upon encountering circle in the first stage, there is 0.5 chance that it will encounter a diamond in the second stage, which the model would get the correct answer in 1 press. However, there is also 0.5 chance that it will encounter a triangle, in which case it will make an error by pressing A4 as it was selected as part of the action sequence, and then the model would choose A2, resulting in 2 presses. Therefore, the sequence learning model will have an asymptotic performance of 1.5 presses/trial in the second stage.
Note that the sequence learning model does not have any model parameters as we assumed perfect memory of the action sequences as well as optimal decision making. Including parameters such as learning rate and inverse temperature would only worsen the performance.
2.2. Experiment 1 Results
2.2.1. Participants do not use flat RL
Participants’ performance improved over Blocks 1–6 (Fig. 2B) and within blocks (Fig. S17). This improvement may reflect the usual process of learning the task observed in most cognitive experiments, as indicated by the improvement between Block 1 and 2 (paired t-test, first stage: t(26) = 2.2,p = 0.03; second stage: t(26) = 3.9,p = 0.0006). However, it could also reflect participants’ ability to create options at three different levels in Blocks 1 and 2, and to successfully reuse them in Blocks 3–6 to adapt to changes in contingencies more efficiently. Below, we present specific analyses to probe option creation in test blocks. We used participants’ performance averaged over Blocks 5 and 6 as a benchmark for comparing against performance in test Blocks 7 and 8.
We probed potential option transfer effects over the first 10 trials for each block (Fig. 2C), before behavior reached asymptote (Fig. S17). In the first stage, there was a main effect of block on number of key presses (1-way repeated measure ANOVA, F(2, 48) = 6.9, p = 0.002). Specifically, participants pressed significantly more times in Block 7 than Blocks 5–6 and Block 8 (paired t-test, Blocks 5–6: t(24) = 3.0, p = 0.006; Block 8: t(24) = 3.0, p = 0.006). We also found no significant difference between the performance of circle and square in Block 7 (Potential Asymmetry in Block 7 of Experiment 1 in Supplementary section). These results provide preliminary evidence for negative transfer of previously learned HO in Block 7: participants might attempt to reuse HO1 or HO2, since either policy is successful for half the trials, but is incorrect and thus results in more key presses in the first stage for the other half of the trials. There was no significant difference between Block 8 and Blocks 5–6 (paired t-test, t(24) = 0.25, p = 0.81). This provides initial evidence for positive transfer of HO1 in Block 8, since performance in the first stage of Block 8 was on par with Blocks 5–6.
In the second stage (Fig. 2C), there was also a main effect of block in number of key presses (1-way repeated measure ANOVA, F(2, 48) = 11, p < 0.0001). Specifically, participants pressed significantly more times in Block 8 than Block 7 and Blocks 5–6 (paired t-test, Block 7: t(24) = 2.4, p = 0.025; Blocks 5–6: t(24) = 5.8, p < 0.0001). The difference between Block 7 and Blocks 5–6 was marginally significant (paired t-test, t(24) = 2.0, p = 0.06). These results suggests that participants negatively transferred MO in the second stage of Block 8, where the first stage choice that respected the current MO was followed by a new LO for correct performance, and thus necessitated to create a new MO.
Behavioral results in both the first and second stages provide initial evidence for option learning and transfer at distinct levels, both positive – when previous policies can be helpfully reused – and negative – when they impair learning. To further validate our hypothesis that participants learned options, we compared the simulations of five models with human behavior (Table 1).
Among the five models (Fig. 3A), only the Option Model and the Task-Set Model could account for the transfer effects in the second stage shown by the number of key presses. The Naive Flat Model could not achieve reasonable performance in the second stage because it ignored the non-Markovian aspect of the task - it was unable to learn two different sets of correct choices for a given second stage stimulus, because this required conditioning on the first stage stimulus (Fig. 2B). Thus, it serves to illustrate the limitations of classic RL, but is a straw man model in this task. The Flat Model achieved reasonable performance in both the first and second stages, being able to take into account the first stage in second stage decisions, but did not demonstrate any transfer effects. The sequence learning model can never achieve reasonable asymptotic performance in the second stage (Fig. 3D). This is because the learned action sequences disregard the state in the second stage (see Sec. 2.1.5): the model cannot disambiguate which action sequence to choose in the first stage without knowing which shape will be shown in the second stage, which is random. Thus the model is equally likely to need 1 or 2 presses in the second stage, resulting in an average of 1.5 presses/trial. Note that, despite assuming perfect memory and choice of sequences, this performance is much worse than participants’ performance, which reaches ceiling performance in the last 10 trials (trials 51–60) of Blocks 5 and 6 at around 1.1 presses/trial (Fig. 3D). This suggests that participants behavior in this task cannot be accounted for by a pure sequence learning model.
Figure 3:
Experiment 1 second stage analysis. (A) Average number of second stage key presses in the first 10 trials of Block 5–8 for participants as well as model simulations. We ran 500 simulations of each hierarchical model (top) and flat model (bottom). See Table 1 for model parameters. Behavioral results show patterns of positive and negative transfer predicted by hierarchical, but not flat RL models. (B) Error type analysis of the second stage choices in Block 8. Top: We defined 1-to-1 mappings from the 4 actions to 4 choice types, 3 of which are error types. Bottom: Participants made significantly more option transfer errors than other errors. This was predicted by the Option Model, but not by the Task-Set Model. (C) Probability of a correct first key press for the second stage of the first trial of each of the 4 branches in Blocks 7–8 reveals positive and negative transfer prior in first attempt (left), as predicted by the Option Model (right). (D) While participants’ performance is close to ceiling, the sequence learning model cannot do better than 1.5 presses/trial on average in the second stage because it ignores the stimulus-dependency in the second stage.
Since both the Option Model and the Task-Set Model demonstrate the transfer effects in terms of average number of presses in the first and second stages, results so far invalidate other models and replicate previous findings that participants create one-step policies or task-sets, that they can reuse in new contexts, leading to positive and negative transfer (Collins et al., 2014; Collins & Frank, 2013, 2016). However, results so far do not discriminate between the Option Model and the Task-Set Model. We now present new analyses to show that the findings extend to creating multi-step policies or options.
2.2.2. Second stage choices reveal option transfer
To strengthen our results, we further examined the specific errors that participants made, as they can reveal the latent structure used to make decisions. To further disambiguate between the Option Model and the Task-Set Model, we categorized errors into meaningful choice types (Collins & Frank, 2013). We focused on the second stage choices for model comparison (Fig. 3), the part of the experiment designed so that temporally-extended policies could have an impact on decision making.
We hypothesized that participants learned MOs that paired the policies in the first and second stages into a single mid-level, temporally-extended option. Therefore, positive transfer in the second stage of Block 7 and negative transfer in the second stage of Block 8 should be due to participants selecting the entire MO that was previously learned in response to a first stage stimulus, including the correct key press for the first stage stimulus as well as the corresponding LO for the second stage. We defined choice types based on this hypothesis (Fig. 3B). For example, for the second stage of Block 8, consider the diamond following the circle in Block 8 (Fig. 2A): A2 is the correct action; an A1 error corresponds to the correct action in the first stage (“f-choice” type); an A4 error would be the correct action if selecting MO1 as a whole (“option transfer” type); an A3 error is labeled “other” type. Therefore, we have a 1-to-1 mapping between the four possible actions and four choice types, three of which are error types.
We computed the proportion of the 3 error types for the first 3 trials of each of the 4 branches in the second stage of Block 8 (Fig. 3B). Note that we picked the first 3 repetitions to match the time frame of the first 10 trials used in previous analyses (Fig. 2C); results for the first 2 repetitions were qualitatively similar. There was a main effect of error type (1-way repeated measure ANOVA, F(2, 48) = 44, p < 0.0001). In particular, we found more “option transfer” errors than the “other” errors (paired t-test, t(24) = 2.5, p = 0.02), suggesting that participants selected previously learned MOs as a whole at the beginning of the second stage of Block 8. The Option Model could reproduce this effect because the agent selects an entire option (MO) in the first stage: not only its immediate response to the first stage stimulus, but also its policy over LO choice in the second stage. The Task-Set Model could not reproduce this effect, because the first stage choice was limited to the first stage, and the second stage did not use any information from the first stage. Therefore, the error type profile in Block 8 could not be accounted for by transfer of one-step task-sets alone, ruling out the Task-Set Model.
There was also more “other” type than “f-choice” errors (paired t-test, t(24) = 8.8, p < 0.0001). There were few “f-choice” errors, likely due to meta-learning (Harlow, 1949; Wang et al., 2018): participants observed that the correct action in the second stage was always different from the first stage (Fig. 2A). We included a free meta-learning parameter m in all models (Sec. 2.1.5) to capture this heuristic and quantitatively capture behavior better.
We next analyzed Block 7 second stage errors. Because Block 7 allowed for full MO transfer, we predicted that there would not be any specific error pattern in the second stage. The same choice type definitions were not well-defined for the second stage of blocks other than Block 8. Therefore, we categorized errors differently in Blocks 1–7. For example, consider the diamond following the circle in Blocks 1, 3, and 5 (Fig. 2A): A4 is the “correct” choice; an A1 error corresponds to the correct choice in the first stage (“f-choice” type); an A2 error corresponds to the correct action for the other second stage stimulus, triangle, in the same LO, thus we defined it to be the “sequence” type, because A2 followed the first stage correct action A1 half of the time, as opposed to the “non-sequence” action A3, which never happened after A1. Indeed, aggregating the first 3 trials for each of the 4 branches in the second stage of Blocks 5–7 (Fig. S6), we did not find any significant difference in any of the 4 choice types between the second stage of Block 7 and that of Blocks 5–6 (paired t-test, all (t(24) ≤ 1, all p’s> 0.30). While participants were pressing marginally more times in Block 7 compared to Blocks 5 and 6 (Fig. 2C), this is likely due to the sudden change in the mappings. The similarity in choice type distributions indicates that the positive transfer in the second stage of Block 7 was not interfered by the negative transfer in the first stage of Block 7, further confirming that participants were selecting learned MOs as a whole, but re-composing them together into a new HO. The Option Model is also able to quantitatively capture the similarity of the choice type profiles between Block 7 and Blocks 5–6 (Fig. S6). We also compared the reaction time of the “sequence” and “non-sequence” types to look for potential signatures of sequence learning (see supplement for details).
2.2.3. The first press in the second stage reveals theoretical benefit of options
While the first several trials demonstrated transfer effects, the Option Model predicts immediate transfer effect on the first press in the second stage of a new block without any experience. Therefore, we computed the probability of a correct choice on the first press for the 4 branches in the second stage (Fig. 3C), and compared to chance (, accounting for the meta-learning effect that the correct action in the second stage was always different from the first stage). The probability of a correct first key press in Block 7 and Blocks 5–6 was significantly above chance (sign test, Block 7: p = 0.015; Blocks 5–6: p < 0.0001), without significant difference between the two (sign test, p = 0.26). These positive transfer effects on the first press supports our prediction that participants were using previously learned MO to guide exploration and thus speed up learning even without any experience in Blocks 5–7. Block 8 was significantly below chance (sign test, p = 0.004), independently indicating, via negative transfer, exploration with previously learned MO in the very first trials. The Option Model was able to quantitatively reproduce these positive and negative transfer effects evident in the first press in the second stage, since the first stage choice can immediately help inform which LO to use in the second stage.
2.2.4. First stage choices reveal transfer of policies over options
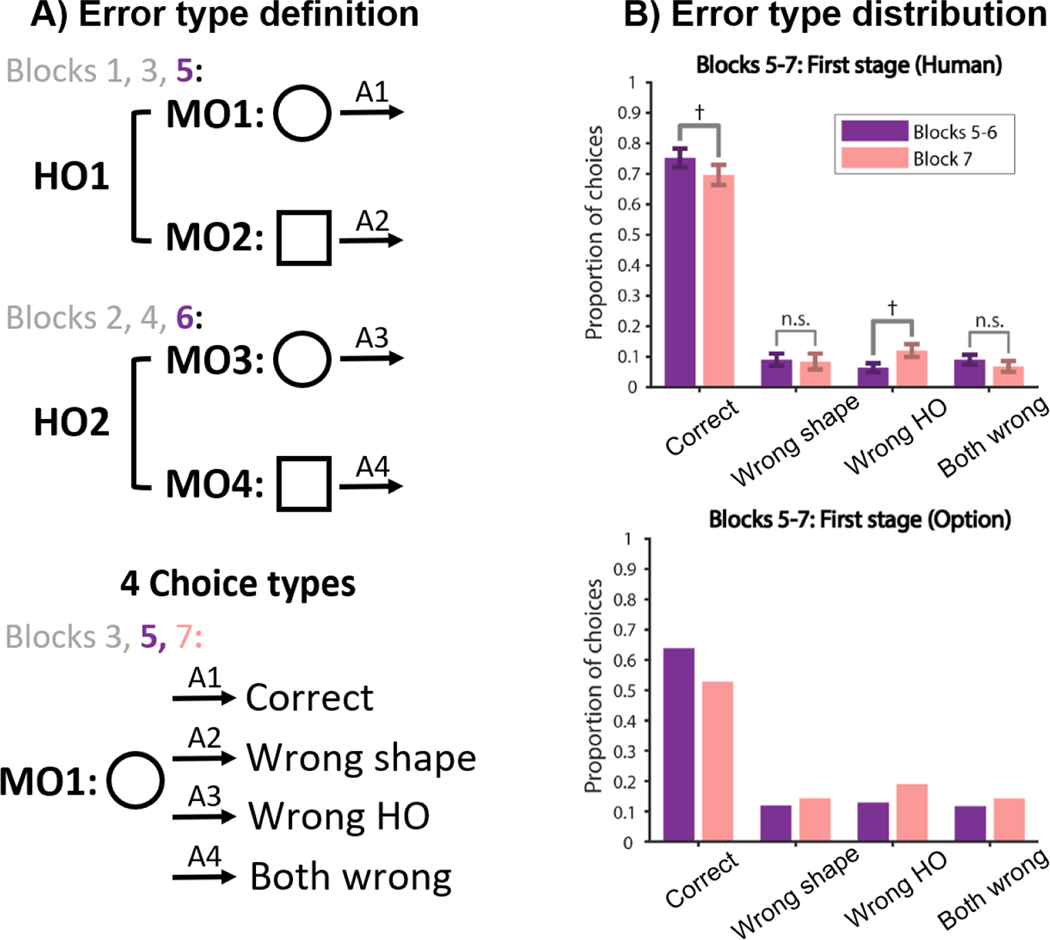
To test whether participants learned HOs in the first stage, we investigated errors in the first stage. We hypothesized that the increase in key presses in the first stage of Block 7 (Fig. 2C) was due to selecting a previously learned but now wrong HO in the first stage, which would be characterized by a specific error. We categorized first stage errors (Fig. 4A) into 3 types (“wrong shape”, “wrong HO”, and “both wrong”), which we exemplify for the circle in Blocks 1, 3, and 5 (Fig. 2B): A1 is the “correct” action; an A2 error corresponds to the correct action for the square in the same block (“wrong shape” type); an A3 error corresponds to the correct action for the circle in Blocks 2, 4, and 6 (“wrong HO” type); and A4 is the “both wrong” type.
Figure 4:
Experiment 1 first stage choices. (A) Definition of choice types in the first stage. (B) Choice type analysis of the first stage in Blocks 5–7 for participants (top) and the Option Model (bottom). Participants made significantly more wrong HO errors in Block 7 than in Blocks 5–6, but no change for the other two error types. This suggests that participants were negatively transferring HO in the first stage of Block 7, as predicted by the Option Model.
According to our hypothesis, we expected that the worse performance in the first stage of Block 7 (Fig. 2C) should be primarily due to the “wrongour hypothesis, we expeHO” errors. We found a main effect of choice type (2-way repeated measure ANOVA, F(3, 72) = 195, p < 0.0001) and a significant interaction between block and choice type (F(3, 72) = 2.9, p = 0.04). In particular, this significant interaction was driven by an increase in Block 7 “wrong HO” errors (Fig. 4B), compared to Blocks 5–6, although the direct comparison did not reach significance (paired t-test, Wrong HO, t(24) = 1.9, p = 0.07; other two error types: paired t-test, both p’s > 0.28). The Option Model predicted this choice type profile in the first stage (Fig. 4C), by attempting to transfer previously learned HO, which would hurt performance in the first stage of Block 7.
2.2.5. Experiment 1 Mturk replicates option transfer in the second stage
While in-lab participants’ behavior showed promising evidence in favor of transferring multi-step options, we sought to replicate our results in a larger and more diverse population. Therefore, we ran a shorter version of Experiment 1 on Mturk (Fig. 5). In the second stage, we replicated the main effect of block on the number of presses (1-way repeated measure ANOVA, F(2, 108) = 19, p < 0.0001). Specifically, the average number of key presses (Fig. 5A) in the first 10 trials of Block 7 was not significantly different from that of Blocks 5–6 (paired t-test, t(54) = 0.72, p = 0.47). Participants pressed significantly more times in Block 8 compared to Block 7 and Blocks 5–6 (paired t-test, Block 7: t(54) = 4.5, p < 0.0001; Blocks 5–6: t(54) = 5.3, p < 0.0001), replicating results from in-lab participants (Fig. 2C).
Figure 5:
Experiment 1 Mturk results. (A) Average number of key presses for the first 10 trials of Blocks 5–8 for the second stage for participants (left) and the Option Model (right). (B) Error type analysis of the second stage in Block 8 for participants (left) and the Option Model (right). We replicated the same pattern as the in-lab population (Fig. 3B). (C) Probability of a correct first key press for the second stage of the first trial of each of the 4 branches in Blocks 7–8 for participants (left) and the Option Model (right).
In the second stage of Block 8 (Fig. 5B), there was a main effect of error type (1-way repeated measure ANOVA, F(2, 108) = 62, p < 0.0001). The “option transfer” errors were significantly more frequent than the “other” type errors (paired t-test, t(54) = 4.7, p < 0.0001), and the “other” type was significantly more frequent than the “f-choice” type (paired t-test, t(54) = 6.7, p < 0.0001). This also replicates the error type profile of in-lab participants.
For the probability of correct choice in the first press (Fig. 5C), we also found participants were performing significantly above chance in the second stage of Blocks 3–4, Blocks 5–6 and Block 7 (sign test, Blocks 3–4: p = 0.001; Blocks 5–6: p = 0.003; Block 7: p = 0.001), but not significantly different from chance in Block 8 (sign test, p = 0.18). There was also no significant difference between Block 7 and Blocks 5–6 (sign test, p = 1). This supported the previous finding that participants used temporally-extended MOs to explore in a new context.
We did not replicate the negative transfer in the first stage of Block 7 (Fig. S8B) shown in in-lab participants (Fig. 2C). There was no main effect of block on the number of presses (1-way repeated measure ANOVA, F(2, 108) = 0.19, p = 0.83). Mturk participants did not press significantly more times in the first stage of Block 7 than Block 8 or Blocks 5–6 (paired t-test, Block 7: t(54) = 0.30, p = 0.77; Blocks 5–6: t(54) = 0.32, p = 0.75). This is potentially due to the lack of motivation among Mturk participants to exploit structure in the first stage, since participants did not receive points for being correct in the first stage. On the other hand, participants received points for choices in the second stage, which, as indicated by the Mturk experiment instruction, would impact their bonus. This might explain why the transfer effects in the first stage did not replicate, but the second stage transfer did. Note that in this case, the absence of transfer allowed the Mturk participants to make fewer errors in Block 7 than they might otherwise, highlighting the fact that engaging in a cognitive task and building and using structure is not always beneficial.
The Option Model was able to account for Experiment 1 Mturk data, despite the lack of transfer in the first stage, by assuming either a faster forgetting of HOs (higher f1) or a lower prior for reusing previously learned HO policies (higher γ1, Table 1). Indeed, simulations reproduced the lack of transfer in the first stage (Fig. S8B), and also captured all option transfer effects demonstrated by Mturk participants in the second stage (Fig. 5).
We conclude that, in the Mturk sample, similar to the in-lab sample, we successfully replicated the main option transfer effects in the second stage due to selecting a temporally-extended policy MO as a whole. This is reflected by number of presses, proportion of error types in Block 8, and the probability of correct choice in the first press (Fig. 5). While we did not replicate transfer of high-level options (task-sets of options), this could be accommodated by the model, and understood as a lack of motivation at learning the highest level of hierarchy HO.
3. Experiment 2
Experiment 2 was administered to UCB undergraduates in exchange for course credit. 31 (21 females; age: mean = 20.2, sd = 1.8, min = 18.3, max = 26.3) UCB undergraduates participated in Experiment 2. 4 participants in Experiment 2 were excluded due to incomplete data or below chance performance, resulting in 27 participants for data analysis.
3.1. Experiment 2 Protocol
Experiment 1’s Block 8 comes after a first testing block that includes re-composing of previous options, which could interfere with our interpretation of positive and negative transfer results in Block 8, for example by making participants aware of the potential for structure transfer. In Experiment 2, we removed Block 7 of Experiment 1 to eliminate this potential interference (Fig. 6A). Therefore, Block 7 in Experiment 2 was identical to Block 8 in Experiment 1. In addition, to limit experiment length and loss of motivation at asymptote in each block, we decreased the length of Blocks 3–7 to 32 trials each, with each first stage stimulus leading to each second stage stimulus 8 times. All other aspects were identical to Experiment 1.
Figure 6:
Experiment 2 protocol and results. (A) To eliminate potential interference of Block 7 on Block 8 in Experiment 1, Block 7 of Experiment 1 was removed in Experiment 2. Therefore, Block 7 in Experiment 2 was identical to Block 8 in Experiment 1. (B) Average number of key presses for the first 10 trials of Blocks 5–7 for the second stage for participants (left) and the Option Model (right). (C) Error type analysis of the second stage in Block 7 for participants (left) and the Option Model (right). We replicated the same pattern as in Block 8 of Experiment 1 (Fig. 3C, Fig. 5B). (D) Probability of a correct first key press for the second stage of the first trial of each of the 4 branches in Blocks 5–7 for participants (left) and the Option Model (right).
3.2. Experiment 2 Results
3.2.1. Second stage choices replicate option transfer
Participants were able to learn the correct actions in both the first and second stages and their performance improved over Blocks 1–6 (Fig. S9A). The within-block learning curves also showed that participants performance improved and then reached asymptote as they progressed within a block (Fig. S19).
We replicated the negative transfer effects in the second stage of Experiment 1 (Fig. 2C) both in terms of number of presses (Fig. 6B) and error types in Block 7 (Fig. 6C). Participants pressed significantly more times in the second stage of Block 7 compared to Blocks 5–6 (paired t-test, t(25) = 6.4, p < 0.0001). In Block 7 specifically, there was a main effect of error type (1-way repeated measure ANOVA, F(2, 50) = 30, p < 0.0001). The proportion of the error type “option transfer” was significantly higher than the error type “other” (paired t-test, t(25) = 3.2, p = 0.004).
We also observed transfer effects on the first press in the second stage (Fig. 6D). We found that the probability of a correct choice was significantly above chance in Blocks 3–4 and Blocks 5–6 (sign test, Blocks 3–4: p = 0.0094; Blocs 5–6: p < 0.0001), and significantly below chance in Block 7 (sign test, p < 0.0001). This replicates results in Blocks 3–6 and 8 in Experiment 1 (Fig. 3C). The Option Model could quantitatively reproduce all these transfer effects (Fig. 6B-D).
3.2.2. Second stage choices in Block 7 reveal interaction between meta-learning and option transfer
Because there was no Block 7 from Experiment 1, we had a less interfered test of negative transfer in the second stage of Block 7 of Experiment 2. Therefore, we further broke down the second stage choice types for each of the 4 branches in the second stage of Block 7 in Experiment 2 (Fig. 7A). Consider (Fig. 2A) the two first stage stimuli as F1 (circle) and F2 (square), and the two second stage stimuli as S1 (diamond) and S2 (triangle). We found a main effect of error type on proportion of errors and a marginally significant interaction between branch and error type (2-way repeated measure ANOVA, error type: F(2, 36) = 20, p < 0.0001; interaction: F(6, 108) = 2.1, p = 0.055). Specifically, we found the error type profile in Fig. 6C was mainly contributed by , i.e. circle in the first stage followed by diamond in the second stage, and (paired t-test, : t(23) = 2.7, p = 0.013; : t(23) = 3.1, p = 0.005). On the other hand, there was no significant difference between the “option transfer” and “other” error types for and (paired t-test, : t(22) = 0.9, p = 0.38; : t(22) = 0.81, p = 0.43). It is striking that this highly non-intuitive result is perfectly predicted by the Option Model (Fig. 7B).
Figure 7:
Experiment 2 second stage choice shows interaction between option transfer and meta learning. Error type analysis for each of the 4 branches in the second stage of Block 8 for participants (A) and the Option Model (B). The option transfer error was more than other error only for and , which was predicted by the Option Model. (C) Example schematic for the interaction: learning A2 for the diamond activates LO3; learning A3 for the triangle activates LO2; meta-learning only suppresses LO2 but not LO3.
The Option Model offers an explanation as the interaction between option transfer and meta-learning (Fig. 7C). Meta-learning discourages participants from selecting second-stage actions that repeat the correct first-stage action, and as such, discourage them from sampling some, but not other LOs (e.g. LO2 in the example of Fig. 7C). This interference in the exploration of potential LOs leads to some transfer errors being more likely, in an asymmetrical way.
3.2.3. Influence of the second stage on the first stage
For the first stage choices (Fig. S9B), we found that participants pressed significantly more times in the first 10 trials of Block 7 compared to Blocks 5–6 (paired t-test, t(25) = 2.4, p = 0.024). This effect was not found in Experiment 1 between Block 8 and Blocks 5–6 (Fig. 2C), and was not predicted by the model.
One potential explanation for this surprising result is that the error signals in the second stage propagated back to the first stage. Specifically, the errors participants made by selecting the wrong LO in the second stage are credited to the chosen LOs policy, but participants might also credit these errors to using the wrong HO in the first stage. Going back to our example, if your meal is not tasty, it might not be because you roasted the potatoes instead of boiling them, but it might be because you wanted meat instead of potatoes in the first place. To test this explanation, we further probed choice types in the first stage of Experiment 2 (Fig. S10). Indeed, we found significantly more “wrong HO” errors in Block 7, compared to Blocks 5–6 (paired t-test, p = 0.045). Therefore, the increase in number of key presses in the first stage of Block 7 was mainly contributed by more “wrong HO” errors, indicating that participants explored another high-level option (making carrots). The same effect was not seen in the first stage of Experiment 1 between Block 8 and Blocks 5–6 (Fig. 2C), potentially due to the interference of Block 7 in Experiment 1.
The Option Model could not capture this effect, since the selection of HO was only affected by learning in the first stage (Sec. 2.1.5), as a way of simplifying credit assignment (see Sec. 6.1.3 for a more detailed discussion on credit assignment). This will be a target for future model improvements.
4. Experiment 3
Experiment 3 was administered to UCB undergraduates in exchange for course credit. 35 (22 females; age: mean = 20.5, sd = 2.5, min = 18, max = 30) UCB undergraduates participated in Experiment 3. 10 participants in Experiment 3 were excluded due to incomplete data or below chance performance, resulting in 25 participants for data analysis.
An additional 65 (37 female; see age range distribution in Table 3) Mturk participants finished the experiment. 34 participants were further excluded due to poor performance, resulting in 31 participants for data analysis (62 of these 65 participants were above chance in the second stage, but only 32 were above chance in the first stage, so Mturk participants were mostly excluded due to performance in the first stage; see Sec. 2.1.4 for more details).
4.1. Experiment 3 in-lab Protocol
In Experiment 1, to perform well in the second stage, participants had to learn option-specific policies, due to the non-Markovian nature of the task (the correct action for the same second stage stimulus was dependent on the first stage stimulus). In Experiment 3, we removed this non-Markovian feature of the protocol and tested whether the removal would reduce or eliminate option transfer. Based on previous research on task-sets showing that participants build structure when it is not needed (Collins et al., 2014; Collins & Frank, 2016), we predicted that participants might still show some evidence of transfer. However, we predicted that any evidence of transfer would be weaker than in previous experiments.
In Experiment 3, the second stage stimuli following the two first stage stimuli were different (Fig. 8A). This eliminated the key non-Markovian feature from Experiment 1, since participants could simply learn the correct key for each of the 4 second stage stimuli individually without learning option-specific policies. Blocks 1 and 2 had 60 trials; we shortened Blocks 3 to 8 to 32 trials for the same reason as in Experiment 2. All other aspects of the protocol were identical to Experiment 1.
Figure 8:
Experiment 3 protocol and Mturk results. (A) The second stage stimuli following each first stage stimuli were different: for example, diamond and triangle followed circle; hexagon and star followed square. All state-action assignments remained the same as Experiment 1. This manipulation allowed us to test whether participants would naturally learn and transfer options in the second stage even when they could simply learn the correct key for each of the 4 second stage stimuli individually, rather than needing to take into account first stage information. (B) Error type analysis of the second stage in Block 8 for participants (left) and the Option Model (right). For Mturk participants, the proportion of option transfer error was not significantly different from other error, unlike Experiment 1 and Experiment 2, suggesting a lack of option transfer. (C) Probability of a correct first key press for the second stage of the first trial of each of the 4 branches in Blocks 7–8 for participants (left) and the Option Model (right). (D) Comparison of Experiment 1 Mturk and Experiment 3 Mturk participants in terms of error types in the second stage of Block 8: There was no significant effect of experimental condition.
4.2. Experiment 3 Mturk Protocol
In the Mturk version, Blocks 1 and 2 had a minimum of 32 and a maximum of 60 trials, but participants moved on to the next block as soon as they reached a criterion of less than 1.5 key presses per second stage trial in the last 10 trials (the 31 Mturk participants included for data analysis on average used 36 (SD = 7, median = 32, min = 32, max = 60) trials in Block 1 and 35 (SD = 4, median = 32, min = 32, max = 59) trials in Block 2). Blocks 3 to 8 all had 32 trials each. Experiment 3 MTurk was thus perfectly comparable to Experiment 1 MTurk in terms of trial numbers, as such, we focus first on MTurk results, since the same comparison could not be drawn between Experiments 1 and 3 for in-lab participants.
4.3. Experiment 3 Results
4.3.1. Mturk participants show weak evidence of options
Mturk participants were able to learn the correct actions in both the first and second stages, and their performance improved over Blocks 1–6 (Fig. S11A). The within-block learning curves also showed that participants performance improved and then reached asymptote as they progressed within a block (Fig. S20).
We first analyzed the average number of key presses in the first 10 trials of each block and stage. For the first stage (Fig. S12), we found no effect of block on number of presses across Blocks 5–8 (1-way repeated measure ANOVA, F(2, 60) = 0.13, p = 0.88), as in Experiment 1 MTurk. For the critical second stage (Fig. S11B), there was a main effect of Block (1-way repeated measure ANOVA, F(2, 60) = 3.3, p = 0.043). Specifically, there was no significant difference between Block 7 and Blocks 5–6 (paired t-test, t(30) = 0.25, p = 0.81). Participants pressed significantly more times in Block 8 than in Block 7 and Blocks 5–6 (paired t-test, Block 7: t(30) = 2.1, p = 0.048; Blocks 5–6: t(30) = 2.2, p = 0.036).
The negative transfer effect observed in the first stage of Block 7 in Experiment 1 (Fig. 2C) was not present here in Experiment 3 (Fig. S12). In addition to the fact that the first stage was never explicitly rewarded, as in Experiment 1, participants in Experiment 3 were even less motivated to exploit structure in the first stage. This is because the first stage in Experiment 3 was not necessary for resolving the second stage actions (Fig. 8A), while the non-Markovian aspect of Experiment 1 (Fig. 2A) forced participants to incorporate first stage information to resolve the correct choice for the second stage.
We calculated the proportion of error types in the second stage of Block 8 (Fig. 8B). Unlike in Experiment 1, we did not observe significantly more “option transfer” error than “other” error (paired t-test, t(30) = 1.6, p = 0.11). This choice type profile, compared to that in Experiment 1 and Experiment 2 (Fig. 3B, Fig. 5B, Fig. 6C), suggests a lack of option transfer in the second stage.
We also calculated the probability of a correct second stage first press for each of the 4 branches in the second stage (Fig. 8C). The probability was significantly above chance in Blocks 3–4 and Blocks 5–6 (sign test, Blocks 3–4: p = 0.0002; Blocks 5–6: p < 0.0001). It was marginally above chance in Block 7 (sign test, p = 0.07) and not significantly different from chance in Block 8 (sign test, p = 1). Compared to the results in Experiment 1 (Fig. 3C, Fig. 5C), these results suggest participants were still taking advantage of previously learned options to speed up learning at the beginning of each block, but potentially to a lesser extent compared to Experiment 1 and Experiment 2.
To formally quantify the effect of the experimental manipulation, we compared Experiment 1 and Experiment 3 for Mturk participants. In particular, we compared the proportion of “option transfer” and “other” error types in the second stage of Block 8 between the two experiments (Fig. 8D). We found a main effect of error type (2-way mixed ANOVA, F(2, 168) = 76, p < 0.0001), but there was no interaction between experiment and error type (2-way mixed ANOVA, F(2, 168) = 0.89, p = 0.41). In particular, the proportion of “option transfer” error type was not significantly higher in Experiment 1, compared to that in Experiment 3 (unpaired t-test, t(84) = 1, p = 0.32). This further shows that while there might be a lack of option transfer in the second stage of Block 8 based on the error type profile (Fig. 8B), learning might still not be completely flat in Experiment 3 (Fig. S11B).
The Option Model could capture the lack of option transfer (Fig. 8BC), with an increase in the second stage clustering coefficient , which controls how likely the model is to select a new blank policy compared to previously learned LOs in the second stage, as well as the forgetting parameter in the second stage, f2, which increases the speed at which the model forgets previously learned LO (Table 1).
4.3.2. In-lab participants replicate results from Mturk participants
In-lab participants replicated all aforementioned trends shown in Mturk participants (Fig. S13). In particular, there was a main effect of block on number of choices in the second stage (F(2, 46) = 7.2, p = 0.002). In-lab participants also pressed significantly more times in the second stage of Block 8 than Blocks 5–6 (paired t-test, t(23) = 3.6, p = 0.0017), but only marginally more than Block 7 (paired t-test, t(23) = 1.9, p = 0.067). Moreover, similar to Mturk participants, the proportion of “option transfer” error type was not significantly different from “other” error type (paired t-test, t(23) = 0.8, p = 0.43). These results replicated a lack of option transfer in the second stage in a separate in-lab population. Note that we could not do the same comparison between Experiment 1 and Experiment 3 for in-lab participants, because the number of trials per block for Experiment 1 and Experiment 3 was different in-lab.
5. Experiment 4
Experiment 4 was administered to UCB undergraduates in exchange for course credit. 31 (23 females; age: mean = 20.2, sd = 1.4, min = 18, max = 23) UCB undergraduates participated in Experiment 4. 12 participants were excluded due to incomplete data or below chance performance, resulting in 19 participants for data analysis.
An additional 110 (50 females; see age range distribution in Table 3) Mturk participants finished the experiment. 49 participants were excluded due to poor performance, resulting in 61 participants for data analysis (106 of the 110 participants were above chance in the second stage, but only 61 were above chance in the first stage; thus most Mturk participants were excluded by performance criterion in the first stage; see Sec. 2.1.4 for more details).
5.1. Experiment 4 in-lab Protocol
Experiment 4 (Fig. 9A) was designed to test whether participants were able to compose options learned separately, for example by expanding a low-level option’s initiation set and selecting it as part of a new mid and high-level option. Specifically, the protocol was identical to Experiment 1, except for Blocks 7 and 8. Block 8 in Experiment 4 was similar to Block 8 in Experiment 1, introducing two new LOs (LOnew) at the second stage as a benchmark for pure negative transfer.
Figure 9:
Experiment 4 protocol and results. (A) Experiment 4 design. In Experiment 4, we tested participants’ ability to recompose LO policies within MO policies. Blocks 1–6 were identical to Experiment 1. In Block 7, green indicates positions of potential positive transfer: MO2 followed by LO2 was learned in Blocks 1, 3, 5. Orange indicates positions of option composition: although MO1 previously included LO1 for second stage stimuli, it was modified to LO3 in Block 7. In Block 8, red indicates positions of negative transfer: LO5 and LO6 were completely novel to participants. Blocks were color coded for later analysis: Blocks 1–4 gray; Blocks 5–6 purple; Block 7 orange; Block 8 blue. (B) Second stage behavioral results. (1) Average number of key presses for the first 3 trials for each of the 4 branches in the second stage of Blocks 5–8 for participants (left) and the Option Model (right). Block 7 was split into LOmatch and LOmismatch; Block 8 corresponded to LOnew. (2) Proportion of correct choices on the first press of trials 1–3 for each of the 4 branches in the second stage for LOmatch, LOmismatch and LOnew for participants (left) and the Option Model (right). (3) Proportion of correct choices on the second press (for trials 1–3 for each of the 4 branches with an incorrect first key press) for the mismatch (left) and the new (right) condition. (4) Probability of a correct first key press for the second stage of the first trial of each of the 4 branches in Blocks 5–8 for participants (left) and the Option Model (right). (5)–(8) Same as (1)–(4) for Mturk participants.
The main difference between Experiment 4 and Experiment 1 was Block 7. In Block 7, one of the first stage stimuli (e.g. square) elicited the same extended policy MO2 (A2 followed by LO2 in the second stage), allowing positive MO transfer (“match” condition LOmatch). In contrast, the other first stage stimulus (e.g. circle) elicited a new policy recomposed of old subpolicies: participants needed to combine what they learned in the first stage of MO1 in Blocks 1, 3, and 5 (A1) (allowing for first stage transfer of HO1), and the second stage of Blocks 2, 4, and 6 (LO3; “mismatch” condition LOmismatch). Extending the food analogy, in Blocks 1, 3, 5, participants learned to make potatoes (MO1) by cutting potatoes (the first stage) and then roasting (LO1). In Block 7, participants also needed to cut potatoes, but then steam them (LO3), which was already learned as part of MO3 (make carrots) in Blocks 2, 4, 6. All blocks had 60 trials each.
5.1.1. Experiment 4 Mturk Protocol
The Mturk version was shortened for online workers. Blocks 1 and 2 had a minimum of 32 and a maximum of 60 trials, but participants moved on to the next block as soon as they reached a criterion of less than 1.5 key presses per second stage trial in the last 10 trials (the 61 Mturk participants included for data analysis on average used 46 (SD = 11, median = 42, min = 32, max = 60) trials in Block 1 and 43 (SD = 11, median = 38, min = 32, max = 60) trials in Block 2). All other blocks had 32 trials each.
5.2. Experiment 4 Results
5.2.1. Mismatch impacted performance of in-lab participants
Participants’ performance improved over Blocks 1–6 (Fig. S14A) and within each block (Fig. S22). To test more specifically whether participants were able to compose options, we focused on comparing the second stage behavior for old LOs (LOmatch and LOmismatch) and the average of LO5 and LO6 (LOnew) in Blocks 7–8. The Option Model predicted that performance for LOmatch in Block 7 should be the best due to positive transfer, since participants should have learned the extended MO2 policy whereby LO2 followed A2 in Blocks 1, 3, and 5 (Fig. 9A). LOnew should be the worst due to negative transfer, with all 4 stimulus-action assignments in the second stage novel. Performance for LOmismatch in Block 7 should fall in between (as observed in the number of key pressed, Fig. 9B1). While there should be negative transfer, as MO1 was usually followed by LO1, LO3 had been previously learned, so its performance should still surpass the performance in the second stage of Block 8, where LO5 and LO6 were completely novel to the participants. Therefore, we predicted LOmatch > LOmismatch > LOnew in terms of performance.
In the second stage (Fig. 9B1), there was a main effect of block on number of presses (1-way repeated measure ANOVA, F(2, 36) = 9.9, p = 0.0004). Specifically, the average number of key presses in LOnew (Block 8) was significantly more than Blocks 5–6 and LOmatch (paired t-test, Blocks 5–6: t(18) = 4.1, p = 0.0007; LOmatch: t(18) = 3.6, p = 0.002). There was no significant difference between Blocks 5–6 and LOmatch (paired t-test, t(18) = 0.7, p = 0.49), supporting the model’s prediction of positive MO transfer in this condition. The model predicted that LOmismatch performance should be between LOnew and LOmatch: LOmismatch performance should reflect positive LO transfer but negative MO transfer. Indeed, we observed a significant effect of LO condition on performance (1-way repeated ANOVA, F(2, 36) = 5, p = 0.01), driven by the predicted qualitative pattern. However, the paired comparisons were not significant (paired t-test, LOmatch: t(18) = 1.6, p = 0.13; LOnew: t(18) = 1.4, p = 0.18). These results replicate the negative transfer effects in the second stage of Block 8 shown in Experiment 1 (Fig. 2C) and Experiment 2 (Fig. 6B). In addition, they provide initial support for the compositionality hypothesis of the model, with intermediary transfer in the mismatch condition.
We confirmed the previous results by analyzing the proportion of trials in which the first key press was correct. We found that, in the first 3 trials for each of the 4 branches in the second stage (Fig. 9B2), there was a main effect of LO condition (1-way repeated measure ANOVA, F(2, 36) = 7.2, p = 0.002) on the proportion of correct choices for the first press of each trial. In particular, we found no significant difference between LOmismatch and LOnew (paired t-test, t(18) = 0.56, p = 0.58), while the performance of LOmatch was significantly higher than LOmismatch and LOnew (paired t-test, LOmismatch: t(18) = 2.6, p = 0.017; LOnew: t(18) = 4.4, p = 0.0003). These results suggested that the mismatch between MO1 and LO3 impacted participants’ performance, a marker of negative option (MO) transfer. The first three iterations indicated that participants were not able to efficiently re-compose the LOmismatch into a new mid-level option.
To better investigate participants’ choices before they experienced any new information in a new block, we also computed the probability of a correct first key press for the second stage of the first trial of each of the 4 branches in the Blocks 5–8 (Fig. 9B4). We found a main effect of block (Friedman Test, χ2(2, 36) = 20, p < 0.0001). Specifically, Blocks 5–6 and LOmatch were significantly above chance (sign test, both p < 0.0001); LOmismatch was not significantly different from chance (sign test, p = 0.34); LOnew was significantly below chance (sign test, p = 0.0007). There was a marginal difference between LOmatch and LOmismatch (sign test, p = 0.09), but no significant difference between LOmismatch and LOnew (sign test, p = 0.24). These results further showed that the mismatch condition impacted participants’ performance on the first press due to negative option (MO) transfer, and replicated the strong negative transfer in Block 8 in Experiment 1 and Experiment 2. The Option Model captured participants’ behavior well (Fig. 9B1, 2, 4, see Table 1 for model parameters).
5.2.2. Second press reveals benefit of option composition
The results so far supported one of our predictions, LOmatch > LOmismatch, by showing that performance in the mismatch condition was impacted due to negative MO transfer. We next sought evidence for our second prediction, LOmismatch > LOnew, where we hypothesized better performance in the mismatch condition by composing the first stage policy of MO1 and LO3.
In terms of performance on the first press in each trial, we did not find a significant difference between the two conditions (Fig. 9B2). However, this might be because the negative MO transfer reduced the benefit of compositionality, making it less detectable on the first press, also reflected by the small effect from the Option Model in Fig. 9B2. Positive LO transfer thus might only show a more significant effect after the first press unexpectedly failed (from negative transfer of MO1).
Therefore, we further computed the proportion of correct choices on the second press in those trials where the first press was incorrect (Fig. 9B3). Indeed, we found that the proportion of correct choices on the second press was significantly higher in the mismatch condition than the new condition (paired t-test, t(17) = 2.8, p = 0.012). This result supports our second prediction, LOmismatch > LOnew, revealing a benefit in the mismatch condition compared to the new condition in participants re-composing an old LO into a non-matching MO.
5.2.3. Mturk participants showed benefits of option composition
We collected a larger and independent sample on Mturk. Mturk participants also improved over Blocks 1–6 (Fig. S14B) and within block (Fig. S23), though their asymptotic performance (Blocks 5–6) was lower than the in-lab population. Specifically, we compared the average number of key presses in Blocks 5–6 in the first and second stages for both in-lab and Mturk populations. There was a main effect of stage and a marginal interaction of population and stage (2-way mixed ANOVA, stage: F(1, 78) = 7.1, p = 0.009; interaction: F(1, 78) = 3.1, p = 0.08). In particular, for the first stage, Mturk population was not significantly worse than the in-lab population (unpaired t-test, t(78) = 0.17, p = 0.86); but for the second stage, which was the focus of our analysis, Mturk population was significantly worse than the in-lab population (unpaired t-test, t(76) = 3.2, p = 0.002).
In the second stage (Fig. 9B5), there was a main effect of block on number of presses (1-way repeated measure ANOVA, F(2, 120) = 17, p < 0.0001). Specifically, the average number of key presses in LOnew was significantly more than LOmatch and LOmismatch (paired t-test, LOmatch: t(60) = 4.6, p < 0.0001; LOmismatch: t(60) = 3.8, p = 0.0004). LOmatch was not significantly different from Blocks 5–6 and LOmismatch (paired t-test, Blocks 5–6: t(60) = 0.26, p = 0.8; LOmismatch: t(60) = 0.8, p = 0.42).
The proportion of correct first press choices (Fig. 9B6) showed a similar pattern: there was a main effect of LO condition (1-way repeated measure ANOVA, F(2, 120) = 15, p < 0.0001) on the proportion of correct choices. In particular, the proportion of correct choice for LOnew was significantly lower than LOmismatch and LOmatch (paired t-test, LOmismatch: t(60) = 4.7, p < 0.0001; LOmatch: t(60) = 5.1, p < 0.0001) in Block 7. There was no significant difference between LOmismatch and LOmatch performance (paired t-test, t(60) = 0.54, p = 0.59). There was no difference between the mismatch condition and the new condition for second key presses (paired t-test, t(52) = 0.08, p = 0.94, Fig. 9B7), contrary to in-lab participants (Fig. 9B3). This difference could be attributed to MTurk participants’ lower task engagement. Indeed, contrary to in lab participants, MTurk participants’ performance was at chance for second key press (paired t-test against 0.5, Mturk: t(53) = 1.6, p = 0.13; in-lab: t(17) = 3.4, p = 0.003). Directly comparing MTurk and in-lab population for the proportion of correct second key press in both the mismatch and new conditions revealed a marginal effect of condition and a marginal interaction of population and condition (2-way mixed ANOVA, condition: F(1, 69) = 3.3, p = 0.07; interaction: F(1, 69) = 3.7, p = 0.06). This supports our interpretation that MTurk participants did not attempt to find the correct answer following an error, making the second press error analysis in this population difficult to interpret.
Finally, we looked at the probability of a correct first press in the very first trial of each of the 4 branches in the second stage (Fig. 9B8). There was a main effect of block (Friedman test, χ2(2, 120) = 17, p = 0.0002). In particular, Blocks 5–6 and LOmismatch were significantly above chance (sign test, both p = 0.004); LOmatch was marginally above chance (sign test, p = 0.07); LOnew was significantly below chance (sign test, p < 0.0001).
These results can be interpreted in one of two ways. The similar performance between LOmatch and LOmismatch suggests that participants were able to efficiently re-compose the first stage of MO1 with LO3 in the mismatch condition in Block 7, so that they did not suffer from MO negative transfer, as did in-lab participants. Alternatively, this result might indicate a lack of MO transfer (and only positive LO transfer) in both the match and mismatch condition. The latter interpretation is supported by the fact that second stage performance in LOmatch was lower in MTurk participants than it was for in-lab participants in all measures (unpaired t-test, number of key presses in the first 10 trials of Blocks 5–6: t(78) = 1.8, p = 0.08; proportion of correct choices in match condition: t(78) = 2.4, p = 0.019).
The Option Model could capture the negative transfer effect in LOnew and thus the difference between LOnew and LOmismatch (Fig. 9B5, 6). However, it could not fully reproduce the lack of difference between LOmatch and LOmismatch, since the model would first try to transfer LO1 in the mismatch condition, resulting in worse performance for LOmismatch. One possibility for this discrepancy might be that Mturk participants did not learn or transfer MO well, reflected by their overall worse performance in the second stage compared to in-lab participants (Fig. 9B).
This interpretation might suggest that the Task-Set Model explains the Mturk population better, indicating a lack of temporally-extended options, and makes a specific prediction: second stage errors should not be impacted by first stage information. To test this prediction, we analyzed the specific errors participants made, as this is a hallmark of temporally-extended option transfer vs. task-sets (Fig. 3B). Contrary to the prediction made by the Task-Set model, but consistent with the Option Model prediction, Mturk participants did demonstrate the behavioral signature of negative option (MO) transfer in the mismatch condition (Fig. S15): they made significantly more “option transfer” errors than “other” errors (paired t-test, t(53) = 4.8, p < 0.0001). While the comparison was not significant for in-lab participants (paired t-test, t(17) = 1.5, p = 0.16), a direct comparison between in-lab and Mturk populations did not reveal an effect of population (2-way mixed ANOVA, F(2, 140) = 0.74, p = 0.48), but did reveal an effect of error type (2-way mixed ANOVA, F(2, 140) = 39, p < 0.0001). Thus, our results indicate that both MTurk participants and in-lab participants used temporally-extended MOs, although MTurk participants were overall less successful at transferring them to facilitate decision making in the second stage. The results are consistent with participants re-composing low-level options into higher-level options.
6. Discussion
Our findings provide novel insight into how humans learn hierarchical representations they can compose for flexible generalization. They offer strong support for the acquisition of option-like representations in healthy human adults. Options can be thought of as choices that are more abstract, complex, and extended than simple motor actions, but can similarly be selected in a single decision. Using a novel two-stage protocol, we provide evidence that humans create multi-step policies than can be selected as a whole (options), and flexibly transfer and compose previously learned options. This transfer and composition ability guides exploration in novel contexts and speeds up learning when the options are appropriate, but impairs performance otherwise, as predicted by the options framework (Botvinick et al., 2009). Model simulations showed that only a model including temporal hierarchy could account for all results, suggesting that human participants not only build state abstractions with one-step task-sets (Monsell, 2003), but also temporal abstractions in the action space with multi-step options.
6.1. The Option Model
We developed a new model, the Option Model, to account for participants’ behavior. The Option Model includes features from our previous hierarchical structure learning model (Collins et al., 2014; Collins & Frank, 2013, 2016) and the hierarchical reinforcement learning (HRL) options framework (Sutton et al., 1999). In our previous hierarchical structure learning model, we used non-parametric priors (Chinese restaurant Process, or CRP (Pitman, 2006)) over latent variables that represented the currently valid policy to create state abstractions: this allowed the model to cluster different contexts together if the same task-set applied. This CRP prior enables the agent to identify (via Bayesian inference) novel contexts as part of an existing cluster if the cluster-defined task-set proves successful, resulting in more efficient exploration and faster learning.
On the other hand, the original formulation of the HRL options framework (Sutton et al., 1999) augments the action space of traditional flat RL with temporal abstractions called options. Each option is characterized by an initiation set that specifies in which states the option can be activated, a termination function that maps states to a probability of terminating the current option, and an option-specific policy (that leads the agent to a potentially meaningful and useful subgoal). Multi-step options allow even more efficient transfer than task-sets, which can be thought of as simpler one-step options.
Our Option Model is inspired by the fact that task-sets and options are similar in essentials: they are policies that an agent can select as a whole, and then apply at a lower level of abstraction (applying it to make a motor choice in response to a stimulus for task-sets, or applying it across time until termination in the case of an option (Collins, 2018)). Thus, our model brings together state and temporal abstractions by using option-specific CRP priors to implement option-specific policies that can be flexibly selected in different contexts if they share the same environmental contingencies. Our model captures the essence of the options framework despite some subtle differences. Here, we further discuss how our Option Model relates to each part of the HRL options framework.
6.1.1. Option-specific policy
The most important component of an option is the option-specific policy: what lower level-choices (either simpler options or basic actions) it constrains. In this paper, we focused on the transfer of option-specific policy to test theoretical benefits of the options framework.
Theoretical work (Botvinick et al., 2009) suggested that useful options should facilitate exploration and speed up learning. Indeed, we observed speed up in learning through the positive transfer effects. For example, in Experiment 1, the second stage of Block 7 provided a test of positive option transfer in terms of choice types (Fig. S6). Importantly, this positive transfer was not interfered by the negative transfer in its first stage (Fig. 2C), suggesting that participants transferred mid-level options (MO) as a whole. Moreover, the learning benefit was evident even in the first press (Fig. 3C, Fig. 5C, Fig. 6D): participants were already significantly above chance in the first press, indicating that they could explore more efficiently by immediately transferring previously learned options.
Previously learned option-specific policies also helped with option composition in the mismatch condition of Experiment 4 (Fig. 9). While MO1 was usually followed by LO1 in Blocks 1, 3, 5, in the mismatch condition, MO1 was followed by LO3 instead. This change indeed resulted in “option transfer” errors (Fig. S15). However, the fact that LO3 had been previously learned helped participants explore more efficiently. For example, once participants figured out A2 was correct for the diamond, they would more likely explore LO3, and thus A4 for triangle.
The HRL options framework also suggested that non-useful options can slow down learning (Botvinick et al., 2009). Indeed, we observed negative option transfer effects in the second stage across multiple experiments in terms of number of presses (Fig. 2C, Fig. 5A, Fig. 6B, Fig. 9B1, 5), and more importantly, error types (Fig. 3B, Fig. 5B, Fig. 6C, Fig. 7, Fig. S15), that are consistent with the predictions of the options framework. Note that the slow down was due to negative transfer of previously learned option-specific policies. Thus testing how having a wrong subgoal can impact learning performance is an interesting future direction.
We sought to confirm that participants were indeed learning option-specific policies, not just action sequences. Our protocol specifically used two second stage stimuli following each first stage stimulus (Fig. 2A) to avoid this potential confound. If, for example, circle was always followed by diamond and square by triangle, participants would not need to pay attention to the actual stimulus in the second stage, and could instead plan a sequence of actions in the first stage. In contrast, here, participants could only perform well by selecting options (i.e. stimulus-dependent temporally-extended policies). Indeed, we showed (Fig. 3D) that a sequence learning model would show ceiling performance at 1.5 presses per second-stage trials, while participants’ asymptotic performance were significantly better than 1.5 presses across all datasets (paired t-test, all p’s < 0.002, Fig. S16). While pure sequence learning could not account for our results, we investigated whether it could contribute to some of its aspects. Sequence learning would predict faster reaction times for actions that often follow in a sequence (Clegg, DiGirolamo & Keele, 1998). Therefore, we compared the reaction time for the “sequence” and “non-sequence” error types in the second stage. We did not find significant difference between the reaction time for “sequence” and “non-sequence” error types at the beginning of blocks; we only found such difference at the end of blocks (see supplement for full details). This suggests that while the transfer effects we observe at the beginning of each block could not be explained by pure sequence learning, participants might develop sequence learning-like expectations over time in a block, speeding up choices that came more frequently after each other.
6.1.2. Initiation set
The initiation set of an option specifies the set of states where the option can be selected. The observable states in our tasks are the shapes shown on the screen. Therefore, at first, the initiation sets of HO and MO are first stage stimuli (e.g. circle and square, Fig. 2A), whereas the initiation sets of LO are second stage stimuli. However, the optimal policies were also dependent on the block; thus participants needed to infer the latent states (state abstraction) dictated by block. Our extension of classic options with a CRP prior inference process over latent states can thus be thought of as continuously adding new block contexts to the initiation set of an option throughout the task. The ability to add new contexts to the initiation sets provides our Option Model the crucial flexibility needed to achieve transfer and composition, as demonstrated by human participants. For example, if LO3 was tied solely to the context of Block 2, where it was first learned, we would not observe the benefit of option composition in Experiment 4 in the mismatch condition.
6.1.3. Termination function
An option’s termination function maps each state to the probability of terminating the current option (i.e. not using its policy anymore). How to terminate an option is closely related to the underlying theoretical question of credit assignment, which arises naturally in tasks that require hierarchical reasoning (Sarafyazd & Jazayeri, 2019): if the current policy does not generate any (pseudo-) reward for a while, should the agent continue improving the current policy or terminate it and use another policy or even something new?
With a termination function as described in the original HRL options framework, credit assignment happens in a very specific way: the policy of the currently selected option (or options if multiple nested options are selected) is updated until termination is reached. However, this would make behavior very inflexible. For example, in our task, when an agent enters the second stage of Block 8 in Experiment 1 (Fig. 2A) for the first time after having correctly made a choice for the circle in the first stage, the agent would likely use LO1 due to negative transfer of MO1 and thus not receive reward. Because the termination function only takes state as an input, the agent would keep overwriting the LO1 policy with LO5 policy until termination, and thus not be able to reuse LO1 down the line.
Thus, our Option Model, uses a more flexible form of option termination. Specifically, we use Bayesian inference (Sec. 2.1.5), which was introduced in our previous hierarchical structure learning model (Collins & Frank, 2013). At the end of each choice, the model updates the likelihood of each option being valid based on the observed reward feedback, which then determines whether the model should stop using the current option. Moreover, Q-learning only operates on the option that has the highest posterior, thus assigning credit retrospectively to the best cause (Moran, Keramati, Dayan & Dolan, 2019). Therefore, the Option Model is more likely to create a new LO5 and learn its policy from scratch, making it more flexible at learning and selecting options. The crucial benefit of our new Option Model termination policy is that the agent can create a new LO5 and learn its policy from scratch, without overwriting the original LO1 policy. While the Option Model can capture participants’ choices well across all four experiments, the current experimental protocol was not designed specifically to test credit assignment to options. This remains an important question for future research.
There is another credit assignment problem that is not fully addressed by our current protocol and modeling: choices by lower level options may affect the termination of higher level options. For example, if you get punished for roasting potatoes, should you credit this to the lower level option (roasting) or to the higher level option (making potatoes) in the first place? Should you plan to cook meat instead, or just boil the potatoes? We have some evidence for both levels of credit assignment (e.g. in Block 7 of Experiment 2, or Block 8 in Experiment 1; Fig. 2C), when participants were experiencing many errors in the second stage using LO1 and LO2. Participants might not only consider terminating or re-learning the current LO, but also naturally attribute some of the negative feedback to the choices they made in the first stage regarding MO or HO. Indeed, we observed that second stage errors potentially resulted in more “wrong HO” errors in the first stage of Experiment 2 (Fig. S9B, Fig. S10).
In our Option Model (Sec. 2.1.5), for simplicity, first stage choices were only determined by learning within the first stage and were not sensitive to reward feedback in the second stage. It will be important in future research to better understand interactions between option levels for credit assignment. When considered together with the termination problem, these future directions may help trace the underlying neural mechanisms for credit assignment in human learning and hierarchical decision making.
6.2. Possible extensions
We tested predictions of HRL options framework through positive and negative transfer of option-specific policies in the simplest possible set up of tabular representation of state and action space. Multiple aspects could be expanded on in future research to increase the generalizability of the policy in real world scenarios.
First, real world policies apply to much more complex (continuous, multidimensional) state spaces. Recent work in AI expands the options framework to more realistic situations (Konidaris & Barto, 2007), where artificial agents learn how to navigate a sequence of rooms with different shapes and sizes. If each state in a room is naively paramatrized in a tabular way by (x, y) coordinates, when the agent is placed in a new room of a different shape, previously learned policy would be of not use. It is thus crucial to identify meaningful features of the state space shared by different rooms. (Konidaris & Barto, 2007) proposed learning options in a state space parametrized by distance from goals (“agent space”) to bypass this limitation.
Second, the low-level action space in real life conditions is also more complex. A good example is our flexible use of tools (Allen, Smith & Tenenbaum, 2019). We can conceptualize using various tools as taking actions. Humans demonstrate great flexibility when improvising using different tools to solve the same problem or even crafting new tools. If we simply represent actions in a tabular way, after participants associated a particular tool (action) to solve a task, the policy would be of no use if this particular tool is no longer provided in the future. The key might again be figuring out meaningful dimensions of the tool (action) space that are shared in different task scenarios, such as shape and weight of the tool.
Finally, even if two problems are different in terms of both state and action space (e.g. learning to play piano vs learning to play violin (Franklin & Frank, 2018)), knowledge of one might still help the other. Once one learned a piece on the piano, the knowledge of music theory might serve as a model to guide option transfer when learning the same piece on violin. These are important future directions for testing how humans transfer in those more real life scenarios, which might provide insight into developing more flexible and human-like AI systems with the HRL options framework.
6.3. Option discovery
One of the most important questions regarding options in AI is how to discover meaningful options. Discovering useful options entails learning all components of an option: initiation set, termination function, and option-specific policy that leads to a meaningful sub-goal. In this paper, we designed a protocol that focused on learning option-specific policies by making all other features, including subgoals, trivial.
Discovering options may be useful because of a key feature of our interactions with our environment. In real world scenarios, it is frequent that for a given observable state, the right choice to make depends on hidden context, task demand, or past information. This property is refered to as non-Markovian: the current observable information is insufficient to determine the next step. For example, when potatoes are peeled, we can use them to make either roasted potatoes or mashed potatoes. Therefore, the state “ peeled potatoes” is a meaningful subgoal state, and peeling potatoes is its corresponding option-specific policy.
This non-Markovian property might encourage the hierarchical and compositional nature of human behavior. It is central to the original formulation of the options framework (Sutton et al., 1999), and is also a natural objective for option discovery. In relation to our protocol, the correct action for diamond (Fig. 2B) varies from time to time in the same block. It makes sense to create different options to capture this, and relate it to the inferred hidden cause for why the correct actions change. Indeed, we observed that the non-Markovian feature in our experiments encouraged participants to create and transfer options at multiple levels of abstractions.
We tested whether the environment needs to be non-Markovian to trigger option creation. Specifically, we designed Experiment 3 by eliminating the non-Markovian property from Experiment 1 and testing if that affects option learning and transfer (Fig. 8A). Unsurprisingly, we found weaker option transfer effects in Experiment 3; however, participants’ behavior was still not flat (Fig. 8, Fig. S13). Thus, our results hint at the possibility that participants create temporal options (MO), even in the absence of a need for it, echoing past results showing that humans tend to create structure unnecessarily (Collins, 2017; Collins & Frank, 2013; Collins & Frank, 2016; Yu & Cohen, 2009). Furthermore, this may also show that objectives for option discovery are not limited to solving non-markovian problems. For example, (Diuk, Schapiro et al., 2013) showed that humans could identify bottleneck states from transition statistics, reflecting graph-theoretic objectives for option discovery in humans.
6.4. The options framework and other learning systems and models
While our Option Model uses a simple form of model-free RL (Q-learning; (Sutton & Barto, 2018)) to learn option-specific policies, the options framework is general and not limited to just Q-learning. Options can be learned or used with model-free methods (Botvinick et al., 2009) and model-based methods (Botvinick & Weinstein, 2014). It also has strong connections to successor representations (Momennejad et al., 2017; Stachenfeld, Botvinick & Gershman, 2017), which might provide objectives for subgoal discovery.
Moreover, in this paper, we gave examples of potential interaction of options with the meta-learning system (Fig. 7) and sequence learning (see supplement) in human participants. How options might interact with other learning systems is an important question for future research.
Finally, the options framework is not the first attempt to incorporate hierarchy and compositionality to model complex human cognition. Within psychology in particular, the concept of “options” echoes the idea of “chunking” in the cognitive architecture literature (Anderson et al., 2004; Lehman, Laird, Rosenbloom et al., 1996). Cognitive architectures models such as ACT-R (Anderson et al., 2004) rely strongly on the hierarchical representation of behaviors, whereby procedures frequently executed in successions can become “chunks” that can be selected at a higher level of abstraction. However, we were not able to find examples of such cognitive models that focused on how humans might rapidly learn and transfer hierarchical representations. Furthermore, a distinct aspect of the RL options framework (compared to cognitive architectures) is its objective of reward maximization (Botvinick et al., 2009), which is inherited as an augmentation of traditional flat RL. In that sense, options proposes a computational framework at Marr’s computational level of analysis (Niv & Langdon, 2016), not only at the “algorithm and representation” one. In our model, this reward objective also allows us to naturally include Bayesian inference as a way of optimal option selection and transfer. However, there have also been initial attempts to combine ideas from reward maximization of RL with cognitive architectures (Fu & Anderson, 2006; Nason & Laird, 2005). It would be especially interesting to consider potential connections between the options framework and various cognitive architectures, which were designed to explain a wide range of human cognition and not limited to structural learning from trial-by-trial interactions with the environment and reward feedbacks.
7. Conclusion
In summary, we found compelling evidence of option learning and transfer in human participants by examining the learning dynamics of a novel two-stage experimental paradigm. Through analyzing participants’ behavioral patterns and model simulations, we demonstrated the flexibility of option transfer and composition at distinct levels in humans. We proposed a novel computational framework, unifying temporal and state abstraction in a hierarchical reinforcement learning framework, to account for human flexible decision making.
Humans’ ability to flexibly transfer previously learned skills is crucial for learning and adaptation in complex real world scenarios. This ability is also one of the fundamental gaps that sets humans apart from current state-of-the-art AI algorithms. Therefore, our work trying to probe learning and transfer in humans might also help provide inspirations for AI algorithms to be more flexible and human-like.
Supplementary Material
8. Acknowledgements
We thank Katya Brooun, Ham Huang, Helen Lu, Sarah Master, and Wendy Shi for their substantial contribution to the project. We thank Rich Ivry, Milena Rmus and Amy Zou for feedback on this draft. This work was supported by NIMH RO1MH119383.
References
- Allen KR, Smith KA & Tenenbaum JB (2019). The tools challenge: Rapid trial-and-error learning in physical problem solving. arXiv preprint arXiv:1907.09620.
- Anderson JR, Bothell D, Byrne MD, Douglass S, Lebiere C & Qin Y (2004). An integrated theory of the mind. Psychological review, 111(4), 1036. [DOI] [PubMed] [Google Scholar]
- Andreas J, Klein D & Levine S (2017). Modular multitask reinforcement learning with policy sketches. In Proceedings of the 34th international conference on machine learning-volume 70 (pp. 166–175). JMLR. org. [Google Scholar]
- Badre D (2008). Cognitive control, hierarchy, and the rostro–caudal organization of the frontal lobes. Trends in cognitive sciences, 12(5), 193–200. [DOI] [PubMed] [Google Scholar]
- Badre D & D’Esposito M (2007). Functional magnetic resonance imaging evidence for a hierarchical organization of the prefrontal cortex. Journal of cognitive neuroscience, 19(12), 2082–2099. [DOI] [PubMed] [Google Scholar]
- Badre D & D’esposito M (2009). Is the rostro-caudal axis of the frontal lobe hierarchical? Nature Reviews Neuroscience, 10(9), 659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badre D & Frank MJ [Michael J]. (2011). Mechanisms of hierarchical reinforcement learning in cortico–striatal circuits 2: Evidence from fmri. Cerebral cortex, 22(3), 527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, Dezfouli A, Ito M & Doya K (2015). Hierarchical control of goal-directed action in the cortical–basal ganglia network. Current Opinion in Behavioral Sciences, 5, 1–7. [Google Scholar]
- Biederman I (1987). Recognition-by-components: A theory of human image understanding. Psychological review, 94(2), 115. [DOI] [PubMed] [Google Scholar]
- Bill J, Pailian H, Gershman SJ & Drugowitsch J (2019). Hierarchical structure is employed by humans during visual motion perception. bioRxiv, 758573. [DOI] [PMC free article] [PubMed]
- Botvinick MM (2007). Multilevel structure in behaviour and in the brain: A model of fuster’s hierarchy. Philosophical Transactions of the Royal Society B: Biological Sciences, 362(1485), 1615–1626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM (2012). Hierarchical reinforcement learning and decision making. Current opinion in neurobiology, 22(6), 956–962. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Niv Y & Barto AC (2009). Hierarchically organized behavior and its neural foundations: A reinforcement learning perspective. Cognition, 113(3), 262–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM & Plaut DC (2004). Doing without schema hierarchies: A recurrent connectionist approach to normal and impaired routine sequential action. Psychological review, 111(2), 395. [DOI] [PubMed] [Google Scholar]
- Botvinick MM & Weinstein A (2014). Model-based hierarchical reinforcement learning and human action control. Phil. Trans. R. Soc. B, 369(1655), 20130480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clegg BA, DiGirolamo GJ & Keele SW (1998). Sequence learning. Trends in cognitive sciences, 2(8), 275–281. [DOI] [PubMed] [Google Scholar]
- Collins AG (2017). The cost of structure learning. Journal of Cognitive Neuroscience, 29(10), 1646–1655. [DOI] [PubMed] [Google Scholar]
- Collins AG (2018). Learning structures through reinforcement. In Goal-directed decision making (pp. 105–123). Elsevier.
- Collins AG (2019). Reinforcement learning: Bringing together computation and cognition. Current Opinion in Behavioral Sciences, 29, 63–68. [Google Scholar]
- Collins AG, Cavanagh JF & Frank MJ (2014). Human eeg uncovers latent generalizable rule structure during learning. Journal of Neuroscience, 34(13), 4677–4685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG & Frank MJ [Michael J]. (2012). How much of reinforcement learning is working memory, not reinforcement learning? a behavioral, computational, and neurogenetic analysis. European Journal of Neuroscience, 35(7), 1024–1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG & Frank MJ [Michael J]. (2013). Cognitive control over learning: Creating, clustering, and generalizing task-set structure. Psychological review, 120(1), 190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG & Frank MJ [Michael J]. (2016). Neural signature of hierarchically structured expectations predicts clustering and transfer of rule sets in reinforcement learning. Cognition, 152, 160–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG & Frank MJ [Michael Joshua]. (2016). Motor demands constrain cognitive rule structures. PLoS computational biology, 12(3), e1004785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dezfouli A & Balleine BW (2012). Habits, action sequences and reinforcement learning. European Journal of Neuroscience, 35(7), 1036–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dezfouli A & Balleine BW (2013). Actions, action sequences and habits: Evidence that goal-directed and habitual action control are hierarchically organized. PLoS computational biology, 9(12), e1003364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diuk C, Schapiro AC, Cordova N, Ribas-Fernandes JJ, Niv Y & Botvinick MM (2013). Divide and conquer: Hierarchical reinforcement learning and task decomposition in humans. In Computational and robotic models of the hierarchical organization of behavior (pp. 271–291). Springer. [Google Scholar]
- Diuk C, Tsai K, Wallis J, Botvinick MM & Niv Y (2013). Hierarchical learning induces two simultaneous, but separable, prediction errors in human basal ganglia. Journal of Neuroscience, 33(13), 5797–5805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MK & Collins AG (2019). Computational evidence for hierarchically-structured reinforcement learning in humans. bioRxiv, 731752. [DOI] [PMC free article] [PubMed]
- Farashahi S, Rowe K, Aslami Z, Lee D & Soltani A (2017). Feature-based learning improves adaptability without compromising precision. Nature communications, 8(1), 1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox R, Krishnan S, Stoica I & Goldberg K (2017). Multi-level discovery of deep options. arXiv preprint arXiv:1703.08294.
- Frank MJ [Michael J] & Badre D. (2011). Mechanisms of hierarchical reinforcement learning in corticostriatal circuits 1: Computational analysis. Cerebral cortex, 22(3), 509–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin NT & Frank MJ [Michael J]. (2018). Compositional clustering in task structure learning. PLoS computational biology, 14(4), e1006116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu W-T & Anderson JR (2006). From recurrent choice to skill learning: A reinforcement-learning model. Journal of experimental psychology: General, 135(2), 184. [DOI] [PubMed] [Google Scholar]
- Gläscher J, Daw N, Dayan P & O’Doherty JP (2010). States versus rewards: Dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron, 66(4), 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harlow HF (1949). The formation of learning sets. Psychological review, 56(1), 51. [DOI] [PubMed] [Google Scholar]
- Holroyd CB [Clay B] & Yeung N. (2012). Motivation of extended behaviors by anterior cingulate cortex. Trends in cognitive sciences, 16(2), 122–128. [DOI] [PubMed] [Google Scholar]
- Jayaraman D, Ebert F, Efros AA & Levine S (2018). Time-agnostic prediction: Predicting predictable video frames. arXiv preprint arXiv:1808.07784.
- Jiang Y, Gu S, Murphy K & Finn C (2019). Language as an abstraction for hierarchical deep reinforcement learning. arXiv preprint arXiv:1906.07343.
- Koechlin E & Jubault T (2006). Broca’s area and the hierarchical organization of human behavior. Neuron, 50(6), 963–974. [DOI] [PubMed] [Google Scholar]
- Koechlin E, Ody C & Kouneiher F (2003). The architecture of cognitive control in the human prefrontal cortex. Science, 302(5648), 1181–1185. [DOI] [PubMed] [Google Scholar]
- Konidaris G & Barto AG (2007). Building portable options: Skill transfer in reinforcement learning. In Ijcai (Vol. 7, pp. 895–900). [Google Scholar]
- Krigolson O & Holroyd C (2006). Evidence for hierarchical error processing in the human brain. Neuroscience, 137(1), 13–17. [DOI] [PubMed] [Google Scholar]
- Lake BM, Salakhutdinov R & Tenenbaum JB (2015). Human-level concept learning through probabilistic program induction. Science, 350(6266), 1332–1338. [DOI] [PubMed] [Google Scholar]
- Lake BM, Ullman TD, Tenenbaum JB & Gershman SJ (2017). Building machines that learn and think like people. Behavioral and brain sciences, 40. [DOI] [PubMed]
- Lee TS & Mumford D (2003). Hierarchical bayesian inference in the visual cortex. JOSA A, 20(7), 1434–1448. [DOI] [PubMed] [Google Scholar]
- Lehman JF, Laird JE, Rosenbloom P et al. (1996). A gentle introduction to soar, an architecture for human cognition. Invitation to cognitive science, 4, 212–249. [Google Scholar]
- Leong YC, Radulescu A, Daniel R, DeWoskin V & Niv Y (2017). Dynamic interaction between reinforcement learning and attention in multidimensional environments. Neuron, 93(2), 451–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado MC [Marios C], Bellemare MG & Bowling M. (2017). A laplacian framework for option discovery in reinforcement learning. In Proceedings of the 34th international conference on machine learning-volume 70 (pp. 2295–2304). JMLR. org. [Google Scholar]
- Machado MC [Marlos C], Rosenbaum C, Guo X, Liu M, Tesauro G & Campbell M. (2017). Eigenoption discovery through the deep successor representation. arXiv preprint arXiv:1710.11089.
- McGovern A & Barto AG (2001). Automatic discovery of subgoals in reinforcement learning using diverse density.
- Menache I, Mannor S & Shimkin N (2002). Q-cut—dynamic discovery of sub-goals in reinforcement learning. In European conference on machine learning (pp. 295–306). Springer. [Google Scholar]
- Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, ... Ostrovski G. et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529. [DOI] [PubMed] [Google Scholar]
- Momennejad I, Russek EM, Cheong JH, Botvinick MM, Daw ND & Gershman SJ (2017). The successor representation in human reinforcement learning. Nature Human Behaviour, 1(9), 680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monsell S (2003). Task switching. Trends in cognitive sciences, 7(3), 134–140. [DOI] [PubMed] [Google Scholar]
- Moran R, Keramati M, Dayan P & Dolan RJ (2019). Retrospective model-based inference guides model-free credit assignment. Nature communications, 10(1), 750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair S & Finn C (2019). Hierarchical foresight: Self-supervised learning of long-horizon tasks via visual subgoal generation. arXiv preprint arXiv:1909.05829.
- Nason S & Laird JE (2005). Soar-rl: Integrating reinforcement learning with soar. Cognitive Systems Research, 6(1), 51–59. [Google Scholar]
- Niv Y (2009). Reinforcement learning in the brain. Journal of Mathematical Psychology, 53(3), 139–154. [Google Scholar]
- Niv Y & Langdon A (2016). Reinforcement learning with marr. Current opinion in behavioral sciences, 11, 67–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paolacci G, Chandler J & Ipeirotis PG (2010). Running experiments on amazon mechanical turk. Judgment and Decision making, 5(5), 411–419. [Google Scholar]
- Peng XB, Chang M, Zhang G, Abbeel P & Levine S (2019). Mcp: Learning composable hierarchical control with multiplicative compositional policies. arXiv preprint arXiv:1905.09808.
- Pitman J (2006). Combinatorial stochastic processes: Ecole d’eté de probabilités de saint-flour xxxii–2002. Springer. [Google Scholar]
- Ribas-Fernandes JJ, Shahnazian D, Holroyd CB & Botvinick MM (2019). Subgoal-and goal-related reward prediction errors in medial prefrontal cortex. Journal of cognitive neuroscience, 31(1), 8–23. [DOI] [PubMed] [Google Scholar]
- Ribas-Fernandes JJ, Solway A, Diuk C, McGuire JT, Barto AG, Niv Y & Botvinick MM (2011). A neural signature of hierarchical reinforcement learning. Neuron, 71(2), 370–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarafyazd M & Jazayeri M (2019). Hierarchical reasoning by neural circuits in the frontal cortex. Science, 364(6441), eaav8911. [DOI] [PubMed] [Google Scholar]
- Schapiro AC, Rogers TT, Cordova NI, Turk-Browne NB & Botvinick MM (2013). Neural representations of events arise from temporal community structure. Nature neuroscience, 16(4), 486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver D, Hubert T, Schrittwieser J, Antonoglou I, Lai M, Guez A, ... Graepel T. et al. (2018). A general reinforcement learning algorithm that masters chess, shogi, and go through self-play. Science, 362(6419), 1140–1144. [DOI] [PubMed] [Google Scholar]
- Şimşek Ö & Barto AG (2004). Using relative novelty to identify useful temporal abstractions in reinforcement learning. In Proceedings of the twenty-first international conference on machine learning (p. 95). ACM. [Google Scholar]
- Solway A, Diuk C, Córdova N, Yee D, Barto AG, Niv Y & Botvinick MM (2014). Optimal behavioral hierarchy. PLoS computational biology, 10(8), e1003779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stachenfeld KL, Botvinick MM & Gershman SJ (2017). The hippocampus as a predictive map. Nature neuroscience, 20(11), 1643. [DOI] [PubMed] [Google Scholar]
- Sutton RS & Barto AG (2018). Reinforcement learning: An introduction. MIT press. [Google Scholar]
- Sutton RS, Precup D & Singh S (1999). Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial intelligence, 112(1–2), 181–211. [Google Scholar]
- Taatgen NA, Lebiere C & Anderson JR (2006). Modeling paradigms in act-r. Cognition and multi-agent interaction: From cognitive modeling to social simulation, 29–52.
- Tomov M, Yagati S, Kumar A, Yang W & Gershman S (2018). Discovery of hierarchical representations for efficient planning. BioRxiv, 499418. [DOI] [PMC free article] [PubMed]
- Van Essen DC & Maunsell JH (1983). Hierarchical organization and functional streams in the visual cortex. Trends in neurosciences, 6, 370–375. [Google Scholar]
- Wang JX, Kurth-Nelson Z, Kumaran D, Tirumala D, Soyer H, Leibo JZ, ... Botvinick MM. (2018). Prefrontal cortex as a meta-reinforcement learning system. Nature neuroscience, 21(6), 860. [DOI] [PubMed] [Google Scholar]
- Wessinger C, VanMeter J, Tian B, Van Lare J, Pekar J & Rauschecker JP (2001). Hierarchical organization of the human auditory cortex revealed by functional magnetic resonance imaging. Journal of cognitive neuroscience, 13(1), 1–7. [DOI] [PubMed] [Google Scholar]
- Wingate D, Diuk C, O’Donnell T, Tenenbaum J & Gershman S (2013). Compositional policy priors.
- Xu D, Martιn-Martιn R, Huang D-A, Zhu Y, Savarese S & Fei-Fei L (2019). Regression planning networks. arXiv preprint arXiv:1909.13072.
- Xu D, Nair S, Zhu Y, Gao J, Garg A, Fei-Fei L & Savarese S (2018). Neural task programming: Learning to generalize across hierarchical tasks. In 2018 ieee international conference on robotics and automation (icra) (pp. 1–8). IEEE. [Google Scholar]
- Yu AJ & Cohen JD (2009). Sequential effects: Superstition or rational behavior? In Advances in neural information processing systems (pp. 1873–1880). [PMC free article] [PubMed]
- Zarr N & Brown JW (2016). Hierarchical error representation in medial prefrontal cortex. NeuroImage, 124, 238–247. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.