Mapping the Rest of the Human Connectome: Atlasing the Spinal Cord and Peripheral Nervous System

Abstract

The emergence of diffusion, structural, and functional neuroimaging methods has enabled major multi-site efforts to map the human connectome, which has heretofore been defined as containing all neural connections in the central nervous system (CNS). However, these efforts are not structured to examine the richness and complexity of the peripheral nervous system (PNS), which arguably forms the (neglected) rest of the connectome. Despite increasing interest in an atlas of the spinal cord (SC) and PNS which is simultaneously stereotactic, interactive, electronically dissectible, scalable, population-based and deformable, little attention has thus far been devoted to this task of critical importance. Nevertheless, the atlasing of these complete neural structures is essential for neurosurgical planning, neurological localization, and for mapping those components of the human connectome located outside of the CNS. Here we recommend a modification to the definition of the human connectome to include the SC and PNS, and argue for the creation of an inclusive atlas to complement current efforts to map the brain’s human connectome, to enhance clinical education, and to assist progress in neuroscience research. In addition to providing a critical overview of existing neuroimaging techniques, image processing methodologies and algorithmic advances which can be combined for the creation of a full connectome atlas, we outline a blueprint for ultimately mapping the entire human nervous system and, thereby, for filling a critical gap in our scientific knowledge of neural connectivity.

1. Introduction

Originating with the influential work of Brodmann (1909), anatomical atlases of the brain form the foundation of modern neuroscience research and provide the modern basis of neurosurgical practice and education. Prior to the advent of modern neuroimaging, most atlases of human neuroanatomy consisted of artistic drawings and/or photographs taken during post mortem dissections. Typically, such atlases conveyed neuroanatomical information obtained from only a single human subject. The extent of inter-subject variability across the general population is difficult—if not impossible—to extract with acceptable accuracy from such representations. Partly for this reason, much effort in the past 30+ years has been devoted to compiling neuroanatomical atlases which not only capture brain architecture, but also convey its structural variability across subjects in both health and in disease. Because interactive three-dimensional (3D) atlases provide rapid appreciation of spatially-relative neuroanatomy useful for basic research and efficient surgical planning, numerous digital brain atlases have been designed (Thompson and Toga 1996, Thompson, Woods et al. 2000, Nowinski, Johnson et al. 2012).

Most recently, considerable attention has been granted to mapping the human connectome (Toga, Clark et al. 2012, Van Essen, Smith et al. 2013, Bookheimer, Salat et al. 2019, Van Essen, Donahue et al. 2019). As originally defined, the human connectome refers to “a comprehensive structural description of the network of elements and connections forming the human brain” (Sporns, Tononi et al. 2005). Since the brain stem and cerebellum are traditionally categorized as parts of the brain (Duvernoy 2012), these structures are typically considered to belong to the central nervous system (CNS), such that the human connectome includes them, according to many authors (Bota, Sporns et al. 2015, Quartarone, Cacciola et al. 2020). Nevertheless, a substantial and critically important portion of nervous system (NS) connections consist of neurons, connections, and circuits outside the brain itself, i.e. in the spinal cord (SC) and peripheral nervous system (PNS). Since 2010, the National Institutes of Health (NIH) have financially supported the Human Connectome Project (HCP) and its derivative projects (https://neuroscienceblueprint.nih.gov/human-connectome/connectome-programs), whose purpose is to allow navigation of the brain in ways which were previously impossible, to study major brain pathways, and to compare major circuits from the standpoint of their architecture and function. While critically important, HCP efforts have focused exclusively on mapping the neuronal pathways within the central nervous system (CNS). This leaves connections involving the SC and PNS as contributors to the human connectome largely overlooked and, thus, points to the HCP as only a partial—rather than comprehensive—mapping of the body’s neuronal connections.

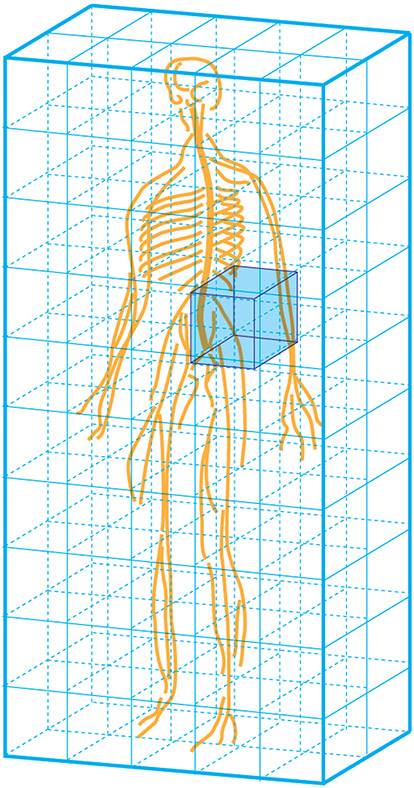
Despite intense interest from clinicians and researchers in the task of employing modern imaging methods (Figure 1), addressing the injuries and diseases which affect the SC (Yoon, Kim et al. 2013, Gupta, Gupta et al. 2014, Koskinen, Hakulinen et al. 2014, Hawasli, Rutlin et al. 2018), and the nerves which form the PNS (Cauley and Filippi 2013, Mathys, Aissa et al. 2013, Stoll, Wilder-Smith et al. 2013) (Figure 2), little attention has thus far been devoted to the goal of creating a population-based 3D atlas of these complex and wide-ranging structures. To satisfy the high standards of contemporary scientific and medical practice, such an atlas should be stereotactic, interactive, electronically dissectible, extendable, accurate, scalable, deformable, and completely labeled (Nowinski, Johnson et al. 2012, Nowinski, Chua et al. 2013). Furthermore, its navigation principles should include dynamic (de)composition, manipulation-independent 3D labeling, interaction combined with animation and quantification. Nevertheless, such organization, exploration, and visualization of these rich, whole-body connectomic data sets can be expected to form unprecedented challenges for the neuroinformatics community. With this in mind, we here propose that the concept and definition of the connectome should be augmented to include neuronal elements and connections within the entirety NS, rather than in the brain alone. Additionally, we advocate for the continued refinement of population-level, stereotactic, human atlas of the SC and PNS to complement current NIH-supported efforts to map the human brain connectome and thereby to fill a serious gap in the scientific state-of-the-art.

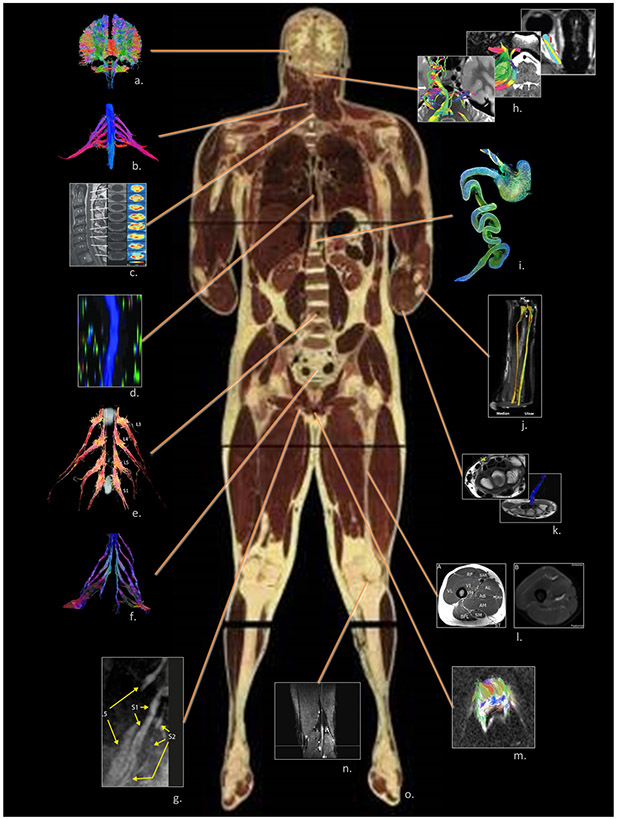
Figure 1.

The complete human connectome comprises not only the CNS but also nervous tissues located throughout the body which are suitable for neuroimaging. These include: a. the CNS (the authors); b. brachial plexus (Gasparotti 2011); c. cervical spinal cord (Vedantam, Jirjis et al. 2014); d. thoracic spinal cord (Alizadeh, Fisher et al. 2018); e. lumbar spinal cord (Eguchi, Ohtori et al. 2011); f. sacral spinal cord (van der Jagt, Dik et al. 2012)^◊; g. sciatic nerve (Cervantes, Van et al. 2018); h. cranial nerves (Zolal, Sobottka et al. 2016)^◊; i. the enteric nervous system (Stowers Institute for Medical Research)^◊; j. extremity: forearm (Haakma, Jongbloed et al. 2016)^◊; k. extremity: wrist (Lindberg, Feydy et al. 2013)^◊; l. extremity: thigh (Charles, Suntaxi et al. 2019)^♦; m. the reproductive system (Hedgire, Tonyushkin et al. 2016); n. extremity: tibial nerve (Simon, Lagopoulos et al. 2016); o. visible human (male), National Library of Medicine, National Institute of Health, Bethesda, USA.^♦

^◊ Reproduced with author’s/publisher’s permission; ^♦ Open access, unrestricted use.

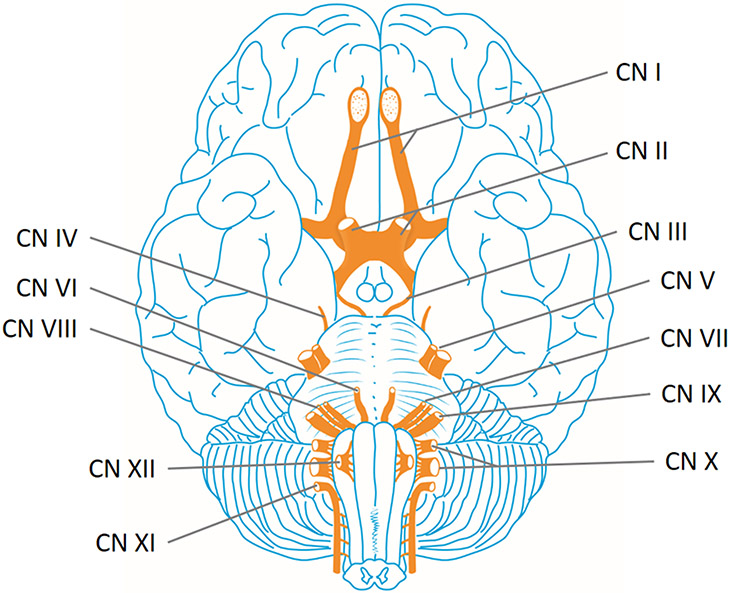
Figure 2.

Cranial nerves of the brain. The cranial nerves provide motor and sensory innervation mainly to the structures within the head, neck, and into the upper torso. Sensory innervation includes both general sensations such as temperature and touch, and specialized innervations such as taste, vision, smell, balance and hearing. The olfactory nerve (I) conveys the sense of smell. The optic nerve (II) transmits visual information. The oculomotor nerve (III), trochlear nerve (IV) and abducens nerve (VI) coordinate eye movement. The trigeminal nerve (V) comprises three distinct parts: The Ophthalmic (V1), the Maxillary (V2), and the Mandibular (V3) nerves. Lesions of the facial nerve (VII) may manifest as facial palsy. The vestibulocochlear nerve (VIII) splits into the vestibular and cochlear nerve. The vestibular part is responsible for innervating the vestibules and semicircular canal of the inner ear; this structure transmits information about balance, and is an important component of the vestibuloocular reflex, which keeps the head stable and allows the eyes to track moving objects. The cochlear nerve transmits information from the cochlea, allowing sound to be heard. The glossopharyngeal nerve (IX) innervates the stylopharyngeus muscle and provides sensory innervation to the oropharynx and back of the tongue. The vagus nerve (X) provides sensory and autonomic (parasympathetic) motor innervation to structures in the neck and also to most of the organs in the chest and abdomen. Damage to the accessory nerve (XI), involved in head motion and the movement of the shoulders, will lead to ipsilateral weakness in the trapezius muscle. The hypoglossal nerve (XII), responsible for tongue movement, is unique in that it is innervated from the motor cortices of both hemispheres of the brain. See also Table 1.

For the benefit of both scientific research and medical practice, we provide a general overview of existing neuroimaging techniques, image processing methodologies, algorithmic, and informatics advances which can be combined for the purpose of this important and momentous neuroimaging undertaking. Furthermore, recommendations and guidelines concerning the implementation of such a scientifically ambitious program are outlined and discussed.

2. Significance of SC and PNS connectome mapping

In neuroscience and many medical specialties—neurology, neurosurgery, and psychiatry, in particular—atlases of the NS and of its connections are essential for a variety of purposes, including neuroanatomy instruction, academic material preparation, clinical training, formal evaluation of medical practitioners, self-testing, neurosurgical planning, neurological localization, and many more (Brazis, Masdeu et al. 2011). Neuroanatomical knowledge of the cranial nerves (Table 1), of the musculature associated with the spinal nerves (Table 2), of their various nuclei and of their branching patterns has long been essential to medical students, neurologists, and neurosurgeons for purposes like 3D localization, surgical planning, stereotactic navigation during operating room interventions, and many more potential applications (Lo and Chiang 2016). The somatic nervous system (SNS or voluntary nervous system), for instance, is associated with the voluntary control of body movements via skeletal muscles. The system governs the process of voluntary reflex arcs which link sensory input to specific motor output. In contrast, the autonomic nervous system is a control system, acting largely below the level of consciousness, which regulates bodily functions, such as the heart rate, digestion, respiratory rate, pupillary response, urination, and sexual arousal. The system is the primary mechanism in control of initial physiological responses associated with the fight-or-flight response. These and other systems have been classically examined and characterized from post-mortem anatomy, although their mapping using neuroimaging is scant. Their importance to the overall nervous system architecture of the human body is undeniable.

Table 1.

The cranial nerves, their sensory modality, and basic functions. After Wilson-Pauwels, L., Akesson, E.J., and Stewart, P.A. (1988) Cranial Nerves: Anatomy and Clinical Comments. B.C. Decker, Philadelphia.

Modality
Nerve	Number	Somatic Motor	Brachial Motor	Visceral Motor	Visceral Sensory	General Sensory	Special Sensory	Function
Olfactory	I						✓	Smell
Optic	II						✓	Vision
Oculomotor	III	✓						Motor control of all extraocular muscles except the superior oblique and lateral rectus muscles
				✓				Parasympahetic supply to ciliary and pupillary constrictor muscles
Trochlear	IV	✓						Motor control of the superior oblique muscle
Trigeminal	V		✓					Motor control to muscles of mastication, etc. (V3)
						✓		Sensory function from the surface of head and neck, sinuses, meninges, and lymphatic membrane (external surface)
Abducens	VI	✓						Motor control to lateral rectus muscles
Facial	VII		✓					Motor control to the muscles of facial expression, etc.
				✓				Parasympathetic supply to all glands of the head except the parotid and integumentary glands
						✓		General sensation from a small area around the external ear, tympanic membrane (external surface)
							✓	Taste, anterior two-thirds of tongue
Vestibulocochlear	VIII						✓	Balance
							✓	Hearing
Glossopharangeal	IX		✓					Motor control of the stylopharyngeus muscle
				✓				Parasympathetic supply to parotid gland
					✓			Visceral sensation from carotid body
						✓		General sensation from posterior one-third of tongue and internal surface of the tympanic membrane
							✓	Taste, posterior one-third of tongue
Vagus	X		✓					Motor control of pharynx and larynx
				✓				Parasympathetic supply to pharynx, larynx, thoracic and abdominal viscera
					✓			Visceral sensory input from pharynx, larynx, and viscera
						✓		General sensation from small area around external ear
Accessory	XI		✓					Motor control of sternomastoid and trapezius muscles
Hypoglossal	XII	✓						Motor control of intrinsic and extrinsic muscles of the tongue except palatoglossus

Table 2.

Spinal segment innervation of major muscles. Spinal segments: C = cervical; T = thoracic; L = lumbar; S = sacral; major spinal segments indicated in bold.

Limb/Joint	Movement	Peripheral Nerve (Muscle)	Spinal Cord Segment
Arm	Abduction	Supracapular (supraspinatus)	C5, C6
Elbow	Flexion	Musculocutaneous (brachialis, biceps)	C5, C6
		Radial (brachioradialis)	C5, C6
	Extension	Radial (triceps)	C6, C7, C8
Wrist	Flexion	Median, ulnar	C6, C7, C8
	Extension	Radial	C5, C6, C7, C8
Hand	Finger movements	Median, radial, ulnar	C7, C8, T1
	Thumb movements	Median, radial, ulnar	C7, C8, T1
Hip	Flexion	Lumbar spinal nerves, femoral (iliopsoas)	L1, L2, L3
	Extension	Inferior gluteal (gluteus maximus)	L5, S1, S2
Knee	Flexion	Sciatic (hamstrings)	L5, S1, S2
	Extension	Femoral (quadriceps)	L2, L3, L4
Ankle	Dorsoflexion	Sciatic → peroneal (tibiaslis anterior)	L4, L5
	Plantar flexion	Sciatic → tibial (gastrocnemius)	S1, S2

Virtual navigation of 3D stereotactic atlases via well-designed, user-friendly software is likely to decrease the perceived difficulty of human anatomy and to increase motivation by medicine and neuroscience trainees to study material with fewer time constraints imposed by surgery or by cadaveric dissections. In addition, 3D scenes and images obtained from 3D atlases can typically be saved in electronic format to provide high quality materials and to enable prompt preparation of anatomical materials in both print and in electronic formats.

It was not until the advent and popularization of magnetic resonance imaging (MRI) and computed tomography (CT) that sophisticated noninvasive 3D imaging of the CNS, PNS and SC became feasible (see Smith, Pekar et al. 2012, for overview). Although both methods have been widely used to image various anatomic components of the CNS and PNS, insufficient progress has been made toward creating a stereotactic, electronically dissectible, population-level 3D atlas of neural connections outside the brain. In complement to the benefits of MRI and CT, opportunities to perform virtual dissections of white matter (WM) tracts in the SC and to visualize nerve pathways in the human body are among the most promising applications of diffusion weighted imaging (DWI) and of diffusion tensor imaging (DTI) tractography within the fields of SC imaging and neurography. The spinocerebellar tracts, which provide a rich neural representation of the musculature in the trunk and extremities (Table 3), are of particular interest (e.g. Flechsig’s tract) in the study of proprioception and limb coordination (see Koh and Markovich 2020, for a recent review). By applying motion-probing gradients (MPGs) which suppress signals from locations with relatively unimpeded diffusion, DWI and DTI can reveal the trajectories of peripheral nerves and SC tracts along the lengths of their myelin sheaths, and allow one to distinguish vascular elements from neural ones (Skorpil, Rolheiser et al. 2011). For these reasons, aside from standard T₁- and T₂-weighted MRI (which can image nervous pathways accurately), DWI/DTI methodologies tailored for SC and PNS imaging are important in a variety of clinical applications (Takahara and Kwee 2010, Hiltunen, Kirveskari et al. 2012), and their use can complement current efforts to map the human brain connectome. For example, one metric provided by DWI is mean diffusivity (MD), which quantifies the average extent of water diffusion along WM and nerve axons. It has been proposed that an abnormal MD increase along nerves reflects inflammation, whereas an MD decrease may be associated with demyelination, axonal loss, or with an increase in isotropic water volume (Eppenberger, Andreisek et al. 2014). A growing number of studies have pointed out that the lack of normative values for metrics like MD make statistical comparisons of individual patient lesions to the normal population difficult at best (Renoux, Facon et al. 2006, Shanmuganathan, Gullapalli et al. 2008, Theaudin, Saliou et al. 2012). Thus, the development of novel neuroimaging approaches for the accurate representation and quantification of SC and PNS connections is imperative and would be extremely useful to the clinical community. Such development could provide an adequate level of granularity when attempting to map the neuroanatomical innervation of the body (e.g. the afferents and efferents of the viscera; see Figure 3), to improve lesion localization, to improve diagnostic accuracy, to guide surgery and to enhance treatment planning, (Takahara and Kwee 2010).

Table 3.

The major spinocerebellar tracts.

	posterior spinocerebellar tract	anterior spinocerebellar tract	cuneocerebellar tract
origin	Clarke’s nucleus (T1-L2/L3)	spinal border cells (T12-L5)	lateral cuneate nucleus (medulla)
body part represented	trunk, lower extremities	trunk, lower extremities	trunk, upper extremities
principle inputs	mechanoreceptors in muscles, joints, skin	mechanoreceptors, movement-related interneurons	mechanoreceptors in muscles, joints, skin
midline crossing	none	once in spinal cord, again in cerebellum	None
peduncle used to enter cerebellum	inferior	Superior	Inferior

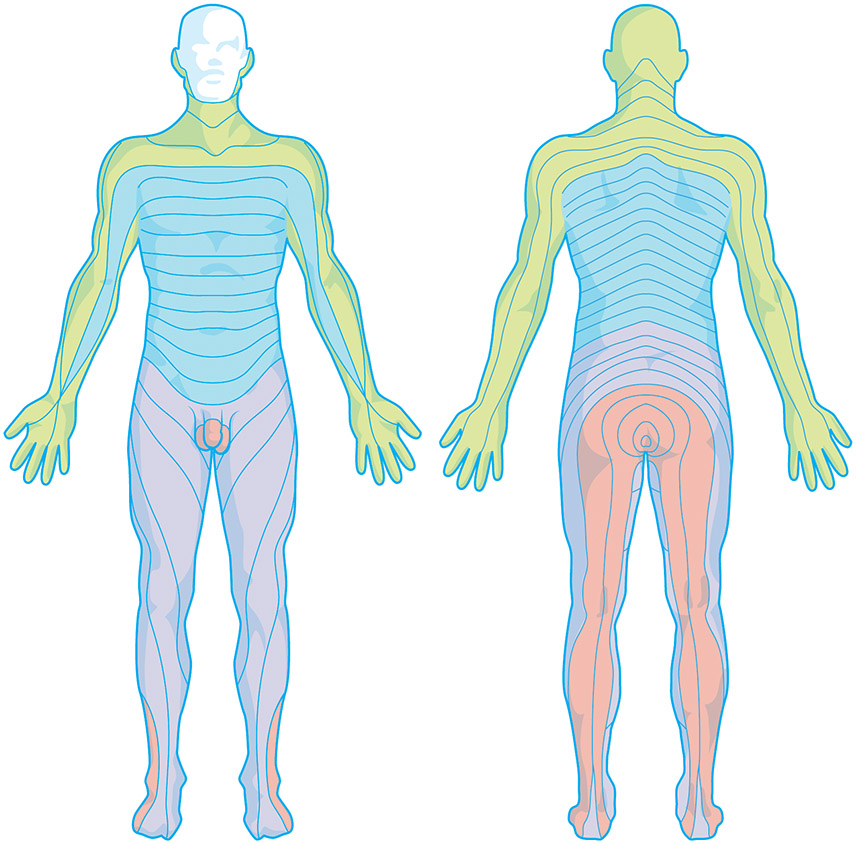
Figure 3.

The dermatomes of the body innervated by spinal nerves. A dermatome is an area of the skin which is primarily supplied by a single spinal nerve. There are 8 cervical nerves (C1 being an exception with no dermatome), 12 thoracic nerves, 5 lumbar nerves and 5 sacral nerves. Each of these nerves relays sensation (notably pain information) from a particular region of skin to the brain. Along the thorax and abdomen of the human body the dermatomes are like a stack of discs, each supplied by a different spinal nerve. Along the arms and the legs, the pattern is different: the dermatomes run longitudinally along the limbs. Although the general pattern is similar in all humans, the precise zones of innervation are unique to each individual.

3. Advances required for SC imaging

A panel of clinicians familiar with the aims and strategic goals of the International Spinal Research Trust (spinal-research.org) and of the Wings for Life Foundation (wingsforlife.com) have noted that only very few research groups in the world are actively involved in the development of SC imaging methods, and that “the potential outcomes of advancing these methods are tremendous, enhancing our basic understanding of healthy human SC function, and impacting our ability to accurately diagnose and treat injury and disease, and [to] predict outcomes” (Stroman, Wheeler-Kingshott et al. 2014). These clinicians specializing in the treatment of SC pathologies additionally pointed out that there is an acute paucity of imaging methods tailored to address the unique challenges of imaging the human SC and its connections to the rest of the NS. Specifically, imaging this structure is inherently difficult (Thurnher and Law 2009) due to 1) the presence of bone surrounding the spinal canal, 2) physiological motion of the SC and adjacent tissues, 3) the SC’s small cross-sectional dimensions, and/or 4) the possible presence of metallic implants in injured patients.

Due to large differences in magnetic susceptibility between bone, soft tissue and air, magnetic field inhomogeneity in the vicinity of the SC is appreciable, and this can lead to poor image quality. Whereas shimming may alleviate the effects of this phenomenon, shimming cannot typically compensate for the presence of sharp, localized magnetic field variations, like within the cartilaginous disks between vertebrae (Stroman, Krause et al. 2001). Most MRI methods are either based on a gradient echo (GE) or a spin echo (SE) pulse sequence. As echo time (T_E) increases, such sequences gradually become T₂*- or T₂-weighted, respectively. SE uses a refocusing pulse to briefly reverse static field inhomogeneity effects, such that, in SE MRI, the signal is relatively free of field inhomogeneity artifacts at the peak of the refocusing pulse. For this reason, SE scans provide advantages for SC imaging (Stroman, Wheeler-Kingshott et al. 2014). Nevertheless, recent efforts have led to the tailored development of GE sequences which are also suitable for this purpose (Cohen-Adad and Wheeler-Kingshott 2014, Levy, Benhamou et al. 2015, De Leener, Levy et al. 2017, Grussu, Battiston et al. 2020).

Cerebrospinal fluid (CSF) in the spinal canal flows back and forth in the head-to-foot direction with every heartbeat, which can make SC imaging very challenging due to the motion artifacts induced by this phenomenon (Feinberg and Mark 1987, Matsuzaki, Wakabayashi et al. 1996). For this reason, one important requirement for effective PNS imaging is minimizing the possible presence of phasic motion artifacts due to respiration during the short diffusion-encoding time when MPGs are applied (Muro, Takahara et al. 2005, Koh, Takahara et al. 2007). The periodic physiological motion of the cord due to heart beats and breathing can be partially addressed by synchronizing the slice acquisition intervals with the cardiac and respiratory cycles. Specifically, images can be acquired during the quiescent part of the cardiac cycle by means of peripheral gating or cardiac monitoring, with an appropriate delay specified for each subject so that data sampling can be performed during the cardiac diastole (Fenyes and Narayana 1999, Summers, Staempfli et al. 2006, Loy, Kim et al. 2007, Summers, Ferraro et al. 2010). Although this can increase the acquisition time by a factor of 2 or 3 and may also result in a variable repetition time (T_R) for image acquisitions, the approach has been found to be adequate in several studies (Gudbjartsson, Maier et al. 1996, Spuentrup, Buecker et al. 2003, Madi, Hasan et al. 2005, Kim, Loy et al. 2007). Techniques like dynamic shimming have been proposed to correct artifacts related to dynamic B₀ variations due to respiration (van Gelderen, de Zwart et al. 2007).

To reduce T₁-induced signal variation due to variable T_R, long T_R values (typically in excess of 5 s) have been employed. Other techniques like motion-compensating gradients and averaging of the MR signal across multiple phases of motion can also be applied to reduce artifacts. Because the SC can undergo not only translational but also rotational motion during MR image acquisition, nonlinear phase navigation methods have been proposed to correct for bulk motion artifacts due to SC rotation (de Crespigny, Marks et al. 1995, Bammer, Fazekas et al. 2000). In addition, to account for motion-related changes in SC curvature, line scan imaging sequences have been implemented (Gudbjartsson, Maier et al. 1996, Maier, Gudbjartsson et al. 1998) and specialized spinal phantoms which simulate physiological sources of noise in spinal MRI have been developed (De Tillieux, Topfer et al. 2018). Machine learning methods have been applied to speed up processing by removing DWI volumes which have been degraded by motion (Li, Shi et al. 2012, Li, Shi et al. 2014). Additionally, faster DWI imaging can be attained using constrained reconstruction (Kim and Haldar 2016) and compressed sensing methods (Sharma, Fong et al. 2013) which under-sample k space and then impute un-sampled data, resulting in fully acquired image volumes. When imaging the SC, axial scans have been favored due to their ability to reveal more information about specific WM fiber bundles (Holder, Muthupillai et al. 2000, Schwartz, Chin et al. 2005, Cohen-Adad, Benali et al. 2008, Ellingson, Ulmer et al. 2008, Smith, Edden et al. 2008). To reduce image artifacts and spatial distortion, various correction methods can be applied, including the estimation of a nonlinear warping field constrained in the phase-encoding direction. This field can be estimated based on the phase difference between two GE images acquired at slightly different T_E values (Schneider and Glover 1991, Wilson, Jenkinson et al. 2002, Cusack, Brett et al. 2003).

Enhanced imaging sequences can be used in conjunction with offline motion correction algorithms which take into account the non-rigid nature of the spinal column in contrast to that of the head. The algorithms which have been found to be most valuable for this purpose are based on slice-wise motion correction, where B₀ images are interspersed throughout the DWI acquisition process. Motion is then estimated based on the B₀ images because they have the same contrast—although higher signal-to-noise ratios (SNRs)—compared to DWI images, and are thus easier to co-align. When combined with eddy current correction and robust diffusion tensor fitting, this type of imaging has been found to produce the highest contrast-to-noise ratio (CNR) and least variation in fractional anisotropy (FA) maps (Mohammadi, Freund et al. 2013)

The physical properties of the SC suggest that high spatial resolution is paramount for its precise and accurate imaging. For example, the widest cervical enlargement of the spinal canal is ~15 mm across, with average transverse areas of ~50, ~25 and ~30 mm² in the cervical, thoracic and lumbar regions, respectively (Ellingson, Ulmer et al. 2007, Bosma and Stroman 2012). High-resolution slices can reduce partial volume effects, although reduced voxel size also comes at the cost of decreased SNR, and optimization strategies have been developed to achieve an acceptable balance between the two (Stroman 2005). Whereas axial slices with high in-plane resolution and greater thickness can be acquired with high SNR, the scan time in this approach is higher than desirable. By contrast, sagittal slices allow greater coverage but suffer from greater partial volume effects unless slice thickness is very small (Clark, Barker et al. 1999, Ries, Jones et al. 2000).

4. Challenges of imaging the PNS

Whereas imaging of the SC is challenging primarily due to the magnetic susceptibility profile of this organ and to the large number of degrees of freedom involved in its motion, PNS imaging is additionally difficult because of the small cross section and abundant branching structure of the peripheral nerves and of their connections to one another. Nevertheless, MRI/DWI sequences which are particularly suitable for peripheral nerve neurography have been designed; these include short-tau inversion recovery (STIR), chemical shift selective (CHESS) techniques, spectral adiabatic inversion recovery (SPAIR), reversed fast imaging with steady-state precession (PSIF), suppression of heavily isotropic objects imaging (SUSHI), etc. For example, an STIR pre-pulse can implement robust fat suppression over a large FOV even in body areas which are subjected to substantial magnetic field inhomogeneities, such that the resulting imaging volumes can be post-processed using slab minimum intensity projections (MIPs) or the so-called soap-bubble projection (Wrazidlo, Brambs et al. 1991, Etienne, Botnar et al. 2002) with minimal image degradation due to artifacts (Takahara and Kwee 2010). 3D DW-PSIF has been used to evaluate cranial nerves, the lumbar plexus and peripheral nerves with good suppression of moving structures—including vascular flow—which makes this sequence particularly amenable to nerve localization and/or presurgical evaluation (Hodaie, Quan et al. 2010, Chhabra, Subhawong et al. 2011). The use of a hyperbolic secant adiabatic inversion pulse might be advisable for imaging peripheral nerves in the neck and chest, where fat signals over the large FOV can obscure critical signals from areas deep within the body. DWI neurography techniques tailored specifically for whole body imaging, such as DWIBS—diffusion-weighted whole-body imaging with background body signal suppression (Kwee, Takahara et al. 2008, Sasatomi and Ogata 2009, Yamashita, Kwee et al. 2009)—are particularly suitable for imaging nerves throughout the entire body for the purpose of PNS atlasing and connectomic mapping.

To address the imaging challenges posed by the length and small cross-section of the SC and peripheral nerves, reduced field of view (rFOV) methods have been developed and compared favorably to conventional single-shot echo-planar imaging (EPI) sequences (Zaharchuk, Saritas et al. 2011). In rFOV, a two-dimensional (2D) echo-planar radio frequency (RF) pulse is used to excite and subsequently to read out a rectangularly-shaped FOV by traversing k-space faster than usual for some given spatial resolution. In parallel imaging, which is a type of rFOV technique, images are acquired simultaneously from multiple coils and spatial information from each coil is used. This type of imaging has been highlighted as particularly useful for both SC and nerve imaging because the total number of phase-encoding steps is substantially reduced, the total acquisition time is decreased and the effects of susceptibility gradients are attenuated (Bosma and Stroman 2012). Two types of parallel imaging are commonly used, namely sensitivity encoding (SENSE) and generalized auto-calibrating partially parallel acquisition (GRAPPA) (Blaimer, Breuer et al. 2004), both of which reduce susceptibility artifacts at the price of SNR. To compensate for this latter drawback, parallel imaging to reduce the EPI factor or the echo train length (ETL) can be enhanced by acquiring multiple thin image sections which are subsequently averaged for SNR enhancement. Aside from parallel imaging sequences like GRAPPA and SENSE, rFOV techniques which can correct motion artifacts include zonally magnified oblique multi-section (ZOOM) EPI sequences (Finsterbusch and Frahm 1999, Dowell, Jenkins et al. 2009, Mohammadi, Freund et al. 2013) and saturation band methods (Martin, Aleksanderek et al. 2016).

Myelin imaging techniques are particularly promising for PNS mapping. Myelin water-fraction (MWF) MRI, for example, indicates the fraction of tissue water bound to the myelin sheath, which is a valuable marker for myelination (Whittall, MacKay et al. 1997, Wu, Alexander et al. 2006). The MWF is significantly lower in patients with multiple sclerosis (MS) and with other pathological conditions (Laule, Leung et al. 2006), and this technique is thus very suitable when comparing the myelination of axons in the spine of a given patient to that typical of the general population. Because the MWF could be used as a neuroanatomical indicator of disease severity, inclusion of its values and descriptive statistical parameters in a SC atlas is highly recommended, like in that of Liu et al (2020). Other techniques which can be leveraged to image myelin include magnetization transfer imaging (MTI) (Schmierer, Scaravilli et al. 2004), quantitative magnetization transfer MRI (qMT-MRI) (Ou, Sun et al. 2009), inhomogeneous MT (ihMT) MRI (Taso, Girard et al. 2016) and ultrashort TE (UTE) MRI (Pang, Bow et al. 2018). MTI can indirectly characterize water protons in macromolecular structures like myelin and is particularly useful for investigating WM integrity because it provides a sensitive way to quantify WM abnormalities in the spinal cord and other structures containing WM (Zackowski, Smith et al. 2009). qMT MRI can capture the interactions between free water protons and immobile macromolecular protons in myelin, yielding indices like the macromolecular proton fraction (MPF), which correlates with WM myelin content (Smith, Dortch et al. 2014). ihMT MRI is a dipolar-order relaxation time-weighted imaging technique with enhanced selectivity for myelin-rich structures and which has been validated against the gold standard of green fluorescence protein microscopy (Duhamel, Prevost et al. 2019). Finally, UTE MRI facilitates the direct detection of myelin signal using whole body clinical MRI scanners. In its basic form, a 2D UTE sequence uses a half pulse or short rectangular pulse for signal excitation, followed by radial mapping of k-space from the center out. The data from these excitations are added to produce a single radial line of k-space and raw data are reconstructed after re-gridding using an inverse Fourier transform. Because myelin accounts for a small fraction of the total signal acquired, the primary signal are from long-T₂ gray matter (GM) and long-T₂ WM, which are then suppressed to generate high contrast specific to myelin (Ma, Jang et al. 2020).

An important consideration for PNS imaging is how to best leverage high-field imaging to map the SC and peripheral nerves in detail. High-resolution SC and nerve imaging at high field strengths (7 T and above) has been implemented with promising results and the results of such studies have been compared very favorably to those involving 1.5 T or 3 T imaging using the rigorous Kellman method for SNR estimation (Kellman and McVeigh 2005, Barry, Vannesjo et al. 2017). High field imaging has been shown to benefit from increased ability to identify structures otherwise undistinguishable at lower field strengths, like denticulate ligaments and nerve roots (Sigmund, Suero et al. 2012). Resting state functional MRI has also been successfully explored at 7 T in healthy subjects (Barry, Rogers et al. 2016) as well as in patients with MS (Dula, Pawate et al. 2016). One technique suitable for the comprehensive imaging of the PNS in cadavers is that of micro-neurography (Bilgen, Heddings et al. 2005), which allows involves the use of 9 T scanners with gradients of 400 mT/m to obtain images with stunning histological precision, at a spatial resolution of ~30 μm. Intrinsic connectivity mapping of the SC in nonhuman examinations at 9.4 T has shown much potential (Chen, Mishra et al. 2015, Wu, Wang et al. 2018) and applications in human samples can be expected. Thus, it can be argued that imaging neural connections located outside the brain at high fields is equally as useful and promising of an approach as it is in the case of mapping the brain connectome.

5. Devising a full-body stereotactic coordinate system

Whereas consideration of the level of dermatomes provides a course level of localization (Figure 4), establishing a coordinate system convention which accommodates the entire body (including the trunk, abdomen and limbs) is essential for generating a comprehensive, stereotactic atlas of the PNS. One essential advantage of a stereotactic atlas is the ability to provide a reference coordinate system for the unique identification of any anatomic location and for facilitating the process of mapping such locations from the atlas to any individual subject and vice versa. In the case of brain atlases, such coordinate systems have been not only proposed, but are also being used widely by the neuroscience community. Such atlases include the original Talairach & Tournoux (1988) coordinate system, which was based on a single brain, as well as more sophisticated atlases which are based on populations of healthy adult subjects, such as the Montreal Neurological Institute (MNI) atlas (Evans, Collins et al. 1993). Although such reference coordinate systems for the brain are well established, analogous coordinate systems which encompass the rest of the human body have been proposed relatively recently (De Leener, Fonov et al. 2018).

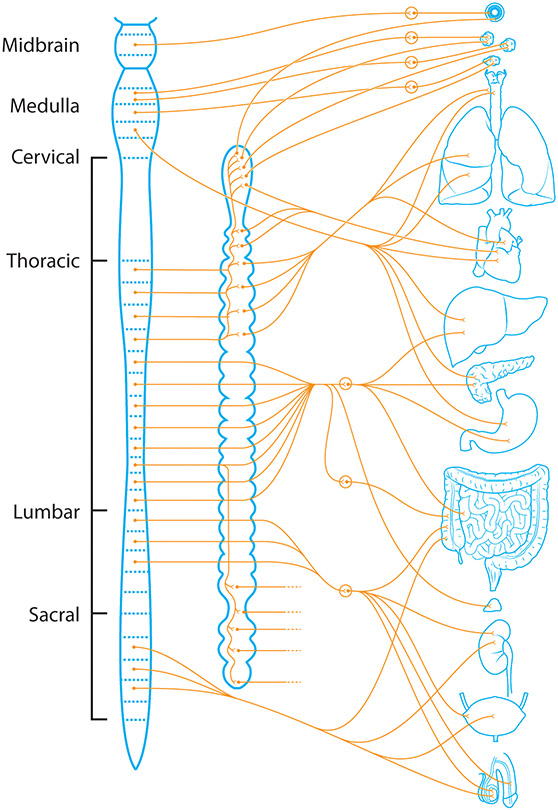
Figure 4.

Spinal afferents and efferents of the viscera (the soft internal organs of the body, especially those contained within the abdominal and thoracic cavities). These include, the lungs, heart, liver, pancreas, stomach, intestines, kidneys, bladder, and genitalia, among other smaller organs.

The only full-body reference system which is broadly familiar to both life scientists and clinicians is that defined by the three ‘natural’ axes of the human body, namely the anterior-posterior (sagittal), mediolateral (left-right, or transverse), and longitudinal (superior-inferior, or sagittal) axes. This coordinate system is widely used not only in these two fields, but also in engineering and other areas of science (Gietzelt, Schnabel et al. 2012). If the human body is represented in standing position, the longitudinal axis is usually labeled as the z axis, whereas the antero-posterior and mediolateral axes typically correspond to the x and y axes, respectively. The origin of the coordinate framework is often within the sternum. Although this convention is certainly useful, it is by no means universal. For example, the origin of such a coordinate system often differs from context to context, as does the labeling of axes. If the body is in supine position, the antero-posterior axis can be conveniently labeled as the z axis, such that the body roughly lies in the x-y plane. Similarly, the origin of the coordinate system can be arbitrarily positioned in the trunk or upper abdomen, or anywhere along the longitudinal axis, for that matter. Thus, although this convention is a starting point for defining a coordinate system for the human body, it is far from being a consistent one, and furthermore it does not provide a stereotactic reference system.

Several studies have attempted to provide a consistent reference system for the entire human body. In 1977, Malmivuo et al. proposed both a rectangular as well as a spherical polar coordinate system for the human torso (Malmivuo, Wikswojun et al. 1977). These authors noted that a rectangular coordinate system should be right-handed—to be consistent with the conventions of physical sciences—and proposed that the center of the coordinate system should be the geometric center of the heart. Although this convention can be very useful for the study of the cardiovascular system, it suffers from at least one important disadvantage, namely that the heart and the other thoracic organs move during respiration. This means that co-registering CT or MRI volumes acquired from different subjects can be particularly difficult if the center of the coordinate system changes location during the imaging scan.

Wang et al. (2008) proposed that (A) coordinate values should be normalized by individual thoracic size so that they are universal to the human population, and that (B) the origin of the coordinate system should be at the center of one of the thoracic vertebrae. One argument in favor of the latter convention is that only the spine is relatively stationary during respiration, which makes the spinal canal more suitable as a line of reference. To generate a coordinate system for the entire torso, Wang et al. identified the geometric centers of the fifth and tenth thoracic vertebrae (T5 and T10, respectively) and selected the line passing through these two points as the z axis, with the coordinate system origin at the geometric center of T10 and z increasing toward the head. T5 and T10 were selected because they are not adjacent to either the cervical or the lumbar vertebrae, such that the effect of neck or waist motion is minimized. The antero-posterior plane was defined as the sagittal mid-plane of the human trunk because this plane is stationary during respiration. With these assumptions, the x and y axes can be readily found since they are orthogonal with respect to each other and to the z axis.

Aside from the obvious advantages of the procedure described by Wang et al. for defining a coordinate system for the entire trunk, these authors’ strategy suffers from the drawback that small lateral flexions of the spinal column, together with subtle movements of the sagittal mid-plane, can introduce small motion artifacts which may systematically bias the procedure of co-registering any two distinct bodies, or even longitudinal scans of the same body. A more sophisticated approach is that of Vrtovec et al. (2005), who advocate the automatic definition and extraction of the spinal curve c(n) as a function of a continuous independent variable n which parametrizes the curve in terms of Cartesian coordinates, i.e. c(n) = [x(n),y(n),z(n)]. To render a complete 3D representation of the coordinate system, Vrtovec et al. use three directional, mutually orthogonal variables u, v and w, where v can be used to specify the extent of spinal column rotation at each point along the cord. One can define the quantity φ(n), parametrized as φ(v(n),y′(n)), as the angle between v and the corresponding projection y′(n) of the Cartesian coordinate y onto the plane orthogonal to the spine curve. By means of this procedure, any subject’s spine can be described by a specific curve, and co-registration of different subjects’ spines can be accomplished by nonlinearly mapping one curve onto the other, or by mapping the curves onto a reference curve specified by an atlas. This powerful technique not only allows co-registration of any given subject’s trunk from her/his coordinate system to that of an atlas or vice versa, but also creates an appropriate context for defining a consistent, unique and reliable origin of a stereotactic atlas coordinate system.

Whereas the procedures described thus far for creating a stereotactic coordinate system can be applied to the human trunk, further complexities are introduced by the additional degrees of freedom associated with limb movement. Fortunately, however, the Standardization and Terminology Committee (STC) of the International Society of Biomechanics (ISB) has introduced standards for defining Cartesian coordinate systems for all joints of the upper and lower limbs, all of which are reviewed extensively by Wu et al. (2002, 2005). Based on the ISB conventions, the task of generating a full-body stereotactic coordinate system and of handling the considerable number of degrees of freedom involved can be made substantially simpler. Specifically, one can first assume rigidity of all joints in, say, the well-known posture of the Vitruvian Man proposed by Leonardo da Vinci around the year 1490. This allows one to reduce the problem at hand to one where only the angle between each limb and the sagittal plane of the spinal curve must be specified, such that a stereotactic coordinate system for the entire body can be created. Incidentally and significantly, conversion of coordinates between this system and either of the Talairach and MNI coordinate systems can be accomplished straightforwardly using a set of easily predefined scalings, rotations, and translations, all of which are affine transformations.

6. Atlasing extracranial neural connections

At least three essential requirements of robust PNS atlas design have been identified, namely modularity, scalability and decomposition (Nowinski, Johnson et al. 2012). A connectomic atlas which satisfies all these three features has individual components in the virtual model which can be composed and decomposed freely, and which can be shown, highlighted, hidden, measured and manipulated with ease. A deformable atlas of neural connections outside the brain could not only accommodate anatomic variations across different subjects, but could also offer the opportunity to explore and to classify variations in anatomy related to development or pathology (Thompson and Toga 1996).

Although the standard neuroanatomy of human cranial nerves in the context of their surrounding structures is illustrated in a variety of articles (Saylam, Ucerler et al. 2007, Skorpil, Rolheiser et al. 2011), anatomical treatises, textbooks and software suites (Snell 2010), hardly any resource makes this information available in 3D together with depictions of surface neuroanatomy, vasculature, inter-connectivity and MRI. For example, Kakizawa et al. (2007) developed an interactive 3D model of the skull and cranial nerves based on measurements from several human specimens. Similarly, Yeung et al. (2011) created a computer-assisted learning module in 3D based on the Visible Human Project dataset. Although interactive, this module does not allow free rotation or translation and the level of detail provided is not as high as in the model of Kakizawa et al. The commercially available 3D Skull Atlas developed by Brown & Herbranson (eHuman.com) enables free display—although not manipulation—of individual cranial nerves or nuclei.

One atlas of the cranial nerves which comes close to satisfying many of the stringent criteria set by today’s clinicians for purposes such as neurosurgical planning is that of Nowinski et al. (2012). These authors employed a ‘pyramidal principle from blocks to brain’ to construct virtual geometric models of individual cranial nerves and nuclei and to integrate these models with an existing brain atlas. Subsequent to initial extraction of cranial nerves and of their nuclei from MRI volumes, these authors implemented fine tuning, post-processing and synthesizing of each extracted structure via tubular iso-surface modeling followed by adaptive compression of each polygonal object to facilitate interactivity. Cranial nerves were (1) corrected against self-intersections as well as against intersections with major vessels (such as the internal carotid artery, the cerebellar arteries and the internal jugular vein) and with the brain, (2) labeled according to Terminologia Anatomica (FCAT 1998), and (3) uniquely colored and capped at each end.

One disadvantage of many atlases is that they are based on only one or a few specimens, which implies that they do not offer adequate information on inter-subject variability in the location, spatial configuration, and physical properties of neuroanatomical structures. In addition, an undesirable consequence of using standard MRI sequences to perform PNS imaging is the reduced ability to identify small branches of cranial nerves and of other nerves, which can only be appropriately imaged in post-mortem human specimens and/or with more advanced MRI scanning sequences which are specifically designed and customized for the task.

7. Algorithmic advances required for next-generation PNS and SC imaging

The creation of a 3D stereotactic atlas of neural connections outside the brain requires the development and implementation of highly robust and accurate non-rigid registration and deformation algorithms which can accommodate the large variability in human body shape and in the specific position of the limbs, trunk, neck and other body parts during MRI scanning. To address such challenges, warping algorithms must be developed to calculate 3D deformation fields which can be used to register one subject to another in a nonlinear fashion, and subsequently to transfer anatomic data from distinct individuals to a unique anatomic template, which can enable information from different subjects to be integrated (Thompson, Woods et al. 2000). In other contexts, density-based approaches with high spatial dimensions (Christensen, Rabbitt et al. 1994) have been proposed to compute elastic matching transformation mappings between an atlas and a target subject, and to preserve atlas topology and connectivity under these complex transformations. In fragment bundling (Dorfer, Donner et al. 2013), by contrast, MRI or CT scans of body sections are treated as ‘fragments’ of a larger structure (the whole body), which can be reconstructed by ‘bundling’ the volumes together to create a larger atlas which incorporates all available fragments.

In addition to deformable atlases which can be elastically transformed into the individual anatomic space of any particular subject, probabilistic atlases of neural connections outside the brain are also needed to generate anatomical templates which can serve as expert diagnostic systems and as knowledge-based imaging tools which retain quantitative information on inter-subject variability (Thompson, Woods et al. 2000). Importantly, the statistics associated with the physical properties of WM bundles in the PNS can be encoded locally to specify the magnitude and directional biases of anatomical variation, as well as the effects of pathology and of other factors upon the SC and PNS (Collins, LeGoualher et al. 1996, Davatzikos 1998). Yao & Summers (2009) demonstrated a statistical location model (SLM) to build a probabilistic density model for each organ which incorporates automated spinal column extraction and partitioning accompanied by abdominal cavity standardization, the latter being especially useful due to large variability among subjects. Similarly, Reyes et al. (2009) used principal factor analysis (PFA) to describe anatomical variability of body shape and structure and to create point distribution models of the human body whose principles can also be applied to the creation of a PNS atlas. Other approaches include fuzzy connectedness (Zhou and Bai 2007), expectation maximization (EM) (Lorenzo-Valdes, Sanchez-Ortiz et al. 2004), active contour models (Qatarneh, Noz et al. 2003), and thin plate spline (TPS) warping transforms (Park, Bland et al. 2003).

When designing a 3D stereotactic atlas of the SC and PNS, previous methods for creating analogous atlases of WM fibers in the human brain (Mori, Oishi et al. 2008) can be used as sources of inspiration and as starting points for the development of novel methodologies. Specifically, as in the case of the atlas template created by the International Consortium of Brain Mapping (ICBM), the task of creating SC and PNS atlases involves the opportunity to establish a PNS WM coordinate system, to study pathology mechanisms in relationship to WM anatomy, and to understand disease patterns in the context of population-level statistical analyses. Establishing a WM structural map of the SC and PNS which is similar in concept to previously created brain maps is therefore very important. SC atlases available thus far include the spinal fMRI 8 atlas of Stroman et al. (Stroman, Wheeler-Kingshott et al. 2014), the Spinal Cord Toolbox (De Leener, Levy et al. 2017), groupwise multi-atlas segmentation via the Java Image Science Toolkit (JIST) (Chen, Carass et al. 2013) and SpineSeg (Bergo, Franca et al. 2012).

Whereas a notable amount of effort has been dedicated to the task of performing automatic segmentation of the SC from MRI and CT, very little attention has been dedicated to the creation of an atlas of the PNS. Nevertheless, valuable insight can be gained in this respect from at least two sources, namely from (1) previous experience in mapping the lymphatic system, as well as from (2) methods for atlasing human vasculature. Because the lymphatic and vascular systems both involve tubular vessels which branch richly throughout the entire body, imaging analysis algorithms developed for these systems can be used as starting points for the development of PNS atlases (Figure 5).

Figure 5.

Idealized depiction of the CNS and PNS represented in a 3D Cartesian coordinate system. Such a system can be formed by rotating and extending the classic Talairach and Tournoux brain atlas laterally, along the anterior/posterior axis, and inferiorly until it contains the limits of the body.

Approaches which have been used for the development of 3D atlases of cerebral vasculature can, for the most part, also be applied to the creation of a PNS atlas. In the following order, these include: 1) nerve segmentation, 2) extraction of nerve centerline and radius, 3) centerline editing, correction and smoothing, 4) modeling of nerve segments and bifurcations, and 5) nerve labeling.

Nerve segmentation can be performed in a manner analogous to that of vasculature segmentation, where segmentation seeding is followed by tracking the image intensity ridge representing the vessel skeleton in 3D (Bullitt, Muller et al. 2005). Subsequent to this, the tree structure of vessels (or nerves, in this case) can be calculated using parent-child relationships which can be mapped using a minimum spanning tree algorithm (Bullitt, Aylward et al. 2001). Additional information which can be extracted involves the number of nerves, their radii and branching frequencies. The entire process has been referred to as ‘skeletonization’ (Nowinski, Thirunavuukarasuu et al. 2005) and its implementation typically involves the application of distance transforms in step (3) and of sliding average filters in step (4) (Yi and Hayward 2002). A tubular geometry has typically been adopted to model vascular segments, and this is also applicable to the modeling of nerves. Bifurcations have been rendered using so-called B-subdivisions (Nowinski, Thirunavuukarasuu et al. 2005) which involve bicubic uniform B-spline surface refinement (Catmull and Clark 1978). Once defined, such an atlas may be deformed accordingly to a variety of representations (Figure 6a, 6b, 6c).

Figure 6.

A. The CNS/PNS represented on a 2D planar projection system in which various nerves have been laid flat. B. Alternative version of A displaying a limb arrangement similar to that of the familiar Vitruvian Man pose. C. Spinal and peripheral nerves superimposed and projected onto the surface of a sphere to provide a latitude and longitude-based—or azimuth and elevation-based—polar coordinate system, similar to the commonly utilized spherical representations of the hemispheres of the brain.

8. Accounting for inter-subject variability

Information on the inter-subject statistical variability of neuroanatomic inter-connectivity outside the brain, particularly as this pertains to statistical estimates of the thickness, shape, length and other physical properties of the SC at specific locations within the vertebral column, has recently become available, as this pertains to spinal vs. vertebral levels (Cadotte, Cadotte et al. 2015), the morphometry of the SC and of its GM (Fradet, Arnoux et al. 2014), and the microstructure of the human spinal cord (Duval, Saliani et al. 2019) and the inter-subject variability of cord morphometry (De Leener, Fonov et al. 2018). Information regarding the inter-subject variability of spinal nerve thickness values and spatial trajectories is also slowly becoming available. Whereas these resources address the previous paucity of such information despite obvious prior and current need for it in the medical field, analogous knowledge pertaining to other nerves in the PNS is relatively lacking. For example, there is currently no accurate set of atlasing methods which can allow one to stereotactically map and quantify fine scale nerve branchings throughout the human body, the spatial location and inter-subject variability thereof, as well as basic physical parameters of peripheral nerves such as thickness, length, degree of myelination and connectivity with other neural pathways.

Information regarding the statistical variability of physical properties and of connectivity patterns pertaining to nerves and to the SC across the healthy adult population is very difficult to retrieve from available literature. Because off this, it is currently very challenging to assess and to compare the extent of nerve or SC damage in a given patient to normative values of these measures. This situation obviously constitutes a tremendous setback to the clinical task of evaluating the severity of various forms of PNS pathology, particularly in the context of current efforts aimed at implementing patient tailored approaches to treatment. At this time, for example, it is not altogether feasible or straightforward to assess the severity of nerve demyelination or of various forms of PNS injury by performing a personalized statistical comparison between the pathology profile of some given patient and the normative values for the physical parameters of the affective nerve as derived from the general, healthy adult population. Consequently, the current unavailability of a 3D stereotactic SC and PNS atlas which incorporates information pertaining to inter-subject variability in humans is of great detriment to neurological and neurosurgical practice.

Based only upon ex vivo dissection methods, information is poor regarding the inter-subject variability of the physical properties, spatial configurations and connectomic patterns of the SC and of PNS structures (Gulekon, Anil et al. 2005). Recently, the compilation of Lang et al. (1995) was identified as “the most comprehensive, though far from being complete, account on measurements of the cranial nerves on 52 head halves” (Nowinski, Johnson et al. 2012). In their own study, Nowinski et al. attempted to infer the absolute ranges of cranial nerve diameters, although even this is challenging when only several specimens are available. As these authors pointed out, the task is made even more difficult by the presence of systemic inaccuracies, contradictions and obvious mistakes in the neuroanatomy literature. For the SC and other nerves excluding the cranial nerves, even such information appears to be lacking, which highlights the need for creating an atlas which can fill these lacunae in current knowledge. The availability of statistical normative values of PNS structures within a stereotactic, connectomic atlas could enhance the ability to evaluate neurogenic tumors, the extent of abnormal nerve thickening due to inflammatory processes, as well as the severity of nerve thinning resulting from traumatic injuries (Takahara and Kwee 2010). Quantitative measures afforded by DTI—e.g. FA, MD and the apparent diffusion coefficient (ADC)—have been measured in peripheral nerves (Kabakci, Gurses et al. 2007, Khalil, Hancart et al. 2008) and can be altered substantially in the presence of pathology. Nevertheless, it remains challenging to use such measures to quantify disease severity unless the statistical distribution parameters associated with each of these metrics in the healthy population is known a priori at the time of the neurological examination.

In the case of MS, studies involving statistical comparisons between the values of DTI-derived metrics (FA, MD, ADC) acquired from MS patients and corresponding values acquired from healthy control (HC) subjects have been hampered by problematic issues related to the unavailability of a sufficiently large sample size which could allow one accurately to capture the variance in DTI measurements across the healthy adult population (Valsasina, Rocca et al. 2005, Ohgiya, Oka et al. 2007, Cruz, Domingues et al. 2009). In SC injury (SCI), increases in MD compared to HCs have been observed at injury sites whereas, in amyotrophic lateral sclerosis (ALS), decreases in FA and MD have been measured (Cosottini, Giannelli et al. 2005, Agosta, Rocca et al. 2009, Nair, Carew et al. 2010). Similar analyses have been implemented in progressive muscular atrophy (PMA), myelitis (Renoux, Facon et al. 2006, Lee, Park et al. 2008), tumors (Liu, Germin et al. 2011), SC ischemia (Loher, Stepper et al. 2001, Loher, Bassetti et al. 2003, Fujikawa, Tsuchiya et al. 2004, Kuker, Weller et al. 2004) and in other conditions. In many of these and other studies, the recent availability of normative samples has partially facilitated the application of statistical inference techniques, e.g. in studies of chronic pain (Albrecht, Ahmed et al. 2018), ALS (Paquin, El Mendili et al. 2018), spinal muscular atrophy (Querin, El Mendili et al. 2019), cervical myelopathy (Martin, De Leener et al. 2018) and MS (Yiannakas, Mustafa et al. 2016).

9. Sex-specific PNS mapping

The sex specificity of the PNS needs to be taken into consideration if the imaging community is to provide maximal clinical utility involving sexual dimorphism. For instance, pelvic pain due to endometriosis in women has recently been examined using diffusion imaging methods (Manganaro, Porpora et al. 2014). In this condition, tractography analysis has provided evidence of altered sacral roots microstructure, with FA values reduced along S1-S3 in endometriosis compared to HC females. Thus, from such studies, arises the possibility that sacral nerve root alterations can help to describe and explain the nature of endometriosis-related chronic pelvic pain. Likewise, DTI imaging of the female breast (Partridge, Murthy et al. 2010, Baltzer, Schafer et al. 2011) has been shown to have promise for mapping breast tumor and lesions resulting from cancer biopsies and excision surgeries (Partridge, Ziadloo et al. 2010, Tsougos, Svolos et al. 2014). Although tractography of nerve pathways in the breast has only been reported at 1.5 T (Wang, Zhang et al. 2014), such imaging at higher magnetic field strengths could critically complement the assessment of nerve damage during surgery or that of lesions due to radiation therapy. In males, DWI of the healthy prostate gland has been undertaken (Li, Chen et al. 2011) and DTI tractography has been shown to be particularly apt for mapping the periprostate fiber plexus (Panebianco, Barchetti et al. 2013). Such imaging of nerves pathways within and proximal to the prostate may be useful for patients with (suspected) prostate cancer (Park, Kim et al. 2014), where DTI may have specific diagnostic advantages over traditional transrectal ultrasound approaches (Chen, Pu et al. 2011). Thus, because of the need for sex specificity in many medical applications, imaging scientists should aim to create distinct PNS atlases for each sex.

10. Validation of SC and PNS atlasing

Some of the most noteworthy and widely used brain atlases, including that of Talairach & Tournoux (1988), have been utilized—often detrimentally (see Laird, Robinson et al. 2010, for review)—without validation. The task of validation is exceptionally important when compiling an atlas of the SC and PNS because of (1) the large number of individual neuroanatomical structures involved and (2) the large inter-subject variability of their spatial locations, configurations, physical properties and connectomic patterns. Yeung et al., for example, had their anatomic models assessed by a board-certified otolaryngologist, by a neuroanatomist, as well as by graduate students (Yeung, Fung et al. 2011). Nowinski et al. validated their atlas by verifying that their constructed cerebral model conformed to typical human anatomy, topology and geometry based on compilations from the literature in terms of nerve origin, supply/terminal regions, course, branches, surrounding structures, definition and physical features (Nowinski, Thirunavuukarasuu et al. 2005). When undertaking atlas validation, it is very important to assess both intra- and inter-observer variability of nerve trajectories, diffusion properties (FA, MD, etc.) and other quantitative measures. This can be accomplished by calculating measures like the intra-class correlation coefficient (ICC) while accounting for two-way random effects, including observer effects and measurement effects (Guggenberger, Eppenberger et al. 2012, Guggenberger, Nanz et al. 2012). Other strategies like Bland-Altman analysis (Bland and Altman 1986) are also useful.

Manual segmentation of the SC and of the nerves can be used in combination with automatic and semi-automatic methods of segmentation to achieve cross-validation of atlas models. To this end, semi-automatic SC segmentation methods with intrinsic smoothness constraints have been proposed based on active surface (AS) models of the SC (Horsfield, Sala et al. 2010). Importantly, the intra- and inter-observer reproducibility of such automated methods has been compared favorably with that of manual methods (Coulon, Hickman et al. 2002, McIntosh and Hamarneh 2006). One advantage of AS models is that the centerline of the SC can be resampled into a plane in which the former is embedded as a straight line, thus allowing co-registration of SCs from different patients into the same morphological and anatomical space. More advanced techniques involving voxel-based morphometry (VBM) of the SC have been used to test the correlation between SC tissue loss and aging (Valsasina, Horsfield et al. 2012), to assess WM and GM atrophy due to SCI, as well as for other clinical purposes. Methods are now available for the fully automatic 3D segmentation of the thoracolumbar spinal cord and of the vertebral canal using K-means clustering (Sabaghian, Dehghani et al. 2020), variational segmentation methods (Tsagkas, Horvath et al. 2019), deep learning (Paugam, Lefeuvre et al. 2019), convolutional neural networks for contusion injury segmentation (Gros, De Leener et al. 2019, McCoy, Dupont et al. 2019), and tubular deformable models (De Leener, Kadoury et al. 2014, De Leener, Cohen-Adad et al. 2015). The reader is referred elsewhere (De Leener, Taso et al. 2016) for a comprehensive review of these methods.

For the CNS, to minimize mis-registration due to motion- and eddy-current image distortion, co-registration using 12-parameter affine transformation (Jenkinson, Bannister et al. 2002) and diffusion tensor multi-linear fitting can be applied to DWI volumes. The resulting transformation matrix can be applied to the calculated diffusion tensor fields (Alexander, Pierpaoli et al. 2001, Xu, Mori et al. 2003) and the linearly transformed fields from individual subjects can be averaged via scalar averaging of tensor elements, such that DTI metrics like FA, MD and the averaged tensor field can be recalculated. After this, nerves can be labeled according to standard neuroanatomical nomenclature. Registration quality can be assessed by placing landmarks at desired locations within the topological space of each subject, and affine transformation of the landmarks into atlas space can then be applied. The residual distances of the landmark displacements between the subjects and the atlas can then be compared statistically to craft probabilistic atlases. For the PNS, however, analogous data processing algorithms need to be developed, tested, and validated, which likely requires considerable effort by mathematicians, data specialists, and neuroinformaticians. For any new PNS atlasing effort, the task of determining how best to define, represent and manipulate a PNS atlas space will require considerable reflection and effort.

11. The neuroinformatics of NS-wide atlasing

The computer science and informatics needed to support the comprehensive mapping of the SC and PNS will be a serious and critical consideration for any major atlasing enterprise. Since the earliest days of brain mapping (Fox, Mikiten et al. 1994, Mazziotta, Toga et al. 1995), databases of human brain primary and derived data have provided critical means for aggregating image volumes for atlasing and quantifying normal variability. Archives of anonymized raw and processed data, in addition to summary results, now permit researchers to explore data which were previously available only to the researchers who had acquired the original data. Data sharing of such archives has been proposed as an essential element of modern neuroimaging (Poline, Breeze et al. 2012), enabling the widest possible audience to utilize such data; the byproducts of such secondary analyses have been both novel and wide-ranging (Van Horn and Ishai 2007). Nevertheless, existing archives designed primarily for databasing brain volumes are likely ill-equipped for storing, representing, and facilitating additional SC and PNS neuroimaging data sets. For instance, HCP diffusion imaging datasets of the brain acquired using the 3 T Connectome MRI scanner at the Massachusetts General Hospital typically require storage on the order of tens of Gigabytes per subject after conversion from standard DICOM file format to uncompressed NIFTI format (http://nifti.nimh.nih.gov/nifti-1). By contrast, MRI datasets of the entire body can be expected to larger by a factor greater than 10. Moreover, such datasets are likely to be acquired not as a single MR volume but rather as several volumes of the torso, limbs, and portions thereof. If high-resolution multimodal data (e.g. T₁-, T₂-weighted structural MRI, DWI, etc.) are acquired from the same bodily segments, aggregate full-body datasets will likely be relatively large compared to brain-only datasets. For this reason, a robust and reliable data storage and databasing infrastructure is likely required to accommodate such big data.

If data are obtained as a series of distinct scans for various body segments, then the harmonization, co-registration and unification of such scans into a single, complete and multimodal volume of the whole body for subsequent image manipulations and analysis will greatly challenge the capabilities of today’s most commonly available image processing platforms. Modern scientific workflows capable of executing processing tasks in parallel on large computational clusters will be required to apply novel methods for combining data volumes with differing dimensions and native coordinate systems. This will necessitate efficient software design practices for the judicious use of computer memory and rapid processing speed. Additionally, novel file formats may be needed to accommodate the aggregate datasets and results, to permit the exchange of PNS connectivity information, and to set the stage for subsequent atlasing efforts.

The coordinate system of the atlas used to represent SC and PNS connectivity will require careful consideration. Initially, there may not exist a single representation at all, but rather a family of linked spaces of different Cartesian coordinates in addition to 2D representations, 3D spherical projections and to other such atlas frameworks. The use of 2D projections for representing brain morphometry and connectivity have become common in the connectomics literature, e.g. for connectograms (Irimia, Chambers et al. 2012, Van Horn, Irimia et al. 2012); similar methods can be expected to provide similar utility for mapping SC and PNS connectivity. Spherical representations of brain anatomy are commonplace and imply the use of latitude/longitude coordinate systems for brain surface topology (Van Essen and Drury 1997). In each case, the coordinate systems provide abstracted but useful means for the organization and consideration of underlying information on brain anatomy and wiring. It can be expected that a considerable informatics effort will be required to a) create such 2D/3D representations, and then to b) craft computer algorithms and software for the efficient conversion of native data into these graphical representations and for their inclusion into large archives using appropriate file types.

12. Modeling whole-body connectomic network properties

Network modeling approaches (Bassett and Sporns 2017), which have been so readily applied to data obtained in diffusion (Irimia and Van Horn 2016) and functional (Friston, Moran et al. 2013) imaging studies of the CNS, may also be applied to the PNS and, potentially, the complete NS. Several recent studies suggest this is possible. For example, Kerkman and colleagues (2018) utilized network analysis to examine the relationship between anatomical and functional connectivity in the musculoskeletal system as presented in the Hosford Muscle Tables (Hosford 1998). Anatomical networks were defined by the physical connections between 36 distinct muscles, while functional networks were based on intermuscular coherence assessed during postural tasks. They identified a modular structure of functional networks which was strongly shaped by the anatomical constraints of the musculoskeletal system. Changes in postural tasks were associated with frequency-dependent reconfigurations of the coupling between functional modules. In a similar study, Murphy et al. (2018) constructed a simplified whole-body musculoskeletal network, also based on the Hosford tables, wherein single muscles were connected to multiple bones. Using this streamlined approach, they determined that a muscle's role in the network offered theoretical predictions for the susceptibility of surrounding components to secondary injury. Importantly, they illustrated that sets of muscles cluster into network communities which mimic the organization of control modules in primary motor cortex. Where systems could also be also informed by underlying NS connectomic imaging, fully predictive computational frameworks for assessment of system properties would be undoubtedly be feasible. These might have implications for clinical neurological disorders having primary motor symptomatology (e.g. Parkinson’s, Multiple Sclerosis, etc). Applications to other body-wide systems (such as the enteric system (Barth and Shen 2018) and/or gut-brain axis (Osadchiy, Martin et al. 2019)) may offer unique insights and a wider appreciation of overall system dynamics in health and in disease, at the individual and/or population level. However, the Hosford tables of musculoskeletal anatomy are likely to be insufficient to describe the neuronal properties of the CNS+PNS connectome, nor will they account for subject-to-subject variations. Though this may be helpful for identifying the positions of the joints and the motion of the limbs with respect to them, 3D motion capture is distinct from the mapping of neural pathways, which would be a superseding goal of any whole body connectomic atlas. For this, medical imaging is likely needed.

One might imagine considerable community-driven effort in the definition of the nodal structure of whole-body network models. For instance, as noted above, initial nodes defined at the neuromuscular junction for major muscle groups, based upon published tables thereof, has been employed in prior work to then explore PNS network structure. However, further refinement might be required to enhance the density of connectivity and explore in more detail the properties of networks with increasing density. Moreover, (my)enteric systems, autonomic, and somatic nervous system components may necessitate distinct network modeling. Cranial Nerve X alone innervates the heart, esophagus, stomach, and other organs via numerous branches and any simple nodal structure may not fully capture this extensive connectivity. Additionally, the nodal architecture may be multi-scaled, involving connections representing neuromuscular junctions, enteric nervous system, the sensorimotor systems, joints, and so on. Moreover, simply defining nodes without accompanying network edges determined from neuroimaging would likely be insufficient for the examination of whole-body networks wherein. Spinal reflexes or the nuclei of the medulla, for example, include additional synaptic relays which current graph theoretical network applications do not often account for. At this time, in the absence of complete medical imaging data sets involving these varied systems, it would be hasty to be overly prescriptive on how such work might proceed. Indeed, these and other considerations suggest that the connectomics of the whole body do not simply involve scaling-up the type of mapping presently undertaken for the CNS alone. Determining the locations of nodal endpoints for the Vagus nerve alone is likely to require collective, multi-disciplinary input in order to achieve actionable consensus.

13. Potential clinical impact of full-body connectome mapping

Because DWI and DTI have the promise to facilitate the visualization of cranial, spinal and peripheral nerves—as well as of the SC itself—in 3D, the use of these modalities in the context of a stereotactic, deformable, population-level connectomic atlas has the potential to a) improve clinical understanding of PNS reflex processes (Table 4) and to b) enable finer diagnosis and characterization of peripheral nerve disorders. Additionally, this can optimize lesion localization, assist in mapping the entire human connectome, and also enable more straightforward evaluation of neural dysfunction compared to the extent to which this can be accomplished using conventional MRI alone (Takahara and Kwee 2010). GE MRI and DTI neurography could also be useful for determining the location and extent of injuries outside the SC or extradural space, particularly when findings can be corroborated by electroneurographic recordings (Yoshikawa, Hayashi et al. 2006).

Table 4.

Peripheral nerves, their spinal segments, and their reflexes commonly assessed by clinicians. Spinal segments: C = cervical; T = thoracic; L = lumbar; S = sacral.

Peripheral nerve	Reflex	Muscles involved	Principal SC segment
Musculocutaneous	Biceps	Biceps brachii	C5
Radial	Brachioradialis	Brachioradialis	C6
Radial	Triceps	Triceps brachii	C7
Femoral	Knee-jerk (patellar)	Quadriceps femoris	L4
Tibial	Ankle-jerk (Achilles)	Gastrocnemius, soleus	S1

Understanding the anatomic and connectomic variability of the SC and spinal nerves across patients is crucial in many clinical settings. A review of the recent clinical literature on PNS disorders suggests that a sophisticated 3D atlas of the PNS could substantially enhance the ability to diagnose a wide range of conditions, including peripheral neuropathy or plexopathy (Takahara and Kwee 2010, Healy, Redmond et al. 2020), peripheral and optic neuritis (Dailey, Tsuruda et al. 1997, Maravilla and Bowen 1998, Moore, Tsuruda et al. 2001, Meltzer, Frohman et al. 2018), peripheral nerve sheath tumors (Weber, Montandon et al. 2000, Lee, Kim et al. 2020), traumatic injuries, neuralgias and nerve compressions (DeSouza, Hodaie et al. 2014, Konieczny, Reinhardt et al. 2020), axonotmesis and neurotmesis (Chen, Carass et al. 2011, Chen, Carass et al. 2013), nerve root irregularities and loss of unidirectional nerve course, nerve entrapment due to carpal tunnel syndrome (Kabakci, Gurses et al. 2007, Khalil, Hancart et al. 2008, Stein, Neufeld et al. 2009, Hiltunen, Kirveskari et al. 2012, Negm, Nagm et al. 2017), etc. For many other conditions, preliminary studies indicate that the availability of a stereotactic, deformable, population-based and connectomic atlas of the SC and PNS would be useful for predicting the course of disease, for monitoring disease progression, and for monitoring the effects of therapeutic interventions (Valsasina, Rocca et al. 2005, Ohgiya, Oka et al. 2007, Cruz, Domingues et al. 2009, Bosma and Stroman 2012, Tarawneh, D'Aquino et al. 2020). Such an atlas would greatly improve the ability of DTI tractography to quantify the severity of neurological deficits due to MS (Schwartz, Duda et al. 2005, Durand-Dubief 2020), ALS (Agosta, Rocca et al. 2009, Nair, Carew et al. 2010, Valsasina, Horsfield et al. 2012, Paquin, El Mendili et al. 2018), encephalomyelitis (Constantinescu, Farooqi et al. 2011, Koelman, Benkeser et al. 2017), traumatic SCI (Deboy, Zhang et al. 2007, Rao, Zhao et al. 2013, Seif, Curt et al. 2018), SC tumors and vascular disorders of the SC (Ozanne, Krings et al. 2007, Setzer, Murtagh et al. 2010), spinal dysraphism (Hatem, Attal et al. 2009), Brown-Sequard Syndrome (Tattersall and Turner 2000), cervical disc herniation (Chen, Carass et al. 2011, Chen, Carass et al. 2013, Varlotta, Ge et al. 2020), irritable bowel syndrome (Labus, Naliboff et al. 2008), etc. Finally, a detailed and multimodal atlas of the type proposed here would be invaluable for assessing the severity of traumatic axonal injury at various locations along either nerves or along the SC (Song, Sun et al. 2003, Loy, Kim et al. 2007, Kim, Loy et al. 2010, Noristani, Boukhaddaoui et al. 2017) using such metrics as local FA, ADC and MD, which have been shown to be sensitive markers of change in axonal integrity.

14. Conclusion

Mapping the connectome of the human brain has been a task of tremendous importance and whose achievement remains likely to facilitate a broad range of scientific advances in clinical practice in addition to numerous substantial discoveries in neuroscience (Toga, Clark et al. 2012). Such mappings of CNS connectivity are now being actively examined across the lifespan in large-scale studies from North America (Kruggel, Masaki et al. 2017, Hagler, Hatton et al. 2019), Europe (Amunts, Ebell et al. 2016), and elsewhere. Nevertheless, because a large proportion of NS processes in the human body lie completely outside the brain, our desired understanding of structural and functional neural patterns and of their importance in health and disease remains incomplete without the availability of a connectomic, stereotactic atlas of the SC and PNS. Although useful technological advances have been made to facilitate connectome mapping, our knowledge of neural connections outside the brain remains unsystematic, fragmentary and often disorganized. Importantly, no major research enterprise has been dedicated to the tasks of (1) synthesizing the plethora of neuroimaging techniques now available for PNS and SC imaging and (2) developing novel medical imaging techniques for mapping nerve pathways outside the brain at a level of detail which can rival the state of the art in brain connectomics. Because such progress is critical for the advancement of both scientific knowledge and clinical practice, we hereby propose the implementation of a large-scale scientific effort to map neural connections outside the brain, thereby complementing current WM brain mapping efforts and completing the task of charting the entirety of the human connectome.