The Effect of Transmit B₁ Inhomogeneity on Hyperpolarized [1-¹³C]-Pyruvate Metabolic MR Imaging Biomarkers

Abstract

Purpose:

A specialized Helmholtz-style ¹³C volume transmit “clamshell” coil is currently being utilized for ¹³C excitation in pre-clinical and clinical hyperpolarized ¹³C MRI studies aimed at probing metabolic activity of tumors in various target anatomy. Due to widespread use of this ¹³C clamshell coil design, it is important that the effects of the ¹³C clamshell coil B₁⁺ profile on HP signal evolution and quantification are well understood. The goal of this study was to characterize the B₁⁺ field of the ¹³C clamshell coil and assess the impact of inhomogeneities on semi-quantitative and quantitative hyperpolarized MR imaging biomarkers of metabolism.

Methods:

The B₁⁺ field of the ¹³C clamshell coil was mapped by hand using a network analyzer equipped with a S-parameter test set. Pharmacokinetic models were used to simulate signal evolution as a function of position dependent local excitation angles, for various nominal excitation angles, which were assumed to be accurately calibrated at isocenter. These signals were then quantified according to the normalized lactate ratio (nLac) and the apparent rate constant for the conversion of pyruvate to lactate (k_PL). The percent difference between these metabolic imaging biomarker maps and the reference value observed at isocenter of the clamshell coil was calculated to estimate the potential for error due to position within the clamshell coil. Finally, regions were identified within the clamshell coil where deviations in B₁⁺ field inhomogeneity or imaging biomarker errors imparted by the B₁⁺ field were within ±10% of the value at isocenter.

Results:

The B₁⁺ field maps show that a limited volume encompassed by a region measuring approximately 12.9 × 11.5 × 13.4 cm (X-direction, Y-direction, Z-direction) centered in the ¹³C clamshell coil will produce deviations in the B₁⁺ field within ±10% of that at isocenter. For the metabolic imaging biomarkers that we evaluated, the case when the pyruvate excitation angle (θ_P) and lactate excitation angle (θ_L) were equal to 10° produced the largest volumetric region with deviations within ±10% of the value at isocenter. Higher excitation angles yielded higher signal and SNR, but the size of the region in which uniform measurements could be collected near the isocenter of the coil was reduced at higher excitation angles. The tradeoff between the size of the homogenous region at isocenter and signal intensity must be weighed carefully depending on the particular imaging application.

Conclusion:

This work identifies regions and optimal excitation angles (θ_P and θ_L) within the ¹³C clamshell coil where deviations in B₁⁺ field inhomogeneity or imaging biomarker errors imparted by the B₁⁺ field were within ±10% of the respective value at isocenter, and thus where excitation angles are reproducible and well calibrated. Semi-quantitative and quantitative metabolic imaging biomarkers can vary with position in the clamshell coil as a result of B₁⁺ field inhomogeneity, necessitating care in patient positioning and the selection of an excitation angle set that balances reproducibility and SNR performance over the target imaging volume.

Introduction

Dissolution dynamic nuclear polarization (dDNP) has attracted interest in recent years as a way to enhance the sensitivity of various molecular imaging agents beyond the capabilities of conventional magnetic resonance imaging (MRI).^1,2 dDNP can be utilized to create hyperpolarized (HP) substrates which enable the investigation of metabolic pathways in vivo with sensitivity and spatiotemporal resolution that was previously impossible.³ HP ¹³C MRI can be used to quantify the conversion of HP pyruvate into lactate as an indicator for glycolytic exchange in vivo.⁴ HP [1‐¹³C]-pyruvate and its downstream metabolites have shown tremendous potential for characterization of tumor metabolism and detection of tumor response to therapy.^5–9 Robust quantification of HP ¹³C data will improve the clinical utility of this metabolic imaging method. Therefore, a major goal for the field of HP MRI is the establishment of HP imaging methods that are quantitative, robust, and reproducible.

The standard ¹H body coil within clinical MR systems is used to achieve homogeneous signal excitations for traditional MRI. However, because the ¹H body coil does not support ¹³C signal transmit, specialized ¹³C transmit and receive coils must be integrated into the imaging setup in order to conduct ¹³C imaging studies. A specialized Helmholtz-style ¹³C volume transmit “clamshell” coil^10,11 was originally designed to support the acquisition of clinical ¹³C data in the setting of prostate cancer⁷ and has supported acquisitions in other anatomical regions, such as the heart, brain, kidneys, and elsewhere.^12–15 At present there are twelve sites internationally carrying out HP [1-¹³C]-pyruvate studies in human subjects and almost all of these sites utilize the ¹³C clamshell coil for signal excitation outside of brain.

Unlike conventional MRI, HP ¹³C MRI magnetization is non-recoverable and is limited by ¹³C signal decay and losses due to signal excitation. Excitations effect signal evolution and quantification by depleting spin labels on metabolic precursors and products in and around target anatomy. Accurate knowledge of excitation angles is critical for HP imaging because excitation losses must be accounted for in order to accurately determine apparent chemical conversion rates in vivo.¹⁶ A simple ¹³C reference standard is often used to calibrate the ¹³C center frequency and transmit power for imaging prior to injection of HP [1‐¹³C]-pyruvate.^7,17–19 Unfortunately, calibration using a small reference phantom only provides information about excitation fields at the location of the phantom.

Methods to calibrate and map B₁ for ¹³C coils have been proposed to improve the efficient use of HP signal and the accuracy and robustness of HP ¹³C imaging. Grist, et al. used the endogenous signal derived from ²³Na nuclei as a reference for ¹³C imaging.²⁰ Tang, et al. used regional bolus tracking to trigger Bloch-Siegert B₁ mapping and real-time B₁ calibration based on regional B₁ measurements.²¹ These methods are useful in reducing B₁ transmit errors and accounting for transmit errors due to B₁ inhomogeneities that can’t be controlled by careful placement of anatomy within the ¹³C coil. Comprehensive B₁⁺ maps of the entire volumetric region of the coil could also provide valuable information about the spatial dependencies of semi-quantitative and quantitative imaging biomarkers, along with critical guidance for placement of anatomical structures within the coil to minimize experimental variations. This information can be used to determine the location and extent of a region in the ¹³C clamshell coil where B₁⁺ inhomogeneity is acceptably low. Accurate positioning of target anatomy in this homogeneous region will ensure accurate excitation and improve quantitative accuracy.^4,16

In this research, we measured the B₁⁺ field of a ¹³C volume transmit clamshell coil by hand and created comprehensive B₁⁺ field maps that provide information about the inhomogeneity across the entire field-of-view (FOV). We then used these B₁⁺ field maps to generate synthetic pyruvate and lactate curves using several excitation angle cases in order to evaluate how semi-quantitative and quantitative metabolic imaging biomarkers can vary with position in the clamshell coil. We focus on the normalized lactate ratio (nLac) and the apparent rate constant for the conversion of pyruvate into lactate (k_PL). The resultant biomarker maps permitted identification of acceptable regions within the ¹³C clamshell coil where deviations in B₁⁺ field inhomogeneity or imaging biomarker errors imparted by the B₁⁺ field were within ±10% of their nominal values at isocenter.

Methods

Bench Measurement of the B₁⁺Field Sensitivity

Local B₁⁺ field sensitivity of the ¹³C clamshell coil (GE Healthcare, Waukesha, WI, USA) was measured by hand using a network analyzer (4395A, Agilent, Santa Clara, CA, USA) equipped with a S-parameter test set (87511A, Agilent, Santa Clara, CA, USA). S₂₁ at the Larmor frequency for ¹³C at 3T (32.12 MHz) was measured as a function of position using a custom-built, small untuned 13 mm diameter loop “sniffer” probe. A purpose-built and electromagnetically transparent platform was constructed to ensure consistent and repeatable positioning and measurements (Figure 1). 238 measurements were collected in the XZ plane, over a 40 × 40 cm grid, and these measurements were repeated at eight heights in the Y-direction for a total of 1,904 measurements covering the entire FOV of the clamshell coil.

Figure 1.

The electromagnetically transparent B1+ field sensitivity bench measurement setup used to produce consistent and repeatable positioning and hand measurements. Position in the X- and Z-direction was measured consistently by utilizing the evenly spaced holes present in the pegboard. The sniffer probe was held in place using a plastic clamp and the clamshell coil was placed on a plastic cart to minimize perturbation of the RF field distribution.

The relative magnetic field intensity produced by the ¹³C clamshell coil at the position of the sniffer probe was calculated from S₂₁ measurements and analyzed using MATLAB R2020b (The MathWorks, Natick, MA, USA). Bilinear interpolation of the data was performed throughout the volumetric region of the clamshell coil and all values were normalized to the value at isocenter. Axial, sagittal, and coronal B₁⁺ field maps at coil isocenter were created, as well as a multi-plane 3D B₁⁺ field map showing an intersecting axial, sagittal, and coronal quadrant at isocenter. Isosurface contour values from −70% to +50% were used to display the percent deviation in B₁⁺ field inhomogeneity from the isocenter of the clamshell coil.

Metabolic Imaging Biomarkers

The conversion of HP pyruvate into lactate in vivo is often semi-quantitatively summarized using normalized lactate (nLac), which is the ratio of the area-under-the-curve (AUC) over time for HP lactate to the combined sum of the AUCs for HP pyruvate and lactate. Alternatively, HP lactate production may be quantitatively summarized using k_PL, the apparent rate constant for the conversion of pyruvate to lactate obtained through pharmacokinetic (PK) modeling. The effect of B₁⁺ inhomogeneity on nLac and k_PL was assessed for six excitation angle cases, including four cases in which pyruvate and lactate were subjected to equal excitation angles (θ_P = θ_L = 10°, 20°, 30°, and 60°), and two cases in which lactate was excited at a higher level than pyruvate (θ_P = 10°, θ_L = 30° and θ_P = 20°, θ_L = 30°). In current practice, constant excitation angle cases are often used with typical values ranging from 10–30°, and spectral-spatial RF pulses are often used to impart differing excitation angles on pyruvate and lactate.¹⁸ We assessed these excitation angle cases, as well as a 60° constant excitation angle case in order to explore the effects of B₁⁺ inhomogeneity on nLac and k_PL at higher excitation angles. These results were then used to estimate how nLac and k_PL could vary spatially within the volume of the ¹³C clamshell coil due only to variations in B₁⁺.

Pharmacokinetic Modeling

In this work, we consider two PK models.^4,19,22 Model A (Equation 1) contains two chemical pools (HP pyruvate and lactate) and one physical compartment. This precursor-product relationship between pyruvate and lactate is an approximation that assumes all observed substrate has the ability to interact with intracellular enzymes that enable exchange:

$$\left[M_{L,z}(n)\right]=e^{-TR/T_{1,L}}\left[\cos \left({\theta }_L\right)\cdot M_{L,z}(n-1)\right]+k_{PL}{\int }_{(n-1)\cdot TR}^{n\cdot TR}{e}^{(n\cdot TR-\tau )/T_{1,L}}\left[M_{P,z}(\tau )\right]d\tau$$ (1)

Here, M_L,z(n) refers to the longitudinal lactate magnetization just prior to the n^th excitation pulse. M_L,z(0) refers to the initial lactate magnetization. T_1,L, the longitudinal relaxation rate for HP [1-¹³C]-lactate, was assumed to be accurately known a priori in these simulations. The transverse magnetization is calculated from longitudinal magnetization according to the excitation angle.

Model B (Equations 2–4) contains two chemical pools and two physical compartments, where the intravascular (iv) space is separated from an extravascular space (ev) that is assumed to be well-mixed and homogenized by rapid diffusion and membrane transport. Chemical conversion of HP pyruvate to lactate occurs only in the extravascular space, and the reverse reaction is assumed to be negligible. Nuisance parameters that must be included but are not of particular interest in the analysis, including T_1,P and T_1,L, and parameters that account for microvascular function, were assumed to be accurately known throughout. The rate of pyruvate extravasation is given by k_ve, while v_b denotes the vascular blood volume fraction. In this model, extravascular HP signal evolution follows:

$$\left[\begin{array}{l}{M}_{P,ev,z}(n)\hfill \\ M_{L,ev,z}(n)\hfill \end{array}\right]=e^{A\cdot TR}\left[\begin{array}{l}\cos \left({\theta }_P\right)\cdot M_{P,ev,z}(n-1)\hfill \\ \cos \left({\theta }_L\right)\cdot M_{L,ev,z}(n-1)\hfill \end{array}\right]+\frac{k_{ve}}{1-v_b}{\int }_{(n-1)\cdot TR}^{n\cdot TR}{e}^{A(n\cdot TR-\tau )}\left[\begin{array}{l}{M}_{P,iv}(\tau )\hfill \\ M_{L,iv}(\tau )\hfill \end{array}\right]$$ (2)

Where

$$A=\left[\begin{array}{cc}-\left(\frac{k_{ve}}{1-v_b}+k_{PL}+\frac{1}{T_{1,P}}\right)& 0\\ k_{PL}& -\frac{1}{T_{1,L}}\end{array}\right]$$ (3)

The observed transverse magnetization is calculated from the longitudinal magnetization according to excitation angles for pyruvate and lactate, and the volume-weighted combination of intravascular and extravascular compartments follows:

$$\left[\begin{array}{l}{M}_{P,xy}(n)\hfill \\ M_{L,xy}(n)\hfill \end{array}\right]=\left[\begin{array}{c}\sin \left({\theta }_P\right)\\ \sin \left({\theta }_L\right)\end{array}\right]\cdot \left\{v_b\left[\begin{array}{c}{M}_{P,iv}(n)\\ M_{L,iv}(n)\end{array}\right]+1-v_b\left[\begin{array}{l}{M}_{P,ev,z}(n)\hfill \\ M_{L,ev,z}(n)\hfill \end{array}\right]\right\}$$ (4)

More physiologically accurate PK models for HP [1-¹³C]-pyruvate have been described⁴, which account for transport of HP agents across cellular membranes prior to interaction between HP pyruvate and the intracellular enzymes that mediate chemical conversion. However, these models are rarely used because of their complexity and the difficulty in resolving signals in the extravascular/extracellular space from those in the intracellular space.

Synthetic Data Generation

Synthetic dynamic pyruvate and lactate curves were generated for the six previously defined excitation angle cases using a two compartment model (Model B). Hand measured B₁⁺ maps were scaled to achieve the correct excitation angle at isocenter. The default value for T_1,P was assumed to be 43 s and T_1,L was assumed to be 33 s.²³ The vascular input function (VIF) shape was modeled as a gamma-variate function.²⁴ The rate constant of pyruvate extravasation (k_ve) was set to 0.020 s⁻¹ and the vascular blood volume fraction (v_b) was 0.050. The input k_PL was defined to be 0.050 s^-1. We simulated data using TR = 2 s over a time interval of 128 s.

Analysis of Synthetic Data

nLac was calculated by taking the ratio of the time integrated AUC for HP lactate to the combined AUCs for HP pyruvate and lactate, using synthetic data generated by model B as described above.

The k_PL for each set of synthetic signal curves was fit using both model A and model B. All fitting was completed with a non-linear least-squares algorithm in MATLAB using the PK models described above. Data generated by model B was not only fit using model B (denoted hereafter as k_PLBB) but also fit using model A (denoted as k_PLBA). For analysis using model A, we fit k_PLBA and for analysis using model B, we fit k_PLBB and a scaling factor for the VIF. All other parameters were assumed to be known and identical to the parameters previously stated in the synthetic data generation section above. Isosurface contour lines were used to display the spatially dependent percent deviation in nLac, as well as k_PLBA and k_PLBB reference values at isocenter of the coil. It is important to note that the excitation angle value at isocenter of the clamshell coil was assumed to be calibrated accurately.

Results

The hand measured B₁⁺ field maps (Figure 2) show that a volumetric region (X-direction, Y-direction, Z-direction) measuring 12.9 × 11.5 × 13.4 cm centered at coil isocenter will contain deviations in the B₁⁺ field within ±10% of the field at the center of the coil. The axial (Figure 2a) and sagittal (Figure 2b) views of the hand measured B₁⁺ field maps show increased B₁⁺ field intensity in the Y-direction near the coil elements, with a reduction in B₁⁺ field intensity in the X- and Z-direction which produces a distinct hourglass shape in the transmit field profile. The axial, sagittal, and coronal multi-plane 3D view (Figure 2d) better illustrates a portion of the volume that will produce deviations in the B₁⁺ field within ±10% of the value at isocenter.

Figure 2.

(a) Axial, (b) sagittal, (c) coronal, and (d) multi-plane 3D view of hand measured B1+ field maps for the 13C clamshell coil, referenced from coil isocenter. The red contour lines in all subfigures highlight the boundaries of the volumetric region that produces deviations in the B1+ field within ±10% of the value of at isocenter.

nLac values calculated at isocenter for the six excitation angle cases (Figure 3) reveal that the θ_P = 10°, θ_L = 30° case (Figure 3e) produced the largest value of nLac (0.64), followed by the θ_P = θ_L = 10° case (Figure 3a) which produced a nLac value at isocenter of 0.55. The θ_P = θ_L = 60° case (Figure 3d) produced the smallest value of nLac at isocenter (0.12). As excitation angles increased, the observed nominal value of nLac generally decreased and the physical extent of the uniform region decreased in size. A summary of nLac values as a function of excitation angle and the volumetric region that will produce deviations within ±10% nLac of the nLac value found at isocenter for the six excitation angle cases can be found in Table I. The case when θ_P = θ_L = 10° (Figure 3a) produced the largest volumetric region that produces deviations within ±10% nLac at isocenter. However, the exact dimensions of this region are outside of the FOV.

Figure 3.

Axial, sagittal, and coronal 3D nLac maps as a function of nominal excitation angles for pyruvate and lactate, when: (a) θP = θL = 10°; (b) θP = θL = 20°; (c) θP = θL = 30°; (d) θP = θL = 60°; (e) θP = 10°, θL = 30°; (f) θP = 20°, θL = 30°. The dashed red contour lines in (a) and (b) highlight the boundaries of the volume that produces deviations in nLac within ±5% of the nLac value found at isocenter of the coil. The solid red contour lines in (b) through (f) highlight the boundaries of the volume that produces deviations in nLac within ±10% of the nLac value found at isocenter.

Table I.

The volumetric region that produces deviations within ±10% nLac of the nLac value found at isocenter of the coil.

Excitation Angle Case	nLac	X (cm)	Y (cm)	Z (cm)
θP = θL = 10°*	0.55	-	-	-
θP = θL = 20°	0.46	20.5	15.6	20.8
θP = θL = 30°	0.35	13.5	12.1	13.9
θP = θL = 60°	0.12	8.0	7.7	7.9
θP = 10°, θL = 30°	0.64	21.4	16.0	21.7
θP = 20°, θL = 30°	0.46	15.9	13.5	16.4

^*10% contour lines were outside the FOV

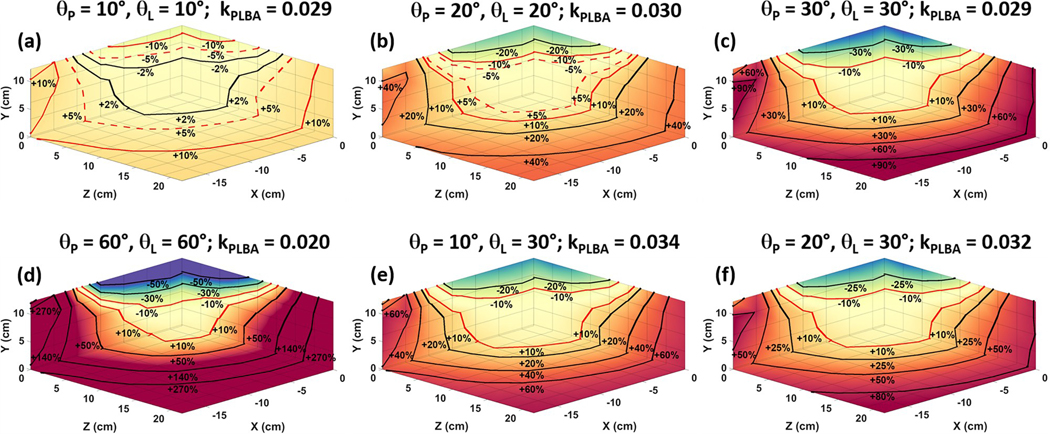
Due to the fact that k_PLBA (Figure 4) data was generated using a two compartment model (Model B) and fit using a simple precursor-product relationship (Model A), there was a discrepancy between the fitted k_PLBA and the k_PL (0.050 s⁻¹) used for data generation. Analysis using the precursor-product relationship is known to underestimate k_PL because it assumes that all observed pyruvate is in direct biological contact with enzymes that mediate the conversion of pyruvate into lactate. The excitation angle case when θ_P = θ_L = 60° (Figure 4d) produced the lowest k_PLBA value at isocenter of the coil (0.020 s⁻¹) and the θ_P = 10°, θ_L = 30° case (Figure 4e) produced the largest value of k_PLBA (0.034 s⁻¹). Therefore, at higher excitation angle cases, the value of k_PLBA at isocenter decreases as well as the size of the volumetric region that will produce deviations within ±10% k_PLBA. A summary of k_PLBA values and the volumetric region that will produce deviations within ±10% k_PLBA of the k_PLBA value found at isocenter for the six excitation angle cases (Figure 4) can be found in Table II. The case when θ_P = θ_L = 10° (Figure 4a) produced the largest volumetric region (29.2 × 19.6 × 32.6 cm) that produces spatially dependent deviations within ±10% k_PLBA of the k_PLBA value found at isocenter.

Figure 4.

Axial, sagittal, and coronal 3D kPLBA maps as a function of changes in pyruvate and lactate excitation angle, when: (a) θP = θL = 10°; (b) θP = θL = 20°; (c) θP = θL = 30°; (d) θP = θL = 60°; (e) θP = 10°, θL = 30°; (f) θP = 20°, θL = 30°. The dashed red contour lines in (a) and (b) highlight the boundaries that produce deviations in kPLBA within ±5% of the kPLBA value found at isocenter. The solid red contour lines in (a) through (f) highlight the boundaries that produce deviations in kPLBA within ±10% of the kPLBA value found at isocenter.

Table II.

The volumetric region that produces deviations within ±10% k_PLBA of the k_PLBA value found at isocenter of the coil.

Excitation Angle Case	kPLBA (s−1)	X (cm)	Y (cm)	Z (cm)
θP = θL = 10°	0.029	29.2	19.6	32.6
θP = θL = 20°	0.030	15.6	13.3	16.1
θP = θL = 30°	0.029	11.3	11.0	12.1
θP = θL = 60°	0.020	7.5	7.3	7.4
θP = 10, θL = 30°	0.034	12.5	11.7	13.1
θP = 20, θL = 30°	0.032	12.0	11.4	12.7

k_PLBB (Figure 5) values were calculated by using the same two compartment PK model (Model B) for synthesis and analysis, and as a result, the value of k_PLBB at isocenter remained unchanged (0.050 s⁻¹), regardless of the excitation angle case employed. However, at higher excitation angle cases (Figure 5d), the size of the volumetric region that will produce deviations within ±10% k_PLBB decreased considerably when compared to the lowest excitation angle case (Figure 5a). A summary of k_PLBB values as a function of excitation angle and the volumetric region that will produce deviations within ±10% k_PLBB of the k_PLBB value found at isocenter of the coil for the six excitation angle cases can be found in Table III. The case when θ_P = θ_L = 10° produced the largest volumetric region that produces spatially dependent deviations within ±10% k_PLBB of the k_PLBB value found at isocenter of the ¹³C clamshell coil. However, the exact dimensions of this region are outside of the FOV.

Figure 5.

Axial, sagittal, and coronal 3D kPLBB maps as a function of changes in pyruvate and lactate excitation angle, when: (a) θP = θL = 10°; (b) θP = θL = 20°; (c) θP = θL = 30°; (d) θP = θL = 60°; (e) θP = 10°, θL = 30°; (f) θP = 20°, θL = 30°. The dashed red contour lines in (a) and (b) highlight the boundaries that produce deviations in kPLBB within ±5% of the kPLBB value found at isocenter. The solid red contour lines in (b) through (f) highlight the boundaries that produce deviations in kPLBB within ±10% of the kPLBB value found at isocenter.

Table III.

The volumetric region that produces deviations within ±10% k_PLBB of the k_PLBB value found at isocenter of the coil.

Excitation Angle Case	kPLBB (s−1)	X (cm)	Y (cm)	Z (cm)
θP = θL = 10°*	0.050	-	-	-
θP = θL = 20°	0.050	19.4	14.6	19.7
θP = θL = 30°	0.050	12.3	11.3	13.0
θP = θL = 60°	0.050	7.1	7.1	7.1
θP = 10°, θL = 30°	0.050	15.6	13.0	13.4
θP = 20°, θL = 30°	0.050	14.3	12.2	15.0

^*10% contour lines were outside the FOV

Discussion

There are several observable trends that can be seen when looking at the nLac maps (Figure 3 a–d), k_PLBA maps (Figure 4 a–d), and k_PLBB maps (Figure 5 a–d) for equal excitation angles. As excitation angle is increased, the volumetric region that produces deviations within ±10% error from the reference value of nLac, k_PLBA, and k_PLBB observed at clamshell isocenter decreases. As a result, when excitation angles increase, nLac or k_PL becomes more sensitive to location in the coil due to B₁⁺ non-uniformity. Furthermore, as excitation angles increase, error in measurements that are taken further from coil isocenter become large, further highlighting the importance of target anatomy placement within the central region of the clamshell coil where B₁⁺ deviations are minimal.

Generally, lactate signal in ¹³C studies is much lower than pyruvate signal, and it is sometimes beneficial to utilize strategies where the lactate excitation angle is greater than the pyruvate excitation angle. The use of a lower excitation angle for pyruvate allows for the preservation of hyperpolarized pyruvate magnetization, which could be chemically converted into lactate. The results from this work show that using an excitation angle case of θ_P = θ_L = 10° produces the largest volumetric region that produces deviations within ±10% nLac, k_PLBA, and k_PLBB. However, low excitation angles can lead to low signal-to-noise ratio (SNR). Lower excitation angles may produce better absolute excitation uniformity, but this will come at the expense of a reduction in SNR. Therefore, a tradeoff must be made in order to balance SNR and excitation angle homogeneity. Lower excitation angles could also promote a temporal averaging effect that will reduce sensitivity to dynamic content with a higher temporal frequency.²⁵

In this work, synthetic data was used to evaluate how semi-quantitative and quantitative metabolic imaging biomarkers can vary with position in the clamshell coil due solely to variations in the B₁⁺ field. At present, no means exist to generate perfectly uniform magnetization and chemical conversion over the large interior volume of this coil, and therefore it would be impractical to perform this study experimentally.

Another minor limitation of this study is that the B₁⁺ field of the clamshell coil was measured by hand, without loading. It is possible that our results may change slightly once the coil is loaded, however, we don’t expect the B₁⁺ field to change dramatically because the RF wavelength is much larger than body size at the ¹³C resonance frequency of 32.12 MHz, and thus the B₁⁺ field obtained by hand measurements should be a fair representation of the fields inside the body.²⁶

While it may be possible to utilize the hand measured B₁⁺ maps in this work to correct the effects of B₁⁺ inhomogeneities in acquired image data, this would require very careful registration between the B₁⁺ maps, clamshell coil, and patient/target of interest. While we expect perturbations due to body loading to be small, any mismatch could lead to miscalibration and/or errors when correcting image data for the excitation angle at each point in space. This correction would be particularly error prone in regions where excitation angles and SNR are too low, or where excitation angles are too high and HP magnetization is depleted too quickly. Also, semi-quantitative approaches, such as nLac and Model A, will be challenging to correct because different pyruvate excitation angles will deplete pyruvate signal, and thus subsequent lactate signal, at different rates. These errors can be seen in Table I and Table II where there is a clear variation in nLac and k_PLBA values at isocenter, as a function of known excitation angles. However, this error is not observed in the k_PLBB maps (Table III) because Model B more accurately accounts for excitation losses in extravascular pyruvate. Our primary focus in this body of work was to characterize potential errors induced by transmit inhomogeneities and to identify the range over which we can make accurate measurements without additional sets of corrections. The framework outlined in this manuscript can be used to evaluate the effects of inhomogeneities in other transmit coils that are used for HP MRI studies.

Given the results of the volumetric regions that produce deviations within ±10% nLac, k_PLBA, and k_PLBB, as well as SNR limitations, we suggest employing excitation angle cases of θ_P = 10°, θ_L = 30° and θ_P = θ_L = 20° for nLac, k_PLBA, and k_PLBB measurements when utilizing the clamshell coil. These excitation angle cases would yield the highest nLac and k_PL values as well as the largest volumetric regions that produce deviations within ±10% error from the reference value of nLac, k_PLBA, and k_PLBB observed at clamshell isocenter. Furthermore, these excitation angle cases would reduce B₁⁺ errors in metabolic analysis of hyperpolarized pyruvate when utilizing the clamshell coil while still maintaining lactate and pyruvate SNR. It is important to note that the tradeoff between the size of the homogenous region at isocenter and signal intensity must be weighed carefully depending on the particular imaging application.

Conclusion

We explored the effect of B₁⁺ field inhomogeneity using a ¹³C volume transmit body coil and produced various B₁⁺ field maps and molecular biomarker deviation maps in order to aid in the positioning of target anatomy for various HP MRI studies. Kinetic modeling and metabolic biomarkers are highly influenced by RF excitation angles^16,27 which require precise B₁⁺ calibration for accurate quantitative measurements. By defining acceptable limits of error to be within ±10% deviation in nLac, k_PLBA, and k_PLBB we were able to create maps that highlight these boundaries across the range of several excitation angle cases that are currently used in research studies today. These hand measured maps will serve as a valuable visualization tool when placing target anatomy in the clamshell coil to aid in reducing B₁⁺ field inhomogeneity and its effect on nLac and k_PL measurements. Establishing HP methods that are quantitative, robust, and reproducible is critical for the field of HP MRI. In order to facilitate the widespread clinical application of HP metabolic imaging methods, collaboration and the comparison of clinical HP data gathered at different institutions will require uniform standards in image acquisition protocols and data analysis that enable multicenter trials. Better understanding of the spatial variations of transmit field heterogeneity is important for guiding the physical setup of imaging measurements, and for establishing imaging protocols that will maximize reproducibility and accuracy. This work identifies regions and optimal excitation angles (θ_P and θ_L) within the ¹³C volume transmit clamshell coil where excitation angles will be reproducible and well calibrated, leading to a reduction of errors in metabolic quantification.