AC Insulator-based Dielectrophoretic Focusing of Particles and Cells in an “Infinite” Microchannel

Abstract

It is often necessary to pre-focus particles and cells into a tight stream for subsequent separation and/or analysis in microfluidic devices. DC electric field has been widely used for particle and cell focusing in insulator-based dielectrophoretic (iDEP) microdevices, where a large field magnitude, a high constriction ratio, and/or a long microchannel are usually required to enhance the iDEP effect. We demonstrate in this work an AC iDEP focusing technique, which utilizes a low-frequency AC electric field to generate both an oscillatory electrokinetic flow of the particle/cell suspension and a field direction-independent dielectrophoretic force for particle/cell focusing in a virtually “infinite” microchannel. We also develop a theoretical analysis to evaluate this focusing in terms of the AC voltage frequency, amplitude, and particle size, which are each validated through both experimental demonstration and numerical simulation. The effectiveness of AC iDEP focusing increases with the second order of electric field magnitude, superior to DC iDEP focusing with only a first-order dependence. This feature and the “infinite” channel length together remove the necessity of large electric field and/or small constriction in DC iDEP focusing of small particles.

Graphical Abstract

INTRODUCTION

Microfluidic devices have been increasingly used for particle and cell manipulation in various biomedical, chemical, and environmental applications.^1–5 Focusing particles and cells into a tight stream is often necessary prior to separating and analyzing them in these devices (e.g., microflow cytometer).^6–9 A variety of force fields (e.g., acoustic,^10–12 magnetic,^13,14 etc.) have been demonstrated for this purpose, among which DC electric field is frequently used because of the ease of connection, operation, integration, etc.^15–17 It generates three primary electrokinetic phenomena in microchannels including fluid electroosmosis, particle electrophoresis, and particle dielectrophoresis (DEP).^18–20 The former two motions are both linear electrokinetic phenomena parallel to the applied electric field, and have been demonstrated to focus the suspended particles or cells via the so-called sheath-flow focusing.^21–25 This type of approaches consumes a relatively large amount of sheath fluid, which not only dilutes the particle or cell concentration but also increases the material cost. Moreover, the electrokinetic flows of both the particle/cell suspension and the shear fluid(s) need to be each precisely controlled for an effective focusing.^15,21

DEP is the particle motion induced by electric field gradients, which is a nonlinear electrokinetic phenomenon that may have components both along and normal to the electric field direction.^26,27 It has been demonstrated for particle and cell focusing in electrode-free microchannels through two different forms. One form is to utilize the dielectrophoretic-like force resulting from the transversely asymmetric electric field around an off-center dielectric particle or cell to direct it toward the channel centerline.^28,29 However, this wall-induced electrical lift decays very rapidly with the increasing particle-wall separation distance.^30–32 Therefore, a large electric field and/or a long microchannel must be used in order for an efficient focusing, especially for smaller particles and cells.^33,34 These requirements increase the power consumption and fabrication cost. They may also cause adverse impacts on both the sample and the device itself through, for example, electric shock³⁵ and Joule heating-induced thermal effects.³⁶ Another form is to use the insulator-based dielectrophoretic (iDEP) force to push a dielectric particle or cell away from the high electric field region near an insulator, which may be either a hurdle on the channel wall or the wall itself if the wall has a non-zero curvature.^37–40 This DC iDEP focusing technique experiences a similar issue to the above wall-induced dielectrophoretic-like focusing because DEP acts upon particles within a short range. DC-biased AC electric field with a frequency of 1 kHz order has been employed to partially mitigate this issue.⁴¹ Alternately, there have been reports on the use of 3D insulator with a large constriction ratio⁴² or an array of insulators for enhanced DC iDEP focusing.⁴³

We propose the use of low-frequency AC electric field to generate an oscillatory electrokinetic flow of the particle or cell suspension and simultaneously an iDEP focusing of the particles or cells in a ratchet microchannel. This idea is borrowed from the recently proposed oscillatory hydrodynamic flow-based inertial⁴⁴ and viscoelastic⁴⁵ focusing of particles in practically “infinite” microchannels, where the flow-induced inertial^46–49 and viscoelastic^50–53 lift forces preserve their directionality when the flow direction is switched. Our proposed AC iDEP focusing technique sacrifices time to gain a virtually “infinite” channel length, which decreases the above-mentioned requirements for DC iDEP focusing of particles. Its novelty consists in the synergy of long-range transient electrokinetic flow and short-range time-averaged dielectrophoretic particle motion. In particular, as we will demonstrate below through a combined theoretical, experimental, and numerical study of the related parameters, the effectiveness of the proposed AC iDEP focusing scales with the electric field magnitude at a higher order than DC iDEP focusing, which further helps lowering the electric field requirement. Moreover, it does not have the issues accompanied with the generation of oscillatory hydrodynamic flows in microchannels, where the mechanical moving part and tubing connection may both make the microfluidic devices prone to fouling.⁵⁴

MATERIALS AND METHODS

Experimental Setup

The ratchet microchannel was fabricated in polydimethylsiloxane (PDMS) using the standard soft lithography technique. Detailed fabrication procedure is referred to our earlier paper.⁵⁵ As shown in Figure 1a, the channel is composed of two opposing identical arrays of 20 triangular ratchets along its sidewalls. The peak-to-peak distance of two consecutive ratchets, i.e., the spatial period of ratchets, is 250 μm, making the overall ratcheted region 5 mm long. The widest part of the channel is 500 μm, while the narrowest part (i.e., the distance of opposing ratchet tips) is 100 μm. The microchannel is uniformly 40 μm deep and overall 8 mm long, with a 5 mm diameter circular extension at each end acting as a fluid reservoir. The AC iDEP focusing was demonstrated using spherical polystyrene particles of 3, 5, and 10 μm diameter (Sigma-Aldrich), which were each re-suspended into 1 mM phosphate buffer solution (with a measured electric conductivity of 200 μS/cm) to a concentration of 10⁶ – 10⁷ particles per mL. Yeast cells (ATCC9763, Saccharomyces cerevisiae) were used to demonstrate the biological applications of the AC iDEP focusing technique. They were cultured in Sabouraud dextrose broth (Becton, Dickinson and Company) at 35° C for 24 hours before being harvested and washed with phosphate-buffered saline solution (Fisher Scientific) three times. They were re-suspended in 1 mM phosphate buffer to a final concentration of around 10⁶ cells/mL and measured to have an average diameter of approximately 7 μm. A small amount of Tween 20 (0.5% in volume, Fisher Scientific) was added to each prepared suspension for preventing particles or cells from adhering to the channel walls.

Figure 1.

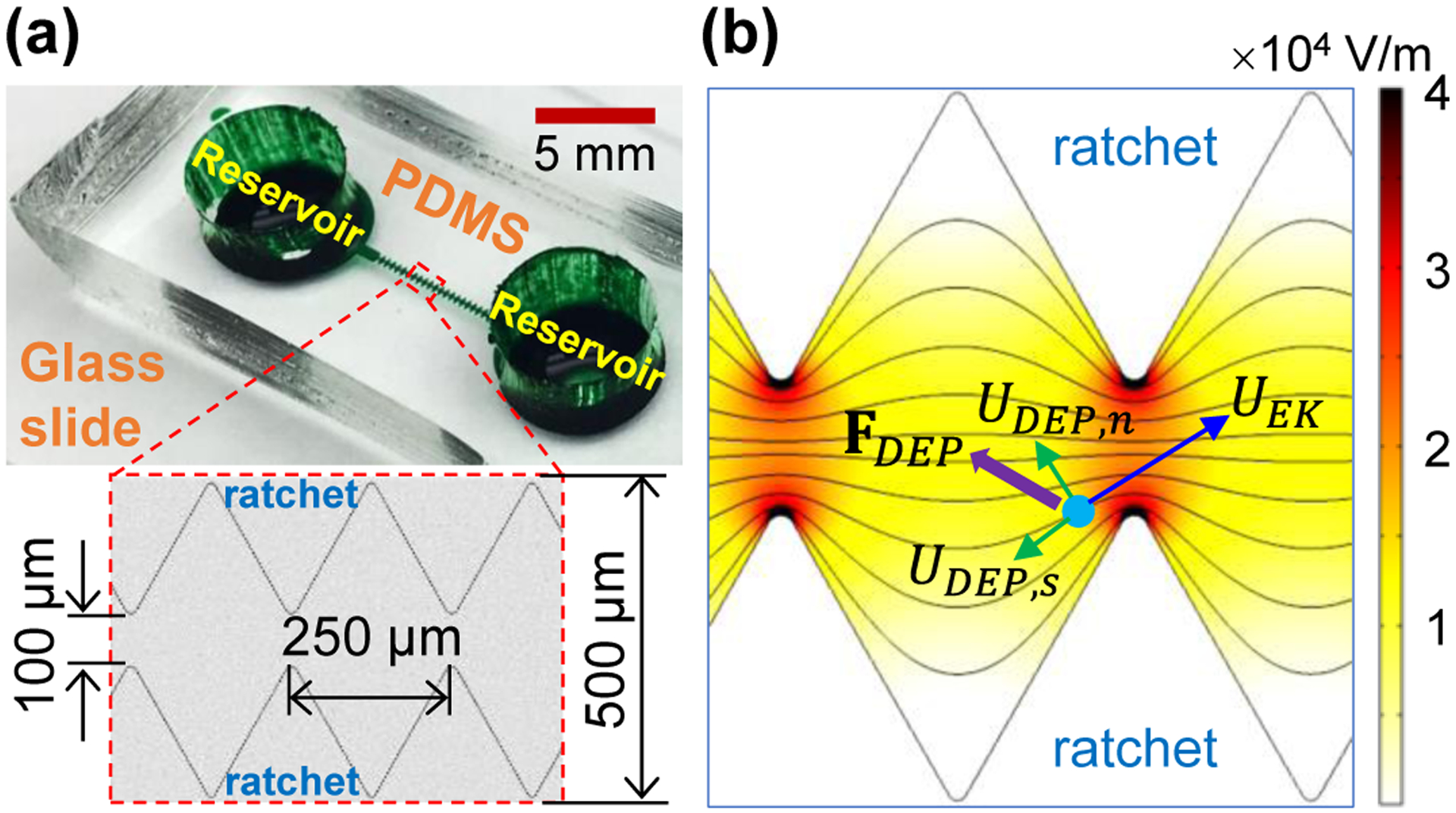
AC iDEP focusing of particles in a ratchet microchannel: (a) Picture of the microchannel (filled with green dye for visual clarity), where the inset shows the dimensions of each ratchet; (b) Illustration of the particle focusing mechanism, where F_DEP is the dielectrophoretic force induced by the electric field gradients (see the contour under an applied 100 V AC voltage, the darker color the larger magnitude) around the insulating ratchets, U_DEP,s is the stream-wise dielectrophoretic particle velocity, and U_DEP,n is the cross-stream dielectrophoretic particle velocity that competes with the electrokinetic particle velocity, U_EK (dominant over U_DEP,s in this work) for a focusing effect. The background lines shows the electric field lines or equivalently the fluid streamlines.

Immediately before experiment, the liquid heights in the two reservoirs were carefully balanced to remove the pressure-driven flow. AC electric voltage was supplied by a function generator (Agilent Technologies, Santa Clara, CA, USA) in conjunction with a high-voltage amplifier (Trek, Lockport, NY, USA). It was imposed upon the platinum electrode inserted into the liquid in one reservoir while the other electrode was grounded. The frequency and magnitude of the AC voltage were each varied to study their respective effects. The particle or cell motion was visualized in the middle of the microchannel via a CCD Camera (Nikon DS-Qi1Mc, Nikon Instruments) attached to an inverted microscope (Nikon Eclipse TE2000U). Images were recorded at a rate of 15 frames per second and post-processed in the Nikon imaging software (NIS-Elements AR 2.30). The data in the plot for probability density function (PDF) of particles were extracted from the digital images using the ImageJ software (National Institute of Health), which illustrate the particle distribution in the channel width direction or equivalently the particle focusing effect. The electrokinetic velocity for each type of particles under an applied small DC electric field was measured in the ratchet-free region, where particle DEP vanishes. It was then used to determine the electrokinetic particle mobility, μ_EK, i.e., electrokinetic velocity per unit DC electric field, which was found to remain at 1.8×10⁻⁸ m²/(V·s) for all the three types particles in our test.

Theoretical Analysis

Owing to the insulating nature, the ratchets in the microchannel create electric field gradients around them (see the contour of electric field in Figure 1b; the darker color the larger magnitude), leading to a dielectrophoretic force, F_DEP, acting on the suspended particle or cell,¹⁷

$$F_{DEP}=-\frac{1}{8}\pi d^3\epsilon \nabla E^2$$ (1)

where d is the diameter of the assumed spherical particle or cell, ε is the fluid permittivity, and E is the root-mean-square electric field. Note that we have set the so-called Clausius-Mossotti factor to −0.5 because the electric conductivity of microscale particles or cells is much smaller than that of the suspending buffer solution.³⁵ Therefore, F_DEP directs the particle or cell toward the lower electric field region, i.e., away from the tip of each ratchet in all directions of the horizontal plane. Considering that the electric field lines (see the background lines in Figure 1b) are equivalent to the fluid streamlines in pure electrokinetic flows,⁵⁶ we may conveniently break down the resulting dielectrophoretic particle velocity, U_DEP, in the streamline coordinates,¹⁷

$$U_{DEP}=U_{DEP,s}\widehat{s}+U_{DEP,n}\widehat{n}=-{\mu }_{DEP}\left(\frac{\partial E^2}{\partial s}\widehat{s}+2\frac{E^2}{\Re }\widehat{n}\right)$$ (2)

$${\mu }_{DEP}=\frac{d^2\epsilon }{24\eta }$$ (3)

where U_DEP,s is the dielectrophoretic velocity component in the streamline direction with the unit vector ŝ, U_DEP,n is that normal to the streamline direction with the unit vector $\widehat{n}$, μ_DEP is the dielectrophoretic particle mobility with η being the fluid viscosity, and ℜ is the radius of curvature of the electric field line. Note that the negative sign on the most right hand side of Eq. (2), as well as Eq. (1), indicates a negative DEP.

As viewed from the particle velocity analysis in Figure 1b, the streamwise particle velocity is the addition of U_DEP,s and electrokinetic particle velocity, U_EK, where the latter dominates the former motion in this work. It is because only small electric fields are needed to achieve the AC iDEP focusing of particles and cells, wherein no particle or cell trapping^57–59 occurs. Note that U_EK is a combination of fluid electroosmosis and particle electrophoresis given by U_EK = μ_EK E = ε (ζ_p − ζ_w) E/η under the approximation of thin electric double layer, where ζ_p and ζ_w are the particle and wall zeta potentials, respectively.¹⁹ The cross-stream particle velocity, U_DEP,n, points toward the centerline of the ratchet microchannel, which competes with the streamwise particle velocity within each period of ratchets yielding a focusing effect. The effectiveness of such an iDEP focusing under an applied low-frequency AC voltage may be evaluated by a dimensionless focusing number, which, as shown in the equation below, reflects both the focusing effectiveness within one ratchet period in terms of the particle velocity ratio¹⁷ and the number of ratchets that particles or cells can pass through within one half period of the AC voltage application,

$$\beta =\frac{\left|U_{DEP,n}\right|}{U_{EK}}\cdot \frac{\frac{1}{2f}{U}_{EK}}{T}=\frac{\left|U_{DEP,n}\right|}{2fT}=\frac{\epsilon }{24\eta }\cdot \frac{1}{T\Re }\cdot d^2\cdot \frac{E^2}{f}$$ (4)

where T is the spatial period of the ratchets, and the four terms on the most right hand side represent the parameters associated with the fluid, microchannel, particle, and electric field, respectively. This focusing number, β, exhibits a quadratic dependence on both the particle diameter and the applied AC electric field (or equivalently the AC voltage). It is also an inverse function of the AC voltage frequency. Note that a greater value of β indicates a stronger particle focusing effect.

Numerical Simulation

We developed a 2D numerical model in COMSOL^® (Multiphysics 5.5) to track the motion of particles and simulate the AC iDEP focusing process in a ratchet microchannel. This model needs only the electric field in the fluid domain to calculate the particle velocity for tracing, which has been validated through comparison with experiment in our previous studies.^41,43 Briefly, the electric field is solved from the Laplace equation using the “Electric Currents (ec)” module,

$${\nabla }^2\varphi =0$$ (5)

where ϕ is the electric potential satisfying E = −∇ϕ, and is imposed with the time-varying AC voltage in one reservoir and 0 in the other. The microchannel and reservoir walls are electrically insulating. The particle motion was predicted using the “Particle Tracing (pts)” module with the particle velocity, U_P, being a vector addition of the electrokinetic and dielectrophoretic components,

$$U_P=U_{EK}+U_{DEP}={\mu }_{EK}E+\lambda {\mu }_{DEP}\nabla E^2$$ (6)

where μ_EK is the electrokinetic mobility and was determined experimentally as noted above, and λ is the correction factor introduced for the particle size effect on DEP since its disturbance to the electric field is not considered in the model.⁶⁰ The value of λ was set to 0.6, 0.7 and 0.8 for 3, 5, and 10 μm-diameter particles, respectively, with which the predicted particle trajectories were found to match the experimental observations. The dielectrophoretic mobility of particles, μ_DEP, was calculated from Eq. (3). The fluid viscosity and permittivity were both assumed equal to the values of water at room temperature. One hundred particles were considered in the model, and their initial positions in the middle four ratchet periods were randomly chosen using the built-in function generator. Note that our model considers the transient electrokinetic and dielectrophoretic motions of particles because of the time varying E in Eq. (6).

RESULTS AND DISCUSSION

Demonstration of Particle Focusing

Figure 2a shows the top-view images of 5 μm diameter particles in the middle of the ratchet microchannel (specifically, the 10^th and 11^th ratchets) under an applied 100 V AC voltage with a 0.1 Hz square wave. The corresponding AC electric field is 125 V/cm on average over the 0.8 cm long microchannel. We also tested the more common sine wave AC voltage as well as other less common wave forms (e.g., saw wave) (data not shown), among which the square wave was found to yield minimal particle pearl chaining effect. This may be attributed to the added particle acceleration and deceleration under a non-square wave AC voltage (whose direction and magnitude both change periodically) to those caused by the ratchets alone. Initially, particles are scattered throughout the microchannel with random positions. Once the AC voltage is applied, they start traveling through the ratchets in one direction while being pushed away from the ratchet tips by the iDEP force until the AC voltage switches its sign. After that moment, all particles reverse their motion to travel back through the ratchets they have just passed while the iDEP force remains in the same direction to direct particles toward the channel centerline. This AC iDEP focusing process is repeated periodically, such that most of the particles migrate into the central part of the channel after being exposed to the AC electric field for 15 s. After another 15 s, all particles flow in a tight stream along the channel centerline. They appear to move in a single file at 60 s as seen from the image in Figure 2a. The experimentally observed time development for the AC iDEP focusing of particles is reasonably simulated by our 2D numerical model.

Figure 2.

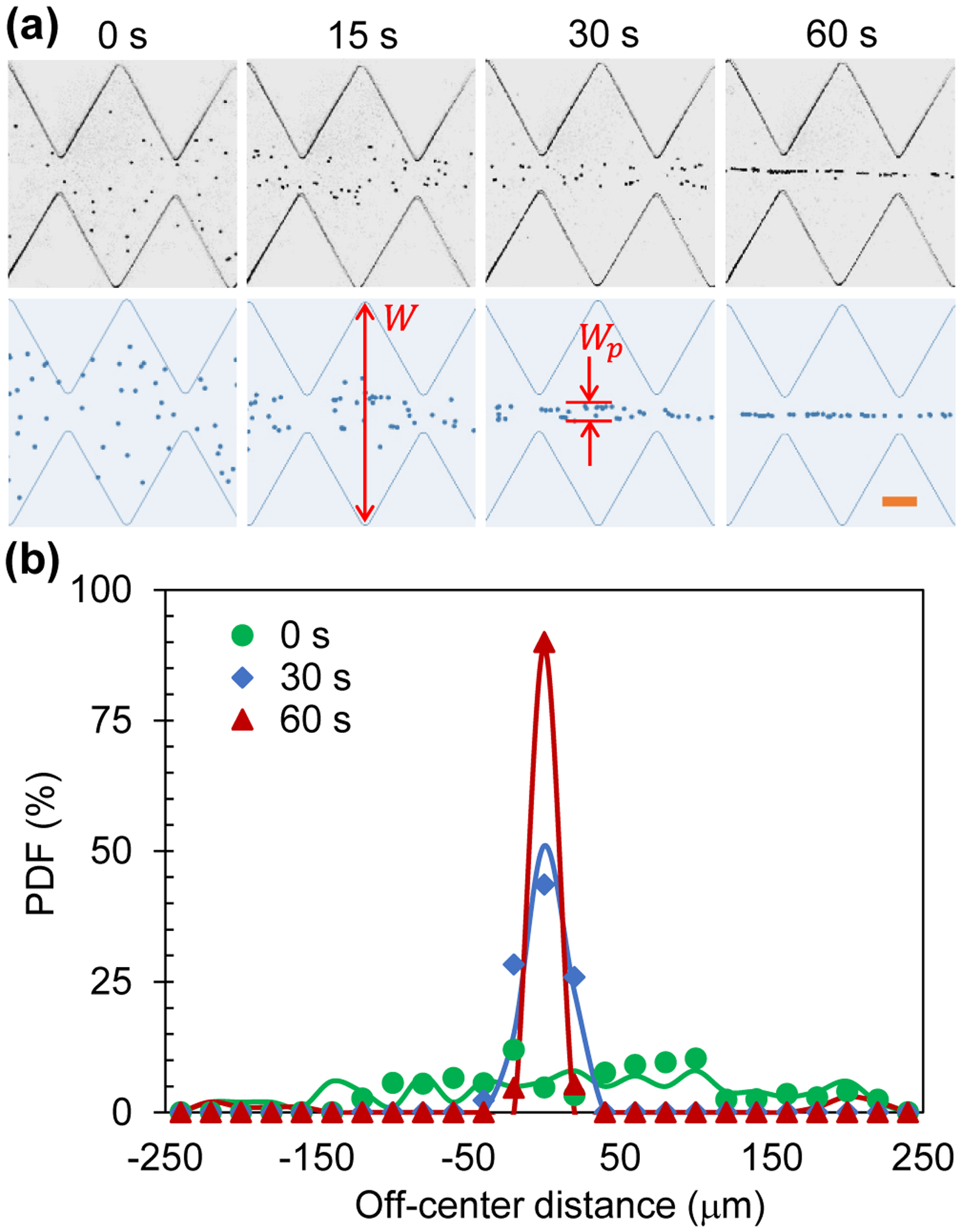
AC iDEP focusing of 5 μm diameter particles under an applied 100 V AC voltage with a 0.1 Hz square wave: (a) Comparison of experimentally (upper row) and numerically (lower row) obtained particle images at varying time instants after the voltage application; (b) Comparison of experimentally (symbols) and numerically (lines) obtained particle PDF plots across the microchannel width. The highlighted dimensions, W and W_p, on the numerical images in (a) denote the widths of the microchannel and focused particle stream, respectively, which are used to determine the focusing ratio in Eq. (7). The scale bar on the lower-right image in (a) represents 100 μm.

It is important to note that the observed particle patterns at different time instants in Figure 2a actually remain unvaried throughout the ratchet region. In other words, our proposed AC iDEP focusing technique is essentially independent of the channel length and develops with time only. It is a result of the continuous action of the electric field direction-independent dielectrophoretic force on the suspended particles or cells in an electrokinetically oscillating fluid. Figure 2b shows the experimentally and numerically obtained PDF plots for particles across the width of the microchannel at 0, 30 and 60 s of the test. A good agreement is seen at all three tested time instants. We observe a Gaussian distribution for the focused particle stream, whose standard deviation decreases as time evolves. To evaluate the AC iDEP focusing of particles, we define a dimensionless focusing ratio,

$$\text{focusing ratio}=\frac{W}{W_p}$$ (7)

where W = 500 μm is the main width of the ratchet microchannel, and W_p is the stream width that contains at least 90% of the particles that travel through the measuring place within one period of the voltage application (see the highlighted dimensions on the numerical images in Figure 2a). The obtained focusing ratio is roughly 30 for 5 μm particles in both the experiment and simulation at 60 s after the AC voltage application.

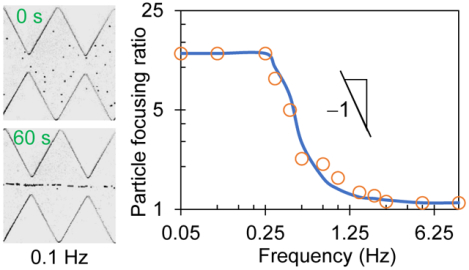
Effect of AC Voltage Frequency

Figure 3a compares the experimental and numerical images of 5 μm diameter particles in the ratchet microchannel 30 s after the application of a 100 V square-wave AC voltage, where a visual consistency is seen for all four illustrated frequencies. Interestingly, the AC iDEP focusing effect is visually comparable between the 0.05 Hz and 0.25 Hz cases, which also shows a similarity to the 0.1 Hz case at 30 s in Figure 2a. It, however, gets apparently weaker at 0.4 Hz and becomes even worse at 1 Hz. Figure 3b shows the experimentally and numerically determined particle focusing ratios against the AC voltage frequency in a log-log space. The spectrum indicates the existence of both a low, f_low ≈ 0.25 Hz, and a high frequency threshold, f_high ≈ 1.25 Hz, which may be explained as follows. The high-frequency threshold corresponds to the situation, where even the particle that travels along the channel centerline with the shortest distance is barely able to complete one half spatial period of the ratchets within one half (time) period of the AC voltage application (see the inset of Figure 3b), i.e.,

$$\frac{U_{p\_\mathit{\text{center}}}}{f}\le T$$ (8)

The computed average electric field along the centerline of the ratchet region is E_{r_center} = 160 V/cm, which, as expected, is higher than that over the entire channel length with E = 125 V/cm. Neglecting the influence of the streamwise dielectrophoretic velocity, we estimate the velocity in Eq. (8) as, U_{p_center} ≈ U_{EK_center} = μ_EK E_{r_center} = 288 μm/s for the particle travelling along the channel centerline. Referring to the special period of ratchets, T = 250 μm, gives f ≥ 1.15 Hz, which closely matches the observed high-frequency threshold, f_high ≈ 1.25 Hz, in Figure 3b. No significant AC iDEP focusing of particles can be achieved for f > f_high.

Figure 3.

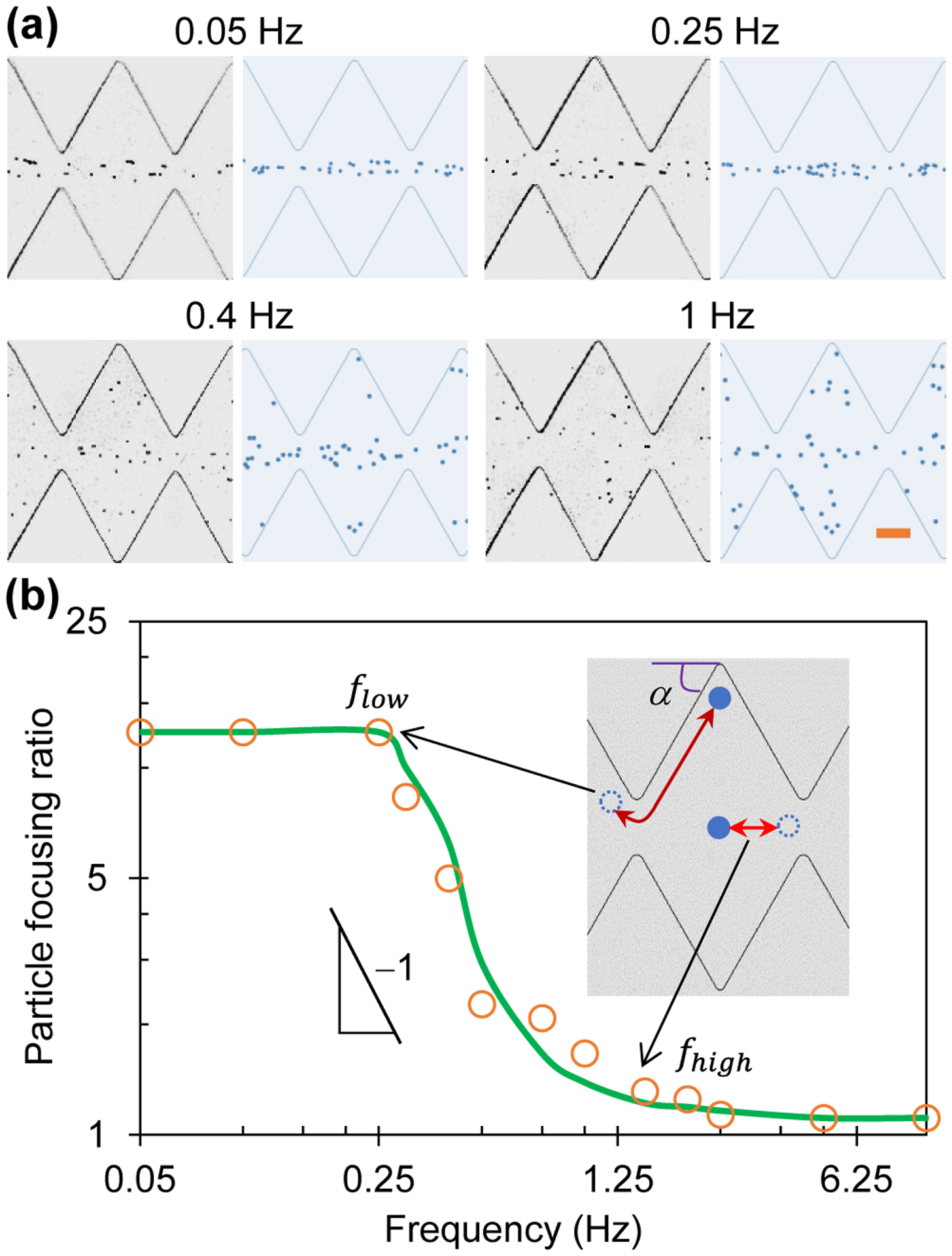
Frequency effect on AC iDEP focusing of 5 μm diameter particles under an applied 100 V AC voltage with a square wave: (a) Comparison of experimental (left) and numerical (right) images 30 s after the application of AC voltages at four different frequencies; (b) Comparison of experimentally (symbols) and numerically (line) determined focusing ratios in a range of AC voltage frequencies in the log-log space, which exhibit a linear relationship in the regime f_low ≤ f ≤ f_high with a slope of −1 indicating a reciprocal dependence. The inset illustrates the situations for the low, f_low, and high-frequency, f_high, thresholds, respectively. The scale bar on the lower-right image in (a) represents 100 μm.

In contrast, the low-frequency threshold corresponds to the situation, where even the particle that travels adjacent to a channel sidewall with the longest distance is able to complete one half spatial period of the ratchets within one half (time) period of the AC voltage application (see the inset of Figure 3b), i.e.,

$$\frac{T}{cos\left(\alpha \right)}\le \frac{U_{p\_\mathit{\text{wall}}}}{f}$$ (9)

where α is the angle of the ratchet edge with respect to the channel wall. Considering the average electric field in the near-wall region from the base to tip of a ratchet is only about half of that along the channel centerline in the ratchet region, we estimate the locally average particle velocity as, U_{p_wall} ≈ 0.5U_{EK_center} = 144 μm/s. Referring to tan(α) = 200/125 = 1.6 and hence cos(α) = 0.53 yields f ≤ 0.30 Hz, which agrees well with the observed low-frequency threshold, f_low ≈ 0.25 Hz, in Figure 3b. No further enhancement in the AC iDEP focusing of particles can be achieved for f < f_low because the iDEP effect remains identical among all the ratchets. In other words, the AC iDEP focusing effect should not depend on if the particles are oscillating through single or multiple ratchets within one period of the AC voltage application. For the AC voltage frequency that satisfies f_low ≤ f ≤ f_high, the defined particle focusing number, β, in Eq. (4) has the form of a reciprocal function with respect to the frequency. This analysis is supported by the experimentally and numerically obtained particle focusing ratios in Figure 3b that both exhibit a linear trendline in the log-log space with a slope of −1.

Effect of AC Voltage Amplitude

Figure 4a compares the experimental and numerical images of 5 μm diameter particles in the ratchet microchannel 30 s after the application of 50 V and 150 V square-wave AC voltages, respectively. A good agreement is viewed for both cases. Consistent with the prediction of the particle focusing number in Eq. (4), the AC iDEP focusing effect increases significantly with the increase of the voltage amplitude (see also the 100 V case at 30 s in Figure 2a). A tight focusing of 5 μm particles has been achieved after only 30 s application of the 150 V AC voltage. Figure 4b shows the experimentally and numerically determined particle focusing ratios against the AC voltage amplitude, which exhibits a linear relationship in the log-log space. This trendline indicates that the particle focusing ratio is a quadratic function of the applied AC electric field, which is consistent with the prediction of the defined AC iDEP focusing number, β, in Eq. (4). This dependence is superior to the traditional DC iDEP focusing because the focusing number of the latter, i.e., |U_DEP,n|/U_EK in Eq. (4), is just a first-order function of the applied electric field magnitude.¹⁷ Therefore, our proposed AC iDEP focusing technique can save not only space (and hence the reduced fabrication cost) but also electric power (and hence the reduced Joule heating effects⁶¹).

Figure 4.

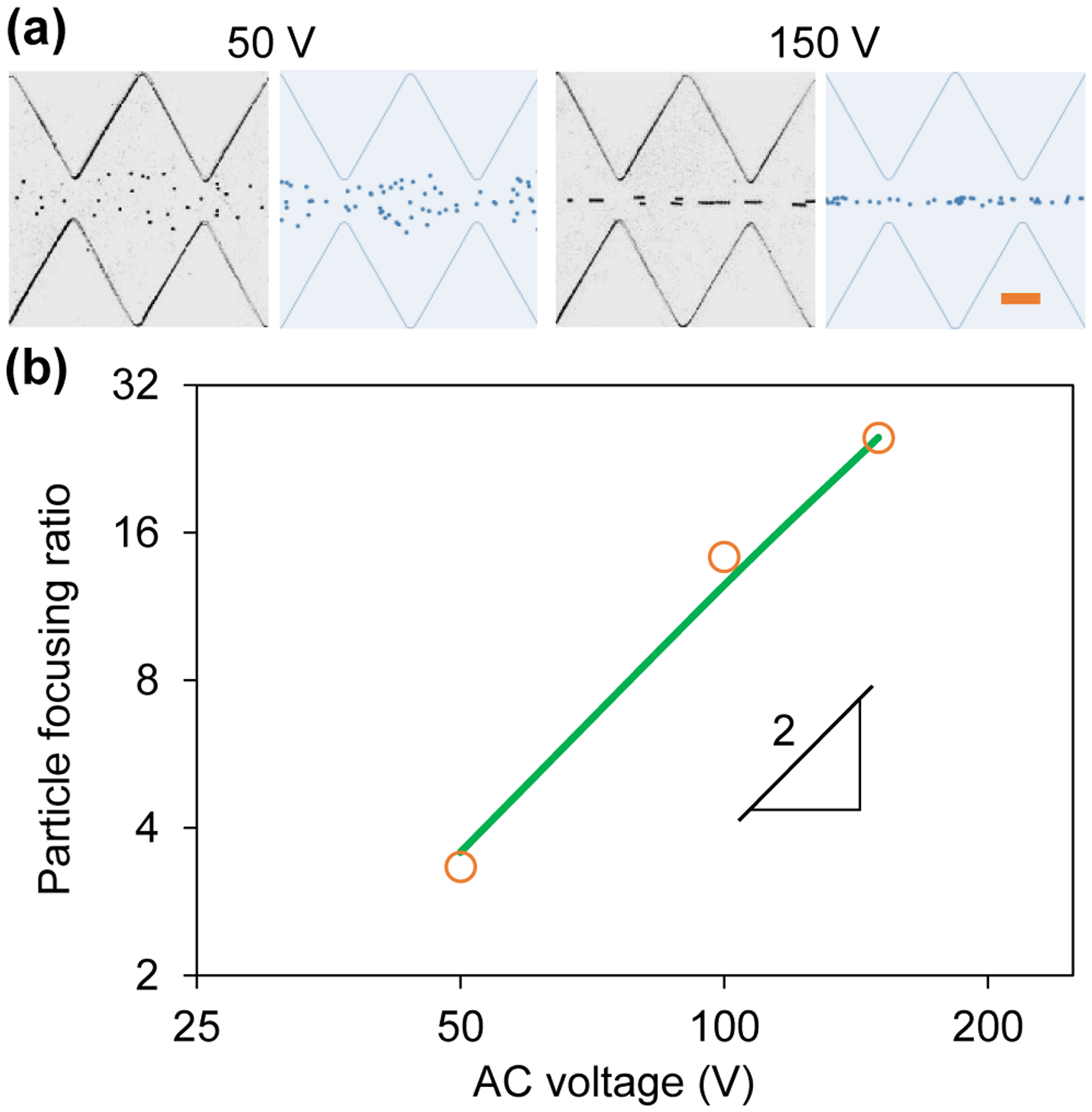
Amplitude effect on AC iDEP focusing of 5 μm diameter particles under varying AC voltages with a 0.1 Hz square wave: (a) Comparison of experimental (left) and numerical (right) images 30 s after the application of 50 V and 150 V voltages; (b) Comparison of experimentally (symbols) and numerically (line) determined focusing ratios vs. AC voltage amplitude, which exhibits a linear relationship in the log-log space with a slope of 2 indicating a quadratic dependence. The scale bar on the right-most image in (a) represents 100 μm.

Effect of Particle Size

Figure 5a compares the experimental and numerical images of 3 μm and 10 μm diameter particles in the ratchet microchannel 30 s after the application of a 100 V AC voltage with a 0.1 Hz square wave. We see a good agreement in both cases. As predicted from the focusing number in Eq. (4), the AC iDEP focusing of particles gets apparently stronger for larger particles (see also the images for 5 μm particles at 30 s in Figure 2a). An almost single-line focusing is achieved for 10 μm particles while 3 μm ones are still scattered over the narrow section in between the opposing ratchet tips. Figure 5b shows the experimentally and numerically determined particle focusing ratios against the particle diameter, which, similar to the voltage amplitude effect in Figure 4b, also exhibits a linear relationship in the log-log space. Therefore, the AC iDEP focusing ratio is a quadratic function of the particle diameter, which agrees with the prediction of the defined focusing number in Eq. (4). We note that the AC and DC iDEP focusing effects both show a second-order dependence on the particle size. This is because DEP, whose direction is independent of that of the applied electric field (i.e., regardless of AC or DC field), is the only motion in both techniques that varies with the particle size [see Eq. (1)].

Figure 5.

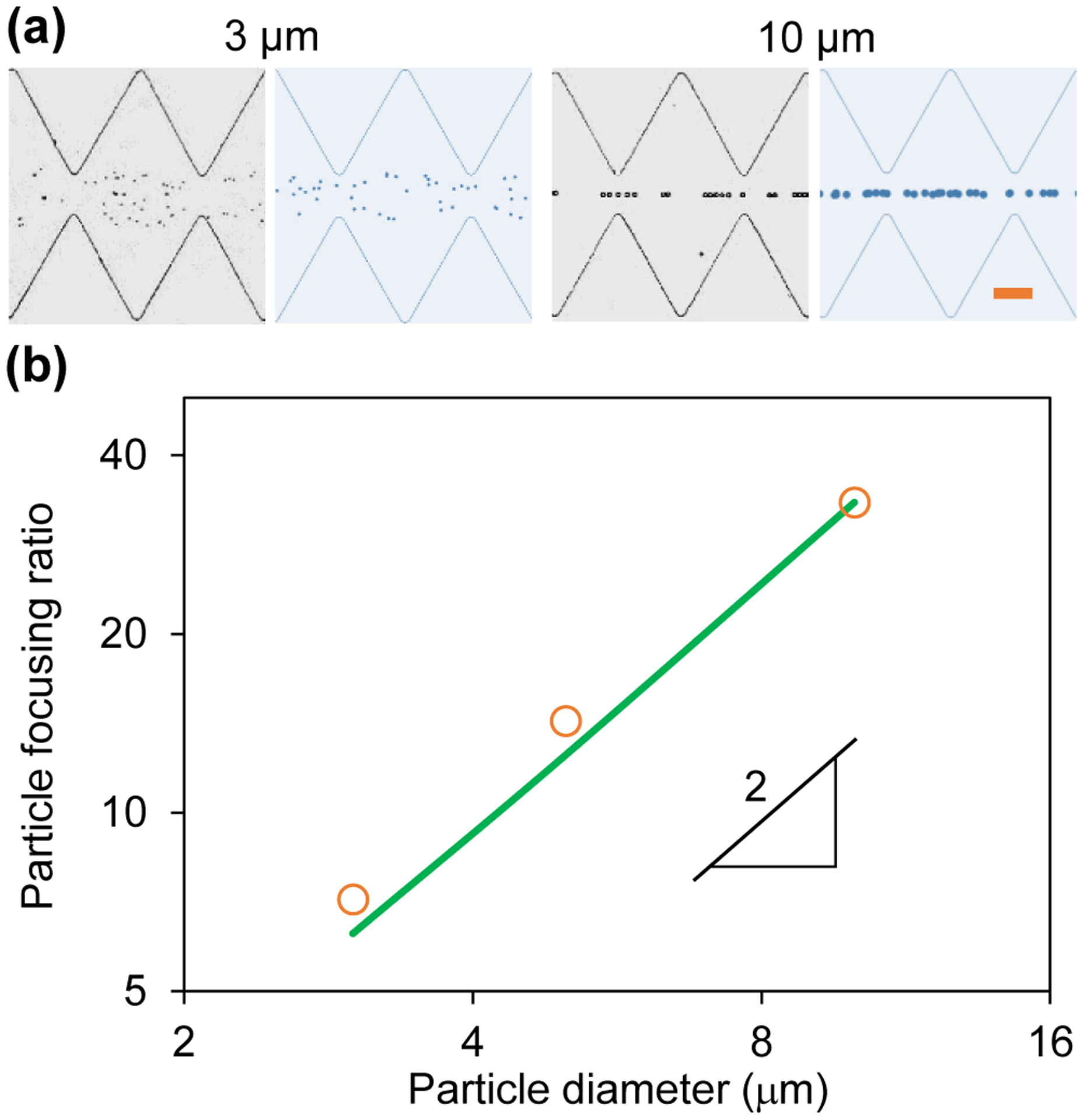
Particle size effect on AC iDEP focusing under an applied 100 V AC voltage with a 0.1 Hz square wave: (a) Comparison of experimental (left) and numerical (right) images of 3 μm and 10 μm diameter particles 30 s after the voltage application; (b) Comparison of experimentally (symbols) and numerically (line) determined focusing ratios vs. particle diameter, which exhibits a linear relationship in the log-log space with a slope of 2 indicating a quadratic dependence. The scale bar on the right-most image in (a) represents 100 μm.

Application to Cell Focusing

The potential for biological applications of our proposed AC iDEP focusing technique is demonstrated through the use of yeast cells in the same ratchet microchannel as for the particles in the above tests. Figure 6 shows the top-view snapshot images of cells at different time instants after the application of a 100 V AC voltage with a 0.1 Hz square wave. Similar to the observation of 5 μm polystyrene particles in Figure 2a, the AC iDEP focusing of yeast cells with an average diameter of 7 μm also shows an increasing effect with a longer exposure time to the AC voltage. It, is however, not visually as good as that of 5 μm particles because yeast cells have a much larger size deviation (the smallest diameter can be only 3 μm) than the particles. The electric current was monitored and no visible increase was noticed during the test, indicating minimal Joule heating effects under the experimental conditions.⁶¹ We further did a viability test for the cells collected after the focusing experiment using trypan blue. Similar to our previously studied DC iDEP focusing of yeast cells in the same ratchet microchannel as in this work,⁴³ more than 95% of the cells were found still alive after the experiment.

Figure 6.

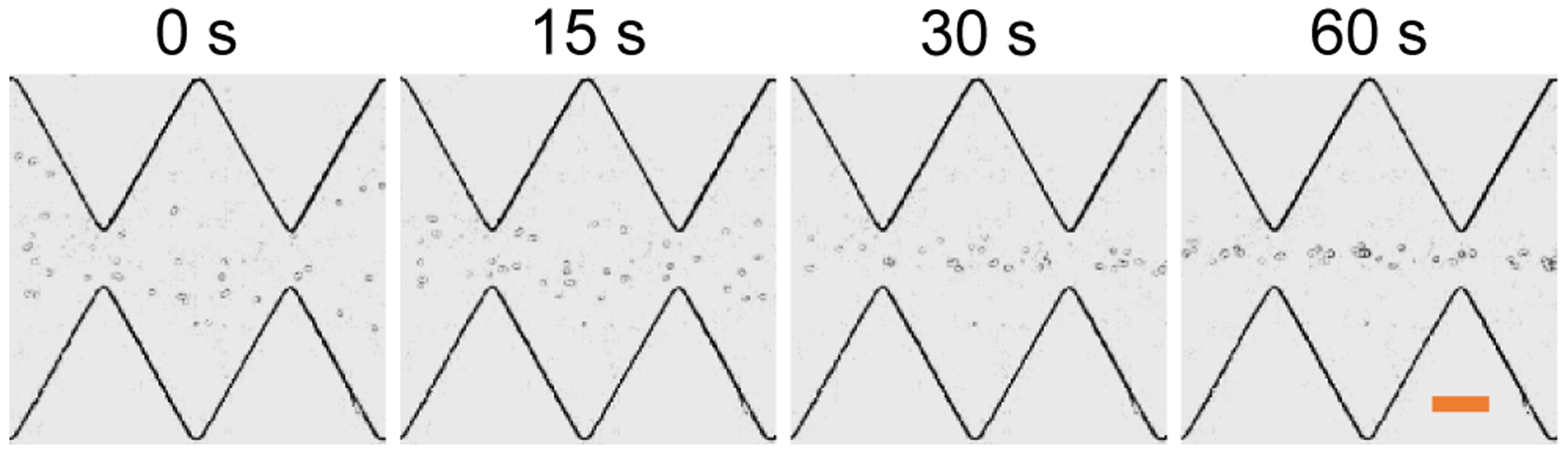
Demonstration of AC iDEP focusing of yeast cells in the ratchet microchannel under an applied AC voltage of 100 V with a 0.1 Hz square wave. The scale bar on the right-most image represents 100 μm.

CONCLUSIONS

We have developed a low-frequency AC iDEP technique that sacrifices time to gain a virtually “infinite” channel length for particle and cell focusing under a small electric field. The effects of the AC voltage frequency and amplitude as well as particle size on the AC iDEP focusing of particles are studied experimentally in a ratchet microchannel. The obtained particle focusing ratios in each of these parametric studies match the predictions of a 2D numerical simulation. Moreover, we have defined a dimensionless focusing number based upon a theoretical analysis, which is found to predict correctly the observed dependences of the particle focusing ratio on the three tested parameters. In particular, we demonstrate that the effectiveness of the proposed AC iDEP focusing is a quadratic function of the applied electric field magnitude, in contrast to the first order dependence of the traditional DC iDEP focusing. This feature along with the “infinite” channel length may enable the AC iDEP focusing of nanoparticles for applications like nanoscale flow cytometry.^62,63 Moreover, as the low and high-frequency thresholds both increase under a larger electric field for a smaller ratchet structure, we envision the proposed AC iDEP focusing technique can be potentially driven by a 50 Hz utility power and hence be used in resource-limited settings.