Bio-inspired Haptic Feedback for Artificial Palpation in Robotic Surgery

Abstract

Adding haptic feedback has been reported to improve the outcome of minimally invasive robotic surgery. In this study, we seek to determine whether an algorithm based on simulating responses of a cutaneous afferent population can be implemented to improve the performance of presenting haptic feedback for robot-assisted surgery. We propose a bio-inspired controlling model to present vibration and force feedback to help surgeons localize underlying structures in phantom tissue. A single pair of actuators was controlled by outputs of a model of a population of cutaneous afferents based on the pressure signal from a single sensor embedded in surgical forceps. We recruited 25 subjects including 10 expert surgeons to evaluate the performance of the bio-inspired controlling model in an artificial palpation task using the da Vinci surgical robot. Among the control methods tested, the bio-inspired system was unique in allowing both novices and experts to easily identify the locations of all classes of tumors and did so with reduced contact force and tumor contact time. This work demonstrates the utility of our bio-inspired multi-modal feedback system, which resulted in superior performance for both novice and professional users, in comparison to a traditional linear and the existing piecewise discrete algorithms of haptic feedback.

I. Introduction

The original aims of Robotic Minimally Invasive Surgery were to address some of the shortcomings of traditional Minimally Invasive Surgery tools with improved depth perception, dexterity, and a reduction of hand tremors [1]. In comparison to endoscopic or laparoscopic techniques, however, robotic surgical systems suffered from a complete loss of haptic feedback to the user [2]. Consequently, surgeons relied on visual cues and their experience in order to perform the accurate motor movements required for operations [3]. In inexperienced hands, the absence of haptic feedback has resulted in prolonged procedural times and a greater risk for surgical error [4]. Furthermore, studies have found that even considering professional robotic-surgeons, a partial presentation of haptic feedback decreased the number of errors during blunt dissection tasks [5] and reduced the frequency of intraoperative tissue damage. During open surgery, abnormal tissue (e.g., tumor or inflamed soft tissue) is detected by its different mechanical properties compared to the surrounding normal tissue [6]. Some of these differences (e.g., texture, stiffness, and compliance) are not easily detectable through vision and require a surgeon’s touch [7]. Appropriate tactile and kinesthetic feedback, which enables the rapid and precise localization of anatomical structures buried under tissue (e.g., a mesentery vessel or the ureter), thus serves a critical role in reducing injury to delicate neighboring structures [8]. One approach to identify abnormal tissue has been to use a sophisticated sensor system with a graphic output, that allows the user to visually identify properties of the tissue [9]. We aim, instead, to provide haptic feedback to the user, with an ultimate goal of having the surgeon feel the tissue.

Haptic feedback systems for robotic surgery consist of two key components: sensors and actuators. Sensors detect forces applied to tissue by surgical instruments while actuators relay signal detected by sensors to the surgeon’s fingertips. Current actuators can only provide simple feedback such as vibration and static pressure, which is often different from the signal detected by sensor. How to convert the sensor data to best control the actuator is an important design factor that has not been adequately considered. The most basic approach is a simple linear function. Such linear control algorithms are easily implemented and provide surgeons with a sense of artificial force feedback [10], [11]. In our previous work, we have utilized piecewise discrete control systems, which quantize pressure output and make jumps in force more noticeable to the user [12], [13]. However, the perception produced by an actuator using a linear control method or our piecewise discrete method may not be consistent with the perception corresponding to the stimulus signal detected by the sensor. That is, the sample feedback method does not replicate the natural sense of touch. On the other hand, if we can build an accurate model replicating the perception of the stimulus as detected by the sensor, then we can better reproduce the natural haptic perception.

A natural haptic feedback system should be designed to encode tactile information in a similar fashion to the nervous system. Findings from neurophysiological experiments suggest that mechanosensory information regarding edge orientation [14], shape [15], [16], roughness [17], and texture [18], are encoded in the firing patterns of cutaneous afferent population responses (CAPR) in the peripheral nervous system. In humans, there are 3 types of cutaneous afferent neurons involved in encoding these stimuli: slowly adapting type 1 (SA1), rapidly adapting type 1 (RA1), and Pacinian corpuscles (PC) and each of these plays a different role in tactile perception [19]. Here, we take advantage of the fact that SA1 afferents uniquely respond to static pressure, such as that provided by our pneumatic actuator, and RA1 and PC afferents preferentially respond to dynamic changes, which can be mimicked by our vibration actuator. We hypothesized that if we can convert the information from a sensor to the two classes of actuators in a way consistent with the way the information is parsed in the skin, then performance should be superior to that when utilizing previous control functions. Indeed, implementing a CAPR model in a prosthesis has achieved a better outcome than traditional controlling methods [20].

In this paper, we designed a bio-inspired controlling algorithm using a CAPR model to present haptic feedback for robotic surgery. In this bio-inspired haptic feedback algorithm, the actuators are not controlled linearly by the detected signal but by the perceived intensity of the afferent populations, as predicted by the CAPR model. We utilized a single sensor and a single pair of actuators to test our hypothesis and compared the performance of our bio-inspired control algorithm to performance with no haptic feedback (i.e., visual feedback alone), piecewise discrete haptic feedback and linear haptic feedback control methods. We recruited novice subjects and expert surgeons to perform a psychophysical experiment to evaluate the efficacy of this feedback in improving the ability to quickly localize underlying structures in a tissue phantom. The experiment was aimed to test whether the bio-inspired controlling method would allow subjects to have better localizing accuracy and applied force than the other two haptic feedback algorithms and when no haptic feedback was provided.

II. Methods

We will first describe the current haptic feedback system and two previous haptic feedback algorithms. Then we will describe our controlling method using a CAPR model. We will finish by describing the psychophysical experiment we used to test subjects’ performance using the different controlling methods.

The current haptic feedback system, which was designed by CASIT at UCLA, consists of a haptic sensor, haptic controller, haptic driver, and haptic actuators as illustrated in Fig. 1a [7]. A single haptic sensor is used to encode the overall contact force. The sensor was calibrated before installation on the surgical instrument. The fitted curve of pressure changes as a function of AD value is shown in Fig 1b. [21]. The sensor data in the controller was updated at a rate near 50 Hz. The controller sent commands through Wi-Fi to the haptic driver in order to activate the haptic actuators (a pneumatic balloon and vibration motor).

Fig. 1.

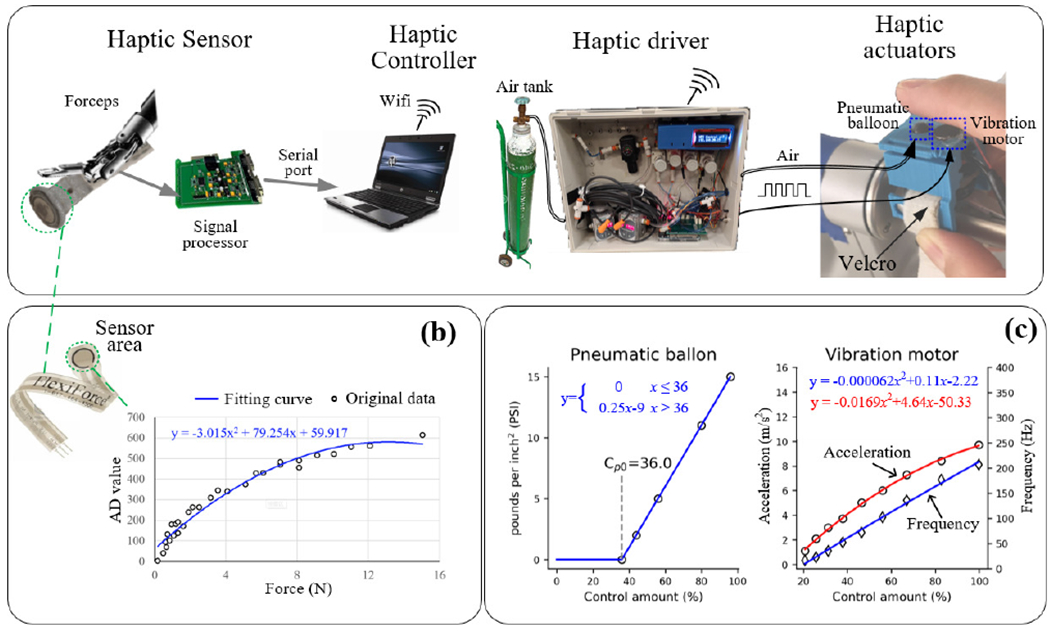
Block diagram of the hardware of haptic feedback system for the surgical robot. (b) Output characteristics of haptic sensor (FlexiForce A201 force) detected by 10-bit AD converter. (c) Output characteristics of pneumatic balloon (left) and vibration motor (right) under different controlling amounts.

The pneumatic ballon actuator was made at UCLA, using a well established method [22]. The maximum pressure of the pneumatic ballon was set to 20 PSI using the regulator installed on the air tank. The pressure produced by the pneumatic ballon as a function of the control amount (as controlled by a solenoid valve array) is shown in Fig. 1c left [21]. For the vibration actuator, we used an 8 mm Uxcell coin vibration motor, as used in reference [23]. For this particular actuator, the vibration amplitude and frequency cannot be modulated independently: both increase as function of the driving voltage (PWM duty) as shown in Fig 1c right. The control amounts for the pneumatic balloon and vibration motor (c_p, c_v) are the proportion of opening solenoid valve and the duty of PWM respectively, thus they can represented as variables ranging from 0 to 100.

In order to recreate a natural sense of touch through the current hardware, we aimed to control the pneumatic balloon and vibration motor in a way that was the equivalent to the human tactile signals coming from the sorts of afferents that encode the sensory stimuli. Importantly, we wanted to compare this to controlling algorithms currently used in the literature: a piecewise discrete algorithm and a linear algorithm. An algorithm previously designed by CASIT at UCLA for the haptic feedback system adopted a piecewise discrete control strategy in which the sensor value was classified into several ranges for activating different actuators as shown in ref. [7], [21]. This algorithm was implemented because jumps in feedback pressure were more noticeable than a continuous gradient. The linear controlling algorithm we used converted the sensor signal linearly to the control amount of the actuator in its dynamic range, as illustrated in equation (1):

$$\text{c}=\frac{s-s_{min}}{s_{max}-s_{min}}\left(c_{max}-c_{min}\right)+c_{min}$$ (1)

Where s, c is the sensor value and control amount of each actuator respectively. Similar algorithms have been used in previous studies, including one in which non-linear data were intentionally linearized [10], [11].

A. Bio-inspired control model

The bio-inspired control model is illustrated in Fig 2. The aim of the CAPR model is to simulate the responses evoked in a population of cutaneous afferents to a given stimulus and to use the output of this model to activate the appropriate actuators. In this system, the pneumatic balloon mostly indicates the magnitude of the applied force, which is typically encoded by SAI afferents [12], while the vibration motor can be thought of as indicating the dynamic aspect of touch, which is encoded in the SA1, RA1 and PC afferents [15]. While it is possible that this could be modeled by simply sending the static component of the input to the balloon actuator and the dynamic component to the vibration motor, the model allows us to present output signals to the user’s skin optimized for the afferent population. It also gives us the potential to scale up to handle more sensors and actuators. The control model works as follows: we first run the CAPR model to generate the population activity of three afferent classes by inputting the pressure data from the sensing area, we then compute the perceived intensities from the population response activity and then substitute the intensities to the inverse function of the psychophysical data (as in Fig. 3) to control the two actuators. The code of the Bio-inspired feedback control model is available at the link: https://github.com/ouyangqq/Bioinspired_Haptic_Feedback_sys.

Fig. 2.

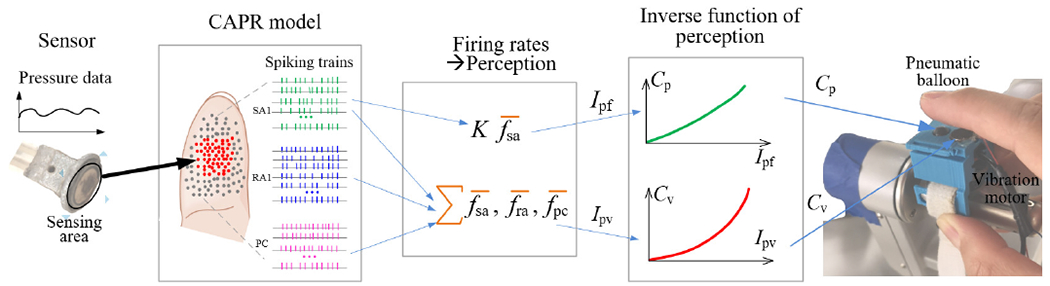
Schematic diagram of Bioinpired contrlling haptic feedback. A red dot and gray dot in the fingertip represents a activated and inactived afferent neuron respectively, the green, blue and purple tick trace represents the firing spiking trian of a SA1, RA1 and neuron respectively. f_sa, f_ra and f_pc is firing rate of a SA1, RA1 and PC neuron respectively, which is calculated as spike number per second in a spiking train. The orange symbol ”∑” respresents weightted summation. The orange symbol ”⁻” respresents operator of calculating the average firing rate over all afferent neurons of one type in the fingertip.

Fig. 3.

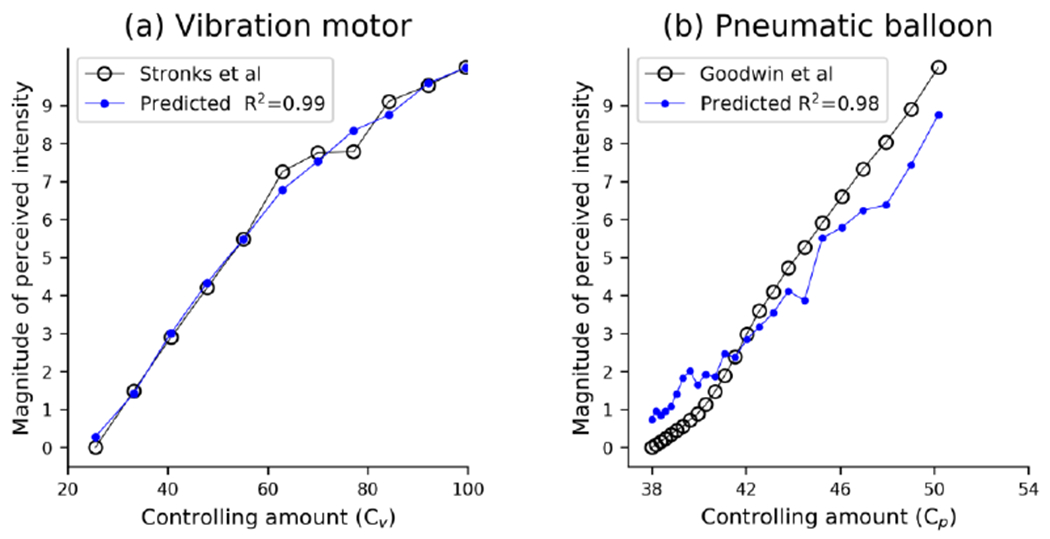
Perceived intensity predicted by our CAPR model and it estimated magnitude obtained in psychophysical experiment. (a) Predicted perceived intensity for motor. (b) Predicted perceived intensity for pneumatic ballon. In (a) and (b), black circles respresent psychophysical data about perceived intensities (adapted from ref. [24] and [23]).

1). Description of our previous CAPR model

The CAPR model adopted in the current work was presented previously [24] and is described only briefly here. The CAPR model was designed based on a resistance network, to mimic the distribution of pressure across the skin, and two-channel filters to separate out the static and dynamic components of skin indentation. These then describe the responses of populations of SA1, RA1 and PC afferents on fingertip [25].

The input to the CAPR model was pressure data detected by the sensor as illustrated in Fig 2. The output of the CAPR model is the firing rates of the 3 afferent types. The relationship between the firing rate of each afferent type and pressure is determined by following transfer function.

$$H_{(\text{s})}=\frac{f_r(\text{S})}{P(\text{S})}=\underset{\text{BPF}}{\underbrace{\frac{K_{b1}\cdot \frac{2\pi \cdot f_{\text{b}}}{Q}\cdot S+K_{b2}\cdot S^2}{S^2+\frac{2\pi \cdot f_{\text{b}}}{Q}\cdot S+4{\pi }^2\cdot f_{\text{b}}{}^2}\cdot \frac{2\pi \cdot f_{\text{b}}}{S+2\pi \cdot f_{\text{b}}}}}+\underset{\text{LPF}}{\underbrace{\frac{K_u\cdot 2\pi \cdot f_1}{S+2\pi \cdot f_1}}}$$ (2)

Where P and f_r is the pressure the output firing rate, S is the complex operator, f_b (Hz), Q and f₁ (Hz) are the center frequency of the band-pass filter (BPF), which carries the dynamic information, the quality factor of the BPF (band-passing filter) and the cutoff frequency of the low-pass filter (LPF), which carries the static pressure information. The full code of the CAPR model is available online at the following link: https://github.com/ouyangqq/model_tactile_pop_response/.

2). Modelling perception from firing rates outputted by CAPR model

Previous studies indicate that the perceived force is almost linearly related to the average firing rate of activated SA1 response [26]. The estimated magnitude of perceived intensity of static force (I_pf) is illustrated by equation (3):

$$I_{\text{pf}}=\frac{K_{\text{pf}}\cdot \overline{f_{sa}}}{10}$$ (3)

where K_pf is a proportion coefficient for normalizing perceived intensity of static force and $\overline{f_{sa}}$ is the average firing rate of the activated SA1 afferents.

Previous studies also indicate that the perceived vibration intensity is 97% accounted for by the average firing rate of activated afferent neurons located under or near the locus of stimulation, weighted by afferent type [27]. The estimated magnitude of perceived vibration intensity (I_pv) can be obtained via equation (3).

$$I_{\text{pv}}=\frac{K_{\text{pv}}\cdot \left(C_{s\text{a}}\overline{f_{sa}}+C_{\text{ra}}\overline{f_{ra}}+C_{\text{pc}}\overline{f_{pc}}\right)}{10}$$ (4)

where K_pv is a proportion coefficient for normalizing perceived intensity of vibration. C_sa1, C_ra, C_pc are the weights for each afferent type, which were set to 0.29, 0.36, 0.46 referring to study [27]. In equations (3) and (4), $\overline{f_{sa}}$, $\overline{f_{ra}}$, $\overline{f_{pc}}$ are the average firing rates of the activated SA1, RA1, PC afferents respectively. We used psychophysical data about perceived intensities as shown in the black curve in Figs. 3a and 3b to optimize K_pf, K_pv respectively. In Fig. 3, the data of perceived intensities captured from the previous references was normalized to 0-10.

3). Inverse function of perception

The inverse function of perception for each actuator is a function that relates the control amount to perceived intensity changes. To obtain the inverse functions, we used psychophysical data about the perceived intensities of vibration and static force. For vibration, ref. [24] provided the psychophysical data about the perceived intensity, as shown in Fig. 3b. Whereas for the pneumatic actuator, we used the psychophysical data from ref [28]. We used the following equation to calculate the controlling amount of pressure (C_p) for the pneumatic balloon for a given force (F_p).

$$C_{\text{p}}=\frac{5F\text{p}}{K_{\text{psi}}\cdot \pi \cdot r_{\text{p}}{}^2}+C_{\text{p}0}$$ (5)

where C_p0 is the minimal control amount that the balloon pressure can be discerned. K_psi (6.896e-3) is the coefficient for converting PSI to N/mm².

Since the magnitude of the perceived intensities, as shown in the blue curves in Fig. 3, fits the human data well, we used the following exponential function to obtain control amount changing as a function of the magnitude of perceived intensity for each actuator.

$$C=C_0\cdot {(1+w)}^I$$ (6)

where C is the control amount, w is the Weber fraction defined as the ratio of the perceptual threshold to the intensity of the original stimulus. C₀ is the control amount threshold to make the stimulus discernible.

B. Analyzing performance of the Bio-inspired control model in predicting haptic perception.

After determining the two coefficients (K_pf, K_pv) for normalizing perceived intensity, we further analyzed the performance of the current model in predicting haptic perception as shown in the blue curve in Figs. 3a and 3b. We computed the relevance coefficient (R²) between the blue and black curves to show how much of the variance of the psychophysical data can be explained by the current model. We found that the predicted intensities from the current model for the vibration and pneumatic actuators were well correlated with the psychophysical data (R²=0.99 and 0.98, respectively). In accordance with the psychophysical data in Fig. 3a, the perceived intensity predicted by the CAPR model for vibration motor changed approximately logarithmically with control, which indicates that the predicted results are fit well by the human Weber function, which describes the relationship between the change in a stimulus and the perceived change. As shown in Fig. 3b, the perceived intensity predicted by the CAPR model for pnumatic balloon changed approximately linearly with the pressure. It also matched the psychophysical data, since the static pressure produced by the pneumatic balloon is below the force level that causes SA1 afferent responses to saturate.

Although the coefficients were optimizated using psychophyscial data ranging from 0 to 10, the model uses the same coefficients when inputting the full mage of signals detected by the sensor.

C. Comparison between different control algorithms

As illustated in Fig. 2, the bio-inspired control model was established by combining the CAPR model with the haptic perception model from the afferent population response. To compare the current bio-inspired control model with the two previous control models, we presented the output characteristics of different control models for various fabricated trapezoidal pressure waves, as shown in Fig. 4. The linear control algorithm is simple, in which a control amount for 2 actuators changes linearly with input pressure signal. In the piecewise discrete controlling model, the control amount for the 2 actuators changed as a step function with pressure. The steps used in this study were based on optimization of this algorithm in a previous study [29]. In the bio-inspired system, as illustrated in Fig. 2, the balloon actuator was controlled according to the responses of SA1 afferents, which respond to the onset and hold phase (but typically not its offset of a rampand-hold stimulation wave [30]). The output control amount for the balloon actuator in response to trapezoidal pressure waves changes in almost same way as SA1 afferent responses. Whereas the vibration motor was controlled by following the responses of all 3 afferents [31] [32]. RA1 and PC afferent neurons respond strongly to onset and offset of simulation do not respond during static simulation. The output control amount for vibration has also similar response properties with RA1 and PC afferents. Overall, the output characteristics of this model match cutaneous afferent response properties as measured in neurophysiological experiments.

Fig. 4.

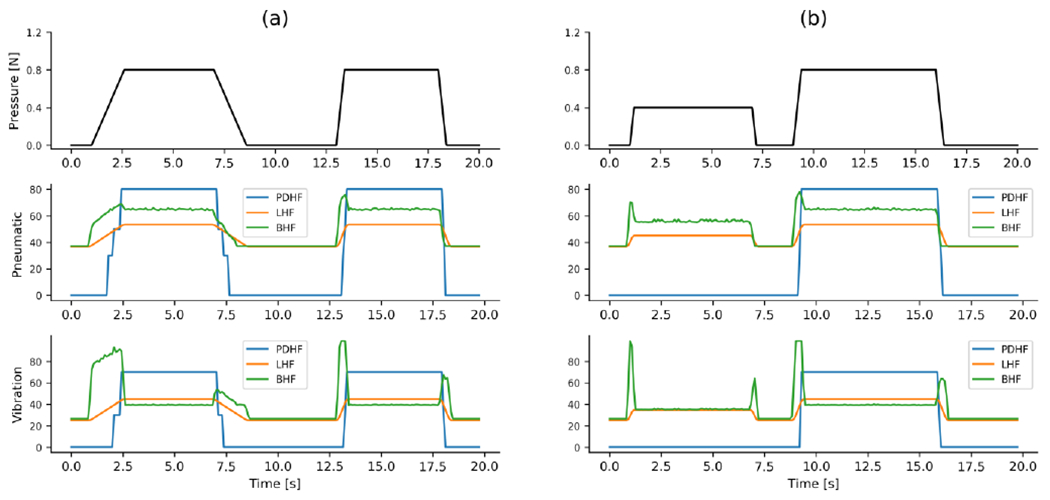
The outputs of the 3 control models to simulated trapezoidal pressure waves with (a) different changing rate but same peak value, (b) different peak value but same changing rate. PDHF: piecewise discrete haptic feedback; LHF: linear haptic feedback; BHF: bio-inspired haptic feedback.

D. Experimental evaluation of the control algorithms

The aim of the experiment was to evaluate the performance of different feedback methods in aiding users to identify tumors (of varied stiffness) embedded in phantom tissue made of a sponge. A repeated measures study design was used whereby study subjects were asked to palpate soft tissue phantoms with the artificial palpation probe mounted on a da Vinci surgical forceps (Intuitive Surgical, Sunnyvale, CA) in attempt to localize the tumor hidden in the phantom.

Each subject was asked to perform the same task in 4 trials: once with no haptic feedback (i.e., visual feedback alone), once with the feedback controlled by the piecewise discrete algorithm, once with linear haptic feedback, and once with the bio-inspired haptic feedback algorithm. Work with human subjects was approved by the Institutional Review Board under protocol #11-000077.

1). Participants

The first group of subjects was comprised of 15 novice subjects (male: 7, female: 8) with little or no experience with robotic surgery. The second group of subjects was comprised of 10 expert robotic surgeons (male: 7, female: 3) recruited from the Ronald Reagan Hospital at UCLA. Of the 25 participants, 24 were right-handed and 1 was left-handed.

2). Phantom of tumor

A tumor phantom was fabricated using a sponge (QEP 70005Q-6D 14x14x4.8 cm) on the basis of the actual dimensions and stiffness of tissue. There were 7 holes distributed in different sites of the phantom base as shown in Fig. 5 (right panel). Different materials were used to simulate different types of tumors: foam, Silica gel, and rubber to fabricate soft (S), medium (M) and hard (H) tumors, respectively. The elastic modulus of the sponge, S tumor, N tumor, and H tumor is approximately 50, 58, 70, and 120 kPa respectively. In general, softer tumors were more difficult for subjects to localize. The fabricated tumors (approximately 1 cm in diameter, 3 cm in height) could be inserted in different holes on the phantom base and could easily be palpated without visualization from the sponge surface. In order to facilitate the recording of subjects’ reported tumor locations, a coordinate map was drawn on top of the tissue phantom.

Fig. 5.

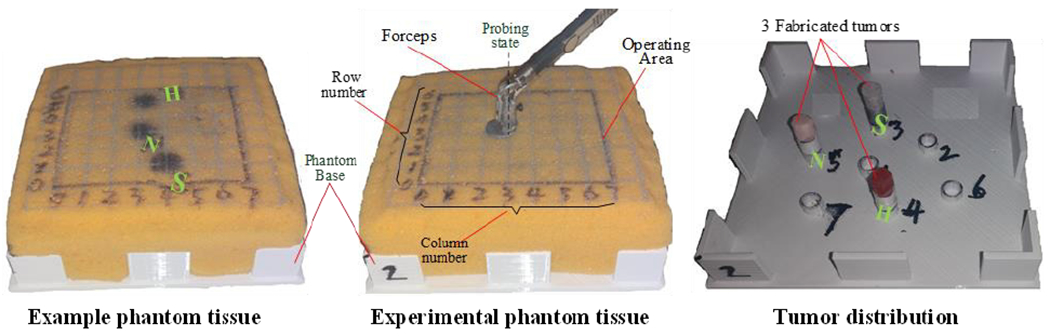
Phantom composed of soft sponge material. The distribution of 7 tumor holes on the phantom base.

3). Experimental precautions and procedure

Before each trial, the subjects were given up to 5 minutes to get used to the feedback mechanism being tested using the example phantom tissue, on which the locations of 3 different types of tumors were marked. This allowed the subjects to become familiar with the sensor manipulation and localization tasks. Subjects were also instructed to keep their fingers closed to hold the pressure sensor, and try to position the forceps orthogonal to the surface of the sponge as illustrated in the middle panel of Fig. 5. Subjects were told to try to apply the least amount of pressure and find the tumors as quickly as possible when probing, since large applied force for a long period may cause damage to the tissue in real surgery [33]. In each trial, we placed one soft, medium and hard tumor pseudo randomly among the 7 holes. The subjects were not told how many tumors they would need to find and were only required to indicate whether there was a tumor present. The subjects were instructed to follow the grid, checking each location one by one. In each session, subjects performed four trials, one with each of the four haptic feedback mechanisms. The order of these trials was counterbalanced across subjects. Once the trial began, the subjects were asked to find tumors in the experimental phantom tissue within the operating area marked as black rectangle on the sponge (see Fig. 5, middle). Once they found a tumor, subjects were required to report its position by its column and row number. In each trial, the locations of the 3 tumors and were pseudo-randomly moved to be different from the previous trial. Between each trial, the subjects had a 30-second break, but were asked to stay seated while not operating the robot.

4). Statistical Analyses

Statistical analyses were performed on four recorded metrics: localizing accuracy, mean force, time to completion and time spent in contact with the tumor (tumor contact time). We defined a reported tumor location that was not more than 1 grid of distance away from the actual tumor site as being correctly localized. The localizing accuracy was calculated as the proportion of correct judgments to total reports. The completion time was the time from when subjects start probing to when they finished checking on the phantom and were sure they had found all the tumors. The time spent in tumor contact was defined as time when pressing force exceed a preset level (horizontal black dotted line in Fig. 6). And the mean force was the average of the pressure data during tumor contact.

Fig. 6.

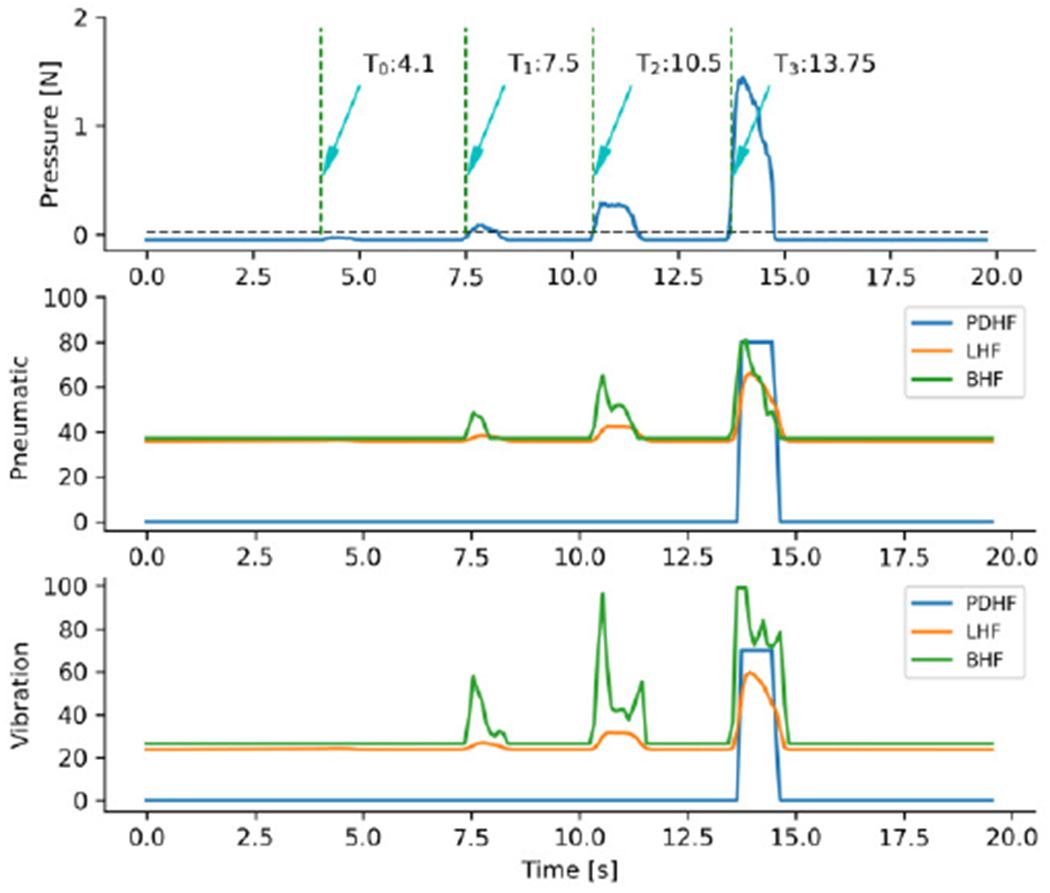
Output characteristics of linear, piecewise discrete and Bio-inspired control to detected signal of pressing normal tissue and tumor site. T₀, T₁, T₂ and T₃ indicates starting time of pressing normal tissue, soft tumor, medium tumor and hard tumor, respectively. PDHF: piecewise discrete haptic feedback; LHF: linear haptic feedback; BHF: bio-inspired haptic feedback.

Because most of the recorded parameters were not normally distributed, non-parametric tests were used to analyze the data. To test for differences between novice subjects and surgeons, we used a Wilcoxon Rank Sum test to compare performance from each metric (n=4) for each control algorithm (n=4). Despite performing 16 tests, we found no evidence that the subject groups performed differently (p-values all greater than 0.14; median p-value 0.55), so the remaining analyses were performed on all subjects combined. However, we plot the data separately to show the similarities between subject groups. For each tested metric, we performed a Kruskal-Wallis test, with the metric as the dependent variable and the control algorithm as the independent variable. If we found a main effect of control algorithm, we used the post-hoc analyses of the Kruskal-Wallis test to identify individual significant differences.

III. Results

A. Test of different control methods

An example of the different feedback methods when a subject palpated different site of the tissue phantom is presented in Fig. 6. The piecewise discrete controlling method missed the soft and medium tumor, and only responded to the hard tumor. In the linear and bio-inspired controlling methods, the pneumatic and vibration actuators were activated with different intensities for the three different tumor types. Critically, the linear and bio-inspired controlling methods differ in their temporal profiles. The bio-inspired method activated stronger intensities for the two actuators, thus increasing the difference in response between the different tumor types.

B. Performance of different control methods

In order to further identify which of the three controlling methods was best suited for users to find tumors, we calculated the localizing accuracy, mean force, completion time and time in which the user was in contact with a tumor (tumor contact time)

As noted above and shown in Fig. 7a, we found no evidence that novice subjects performed differently than surgeon subjects (p>0.41, Wilcoxon Rank Sum tests). When using the bio-inspired haptic feedback system subjects achieved median localizing accuracy of 0.83. Although this was not statistically distinguishable from the median localizing accuracy when using the linear method (0.75; p=0.23), it was significantly greater than the accuracies when using the piecewise discrete method (0.67; p=0.0032), or when there was no feedback (0.33; p=1.4x10⁻¹³). Likewise, accuracies using the linear and piecewise methods were both significantly better than with no feedback (p=2.2x10⁻⁴ and p=0.049, respectively).

Fig. 7.

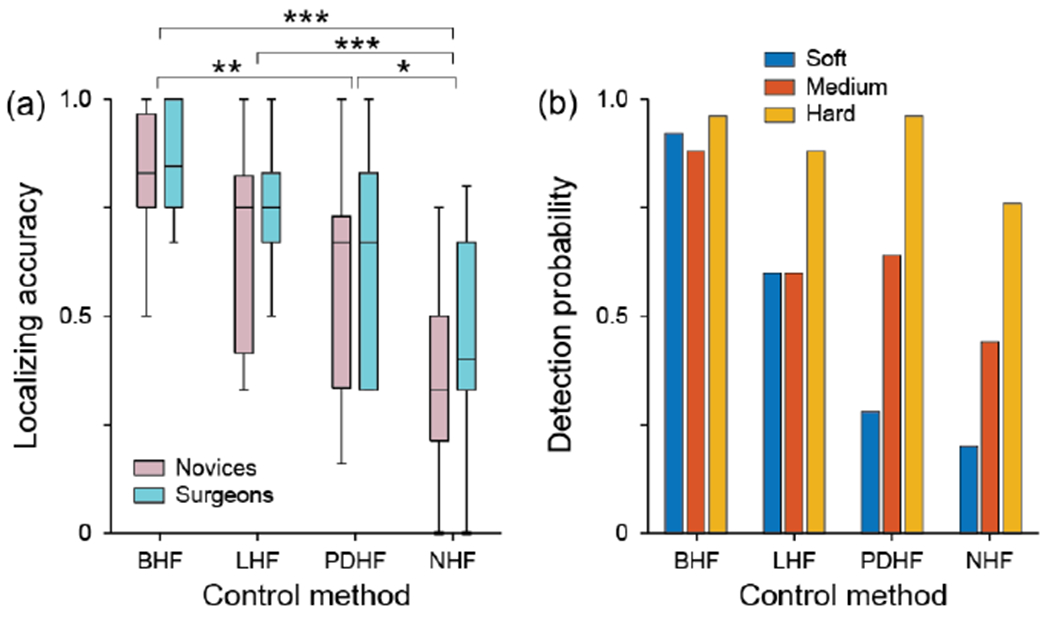
(a) box-plot of localizing accuracy for the 4 feedback control methods. (b) Detection probabilities for the different tumor classes for the 4 feedback control algorithms. * indicates p<0.05; ** indicates p<0.01; *** indicates p<0.001 from post-hoc tests following Kruskal-Wallis tests. BHF: bio-inspired haptic feedback; LHF: linear haptic feedback; PDHF: piecewise discrete haptic feedback; NHF: no feedback.

In order to evaluate the performance of each feedback method for each tumor type, we calculated the detection probability. Because each subject performed each condition once, the detection probability was calculated across subjects. As such, the detection probability for a particular tumor in a particular condition was the number of times it was correctly located across all the subjects in that condition divided by the number of subjects. As seen in Fig. 7b, subjects using the bio-inspired haptic feedback system detected each tumor class equally well. To test this, we used a Kruskal-Wallis test with detection as the dependent variable and tumor class as the independent variable. We found no evidence that the subject pools performed differently with the three tumor types (p=0.58). Using the linear method, subjects’ performance was affected by tumor class (p=0.048), but not as strongly as subjects using the piecewise discrete method (p=5.0x10⁻⁶) or without feedback (p=4.0x10⁻⁴). In these cases, subjects were significantly worse at detecting the soft tumor compared to the hard tumor (post-hoc test p-values <0.001).

Analyses of the remaining metrics are shown in Fig. 8, which show boxplots for mean force (Fig. 8a), completion time (Fig. 8b) and tumor contact time (Fig. 8c) as a function of subject group and control algorithm. As noted above, we found no significant differences between novices and expert surgeons (p>0.14, Wilcoxon Rank Sum tests) for any of the metrics, so the following Kruskal-Wallis tests were performed on the pooled data. We plot the subject groups separately for illustration purposes only.

Fig. 8.

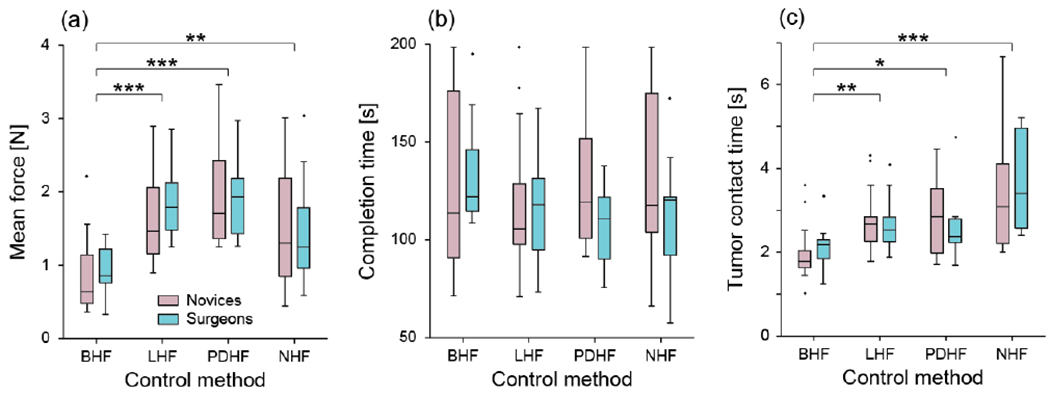
Boxplots showing the effects of the four control methods in the two subject pools on mean force (a), completion time (b) and tumor contact time (c). * indicates p<0.05; ** indicated p<0.01 and *** indicates p<0.001 from post-hoc tests following Kruskal-Wallis tests. BHF: bio-inspired haptic feedback; LHF: linear haptic feedback; PDHF: piecewise discrete haptic feedback; NHF: no feedback.

We found a main effect of mean force (p=1.73x10⁻⁷), no main effect of completion time (p=0.684) and a main effect of tumor contact time (p=1.23x10⁻⁵). Given that median force and tumor contact time both showed a main effect of control algorithm, we further analyzed the data to see where there were significant differences among the feedback methods.

Using the bio-inspired haptic feedback method, subjects used significantly less mean force (Fig. 8a) than when using the linear feedback method (p=4.32x10⁻⁵, post-hoc test), the piecewise discrete method (p=2.38x10⁻⁷) or when there was no feedback (p=0.0099). We found no evidence of differences in mean force among the remaining 3 conditions (all p-values >0.08).

We also found that subjects spent considerably less time in contact with the tumors (Fig. 8c) when using the bio-inspired feedback method (median 1.9s) than when using the linear method (2.7s; p=0.0048), the piecewise discrete method (2.5s; p=0.014) or when there was no feedback (3.1s; p=4.7x10⁻⁶). Again, we found no differences in contact time among the remaining 3 feedback methods (all p-values >0.21).

IV. Discussion

We implemented an innovative control model based on the responses of touch receptors and presented feedback to users of a surgical robot. For this algorithm, the actuators were controlled according to the perceived intensity as predicted by our CAPR model, which simulated the response of three different cutaneous afferent populations. Even when using only a single sensor and pair of actuators, this feedback system helped subjects more effectively localize tumors than other control methods, leading to less contact force, shorter time in contact with the tumor and better localization accuracy. While each of the feedback systems allows users to localize tumors better than with no feedback, only the bio-inspired control method allowed users to find the soft and medium tumors as easily as the hard tumors.

For the linear control algorithm, the pneumatic and vibration actuators were always activated simultaneously when interacting with soft tissue. Tins feature does not correspond to natural tactile sensation since one does not feel vibrations when pressing down on an object statically. The piecewise-discrete control algorithm was originally designed to be highly flexible to fit the needs of the task at hand. This was accomplished by changing the feedback activation rule set to convey meaningful information to the user (e.g., vibrate upon contacting a tumor for palpation, or when a suture is about to break for knot tying). While this strategy allows for an easily adaptable setup, it has drawbacks that can affect its performance. Primarily, it is highly dependent on prior knowledge of the forces involved in the task. Specifically, the ruleset must be established to activate in ranges that a user would experience during the task. If the minimum and maximum force ranges are not set optimally there will be a decrease in the amount of useful information conveyed to the user. In this study it is possible that a different ruleset for the piecewise algorithm may have provided more favorable results for that algorithm, particularly if it was tuned for a specific tumor. However, the fact that the bio-inspired feedback system did so well without any adjustments highlights its benefit over other algorithms that rely on being customized properly.

To the best of our knowledge, this study represents the first time that a bio-inspired haptic feedback system has been used for haptic feedback. However, a similar model to our CAPR (Touchsim) has been implemented for biomimetic sensory feedback [16]. In that study, the Touchsim model was used to convert the pressure sensor signal to action potentials of the three classes of afferents, which were then provided to the residual nerve using an electrode array.

The bio-inspired feedback method was more sensitive than any of the traditional control methods, especially for recognizing the soft tumor as illustrated in Fig. 6 and Fig. 7b. This is due, in part, because the vibration actuator is primarily driven by the RA and PC components of the response, so it only vibrates during the dynamic phase of contact. As the subjects probe the tumor, they feel the higher intensity of the vibration. Therefore, the biofeedback method is more beneficial for surgeons to find soft structures under the tissue more quickly and with less applied force, thus translating to a decreased amount of potential tissue damage.

In this experiment, the actuators were continuously controlled in order to present haptic feedback to the user. It may not be necessary to control the actuators continuously since a human’s perception levels of stimulus intensity are limited and the difference between two stimuli must exceed a threshold to permit discrimination. In future designs it may be beneficial to set several stimulus levels for each actuator, and record the population spike trains for each level. Then, each actuator may be controlled with the stimulus level and spike train most approximate to the output action potentials evoked by the sensor signals. Using this discrete method, the complexity of the current control model may be simplified. In the current work, we simulated the responses of 167 SA1, 329 RA1, and 52 PC afferents which distribute evenly over the fingertip according the real afferent densities in the fingertip [34]. However, it may not be necessary to simulate as many tactile afferents for a pressure sensor of a single point. As such, we may be able to further improve the computation efficiency by decreasing the afferent density of the simulated tactile units. In this work, a single sensor was used to detect the pressure signals, so only temporal information was captured; the spatial characteristics of the soft tissue were lost. The current control model can easily be expanded with distributed pressure sensors by changing the input to the model with the spatial parameters of the sensor distribution. Likewise, the output of the model can be configured to any array of actuators, from the coarse pneumatic-only array we have used previously [13] to more advanced arrays of the future. Other than the sort of haptic system for artificial palpation presented in current work, it is possible that we could implement our bio-inspired haptic feedback method in other haptic systems for other surgical simulations like the haptic warning system designed by CASIT for suture breakage [35].

V. Conclusion

Our bio-inspired haptic feedback system aimed to parse dynamic tactile information to afferents via a vibration actuator and static tactile information to SA1 afferents via a pneumatic balloon actuator based on the responses of these afferents in our model. Using a single sensor and single pair of actuators, the system allowed novices and expert surgeons alike to identify the locations of all classes of tumors more easily and did so with reduced contact force and tumor contact time compared to previous control functions and when no haptic feedback was provided. These results show the benefit of utilizing a bio-inspired algorithm, particularly one which can be easily scaled up for use with more advanced sensor and actuator arrays.