Regional variation in the impacts of the COVID-19 pandemic on the quantity and quality of data collected by the project eBird

Abstract

The COVID-19 pandemic has likely affected natural systems around the world; the curtailment of human activity has also affected the collection of data needed to identify the indirect effects of this pandemic on natural systems. We describe how the outbreak of COVID-19 disease, and associated stay-at-home orders in four political regions, have affected the quantity and quality of data collected by participants in one volunteer-based bird monitoring project, eBird. The four regions were selected both for their early and prolonged periods of mandated changes to human activity, and because of the high densities of observations collected. We compared the months of April 2020 with April in previous years. The most notable change was in the landscapes in which observations were made: in all but one region human-dominated landscapes were proportionally more common in the data in April 2020, and observations made near the rarer wetland habitat were less prevalent. We also found subtler changes in quantity of data collected, as well as in observer effort within observation periods. Finally, we found that these effects of COVID-19 disease varied across the political units, and thus we conclude that any analyses of eBird data will require region-specific examination of whether there have been any changes to the data collection process during the COVID-19 pandemic that would need to be taken into account.

1. Introduction

Citizen science data have long been important for ecological and conservation research (e.g., Greenwood et al., 1995), and the diversity of uses has only increased through time (e.g., Fink et al., 2020; La Sorte et al., 2018; Reynolds et al., 2017; Robinson et al., 2018); however, changes in human behaviour can cause variation in how these data are collected. The sampling processes of citizen science projects with relatively unstructured data-collection protocols — with observers choosing when, where and for how long to make observations — have the potential to systematically change through time, both within and among years, with changes in observers' motivation and life circumstances. It is important to identify the sources of temporal variation in the sampling process that must be controlled during data analysis, particularly when describing changes through time in distribution and abundance. The emergence of COVID-19 disease starting in late 2019 has disrupted human activity around the world, including disruptions to highly structured monitoring of bird populations. For example, in 2020 data collection for the North American Breeding Bird Survey was cancelled (BBS National Offices, 2020), and the British Breeding Bird Survey activity was highly curtained (The BTO Team, 2020). Although less structured citizen science projects have not ceased activity, the volume and type of observations submitted may have been significantly altered due to restrictions imposed on human movement. If we want to use data from relatively unstructured projects in order to understand the effects of this pandemic on natural systems (Rutz et al., 2020), or to use such data in lieu of those from more structured monitoring programs in 2020, it will be necessary to understand whether and how observer behaviour has changed in response to the COVID-19 pandemic.

Changes in the quantity of data that are collected are the most basic of the potential impacts of changes in observer behaviour. We do not have a clear expectation of whether the quantity of data will have increased or decreased as a consequence of the COVID-19 pandemic. Stay-at-home orders may have curtailed the activities of observers because of restrictions preventing observers from travelling to their preferred locations for bird watching. However, anecdotally there are also suggestions that these same restrictions may have increased the desire of people to connect with the natural world (e.g., Flaccus, 2020), and in some regions bird watchers have been actively encouraged to report birds that they see from their homes (anonymous, 2020; Bird Count India, 2020; Domingues, 2020). Thus, new data may have entered the database at a higher, and not lower rate.

Not just the quantity but the quality (i.e. the relative information content of each observation) may have changed. One aspect of quality of the entire dataset is the evenness with which observations are distributed across a region; evenly spaced observations contain greater independent information than the same number of observations that are clustered together. I.e. spatial autocorrelation are routinely higher, and thus each datum provides a lower amount of independent ecological information, for locations that are in closer proximity (e.g., Koenig, 1999). Because of restrictions of human movement, we expect that observations will be more clustered, and that urbanized landscapes will be represented more frequently in the data collected during the pandemic, exacerbating an existing bias toward the collection of observations near to urban centers (e.g., Tulloch and Szabo, 2012; unpubl. data from eBird), and the reporting of species that more commonly are found near people. We also expect that rare habitat types such as wetland areas, and their associated faunas, will be under-sampled because the curtailment of long-distance movement has made it less likely that observers will travel to these habitats.

The probabilities of detecting birds that are actually present can also be affected by pandemic-related changes in the behaviour of observers. Differences in the habitats visited by observers can impact data not just because species have different habitat associations, but also because detection rates can differ between habitat types (Ruiz-Gutiérrez et al., 2010). Detection rates will also vary with multiple aspects of observer behaviour such as the durations of observation periods and distances travelled during observation periods (Johnston et al., 2020). Both of these may have changed during the pandemic. We do not have a clear expectation for whether pandemic-related restrictions to observers' movements will have decreased durations of observation periods (i.e. less motivation because of low avian diversity in urban areas), or increase the durations of observation periods because of additional time being available. We expect that a greater proportion of counts will be made by people who are stationary (e.g., counting birds from within their homes), and that those observers who are moving during observation periods will travel shorter distances. Impacts of the COVID-19 pandemic on the factors that affect probabilities of detection need to be identified and taken into account so that differences in probabilities of detection are not erroneously interpreted as changes in abundances.

The eBird project (Sullivan et al., 2014) is a useful candidate for examining the effects of the COVID-19 pandemic on the quantity and quality of citizen science data being collected, given its prominence as a source of information about bird distribution and abundance in many parts of the world (Amano et al., 2016). eBird has been described as a “semi-structured” citizen science project (Kelling et al., 2019); observation location, time and effort are all determined by project participants, but ancillary information is collected in order to enable the filtering of raw data and modelling of the effects of this sampling variation.

In this paper, we test our expectations that several facets of the quantity and quality (i.e. information content) of data submitted to the eBird project have changed as a consequence of the COVID-19 pandemic. We have looked for evidence of effects in four political regions that we will use as examples of the potential impacts of the pandemic on the data being collected by the eBird project. These regions are the U.S. states of California and New York, and the countries of Portugal and Spain. Spain underwent a longer and stricter curtailment of human activity in the spring of 2020 than in the other regions, and our expectation is that Spain may have some of the largest differences in data being collected during the pandemic. For each of these political units we assess whether the quantities of data were affected by comparing data submissions from April 2020 — when all four political units were under stay-at-home decrees — to the data collected in April of previous years. We also assessed changes in various facets of data quality. We looked for greater representation of urban landscapes within the data from April 2020 across the four political units; additionally, we looked for evidence of a decline in representation of wetland habitat. Also, we carried out analyses to look for evidence of other potential changes in the behaviour of observers that might have led to deviation in the detection rates of birds in April 2020 compared to the same month in previous years.

2. Methods

Rather than attempting to describe this globally, our purpose is to conduct a detailed case studies of the potential impacts over a one-month period in four geographically contiguous political units. For this, we selected the states of California and New York, and the countries of Spain and Portugal (excluding their overseas territories: the Spanish autonomous communities of the Canary Islands, Cueta and Melilla; the Portuguese autonomous regions of the Azores and Madeira Islands). We chose California and New York both because of the large quantities of data available in these two states, and also because the restrictions imposed on citizens of these states were among the strongest and earliest in the United States. In both of these states, stay-at-home orders came into effect in late March 2020, and continued throughout and beyond the month of April. The governments of Spain and Portugal, countries with partner organizations coordinating nation-specific versions of eBird (eBird España, and PortugalAves) and high participation by resident bird watchers, also decreed stay-at-home restrictions that were in place throughout April 2020, and in Spain these restrictions placed very severe limits on peoples' ability to leave their places of residence. We are restricting our analyses to data from the month of April, and comparing the data from April 2020 to those collected in April of preceding, typically 3–4, years. Note that 2020 was the first year of data collection for the third New York Breeding Bird Atlas, for which eBird is serving as the data-collection and management platform, which independently may have affected the quantity and quality of data within eBird. It is not possible to separate atlas-specific observations from those made for other purposes; however, April is prior to nesting of most bird species in New York state, and thus prior to the greatest focus of data collection for the breeding bird atlas.

We extracted the data from the eBird Sampling Event Data (eBird SED), a data product in which each row of data contains only information about each observation event's sampling process (e.g., date, time, location, effort), but no information about the bird species observed. The version of the SED that we used was released in May 2020, and contains all observations submitted to the database prior to mid-May 2020. Because data entry for eBird is entirely done through a web data-entry page or increasingly from smartphones, there was no need to wait multiple months for the data compliation to contain records of essentially all observations made in April 2020. We found that only a small proportion (<1%) of observation records from the month of April 2020 first appeared in the compilations of these data that were created in mid-June or mid-July 2020. We used the R package auk (Strimas-Mackey et al., 2018) to extract only the records from the month of April for the four regions described above. We filtered these records to only include data from those observation events that are routinely used in analyses at the Cornell Lab of Ornithology, which is the lead organization maintaining the eBird enterprise; these practices and the reason for their use are summarized in Johnston et al. (2020). We retained data only from “complete checklists” (i.e. observation events for which the non-detections could be inferred for all species not reported). For most of our analyses, except when counting the number of observers, we used auk to reduce “shared checklists”, which are multiple versions of the same observation event, to one record for each shared group. We only retained records for which observation effort was within these criteria: durations of observation periods were between 3 and 300 min, and travel distances were no more than 5 km (for rationale see Johnston et al., 2020).

In order to describe the environments around all of the sampling locations, we calculated the proportions of land cover classes based on the University of Maryland (UMD) classification of MODIS MCD12Q1 Version 6 remote sensing data (Friedl and Sulla-Menashe, 2019; Sulla-Menashe and Friedl, 2018). These data classify land cover within pixels 500 m on a side, and for each location we summarized the proportions of pixels classified as belonging to each of the 16 land cover types from a 5-by-5 grid of pixels centered on the pixel containing the reported location. A separate land cover classification is available, and was used, for each calendar year up to and including 2018; for eBird observations from 2019 and 2020 we assigned land covers based on the 2018 land cover classification. We chose this spatial extent for the summary of habitat information because this is the standard extent across which habitat information is summarized in analyses of eBird data at the Cornell Lab of Ornithology, and past studies have demonstrated that this spatial extent provides biologically relevant informative on species' habitat preferences (e.g., Fink et al., 2020).

We divided each political unit into a grid of equal-area hexagonal cells whose centers were approximately 95 km apart (each grid cell 7774.2km² in area) by specifying the res = 9 argument in the dgconstruct() function of dggridR R package (Barnes, 2018). In analyses for which multiple data were present within each grid cell in each year, we used the grid cell ID as a random intercept, so that the pattern of interest in each analysis was modelled as each observation's deviation from its grid cell's pre-2020 average value across years. There were data in 104 grid cells for California, 32 for New York state, 108 for Spain, and 34 for Portugal.

Typical parametric analyses, like generalized linear models, only describe variation in the mean value of a response variable. However, geographically uneven responses within a country, state or other region also could have resulted in a change in the range of variation (i.e. variance), or the extremes (i.e. skewness, kurtosis) of the responses across the grid cells. Any such changes could affect the species of birds observed or their reported numbers; thus we needed to identify all types of changes in distribution. Generalized additive models for location, scale and shape (GAMLSS) are designed to allow each of these moments of distribution to vary independently, with variation in each being described using separate sets of predictor variables. For our analyses we used the implementation of GAMLSS models in the R package gamlss (Mayr et al., 2012).

2.1. Modelling deviations from expected densities of observation events

The first potential consequence of the COVID-19 pandemic that we described with statistical models was whether the quantity of data collected was altered in April 2020. We measured quantities as the number of separate observation events within each hexagonal grid cell, summed across all days in the month of April separately for each year. For the U.S. states we calculated these summaries between 2005 and 2020 inclusive (eBird began in 2002 in the U.S.). eBird was formally adapted substantially later in Portugal and Spain, and we created these summaries only for the years from 2015 and 2017 onward, for Portugal and Spain respectively. The quantity of data being collected by eBird is increasing through time (Sullivan et al., 2014), and thus the potential impact of COVID-19 disease for which we looked was a deviation in the number of observation events in 2020 relative to the number expected based on the trend from prior years. We modelled the distributions of these responses using generalized inverse Gaussian (GIG) distributions, in which the response could take any value from zero to positive infinity with the shape of the distribution controlled by specifying mean, variance, and skewness. Preliminary analyses showed the GIG distribution to be the best available choice with which to model the data, based on inspection of Q-Q plots created by R's gamlss package. We found that GIG regression models only slightly under-predicted the very largest observed values. We created a set of 20 candidate models (the combinations of fixed effects are listed in Table A1) in which we allowed each of mean, variance, and skewness to vary as a function of some combination of calendar year (continuous variable, hereafter “CalYr”), and whether the data were from the COVID-19 year (i.e. 2020 versus all other calendar years; “COVIDYr”). In this model set, CalYr was always included as a predictor of variation in the mean number of checklists because of our expectation that numbers of observation events have increased through time. The predictor variable COVIDYr was present as a main effect in some models of variation in the mean, and presence or absence of COVIDYr in otherwise identical models allowed us to determine whether there was a statistically important deviation in 2020 from the numbers of observation events expected based on the trend in prior years that was described by CalYr. We modelled changes in variance and skewness similarly, except that we also included models in which variance and skewness remained constant through time (i.e. intercept-only models of variance or skewness). We identified well-supported models based on their AIC scores, considering the well-supported models to be those within ΔAIC ≤8 of the best-supported model (Burnham and Anderson, 2002).

Table A1.

Fixed effect predictor variables for each model in the set of twenty models fitted separately to data from each of the four political units, in order to identify the best-supported model(s) describing inter-annual variation in numbers of observation events across the equal-area hexagonal grid cells into which each political unit was divided. An “X” within a column indicates that this predictor variable was included in the model described by a row within this table. The fixed effect predictor “CalYr” is a continuous variable that describes monotonic changes across the calendar years in each moment of the distribution (i.e. mean, variance, and skewness) “COVIDYr” is a 2-value categorical variable that indicates whether the calendar year was 2020; this predictor functions to allow the moment of distribution to deviate in 2020 from the longer-term trend described by “CalYr”. All models converged, except for fitting of models for Portugal; here, 3 models failed to converge^a.

Model number	Mean		Variance		Skewness
	CalYr	COVIDYr	CalYr	COVIDYr	CalYr	COVIDYr
1	X
2	X	X
3	X		X
4	X	X	X
5	X		X	X
6	X	X	X	X
7	X				X
8	X	X			X
9	X				X	X
10	X	X			X	X
11	X		X		X
12	X	X	X		X
13	X		X		X	X
14	X	X	X		X	X
15	X		X	X	X
16	X	X	X	X	X
17	X		X		X	X
18	X	X	X		X	X
19	X		X	X	X	X
20	X	X	X	X	X	X

^aModels # 13, 17 and 20 did not converge when fitted to the data from Portugal.

2.2. Modelling deviations from expected habitat representation in observations

Our approach to testing for effects of COVID-19 on the other response variables (proportion of urban habitat, probability of any nearby wetlands, duration of observation period, probability of observer movement during the observation period, distance travelled by moving observers) was different from the method outlined above for examining variation in the number of observation events. Based on prior work with eBird data (D. Fink, pers. comm.), at least in North America we expected that in recent years the typical values of the responses of interest — habitats surveyed, and observer effort — should be approximately constant through time, unless the COVID-19 pandemic had an impact on observers' behaviour in 2020. Thus, our tests for effects of COVID-19 did not model a systematic trend across years, but instead we treated CalYr as a categorical variable and compared observer behaviour in April 2020 to behaviour in the month of April of the preceding 4 years: 2016–2019, inclusive (or the 3 years 2017–2019 for Spain). We again created sets of candidate models with which to examine effects of COVID-19 on inter-annual variation in each moment of distribution (e.g., mean, variance, skewness) of the reponse. The year 2020 was set to be the reference category; in other words, the regression coefficient for CalYr = 2020 describes a baseline value of the response (i.e. it is the intercept), and the regression coefficients for each of the other years describe the deviation from the 2020 value. By parameterizing the model in this way, we are conveniently able to evaluate whether there was a consistent difference between 2020 and all earlier years, because differences would be indicated by the regression coefficients for the other years being either all above zero, or all below zero. In this paper, we will describe 2020 as being statistically different if other years' coefficients were all positive (or all negative) and if the 95% confidence limits around all of these coefficients did not overlap zero.

In order to examine whether the proportion of urban habitat around observation locations was different in April 2020 than in previous years, we fitted separate models to the data from each of the four political units. We fitted models using an inflated Beta error distribution (the “BEINF” distribution family in the gamlss package). This is a beta distribution (response values of between 0 and 1) modified to allow excess or deficit in the presence of response values of 0 or 1. The use of this distribution enabled modelling of the effects of predictor variables on mean, variance, skewness, and kurtosis. We used only one fixed effect predictor variable, CalYr (categorical predictor). For each political unit, we fitted a set of models in which each moment of the distribution could be either constant or a function of CalYr. In all models, the grid cell in which each observation was made was used as a random intercept for the mean proportion of urban habitat. All possible combinations of fixed effects were modelled, producing a model set of 16 models (Table A2). The best-supported model(s) were identified based on ΔAIC values of the models within each set.

Table A2.

Fixed effect predictor variables for each model in the set of sixteen models fitted separately to data from each of the four political units, in order to identify the best-supported model(s) describing inter-annual variation in proportion of urban landcover within the 2.5 km × 2.5 km areas centered on the locations of observation events. In these models each of the four moments of distribution — mean, variance, skewness and kurtosis — could vary independently as a function of their own set of predictor variables. An “X” within a column indicates that this predictor variable was included in the model described by a row within this table. The fixed effect predictor “intercept” indicates that the moment of variation was constant across years. “Year” was a categorical predictor variable that describes variation among years that is arbitrary and potentially non-systematic in pattern; note that when “Year” was included as a predictor of a moment of distribution the year 2020 was treated as the intercept.

Model number	Mean		Variance		Skewness		Kurtosis
	Intercept	Year	Intercept	Year	Intercept	Year	Intercept	Year
1	X		X		X		X
2	X			X	X		X
3	X		X			X	X
4	X		X		X			X
5	X			X		X	X
6	X			X	X			X
7	X		X			X		X
8	X			X		X		X
9		X	X		X		X
10		X		X	X		X
11		X	X			X	X
12		X	X		X			X
13		X		X		X	X
14		X		X	X			X
15		X	X			X		X
16		X		X		X		X

We also examined whether one rare habitat, wetlands, differed in representation in April 2020 compared to this same month in prior years (2016–2019; 2017–2019 for Spain). The presence of any amount of wetland habitat was uncommon (only between 20% and 40% of observations had any landcover classified as wetland within 2.5 km of the sampling location, in any year and political unit). As a consequence, we chose to treat the presence of wetland habitat as a binary response: either there was, or there was not any nearby wetland habitat. We fitted these binary-response data using a single model for the data from each political unit. This model contained CalYr as a categorical fixed effect (2020 was the reference/intercept year). The grid cell in which an observation was made was treated as a random intercept, which controlled for variation in the prevalence of wetlands across each political unit. Given the small number of predictor variables and our ability to test for the predicted effect based on the regression coefficients for the only fixed effect, we do not believe that there is need to examine multiple statistical models.

2.3. Modelling deviations from expected observer effort

The species of birds detected, and the numbers of individuals counted are affected by the amount of effort expended by observers during an observation period. We know that the duration of an observation period is an important determinant of the number of birds detected (e.g., Kelling et al., 2015). In our analyses of variation in the lengths of observation periods, we needed to account for the fact that ranges of effort were truncated in the process of filtering the raw records in order to create the set of data that we used. For our analyses of variation in the duration of the observation period, the data were filtered to leave only observation periods of between 3 and 300 min, inclusive; we modelled these data using a truncated version of the gamlss generalized inverse Gaussian family that allowed only response values of between 3 and 300 min. The fixed effects of the models that we used are shown in Table A3.

Table A3.

Fixed effect predictor variables for each model in the set of seven models fitted separately to data from each of the four political units, in order to identify the best-supported model(s) describing inter-annual variation in observer effort (separately duration of count periods, and distances travelled for non-stationary counts). In these models each of three moments of distribution — mean, variance and skewness — could vary independently as a function of their own set of predictor variables. An “X” within a column indicates that this predictor variable was included in the model described by a row within this table. The fixed effect predictor “intercept” indicates that the moment of variation was constant across years. “Year” was a categorical predictor variable that describes variation among years that is arbitrary and potentially non-systematic in pattern; note that when “Year” was included as a predictor of a moment of distribution the year 2020 was treated as the intercept. Note that several models failed to converge, both for modelling of variation in count durations and travel distances, in spite of our efforts to adapt the model-fitting process^a. See footnotes for Table A8, Table A9 for lists of the models that did not converge for each political unit.

Model number	Mean		Variance		Skewness
	Intercept	Year	Intercept	Year	Intercept	Year
1		X	X		X
2	X			X	X
3	X		X			X
4		X		X	X
5		X	X			X
6	X			X		X
7		X		X		X

^aWe adapted the default model-fitting process in two ways. First, we increased the number of iterations allowed for model fitting from the default 20 to 100, and halved the “step.length” value with which the algorithm would adjust parameter values in each iteration of the model-fitting algorithm; the convergence criterion was never altered. Second, at times model convergence failed in fewer than the 20 iterations allowed by default, and in these cases we would change the algorithm used from the default “method = RS”, to instead use a mixture of the two available algorithms (“method = mixed”) and then vary the number of iterations using the first algorithm before starting to use the second.

The distance travelled will also affect the number of birds detected, with longer distances leading to the detection of more birds, and we expect that the distances that observers travelled during observation periods will have been decreased by the restrictions on human movement. We have divided our examination of variation in these travel distances into two components, asking whether in April 2020: (1) a greater proportion of observation periods were made by non-moving observers (i.e. whether the observation was an eBird “stationary count”), and (2) whether the distances travelled by non-stationary observers were different than in prior years. We have separated our analyses into these two components because our prior experience with these data has shown that a “stationary count” is not simply a travelling count of zero distance. Our analyses for component (1) were logistic regression models in which a single model was fitted to the data from each political unit. This model has a single fixed effect predictor, CalYr (categorical variable; 2020 is the reference/intercept year) and the grid cell of each observation as a random intercept. For our analyses of component (2) we fitted the same set of models that we used to examine variation in the duration of observation periods (Table A3). The distribution of the response variable was truncated, and we fitted data using a truncated generalized inverse Gaussian distribution, this time allowing values to range between 0.01 km and 5 km, the range produced by our filtering of the total set of data and removing all data from stationary counts.

GAMLSS models did not always converge to solutions using the default settings within R's gamlss package. In most, but not all, cases we were able to produce model convergence by altering two aspects of the model fitting process that we describe in a footnote to Table A3. In spite of this some of the models of variation in observer effort failed to converge (duration of observation period and distance travelled; models listed in footnotes to Table A8, Table A9). Based on inspection of the data, our experimentation with adjusting model fitting, and conversations with colleagues, we suggest that the lack of model convergence was the result of intrinsic difficulties in fitting GAMLSS models. The large number of parameters estimated in GAMLSS models is particularly challenging with truncated response distributions, for which we suspect that truncation removed exactly the information required in order to identify distribution variance and skewness.

Table A8.

Estimated regression coefficients describing the differences in duration of observation periods among years. Results are presented only for analyses of data from Portugal, California and New York state, because no models converged to solutions for data from Spain. Coefficients are from the single successfully fitted^a model of a set of 7 that was best supported by the data based on ranking models by AIC values. We fitted the data to models (Table A3) in which mean, variance, and skewness (i.e. moments of the distribution) could be modelled as being independently affected by predictor variables. All “Year (201*)” coefficients describe differences between the specified year and 2020. The coefficients for describing mean and variance are presented on the ln-link scale, while skewness was calculated on the scale of measurement (“identity link” in the parlance of gamlss). Coefficients and standard errors in bold font indicate coefficients for which the 95% confidence intervals did not overlap with zero, indicating statistically reliable estimates.

State	Moment	Predictor	Coefficient	SE
Portugal	Mean	Intercept	3.98	0.02
		Year (2016)	0.28	0.01
		Year (2017)	0.33	0.03
		Year (2018)	−0.15	0.03
		Year (2019)	−0.06	0.03
	Variance	Intercept	0.34	0.01
	Skewness	Intercept	−0.07	0.02
Spain	Mean	Intercept	4.22	0.01
		Year (2017)	0.38	0.02
		Year (2018)	0.08	0.01
		Year (2019)	0.07	0.01
	Variance	Intercept	0.31	0.01
		Year (2017)	0.10	0.02
		Year (2018)	0.05	0.01
		Year (2019)	0.04	0.01
	Skewness	Intercept	0.31	0.02
New York	Mean	Intercept	3.87	0.003
	Variance	Intercept	0.61	0.01
	Skewness	Intercept	0.68	0.01
		Year (2016)	−0.06	0.02
		Year (2017)	−0.04	0.01
		Year (2018)	−0.08	0.01
		Year (2019)	0.003	0.02
California	Mean	Intercept	4.06	0.005
		Year (2016)	0.08	0.01
		Year (2017)	0.07	0.01
		Year (2018)	0.04	0.01
		Year (2019)	0.03	0.01
	Variance	Intercept	0.6524	0.01
	Skewness	Intercept	0.91	0.06

^aFor modelling of count duration the following models did not converge in each political unit: Portugal Models 3, 5, 6 and 7; Spain 3, 5, 6 and 7; California 2, 4, 6 and 7; New York state 7.

Table A9.

Estimated regression coefficients describing the differences among years in distances travelled during of observation periods in April, for non-stationary counts. Coefficients are from the best-supported statistical model of a 7-model set, although not all models in this set were able to fit the data^a. We fitted the data to models in which mean, variance, and skewness (i.e. moments of the distribution) could be modelled as being independently affected by the predictor calendar year. All “Year (201*)” coefficients describe differences between the specified year and 2020. The coefficients for describing mean and variance are presented on the ln-link scale, while skewness was calculated on the scale of measurement (“identity link” in the parlance of gamlss). Coefficients and standard errors in bold font indicate coefficients for which the 95% confidence intervals did not overlap with zero, indicating statistically reliable estimates.

Region	Moment	Predictor	Coefficient	SE
Portugal	Mean	Intercept (2020)	0.74	0.02
		Year (2016)	0.04	0.03
		Year (2017)	0.16	0.03
		Year (2018)	0.05	0.03
		Year (2019)	−0.03	0.03
	Variance	Intercept	0.36	0.02
	Skewness	Intercept	1.21	0.03
California	Mean	Intercept (2020)	0.70	0.01
		Year (2016)	−0.04	0.01
		Year (2017)	−0.05	0.01
		Year (2018)	−0.07	0.01
		Year (2019)	−0.07	0.01
	Variance	Intercept	0.59	0.005
	Skewness	Intercept (2020)	1.34	0.02
		Year (2016)	−0.25	0.03
		Year (2017)	−0.25	0.02
		Year (2018)	−0.15	0.02
		Year (2019)	−0.08	0.02
New York	Mean	Intercept	0.55	0.003
	Variance	Intercept (2020)	1.00	0.04
		Year (2016)	−0.28	0.05
		Year (2017)	−0.19	0.07
		Year (2018)	−0.23	0.05
		Year (2019)	−0.29	0.05
	Skewness	Intercept	1.37	0.01

^aFor modelling of travel distance the following models did not converge in each political unit: Portugal Models 2–7; Spain 1–7; California 2, 4, 6 and 7; New York state 7.

3. Results

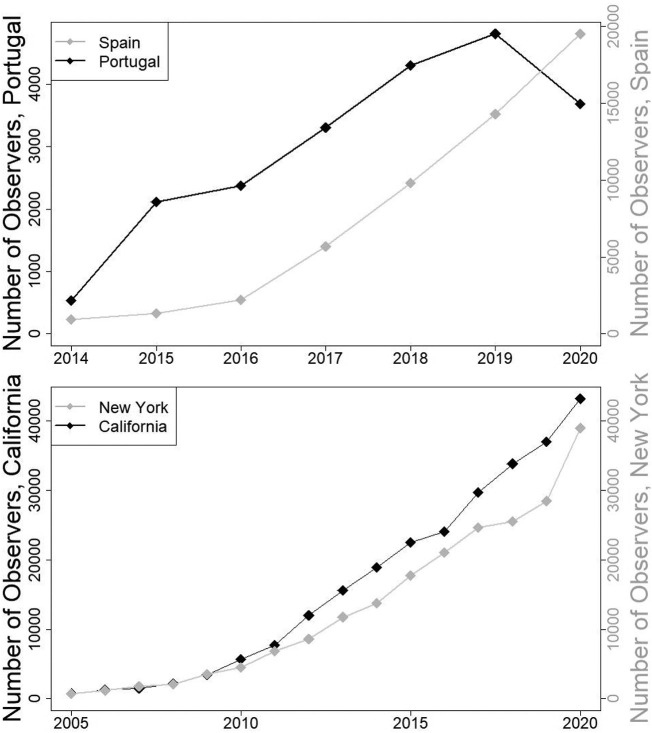
Across the political units that we have considered, the restrictions imposed on the populations had markedly different effects on the abilities and motivations of people to make observations, as evidenced by changes to the numbers of people collecting observations (Fig. 1 ). All year-to-year changes in numbers of observers were increases, except in Portugal where there was a decline in the number of people participating in data collection in April 2020 compared to April 2019. Exploring the causes of these differences (e.g., how much of the decline in Portugal was because of the absence of tourist bird watchers?) is out of scope for this paper, because we were investigating of the COVID-19 pandemic for data quantity and quality, and not the causes of changes in human behaviour.

Fig. 1.

The number of volunteer observers contributing data into the eBird database in April of each calendar year. Plotted is the number of unique observer ID values, regardless of whether these observers were associated with a unique observation event or with groups of observers collectively making observations (i.e. eBird “shared checklists”). Note that the ranges of years plotted on the x-axes differ between the graphs, because the active promotion of eBird to local bird watchers began later on the Iberian Peninsula than in North America. Also note that left and right y-axis scales on each graph are not identical.

3.1. Deviation from expected densities of observation events in 2020

The distribution, and not just the number, of observation events determines the information content of eBird's data within a larger region. We described variation in the distribution of observations within each of our four political units based on the number of observation events recorded within each of the hexagonal equal-area grid cells within that political unit. The majority of grid cells had relatively few observation events, but a small number of grid cells contained a very large number of observations (Fig. 2 ).

Fig. 2.

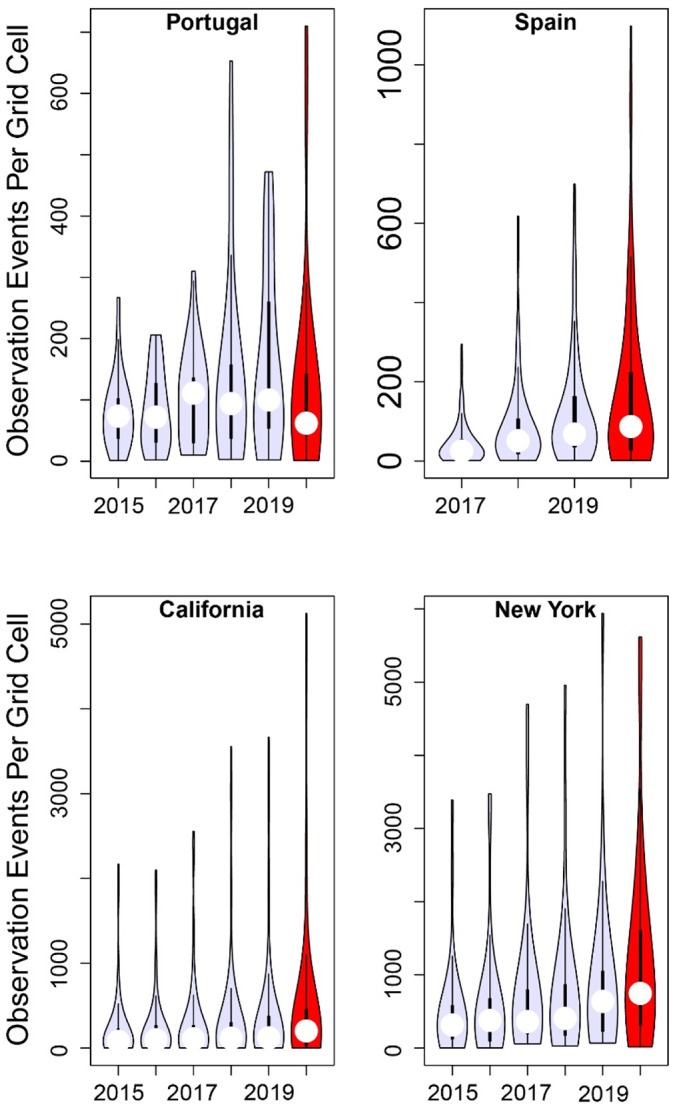
The numbers of observation events in April 2020 were largely consistent with the patterns of interannual change across prior years. Data points were the numbers of observation events within each hexagonal grid cell inside each political unit. The width of each vertical bar of these violin plots is a smoothed representation of the proportion of grid cells with a given number of observation events. White dots within the “violins” are the median number of observation events, and thicker black bars denote the inter-quartile ranges.

We found no statistical evidence that the numbers of observations per grid cell in April 2020 differed from the expected trend of increasing average numbers seen in prior years, with AIC-based support spread across most of the models in all four political units. Because different aspects of the shapes of these distributions could vary among years, we statistically tested whether any of three moments of distribution — mean, variance or skewness — were consistently different in 2020 relative to the prior years. With the data from Spain, model support was spread across the models, which were all within ΔAIC <5.3 of the best-supported model. With the data from Portugal, model support was spread across the converging 17 models (see footnote to Table A1) that were all within ΔAIC <7.1 of the best-supported model. For California data, there were 13 models within ΔAIC ≤8 of the best-supported model. From our analyses of data from New York state, there were 14 models within ΔAIC ≤8 of the best-supported model. For the model sets from each of the four of the political units, all regression parameters describing deviations of 2020 from prior years were estimated with 95% confidence limits that overlapped with zero. In other words, there is no statistical support for the existence of differences in the number of observations per grid cell between April 2020 and April of prior years.

3.2. Changes in the habitats surveyed

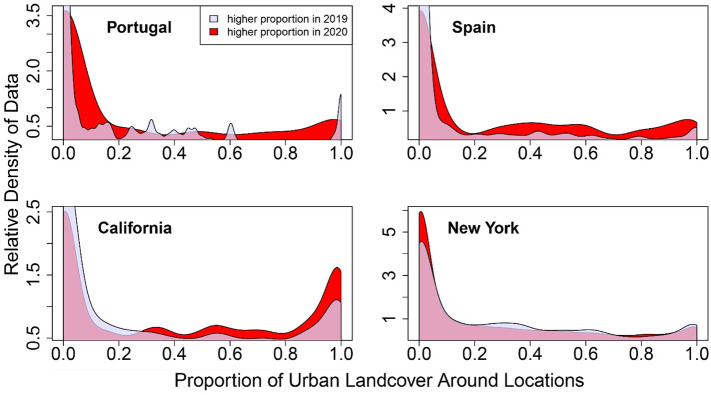
In all four political units, we detected statistical differences in the amounts of urbanized landscape surrounding locations of observation in April 2020 compared to previous years (Fig. 3 ). The mean proportion of urban habitat was higher in 2020 in all four of the political units examined (Fig. 3, Table A4, Table A5, Table A6, Table A7). Not only were the mean proportions of urban habitat different in 2020, but the overall shapes of the distributions changed. The variance in amounts of urban landscape was higher in Portugal for data from 2020. The skewness was lower in 2020 in Spain, Portugal, and California. Kurtosis was higher in 2020 in the data from Portugal and California. For our purposes in this paper, the implication of a change in each moment of distribution is not relevant; instead, the relevant information is that multiple aspects of distribution have changed. On a related topic, note that while the mean is typically the only moment of a distribution that is statistically evaluated for change, only in New York state was the mean the only moment of distribution to vary.

Fig. 3.

The relative frequency with which landscapes containing different proportions of urban landcover were sampled in 2020 compared to 2019. In red (or the darkest shade of grey in greyscale reproduction) are the proportions of urbanization that were more frequently sampled in 2020, relative to 2019. In the data from Portugal, Spain and California, more urbanized landscapes were sample at higher frequency in 2020 than 2019. Qualitatively similar results were found when the data from 2020 were compared to data from years prior to 2019. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table A4.

In Portugal, the proportion of urban landscape in the area around observation locations differed in April 2020 compared to the prior four years. For each of the four moments of the distributions — mean, variance, skewness, and kurtosis — the coefficient describing the 2020 value is the reference category, and the coefficients for all other years describe deviations from the 2020 reference value. Coefficient and standard error values printed in bold font denote coefficients that were estimated with high statistical precision: the 95% confidence intervals around these coefficients did not overlap zero. Thus, if the coefficients for effects in the years 2016–2019 either all positive or all negative, and all are displayed in bold font, then in 2020 a moment of distribution is consistently different than in all prior years examined. The coefficients for describing mean and variance are presented on the logit scale, while skewness and kurtosis are presented on the ln-link scale.

Moment	Predictor	Coefficient	SE
Mean	Intercept (2020)	−0.53	0.03
	Year (2016)	−0.14	0.05
	Year (2017)	−0.20	0.05
	Year (2018)	−0.29	0.04
	Year (2019)	−0.31	0.04
Variance	Intercept (2020)	0.34	0.03
	Year (2016)	−0.20	0.05
	Year (2017)	−0.21	0.04
	Year (2018)	−0.44	0.03
	Year (2019)	−0.31	0.04
Skewness	Intercept (2020)	0.09	0.04
	Year (2016)	1.03	0.06
	Year (2017)	0.88	0.05
	Year (2018)	0.24	0.05
	Year (2019)	0.68	0.05
Kurtosis	Intercept (2020)	−1.70	0.07
	Year (2016)	−0.90	0.17
	Year (2017)	−0.67	0.12
	Year (2018)	−0.79	0.11
	Year (2019)	−0.48	0.11

Table A5.

In Spain, the mean proportion of urban landscape in the area around observation locations was higher in April 2020 compared to the prior four years. For each of the four moments of the distributions — mean, variance, skewness, and kurtosis — the coefficient describing the 2020 value is the reference category, and the coefficients for all other years describe deviations from the 2020 reference value. Coefficient and standard error values printed in bold font denote coefficients that were estimated with high statistical precision: the 95% confidence intervals around these coefficients did not overlap zero. Thus, if the coefficients for effects in the years 2017–2019 either all positive or all negative, and all are displayed in bold font, then in 2020 a moment of distribution is consistently different than in all prior years examined. The coefficients for describing mean and variance are presented on the logit scale, while skewness and kurtosis are presented on the ln-link scale.

Moment	Predictor	Coefficient	SE
Mean	Intercept (2020)	−0.06	0.01
	Year (2017)	−0.57	0.03
	Year (2018)	−0.28	0.02
	Year (2019)	−0.34	0.02
Variance	Intercept	0.02	0.01
	Year (2017)	−0.01	0.03
	Year (2018)	0.09	0.02
	Year (2019)	0.003	0.02
Skewness	Intercept	−0.25	0.02
	Year (2017)	1.22	0.04
	Year (2018)	0.98	0.03
	Year (2019)	0.86	0.03
Kurtosis	Intercept	−2.45	0.03

Table A6.

In California, the mean, variance and kurtosis of the proportion of urban landscape in the area around observation locations differed in April 2020 compared to the prior four years. For each of the four moments of the distributions — mean, variance, skewness, and kurtosis — the coefficient describing the 2020 value is the reference category, and the coefficients for all other years describe deviations from the 2020 reference value. Coefficient and standard error values printed in bold font denote coefficients that were estimated with high statistical precision: the 95% confidence intervals around these coefficients did not overlap zero. Thus, if the coefficients for effects in the years 2016–2019 either all positive or all negative, and all are displayed in bold font, then in 2020 a moment of distribution is consistently different than in all prior years examined. The coefficients for describing mean and variance are presented on the logit scale, while skewness and kurtosis are presented on the ln-link scale.

Moment	Predictor	Coefficient	SE
Mean	Intercept	−0.03	0.01
	Year (2016)	−0.29	0.01
	Year (2017)	−0.27	0.01
	Year (2018)	−0.20	0.01
	Year (2019)	−0.19	0.01
Variance	Intercept	0.07	0.01
	Year (2016)	−0.01	0.01
	Year (2017)	0.01	0.01
	Year (2018)	0.04	0.01
	Year (2019)	0.01	0.01
Skewness	Intercept	−1.07	0.01
	Year (2016)	0.48	0.02
	Year (2017)	0.53	0.02
	Year (2018)	0.34	0.02
	Year (2019)	0.42	0.02
Kurtosis	Intercept	−1.67	0.02
	Year (2016)	−0.57	0.03
	Year (2017)	−0.43	0.03
	Year (2018)	−0.33	0.03
	Year (2019)	−0.25	0.03

Table A7.

In New York, the mean proportion of urban landscape in the area around observation locations was lower in April 2020 compared to the prior four years. For each of the four moments of the distributions — mean, variance, skewness, and kurtosis — the coefficient describing the 2020 value is the reference category, and the coefficients for all other years describe deviations from the 2020 reference value. Coefficient and standard error values printed in bold font denote coefficients that were estimated with high statistical precision: the 95% confidence intervals around these coefficients did not overlap zero. Thus, if the coefficients for effects in the years 2016–2019 either all positive or all negative, and all are displayed in bold font, then in 2020 a moment of distribution is consistently different than in all prior years examined. The coefficients for describing mean and variance are presented on the logit scale, while skewness and kurtosis are presented on the ln-link scale.

Moment	Predictor	Coefficient	SE
Mean	Intercept	−0.56	0.01
	Year (2016)	−0.10	0.01
	Year (2017)	−0.09	0.01
	Year (2018)	−0.07	0.01
	Year (2019)	−0.04	0.01
Variance	Intercept	0.07	0.01
	Year (2016)	−0.01	0.01
	Year (2017)	−0.02	0.01
	Year (2018)	0.01	0.01
	Year (2019)	0.03	0.01
Skewness	Intercept	−0.43	0.01
	Year (2016)	0.06	0.02
	Year (2017)	−0.05	0.02
	Year (2018)	−0.15	0.02
	Year (2019)	−0.23	0.02
Kurtosis	Intercept	−2.91	0.03
	Year (2016)	−0.02	0.05
	Year (2017)	0.07	0.05
	Year (2018)	0.15	0.05
	Year (2019)	0.07	0.05

Observers in Spain, Portugal and California made fewer observations near wetland habitat in April 2020 than in the preceding years; we found no consistent pattern of inter-annual variation in the data from New York (Table 1 ).

Table 1.

Estimated regression coefficients describing the differences in the probability of an observation event in April being near wetland habitat among years. Coefficients are from the single logistic regression model fitted to data from each of the four political units separately. These models were parameterized so that the April 2020 proportion of observations near any wetlands is the intercept/reference value, and the coefficients for all earlier years represent deviations from the 2020 proportions. Thus, positive values for regression coefficients for the years prior to 2020 indicate that the proportion near wetlands were higher in these years than in 2020. Coefficients and standard errors in bold font indicate coefficients for which the 95% confidence intervals did not overlap with zero, indicating statistically reliable estimates. The final column, presenting the estimated proportions of observation events made near wetlands, were calculated based only on the fixed effect in the model (i.e. setting the random effect coefficient to zero).

Region	Predictor	Coefficient	SE	Proportion near wetlands
Spain	Intercept (2020)	−3.74	0.31	0.0232
	Year (2017)	1.29	0.06	0.0796
	Year (2018)	1.09	0.05	0.0660
	Year (2019)	1.04	0.05	0.0627
Portugal	Intercept (2020)	−3.57	0.43	0.0274
	Year (2016)	0.43	0.09	0.0414
	Year (2017)	0.62	0.09	0.0497
	Year (2018)	0.44	0.08	0.0418
	Year (2019)	0.83	0.08	0.0610
California	Intercept (2020)	−3.46	0.31	0.0305
	Year (2016)	0.38	0.03	0.0440
	Year (2017)	0.44	0.03	0.0468
	Year (2018)	0.27	0.03	0.0396
	Year (2019)	0.21	0.02	0.0374
New York	Intercept (2020)	−1.97	0.37	0.123
	Year (2016)	−0.005	0.02	0.122
	Year (2017)	0.07	0.02	0.131
	Year (2018)	0.04	0.02	0.127
	Year (2019)	0.07	0.02	0.130

3.3. Changes in observer effort

We found statistical evidence that count durations varied between 2020 and prior years in both Spain and California. For the data from Spain both the mean and variance of observation durations were lower in 2020 than in any of the prior years (Table A8). The best-supported model for data from California modelled only the mean count duration as varying among years, and mean count duration was lower in April 2020 than in the four prior years (Table A8). For Portugal the best-supported model describes inter-annual variation only in mean duration of the observation period, but in the years prior to 2020 the mean durations of observation periods were both higher and lower than in 2020 (Table A8). The best-supported model for data from New York state only modelled skewness of count durations to vary among years, with mean and variance being constant. However, while there were year-to-year differences in skewness, the observations in April 2020 did not differ consistently from those in all other years, and the skewness of count durations was most similar between 2019 and 2020 (Table A8). Given that several of the models did not converge to solutions (see Table A8), this emphasizes the challenges of identifying whether or how count durations varied among years given the presence of the trunctated response variable.

Our prediction that stationary counts would be more common in 2020 was confirmed, except in New York state (Table 2 ). In Spain, Portugal, and California a greater proportion of observation periods were stationary counts in April 2020 compared to April of prior years. This change was most dramatic in Spain, where the proportion of stationary counts was over 80% in 2020, more than doubling the percentage of any of the prior three years. In all three of the aforementioned political units, the 95% confidence intervals around these estimates did not overlap zero, meaning that these differences were statistically robust. New York state was the exception, with only one of the four prior years having a lower proportion of stationary counts; only 2 of these 4 differences from the 2020 proportion of stationary counts were statistically robust, and both of these coefficients were for larger, and not smaller, proportions of stationary counts in prior years.

Table 2.

Estimated regression coefficients describing the differences in the probability of an observation event being a stationary (i.e. point) count among years, in April. Coefficients are from the single logistic regression model fitted to data from each of the four political units separately. These models were parameterized so that the April 2020 proportion of stationary counts is the intercept/reference value, and the coefficients for all earlier years represent deviations from the 2020 proportions. Thus, negative values for regression coefficients for the years prior to 2020 indicate that the proportion of stationary counts was lower in these years than in 2020. Coefficients and standard errors in bold font indicate coefficients for which the 95% confidence intervals did not overlap with zero, indicating statistically reliable estimates. The final column, presenting the estimated proportions of observation events that were from stationary counts, was calculated calculating based only on the fixed effect in the model (i.e. setting the random effect coefficient to zero).

Region	Predictor	Coefficient	SE	Proportion stationary
Spain	Intercept (2020)	1.59	0.06	0.831
	Year (2017)	−1.97	0.04	0.408
	Year (2018)	−2.13	0.03	0.368
	Year (2019)	−2.34	0.03	0.322
Portugal	Intercept (2020)	0.12	0.08	0.529
	Year (2016)	−1.13	0.07	0.267
	Year (2017)	−0.89	0.06	0.316
	Year (2018)	−0.32	0.05	0.450
	Year (2019)	−0.58	0.05	0.386
California	Intercept (2020)	−0.39	0.05	0.404
	Year (2016)	−0.40	0.02	0.313
	Year (2017)	−0.36	0.02	0.322
	Year (2018)	−0.45	0.02	0.303
	Year (2019)	−0.44	0.02	0.303
New York	Intercept (2020)	−0.19	0.07	0.453
	Year (2016)	0.13	0.02	0.486
	Year (2017)	0.10	0.02	0.478
	Year (2018)	0.0002	0.02	0.453
	Year (2019)	−0.001	0.02	0.453

Only for the two U.S. states did we find statistical evidence that the distribution of travel distances was consistently different in 2020 compared to prior years. We fitted a set of 7 models (Table A3) to the travel-distance data from each country or state. For Portugal's data, the single converging model describes inter-annual differences in mean travel distance, but there was no consistent direction to this variation in the years prior to 2020 (Table A9). The best-supported model from California's data described both higher mean and skewness of travel distances in 2020, relative to prior years, and for data from New York the best supported model was of higher variance in travel distances in 2020 compared to prior years (Table A9). Note that many models, including all models of data from Spain, did not converge to solutions (Table A9). Regarding non-convergence of the models of travel distance in Spain, there were relatively fewer data on travel distance in 2020, given that roughly 80% of all observations were made by stationary observers in April 2020; in contrast, the majority of observations were made by people who were moving during their observation periods in all other political units.

4. Discussion

The effects of the stay-at-home decrees in April 2020 are visible in the way that eBird data were gathered. However, these effects varied among the four political units whose data we examined. We found a reduction in the proportion of travelling observation events, and in the two U.S. states we also found subtle changes in the distances travelled for those observation events that were “travelling counts” (Fig. 4 ). We also found shifts toward making observations in more human-dominated landscapes and away from landscapes containing wetlands, with the exception of New York state for which urban-dominated landscapes were statistically less likely to be sampled in 2020 (Fig. 3; Table 1). Of note, we found that not all of these changes were shifts in averages. We fitted models that simultaneously described changes in mean, variance, skewness, and (for the proportion of urban habitat) kurtosis, and each of these moments of distribution was significantly different in 2020 in one or more analyses. We have not attempted to provide separate interpretations for variance, skewness and kurtosis, but instead for the purpose of our paper we emphasize that changes in any and all of these moments of distribution are associated with changes in the shapes of distributions of observer activity. These changes in distribution of data are best interpreted by examination of graphs that visualize the changes in shapes of distributions, as this encompasses changes in all of the parameters. Our most important conclusion is that any use of eBird data to infer changes in the abundance or distribution of birds in 2020 must account for changes in the checklists that were contributed during periods of altered daily patterns of human activity. This applies to studies designed to infer impacts of the COVID-19 pandemic or those that include data from this year for other purposes. Important aspects of change to data contributions to consider are: the spatial distribution of observers' activity, the specific habitats visited by observers, and the amount and type of effort expended during the collection of these data. If assessments do not account for changes to observer behaviour and data submissions, misleading conclusions will often be made regarding changes to bird populations and communities in 2020.

Fig. 4.

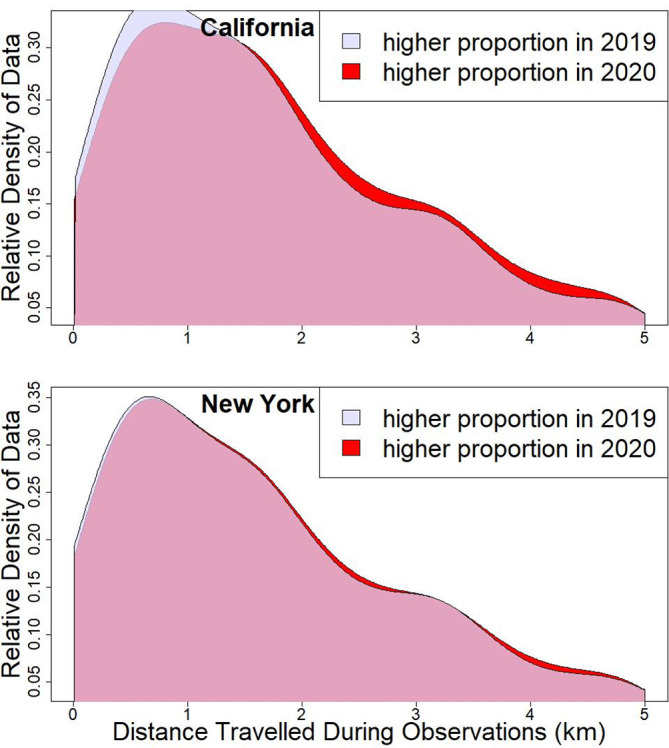
The relative frequency with which observers travelled different distances during observation periods in 2020 compared to 2019. In red (or the darkest shade of grey in greyscale reproduction) are the distances frequently travelled in 2020, relative to 2019. In the data from California mean travel distance was greater in 2020, whereas in the data from New York state only the variance but not the mean travel distance was greater in 2020. Qualitatively similar results were found when the data from 2020 were compared to data from years prior to 2019. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Our results indicate that it is impossible to create a universal prescription for dealing with the impacts of the changed behaviour of bird watchers. Instead, any use of the data from 2020 will require analysts to determine how the COVID-19 pandemic has affected their data and apply the necessary corrections (e.g., Johnston et al., 2020). Further, those analysing data from broad geographic areas will need to consider that the impacts of the pandemic will have varied across their study region. This point is illustrated by the differences found between California and New York in the United States, and especially between the neighbouring countries of Spain and Portugal. The differences that we found in the data from Portugal and Spain are consistent with differences in the severity with which stay-at-home restrictions were imposed in these two countries: in Spain the prohibition on leaving one's place of residence was almost absolute, whereas in Portugal people were able to walk outside within a few kilometers of their homes. Additionally, the restrictions imposed in Portugal were relaxed in the last week of April. We suggest that the differences between New York state and the other three political units (e.g., Fig. 3) illustrate that responses to the COVID-19 pandemic may not have been the only cause of variation in observer behaviour in 2020. The shifting of observer activity away from urban landscapes in New York is consistent both with observers in New York state generally avoiding urban areas, as well as with observers shifting their efforts toward searching areas with a greater diversity of nesting species for the third New York Breeding Bird Atlas. Our findings have a more general implication for the analyses of broad-scale ecological data in that analytical approaches proposed for dealing with spatial variation assume gradual variation through space (e.g., Fink et al., 2010; Osborne et al., 2007; Royle and Young, 2008), but the potential for sharp differences in observer behaviour across political boundaries cannot be ignored.

The fact that habitats have been visited in different proportions in April 2020, compared to the same month in previous years, will result in fewer reported observations of species that are most prevalent in the habitats under-sampled in 2020, such as wetland-associated species, and more observations of species in the over-sampled habitats. Thus, in order to appropriately describe how the distribution and abundance of a bird species may have changed in 2020 compared to previous years, the habitat associations of species and changes in frequency of sampling within habitats need to be incorporated into analyses (Johnston et al., 2020). When using datasets that include detection/non-detection, it is possible to analytically separate the habitats surveyed from the species presence, although care is required to design analyses that will accommodate changes in habitats sampled. With presence-only data (for example iNaturalist or Observation.org) it would be much more challenging to separate these two processes, because at best the sampling of habitats can only be inferred indirectly (Isaac and Pocock, 2015; Isaac et al., 2014).

Different rates of species detection also will have resulted from any differences in the duration of observation periods and distances travelled during non-stationary observation periods. For any specific region these changes in detection frequency will vary with the magnitude of change in observer effort, and will also differ among species. This underlines the importance of including effort variables in models, to describe the heterogeneity in detectability between observations (Kelling et al., 2019). Including observer effort as a predictor variable can be complicated because, for example, 1 h of observation effort or 1 km of distance travelled likely will produce different counts of birds or different lists of species for observers who are in different habitats. Describing such interactions can be a complex task when parametric statistical models are being specified, although machine-learning models such as random forest or boosted regression trees models should automatically detect important interactions among factors that affect detection rates (e.g., Elith et al., 2008).

In conclusion, we found that bird watchers participating in data collection for eBird did alter their behaviours in April 2020 in response to the restrictions on human movement that resulted from the COVID-19 pandemic. Given the magnitude of the change to daily life, it is perhaps notable that the changes observed in eBird data are not more substantial. Nevertheless, the behaviour of observers did change in ways that will require analyses of eBird's data to account for differences in the proportional representation of habitats in observations, and differences in observer effort. While we have only looked for changes in observer activity in four political units, we have found different effects on the activities of project participants among these political units. We expect such differences have occurred globally, given the substantial differences in political and policy responses to the pandemic around the globe and the different environments in which observers live. These regional differences in effects on participants' behaviour will need to be taken into account for most any use of these data. This applies to examining whether behaviour and local distribution of wild animals was altered by pandemic-related changes in human behaviour. This conclusion also applies more broadly to the use of data from eBird collected during the pandemic for other purposes including montoring of longer term changes in distribution and abundance. We have only looked at changes in the behaviour of participants in one project, eBird. However, we expect that similar changes in observer behaviour in 2020 have occurred for other projects for which volunteer participants choose how much effort to expend, where to expend their effort, and when to expend their effort. Thus, similar analytical challenges await anyone using data collected by these other projects during the COVID-19 pandemic.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.