Investigating the Stability of mcDESPOT Myelin Water Fraction Values Derived Using a Stochastic Region Contraction Approach

Abstract

Purpose

Multicomponent driven equilibrium single pulse observation of T₁ and T₂ (mcDESPOT) is an alternative to established multi-echo T₂-based approaches for quantifying myelin water fraction, affording increased volumetric coverage and spatial resolution. A concern with mcDESPOT, however, is the large number of model parameters that must be estimated, which may lead to non-unique solutions and sensitivity to fitting constraints. Here we explore mcDESPOT performance under different experimental conditions to better understand the method’s sensitivity and reliability.

Methods

To obtain parameter estimates, mcDESPOT uses a stochastic region contraction (SRC) approach to iteratively contract a pre-defined solution search-space around a global optimum. The sensitivity of mcDESPOT estimates to SRC boundary conditions, and tissue parameters, was examined using numerical phantoms and acquired in vivo human data.

Results

The SRC approach is described and shown to return robust myelin water estimates in both numerical phantoms and in vivo data under a range of experimental conditions. However, care must be taken in choosing the initial SRC boundary conditions, ensuring they are broad enough to encompass the ‘true’ solution.

Conclusions

Results suggest that under the range of conditions examined, mcDESPOT can provide stabile and precise values.

Introduction

Non-invasive myelin content imaging may be potentially useful in a variety of neurological disorders, such as multiple sclerosis (MS), as well as in investigations of white matter plasticity during learning, development, and rehabilitation. Multi-component analysis of relaxation data (MCR) has been shown to inform on white matter microstructure, providing quantitative measures preferentially sensitive to myelin content^1–6.

The established gold standard MCR approach is the multi-echo Carr-Purcell-Meiboom-Gill (CPMG) T₂ method^2–6. An attractive alternative approach to myelin water imaging, termed mcDESPOT^7,8 (multi-component Driven Equilibrium Single Pulse Observation of T₁ and T₂), has recently been presented and applied to studies of neurodevelopment and MS-related demyelination^9–13. mcDESPOT utilizes spoiled and fully refocussed steady state imaging (SPGR and bSSFP, respectively), potentially affording improved SNR, reduced acquisition times, and increased spatial resolution and volumetric coverage compared to the established T₂ approach, though at the expense of a more complicated signal model that must include the effects of water exchange. While preliminary mcDESPOT results are promising, demonstrating myelin development in healthy infants⁹ that closely mirrors the expected spatio-temporal pattern, and myelin loss in MS that reflects clinical disability¹¹, mcDESPOT-derived myelin water fraction values (VF_M) are consistently larger than corresponding CPMG T₂-based myelin water fraction values⁸. While the cause of this discrepancy remains unknown, potential explanations include magnetization transfer, diffusion effects, off-resonance effects, an ill-posed tissue model, or an ill-conditioned fitting approach.

This last explanation was recently explored theoretically by statistically examining the stability of the mcDESPOT solution when either completely unconstrained (i.e. parameters could have any value regardless of their biological plausibility); or with individual parameters held fixed¹⁴. Results showed that derived mcDESPOT VF_M values were non-unique and unstable, not surprising given the large number of free-parameters (nine) and the near infinite solution space. This theoretical result, however, contradicts prior numerical analysis of mcDESPOT precision⁸, as well as in vivo results^9–13, which are performed using a constrained solution-space approach that limits the range of each model parameter.

In this work, we sought to further explore mcDESPOT VF_M stability by examining the influence of solution-space constraints (boundaries or priors) used in the fitting on both simulated numerical data and in vivo data. We find that mcDESPOT values are stable and can be derived precisely with little influence of fitting constraints, provided the fitting boundaries are chosen to encompass the likely solution.

Method

Theory & Fitting

Detailed previously^7,8, mcDESPOT comprises at least 8 T₁-weighted SPGR images and 8 T₁/T₂-weighted bSSFP images, each at two different radio-frequency (RF) phase-cycling patterns. To these data, a 3-pool model⁸ is fit that includes nine free parameters: T_1,M, T_2,M, T_1,IE, T_2,IE, T_1,F, T_2,F, τ_M, VF_M and VF_F, where the M, IE and F subscripts denote the myelin, cellular and CSF water, τ_M is the myelin water residence time, and VF_F is the CSF water volume fraction. An additional parameter, Δω, the off-resonance with respect to the central water peak may also be fit or estimated from a B₀ field mapping scan. Fitting of the proton density terms are avoided by normalizing the SPGR and bSSFP signals by their mean values. Due to the influence of T₁ on the SPGR and bSSFP signals, water exchange is included between the myelin-associated and intra/extra-cellular water pools.

To fit this model, a variety of fitting approaches, including genetic algorithms⁷, simulated annealing¹⁵, and swarming¹⁵, or stochastic region contraction (SRC)^8,17 may be used. In SRC, a broad search-space is iteratively contracted around the optimal solution. Applied to mcDESPOT, the default search-space encompasses a broad range taken from prior literature reports^2–6, except for the axonal water T_1,IE range, which is calculated based on the single-component T_1,DESPOT value derived using DESPOT1. When VF_M is 0, T_1,IE must equal T_1,DESPOT, thus, the lower bound for T_1,IE is set to 0.9×T_1,DESPOT to allow the solution to converge around this value. To determine the upper bound for T_1,IE (T_1,max), we calculate the T_1,IE that would provide the measured T_1,DESPOT with the maximum VF_M and minimum T_1,M. This provides a safe upper bound that, in general, exceeds 5000ms.

Beyond the defined search-space, two additional constraints are applied: VF_IE = 1.00 − (VF_M + VF_F), and VF_M + VF_F ≤ 0.95; i.e., there are only three water pools; and T_1,M < T_1,IE < T_1,F and T_2,M < T_{2, IE} < T_2,F.

The SRC algorithm proceeds by creating N_S = 5000 random sets of <T_1,M, T_1,IE,T_1,F, T_2,M, T_2,IE, T_2,F, VF_M, VF_F, τ_M> chosen from the defined search-space. In our implementation, values are chosen from a uniform distribution for the first iteration, and from a Gaussian distribution for subsequent iterations. This speeds contraction and reduces the number of iterations required, however, at the potential expense of converging on a non-optimal solution. For each parameter set, theoretical SPGR and bSSFP signals are estimated, normalized by their mean, and the sum-of-squares residuals calculated with respect to the acquired data. From the N_S potential solutions, the top N_T = 50 with the lowest residuals are selected and the minimum and maximum values of each parameter set the new bounds of the search-space. To help avoid inadvertently over-contracting, the searchspace is expanded by (maximum-minimum)/N_T. Finally, a Gaussian is fit to the top solutions to guide the creation of the N_S sets in the following iteration. When creating each set from the Gaussian distributions, if the chosen value exceeds the parameter bounds, a new sample is selected.

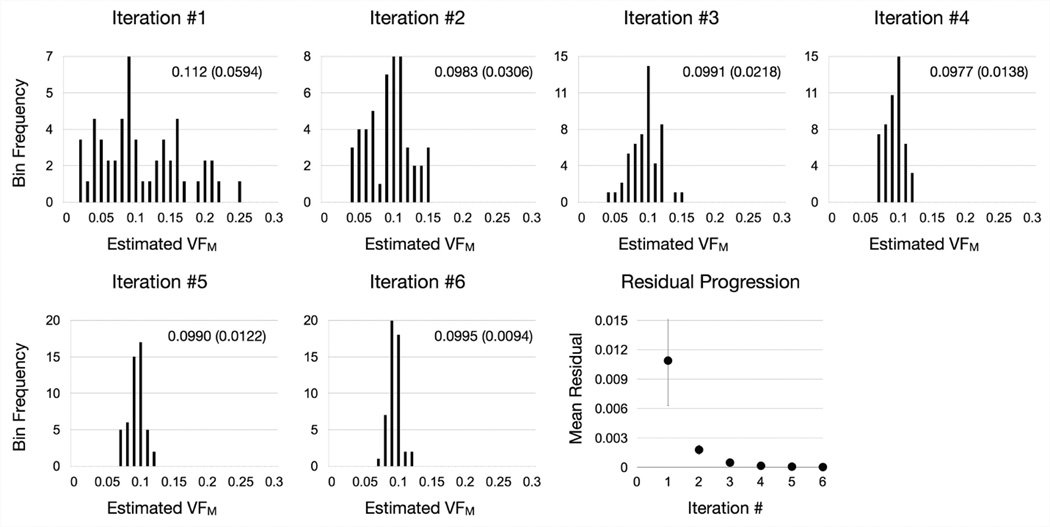
The algorithm is repeated until the difference between the minimum and maximum values of each parameter drops below 1%, or until a set number of repeats (N_R = 7) are performed. For additional precision, N_R may be increased at the expense of computation time. An illustration of the algorithm applied to a numerical phantom with T_1,M = 465ms, T_1,IE = 965ms, T_1,F = 3500ms, T_2,M = 12ms, T_2,IE = 90ms, T_2,F = 250ms, VF_F = 0.0, τ_M = 125ms, and VF_M = 0.10, is provided in Fig. 1, showing the contraction of the estimates around the solution (VF_M = 0.10), with the expected decrease in the mean residual. For each voxel, computation time is 4s for N_R = 7 on a 2.6GHz Intel Core i7 processor.

Figure 1.

Convergence of SRC algorithm around the true value of VF_M = 0.1 illustrated by histograms of the top 50 solutions from each algortihm iteration and the corresponding mean residual of the top 50 solutions (error bars denote the standard deviation) at each step. The mean estimated VF_M value (and standard deviation) are also provided for each step.

Theoretical Simulations

Simulation #1: Effect of Initial SRC Boundary Conditions

Systematic investigation of mcDESPOT VF_M estimate accuracy and precision over all T_1,M, T_1,IE, T_1,F, T_2,M, T_2,IE, T_2,F, VF_M, VF_F, and τ_M combinations is impractical, as even 10 examples of each parameter would lead to 10⁹ possible combinations. We instead investigated the influence of the initial SRC bounds using four generic numerical phantoms with common T_1,M = 465ms, T_1,IE = 965ms, T_1,F = 3500ms, T_2,M = 12ms, T_2,IE = 90ms, T_2,F = 250ms, VF_F = 0.0, and τ_M = 125ms, but varied VF_M values of (0.05, 0.10, 0.15 and 0.20). For simulation #1, the SRC bounds for each parameter; combination of parameters (T_1,M, T_1,IE and VF_M, T_2,M, T_2,IE and VF_M); and all parameters, were systematically enlarged with the VF_M accuracy and precision calculated. Default boundary conditions were as follows: 0.00 < VF_M < 0.35; 300ms < T_1,M < 650ms; 1ms < T_2,M < 30ms; 0.9×T_1,DESPOT < T_1,IE < T_1,MAX; 50ms < T_2,IE < 165ms; 25ms < τ_M < 600ms. Expanded bounds were: 0.00 < VF_M < 0.5; 50ms < T_1,M < 1000ms; 1ms < T_2,M < 100ms; 0.7×T_1,DESPOT < T_1,IE < 1.6×T_1,MAX; 20ms < T_2,IE < 350ms; and 1ms < τ_M < 1000ms. In all simulations, algorithm parameters were constant: N_S = 5000, N_T = 50, and N_R = 7.

For each parameter or combination, the simulation was repeated 1000 times with Gaussian-distributed noise added to the theoretical SPGR and bSSFP signal values such that the peak SPGR signal had a signal-to-noise ratio of 100 (comparable to in vivo mcDESPOT data). Simulated acquisition parameters were: SPGR TR = 5.6ms, flip angles = {4, 5, 6, 7, 9, 11, 14, 18}°; SSFP TR = 4.4ms, flip angles = {12, 16, 19, 23, 27, 34, 50, 70}°, with phase-cycling patterns of 0° and 180°. No off-resonance was assumed in the simulated data.

Accuracy was defined as the absolute percent difference between the mean of the 1000 estimations and the known value, and precision was calculated as the mean divided by the standard deviation.

Simulation #2: Variable Numerical Phantom Parameters

Using the default search-space bounds, we next altered the values of each parameter of the numerical phantom (except T_1,F, T_2,F, since these are modeled as pure water). Altered values were: T_1,M = (365, 415, 515)ms, T_1,IE = (765, 1165, 1365)ms, T_2,M = (6, 18, 24)ms, T_2,IE = (75, 105, 120)ms, and τ_M = (75, 200, 275)ms. VF_M accuracy and precision were calculated as defined above for each case.

Simulation #3: mcDESPOT Performance vs. VF_M

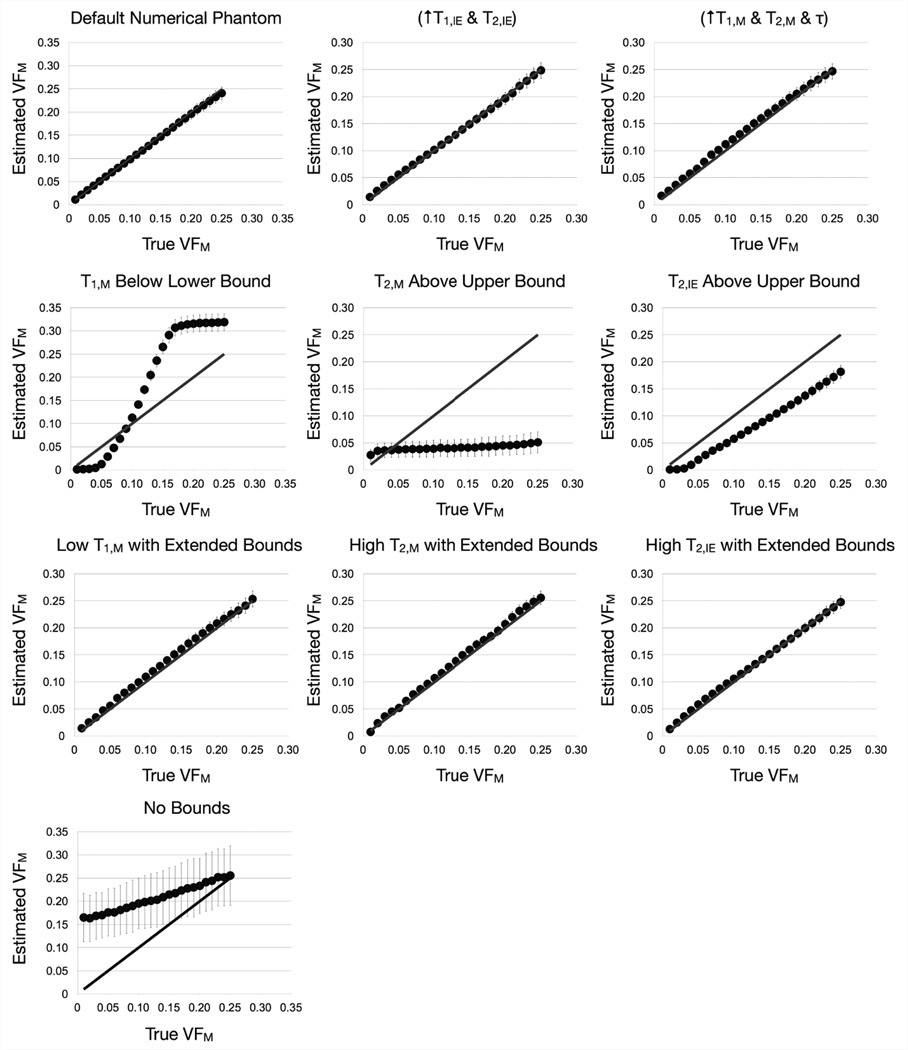
We also sought to investigate its performance across a VF_M continuum from 0.01 to 0.25 under a variety of conditions: (1) the default numerical phantom; (2) a case mimicking inflammation or axonal swelling, with increased T_1,IE (to 1500ms) and T_2,IE (to 150ms); and (3) a case mimicking increased space between the myelin layers, with increased T_1,M (to 600ms), T_2,M (to 25ms), and τ (to 250ms). We also sought to explore the response of the algorithm when the true parameter value lies outside of the initial boundary conditions, i.e., when T_1,M is 120ms; T_2,M = 50ms; and T_2,IE = 200ms. Finally, we examined the effect of eliminating all boundary constraints, setting the bounds of each parameter to: T_1,M, T_1,IE and T_1,F = 0–5000ms; T_1,IE = 0–5000ms; T_2,M, T_2,IE, and T_2,F = 0–5000ms; τ = 0–10000ms; VF_M = 0–1 and VF_F = 0–1.

Simulation #4: Signal Ambiguity

Prior analysis has shown that different parameter combinations can yield similar SPGR and bSSFP signal profiles⁸, making it difficult to accurately disambiguate them depending on SNR. Three such parameter combinations are: <T_1,M, T_1,IE, T_2.M, T_2,IE, VF_M, τ> = <415, 970, 12, 80, 0.15, 90>, <527, 965, 16.6, 83.7, 0.23, 149> and <579, 965, 19.3, 86.9, 0.28, 200>. As above, we examined the ability to differentiate between these combinations (assuming T_1,F = 3500ms, T_2,F = 250ms and VF_F = 0) with SNR values of 100 and 25. VF_M values were estimated using the default bounds.

In Vivo Imaging

Simulations results were complimented with in vivo data from a healthy infant and adult, as well an adult female MS patient. VF_M maps were calculated using the default, and each of the expanded boundary conditions used in simulation #1. Participant details and data acquisition parameters are provided in Table 1. All data were acquired on a Siemens Tim Trio 3T scanner with a 12 (infant) or 32 channel head RF array. All imaging was performed with appropriate IRB approval from the host institutions and informed consent. Total acquisition time for the infant was approx. 18 minutes, while for the adult, acquisition time was approx. 12 minutes.

Table 1.

In vivo Acquisition parameters

Healthy 12-Month Old Infant
	SPGR	IR-SPGR	bSSFP
Field of View	(18 × 18 × 16)cm3	(18 × 18 × 16)cm3	(18 × 18 × 16)cm3
Slice Thickness (mm)	1.8	3.6	1.8
Imaging Matrix	96 × 96 × 88	96 × 96 × 44	96 × 96 × 88
TE/TR/TI (ms)	5.7/14	5.7/14/600, 900	5.56/11.1
α (degrees)	(2,3,4,5,6,7,10,14)	5	(12,16,19,23,27,35, 50,70)
Bandwidth (Hz/Pixel)	350	350	350
Healthy 55 Year-Old Adult
	SPGR	IR-SPGR	bSSFP
Field of View	(22 × 22 × 16)cm3	(22 × 22 × 16)cm3	(22 × 22 × 16)cm3
Slice Thickness (mm)	1.7	1.7	1.7
Imaging Matrix	124 × 124 × 96	124 × 124 × 48	124 × 124 × 96
TE/TR/TI (ms)	2.4/5.4	2.4/5.4/450	2.2/4.4
α (degrees)	(3,4,5,6,7,9,13,18)	5	(10,13,17,23,30,43, 60)
Bandwidth (Hz/Pixel)	450	450	450
47 Year-Old MS Patient Expanded Disability Status Scale = 4.0, Disease Duration = 36 months
	SPGR	IR-SPGR	bSSFP
Field of View	(22 × 22 × 16)cm3	(22 × 22 × 16)cm3	(22 × 22 × 16)cm3
Slice Thickness (mm)	1.7	1.7	1.7
Imaging Matrix	128 × 128 × 96	128 × 128 × 48	128 × 128× 96
TE/TR/TI (ms)	2.6/5.6	2.6/5.6/450	2.3/4.6
α (degrees)	(3,4,5,6,7,9,13,18)	5	(10,13,16,23,30,43,60)
Bandwidth (Hz/Pixel)	400	400	560

Following acquisition, data were linearly co-registered to account for subtle intra-scan motion, non-brain parenchyma signal removed, B₀ and B₁ field calibration maps calculated, and the 10 VF_M maps calculated^8,18. Average VF_M values were determined from regions of interest (ROIs) placed throughout white and gray matter in each volunteer and statistically compared across the 10 maps using a paired t-test with a significant difference defined as p < 0.05 (uncorrected for multiple comparisons).

Results

Theoretical Simulation Results

Simulations #1 and #2

Results from simulations #1 and #2 are summarized as follows. In all cases, varying the initial algorithm boundary conditions, or the phantom parameter values, yielded little deviation in the estimated VF_M values, though estimate accuracy and precision increased with VF_M. For the default boundary conditions in simulation #1, the estimated mean VF_M and standard deviation values were: 0.054 (±0.005), 0.107 (±0.008), 0.148 (±0.01), and 0.201 (±0.011). For the remaining cases: Expanded T_1,M: 0.052 (±0.005), 0.102 (±0.008), 0.147 (±0.01), and 0.202 (±0.011); Expanded T_2,M: 0.053 (±0.005), 0.099 (±0.008), 0.146 (±0.01), and 0.201 (±0.011); Expanded T_1,IE: 0.055 (±0.005), 0.102 (±0.008), 0.158 (±0.01), and 0.20 (±0.011); Expanded T_2,IE: 0.054 (±0.005), 0.102 (±0.008), 0.158 (±0.01), and 0.20 (±0.011); Expanded T_1,M & T_1,IE: 0.054 (±0.005), 0.107 (±0.008), 0.148 (±0.01), and 0.203 (±0.011); Expanded T_2,M & T_2,IE: 0.044 (±0.005), 0.112 (±0.008), 0.144 (±0.01), and 0.202 (±0.011); Expanded τ: 0.053 (±0.005), 0.103 (±0.008), 0.154 (±0.01), and 0.20 (±0.011); and All Expanded: 0.055 (±0.005), 0.104 (±0.008), 0.153 (±0.01), and 0.201 (±0.011). Averaged across all conditions, mean estimated VF_M (and corresponding mean absolute % error and precision) were: 0.053 (7.8%, 10.2); 0.104 (4.1%, 13.1); 0.148 (2.6%, 14.7); and 0.201 (0.6%, 18.8).

Similarly, for simulation #2, estimated mean VF_M and standard deviation values for each parameter variation were: For varied T_1,M: 0.101 (±0.009), 0.111 (±0.01), and 0.098 (±0.007); varied T_2,M: 0.113 (±0.007), 0.097 (±0.011), and 0.096 (±0.013); varied T_1,IE: 0.106 (±0.01), 0.094 (±0.009), and 0.097 (±0.007); varied T_2,IE: 0.106 (±0.009), 0.091 (±0.006), and 0.092 (±0.006); varied VF_F: 0.109 (±0.009), 0.104 (±0.01), and 0.109 (±0.011); and varied τ: 0.105 (±0.012), 0.096 (±0.01), and 0.094 (±0.009). Thus, varying the parameters of the numerical phantom resulted in subtle deviation of the estimated VF_M, with the absolute % error ranging from a minimum of 1% (when T_1,M = 365ms), to a maximum of 11.5% (when T_2,M = 6ms). These results show VF_M is not independent of the other parameters. For example, when T_2,M was varied from 6ms to 24ms, a change in the estimate of VF_M from 0.107 to 0.096 (10.3% difference) was observed. Similar results were observed for T_2,IE, with a 12.3% difference between the highest and lowest estimate. For the remaining parameters, the minimum-maximum percent difference were less than 6% (5.4% for T_1,M; 5.8% for T_1,IE; 4.6% for VF_F; and 5.8% for τ). Thus, VF_M is most susceptible to T₂ estimates errors. This finding agrees with prior results⁷, showing correlations between VF_M and T_2,M and T_2,IE of 0.87 and 0.86. However, a dependence between myelin water fraction and T₂ is not unique to mcDESPOT, having been previously demonstrated in the CPMG approach¹⁹.

Simulation #3

Results of simulation #3 are displayed in Fig. 2 and Table 1, and show that provided the initial SRC search-space encompasses the true solution, the algorithm tends to converge to the correct solution, with a mean accuracy of 2.7% for the default phantom; 5.1% when T_1,IE and T_2,IE were increased; and 9.2% difference when T_1,M, T_2,M and τ were increased. However, if the algorithm is over-constrained, widely inaccurate VF_M results are obtained. When the T_1,M, T_2,M and T_2,IE boundaries were expanded, good correspondence between the estimated VF_M values and the ‘true’ value with percent error values of 8.8%, 7.4% and 6.1%, respectively. This result highlights the importance of ensuring broad initial boundaries, particularly when dealing with pathology that may cause unanticipated changes in tissue parameters. Examination of all derived parameter maps can also provide insight into possible boundary issues. For example, when the true values were outside of the boundary conditions, the calculated T_1,M values were clustered at the lower boundary, while the T_2,M and T_2,IE values were clustered at the upper boundary (data not shown). This clustering was not seen when the boundaries were expanded to encompass the true solution. Therefore, it is important to examine all maps when performing mcDESPOT in vivo and in pathology to ensure parameters are not converging to one boundary.

Figure 2.

Results from the third simulation that examined estimated VF_M over a continuum of “true” VF_M values under differential conditions. Plotted points represent the mean estimated value with the standard deviation shown by the error bars. The grey line denotes unity between the ‘true’ and estimated values. While the method performs well provided the solution is within the initial parameter boundaries, it provides spurious results when this condition is not met (middle row). The final image corresponds to the case where minimal bounds were imposed. In this case accuracy and precision drop significantly, as was demonstrated in prior theoretical analysis¹³.

Finally, we examined the case where the search-space was unbounded. Results of this simulation agree with prior theoretical analysis¹⁴, with the estimated values having extremely poor precision (mean = 3.5) and, at low VF_M (less than 0.15), poor accuracy. It is interesting to note, however, that despite the low accuracy and precision of the estimates, there is still a linear relationship between the estimated and true values and, thus, changes in the estimated value are still reflective of changes in the true value.

Results from simulation #3 clearly demonstrates the need to limit the SRC search-space in order to achieve acceptable accuracy and prevision, however, over-constraining can also lead to inaccuracy and aberrant behavior of the algorithm.

Simulation #4: Signal Ambiguity

Examining the ability to discriminate between closely matching signal curves, VF_M estimates were calculated for 3 parameter sets under high and low noise conditions with ‘true’ VF_M values of 0.15, 0.23 and 0.28. For the low noise condition, VF_M mean and standard deviation were: Set #1: 0.15 (0.006) ; Set #2: 0.22 (0.011); and Set #3: 0.26 (0.01); and for the high noise condition: Set #1: 0.18 (0.013) ; Set #2: 0.19 (0.018); and Set #3: 0.24 (0.017).

In Vivo Imaging

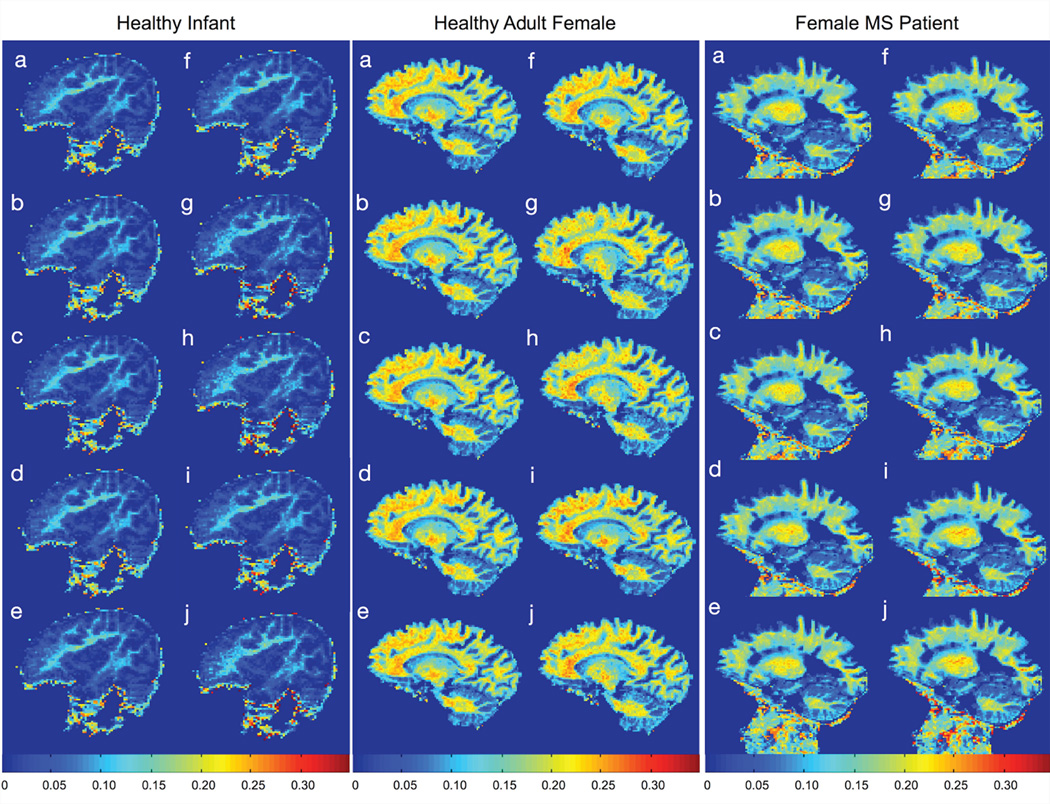
In vivo results are shown in Figs. 3 and 4. Figure 3 displays each of the ten calculated VF_M maps for each participant with the same scaling and display settings. To demonstrate the consistency of the estimated VF_M values across the ten maps, 3 spatially-consistent ROIs were superimposed on each brain and mean and standard deviation values extracted and compared (Fig. 4). In each ROI, no significant difference was calculated between any pair of VF_M values using a paired t-test, uncorrected for multiple comparisons. These results suggest the default SRC boundary conditions used for mcDESPOT fitting are sufficiently broad across a range of biological stages (infant, adult, and MS pathology). Results also further the simulation result showing improved estimate precision with increasing VF_M, as evidence by the error bars on values in grey matter vs. white matter in the infant data. Mean white matter signal-to-noise ratio values for the in vivo data, calculated from the high angle SPGR image were: 124 for the infant, 248 for the healthy adult, and 234 for the MS patient, higher than that modeled in the simulations.

Figure 3.

Comparison of in vivo VF_M maps, corresponding to the same slice, calculated using (a) default model boundaries; and expanded (b) T_1,M boundaries; (c) T_1,IE boundaries; (d) T_1,M and T_1,IE boundaries; (e) τ boundaries; (f) T_2,M boundaries; (g) T_2,IE boundaries; (h) T_2,M and T_2,IE boundaries; (i) VF_M boundaries; and (j) all boundaries.

Figure 4.

Comparison of mean VF_M values taken from gray and white matter ROIs in each participant (left=infant, middle=healthy adult, right=adult MS patient) in each of the 10 calculated VF_M maps. Note the difference in scale between the infant and adult plots. Plotted bars correspond to the ROI mean with the error bars denoting the standard deviation. For each region, no significant difference was found between any combination of the 10 estimates.

Of potential interest is the estimated myelin water T_1,M. Recent investigations of multicomponent T₁ relaxation¹⁷ has suggested a myelin T₁ of approximately 120ms. Values obtained herein are 440±21ms using the default boundaries and 442±20ms using the expanded T_1,M boundaries.

Discussion

Results of this numerical and in vivo analysis show SRC fitting can provide consistent VF_M values under a variety of experimental and algorithmic conditions. However, this analysis does not address the mechanism underlying the discrepancy between mcDESPOT VF_M and established T₂-based myelin water fraction values. Possible explanatory and contributing mechanisms for this difference could include magnetization transfer (MT) effects, diffusion effects, off-resonance effects, or an ill-posed tissue model, none of which can be directly addressed by the analysis herein. However, each makes testable predictions.

MT effects in bSSFP are most pronounced with short repetition times and short RF pulse widths²⁰. Thus, experiments examining mcDESPOT VF_M values as a function of TR and pulse width, whilst maintaining similar flip angles, could shed light on the relative influence of MT. Numerical analysis of MT effects has been performed previously in the context of deriving myelin water estimates using just bSSFP data²¹, showing that MT effects may be negated for RF pulses longer than 2ms, though correction for finite RF pulses becomes necessary. The pulse duration used in the current study was 800us, suggesting these effects may still be present. The work of Lenz et. al.²¹ differs in that all parameters were held fixed apart from VF_M. Examining the dependance of the fixed values, the authors reported subtle deviations in VF_M in response to changes in T_1,M, T_2,M, and τ, but large deviations in response to T_1,IE and T_2,IE. We found similar dependence on T_2,IE, though also found a strong dependence on T_2,M.

Recent work examining orientation differences in susceptibility weighted imaging²² suggest likely differences in the resonance values of proton spins within the myelin sheath compared to those further away. In the current mcDESPOT model, the off-resonance value of all water pools are considered the same. This assumption could be removed from the model, allowing each pool’s Δω to be fit independently, however, this introduces an additional 2 free parameters, likely decreasing precision. Finally, the three-pool tissue model used in mcDESPOT assumes similar T₁ and T₂ values for both the intra and extra-axonal water pools, which may not be correct. Unfortunately, modeling these pools separately is not straight-forward since mcDESPOT includes water exchange. Thus, an accurate model of which pools can exchange is necessary. For example, can intra and extra-axonal water exchange directly (i.e., through the nodes of Ranvier)? Modeling these pools separately would also introduce an additional 4 parameters (T₁, T₂, relative volume fraction, and relative exchange rate), likely necessitating the acquisition of more data to reliably fit.

The need to include exchange is an important distinction between mcDESPOT and CPMG T₂-based approaches. Several attempts have been made to assess the exchange timescale, which have been hindered by its dependence on temperature, pH and tissue system^23–25. τ values obtained in adult brain using mcDESPOT range from 60–200ms, with a mean of 127ms. This value is in broad agreement with prior measurements, with a mean of 200ms^23–25, and suggests strict T₂-based analysis may not need to consider exchange effects.

In this work we have sought to more fully explain the mcDESPOT SRC fitting approach and examine its limitations. We have shown that accurate and reproducible VF_M values can be derived that are independent of initial boundary conditions, provided they are sufficiently broad to encompass the actual solution. It is, therefore, important to examine all derived parameter maps to ensure values are not clustering at boundaries. However, our analysis does not preclude the possibility of non-unique mcDESPOT solutions (i.e, 2 or more VF_M values with other differing parameters that provide the same least-squares residual value), since not all parameter combinations could be systematically examined here. In these cases, the algorithm could jump between possible solutions, or be preferentially biased towards one. If the former, we would expect this to be easily visualized with neighboring voxels in the VF_M map taking on a noise-like appearance without anatomical structure. In the human development and pathology cases previously examined using mcDESPOT^9–13, this has not been reported.

In prior numerical analysis of mcDESPOT stability, results generally showed VF_M measures to have poor precision. This analysis, however, examined either unbounded solutions, or solutions in which one or more parameter was held fixed. In this way, the results of [14] are similar to those of [21], which also showed holding values fixed lead to poor stability. In this work, we show that robust VF_M values can be obtained provided appropriate bounds and image SNR. The main differences between the analysis herein and prior analysis^14,21 are: 1. the use of a three-pool model; 2. a bounded probabilistic fitting approach; 3. the use of RF phase-cycling in the bSSFP acquisitions; and 4. simultaneous estimation of all parameters. Holding 1 or more parameter fixed may introduce or magnify VF_M error since any signal deviation can only be accounted for by the remaining free parameters. As discussed in [14], the use of RF phase cycling yields a substantial improvement in parameter estimate precision, and is necessary to account for B₀ field inhomogeneity²¹. Our analysis does, however, introduce the problems of how to choose the appropriate bounds, and what SNR is acceptable. In general, we have found that examining all parameter maps is important to ensuring correct bounds. When the bounds are too strict, one or more parameter will converge to a boundary. When the bounds are too loose, the resultant VF_M map will appear as noise, lacking anatomical detail. In terms of SNR, we have found 100 provides acceptable results and can be easily achieved in near clinical time-frames (Table 1).

Additional work examining the influence of MT, diffusion or other effects, therefore, is still required to fully understand their affect on mcDESPOT. Finally, while preliminary comparisons between mcDESPOT and myelin histology²⁶ have been performed, more rigorous histological comparisons are required to better understand the limitations of the method and how changes in derived parameters reflect differential pathology.

Table 2.

Summary of simulation #3 results.

Condition	Estimated VFM % Error (Min/Max)	Estimated VFM Precision (Min/ Max)
Default Phantom	2.65 (0.04/9.4)	18.1 (8.9/26.7)
“Inflammation: ↑ T1,IE & T2,IE	5.08 (0.07/30.1)	21.5 (8.4/33.7)
“Myelin Swelling” ↑ T1,M & T2,M & τ	9.22 (0.13/29.7)	11.1 (2.3/19)
T1,M Under Lower Bound	191 (21/686)	24.4 (1.4/42.2)
T2,M Over Upper Bound	210 (9/389)	2.5 (2.4/2.7)
T2,IE Over Upper Bound	229 (38/1142)	15.9 (2.5/22.5)
Low T1,M, Expanded Bounds	8.8 (0.5/30.1)	16.2 (2.9/29.1)
High T2,M, Expanded Bounds	7.4 (2.2/29.2)	17.4 (1.4/40.6)
High T2,IE, Expanded Bounds	6.1 (0.9/22.8)	19.7 (12.8/25.8)
No Bounds	178 (2.2/1550)	3.5 (3.1/4.1)