Determining structures in a native environment using single-particle cryoelectron microscopy images

Abstract

Cryo-electron tomography is a powerful tool for structure determination in the native environment. However, this method requires the acquisition of tilt series, which is time-consuming and severely slows structure determination. By treating the densities of non-target protein as non-Gaussian noise, we developed a new target function that greatly improves the efficiency of recognizing the target protein in a single cryo-electron microscopy image. Moreover, we developed a sorting function that effectively eliminates the model dependence and improved the resolution during the subsequent structure refinement procedure. By eliminating model bias, our method allows using homolog proteins as models to recognize the target proteins in a complex context. Together, we developed an in situ single-particle analysis method. Our method was successfully applied to solve structures of glycoproteins on the surface of a non-icosahedral virus and Rubisco inside the carboxysome. Both data were collected within 24 h, thus allowing fast and simple structural determination.

Graphical abstract

Public summary

• •Structures could be achieved when proteins are overlapped with surroundings free of tilt series
• •The particle detection efficiency is significantly improved
• •Allowing the usage of homolog proteins as templates
• •The throughput of structure determination is remarkably enhanced

Introduction

Considerable progress has been made in recent years in determining the structures of proteins in their native context. The in situ structure of working protein machinery in their native context allows for more physiological structural information, together with identifying the interactions with other proteins nearby. One of the current technologies well suited for determining high-quality in situ structures is cryo-electron tomography.^1,2 In situ protein structures have recently been determined both at nanometer resolution on cryo-sectioning samples3, 4, 5, 6, 7 and even sub-nanometer resolution on non-cryo-sectioning samples.8, 9, 10, 11, 12, 13, 14, 15 This was made possible by combining tomography with a sub-tomogram averaging technique,^16,17 which increases the signal-to-noise ratio (SNR) of target protein complexes by aligning and averaging multiple copies of the three-dimensional (3D) volume of the protein complex in the tomogram.

While tomography allows for near nanometer-resolution structure determination, it also requires the acquisition of a tilt series to achieve the tomogram. A tilt series typically contains more than 30 images taken at a range of tilt angles typically acquired within a time of 30 min, resulting in a slowdown of data collection throughput. The recent development of a stable sample stage using during electron microscopy allows faster data collection by decreasing the waiting time of the stage.¹⁸ However, the feasible data throughput remains at least one magnitude slower than the collection of single-particle data.

When the target protein complex is located in a crowded environment during single-particle imaging, the density of the target protein complex in the image is overlapped by other densities originating from surrounding proteins or other biological macromolecules. These overlapping densities can be considered as noise that decreases the SNR, especially within the range of low spatial frequencies, where the shot noise is much lower than signals. These low-frequency signals exhibiting high SNR are essential for determining the initial position and orientation of the protein complex. These parameters are necessary for a conventional iterative single-particle algorithm.

A previous study showed that, by using a high-resolution model of the target protein complex, the initial position and orientation of this protein complex can be determined from the protein background, namely by incorporating the high-frequency signals of the target protein into the location and orientation search.¹⁹ However, the usage of the high-resolution structure of the target protein renders the method impractical for unavailable structures. A whitening filter was applied to both the reference and the image before calculating the correlation coefficient,¹⁹ which failed to account for both the overlapping density and SNR oscillation. This oscillation stems from the signal oscillation induced by the contrast transfer function (CTF). Furthermore, the shot noise in the image is approximately modeled by a Gaussian distribution with a smooth background in Fourier space. Therefore, CTF-like weighting has been widely used in score function.^20,21 However, the overlapping densities can be treated as part of the noise that fails to follow a Gaussian distribution. How to optimize the score function when considering the noise distributed in a non-Gaussian manner has remained elusive.

Ours and other previous studies showed that, in cases where the density of target protein complexes is overlapped with other densities, after extracting information of the initial center and orientation of the protein complex from single-particle results²² or sub-tomogram averaging,²³ the structure of a protein complex can be effectively refined using traditional local refinement procedures without requiring subtraction of overlapping densities. Both of these methods provide accurate initial center as well as the orientation parameters of the target protein complexes, as the low-frequency signal in their data used for the calculation possesses a high SNR. However, the determination of the initial center and orientation of a protein complex by incorporating a high-frequency signal with low SNR introduces false-positive solutions, resulting in a reference bias problem²⁴ in the structure refinement procedure, which therefore limits the resolution of the reconstruction. Thus, an effective method to solve this challenge and to improve the resolution is urgently required.

Here, we set out to develop a single-particle-like data processing method that allows the structure determination of protein complexes in the native context. To this end, we combined an optimized score function providing the initial orientation and location of a target protein with a sorting algorithm that distinguishes the correct solutions from the false-positive solutions, therefore reducing the model bias problem.

Results

During the derivation of the weighting function, we treated the overlapping protein densities as CTF-modulated noise, and approximated the ratio of overlapping proteins intensity to target protein intensity as a constant n. The details are provided in the supplemental information.

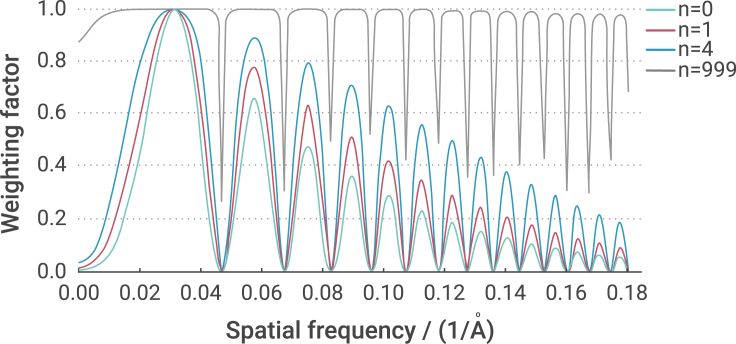
Weighting functions from a typical cryoelectron microscopy (cryo-EM) micrograph with different values of n applied were plotted in Figure 1. Here, SSNR was estimated from the power spectrum of the image (see the Data S1) and FSC was set to 1. An increase of n indicates more noise from overlapping protein densities, which decreases the SNR. However, the SNR at low-frequency range decreases faster than that at high-frequency range. Therefore, the relative weight of the score at the high-frequency range increases along with an increase of n. Moreover, the shape of the peak of the oscillation of the weighting function expended in the x direction with an increasing n. When n is much larger than 1/SSNR(k) (Figure 1, n = 999) (i.e., ignoring the shot noise), our weighting function is similar to a whitening filter.¹⁹ Under different conditions when n is zero (i.e., free of the overlapping densities), our weighting function is a dot product of CTF(k) (absolute value when applied to our signal-whitened images), SSNR(k), and FSC(k). Without considering the overlapping densities, similar weighting functions have been used in CisTEM,²⁵ EMAN,²⁶ and for CTF refinement in RELION.²⁷ In our picking, n is normally estimated to 3 or 4 in real cryo-EM data (see below).

Figure 1.

Weighting functions

Weighting factors damp and oscillate with spatial frequency (green, red, blue, and gray) at different n (0, 1, 4, 999).

Particle detection efficiency

We tested the weighting function by finding protein complexes of different sizes in cryo-EM images in three icosahedral viruses, e.g., herpes simplex virus (HSV) (Figure 2A), alphavirus, and reovirus. Protein complexes are overlapped with densities from other proteins and the genome of the virus, which mimic a complex environment. High-resolution single-particle analysis^28,29 on these viruses ensured an accurate determination of rotational and translational parameters of each 2D image. We extracted the center and the orientation of target protein complexes on the virus and used these known parameters as positive controls. Thirty virus particles from each of the HSV-2 and reovirus datasets were selected for testing. The projection list of the initial model was generated by EMAN³⁰ with the incremental rotation angle set to 5°. Then the CCGs (Cross Correlation Grams) (Figure S1) were calculated between projections and images. For both HSV-2 and reovirus datasets, any results with the translational error larger than 5 pixels and the rotational error larger than 6° were considered as false-positive results.

Figure 2.

The efficiency of particle detection

(A) Left: projection of HSV-2 hexamer model. Right: HSV-2 virus particle imaged at 2.75 μm defocus with 25 electrons per Å⁻². The location of the projection on the virus particles is indicated by a white square.

(B) Precision-recall curves for detections on reovirus datasets using a model at 900 kDa molecular weight at n = 0 (red), 1 (dark blue), 2 (light blue), 3 (gray), 4 (light yellow), 5 (yellow), 6 (purple), 50 (green), and whitening filter (black).

(C) Precision-recall curves for detections on HSV-2 datasets with the same processing as in (B).

(D) Precision-recall curves (dark blue, red, green, and black) for detections (n = 3) on alphaviruses using models at different molecular weights (960, 800, 640, and 480 kDa).

(E) Precision-recall curves for the lower abundance of a 960 kDa protein on alphavirus (yellow for 5 times, purple for 10 times, green for 100 times, and red for 200 times lower abundance), 960 kDa at the abundance of 60 copies per 672 × 672 image (dark blue) and 480 kDa at the abundance of 60 copies per 672 × 672 image (black).

In our weighting function, n regulates the ratio of protein density noise to shot noise. To pick these protein complexes, we tested different picking functions, with n ranging from 0 to 50. The results are displayed as precise-recall curves (Figures 2B and 2C), where precision is the ratio of true detections to false positives and recall is the ratio of detected particles to total particles presented. When n increases from 0 to 3, the ratio of correct results increases in the datasets of HSV-2 and reovirus. The ratio becomes steady when n is between 3 and 6. Thus, we used 4 as the default value of n in the picking function. The ratio decreases when n increases further. The precise-recall curve of the whitening filter where n approaches infinity shows a much lower ratio of correct results compared with the curve of n = 4 (Figures 2B and 2C).

Our picking function was tested on recognizing protein complexes of different molecular weights on alphavirus data. As shown in Figure 2D, the ratio of correct results versus all results decreases quickly as the size of the protein complexes decreases. This finding suggests that our picking function also generates a significant amount of incorrect particles. These false-positive results are very similar to the model for picking according to the high score of our picking function, which will induce high-resolution noise in the structure refinement procedure.

Also, the abundance of the target also affects the efficiency assuming that different ratios of the target protein are randomly removed from the micrographs to change the abundance of the protein. Although the recall of the protein (percentage of the target protein that is picked) remains unchanged using a fixed cutoff threshold of CC (Corss Correlaion), the number of picked target protein decreases along with the decreasing of abundance. Since the background noise remains almost the same, we assume that the number of the false-positive result remains unchanged too. Thus, we recalculated the precision-recall curves of a 960 kDa protein as shown in Figure 2E. When the precision drops to 0.1, the recall of the 960 kDa protein with 100 times decrease of abundance is still higher than that of a 480 kDa protein. Thus, the size of the protein is a more important factor than the abundance.

Application on test data

To investigate the ability of our method to determine the protein structure in a crowded environment, we selected a part of the HSV-2 capsid as a target protein. This part is approximately 900 kDa in molecular weight and consists of VP5 and VP26 trimetric capsid proteins as well as the surrounding triplex (two copies of VP23 and one copy of VP19C).²⁸

We set n to 4 and used the frequencies ranging from 1/100 to 1/8 Å⁻¹ for particle detection. Possible locations and orientations of the target protein complex were calculated and sorted according to the score of our picking function following the workflow of in situ single-particle analysis (isSPA) (Figure S2). After merging the results with similar orientations (within 7°) in neighbor locations (within 10 pixels) into a single result, the first 500 putative target protein complexes with the highest score from each virus particle were selected for further data processing, in which around 88% were false-positive results according to the criteria we set above. We performed 3D classification in RELION skipping alignment using the locations and orientations provided by our picking function. As shown in Figure 3A, 2 out of 10 classes containing the lowest percentages of false-positive results were selected, among which ∼50% were false-positive results. Further classification failed to improve the ratio of the correct result.

Figure 3.

Data processing of HSV-2 hexamer

(A) Upper panel: 3D classification of raw picked positives in ten classes, the percentage of true detections in each class is shown at the top left corner. The two selected classes are indicated by squares in red. Lower panel: 3D classification of selected particles in three classes, and the percentage of true detections in each class is noted at the top left corner.

(B) Upper panel: 3D reconstruction of the HSV-2 hexamer. Lower panel: FSC curves denote 3 reconstructions in different conditions using 2,000 viral particles before PR sorting (dash) and after PR sorting (black), using 8,000 virus particles and after PR sorting (blue)

(C) True and false particle distribution with MaxValueProbDistribution term in RELION.

(D) True and false particle distribution with phase residual using data from 1/20 to 1/8 Å⁻¹.

(E)True and false particle distribution with phase residual using data from 1/8 to 1/5 Å⁻¹ .

Next, we performed auto refinement locally, which resulted in a reconstruction at 4.3 Å resolution. The FSC curve as shown in Figure 3B drops quickly at the frequency of ∼1/8 Å⁻¹ and exhibits a shoulder around the frequency of 1/5 Å⁻¹, indicating a reference bias problem (below 1/8 Å⁻¹) and noise problem (above 1/8 Å⁻¹) in the reconstruction. We also tried to use fewer putative target protein complexes at the top of the sorting list to increase the ratio of correct results. However, this approach also decreased the number of correct results. When we reduced the number of putative target protein complexes in the refinement procedure, the resolution of the reconstruction improved (Figure S3A), presumably due to the increase of the ratio of correct results before decreasing because of the lack of particles.

To further reduce the ratio of false-positive results, we calculated the score between the reference and the raw image according to refined parameters using phase residual (Equation S20). For this calculation, we only used frequencies ranging from 1/8 to 1/5 Å⁻¹. The particles were sorted according to their scores. As shown in Figure 3B, the sorting efficiently separated the correct results from false-positive results by two Gaussian-like peaks (Figures S3B and S3C). When the sorting was based on the score from our picking function using the frequencies ranging from 1/20 to 1/8 Å⁻¹, the ability of separation decreased markedly (Figure 3C). This range of frequency was involved in particle picking, which performed a global search of the location and orientation of the target protein on a whole virus. For instance, in a combination of translational (step size of 2.76 Å) and rotational parameters (step size of 5°), $7.5\times {10}^{10}$ possible locations of the protein complex were searched, from which the top 500 possible locations were selected by the program. Thus, each false-positive result was selected from $7.5\times {10}^{10}$ possible locations. However, further refinement using only a local search improved the resolution to ∼4.3 Å. The local search strictly limited the possible locations. Thus, in the range of frequencies from 1/8 to 1/4.3 Å⁻¹, the false-positive result exhibits differences from the model. Therefore, excluding the range of frequencies involved in picking a function for sorting exhibits less reference bias. In addition, the refinement only performing the local search was based on the maximum likelihood score function in RELION. We tested “MaxValueProbDistribution” generated in RELION as a score to sort the particles, however, the correct results were barely differentiated from the false-positive results (Figure 3D). The sorting according to the parameter of “NrOfSignificantSamples” exhibited a similar result to that of MaxValueProbDistribution. Thus, it is possible that using scores different from the one used in the refinement for sorting also helps to reduce the reference bias problem encountered in the refinement.

After sorting by the score calculated using only the frequencies from 1/8 to 1/5 Å⁻¹, 40,000 particles (the top 40% particles contained ∼93% correct results) were selected. Further refinement of this dataset led to a resolution of 4.0 Å (Figure 3E). By adding in a further 6,000 viral particles, 180,000 hexamer particles were selected after non-alignment 3D classification and sorting. The gold standard resolution was 3.7 Å. By combining with CTF refinement in RELION using our optimized weighting function, the resolution was improved to 3.5 Å. The original CTF refinement procedure implanted in RELION produced a map of 3.6 Å resolution.

Determining protein structure using a homologous structure as a picking model

Since the expected structure is usually unknown, we explored the possibility of using homologous structure as a picking model. The differences between homologous structure and expected structure were treated as noise ($N^{\prime }$), resulting in a different term named FSC_m (between the cryo-EM map of homologous structure and the expected structure) in the weighting function to replace the FSC.

$$W\left(k\right)=\frac{CTF\left(k\right)\cdot FS{C}_m\left(k\right)}{\frac{1}{SSNR\left(k\right)}+n\cdot CT{F}^2\left(k\right)}$$ (Equation 1)

To search for a similar protein complex on the HSV-2 capsid core, we used a homologous protein complex present in the HSV-1 capsid core as the model. First, we extracted the 3D model of the homologous protein complex from a 4.2 Å map of HSV-1.³¹ The FSC curve between protein complexes from HSV-1 and HSV-2 showed similarity in the structures with the FSC value decreasing to 0.7 at the frequency of 1/8 Å⁻¹ (Figure 4A). Three million potential particles of the protein complex on the HSV-2 capsid were selected based on the score produced by our picking function. After local 3D classification and further selection by sorting, 60,000 particles were finally selected. As shown in Figure 4B, the local refinement resulted in a 4.0 Å resolution map. We calculated the FSC curves between this map and the corresponding 3.1 Å map from the single-particle result of HSV-2 and between this map and the corresponding 4.2 Å map of HSV-1.³¹ As shown in Figures 4C and 4D, our refined structure is closer to the corresponding structure in HSV-2 than that in HSV-1. Assuming that the 3.1 Å map represents a perfect map, the FSC between the 3.1 Å map and our map reported a resolution of 4.0 Å using a threshold of 0.5. This result is in agreement with the resolution (4.0 Å) reported by FSC between two half maps using a threshold of 0.143. Besides, we also detected proteins at a molecular weight of 900 kDa on a reovirus with a homologous crystal structure as the 3D model successfully (Figure S4). Together, these results show that the procedure we used in the reconstruction avoids reference bias induced by homologous models.

Figure 4.

Homologous structure as a picking model

(A) FSC curve of a HSV-1 hexamer with a HSV-2 hexamer.

(B) The resolutions were determined by gold standard FSC at a threshold 0.143 for the HSV-2 hexamer reconstructed from a HSV-1 hexamer.

(C) PDB of the HSV-1 hexamer (yellow) and the HSV-2 hexamer (green) fitting to the density of the 4.0 Å cryo-EM map, the disagreements between the two PDBs are indicated by red arrows.

(D) FSC curves show similarities between our map and the HSV-1 hexamer (red) and the HSV-2 hexamer (blue), respectively.

(E) Precision-recall curves of the ∼2 MDa protein of HSV-2 at a series of scales corresponding to Figure S5.

(F) Precision-recall curves of the ∼1.8 MDa protein of reovirus at a series of scales corresponding to Figure S5.

To evaluate the ability to find protein complexes by homologous models of different similarities between their structures and the structure of the target protein complex, we simulated homologous models by applying different scale factors to the structure of the target protein. As shown in Figure S5, the similarities between the re-scaled models and the original map are indicated by FSC curves. The precision-recall curves show that the ability to find a protein complex decreases along with the reduction of the similarity between the homologous model and the protein complex (Figures 4E and 4F). We downloaded PDB files of different homologous proteins and calculated the potential density maps, and then calculated the FSCs between pairs of homologous maps. As shown in Figure S6, the similarity between proteins varies greatly. These homologous proteins with high similarities can be used as picking models in our method.

Determining structures at high resolution using isSPA

To evaluate our program, we first processed a dataset of a bunyavirus (Figure 5A) by 2D and 3D classification. As shown in Figure 5B, only approximately 28% of the viral particles (3,140 particles) exhibited an icosahedral symmetry. Further refinement on the icosahedral viral particles resulted in an 11.8 Å map due to the flexibility. To compensate for this limitation in flexibility, one block (one pentamer and five surrounding hexamers) centered on a pentamer was extracted and refined,²⁴ which led to a map of 8.7 Å resolution. A centered sub-block (pentamer) and a sub-block adjacent to the pentamer that centered on a hexamer segmented from the 8.7 Å block were used as 3D models to pick the protein complex on the non-icosahedral virus particles previously excluded from data processing. Through global detection by isSPA, 20 potential solutions were selected from each virus and ∼27,000 particles in total were selected according to 3D non-alignment classification, resulting in a 7.7 Å resolution map (Figures 5C and 5D). In the search for hexamers, 1 hexamer from the 5 surrounding a pentamer was segmented as the model, and 200 potential solutions were selected from each virus. After 3D non-alignment classification, ∼87,000 particles were selected and refined to 8.3 Å resolution (Figure 5E).

Figure 5.

Application

(A) A micrograph of bunyavirus particles.

(B) Upper panel: 2D classification of viral particles binned by 4. Lower panel: 3D classification of viral particles selected from 2D classification.

(C) Densities in the 7.7 Å map of the pentamer.

(D) FSC curve shows the resolution of the hexamer map.

(E) FSC curve shows the resolution of the pentamer map.

(F) An image of a carboxysome; Rubiscos are packaged inside. Scale bar represents 10 nm.

(G) The 3.7 Å map of Rubisco was reconstructed using our isSPA method (right) and the FSC curve showing the resolution of the 3.7 Å map at gold standard (left).

(H) Distribution of particle numbers to scores fitted by two Gaussian functions.

In the second sample, carboxysomes were purified from Halothiobacillus neapolitanus and the cryo-EM data were collected on this sample (Figure 5F). The size of the carboxysomes ranged from 100 to 150 nm. We also purified Rubisco from fractured carboxysomes by adding extra freeze-thaw cycles before the centrifugation step for carboxysome purification. We collected the cryo-EM data of purified Rubisco, and obtained a 2.7 Å map of this complex (around 500 kDa). This complex was then used as a model to pick the Rubisco inside the carboxysome in the cryo-EM images. Frequencies between 1/100 and 1/8 Å⁻¹ were used for picking. From the collected micrographs, ∼5,200 carboxysome images were extracted, and each image was cross-correlated with the 2.7 Å model at frequencies ranging from 1/100 to 1/8 Å⁻¹. This procedure yielded a large group of locations and orientations, from which on average 150 solutions were picked per carboxysome for further processing. The non-alignment 3D classification was performed using RELION. Approximately 150,000 particles were selected, and a further auto local refinement with an angular sampling of 0.9° and translational sampling of 1.04 Å in RELION reported a 4.3 Å resolution map. To remove the reference bias, the refined particles were sorted with phase residual using frequencies from 1/8 to 1/5 Å⁻¹. We tested three cutting thresholds (0.07, 0.08, and 0.09) and selected ∼82,000, ∼46,000, and ∼21,000 particles to the second-round refinement individually, resulting in 4.0, 3.9, and 3.9 Å resolution. Further CTF refinement subsequently improved the resolutions to 3.9, 3.9, and 3.7 Å (Figure 5G). According to the fitting of two Gaussian distributions (Figure 5H), the portion of true solutions at a threshold of 0.09 was estimated to be ∼90%. The reconstructions of all particles, particles scored above and below 0.09 were compared with the initial 3D model, respectively, and the FSCs exhibited the ability to sort (Figure S7). We also tried classical picking methods (e.g., RELION autopicking) on these data, followed by 2D and 3D classification, and the result shows that RELION failed in our case (Figure S8).

The success on the Rubisco dataset may be owing to the high symmetry (D4) and its high abundance. We have shown above that our workflow can handle proteins picked with precision below 0.1. According to the description of the alphavirus, the recall of the 960 kDa protein with 200 times decreasing of abundance remains the same as a 480 kDa protein at a precision of 0.1. Thus, it is possible that a ∼1 MDa protein in carboxysome thickness with 200 times lower abundance than that of Rubisco can be solved at a pseudo atomic resolution.

Discussion

In this work, we showed that the isSPA method can resolve proteins (larger than 400 kDa) in the native context at high resolution with non-cryo-sectioning data when the thickness of the sample is around 100 nm. The ability to find the initial rotational and translational parameters of the target protein is closely associated with the size of the target protein and the thickness of the cryo-EM sample. Our recent results show that 50% of ∼350 kDa membrane proteins can be found and reconstructed on 50-nm-diameter liposomes. Thus, the isSPA method can very efficiently help to solve structures of different kinds of membrane proteins on liposomes constituted by their native lipid membrane. Due to the thickness and the quality of the cryo-sectioning data, we believe that there is more limitation in the size of protein complexes in cryo-sectioning data for this method. The major obstacle of this method is to determine the initial parameters of protein complexes. This method will benefit greatly from hardware, such as a new generation of direct detectors or phase plates that improve the SNR of images, especially at frequencies ranging from 1/20 to 1/8 Å⁻¹ (0.1–0.25 Nyquist at a pixel size of 1 Å).

When a protein in a complex environment is imaged, the overlapping densities ruin the SNR of low-frequency signals of the target protein. The SPA algorithms improve the 3D structure iteratively from a low-resolution 3D map to a high-resolution 3D map. However, such a method becomes invalid when the low-frequency signals of the target protein are ruined by overlapping densities. Thus, routine none-reference 2D classification and 3D classification starting from a low-resolution initial model usually converge to wrong results. Thus, starting from the local refinement in both structure refinement and 3D classification is strongly suggested in isSPA. The structural information of a template with a frequency above 1/8 Å⁻¹ is involved in picking the particle, therefore the FSC curves below 1/8 Å⁻¹ are not calculated from two completely independent datasets. However, the FSC beyond 1/8 Å⁻¹ is not affected by the template and can be considered as gold standard.

Generally, isSPA is developed for high-throughput structural determination of proteins in a crowded environment. However, isSPA cannot detect all the target proteins correctly due to the relatively low accuracy, therefore it is not an accurate tool to analyze the distribution of protein complexes in the cellular environment. Moreover, the z height of the protein in the sample is determined by its defocus value in the micrograph. Although the per-particle CTF refinement improves the defocus value of the protein, there remains errors in the defocus value, which prevents an accurate localization of the target protein along the z direction. Thus, if the distribution of target proteins is unknown, we suggest that a tomographic study prior to isSPA can be used to show the distribution of target protein in the in situ environment and provide a medium resolution template if it is necessary. Missing a portion of target proteins or certain defocus error did not prevent us from achieving high-resolution structures of the target protein, more high-throughput single-particle data can be collected, and we can further improve the resolution of the target protein by applying the isSPA method to this dataset with the medium-resolution structure being a template.

Published Online: September 8, 2021

Lead contact website

http://www.ibp.cas.cn/sourcedb_ibp_cas/cn/ibpexport/swdfzgjzdsys/201912/t20191202_5447224.html.