Significance
Early warning signals (EWS) of tipping points are vital to anticipate system collapse or other sudden shifts. However, existing generic early warning indicators designed to work across all systems do not provide information on the state that lies beyond the tipping point. Our results show how deep learning algorithms (artificial intelligence) can provide EWS of tipping points in real-world systems. The algorithm predicts certain qualitative aspects of the new state, and is also more sensitive and generates fewer false positives than generic indicators. We use theory about system behavior near tipping points so that the algorithm does not require data from the study system but instead learns from a universe of possible models.
Keywords: dynamical systems, machine learning, bifurcation theory, theoretical ecology, early warning signals
Abstract
Many natural systems exhibit tipping points where slowly changing environmental conditions spark a sudden shift to a new and sometimes very different state. As the tipping point is approached, the dynamics of complex and varied systems simplify down to a limited number of possible “normal forms” that determine qualitative aspects of the new state that lies beyond the tipping point, such as whether it will oscillate or be stable. In several of those forms, indicators like increasing lag-1 autocorrelation and variance provide generic early warning signals (EWS) of the tipping point by detecting how dynamics slow down near the transition. But they do not predict the nature of the new state. Here we develop a deep learning algorithm that provides EWS in systems it was not explicitly trained on, by exploiting information about normal forms and scaling behavior of dynamics near tipping points that are common to many dynamical systems. The algorithm provides EWS in 268 empirical and model time series from ecology, thermoacoustics, climatology, and epidemiology with much greater sensitivity and specificity than generic EWS. It can also predict the normal form that characterizes the oncoming tipping point, thus providing qualitative information on certain aspects of the new state. Such approaches can help humans better prepare for, or avoid, undesirable state transitions. The algorithm also illustrates how a universe of possible models can be mined to recognize naturally occurring tipping points.
Many natural systems alternate between states of equilibrium and flux. This has stimulated research in fields ranging from evolutionary biology (1) and statistical mechanics (2) to dynamical systems theory (3). Dynamical systems evolve over time in a state space described by a mathematical function (3). Thus, dynamical systems are extremely diverse, ranging in spatial scale from the expanding universe (4) to quantum systems (5) and everything in between (6–8).
Different dynamical systems exhibit vastly different levels of complexity, and correspondingly diverse behavior far from equilibrium states. Sometimes, a system that is close to equilibrium may experience slowly changing external conditions that move it toward a tipping point where its qualitative behavior changes (we note that “tipping point” has been used to refer to a variety of phenomena (9), but here we will treat it as being synonymous with a local bifurcation point). In these circumstances, dynamical systems theory predicts that even very high-dimensional systems will simplify to follow low-dimensional dynamics (10, 11). Moreover, there exist a limited number of typical bifurcations of steady states, each of which may be described by a “normal form”—a canonical example capturing the dynamical features of the bifurcation (Box 1) (3). For instance, in a fold bifurcation, the system exhibits an abrupt transition to a very different state. A transcritical bifurcation usually causes a smooth transition, although it may sometimes cause an abrupt transition (12). Or, a Hopf bifurcation can lead the system into a state of oscillatory behavior via a smooth (supercritical) or abrupt (subcritical) transition.
Box 1. Dimension Reduction Close to a Bifurcation
As a high-dimensional dynamical system approaches a bifurcation, its dynamics simplify according to the center manifold theorem (10). That is, the dynamics converge to a lower-dimensional space, which exhibits dynamics topologically equivalent to those of the normal form of that bifurcation. Examples of a fold, (supercritical) Hopf, and transcritical bifurcation are shown in Box 1a–c. Dynamics close to the bifurcation (gray box) are topologically equivalent to the normal forms
| [1] |
| [2] |
| [3] |
respectively, where and are state variables that depend on time , and is the bifurcation parameter. The bifurcation of each system occurs at . These normal forms are contained within the set of two-dimensional dynamical systems with third-order polynomial right-hand sides, motivating this as the framework for training the deep learning (DL) algorithm (see Materials and Methods).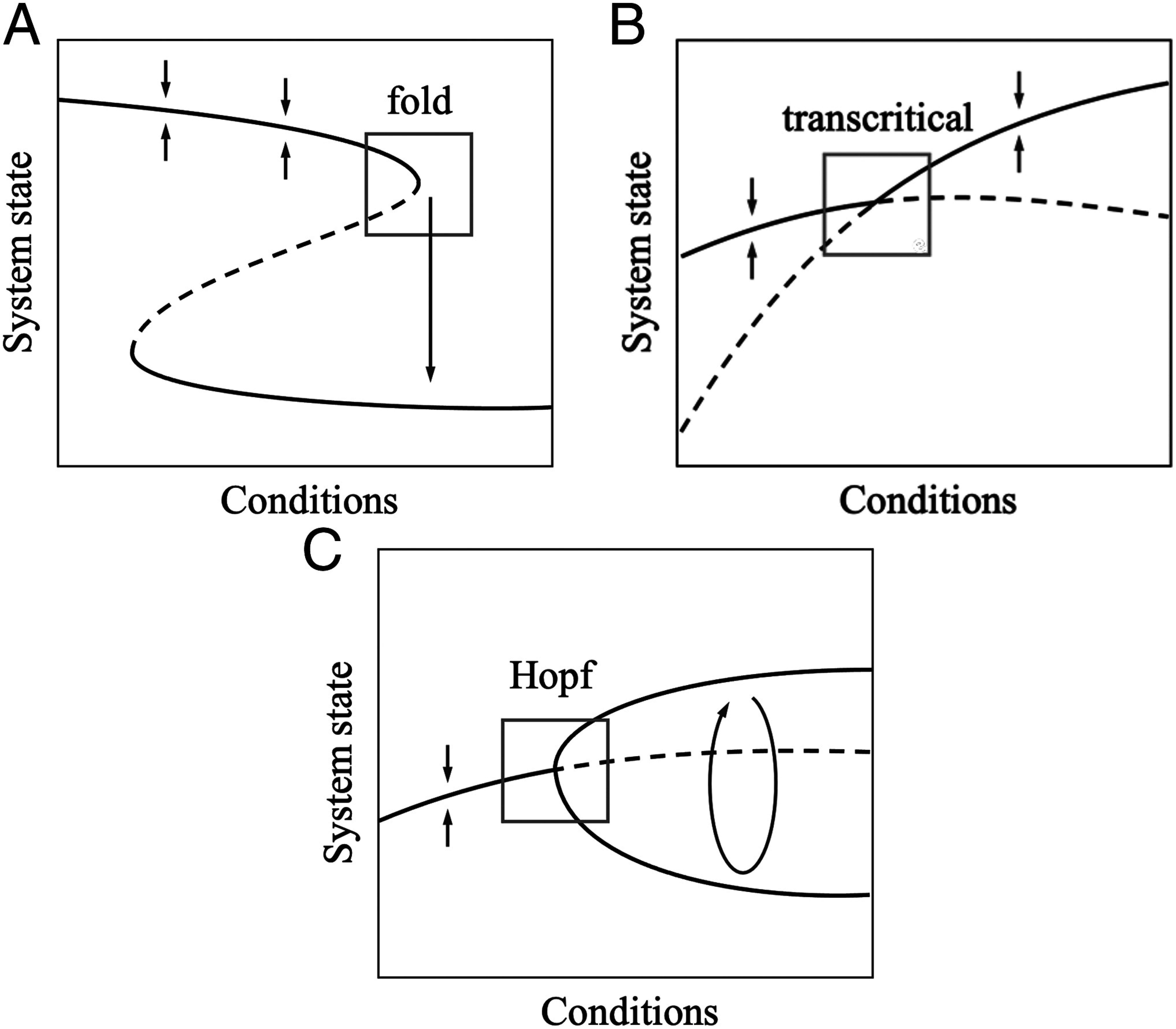
Different bifurcation types correspond to distinct types of dynamical behavior. Moreover, other behaviors can emerge near the bifurcation that are common to many normal forms. For example, all local bifurcations, that is, those where eigenvalues of the respective matrices cross the imaginary axis, are accompanied by critical slowing down (3, 13). This is where system dynamics become progressively less resilient to perturbations as the transition approaches, causing dynamics to become more variable and autocorrelated. As a result, statistical indicators such as rising variance and lag-1 autocorrelation (AC) of a time series often precede tipping points in a variety of systems (14–16). These generic early warning indicators have been found to precede catastrophic regime shifts in systems including epileptic seizures, Earth’s paleoclimate system, and lake manipulation experiments (17–19).
Mathematically, critical slowing down occurs when the real part of the dominant eigenvalue (a measure of system resilience; Box 2) diminishes and eventually passes through zero at the bifurcation point. This happens for fold, Hopf, and transcritical bifurcations, and thus critical slowing down is manifested before these three bifurcations types (16). Generic early warning indicators are intended to work across a range of different types of systems by detecting critical slowing down. But this strength is also their weakness, since these indicators do not tell us which type of bifurcation to expect (16).
Box 2. Significance of Higher-Order Terms Close to a Bifurcation
The local behavior of a dynamical system about an equilibrium point is often well described by a linear approximation of the equations that govern its dynamics. However, for systems nearing a bifurcation, higher-order terms become significant. We illustrate this for a one-dimensional system with equilibrium , that is, . The dynamics about equilibrium following a perturbation by satisfy
where , , are coefficients of the Taylor expansion, and is referred to as the dominant eigenvalue. The potential landscape of this system centered on is given by
where we have dropped the arbitrary integration constant. Far from a bifurcation in a regime of small noise, displacement from equilibrium () is small, and so the visited part of the potential landscape is well described by the first-order (linear) approximation (Box 2a). As a local bifurcation is approached, , which corresponds to critical slowing down, and a flattening of the first-order approximation to the potential landscape (Box 2b). This allows noise to push the system farther from equilibrium, where higher-order terms become significant.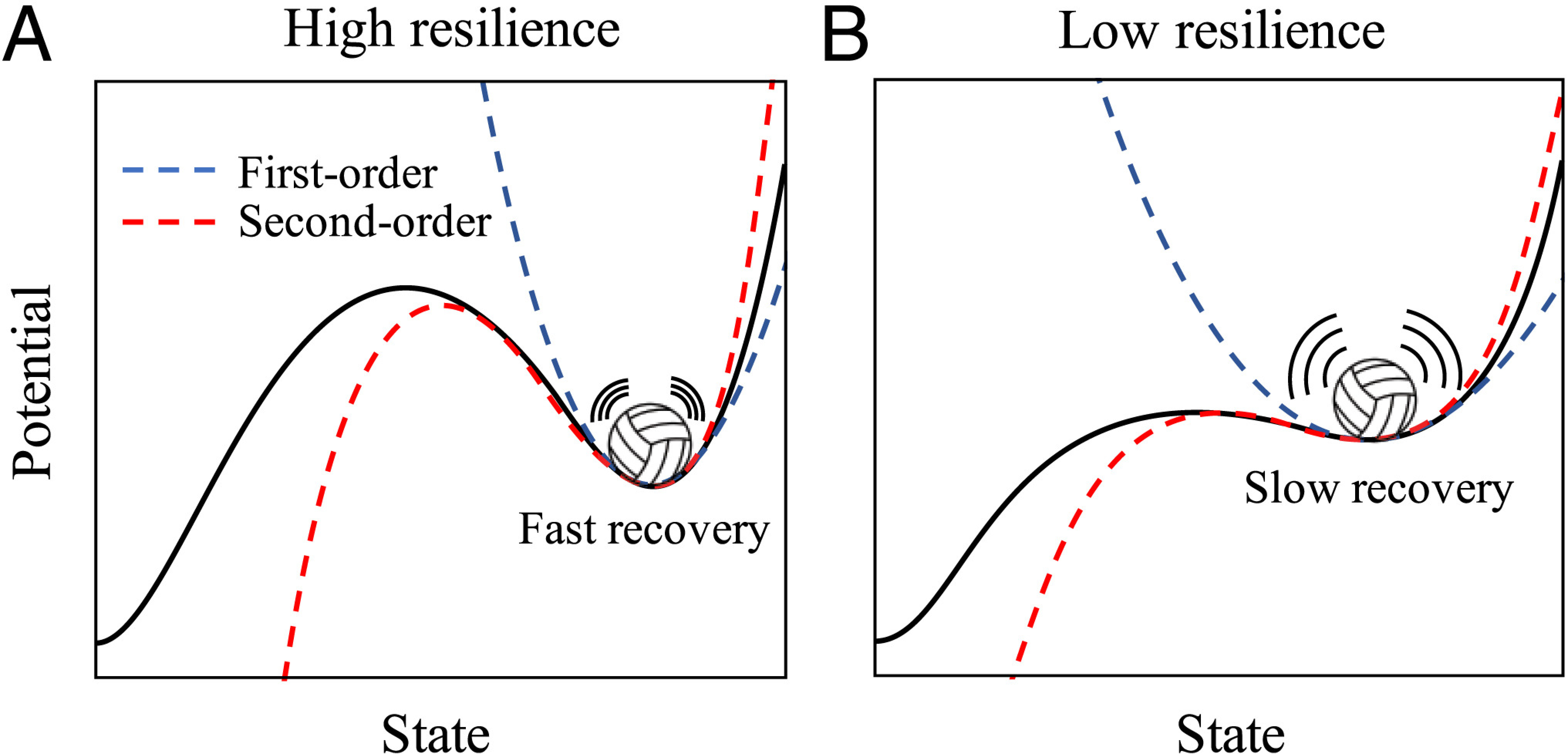
The dominant eigenvalue is derived from a first-order approximation to dynamics near the equilibrium. Higher-order approximations can distinguish between different types of bifurcations. But they are not often used to develop early warning indicators because 1) the first-order approximation dominates dynamics sufficiently close to the equilibrium, causing critical slowing down to generate the strongest signal, and 2) the first-order approximation is more tractable to mathematical analysis of stochastic systems than the higher-order approximations (20). However, as a system gets closer to a bifurcation, it can drift farther from equilibrium due to critical slowing down. As a consequence, the higher-order terms become significant and may be large enough to provide clues about the type of transition that will occur. Statistical measures such as skew and kurtosis reflect the influence of these highest-order terms, for instance (20–22). Higher-order terms could be associated with features in time series data that are subtle but detectable, if we knew what to look for. Knowing qualitative information about the tipping point (such as whether it will be sudden or gradual) and the state that lies beyond it (such as whether it will oscillate or be stable) based on predicting the bifurcation type could be valuable in a range of applications.
Deep Learning and Bifurcation Theory
Generic early warning indicators such as variance and lag-1 AC use insights from dynamical systems theory to detect patterns that emerge before a bifurcation (Box 2). Supervised DL algorithms can also detect patterns (features) in time series, and have achieved state of the art in time series classification (23)—the ability to classify time series based on characteristic features in the data. We hypothesized that DL algorithms can detect both critical slowing down and other subtle features that emerge in time series prior to each type of bifurcation, such as the features generated by higher-order terms.
However, supervised DL algorithms require many thousands of time series to learn classifications—something we do not have for many empirical systems (24). And they can only classify time series similar to the type of data they were trained on. Here, we propose that simplification of dynamical patterns near a bifurcation point provides a way to address the problem of limited empirical data, and allows us to relax the restriction that DL algorithms can only classify time series from systems that they were trained on. Our first hypothesis (H1) is that, if we train a DL algorithm on a sufficiently large training set generated from a sufficiently diverse library of possible dynamical systems, the relevant features of any empirical system approaching a tipping point will be represented somewhere in that library. Therefore, the trained algorithm will provide early warning signals (EWS) in empirical systems that are not explicitly represented in the training set. Thus, even a relatively limited library might contain the right kinds of features that characterize higher-order terms in real-world time series. Our second hypothesis (H2) is that the DL algorithm will detect EWS with greater sensitivity (more true positives detected) and specificity (fewer false positives) than generic early warning indicators. Our third hypothesis (H3) is that the DL algorithm will also predict qualitative information about the new state that lies beyond the tipping point, on account of being able to recognize patterns associated with higher-order terms. All three hypotheses are based on the simplification of complex dynamics close to a bifurcation point (Boxes 1 and 2).
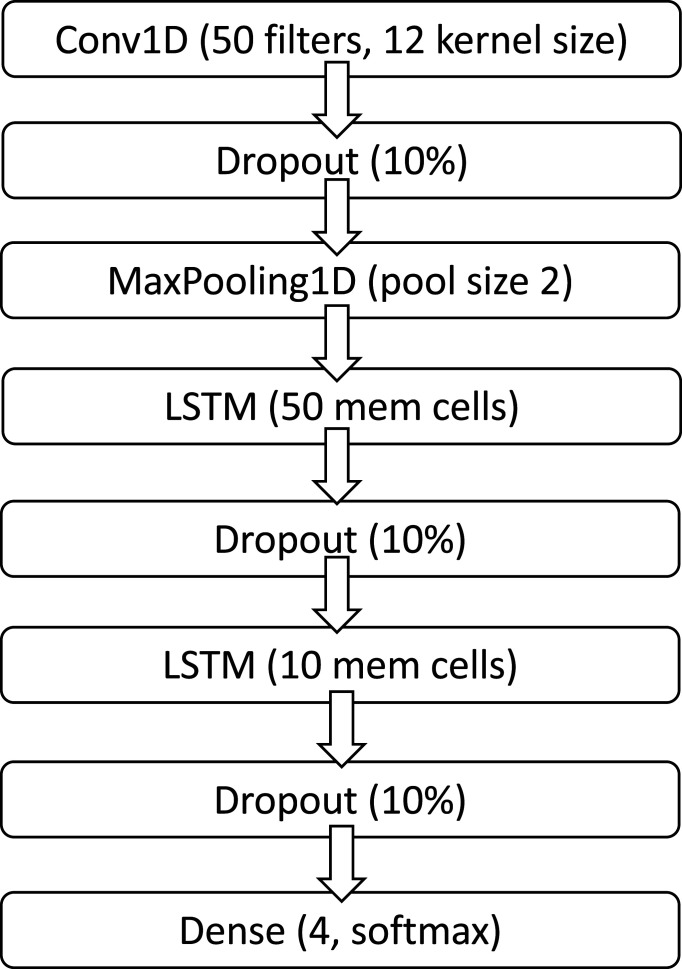
To test these hypotheses, we developed a DL algorithm to provide EWS for tipping points in systems it was not trained upon. We used a CNN-LSTM architecture (convolutional neural network—long short-term memory network; see Materials and Methods). CNN-LSTM sandwiches two different types of neural network layers. The CNN layer reads in subsequences of the time series and extracts features that appear in those subsequences. The LSTM layer then reads in the output of the CNN and interprets those features. The LSTM layer loops back on itself to generate memory, enabling the layer to recognize the same feature appearing at different times in a long time series. As a result, this approach excels at pattern recognition and sequence prediction (25, 26).
We created a training set consisting of simulations from a randomly generated library of mathematical models exhibiting local bifurcations (see Materials and Methods). Specifically, we generated three classes of simulations eventually going through a fold, Hopf, or transcritical bifurcation, and a fourth neutral class that never goes through a bifurcation. (We note that other types of state transitions are possible, such as those caused by a global bifurcation (27), but we restrict attention to local codimension-one bifurcations in this paper.) Then, we trained the CNN-LSTM algorithm on the training set to classify any given time series into one of the four categories based on the prebifurcation portion of the simulation time series. The F1 score of the algorithm—a combined measure of precision (how many positive classifications are true positives) and sensitivity/recall (how many of the true positives are detected)—tested against a hold-out portion of the training set was when training on time series of length 1,500 data points, and was when training on time series of length 500 data points.
We evaluated the out-of-sample predictive performance of the algorithm, using data from study systems that were not included in the training set. We tested three model systems and three empirical systems. The model systems included a simple harvesting model consisting of a single equation that exhibits a fold bifurcation (28); a system of two equations representing a consumer−resource (predator−prey) system exhibiting both Hopf and transcritical bifurcations (29); and a system of five equations representing the coupled dynamics of infection transmission and vaccine opinion propagation, and exhibiting a transcritical bifurcation (12). The three empirical datasets consisted of data from paleoclimate transitions (17), transitions to thermoacoustic instability in a horizontal Rijke tube which is a prototypical thermoacoustic system (30), and sedimentary archives capturing episodes of anoxia in the eastern Mediterranean (31) (see Materials and Methods). We selected these empirical datasets because, in each case, they have been previously argued to show critical slowing down before a tipping point, based on lag-1 AC and/or variance trends, followed by observation of a state transition. We compared the performance of the DL algorithm against lag-1 AC and variance for all six study systems.
Results
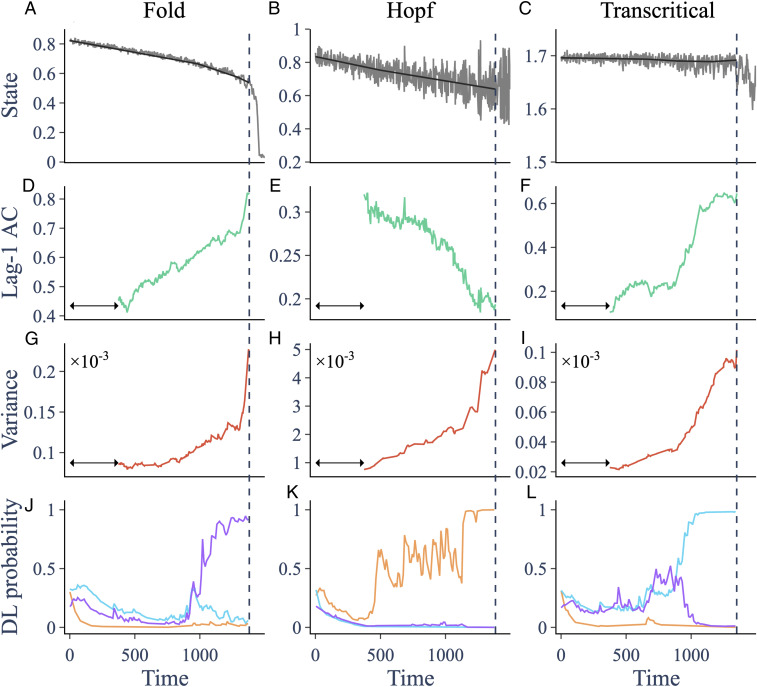
The EWS provided by lag-1 AC, variance, and the DL algorithm can be compared as progressively more of the time series leading up to the bifurcation is made available for their computation, as might occur in real-world settings where a variable is monitored over time. A clear trend in variance or lag-1 AC is taken to provide an early warning signal of an upcoming state transition (32). For the two ecological models exhibiting the fold, Hopf and transcritical bifurcations (Fig. 1 A–C), the lag-1 AC and variance increase progressively before all three transition types except for the Hopf bifurcation, where lag-1 AC decreases due to the presence of an oscillatory component to the motion (20) (Fig. 1 D–I). Hence the trends in these two indicators suggest that a transition will occur.
Fig. 1.
Trends in indicators prior to three different bifurcations in ecological models. (A–C) Trajectory (gray) and smoothing (black) of a simulation of an ecological model going through a fold, Hopf, and transcritical bifurcation, respectively. (D–F) Lag-1 AC computed over a rolling window (arrow) of width 0.25. (G–I) Variance. (J–L) Probabilities assigned to the fold (purple), Hopf (orange), and transcritical (cyan) bifurcation by the DL algorithm. The vertical dashed line marks the time at which the system crosses the bifurcation.
The DL algorithm assigns a probability for each of the four possible outcomes (fold, transcritical, Hopf, and neutral) that the time series will culminate in that outcome. Therefore, a heightened probability assigned to one of the outcomes compared to the other three is taken to provide an early warning signal of that outcome. According to this criterion, the DL algorithm also provides early warning of a transition in the two ecological models, and correctly predicts the type of bifurcation in each of the three cases (Fig. 1 J–L). Inspection of the time series provides supporting evidence for our first two hypotheses. Firstly, these model equations were not used to develop our training library (although we note that our hypothesis relies on the training library including a representative type of dynamics from the models, such as fold bifurcations). Secondly, the algorithm initially assigns similar probabilities to all three transition types in the earlier part of the time series, but, after a specific time point, the algorithm becomes highly confident in picking one of the three bifurcation types as the most probable outcome. This is consistent with the algorithm being able to distinguish features based on higher-order terms that are held in common between dynamical systems exhibiting each bifurcation type, but that distinguish the bifurcation types from one another. Examples of these time series for the other four study systems appear in SI Appendix, Figs. S1–S10.
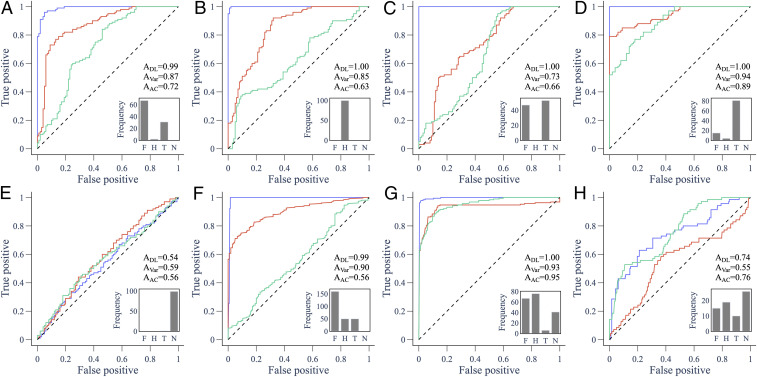
These time series, however, do not address how the approaches might perform when faced with a neutral time series where no transition occurs, and whether they might mistakenly generate a false positive prediction of an oncoming state transition (33). Hence, we compared the performance of these approaches with respect to both true and false positives through a receiver operator characteristics (ROC) curve. The ROC curve shows the ratio of true positives to false positives, as a discrimination threshold that determines whether a classifier predicts a given outcome (such as transition versus no transition) is varied. The area under the ROC curve determines how well the classifier does with respect to both sensitivity/recall (how many true positives are detected) and specificity (how many false positives are avoided). The AUC is one for a perfect classifier, and 0.5 for a classifier that is no better than random. For variance and lag-1 AC, higher positive values of the Kendall statistic indicate a more strongly increasing trend. Therefore, these indicators were taken to predict a given outcome when the Kendall statistic exceeded the discrimination threshold. The DL algorithm was taken to predict a given outcome simply when the probability assigned to that outcome exceeded the discrimination threshold.
We compared ROC curves for the criterion of predicting any transition for lag-1 AC, variance, and the DL algorithm, for eight comparisons across all six study systems (Fig. 2). In support of our second hypothesis, the DL algorithm strongly outperforms lag-1 AC and variance in six of the comparisons. There are two interesting comparisons where the performance of the DL algorithm is similar to that of lag-1 AC or variance. For the SEIRx (Susceptible-Exposed-Infectious-Removed-vaccinator) coupled behavior−disease model, all three classifiers are little better than random in the model variable for the number of infectious persons (; Fig. 2E). This occurs due to nonnormality of the system associated with differing timescales for demographic and epidemiological processes (34). However, the early warning signal is apparent in the variable for the prevalence of provaccine opinion, and the DL algorithm outperforms both lag-1 AC and variance in this respect. Also, for the paleoclimate data, the DL algorithm performs about as well as lag-1 AC, and both perform better than variance (Fig. 2H). This may occur because the variance actually decreases before the transition in several of the empirical time series, because the sampling data does not have high enough resolution, or because the system was forced too quickly.
Fig. 2.
ROC curves for predictions using 80 to 100% of the pretransition time series for model and empirical data. ROC curves compare the performance of the DL algorithm (blue), variance (red), and lag-1 AC (green) in predicting an upcoming transition. The area under the curve (AUC), abbreviated to A, is a measure of performance. Insets show the frequency of the favored DL probability among the forced trajectories: (F)old, (T)ranscritical, (H)opf, or (N)eutral. (A) May’s harvesting model going through a fold bifurcation; (B and C) consumer−resource model going through a (B) Hopf and (C) transcritical bifurcation; (D and E) behavior−disease model going through a transcritical bifurcation using data from (D) provaccine opinion () and (E) total infectious (); (F) sediment data showing rapid transitions to an anoxic states in the Mediterranean sea; (G) data of a thermoacoustic system undergoing a Hopf bifurcation; and (H) ice core records showing rapid transitions in paleoclimate data. The diagonal dashed line marks where a classifier works no better than a random coin toss.
In support of our third hypothesis, we note that the DL algorithm usually predicts the correct type of bifurcation in all eight comparisons (Fig. 2). An exception occurs for the thermoacoustic system (Fig. 2G), where the frequency of the favored DL probability for the Hopf bifurcation is only slightly higher than for the fold bifurcation. This could be due to our down-sampling of the data to enable the time series to be accommodated by the DL algorithm code.
These ROC curves came from classifiers with access to 80 to 100% of the time series (in other words, using the last of the time series). We also computed the ROC curves when the three classifiers had access to 60 to 80% (the fourth quintile) of the time series (SI Appendix, Fig. S11). This allows us to assess the reliability of the approaches when they are required to provide early warning for a system that is still far from the tipping point. We observe that the DL algorithm provides early warning with greater sensitivity and specificity than either lag-1 AC or variance, in all comparisons except the variable of the SEIRx model, where they perform equally poorly. This result suggests that the DL algorithm can provide greater forewarning of coming state transitions, although additional statistical tests would be required to show this conclusively.
Discussion
We tested our DL algorithm on data from systems that exhibited critical slowing down before a local bifurcation. However, other types of transitions are possible, such as global bifurcations that do not depend on changes to the local stability of equilibria (27). EWS of global bifurcations are more challenging to detect. State transitions may also occur through codimension-two bifurcations where two forcing parameters are varied simultaneously (16, 35, 36), or bifurcations of periodic orbits (22), for which EWS are more apparent. In general, DL algorithms only work for the specific problems they are trained to do. In order for our DL algorithm to provide early warning of other such bifurcations, we speculate that the training set would need to be expanded to include simulated data exhibiting those dynamics.
Bifurcations are not inherent to real-world systems but rather are a property of our mathematical model of the systems. We trained the DL algorithm on data from mathematical models, but we applied it to empirical data from systems that have been previously studied in the literature on EWS of tipping points. The algorithm still detects bifurcations in the empirical systems because that is what it was trained to do. However, it could be said that the algorithm is really predicting the type of bifurcation that researchers would use to describe an observed transition in the real-world system. This reflects the more general issue of how humans leave their imprint—for better or worse—on the classifications provided by supervised machine learning algorithms (37).
Early warning indicators generally require high-resolution data from a sufficiently long time series leading up to the tipping point (38). This applies to DL algorithms as well as to lag-1 AC and variance. We did not analyze how the performance of the DL algorithms, lag-1 AC, and variance compare as the time series becomes shorter. Similarly, none of these approaches can predict exactly when a transition will occur. This task lies in the domain of time series forecasting instead of classification and is a difficult undertaking, given that stochasticity could cause a system to jump prematurely to a new basin of attraction even before the system has reached the tipping point (39). Also worth noting is that we generated a training set based on models with two state variables and second-order polynomial model equations. This limits its ability to detect features such as deterministic chaos (22), which require at least three state variables (40).
We did not analyze whether the DL algorithm is using the higher-order terms in the normal form equations, or whether it is primarily relying on some other features in the data. This could be addressed in future work by controlled tests of whether the algorithm can distinguish supercritical and subcritical Hopf bifurcations (which differ in the cubic term), for instance. Finally, we note that, even though the DL algorithm can predict certain qualitative features of the new regime (such as oscillations after a Hopf bifurcation, or a stable state after a fold bifurcation), it cannot say much else about the new regime. For instance, a fold bifurcation could lead an ecosystem into either a stable collapsed state or a stable healthy state (41).
Other early warning approaches have been developed to predict the type of bifurcation (20, 22, 34). However, these approaches tend to be system specific. Our results show that DL algorithms not only can improve the sensitivity and specificity of EWS for regime shifts but also apply with a great degree of generality across different systems. Moreover, as long as the generic dynamical features (the normal forms) of the system near a tipping point are represented in the training set (Boxes 1 and 2), data from the study system are not required to train the algorithm. In summary, by combining dynamical systems insights with DL approaches, our results show how to obtain EWS of tipping points with much greater sensitivity, specificity, and generalizability across systems than is currently possible, as well as predicting the type of tipping point, and thus providing specific qualitative information about the new state that lies beyond the tipping point. This information is important to know for both theoretical and practical purposes, since tipping points in many systems can lead to undesirable collapse (14). Improved EWS can help us better prevent or prepare for such state transitions (41).
Materials and Methods
Generation of Training Data for the DL Classifier.
Training data consist of simulations of randomly generated, two-dimensional dynamical systems of the form
| [4] |
| [5] |
where and are state variables, and are parameters, and is a vector containing all polynomials in and up to third order,
An individual model is generated by drawing each and from a normal distribution with zero mean and unit variance. Then, half of these parameters are selected at random and set to zero. The parameters for the cubic terms are set to the negative of their absolute value to encourage models with bounded solutions.
For a DL algorithm to be effective, the training data should cover a wide representation of the possible dynamics that could occur in unseen data. For this reason, we generate many versions of the model in Eqs. 4 and 5, each with a different set of parameter values. We continue to generate models until a desired number of each type of bifurcation has been found. For each bifurcation, we run simulations that are used as training data for the DL algorithm. In this study, we consider codimension-one bifurcations of steady states, including the fold, Hopf, and transcritical bifurcation. The pitchfork bifurcation is another example; however, it only occurs in models with symmetrical dynamics that are not often found in ecological models.
We generated two different training sets: one consisting of time series of length 500 data points, and one consisting of time series of length 1,500 data points. This was done because the time series lengths in the three empirical and three model systems are highly variable. The algorithm was trained separately on these two training sets (see next subsection), resulting in a “500-classifier” and a “1,500-classifier.” The 500-classifier was used on shorter time series, while the 1,500-classifier was used on the longer time series. For the model time series in Fig. 1, we use the 1,500-classifier. For the ROC curves in Fig. 2, we used the 500-classifier for the paleoclimate data and the ecological models, and used the 1,500-classifier for the thermoacoustic data, anoxia data, and disease model.
Upon generation of a model, we simulate it for 10,000 time steps from a randomly drawn initial condition and test for convergence to an equilibrium point. Convergence is required in order to search for bifurcations. The simulation uses the odeint function from the Python package Scipy (42) with a step size of 0.01. We say the model has converged if the maximum difference between the final 10 points of the simulation is less than . Models that do not converge are discarded. For models that converge, we use AUTO-07P (43) to identify bifurcations along the equilibrium branch as each nonzero parameter is varied within the interval . For each bifurcation identified, we run a corresponding “null” and a “forced” stochastic simulation of the model with additive white noise. Null simulations keep all parameters fixed. Forced simulations increase the bifurcation parameter linearly in time from its original value up to the bifurcation point. Stochastic simulations are run using the Euler Maruyama method with a step size of 0.01, an initial condition given by the model’s equilibrium value and a burn-in period of 100 units of time. The noise amplitude is drawn from a triangular distribution centered at 0.01 with upper and lower bounds 0.0125 and 0.0075, respectively, and weighted by an approximation of the dominant eigenvalue of the model (SI Appendix, Supplementary Note).
For each simulation, we set a sampling rate , the number of data points collected per unit of time, which is drawn randomly from . Using a varied sampling rate provided a wider distribution of lag-1 AC among the training data entries, which is important for representing a wide range of systems and timescales. The simulation is then run for time units for the 500-classifier and time units for the 1,500-classifier, providing 700 and 1,700 points, respectively, when sampled at a frequency .
Due to noise, the simulations often transition to a new regime before the bifurcation point is reached. We only want the DL classifier to see data prior to the transition. Therefore, we use a change-point detection algorithm contained in the Python package ruptures (44) to locate a transition point if one exists. If a transition point is detected, the preceding 500 (1,500) points are taken as training data. If the transition occurs earlier than 500 (1,500) data points into the simulation, the model is discarded. If no transition point is detected, the final 500 (1,500) points are taken as training data.
DL Algorithm Architecture and Training.
We used a CNN-LSTM DL algorithm (25, 26). We also experimented with a residual network, functional convolutional network, and recurrent neural network but found that the CNN-LSTM architecture yielded the highest precision and recall on our training set. The code was written using TensorFlow 2.0 in Anaconda 2020.02. The CNN-LSTM architecture appears in Fig. 3. The algorithm was trained for 1,500 epochs with a learning rate of 0.0005, and the hyperparameters were tuned through a series of grid sweeps. The same hyperparameter values were used for training on both 500-classifier and 1,500-classifier (see previous subsection).
Fig. 3.
CNN-LSTM architecture.
The simulation output time series from the random dynamical systems were detrended using Lowess smoothing with a span of 0.2 to obtain the residual time series that formed the training set. Each residual time series was normalized by dividing each time series data point by the average absolute value of the residuals across the entire time series. We used a train/validation/test split of for both the 500- and 1,500-classifiers. The test set was chosen as a small percentage because a test set of a few thousand time series is adequate to provide a representative estimate of the precision and recall. The f1 score, precision, and recall for an ensemble of ten 500-classifier models were , , and , respectively. The f1 score, precision, and recall for an ensemble of ten 1,500-classifier models were , , and , respectively.
For testing the ability of the DL algorithm to provide EWS of bifurcations, we developed variants where the algorithm was trained on censored versions of the training time series. For the 500 (1,500) length classifier, one variant was trained on a version of the training set where the residuals of the simulation time series were padded on both the left and right by between 0 and 225 (725) zeroes, with the padding length chosen randomly from a uniform distribution. This allowed the algorithm to train on time series as short as 50 (50), not necessarily representing the time phase just before the transition. The intention was to boost the performance of the DL algorithm for detecting EWS features from shorter time series and from the middle sections of time series. The second variant was trained on a version of the training set where the residuals of the simulation time series were padded only on the left, by between 0 and 450 (1,450) zeroes, where the padding length was chosen randomly from a uniform distribution. This allowed the algorithm to train on time series as short as 50 (50), representing time series of various lengths that lead up to the bifurcation (except for the neutral class). As a result, the classifier could better detect features that emerge most strongly right before the bifurcation. Ten trained models of each variant were ensembled by taking their average prediction at each point to generate all of our reported results.
Theoretical Models Used for Testing.
We use models of low and intermediate complexity to test the DL classifier. Models are simulated using the Euler Maruyama method with a step size of 0.01 unless otherwise stated. To test detection of a fold bifurcation, we use May’s harvesting model (28) with additive white noise. This is given by
where is biomass of some population, is its carrying capacity, is the harvesting rate, characterizes the nonlinear dependence of harvesting output on current biomass, is the intrinsic per capita growth rate of the population, is the noise amplitude, and is a Gaussian white noise process. We use parameter values , , , , and . In this configuration, a fold bifurcation occurs at . The parameter is kept fixed at its lower bound for null simulations and is increased linearly to its upper bound in forced simulations.
To test the Hopf and transcritical bifurcations, we use the Rozenzweig−MacArthur consumer−resource model (29) with additive white noise. This is given by
where is the intrinsic per capita growth rate of the resource (), is its carrying capacity, is the attack rate of the consumer (), is the conversion factor, is the handling time, is the per capita consumer mortality rate, and are noise amplitudes, and and are independent Gaussian white noise processes. We fix the parameter values , , , , , , and . In this configuration, the deterministic system has a transcritical bifurcation at and a Hopf bifurcation at . For the transcritical bifurcation, we simulate null trajectories with and forced trajectories with ; for the Hopf bifurcation, we use and , respectively.
To test the DL algorithm on a model of higher dimensionality than the ecological models, we used a stochastic version of the SEIRx model that captures interactions between disease dynamics and population vaccinating behavior (12, 45) given by
where is the number of susceptible individuals, is the number of exposed (infected but not yet infectious) individuals, is the number of infectious individuals, is the number of recovered/immune individuals, is the number of individuals with provaccine sentiment, is the per capita birth and death rate, is the transmission rate, is the per capita rate at which exposed individuals become infectious, is the per capita rate of recovery from infection, is the social learning rate, is the strength of injunctive social norms, and is the perceived relative risk of vaccination versus infection. For our simulations, we used , (based on ), , , , , and , representing a typical pediatric infectious disease (12). Simulations were perturbed weekly with for , and . On account of the large timescale difference in vital dynamics and infection processes, the system is nonnormal (34). We note that , and therefore, since can be obtained as , the model is four-dimensional. The forcing parameter was gradually forced from 0 to 100. As perceived vaccine risk increases along the branch corresponding to full vaccine coverage, the model has a transcritical bifurcation at (12), which leads to a critical transition corresponding to a drop in the proportion of individuals with provaccine sentiment and a return of endemic infection.
Empirical Systems Used for Testing.
We use three different sources of empirical data to test the DL classifier.
-
1)
The first source is sedimentary archives from the Mediterranean Sea (46). These provide high-resolution reconstructions of oxygen dynamics in the eastern Mediterranean Sea. Rapid transitions between oxic and anoxic states occurred regularly in this region in the geological past. A recent study has shown that EWS exist prior to the transitions (31). The data consist of output from three cores that, together, span eight anoxic events. Variables include molybdenum (Mo) and uranium (U), proxies for anoxic and suboxic conditions, respectively, giving us a total of 26 time series for anoxic events (some are captured by multiple cores). The sampling rate provides 10- to 50-y resolution depending on the core, with an almost regular spacing between data points. We perform the same data preprocessing as Hennekam et al. (31). Interpolation is not done, as most data points are equidistant, and it can give rise to aliasing effects that strongly affect variance and AC. Data 10 ky prior to each transition are analyzed for EWS. Null time series of the same length are generated from an AR (1) (autoregressive lag 1) process fit to the initial 20% of the data. Residuals are obtained from smoothing the data with a Gaussian kernel with a bandwidth of 900 y, and EWS are computed using a rolling window of 0.5.
-
2)
The second source is thermoacoustic instability. Thermoacoustic systems often exhibit a critical transition to a state of self-sustained large-amplitude oscillations in the system variables, known as thermoacoustic instability. The establishment of a positive feedback between the heat release rate fluctuations and the acoustic field in the system is often the cause for this transition. We perform experiments in a horizontal Rijke tube which consists of an electrically heated wire mesh in a rectangular duct (30). We pass a constant mass flow rate of air through the duct and control the voltage applied across the wire mesh to attain the transition to thermoacoustic instability via subcritical Hopf bifurcation as the voltage is increased. We have data for 19 forced trajectories where the voltage is increased over time at different rates (2 mV/s to 24,000 mV/s). We also have 10 steady-state trajectories where the voltage is kept at a fixed value between 0 and 4 V. Experimental runs at fixed higher voltages are not used, as they exhibit limit cycle oscillations. We downsample the data from 4 kHz to 10 kHz in experiments to 2kHz. Transition times are picked by eye. For each forced time series, we analyze data 1,500 points prior to the transition. From the steady-state time series, we extract two random sections of length 1,500 to serve as null time series, giving a total of 20 null time series. Data are detrended using Lowess smoothing with a span of 0.2 and degree 1. EWS are computed from residuals using a rolling window of 0.5.
-
3)
The third source is paleoclimate transitions (47–50). We use data for seven out of the eight climate transitions that were previously analyzed for EWS by Dakos et al. (17). Time series for the desertification of North Africa was not included due to insufficient data. We use the same data preprocessing as Dakos et al. (17), which involves using linear interpolation to make the data equidistant, and detrend with a Gaussian kernel smoothing function. Bandwidth of the kernel is specified for each time series (17) to remove long-term trends while not overfitting. For each time series, we generate 10 null time series of the same length from an AR (1) process fit to the initial 20% of the residuals, yielding a total of 70 null time series and 7 forced time series.
Computing Early Warning Indicators and Comparing Predictions with the DL Classifier.
Generic early warning indicators are computed using the Python package ewstools (20) which implements established methods (51). This first involves detrending the time series to obtain residual dynamics. This is done using Lowess smoothing (52) with span 0.2 and degree 1 unless stated otherwise. Variance and lag-1 AC are then computed over a rolling window of length 0.5. To assess the presence of an early warning signal, we use the Kendall value, which serves as a measure of increasing or decreasing trend. The Kendall value at a given time is computed over all of the preceding data.
To compare predictions made between variance, lag-1 AC, and the DL classifier, we use ROC. The ROC curve plots the true positive rate vs. the false positive rate as a discrimination threshold is varied. For variance and lag-1 AC, the discrimination threshold is taken as the Kendall value, whereas, for the DL classifier, the discrimination threshold is taken as the DL probability.
Supplementary Material
Acknowledgments
We thank Ryan Kinnear for helpful discussions on time series analysis and Rick Hennekam and Gert-Jan Reichart for providing the anoxia dataset. This research was supported by Natural Sciences and Engineering Research Council Discovery Grants to C.T.B. and M.A.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2106140118/-/DCSupplemental.
Data Availability
Thermoacoustic data and machine learning and training set code have been deposited in GitHub (https://github.com/ThomasMBury/deep-early-warnings-pnas). The geochemical data (46) are available at the PANGAEA repository (https://doi.pangaea.de/10.1594/PANGAEA.923197). The paleoclimate data (47) are available from the World Data Center for Paleoclimatology, National Geophysical Data Center, Boulder, Colorado (http://www.ncdc.noaa.gov/paleo/data.html).
References
- 1.Gould S. J., Eldredge N., Punctuated equilibrium comes of age. Nature 366, 223–227 (1993). [DOI] [PubMed] [Google Scholar]
- 2.Prigogine I., Time, structure, and fluctuations. Science 201, 777–785 (1978). [DOI] [PubMed] [Google Scholar]
- 3.Strogatz S. H., Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Westview, 2014). [Google Scholar]
- 4.Wainwright J., Ellis G. F. R., Dynamical Systems in Cosmology (Cambridge University Press, 2005). [Google Scholar]
- 5.Ostlund S., Pandit R., Rand D., Schellnhuber H. J., Siggia E. D., One-dimensional Schrödinger equation with an almost periodic potential. Phys. Rev. Lett. 50, 1873 (1983). [Google Scholar]
- 6.Grenfell B. T., Bjørnstad O. N., Kappey J., Travelling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 (2001). [DOI] [PubMed] [Google Scholar]
- 7.Hastings A., et al. , Transient phenomena in ecology. Science 361, (2018). [DOI] [PubMed] [Google Scholar]
- 8.Bury T. M., Bauch C. T., Anand M., Charting pathways to climate change mitigation in a coupled socio-climate model. PLOS Comput. Biol. 15, e1007000 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.van Nes E. H., et al., What do you mean, ‘tipping point’? Trends Ecol. Evol. 31, 902–904 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Kuznetsov Y. A., Elements of Applied Bifurcation Theory (Applied Mathematical Sciences, Springer Science & Business Media, 2013), vol. 112. [Google Scholar]
- 11.Campbell S. A., “Calculating centre manifolds for delay differential equations using maple” in Delay Differential Equations, Erneux T., Ed. (Springer, 2009), pp. 1–24. [Google Scholar]
- 12.Oraby T., Thampi V., Bauch C. T., The influence of social norms on the dynamics of vaccinating behaviour for paediatric infectious diseases. Proc. R. Soc. B Biol. Sci. 281, 20133172 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wissel C., A universal law of the characteristic return time near thresholds. Oecologia 65, 101–107 (1984). [DOI] [PubMed] [Google Scholar]
- 14.Scheffer M., et al., Anticipating critical transitions. Science 338, 344–348 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Boettiger C., Ross N., Hastings A., Early warning signals: The charted and uncharted territories. Theor. Ecol. 6, 255–264 (2013). [Google Scholar]
- 16.Kéfi S., Dakos V., Scheffer M., Van Nes E. H., Rietkerk M., Early warning signals also precede non-catastrophic transitions. Oikos 122, 641–648 (2013). [Google Scholar]
- 17.Dakos V., et al., Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. U.S.A. 105, 14308–14312 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Butitta V. L., Carpenter S. R., Loken L. C., Pace M. L., Stanley E. H., Spatial early warning signals in a lake manipulation. Ecosphere 8, e01941 (2017). [Google Scholar]
- 19.Meisel C., Kuehn C., Scaling effects and spatio-temporal multilevel dynamics in epileptic seizures. PLoS One 7, e30371 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bury T. M., Bauch C. T., Anand M., Detecting and distinguishing tipping points using spectral early warning signals. J. R. Soc. Interface 17, 20200482 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Carpenter S. R., Brock W. A., Early warnings of regime shifts in spatial dynamics using the discrete Fourier transform. Ecosphere 1, 1–15 (2010). [Google Scholar]
- 22.Wiesenfeld K., Virtual Hopf phenomenon: A new precursor of period-doubling bifurcations. Phys. Rev. A Gen. Phys. 32, 1744–1751 (1985). [DOI] [PubMed] [Google Scholar]
- 23.Fawaz H. I., Forestier G., Weber J., Idoumghar L., Muller P.-A., Deep learning for time series classification: A review. Data Min. Knowl. Discov. 33, 917–963 (2019). [Google Scholar]
- 24.Scheffer M., Carpenter S. R., Dakos V., van Nes E. H., Generic indicators of ecological resilience: Inferring the chance of a critical transition. Annu. Rev. Ecol. Evol. Syst. 46, 145–167 (2015). [Google Scholar]
- 25.Mutegeki R., Han D. S., “A CNN-LSTM approach to human activity recognition” in 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Lee J. H., Park S., Eds. (Institute of Electrical and Electronics Engineers, 2020), pp. 362–366. [Google Scholar]
- 26.Vidal A., Kristjanpoller W., Gold volatility prediction using a CNN-LSTM approach. Expert Syst. Appl. 157, 113481 (2020). [Google Scholar]
- 27.Adamson M. W., Dawes J. H. P., Hastings A., Hilker F. M., Forecasting resilience profiles of the run-up to regime shifts in nearly-one-dimensional systems. J. R. Soc. Interface 17, 20200566 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.May R. M., Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 269, 471–477 (1977). [Google Scholar]
- 29.Rosenzweig M. L., MacArthur R. H., Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209–223 (1963). [Google Scholar]
- 30.Pavithran I., Sujith R. I., Effect of rate of change of parameter on early warning signals for critical transitions. Chaos 31, 013116 (2021). [DOI] [PubMed] [Google Scholar]
- 31.Hennekam R., et al., Early-warning signals for marine anoxic events. Geophys. Res. Lett. 47, e2020GL089183 (2020). [Google Scholar]
- 32.Dakos V., Carpenter S. R., van Nes E. H., Scheffer M., Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 370, 20130263 (2015). [Google Scholar]
- 33.Boettiger C., Hastings A., Early warning signals and the prosecutor’s fallacy. Proc. R. Soc. B Biol. Sci. 279, 4734–4739 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.O’Regan S. M., O’Dea E. B., Rohani P., Drake J. M., Transient indicators of tipping points in infectious diseases. J. R. Soc. Interface 17, 20200094 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Williamson M. S., Lenton T. M., Detection of bifurcations in noisy coupled systems from multiple time series. Chaos 25, 036407 (2015). [DOI] [PubMed] [Google Scholar]
- 36.Baurmann M., Gross T., Feudel U., Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. J. Theor. Biol. 245, 220–229 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Zou J., Schiebinger L., AI can be sexist and racist—It’s time to make it fair. Nature 559, 324−326 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Boers N., Early-warning signals for Dansgaard-Oeschger events in a high-resolution ice core record. Nat. Commun. 9, 2556 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang R., et al., Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature 492, 419–422 (2012). [DOI] [PubMed] [Google Scholar]
- 40.Pathak J., Hunt B., Girvan M., Lu Z., Ott E., Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach. Phys. Rev. Lett. 120, 024102 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Bauch C. T., et al., Early warning signals of regime shifts in coupled human–environment systems. Proc. Natl. Acad. Sci. U.S.A. 113, 14560–14567 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Virtanen P., et al., SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Doedel E. J., et al., Auto-07p: Continuation and bifurcation software for ordinary differential equations. https://re.public.polimi.it/handle/11311/560353. Accessed 7 September 2021.
- 44.Truong C., Oudre L., Vayatis N., Selective review of offline change point detection methods. Signal Processing 167, 107299 (2020). [Google Scholar]
- 45.Pananos D. A., et al., Critical dynamics in population vaccinating behavior. Proc. Natl. Acad. Sci. U.S.A. 114, 13762−13767 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hennekam R., et al. , Calibrated XRF-scanning data (mm resolution) and calibration data (ICP-OES and ICP-MS) for elements Al, Ba, Mo, Ti, and U in Mediterranean cores MS21, MS66, and 64PE406E1. PANGAEA. 10.1594/PANGAEA.923197. Accessed 21 September 2020. [DOI]
- 47.Hughen K., et al. , Cariaco Basin 2000 deglacial 14C and grey scale data. IGBP PAGES/World Data Center A for Paleoclimatology Data Contribution Series #2000-069. NOAA/NGDC Paleoclimatology Program. https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=noaa-ocean-5853. Accessed 7 January, 2021.
- 48.Petit J. R., et al. , Vostok ice core data for 420,000 years. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2001-76. ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/vostok/dustnat.txt. Accessed 7 January, 2021.
- 49.Alley R., GISP2 Ice core temperature and accumulation data, IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series no. 2004-013. NOAA/NGDC Paleoclimatology Program. ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/greenland/summit/gisp2/isotopes/gisp2_temp_accum_alley2000.txt. Accessed 7 January, 2021.
- 50.Tripati A., et al. Eocene greenhouse-icehouse transition carbon cycle Data. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series no. NOAA/NGDC Paleoclimatology Program. https://www.ncei.noaa.gov/pub/data/paleo/contributions_by_author/tripati2005/tripati2005.txt. Accessed 7 January 2021.
- 51.Dakos V., et al., Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS One 7, e41010 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cleveland W. S., Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 74, 829–836 (1979). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Thermoacoustic data and machine learning and training set code have been deposited in GitHub (https://github.com/ThomasMBury/deep-early-warnings-pnas). The geochemical data (46) are available at the PANGAEA repository (https://doi.pangaea.de/10.1594/PANGAEA.923197). The paleoclimate data (47) are available from the World Data Center for Paleoclimatology, National Geophysical Data Center, Boulder, Colorado (http://www.ncdc.noaa.gov/paleo/data.html).