Significance
Do we talk about some colors more often than others? And do the colors we communicate about most frequently vary across cultures? A classic finding shows that languages around the world partition colors into words in remarkably similar, although not identical, ways. The biology of human color perception helps explain similar color vocabularies across languages, but less is known about how often speakers need to reference different colors. The inference method we develop reveals extensive variation in communicative needs across colors, and a diversity in needs across 130 languages, which helps explain variation in their color vocabularies. Our results open the door to studying cross-cultural variation in demands on different colors, and factors that drive color demands in linguistic communities.
Keywords: color categories, language evolution, cultural evolution, collective behavior, information theory
Abstract
Names for colors vary widely across languages, but color categories are remarkably consistent. Shared mechanisms of color perception help explain consistent partitions of visible light into discrete color vocabularies. But the mappings from colors to words are not identical across languages, which may reflect communicative needs—how often speakers must refer to objects of different color. Here we quantify the communicative needs of colors in 130 different languages by developing an inference algorithm for this problem. We find that communicative needs are not uniform: Some regions of color space exhibit 30-fold greater demand for communication than other regions. The regions of greatest demand correlate with the colors of salient objects, including ripe fruits in primate diets. Our analysis also reveals a hidden diversity in the communicative needs of colors across different languages, which is partly explained by differences in geographic location and the local biogeography of linguistic communities. Accounting for language-specific, nonuniform communicative needs improves predictions for how a language maps colors to words, and how these mappings vary across languages. Our account closes an important gap in the compression theory of color naming, while opening directions to study cross-cultural variation in the need to communicate different colors and its impact on the cultural evolution of color categories.
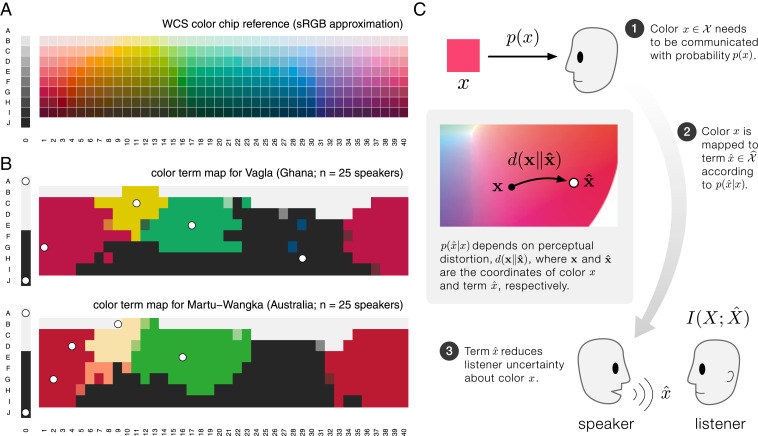
What colors are “green” to an English speaker? Are they the same as what a French speaker calls “vert?” Berlin and Kay (1) and Kay et al. (2) studied this question on a worldwide scale, surveying the color vocabularies of 130 linguistic communities using a standardized set of color stimuli (Fig. 1A). They found that color vocabularies of independent linguistic origin are remarkably consistent in how they partition color space (1). In languages with two major color terms, one term typically describes white and warm colors (red/yellow), and the other describes black and cool colors (green/blue). If a language has three color terms, there is typically a term for white, a term for red/yellow, and a term for black/green/blue. Languages with yet larger color vocabularies remain largely predictable in how they partition the space of perceivable colors into discrete terms (3–6) (Fig. 1B).
Fig. 1.
Cross-linguistic patterns in color naming and the rate−distortion hypothesis. B&K (1) and WCS (2) studied color vocabularies in 130 languages around the world (see WCS). (A) The 330 color chips named by native speakers in the WCS study. Colors shown here are best approximations in Standard RGB (sRGB) color space. (B) Empirical color vocabularies for two example languages in the WCS, each with six basic color terms. Color chips correspond to A, but they have been colored according to the focal color of the term chosen by the majority of speakers surveyed (or by a mixture of the best choice focal colors when there was more than one best choice). The languages Vagla and Martu-Wangka, although linguistically unrelated and separated by a distance of nearly 14,000 km, have remarkably similar partitions of colors into basic color terms (2). (C) Schematic diagram of rate−distortion theory applied to color naming. A speaker needs to refer to color with probability . The speaker uses a probabilistic rule to assign color terms, , to colors, . This rule depends on the perceptual distortion d introduced by substituting for the true color, , where each term is associated with a coordinate in color space. The choice of the term by the speaker reduces the listener’s uncertainty about the true color being referenced, measured, on average, by the mutual information . While any probabilistic mapping from colors to terms, , is possible, some mappings are more efficient than others. Rate−distortion theory provides optimal term mappings that allow a listener to glean as much information as possible, for a given level of tolerable distortion and distribution of communicative needs .
What explains these shared patterns? To talk about color, a language must represent the vast space of human perceivable colors with a comparatively small set of color terms. The compression theory of color naming (7–10) seeks to explain color vocabularies as an efficient mapping from colors to terms, based on the psychophysics of human color perception and the utility, or need, to reference different colors.
Judgments of color appearance by humans with normal color vision are remarkably stable despite genetic variability in photoreceptor spectral sensitivities (11), age-dependent variability in light filtering of the eye (12), and variation in the proportion of different classes of retinal cone photoreceptors (13, 14). The shared psychophysics of perception therefore provides a common metric for color similarity, and common limits on the gamut of perceivable colors, which each contribute to shared patterns in color naming across languages (1, 8, 15–22).
Recent work (23–25) has also found that color terms tend to reflect how often speakers need to refer to different colors, with a trend that emphasizes communication about warm hues (red/yellow) over cool hues (blue/green). Shared communicative needs of colors—for example, emphasizing the colors of greatest importance to ancestral humans, such as those of ripe fruits or dangerous animals (26)—also helps explain shared patterns in color naming across languages.
However, estimating communicative needs is nontrivial. Several approaches have been proposed: using the statistics of surface reflectances in natural scenes (7), assuming a uniform distribution over highly saturated colors (8), using a worldwide average of capacity-achieving priors (10, 27), or extrapolating from English word frequency corpus data (28). The aim of all of these approaches is to approximate a single distribution of needs common to all languages worldwide. But, unlike perception, needs may vary across cultures—and this variation might explain why color vocabularies, though similar, are far from identical across languages. A complete theory of color naming must explain cross-language variation as well as shared trends. However, to date, language-specific communicative needs are unknown.
Here, we seek to close this gap in the compression theory of color naming by providing a way to directly estimate language-specific communicative needs of colors. Without making strong assumptions about the origins or characteristics of communicative needs, we derive an algorithm to solve a natural inverse problem; we infer the most conservative (maximum entropy) distribution of communicative needs across colors consistent with positions of focal colors in a language’s vocabulary—for example, the “reddest red” and the “greenest green.” Our approach explains focal colors as a natural part of the compression theory of color naming, and it allows us to test predictions for term maps against independent empirical data that were not used in fitting our model.
Applying our method, we infer the language-specific communicative needs for 130 languages around the world. We confirm that shared trends in communicative needs across languages are related to the colors of salient objects (23), but we also find substantial variation in communicative needs across languages. This variation is consequential: Accounting for variation in needs substantially improves the prediction of color terms in each language. Moreover, this variation in needs across linguistic communities is meaningful: It correlates with differences in geographic location and local biogeography. Our account supports an emerging, unified view of the color word problem that integrates the shared psychophysics of color perception with language-specific communicative needs for colors. We show that this view is consistent with both shared patterns and observed variability across languages.
Color Naming as a Compression Problem
In the compression model of color naming first introduced by Yendrikhovskij (7) and with recent extensions by Zaslavsky et al. (10), a color in the set of all perceivable colors, , needs to be communicated with some probability, , to a listener. The speaker cannot be infinitely precise when referring to , and must instead use a term, , from their shared color vocabulary, . Many colors in map to the same term, so that a listener hearing will not know exactly which color was referenced. Color naming is then distilled to the following problem: How do we choose the mapping from colors to color terms? Rate−distortion theory (29–32), the branch of information theory concerned with lossy compression, provides an answer.
Mapping colors to a limited set of terms necessarily introduces imprecision or “distortion” in communication. The amount of distortion depends on a listener’s expectation about what color, , a speaker is referencing when she utters color term . Under the rate−distortion hypothesis, a language’s mapping from colors to terms allows a listener to glean as much information as possible about color from a speaker’s choice of term (Fig. 1C).
Each color is identified with a unique position, denoted , in a perceptually uniform color space. Here we use CIE (Commission Internationale de l’Eclairage) Lab as in Regier et al. (8). The coordinates corresponding to a color term are given by its centroid: the weighted average of all colors a speaker associates with that term, . The distortion introduced when a speaker uses to refer to is simply the squared Euclidean distance between and in CIE Lab, denoted . Intuitively, colors that are near are more likely to be assigned to the term than colors that are far (Fig. 1C), and the centroid minimizes the average distortion of all the points assigned to that term, that is, .*
The mathematics of compression provides optimal ways to represent information for a given level of tolerable distortion. The size of a compressed representation, , is measured by the amount of information it retains about the uncompressed source, , given by the mutual information . Terms represent colors by specifying the probability of using a particular term to refer to a given color , denoted . Rate−distortion efficient mappings are choices of the mapping that minimize such that the expected distortion, , does not exceed a given tolerable level. Efficient mappings and centroid positions can be found for a large class of distortion functions known as Bregman divergences, which includes the CIE Lab measure of perceptual distance (SI Appendix, section 1).
Communicative Needs of Colors
Rate−distortion theory provides an efficient mapping from colors to terms that depends on three choices: the distortion function in color space, the degree of distortion tolerated by the language, and the probability that each color needs to be referenced during communication, called the “communicative need.” Previous studies have largely focused on communicative needs that are shared across all languages, considering distributions that are either uniform across the World Color Survey (WCS) color stimuli (5), correlated with the statistics of natural images (7) or the color of salient objects (23), approximated by a worldwide average “capacity achieving prior” (10, 27), or related to linguistic usage (33) as, for example, approximated by the frequencies of words for color in English language corpus data (28). As a result, prior studies have drawn conflicting conclusions about whether communicative needs matter for color naming, and little is known about whether communicative needs vary across languages or whether such variation is significant for their color vocabularies. While the potential importance of language-specific communicative needs has been discussed (33), here we resolve these questions by directly estimating the communicative needs of colors for each of the 130 languages in the combined Berlin and Kay plus WCS (B&K+WCS) dataset under the compression theory of color naming.
Algorithm to Infer Communicative Needs.
How can we infer the underlying communicative needs of colors from limited empirical data? Here we derive an algorithm that finds the maximum entropy estimate of the underlying communicative needs consistent with a rate−distortion optimal vocabulary with known centroid coordinates and term frequencies , for any Bregman divergence measure of distortion.
The estimate of communicative needs has the form , with
| [1] |
In words, the optimal is the choice of that maximizes the entropy, , among the set of conditional probability distributions whose predicted focal color coordinates match the observed coordinates for each color term. We construct this solution via an iterative alternating maximization algorithm (SI Appendix, section 2 for its derivation),
| [2] |
where the vectors are chosen so that predicted focal color coordinates match observed coordinates (SI Appendix, section 2).
This algorithm provably converges to a unique, globally optimal, maximum entropy estimate of the true communicative need (SI Appendix, sections 2A and 2B). Remarkably, we can construct this solution knowing only that the observed coordinates are rate−distortion optimal centroids, without knowledge of the specific distortion measure (SI Appendix, section 2C and Fig. S1).
Inference from Focal Colors.
Our algorithm infers a language’s communicative needs from knowledge of the centroids associated with its color terms. Berlin and Kay (1) measured the “focal color” of each color term by asking native speakers to choose, from among the Munsell stimuli (Fig. 1A), the “best example” of that term. We propose that the measured focal colors are, in fact, the centroids for each term.† This hypothesis may appear problematic, since laboratory experiments suggest focal colors and category centroids are distinct points in color space (34–36). However, centroids in those studies were calculated under the implicit assumption of uniform communicative needs, leaving open the possibility that focal colors are centroids under the true distribution of nonuniform needs (SI Appendix, section 1C).
Our approach provides an entropy-maximizing inference of language-specific communicative needs that does not make strong assumptions about the form of or depend on additional, unmeasured quantities for each WCS language. Prior work on a universal distribution of needs relies on strong assumptions about the form of (SI Appendix, sections 2C and 4), and so applying it to individual languages in the WCS produces implausible inferences (SI Appendix, Fig. S4). Alternatively, there is a prior language-specific approach based on word frequency data, but this approach cannot be applied to the vast majority of languages in the WCS that lack this information (SI Appendix, section 4A and Fig. S10B). Moreover, unlike prior work, our inference of language-specific needs does not rely on knowing the empirical mapping from colors to terms, , which is the quantity that we ultimately wish to predict from any theory of color naming (SI Appendix, Fig. S9).
Different Colors, Different Needs.
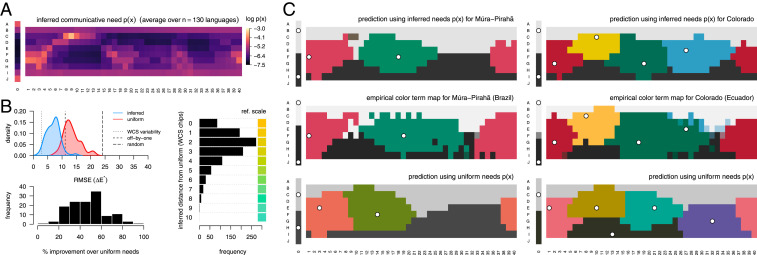
Our analysis reveals extensive variation in the demand to speak about different regions of color space (Fig. 2A). Averaged over all 130 B&K+WCS languages, the inferred communicative needs emphasize some colors (e.g., bright yellows and reds) up to 36-fold more strongly than others (e.g., blue/green pastels and browns). This conclusion stands in sharp contrast to prior work that assumed a uniform distribution of needs (8) and attributed color naming to the shape of color space alone.
Fig. 2.
Inferred distributions of communicative needs. (A) The mean inferred distribution of communicative need, , averaged across the WCS and B&K survey data ( languages). Color chips correspond to those shown in Fig. 1A. We infer 36-fold variation in communicative need across color chips, with greater demand for communication about yellows and reds, for example, than for blues and greens. (B) The color vocabulary of a language predicted by rate−distortion theory better matches the empirical vocabulary when we account for variation in the need to communicate about different colors. (Top Left) The error between the predicted and empirical focal color positions across languages, where predictions are rate−distortion optimal vocabularies assuming either a uniform (red) or the inferred (blue) distribution of communicative needs. RMSE is measured in units of CIE Lab perceptual distance (denoted ; RMSE of Focal Color Predictions). Reference lines show RMSE when empirical focal points are compared to random focal points (“random”), displaced by one WCS column or row (off-by-one), and by sampling from participant responses (“WCS variability”) (see SI Appendix, section 3A). (Bottom Left) The relative improvement (reduction in error) using the inferred versus uniform distribution of communicative need. (Right) Difference in focal point positions of rate−distortion optimal vocabularies, under inferred versus uniform communicative needs. (C) Two example languages, Múra-Pirahã (Left), and Colorado (Right), that illustrate how predicted term maps are improved when accounting for nonuniform communicative needs of colors. The region corresponding to each term is colored by the WCS chip closest to the term’s focal point (white points). The predicted term maps (Top) based on the inferred distribution of communicative needs and (Bottom) based on a uniform distribution of communicative need; (Middle) the empirical term maps in the WCS data.
Our ability to predict the color vocabulary of a language is substantially improved once we account for nonuniform communicative needs (Fig. 2B). We find improvement in an absolute sense, as measured by the root-mean-squared error (RMSE) between predicted and empirically measured focal colors, and also in a relative sense, measured by percent improvement over a uniform distribution of needs. The typical change in predicted focal color once accounting for nonuniform needs is easily perceivable, corresponding to a median change of two WCS color chips (Fig. 2B, Right). Not only are the predicted focal points in better agreement with the empirical data, once accounting for nonuniform needs, but the entire partitioning of colors into discrete terms is substantially improved, as seen in the example languages Múra-Pirahã and Colorado (Fig. 2C).
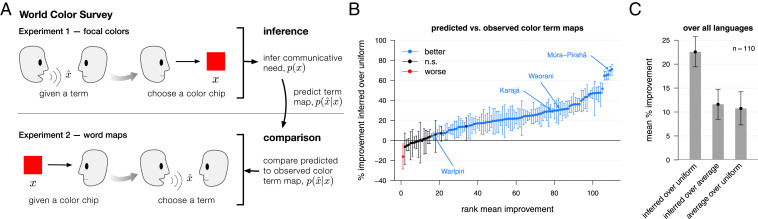
We infer communicative needs and predict color terms using data from the first of two experiments in the WCS, which measured focal colors (Fig. 3A). This inference and prediction requires fitting one parameter that controls the “softness” of the partitioning and one hyperparameter to control overfitting (SI Appendix, section 3). Without any additional fitting, we can then compare the predicted mappings from colors to terms to the empirical term maps measured in the second WCS experiment. For nearly all of the WCS languages analyzed (), the color term maps predicted by rate−distortion theory are significantly improved once accounting for nonuniform communicative needs (improvement in 84% of languages; Fig. 3B). Only 15% of languages show little or no improvement, with an additional single outlier, Huave (Huavean, Mexico), that may violate model assumptions in some significant way (see Discussion). The substantial improvement in predicted term maps can be attributed both to universal patterns in communicative needs, shared across languages, and to language-specific variation in needs (Fig. 3C).
Fig. 3.
Inference and prediction within the WCS. (A) WCS (2) included two separate experiments with native speakers of each language. In this study, we used only the WCS focal color experiment to infer the communicative needs of colors, , and to predict a language’s mapping from colors to terms, . Without any additional fitting, we then compared the predicted term maps to the empirical term maps observed in the second WCS experiment. (B) Predicted term maps tend to agree with the observed term maps (Fig. 2C and SI Appendix, Fig. S2C). Moreover, the predicted term maps show better agreement with the empirical data than would predictions assuming a uniform distribution of communicative needs. Shown are the rank ordered mean percentage improvement in predicted versus observed term maps using the inferred communicative need compared to a uniform communicative need, with 95% CIs (bootstrap resampling; see Measuring Distance between Distributions over Colors). Languages (points) colored black have 95% CIs overlapping 0%; blue indicates significant improvement. Languages that do worse under the inferred distribution of needs (red points) violate model assumptions. (C) Over all languages, the mean percentage improvement (and 95% CIs) in predicted vocabularies when using language-specific commutative needs compared to uniform needs (“inferred over uniform”), language-specific versus average needs over all languages (“inferred over average”), and average versus uniform needs (“average over uniform”). Some improvement in predictive accuracy is attributable to commonalities in communicative needs across languages (third comparison), and yet more improvement is attributable to variation in needs among languages (second comparison).
In contrast to prior work on the compression model of color naming (10, 28), no part of our inference procedure uses empirical data on a language’s mapping from colors to terms, . Nor are our predicted color terms simply an out-of-sample prediction, since the predicted quantities, , are not used to parameterize the model. Therefore, our analysis is not simply a fit of the compression model to data but rather an empirical test of its ability to predict color naming from first principles.
Communicative Needs and the Colors of Salient Objects.
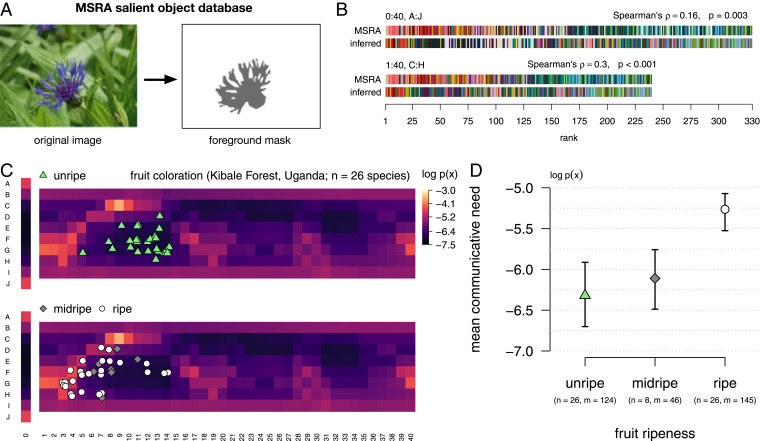
We can interpret the inferred communicative needs of colors by comparing them to what is known about the colors of salient objects. Prior work (23) suggests a warm-to-cool trend in communicative need, related to the frequency of colors that appear in foreground objects as identified by humans in a large dataset of natural images (37) (Fig. 4A). We find that the same correlation holds, at least when restricting to the middle range of lightness (color chips in rows C–H in Fig. 4C; two-sided Spearman’s , p 0.001, ). However, the pattern of communicative needs is more complex than this warm−cool gradient alone. Pastels that are greenish blue or blue, as well as brownish greens, need to be communicated less often than dark green or dark blue, for example. Moreover, dark colors in general (e.g., color chips in rows I and J in Fig. 4C) show a relatively high communicative need under our inference compared to their frequency in foreground objects of natural images (Fig. 4B).
Fig. 4.
Inferred distributions of communicative needs correlate with the colors of salient objects. (A) Human participants in the MSRA salient object study were asked to identify the foreground object in images; example foreground mask is illustrated in gray. (B) WCS color chips ordered by their rank frequency in the foreground of MSRA images [rows “MSRA”; see Gibson et al. (23)], and in the inferred distribution of communicative need (rows “inferred”), averaged across the languages in the B&K+WCS survey data. There is a weak positive correlation between the colors that are considered salient, in the MSRA dataset, and the colors with greatest inferred communicative need, across all WCS color chips (Top). This relationship is strengthened after removing achromatic chips (WCS column 0, rows B and I) from the comparison (Bottom). (C) Colors of unripe (Top) and midripe and ripe (Bottom) fruit in the diets of catarrhine primates, derived from fruit spectral reflectance measurements collected in the Kibale Rainforest, Uganda, by Sumner and Mollon (38, 39). The colors of ripe fruit tend to correspond with the colors of greatest inferred communicative need. (D) Average log-probability in the inferred distribution of communicative need of color corresponding to unripe, midripe, and ripe fruit; denotes the number of fruit species, and denotes the total number of spectral measurements. Error bars show CIs of the means (nonparametric bootstrap by species).
We also compared communicative needs to spectral measurements by Sumner and Mollon (38, 39) of unripe and ripe fruit in the diets of catarrhine primates, which have trichromatic color vision and spectral sensitivities similar to humans. When projected onto the WCS color chips (SI Appendix, Fig. S6), unripe, midripe, and ripe fruit occupy distinct regions of perceptual color space (Fig. 4C) corresponding to low, medium, and high values of inferred communicative need, respectively (Fig. 4D). The morphological characteristics of fruit, including color, are known to be adapted to the sensory systems of frugivores that act as their seed dispersers, for vertebrates in general (40–42) and primates in particular (43–45). Therefore, our results support the hypothesis that shared communicative needs in human cultures emphasize the colors of salient objects that stand out or attract attention in our shared visual system across a typical range of environments.§
Cross-Cultural Variation.
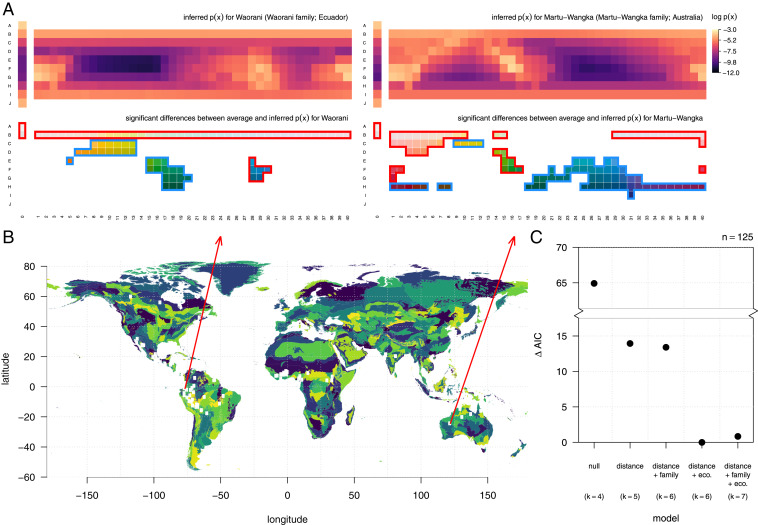
Languages vary considerably in their needs to communicate about different parts of color space (Fig. 5A and SI Appendix, Figs. S11–S27). The inferred needs for the language Waorani (Ecuador), for example, emphasize white and midvalue blues, while deemphasizing yellows and greens, relative to the average needs of all B&K+WCS languages, whereas Martu-Wangka (Australia) emphasizes pinks and midvalue reds, as well as light greens, while deemphasizing blues and dark purples (Fig. 5A). In fact, the median distance between language-specific communicative needs and the across-language average needs is nearly as large as the distance between the average needs and uniform needs (9.9 and 11.2, respectively, in units of ).
Fig. 5.
The communicative needs of colors vary across languages, and they are correlated with geographic location and ecological region. (A) The inferred distribution of communicative needs for two example languages (Top). For each language, many color chips have significantly elevated (red border) or suppressed (blue border) communicative need compared to the across-language average (Bottom; deviations that exceed with 95% confidence are highlighted in red or blue). (B) The approximate locations of WCS native language communities (red points) shown on a world map colored by ecoregions (47). (C) Languages spoken in closer proximity to each other and sharing the same ecoregion tend to have more similar inferred communicative needs (type II Wald χ2 tests; 20.98, df = 1, ; and 12.91, df = 1, ), whereas shared language family does not have a significant effect ( 1.022, df = 1, ). Distance and shared ecoregion each substantially improve the fit of GLMMs predicting the distance between pairs of inferred communicative needs. GLMMs were fit using log-normal link function and a random effects model designed for regression on distance matrices (69) (see Correlates of Cross-Cultural Differences in Communicative Need); denotes the total number of fixed and random effects in each model.
Why do language communities vary in their needs to communicate different colors? Detailed study of this question requires language-specific investigation beyond the scope of the present work. However, we can at least measure how variation in linguistic origin, geographic location, and local biogeography (Fig. 5B) relate to differences in communicative needs. We quantified these factors for pairs of languages by determining 1) whether or not they belong to the same linguistic family in Glottolog (46); 2) the geodesic distance between communities of native speakers; and 3) whether or not language communities share the same “ecoregion,” a measure of biogeography (47) that delineates boundaries between terrestrial biodiversity patterns (48). Our statistical analysis also controls for differences in the number of color terms between languages, because we seek to understand cross-cultural variation above and beyond any relationship between vocabulary size and (inferred) communicative needs (SI Appendix, section 3C).
While language differences are largely idiosyncratic, we find a small but measurable impact of distance and biogeography on communicative needs (Fig. 5C and Correlates of Cross-Cultural Differences in Communicative Need). In particular, increasing the geodesic distance between language communities by a factor of 10 decreases the mean similarity in their communicative needs by a factor of 2.9% ( CI), while sharing the same ecoregion increases the mean similarity by a factor of ( CI). By contrast, we find no significant effect of language genealogy on communicative needs, at least at the coarse scale of language family. Taken together, these results suggest that color vocabularies are adapted to the local context of language communities.
Discussion
We have inferred language-specific needs to communicate about different colors, using an algorithm that applies to any rate−distortion Bregman clustering. Accounting for nonuniform needs substantially improves our ability to predict color vocabularies across 130 languages. Neither our predictions of term maps nor, in contrast to prior work, our inferences of needs use empirical information on the mappings from colors to terms, allowing us to test the compression model of color naming against independent data.
The distribution of communicative needs, averaged across languages, reflects a warm-to-cool gradient, as hypothesized in Gibson et al. (23), and it is related to object salience more generally, as indicated by the positioning of ripe fruit coloration in regions of highest need. This is true even though the needs that we infer by maximum entropy differ from the notion of communicative efficiency, or surprisal, used in prior work (SI Appendix, section 3F.1). We also document extensive variation across languages in the demands on different regions of color space, correlated with geographic location and the local biogeography of language communities.
Our analysis provides clear support for the compression model of color naming. Whereas prior work has established the role of shared perceptual mechanisms for universal patterns in color naming, our results highlight communicative need as a source of cross-cultural variation that must be included for agreement with empirical measurements. A catalog of language-specific needs (SI Appendix, Figs. S11–S27) will enable future study into what drives cultural demands on certain regions of color space, and how they relate to contact rates between linguistic communities, shared cultural history, and local economic and ecological contexts. Our methodology also provides a theoretical framework and inference procedure to study categorization in other cognitive domains, including other perceptual domains of diverse importance worldwide (49), and even in nonhuman cognitive systems that exhibit categorization [e.g., Zebra finches (50, 51), the songbird Taeniopygia guttata].
Several languages have been advanced as possibly invalidating the universality of color categories (52–54). Languages are known to vary in the degree to which different sensory domains are coded (49, 55, 56), and, in Pirahã and Warlpiri, the existence of abstract terms for colors has been disputed (57, 58). Moreover, the color vocabularies in Karajá and Waorani notably lack alignment with the shape of perceptual color space (5). Once we account for communicative needs, however, we find that the color terms of Karajá and Waorani are well explained by rate−distortion theory. Likewise, while Pirahã may seem exceptional when assuming uniform communicative needs, we recover accurate predictions once accounting for a nonuniform distribution of needs (Figs. 2C and 3B).¶
Nevertheless, several languages show little or no improvement in predicted term maps using inferred versus uniform communicative needs, and Warlpiri is among these cases. Before drawing conclusions about exceptionalism, however, we note that several technical assumptions of our analysis may be violated for these languages. For one, we assumed that basic color terms are used with equal frequency, to first approximation. This is a reasonable assumption given that basic color terms are elicited with roughly equal frequency under a free naming task in, for example, English (36). Moreover, the inferred distribution of needs for WCS and B&K languages are relatively insensitive to nonuniformity of color term frequency, up to variation by a factor 1.5 (SI Appendix, section 3B and Fig. S2D). Still, this assumption may not be accurate enough for all languages, and the frequencies of color terms require future empirical study. Another possibility is that the choice of the WCS stimuli themselves, that is, the set of Munsell chips, , may work well for identifying focal colors of most languages, but may be too restrictive in the languages that show little improvement. Future field and laboratory work could remedy this by broadening the range of color stimuli used in surveys.
Another limitation of the WCS is variability in chroma across the Munsell color chips used as stimuli, which might bias participants’ choice of focal color positions (25, 60–63). While there is no relationship between chroma and language-specific communicative needs (SI Appendix, section 3F.2 and Fig. S8B), we do find a small but statistically significant correlation (two-sided Spearman’s , , ) between chroma and the inferred distribution of communicative need averaged across WCS languages. However, if this bias dominated the choice of focal colors in the WCS, then we would not expect distributions of need inferred from focal colors to improve predictions of color term maps. The fact that we do see substantial improvement suggests that, whatever bias this effect may have, it is evidently not large enough to impact the relationship between focal color positions and color term maps for most languages. Nor would chromatic bias in stimuli explain the cross-cultural variation in communicative needs that we observe, since the set of stimuli was held constant across languages.
Our study has focused on how languages partition the vast space of perceivable colors into discrete terms, and how communicative needs shape this partitioning. Why some languages use more basic color terms than others remains an open topic for cross-cultural study. In principle, the issue of tolerance to imprecision in color communication is orthogonal to the distribution of communicative needs in a community. In practice, the number of color terms has a small impact on the resolution of inferred needs (SI Appendix, Fig. S3A), which we control for in cross-cultural comparisons (SI Appendix, Fig. S3B). Nonetheless, languages that have similar vocabulary sizes tend to have more similar communicative needs across colors, and this covariation is greater than any effect of vocabulary size on the resolution of our inferences (SI Appendix, Fig. S3). These results suggest that causal factors driving vocabulary size may also influence a culture’s communicative demands on colors—a hypothesis for future research.
Future empirical work may begin to unravel why cultures vary in their communicative demands on different regions of color space. It is already known that natural environments vary widely in their color statistics (64, 65), and this variation matters for color salience (66). The need to reference certain objects, as well as their salience relative to similar backgrounds, may help explain why communities that share environments prioritize similar regions of color space, as we have seen. Therefore, shared environment, physical proximity, and shared linguistic history at a finer scale than language family are all plausible avenues for future study on the determinants of color demands. Beyond these factors, there remains substantial interest in cultural features that we have not studied here, including religion, agriculture, trade, access to pigments and dies, and different ways of life, that can all shape a community’s needs to refer to different colors, and the resulting language that emerges.
Materials and Methods
WCS.
Berlin and Kay (1) and Kay et al. (2) surveyed color naming in 130 languages around the world using a standardized set of color stimuli. The stimuli (Fig. 1A), a set of Munsell color chips, were designed to cover the gamut of human perceivable colors at maximum saturation, across a broad range of lightness values.# Native speakers were asked to choose among the basic color terms in their language to name each color chip, one at a time, in randomized order. The WCS study surveyed 25 native speakers in each of 110 small, preindustrial language communities; the B&K study surveyed one native speaker in each of 20 languages from a mixture of both large (e.g., Arabic, English, and Mandarin) and comparatively small (e.g., Ibibio, Pomo, and Tzeltal) preindustrial and postindustrial societies.
The stimuli provided by the Munsell color chips are a function of the color pigment of the chips and the ambient light illuminating them. The ambient light source was approximately controlled by conducting the survey at noon and outdoors in shade, corresponding to CIE standard illuminant C. To the extent possible, participants were surveyed independently, although preventing the discussion of responses among participants was not always possible [discussed in Regier et al. (59)].
In our treatment of the color naming data, for each language, we include all recorded terms that had an associated focal color, was used by at least two surveyed speakers (unless a B&K language, in which case only one speaker was surveyed), and was considered the best choice for at least one WCS color chip.
The 20 B&K languages were included in our analyses where appropriate: comparisons based on focal colors and inferred communicative needs. They were excluded from term map comparisons, because the methods of estimating term maps differed methodologically from those in the WCS (67), and they do not provide straightforward estimates of . In addition, B&K languages with significant geographic extent, for example, Arabic and English, were excluded from statistical analysis of the correlates of cross-cultural differences in communicative needs, because estimating geographic distance or local biogeography would make little sense for these languages.
RMSE of Focal Color Predictions.
Language-specific focal color positions were compared to model predictions using the RMSE between observation and prediction in units of CIE Lab , computed for each WCS language according to
| [3] |
where the superscript specifies the coordinate in the CIE Lab color space of position vectors and , corresponding, respectively, to the predicted and empirically observed coordinates of the focal color for term in language ’s vocabulary, . Here denotes the number of basic color terms in language ’s vocabulary.
Spectral Measurements of Ripening Fruit.
Spectral measurements of ripening fruit in the diets of catarrhine primates were obtained from the Cambridge database of natural spectra. Reflectance data for fruit taken from the Kibale Forest, Uganda, were converted to CIE XYZ 1931 color space coordinates using CIE standard illuminant C. We then converted points from XYZ to CIE Lab space using the XYZ values for CIE standard illuminant C ( standard observer model) as the white point, in order to match the WCS construction of CIE Lab color chip coordinates. Calculations were performed in R (v3.6.3) using the package colorscience (v1.0.8).
Indicators of fruit ripeness include color, odor, and smell. Therefore, to measure visual salience, we considered only fruit that had a discernable (in terms of CIE Lab ) difference between unripe and ripe measurements (see SI Appendix, Fig. S6A for determination of statistical threshold on change in chromaticity). For fruits with detectable changes in chromaticity, we projected their unripe, midripe, and ripe positions onto the WCS color chips such that absolute lightness, , and the ratio of to was preserved (SI Appendix, Fig. S6B).
Measuring Distance between Distributions over Colors.
We quantified the perceptual difference between any two distributions over the WCS color chips in terms of their Wasserstein distance (used in Fig. 5C), defined as
| [4] |
where is the set of joint distributions satisfying and . The CIE Lab coordinates of and are given by and , respectively, and the Euclidean distance between them approximates their perceptual dissimilarity, by design of the CIE Lab system. Under this measure, a small displacement in CIE Lab space of distributional emphasis is distinguishable from a large displacement. For example, for discrete distribution when , and otherwise, let distribution be defined identically except substituting for . Then the Wasserstein distance between and will increase with the Euclidean distance between and , whereas, for example, the Kullback–Leibler divergence between and would remain constant for any .
We used a generalization of this distance measure to quantify the match between predicted and measured term maps. To make this comparison, we find the minimum-CIE partial matching between predicted and measured term map categories, , for each term (used in Fig. 3B). To do this, we find the minimum cost achievable by any assignment of chips empirically labeled by to those predicted to be labeled , weighted by the measured and predicted . The best partial matching accommodates for the fact that predicted and measured categories can differ in total weight. This measure is known as the Earth mover’s distance (68), which has the Wasserstein distance as a special case with matching total weights. Both measures were computed in R (v3.6.3) using the emdist (v0.3-1) package.
Correlates of Cross-Cultural Differences in Communicative Need.
We modeled the pairwise dissimilarity in communicative need between B&K+WCS languages as a log-linear function of the geodesic distance between language communities, shared linguistic family, and shared ecoregion, using a maximum-likelihood population effects model (MLPE) structure to account for the dependence among pairwise measurements (69). For languages , , we use a generalized linear mixed effects model (GLMM) with form
| [5] |
| [6] |
| [7] |
| [8] |
where is the Wasserstein distance between the inferred distributions of communicative need for languages and ; is their estimated geodesic distance (Haversine method) in standardized (normalized by SD) units based on geographic coordinates in Glottolog (and restricting to languages with small geographic extent); is a binary indicator of being in the same linguistic family or not (one or zero, respectively); is a binary indicator of being in the same ecoregion or not (one or zero, respectively); and is the difference in their number of color terms, which we include as a control. The random effects model the dependence structure of the pairwise measurements. Model diagnostics suggest reasonable behavior of residuals using a -link function (SI Appendix, Fig. S7). Fitted coefficients indicate a positive increase in dissimilarity with geodesic distance, and a decrease in dissimilarity with ecoregion, but no significant effect of shared language family (SI Appendix, Fig. S7). GLMM fits were performed in R (v3.6.3) using the lme4 (v1.1-21) package, with MLPE structure based on code from resistanceGA (70). Model diagnostics based on simulated residuals were done using package DHARMa (v0.2.6).
Pseudo- measuring overall model fit was computed as , where is the model-predicted value for , based on Zheng and Agresti (71). For our model, . However, there is no standard, single measure of for models with mixed effects. A recent proposal (72, 73) suggests reporting two separate quantities, a conditional and marginal , which can be interpreted as measuring the variance explained by both fixed and random effects combined (), and the variance explained by fixed effects alone (). For our model, we computed these as and , respectively, where based on Nakagawa and Schielzeth (73). For our model, conditional , and marginal . We based the inclusion of fixed effects on AIC (Akaike Information Criterion) (Fig. 5C) following best practices for MLPE models (74).
Supplementary Material
Acknowledgments
We thank Bevil R. Conway for providing a copy of the MSRA salient object data used by E. Gibson et al.; Danielle S. Bassett, Andrew T. Hartnett, Henry S. Horn, and Alan A. Stocker for helpful questions and early discussions; and our two anonymous reviewers. C.R.T. was supported by a MindCORE (Center for Outreach, Research, and Education) Postdoctoral Research Fellowship. G.R. acknowledges the support of an NSF Grant (Award 1946 882). J.B.P. acknowledges funding from The David and Lucile Packard Foundation.
Footnotes
The authors declare no competing interest.
*The property that the mean coordinates, or centroid, is the minimizer holds for the sum of squared Euclidean distances. But this is not true for the summed Euclidean distance, which has neither unique nor closed-form solutions in general.
†More precisely, we propose the measured focal colors are the best approximation to the true centroid among the set of WCS color stimuli.
Nor do we use empirical term maps for selection among the small set of nonunique rate−distortion optimal solutions. In this study, selection is based on focal points alone. See SI Appendix, section 3.
§Note that these results do not imply that shared communicative needs are determined by the need to name fruit specifically.
¶Note that this result does not imply that color terms in Pirahã are abstract necessarily; see Regier et al. (59).
#The Munsell color system was created as a means to index human perceivable color by hue, value, and chroma, at empirically measured perceptually uniform intervals along each dimension. In the WCS notation, rows correspond to equally spaced Munsell values, and columns 1–40 correspond to equally spaced Munsell hues. For column 0, Munsell chroma is 0; for all other columns, Munsell chroma was chosen as the maximum for the given hue and value.
This article is a PNAS Direct Submission. J.W. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2109237118/-/DCSupplemental.
Data Availability
All data came from preexisting datasets. Color vocabulary data were sourced from the WCS online repository (www1.icsi.berkeley.edu/wcs/data.html) (75). Additional language data were sourced through Glottolog v3.4, available online (https://glottolog.org/meta/downloads) (76). Data on biogeographic regions were provided by the World Wildlife Foundation, available online (https://www.worldwildlife.org/publications/terrestrial-ecoregions-of-the-world) (77). Fruit reflectance data came from the Cambridge database of natural spectra, available online (vision.psychol.cam.ac.uk/spectra) (78). Salient object data originating from the Microsoft Research Asia (MSRA) dataset are not publicly available, but were kindly provided to us on request by the corresponding authors of Gibson et al. (23). Data generated by our inference method and used to estimate the average communicative needs across languages (Fig. 2A) and language-specific communicative needs (SI Appendix, Figs. S11–S27) is shared under a creative commons license and is available in both our supporting information and online (https://github.com/crtwomey/twomey2021). Custom code was developed to infer communicative needs using the algorithm derived in this paper (SI Appendix, section 2). This code is open source (GNU GPLv3) and publicly available online (https://github.com/crtwomey/twomey2021).
References
- 1.Berlin B., Kay P., Basic Color Terms: Their Universality and Evolution (University of California Press, Berkeley, CA, 1969). [Google Scholar]
- 2.Kay P., Berlin B., Maaffi L., Merrifield W., Cook R., The World Color Survey (Center for the Study of Language and Information, Stanford, CA, 2009). [Google Scholar]
- 3.Kay P., Regier T., Resolving the question of color naming universals. Proc. Natl. Acad. Sci. U.S.A. 100, 9085–9089 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kay P., Color categories are not arbitrary. Cross-Cultural Res. 39, 39–55 (2005). [Google Scholar]
- 5.Regier T., Kay P., Cook R. S., Focal colors are universal after all. Proc. Natl. Acad. Sci. U.S.A. 102, 8386–8391 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lindsey D. T., Brown A. M., World Color Survey color naming reveals universal motifs and their within-language diversity. Proc. Natl. Acad. Sci. U.S.A. 106, 19785–19790 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yendrikhovskij S. N., Computing color categories from statistics of natural images. J. Imaging Sci. Technol. 45, 409–417 (2001). [Google Scholar]
- 8.Regier T., Kay P., Khetarpal N., Color naming reflects optimal partitions of color space. Proc. Natl. Acad. Sci. U.S.A. 104, 1436–1441 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Komarova N. L., Jameson K. A., Narens L., Evolutionary models of color categorization based on discrimination. J. Math. Psychol. 51, 359–382 (2007). [Google Scholar]
- 10.Zaslavsky N., Kemp C., Regier T., Tishby N., Efficient compression in color naming and its evolution. Proc. Natl. Acad. Sci. U.S.A. 115, 7937–7942 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Webster M. A., Miyahara E., Malkoc G., Raker V. E., Variations in normal color vision. II. Unique hues. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 17, 1545–1555 (2000). [DOI] [PubMed] [Google Scholar]
- 12.Schefrin B. E., Werner J. S., Loci of spectral unique hues throughout the life span. J. Opt. Soc. Am. A 7, 305–311 (1990). [DOI] [PubMed] [Google Scholar]
- 13.Brainard D. H., et al., Functional consequences of the relative numbers of L and M cones. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 17, 607–614 (2000). [DOI] [PubMed] [Google Scholar]
- 14.Neitz J., Carroll J., Yamauchi Y., Neitz M., Williams D. R., Color perception is mediated by a plastic neural mechanism that is adjustable in adults. Neuron 35, 783–792 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Kay P., McDaniel C. K., The linguistic significance of the meanings of basic color terms. Language 54, 610–646 (1978). [Google Scholar]
- 16.Heider E. R., Universals in color naming and memory. J. Exp. Psychol. 93, 10–20 (1972). [DOI] [PubMed] [Google Scholar]
- 17.Rosch E., Natural categories. Cognit. Psychol. 4, 328–350 (1973). [Google Scholar]
- 18.Sun R. K., Perceptual distances and the basic color term encoding sequence. Am. Anthropol. 85, 387–391 (1983). [Google Scholar]
- 19.MacLaury R. E., Color-category evolution and Shuswap yellow-with-green. Am. Anthropol. 89, 107–124 (1987). [Google Scholar]
- 20.MacLaury R. E., From brightness to hue: An explanatory model of color-category evolution. Curr. Anthropol. 33, 137–186 (1992). [Google Scholar]
- 21.Jameson K., D’Andrade R. G., “It’s not really red, green, yellow, blue: An inquiry into perceptual color space” in Color Categories in Thought and Language, Hardin C. L., Maffi L., Eds. (Cambridge University Press, Cambridge, UK, 1997), pp. 295–319. [Google Scholar]
- 22.Webster M. A., Kay P., “Individual and population differences in focal colors” in Anthropology of Color: Interdisciplinary Multilevel Modeling, MacLaury R. E., Paramei G. V., Dedrick D., Eds. (John Benjamins, Philadelphia, PA, 2007), pp. 29–53. [Google Scholar]
- 23.Gibson E., et al., Color naming across languages reflects color use. Proc. Natl. Acad. Sci. U.S.A. 114, 10785–10790 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gibson E., et al., How efficiency shapes human language. Trends Cogn. Sci. 23, 389–407 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Conway B. R., Ratnasingam S., Jara-Ettinger J., Futrell R., Gibson E., Communication efficiency of color naming across languages provides a new framework for the evolution of color terms. Cognition 195, 104086 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shepard R. N., “The perceptual organization of colors: An adaptation to regularities of the terrestrial world?” in Adapted Minds, Barkow J., Cosmides L., Tooby J., Eds. (Oxford University Press, Oxford, UK, 1992), pp. 495–532. [Google Scholar]
- 27.Zaslavsky N., Kemp C., Tishby N., Regier T., Color naming reflects both perceptual structure and communicative need. Top. Cogn. Sci. 11, 207–219 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Zaslavsky N., Kemp C., Tishby N., Regier T., Communicative need in colour naming. Cogn. Neuropsychol. 37, 312–324 (2020). [DOI] [PubMed] [Google Scholar]
- 29.Shannon C. E., A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948). [Google Scholar]
- 30.Shannon C. E., Coding theorems for a discrete source with a fidelity criterion. IRE Natl. Con. Rec. 7, 142–163 (1959). [Google Scholar]
- 31.Cover T. M., Thomas J. A., Elements of Information Theory (Wiley-Interscience, ed. 2, 2006). [Google Scholar]
- 32.Sims C. R., Rate-distortion theory and human perception. Cognition 152, 181–198 (2016). [DOI] [PubMed] [Google Scholar]
- 33.Kemp C., Xu Y., Regier T., Semantic typology and efficient communication. Annu. Rev. Linguist. 4, 109–128 (2018). [Google Scholar]
- 34.Boynton R. M., Olson C. X., Locating basic colors in the OSA space. Color Res. Appl. 12, 94–105 (1987). [Google Scholar]
- 35.Sturges J., Whitfield T. W. A., Locating basic colours in the Munsell space. Color Res. Appl. 20, 364–376 (1995). [Google Scholar]
- 36.Lindsey D. T., Brown A. M., The color lexicon of American English. J. Vis. 14, 17 (2014). [DOI] [PubMed] [Google Scholar]
- 37.Liu T., Sun J., Zhen N. N., Tang X., Shum H. Y., “Learning to detect a salient object” in IEEE Conference on Computer Vision and Pattern Recognition (Minneapolis, MN, (2007), pp. 1–8. [Google Scholar]
- 38.Sumner P., Mollon J. D., Catarrhine photopigments are optimized for detecting targets against a foliage background. J. Exp. Biol. 203, 1963–1986 (2000). [DOI] [PubMed] [Google Scholar]
- 39.Sumner P., Mollon J. D., Chromaticity as a signal of ripeness in fruits taken by primates. J. Exp. Biol. 203, 1987–2000 (2000). [DOI] [PubMed] [Google Scholar]
- 40.Lomáscolo S. B., Levey D. J., Kimball R. T., Bolker B. M., Alborn H. T., Dispersers shape fruit diversity in Ficus (Moraceae). Proc. Natl. Acad. Sci. U.S.A. 107, 14668–14672 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nevo O., et al., Frugivores and the evolution of fruit colour. Biol. Lett. 14, 20180377 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Valenta K., Nevo O., The dispersal syndrome hypothesis: How animals shaped fruit traits, and how they did not. Funct. Ecol. 34, 1158–1169 (2020). [Google Scholar]
- 43.Regan B. C., et al., Frugivory and colour vision in Alouatta seniculus, a trichromatic platyrrhine monkey. Vision Res. 38, 3321–3327 (1998). [DOI] [PubMed] [Google Scholar]
- 44.Regan B. C., et al., Fruits, foliage and the evolution of primate colour vision. Philos. Trans. R. Soc. Lond. B Biol. Sci. 356, 229–283 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Onstein R. E., et al., Palm fruit colours are linked to the broad-scale distribution and diversification of primate colour vision systems. Proc. Biol. Sci. 287, 20192731 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hammarström H., Forkel R., Haspelmath M., Bank S., Glottolog 4.2.1 (Max Planck Institute for the Science of Human History, 2020). [Google Scholar]
- 47.Olson D. M., et al., Terrestrial ecoregions of the world: A new map of life on Earth. Bioscience 51, 933–938 (2001). [Google Scholar]
- 48.Smith J. R., et al., A global test of ecoregions. Nat. Ecol. Evol. 2, 1889–1896 (2018). [DOI] [PubMed] [Google Scholar]
- 49.Majid A., et al., Differential coding of perception in the world’s languages. Proc. Natl. Acad. Sci. U.S.A. 115, 11369–11376 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Caves E. M., et al., Categorical perception of colour signals in a songbird. Nature 560, 365–367 (2018). [DOI] [PubMed] [Google Scholar]
- 51.Zipple M. N., et al., Categorical colour perception occurs in both signalling and non-signalling colour ranges in a songbird. Proc. Biol. Sci. 286, 20190524 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Davidoff J., Davies I., Roberson D., Colour categories in a stone-age tribe. Nature 398, 203–204 (1999). [DOI] [PubMed] [Google Scholar]
- 53.Roberson D., Davies I., Davidoff J., Color categories are not universal: Replications and new evidence from a stone-age culture. J. Exp. Psychol. Gen. 129, 369–398 (2000). [DOI] [PubMed] [Google Scholar]
- 54.Roberson D., Davidoff J., Davies I. R. L., Shapiro L. R., Color categories: Evidence for the cultural relativity hypothesis. Cognit. Psychol. 50, 378–411 (2005). [DOI] [PubMed] [Google Scholar]
- 55.Majid A., Kruspe N., Hunter-gatherer olfaction is special. Curr. Biol. 28, 409–413.e2 (2018). [DOI] [PubMed] [Google Scholar]
- 56.Majid A., Burenhult N., Stensmyr M., de Valk J., Hansson B. S., Olfactory language and abstraction across cultures. Phil. Trans. R. Soc. B 373, 20170139 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Everett D. L., Cultural constraints on grammar and cognition in Pirahã: Another look at the design features of human language. Curr. Anthropol. 46, 621–646 (2005). [Google Scholar]
- 58.Wierzbicka A., Why there are no ‘colour universals’ in language and thought. J. R. Anthropol. Inst. 14, 407–425 (2008). [Google Scholar]
- 59.Regier T., Kay P., Khetarpal N., Color naming and the shape of color space. Language 85, 884–892 (2009). [Google Scholar]
- 60.Lindsey D. T., Brown A. M., Brainard D. H., Apicella C. L., Hunter-gatherer color naming provides new insight into the evolution of color terms. Curr. Biol. 25, 2441–2446 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Witzel C., New insights into the evolution of color terms or an effect of saturation? i-Perception 7 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lindsey D. T., Brown A. M., Brainard D. H., Apicella C. L., Hadza color terms are sparse, diverse, and distributed, and presage the universal color categories found in other world languages. i-Perception 7, (2016). 10.1177/2041669516662040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Witzel C., Variation of saturation across hue affects unique and typical hue choices. i-Perception 10, (2019). 10.1177/2041669519872226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Webster M. A., Mollon J. D., Adaptation and the color statistics of natural images. Vision Res. 37, 3283–3298 (1997). [DOI] [PubMed] [Google Scholar]
- 65.Webster M. A., Mizokami Y., Webster S. M., Seasonal variations in the color statistics of natural images. Network 18, 213–233 (2007). [DOI] [PubMed] [Google Scholar]
- 66.McDermott K. C., Malkoc G., Mulligan J. B., Webster M. A., Adaptation and visual salience. J. Vis. 10, 17 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kay P., Berlin B., Maffi L., Merrifield W., “Color naming across languages” in Color Categories in Thought and Language, Hardin C. L., Maffi L., Eds. (Cambridge University Press, Cambridge, UK, 1997), pp. 21–56. [Google Scholar]
- 68.Rubner Y., Tomasi C., Guibas L. J., “A metric for distributions with applications to image databases” in IEEE Sixth International Conference on Computer Vision (Bombay, India: ), pp. 59–66 (1998). [Google Scholar]
- 69.Clarke R. T., Rothery P., Raybould A. F., Confidence limits for regression relationships between distance matrices: Estimating gene flow with distance. J. Agric. Biol. Environ. Stat. 7, 361–372 (2002). [Google Scholar]
- 70.Peterman W. E., Resistance G. A., An R package for the optimization of resistance surfaces using genetic algorithms. Methods Ecol. Evol. 9, 1638–1647 (2018). [Google Scholar]
- 71.Zheng B., Agresti A., Summarizing the predictive power of a generalized linear model. Stat. Med. 19, 1771–1781 (2000). [DOI] [PubMed] [Google Scholar]
- 72.Nakagawa S., Schielzeth H., The coefficient of determination and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Methods Ecol. Evol. 4, 133–142 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Nakagawa S., Johnson P. C. D., Schielzeth H., The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. R. Soc. Interface 14, 20170213 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Row J. R., Knick S. T., Oyler-McCance S. J., Lougheed S. C., Fedy B. C., Developing approaches for linear mixed modeling in landscape genetics through landscape-directed dispersal simulations. Ecol. Evol. 7, 3751–3761 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cook R., Kay P., Regier T., BK-dict.txt, BK-foci.txt, BK-term.txt, cnum-vhcm-lab-new.txt, foci-exp.txt, term.txt. WCS Data Archives. https://www1.icsi.berkeley.edu/wcs/data.html. Accessed 2 August 2017.
- 76.Hammarström H., Forkel R., Haspelmath M., tree_glottolog_newick.txt. Glottolog 3.4. https://glottolog.org/meta/downloads. Accessed 25 April 2019.
- 77.Olson D. M., et al., wwf_terr_ecos.lyr, wwf_terr_ecos.prj, wwf_terr_ecos.sbn, wwf_terr_ecos.sbx, wwf_terr_ecos.shp, wwf_terr_ecos.shp.xml, wwf_terr_ecos.shx. Terrestrial Ecoregions of the World. https://www.worldwildlife.org/publications/terrestrial-ecoregions-of-the-world. Accessed: 20 May 2019.
- 78.Sumner P., Regan B., Mollon J., fruit.html, ugfruit.txt, ugillums.txt. Cambridge Database of Natural Spectra. http://vision.psychol.cam.ac.uk/spectra/uganda/. Accessed 26 June 2019.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data came from preexisting datasets. Color vocabulary data were sourced from the WCS online repository (www1.icsi.berkeley.edu/wcs/data.html) (75). Additional language data were sourced through Glottolog v3.4, available online (https://glottolog.org/meta/downloads) (76). Data on biogeographic regions were provided by the World Wildlife Foundation, available online (https://www.worldwildlife.org/publications/terrestrial-ecoregions-of-the-world) (77). Fruit reflectance data came from the Cambridge database of natural spectra, available online (vision.psychol.cam.ac.uk/spectra) (78). Salient object data originating from the Microsoft Research Asia (MSRA) dataset are not publicly available, but were kindly provided to us on request by the corresponding authors of Gibson et al. (23). Data generated by our inference method and used to estimate the average communicative needs across languages (Fig. 2A) and language-specific communicative needs (SI Appendix, Figs. S11–S27) is shared under a creative commons license and is available in both our supporting information and online (https://github.com/crtwomey/twomey2021). Custom code was developed to infer communicative needs using the algorithm derived in this paper (SI Appendix, section 2). This code is open source (GNU GPLv3) and publicly available online (https://github.com/crtwomey/twomey2021).