Shear-induced orientational ordering in an active glass former

Significance

Dense active matter systems are ubiquitous in nature, with examples ranging from the cytoplasm to tissues of motile cells to vehicular traffic jams. Many recent studies have explored the dynamical and transport aspects of such active glasses. However, an understanding of the rheological behavior of these fascinating out-of-equilibrium systems (i.e., their response to mechanical deformation) remains elusive. Using extensive molecular dynamics simulation of a model active glassy system under steady shear, we establish the existence of different dynamical states: disordered, propulsion-induced ordered, and shear-induced ordered (SIO). Combining simulation results with an analytical theory, we rationalize the qualitative features of the SIO state, which is facilitated by the applied shear and appears without any alignment interactions or particle shape anisotropies.

Abstract

Dense assemblies of self-propelled particles that can form solid-like states also known as active or living glasses are abundant around us, covering a broad range of length scales and timescales: from the cytoplasm to tissues, from bacterial biofilms to vehicular traffic jams, and from Janus colloids to animal herds. Being structurally disordered as well as strongly out of equilibrium, these systems show fascinating dynamical and mechanical properties. Using extensive molecular dynamics simulation and a number of distinct dynamical and mechanical order parameters, we differentiate three dynamical steady states in a sheared model active glassy system: 1) a disordered state, 2) a propulsion-induced ordered state, and 3) a shear-induced ordered state. We supplement these observations with an analytical theory based on an effective single-particle Fokker–Planck description to rationalize the existence of the shear-induced orientational ordering behavior in an active glassy system without explicit aligning interactions of, for example, Vicsek type. This ordering phenomenon occurs in the large persistence time limit and is made possible only by the applied steady shear. Using a Fokker–Planck description with parameters that can be measured independently, we make testable predictions for the joint distribution of single-particle position and orientation. These predictions match well with the joint distribution measured from direct numerical simulation. Our results are of relevance for experiments exploring the rheological response of dense active colloids and jammed active granular matter systems.

Glassy or slow dynamics has been observed and thoroughly investigated in recent years in dense living or synthetic active matter systems across a range of scales, for example, dense assemblies of cells (1), crowded cellular cytoplasm (2), glassy liquids formed by self-propelled Janus colloids (3, 4), and jammed active granular solid (5); refs. 6 and 7 have recent reviews. Simulations and experiments have shown many nontrivial dynamical signatures, such as active jamming (8), shape-dependent fluidization in a self-propelled Voronoi model (9, 10), glassy swirls in active dumbbells (11), intermittent dynamics with transient jamming (12), and nonmonotonic response in a glassy assembly of Janus colloids (3, 4), along with the strong dynamical heterogeneity and slow density relaxation (13–15) that are typical to passive supercooled liquids. Although dynamical aspects and transport in such active glassy systems have been looked at quite extensively, the response of such out-of-equilibrium systems to mechanical perturbation (i.e., their rheology) remains largely unexplored. In one recent example, Barrat and coworkers (16) investigated the rheological response of a particular model dense active material that mimics the dynamics of tissue. In this model, the number of particles is not conserved, and particle death (apoptosis) and birth are modeled as a stochastic process. The authors of ref. 16 observe a Newtonian cross-over in the flow curves (stress vs. strain rate), which is set by the cell death rate. In contrast to widely studied active particle classes, such as active Brownian particles (ABPs) (17–20) or active Ornstein–Uhlenbeck particles (21, 22), the particles in ref. 16 lack orientational degrees of freedom and active propulsion forces. The rheological response of ABPs has also been explored (23), and an interesting velocity reversal phenomenon was observed near the boundary, although this study was limited to low-density suspensions of self-propelled particles. Further studies exist of the shear response of active polar (24, 25) systems, again in the dilute regime, as well as nematic systems (26, 27) where liquid–crystalline ordering phenomena appear. However, the overall understanding of the response to steady shear of active glassy systems made of isotropic particles with orientational degrees of freedom remains an open question in the literature.

In this article, we report on types of orientational ordering in a glassy assembly of ABPs. This orientational order appears without any mutual alignment interaction between the particles of Viscek type (28), for example, or arising from anisotropic particle shapes and is facilitated by shear. Using different physical quantities in steady shear, specifically 1) nonaffinity in the velocity profile, 2) shear stress, and 3) an orientational order parameter, we can differentiate between a number of qualitatively distinct steady states. Even though shear might naively be thought of as injecting additional fluctuations into the system and thus, suppressing ordering, we find that it can in fact help the system to order orientationally (we return to the relation to other shear ordering phenomena in Discussion). The three states we observe are 1) a disordered state, 2) a propulsion-induced ordered (PIO) state, and 3) a shear-induced ordered (SIO) state. To understand the most intriguing one, which is the SIO state, we use a Fokker–Planck equation as an effective description of the single-particle dynamics. Using a Galerkin truncation, we evaluate the steady-state joint probability distribution $P\left(\theta ,y\right)$ of particle position (in the shear gradient direction) and orientation in closed form. The theoretically predicted distributions $P\left(\theta ,y\right)$, for which all parameters can be determined independently, are in very good qualitative agreement with our simulation results in the SIO state.

Model

We study a model active glass (12, 29) that can be viewed as essentially a passive glass former but with the dynamics of each particle driven by a self-propulsion force in addition to the usual force from interaction with its neighbors. For the underlying passive glass former, we use the well-known Kob–Andersen model (30, 31), which is a $65:35$ binary mixture of soft particles with nonadditive Lennard–Jones (LJ) interactions. For their dynamics, we assume an ABP form (17–20) (in terms of active forcing) with added steady shear:

$$m{\dot{\mathbf{v}}}_i=-\gamma \left({\mathbf{v}}_i-{\mathbf{v}}_F\left(y_i\right)\right)+{\mathbf{F}}_i+f{\mathbf{n}}_i.$$ [1]

Here, $m$ is the mass of each particle, and $\gamma$ is the friction coefficient; we set both to one in our study. We denote by ${\mathbf{v}}_i$ the velocity of the $i$th particle and by ${\mathbf{v}}_F\left(y_i\right)$ the local affine flow velocity from the applied shear; viscous damping is taken as relative to this flow and can thus be viewed as resulting from an affinely sheared solvent. With an imposed shear rate $\dot{\gamma }$, the affine velocity field is ${\mathbf{v}}_F\left(y\right)=\dot{\gamma }y{\widehat{\mathbf{e}}}_x$ if $y$ denotes the position coordinate along the shear gradient direction and ${\widehat{\mathbf{e}}}_x$ is the unit vector in the shear ($x$) direction. To implement the constant shear rate, we move all the particles in an upper wall with a constant velocity $v_w$, while the particles in the corresponding lower wall are static. The upper-wall velocity then sets the imposed shear rate through the relation $\dot{\gamma }=v_w/L$, where $L$ is the distance between the upper and lower walls. We generally use $L=50$, with a full box height including walls of $L_0=57.73$ (an illustration is in Fig. 1A). We return below to the importance of implementing the shear deformation with explicit walls.

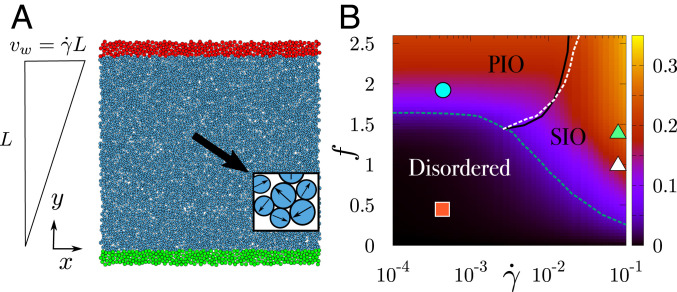
Fig. 1.

(A) Schematic of the active glass under steady shear, showing the upper wall (red particles) that moves steadily with velocity $v_w$, the static lower wall (green particles), and the bulk (blue particles); arrows represent the active forcing direction on each particle (see zoom on small region in the Inset). (B) State diagram constructed from numerical molecular dynamics simulation of the sheared active glass for ${\tau }_p=10^3$, showing different dynamical states: 1) disordered: the orientationally disordered state; 2) PIO: the PIO state; and 3) SIO: the SIO state. The color bar in the state diagram shows the average value of the orientational order parameter $\psi$ in the steady state. The dashed blue line marks the boundary between the orientationally ordered and disordered states; the solid black and dotted white lines delineate the separation between the PIO and the SIO states according to two complementary criteria (the text has details).

Returning to the remaining terms in Eq. 1, ${\mathbf{F}}_i$ is the total force on particle $i$ resulting from the Kob–Andersen LJ interactions (30, 31). The active force has constant magnitude $f$ and direction ${\mathbf{n}}_i=\left(\cos {\theta }_i,\sin {\theta }_i\right)$ for the $i$th particle. Each angle ${\theta }_i$ changes diffusively, explicitly ${\dot{\theta }}_i={\left(2/{\tau }_p\right)}^{1/2}{\eta }_i\left(t\right)$ with ${\eta }_i\left(t\right)$ unit variance white noise; ${\tau }_p$ is thus the persistence time of the active forcing (12, 29).

Following the approach in refs. 12 and 29, we keep number density high ($\rho =1.2$) and focus mainly on the athermal limit ($T=0$). We will see later, however, that for small persistence times ${\tau }_p=O\left(1\right)$, the active system can be mapped to an equivalent passive thermal system. Note also that while our equation of motion does contain an inertial term, the value of the friction coefficient ($\gamma =1$) that we use ensures that the dynamics is mostly overdamped (32). We focus mostly on the two extreme limits of very small and very large persistence times ${\tau }_p$, choosing specifically ${\tau }_p=1$ and ${\tau }_p=10^3$. The key parameters for the state diagrams we construct in this study are then the magnitude $f$ of the self-propulsion force and the imposed shear rate $\dot{\gamma }$.

Results

Small Persistence Time.

We first performed steady shear simulations in the small persistence time limit (${\tau }_p=1$) of our model active glass. In this regime, the behavior can be understood using the idea of an effective temperature generated by the rapidly fluctuating active forcing. We measured the steady-state shear stress $⟨{\sigma }_{xy}⟩$ for different applied shear rates $\dot{\gamma }$ and compared the flow curve of the active glass with ${\tau }_p=1$ and $f=0.7$ with the flow curve of the corresponding passive system ($f=0$) at an equivalent effective temperature $T_{\mathrm{e}\mathrm{ff}}=0.1$. These two sets of flow curves match very well as shown in SI Appendix, Fig. S1B; SI Appendix also has further discussion of the effective temperature. Indeed, from the time correlations of the active forces, one expects $T_{\mathrm{e}\mathrm{ff}}$ to scale as ${\tau }_p{f}^2$, and this effective temperature description generally works well for active glasses in the small persistence time limit (12, 29). For most of the stress measurements in this study, we use the virial stress, defined as ${\sigma }_{\alpha \beta }=-V^{-1}{\sum }_{i=1}^N{r}_i^{\alpha }{F}_i^{\beta }$, where ${\mathbf{r}}_i$ is the position of the $i$th bulk particle, ${\mathbf{F}}_i$ is the total interaction force on this particle, $V$ is the volume of the bulk, and $N$ is the number of particles in the bulk. We have also looked at the active stress defined as ${\sigma }_{\alpha \beta }^a=-V^{-1}{\sum }_{i=1}^N{r}_i^{\alpha }{f}_i^{\beta }$, where ${\mathbf{f}}_i=f{\mathbf{n}}_i$ is the active force acting on particle $i$. We observe that it fluctuates around zero (SI Appendix, Fig. S1C) and so, can be ignored in the average stress; its fluctuation amplitude depends strongly on the active force magnitude ($f$) but only very weakly on the shear rate ($\dot{\gamma }$) (SI Appendix, Fig. S1C). As we are dealing with an active system, where the definition and meaning of stress have been the subject of much discussion (33, 34), we also checked whether the virial stress calculated from the bulk matches with the direct measurement of stress from the forces on the walls. We see good agreement between the two approaches, both in a plot of stress vs. strain as shear is started up at fixed shear rate and in the flow curve ($⟨{\sigma }_{xy}⟩$ vs. $\dot{\gamma }$). We refer to SI Appendix for further discussion of the different stress definitions and their comparison (in particular, SI Appendix, Fig. S2).

Large Persistence Time.

We observe the physically most interesting behavior for large values of the persistence time, in particular with regard to spatial ordering of the orientation of the active particles (as given by the direction of their propulsive force). We therefore now fix the persistence time to the large value ${\tau }_p=10^3$ (we keep this fixed for all the results described in the text below) and vary active forcing $f$ and shear rate $\dot{\gamma }$ within a broad range of values $f\in \left[\mathrm{0,2.6}\right]$, $\dot{\gamma }\in \left[10^{-4},10^{-1}\right]$. We find three types of dynamical states (Fig. 1B): 1) disordered, 2) PIO, and 3) SIO. To differentiate these states, we use first an orientational order parameter. This is determined from the joint distribution $P\left(\theta ,y\right)$ of the $y$ coordinates and orientations $\theta$ of the bulk particles as

$$\psi ={\int }_{-L/2}^{L/2}P\left(y\right)\varphi \left(y\right)\sin \left(\frac{2\pi y}{L}\right)dy.$$ [2]

Here, $\varphi \left(y\right)$ is in turn defined as

$$\varphi \left(y\right)=\frac{{\int }_{-\pi }^{\pi }P\left(\theta ,y\right)\sin \theta \hspace{0.17em}d\theta }{P\left(y\right)},\hspace{1em}P\left(y\right)={\int }_{-\pi }^{\pi }P\left(\theta ,y\right)d\theta .$$ [3]

Intuitively, $\varphi \left(y\right)$ measures the dominant nonuniformity in the orientation distribution as a function of $y$ and is positive if particles point primarily toward the upper wall ($\theta \approx \pi /2$) and negative in the opposite case. The global order parameter $\psi$ thus detects whether the preferred particle orientation varies significantly in space, such that particles in the upper half of the system tend to point to the upper wall while those in the lower half point in the opposite direction. Note that in addition to the “up/down”-type orientational ordering described by the order parameter $\psi$, the system also shows a rather weaker “left/right”-type alignment that can be captured by an analogous order parameter (SI Appendix has details). Both $\varphi \left(y\right)$ and $\psi$ vanish for a uniform orientational distribution, $P\left(\theta ,y\right)=P\left(y\right)/\left(2\pi \right)$. The color bar in the state diagram (Fig. 1B) in the $\left(\dot{\gamma },f\right)$ plane shows the average value of the orientational order parameter $\psi$ in the steady state; the blue line is the contour for a small constant $\psi$ (we choose $\psi =0.05$) and so, marks the boundary between orientationally ordered and disordered states.

The black solid line and the white dashed line together mark the boundary between PIO and SIO, according to two complementary criteria. The black solid line was calculated from the average stress and separates the regions of small and large stresses by a contour of constant $⟨{\sigma }_{xy}⟩=0.4$ (roughly halfway between the typical values $\ll 1$ for PIO and $\approx 1$ for SIO). The white dashed line was determined from the strength of velocity fluctuations away from the affine flow field; it thus marks the boundary between states with predominantly affine flow and those with significantly nonaffine flow. In particular, we measure the average velocity in the shear direction $⟨v_x\left(y\right)⟩$ as a function of $y$ and define $v^{\mathrm{N}\mathrm{A}}$ as the rms deviation of this (Materials and Methods has the definition) from the affine flow velocity $v_{Fx}\left(y\right)$. The white dashed line in Fig. 1B is then the contour $v^{\mathrm{N}\mathrm{A}}/v_w=0.2$, where we use the upper-wall velocity $v_w=\dot{\gamma }L$ as a natural velocity scale for the affine flow. Our data here suggest that the transition from the PIO to SIO state is a smooth cross-over between two dynamical steady states and not a thermodynamic phase transition.

In the disordered state, the system behaves like a typical supercooled or glassy solid with Herschel–Bulkley rheology and a nonzero yield stress, around which stress fluctuations are seen in the steady state (Fig. 2B). Note that the system is dynamically arrested or glass like in the absence of shear for the parameters used to generate the disordered state in Fig. 2. The particle orientations do not show any ordering (Fig. 2 A and D and Movie S1) as $P\left(\theta ,y\right)/P\left(y\right)$ remains close to $1/2\pi$. The velocity profile remains linear with almost negligible nonaffine fluctuations (Fig. 2C). These small nonaffine fluctuations increase with the active forcing $f$ but decrease with increasing shear rate $\dot{\gamma }$ (data not shown). These trends can be seen as the precursors of, respectively, the PIO state, which appears at larger $f$ and exhibits significantly nonaffine velocities as we discuss next, and the SIO state at larger $\dot{\gamma }$ with its essentially affine flow.

Fig. 2.

Disordered state (marked by the red square in the state diagram in Fig. 1B). (A) Orientational order parameter $\psi$ (the text has details) shows no emergent order in steady state. (B) Shear stress ${\sigma }_{xy}$ exhibits initial growth during start-up of steady shear, with fluctuations around a finite value in steady state. (C) Instantaneous velocity profile (Materials and Methods has details) in steady state is essentially linear with small nonaffine fluctuations. Note that the walls end at a distance of 0.07 from both ends in units of $L_0$. (D) A snapshot of the system in the steady state shows uniform distribution of particle orientation $\theta$ as indicated by the color bar.

Upon increasing $f$ at small shear rate $\dot{\gamma }$, one enters the PIO state. This has a moderate amount of orientational ordering (Fig. 3 A and D) but strong nonaffine flows created by the “stirring” arising from the substantial active forces (Fig. 3C). The system also shows significant density inhomogeneities (SI Appendix has details) ranging up to the formation of transient cavities (Movie S2) that remodel dynamically. The spatial segregation into dense regions and cavities with almost zero density can be thought of as an inverted type of motility-induced phase separation (35–37). Because of this dynamic cavity formation and strong internal flows during the steady shear, the system is unable to sustain any significant shear stress in the steady state; the average stress reaches very low values, with strong fluctuations around the mean (Fig. 3B). We call this state “PIO” because the spatial segregation is observable even for $\dot{\gamma }\to 0$, where the motion of the particles and hence, the overall physics are dominated by the active propulsion forces. In line with this terminology, the unperturbed system at $\dot{\gamma }=0$ also becomes orientationally ordered in the presence of explicit walls.

Fig. 3.

PIO state (the cyan circle in the state diagram in Fig. 1B). (A) Orientational order parameter $\psi$ shows growth during start-up of steady shear, with saturation for $t\approx {\tau }_p$. (B) Shear stress ${\sigma }_{xy}$ fluctuates around zero in the steady state. (C) Instantaneous velocity profile in steady state demonstrates very strong nonaffine fluctuations. (D) A snapshot of the system shows weak orientational order (color bar) and strong density inhomogeneities including transient cavity formation.

To understand the PIO state in more detail, we evaluated the Fourier space longitudinal velocity correlation [defined as ${\omega }_{\Vert }\left(q\right)=\frac{1}{N}⟨|\widehat{\mathbf{q}}\cdot \mathbf{v}\left(\mathbf{q}\right){|}^2⟩$] and estimated a correlation length ${\zeta }_{\parallel }$ from there. The values of ${\zeta }_{\parallel }$ we find (SI Appendix, SI Text and Fig. S7 have details) are significantly smaller than the system size $L=50$ and also do not change much when we consider different system sizes within the PIO state or move from a PIO state to the disordered state, despite the concomitant large orientational order parameter changes. This points to the fact that the relevant physics for propulsion-induced orientational ordering is not connected to the recently discovered long-range velocity correlation effects in dense active matter (38–40); rather, it is driven by the orientational phase segregation, which under shear, generates macroscopic nonaffine velocity fields (SI Appendix, Fig. S6B). A separate analysis of how the order parameter ($\psi$) changes as a function of active forcing $f$ for different system sizes $N$ also suggests that the transition point from the disordered state to PIO does not vary significantly within the range of system sizes ($N\in \left[\mathrm{1,000,8,000}\right]$) studied, although a full analysis of finite size effects on the observed ordering remains an interesting open question. However, the system sizes we study are quite typical of a range of experimental systems (3, 4, 8) and so, remain relevant irrespective of the asymptotic behavior for infinite system sizes.

We next consider the SIO state. This can also be reached from the disordered state but along a different route: starting at moderate active forcing, $f\sim 1$, in the disordered state, one increases the shear rate $\dot{\gamma }$ from a very low value $\sim 10^{-3}$ to a quite substantial rate $\sim 10^{-1}$. The resulting SIO state shows liquid-like properties in many respects. For example, it has an almost linear velocity profile with negligible nonaffine fluctuations (Fig. 4C). The shear stress increases after shear start-up and reaches a constant steady-state value on timescales around or above ${\tau }_p$ (Fig. 4B). Surprisingly, however, these liquid-like features are combined with strong spatial order in the particle orientations (Fig. 4 A and D and Movie S3).

Fig. 4.

SIO state (marked by the green triangle in the state diagram in Fig. 1B). (A) Orientational order parameter $\psi$ indicates a strongly ordered steady state. (B) Shear stress remains finite in steady shear, reaching a constant value at $t\approx {\tau }_p$. (C) Instantaneous velocity profile at steady state shows linear velocity profile with negligible nonaffine fluctuations. (D) A snapshot of the system shows strong orientational order (color bar) but essentially homogeneous density.

Summarizing our findings for the properties of the two ordered states PIO and SIO, these differ substantially in the spatial uniformity of the number density, in the presence or absence of nonaffine flow, and in their ability to support significant shear stress. The PIO state is dominated by the physics of orientational phase segregation, and shear does not play a significant role in its formation or stability. The SIO state, on the other hand, exists only at reasonably large shear rates, and active propulsion does not on its own guarantee the existence or stability of such a state. The ordering effect is strongly dependent on the presence of a physical wall and will not appear for artificial boundary conditions of, for example, Lees–Edwards type. Outside of equilibrium statistical physics, such qualitative consequences of the choice of boundary conditions are to be expected, and the case of physical walls we consider here is clearly the one that is more representative of natural or experimental systems.

We next show that the qualitative behavior of the SIO state as an affinely flowing yet orientally ordered state can be understood by a simple analytical approach. This is based on an effective Fokker–Planck description of the single-particle dynamics and will allow us to make quantitative predictions that can be verified in our simulations.

Effective Single-Particle Description.

The dynamics of our model glass can in principle be described by a Fokker–Planck equation for the $3N$ particle coordinates and orientations $\left(x_i,y_i,{\theta }_i\right)$, together with the associated momenta and supplemented by terms describing the wall motion. As the qualitative physics we are describing corresponds to an overdamped limit, the momenta can be ignored to a good approximation. The equation of motion for a single particle can then formally be derived by integrating out all other degrees of freedom (41). We neglect the memory effects that generically occur in such a reduction (e.g., refs. 42 and 43) and write an approximate Fokker–Planck equation for the joint distribution $P\left(\theta ,y\right)$ of the orientation $\theta$ and $y$ position of a single particle:

$$\begin{array}{l}\hfill \frac{\partial P\left(\theta ,y\right)}{\partial t}+\mu f\sin \theta \frac{\partial P\left(\theta ,y\right)}{\partial y}=D\frac{{\partial }^{2}P\left(\theta ,y\right)}{\partial y^2}+D_{\theta }\frac{{\partial }^{2}P\left(\theta ,y\right)}{\partial {\theta }^2}.\\ \hfill \end{array}$$ [4]

Here, $\mu$ is the effective mobility, $f$ is the active force magnitude as before, $D$ is the effective diffusion constant, and $D_{\theta }=1/{\tau }_p$ is the orientational diffusion constant. The second term on the left-hand side represents advection of probability due to active forcing, with the average $y$ velocity of the particle being proportional to the $y$ component $f\sin \theta$ of the active force. The terms on the right-hand side describe translational and rotational diffusion, respectively. Our aim is now to obtain the steady-state solution $P\left(\theta ,y\right)$, from which predictions for the orientational order parameter can be derived according to Eqs. 2 and 3. A Fourier decomposition of the angular dependence gives

$$P\left(\theta ,y\right)=\sum _{m=-\infty }^{\infty }{e}^{im\theta }{P}_m\left(y\right),$$ [5]

where $P_m\left(y\right)$ is the $y$-dependent coefficient of the $m$th Fourier mode. Substituting the representation Eq. 5 into Eq. 4, we obtain a system of coupled equations for the $P_m\left(y\right)$:

$$\begin{array}{l}\hfill \frac{\mu f}{2i}\left[\frac{\partial P_{m-1}\left(y\right)}{\partial y}-\frac{\partial P_{m+1}\left(y\right)}{\partial y}\right]=D\frac{{\partial }^2{P}_m\left(y\right)}{\partial y^2}-m^2{D}_{\theta }{P}_m\left(y\right).\\ \hfill \end{array}$$ [6]

To find a closed form approximation for $P\left(\theta ,y\right)$, we use a Galerkin truncation (44); specifically, we truncate the series in Eq. 5 after the leading terms with $m=0,\pm 1$. We have checked that the inclusion of higher modes does not change the predictions qualitatively (SI Appendix, Fig. S4 A and B). The boundary conditions required to fix the solution for $P\left(\theta ,y\right)$ arise from the fact that the upper and lower walls in our system are impermeable so that the probability current in the $y$ direction, which is given by

$$J_y=\left(\mu f\sin \theta \right)P-D\frac{\partial P}{\partial y},$$ [7]

has to vanish there:

$$J_y=\left\{\begin{array}{cc}0,\hspace{1em}\hfill & \text{at}y=-L/2\hfill \\ 0,\hspace{1em}\hfill & \text{at}y=+L/2\hfill \end{array}\right..$$ [8]

Away from the walls, we find that $J_y$ is generically nonzero, reflecting the nonequilibrium character of the system. The full current vector $\left(J_{\theta },J_y\right)$ exhibits interesting structure, with the corresponding flow splitting the $\left(\theta ,y\right)$ plane into a number of distinct regions as shown in SI Appendix, Fig. S3C. With the above boundary conditions, we find the steady-state solution for the dominant Fourier modes as

$$P_0\left(y\right)=\frac{1}{2\pi }\frac{\cosh \left(\alpha y\right)+\zeta \cosh \left(\alpha L/2\right)}{\zeta L\cosh \left(\alpha L/2\right)+\frac{2}{\alpha }\sinh \left(\alpha L/2\right)}$$ [9]

and

$$P_1\left(y\right)=-i\frac{\alpha D}{\mu f}\frac{1}{2\pi }\frac{\sinh \left(\alpha y\right)}{\zeta L\cosh \left(\alpha L/2\right)+\frac{2}{\alpha }\sinh \left(\alpha L/2\right)}$$ [10]

with $P_{-1}\left(y\right)=-P_1\left(y\right)$. Here, the inverse length scale $\alpha$ is defined via ${\alpha }^2=\left({\mu }^2{f}^2+2D{D}_{\theta }\right)/\left(2D^2\right)$. Inserting into the Fourier expansion of Eq. 5 with our Galerkin truncation

$$P\left(\theta ,y\right)=e^{i\theta }{P}_1\left(y\right)+e^{-i\theta }{P}_{-1}\left(y\right)+P_0\left(y\right)$$ [11]

gives the desired steady-state joint distribution

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P\left(\theta ,y\right)=& \frac{\alpha D}{\mu f}\hspace{0.17em}\frac{2\sin \theta \sinh \left(\alpha y\right)}{2\pi \left(\zeta L\cosh \left(\alpha L/2\right)+\frac{2}{\alpha }\sinh \left(\alpha L/2\right)\right)}\hfill \\ \hfill & +\frac{\cosh \left(\alpha y\right)+\zeta \cosh \left(\alpha L/2\right)}{2\pi \left(\zeta L\cosh \left(\alpha L/2\right)+\frac{2}{\alpha }\sinh \left(\alpha L/2\right)\right)}.\hfill \end{array}\end{array}$$ [12]

From this, we can finally deduce the local orientational order parameter $\varphi \left(y\right)$ defined in Eq. 3:

$$\varphi \left(y\right)=\frac{\alpha D}{\mu f}\frac{\sinh \left(\alpha y\right)}{\cosh \left(\alpha y\right)+\zeta \cosh \left(\alpha L/2\right)}.$$ [13]

To assess these theoretical predictions, we can take most parameters directly from simulations and use for a typical SIO state $f=1$, ${\tau }_p=10^3$, and $L=50$. The remaining two effective single-particle parameters can be measured directly from the simulation (Fig. 5 A and B); the mobility $\mu =v_y/\left(f\sin \theta \right)$ can be determined from the relation between the average velocity of the particles and their orientation, and the diffusion constant can be extracted from $D_m=⟨{\mathrm{\Delta }y\left(t\right)}^2⟩/\left(2t\right)$ (Materials and Methods). As the diffusive description is approximate (see below), we take a somewhat larger $D$ in the theory, $D=3.3D_m$. With $\mu$ and $D$ fixed, there are no remaining free parameters in the theory. Fig. 5 C and D shows the comparison of the theoretically predicted $P\left(\theta ,y\right)$ and the steady-state simulation data in the corresponding SIO state. We observe very good qualitative and semiquantitative agreement, particularly given the approximations inherent in the theory: 1) The simulations show a superdiffusive growth of the mean-squared particle displacement, suggesting that memory effects cannot be fully neglected as we have done; and 2) the effective diffusivity $D$ and mobility $\mu$ may exhibit some dependence on density and therefore, $y$, whereas we have taken these parameters as constant. Overall, our simple single-particle theory offers a remarkably good description of the SIO state and its orientational ordering. Within the theoretical picture, the degree of orientational ordering is governed by the competition between the orientational bias of the particle velocities in the shear gradient direction on the one hand and the disordering tendency of the rotational diffusion on the other. Ordering is observable when the steady shear leads to a sufficiently large effective mobility and hence, a stronger tendency toward orientational order.

Fig. 5.

Single-particle parameters in SIO state marked in Fig. 1B (the open triangle). (A) Average velocity of particles around $y=0$ in shear gradient ($y$) direction, plotted against $\sin \theta$, giving a linear relation as assumed in our single-particle theory; the slope identifies the mobility $\mu$. (B) Mean-squared displacement of particles starting around $y=0$ (marked by red points) and a linear fit (blue dashed line) to extract $D_m$. (C and D) Comparison of steady-state $P\left(\theta ,y\right)$ from the analytical single-particle theory and from simulation, showing good agreement without fit parameters.

Discussion

In this work, we explored the effect of steady shear deformation in a model active glassy material and report a type of orientational ordering that is facilitated by shear. Using different physical quantities including nonaffinity in the velocity profile, steady-state shear stress, and an orientational order parameter, we were able to distinguish a number of qualitatively distinct dynamical steady states: 1) a disordered state, 2) a PIO state, and 3) an SIO state. We observe in particular that shear can help the system to order orientationally, effectively by mobilizing particles sufficiently to follow their orientational bias. For the SIO state, which exhibits strong orientational ordering yet essentially affine flow, we constructed a single-particle Fokker–Planck theory that predicts the joint steady-state distribution $P\left(\theta ,y\right)$ and hence, the degree of orientational order in the system. The predictions compare well with simulation data. There are no free fit parameters in this comparison as the two required effective single-particle quantities (mobility and order or magnitude of diffusion constant) can be measured directly in the simulations.

Shear-induced phase transitions and ordering phenomena in passive systems have been an active topic of research for some time (45–48). It has been shown that although shear can destroy order by melting a system (47), it can also induce ordering in the sense of crystallization (45, 47–51) or alignment for elongated particles (52, 53). Shear-induced crystallization has also been reported very recently in passive colloidal Janus particles (54). Our results demonstrate that other forms of shear-induced ordering can arise in active systems, which are inherently out of equilibrium even without shear. This will add further directions to the exciting paradigm of ordering through steady shear driving.

It will be an interesting challenge to see whether our theoretical approach can be extended into a complete theory for all states we see, including a prediction of the state boundaries. This would require in particular keeping track of the spatial inhomogeneities of the PIO state. Another interesting direction would be to study shear ordering in chiral active systems, where qualitatively new phenomena might be expected. The orientational ordering we have found can also be explored and exploited in synthetic active glassy systems using controlled experiments on active colloids or active granular matter.

Materials and Methods

As mentioned in Model, the particles interact through a Lennard–Jones potential, which has the form

$$V_{L\hspace{0.17em}J}\left(r_{ij}\right)=4{ϵ}_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right],$$ [14]

where $r_{ij}$ is the distance between particle $i$ and $j$. We have chosen interaction parameters ($\sigma$, $ϵ$) and a mixture ratio ($n_A:n_B$) of particles of type A and B that correspond to the Kob–Andersen glass in two dimensions (30, 31). We use reduced LJ units throughout the paper, with the energy scale set by the interaction strength ${ϵ}_{AA}$ between A-type particles, the length scale by the diameter ${\sigma }_{AA}$ of such particles, and the unit of time by ${\tau }_{L\hspace{0.17em}J}=\frac{m{\sigma }_{AA}^2}{{ϵ}_{AA}}=1$. We also set $m=1$ and $\gamma =1$, and this fixes the damping (Brownian) timescale ${\tau }_{\mathrm{d}\mathrm{a}\mathrm{m}\mathrm{p}}=\frac{\gamma {\sigma }_{AA}^2}{{ϵ}_{AA}}=1$ and vibrational (inertial) timescale ${\tau }_{\mathrm{v}\mathrm{i}\mathrm{b}}=\frac{m}{\gamma }=1$ in L J time units.

The simulations were performed in two spatial dimensions with a square box with periodic boundary condition implemented along the direction of flow. We used modified Langevin dynamics (55) for the simulation with $dt=0.002$. We averaged all steady-state quantities over a timescale of $t=10^4$ after first allowing the same amount of time for the system to reach a steady state. This is ample as for our largest ${\tau }_p=10^3$, the relaxation to the steady state still happens on a timescale of order ${\tau }_p$. Apart from this temporal averaging, the order parameter $\psi$, shear stress ${\sigma }_{xy}$, and other relevant quantities are also averaged over 128 independent simulations. We compared simulations with $N_0=\mathrm{1,000}$ and $N_0=\mathrm{4,000}$ particles to check for finite size effects; all results shown were generated for $N_0=\mathrm{4,000}$. Here, $N_0$ includes both the bulk and boundary (wall) particles. This corresponds to a box size of $L_0=57.73$ (as number density is $\rho =1.2$) with a distance between the two walls of $L=50$ and a wall thickness of approximately $4{\sigma }_{AA}$. Velocity profiles are calculated by dividing the whole system into $N_s=50$ slabs in the $y$ direction. For the calculation of $v^{NA}$, we average the squared fluctuations around the affine velocity $v_{Fx}\left(y\right)$ across slabs and evaluate the root of this mean-squared fluctuation. This means that for $N_0=\mathrm{4,000}$, averages within a slab are taken over 80 particles on average. To determine the measured effective diffusion constant $D_m$, we divided the system into five slabs and measured $⟨{\left(\mathrm{\Delta }y\left(t\right)\right)}^2⟩$ in each of them. The diffusion constant was then determined from $⟨{\left(\mathrm{\Delta }y\left(t\right)\right)}^2⟩/\left(2t\right)$ at the time $t$ where ${⟨{\left(\mathrm{\Delta }y\left(t\right)\right)}^2⟩}^{1/2}\sim 10$, which is the size of each slab in the $y$ direction.

Data Availability

All the data used in the main text and in the supplementary information are available under Göttingen Research Online, https://doi.org/10.25625/I06CGQ.