Emergent probability fluxes in confined microbial navigation

Significance

Motile microorganisms commonly live in porous media comprising microhabitats filled with interfaces of complex shape. On such small scales, the interactions with these interfaces, rather than external gradients, dominate their motion in the search for favorable living conditions. We demonstrate with experiments and theory that the geometry of confining interfaces shapes the topology of the most likely, average trajectory, leading to directed fluxes of probability that are not exclusively localized at the near-wall region. Employing this principle allows us to actively shape a microbe’s average direction of movement, which could be of use in the design of topological transport mechanisms for microfluidic environments.

Abstract

When the motion of a motile cell is observed closely, it appears erratic, and yet the combination of nonequilibrium forces and surfaces can produce striking examples of organization in microbial systems. While most of our current understanding is based on bulk systems or idealized geometries, it remains elusive how and at which length scale self-organization emerges in complex geometries. Here, using experiments and analytical and numerical calculations, we study the motion of motile cells under controlled microfluidic conditions and demonstrate that probability flux loops organize active motion, even at the level of a single cell exploring an isolated compartment of nontrivial geometry. By accounting for the interplay of activity and interfacial forces, we find that the boundary’s curvature determines the nonequilibrium probability fluxes of the motion. We theoretically predict a universal relation between fluxes and global geometric properties that is directly confirmed by experiments. Our findings open the possibility to decipher the most probable trajectories of motile cells and may enable the design of geometries guiding their time-averaged motion.

The presence of hidden order and regularities in living systems—seemingly intractable from the point of view of mathematics and physics—was first intuited by Erwin Schrödinger (1). More recently, there has been a renaissance of discoveries of physical principles governing living matter (2, 3). In systems of motile microorganisms, activity and geometry often conspire to create organized collective states (4–15). The robustness of these results invites the question: At what level does such order start emerging? Specifically, is there a lower bound in either the number of participating microbes or the available space for regularities to affect the activity of the cells? While the dynamics of active microswimmers, which propel themselves—e.g., by the periodic beating of one or multiple flagella (16, 17)—are often studied in idealized bulk situations, these microorganisms live in the proximity of interfaces, prosper in wet soil, inhabit porous rocks, and generally encounter complex boundaries regularly (18–20). When colliding with a solid boundary, a microswimmer may interact with it through hydrodynamic interactions mediated by the fluid (21, 22), through steric interactions (23), or through a combination of the two (24, 25). Studies of puller-type microswimmers like Chlamydomonas reinhardtii suggest that, for such microswimmers, steric interactions dominate the dynamics in the presence of such boundaries (23, 26–28). C. reinhardtii naturally lives in wet soil (29), an environment dominated by fluid–solid interfaces. A common observation is that such microswimmers are more likely to be found at or in close proximity to the boundary, rather than within the interior (30–33), showing a preference for regions of high wall curvature (28, 30, 34).

Here, we report experiments on a single C. reinhardtii cell confined in a compartment with varying boundary curvature, analytical calculations, and simulations that model the microswimmer as an asymmetric dumbbell undergoing active Brownian motion and interacting sterically with the compartment wall. We find that when the compartment’s boundary exhibits nonconstant curvature, the accessible space is partitioned by loops of probability flux that direct and organize the cell’s motion. This finding becomes evident when the nonequilibrium fluxes are extracted from the analysis of experimental and simulation data and also estimated through the Fokker–Planck description of our system. The cell’s front–back asymmetry results in a torque, which, in turn, causes an active reorientation when interacting with the wall. Such shape asymmetry proves crucial for the quantitative agreement of experiments and simulations, making steric effects dominant over hydrodynamics in situations of strong confinement for such flagellated microorganisms. We show that the loops of probability flux are directly linked to the boundary’s gradient of curvature and can be quantified by a dimensionless number $\chi$ accounting for the relevant ratio of length scales.

We conduct experiments on single biflagellated C. reinhardtii cells, wild-type strain SAG 11-32b, confined within a quasi-two-dimensional (quasi-2D) microfluidic compartment in the absence of any inlets or outlets. We employ optical bright-field microscopy and particle-tracking techniques to extract cell trajectories over extended time periods (28). Experiments are performed in elliptical compartments with eccentricities varying in the range 0.5 to 0.9 and accessible areas of $\left(7-200\right)\times 10^3$ $\mathrm{\mu }{\mathrm{m}}^2$. The height of all compartments is ∼22 $\mathrm{\mu }$m, i.e., slightly larger than one cell diameter, comprising cell body and flagella, such that the cell’s motion is confined in two dimensions (Materials and Methods).

We statistically investigate the average motion by tracking the cell’s position over long trajectories. Fig. 1A shows the overlaid positions of a single C. reinhardtii cell confined within a sealed elliptical compartment. While a certain preference to travel alongside the boundary is noticeable, frequent excursions across the microfluidic microhabitat are evident. Periods of time when the cell travels along the boundary are interrupted by rapid reorientations, crossing of the compartments, or curved arcs. The short-time motion of the cell is influenced by the stochasticity associated to the biological motors powering the flagella and their coordination (16, 21, 35) and the small-scale hydrodynamic fluctuations of the fluid stirred by the swimming cell.

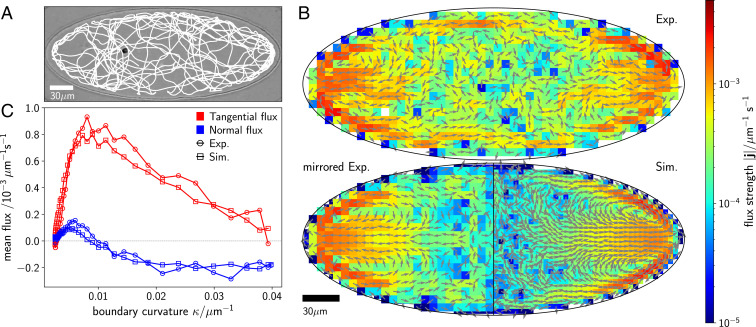
Fig. 1.

Cell trajectory and emerging nonequilibrium fluxes inside an elliptical compartment. (A) Optical micrograph of a single C. reinhardtii cell contained in a quasi-2D elliptical compartment with a major semiaxis of $157\hspace{0.17em}\mathrm{\mu }$m and a minor semiaxis of $63\hspace{0.17em}\mathrm{\mu }$m. A representative section of the fully tracked cell trajectory is overlaid in white. The cell is visible at the left of the center. (B) Steady-state nonequilibrium fluxes with arrows indicating their direction and their strength encoded with color. The fluxes obtained by direct analysis of the experimental (exp.) trajectories are shown in B, Upper. Considering the system’s symmetry, we can increase the available statistics by mirroring along the major and minor axes of the ellipse and, thus, reducing the noise in the fluxes (B, Lower, left). The fluxes resulting from Brownian dynamics simulations (see Numerical Model and Simulation Parameters and SI Appendix for details on our model) are shown in B, Lower, right. (C) Steady-state fluxes in a strip within $20\hspace{0.17em}\mathrm{\mu }$m from the wall in tangential (red) and normal (blue) directions comparing experiments (circles) and simulations (rectangles). Positive tangential fluxes denote fluxes toward lower curvature; positive normal fluxes denote the direction away from the wall.

To investigate the nonequilibrium dynamics of the cell’s motion, we compute the trajectory transition rates as follows. Starting from the cell’s trajectories obtained via particle tracking, we divide the space in the compartment with a square grid and determine the probabilities to traverse a certain box in either direction by averaging over all passages of the trajectory on that box. By counting the directed transitions between adjacent boxes $\alpha$ and $\beta$, we can extract the net transition rates $w_{\alpha ,\beta }$ from which the $x$ and $y$ components of the flux $\mathit{j}$ are computed (SI Appendix, section I) (36, 37). This analysis reveals loops in the experimental probability fluxes, underlying the run-and-tumble-like motion (21) of the cell within the compartment (Fig. 1B). Because of the symmetry of the system and the absence of any preferential direction in the cell’s motion, the loops are symmetrically placed within the ellipse. The fluxes form a strong equatorial current pointing directly toward the ellipse’s apices (the two points on the boundary with the highest curvature) and are then redirected along the boundary away from the apices. These loops are a manifestation of the inherent nonequilibrium nature of the cell’s active motion, which explicitly breaks the invariance of the dynamics between a transition from one state to another and the inverse transition.

Numerical simulations of our system lend insight into the properties of these flux loops. We employ a minimal mechanistic model of C. reinhardtii cells as asymmetric dumbbells (SI Appendix, Fig. S1), representing the characteristic fore–aft asymmetry of the cell’s body and of a larger space spanned by the stroke-averaged flagella (30, 38, 39). Note that other microswimmer geometries produce fluxes as well, though without matching experiments quantitatively (SI Appendix, section V). The translational dynamics of the dumbbell are governed by an overdamped Langevin equation: $\text{d}\mathit{r}/\text{d}t=v_0\mathit{e}+{\mu }_w{\mathit{F}}_w+\mathit{\eta }$, where $\mathit{r}$ is the position of the geometric center of the dumbbell, $v_0$ is the self-propulsion velocity, $\mathit{e}$ is the orientation of the dumbbell, ${\mu }_w$ is the mobility, and ${\mathit{F}}_w$ is the force stemming from steric wall interactions. Furthermore, $\mathit{\eta }$ is a Gaussian white noise to account for translational diffusion with coefficient $D_T=k_{B}T{\mu }_w$. The orientational dynamics are governed by the equation: $\text{d}\mathit{e}/\text{d}t=\left({\mathit{T}}_w/{\tau }_w+\mathit{\xi }\right)\times \mathit{e}$, where ${\mathit{T}}_w$ is the torque acting at the wall, ${\tau }_w$ is the rotational drag coefficient, and $\mathit{\xi }$ is a Gaussian white noise accounting for rotational diffusion with coefficient $D_R$. All parameters entering the equations of motion were either directly measured in our experiments or extracted from the literature (Materials and Methods).

Fig. 1 B, Lower also shows the results of our simulations for the probability flux for a single cell moving according to the above Langevin equations within an elliptical compartment with the same area and eccentricity as in the experiments. We find the analogous structure of flux loops emerging from the numerical results. Strong directional fluxes point from the central region of the compartment toward the apices and then move away along the boundary, closing the flux loops. For any point on the compartment boundary, the fluxes $\mathit{j}$ can be decomposed in a component tangential and one normal to the boundary. We choose the positive normal direction to point into the compartment and the positive tangential direction to always point down the gradient of curvature. The flux analysis reveals that, in the bulk, the cell is most likely to be on a path leading toward a region of high curvature $\kappa$, as indicated by the negative normal fluxes in Fig. 1C; after colliding with the wall, a smaller reorientation is needed to escape again at regions of low curvature, whereas escaping at high curvature requires larger turns, which are statistically less likely. This leads to a net statistical flux along the wall toward regions of lower curvature, resulting in a rise of tangential flux with decreasing $\kappa$. The strong, outward equatorial fluxes (Fig. 1B) meet the boundary and turn up or down along regions of lower curvature. At those turning points (close to the ellipse apices), the normal fluxes change sign, while the tangential flux become strongest. The quantitative agreement between experiments and simulations in Fig. 1C confirms the fundamental role of the force and torque applied by the boundary on the cell.

For a more general understanding of the origin of the flux loops, we now turn to a continuum-mechanics approach of the probability flow by computing the Fokker–Planck equation for the system, which reads

$$\begin{array}{ll}\hfill \frac{\partial p}{\partial t}=& -\nabla \cdot \left(v_0\mathit{e}+{\mu }_w{\mathit{F}}_w-D_T\nabla \right)p\hfill \\ \hfill & -\mathit{e}\times \frac{\partial }{\partial \mathit{e}}\cdot \left(\frac{1}{{\tau }_w}\mathit{e}\times {\mathit{G}}_w-D_R\mathit{e}\times \frac{\partial }{\partial \mathit{e}}\right)p,\hfill \end{array}$$ [1]

where the gorque ${\mathit{G}}_w$ is a more convenient way to treat the torque ${\mathit{T}}_w=\mathit{e}\times {\mathit{G}}_w$. A moment expansion of the probability distribution function $p=p\left(\mathit{r},\mathit{e},t\right)$ in terms of density $\rho \left(\mathit{r}\right)$ and polarization $\mathit{P}\left(\mathit{r}\right)$ allows us to identify the nonequilibrium flux in position space ${\mathit{j}}_r=v_0\mathit{P}+{\mu }_w{\mathit{F}}_w\rho -D_T\nabla \rho$. The probability flux ${\mathit{j}}_r$ obeys a solenoidal condition $\nabla \cdot {\mathit{j}}_r=0$ (SI Appendix, section II), which is obeyed in both the experimental and simulated fluxes (Fig. 1B). We can solve the dynamics of the probability loops by introducing a stream function ${\mathit{j}}_r=\nabla \times \mathit{\psi }$, which satisfies the governing Poisson equation

$$\mathrm{\Delta }\psi =-\omega \left({\mathit{F}}_w,{\mathit{G}}_w,\nabla \kappa \right),$$ [2]

where the vorticity $\omega =\nabla \times {\mathit{j}}_r$ is a function of the forces ${\mathit{F}}_w$ and gorques ${\mathit{G}}_w$ exerted by the boundary on the swimming cell. Additionally, because of the anisotropic shape of the microswimmer, the vorticity crucially couples with the gradient of curvature $\nabla \kappa$.

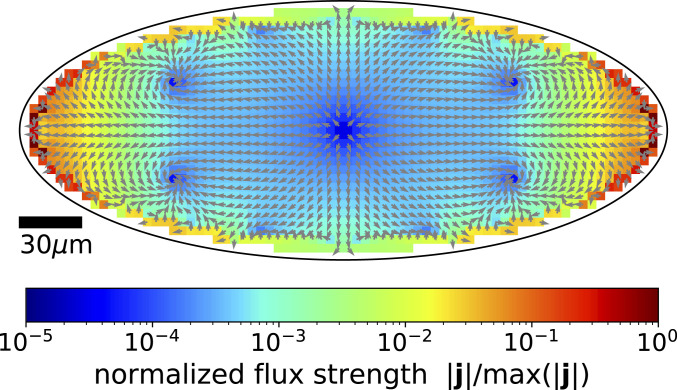
The flux equation [2] with elliptical boundary conditions can be solved analytically (SI Appendix, section III). Fig. 2 shows the resulting fluxes. The qualitative features of the nonequilibrium fluxes found in experiments and simulations are reproduced by the solution of Eq. 2. Four symmetrically placed flux loops emerge in the region close to the apices. This fact points to a general connection between fluxes and the boundary’s curvature. We elucidate this relationship in the following.

Fig. 2.

Topology of the nonequilibrium fluxes in an elliptical geometry. The structure of the flux loops is derived analytically from Eq. 2. Nonuniform wall curvature induces four loops in the nonequilibrium fluxes and strong equatorial fluxes pointing toward the ellipse’s apices. Fluxes result from the interplay of the gradient of curvature and the polarization of active motion. See SI Appendix, section II for details of the analytics.

We can deduct a quantitative relation of the fluxes from the above arguments. From our general arguments (SI Appendix, section II), the steady-state expression for the polarization in close proximity of the wall ${\mathit{P}}_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}\approx -{\left(2\nabla \cdot {\mathit{F}}_w\right)}^{-1}\left(v_0\nabla +{{\tau }_w}^{-1}{\mathit{G}}_w\right)\rho$. Recalling the definition of ${\mathit{j}}_r$, and the fact that close to the boundary the probability density is proportional to the curvature $\rho \propto \kappa$ (28)—i.e., the cell is more likely to spend more time in regions of high local curvature—we find that, generally, the flux depends on the curvature $\kappa$ and its gradient $\nabla \kappa$. In a circular domain, where the curvature is constant, symmetry prevents the emergence of fluxes (SI Appendix, section IV), even though the system is out of equilibrium. A local dependence of curvature breaks the symmetry and allows for nonzero fluxes. Thus, we expect the fluxes to depend on $\nabla \kappa$, but not directly on $\kappa$, as observed in our experiments and simulations.

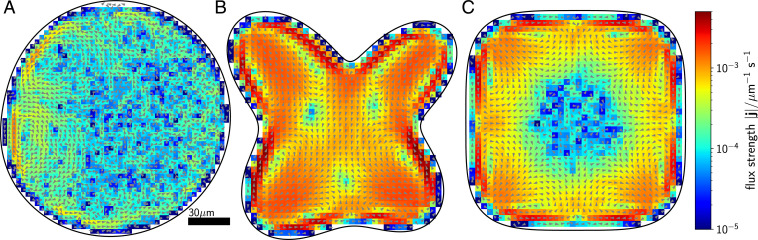
We now generalize our arguments to more complex shapes by inferring the following effective rules: 1) Because flux loops are generated by curvature gradients, the number of flux loops equals the number of zero crossings of curvature gradient, $\nabla \kappa =0$; 2) the magnitude of a flux loop is proportional to the integrated change in curvature $\int \left|\frac{\partial \kappa }{\partial l}\right|\mathrm{d}l$ along a portion of the boundary with arc length $l$; and 3) the number of stagnation points in the flux ($\left|{\mathit{j}}_r\right|\approx 0$) is at most one for every two flux loops. These predictions are in line with the topological structure of the fluxes for simulations of our model in compartments of growing complexity with multiple lobes and points of both positive and negative curvature, as shown in Fig. 3.

Fig. 3.

Complexity and topology of flux loops. Simulations of a model microswimmer in complex geometric confinement confirm the general topological features of the flux loops. The nonequilibrium fluxes (displayed as arrows) are extracted from our active Brownian dynamics simulations. Fluxes are dominated by gradients of wall curvature. More compartment geometries are shown in SI Appendix, Fig. S4. The mathematical equations of the shown compartments A, B, and C are provided in SI Appendix, section VI.

Although Eq. 2 reveals the importance of forces acting at the boundaries, the nonequilibrium nature of the probability distribution imposes a nonlocal spatial distribution of the fluxes. It is then natural to consider the integral of the flux over an area of the compartment

$$\mathcal{F}\equiv \frac{1}{v_0}{\int }_S\left|\mathit{j}\right|\text{d}S,$$ [3]

which gives an effective measure for the strength of the nonequilibrium fluxes within the region $S$ (we choose a strip of $20\hspace{0.17em}\mathrm{\mu }$m along the boundary where the fluxes are clearly distinguishable from statistical noise) and where self-propulsion velocity $v_0$ is used to nondimensionalize $\mathcal{F}$. Through $\mathit{j}$, $\mathcal{F}$ inherits the dependence on $\nabla \kappa \sim \partial \kappa /\partial l$. To capture the global characteristics of the geometry, we are naturally led to define the dimensionless number

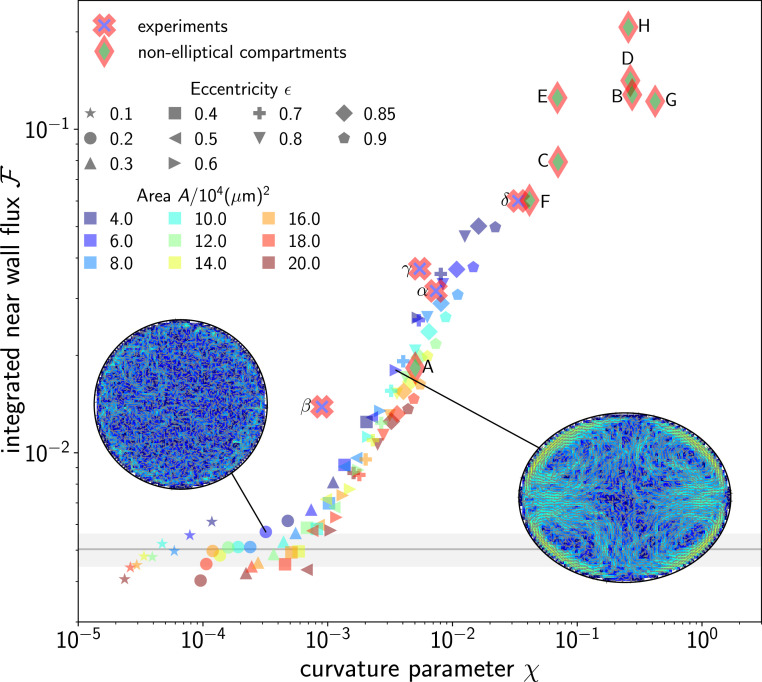
$$\chi \equiv A_c\frac{\int \left|\frac{\partial \kappa }{\partial l}\right|\mathrm{d}l}{\int \mathrm{d}l},$$ [4]

comparing the global change in curvature over the total perimeter $\int \mathrm{d}l$ of the boundary with the typical area of the cell $A_c$ calculated by squaring the swimmer’s length (Materials and Methods). We find that the integral flux strength $\mathcal{F}$ depends uniquely on $\chi$ for both experiments and simulations of elliptical compartments with various areas $A$ and eccentricities $ϵ$ (Fig. 4). The cross-over in the integrated fluxes at $\chi \approx 10^{-3}$ corresponds to the point at which the fluxes can be effectively distinguished from noise, given the available statistics. In fact, to quantify the effect of statistical noise, we consider simulations in circular compartments—where fluxes are strictly absent—and use the same amount of statistics as elliptical compartments; we find an average value ${\mathcal{F}}_{\text{noise}}=5\times 10^{-3}$, marked with a horizontal gray line; the shaded area marks the standard deviation (SD) derived from simulations of circular compartments with the same areas as the ellipses.

Fig. 4.

Relation between boundary curvature gradient and nonequilibrium fluxes. The integrated flux strength $\mathcal{F}$ depends solely on the curvature parameter $\chi$. Experiments and simulations for elliptical compartments with different eccentricities (filled symbols) and areas (color code) collapse on a master curve. The data gathered from experimentally recorded trajectories in elliptical compartments (framed crosses), as well as the simulations in complex shapes shown in Fig. 3, are also included here (framed diamonds). Experiments were performed in compartments of eccentricities ${ϵ}_{\alpha }\approx 0.92$, ${ϵ}_{\beta }\approx 0.55$, ${ϵ}_{\gamma }\approx 0.55$, and ${ϵ}_{\delta }\approx 0.92$ with compartment areas $A_{\alpha }\approx 14.23\times 10^4\hspace{0.17em}\mathrm{\mu }{\text{m}}^2$, $A_{\beta }\approx 19.09\times 10^4\hspace{0.17em}\mathrm{\mu }{\text{m}}^2$, $A_{\gamma }\approx 3.13\times 10^4\hspace{0.17em}\mathrm{\mu }{\text{m}}^2$, and $A_{\delta }\approx 3.11\times 10^4\hspace{0.17em}\mathrm{\mu }{\text{m}}^2$. The cross-over in the data at $\chi \approx 10^{-3}$ marks a transition from weak fluxes indistinguishable from noise with the available statistics to fully developed flux loops. The gray horizontal line and gray shaded area mark the average and SD, respectively, for circular compartments with the same areas as the ellipses and the same amount of statistics.

For values of scaled curvature gradients $\chi <10^{-3}$, the fluxes are rather weak, whereas for $\chi \ge 10^{-3}$, strong fluxes emerge and exhibit closed loops, such that their impact on the global dynamics within the compartment is much stronger. The near collapses of both experiments and simulations for all shapes confirm that the boundary’s geometry determines the strength and shape of flux loops within the interior of the compartment.

Taken together, our results show that the boundary of the confining domain imposes a robust topology of loops of probability fluxes at the level of a single active cell. Our experimental and theoretical results demonstrate the intimate connection between the geometric properties of the boundary and the interior of a compartment confining a motile cell. The ensuing probability fluxes impose an organizing structure to the whole compartment’s interior, which statistically guides the cell’s motion. Our study shows that C. reinhardtii cells are very efficient at exploring the available space and that simple geometric features can leave an imprint on the cells’ overall motion in their microhabitat.

Harnessing the motion of microorganisms is a promising direction of technological development in active matter (25, 40). Improved efficiency of micromachines will require a better understanding of how microbial cells navigate complex environments and interact with their boundaries. Inducing a statistical bias to directional motion, as a consequence of the nonequilibrium nature of the motion and confining boundaries, might, in fact, help in producing efficient microdevices, even at the scale of a single cell.

Materials and Methods

Cell Cultivation.

All experiments were performed by using the wild-type Chlamydomonas reinhardtii strain SAG 11-32b (provided by the Göttingen Algae Culture Collection; SAG). The cells were cultivated axenically in Tris–acetate–phosphate medium in a Memmert IPP110Plus incubator on a 12-h-day–12-h-night cycle. The temperature of the cell cultures in the incubator was kept at 24 $°$C during the day (white light; light intensity of about $3\times 10^{19}$ photons/(m² s) in the center of the incubator) and reduced to a temperature of 22 $°$C during the night (no illumination), respectively. Prior to every experiment, about 50 mL of cell culture was centrifuged (Eppendorf 5804R) for about 10 min at an acceleration of 100 $g$ at ambient temperature. About 40 to 45 mL of the suspension was then removed, and the remaining 5 to 10 mL was allowed to relax for 90 to 120 min in the incubator to ensure that the cells had a sufficient amount of time to eventually regrow their flagella. Finally, this suspension was diluted with cell-culture medium to very low cell concentrations in order to enhance the probability of capturing precisely one single cell per compartment.

Microfluidics.

The experimental chambers were composed of 2D arrays of stand-alone elliptical microfluidic compartments exhibiting a height of about 22 $\mathrm{\mu }$m. These compartment arrays were manufactured by employing soft-lithography techniques using a curable elastomer (polydimethylsiloxane [PDMS]; Sylgard 184 Elastomer Kit, Dow Inc.) and master structures, which we produced by means of photolithography techniques in a clean room. Before filling the chambers with the cell culture, the PDMS-based microfluidic device and a glass microscope slide were treated with air plasma (Pico; Diener Electronic) for 30 s to render their surfaces hydrophilic. A droplet of the diluted cell suspension was placed onto the feature side of the microfluidic device, such that the compartment array was completely filled, and, subsequently, the glass slide was placed atop and gently pressed to tightly seal the experimental compartment. The confining surfaces at the top and bottom prevented the organism from turning out of the plane, enabling a 2D description.

Microscopy.

For time-resolved cell imaging, we employed bright-field microscopy (Olympus IX-81 inverted microscope) in controlled light conditions (closed box). During all experiments, the microfluidic compartment was illuminated by using a narrow red-light bandpass filter (671 nm, full-width at half-maximum = 10 nm) in order to exclude any photoactive response of the cell, including phototaxis (41, 42) and light-induced adhesion to surfaces (43, 44). A Canon 600D camera (at 25 frames per second; resolution: 1,920 $\times$ 1,080 pixels) was used to record videos of single cells swimming in isolated elliptical compartments for about 5 to 30 min each. In order to increase the statistics substantially, these single-cell recordings were independently repeated three to eight times for each chamber geometry.

Image Processing and Cell Tracking

All videos were converted into sequences of 8-bit grayscale images with improved contrast using a custom-made MATLAB algorithm. The compartment boundaries were manually identified to restrict the cell tracking to the region available to the motion of the cell. Finally, 2D cell tracking was performed by using MATLAB based on the protocol developed by Crocker and Grier (45).

Numerical Model and Simulation Parameters

The C. reinhardtii cells are modeled as asymmetric dumbbells (SI Appendix, Fig. S1) with a large sphere in front and a smaller sphere in the back, representing the fore–aft asymmetry of body and appendages (38, 39). The equation of motion for the position $\mathit{r}$ of the active dumbbell is given by

$$\frac{\text{d}\mathit{r}}{\text{d}t}=v_0\mathit{e}+{\mu }_w{\mathit{F}}_w+\mathit{\eta }.$$ [5]

Here, $v_0=100\hspace{0.17em}\mathrm{\mu }\text{m/s}$ is the self-propulsion speed of the cell, and $\mathit{\eta }$ is a Gaussian white noise with correlator $⟨\mathit{\eta }\left(t\right)\mathit{\eta }\left(t^{\prime }\right)⟩=2k_{\mathrm{B}}T{\mu }_w\mathbf{1}\delta \left(t-t^{\prime }\right)$ and translational diffusion coefficient $k_{\mathrm{B}}T{\mu }_w=250\hspace{0.17em}\mathrm{\mu }$m²/s (both numerical values are taken from ref. 28). The term ${\mathit{F}}_w$ accounts for steric wall interactions of the dumbbell and was computed by ${\mathit{F}}_w={\mathit{F}}_1+{\mathit{F}}_2$ with ${\mathit{F}}_{\alpha }=-\nabla U_{\alpha }\left(r\right)$, $\alpha =\mathrm{1,2}$, where 1 and 2 refer to the large and small sphere of the dumbbell, respectively. To compute the respective steric forces, we used the Weeks–Chandler–Anderson potential (46)

$$U_{\alpha }\left(d\right)/\left(k_{\mathrm{B}}T\right)=4U_0\left[{\left(\frac{a_{\alpha }}{d}\right)}^{12}-{\left(\frac{a_{\alpha }}{d}\right)}^6\right]+U_0\hspace{0.17em},$$ [6]

if $d<2^{1/6}{a}_{\alpha }$, and zero otherwise, where $d$ is the distance of the sphere $\alpha \in \left\{\mathrm{1,2}\right\}$ to the wall of the compartment. The radii of the large (1) and small (2) circles of the dumbbell are $a_1=5\hspace{0.17em}\mathrm{\mu }$m and $a_2=2.5\hspace{0.17em}\mathrm{\mu }$m, and we use $\epsilon =10$ to obtain a sufficiently strong screening (the values are taken from ref. 28).

The orientation $\mathit{e}$ is defined as the unit vector pointing from the small to the large circle of the dumbbell. The equation of motion for the orientation is given by

$$\frac{\text{d}\mathit{e}}{\text{d}t}=\left({\mathit{T}}_w/{\tau }_w+\mathit{\xi }\right)\times \mathit{e}.$$ [7]

Here, $\mathit{\xi }$ is a Gaussian white noise with correlator $⟨\mathit{\xi }\left(t\right)\mathit{\xi }\left(t^{\prime }\right)⟩=\frac{2k_{\mathrm{B}}T}{{\tau }_p}\mathbf{1}\delta \left(t-t^{\prime }\right)$ and rotational diffusion coefficient ${\tau }_p/k_{\mathrm{B}}T=2\hspace{0.17em}\text{s}$ (23). The torque acting at the wall is computed by ${\mathit{T}}_w={\mathit{T}}_1+{\mathit{T}}_2$, where we use ${\mathit{T}}_1=\left({\mathit{r}}_1-\mathit{r}\right)\times {\mathit{F}}_1=l\left(\mathit{e}\times {\mathit{F}}_1\right)/2$, ${\mathit{T}}_2=-l\left(\mathit{e}\times {\mathit{F}}_2\right)/2$, and $l=5\hspace{0.17em}\mathrm{\mu }$m. For the shear time at the wall, we use ${\tau }_w/k_{\mathrm{B}}T=0.15\hspace{0.17em}\text{s}$ (23). In addition to Eq. 7, we include a run-and-tumble motion of the cell. Each tumbling event is instantaneous, and the time between each tumbling event is sampled for an exponential distribution with mean ${\tau }_p/k_{\mathrm{B}}T$. The relative tumbling angle ${\varphi }_{\mathrm{t}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{l}\mathrm{e}}$ is drawn from a Gaussian distribution with an SD of 0.1 and a mean of $\pi /2$.

Data Availability

Motile cell trajectory data, analysis and simulation code have been deposited at zenodo.org (DOI: 10.5281/zenodo.5497768) (47).