Real-Time Gait Phase Estimation for Robotic Hip Exoskeleton Control During Multimodal Locomotion

Abstract

We developed and validated a gait phase estimator for real-time control of a robotic hip exoskeleton during multimodal locomotion. Gait phase describes the fraction of time passed since the previous gait event, such as heel strike, and is a promising framework for appropriately applying exoskeleton assistance during cyclic tasks. A conventional method utilizes a mechanical sensor to detect a gait event and uses the time since the last gait event to linearly interpolate the current gait phase. While this approach may work well for constant treadmill walking, it shows poor performance when translated to overground situations where the user may change walking speed and locomotion modes dynamically. To tackle these challenges, we utilized a convolutional neural network-based gait phase estimator that can adapt to different locomotion mode settings to modulate the exoskeleton assistance. Our resulting model accurately predicted the gait phase during multimodal locomotion without any additional information about the user’s locomotion mode, with a gait phase estimation RMSE of 5.04 ± 0.79%, significantly outperforming the literature standard (p < 0.05). Our study highlights the promise of translating exoskeleton technology to more realistic settings where the user can naturally and seamlessly navigate through different terrain settings.

I. Introduction

GAIT phase is a continuous state variable that represents the user’s movement during the gait cycle. This variable is defined as a linearly increasing value between 0 and 100 where both 0 and 100 represent a single deterministic gait event (e.g., heel contact or toe-off). This is critical information for controlling wearable devices, such as robotic exoskeletons, as recent studies have shown that providing exoskeleton assistance with accurate timing is crucial for maximizing user benefit [1]–[3].

A conventional gait phase estimation method in the field is time-based estimation (TBE) which utilizes a mechanical sensor (e.g., a foot switch placed at the user’s heel) to detect the user’s heel contact during locomotion [4], [5]. Using this heel contact information, the user’s gait phase is estimated by dividing the time since the most recent heel contact by the user’s average stride duration from previous strides. While this method may work reliably on a treadmill at a constant walking speed, it fails to provide an accurate estimate once the user dynamically changes walking speeds (gait phase estimation either leads or lags). Moreover, when walking overground in different locomotion modes (e.g., ramps and stairs), TBE can show greater error in gait phase estimation as the stride duration can drastically change from one locomotion mode to another. Therefore, a robust gait phase estimation method is needed to translate robotic exoskeleton technology to more realistic settings.

Previously, different research groups have tackled the development of a robust gait phase estimator [6]–[9]. Ronsse et al. leveraged the sinusoidal nature of hip joint angle during locomotion and computed the user’s gait phase using an adaptive oscillator approach [6]. Villarreal et al. estimated the user’s gait phase by mapping the hip joint angle into a time-independent phase variable [9]. While these heuristic methods showcased promising results by adapting to different user states (changing walking speeds), they are still inherently limited as they require a gradual change from one state to another (e.g., slowly accelerating to another speed). This is not representative of the real world, as the user will dynamically change into different locomotion modes and accelerate/decelerate.

One possible solution to this challenging problem is to use deep learning [10]. Previously, we implemented a neural network-based gait phase estimator in real-time and validated that a machine learning (ML) model can robustly estimate the user’s gait phase during different walking speeds [11]. However, the study was limited to level ground treadmill walking and did not validate the feasibility of translating this estimation approach to other terrain settings. One advantage that deep learning models have over other ML models is that they do not require any manual feature engineering and therefore are not limited to the specific features that a researcher engineers. Thus, in this study, we exploited our previous findings and the end-to-end capability of deep learning models to extend gait phase estimation to an overground scenario with multiple locomotion settings.

The primary contribution of our study is that we have presented a deep learning-based estimation strategy that can predict the user’s gait phase across different locomotion modes (including mode transitions) without any additional information about the user’s current locomotion mode. This is an important contribution to autonomous exoskeleton control because gait phase is a critical state variable that is directly related to accurate exoskeleton control. Thus, to translate the exoskeleton technology to a real-world scenario, a model that can robustly predict the user’s gait phase during multimodal locomotion is necessary.

II. Gait Phase Estimation Development

A. Robotic Hip Exoskeleton

We used the Gait Enhancing and Motivating System (GEMS), a bilateral hip exoskeleton developed by Samsung Electronics (Suwonsi, Gyeonggi-do, South Korea) [12], which has a mass of 2.1 kg and can provide a peak torque of 12 Nm in hip flexion and extension (Fig. 1A). We recorded 6-axis inertial measurement unit (IMU) data of the trunk and bilateral hip encoder position and velocity from the onboard sensors at 200 Hz. We incorporated an additional onboard machine learning co-processor (Jetson Nano, NVIDIA, USA) for real-time inference of the deep learning model. The exoskeleton and the co-processor communicated via an ethernet cable using TCP/IP to transfer data.

Fig. 1.

(A) Robotic hip exoskeleton. Different mechanical sensors on the device measure the user’s kinematic information during walking. The Jetson co-processor estimates the user’s gait phase in real-time. (B) The terrain park used for the human subject experiment consisting of five locomotion modes. The red line indicates the path that each subject walked across the terrain park.

B. Biological Torque Controller

The exoskeleton was controlled using a biological torque controller, in which the reference signal for each locomotion mode was shaped to fit normative biological hip joint moment profiles per locomotion mode (LG - Level Ground, RA - Ramp Ascent, RD - Ramp Descent, SA - Stair Ascent, SD - Stair Descent) (Fig. 2). The normative hip joint moment profiles used for the controller were based on an open-source biomechanics data set [13]. The assistance profile was scaled to mimic the change in biological hip joint moment demands with varying locomotion modes where the peak torque magnitudes were chosen with similar values to those used in two previous hip exoskeleton studies, which reduced the metabolic cost of level [12] and uphill [14] walking using a similar controller and hardware.

Fig. 2.

Reference hip torque trajectories generated by the developed biological torque controller using a sum of univariate Gaussians. Five colored lines represent torque profiles for different locomotion modes where 0% of the gait phase represents toe-off.

This controller was used since it is an effective assistance strategy for augmenting human walking [3], [15]–[18] and is generalizeable to multiple locomotion modes [14]. To ensure continuous and periodic assistance, each assistance trajectory was fit to the corresponding joint torque profile using a sum of univariate Gaussians [19]–[21]. Given the current gait phase x, the desired assistance torque τ was computed using the locomotion mode-specific shaping constants (a, μ, and σ which were manually tuned to represent a smooth hip torque profile based on the biological hip moment) using Equation (1),

$$\tau =\sum _{i=1}^n{a}_i\mathcal{N}\left(x,{\mu }_i,{\sigma }_i\right),$$ (1)

where the Gaussian distribution $\mathcal{N}$ was defined as

$$\mathcal{N}(x,\mu ,\sigma )=e^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}.$$ (2)

The amplitude coefficients (a) were selected to scale the peak assistance torque to 6, 4.5, and 3 Nm for ascent, level, and descent locomotion modes, respectively, to ensure that the assistance level was scaled for each mode. The finalized assistance level showed a similar order of magnitude compared to other literature studies that have successfully improved human locomotion [14], [22].

To provide this assistance in real-time, the exoskeleton onboard processor communicated with the experimenter’s computer over Bluetooth. Using the keyboard, the experimenter manually selected the user’s locomotion mode in real-time. This selection queued the next locomotion mode for the exoskeleton, which transitioned into that mode at toe-off on each side. The onboard exoskeleton processor then selected the appropriate reference torque trajectory based on the current locomotion mode per leg. Based on the gait phase estimate from the TBE or ML model, the instantaneous commanded assistance was then determined using Equation (1), using the locomotion mode-specific constants.

C. Training Data Collection

We recruited ten able-bodied subjects with an average age of 25.2 ± 5.0 years, height of 1.72 ± 0.08 m, and body mass of 66.7 ± 7.6 kg (3 females/7 males) to obtain the initial training data set. The study was approved by the Georgia Institute of Technology Institutional Review Board and informed written consent was obtained for all subjects. All subjects were asked to walk across a terrain park with the exoskeleton at their preferred walking speed for 5 circuit trials (walking in both clockwise and counter-clockwise directions to include all locomotion modes). Each trial included five locomotion modes (level ground, ramp ascent/descent at 11°slope, and stair ascent/descent at 15.24 cm height) (Fig. 1B). As the user navigated the terrain park, the experimenter specified the user’s locomotion mode in the biological torque controller via manual keyboard input, resulting in the corresponding hip assistance.

The controller utilized the TBE method for estimating the user’s gait phase using the stride duration from a single previous gait cycle (to minimize the delay in responding to the mode transition). While the implementation of a robust TBE method (e.g., multiple peak detection to estimate gait phase in several discrete gait events) was possible, we wanted to compare to a gait phase estimation strategy that was commonly used in previous literature studies due to its ease of implementation. We utilized TBE-based assistance during training data collection rather than the transparent mode to minimize any potential discrepancies in the kinematic information (when provided with enough assistance magnitude) between the assistance mode and the transparent mode. The mode transition was marked during the stance phase prior to the transiting mode (the mode-dependent controller switched the assistance profile for the following swing phase). Throughout the experiment, all mechanical sensor data from the exoskeleton were recorded.

D. Ground Truth Labeling

Our previous study utilized a force-sensitive resistor (FSR) sensor at the heel to detect a deterministic point in the gait cycle (e.g., heel contact) to label the ground truth gait phase [11]. This method can be problematic as the FSR can fail to detect accurate ground contact events when foot contact locations are inconsistent (e.g., stair descent). Another disadvantage is that requiring an additional sensor outside of the exoskeleton sensor suite and interface area is not ideal from an exoskeleton designer’s perspective. Instead, we utilized the user’s hip joint position from the encoder. We marked the user’s maximum hip extension (corresponding to toe-off) as 0% of the gait cycle and labeled the data correspondingly. Similar to our previous approach, we converted the labeled gait phase percentage into Cartesian coordinates to avoid discontinuity in the boundary condition of toe-off (sudden drop from 100% to 0%), as this would be detrimental to the model’s learning and evaluation.

E. Offline Model Optimization

Two deep neural networks were explored for optimizing our gait phase estimator. The first was a convolutional neural network (CNN) and the second was a long-short term memory (LSTM) Network. These two networks were specifically chosen for our model optimization as each network has its own strengths in solving the gait phase estimation problem. The CNN is a powerful deep learning technique where feature information (which is hand-engineered in a conventional machine learning approach) is extracted inherently within the neural network architecture, and the model is quick to train [23]. The LSTM is a recurrent neural network-based approach where the estimated variables contribute to the network’s memory (leveraging the sequential nature of the input data) and are utilized in the estimation of the next time step [24]. To make a fair comparison between the two models, we ensured that the space of tunable hyperparameters (e.g., the number of nodes and layers) was kept similar. A variety of hyperparameter configurations were compared when optimizing each model, where model performance was evaluated using 5-fold cross-validation for each subject (each validation fold consisted of all five locomotion modes). To ensure that the gait phase error was evaluated accurately during the transition from one gait cycle to the next, where 100 and 0 represent the same value, we used an angular similarity metric by computing the cosine distance between the predicted and the ground truth Cartesian coordinates. The root mean square error (RMSE) of each stride was then computed as the percentage representation of the root mean square of the angular similarity metric over the gait cycle.

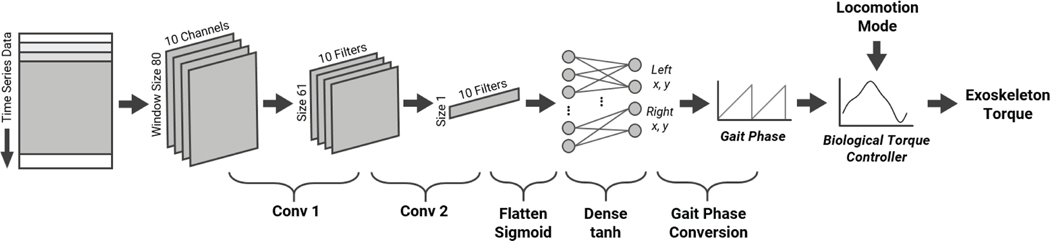
We leveraged the bilateral nature of the hip exoskeleton by fusing sensor data from both joints to increase the overall gait phase estimation accuracy [25]. The fully optimized CNN was trained using a stochastic gradient descent (SGD) optimizer with a learning rate of 0.01 and a batch size of 128, iterating over a maximum of 200 epochs. For all hyperparameters, we have validated our model performance on the extreme cases (i.e., values outside of our hyperparameter range) to ensure that our optimized parameters did not fall into local minima. Early stopping was used on a hold-out validation set during final training to avoid overfitting with stopping criteria based on the change in validation loss. The model had a data input size of 10 channel values (left/right hip position/velocity and trunk IMU) for every time step of 5 ms with a window size of 80 data samples (Fig. 3). The first layer consisted of a batch normalization, where the input values were normalized to a zero mean and unit variance. The second layer consisted of a 1D convolution of 10 filters striding temporally, where each filter had a kernel size of 20. The third layer was another 1D convolution of 10 filters, where each filter had a kernel size of the previous layer’s window size and compressed the data into a single row vector (representing the extracted feature information). A sigmoid activation function was applied to this vector and passed the data to a fully connected dense layer with a tanh activation function. The final output of the CNN consisted of 4 values (x and y Cartesian coordinates for each leg), where the gait phase conversion was applied using Equation (3).

Fig. 3.

Locomotion mode independent gait phase estimation strategy using a convolutional neural network. Time series data from the exoskeleton is read with defined window size. Two convolutional layers with an additional fully connected dense layer map the raw data to the corresponding gait phase. The converted gait phase along with locomotion mode information are utilized as inputs to the biological torque controller.

$$gaitphase=\left(\left(ta{n}^{-1}\left(\frac{y}{x}\right)+2\pi \right)mod2\pi \right)\times \frac{100}{2\pi }$$ (3)

Similar to the CNN, the LSTM was optimized using a standard model architecture and hyperparameter sweep. The fully optimized LSTM was trained using an SGD optimizer with a learning rate of 0.01 and a batch size of 128, iterating over a maximum of 100 epochs with early stopping. The final LSTM had a data input size of 10 channel values with a window size of 60 data samples. The architecture consisted of a batch normalization layer, followed by an LSTM layer consisting of 60 LSTM cells with a tanh activation function and a hidden state size of 20. The output hidden state of the final cell in the LSTM layer was then passed down to a fully connected dense layer with a tanh activation function, where the final output had 4 values representing each leg’s gait phase in Cartesian coordinates. Similar to the CNN, the gait phase conversion Equation (3) was used to calculate the final gait phase percentage.

Overall, the optimized model performances were nearly the same between the CNN and LSTM (Section IV-A). Given that the LSTM had a longer training time, as it requires to be processed sequentially, we chose to use the CNN for real-time implementation. For real-time inference, we trained an optimized, user-dependent model for each subject using data from all 5 trials. The trained model configuration and weights were saved to an hd5 file.

III. Real-Time Inference Validation

A. Online Inference Deployment

The online inference was performed on the Jetson using Keras [26] with a TensorFlow backend [27]. We ran a Python script that used the CNN model and weights for the current subject from the saved hd5 file. The Jetson was connected to the exoskeleton using TCP/IP, where a static buffer was sized equally to the CNN model’s window size. The Jetson received the mechanical sensor data, computed an estimate of the user’s gait phase, and communicated the estimate back to the exoskeleton at 200 Hz. The estimated gait phase was then used as an input to the biological torque controller.

B. Human Subject Experiment

We evaluated the performance of the gait phase estimator on the same ten subjects that participated in the initial data collection on a separate day. All subjects were asked to walk with the exoskeleton at their preferred walking speed across the terrain park. Each subject walked 3 circuits along the same path as the training data collection, with the hip assistance generated using either the baseline TBE method or the optimized ML model (total of 6 circuits). The corresponding torque profile for each locomotion mode was generated based on the estimated gait phase from the CNN or TBE, and the locomotion mode was input to the exoskeleton manually by the experimenter during walking (locomotion mode input was only utilized to generate a relevant torque profile for each mode). For all trials, the gait phase estimates and all mechanical sensor data were recorded. The performance metric for the model was the gait phase estimation RMSE. The model was evaluated within each steady-state locomotion mode and during a transition gait cycle between two locomotion modes (e.g., one gait cycle that includes LG and RA).

C. Statistical Analysis

To evaluate the model performance across all terrain conditions, we conducted a two-way repeated measures analysis of variance (ANOVA) with an α value set to 0.05. Additionally, a Bonferroni post-hoc correction for multivariate analysis was utilized to compute the statistical difference between each controller and terrain condition (Minitab 19, USA).

IV. Results

A. Model Optimization and Online Performance

The final model from an offline model optimization had an average gait phase estimation RMSE across all subjects of 4.37 ± 0.68% and 4.41 ± 0.67% for the CNN and the LSTM, respectively. Using the optimized CNN-based architecture for the online performance validation, the ML model on average had a 71.08 ± 5.72% lower gait phase estimation RMSE than the TBE method, across all subjects (p < 0.05, Fig. 4A). For each specific mode, the ML model on average had a 75.17 ± 6.79%, 50.0 ± 20.6%, 74.86 ± 7.41%, 61.59 ± 13.78%, and 67.07 ± 5.91% lower gait phase estimation RMSE than the TBE method across all subjects, for LG, RA, RD, SA, and SD, respectively (p < 0.05, Fig. 4B). Across all locomotion modes, the ML model on average had a 62.62 ± 5.62% lower corresponding commanded torque RMSE than the TBE method, across all subjects (p < 0.05, Fig. 5).

Fig. 4.

(A) Overall gait phase estimation performance for the CNN-based ML model (blue) and the time-based estimation method (red). (B) Gait phase estimation performance for each specific locomotion mode. (C) Gait phase estimation performance during a transition gait cycle. Error bars represent ± 1 standard deviation. Asterisks indicate statistical significance (p < 0.05).

Fig. 5.

Time series plot of the real-time gait phase estimation using (A) the CNN-based ML model and (B) the time-based estimation method from a single subject with a gait phase estimation error very near the average of the 10 subjects. Each segment in the graph represents a single gait cycle within each locomotion mode (steady-state and transition). The top subplot represents the estimated gait phase and the bottom represents the corresponding exoskeleton torque commanded to the user. The grey line for the gait phase and torque profile indicates the ground truth trajectory with a corresponding gait phase estimation and torque RMSE within each locomotion mode type.

B. Transition Gait Cycle Analysis

During transition gait cycles, the ML model on average had a 61.48 ± 13.04%, 79.20 ± 6.29%, 66.48 ± 9.60%, and 56.21 ± 5.07% lower gait phase estimation RMSE than the TBE method for RA, RD, SA, and SD transitions, across all subjects, respectively (p < 0.05, Fig. 4C). During a transition gait cycle, the ML model on average had a 34.33 ± 11.02% lower corresponding commanded torque RMSE than the TBE method, across all subjects (p < 0.05).

V. Discussion

The key contribution of our study was to develop a gait phase estimator robust to variations in the user’s locomotion mode for real-time control of a robotic hip exoskeleton. Overall, our ML model was able to accurately estimate the user’s gait phase in real-time without additional information about the user’s locomotion mode (except for manual keyboard input for the torque controller) and provide corresponding hip assistance to the user across all locomotion modes (Fig. 5). Not only did our ML model outperform the TBE method during the transition gait cycle by reducing the error rate by 67%, but it also had better performance compared to the TBE method within each specific mode, reducing the error rate by 69%. One of the main factors that induced a greater error in the TBE method was the false peak detection (especially for descent modes where the hip joint trajectory is not smooth), which incorrectly reset the user’s estimated gait phase to 0% during the stride. Additionally, changes in walking speed resulted in inaccurate stride duration, causing the TBE method to either lead or lag in gait phase estimation. Conversely, the ML model was able to dynamically adapt to the user’s walking speeds and locomotion modes.

For the TBE method, LG, RA, and SA modes generally had a better performance than the RD and SD modes across all subjects. These results were expected since the hip kinematics for LG and ascent modes included a single maximum in hip extension angle in contrast to the descent modes, which included multiple local maxima in hip extension angle, leading to false peak detection. On the other hand, the ML model did not show any significant performance differences between locomotion modes (ML’s worst performing SD had 1.6% lower RMSE than the TBE’s best performing SA). This exciting result illustrates the power of a deep learning approach, where the estimator was able to generalize the kinematic information at the hip across different locomotion modes to accurately estimate the user’s gait phase, regardless of any local noise induced during individual modes (RD and SD).

The TBE method estimated the user’s gait phase with a better performance during a transition from level to ascent modes compared to descent modes by 46%. This was because the user’s stride duration value (from LG to RA or SA) was updated in an increasing direction. In such cases, the exoskeleton torque command may have a shifted onset timing (e.g., assistance being early), which is not a critical problem as the user is still moving in the same direction as the exoskeleton. However, transitions from level to descent modes can be problematic. Descent mode transitions cause the user’s stride duration value (from LG to RD or SD) to decrease, which can cause the exoskeleton to generate delayed assistance. In such scenarios, the delayed torque command caused a false peak that resisted the user’s movement. During our experiment, this phenomenon caused the controller to oscillate between stance and swing states after mode transition, causing the system to reach instability (the exoskeleton movement was out of sync with the user). However, this problem was not observed in any of our ML model cases, as the ML model learned the user’s gait dynamics during different locomotion mode transitions from the training data set.

The torque profile tracking results from the TBE method (Fig. 5B) clearly indicate that this method is inadequate for usage in an overground situation, as the torque profile generated using this method was sub-optimal to the user (if the exoskeleton is out of sync it will impede the user’s movement). Our results showed that the overall gait phase estimation error corresponded to a commanded torque RMSE of 2.08 Nm for the TBE method. While our exoskeleton’s commanded torque range was within the boundary of the user’s physical capability, this error could be detrimental to the user if the exoskeleton, using the TBE method, generated a greater joint torque than the user could resist. In contrast, our ML model showed a commanded torque RMSE of only 0.77 Nm across all locomotion modes, illustrating its ability to safely determine the exoskeleton assistance for the user (seen visually in Fig. 5A).

Our ML model showed comparable performance to our previous work [11], where we were able to achieve a gait phase estimation error rate of 4%. The key difference is that our previous model was only evaluated on a treadmill, whereas our new approach expanded its application to different locomotion modes and was able to achieve real-world usefulness at the cost of 1% gait phase estimation accuracy. This was possible by leveraging the end-to-end CNN approach to extract additional feature information instead of the conventional manual feature engineering approach [28]. Currently, the state-of-theart method in estimating the user’s gait phase is to use the non-user-specific adaptive oscillator approach, which has a gait phase estimator error rate of 3% [29], [30]. However, this method was only evaluated during steady-state, treadmill walking, which is not representative of real-world locomotion. Moreover, this method requires an additional sensor to be placed outside the device interface region, such as a capacitance sensor around the shank. Considering that our ML model only utilized the sensors internal to the exoskeleton (hip encoder and trunk IMU), our model is more promising from an exoskeleton design perspective.

One limitation of the study is that the developed ML model was trained on a user-specific basis. However, our user-dependent approach only required approximately 5 minutes of data collection, which is not unreasonable to expect from a novel exoskeleton user. Another limitation is that our study did not showcase the ability of the network to generalize to environments and circumstances beyond the training data set (e.g., different ramp slopes and stair heights). However, our main objective in this work was to demonstrate that deep learning techniques could be used to estimate gait phase across locomotion modes. Future directions based on our findings will focus on developing a model that can generalize its performance to unseen conditions (different user and environmental settings) and evaluating its effect on human outcome measures.

VI. Conclusion

Our CNN-based gait phase estimator effectively characterized the user’s gait phase across multiple locomotion modes and transitions online. Not only did our model reach state-of-the-art performance, but it was also able to generalize to other terrain settings. Our results showed great promise in translating laboratory-based exoskeleton technology to a more realistic setting where the user can dynamically receive assistance regardless of locomotion mode. Future directions from this study will focus on developing and evaluating human outcomes using a user-independent gait phase estimator during multimodal locomotion.