Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Sep 20;125(38):21077–21086. doi: 10.1021/acs.jpcc.1c06835

Exploring Librational Pathways with on-the-Fly Machine-Learning Force Fields: Methylammonium Molecules in MAPbX3 (X = I, Br, Cl) Perovskites

Menno Bokdam †,‡,*, Jonathan Lahnsteiner †, D D Sarma §
PMCID: PMC8488963  PMID: 34621459

Abstract

graphic file with name jp1c06835_0012.jpg

Two seemingly similar crystal structures of the low-temperature (∼100 K) MAPbX3 (X = I, Br, Cl) perovskites, but with different relative methylammonium (MA) ordering, have appeared as representatives of this orthorhombic phase. Distinguishing them by X-ray diffraction experiments is difficult, and conventional first-principles-based molecular dynamics approaches are often too computationally intensive to be feasible. Therefore, to determine the thermodynamically stable structure, we use a recently introduced on-the-fly machine-learning force field method, which reduces the computation time from years to days. The molecules exhibit a large degree of anharmonic motion depending on temperature: that is, rattling, twisting, and tumbling. We observe the crystal’s “librational pathways” while slowly heating it in isothermal–isobaric simulations. Marked differences in the thermal evolution of structural parameters allow us to determine the real structure of the system via a comparison with experimentally determined crystal structures.

Introduction

The crystal structure of hybrid halide perovskites is a topic of study that has surfaced several times in the past four decades. X-ray powder diffraction experiments of Weber et al. on methylammonium (MA)-PbX3 with halogens X = {I, Br, Cl} have established a high-temperature cubic phase for all X.1 A perovskite structure is formed by PbX6 corner-sharing octahedra enclosing the MA molecules. In later years, the low-temperature phases and librational modes of the MA molecule at various temperatures were studied.2−6 The development of high-efficiency solar cells based on these perovskites sparked a rival of interest in its structure characterization.7−10 It was shown by high-quality powder neutron-diffraction experiments9 that the low-temperature orthorhombic phase of MAPbI3 actually belongs to the Pnma space group. This is the space group that was also determined for MAPbBr311 and MAPbCl3.12 The potential for optoelectronic applications raised new questions that are all (in)directly related to the atomic structure: the effect of MA rotation on charge dynamics,13,14 dynamic or permanent deformations of the PbX6 octahedra,15−18 the extent of electron–phonon coupling,19−21 and the Rashba effect,22−27 to name a few. Considerable progress has been made, but consensus has not always been achieved. This is in part the result of differences in interpretation of the local microscopic structure. The disorder, be it static or dynamic, of the molecular C–N axes is a well-known problem for diffraction techniques that makes it difficult to determine their precise orientation.18,28 First-principles (FP) methods such as density functional theory (DFT) have shown to be very useful for the determination of the crystal structure by augmenting the experimentally resolved inorganic framework with the ordering of the molecules.29−37 However, even though commonly used density functional approximations (DFAs) have the required chemical accuracy,38 their computational complexity prohibits the large length-and-timescale molecular dynamics (MD) calculations necessary to resolve the free energy landscape and thereby the finite-temperature crystal structure.31 We will use the on-the-fly machine-learning force field (MLFF) method,39,40 which makes it possible to explore the full diversity of atomic structures while going through the entropy-driven phase transformations in hybrid perovskites. This method substantially reduces the computational cost while retaining near-FP accuracy. Recently, it has been shown to be capable to resolve the orthorhombic–tetragonal (Ort–Tet) and tetragonal–cubic (Tet–Cub) phase transitions in MAPbI3 and the inorganic halide perovskites CsPbX3 in good agreement with experiment.39 Furthermore, it can be systematically extended to describe mixed MAxFA1–xPbI3 perovskites under isothermal–isobaric conditions.41

The starting points of our search for the low-temperature (∼100 K) orthorhombic structure of MAPbX3 are two seemingly similar but distinctly different structures: sA and sB. They have the same lattice vectors and inorganic coordinates but a different molecular ordering pattern, as sketched in Figure 1. We have labeled the lattice vectors such that the molecules lie in the ab-plane. sB is created out of sA by an in-plane rotation of half of the molecules by 180°, as indicated by the curved arrows. Note that in both arrangements, the neighboring molecules in the c-direction (not shown in the figure) are antiparallel. These structures have been prepared in a 2 × 2 × 2 supercell such that it accommodates the (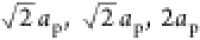Inline graphic) basis of X = I, Br as well as the (2ap, 2ap, 2ap) basis of X = Cl, where ap is the pseudocubic lattice constant of the parent Pm3̅m cell.12 The molecules in the often-referenced experimental (Pnma) structures for X = I, Br, and Cl of refs (8)(11), and (12) are arranged as in the sB, sA, and sA configuration, respectively. Other experimental works did not distinguish between these two arrangements7,42 since refinement of the model structure by permuting N and C with respect to the measured diffraction spectra does not lead to significant improvements of the fit.18 To date, even for the extensively studied MAPbI3 perovskite, different studies report opposite arrangements: sA32,43,44 and sB.29,34,45,46 This is unexpected because if we focus only on the dipole moment of the MA molecule and compute the total electrostatic energy in the point-dipole approximation, then the sB pattern is clearly favored. This pattern shows a closer resemblance to the “head–tails” ground state of a point-dipole model.47

Figure 1.

Figure 1

Open in a new tab

Initial low-temperature crystal structures of MAPbX3 with molecules in the sA and sB arrangement. Lattice vectors and Pb,X atom coordinates are adapted from refs (8)(11), and (12). Only one of the two layers of molecules in the ab-plane is shown. Molecules in the second layer (into the paper) are antiparallel to the first. sB is created by rotating half of the molecules of sA by 180° in the ab-plane. The distortions of the PbCl6 octahedra are indicated in the top right figure by the long (green) and short (orange) Pb–Cl bonds.

In this work, we will analyze the “librational pathways” of the MA molecules and PbX6 octahedra in MAPbX3 and use them to identify the most representative low-temperature orthorhombic structure. We sample structures of the crystal by slowly heating up two plausible low-temperature structures (sA and sB) in isothermal–isobaric MD simulations. Structures on the explored pathways through the structural phase space are thermodynamically linked to the starting configuration and result in marked differences in lattice and order parameters that are compared to temperature-dependent diffraction studies.

Computational Details

The DFT calculations are performed with the projector-augmented wave method,48 as implemented in the VASP code49,50 using the metagradient-corrected SCAN51 DFA, which has shown good performance when compared to high-quality many-body perturbation theory reference calculations.38 A plane-wave basis with a cutoff of 350 eV, Gaussian smearing with a width of 10 meV, and 4 (I, Br) or 8 (Cl) k-points of the Γ-centered 2 × 2 × 2 Monkhorst–Pack grid are set, which suffice to obtain the required accuracy of the calculations.36 The computed lattice parameters as a function of temperature should (qualitatively) agree with experiment over the whole temperature range. Therefore, by not limiting the study to a 0 K DFT-based relaxation of the internal energy, biases related to the chosen DFA can be detected.38 Before starting the MD simulations, the starting structures of Figure 1 were shortly relaxed by a conjugate gradient algorithm.

MLFFs are trained during MD simulations with the VASP based on calculated total energies, forces, and stress tensors for automatically (on-the-fly) selected structures in the isothermal–isobaric ensemble. This approach is described in detail in refs (39) and (40). In short, a Bayesian error estimation of the predicted forces is used to select either DFT or MLFF forces to propagate the structure in time (tn → tn+1). Whenever the predicted errors exceed the threshold, a new reference structure is picked up, a DFT calculation is performed, and the coefficients of the MLFF are reoptimized. In Figure 3c,f, a “density-of-states”-like function of the temperature (note, equivalent to simulation time) shows when in the training MD most DFT calculations were performed. It is calculated using 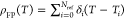Inline graphic, where δ(T) is a Lorentzian function. This function is normalized to the total number of DFT reference structures picked up in training, Nref = ∫ρFP(T) dT. The automatically picked-up reference structures form a minimal training database (containing total energies, forces, stress tensors, and atomic coordinates) that is well spread over the available structural phase space. We have shared this database via the 4TU.DataBase repository61 to encourage development of ML potentials based on minimalistic data sets.

Figure 3.

Figure 3

Open in a new tab

On-the-fly heating MD at 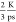Inline graphic of MAPbBr3 starting from the sA and sB arrangement. a, b (a,d) and c (b,e) lattice parameters (blue/red/green) of the orthorhombic system and their running averages (thick lines, window size 5 K). Experimental reference data from ref (11): lattice parameters (symbols) and transition temperatures (thick vertical lines). (c,f) Density ρFP(T) of performed DFT calculations as function of temperature (black line).

A variant of the GAP-SOAP52,53 method is used as a descriptor of the local atomic configuration around each atom. Within a cutoff of 7 Å, a two-body radial probability distribution ρi(2)(r) is built, as well as three-body angular distribution ρi(3)(r,s,θ) within a cutoff of 4 Å. The atomic coordinates are smeared in the distributions by placing Gaussians with a width of 0.5 Å. The obtained distributions are projected on a finite basis set of spherical Bessel functions multiplied with spherical harmonics. The Bessel functions are of the order 6 and 7 for the radial and angular part, respectively. Only the angular part has a maximal angular momentum of lmax = 6. The coefficients of the projections are gathered in the descriptor vector Xi. A kernel-based regression method54 is applied to map the descriptor to a local atomic energy. The similarity between two local configurations is calculated by a polynomial kernel function: 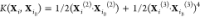Inline graphic.

For each of the six on-the-fly heating trajectories, a Supplementary Movie was generated. A running average (window size of 25 K) over each atomic coordinate is computed to smoothen out high frequency movements. At high temperature, where the molecules rotate fast, this contracts the atoms in the molecule to a point. The movies show the 2 × 2 × 2 supercell under periodic boundary conditions and from two perspectives (from the top and side).

Results and Discussion

To introduce the librational pathways of MAPbX3, we will illustrate them by weighted sums of pair distribution functions (PDFs) in Figure 2. The PDF for the atom types α and β is defined as

graphic file with name jp1c06835_m004.jpg

where ri and rj are the coordinates of the Nα and Nβ atoms, rij = ri − rj, V is the volume of the simulation box, and ⟨ ⟩ denotes the ensemble average. In ginorganic(r), the pairs of framework components Pb–X, X–X, Pb–Pb are included, and only the C–N pairs of the MA molecules are included in gC,N(r). For all halides, X, we see that ginorganic(r) retains most of its structure throughout the whole temperature range and that gC,N(r) shows a transition whereby part of the order is lost. The intramolecular part (r ≈ 1.5 Å) remains intact, but the intermolecular pairs show dual peaks merging into a single broad peak centered around the nearest-neighbor distances of the consecutive cubic unit cells, that is, 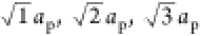Inline graphic. This is the result of the unfreezing of the molecules, whereby they reorient (C4) rapidly.4 Around room temperature, neighboring MA molecules are still dynamically correlated to their neighbors.34 The differences in the DSF between the halides X are, among other things, related to different Pb–X bond lengths and to the relative orientation of the molecules in the low-temperature phase. As we will show hereafter, the thermodynamically stable molecular configurations at low temperature (sA or sB) depend on the halide type X.

Figure 2.

Figure 2

Open in a new tab

Combined pair distribution functions of the inorganic (Pb,X) components compared to gC,N(r) in the MAPbX3 (X = I, Br, and Cl) perovskites for increasing temperatures with steps of 20 K. The crystals librate from the initial structures I-sB, Br-sA, and Cl-sA. Vertical dashed lines indicate typical bond lengths (left) and neighbor distances based on the lattice constant a in the cubic phase (right).

The starting structures (Figure 1) are slowly heated at a rate of 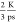Inline graphic using DFT-based MD with a Langevin thermostat and a time step of 2 fs. The PDFs at different temperatures have been obtained by partitioning the resulting trajectory in parts of equal length. In the NPT ensemble, all lattice degrees of freedom are allowed to change, as shown for MAPbBr3 in Figure 3. The two plots correspond to the heating trajectories starting from the sA and sB structures. Thermal fluctuations in structural parameters are smoothed by applying running averages. To accelerate the MD, a MLFF is trained on-the-fly, as described in refs (39) and (40). The algorithm switches between MLFF and DFT forces based on the predicted error of the MLFF. Structural reference configurations to train the MLFF are automatically picked up and by construction lie outside the already “learned” part of the phase space. This can be seen by the sharp increase in the density of FP calculations (ρFP(T)) shown in Figure 3c,f. The on-the-fly algorithm decides to do a large number of DFT calculations in the region between 150 and 170 K, that is, when the system undergoes the Ort–Tet phase transition. The total number of DFT reference structures picked up in training, Nref = ∫80280ρFP(T) dT, are Nref = 933 and NrefsB = 1074. This transition temperature is expected to be retarded because the system is out of thermal equilibrium as a result of the still considerable heating rate. Even though, the agreement with the experimental lattice parameters shown by the symbols in Figure 3 is remarkable. We show that the structural transformation and the related librational pathways of the molecules and octahedra (see Supplementary Movies) are accurately described in the on-the-fly heating MD. This opens up the possibility of exploring many different perovskites because only ∼1.000 out of the total of 150.000 MD steps per heating run were DFT calculations. This reduces the computing time from years to days.

Librational Pathway Analysis

Figure 3 indicates that apart from a small step in the c lattice constant in the sB case, both trajectories qualitatively and quantitatively agree with the experimental data. This means that the lattice parameters alone provide insufficient information to select either the sA or the sB as the thermodynamically stable low-temperature structure. Therefore, we analyze the structural motif presented by the atomic coordinates in the six heating trajectories. First, we solely extract the orientation of the molecular C–N axes in time. The total electrostatic energy (Hlr) corresponding to the dipole moments of the molecules is calculated.47 In short, this point-dipole model assumes a fixed dipole moment on all molecules, no screening, and includes all dipole–dipole interactions up to the third nearest neighbor. In Figure 4a, Hlr is plotted as a function of temperature for the three halides starting from the sA (black lines) and sB (red lines) configurations. The sB configuration is clearly lower in energy. With increasing temperature, the molecules flip/reorder and the stable arrangement is broken down, eventually leading to a disordered state with Hlr = 0.55 For X = I, the sA pattern flips to the stable sB pattern before reaching the Ort–Tet phase transition, which shows that the initial structure was out of equilibrium. However, for X = Br and Cl, the pattern remains largely frozen in until the phase transition. The sA configuration can only be stable at low-T if either a potential energy contribution arising from the inorganic framework or the entropy compensates this internal energy difference.

Figure 4.

Figure 4

Open in a new tab

Energies during the heating trajectories of the MAPbX3 perovskites. (a) Electrostatic energy of the molecular dipoles in the point-dipole approximation (Hlr) and (b) DFT internal energy differences (ΔE). (running averages over 25 K).

The DFT/MLFF-calculated internal energy (E) is shown in Figure 4b as the energy difference (ΔE = EsA – EsB) between the heating trajectory starting with the sA and the sB structure. At low temperature and ambient pressure, the volume and entropy contributions to the Gibbs free energy are small, and a sizable positive/negative ΔE would indicate that the sB/sA configuration is favored, respectively. For MAPbCl3, it is clear that the sA structure is favored even though its electrostatic energy in the dipole model was unfavored. Above ∼175 K, the difference between the two initial configurations has been lifted by thermally induced structural rearrangements. For MAPbI3 and MAPbBr3, the situation is less clear; at low temperature, ΔE is positive; however, it is of the size of the fluctuations. Even for the fully DFT-relaxed (0 K) structures, ΔE values are small: 33, 3, and −72 meV/formula unit for I, Br, and Cl, respectively. Increasing the precision of the calculation by doubling the k-point grid density and applying the tetrahedron method56 results in 33, −6, and −75 meV/f.u., respectively. This indicates that, especially for MAPbBr3, we cannot distinguish sA from sB based on the internal energy alone.

The changes of the structural motif as a function of the temperature are compared in Figure 5 and in Supplementary Movies. Order parameters describing the interoctahedral (O) and intermolecular (M) order are shown for all heating trajectories in Figure 5a. The M/O order parameters are based on the dot products of X–Pb–X/C–N connection vectors located on nearest neighboring sites. A detailed description can be found in refs (39) and (47). Looking at M for I-sA, we see that the molecular ordering pattern rapidly changes starting from M120K = (0.9,0.7,0.7) and transforming to the same order observed for I-sB M160K = (0.9,0.3,0.3), in agreement with the previously seen change in Hlr. At the same time, the interoctahedral order parameter for the inorganic framework, O, changes only little. The breakdown of the initial molecular order occurs at a lower temperature in the Br case and coincides with the Ort–Tet phase transformation. This shows that the sA and sB molecular orders are more energetically competitive in orthorhombic X = Br than in I and that an additional measure is required to determine the stable arrangement. The O values for the experimental low-temperature structures indicated by the circles in Figure 5a provide this measure. Based on their comparison to the simulation, the Br-sA is the stable low-temperature orthorhombic structure.

Figure 5.

Figure 5

Open in a new tab

Heating trajectories of MAPbX3 starting in the sA and sB configuration. (a) Structural order parameters for the octahedra (O) and molecules (M). The red line shows the classified perovskite crystal based on O. (b) Pseudocubic lattice constants refined in the classified phase (running averages over 25 K). The solid circles represent (a) the O values for the experimental low-temperature structures8,11,12 and (b) experimental lattice parameters.11,12,42 Note that the experimental Br O lies outside the scale of the graph (a) at 11 K.

To automatically classify the instantaneous crystallographic phase of all structures within the MD trajectory, we applied a new approach based on the O order parameter. This allows, for example, to still assign the orthorhombic phase to a structure that is strained in a box with a ≈ b ≈ c. Whenever the variance of the components of O is below a threshold, it is classified as Cub, and otherwise, it is Ort or Tet. We can then differentiate between the last two by counting the number (1 → Ort, 2 → Tet) of components larger than their mean value. The red line in Figure 5a shows the result of this phase classification. Note that no Tet phase in MAPbCl3 is recognized. This could be caused by a very small temperature window in which the Tet phase is stable or that the c/a ratio is too small to be noticed in the supercell.

Lattice parameters as a function of temperature are shown in Figure 5b. The parameters are refined in the unit cell corresponding to the classified phase and converted to pseudocubic lattice parameters (ap). Experimentally obtained parameters are shown by the circles. Surprisingly, the plots for MAPbBr3 and MAPbCl3 show good to very good agreement with the experiment. Especially for MAPbI3, we notice the effect of our limited MD setup, suppressing the Tet phase on the T-axes. From our previous study, we know that this can be improved with a lower heating rate and by applying a larger 4 × 4 × 4 supercell. Still, it is noteworthy that under the same computational settings, the Ort–Tet phase transition becomes more retarded, going from Cl, Br, to I.

Combining all the above presented analysis leads to the favored initial configurations, I: sB, Br: sA, and Cl: sA. These configurations are highlighted by the colored rectangles in Figure 5.

Training System Size Dependence

The PDFs in Figure 2 are plotted beyond half of the simulation box width since the 2 × 2 × 2 supercell has an average width of 2ap. They are computed in 4 × 4 × 4 supercells, which are created by replicating the original 2 × 2 × 2 cell, enabling us to sample the PDF on the [0, 2ap] domain. These results are compared to a training run performed with a 4 × 4 × 4 supercell. Specifically, we have made a test for MAPbBr3 starting in the sA configuration and applied the same on-the-fly training directly on the 4 × 4 × 4 supercell. In this supercell, the k-points of the k-grid (applied with the 2 × 2 × 2 supercell) all fold down on the gamma point. For computational tractability, we slightly lowered the plane-wave cutoff from 350 to 300 eV and retrained the 2 × 2 × 2 cell with the same cutoff for a fair comparison. The smaller plane-wave basis results in higher Pulay stress, which slightly affects the volume but does not qualitatively change the crystal structure.36

Figure 6 shows ginorganic(r) and gC,N(r) for the standard supercell and the 8 times larger cell. The ginorganic(r) of the two systems are almost identical. The main deviations in gC,N(r) are the result of a different temperature at which the system switches from the Ort to Tet phase. This is to be expected for simulations with finite system size. The MD trajectory is chaotic, and the transition does not occur at the same temperature even when the initial conditions are the same. This very good agreement indicates that the applied 2 × 2 × 2 supercell is large enough to capture the crystal symmetry. This is in agreement with a fully ab initio MD study of the system size dependence of MAPbI3 going up to the 6 × 6 × 6 supercell.34

Figure 6.

Figure 6

Open in a new tab

Influence of the supercell dimension. PDF of the inorganic (Pb and Br) components (top) and the C and N pairs (bottom) in MAPbBr3 obtained during on-the-fly heating MD in a 2 × 2 × 2 and 4 × 4 × 4 supercell. Increasing temperatures shown with steps of 40 K.

The accuracy of the MLFF model over the entire collected data set of structures, which includes three different perovskite phases is very high. The DFT reference energy (UDFT) and predicted MLFF energy (UMLFF) for the test systems are plotted in Figure 7 and show a clear linear relation over a large energy range. Note that both point clouds nicely overlap, whereby the larger variations are, as would be expected, observed for the smaller supercell. The overall root-mean-square (rms) error on the energy is only 1.7 and 0.88 meV/atom for the MLFF trained on the 2 × 2 × 2 and 4 × 4 × 4 supercells, respectively. This is small and of the same order of magnitude of state-of-the-art ML potentials (kernel-regression,57 neural networks,58 etc.). Furthermore, for the two system sizes, the errors in the force are 0.081 and 0.077 eV/Å and 1.1 and 0.46 kB in the stress. These error estimates are typical for all MLFFs presented in this work. For instance, the rms errors in the energy of the six MLFFs (X = I, Br, Cl/sA or sB) are all in the 1.2–1.8 meV/atom range.

Figure 7.

Figure 7

Open in a new tab

DFT internal energies versus predicted MLFF energies for the structures in the MAPbBr3 training set obtained during on-the-fly heating MD in a 2 × 2 × 2 and 4 × 4 × 4 supercell.

Octahedral Distortions: Dynamic or Permanent?

The central question remains: why is the sA configuration more stable in MAPbCl3 and to a less extent in MAPbBr3 as compared to sB? Chi et al. have already shown that the PbCl6 octahedra are distorted.12 This polar distortion is highlighted in Figure 1 by the green and orange lines indicating the difference between two Pb–Cl bond lengths (3.02 and 2.73 Å) in the crystallographic a-direction and is in good agreement with our simulations. However, we find no noticeable distortion of the PbI6 and PbBr6 octahedra above 80 K, as shown in Figure 8, again, in agreement with experiments of refs (10)(11), however, opposite to the findings of refs (16) and (17) where a permanent octahedra distortion is found in MAPbBr3 around room temperature. In Figure 8a, the distribution of the Pb–X bond lengths as a function of temperature is shown. The heating trajectories were cut in parts of equal length, and all bond lengths in the a-direction were added to the distribution. The low-temperature distribution for Pb–Cl has two peaks. This distortion is neither observed when starting from the Cl-sB structure, nor when starting from the Br-sB or I-sA structures. The distribution is well described by a combination of two Gaussian distribution functions, 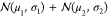Inline graphic. For Cl-sA, the mean values (μ) and the standard deviations (σ) as a function of temperature are shown in Figure 8b. These values have been obtained from a separate heating trajectory with the finished MLFF on a 4 × 4 × 4 MAPbCl3 supercell. The so-obtained distributions agree with Figure 8a and improve statistical accuracy. Experimentally determined bond lengths from refs (12) and (18) have been added to Figure 8b and agree within the standard deviation. In the simulations, a single Gaussian suffices above ∼175 K, that is, |μ1 – μ2| < (σ1 + σ2). At this temperature, the octahedral polar distortion is no longer observed on time average and the crystal is in the cubic phase. As for I and Br, instantaneous distortions of the octahedra do occur at these elevated temperatures.

Figure 8.

Figure 8

Open in a new tab

(a) Distributions of Pb–X bond lengths as a function of temperature. (b) Mean values (μ) and the standard deviations (±σ error bars) as a function of temperature for the Pb–Cl bond lengths. The experimental values from refs (12) and (18) are shown by the circles and squares, respectively.

The following scenario now becomes plausible, the sA ordered molecules are stabilized in the MAPbCl3 orthorhombic phase by an antiferroelectric striped pattern of dipolar octahedra in the a-direction. As argued in ref (12), the volume of the perovskite has to be sufficiently small to induce these distortions, whereby the “hard” MA deforms the “soft” octahedra. However, the striped pattern cannot be the only stabilization mechanism because no distortion is observed in Br-sA.

We would like to note that our “ensemble average” view on the structural model results in PDFs for MAPbBr3 that qualitatively agree with those obtained from X-ray diffraction experiments of ref (17). In Figure 9a, ginorganic(r) has been plotted on the same length scale as Figure 2 in ref (17), whereby the vertical dashed lines indicate the experimental peak positions. Starting from sA, we also do not observe any relevant structural change in the 150–280 K temperature range apart from thermal broadening of the peaks. However, our approach classifies tetragonal and cubic structures within this range and does not indicate that an orthorhombic structure would be a better fit throughout this temperature range. Starting from sB results in structural changes (indicated by *), in disagreement with the PDF of ref (17). This is another indication that the sB pattern is not the stable low-temperature structure. The different structural interpretation of the crystal at elevated temperatures becomes apparent in the H–X bonding, as shown by gH,X(r) in Figure 9b. We find a halogen-dependent first peak position. This finding is different from the 2.5 Å peak observed in the neutron PDFs of both MAPbBr3 and MAPbCl3.18

Figure 9.

Figure 9

Open in a new tab

PDF of the (a) inorganic components in MAPbBr3 and (b) gX,H(r) for increasing temperatures with steps of 20 K. Vertical dashed lines in (a) show the peak positions in the X-ray PDF of ref (17) and (b) the first peaks in the calculated gX,H(r).

MA C3 Dynamics

We would like to note that training of a very accurate MLFF for the hybrid perovskites is not fully completed by the here-performed single heating run. Precise values for phase-transition temperatures, c/a ratios, and so forth were not the aim of this work but can be obtained with an accurate MLFF which enables long MD trajectories on large supercells.39 Limits to the accuracy can be seen in the C3 torsion/rotation degree of freedom of the molecule, for example. Figure 10 shows the NH3 versus the CH3 group dihedral angle (ϕMA) of all MAs in MAPbBr3 in NPT ensembles with the finished MLFF. Torsion (ϕMA < 60°) unfreezes at ∼25 K,59 and also, rotations (ϕMA > 60°) occur around our starting temperature (80 K) of the on-the-fly training.

Figure 10.

Figure 10

Open in a new tab

Threefold dynamics of the NH3 versus the CH3 group. (a) Sketch of the angle ϕMA in the MA molecule. (b) ϕMA,i as a function of time for each of the eight molecules at 270 K. (c) Dihedral potential obtained by a Boltzmann inversion of the distribution (P) at 270 K. (d) Barrier heights as a function of temperature.

Figure 10b shows that ϕMA,i(t) of a single molecule shows step-like behavior, occasionally jumping between planes separated by 120° and is superimposed by a fast oscillation. For each of the eight molecules in the supercell, a probability distribution of ϕMA as in Figure 10c was made. We then calculate the C3 rotational energy barrier in the two MLFFs of MAPbBr3 (sA and sB) by a Boltzmann inversion of the distribution. A barrier was only assigned at a temperature T when the number of 120° rotations in the ∼100 ps long MD trajectories exceeded the number of molecules in the supercell. The error bars in Figure 10d correspond to ±σ, the standard deviation of the eight obtained barriers. The barrier is, within our statistical accuracy, temperature-independent and, surprisingly, different between sA and sB. It is tempting to conclude that the sA structure for Br affords a more facile C3 rotational degree of freedom compared to the sB structure within the orthorhombic phase. However, the difference should not persist in the high-temperature cubic phase, in which the MAs are orientationally disordered. This should be a warning that training is not yet complete and the MLFF still shows a bias depending on the initial conditions.

We are able to measure the barriers of a single molecule in vacuum in the same manner. The absence of a surrounding Pb–Br framework does not destabilize the molecule. Barriers obtained in this way are slightly lower than the DFT value of 105 meV for MA in vacuum. This value was calculated as the difference in internal energies of the optimized ϕMA = 0 and 60° molecule, for which all internal degrees of freedom were relaxed under the constraint of ϕMA. Using these two structures, the barriers for the Br-sA and Br-sB MLFFs are 78 and 89 meV, respectively.

Since both Br-sA and Br-sB show C3 rotations at temperatures below the Ort–Tet phase-transition temperature, we can conclude that the unfreezing of this motion does not drive it. This is in agreement with the findings of the computational study of Kieslich et al.60 This phase transition is driven by an increase in C4 configurational entropy of the molecules.4 This, however, does not preclude the possibility that entropy related to C3 dynamics is involved in this phase transition. Based on the observed initial condition dependence (sA or sB) of the barrier, we speculate that Br-sA is entropically stabilized by the C3 torsion/rotation degree of freedom of the molecule and thereby determines the orthorhombic structure below the phase-transition temperature.

Conclusions

In conclusion, we have shown that on-the-fly MLFFs are a very powerful tool in determining the atomic structure in dynamic, entropically stabilized solids. Already during the training-by-heating MD, important structural characteristics are qualitatively correct and even quantitatively useful. As a prime example, the low-temperature ordering pattern of MA molecules in MAPbX3 perovskites, which is not uniquely resolved by diffraction experiments, was studied. We determined the most likely structure by slow-heating DFT-based MD and analyzing the librational pathways. By comparing this analysis with reported temperature-dependent lattice parameters and refined structures, we show that the ordering of the molecules (sA or sB) in orthorhombic phases of MAPbBr3 and MAPbCl3 is similar (sA), while in MAPbI3, they are differently ordered (sB). This is unexpected since the sA pattern is energetically unfavorable when considering solely the intrinsic dipole moment of the MA molecules. The sA order induces a permanent structural distortion of the PbCl6 octahedra at low temperature, resulting in an antiferroelectric striped pattern in the crystallographic a-direction. In the higher-temperature cubic phase, this distortion is no longer observed in the ensemble average; instead, instantaneous dynamic distortions appear. No permanent distortion is observed in the PbBr, nor PbI, octahedra, even down to the lowest simulated temperature of 80 K. We have presented indications that the sA order in low-temperature, orthorhombic MAPbBr3 is stabilized by an entropic contribution to the free energy related to the C3 dynamics of the MA molecules. We hope that this paper will stimulate combined experimental and MLFF studies of the structure of many other complex dynamic solids.

Acknowledgments

M.B. and J.L. gratefully acknowledge funding by the Austrian Science Fund (FWF): P 30316-N27. Computations were partly performed on the Vienna Scientific Cluster VSC3 and on the Dutch National e-Infrastructure with the support of SURF Cooperative.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c06835.

  • On-the-fly heating trajectory for I-sA (MOV)

  • On-the-fly heating trajectory for I-sB (MOV)

  • On-the-fly heating trajectory for Br-sA (MOV)

  • On-the-fly heating trajectory for Br-sB (MOV)

  • On-the-fly heating trajectory for Cl-sA (MOV)

  • On-the-fly heating trajectory for Cl-sB (MOV)

  • DFT-SCAN-optimized (0 K) orthorhombic sA structure for MAPbI3 (CIF)

  • DFT-SCAN-optimized (0 K) orthorhombic sB structure for MAPbI3 (CIF)

  • DFT-SCAN-optimized (0 K) orthorhombic sA structure for MAPbBr3 (CIF)

  • DFT-SCAN-optimized (0 K) orthorhombic sB structure for MAPbBr3 (CIF)

  • DFT-SCAN-optimized (0 K) orthorhombic sA structure for MAPbCl3 (CIF)

  • DFT-SCAN-optimized (0 K) orthorhombic sB structure for MAPbCl3 (CIF)

The authors declare no competing financial interest.

Supplementary Material

jp1c06835_si_001.mov (7.7MB, mov)
jp1c06835_si_002.mov (6.6MB, mov)
jp1c06835_si_003.mov (5.9MB, mov)
jp1c06835_si_004.mov (8.4MB, mov)
jp1c06835_si_005.mov (5.8MB, mov)
jp1c06835_si_006.mov (5.6MB, mov)
jp1c06835_si_007.cif (8.2KB, cif)
jp1c06835_si_008.cif (8.2KB, cif)
jp1c06835_si_009.cif (8.3KB, cif)
jp1c06835_si_010.cif (8.3KB, cif)
jp1c06835_si_011.cif (8.3KB, cif)
jp1c06835_si_012.cif (8.3KB, cif)

References

  1. Weber D. CH3NH3PbX3, ein Pb(II)-System mit kubischer Perowskitstruktur / CH3NH3PbX3, a Pb(II)-System with Cubic Perovskite Structure. Z. Naturforsch., B: Anorg. Chem., Org. Chem. 1978, 33, 1443. 10.1515/znb-1978-1214. [DOI] [Google Scholar]
  2. Wasylishen R. E.; Knop O.; Macdonald J. B. Cation rotation in methylammonium lead halides. Solid State Commun. 1985, 56, 581–582. 10.1016/0038-1098(85)90959-7. [DOI] [Google Scholar]
  3. Poglitsch A.; Weber D. Dynamic disorder in methylammoniumtrihalogenoplumbates (II) observed by millimeter-wave spectroscopy. J. Chem. Phys. 1987, 87, 6373–6378. 10.1063/1.453467. [DOI] [Google Scholar]
  4. Onoda-Yamamuro N.; Matsuo T.; Suga H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II)†. J. Phys. Chem. Solids 1990, 51, 1383. 10.1016/0022-3697(90)90021-7. [DOI] [Google Scholar]
  5. Kawamura Y.; Mashiyama H.; Hasebe K. Structural Study on Cubic-Tetragonal Transition of CH3NH3PbI3. J. Phys. Soc. Jpn. 2002, 71, 1694–1697. 10.1143/jpsj.71.1694. [DOI] [Google Scholar]
  6. Mashiyama H.; Kawamura Y.; Kubota Y. The Anti-Polar Structure of CH3NH3PbBr3. J. Korean Phys. Soc. 2007, 51, 850–853. 10.3938/jkps.51.850. [DOI] [Google Scholar]
  7. Stoumpos C. C.; Malliakas C. D.; Kanatzidis M. G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. 10.1021/ic401215x. [DOI] [PubMed] [Google Scholar]
  8. Baikie T.; Fang Y.; Kadro J. M.; Schreyer M.; Wei F.; Mhaisalkar S. G.; Graetzel M.; White T. J. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 2013, 1, 5628–5641. 10.1039/c3ta10518k. [DOI] [Google Scholar]
  9. Weller M. T.; Weber O. J.; Henry P. F.; Di Pumpo A. M.; Hansen T. C. Complete structure and cation orientation in the perovskite photovoltaic methylammonium lead iodide between 100 and 352 K. Chem. Commun. 2015, 51, 4180–4183. 10.1039/c4cc09944c. [DOI] [PubMed] [Google Scholar]
  10. Sharada G.; Mahale P.; Kore B. P.; Mukherjee S.; Pavan M. S.; De C.; Ghara S.; Sundaresan A.; Pandey A.; Guru Row T. N.; et al. Is CH3NH3PbI3 Polar?. J. Phys. Chem. Lett. 2016, 7, 2412–2419. 10.1021/acs.jpclett.6b00803. [DOI] [PubMed] [Google Scholar]
  11. Swainson I. P.; Hammond R. P.; Soullière C.; Knop O.; Massa W. Phase transitions in the perovskite methylammonium lead bromide, CH3ND3PbBr3. J. Solid State Chem. 2003, 176, 97–104. 10.1016/s0022-4596(03)00352-9. [DOI] [Google Scholar]
  12. Chi L.; Swainson I.; Cranswick L.; Her J.-H.; Stephens P.; Knop O. The ordered phase of methylammonium lead chloride CH3ND3PbCl3. J. Solid State Chem. 2005, 178, 1376–1385. 10.1016/j.jssc.2004.12.037. [DOI] [Google Scholar]
  13. Gélvez-Rueda M. C.; Cao D. H.; Patwardhan S.; Renaud N.; Stoumpos C. C.; Schatz G. C.; Hupp J. T.; Farha O. K.; Savenije T. J.; Kanatzidis M. G.; et al. Effect of Cation Rotation on Charge Dynamics in Hybrid Lead Halide Perovskites. J. Phys. Chem. C 2016, 120, 16577–16585. 10.1021/acs.jpcc.6b06722. [DOI] [Google Scholar]
  14. Fabini D. H.; Siaw T. A.; Stoumpos C. C.; Laurita G.; Olds D.; Page K.; Hu J. G.; Kanatzidis M. G.; Han S.; Seshadri R. Universal Dynamics of Molecular Reorientation in Hybrid Lead Iodide Perovskites. J. Am. Chem. Soc. 2017, 139, 16875–16884. 10.1021/jacs.7b09536. [DOI] [PubMed] [Google Scholar]
  15. Beecher A. N.; Semonin O. E.; Skelton J. M.; Frost J. M.; Terban M. W.; Zhai H.; Alatas A.; Owen J. S.; Walsh A.; Billinge S. J. L. Direct Observation of Dynamic Symmetry Breaking above Room Temperature in Methylammonium Lead Iodide Perovskite. ACS Energy Lett. 2016, 1, 880–887. 10.1021/acsenergylett.6b00381. [DOI] [Google Scholar]
  16. Page K.; Siewenie J. E.; Quadrelli P.; Malavasi L. Short-Range Order of Methylammonium and Persistence of Distortion at the Local Scale in MAPbBr3Hybrid Perovskite. Angew. Chem., Int. Ed. 2016, 55, 14320–14324. 10.1002/anie.201608602. [DOI] [PubMed] [Google Scholar]
  17. Bernasconi A.; Malavasi L. Direct Evidence of Permanent Octahedra Distortion in MAPbBr3 Hybrid Perovskite. ACS Energy Lett. 2017, 2, 863–868. 10.1021/acsenergylett.7b00139. [DOI] [Google Scholar]
  18. Bernasconi A.; Page K.; Dai Z.; Tan L. Z.; Rappe A. M.; Malavasi L. Ubiquitous Short-Range Distortion of Hybrid Perovskites and Hydrogen-Bonding Role: the MAPbCl3 Case. J. Phys. Chem. C 2018, 122, 28265–28272. 10.1021/acs.jpcc.8b10086. [DOI] [Google Scholar]
  19. Wright A. D.; Verdi C.; Milot R. L.; Eperon G. E.; Pérez-Osorio M. A.; Snaith H. J.; Giustino F.; Johnston M. B.; Herz L. M. Electron-phonon coupling in hybrid lead halide perovskites. Nat. Commun. 2016, 7, 11755. 10.1038/ncomms11755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sendner M.; Nayak P. K.; Egger D. A.; Beck S.; Müller C.; Epding B.; Kowalsky W.; Kronik L.; Snaith H. J.; Pucci A.; et al. Optical phonons in methylammonium lead halide perovskites and implications for charge transport. Mater. Horiz. 2016, 3, 613–620. 10.1039/c6mh00275g. [DOI] [Google Scholar]
  21. Neukirch A. J.; Nie W.; Blancon J.-C.; Appavoo K.; Tsai H.; Sfeir M. Y.; Katan C.; Pedesseau L.; Even J.; Crochet J. J.; et al. Polaron Stabilization by Cooperative Lattice Distortion and Cation Rotations in Hybrid Perovskite Materials. Nano Lett. 2016, 16, 3809–3816. 10.1021/acs.nanolett.6b01218. [DOI] [PubMed] [Google Scholar]
  22. Stroppa A.; Di Sante D.; Barone P.; Bokdam M.; Kresse G.; Franchini C.; Whangbo M.-H.; Picozzi S. Tunable ferroelectric polarization and its interplay with spin-orbit coupling in tin iodide perovskites. Nat. Commun. 2014, 5, 5900. 10.1038/ncomms6900. [DOI] [PubMed] [Google Scholar]
  23. Azarhoosh P.; McKechnie S.; Frost J. M.; Walsh A.; van Schilfgaarde M. Research Update: Relativistic origin of slow electron-hole recombination in hybrid halide perovskite solar cells. APL Mater. 2016, 4, 091501. 10.1063/1.4955028. [DOI] [Google Scholar]
  24. Leppert L.; Reyes-Lillo S. E.; Neaton J. B. Electric Field- and Strain-Induced Rashba Effect in Hybrid Halide Perovskites. J. Phys. Chem. Lett. 2016, 7, 3683–3689. 10.1021/acs.jpclett.6b01794. [DOI] [PubMed] [Google Scholar]
  25. Etienne T.; Mosconi E.; De Angelis F. Dynamical Origin of the Rashba Effect in Organohalide Lead Perovskites: A Key to Suppressed Carrier Recombination in Perovskite Solar Cells?. J. Phys. Chem. Lett. 2016, 7, 1638–1645. 10.1021/acs.jpclett.6b00564. [DOI] [PubMed] [Google Scholar]
  26. Hutter E. M.; Gélvez-Rueda M. C.; Osherov A.; Bulović V.; Grozema F. C.; Stranks S. D.; Savenije T. J. Direct-indirect character of the bandgap in methylammonium lead iodide perovskite. Nat. Mater. 2017, 16, 115–120. 10.1038/nmat4765. [DOI] [PubMed] [Google Scholar]
  27. Frohna K.; Deshpande T.; Harter J.; Peng W.; Barker B. A.; Neaton J. B.; Louie S. G.; Bakr O. M.; Hsieh D.; Bernardi M. Inversion symmetry and bulk Rashba effect in methylammonium lead iodide perovskite single crystals. Nat. Commun. 2018, 9, 1829. 10.1038/s41467-018-04212-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wiedemann D.; Breternitz J.; Paley D. W.; Schorr S. Hybrid Perovskite at Full Tilt: Structure and Symmetry Relations of the Incommensurately Modulated Phase of Methylammonium Lead Bromide, MAPbBr3. J. Phys. Chem. Lett. 2021, 12, 2358–2362. 10.1021/acs.jpclett.0c03722. [DOI] [PubMed] [Google Scholar]
  29. Filippetti A.; Delugas P.; Mattoni A. Radiative Recombination and Photoconversion of Methylammonium Lead Iodide Perovskite by First Principles: Properties of an Inorganic Semiconductor within a Hybrid Body. J. Phys. Chem. C 2014, 118, 24843–24853. 10.1021/jp507430x. [DOI] [Google Scholar]
  30. Quarti C.; Mosconi E.; De Angelis F. Interplay of Orientational Order and Electronic Structure in Methylammonium Lead Iodide: Implications for Solar Cell Operation. Chem. Mater. 2014, 26, 6557–6569. 10.1021/cm5032046. [DOI] [Google Scholar]
  31. Mattoni A.; Filippetti A.; Saba M. I.; Delugas P. Methylammonium Rotational Dynamics in Lead Halide Perovskite by Classical Molecular Dynamics: The Role of Temperature. J. Phys. Chem. C 2015, 119, 17421–17428. 10.1021/acs.jpcc.5b04283. [DOI] [Google Scholar]
  32. Brivio F.; Frost J. M.; Skelton J. M.; Jackson A. J.; Weber O. J.; Weller M. T.; Goñi A. R.; Leguy A. M. A.; Barnes P. R. F.; Walsh A. Lattice dynamics and vibrational spectra of the orthorhombic, tetragonal, and cubic phases of methylammonium lead iodide. Phys. Rev. B 2015, 92, 144308. 10.1103/physrevb.92.144308. [DOI] [Google Scholar]
  33. Bakulin A. A.; Selig O.; Bakker H. J.; Rezus Y. L. A.; Müller C.; Glaser T.; Lovrincic R.; Sun Z.; Chen Z.; Walsh A.; et al. Real-Time Observation of Organic Cation Reorientation in Methylammonium Lead Iodide Perovskites. J. Phys. Chem. Lett. 2015, 6, 3663–3669. 10.1021/acs.jpclett.5b01555. [DOI] [PubMed] [Google Scholar]
  34. Lahnsteiner J.; Kresse G.; Kumar A.; Sarma D. D.; Franchini C.; Bokdam M. Room-temperature dynamic correlation between methylammonium molecules in lead-iodine based perovskites: An ab initio molecular dynamics perspective. Phys. Rev. B 2016, 94, 214114. 10.1103/physrevb.94.214114. [DOI] [Google Scholar]
  35. Carignano M. A.; Aravindh S. A.; Roqan I. S.; Even J.; Katan C. Critical Fluctuations and Anharmonicity in Lead Iodide Perovskites from Molecular Dynamics Supercell Simulations. J. Phys. Chem. C 2017, 121, 20729–20738. 10.1021/acs.jpcc.7b08220. [DOI] [Google Scholar]
  36. Lahnsteiner J.; Kresse G.; Heinen J.; Bokdam M. Finite-temperature structure of the MAPbI3 perovskite: Comparing density functional approximations and force fields to experiment. Phys. Rev. Mater. 2018, 2, 073604. 10.1103/physrevmaterials.2.073604. [DOI] [Google Scholar]
  37. Maheshwari S.; Fridriksson M. B.; Seal S.; Meyer J.; Grozema F. C. The Relation between Rotational Dynamics of the Organic Cation and Phase Transitions in Hybrid Halide Perovskites. J. Phys. Chem. C 2019, 123, 14652–14661. 10.1021/acs.jpcc.9b02736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Bokdam M.; Lahnsteiner J.; Ramberger B.; Schäfer T.; Kresse G. Assessing Density Functionals Using Many Body Theory for Hybrid Perovskites. Phys. Rev. Lett. 2017, 119, 145501. 10.1103/physrevlett.119.145501. [DOI] [PubMed] [Google Scholar]
  39. Jinnouchi R.; Lahnsteiner J.; Karsai F.; Kresse G.; Bokdam M. Phase Transitions of Hybrid Perovskites Simulated by Machine-Learning Force Fields Trained on the Fly with Bayesian Inference. Phys. Rev. Lett. 2019, 122, 225701. 10.1103/physrevlett.122.225701. [DOI] [PubMed] [Google Scholar]
  40. Jinnouchi R.; Karsai F.; Kresse G. On-the-fly machine learning force field generation: Application to melting points. Phys. Rev. B 2019, 100, 014105. 10.1103/physrevb.100.014105. [DOI] [PubMed] [Google Scholar]
  41. Grüninger H.; Bokdam M.; Leupold N.; Tinnemans P.; Moos R.; De Wijs G. A.; Panzer F.; Kentgens A. P. M. Microscopic (Dis)order and Dynamics of Cations in Mixed FA/MA Lead Halide Perovskites. J. Phys. Chem. C 2021, 125, 1742–1753. 10.1021/acs.jpcc.0c10042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Whitfield P. S.; Herron N.; Guise W. E.; Page K.; Cheng Y. Q.; Milas I.; Crawford M. K. Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide. Sci. Rep. 2016, 6, 35685. 10.1038/srep35685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Ali I. O. A.; Joubert D. P.; Suleiman M. S. H. A theoretical investigation of structural, mechanical, electronic and thermoelectric properties of orthorhombic CH3NH3PbI3. Eur. Phys. J. B 2018, 91, 263. 10.1140/epjb/e2018-90312-5. [DOI] [Google Scholar]
  44. Leveillee J.; Schleife A. Free-electron effects on the optical absorption of the hybrid perovskite CH3NH3PbI3 from first principles. Phys. Rev. B 2019, 100, 035205. 10.1103/physrevb.100.035205. [DOI] [Google Scholar]
  45. Filip M. R.; Giustino F. GW quasiparticle band gap of the hybrid organic-inorganic perovskite CH3NH3PbI3: Effect of spin-orbit interaction, semicore electrons, and self-consistency. Phys. Rev. B 2014, 90, 245145. 10.1103/physrevb.90.245145. [DOI] [Google Scholar]
  46. Lee J.-H.; Bristowe N. C.; Lee J. H.; Lee S.-H.; Bristowe P. D.; Cheetham A. K.; Jang H. M. Resolving the Physical Origin of Octahedral Tilting in Halide Perovskites. Chem. Mater. 2016, 28, 4259–4266. 10.1021/acs.chemmater.6b00968. [DOI] [Google Scholar]
  47. Lahnsteiner J.; Jinnouchi R.; Bokdam M. Long-range order imposed by short-range interactions in methylammonium lead iodide: Comparing point-dipole models to machine-learning force fields. Phys. Rev. B 2019, 100, 094106. 10.1103/physrevb.100.094106. [DOI] [Google Scholar]
  48. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  49. Kresse G.; Furthmüller J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  50. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  51. Sun J.; Ruzsinszky A.; Perdew J. P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
  52. Bokdam M.Minimalistic MAPbX3 Database for Force Field Training, 2021. 10.4121/14710323.v1. [DOI]
  53. Bartók A. P.; Payne M. C.; Kondor R.; Csányi G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. 10.1103/physrevlett.104.136403. [DOI] [PubMed] [Google Scholar]
  54. Bartók A. P.; Kondor R.; Csányi G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. 10.1103/physrevb.87.184115. [DOI] [Google Scholar]
  55. Bishop C.Pattern Recognition and Machine Learning (Information Science and Statistics); Springer-Verlag: New York, 2006. [Google Scholar]
  56. Govinda S.; Kore B. P.; Bokdam M.; Mahale P.; Kumar A.; Pal S.; Bhattacharyya B.; Lahnsteiner J.; Kresse G.; Franchini C.; et al. Behavior of Methylammonium Dipoles in MAPbX3 (X = Br and I). J. Phys. Chem. Lett. 2017, 8, 4113–4121. 10.1021/acs.jpclett.7b01740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Blöchl P. E.; Jepsen O.; Andersen O. K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223–16233. 10.1103/physrevb.49.16223. [DOI] [PubMed] [Google Scholar]
  58. Bartók A. P.; Kermode J.; Bernstein N.; Csányi G. Machine Learning a General-Purpose Interatomic Potential for Silicon. Phys. Rev. X 2018, 8, 041048. 10.1103/physrevx.8.041048. [DOI] [Google Scholar]
  59. Behler J. Four Generations of High-Dimensional Neural Network Potentials. Chem. Rev. 2021, 121, 10037. 10.1021/acs.chemrev.0c00868. [DOI] [PubMed] [Google Scholar]
  60. Sharma V. K.; Mukhopadhyay R.; Mohanty A.; Tyagi M.; Embs J. P.; Sarma D. D. Contrasting Behaviors of FA and MA Cations in APbBr3. J. Phys. Chem. Lett. 2020, 11, 9669–9679. 10.1021/acs.jpclett.0c02688. [DOI] [PubMed] [Google Scholar]
  61. Kieslich G.; Skelton J. M.; Armstrong J.; Wu Y.; Wei F.; Svane K. L.; Walsh A.; Butler K. T. Hydrogen Bonding versus Entropy: Revealing the Underlying Thermodynamics of the Hybrid Organic-Inorganic Perovskite [CH3NH3]PbBr3. Chem. Mater. 2018, 30, 8782–8788. 10.1021/acs.chemmater.8b03164. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

  1. Bokdam M.Minimalistic MAPbX3 Database for Force Field Training, 2021. 10.4121/14710323.v1. [DOI]

Supplementary Materials

jp1c06835_si_001.mov (7.7MB, mov)
jp1c06835_si_002.mov (6.6MB, mov)
jp1c06835_si_003.mov (5.9MB, mov)
jp1c06835_si_004.mov (8.4MB, mov)
jp1c06835_si_005.mov (5.8MB, mov)
jp1c06835_si_006.mov (5.6MB, mov)
jp1c06835_si_007.cif (8.2KB, cif)
jp1c06835_si_008.cif (8.2KB, cif)
jp1c06835_si_009.cif (8.3KB, cif)
jp1c06835_si_010.cif (8.3KB, cif)
jp1c06835_si_011.cif (8.3KB, cif)
jp1c06835_si_012.cif (8.3KB, cif)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES