Insight into the fundamental trade-offs of diffusion MRI from polarization-sensitive optical coherence tomography in ex vivo human brain

Robert Jones; Giorgia Grisot; Jean Augustinack; Caroline Magnain; David A Boas; Bruce Fischl; Hui Wang; Anastasia Yendiki

doi:10.1016/j.neuroimage.2020.116704

. Author manuscript; available in PMC: 2021 Oct 4.

Published in final edited form as: Neuroimage. 2020 Mar 6;214:116704. doi: 10.1016/j.neuroimage.2020.116704

Insight into the fundamental trade-offs of diffusion MRI from polarization-sensitive optical coherence tomography in ex vivo human brain

Robert Jones ^a,¹, Giorgia Grisot ^b,¹, Jean Augustinack ^a, Caroline Magnain ^a, David A Boas ^c, Bruce Fischl ^a, Hui Wang ^a, Anastasia Yendiki ^a,^*

PMCID: PMC8488979 NIHMSID: NIHMS1741539 PMID: 32151760

Abstract

In the first study comparing high angular resolution diffusion MRI (dMRI) in the human brain to axonal orientation measurements from polarization-sensitive optical coherence tomography (PSOCT), we compare the accuracy of orientation estimates from various dMRI sampling schemes and reconstruction methods. We find that, if the reconstruction approach is chosen carefully, single-shell dMRI data can yield the same accuracy as multi-shell data, and only moderately lower accuracy than a full Cartesian-grid sampling scheme. Our results suggest that current dMRI reconstruction approaches do not benefit substantially from ultra-high b-values or from very large numbers of diffusion-encoding directions. We also show that accuracy remains stable across dMRI voxel sizes of 1 mm or smaller but degrades at 2 mm, particularly in areas of complex white-matter architecture. We also show that, as the spatial resolution is reduced, axonal configurations in a dMRI voxel can no longer be modeled as a small set of distinct axon populations, violating an assumption that is sometimes made by dMRI reconstruction techniques. Our findings have implications for in vivo studies and illustrate the value of PSOCT as a source of ground-truth measurements of white-matter organization that does not suffer from the distortions typical of histological techniques.

1. Introduction

Diffusion magnetic resonance imaging (dMRI) is the only technique that allows us to study the wiring of the brain in vivo. It relies on the random thermal motion of water molecules (Stejskal and Tanner, 1965). In the white matter (WM), the displacements of water molecules are obstructed by axons, leading to anisotropic diffusion. The MRI signals acquired with diffusion sensitization in different directions allow us to estimate the preferential direction of diffusion and hence infer axonal orientations (Le Bihan et al., 2001).

The resolution of typical in vivo dMRI scans is on the scale of millimeters, while axons in the human brain measure only micrometers in diameter (Susuki, 2010; Liewald et al., 2014). Thus, dMRI reconstruction methods can only recover bundles of axons that travel parallel to each other, rather than individual axons. Determining the true configuration of axons in a voxel that contains anything more complex than a single, coherent bundle is commonly referred to as the “crossing-fiber problem” (Tournier, 2010). The name implies an assumption that the most representative configuration is a small set of mostly coherent axon bundles, hence the problem reduces to determining how many bundles there are in a voxel and at what angles they cross. This assumption has driven both the methods that have been used to reconstruct diffusion orientations and the simulation of data that are used to evaluate these methods. However, the extent to which this assumption is representative of human WM architecture is not well understood.

Diffusion tensor imaging (DTI) was the first attempt at inferring orientations of axon bundles, by fitting a tensor to the dMRI data at each voxel (Basser et al., 1994). As it reconstructs only a single direction of diffusion in each voxel, it is inaccurate in areas where multiple fiber populations are present (Basser et al., 2000; Tournier et al., 2002). A number of methods have since emerged to amend this by estimating the orientations of multiple axon populations per voxel (Tuch, 2004; Wedeen et al., 2005; Özarslan et al., 2006; Behrens et al., 2007; Descoteaux et al., 2007; Tournier et al., 2007; Aganj et al., 2010; Yeh et al., 2010). Some of these methods are model-based, in the sense that they assume a specific model for the displacements of water molecules within a single axon population, while others are model-free, in the sense that they attempt to derive the distribution of displacements in a voxel non-parametrically. Furthermore, methods differ in terms of the types of dMRI acquisitions that they are designed for, and specifically the q-space sampling schemes (grid, single-shell, or multi-shell) that they can accommodate.

Each of these approaches leads to different estimates of diffusion orientations, which can vary further depending on experimental factors such as spatial resolution or signal-to-noise ratio (SNR). Given that dMRI data can provide only indirect inference on axonal orientations, based on water diffusion in and around the axons, and that all aforementioned analysis methods make further simplifying assumptions on that diffusion, it is important to assess the accuracy of these methods and to determine the optimal dMRI data acquisition and analysis approach. This requires the comparison of dMRI orientation estimates with independent measurements of axonal orientations, from a modality that does not rely on water diffusion.

Different approaches have been proposed to obtain a “gold standard” to compare to orientations estimated from dMRI data. One such approach is with numerical simulations, where a simple configuration of ground-truth bundles, like a 2- or 3-way crossing, is assumed and dMRI data are generated numerically based on a forward model. Diffusion orientations are then estimated from the synthetic dMRI data and compared to the ground truth orientations (Descoteaux et al., 2007; Canales-Rodríguez et al., 2009; Aganj et al., 2010; Daducci et al., 2013). This offers the flexibility of generating data with any set of acquisition parameters without the cost of imaging, but it relies on a simplified mathematical model of diffusion and may introduce a bias towards reconstruction methods that employ similar models. Alternatively, one can use physical phantoms, which are constructed with synthetic fibers that have similar diffusion properties as axons, and can be scanned in an MRI scanner to provide more realistic data (Perrin et al., 2005; Poupon et al., 2008). However, the fiber configurations in these phantoms are still simplistic and likely to underestimate the complexity of human WM.

Other techniques focus on obtaining reference measurements of axonal orientations in post-mortem brain tissue at the micrometer scale from imaging modalities that do not rely on water diffusion (see Table 1 for summary). One such approach is by myelin staining, where fiber orientations can be obtained from the histological sections by manual labeling (Leergaard et al., 2010), Fourier analysis (Choe et al., 2012), or structure tensor analysis (Seehaus et al., 2015; Schilling et al., 2017) and compared to dMRI orientation estimates. An alternative histological approach combines staining with DiI or DiA (fluorescent lipophilic dyes) and imaging with confocal microscopy, where axonal orientations can be obtained with structure tensor analysis (Budde and Frank, 2012). A benefit of this approach is that it can be generalized to extract 3-dimensional (3D) orientations within each histological section (Khan et al., 2015; Schilling et al., 2016, 2018).

Table 1. Summary of literature.

Studies that have compared orientation estimates from dMRI in post-mortem brain tissue to independent measurements of axonal orientations from a reference modality. We list the reference modality, type of tissue, and dMRI acquisition parameters for each study (“iso” indicates isotropic voxels).

	Reference modality		Tissue type	dMRI
				b-values [s/mm²]	Gradient directions	Voxel size [mm]
Leergaard et al. (2010)	Myelin stain	2D	Rat	Max 30452	514	.265 iso
Choe et al. (2012)		2D	Owl monkey	1309	21	.3 iso
Seehaus et al. (2015)		2D	Human	3000	60	.34 iso
Schilling et al. (2017)		2D	Macaque	6000	101	.3-.8 iso
Budde and Frank (2012)	DiI	2D	Rat	1200	30	.156x.156x.5
Khan et al. (2015)		3D	Macaque	2500	63	.2 iso
Schilling et al. (2016)		3D	Squirrel monkey	3200/6400	30/90	.4 iso
Schilling et al. (2018)		3D	Squirrel monkey	3000/6000 9000/12000	100/100 100/100	.2 × .2 × .4
Mollink et al. (2017)	PLI	2D	Human	5000	120	.4 iso
Wang et al. (2014)	PSOCT	2D	Human	4032	20	.3 iso
Present study		2D	Human	Max 40000	514	.25 iso

Open in a new tab

All the aforementioned histological methods require that orientations be either manually traced or estimated by image processing. Alternatively, one can obtain direct measurements of axonal orientations by optical imaging techniques that use polarized light to probe birefringence, an intrinsic optical property of anisotropic materials (De Boer et al., 1997). Birefringent tissues introduce a change in the polarization state of light, meaning that light polarized parallel and perpendicular to the axis of anisotropy (optic axis) of the tissue will experience different indices of refraction. In the WM, birefringence occurs due to the regular pattern of arrays of lipids and proteins in myelin. That is, the optic axis of the tissue is the axis along which axons are oriented. Polarization-based techniques measure the orientation of the optic axis of the tissue within the plane perpendicular to the incident light. Thus these techniques allow us to compare the mesoscopic diffusion orientation estimates obtained from dMRI to microscopic axonal orientations from an independent source of measurements that does not rely on water diffusion.

Polarized light imaging (PLI) is a technique that relies on birefringence and has been used to measure axonal orientations for the purpose of comparing them to those estimated by dMRI (Mollink et al., 2017). Unlike histological techniques, PLI obtains direct measurements of axonal orientations. However, like histological techniques, PLI requires tissue to be cut and mounted before imaging, which introduces severe distortions. This can make it difficult to align consecutive slices to each other and to the dMRI data for voxel-wise comparisons. Mitigating these distortions requires the design of complex registration frameworks (Majka and Wójcik, 2016; Ali et al., 2018). This involves various design choices, such as the deformation model, image similarity metric, regularization metrics, multi-resolution scheme, interpolation method, etc., each of which comes with its own trade-offs.

Polarization-sensitive optical coherence tomography (PSOCT) is another technique that relies on birefringence to measure fiber orientation. It has been used to characterize the optic axis of birefringent biological tissues, including tendon, muscle, heart, and nerve fibers (Hitzenberger et al., 2001; Guo et al., 2004; Nakaji et al., 2008, Li et al., 2018). Unlike PLI, PSOCT images the blockface of a volumetric sample before cutting it, therefore eliminating the problem of nonlinear distortions between slices (Magnain et al., 2014; Wang et al., 2014). OCT is an interferometric technique that exploits the back-scattering property of tissue to provide detailed information on microstructure. In addition to reflectivity, PSOCT uses light polarization to provide additional contrasts that can be used to image axonal fiber orientations at microscopic resolutions (Wang et al., 2010; Wang et al., 2014). In this work, we use PSOCT to obtain direct, undistorted, in-plane measurements of fiber orientations in human WM and compare them to orientation estimates from ex vivo dMRI data acquired at ultra-high field and ultra-high b-values. We analyze regions of interest (ROIs) with varying levels of organizational complexity and study a variety of dMRI reconstruction methods and q-space sampling schemes. We also investigate the impact of acquisition parameters such as spatial and angular resolution and SNR. Our results provide insights on how the acquisition and analysis of dMRI data could be optimized to achieve higher accuracy in regimes that are relevant to in vivo studies.

2. Methods

2.1. Sample identification

The samples used in this study (referred to as block 1 and 2) were extracted from two different human brains. The brains had been obtained from the Massachusetts General Hospital 160 Autopsy Suite and fixed in 10% formalin for at least two months. The fixed hemispheres had previously been scanned in a 3 T Siemens Trio scanner, using a product 32-channel head coil and a 3D diffusion-weighted steady state free precession (DW-SSFP) sequence with TR = 30.21 ms, TE = 25.12 ms, 750 μm isotropic resolution, 8 non-DW (b = 0) volumes, and 60 DW volumes (b = 4000 s/mm², δ = 15 ms, Δ = 19 ms). For the purposes of the present work, the whole-hemisphere scans were used only to identify the block of tissue that we extracted from each brain. Data were collected and analyzed from these blocks as described in the following sections.

Block 1 (deep WM):

It was extracted from the right brain hemisphere of a 43-year-old female (diagnosis: cognitive control; cause of death: cardiac arrest; post-mortem interval: <24 h). The block was sized approximately 3 × 2 × 2 cm and contained an area of complex WM organization, where fiber bundles projecting from the frontal cortex branched into the internal and external capsules.

Block 2 (superficial WM):

It was extracted from the left brain hemisphere of a 70-year-old male (clinical diagnosis: severe coronary artery disease, myocardial infarction, hypertension, hyperlipidemia; neuropathologic diagnosis: mild hypoxic/ischemic changes; cause of death: coronary artery disease and multiorgan failure; post mortem interval: 24 h). The block was sized approximately 2 × 2 × 2 cm and was located just below the superior frontal gyrus. The medial side included the cingulate sulcus, while the lateral side contained parts of the corticospinal tract (CST) and superior longitudinal fasciculus (SLF-I).

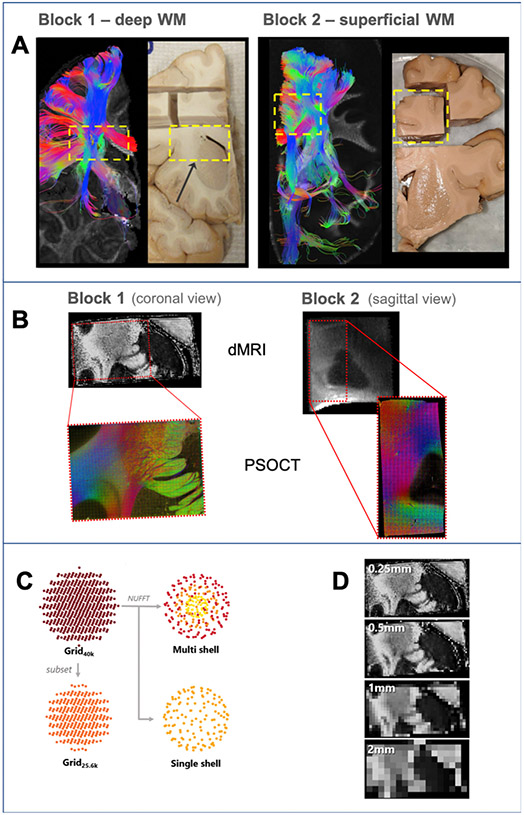
Fig. 1A shows deterministic tensor tractography from the whole-hemisphere dMRI scans of the two brains, and a photograph of the corresponding coronal cross-section of each hemisphere. The two blocks that we extracted are marked by dashed yellow rectangles.

2.2. dMRI data acquisition

We scanned each tissue block in a small-bore 9.4 T Bruker Biospec system with ∣Gmax∣ = 480 mT/m to obtain higher spatial and angular resolution than what would have been feasible for the whole hemisphere. The block was placed in a plastic syringe filled with Fomblin, a chemically inert and proton-free solution, and all air was removed from the syringe to avoid susceptibility artifacts. The block dMRI data were acquired using a 3D echo-planar imaging (EPI) sequence with TR = 750 ms, TE = 43 ms, matrix size 136 × 136 × 176, generalized autocalibrating partial parallel acquisition (GRAPPA) factor 2, and 250 μm isotropic resolution. We collected 515 volumes, corresponding to points on a 11 cubic lattice in q-space enclosed in a sphere, with b_max = 40,000 s/mm², δ = 15 ms, and Δ = 21 ms. The total acquisition time was approximately 48 h.

2.3. PSOCT data acquisition

Fig. 1B shows the area of each tissue block that we selected for PSOCT scanning. We used a polarization maintaining fiber (PMF) based, multicontrast, spectral domain PSOCT system, developed in-house (Wang et al., 2016). Briefly, the light source consisted of two broadband super-luminescent diodes (Thorlabs Inc., LSC2000C), with a center wavelength of 1300 nm and a bandwidth of 170 nm, yielding an axial resolution of 2.9 μm in tissue. The lateral resolution was estimated at 3.5 μm for block 1 and 3.9 μm for block 2. The PSOCT imaging/slicing plane was coronal for block 1, which contained mostly cortico-subcortical fibers traveling superior-inferior, and sagittal for block 2, which contained mostly long-association fibers traveling anterior-posterior and motor fibers traveling superior-inferior.

From a single measurement, PSOCT produces three types of contrast: reflectivity represents the backscattering of light from the tissue; optic axis orientation represents the in-plane (2D) orientation of the fiber axis; and retardance represents the phase shift between oscillating light waves parallel and perpendicular to the optic axis (Wang et al., 2014). The latter offers good white/gray matter contrast and can thus be used for registration to the dMRI data, as we describe in the next section. Serial scanning was performed using a snaked tile configuration scheme, with each tile having a FOV of 1 mm² and 50% overlap between adjacent tiles, resulting in 1120 and 722 imaged tiles per slice, respectively, for block 1 and block 2. Total scan time was approximately 115 h for a 2 × 1.5 × 0.5 cm³ section in block 1 and 85 h for a 0.9 × 0.9 × 2 cm³ section in block 2.

Processed data were saved as 2D en-face maps in the form of four modalities per tile, namely average intensity projection (AIP), maximum intensity projection (MIP), retardance, and optic axis orientation (Wang et al., 2015). The image tiles were stitched using the Fiji software (Preibisch et al., 2009; Schindelin et al., 2012). The en-face slices were then stacked to form a volume. The through-plane resolution, determined by the slice thickness, was 75 μm for block 1 and 100 μm for block 2. For visualization of en-face optic axis orientation slices, RGB images were created using the orientation measurement to determine the hue/color in each pixel, and the retardance to modulate color intensity. Orientation images were despeckled in the RGB domain using Fiji (Schindelin et al., 2012). Finally, the PSOCT data from both blocks were downsampled to 10 μm in-plane resolution to facilitate further analyses. All of the following analyses, unless otherwise stated, use these 10 μm PSOCT data.

2.4. dMRI to PSOCT registration

We aligned the dMRI and PSOCT data from each block by registering the fractional anisotropy (FA) map to the retardance map, as they possess similar gray/white matter contrast (Wang et al., 2014). The absence of non-linear distortions is a key feature of the PSOCT acquisition that facilitates this step, in comparison to alternative histological or optical techniques. Thus, an affine registration was sufficient for the cross-modal alignment. We used a robust registration method that identifies outlier areas of the images and down-weighs them in the registration (Reuter et al., 2010). This approach to registration between dMRI and PSOCT has been further described and evaluated elsewhere (Wang et al., 2014). That work reported a Dice coefficient of 0.96 between tissue masks from the two modalities.

We assessed whether the dMRI datasets used in the present work suffered from nonlinear distortions by registering the low-b dMRI volume to a structural image from the same sample, using both affine and nonlinear registration. The structural scans for blocks 1 and 2 had been collected, respectively, with a 2D rapid acquisition with relaxation enhancement (RARE) at 0.12 × 0.12 × 1 mm resolution and a 3D fast low angle shot (FLASH) acquisition at 0.055 mm isotropic resolution. The intensities of low-b voxels after affine vs. nonlinear registration were highly correlated within each area imaged with PSOCT (block 1: ρ = 0.97, p < 0.001; block 2: ρ = 0.96, p < 0.001). Hence, we did not pursue nonlinear registration further.

All of the dMRI analyses detailed in the following sections were performed in the native space of the dMRI data. We then transformed the dMRI data to PSOCT space by applying the affine registration computed above with nearest-neighbor interpolation. For the dMRI orientation estimates, we applied the rotational component of the affine transformation to the dMRI orientation vectors. This allowed voxel-wise comparisons of the diffusion-based orientation estimates with direct measurements of axonal orientations from PSOCT. These comparisons were performed at the PSOCT resolution (0.01 mm).

2.5. Resampling in q-space

Some of the dMRI reconstruction methods to be compared require data acquired on a grid in q-space, some require data acquired on q-shells, and some can be applied to both types of data. Ideally, we would like to be able to perform all analyses on the same dMRI dataset, to reduce acquisition time for future studies and to ensure as closely matched experimental conditions as possible by avoiding multiple scan sessions. Thus, we propose a method for resampling data from a grid to shells in q-space.

The method consists of two steps: (1) Apply a forward fast Fourier transform (FFT) to the dMRI data, which has been acquired on a uniformly spaced q-space grid, to obtain samples of the diffusion propagator, P(n), n = 1,...,N, and (2) Apply a nonuniform inverse FFT to P(n) to obtain the dMRI data, E_NU, on nonuniformly spaced q-space points:

E_{NU} (q_{m}) = \sum_{n = 0}^{N - 1} P (n) e^{{iq}_{m} n}

(1)

where q_m is the m-th of the target q-space points. In our application, these points were distributed on shells.

Our implementation of (1) used the nonuniform FFT (NUFFT) with min-max interpolation, which was applied previously to the problem of reconstructing MRIs from arbitrary k-space trajectories (Fessler and Sutton, 2003). This method allows fast and accurate computation of Fourier transforms on arbitrary, nonuniformly distributed points in the frequency domain.

We evaluated this approach by comparing dMRI data from block 1 that we resampled from a q-space grid onto q-shells to dMRI data from block 1 that we acquired on q-shells. The grid acquisition was as described in section 2.2. The multi-shell acquisition was performed with identical acquisition parameters, except that it comprised a total of 512 DW images arranged on 4 q-shells (64/64/128/256 directions with b = 4000/12,000/20,000/40,000 s/mm², respectively).

All DW volumes were aligned to the first volume by affine registration to account for distortions or potential displacement of the sample during the long acquisition. For all WM voxels in each DW volume, we calculated the normalized root mean square error (NRMSE) between the acquired and resampled q-space data. Given that the acquired and resampled images came from different acquisitions, hence they were expected to differ due to imaging noise, we also computed the NRMSE between the b = 0 images from the two acquisitions (NRMSE0) for reference. We then computed the relative NRMSE, i.e., the ratio NRMSE/NRMSE0. This quantifies the extent to which resampling introduces additional error, with respect to what the error would have been due to imaging noise alone.

2.6. Comparison of dMRI acquisition schemes

A summary of all the combinations of dMRI acquisition schemes, reconstruction methods, and resolutions for which comparisons to PSOCT are presented in this work is shown inTable 2. In particular, our goal was to compare the accuracy of dMRI orientation estimates obtained from the following q-space sampling schemes (see also Fig. 1C):

Table 2. Summary of experiments.

Each row is a different reconstruction method and each column a different q-space sampling scheme. In each case we list the spatial resolutions (mm) for which we present results.

	Grid_40k	Grid_25.6k	Multi-shell	Single-shell
DTI	0.25, 0.5, 1*, 2	0.25, 0.5, 1*, 2	0.25, 0.5, 1*^†, 2	0.25, 0.5, 1*^†‡, 2
BS	0.25, 0.5, 1*, 2	0.25, 0.5, 1*, 2	0.25, 0.5, 1*^†, 2	0.25, 0.5, 1*^†‡, 2
GQI	0.25, 0.5, 1*, 2	0.25, 0.5, 1*, 2	0.25, 0.5, 1*^†, 2	0.25, 0.5, 1*^†‡, 2
DSI	0.25, 0.5, 1*, 2	0.25, 0.5, 1*, 2	–	–
QBI	–	–	0.25, 0.5, 1*^†, 2	0.25, 0.5, 1*^†‡, 2

Open in a new tab

Asterisks (*), daggers (†), and double daggers (‡) denote regimes for which additional results are presented, respectively, with added noise, with reduced angular resolution, and with reduced single b-values.

Grid: This is the full 11³ Cartesian grid with b_max = 40,000, as described in section 2.2. We will refer to it as Grid_40k.
Grid with reduced diffusion resolution: We generated this dataset by extracting the 257 lower-q volumes from the acquired Grid_40k data, resulting in a 9³ Cartesian grid in q-space with b_max = 25,600 s/mm². We will refer to this dataset as Grid_25.6k.
Single-shell: Using the NUFFT approach of the previous section, we resampled the grid data onto q-space points on a single shell with b = 12,000 s/mm² and 128 uniformly distributed directions (Caruyer et al., 2013).
Multi-shell: Using the NUFFT approach, we resampled the data onto the same 128 directions but 3 q-shells (b = 4,000, 8,000, and 12,000 s/mm²). Given the roughly 4-fold reduction of diffusivity in fixed tissue (D’Arceuil and de Crespigny, 2007; Dyrby et al., 2011; McNab et al., 2009), these b-values were approximately equivalent to in vivo b-values of 1,000, 2000 and 3000 s/mm². The b-values in this multi-shell scheme were thus chosen to reflect the ones used by the WUSTL-UMinn Human Connectome Project (HCP; Van Essen et al., 2013).

2.7. Comparison of dMRI reconstruction methods

We estimated diffusion orientations with the five approaches listed below. In all cases, we used widely available software packages with default parameters unless otherwise noted.

Diffusion tensor imaging (DTI): This approach assumes that water molecule displacements follow a Gaussian distribution (Basser et al., 1994). We performed least-squares fitting of the DTI model with the DSI Studio toolbox, on data from all four acquisition schemes.
Ball and stick (BS): This is a multi-compartment model, with a perfectly isotropic compartment that represents extra-cellular diffusion and N perfectly anisotropic compartments that represent different fiber populations (Behrens et al., 2003; Behrens et al., 2007). We fit the BS model with FSL’s bedpostx and a maximum of N = 3 anisotropic compartments per voxel, on data from all four acquisition schemes. For the datasets with more than one b-value, we used an extension of the BS model that assumes a Gamma distribution of diffusivities to better fit the non-mono exponential signal decay (Jbabdi et al., 2012).
Diffusion spectrum imaging (DSI): This approach reconstructs the diffusion propagator, i.e., the probability distribution function of water molecule displacements, from data sampled on a Cartesian grid in q-space by means of a discrete Fourier transform (Wedeen et al., 2005). We performed DSI reconstructions using the DSI Studio toolbox, with a Hanning filter of width 14 to mitigate ringing artifacts from q-space truncation. We applied this method to the Grid_40k and Grid_25.6k datasets.
Generalized q-sampling imaging (GQI): This method attempts to recover the spin distribution function, a scaled version of the orientation distribution function (ODF) that quantifies the amount of spins undergoing diffusion along each direction (Yeh et al., 2010). We performed GQI reconstruction using the DSI Studio toolbox, with a diffusion length ratio of 0.43 and a maximum of 3 orientation peaks per voxel, on data from all four acquisition schemes.
Q-ball imaging (QBI): This approach estimates the ODF, i.e., the probability distribution function of the orientation of water molecule displacements, from data sampled on a q-shell by means of the Funk-Radon transform (Tuch, 2004). We used an extension to the QBI approach that features a mathematically correct formulation of the ODF, accounting for the quadratic radial growth during integration of the propagator, and that is able to handle multi-shell data (Aganj et al., 2010). We performed QBI reconstruction using FSL’s qboot, with a maximum of three orientation peaks, on both the single- and multi-shell datasets.

2.8. Effect of spatial resolution

We investigated the impact of spatial resolution on the accuracy of dMRI orientation estimates, by downsampling the original data from 0.25 mm to isotropic resolutions of 0.5 mm, 1 mm, and 2 mm. This was done on the acquired Grid_40k data. We then generated the Grid_25.6k, single-shell, and multi-shell data at each resolution level as described in section 2.6, and applied the reconstruction methods of section 2.7. The four resolution levels are illustrated in Fig. 1D.

2.9. Effect of angular resolution

As detailed in the following, our initial results showed that the most substantial gains in accuracy of dMRI orientation estimates occurred when the spatial resolution was increased from 2 mm to 1 mm. Given that an isotropic voxel size of 1 mm or even smaller may be an attainable goal for in vivo dMRI (Eichner et al., 2014; Wu et al., 2016; Setsompop et al., 2018; Wang et al., 2018a), but may require reducing the angular resolution to attain practical acquisition times, we investigated the extent to which using fewer diffusion-encoding directions at 1 mm resolution would affect accuracy. For this purpose, we generated a subset of the single-shell datasets, with only 64 directions at b = 12,000 s/mm², and a subset of the multi-shell datasets, with two 64-direction shells at b = 4000 s/mm² and b = 8000 s/mm², and one 128-direction shell with b = 12,000 s/mm².

2.10. Effect of SNR

Another potential trade-off that may be necessary for attaining a spatial resolution of 1 mm in practice would be to tolerate lower SNR. We investigated this possibility by adding Rician noise to the 1 mm resolution Grid_40k data, and generating Grid_25.6k, multi-shell and single-shell datasets as described above. For each voxel of the original data, lower-SNR data were generated by drawing samples from a Rician distribution with the original signal intensity as the non-centrality parameter and σ = 0.5. This was chosen to reach SNR levels comparable to the in vivo MGH-USC HCP data. Specifically, the b = 0 SNR from a WM ROI was calculated to be 18 for the original 1 mm data, and 10 for the noise-added data, which corresponds to about 45% decrease in SNR. For comparison, the b = 0 SNR in deep WM from a randomly selected MGH-USC HCP subject was 10.5. (Here SNR is defined as the ratio of the average signal intensity to the standard deviation of signal intensities in the ROI).

2.11. Effect of b-value on single-shell acquisitions

For a single-shell acquisition with 64 directions and a spatial resolution of 1 mm, we also evaluated the effects of reducing the b-value from b = 12,000 s/mm² (which was used for the single-shell data analyses in all previous sections) to b = 8000 s/mm² or b = 4000 s/mm².

2.12. Comparison of dMRI and PSOCT orientations

The dMRI orientation estimates that we compared to PSOCT were: a) for DTI, the principal eigenvector of the tensor; b) for the BS model, the orientations of the anisotropic compartments; c) for GQI, DSI, and QBI, the local maxima, or peaks, of the ODF. These orientation vectors were mapped to the space of the PSOCT data as described in section 2.4, and projected onto the PSOCT slice plane. For methods that can reconstruct multiple orientations per voxel (all except DTI), we only considered the orientations whose probability, or volume fraction, was above a threshold of 0.01. Such thresholding is commonly performed when the dMRI orientations are used for tractography. Among the orientations that survived this threshold in each dMRI voxel, we chose the one that minimized the angular difference with each PSOCT orientation in the same voxel. We assessed the accuracy of these dMRI orientations by computing the absolute angular error between them and the orientations measured by PSOCT.

We also examined the number of distinct fiber populations (i.e., anisotropic compartments or ODF peaks) that was identified in each dMRI voxel, with each q-space sampling and reconstruction approach. For comparison to the optical data, we computed fiber orientation distributions (FODs) from the PSOCT orientations within each dMRI voxel. We did this by generating histograms of the optic axis orientation angles from all 0.01 mm PSOCT voxels in each dMRI voxel, with bin widths of 5°. As an equivalent to the number of peaks, we found the local maxima of the PSOCT FOD that were separated by at least 10°. As we allowed dMRI reconstruction methods to find a maximum of three peaks per voxel, we also imposed this constraint on the peak detection of PSOCT FODs. We considered only PSOCT FOD peaks with a magnitude of at least 0.2 times the maximum magnitude in the histogram. We examined the effect of the voxel size on the number of peaks, and how this compared between PSOCT and dMRI.

Finally, given the in-plane (2D) nature of our PSOCT optic axis measurements, one may ask whether voxels with high in-plane error between dMRI and PSOCT orientations may simply be voxels with through-plane bundles, where orientation may be measured correctly by dMRI but not by PSOCT. We investigated this by computing the correlation between the in-plane angular errors between dMRI and PSOCT orientation vectors and the magnitude of the maximum through-plane component among the (normalized) dMRI orientation vectors at the same voxel.

3. Results

3.1. Fiber organization within the samples

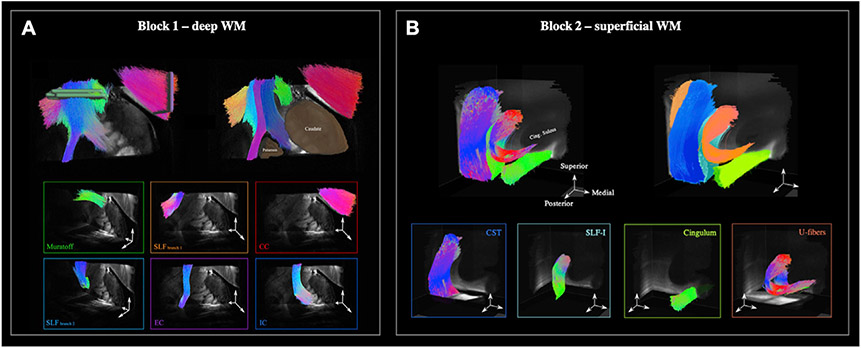
Fig. 2 illustrates the fiber organization of the two WM samples, as seen from the 9.4 T dMRI data at the native, 0.25 mm resolution. We show this using the output of deterministic tractography that we performed on ODFs obtained from the GQI reconstruction of the original data (this tractography is used here for illustrative purposes only and does not factor into the quantitative results presented below).

In the deep WM sample (block 1), we were able to isolate 6 different bundles, traveling both along and across the coronal plane. As tractography streamlines approached the striatum, they split into two branches and merged either with the internal capsule (IC) or with the external capsule (EC). The dorsomedial part of the sample contained the Muratoff bundle, a small WM fascicle located above the caudate and projecting along the anteroposterior axis. Finally, the lateral region of the sample contained branches of the superior longitudinal fasciculus (SLF) that traveled either laterally towards the cortex or caudally in parallel to the EC. We performed the PSOCT scan on this complex area, where bundles branched and crossed at multiple locations (Fig. 1B).

In the superficial WM sample (block 2), the most prominent bundles projected along orthogonal axes. The lateral side of the block contained mainly the corticospinal tract (CST) traveling along the inferior-superior axis. Two bundles could be seen traveling along the anteroposterior axis, namely the cingulum and the superior longitudinal fasciculus (SLF-I). These tracts were nearest to each other in the posterior part of the block but diverged as they projected anteriorly; the cingulum traveled medially, while the SLF-I curved laterally to follow the cingulate sulcus. In doing so, SLF-I fibers protruded into the CST, and it was in this area where more complicated fiber patterns arose. Clusters of U-fibers hugging the cingulate sulcus could also be seen in the proximity of the CST and SLF-I. We performed the PSOCT scan on the area where all of the above bundles met.

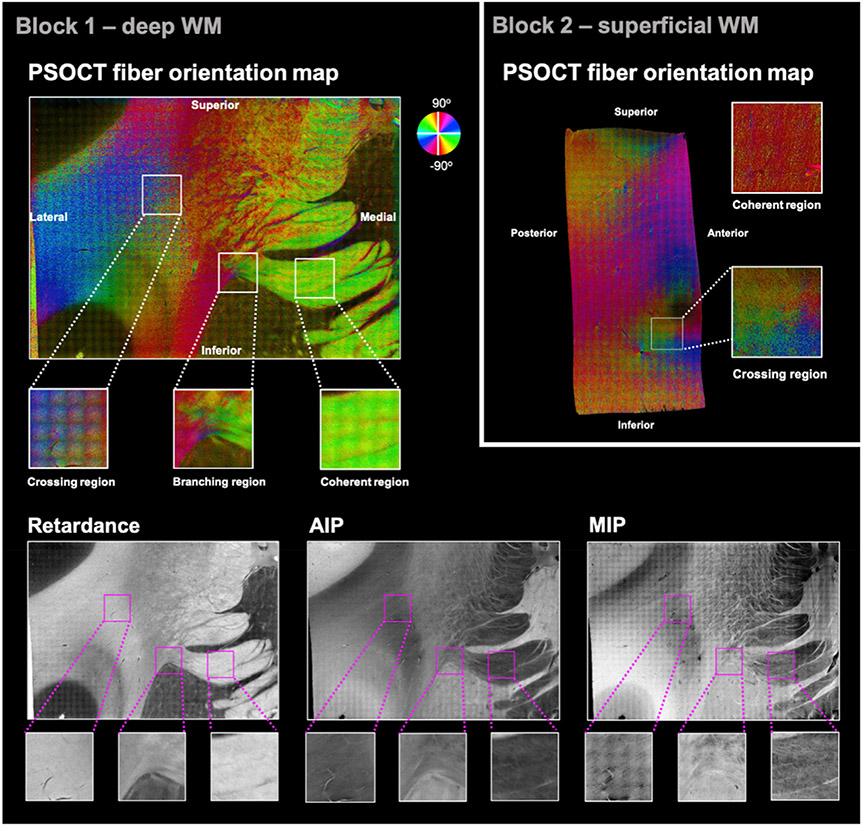
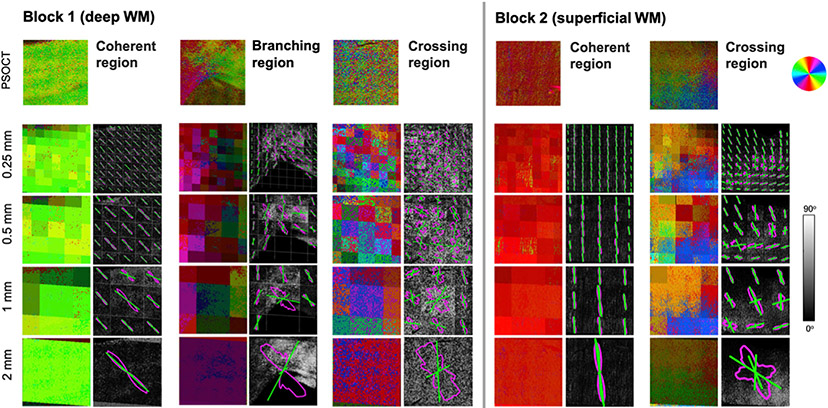
Fig. 3 shows the in-plane optic axis orientation maps (top) obtained with PSOCT for one representative slice of each tissue block. The orientation angles are color-coded as indicated by the color wheel, with brightness modulated by retardance. Note that low retardance within WM indicates the presence of fibers perpendicular to the imaging plane, which our current PSOCT setup cannot capture. Hence, for all comparisons of PSOCT and dMRI orientations, we created a mask to exclude voxels where the retardance was below 57% of the maximum retardance. Fig. 3 also shows the retardance, MIP, and AIP contrasts for block 1 (bottom).

As illustrated by the color-coded PSOCT orientation maps, fiber configurations were heterogeneous throughout both samples. In block 1, there were regions where fibers were organized coherently, traveling in parallel to each other (e.g., the IC and EC, shown as uniformly green and red areas, respectively). In other regions, fibers followed multiple directions, which differed by only a few degrees (e.g., the red/orange/yellow region dorsolateral to the striatum) or by larger angles (e.g., the lateral region where blue, cyan, purple, and green colors alternate at high frequency, suggesting interdigitated fibers). As seen in Fig. 3, we isolated three ROIs from block 1 as examples of different fiber configurations: (i) a coherent region located in the IC, where fibers were organized along a single direction; (ii) a branching region on top of the putamen, where fibers separated into a bundle entering the IC and one entering the EC; and (iii) a crossing region dorsal to the claustrum, where PSOCT orientations suggested an interdigitated pattern of fiber bundles.

In block 2, there were areas with a single dominant fiber orientation, such as the pink bundle moving diagonally on the posterior side of the slice. Following that bundle towards the anterior edge, the orientations showed fanning (the purple/blue area). Other areas, especially where cortex was visible (dark areas that suggest low retardance), were characterized by greater heterogeneity in fiber orientations. As fibers approached the superior edge of the slice, some branched in the anterior and posterior directions (pink/magenta branch to the right and orange/yellow branch to the left, respectively), while others curved to follow the gray-white matter boundary (e.g., yellow-green-cyan transition just below the superior gray matter). We isolated two ROIs from block 2 as examples of different fiber configurations: (i) a coherent region, where fibers were organized along the superior-inferior direction; and (ii) a crossing region near the anterior edge of the displayed slice, where the cingulate sulcus emerged and fiber orientations were particularly heterogeneous. In this crossing ROI from block 2, the different bundles appear to occupy different parts of the 2 mm-sized area, as opposed to the thoroughly interdigitated crossing ROI from block 1.

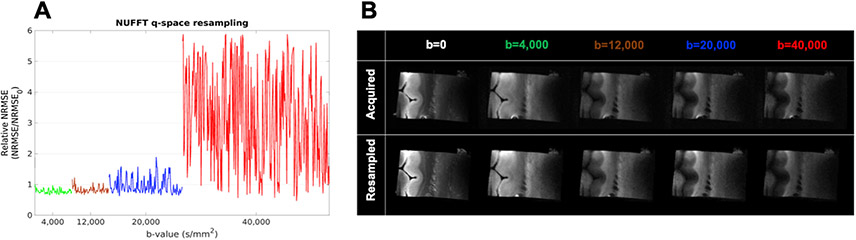
3.2. Resampling in q-space

Results from the evaluation of our q-space resampling method are shown in Fig. 4. We show example images from one slice of a resampled and acquired DW volume for each shell (Fig. 4B). We also plot the relative NRMSE, averaged over all WM voxels, by DW volume (Fig. 4A). Table 3 shows the mean and standard deviation of the relative NRMSE over all DW volumes in each shell. These results demonstrate that, for the b = 4,000, 12,000, and 20,000 s/mm² shells, our q-space resampling introduces negligible approximation error, when compared to the differences between two repeated acquisitions due to imaging noise. (Particularly for the b = 4000 and 12,000 s/mm² shells, the NRMSE between acquired and resampled DW volumes is generally less than the NRMSE between the two independently acquired b = 0 volumes). This suggests that collecting the data on a dense grid in q-space and resampling them onto q-shells introduces less variability into our results than acquiring the grid and shell data separately.

Table 3. Approximation error of q-space resampling.

For each of four shells, we show the relative NRMSE of resampled vs. acquired DW images, with respect to the NRMSE of two independent b = 0 acquisitions. Errors are averaged over WM voxels from all DW images in each shell.

b-value (s/mm²)	Relative NRMSE (mean ± standard deviation)
4000	0.78 ± 0.073
12,000	0.83 ± 0.11
20,000	0.97 ± 0.27
40,000	3.16 ± 1.58

Open in a new tab

The higher approximation error at b = 40,000 s/mm², which is also the highest b-value included in the grid acquisition, is to be expected. It illustrates what happens when there are not enough neighboring samples acquired around the target q-space locations where data are to be resampled. In all the following analyses, however, the b-values at which data are resampled onto shells are between 4000 and 12,000 s/mm², which lie well within the densely sampled area of the q-space grid, where approximation errors are low. Thus, we proceed with using the resampled data in all of the following analyses.

3.3. Overview of PSOCT vs. dMRI comparisons

Fig. 5 shows plots of the angular error between the orientation vectors estimated from dMRI and those measured with PSOCT, averaged over all included voxels from all sections of each sample, as a function of dMRI resolution. The line pattern represents the q-space sampling scheme, while the line color represents the reconstruction method. (Note that, due to the large number of PSOCT voxels, standard error bars are too small to be visible in these plots.) A repeated-measures analysis of variance on the angular error, with factors of q-space sampling scheme, orientation reconstruction method, and spatial resolution showed high significance (p = 0) for all three factors in both samples. Table 4 lists the F-statistics for each factor, showing a reproducible ranking of factors between the two samples.

Table 4. Analysis of variance on the angular error.

F-statistics from a repeated-measures analysis of variance on the angular error between dMRI and PSOCT orientations from each of the two tissue blocks.

	Block 1 (deep WM)	Block 2 (superficial WM)
q-space sampling scheme	3.35	2.87
orientation reconstruction method	8.30	10.29
spatial resolution	16.15	12.96

Open in a new tab

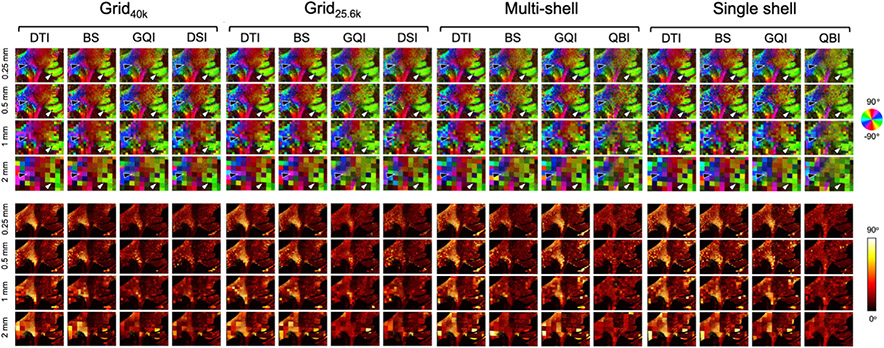
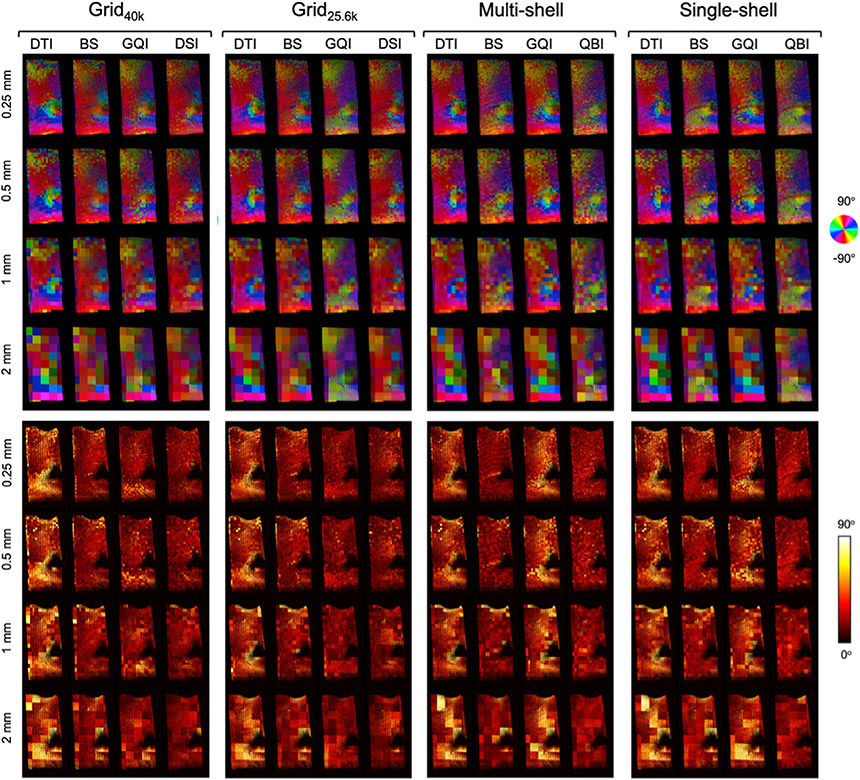
Figs. 6 and 7 show dMRI orientation maps (top) and angular error maps (bottom) from a representative slice of the deep WM and superficial WM sample, respectively. Images are shown for each dMRI orientation reconstruction method and spatial resolution, grouped by q-space sampling scheme. The orientation vectors in these figures are color-coded in the same manner as the PSOCT orientation maps in Fig. 3. For each PSOCT voxel (sized 0.01 mm), the color maps in Figs. 6 and 7 show the dMRI orientation that matches the PSOCT orientation most closely, within the corresponding dMRI voxel (sized 0.25, 0.5, 1, or 2 mm). (This is why, for any dMRI reconstruction method that yields more than one orientation per voxel, there may be multiple colors inside the same dMRI voxel.) The color intensity is modulated by FA. The heat maps in Figs. 6 and 7 show the voxel-wise absolute angular difference between the dMRI orientations seen in the color maps and the corresponding PSOCT orientations.

Fig. 6. — **Top:** Color-coded maps of the orientations obtained from dMRI that match the ones from the PSOCT data (Fig. 3) most closely, for each q-space sampling scheme, orientation reconstruction method, and spatial resolution. The arrows show areas of heterogeneous (black) and coherent (white) fiber orientations. **Bottom:** Absolute angular error between orientations estimated from dMRI and measured with PSOCT.

Fig. 7. — **Top:** Color-coded maps of the orientations obtained from dMRI that match the ones from the PSOCT data (Fig. 3) most closely, for each q-space sampling scheme, orientation reconstruction method, and spatial resolution. **Bottom:** Absolute angular error between orientations estimated from dMRI and measured with PSOCT.

3.4. Effect of dMRI reconstruction method

As seen in the overall average error plots of Fig. 5, the range of angular errors observed in the two samples was similar, with most dMRI reconstruction methods finding the deep WM sample somewhat more challenging than the superficial WM sample. As seen in the voxel-wise error maps of Figs. 6 and 7, error differences between the two samples, as well as performance differences among reconstruction methods, were mostly driven by complex regions containing heterogeneous orientations. Encouragingly, in regions where fibers were organized mostly along a single direction, like the IC and EC in the deep WM sample (Fig. 6) or the superior-inferior fiber bundle in the superficial WM sample (Fig. 7), we found similar error levels in the two samples, and generally similar performance among reconstruction methods, regardless of the q-space sampling scheme.

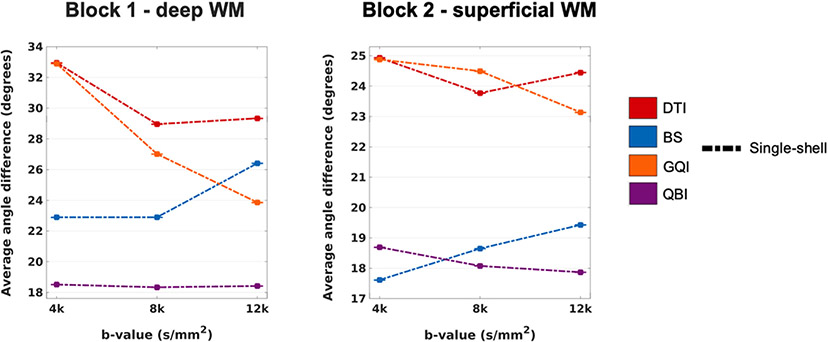
The average error curves of Fig. 5 show that, as expected, DTI had consistently high errors, in both samples and for all q-space sampling schemes. For data sampled on a grid in q-space, DSI and GQI had similarly low errors, with the former only narrowly outperforming the latter. This was observed in both samples. However, GQI did not perform well on the single- or multi-shell data, in either sample. A notable difference in performance between the two samples was observed for the BS model, which performed much better in superficial than in deep WM. In both samples, however, the BS model performed best on multi-shell data and worst on single-shell data, with data sampled on q-space grids landing somewhere in between. Finally, the performance of QBI was remarkably consistent, both between samples and between single- and multi-shell data. In all cases, its errors were somewhat higher than the best-case errors of DSI and GQI on grid data.

The voxel-wise error maps of Figs. 6 and 7 show which areas are driving the performance differences between reconstruction methods. For data sampled on a grid in q-space, DSI and GQI were able to capture the complex orientation patterns in the deep WM sample, such as the branching region dorsal to the striatum, and the most prominent patterns in the crossing region on the lateral portion of the slice (black arrow in Fig. 6). The BS model could also recover, to some extent, the orientations in the branching region, but less accurately so in the crossing region, where its orientation maps were more similar to those from DTI. The performance of the BS model was somewhat closer to that of GQI and DSI in the less challenging, superficial WM sample (Fig. 7).

When the data were sampled on a single shell, DTI and BS performed similarly in the deep WM sample, with BS having only slightly lower errors in the branching region where fibers split into the IC and EC, as well as in the more lateral crossing region (black arrow in Fig. 6). In these single-shell data, GQI performed very similarly to BS and DTI, exhibiting only slightly lower errors in the branching region. However, with multishell acquisitions, orientation estimates from GQI were much less accurate, particularly in the lateral region of the slice, which features extensive interdigitated crossings, and where the angular errors of GQI were similar to those of DTI. In the superficial WM sample (Fig. 7), the reconstruction methods that exhibited higher errors, such as DTI for all q-space sampling schemes and GQI for single- and multi-shell data, did so mainly because of errors in the complex area around the cingulate sulcus, where fibers were crossing and fanning. The BS model performed well on the multi-shell data from both samples, with angular errors in the branching and crossing regions that were similar to GQI and DSI on the grid datasets. Finally, the error maps from both samples confirm that the performance of QBI was remarkably consistent across areas with different fiber configurations, and between single- and multi-shell data.

Peak thresholding had an effect on these results mostly for the BS model. Fig. 6 indicates that the performance of this model in the deep WM sample was very close to that of DTI across all resolutions, for all but the multi-shell data. However, removing the volume fraction threshold of 0.01 yielded color maps and angular errors that are much closer to those obtained with the better-performing methods (Supplementary Figure 1). This suggests that the BS model estimated the orientation of the fiber populations in each voxel with good accuracy, but that it assigned an erroneously low volume fraction to some of them. This would have an impact on tractography, which would not follow those fiber populations by default.

3.5. Effect of dMRI acquisition scheme

When comparing the accuracy of the same reconstruction method across q-space sampling schemes, we found the differences between Grid_40k and Grid_25.6k to be minimal, especially for DSI, and to some extent for GQI. For these reconstruction methods, while Grid_40k performed somewhat better in the deep WM sample, Grid_25.6k performed marginally better for the superficial WM sample. This is perhaps due to the higher diffusion resolution of Grid_40k being even less crucial for capturing the less challenging configurations of the superficial WM, and hence the higher SNR of Grid_25.6k being more beneficial.

The most notable difference in accuracy between the multi- and single-shell data was for the BS model, which performed well with the former in both samples. The GQI reconstruction showed the greatest accuracy improvement when used on data acquired with a Cartesian grid scheme rather than a shell scheme, especially in the crossing-fiber regions of both samples.

3.6. Effect of spatial resolution

As seen in the angular error plots of Fig. 5, as well as the voxel-wise error maps of Figs. 6 and 7, the errors remained mostly stable between the resolutions of 0.25 mm, 0.5 mm, and 1 mm, but increased at 2 mm. This was a consistent trend across all combinations of reconstruction methods and sampling schemes, in both the deep and superficial WM samples. It was the case not only near gray-white matter boundaries, where partial volume effects were most severe, but also within the WM. The regions where fibers were more coherently organized, such the IC and EC in block 1 or the superior-inferior fiber bundle in block 2, could be reconstructed accurately by all methods, even at the lowest resolution. Therefore, the increase in errors with decreasing spatial resolution was greatest for areas with complex fiber configurations.

3.7. ROI-specific analyses

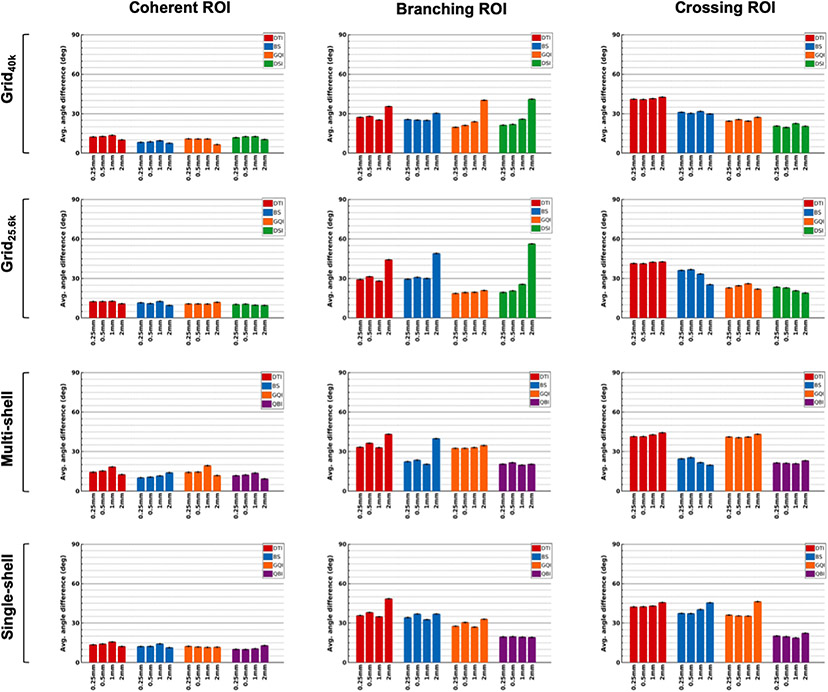
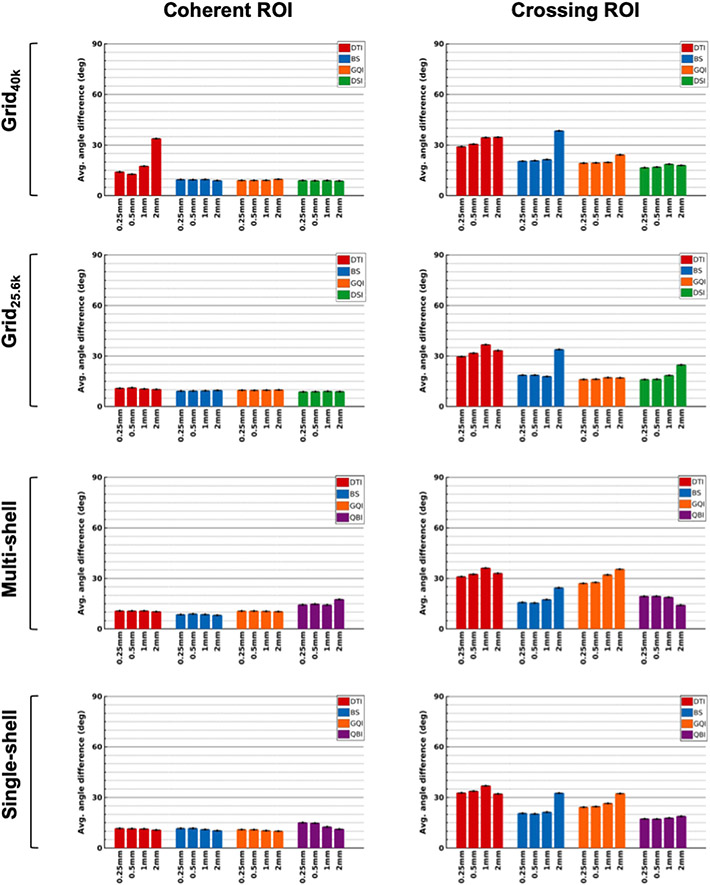
We further examined the differences between areas with varying degrees of organizational complexity by plotting angular errors between dMRI and PSOCT orientations within each of the ROIs shown in Fig. 3 (coherent, branching, and crossing). Fig. 8 shows bar plots of angular errors for each of the three ROIs from the deep WM sample (block 1). Fig. 9 shows the same for the two ROIs from the superficial WM sample (block 2). Average values and standard error bars were obtained from all PSOCT sections that overlapped each ROI.

Fig. 8. — The plots show absolute angular error between orientation vectors estimated from dMRI and measured with PSOCT, averaged over all PSOCT voxels in ROIs containing coherent (left), branching (center), and crossing fibers (right), with standard error bars.

Fig. 9. — The plots show absolute angular error between orientation vectors estimated from dMRI and measured with PSOCT, averaged over all PSOCT voxels in ROIs containing coherent (left) and crossing fibers (right), with standard error bars.

Fig. 10 shows the FODs obtained from PSOCT in each of the five ROIs. Example dMRI orientation vectors (reconstructed by DSI from the original Grid_40k data) are also shown for reference. For each ROI, we show colormaps of the orientation measured by PSOCT (top) and those estimated from dMRI at each spatial resolution (bottom). Note that the dMRI peaks shown in these colormaps are only the ones that were found to be the closest matches to PSOCT orientations in the same voxel – not necessarily all of the peaks detected by dMRI. The FODs computed from the PSOCT orientations in each dMRI voxel are shown as magenta outlines, with all dMRI peaks in the same voxel shown as green lines. These are overlaid on grayscale maps of the angular error between dMRI and PSOCT.

3.7.1. Regions of coherent fibers

All dMRI reconstruction methods were able to capture the fiber orientations in the coherent ROIs from both samples, with a mean angular error around 9°. This was consistent across sampling schemes and spatial resolutions. (Note that there were some errors in the border of the coherent ROI from block 1, due to partial volume effects in the gray-white matter interface.)

3.7.2. Region of branching fibers

As seen from the PSOCT orientations, this ROI contained fibers that split into two branches as they approached the striatum: one that continued into the EC (red/magenta), and one that turned into the IC (green). At the 0.25 mm resolution, dMRI was able to resolve the orientations of the two branches correctly. This was the case even for the DTI model, except at the center of the branching area, where both the EC- and IC-bound orientations were present within the same dMRI voxel. As the voxel size increased, the branching area was still resolved, albeit less precisely, and the reconstruction methods that can estimate multiple fiber populations per voxel benefitted from lower angular errors (Fig. 8, center). An exception was the GQI reconstruction, when performed on single- and multi-shell data, which recovered almost solely a single fiber orientation in each voxel, performing only marginally better than DTI. At a spatial resolution of 2 mm, most reconstruction methods suffered from a radical drop in accuracy and were generally able to recover only one of the two branches. The only two exceptions were QBI (for the shell sampling schemes) and GQI (for the Grid_25.6k sampling scheme), which could still recover both orientations. Interestingly, at 2 mm resolution, the branch corresponding to the least dominant fiber population (i.e., the one entering the EC) was the one reconstructed more consistently by all other methods.

3.7.3. Regions of crossing fibers

The crossing-fiber ROIs chosen from the two tissue blocks had different complexity. The crossing from the deep WM sample contained interdigitated fibers, hence fibers from all crossing bundles were present everywhere in a dMRI voxel. The crossing from the superficial WM sample contained more coherent bundles that occupied different parts of the dMRI voxel. Results show that the former was more challenging to reconstruct with dMRI that the latter (Figs. 8 and 9, right). First, the interdigitated crossing from block 1 exhibited overall higher average errors than the more separable crossing from block 2. Methods that exhibited high angular errors in the former had missed the green orientation shown in the optical data, and instead reconstructed peaks closer to the red and blue ones. This was another example of the less prevalent bundles in a voxel being reconstructed more easily than the more prevalent one. Such occurrences may be explained by differences in myelination between the bundles and merit further investigation. Second, while decreasing the dMRI voxel size from 2 mm to 1 mm allowed the separable crossing from block 2 to be resolved by some reconstruction methods, this was not the case for the interdigitated crossing from block 1, where errors remained high regardless of the spatial resolution.

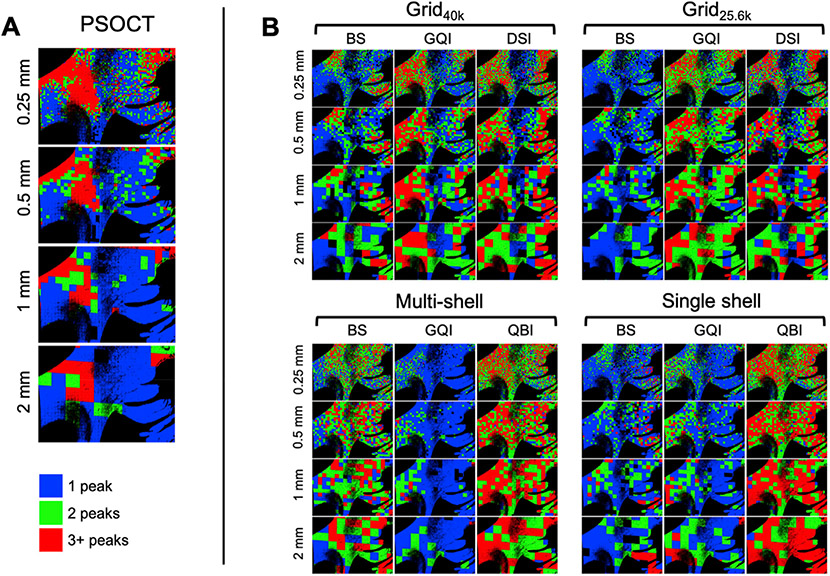
3.8. Number of detected fiber populations

In Fig. 11, we compare the total number of peaks detected by each dMRI reconstruction method at each spatial resolution, grouped by sampling scheme, to the number of peaks in the corresponding PSOCT FODs, for the deep WM sample (block 1). Fig. 11A shows maps of the number of peaks in each voxel (blue = 1, green = 2, and red = 3 or more) for the FODs that we obtained from the PSOCT orientations. The proportion of multi-peak voxels decreased as the resolution got coarser. At voxel sizes of 1 mm and greater, around 70% of voxels appeared to contain only 1 peak, while at a voxel size of 0.25 mm only about 45% of voxels had 1 peak and 35% had 3 peaks. We found the trend to continue when reducing the voxel size beyond the highest dMRI resolution (results not shown here). For example, at a voxel size of 0.1 mm, only 25% of voxels contained 1 peak while over 45% contained 3 peaks.

This trend may seem counter-intuitive at first, as the number of peaks is often used as a proxy for organizational complexity, and one would expect larger voxels to contain more complexity – not less. However, our finding matches that of a prior animal study that used myelin-stained images (Schilling et al., 2017). The general pattern is that, while smaller voxels may be found to contain distinct fiber populations, when more and more fibers are added as the voxel size increases, those fiber populations become more dispersed and may blend into a single fiber population.

The three ROIs that we considered in block 1 shed further light on this. In the coherent-fiber ROI, the PSOCT color map in Fig. 3 reveals that, in addition to the dominant (green) orientation, there is an additional (yellow/red) orientation that occurs with much lower frequency. At higher resolutions, this additional orientation may appear as a separate peak in the PSOCT FODs, even if it is missing at lower resolutions, where only the dominant orientation is present. In the branching-fiber ROI, there are three orientations: that of the descending fibers before they split, and those of the IC and EC bundles that they split into. If more and more of the IC and EC fiber are added as the voxel size increases, those may dominate, and it may appear as though there are two fiber populations instead of three. Finally, in the vicinity of the crossing-fiber ROI, which contains a 3-way intersection of interdigitated fibers, multiple peaks are found consistently at all resolutions.

Fig. 11B shows the number of peaks detected by each of the dMRI reconstruction methods that can model more than one fiber population per voxel, i.e., all except DTI. Here, we found greater variability between different combinations of reconstruction method and q-space sampling scheme than we did across resolutions. Comparing these images to the error maps of Figs. 6 and 7 suggests that, in general, the reconstruction methods that tended to find more peaks were also the ones that had lower angular errors.

Fig. 12 shows the same plots for the superficial WM sample (block 2), where the main trends are reproduced. That is, the number of peaks in the PSOCT FODs increased as the voxel size decreased, even in areas with highly coherent fibers, while the number of peaks detected by dMRI depended more on the reconstruction method than on the spatial resolution.

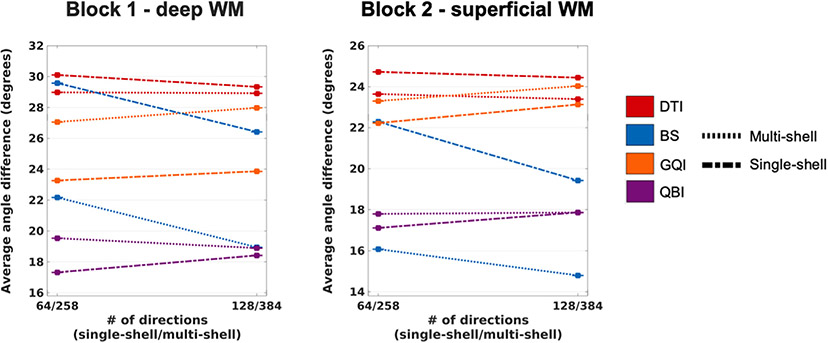
3.9. Effect of angular resolution at 1 mm spatial resolution

Plots of angular error for the multi-shell and single-shell datasets at 1 mm resolution with the original and reduced numbers of directions are shown in Fig. 13. In most cases, reducing the number of directions did not lead to a substantial loss of accuracy. The exception was the BS model, which exhibited much greater angular error with the reduced direction set, for both multi- and single-shell data. Conversely, QBI (for single-shell data) and GQI (for both multi- and single-shell data) exhibited slightly lower errors with the reduced direction set. These trends were remarkably consistent between the two samples.

Fig. 13. — The plots show the absolute angular error, averaged over all included WM voxels from all PSOCT sections in each sample, as a function of the number of gradient directions, at 1 mm spatial resolution. Line styles represent different q-space sampling schemes. Line colors represent different orientation reconstruction methods.

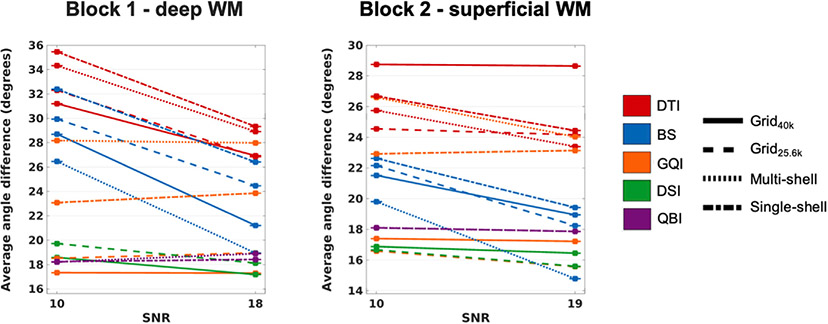
3.10. Effect of SNR at 1 mm spatial resolution

Plots of angular error for the 1 mm resolution data with and without added Rician noise are shown in Fig. 14. The decrease in SNR led to a substantial loss of accuracy only for DTI and BS. All other reconstruction methods were largely unaffected by the addition of noise. This observation was largely reproducible across q-space sampling schemes, and in both tissue blocks.

3.11. Effect of b-value on single-shell acquisitions at 1 mm spatial resolution

Plots of angular error for the single-shell data at 1 mm resolution data with various b-values are shown in Fig. 15. The change in b-value had a greater effect on accuracy in the more complex, deep WM sample than in the superficial WM sample. However, the trends were similar in both samples, e.g., decreasing the b-value led to increased error for GQI but decreased error for BS.

3.12. Effect of through-plane diffusion on in-plane orientation accuracy

In both samples, we found very low correlation coefficients between the in-plane angular error of the dMRI orientation vector and the maximum through-plane component of dMRI peaks in the same voxel (ρ = 0.075 and ρ = 0.0096, respectively, in block 1 and block 2). Results are reported for a DSI reconstruction of the original, full-grid, 0.25 mm-resolution data, but similar trends were observed for other datasets and reconstruction methods. Fig. 16 shows plots of the in-plane angular error vs. the through-plane component of the dMRI orientation. We binned the data into 10 levels of through-plane component magnitude. (This was done for the sake of visibility, given the large number of data points). As seen in the figure, for all levels of through-plane diffusion, the average in-plane error hovered around 15°. Therefore, we did not find any evidence in our data suggesting that high in-plane orientation errors may be explained by through-plane bundles that may be captured by dMRI but not PSOCT measurements.

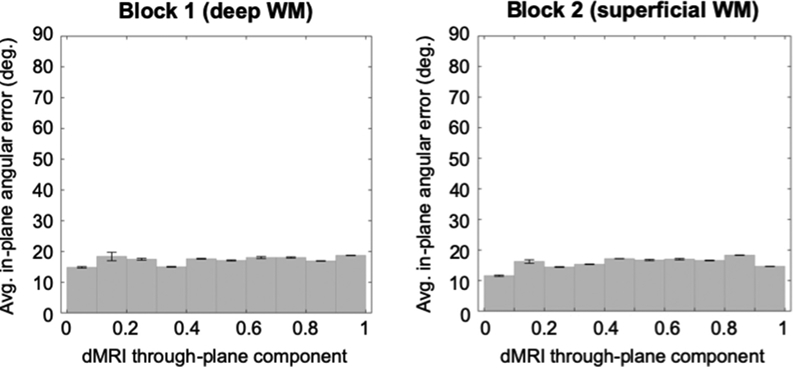
Fig. 16. — In-plane angular error between dMRI and PSOCT orientation vectors is plotted against the through-plane component of dMRI orientation vectors. Average values with standard error bars are shown, binned into 10 levels of through-plane dMRI orientation magnitude.

4. Discussion

This is the first study to compare PSOCT to high angular resolution dMRI in human brain. We compared the accuracy of voxel-wise orientation estimates obtained from a variety of dMRI reconstruction methods and q-space sampling schemes. Our goal was not to perform a “fair” comparison, where all the sampling schemes could be collected in the same amount of time; it was to compare a range of options that one may consider for a research study and to determine if the more demanding ones would pay off in terms of improved accuracy. To this end, we considered a three-shell sampling scheme that represents the state-of-the-art acquisitions used by big data collection efforts such as the HCP. We examined whether a much shorter acquisition, comprising only one of those three shells, would lead to substantially lower accuracy. Conversely, we investigated whether a much more demanding acquisition, with DSI-style, Cartesian-grid sampling and a much higher maximum b-value, would lead to substantially higher accuracy.

4.1. Effect of q-space sampling scheme

Based on the average angular error over all analyzed WM voxels (Fig. 5), the full Cartesian-grid sampling scheme achieves consistently high accuracy. This may be analyzed with DSI or GQI, as they both achieved similarly good performance. However, the reduced diffusion resolution grid, which included only half of the volumes and 2/3 of the maximum b-value, led to only about a 9% loss of accuracy when compared to the full grid in a deep WM sample, and it achieved higher accuracy than the full grid in a superficial WM sample. This was the case with either DSI or GQI, which again performed similarly. Overall, the best performance on the single-shell data was achieved with QBI reconstruction, while the best performance on the multi-shell data was achieved with the BS model. Those two combinations had very similar accuracy to the reduced grid data with DSI/GQI. The single- and multi-shell data included, respectively, about 1/4 and 3/4 of the number of volumes of the full grid data, and they both had 0.3 times the maximum b-value of the full grid data. Thus, it is possible to achieve similar accuracy with single-shell as with multi-shell data, if appropriate analysis methods are used, and to come within 10% of the accuracy of an even more demanding, full Cartesian-grid acquisition.

4.2. Effect of orientation reconstruction method

More generally, as can be seen in Fig. 5, it is how the data are analyzed that has the greatest impact on overall accuracy. For example, in the deep WM sample, there was a roughly 60% reduction in accuracy between the reconstruction method that performed best on the single-shell data (QBI) and the one that performed worst on the same data (DTI). The impact of the reconstruction method on accuracy does not appear to be related to a better fit to the dMRI signal. For example, in some cases, DTI exhibited higher accuracy on the grid data sets than the shell data sets, even though it should be, in principle, better able to fit the latter. Similarly, the BS model exhibited higher accuracy on both grid data sets than the single-shell data set, but lower than the multi-shell data set. This suggests that the goodness of fit to the dMRI signal may not necessarily be a proxy for the anatomical accuracy of model-based reconstruction methods.

4.3. Effect of spatial resolution

Spatial resolution also had an impact on accuracy. While the angular error in dMRI orientation estimates remained fairly stable between the resolutions of 0.25 mm–1 mm, it decreased when the voxel size was increased to 2 mm. This is underappreciated when looking at the overall results of Fig. 5, where the error is averaged over all WM voxels, regardless of the complexity of the axonal configurations that they contain. As can be seen in Figs. 8 and 9 (left column), in areas containing coherent fibers, accuracy is high across all resolutions, even at 2 mm. These areas, however, are unlikely to be the “junction points” where tractography goes wrong because it follows the wrong orientation. Such errors occur mostly in areas with complex configurations, like the spitting-fiber ROI in Fig. 8 (center column), where the angular error increased dramatically when the spatial resolution was reduced from 1 mm to 2 mm.

Before the HCP era, a resolution of 2 mm would have been considered the state of the art for in vivo dMRI. The development of accelerated sequences for simultaneous multi-slice dMRI (Setsompop et al., 2012) allowed the HCP to acquire dMRI data at a resolution of 1.5 mm (Setsompop et al., 2013; Van Essen et al., 2013). The lifespan and disease arms of the HCP are collecting data at 1.75 mm (Harms et al., 2018). Recent work is aimed at making dMRI resolutions of 1 mm or higher feasible in vivo (Eichner et al., 2014; Wu et al., 2016; Setsompop et al., 2018; Wang et al., 2018a). Our findings suggest that such a development could have a significant impact on the accuracy of dMRI orientation estimates in areas of complex axonal configurations. However, it would likely require a reduction in angular resolution or SNR. Our results indicate that a 2-fold reduction in the number of diffusion-encoding directions (Fig. 13) or a roughly 2-fold reduction in SNR (Fig. 14) does not have to offset the gains in accuracy achieved at a spatial resolution of 1 mm, but that analysis methods must be chosen carefully. This provides some insight into the trade-off between spatial and angular resolution and SNR, which could be optimized further using the methodology proposed here.

4.4. Considerations for acquisition and analysis

Our results show that discarding the high-b half of the data points from the Cartesian-grid sampling scheme led to only a moderate reduction in accuracy in the deep WM sample. Our ongoing work suggests that, if we instead omit data points that are distributed throughout q-space, in a compressed-sensing Cartesian grid scheme, we can achieve an even smaller loss of accuracy, with an even greater reduction in the number of volumes that need to be acquired, i.e., 3-fold or more, compared to the full grid (Jones et al., 2019). This type of scheme, combined with the accelerated sequences mentioned above, makes Cartesian-grid acquisitions practical for large-scale population studies (Tobisch et al., 2018).

Although Cartesian-grid sampling schemes achieved high accuracy in our study, a potential drawback is that they are not compatible with certain methods for dMRI orientation reconstruction or microstructural modeling that require data sampled on q-shells. The q-space resampling method that we proposed here can circumvent this. We have shown that the approximation errors incurred when resampling data from a grid to shells in q-space are negligible compared to variability due to imaging noise (Table 3), as long as the target q-shells correspond to lower b-values than the maximum b-value in the acquired grid data.

4.5. Relation to previous studies

In general, our results indicate that there is not a lot to be gained, in terms of the accuracy of the estimated axonal orientations in the human brain, by acquiring data at ultra-high b-values or with a large number of diffusion-encoding directions. This is in agreement with a recent animal study that compared the accuracy of orientations estimated with different single-shell dMRI data sets with respect to histology, in monkey brains (Schilling et al., 2018). That study found that there was negligible improvement in accuracy when the b-value of the single shell was increased from 6000 to 12,000 (the equivalent of 1500–3000 in vivo), or when the number of directions was increased from 64 to 96.

To date there has been no systematic study of the accuracy of different dMRI acquisition schemes in the human brain with respect to independent measurements of axonal orientations from a different modality. In the absence of ground truth, some in vivo human studies have compared different schemes with respect to other criteria. For example, one study used dMRI data oversampled in q-space as the gold standard and compared orientation estimates from those data to estimates from sparser sampling schemes (Kuo et al., 2008). The results showed that the performance of DSI was similar whether the data had been collected on a 515-point Cartesian grid or a grid with about half the data points and 0.6 times the maximum b-value; and that the performance of QBI was similar between data collected on a q-shell with 492 directions and one with 252 directions. Another study, using the goodness of fit to the dMRI signal as its figure of merit, determined that there was not much improvement above 45 directions and b = 3000 s/mm², for single-shell data reconstructed with constrained spherical deconvolution (Tournier et al., 2013). The two aforementioned studies utilized in vivo human dMRI data, collected at spatial resolutions of 2.7 mm and 3 mm, respectively, i.e., far lower than what we have found to be optimal. Nonetheless, they reported a similar trend, in terms of the limited benefit of very high b-values and numbers of directions for the estimation of dMRI orientations. This was also the case for a simulation study that compared a wide range of dMRI reconstruction approaches, using synthetic data generated from idealized combinations of 1–3 coherent axon populations (Daducci et al., 2013). The lowest angular error in that study was achieved with a Cartesian-grid sampling scheme and DSI reconstruction. However, its performance was not dramatically higher than that achieved by methods that utilized a single-shell scheme, even though the maximum b-value of the grid data was 2.7 times higher than the b-value of the single-shell data.

These few prior studies provide converging evidence that we are now able to confirm in real human data by comparison to ground-truth, microscopic measurements of axonal orientations from optical imaging. These findings do not prove that higher-b data, or more densely sampled data, do not contain any additional information that can help resolve different fiber configurations. They do suggest, however, that current reconstruction methods underutilize such data. This is not entirely surprising, as ultimately all of these methods reduce the data to some variant of an ODF.

Previous studies that compared dMRI orientation estimates to a reference considered an estimate satisfactory if the angular error was less than 20° in simulated data (Daducci et al., 2013) and less than 25° in animal data (Schilling et al., 2018). Based on this error tolerance, for each of the four q-space sampling schemes that we considered here, there was at least one reconstruction method that could provide satisfactory estimates at all levels of spatial resolution, on average over all WM voxels (Fig. 5). When examining the accuracy in the three ROIs (Fig. 8), all methods achieved satisfactory accuracy in the coherent-fiber ROI, almost no method achieved satisfactory accuracy in the branching-fiber ROI at a resolution of 2 mm, and the accuracy of DTI was not satisfactory in the branching- or crossing-fiber ROIs at any resolution. In the coherent-fiber ROI of Fig. 8, the average angular error was 9.5°±2.1° across all resolutions, sampling schemes, and reconstruction methods. This is consistent with prior work comparing dMRI to histological stains, where angular errors around 10° in areas with coherent fiber structure have been reported in monkey (Choe et al., 2012; Schilling et al. 2016, 2018) and human tissue (Seehaus et al., 2015). Comparing results in areas with more complex fiber configurations between different studies is not straightforward, as organizational complexity can differ across species and brain locations. In (Schilling et al., 2018), failure to resolve orientations (i.e., angular error consistently above 25°) was reported for voxels where fiber bundles crossed at an angle smaller than 60°. Our branching-fiber and crossing-fiber ROIs featured such angles, as can be seen in Fig. 3. Accordingly, angular errors in the branching-fiber ROI were 39.6°±15.1° at the lowest resolution and 28.5°±7.8° at the highest resolutions.

We were also able to reproduce, in human tissue, a finding from a study that used myelin staining to find the number of distinct fiber populations, or FOD peaks, per voxel in the monkey brain (Schilling et al., 2017). That is, when we computed FODs from the PSOCT orientations within each dMRI voxel, we found that the number of peaks detected in these FODs increased as the size of voxels decreased (Fig. 11). Of course, the complexity of the tissue contained in each voxel does not decrease as the voxel gets larger. On the contrary, for a sample with the organizational complexity shown in Fig. 3, we expect larger voxels to contain more and more complex fiber configurations. However, beyond a certain point, these configurations become so complex that they cannot be modeled as a set of distinct fiber populations with high intra-population coherence, which is what the concept of “peaks” implies. These results suggest that, at the spatial resolutions most commonly used for in vivo human dMRI, the number of FOD/ODF peaks may be a poor measure of WM organizational complexity, and a sparse set of fiber populations (peaks, sticks, etc.) may be a poor model for the underlying fiber architecture. In fact, this may be the reason why the branching-fiber ROI, which diverges from this model, exhibits such a degradation of accuracy at lower dMRI resolutions (between 1 mm and 2 mm).

4.6. Deep vs. superficial WM

In this work we analyzed data from two different brains. While many of the general trends were observed in both samples, several reconstruction methods exhibited higher absolute angular error in the deep WM than the superficial WM sample. The deep WM area contained more complex fiber configurations, including branching and interdigitated crossings. In the superficial WM area, while multiple fiber bundles were present, they were more clearly separated from each other. These observations are consistent with the findings of anatomical tracer injection studies in non-human primates (Lehman et al., 2011; Heilbronner and Haber, 2014; Safadi et al., 2018). Specifically, these studies show that axons leave the cortical injection site in a highly dense, coherent stalk. As they travel through the brain, subgroups of these axons branch off the main stalk and merge with different WM pathways, such as the IC, EC, corpus callosum, uncinate fasciculus, etc. In some of these pathways, axons that came from the same injection site may stay tightly bundled, while in other pathways they may become more dispersed and thus intermingle with axons from other cortical areas. Therefore it is not surprising to find well-organized axon bundles closer to the cortex and more challenging configurations, such as branching and interdigitated bundles, deeper in the WM. Of course, our observations here need to be confirmed by processing more human samples.

4.7. Limitations

A limitation of this study is that we have not evaluated all possible methods for reconstructing orientations from dMRI data. A previous study that compared a wider range of such methods on simulated data showed DTI and DSI to have, respectively, the lowest and highest accuracy (Daducci et al., 2013). Therefore, we expect that the methods tested here are representative of the range of attainable performance. We are currently organizing an open tractography challenge (https://irontract.mgh.harvard.edu). If any methods that we have not evaluated here prove superior to the ones that we have, we will also apply them to the data from the present work.

Post-mortem fixation alters the diffusive properties of tissue. Fixation with formaldehyde (used here) can alleviate significant autolytic degradation and shrinkage of tissue, which would otherwise diminish tissue quality (Dyrby et al., 2011). The extent of such damages is influenced by the length of time between death and fixation, or post-mortem interval (D’Arceuil and de Crespigny, 2007; Dyrby et al., 2011). Previous studies have demonstrated that while fixation decreases diffusivity by 60–80% compared to in vivo, features of diffusion anisotropy and fiber direction are preserved (D’Arceuil et al., 2007; McNab et al., 2009; Dyrby et al., 2011). We used b-values that were 4 times what their equivalent in vivo values would be to account for the decrease in diffusivity. Nonetheless, it is possible that some parameters may not be as accurately extrapolated, as the spin displacement microenvironment probed with the given diffusion time is likely influenced by a range of microstructural factors, such as membrane permeability, that may be altered by fixation (Roebroeck et al., 2019). Here we have focused on the orientation of axon bundles and used an imaging technique that does not introduce histological distortions. Thus we do not expect that structural properties such as the angles between bundles would change from their in vivo state.

A limitation of optical imaging is that measurements of the optic axis of tissues are not sensitive to all aspects of tissue microstructure that dMRI measurements are sensitive to. For example, we would not be able to compare the relative weight of FOD peaks obtained from dMRI to those obtained from optical imaging, as the diffusivity measured in a certain orientation depends not only on the proportion of axons along that orientation but on many other aspects of cell morphology. Hence we have only compared peak orientation angles between modalities here. Although the difference between the contrast mechanisms of the two modalities poses some limitations, there is merit in comparing dMRI orientation measurements against a modality that is independent of water diffusion.

A further limitation of PSOCT is that it measures the orientation of the optic axis within the plane perpendicular to the incident light, hence we restricted our error calculations to the in-plane component of the dMRI orientations. The PSOCT imaging plane must be chosen carefully. As the in-plane component of fiber orientation decreases, the back-scattered light collected by PSOCT also decreases, leading to lower signal and higher noise in the phase measurement. Here, we chose the PSOCT imaging plane for each sample (coronal for block 1, sagittal for block 2) to capture the main orientation of the majority of fibers in the sample. Furthermore, we excluded PSOCT voxels with low retardance, which would indicate fibers with a mostly through-plane optic axis. Finally, we investigated whether the error between the in-plane dMRI and PSOCT orientations could be explained by a high through-plane dMRI orientation component. Our results (Fig. 16) did not show evidence for such an association. Most prior studies that compared dMRI to histology (Leergaard et al., 2010; Budde and Frank, 2012; Choe et al., 2012; Seehaus et al., 2015; Schilling et al., 2017) or PLI (Mollink et al., 2017) have also done so in 2D. A few animal studies used confocal microscopy to compare 3D histological orientations to dMRI (Khan et al., 2015; Schilling et al. 2016, 2018). It is encouraging that the angular errors reported by prior studies seem to be in the same range, whether they were computed in 2D or in 3D, as dMRI is not expected to be less accurate in any direction. However, there is great value in having access to 3D ground-truth axonal orientations in the human brain, particularly for areas that may contain both in- and through-plane crossings. Extending the techniques described in this work to measure 3D orientation will allow such areas to be investigated more fully in the future.

One method that has been proposed to derive 3D orientations from PSOCT data is via structure tensor analysis of reflectivity or retardance volumes (Wang et al., 2015). The structure tensor is a gradient-based technique that has been used extensively for texture analysis (Axelsson, 2008; Krause et al., 2010). It has also been applied to histological sections (Khan et al., 2015; Schilling et al. 2016, 2018) to obtain 3D axonal orientations. It has been noted, however, to be sensitive to the size and type of the kernel used to calculate the spatial derivatives (Wang et al., 2015; Schilling et al., 2018). An alternative approach to reconstructing 3D axonal orientations from PSOCT would be by collecting optic axis measurements with two or more light incidence angles and using them to infer the through-plane orientation. This has been demonstrated in biological tissue (Ugryumova et al., 2006; Ugryumova et al., 2009; Liu et al., 2016).

Finally, a limitation of our current PSOCT setup is that it is unable to resolve multiple orientations within the depth of an optical section, introducing a bias towards the orientation of fibers closer to the superficial layer. In our experiment, we collected PSOCT data along a depth of 75–100 μm, which could reasonably include fibers organized along different orientations. Using a smaller depth profile would reduce this possibility but would also result in SNR loss and longer scan time. Depth resolved axis orientation has been reported in layered structures by modified PSOCT setups and numerical analysis (Kemp et al., 2005; Guo et al., 2004; Fan and Yao, 2013). Future work will aim to integrate depth-resolved, 3D orientation measurement into a novel PSOCT setup that combines serial multi-contrast imaging with automated slicing to enable detailed reconstruction of macroscopic volumes of tissue (Wang et al., 2018b). This should enable direct imaging of WM organization with unprecedented accuracy and detail and provide a true gold standard for dMRI.

5. Conclusion

We have presented the first study to use direct measurements of axonal orientations from PSOCT to evaluate the accuracy of various high angular resolution dMRI techniques in the human brain. Unlike histological approaches, PSOCT does not rely on staining or require image processing (e.g., structure tensor or Fourier analysis) to estimate orientations. Instead, it exploits the birefringence of myelin to obtain direct measurements of the optic axis of axon bundles. Furthermore, it does not suffer from the nonlinear distortions that result from cutting and mounting slices prior to imaging, as is done for histology or PLI. Instead, it images the superficial layer of a tissue block before sectioning it. This obviates the need for registration across slices, and also facilitates their alignment to dMRI volumes. Applying this method on complex areas of WM, we showed that it is possible for single-shell dMRI data to yield orientation estimates with the same accuracy as multi-shell data, and with no more than a 10% accuracy loss compared to a full Cartesian-grid acquisition. Our findings suggest that, with current analytical techniques, there are limited gains from ultra-high b-values or angular resolutions, in terms of the accuracy of dMRI orientation estimates. We also showed degradation in accuracy when the dMRI voxel size increased from 1 mm to 2 mm, particularly for areas of complex axonal configurations. This demonstrates the value of further dMRI sequence development to make high spatial resolutions practical for routine scanning. Finally, we used the PSOCT measurements to show that, at the voxel sizes that are currently common in vivo, axonal configurations in a voxel cannot be modeled by a small set of distinct fiber populations. Our results have implications for both the acquisition and analysis of dMRI data and illustrate the power of the PSOCT technique as a source of ground truth on the wiring of the human brain.

Supplementary Material

Supplementary data

NIHMS1741539-supplement-Supplementary_data.docx^{(2.1MB, docx)}

Acknowledgements

This work was funded by NIH grants R01-EB021265, K99-EB023993, R01-AG057672, R01-EB019956, and U01-MH117023. It was carried out at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies, P41-EB015896, a P41 Biotechnology Resource Grant supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health. This work also involved the use of instrumentation supported by the NIH Shared Instrumentation Grant Program (S10RR025563, S10RR023401, S10RR019307, and S10RR023043). Disclosures: 149 Medical develops a NIRS-DCS device for monitoring the hemodynamics of neonatal brains. Dr. Boas is a co-founder and owns private equity in the company. Humon develops wearable technology which uses NIRS-DCS to monitor hemoglobin levels in the muscles of athletes. Dr. Boas has a financial interest in the company. Dr. Boas’s interests were reviewed and are managed by MGH and Partners HealthCare in accordance with their conflict of interest policies.

Footnotes

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2020.116704.

References

Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N, 2010. Reconstruction of the orientation distribution function in single-and multiple-shell q-ball imaging within constant solid angle. Magn. Reson. Med 64 (2), 554–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ali S, Wörz S, Amunts K, Eils R, Axer M, Rohr K, 2018. Rigid and non-rigid registration of polarized light imaging data for 3D reconstruction of the temporal lobe of the human brain at micrometer resolution. Neuroimage 181, 235–251. [DOI] [PubMed] [Google Scholar]
Axelsson M, 2008. Estimating 3D Fibre Orientation in Volume Images. 2008 19th International Conference on Pattern Recognition. IEEE. [Google Scholar]
Basser PJ, Mattiello J, LeBihan D, 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J 66 (1), 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magn. Reson. Med 44 (4), 625–632. [DOI] [PubMed] [Google Scholar]
Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM, 2003. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 50 (5), 1077–1088. [DOI] [PubMed] [Google Scholar]
Behrens TE, Berg HJ, Jbabdi S, Rushworth MF, Woolrich MW, 2007. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34 (1), 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
Budde MD, Frank JA, 2012. Examining brain microstructure using structure tensor analysis of histological sections. Neuroimage 63 (1), 1–10. [DOI] [PubMed] [Google Scholar]
Canales-Rodríguez EJ, Melie-García L, Iturria-Medina Y, 2009. Mathematical description of q-space in spherical coordinates: exact q-ball imaging. Magn. Reson. Med 61 (6), 1350–1367. [DOI] [PubMed] [Google Scholar]
Caruyer E, Lenglet C, Sapiro G, Deriche R, 2013. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magn. Reson. Med 69 (6), 1534–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
Choe A, Stepniewska I, Colvin D, Ding Z, Anderson A, 2012. Validation of diffusion tensor MRI in the central nervous system using light microscopy: quantitative comparison of fiber properties. NMR Biomed. 25 (7), 900–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
Daducci A, Canales-Rodrı EJ, Descoteaux M, Garyfallidis E, Gur Y, Lin Y-C, Mani M, Merlet S, Paquette M, Ramirez-Manzanares A, 2013. Quantitative comparison of reconstruction methods for intra-voxel fiber recovery from diffusion MRI. IEEE Trans. Med. Imag 33 (2), 384–399. [DOI] [PubMed] [Google Scholar]
De Boer JF, Milner TE, van Gemert MJ, Nelson JS, 1997. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Optics Lett. 22 (12), 934–936. [DOI] [PubMed] [Google Scholar]
Descoteaux M, Angelino E, Fitzgibbons S, Deriche R, 2007. Regularized, fast, and robust analytical Q-ball imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 58 (3), 497–510. [DOI] [PubMed] [Google Scholar]
Dyrby TB, Baaré WF, Alexander DC, Jelsing J, Garde E, Søgaard LV, 2011. An ex vivo imaging pipeline for producing high-quality and high-resolution diffusion-weighted imaging datasets. Hum. Brain Mapp 32 (4), 544–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
D’Arceuil H, de Crespigny A, 2007. The effects of brain tissue decomposition on diffusion tensor imaging and tractography. Neuroimage 36 (1), 64–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
D’Arceuil HE, Westmoreland S, de Crespigny AJ, 2007. An approach to high resolution diffusion tensor imaging in fixed primate brain. Neuroimage 35 (2), 553–565. [DOI] [PubMed] [Google Scholar]
Eichner C, Setsompop K, Koopmans PJ, Lützkendorf R, Norris DG, Turner R, Wald LL, Heidemann RM, 2014. Slice accelerated diffusion-weighted imaging at ultra-high field strength. Magn. Reson. Med 71 (4), 1518–1525. [DOI] [PubMed] [Google Scholar]
Fan C, Yao G, 2013. Imaging myocardial fiber orientation using polarization sensitive optical coherence tomography. Biomed. Optic Express 4, 460–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fessler JA, Sutton BP, 2003. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process 51 (2), 560–574. [Google Scholar]
Guo S, Zhang J, Wang L, Nelson JS, Chen Z, 2004. Depth-resolved birefringence and differential optical axis orientation measurements with fiber-based polarization-sensitive optical coherence tomography. Opt. Lett 29 (17), 2025–2027. [DOI] [PubMed] [Google Scholar]
Harms MP, Somerville LH, Ances BM, Andersson J, Barch DM, Bastiani M, Bookheimer SY, Brown TB, Buckner RL, Burgess GC, 2018. Extending the Human Connectome Project across ages: imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heilbronner SR, Haber SN, 2014. Frontal cortical and subcortical projections provide a basis for segmenting the cingulum bundle: implications for neuroimaging and psychiatric disorders. J. Neurosci 34 (30), 10041–10054. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hitzenberger C, Goetzinger E, Sticker M, Pircher M, Fercher A, 2001. Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography. Optic Express 9 (13), 780–790. [DOI] [PubMed] [Google Scholar]
Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TE, 2012. Model-based analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn. Reson. Med 68 (6), 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jones RJ, Grisot G, Augustinack J, Boas DA, Fischl B, Wang H, Bilgic B, Yendiki A, 2019. Validation of DSI compressed sensing reconstruction in ex vivo human brain. ISMRM (Oral Presentation). [Google Scholar]
Kemp NJ, Zaatari HN, Park J, Rylander III HG, Thomas M, 2005. Depth-resolved optic axis orientation in multiple layered anisotropic tissues measured with enhanced polarization-sensitive optical coherence tomography (EPS-OCT). Optic Express 13, 4507–4518. [DOI] [PubMed] [Google Scholar]
Khan AR, Cornea A, Leigland LA, Kohama SG, Jespersen SN, Kroenke CD, 2015. 3D structure tensor analysis of light microscopy data for validating diffusion MRI. Neuroimage 111, 192–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krause M, Hausherr J-M, Burgeth B, Herrmann C, Krenkel W, 2010. Determination of the fibre orientation in composites using the structure tensor and local X-ray transform. J. Mater. Sci 45 (4), 888–896. [Google Scholar]
Kuo L-W, Chen J-H, Wedeen VJ, Tseng W-YI, 2008. Optimization of diffusion spectrum imaging and q-ball imaging on clinical MRI system. Neuroimage 41 (1), 7–18. [DOI] [PubMed] [Google Scholar]
Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H, 2001. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imag.: Off. J. Int. Soc. Magn. Reson. Med 13 (4), 534–546. [DOI] [PubMed] [Google Scholar]
Leergaard TB, White NS, De Crespigny A, Bolstad I, D’Arceuil H, Bjaalie JG, Dale AM, 2010. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PloS One 5 (1), e8595. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lehman JF, Greenberg BD, McIntyre CC, Rasmussen SA, Haber SN, 2011. Rules ventral prefrontal cortical axons use to reach their targets: implications for diffusion tensor imaging tractography and deep brain stimulation for psychiatric illness. J. Neurosci 31 (28), 10392–10402. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li Q, Karnowski K, Noble PB, Cairncross A, James A, Villiger M, Sampson DD, 2018. Robust reconstruction of local optic axis orientation with fiber-based polarization-sensitive optical coherence tomography. Biomed. Optic Express 9 (11), 5437–5455. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liewald D, Miller R, Logothetis N, Wagner H-J, Schüz A, 2014. Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque. Biol. Cybern 108 (5), 541–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu CJ, Black AJ, Wang H, Akkin T, 2016. Quantifying three-dimensional optic axis using polarization-sensitive optical coherence tomography. J. Biomed. Optic 21 (7), 070501. [DOI] [PubMed] [Google Scholar]
Magnain C, Augustinack JC, Reuter M, Wachinger C, Frosch MP, Ragan T, Akkin T, Wedeen VJ, Boas DA, Fischl B, 2014. Blockface histology with optical coherence tomography: a comparison with Nissl staining. Neuroimage 84, 524–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
Majka P, Wójcik DK, 2016. Possum - a framework for three-dimensional reconstruction of brain images from serial sections. Neuroinformatics 14 (3), 265–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
McNab JA, Jbabdi S, Deoni SC, Douaud G, Behrens TE, Miller KL, 2009. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage 46 (3), 775–785. [DOI] [PubMed] [Google Scholar]
Mollink J, Kleinnijenhuis M, van Walsum A.-M. v. C., Sotiropoulos SN, Cottaar M, Mirfin C, Heinrich MP, Jenkinson M, Pallebage-Gamarallage M, Ansorge O, 2017. Evaluating fibre orientation dispersion in white matter: comparison of diffusion MRI, histology and polarized light imaging. Neuroimage 157, 561–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nakaji H, Kouyama N, Muragaki Y, Kawakami Y, Iseki H, 2008. Localization of nerve fiber bundles by polarization-sensitive optical coherence tomography. J. Neurosci. Methods 174 (1), 82–90. [DOI] [PubMed] [Google Scholar]
Özarslan E, Shepherd TM, Vemuri BC, Blackband SJ, Mareci TH, 2006. Resolution of complex tissue microarchitecture using the diffusion orientation transform (DOT). Neuroimage 31 (3), 1086–1103. [DOI] [PubMed] [Google Scholar]
Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin J-F, LeBihan D, 2005. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Phil. Trans. Biol. Sci 360 (1457), 881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF, 2008. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 60 (6), 1276–1283. [DOI] [PubMed] [Google Scholar]
Preibisch S, Saalfeld S, Tomancak P, 2009. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 25 (11), 1463–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Reuter M, Rosas HD, Fischl B, 2010. Highly accurate inverse consistent registration: a robust approach. Neuroimage 53 (4), 1181–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
Roebroeck A, Miller KL, Aggarwal M, 2019. Ex vivo diffusion MRI of the human brain: technical challenges and recent advances. NMR Biomed. 32 (4), e3941. [DOI] [PMC free article] [PubMed] [Google Scholar]
Safadi Z, Grisot G, Jbabdi S, Behrens T, Heilbronner SR, Mandeville J, Versace A, Phillips ML, Yendiki A, Haber SN, 2018. Functional segmentation of the internal capsule: linking white matter abnormalities to specific connections. J. Neurosci 38 (8), 2106–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schilling K, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2016. Comparison of 3D orientation distribution functions measured with confocal microscopy and diffusion MRI. Neuroimage 129, 185–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schilling K, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW, 2017. Can increased spatial resolution solve the crossing fiber problem for diffusion MRI? NMR Biomed. 30 (12), e3787. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schilling KG, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2018. Histological validation of diffusion MRI fiber orientation distributions and dispersion. Neuroimage 165, 200–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, 2012. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9 (7), 676. [DOI] [PMC free article] [PubMed] [Google Scholar]
Seehaus A, Roebroeck A, Bastiani M, Fonseca L, Bratzke H, Lori N, Vilanova A, Goebel R, Galuske R, 2015. Histological validation of high-resolution DTI in human post mortem tissue. Front. Neuroanat 9, 98. [DOI] [PMC free article] [PubMed] [Google Scholar]
Setsompop K, Cohen-Adad J, Gagoski B, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL, 2012. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 63 (1), 569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL, 2013. Pushing the limits of in vivo diffusion MRI for the human connectome project. Neuroimage 80, 220–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T, 2018. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: simultaneous multislice (g S lider-SMS). Magn. Reson. Med 79 (1), 141–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stejskal EO, Tanner JE, 1965. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys 42 (1), 288–292. [Google Scholar]
Susuki K, 2010. Myelin: a specialized membrane for cell communication. Nat. Educ 3, 59. [Google Scholar]
Tobisch A, Stirnberg R, Harms RL, Schultz T, Roebroeck A, Breteler M, Stöcker T, 2018. Compressed sensing diffusion spectrum imaging for accelerated diffusion microstructure MRI in long-term population imaging. Front. Neurosci 12, 650. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tournier J-D, 2010. The biophysics of crossing fibres. In: Jones DK (Ed.), Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, USA, pp. 465–482. [Google Scholar]
Tournier JD, Calamante F, King M, Gadian D, Connelly A, 2002. Limitations and requirements of diffusion tensor fiber tracking: an assessment using simulations. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 47 (4), 701–708. [DOI] [PubMed] [Google Scholar]
Tournier J-D, Calamante F, Connelly A, 2007. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35 (4), 1459–1472. [DOI] [PubMed] [Google Scholar]
Tournier JD, Calamante F, Connelly A, 2013. Determination of the appropriate b value and number of gradient directions for high-angular-resolution diffusion-weighted imaging. NMR Biomed. 26 (12), 1775–1786. [DOI] [PubMed] [Google Scholar]
Tuch DS, 2004. Q-ball imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 52 (6), 1358–1372. [DOI] [PubMed] [Google Scholar]
Ugryumova N, Gangnus SV, Matcher SJ, 2006. Three-dimensional optic axis determination using variable-incidence-angle polarization-optical coherence tomography. Optics Lett. 31 (15), 2305–2307. [DOI] [PubMed] [Google Scholar]
Ugryumova N, Jacobs J, Bonesi M, Matcher SJ, 2009. Novel optical imaging technique to determine the 3-D orientation of collagen fibers in cartilage: variable-incidence angle polarization-sensitive optical coherence tomography. Osteoarthritis Cartilage 17 (1), 33–42. [DOI] [PubMed] [Google Scholar]
Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, 2013. The Wu-Minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang H, Akkin T, Magnain C, Wang R, Dubb J, Kostis WJ, Yaseen MA, Cramer A, Sakadžić S, Boas D, 2016. Polarization sensitive optical coherence microscopy for brain imaging. Opt. Lett 41 (10), 2213–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang H, Al-Qaisi MK, Akkin T, 2010. Polarization-maintaining fiber based polarization-sensitive optical coherence tomography in spectral domain. Optics Lett. 35 (2), 154–156. [DOI] [PubMed] [Google Scholar]
Wang H, Magnain C, Wang R, Dubb J, Varjabedian A, Tirrell LS, Stevens A, Augustinack JC, Konukoglu E, Aganj I, 2018b. as-PSOCT: volumetric microscopic imaging of human brain architecture and connectivity. Neuroimage 165, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang H, Zhu J, Reuter M, Vinke LN, Yendiki A, Boas DA, Fischl B, Akkin T, 2014. Cross-validation of serial optical coherence scanning and diffusion tensor imaging: a study on neural fiber maps in human medulla oblongata. Neuroimage 100, 395–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang F, Bilgic B, Dong Z, Manhard MK, Ohringer N, Zhao B, Haskell M, Cauley SF, Fan Q, Witzel T, 2018a. Motion-robust sub-millimeter isotropic diffusion imaging through motion corrected generalized slice dithered enhanced resolution (MC-gSlider) acquisition. Magn. Reson. Med 80 (5), 1891–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang H, Lenglet C, Akkin T, 2015. Structure tensor analysis of serial optical coherence scanner images for mapping fiber orientations and tractography in the brain. J. Biomed. Optic 20 (3), 036003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM, 2005. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med 54 (6), 1377–1386. [DOI] [PubMed] [Google Scholar]
Wu W, Poser BA, Douaud G, Frost R, In M-H, Speck O, Koopmans PJ, Miller KL, 2016. High-resolution diffusion MRI at 7T using a three-dimensional multi-slab acquisition. Neuroimage 143, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yeh F-C, Wedeen VJ, Tseng W-YI, 2010. Generalized q-sampling imaging. IEEE Trans. Med. Imag 29 (9), 1626–1635. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary data

NIHMS1741539-supplement-Supplementary_data.docx^{(2.1MB, docx)}

[R1] Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N, 2010. Reconstruction of the orientation distribution function in single-and multiple-shell q-ball imaging within constant solid angle. Magn. Reson. Med 64 (2), 554–566. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Ali S, Wörz S, Amunts K, Eils R, Axer M, Rohr K, 2018. Rigid and non-rigid registration of polarized light imaging data for 3D reconstruction of the temporal lobe of the human brain at micrometer resolution. Neuroimage 181, 235–251. [DOI] [PubMed] [Google Scholar]

[R3] Axelsson M, 2008. Estimating 3D Fibre Orientation in Volume Images. 2008 19th International Conference on Pattern Recognition. IEEE. [Google Scholar]

[R4] Basser PJ, Mattiello J, LeBihan D, 1994. MR diffusion tensor spectroscopy and imaging. Biophys. J 66 (1), 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magn. Reson. Med 44 (4), 625–632. [DOI] [PubMed] [Google Scholar]

[R6] Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM, 2003. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 50 (5), 1077–1088. [DOI] [PubMed] [Google Scholar]

[R7] Behrens TE, Berg HJ, Jbabdi S, Rushworth MF, Woolrich MW, 2007. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34 (1), 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Budde MD, Frank JA, 2012. Examining brain microstructure using structure tensor analysis of histological sections. Neuroimage 63 (1), 1–10. [DOI] [PubMed] [Google Scholar]

[R9] Canales-Rodríguez EJ, Melie-García L, Iturria-Medina Y, 2009. Mathematical description of q-space in spherical coordinates: exact q-ball imaging. Magn. Reson. Med 61 (6), 1350–1367. [DOI] [PubMed] [Google Scholar]

[R10] Caruyer E, Lenglet C, Sapiro G, Deriche R, 2013. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magn. Reson. Med 69 (6), 1534–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Choe A, Stepniewska I, Colvin D, Ding Z, Anderson A, 2012. Validation of diffusion tensor MRI in the central nervous system using light microscopy: quantitative comparison of fiber properties. NMR Biomed. 25 (7), 900–908. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Daducci A, Canales-Rodrı EJ, Descoteaux M, Garyfallidis E, Gur Y, Lin Y-C, Mani M, Merlet S, Paquette M, Ramirez-Manzanares A, 2013. Quantitative comparison of reconstruction methods for intra-voxel fiber recovery from diffusion MRI. IEEE Trans. Med. Imag 33 (2), 384–399. [DOI] [PubMed] [Google Scholar]

[R13] De Boer JF, Milner TE, van Gemert MJ, Nelson JS, 1997. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Optics Lett. 22 (12), 934–936. [DOI] [PubMed] [Google Scholar]

[R14] Descoteaux M, Angelino E, Fitzgibbons S, Deriche R, 2007. Regularized, fast, and robust analytical Q-ball imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 58 (3), 497–510. [DOI] [PubMed] [Google Scholar]

[R15] Dyrby TB, Baaré WF, Alexander DC, Jelsing J, Garde E, Søgaard LV, 2011. An ex vivo imaging pipeline for producing high-quality and high-resolution diffusion-weighted imaging datasets. Hum. Brain Mapp 32 (4), 544–563. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] D’Arceuil H, de Crespigny A, 2007. The effects of brain tissue decomposition on diffusion tensor imaging and tractography. Neuroimage 36 (1), 64–68. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] D’Arceuil HE, Westmoreland S, de Crespigny AJ, 2007. An approach to high resolution diffusion tensor imaging in fixed primate brain. Neuroimage 35 (2), 553–565. [DOI] [PubMed] [Google Scholar]

[R18] Eichner C, Setsompop K, Koopmans PJ, Lützkendorf R, Norris DG, Turner R, Wald LL, Heidemann RM, 2014. Slice accelerated diffusion-weighted imaging at ultra-high field strength. Magn. Reson. Med 71 (4), 1518–1525. [DOI] [PubMed] [Google Scholar]

[R19] Fan C, Yao G, 2013. Imaging myocardial fiber orientation using polarization sensitive optical coherence tomography. Biomed. Optic Express 4, 460–465. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Fessler JA, Sutton BP, 2003. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process 51 (2), 560–574. [Google Scholar]

[R21] Guo S, Zhang J, Wang L, Nelson JS, Chen Z, 2004. Depth-resolved birefringence and differential optical axis orientation measurements with fiber-based polarization-sensitive optical coherence tomography. Opt. Lett 29 (17), 2025–2027. [DOI] [PubMed] [Google Scholar]

[R22] Harms MP, Somerville LH, Ances BM, Andersson J, Barch DM, Bastiani M, Bookheimer SY, Brown TB, Buckner RL, Burgess GC, 2018. Extending the Human Connectome Project across ages: imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Heilbronner SR, Haber SN, 2014. Frontal cortical and subcortical projections provide a basis for segmenting the cingulum bundle: implications for neuroimaging and psychiatric disorders. J. Neurosci 34 (30), 10041–10054. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] Hitzenberger C, Goetzinger E, Sticker M, Pircher M, Fercher A, 2001. Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography. Optic Express 9 (13), 780–790. [DOI] [PubMed] [Google Scholar]

[R25] Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TE, 2012. Model-based analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn. Reson. Med 68 (6), 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Jones RJ, Grisot G, Augustinack J, Boas DA, Fischl B, Wang H, Bilgic B, Yendiki A, 2019. Validation of DSI compressed sensing reconstruction in ex vivo human brain. ISMRM (Oral Presentation). [Google Scholar]

[R27] Kemp NJ, Zaatari HN, Park J, Rylander III HG, Thomas M, 2005. Depth-resolved optic axis orientation in multiple layered anisotropic tissues measured with enhanced polarization-sensitive optical coherence tomography (EPS-OCT). Optic Express 13, 4507–4518. [DOI] [PubMed] [Google Scholar]

[R28] Khan AR, Cornea A, Leigland LA, Kohama SG, Jespersen SN, Kroenke CD, 2015. 3D structure tensor analysis of light microscopy data for validating diffusion MRI. Neuroimage 111, 192–203. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Krause M, Hausherr J-M, Burgeth B, Herrmann C, Krenkel W, 2010. Determination of the fibre orientation in composites using the structure tensor and local X-ray transform. J. Mater. Sci 45 (4), 888–896. [Google Scholar]

[R30] Kuo L-W, Chen J-H, Wedeen VJ, Tseng W-YI, 2008. Optimization of diffusion spectrum imaging and q-ball imaging on clinical MRI system. Neuroimage 41 (1), 7–18. [DOI] [PubMed] [Google Scholar]

[R31] Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H, 2001. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imag.: Off. J. Int. Soc. Magn. Reson. Med 13 (4), 534–546. [DOI] [PubMed] [Google Scholar]

[R32] Leergaard TB, White NS, De Crespigny A, Bolstad I, D’Arceuil H, Bjaalie JG, Dale AM, 2010. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PloS One 5 (1), e8595. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Lehman JF, Greenberg BD, McIntyre CC, Rasmussen SA, Haber SN, 2011. Rules ventral prefrontal cortical axons use to reach their targets: implications for diffusion tensor imaging tractography and deep brain stimulation for psychiatric illness. J. Neurosci 31 (28), 10392–10402. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Li Q, Karnowski K, Noble PB, Cairncross A, James A, Villiger M, Sampson DD, 2018. Robust reconstruction of local optic axis orientation with fiber-based polarization-sensitive optical coherence tomography. Biomed. Optic Express 9 (11), 5437–5455. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Liewald D, Miller R, Logothetis N, Wagner H-J, Schüz A, 2014. Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque. Biol. Cybern 108 (5), 541–557. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Liu CJ, Black AJ, Wang H, Akkin T, 2016. Quantifying three-dimensional optic axis using polarization-sensitive optical coherence tomography. J. Biomed. Optic 21 (7), 070501. [DOI] [PubMed] [Google Scholar]

[R37] Magnain C, Augustinack JC, Reuter M, Wachinger C, Frosch MP, Ragan T, Akkin T, Wedeen VJ, Boas DA, Fischl B, 2014. Blockface histology with optical coherence tomography: a comparison with Nissl staining. Neuroimage 84, 524–533. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Majka P, Wójcik DK, 2016. Possum - a framework for three-dimensional reconstruction of brain images from serial sections. Neuroinformatics 14 (3), 265–278. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] McNab JA, Jbabdi S, Deoni SC, Douaud G, Behrens TE, Miller KL, 2009. High resolution diffusion-weighted imaging in fixed human brain using diffusion-weighted steady state free precession. Neuroimage 46 (3), 775–785. [DOI] [PubMed] [Google Scholar]

[R40] Mollink J, Kleinnijenhuis M, van Walsum A.-M. v. C., Sotiropoulos SN, Cottaar M, Mirfin C, Heinrich MP, Jenkinson M, Pallebage-Gamarallage M, Ansorge O, 2017. Evaluating fibre orientation dispersion in white matter: comparison of diffusion MRI, histology and polarized light imaging. Neuroimage 157, 561–574. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Nakaji H, Kouyama N, Muragaki Y, Kawakami Y, Iseki H, 2008. Localization of nerve fiber bundles by polarization-sensitive optical coherence tomography. J. Neurosci. Methods 174 (1), 82–90. [DOI] [PubMed] [Google Scholar]

[R42] Özarslan E, Shepherd TM, Vemuri BC, Blackband SJ, Mareci TH, 2006. Resolution of complex tissue microarchitecture using the diffusion orientation transform (DOT). Neuroimage 31 (3), 1086–1103. [DOI] [PubMed] [Google Scholar]

[R43] Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin J-F, LeBihan D, 2005. Validation of q-ball imaging with a diffusion fibre-crossing phantom on a clinical scanner. Phil. Trans. Biol. Sci 360 (1457), 881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF, 2008. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 60 (6), 1276–1283. [DOI] [PubMed] [Google Scholar]

[R45] Preibisch S, Saalfeld S, Tomancak P, 2009. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 25 (11), 1463–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Reuter M, Rosas HD, Fischl B, 2010. Highly accurate inverse consistent registration: a robust approach. Neuroimage 53 (4), 1181–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Roebroeck A, Miller KL, Aggarwal M, 2019. Ex vivo diffusion MRI of the human brain: technical challenges and recent advances. NMR Biomed. 32 (4), e3941. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Safadi Z, Grisot G, Jbabdi S, Behrens T, Heilbronner SR, Mandeville J, Versace A, Phillips ML, Yendiki A, Haber SN, 2018. Functional segmentation of the internal capsule: linking white matter abnormalities to specific connections. J. Neurosci 38 (8), 2106–2117. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Schilling K, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2016. Comparison of 3D orientation distribution functions measured with confocal microscopy and diffusion MRI. Neuroimage 129, 185–197. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Schilling K, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW, 2017. Can increased spatial resolution solve the crossing fiber problem for diffusion MRI? NMR Biomed. 30 (12), e3787. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Schilling KG, Janve V, Gao Y, Stepniewska I, Landman BA, Anderson AW, 2018. Histological validation of diffusion MRI fiber orientation distributions and dispersion. Neuroimage 165, 200–221. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, 2012. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9 (7), 676. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R53] Seehaus A, Roebroeck A, Bastiani M, Fonseca L, Bratzke H, Lori N, Vilanova A, Goebel R, Galuske R, 2015. Histological validation of high-resolution DTI in human post mortem tissue. Front. Neuroanat 9, 98. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Setsompop K, Cohen-Adad J, Gagoski B, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL, 2012. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 63 (1), 569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL, 2013. Pushing the limits of in vivo diffusion MRI for the human connectome project. Neuroimage 80, 220–233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley SF, Nummenmaa A, Wang F, Rathi Y, Witzel T, 2018. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: simultaneous multislice (g S lider-SMS). Magn. Reson. Med 79 (1), 141–151. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Stejskal EO, Tanner JE, 1965. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys 42 (1), 288–292. [Google Scholar]

[R58] Susuki K, 2010. Myelin: a specialized membrane for cell communication. Nat. Educ 3, 59. [Google Scholar]

[R59] Tobisch A, Stirnberg R, Harms RL, Schultz T, Roebroeck A, Breteler M, Stöcker T, 2018. Compressed sensing diffusion spectrum imaging for accelerated diffusion microstructure MRI in long-term population imaging. Front. Neurosci 12, 650. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] Tournier J-D, 2010. The biophysics of crossing fibres. In: Jones DK (Ed.), Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, USA, pp. 465–482. [Google Scholar]

[R61] Tournier JD, Calamante F, King M, Gadian D, Connelly A, 2002. Limitations and requirements of diffusion tensor fiber tracking: an assessment using simulations. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 47 (4), 701–708. [DOI] [PubMed] [Google Scholar]

[R62] Tournier J-D, Calamante F, Connelly A, 2007. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35 (4), 1459–1472. [DOI] [PubMed] [Google Scholar]

[R63] Tournier JD, Calamante F, Connelly A, 2013. Determination of the appropriate b value and number of gradient directions for high-angular-resolution diffusion-weighted imaging. NMR Biomed. 26 (12), 1775–1786. [DOI] [PubMed] [Google Scholar]

[R64] Tuch DS, 2004. Q-ball imaging. Magn. Reson. Med.: Off. J. Int. Soc. Magn. Reson. Med 52 (6), 1358–1372. [DOI] [PubMed] [Google Scholar]

[R65] Ugryumova N, Gangnus SV, Matcher SJ, 2006. Three-dimensional optic axis determination using variable-incidence-angle polarization-optical coherence tomography. Optics Lett. 31 (15), 2305–2307. [DOI] [PubMed] [Google Scholar]

[R66] Ugryumova N, Jacobs J, Bonesi M, Matcher SJ, 2009. Novel optical imaging technique to determine the 3-D orientation of collagen fibers in cartilage: variable-incidence angle polarization-sensitive optical coherence tomography. Osteoarthritis Cartilage 17 (1), 33–42. [DOI] [PubMed] [Google Scholar]

[R67] Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium W-MH, 2013. The Wu-Minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Wang H, Akkin T, Magnain C, Wang R, Dubb J, Kostis WJ, Yaseen MA, Cramer A, Sakadžić S, Boas D, 2016. Polarization sensitive optical coherence microscopy for brain imaging. Opt. Lett 41 (10), 2213–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Wang H, Al-Qaisi MK, Akkin T, 2010. Polarization-maintaining fiber based polarization-sensitive optical coherence tomography in spectral domain. Optics Lett. 35 (2), 154–156. [DOI] [PubMed] [Google Scholar]

[R70] Wang H, Magnain C, Wang R, Dubb J, Varjabedian A, Tirrell LS, Stevens A, Augustinack JC, Konukoglu E, Aganj I, 2018b. as-PSOCT: volumetric microscopic imaging of human brain architecture and connectivity. Neuroimage 165, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R71] Wang H, Zhu J, Reuter M, Vinke LN, Yendiki A, Boas DA, Fischl B, Akkin T, 2014. Cross-validation of serial optical coherence scanning and diffusion tensor imaging: a study on neural fiber maps in human medulla oblongata. Neuroimage 100, 395–404. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Wang F, Bilgic B, Dong Z, Manhard MK, Ohringer N, Zhao B, Haskell M, Cauley SF, Fan Q, Witzel T, 2018a. Motion-robust sub-millimeter isotropic diffusion imaging through motion corrected generalized slice dithered enhanced resolution (MC-gSlider) acquisition. Magn. Reson. Med 80 (5), 1891–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Wang H, Lenglet C, Akkin T, 2015. Structure tensor analysis of serial optical coherence scanner images for mapping fiber orientations and tractography in the brain. J. Biomed. Optic 20 (3), 036003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM, 2005. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med 54 (6), 1377–1386. [DOI] [PubMed] [Google Scholar]

[R75] Wu W, Poser BA, Douaud G, Frost R, In M-H, Speck O, Koopmans PJ, Miller KL, 2016. High-resolution diffusion MRI at 7T using a three-dimensional multi-slab acquisition. Neuroimage 143, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Yeh F-C, Wedeen VJ, Tseng W-YI, 2010. Generalized q-sampling imaging. IEEE Trans. Med. Imag 29 (9), 1626–1635. [DOI] [PubMed] [Google Scholar]

PERMALINK

Insight into the fundamental trade-offs of diffusion MRI from polarization-sensitive optical coherence tomography in ex vivo human brain

Robert Jones

Giorgia Grisot

Jean Augustinack

Caroline Magnain

David A Boas

Bruce Fischl

Hui Wang

Anastasia Yendiki

Abstract

1. Introduction

Table 1. Summary of literature.

2. Methods

2.1. Sample identification

Block 1 (deep WM):

Block 2 (superficial WM):

Fig. 1. Overview of experiments.

2.2. dMRI data acquisition

2.3. PSOCT data acquisition

2.4. dMRI to PSOCT registration

2.5. Resampling in q-space

2.6. Comparison of dMRI acquisition schemes

Table 2. Summary of experiments.

2.7. Comparison of dMRI reconstruction methods

2.8. Effect of spatial resolution

2.9. Effect of angular resolution

2.10. Effect of SNR

2.11. Effect of b-value on single-shell acquisitions

2.12. Comparison of dMRI and PSOCT orientations

3. Results

3.1. Fiber organization within the samples

Fig. 2. Organization of imaged WM blocks.

Fig. 3. PSOCT data from one representative slice of each tissue block.

3.2. Resampling in q-space

Fig. 4. Evaluation of q-space resampling.

Table 3. Approximation error of q-space resampling.

3.3. Overview of PSOCT vs. dMRI comparisons

Fig. 5. Angular error between dMRI and PSOCT orientations.

Table 4. Analysis of variance on the angular error.

Fig. 6. Axonal orientations estimated from dMRI in a deep WM sample.

Fig. 7. Axonal orientations estimated from dMRI in a superficial WM sample.

3.4. Effect of dMRI reconstruction method

3.5. Effect of dMRI acquisition scheme

3.6. Effect of spatial resolution

3.7. ROI-specific analyses

Fig. 8. Angular errors in ROIs from a deep WM sample.

Fig. 9. Angular errors in ROIs from a superficial WM sample.

Fig. 10. PSOCT FODs vs. dMRI orientations in ROIs with different fiber configurations.

3.7.1. Regions of coherent fibers

3.7.2. Region of branching fibers

3.7.3. Regions of crossing fibers

3.8. Number of detected fiber populations

Fig. 11. Number of fiber populations detected by PSOCT and dMRI in a deep WM sample.

Fig. 12. Number of fiber populations detected by PSOCT and dMRI in a superficial WM sample.

3.9. Effect of angular resolution at 1 mm spatial resolution

Fig. 13. Effect of angular resolution on the accuracy of dMRI orientation estimates.

3.10. Effect of SNR at 1 mm spatial resolution

Fig. 14. Effect of added noise on the accuracy of dMRI orientation estimates.

3.11. Effect of b-value on single-shell acquisitions at 1 mm spatial resolution

Fig. 15. Effect of b-value on the accuracy of dMRI orientation estimates.

3.12. Effect of through-plane diffusion on in-plane orientation accuracy

Fig. 16. Effect of through-plane diffusion on in-plane orientation accuracy.

4. Discussion

4.1. Effect of q-space sampling scheme

4.2. Effect of orientation reconstruction method

4.3. Effect of spatial resolution

4.4. Considerations for acquisition and analysis

4.5. Relation to previous studies

4.6. Deep vs. superficial WM

4.7. Limitations

5. Conclusion

Supplementary Material

Acknowledgements

Footnotes

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK