Modeling and optimizing an agro-supply chain considering different quality grades and storage systems for fresh products: a Benders decomposition solution approach

Abstract

This paper proposes a mathematical model in the context of agro-supply chain management, considering specific characteristics of agro-products to assist purchase, storage, and transportation decisions. In addition, a new method for determining the required quality score of different types of products is proposed based on their loss factors and purchasing costs. The model aims to minimize total cost imposed by purchasing fresh products, opening warehouses, holding inventories, operational activities, and transportation. Two sets of examples, including small and medium-sized problems, are implemented by general algebraic modeling language (GAMS) software to evaluate the model. Then, Benders decomposition (BD) algorithm is applied to tackle the complexity of solving large-sized instances. The results of both GAMS and BD are compared in terms of objective function values and computational time to demonstrate the efficiency of the BD algorithm. Finally, the model is applied in a real case study involving an apple supply chain to obtain managerial insights.

Introduction

Over recent decades, agricultural logistics has drawn the attention of researchers and practitioners due to increasing concerns in economic, healthy feeding, environmental, and political issues. Hence, good management in post-harvest operations, such as packaging, storing, and distributing agro-products, can add significant value to logistics while satisfying customers’ demands and maintaining food security. Therefore, research on agricultural logistics can speed up modernization and competition abilities in agricultural processes (Otchia 2014).

The specific characteristic of agro-products, such as seasonality, perishability, and long procurement time, make it different from other supply chains, therefore, it is necessary to have accurate information about their effects on supply chain management. These characteristics put restrictions on logistic decisions and make deep concerns over resource depletion and the occurrence of agricultural wastes and losses. According to Widodo et al. (2006), 20–60% of agro-products are wasted along supply chains in any country. Therefore, designing efficient inventory and transportation systems for perishable products plays a vital role in cost-saving and freshness-keeping (Coelho and Laporte 2014). From this perspective, cold chains with proper temperature adjustment can significantly reduce losses (Yu and Xiao 2017).

Although efficient agro-supply chain management prevents storage and transportation losses, facility location problem is another issue strongly affecting the security and safety of foods, especially in developing countries (Morton et al. 2008). Given capacity constraints in warehouses, determining warehouse locations and assigning cold storage rooms under controllable temperature conditions play a pivotal role in loss and waste reduction over a supply chain that may yield a complicated problem (Aung and Chang 2014). Forasmuch as the current study deals with agricultural products with a short shelf life, optimal facility location and storage condition decisions can reduce losses due to the dispersed distribution centers, long distances transportation, etc.

This study presents an agro-supply chain based on a case study involving a wide range of decisions such as supplier selection, facility location, inventory control, and transportation planning. This research aims to optimize the shelf life of products via assigning proper cold storage systems that can prevent postharvest losses. In addition, different quality grades are considered for each type of product, whereby those farmers who have gotten the average quality score are selected to satisfy warehouses’ demands. For these purposes, a mixed-integer nonlinear programming (MINLP) problem is formulated considering several operational constraints. Then, the model is linearized and transformed to mixed-integer linear programming (MILP) problem and solved by GAMS/CPLEX solver in small and medium sizes. Moreover, Benders decomposition (BD) algorithm is proposed to tackle the complexity of the problem caused by increasing the number of binary and integer variables in large sized-instances. Then, the proposed model is implemented for a real case study in Iran covering eight months of a year.

The rest of the paper is organized as follows: Sect. 2 gives an overview in the context of agro-supply chains. In Sect. 3, problem definition, notations, assumptions, and the mathematical model are presented. In Sect. 4, BD algorithm is proposed to tackle the complexity of large-sized instances. In Sect. 5, numerical experiments and a case study are performed to demonstrate the practicality of the proposed model. Section 5 draws conclusions and remarks on some future research directions.

Literature review

Economic costs in agro-supply chains have been implied by inefficient management in purchasing, storage, and distribution of agro-products (Ahumada and Villalobos 2009). Although there are copious studies dealing with facility location and transportation problems, they have not been widely discussed for agricultural products. The facility location problem is a critical element of strategic decisions in agro-supply chains, especially in developing countries (Morton et al. 2008). This is because transportation and storage time will become shorter by properly determining facility locations (Morganti and Gonzalez-Feliu 2015). Therefore, dealing with the capacitated facility location problems with applications in storing and distributing agro-products is an essential component to adapt to environmental and competitive aspects (Validi et al. 2014).

Here, related literature with emphasis on three core parts of agro-supply chains, purchasing, facility location, and transportation decisions, has been reviewed to pinpoint the research gap. In this context, Paam et al. (2016) and Ganesh Kumar et al. (2017) have comprehensively reviewed agro-supply chain models. Then, Banasik et al. (2017) analyzed tradeoffs between economic and environmental benefits of an agro-food closed-loop supply chain with location-allocation decisions and production planning. They attempted to valorize agro-wastes by applying recycling concepts. Ghezavati et al. (2017) proposed a mathematical model for a distribution planning system considering the freshness and ripeness of products. They proposed BD algorithm to solve their problem in a reasonable time. Orjuela-Castro et al. (2017) presented a MILP model for a multi-product facility location problem. They aim to minimize the costs of transportation, installation, and fruit losses and show how intermediate logistics platforms affect fruit losses. Soto-Silva et al. (2017) formulated a two-stage agro-supply chain model for a case study in Chile. The first stage contains particular decisions on supplier selection and transportation planning and the second stage associates with establishing different types of cold chambers to store products and transportation planning. Allaoui et al. (2018) proposed a two-stage programming model for a sustainable agro-food supply chain. In the first stage, a hybrid analytic hierarchy process with an ordered weighted averaging method was used for assigning weights to sustainable indicators. In the second stage, a multi-objective mathematical model was proposed with respect to the results in the first stage. Paam et al. (2018) proposed an agro-supply chain model to optimize the shelf lives of apples with different quality grades in cold storage rooms. Liu et al. (2018) studied optimal purchase decisions and inventory retrieval policies for a single-product finite period agro-supply chain to maximize total profit under fluctuating prices. Jonkman et al. (2019) investigated the impacts of location-allocation, inventory, and transportation decisions on an agro-food supply chain under uncertain conditions. Liu et al. (2019) developed a transportation model for fresh agricultural products considering the impacts of ethephon concentration, time, and temperature on the maturity of soluble solids. They used ant colony algorithm to solve their model. Onggo et al. (2019) assessed stochastic demand in a multi-period inventory routing problem and attempted to minimize inventory, transportation, and shortage costs. They used a local metaheuristic algorithm to tackle the complexity of their model. Paam et al. (2019) proposed a new model for inventory management optimization in an apple supply chain. They analyzed the effects of two scenarios in storage rooms on fruit losses. Yu et al. (2019) investigated the impacts of horizontal and vertical integration on the quantity/quality losses and retailer profits.

The prior work on agro-supply chains is summarized in Table 1 to reveal existing gaps in the literature. The majority of the research has investigated multi-level supply chains under several constraints, without sufficient consideration on specific characteristics of agro-products, farmers, and distribution processes. However, a survey of practical experiences illustrates significant impacts of these properties on spoilage rate, in turn, on the amount of loss and system cost. Therefore, this paper takes several actions to fill the gaps, which are vividly explained as follows:

Table 1.

A literature review on agro-supply chain models

Researchers	Products		SLD	Operational constraints					Solution procedures
	single	multiple		Inventory balance	Transportation decision	Facility location	Quality scores	CFD
Banasik et al. (2017)	–		–		–		–	–	$\epsilon$-constraint
Ghezavati et al. (2017)		–	–		–		–	–	Solver-BD
Orjuela-Castro et al. (2017)	–		–	–	–		–	–	Meta-heuristic
Soto-Silva et al. (2017)	–						–		Solver
Allaoui et al. (2018)	–		–			–	–	–	Solver
P Paam et al. (2018)		–			–	–	–		Solver
Jonkman et al. (2019)	–		–		–		–	–	Solver
Onggo et al. (2019)		–	–			–	–	–	Simulation-meta-heuristic
P. Paam et al. (2019)		–			–	–	–		Solver
Current study	–								Solver-BD

SLD decision on shelf life, CFD decision on cold storage facilities

This study is an extension of the work done by Soto-Silva et al. (2017) in a way to be applicable for an apple supply chain in Iran. In their study, unlike many agro-supply chain models, three types of refrigeration technologies for maintaining different types of agro-products have been proposed that can make a privileged contribution in this context. In spite of their primary step towards sustainability of agro-products, it lacks an in-depth discussion on adjustment of storage conditions and its effects on inventory decisions. However, practical accessibility gave us valuable insights to design a mathematical model for adjusting storage conditions according to costs imposed on the system and its effects on the durability of agro-products. In addition, the storage of agro-products for a long-time mainly depends on their initial quality. Therefore, this study aims to manage the quality of agro-products by giving scores to producers and accordingly selecting them. To the best of the authors’ knowledge, there is no previous effort on quality management despite its importance in handling the shelf life of agro-products. Overall, the main contributions of the paper are as follows:

• A MINLP model has been presented to jointly optimize facility location, transportation, inventory decisions in an agro-supply chain.

• A new method is proposed to assign weights to suppliers based on their loss factor. Accordingly, decisions on supplier selection are made.

• The current research seeks to optimize the shelf life of products through adjusting appropriate storage conditions.

• The proposed MINLP method is linearized and transformed to a MILP model.

• BD algorithm has been utilized to tackle the complexity of the proposed model and solve it in a reasonable time.

• The proposed model is implemented in a real case study in Iran to demonstrate its applicability and efficiency.

Problem definition

This study is an extension of the proposed model by Soto-Silva et al. (2017), who addressed supplier selection, transportation, and facility location decisions in an agro supply chain. However, their study lacks in-depth discussions on quality management and storage and inventory planning. Therefore, we formulate a multi-period MINLP model under some operational constraints to intertwine supplier selection, transportation, storage operation, inventory planning, and facility location decisions in an agro-supply chain. Afterwards, we reformulate it to a MILP model and propose BD algorithm to solve it. Figure 1 is meant to show the process of this paper.

Fig. 1.

Overview of the paper

Figure 2 is a perspective of the proposed agro-supply chain, including producers, warehouses, and a wholesaler. Fresh products should be purchased from the producers who gain the required score based on their quality grades. This approach satisfies the required quality of products to be kept for a long time in cold chambers, which is more profitable for the system. The products are shipped to the warehouses by the private fleet. The reason is that producers, either small or medium sizes, are often located in rural and sparsely populated areas. The long distances between orchards and facilities and busy harvest seasons require the producers to provide flexible operating by their private fleet. The processing operations should carry before the storage of products, by which products are sorted based on their varieties, sizes, etc. Then, each type of products regardless of their sizes, color, etc., are kept in a cold storage room, and the temperature conditions should be adjusted to optimize the shelf life of products. Afterward, the products are delivered to the wholesaler to satisfy customers’ demands. Herein, transportation decisions are made by warehouses. In total, the proposed model aims to minimize the total cost of the agro-supply chain model while satisfying the constraints.

Fig. 2.

Structure of the proposed agro-supply chain

In order to formulate the mathematical model, the following assumptions are considered. In addition, indices, parameters, and decision variables are presented in Table 2.

Table 2.

Indices, parameters, and decision variables

Indices

$i$: Index of products $(i\in I)$ $t,g$: Index of periods $(t,g\in T)$ $c$: Index of temperature conditions $(c\in C)$ $w$: Index of potential warehouses $(w\in W)$ $k$: Index of vehicles $(k\in K)$ $j$: Index of producers $(j\in J)$ $s$: Index of quality grades $(s\in S$) $v$: Index of cold chambers $(v\in V)$

Parameters

${\mathit{CT}}_{\mathit{jw}}:$ Operational costs to transport products from producer $j$ to warehouse $w$ $P_w$: Operational costs in warehouse $w$ ${\mathit{HW}}_c$: Holding cost of products under temperature condition $c$ ${\mathit{CFT}}_k$: Fixed cost of transporting products by vehicle type $k$ ${\mathit{CW}}_w$: Fixed cost of opening a warehouse at location $w$ $W_w$: Available capacity of a cold chamber in warehouse $w$ ${\mathit{FW}}_w$: Number of available cold chambers in a warehouse if it is opened at location w ${\mathit{CV}}_k$: Transportation capacity of vehicle type $k$ ${\mathit{CQ}}_{\mathit{ijs}}$: Purchase cost of product $i$ with quality grade $s$ supplied by producer $j$ $T_{\mathit{ic}}$: Shelf life of product $i$ under temperature condition $c$ $D_{\mathit{it}}$: Quantity of demand for product $i$ in period $t$ ${\mathit{LF}}_{\mathit{ijs}}$: Loss factor of product $i$ with quality grade $s$ purchased from producer $j$ ${\mathit{CF}}_i$: Supply capacity of product type i ${\mathit{WEP}}_{\mathit{ijs}}$: Quality score of product $i$ with quality grade $s$ supplied by producer $j$ $a_{\mathit{it}}$: Binary parameter; 1 if product $i$ is available in period $t$, 0 otherwise ${\alpha }_i$: Minimum acceptable quality score for product i

Variables

${\mathit{QF}}_{\mathit{ijst}}$: Quantity of product $i$ with quality grade $s$ purchased from producer $j$ in period $t$ ${\mathit{LOSS}}_{\mathit{ijs}}$: Quantity of product loss $i$ with quality grade s purchased from producer $j$ ${\mathit{QFW}}_{\mathit{ijwvct}}:$ Quantity of product $i$ purchased from producer $j$ by warehouse $w$ to be kept in cold chamber $v$ under temperature condition c in period $t$ ${\mathit{QW}}_{\mathit{iwvcktg}}$: Quantity of stored product $i$ in warehouse $w$ in cold chamber $v$ under temperature condition $c$ in period $g$ to deliver to the wholesaler by vehicle type $k$ in period $t$ $I_{\mathit{iwvctg}}$: Product $i$ stored in warehouse $w$ in cold chamber $v$ under temperature condition $c$ in period $g$ and remained until period t ${\mathit{TE}}_{\mathit{iwvct}}:$ Storage time for product $i$ in warehouse $w$ in cold chamber $v$ under temperature condition $c$ in time period $t$ $y_{\mathit{kt}}$: Number of vehicles $k$ for transporting products from warehouses to the wholesaler in period $t$ $A_{\mathit{ijst}}$: Binary variable, 1 if product $i$ with quality grade $s$ is supplied by producer $j$ in period $t$, 0 otherwise ${\mathit{AC}}_{\mathit{iwvct}}$: Binary variable; 1 if cold chamber $v$ is turned on in warehouse $w$ under temperature condition $c$ in period $t$, 0 otherwise ${\mathit{AW}}_w$: Binary variable; 1 if a warehouse is opened at location $w$, 0 otherwise

Assumptions

• Shortages are not allowed.

• Three different quality grades are considered for products in orchards.

• Each of the quality grades for each variety of products imposes different amounts of losses.

• Each variety of products is available for purchase at a specific period. Therefore, they are purchased with sufficient quality to be stored in cold chambers in order to meet customers’ demands for a while.

• Decisions on the type of temperature conditions should be made for each cold chamber in warehouses.

Mixed-integer nonlinear model

In this section, a MINLP model is presented as follows:

$$MinZ=\sum _{i\in I}\sum _{j\in J}\sum _{s\in S}\sum _{t\in T}{a_{\mathit{it}}CQ}_{\mathit{ijs}}{\mathit{QF}}_{\mathit{ijst}}+\sum _{i\in I}\sum _{j\in J}\sum _{w\in W}\sum _{v\in V}\sum _{c\in C}\sum _{t\in T}{\mathit{CT}}_{\mathit{jw}}{\mathit{QFW}}_{\mathit{ijwvct}}+\sum _{i\in I}\sum _{w\in W}\sum _{v\in V}\sum _{c\in C}\sum _{k\in K}\sum _{t\in T}\sum _{g\in {\mathit{TE}}_{\mathit{iwvct}}}{P}_w{\mathit{QW}}_{\mathit{iwvcktg}}+\sum _{w\in W}{\mathit{CW}}_w{\mathit{AW}}_w+\sum _{k\in K}\sum _{t\in T}{\mathit{CFT}}_k{y}_{\mathit{kt}}+\sum _{i\in I}\sum _{w\in W}\sum _{v\in V}\sum _{c\in C}\sum _{t\in T}\sum _{g\in {\mathit{TE}}_{\mathit{iwvct}}}{\mathit{HW}}_c{I}_{\mathit{iwvctg}}$$ 1

$$\sum _j\sum _s{a_{\mathit{it}}{\mathit{WEP}}_{\mathit{ijs}}QF}_{\mathit{ijst}}\ge {\alpha }_i\sum _j\sum _s{a_{\mathit{it}}QF}_{\mathit{ijst}}\forall i\in I;t\in T;$$ 2

$$\sum _i\sum _c{\mathit{AC}}_{\mathit{iwvct}}\le 1\forall w\in W;v\in V;t\in T;$$ 3

$${\mathit{TE}}_{\mathit{iwvct}}\le {T_{\mathit{ic}}AC}_{\mathit{iwvct}}\forall i\in I;w\in W;v\in V;c\in C;t\in T;$$ 4

$$\sum _s{A}_{\mathit{ijst}}\le 1\forall i\in I;j\in J;t\in T;$$ 5

$${\mathit{QF}}_{\mathit{ijst}}\le BIG{A}_{\mathit{ijst}}\forall i\in I;j\in J;s\in S;t\in T$$ 6

$$\sum _w\sum _v\sum _c{\mathit{QFW}}_{\mathit{ijwvct}}\le \sum _s{a}_{\mathit{it}}\left({\mathit{QF}}_{\mathit{ijst}},-,{\mathit{LOSS}}_{\mathit{ijst}}\right)\forall i\in I;j\in J;t\in T;$$ 7

$$I_{\mathit{iwvctg}}=I_{iwvct-1g}-\sum _k{\mathit{QW}}_{\mathit{iwvcktg}}\forall i\in I;w\in W;v\in V;c\in C;;t\in T;t-g\le {\mathit{TE}}_{\mathit{icwvg}}\&g\in {\mathit{TE}}_{\mathit{icwg}}\&g<t;$$ 8

$$I_{\mathit{iwvctg}}=\sum _j{\mathit{QFW}}_{\mathit{ijwvct}}-\sum _k{\mathit{QW}}_{\mathit{iwvcktg}}\forall i\in I;w\in W;v\in V;c\in C;t\in T;t=g;$$ 9

$$\sum _j{\mathit{QFW}}_{\mathit{ijwvct}}+\sum _{g(g<t)}{I}_{iwvct-1g}\le W_w{\mathit{AC}}_{\mathit{iwvct}}\forall w\in W;v\in V;c\in C;i\in I;t\in T;$$ 10

$$\sum _w\sum _v\sum _c\sum _k\sum _g{\mathit{QW}}_{iwvcktg(g\le t)}\ge D_{\mathit{it}}\forall i\in I;t\in T$$ 11

$$\sum _i\sum _v\sum _c{\mathit{AC}}_{\mathit{iwvct}}\le {\mathit{FW}}_w{\mathit{AW}}_w\forall w\in W;t\in T;$$ 12

$$\sum _i\sum _w\sum _v\sum _c\sum _g{\mathit{QW}}_{\mathit{iwvcktg}}\le {\mathit{CV}}_k{y}_{\mathit{kt}}\forall k\in K;t\in T$$ 13

$${\mathit{Loss}}_{\mathit{ijst}}={{\mathit{LF}}_{\mathit{ijs}}QF}_{\mathit{ijst}}\forall i\in I;j\in J;s\in S;t\in T$$ 14

$$\sum _j\sum _s{a}_{\mathit{it}}({\mathit{QF}}_{\mathit{ijst}}-{\mathit{LOSS}}_{\mathit{ijst}})\le {\mathit{CF}}_i\forall i\in I;t\in T$$ 15

$${\mathit{QF}}_{\mathit{ijst}},{\mathit{LOSS}}_{\mathit{ijst}},{\mathit{QFW}}_{\mathit{ijwvct}}{,QW}_{\mathit{iwvcktg}},I_{\mathit{iwvctg}}\ge 0;{\mathit{AW}}_w,{\mathit{AC}}_{\mathit{iwvct}},A_{\mathit{ijst}}\in \left\{0,1\right\};y_{\mathit{kt}},{\mathit{TE}}_{\mathit{iwvct}}\in {\mathit{Integer}}^{+}$$ 16

The objective function (1) minimizes total cost consisting of six components, purchasing cost, operational costs including packing, laborers, and transportation costs (from producers to warehouses), operational costs in warehouses, fixed cost of opening warehouses, fixed cost of transportation (from warehouses to the wholesaler), inventory holding costs. Constraints (2) ensure that the purchased products are of satisfactory quality with reasonable prices. Constraints (3) ensure that only one type of product should be stored in each cold chamber under a specific temperature condition. Constraints (4) indicate the effects of temperature conditions on the shelf life of products. Constraints (5) ensure that products with the same quality grade are purchased from a producer. Constraints (6) show the relation between variables $A_{\mathit{ijst}}$ and ${\mathit{QF}}_{\mathit{ijst}}$. Constraints (7) ensure that the amount of product in warehouses should not exceed the amount of purchased product. Equations (8) and (9) show the inventory level of products in warehouses where $g<t$ and $g=t$, respectively. Constraints (10) state the limited storage capacity of cold chambers in warehouses. Constraints (11) are the demand response. Constraints (12) represent the limitation in the number of cold chambers in a warehouse. Constraints (13) are capacity constraints of vehicles for transporting products from warehouses to the wholesaler. Equations (14) calculate the losses after purchasing products from producers. Constraints (15) indicate the available capacity of producers to supply product $i$. Constraints (16) define types of decision variables which are non-negative continuous, binary, or integer variables.

Model linearization and reformulation

In the proposed model, the upper limit of index $g$ is considered as a decision variable making the model nonlinear. In these cases, if–then decisions should be made to remove spoiled products from warehouses. Indeed, if the storage time exceeds the shelf life of products, the products should be removed from warehouses (If $t-g>{\mathit{TE}}_{\mathit{iwvct}}\to I_{\mathit{iwvctg}}=0;{\mathit{QW}}_{\mathit{iwvcktg}}=0)$. Conversely, if the storage time is less than the shelf life of products, Eq. (8) are used to calculate the inventory level of products (If $t-g\le {\mathit{TE}}_{\mathit{iwvct}}\to I_{\mathit{iwvctg}}=I_{iwvct-1g}-{\sum }_k{\mathit{QW}}_{\mathit{iwvcktg}}$). In order to handle the nonlinear formulation and transform the MINLP model to MILP, a linearization technique is derived from Chen et al. (2010).

Consider the following nonlinear equivalents $(f(x)\le b\to g_j(x)\le {b_j}^{{}^{\prime }})$ where $b$ and b’ are the right-hand side of inequalities and $f(x)$ and $g_j(x)$ are the functions of variable $x$. In this case, if $f(x)$ is less than $b$, then $g_j(x)\le {b_j}^{{}^{\prime }}$. The linearization of the if–then constraint is applied as follows:

$$-f\left(x\right)+b\le BIG·y$$ 17

$$g_j\left(x\right)-b_j^{{}^{\prime }}\le BIG·(1-y)$$ 18

where BIG and y are a positive big number and binary variable, respectively. Accordingly, the following equations are presented to linearize the if–then constraints in this paper.

$$t-g{-TE}_{\mathit{iwvcg}}\le BIG·Z_{\mathit{iwvctg}}$$ 19

$$I_{\mathit{iwvctg}}\le BIG·(1-Z_{\mathit{iwvctg}})$$ 20

$${\mathit{QW}}_{\mathit{iwvcktg}}\le BIG·(1-Z_{\mathit{iwvctg}})$$ 21

$$I_{\mathit{iwvctg}}-(I_{iwvct-1g}-\sum _k{\mathit{QW}}_{\mathit{iwvcktg}})\le BIGM·(1-Z_{\mathit{iwvctg}})$$ 22

Solution procedure

The complexity of MILP problems rises by increasing the number of binary and integer variables, consequently, has a strong influence upon the computational time (Keshavarz-Ghorbani and Pasandideh 2021). Therefore, it is necessary to apply efficient solution procedures to overcome the computational burden. BD algorithm is known as one of the powerful algorithms to tackle the complexity of NP-hard problems. BD algorithm uses the concept of "divide and conquers" to reformulate the original problem into a master problem (MP) and dual subproblem (DSP) in a limited number of iterations. Nowadays, advantages of the BD algorithm, such as a limited number of iterations, less computational time, and guaranteed convergence for large-scale problems, make it suitable for many optimization problems (e.g., Pishvaee et al. 2010; Shaw et al. 2016; Ghezavati et al. 2017; Kayvanfar et al. 2018; Babazadeh et al. 2019; Azadi et al. 2019; Mardan et al. 2019; Naderi et al. 2019; Alkaabneh et al. 2020; Gong and Zhang 2021).

The primary steps of the BD algorithm work iteratively by outer linearization and relaxation. In other words, the original problem is decomposed into an MP and subproblem (SP). The MP is a pure integer problem and includes integer and binary variables. The MP is solved and puts its solutions among the SP. In this step, the SP turns into DSP to make the feasible solution space independent from integer solutions. Then the DSP is solved, and its optimal bounded solutions/ unbounded solutions are added as feasibility/optimality cutting planes into the MP. This procedure reduces the computational time compared to the original problem. The convergence of BD comes from closing upper and lower bounds obtained from solving the DSP and MP, respectively. Figure 3 illustrates the steps of the iterative BD algorithm.

Fig. 3.

The flowchart of BD

Benders master problem

To implement BD for the proposed model, the MP is called to minimize a part of the objective function associated with binary and integer variables with respect to constraints (3)–(5), and (12). That is a relaxation of the original problem to obtain lower bounds.

$$\begin{array}{cc}\hfill \mathit{MinZ}& =\sum _{w\in W}C{W}_{w}A{W}_w+\sum _{k\in K}\sum _{t\in T}CF{T}_k{y}_{\mathit{tk}}\hfill \\ \hfill & \sum _i\sum _{c}A{C}_{\mathit{iwvct}}\le 1\forall w\in W;v\in V;t\in T\hfill \\ \hfill & T{E}_{\mathit{iwvct}}\le T_{\mathit{ic}}A{C}_{\mathit{iwvct}}\forall i\in I;w\in W;v\in V;c\in C;t\in T;\hfill \\ \hfill & \sum _s{A}_{\mathit{ijst}}\le 1\forall i\in I;j\in J;t\in T;\hfill \\ \hfill & \sum _i\sum _v\sum _{c}A{C}_{\mathit{iwvct}}\le F{W}_{w}A{W}_w\forall w\in W;t\in T\hfill \\ \hfill & A{W}_w,A{C}_{\mathit{iwvct}},A_{\mathit{ijst}}\in \left\{0,1\right\};y_{\mathit{kt}},T{E}_{\mathit{iwvct}}\in Intege{r}^{+}\hfill \\ \hfill \end{array}$$ 23

Benders subproblem

The SP includes a part of the objective function associated with continuous variables subject to constraints (2), (6)–(11), (13)–(15) that can be seen in Table 3.

Table 3.

Equations related to the SP and its corresponding dual variables

Equations	Dual variables
$MinZ={\sum }_{i\in I}{\sum }_{j\in J}{\sum }_{s\in S}{\sum }_{t\in T}{a_{\mathit{it}}CQ}_{\mathit{ijs}}{\mathit{QF}}_{\mathit{ijst}}+{\sum }_{i\in I}{\sum }_{w\in W}{\sum }_{v\in V}{\sum }_{c\in C}{\sum }_{k\in K}{\sum }_{t\in T}{\sum }_{g\in {\mathit{TE}}_{\mathit{icwt}}}{P}_w{\mathit{QW}}_{\mathit{iwvcktg}}+{\sum }_{i\in I}{\sum }_{j\in J}{\sum }_{w\in W}{\sum }_{v\in V}{\sum }_{c\in C}{\sum }_{t\in T}{\mathit{CT}}_{\mathit{jw}}{\mathit{QFW}}_{\mathit{ijwvct}}+{\sum }_{i\in I}{\sum }_{w\in W}{\sum }_{v\in V}{\sum }_{c\in C}{\sum }_{t\in T}{\sum }_{g\in {\mathit{TE}}_{\mathit{icwt}}}{\mathit{HW}}_c{I}_{\mathit{iwvctg}}$	–
${\mathit{QF}}_{\mathit{ijst}}<BIG{A}_{\mathit{ijst}}$	${\beta 1}_{\mathit{ijst}}$
${\sum }_w{\sum }_v{\sum }_c{\mathit{QFW}}_{\mathit{ijwvct}}\le {\sum }_s{a}_{\mathit{it}}\left({\mathit{QF}}_{\mathit{ijst}},-,{\mathit{LOSS}}_{\mathit{ijst}}\right)$	${\beta 2}_{\mathit{ijt}}$
$I_{\mathit{iwvctg}}=I_{iwvct-1g}-{\sum }_k{\mathit{QW}}_{\mathit{iwvcktg}}$	${\beta 3}_{\mathit{iwvctg}}$
$I_{\mathit{iwvctg}}={\sum }_j{\mathit{QFW}}_{\mathit{ijwvct}}-{\sum }_k{\mathit{QW}}_{\mathit{iwvcktg}}$	${\beta 4}_{\mathit{iwvctg}}$
${\sum }_j{\mathit{QFW}}_{\mathit{ijwvct}}+{\sum }_g{I}_{iwvct-1g}\le W_w{\mathit{AC}}_{\mathit{iwvct}}$	${\beta 5}_{\mathit{iwvct}}$
${\sum }_w{\sum }_v{\sum }_c{\sum }_k{\sum }_g{\mathit{QW}}_{\mathit{iwvcktg}}\ge D_{\mathit{it}}$	${\beta 6}_{\mathit{it}}$
${\sum }_i{\sum }_w{\sum }_v{\sum }_c{\sum }_g{\mathit{QW}}_{\mathit{iwcktg}}\le {\mathit{CV}}_k{y}_{\mathit{kt}}$	${\beta 7}_{\mathit{kt}}$
${\sum }_j{\sum }_s{a}_{\mathit{it}}({\mathit{QF}}_{\mathit{ijst}}-{\mathit{LOSS}}_{\mathit{ijst}})\le {\mathit{CF}}_i$	${\beta 8}_{\mathit{it}}$
${\sum }_j{\sum }_s{a_{\mathit{it}}{\mathit{WEP}}_{\mathit{ijs}}QF}_{\mathit{ijst}}\ge {\alpha }_i{\sum }_j{\sum }_s{a_{\mathit{it}}QF}_{\mathit{ijst}}$	${\beta 9}_{\mathit{it}}$

Dual subproblem

The DSP makes the feasible solution space independent from integer solutions and reaches the same objective function value as the SP. Therefore, the DSP is used instead of the SP to obtain upper bounds for the original problem. In this paper, the DSP is formulated as follows (Table 4):

Table 4.

Dual variables associated with the sub-problem

Dual variables
$\left({\beta 1}_{\mathit{ijst}},\ge ,0\right|\forall i\in I,j\in J,s\in S,t\in T;\left({\beta 2}_{\mathit{ijt}},\ge ,0\right|\forall i\in I,j\in J,t\in T$;$\left({\beta 3}_{\mathit{iwvctg}},\ge ,0\right|\forall i\in I,w\in W,v\in V,c\in C,t\in T,g\in T;\left({\beta 4}_{\mathit{iwvctg}}\right|\forall i\in I,w\in W,v\in V,c\in C,t\in T,g\in T$; $\left({\beta 5}_{\mathit{iwvct}},\ge ,0\right|\forall i\in I,w\in W,v\in V,c\in C,t\in T$;$\left({\beta 6}_{\mathit{it}},\ge ,0\right|\forall i\in I;t\in T$;$\left({\beta 7}_{\mathit{kt}},\ge ,0\right|\forall k\in K,t\in T$;$\left({\beta 8}_{\mathit{it}},\ge ,0\right|\forall i\in I,t\in T$;
$\left({\beta 9}_{\mathit{it}},\ge ,0\right|\forall i\in I,t\in T;$

The DSP and its corresponding variables are presented in Table 5.

Table 5.

The DSP and its corresponding variables

DSP	Variables
$Max\delta ={\sum }_i{\sum }_j{\sum }_s{\sum }_t{\left(-,B,I,G,{\overline{A}}_{\mathit{ijst}}\right)\beta 1}_{\mathit{ijst}}+{\sum }_i{\sum }_w{\sum }_v{\sum }_c{\sum }_t\left(-,W_w,{\overline{\mathit{AC}}}_{\mathit{iwvct}}\right){\beta 5}_{\mathit{iwvct}}+{\sum }_i{\sum }_t{D}_{\mathit{it}}{\beta 6}_{\mathit{it}}+{\sum }_t{\sum }_k{-CV}_k{\overline{y}}_{\mathit{kt}}{\beta 8}_{\mathit{kt}}+{\sum }_i{\sum }_t-{\mathit{CF}}_i{\beta 9}_{\mathit{it}}$	–
$a_{\mathit{it}}(-{\beta 1}_{\mathit{ijst}}+(1-{\mathit{LF}}_{\mathit{ijs}}){\beta 2}_{\mathit{ijt}}-(1-{\mathit{LF}}_{\mathit{ijs}}){\beta 8}_{\mathit{it}}+{(WEP}_{\mathit{ijs}}-{\alpha }_i){\beta 9}_{\mathit{it}})\le {\mathit{CQ}}_{\mathit{ijs}}$	${\mathit{QF}}_{\mathit{ijst}}$
$-{\beta 2}_{\mathit{ijt}}+{\beta 4}_{\mathit{iwvctg}}-{\beta 5}_{\mathit{iwvct}}\le {\mathit{CT}}_{\mathit{jw}}$	${\mathit{QFW}}_{\mathit{ijwvct}}$
$-{\beta 3}_{\mathit{iwvctg}}+{\beta 6}_{\mathit{it}}-{\beta 7}_{\mathit{kt}}\le P_w$	$\left({\mathit{QW}}_{\mathit{iwvcktg}}\right|t>g$; $t-g\le {\overline{\mathit{TE}}}_{\mathit{iwvcg}}$
$-{\beta 4}_{\mathit{iwvctg}}+{\beta 6}_{\mathit{it}}-{\beta 7}_{\mathit{kt}}\le P_w$	$\left({\mathit{QW}}_{\mathit{iwvcktg}}\right|t=g$
$-{\beta 3}_{\mathit{iwvctg}}+{\beta 3}_{iwvct+1g}-{\beta 5}_{iwvct+1}\le {\mathit{HW}}_c$	$\left(I_{\mathit{iwvctg}}\right|\mathrm{t}>\mathrm{g}$; $t-g\le {\overline{\mathit{TE}}}_{\mathit{iwvcg}}$
${\beta 3}_{iwvct+1g}+{\beta 4}_{\mathit{iwvctg}}{-\beta 5}_{iwvct+1}\le {\mathit{HW}}_c$	$t=g$

After solving the DSP, an optimal or feasible cut is added to the MP according to Eq. (24) and an extreme ray of DSP. BD algorithm terminates whenever the stop criterion $\frac{{\mathit{UB}}_{\mathit{iter}}-{\mathit{LB}}_{\mathit{iter}}}{{\mathit{LB}}_{\mathit{iter}}}\le \epsilon$.

$$Z_{\mathit{lower}}\ge \delta +\sum _{w\in W}C{W}_{w}A{W}_w+\sum _{k\in K}\sum _{t\in T}CF{T}_k{y}_{\mathit{tk}}x\in S$$ 24

where $S$ is the feasible solution space of the MP, $\epsilon$ is a small non-zero number. In addition, UB_iter and LB_iter are the upper and lower bounds obtained from solving DSP and MP, respectively. The pseudocode of BD is given as follows:

Experimental results

This section is presented in three parts. In the first part, numerical test problems, including small, medium, and large-sized instances, are executed for assessing the efficiency and applicability of the proposed model and solution approach. These test problems are randomly generated in Excel and presented in Tables 6 and 7. In the second part, the model is implemented in a case study in Iran to derive valuable insights. Finally, a sensitivity analysis is carried out to help decision-makers determining key parameters which should be carefully tracked in the presented model.

Table 6.

Data generation functions

Parameters	Distribution functions
${\mathit{CT}}_{\mathit{jw}}$	$\sim Uniform(1,2)$
$P_w$	$\sim Uniform(1,2)$
${\mathit{HW}}_c$	$\sim Uniform(1,2)$
${\mathit{CFT}}_k$	$\sim Uniform(1,2)$
${\mathit{FW}}_w$	$\sim Uniform(10,20)$
$W_w$	$\sim Uniform(50,100$)
${\mathit{CW}}_w$	$\sim Uniform(1,2)$
${\mathit{CV}}_k$	$\sim Uniform(5,20)$
$D_{\mathit{it}}$	$\sim Uniform(10,100)$
${\mathit{CF}}_i$	$\sim Uniform(50,200)$
${\alpha }_i$	$\sim Uniform(0.6,0.8)$

Table 7.

Data generation functions for products with different quality grades

$s$	$s1$	$s2$	$s3$
${\mathit{CQ}}_{\mathit{ijs}}$	$[900,1000)$	$[1000,1500)$	$[1500,2000]$
${\mathit{LF}}_{\mathit{ijs}}$	$[0.2,0.28]$	$[0.1,0.2)$	$[0.01,0.1)$

Validation of BD

The presented MILP model and BD algorithm are coded in GAMS 27.2 optimization software and solved by a CPLEX solver. Both CPLEX solver and BD algorithm are executed on a computer with Intel^@ Core™ i7-CPU 2.20 GHz and RAM 8.00 GB. Different sizes are presented in Table 8, and numerical results are presented in Table 9, including optimal values of objective functions, the lower and upper bounds of BD, computational time, and gaps between upper and lower bounds of BD and CPLEX solver. BD algorithm continues once it reaches termination criteria which are as follows:

• The number of iterations reaches 200

• A relative gap between lower and upper bounds become less than $0.3\%$

Table 8.

Generated small, medium, and large-sized instances

Instances	$I$	$J$	$W$	$C$	$S$	$V$	$K$
$P1$	3	3	3	3	3	5	3
$P2$	4	3	3	3	3	5	3
$P3$	4	4	4	3	3	5	3
$P4$	3	8	5	3	3	5	3
$P5$	5	8	5	3	3	5	3
$P6$	8	8	5	3	3	5	3
$P7$	10	8	5	3	3	5	3
$P8$	10	10	8	3	3	5	3
$P9$	10	15	10	3	3	5	3
$P10$	12	15	12	3	3	5	3
$P11$	12	15	15	3	3	5	3
$P12$	15	15	20	3	3	10	3
$P13$	15	20	15	3	3	10	3
$P14$	20	20	10	3	3	10	3
$P15$	25	20	10	3	3	10	3
$\mathit{Min}$	3	3	3	3	3	5	3
Max	25	20	20	3	3	10	3

Table 9.

Obtained results from solving small, medium, and large scales instances with GAMS and BD

Size	Instances	CPLEX solver		Benders decomposition algorithm					PRE (%)
		Objective function	CM (s)	LB	UB	CM (s)	Iter	GAP(%)	LB	UB
Small scale	P1	1,692,661	18	1,692,661	1,692,661	31	9	0	0.000	0.000
	P2	1,937,866	25	1,937,512	1,937,893	17	12	0.020	0.018	0.001
	P3	2,014,646	40	2,014,071	2,014,690	20	12	0.031	0.029	0.002
	P4	1,513,379	23	1,509,382	1,513,478	24	11	0.271	0.264	0.007
	P5	2,578,430	35	2,571,032	2,578,488	30	16	0.290	0.287	0.002
Medium-scale	P6	4,488,737	9757	4,476,869	4,489,851	63	19	0.290	0.264	0.000
	P7	5,775,525	28,795	5,773,605	5,787,357	97	19	0.238	0.033	0.205
	P8	5,649,849	> 28,795	5,635,241	5,650,601	495	11	0.273	0.259	0.013
	P9	5,773,698	> 28,795	5,758,896	5,774,913	255	19	0.278	0.256	0.021
	P10	6,652,182	> 28,795	6,652,159	6,653,543	461	22	0.021	0.000	0.020
	P11	6,794,693	> 28,795	6,778,839	6,797,817	621	17	0.280	0.233	0.046
Large scale	P12	Out of memory		8,342,697	8,367,630	2199	26	0.299	–	–
	P13			10,164,640	10,188,150	2555	29	0.231	–	–
	P14			11,570,161	11,600,005	3654	21	0.258	–	–
	P15			13,682,170	13,692,152	3861	34	0.073	–	–

LB lower bound, UB upper bound, s seconds, CM computational time, GAP relative gap between upper and lower bounds, PRE percentage relative gaps between lower or upper bound and optimal values, Iter number of iterations

In addition, the CPLEX solver terminates once the absolute and relative gaps become less than 0.001.

The results in Table 9 point out that the CPLEX solver reaches optimal solutions in less than one minute, whereas the computational time of BD is more than the CPLEX solver in several small sized-instances. As increasing the number of variables in medium sizes, the lower and upper bounds of BD converge to optimal solutions less than an hour, which is remarkably faster than the CPLEX solver. It should be noted, for large sized-instances, the CPLEX solver cannot find optimal solutions and releases an "OUT OF MEMORY" error. In these cases, BD can be utilized to cope with complexity and reach optimal solutions in a reasonable time. Figure 4 demonstrates the changes of computational time for BD and CPLEX solver, in which BD outperforms CPLEX solver, especially in medium and large-sized instances. According to the results, the computational time of the CPLEX solver increases whatever the size of the problem increases. This affirms the efficiency of BD in solving the model in a reasonable time.

Fig. 4.

Comparison of the computational time between GAMS and BD solvers

Besides, the average gap between the upper bounds of BD and the CPLEX solver is about 0.01684. It turns out BD converges to optimal solutions with a near-zero gap. In order to verify the efficiency of BD and its convergence, three instances in small, medium, and large sizes are derived from GAMS/CPLEX solver and presented as follows:

Figure 5 shows that BD provides optimality convergence in less than 17 iterations for a small-sized test (no. p5).

Fig. 5.

The convergence of lower and upper bounds of BD for a small sized-instance (no. p5)

Figure 6 shows that BD provides optimality convergence in less than 12 iterations for a medium-sized test (no. p8).

Fig. 6.

The convergence of lower and upper bounds of BD for a medium sized-instance (no. p8)

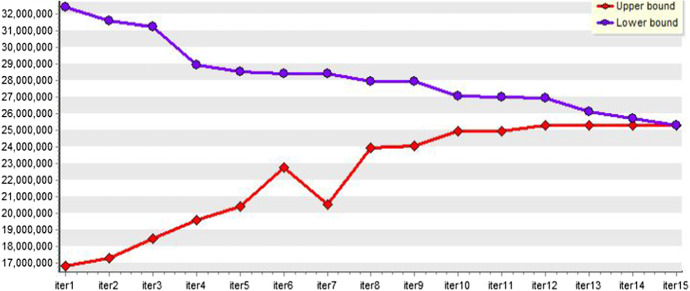
Figure 7 demonstrates that BD provides optimality convergence in less than 23 iterations for a large-sized test problem (no. p14).

Fig. 7.

The convergence of lower and upper bounds of BD for a large sized-instance (no. p14)

A case study

This section devotes a discussion on an apple supply chain belonging to a domestic distributor in Iran to demonstrate the application of the proposed model. The company decides to establish warehouses at four potential locations, namely Tehran, Fars, Isfahan, and Razavi Khorasan, and activate cold chambers under proper temperature conditions. They often purchase different varieties of apples from producers who truck products by private vehicle fleet and located in Tehran, Alborz, Isfahan, West Azerbaijan, East Azerbaijan, and Semnan provinces. The company purchases good storage apples based on quality characters (i.e., texture, cosmetic appearance) to remain for a while in warehouses and satisfy the wholesaler’s demands in different months of a year. Tables 10, 11, 12, 13, 14, 15 and 16 represent input data related to cold storage construction projects (www.damoon-co.com) and purchasing, transportation, and storage planning for eight months. The average demand is obtained based on historical data when the company faces shortages, and also demands should be met by any variety of apples. In addition, the purchasing cost of apples with different quality grades are available in fruit and vegetable fields organization in Iran, and information about temperature conditions in cold chambers are available in (https://pdfsara.ir/container-storage-services-atmospheric-plan/).

Table 10.

Input data related to the varieties of apples

Apples	$T_{\mathit{ic}}$			${\mathit{CF}}_i\times {10}^3$Ton	$a_{\mathit{it}}$
	$c1$	$c2$	$c3$		$t1$	$t2$	$t3$	$t4$	$t5$	$t6$	$t7$	$t8$
Red delicious	1	3	8	3.5	–	–	–	–	1	1	–	–
Golden delicious	1	3	8	3.5	–	–	–	–	1	1	–	–
Golab	1	0	0	4	–	–	1	–	–	–	–	–
Jonathan	1	3	8	3	–	–	–	–	1	1	–	–
Granny Smith	1	3	8	3	–	–	–	–	1	1	–	–
Fuji	1	3	8	3	–	–	–	–	1	1	–	–
Qabaleh	1	3	8	0.7	–	–	–	–	1	1	–	–
Baljei	1	3	8	4	1	–	–	–	–	–	–	–
Soltani	1	3	0	3	–	1	–	–	–	–	–	–
Mashhadi	1	3	0	3.5	–	1	1	–	–	–	–	–
Gardeshiri	1	0	0	3	–	–	–	1		–	–	–
Asadkuhi	1	3	0	3	1	–	–	–	–	–	–	–

Table 11.

Operational costs including transportation, packing, and sorting apples

${\mathit{CT}}_{\mathit{jw}}$($)	Warehouses
producers	Tehran	Fars	Isfahan	Razavi Khorasan
Tehran	12.12	21.76	14.08	21.20
Alborz	12.12	21.76	14.08	21.20
Isfahan	14.36	14.34	12.10	26.01
West Azerbaijan	19.34	29.26	29.18	16.06
East Azerbaijan	6.51	2.48	19.31	26.20
Semnan	21.2	27.14	26.01	5.04

Table 12.

Input data related to the vehicles

	$k1$	$k2$	$k3$	$k4$
${\mathit{CV}}_k$(Ton)	5	10	15	25
${\mathit{CFT}}_k$($)	18.92	25.36	33.2	47.52

Table 13.

Input data related to warehouses

	Tehran	Fars	Isfahan	Razavi Khorasan
${\mathit{CW}}_w$(104 $)	33.66	11.00	18.33	29.33
$W_w$(Ton)	1000	500	500	1000
${\mathit{FW}}_w$	10	6	10	8
$P_w$(10–4 $))	3.31	0.99	1.66	2.64

Table 14.

Holding cost of apples under the different temperature conditions

	$c1$	$c2$	$c3$
${\mathit{HW}}_c$($)	29.4	50.4	159.92

Table 15.

Loss factors for different types of apples with different quality grades and minimum acceptable quality score based on expert’s opinion

${\mathit{LF}}_{\mathit{ijs}}$(%)	$s1$						$s2$						$s3$						${\alpha }_i$
	$j1$	$j2$	$j3$	$j4$	$j5$	$j6$	$j1$	$j2$	$j3$	$j4$	$j5$	$j6$	$j1$	$j2$	$j3$	$j4$	$j5$	$j6$
Red delicious	22	22	21	21	21	21	14	12	12	14	17	13	9	9	7	9	6	5	0.634
Golden Delicious	20	24	25	23	22	20	13	19	17	10	14	11	6	6	7	9	8	6	0.769
Golab	23	21	20	24	24	22	15	13	17	13	10	11	7	5	6	7	5	5	0.710
Jonathan	22	24	26	24	20	21	15	11	13	11	12	11	5	8	7	8	8	5	0.660
Granny Smith	21	24	25	22	25	23	14	12	15	17	19	18	7	6	7	7	5	6	0.658
Fuji	21	21	23	22	23	21	14	16	10	13	11	15	6	7	7	6	6	7	0.645
Qabaleh	24	20	24	26	24	22	16	14	10	15	17	15	9	5	9	6	8	5	0.670
Baljei	21	22	21	20	23	20	14	13	15	11	12	11	5	6	8	7	8	8	0.771
Soltani	24	22	23	26	24	22	15	18	17	16	15	18	8	9	8	6	5	7	0.613
Mashhadi	23	22	26	25	25	21	13	15	19	12	10	16	6	9	6	9	9	7	0.700
Gardeshiri	24	22	23	25	25	23	14	19	11	16	14	13	7	8	5	5	8	6	0.800
Asadkuhi	23	23	23	26	24	24	13	15	16	15	14	15	5	7	7	6	7	5	0.716

Table 16.

Demand for different types of apples

$D_{\mathit{it}}\times {10}^3$(Ton)	$t1$	$t2$	$t3$	$t4$	$t5$	$t6$	$t7$	$t8$
Red delicious	–	–	–	–	1.000	0.900	1.560	1.400
Golden Delicious	–	–	–	–	0.650	0.780	1.000	1.080
Golab	–	–	2.530	1.438	–	–	–	–
Jonathan	–	–	–	–	1.350	1.246	1.321	1.350
Granny Smith	–	–	–	–	1.630	1.630	2.430	2.150
Fuji	–	–	–	–	1.450	1.525	2.350	2.096
Qabaleh	–	–	–	–	0.554	0.324	0.268	–
Baljei	1.500	1.000	1230	1.551	1.470	1.580	–	–
Soltani	–	1.450	1375	–	–	–	–	–
Mashhadi	–	1.250	1250	1.235	–	–	–	–
Gardeshiri	–	–	–	1.542	2.235	–	–	–
Asadkuhi	1.400	1.245	1.115	–	–	–	–	–
$D_t\times {10}^3$(Ton)	2.900	4.945	7.500	5.766	10.0339	7.985	8.929	8.076

The quality score of fruits supplied by different producers (${\mathit{WEP}}_{\mathit{ijs}}$) is calculated based on the minimum and maximum values of loss factor for a product with quality grade s as follows:

$${\mathit{WEP}}_{\mathit{ijs}}=1-\frac{{\mathit{LF}}_{\mathit{ijs}}-{\mathit{MIL}}_{\mathit{is}}}{{\mathit{MAL}}_{\mathit{is}}-{\mathit{MIL}}_{\mathit{is}}}$$ 25

where ${\mathit{MIL}}_{\mathit{is}}$ is the minimum loss factor for product $i$ with quality grade s and ${\mathit{MAL}}_{\mathit{is}}$ is the maximum loss factor for product $i$ with quality grade $s$. Equation (26) illustrates the quality score of producer $j2$ supplying product $i1$ with quality grade $s3$, which equals 1.

$${\mathit{WEP}}_{\mathit{ijs}}=1-\frac{0.06-0.06}{0.09-0.06}=1$$ 26

Numerical results and discussion on a case study

The model has 184,572 discrete variables, 330,049 continuous variables, and 642,748 equations for the case study and is implemented by both CPLEX solver and BD. Herein, the efficiency of the proposed model and related solutions have been discussed. The lower and upper bounds of BD become 25,289,297 and 25,289,302, respectively. In addition, the optimal solution is obtained by the CPLEX solver, which is 25,289,302. The results indicate that BD converges to the optimal solution in a reasonable time. Figure 8 shows the convergence of BD for the case study.

Fig. 8.

The convergence of the lower and upper bounds of BD for the case study

First, producers who gain good scores are selected to supply products. The results show a $44\%$ of apples are of first quality grade, $45\%$ are of second grade, and $12\%$ are of third quality grade. In this respect, the total cost of purchasing apples with different quality grades is about US$ 996,000.

According to the results, it is beneficial to open warehouses in Tehran, Fars, and Isfahan provinces at a total cost of US$ 6,600,000. In this case, the operational costs in warehouses become US$ 147. It is worth mentioning that the presented model is able to show the temperature condition in each cold chamber. Three temperature conditions are utilized for maintaining apples with different shelf life. Accordingly, 73.554%$,$ 19.008%, and 7.438% of products are kept under the temperature levels $c1$, $c2$, and $c3$, respectively at a total cost of US$ 17,520,000. In addition, operational costs, including laborer, packing, and transportation costs from producers to warehouses are about US$ 67,422. Transportation cost between warehouses to the wholesaler is about US$ 107,349 for 2262 trips, of which 1, 1, 3, and 2256 are performed by vehicles types 1, 2, 3, and 4, respectively.

Sensitivity analysis

Sensitivity analysis is performed on the case study to determine the behavior of the model by changing the main parameters. Clearly, there are many reasons affecting the selling price of products and may lead to fluctuation in demands. Changes in the selling price of products may be caused by specific economic conditions (e.g., economic impacts of COVID-19 outbreak), irreversible damage during production (e.g., frost, floods), etc. The customers’ demand may be triggered by these factors or changes in taste and expectation, thereby becoming lesser or higher. From this point of view, it is vital to assess the model behavior during changes in parameters $D_{\mathit{it}}$ and ${\mathit{CQ}}_{\mathit{ijs}}$. In addition, this paper gives four vehicle types for fruits transportation and two cold storage rooms for 500 or 1000 Tons of apples that may change. The containers of different capacities can easily fit onto different forms of trucks and provide other options for transportation planning. Besides, redesign of cold rooms of less capacity may affect the feasibility of the problem. Finally, two remaining parameters are inventory holding costs and operational costs, which may be changed by embracing new technologies, identifying inefficiencies and unused services, etc. Therefore, this section provides an overview of the changes and their impacts to revise the plan after the occurrence. The results are summarized in Table 17.

Table 17.

The results of sensitivity analysis

Parameters	Changes (%)	Objective function values ($)	Percentage changes (%)
${\mathit{HW}}_c$	50	34,048,377	34.63
	25	29,668,828	17.31
	− 25	20,909,811	− 17.31
	− 50	16,530,329	− 34.63
$W_w$	50	23,458,018	− 7.24
	25	24,281,249	− 3.98
	− 25	27,137,910	7.31
	− 50	Infeasible	−
$D_{\mathit{it}}$	50	Infeasible	−
	25	Infeasible	−
	− 25	15,945,152	− 36.94
	− 50	10,358,746	− 59.03
${\mathit{CW}}_w$	50	28,589,282	13.04
	25	26,939,292	6.52
	− 25	23,639,312	− 6.52
	− 50	21,989,421	− 13.04
${\mathit{CQ}}_{\mathit{ijs}}$	50	25,785,923	1.96
	25	25,537,897	0.98
	− 25	25,040,161	− 0.98
	− 50	24,790,887	− 1.97
${\mathit{CV}}_k$	50	25,253,548	− 0.14
	25	25,267,852	− 0.08
	− 25	25,325,095	0.14
	− 50	25,396,595	0.42

The results in Table 17 draw up the sensitivity of the model to parameters $D_{\mathit{it}}$ and ${\mathit{HW}}_c$, where an increase of 25% in parameter $D_{\mathit{it}}$ makes the model infeasible, and a decrease of 50% in parameter $D_{\mathit{it}}$ reduce the total cost by 59%. Indeed, it is necessary to adjust capacity to match it with the changes in demands. We suppose that the available capacity of warehouses or producers is not sufficient in response to increased demands, therefore, the model becomes infeasible. In this case, the capacity of either warehouses or producers may step up to meet the demand. In addition, it is expected to purchase fewer products and avoid overstocks when demand decreases. This may cause a decrease in purchasing costs, operational costs, and inventory holding costs. Besides, a 50% increase in ${\mathit{HW}}_c$ leads to a 34.63% increase in the total cost. This indicates the importance of temperature condition adjustment and its impacts on the total cost.

For further investigation, the effects of the changes in parameters $\mathit{HWc}$, ${\mathit{CQ}}_{\mathit{ijs}}$, $D_{\mathit{it}}$ on operational costs, inventory holding costs, and purchasing costs are presented as follows:

Figure 9 demonstrates the effects of the changes on operational costs.

• The changes in parameter ${\mathit{CQ}}_{\mathit{ijs}}$ have insignificant opposite impacts on the operational costs.

• The changes in parameter $D_{\mathit{it}}$ have the greatest impacts on the operational costs, and a 25% decrease in demand leads to an 18% decrease in operational costs.

Fig. 9.

Impacts of the changes on operational costs

Figure 10 shows the impacts of the changes on inventory holding costs.

• A decrease in parameter ${\mathit{HW}}_c$ significantly reduces inventory holding costs. Indeed, a decrease of 25% in ${\mathit{HW}}_c$ leads to a 25% decrease in inventory holding costs.

• An increase in parameter $D_{\mathit{it}}$ significantly affects the inventory holding costs, and a 25% decrease in $D_{\mathit{it}}$ leads to a 36% decrease in inventory holding costs.

Fig. 10.

Impacts of the changes on inventory holding costs

Figure 11 shows the impacts of the changes on purchase costs.

• Changes in parameter $D_{\mathit{it}}$ have the greatest impacts on the total purchase cost. Indeed, a 25% decrease in $D_{\mathit{it}}$ leads to a 27% decrease in total purchase cost.

• Total purchase cost increases by increasing the amount of parameter ${\mathit{CQ}}_{\mathit{ijs}}$.

Fig. 11.

Impacts of the changes on purchase costs

Conclusion and future directions

Nowadays, an appropriate configuration of agro-supply chains becomes all the more critical issues owing to specific characteristics of agro-products. Hence, in this paper, a multi-product multi-period MINLP model has been developed for an agro-supply chain contributing to purchase, facility location, and transportation decisions. Forasmuch as adjustment of temperature condition affects the quality of products and consequently their shelf lives, this study determines proper temperature conditions based on the varieties of products. This model aims to minimize the total cost of the supply chain considering several operational constraints.

The primary step to solve the proposed model is to linearize the MINLP model and reformulate it into a MILP problem. Then, three sets of numerical examples, small, medium, and large sizes, have been presented to evaluate the performance of the mathematical model. The problem was coded in GAMS software and executed for small and medium test problems. Whatever the size of the problem increases, the computational time increases and the problem becomes difficult to solve. Therefore, BD algorithm has been implemented to tackle the complexity of the problem. Then GAMS/CPLEX solver and BD were compared in terms of objective function values and computational time. The results depict the convergence of BD to optimal solutions in a reasonable time.

Afterward, a precise assessment of the model was carried out by implementing a real case study. The results turn out the optimal purchase decisions of required quality score to be kept for a long time and number of cold chambers under proper temperature conditions. In addition, a sensitivity analysis was performed on the main parameters to predict the effects of the variations.

For future research, first, the model can be revisited for conditions under uncertain demands, thereby proposing efficient scenarios to overcome their associated shortage. Another possible extension of the model is to analyze purchase decisions under discount. This paper assumes only the products of the required quality for long time storage should be purchased. However, a new framework is promising to accommodate the distribution of products with short and long shelf lives that need precise inventory management.

Appendix

Abbreviation	Description
MINLP	Mixed-integer nonlinear programming
BD	Benders decomposition
MILP	Mixed-integer linear programming
MP	Master problem
SP	Subproblem
DSP	Dual sub-problem
SLD	Decision on shelf life
CFD	Decision on cold storage facilities