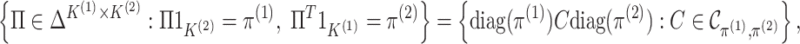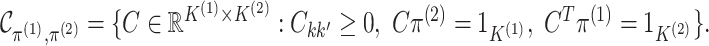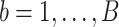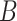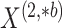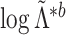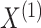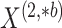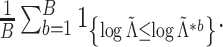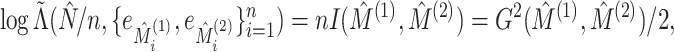Summary
In the Pioneer 100 (P100) Wellness Project, multiple types of data are collected on a single set of healthy participants at multiple timepoints in order to characterize and optimize wellness. One way to do this is to identify clusters, or subgroups, among the participants, and then to tailor personalized health recommendations to each subgroup. It is tempting to cluster the participants using all of the data types and timepoints, in order to fully exploit the available information. However, clustering the participants based on multiple data views implicitly assumes that a single underlying clustering of the participants is shared across all data views. If this assumption does not hold, then clustering the participants using multiple data views may lead to spurious results. In this article, we seek to evaluate the assumption that there is some underlying relationship among the clusterings from the different data views, by asking the question: are the clusters within each data view dependent or independent? We develop a new test for answering this question, which we then apply to clinical, proteomic, and metabolomic data, across two distinct timepoints, from the P100 study. We find that while the subgroups of the participants defined with respect to any single data type seem to be dependent across time, the clustering among the participants based on one data type (e.g. proteomic data) appears not to be associated with the clustering based on another data type (e.g. clinical data).
Keywords: Data integration, Hypothesis testing, Model-based clustering, Multiple-view data
1. Introduction
Complex biological systems consist of diverse components with dynamics that may vary over time, and so these systems often cannot be fully characterized by any single type of data, or at any single snapshot in time. Consequently, it has become increasingly common for researchers to collect multiple datasets, or views, for a single set of observations. In the machine learning literature, this is known as the multiple-view or multi-view data setting.
Multiple-view data have been applied extensively to characterize disease, such as in The Cancer Genome Atlas Project (Cancer Genome Atlas Research Network, 2008). In contrast, The Pioneer 100 (P100) Wellness Project (Price and others, 2017) collected multiple-view data from healthy participants to characterize wellness, and to optimize wellness of the participants through personalized healthcare recommendations. One way to do this is to identify subgroups of similar participants using cluster analysis, and then tailor recommendations to each subgroup.
In recent years, many papers have proposed clustering methods in the multiple-view data setting (Bickel and Scheffer, 2004; Shen and others, 2009; Kumar and others, 2011; Kirk and others, 2012; Lock and Dunson, 2013; Gabasova and others, 2017). The vast majority of these methods “borrow strength” across the data views to obtain a more accurate clustering of the observations than would be possible based on a single data view. Implicitly, these methods assume that there is a single consensus clustering shared by all data views.
The P100 data contains many data views; multiple data types (e.g. clinical data and proteomic data) are available at multiple timepoints. Thus, it is tempting to apply consensus clustering methods to identify subgroups of the P100 participants. However, before doing so, it is important to check the assumption that there exists a single consensus clustering. If instead different views reflect unrelated aspects of the participants, then there is no “strength to be borrowed” across the views, and it would be better to perform a separate clustering of the observations in each view. Before attempting cluster analysis of the P100 data, it is critical that we determine which combinations of views have “strength to be borrowed,” and which combinations do not.
This raises the natural question of how associated the underlying clusterings are in each view. Suppose we cluster the P100 participants twice, once using their baseline clinical data, and once using their baseline proteomic data. Can we tell from the data whether the two views’ underlying clusterings are related or unrelated? Answering this question provides useful information:
Case 1: If the underlying clusterings appear related, then this increases confidence that the clusterings are scientifically meaningful, and offers some support for performing a consensus clustering of the P100 participants that integrates baseline clinical and proteomic views.
-
Case 2: If the underlying clusterings appear unrelated, we must consider two explanations.
(1) Perhaps clinical and proteomic views measure different properties about the participants, and therefore identify complementary (or “orthogonal”) clusterings. If so, then a consensus clustering is unlikely to provide meaningful results, and may cause us to lose valuable information about the subgroups underlying the individual data views.
(2) Perhaps the subgroups underlying the data views are indeed related, but they appear unrelated due to noise. If so, then we might be skeptical of any results obtained on these very noisy data, whether from consensus clustering or another approach.
In Case 2, it would not be appropriate to perform consensus clustering.
To determine from the data whether the two views’ clusterings are related or unrelated, it
is tempting to apply a clustering procedure (e.g. k-means) to each view, then apply
well-studied tests of independence of categorical variables (e.g. the
 -test for independence, the
-test for independence, the
 -test for independence, or Fisher’s exact
test) to the estimated cluster assignments. However, such an approach relies on an
assumption that the estimated cluster assignments are independent and identically
distributed samples from the joint distribution of the cluster membership variables, which
is not satisfied in practice. Thus, there is a need for an approach which takes into account
the fact that the clusterings are estimated from the data.
-test for independence, or Fisher’s exact
test) to the estimated cluster assignments. However, such an approach relies on an
assumption that the estimated cluster assignments are independent and identically
distributed samples from the joint distribution of the cluster membership variables, which
is not satisfied in practice. Thus, there is a need for an approach which takes into account
the fact that the clusterings are estimated from the data.
The rest of this article is organized as follows. In Section 2, we propose a mixture model for two-view data. In Section 3, we use this model to develop a test of the null hypothesis
that clusterings on two views of a single set of observations are independent. We explore
the performance of our proposed hypothesis test via numerical simulation in Section 4. In Section
5, we connect and compare our proposed hypothesis test to the aforementioned
approach of applying the 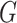 -test for independence to the estimated
cluster assignments and draw connections between this approach and the mutual information
statistic (Meilă, 2007). In Section 6, we apply our method to the clinical, proteomic, and
metabolomic datasets from the P100 study. In Section
7, we provide a discussion, which includes the extension to more than two
views.
-test for independence to the estimated
cluster assignments and draw connections between this approach and the mutual information
statistic (Meilă, 2007). In Section 6, we apply our method to the clinical, proteomic, and
metabolomic datasets from the P100 study. In Section
7, we provide a discussion, which includes the extension to more than two
views.
2. A mixture model for multiple-view data
2.1. Model specification
In what follows, we consider the case of two data views. We will discuss the extension to more than two views in Section 7.
Suppose we have  and
and 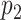 features in the first and second data view, respectively. For a single observation, let
features in the first and second data view, respectively. For a single observation, let
 and
and
 denote the
random vectors corresponding to the two data views and let
denote the
random vectors corresponding to the two data views and let 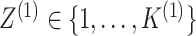 and
and
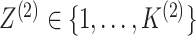 be
unobserved random variables, indicating the latent group memberships of this observation
in the two data views. Here,
be
unobserved random variables, indicating the latent group memberships of this observation
in the two data views. Here, 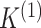 and
and 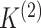 represent the number of clusters in the two data views, which we assume for now to be
known (we will consider the case in which they are unknown in Section 2.4). We assume that
represent the number of clusters in the two data views, which we assume for now to be
known (we will consider the case in which they are unknown in Section 2.4). We assume that 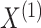 and
and 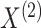 are conditionally independent given
the pair of cluster memberships,
are conditionally independent given
the pair of cluster memberships, 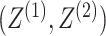 ; this
assumption is common in the multi-view clustering literature (see e.g. Bickel and Scheffer, 2004; Rogers and others, 2008; Kumar and others, 2011; Lock and Dunson, 2013; Gabasova
and others, 2017). Further, suppose that
; this
assumption is common in the multi-view clustering literature (see e.g. Bickel and Scheffer, 2004; Rogers and others, 2008; Kumar and others, 2011; Lock and Dunson, 2013; Gabasova
and others, 2017). Further, suppose that
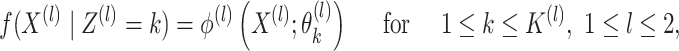 |
(2.1) |
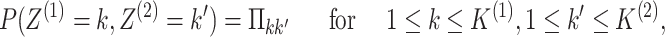 |
(2.2) |
where  denotes a density function with parameter
denotes a density function with parameter 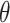 , and
, and
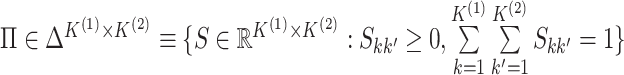 .
Equations (2.1)–(2.2) are an extension of the finite
mixture model (McLachlan and Peel, 2000) to the
case of two data views. We further assume that each cluster has positive probability, that
is
.
Equations (2.1)–(2.2) are an extension of the finite
mixture model (McLachlan and Peel, 2000) to the
case of two data views. We further assume that each cluster has positive probability, that
is 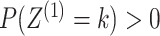 and
and
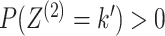 , and so
, and so
 and
and
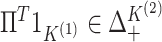 ,
where
,
where 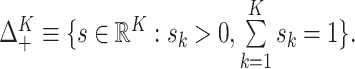
Let  and
and 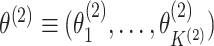 .
The joint density of
.
The joint density of 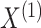 and
and 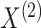 is
is
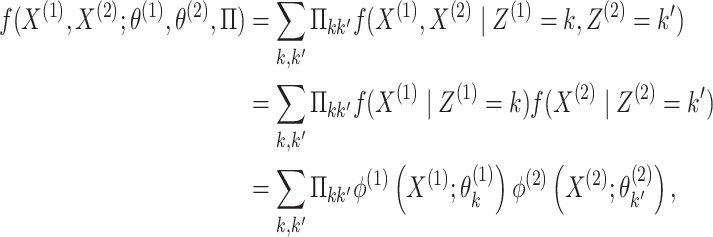 |
(2.3) |
where the second equality follows from conditional
independence of 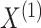 and
and 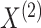 given
given  and
and 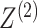 ,
and the last equality follows from (2.1).
,
and the last equality follows from (2.1).
The matrix  governs the statistical dependence
between the two data views. It will be useful for us to parameterize
governs the statistical dependence
between the two data views. It will be useful for us to parameterize
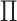 in terms of a triplet
in terms of a triplet
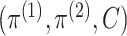 that separates the
single-view information from the cross-view information.
that separates the
single-view information from the cross-view information.
Proposition 1
Suppose
and
. Then,
where
A Proof of Proposition 1 is given in Appendix A.1 of the supplementary material available at Biostatistics online.
Proposition 1 indicates that any matrix 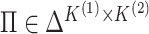 with
with
 and
and
 can be written as the product of its row sums
can be written as the product of its row sums 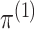 , its column sums
, its column sums
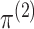 , and a matrix
, and a matrix
 . Therefore, we can rewrite the joint
probability density (2.3) as
follows:
. Therefore, we can rewrite the joint
probability density (2.3) as
follows:
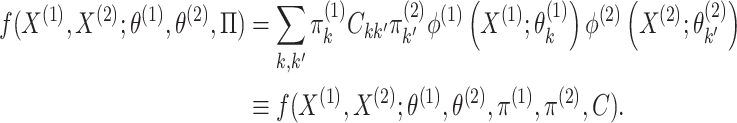 |
(2.4) |
In what follows, we will parametrize the density of 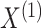 and
and 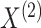 in terms of
in terms of
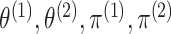 ,
and
,
and  , rather than in terms of
, rather than in terms of
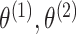 , and
, and
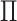 .
.
The following proposition characterizes the marginal distributions of
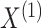 and
and 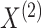 .
.
Proposition 2
Suppose
and
have joint distribution (2.4). Then for
,
has marginal density given by
(2.5)
Proposition 2 follows from (2.1) to
(2.2). Proposition 2 shows that
for 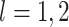 ,
, 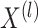 marginally follows a mixture model with parameters
marginally follows a mixture model with parameters 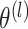 and cluster membership
probabilities
and cluster membership
probabilities 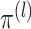 . Note that the marginal density
of
. Note that the marginal density
of 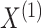 does not depend on
does not depend on
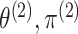 , and
, and
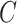 , and similarly, the marginal density of
, and similarly, the marginal density of
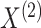 does not depend on
does not depend on
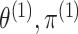 , and
, and
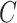 ; this fact will be critical to our
approach to parameter estimation in Section
2.3.
; this fact will be critical to our
approach to parameter estimation in Section
2.3.
The model described in this section is closely related to several multiple-view mixture
models proposed in the literature: see for example Rogers
and others (2008), Kirk
and others (2012), Lock and
Dunson (2013), and Gabasova and
others (2017). However, the focus of those papers is cluster
estimation: they do not provide a statistical test of association, and for the most part,
impose additional structure on the probability matrix 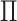 in
order to encourage similarity between the clusters estimated in each data view. In
contrast, the focus of this article is inference: testing for dependence between the
clusterings in different data views. The model described in this section is a step towards
that goal.
in
order to encourage similarity between the clusters estimated in each data view. In
contrast, the focus of this article is inference: testing for dependence between the
clusterings in different data views. The model described in this section is a step towards
that goal.
2.2. Interpreting 
In Figure 1(i)–(iii), 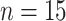 independent pairs
independent pairs  are drawn
from the model (2.1)–(2.2), for three choices of
are drawn
from the model (2.1)–(2.2), for three choices of 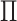 . The
left-hand panel represents the
. The
left-hand panel represents the 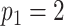 features in the
first data view, and the right-hand panel represents the
features in the
first data view, and the right-hand panel represents the 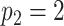 features in the second data view. For
features in the second data view. For 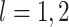 , the observations
, the observations
 in the
in the
 th data view belong to two clusters, where
the latent variables
th data view belong to two clusters, where
the latent variables 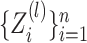 characterize cluster
membership in the
characterize cluster
membership in the 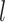 th data view. Light and dark gray
represent the clusters in the first view, and circles and triangles represent the clusters
in the second view.
th data view. Light and dark gray
represent the clusters in the first view, and circles and triangles represent the clusters
in the second view.
Fig. 1.
Clusters in the first view are represented with dark and light shades of gray, and
clusters in the second view are represented with circles and triangles. (i) The
clusterings in the two views are independent, that is, 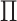 has rank one, so the shade of gray (dark or light) and shape (circle or triangle) are
unassociated. (ii) The clusterings in the two views are the same, that is,
has rank one, so the shade of gray (dark or light) and shape (circle or triangle) are
unassociated. (ii) The clusterings in the two views are the same, that is,
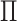 is diagonal (up to permutation of
rows), so the shade of gray (dark or light) and shape (circle or triangle) are
perfectly correlated. (iii) The clusterings in the two view are somewhat dependent,
that is,
is diagonal (up to permutation of
rows), so the shade of gray (dark or light) and shape (circle or triangle) are
perfectly correlated. (iii) The clusterings in the two view are somewhat dependent,
that is,  is neither diagonal nor rank one.
is neither diagonal nor rank one.
Figure 1(i)–(ii) correspond to two special cases of
 that are easily interpretable. In Figure 1(i),
that are easily interpretable. In Figure 1(i),  has rank one, that is
has rank one, that is
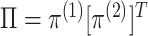 , so that the
clusterings in the two data views are independent. Thus, whether an observation is light
or dark appears to be roughly independent of whether it is a circle or a triangle. In
Figure 1(ii),
, so that the
clusterings in the two data views are independent. Thus, whether an observation is light
or dark appears to be roughly independent of whether it is a circle or a triangle. In
Figure 1(ii),  and
and 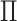 is
diagonal (up to a permutation of the rows), so that the clusterings in the two data views
are identical. Thus, all of the circles are light and all of the triangles are dark.
Another special case is when
is
diagonal (up to a permutation of the rows), so that the clusterings in the two data views
are identical. Thus, all of the circles are light and all of the triangles are dark.
Another special case is when 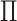 is block diagonal (up to a permutation)
with
is block diagonal (up to a permutation)
with 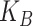 blocks. Then, the clusterings of the
two data views agree about the presence of
blocks. Then, the clusterings of the
two data views agree about the presence of 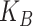 “meta-clusters” in the
data. For example, one clustering might be a refinement of the other, or if one view has
clusters
“meta-clusters” in the
data. For example, one clustering might be a refinement of the other, or if one view has
clusters 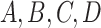 , and the other has clusters
, and the other has clusters
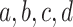 , it could be that
, it could be that

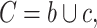 and
and 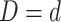 .
.
In general, 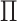 will be neither exactly rank 1 nor
exactly (block) diagonal; Figure 1(iii) provides such
an example. Furthermore,
will be neither exactly rank 1 nor
exactly (block) diagonal; Figure 1(iii) provides such
an example. Furthermore,  (an estimator for
(an estimator for
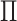 ) almost certainly will be neither.
Nonetheless, examination of
) almost certainly will be neither.
Nonetheless, examination of  can provide insight into the
relationships between the two clusterings. For example, if
can provide insight into the
relationships between the two clusterings. For example, if  is far from rank 1, then this suggests that the clusterings in the two data views may be
dependent. We will formalize this intuition in Section
3.
is far from rank 1, then this suggests that the clusterings in the two data views may be
dependent. We will formalize this intuition in Section
3.
2.3. Estimation
2.3.1. Estimation procedure and algorithm
Given 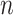 independent pairs
independent pairs
 drawn from the model (2.1)–(2.2), the log-likelihood takes the
form
drawn from the model (2.1)–(2.2), the log-likelihood takes the
form
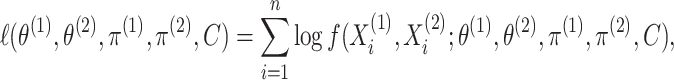 |
(2.6) |
where  is defined in (2.4). A custom
expectation–maximization (EM; Dempster and
others 1977; McLachlan and Krishnan
2007) algorithm could be developed to solve (2.6) for a local optimum (a global optimum is typically
unattainable, as (2.6) is
non-concave). We instead take a simpler approach. Proposition 2 implies that for
is defined in (2.4). A custom
expectation–maximization (EM; Dempster and
others 1977; McLachlan and Krishnan
2007) algorithm could be developed to solve (2.6) for a local optimum (a global optimum is typically
unattainable, as (2.6) is
non-concave). We instead take a simpler approach. Proposition 2 implies that for
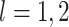 , we can estimate
, we can estimate
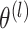 and
and
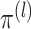 by maximizing the marginal
likelihood for the
by maximizing the marginal
likelihood for the  th data view, given by
th data view, given by
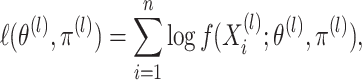 |
(2.7) |
where 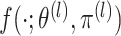 is
defined in (2.5). Each of these
maximizations can be performed using standard EM-based software for model-based
clustering of a single data view. Let
is
defined in (2.5). Each of these
maximizations can be performed using standard EM-based software for model-based
clustering of a single data view. Let  and
and 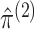 denote the maximizers of
(2.7). Next, to estimate
denote the maximizers of
(2.7). Next, to estimate
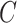 , we maximize the joint log-likelihood
(2.6) evaluated at
, we maximize the joint log-likelihood
(2.6) evaluated at
 and
and 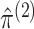 , subject to the
constraints imposed by Proposition 1:
, subject to the
constraints imposed by Proposition 1:
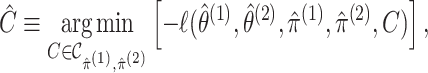 |
(2.8) |
where 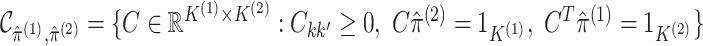 .
Equation 2.8 is a convex
optimization problem, which we solve using a combination of exponentiated gradient
descent (Kivinen and Warmuth, 1997) and the
Sinkhorn–Knopp algorithm (Franklin and Lorenz,
1989), as detailed in Appendix B of the supplementary material available at Biostatistics
online. Details of our approach for fitting the model (2.1)–(2.2) are given in Algorithm 1.
.
Equation 2.8 is a convex
optimization problem, which we solve using a combination of exponentiated gradient
descent (Kivinen and Warmuth, 1997) and the
Sinkhorn–Knopp algorithm (Franklin and Lorenz,
1989), as detailed in Appendix B of the supplementary material available at Biostatistics
online. Details of our approach for fitting the model (2.1)–(2.2) are given in Algorithm 1.
Algorithm 1.
- Maximize the marginal likelihoods (2.7) in order to obtain the marginal MLEs
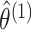 ,
,
 and
and
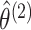 ,
,
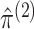 . This can be
done using standard software for model-based clustering.
. This can be
done using standard software for model-based clustering. - Define matrices
 and
and  with elements
with elements 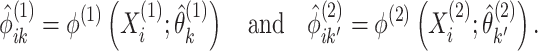
(2.9) - Fix a step size
 . Theorem 5.3 from Kivinen and Warmuth (1997) gives conditions
on
. Theorem 5.3 from Kivinen and Warmuth (1997) gives conditions
on  that guarantee
convergence.
that guarantee
convergence. -
Let
 .
For
.
For 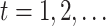 until
convergence:
until
convergence:- (a) Define
 where
where 
-
(b) Let
 and
and
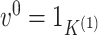 . For
. For
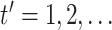 , until
convergence:
, until
convergence:- i.
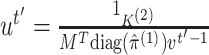 ,
,
 ,
where the fractions denote element-wise vector division.
,
where the fractions denote element-wise vector division.
- (c) Let
 and
and
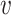 be the vectors to which
be the vectors to which
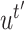 and
and
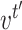 converge. Let
converge. Let
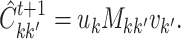
- Let
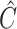 denote the matrix to
which
denote the matrix to
which  converges, and let
converges, and let
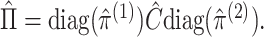
2.3.2. Justification of estimation procedure
The estimation procedure in Section 2.3.1 does not maximize the joint likelihood (2.6); nonetheless, we will argue that it is an attractive approach.
To begin, in Step 1 of Algorithm 1, we estimate
 and
and
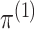 by maximizing the marginal
likelihood (2.7). This decision
leads to computational advantages, as it enables us to make use of efficient software
for clustering a single data view, such as the
by maximizing the marginal
likelihood (2.7). This decision
leads to computational advantages, as it enables us to make use of efficient software
for clustering a single data view, such as the  package (Scrucca and others, 2016) in
package (Scrucca and others, 2016) in
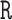 . We can further justify this
decision using conditional inference theory. Equation 3.6 in Reid (1995) extends the definition of ancillary statistics to a
setting with nuisance parameters. We show that
. We can further justify this
decision using conditional inference theory. Equation 3.6 in Reid (1995) extends the definition of ancillary statistics to a
setting with nuisance parameters. We show that 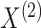 is ancillary (in the extended sense
of Reid 1995) for
is ancillary (in the extended sense
of Reid 1995) for  , and
, and
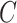 by using the definition of conditional
densities, and Proposition 2, to rewrite (2.4) as
by using the definition of conditional
densities, and Proposition 2, to rewrite (2.4) as
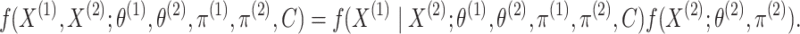 |
Thus, Reid (1995) argues that we should use only
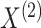 , and not
, and not
 , to estimate
, to estimate
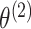 and
and
 . In Step 1 of Algorithm 1, we are doing exactly this.
. In Step 1 of Algorithm 1, we are doing exactly this.
In Steps 3–5 of Algorithm 1, we maximize
 ,
giving
,
giving  , which is a pseudo maximum
likelihood estimator for
, which is a pseudo maximum
likelihood estimator for  in the sense of Gong and Samaniego (1981). This decision also leads to computational
advantages, as it enables us to make use of efficient convex optimization algorithms in
estimating
in the sense of Gong and Samaniego (1981). This decision also leads to computational
advantages, as it enables us to make use of efficient convex optimization algorithms in
estimating  . Results in Gong and Samaniego (1981) suggest that when
. Results in Gong and Samaniego (1981) suggest that when  ,
,
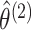 ,
,
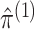 , and
, and
 are good estimates,
are good estimates,
 is so as well.
is so as well.
2.4. Selection of the number of clusters
In Sections 2 and 3, our discussion assumed that  and
and
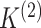 are known. However, this is rarely
the case in practice. Recall that we estimate
are known. However, this is rarely
the case in practice. Recall that we estimate  and
and
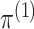 by maximizing the marginal
likelihood (2.7), which amounts to
performing model-based clustering of
by maximizing the marginal
likelihood (2.7), which amounts to
performing model-based clustering of  only. Thus, to
select the number of clusters
only. Thus, to
select the number of clusters 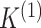 , we can make use
of an extensive literature (reviewed in e.g. Mirkin
2011) on choosing the number of clusters when clustering a single data view. For
example, we can use Akaike Information Criterion (AIC) or Bayesian Information Criterion
(BIC) to select
, we can make use
of an extensive literature (reviewed in e.g. Mirkin
2011) on choosing the number of clusters when clustering a single data view. For
example, we can use Akaike Information Criterion (AIC) or Bayesian Information Criterion
(BIC) to select 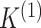 and
and 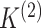 .
.
3. Testing whether two clusterings are independent
3.1. A brief review of pseudo likelihood ratio tests
Let  be the
log-likelihood function for a random sample, where
be the
log-likelihood function for a random sample, where  is the parameter space of
is the parameter space of
 . Given a null hypothesis
. Given a null hypothesis
 for some
for some
 , an alternative
hypothesis
, an alternative
hypothesis 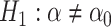 , and an
estimator
, and an
estimator 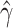 , the pseudo likelihood ratio
statistic (Self and Liang, 1987) is defined to be
, the pseudo likelihood ratio
statistic (Self and Liang, 1987) is defined to be
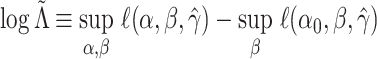 .
Let
.
Let  be the true parameter value for
be the true parameter value for
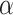 . If
. If 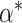 is an interior point of
is an interior point of 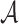 , then under some regularity
conditions, if
, then under some regularity
conditions, if  holds, then
holds, then  where
where  is the dimension of
is the dimension of
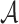 (Chen and Liang, 2010).
(Chen and Liang, 2010).
3.2. A pseudo likelihood ratio test for independence
In this subsection, we develop a test for the null hypothesis that
 , or
equivalently, that
, or
equivalently, that 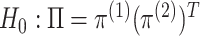 : that
is, we test whether
: that
is, we test whether  and
and  are independent, that is whether the cluster memberships in the two data views are
independent. We could use a likelihood ratio test statistic to test
are independent, that is whether the cluster memberships in the two data views are
independent. We could use a likelihood ratio test statistic to test
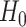 ,
,
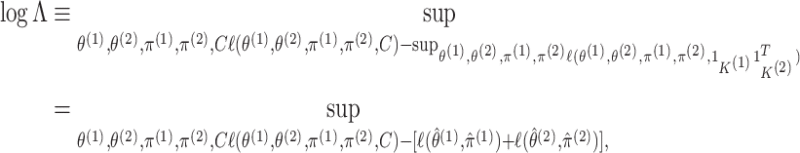 |
(3.10) |
where the second equality follows from noticing that
substituting 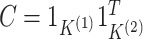 into (2.6) yields
into (2.6) yields
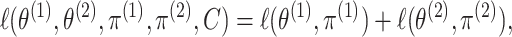 |
(3.11) |
where  for
for
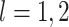 are defined in (2.7), and recalling the definition of
are defined in (2.7), and recalling the definition of
 ,
,
 ,
,  , and
, and
 as the maximizers of (2.7). However, (3.10) requires maximizing
as the maximizers of (2.7). However, (3.10) requires maximizing
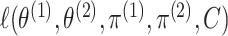 ,
which would require a custom EM algorithm; furthermore, the resulting test statistic will
typically involve the difference between two local maxima (since each term in (3.10) requires fitting an EM
algorithm). This leads to erratic behavior, such as negative values of
,
which would require a custom EM algorithm; furthermore, the resulting test statistic will
typically involve the difference between two local maxima (since each term in (3.10) requires fitting an EM
algorithm). This leads to erratic behavior, such as negative values of
 .
.
Therefore, instead of taking the approach in (3.10), we develop a pseudo likelihood ratio test, as in Section
3.1. We use the marginal MLEs,
 and
and
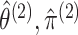 , instead
of performing the joint optimization in (3.10). This leads to the test statistic
, instead
of performing the joint optimization in (3.10). This leads to the test statistic
 |
(3.12) |
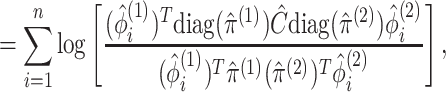 |
(3.13) |
where  in (3.12) is defined in (2.8),
in (3.12) is defined in (2.8),  is defined in Proposition 1,
is defined in Proposition 1, 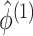 and
and
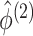 are defined in (2.9), and the last equality follows from
(2.6), (2.7), and (2.9). In addition to taking advantage of the computationally
efficient estimation procedure described in Section
2.3.1, the pseudo likelihood ratio test statistic does not exhibit the erratic
behavior exhibited by the likelihood ratio test statistic. This stability comes from all
three terms in (3.12) involving the
same local maxima (as opposed to different local maxima).
are defined in (2.9), and the last equality follows from
(2.6), (2.7), and (2.9). In addition to taking advantage of the computationally
efficient estimation procedure described in Section
2.3.1, the pseudo likelihood ratio test statistic does not exhibit the erratic
behavior exhibited by the likelihood ratio test statistic. This stability comes from all
three terms in (3.12) involving the
same local maxima (as opposed to different local maxima).
3.3 Approximating the null distribution of 
The discussion in Section 3.1 suggests that
under 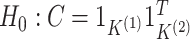 , one
might expect that
, one
might expect that 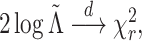 where
where  is the
dimension of
is the
dimension of 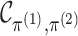 .
However, this approximation performs poorly in practice, due to violations of the
regularity conditions in Chen and Liang (2010).
Furthermore, we will often be interested in data applications in which
.
However, this approximation performs poorly in practice, due to violations of the
regularity conditions in Chen and Liang (2010).
Furthermore, we will often be interested in data applications in which
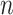 is relatively small. Hence, we propose a
permutation approach. We observe from (3.11) that under
is relatively small. Hence, we propose a
permutation approach. We observe from (3.11) that under 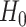 , the log-likelihood is identical under
any permutation of the order of the samples in each view. Hence, we take
, the log-likelihood is identical under
any permutation of the order of the samples in each view. Hence, we take
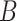 random permutations of the samples
random permutations of the samples
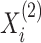 from the second view and compare
the observed value of
from the second view and compare
the observed value of 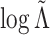 to its empirical
distribution in these permutation samples. Details are given in Algorithm 2. Since
to its empirical
distribution in these permutation samples. Details are given in Algorithm 2. Since 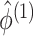 ,
,
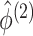 ,
, 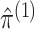 , and
, and  are invariant to permutation,
for each permutation we need only to estimate
are invariant to permutation,
for each permutation we need only to estimate  . This is another
advantage of our test over the likelihood ratio test discussed in Section 3.2, which would require repeating the EM algorithm in every
permutation. Even when we reject the null hypothesis, the clusters could be only weakly
dependent; thus, it is helpful to measure the strength of association between the views.
Recalling from Section 2.2 that
. This is another
advantage of our test over the likelihood ratio test discussed in Section 3.2, which would require repeating the EM algorithm in every
permutation. Even when we reject the null hypothesis, the clusters could be only weakly
dependent; thus, it is helpful to measure the strength of association between the views.
Recalling from Section 2.2 that
 implies independence
of the clusterings in the two data views, we propose to calculate the effective rank
(Vershynin, 2012) of
implies independence
of the clusterings in the two data views, we propose to calculate the effective rank
(Vershynin, 2012) of  , defined in Algorithm 1—the ratio of the sum of the singular values of
, defined in Algorithm 1—the ratio of the sum of the singular values of
 , and the largest singular value of
, and the largest singular value of
 . The effective rank of a matrix is
bounded between 1 and its rank, and the matrix is far from rank-1 when its effective rank
is far from 1. For example, in Figure 1(iii), the
effective rank of
. The effective rank of a matrix is
bounded between 1 and its rank, and the matrix is far from rank-1 when its effective rank
is far from 1. For example, in Figure 1(iii), the
effective rank of 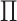 is 1.5, and is upper bounded by 2.
Thus, the effective rank of
is 1.5, and is upper bounded by 2.
Thus, the effective rank of  is bounded between 1 and
is bounded between 1 and
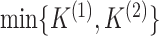 , and
, and
 is far from rank-1 when its
effective rank is far from 1.
is far from rank-1 when its
effective rank is far from 1.
Algorithm 2.
4. Simulation results
To investigate the Type I error and power of our test, we generate data from (2.1)–(2.2), with
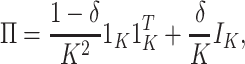 |
(4.14) |
for 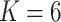 and for a range of
values of
and for a range of
values of 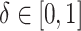 , where
, where
 corresponds to independent
clusterings, and
corresponds to independent
clusterings, and 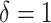 corresponds to identical
clusterings. We draw the observations in the
corresponds to identical
clusterings. We draw the observations in the 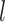 th data view from a
Gaussian mixture model, for which the
th data view from a
Gaussian mixture model, for which the  th mixture component is a
th mixture component is a
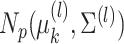 distribution,
with
distribution,
with 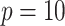 , and with
, and with 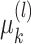 given in Appendix C.1 of the supplementary material available at
Biostatistics online.
given in Appendix C.1 of the supplementary material available at
Biostatistics online.
We simulate 2000 datasets for  for a range of values of
for a range of values of 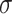 and
and  , and
evaluate the power of the pseudo likelihood ratio test of
, and
evaluate the power of the pseudo likelihood ratio test of  described in Section 3.2 at nominal significance level
described in Section 3.2 at nominal significance level
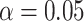 , when the number of clusters is
correctly and incorrectly specified. To perform Step 1 of Algorithm 1, we use the package
, when the number of clusters is
correctly and incorrectly specified. To perform Step 1 of Algorithm 1, we use the package 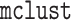 in
in
 to fit Gaussian mixture models
with a common
to fit Gaussian mixture models
with a common  covariance matrix (the “EII”
covariance structure in
covariance matrix (the “EII”
covariance structure in  ). We use
). We use
 permutation samples in Step 2 of
Algorithm 2. Simulations in this article were
conducted using the
permutation samples in Step 2 of
Algorithm 2. Simulations in this article were
conducted using the  package (Bien, 2016) in
package (Bien, 2016) in  . Results are
shown in Figure 2.
. Results are
shown in Figure 2.
Fig. 2.
Power of the pseudo likelihood ratio test of  with
with
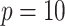 ,
, 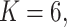 and
and 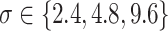 in the
simulation setting described in Section 4. The
in the
simulation setting described in Section 4. The
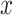 -axis displays
-axis displays 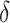 , defined in (4.14), and the
, defined in (4.14), and the
 -axis displays the power.
-axis displays the power.
The pseudo likelihood ratio test controls the Type I error close to the nominal
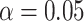 level, even when the number of
clusters is misspecified. Power tends to increase as
level, even when the number of
clusters is misspecified. Power tends to increase as  (defined in (4.14)) increases and
tends to decrease as
(defined in (4.14)) increases and
tends to decrease as  increases. Compared to using the
correct number of clusters, using too many clusters yields lower power, but using too few
clusters can sometimes yield higher power (e.g. in the middle panel of Figure 2). This is because, when the signal-to-noise ratio is low, the
true clusters are not accurately estimated; thus, combining several true clusters into a
single “meta-cluster” can sometimes, but not always, lead to improved agreement between
clusterings across the two data views. We explore the impact of the choice of
increases. Compared to using the
correct number of clusters, using too many clusters yields lower power, but using too few
clusters can sometimes yield higher power (e.g. in the middle panel of Figure 2). This is because, when the signal-to-noise ratio is low, the
true clusters are not accurately estimated; thus, combining several true clusters into a
single “meta-cluster” can sometimes, but not always, lead to improved agreement between
clusterings across the two data views. We explore the impact of the choice of
 on the performance of the pseudo likelihood
ratio test in Appendix C.2.1 of the supplementary materials available at Biostatistics online.
on the performance of the pseudo likelihood
ratio test in Appendix C.2.1 of the supplementary materials available at Biostatistics online.
Additional values of 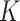 and
and  are
investigated in Appendix C.2.2 of the supplementary material available at Biostatistics online.
are
investigated in Appendix C.2.2 of the supplementary material available at Biostatistics online.
5. Connection to the G-test for independence and mutual information
Let 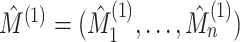 and
and 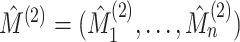 denote the results of applying a clustering procedure to
denote the results of applying a clustering procedure to 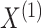 and
and 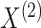 , respectively. In this notation,
, respectively. In this notation,
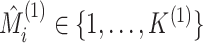 and
and
 denote the estimated cluster assignment for the
denote the estimated cluster assignment for the 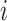 th observation in the two
views. To test whether
th observation in the two
views. To test whether  and
and 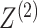 are independent, we could naively apply tests on
are independent, we could naively apply tests on 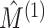 and
and
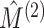 for whether two categorical
variables are independent. For instance, we could use the
for whether two categorical
variables are independent. For instance, we could use the  -test
statistic for independence (Chapter 3.2, Agresti,
2003), given by
-test
statistic for independence (Chapter 3.2, Agresti,
2003), given by
 |
(5.15) |
where 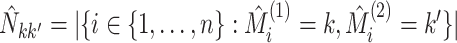 ,
,
 ,
and
,
and 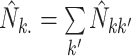 .
Under the model
.
Under the model  the
the 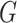 -test statistic for independence (5.15) is a likelihood ratio test
statistic for testing the null hypothesis of independence, that is for testing
-test statistic for independence (5.15) is a likelihood ratio test
statistic for testing the null hypothesis of independence, that is for testing
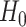 :
: 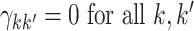 .
Thus, under
.
Thus, under 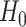 :
: 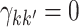 ,
,
 |
(5.16) |
The 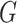 -test statistic for independence (5.15) relies on an assumption which is
violated in our setting, namely that
-test statistic for independence (5.15) relies on an assumption which is
violated in our setting, namely that  are independent and identically distributed samples from the distribution of
are independent and identically distributed samples from the distribution of
 . It is nonetheless a
natural approach to the problem of comparing two views’ clusterings. In fact, the mutual
information of Meilă (2007) for measuring the
similarity between two clusterings of a single
. It is nonetheless a
natural approach to the problem of comparing two views’ clusterings. In fact, the mutual
information of Meilă (2007) for measuring the
similarity between two clusterings of a single  dataset can be
written as a scaled version of the
dataset can be
written as a scaled version of the 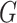 -test statistic; when
applied to instead measure the similarity between
-test statistic; when
applied to instead measure the similarity between  and
and
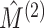 , the mutual information
, the mutual information
 is given by
is given by
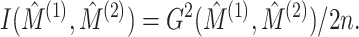 |
(5.17) |
While the proposed pseudo likelihood ratio test statistic (3.13) for testing independence of 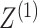 and
and 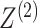 does not resemble the simple
does not resemble the simple
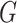 -test statistic for independence in (5.15), we show here that they are in fact
quite related.
-test statistic for independence in (5.15), we show here that they are in fact
quite related.
Let 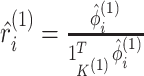 and
and  be the vectors giving the soft-clustering assignment weights (or “responsibilities”) for the
be the vectors giving the soft-clustering assignment weights (or “responsibilities”) for the
 th observation in the two views, where
th observation in the two views, where
 is defined in (2.9). We rewrite the pseudo likelihood
ratio test statistic (3.13) as
is defined in (2.9). We rewrite the pseudo likelihood
ratio test statistic (3.13) as
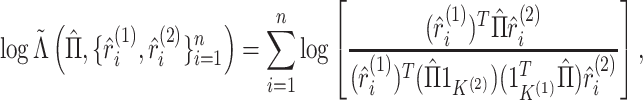 |
(5.18) |
where  is defined in
Algorithm 1. In the following proposition, we
consider replacing the “soft” cluster assignments
is defined in
Algorithm 1. In the following proposition, we
consider replacing the “soft” cluster assignments  and
and
 with “hard” cluster
assignments, and replacing the estimate
with “hard” cluster
assignments, and replacing the estimate  derived from the
“soft” cluster assignments with an estimate derived from “hard” cluster assignments, in
(5.18). In what follows,
derived from the
“soft” cluster assignments with an estimate derived from “hard” cluster assignments, in
(5.18). In what follows,
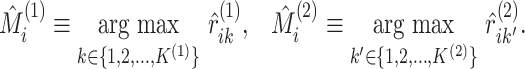 |
(5.19) |
Proposition 3
Let
and
be the estimated model-based cluster assignments in each data view defined by (5.19). Let
be the matrix with entries
containing the number of observations assigned to cluster
in view 1 and cluster
in view 2. Then,
(5.20) where
is defined in (5.18), and
is the unit vector that contains a 1 in the
th element.
Proposition 3 follows by algebra, and says that replacing the soft cluster assignments in
the pseudo likelihood ratio test statistic of Section
3 with hard cluster assignments yields exactly the
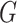 -test statistic for independence (5.15) (and the mutual information given
in (5.17))! In fact, in the special
case of fitting multiple-view Gaussian mixtures with common covariance matrix
-test statistic for independence (5.15) (and the mutual information given
in (5.17))! In fact, in the special
case of fitting multiple-view Gaussian mixtures with common covariance matrix
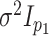 in the first view and
in the first view and
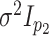 in the second view, we will
show that as
in the second view, we will
show that as 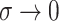 , and the soft cluster
assignments converge to hard cluster assignments, the pseudo likelihood ratio test statistic
converges to the
, and the soft cluster
assignments converge to hard cluster assignments, the pseudo likelihood ratio test statistic
converges to the 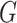 -test for independence. In what follows,
-test for independence. In what follows,
 ,
as in (3.13) and (5.18).
,
as in (3.13) and (5.18).
Proposition 4
Let
. Suppose that to compute
, we fit the model (2.1)–(2.2), for
and
densities of Gaussian distributions with covariance matrices
and
, respectively. Let
and
denote the results of applying k-means clustering on the two data views. Then, as
,
.
Proposition 4 is proven in Appendix A.2 of the supplementary materials available at Biostatistics
online. When 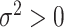 , the pseudo likelihood ratio
test statistic, the
, the pseudo likelihood ratio
test statistic, the 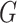 -test statistic, and the mutual information
are not equivalent. We can thus think of the pseudo likelihood ratio test statistic as
reflecting the uncertainty associated with the clusterings obtained on the two views, and
the
-test statistic, and the mutual information
are not equivalent. We can thus think of the pseudo likelihood ratio test statistic as
reflecting the uncertainty associated with the clusterings obtained on the two views, and
the 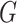 -test statistic and the mutual information as
ignoring the uncertainty associated with the clusterings. This suggests that the pseudo
likelihood ratio test of Section 3.2 outperforms
the
-test statistic and the mutual information as
ignoring the uncertainty associated with the clusterings. This suggests that the pseudo
likelihood ratio test of Section 3.2 outperforms
the 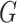 -test for independence when the sample size is
small and/or there is little separation between the clusters.
-test for independence when the sample size is
small and/or there is little separation between the clusters.
To confirm this intuition, we return to the simulation set-up described in Section 4, and compare the performances of the pseudo
likelihood ratio test (3.13) and the
G-test for independence (5.15) for
testing 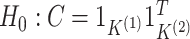 . We obtain
p-values for (5.15) using the
. We obtain
p-values for (5.15) using the
 approximation from (5.16), and using a permutation approach,
where we take
approximation from (5.16), and using a permutation approach,
where we take 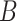 permutations of the elements of
permutations of the elements of
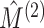 , and compare the observed value
of (5.15) to its empirical
distribution in these permutation samples. The results are shown in Figure 3; we see that the two tests yield similar power when the sample
size is larger and/or the value of
, and compare the observed value
of (5.15) to its empirical
distribution in these permutation samples. The results are shown in Figure 3; we see that the two tests yield similar power when the sample
size is larger and/or the value of  is smaller, and that
the pseudo likelihood ratio test yields higher power than the G-test for independence when
the sample size is smaller and/or the value of
is smaller, and that
the pseudo likelihood ratio test yields higher power than the G-test for independence when
the sample size is smaller and/or the value of  is larger. We note
that the
is larger. We note
that the  approximation for the G-test from
(5.16) does not control the Type I
error. Additional values of
approximation for the G-test from
(5.16) does not control the Type I
error. Additional values of 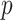 and
and 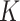 ,
additional values of
,
additional values of 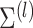 , and non-Gaussian finite mixture
models are investigated in Appendices C.3.1, C.3.2, and C.3.3 of the supplementary materials available at
Biostatistics online, respectively; the results are similar to those
described in this section.
, and non-Gaussian finite mixture
models are investigated in Appendices C.3.1, C.3.2, and C.3.3 of the supplementary materials available at
Biostatistics online, respectively; the results are similar to those
described in this section.
Fig. 3.
For the simulation study described in Section 5,
power of the pseudo likelihood ratio test and the  -test
of independence for
-test
of independence for 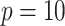 ,
,  and
and  , with
, with
 , defined in (4.14), on the
, defined in (4.14), on the
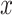 -axis and power on the
-axis and power on the
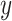 -axis.
-axis.
6. Application to the Pioneer 100 Wellness Project
6.1. Introduction to the scientific problem
In the P100 Wellness Project (Price and others, 2017), multiple biological data types were collected at multiple timepoints for 108 healthy participants. For each participant, whole genome sequences were measured, activity tracking data were collected daily over 9 months, and clinical laboratory tests, metabolomes, proteomes, and microbiomes were measured at 3-month, 6-month, and 9-month timepoints. The P100 study aims to optimize wellness of the participants through personalized healthcare recommendations. In particular, clinical biomarkers measured at baseline were used to make personalized health recommendations.
As an alternative approach, we could identify subgroups of individuals with similar clinical profiles using cluster analysis, and then develop interventions tailored to each subgroup. It is tempting to identify these subgroups using not just clinical data at baseline, but also other types of data (e.g. proteomic data) at other timepoints. We could do this by applying a multi-view consensus clustering method (e.g. Shen and others 2009). However, such an approach assumes that there is a single true clustering underlying all data types at all timepoints. Therefore, before applying a consensus clustering approach, we should determine whether there is any evidence that the clusterings underlying the data types and/or timepoints are at all related (in which case consensus clustering may lead to improved estimation of the clusters) or whether the clusterings are completely unrelated (in which case one would be better off simply performing a separate clustering of the observations in each view). In what follows, we will use the hypothesis test developed in Section 3 to determine whether clusterings of P100 participants based on clinical, proteomic, and genomic data are dependent across timepoints, and across data types.
6.2. Data analysis
At each of the three timepoints, 207 clinical measurements, 268 proteomic measurements,
and 642 metabolomic measurements were available for 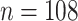 observations. In the following, we define a data view to be a single data type at a single
timepoint. In each view, we removed features missing in more than 25% of participants, and
removed participants missing more than 25% of features. Next, features in each view with
standard deviation 0 were removed. The remaining missing data were imputed using nearest
neighbors imputation in the
observations. In the following, we define a data view to be a single data type at a single
timepoint. In each view, we removed features missing in more than 25% of participants, and
removed participants missing more than 25% of features. Next, features in each view with
standard deviation 0 were removed. The remaining missing data were imputed using nearest
neighbors imputation in the 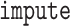 package in
package in
 (Hastie and others, 2017). Features in each view were then
adjusted for gender using linear regression. Finally, the remaining features were scaled
to have standard deviation 1. As in Section 4, we
consider the model (2.1)–(2.2) under the assumption that each
component in the mixture is drawn from a Gaussian distribution. For each data view, we fit
the model using the
(Hastie and others, 2017). Features in each view were then
adjusted for gender using linear regression. Finally, the remaining features were scaled
to have standard deviation 1. As in Section 4, we
consider the model (2.1)–(2.2) under the assumption that each
component in the mixture is drawn from a Gaussian distribution. For each data view, we fit
the model using the 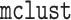 package in
package in
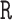 , with a common
, with a common
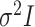 covariance matrix (the “EII”
covariance structure in
covariance matrix (the “EII”
covariance structure in 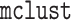 ). To test
). To test
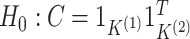 , we
compute p-values using the permutation approximation discussed in Section 3.3 with
, we
compute p-values using the permutation approximation discussed in Section 3.3 with 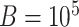 . Based on the
results in Appendix C.2.1 of the supplementary material available at Biostatistics online, we
choose the number of clusters in each view by BIC under the constraint that the number of
clusters is greater than 1.
. Based on the
results in Appendix C.2.1 of the supplementary material available at Biostatistics online, we
choose the number of clusters in each view by BIC under the constraint that the number of
clusters is greater than 1.
We now compare the clusterings in the clinical data at the first and third timepoints, the clustering in the proteomic data at the first and third timepoints, and the clusterings in the metabolomic data at the first and third timepoints. The sample sizes and results are reported in Table 1. For each data type, the clusters found at each timepoint are displayed in Figure 4.
Table 1.
Results from the test of 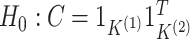 developed in Section 3.1 applied to
clinical, proteomic, and metabolomic data at the first and third timepoints, and
applied to pairs of data views defined by different data types. Sample sizes
developed in Section 3.1 applied to
clinical, proteomic, and metabolomic data at the first and third timepoints, and
applied to pairs of data views defined by different data types. Sample sizes
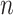 , dimensions in each view
, dimensions in each view
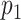 and
and 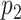 , and p-values obtained using the
permutation approximation from Section 3.3
are reported.
, and p-values obtained using the
permutation approximation from Section 3.3
are reported.
| View 1 | View 2 |

|
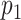
|

|
p-value |
|---|---|---|---|---|---|
| Clinical at Timepoint 1 | Clinical at Timepoint 3 | 83 | 204 | 198 |
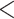 0.0001 0.0001 |
| Proteomic at Timepoint 1 | Proteomic at Timepoint 3 | 66 | 249 | 257 |
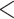 0.0001 0.0001 |
| Metabolomic at Timepoint 1 | Metabolomic at Timepoint 3 | 88 | 641 | 640 |
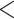 0.0001 0.0001 |
| Clinical at Timepoint 1 | Proteomic at Timepoint 1 | 70 | 204 | 249 | 0.236 |
| Clinical at Timepoint 2 | Proteomic at Timepoint 2 | 60 | 205 | 254 | 0.091 |
| Clinical at Timepoint 3 | Proteomic at Timepoint 3 | 66 | 198 | 257 | 0.950 |
| Clinical at Timepoint 1 | Metabolomic at Timepoint 1 | 98 | 204 | 641 | 0.034 |
| Clinical at Timepoint 2 | Metabolomic at Timepoint 2 | 89 | 205 | 641 | 0.073 |
| Clinical at Timepoint 3 | Metabolomic at Timepoint 3 | 81 | 198 | 640 | 0.328 |
| Proteomic at Timepoint 1 | Metabolomic at Timepoint 1 | 72 | 249 | 641 | 0.402 |
| Proteomic at Timepoint 2 | Metabolomic at Timepoint 2 | 67 | 254 | 641 | 0.004 |
| Proteomic at Timepoint 3 | Metabolomic at Timepoint 3 | 73 | 257 | 640 | 0.020 |
Fig. 4.
For three different data types, a comparison of the clustering at the first timepoint
(represented with colors) with the clustering at the third timepoint (represented with
shapes). In each data type, there is strong evidence of dependence (p-value
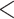 0.0001). The data types are (i)
clinical measurements, (ii) proteomic measurements, and (iii) metabolomic
measurements.
0.0001). The data types are (i)
clinical measurements, (ii) proteomic measurements, and (iii) metabolomic
measurements.
We find strong evidence that for each data type, the clusterings at the first and third
timepoints are not independent. We further measure the strength of dependence through the
effective rank of  , as described in Section 3.3. For the clusterings in the clinical
data, the effective rank of
, as described in Section 3.3. For the clusterings in the clinical
data, the effective rank of  is 1.63 and is upper bounded by 2.
For the clusterings in the proteomic data, the effective rank of
is 1.63 and is upper bounded by 2.
For the clusterings in the proteomic data, the effective rank of  is 1.90 and is upper bounded by 5. For the clusterings in the metabolomic data, the
effective rank of
is 1.90 and is upper bounded by 5. For the clusterings in the metabolomic data, the
effective rank of  is 1.2 and is upper bounded by 3.
These results suggest that the strengths of association for the clusterings estimated on
the clinical data, the proteomic data, and the metabolomic data, are strong, moderate, and
weak, respectively. The fact that the clusterings estimated on some data types are
strongly dependent over time provides evidence that they are scientifically meaningful.
Furthermore, it suggests that performing consensus clustering on some data types (e.g.
clinical data and proteomic data) across timepoints may be reasonable.
is 1.2 and is upper bounded by 3.
These results suggest that the strengths of association for the clusterings estimated on
the clinical data, the proteomic data, and the metabolomic data, are strong, moderate, and
weak, respectively. The fact that the clusterings estimated on some data types are
strongly dependent over time provides evidence that they are scientifically meaningful.
Furthermore, it suggests that performing consensus clustering on some data types (e.g.
clinical data and proteomic data) across timepoints may be reasonable.
We now focus on comparing clusterings in the clinical, proteomic, and metabolomic data at a single timepoint. The sample sizes and results are reported in Table 1.
The results provide modest evidence that proteomic and metabolomic data at a given timepoint are dependent and provide weak evidence that clinical and metabolomic data are dependent. However, on balance, the evidence that the clusterings are dependent across data types is weaker than we might expect. This suggests to us that the underlying subgroups defined by the three data types are in fact quite different, and that we should be very wary of performing a consensus clustering type approach across data types, or any analysis strategy that assumes that all three data types are getting at the same set of underlying clusters.
7. Discussion
Most existing work on multiple-view clustering has focused on the problem of estimation: namely, on exploiting the availability of multiple data views in order to cluster the observations more accurately. In this article, we have instead focused on the relatively unexplored problem of inference: we have proposed a hypothesis test to determine whether clusterings based on multiple data views are independent or associated.
In Section 6, we applied our test to the P100 Wellness Study (Price and others, 2017). We found strong evidence that clusterings based on clinical data and proteomic data persist over time, that is that the subgroups defined by the clinical data and the proteomic data are similar at different timepoints. This suggests that if we wish to identify participant subgroups based on (say) clinical data, then it may be worthwhile to apply a consensus clustering approach to the clinical data from multiple timepoints. However, we found only modest evidence that clusterings based on different data types are dependent! This suggests that we should be cautious about identifying participant subgroups by applying consensus clustering across multiple data types, as the clusterings underlying the distinct data types may be quite different.
Throughout this article, we compared clusterings on  data
views. We may also wish to compare clusterings across
data
views. We may also wish to compare clusterings across 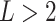 views. Let
views. Let  for
for
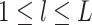 be the random vectors
corresponding to the
be the random vectors
corresponding to the  views. Suppose
views. Suppose 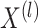 are generated according to (2.1) for
are generated according to (2.1) for
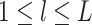 , where
, where
 are unobserved
multinomial random variables with probabilities given by
are unobserved
multinomial random variables with probabilities given by  for
for 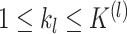 and
and
 , where the sum of
, where the sum of
 over all indices is 1 and
over all indices is 1 and
 . Results
analogous to Propositions 1 and 2 hold in this setting. Thus, we can estimate the parameters
in the extended model much as we did in Section
2.3.1, replacing the Sinkhorn–Knopp algorithm for matrix balancing with a tensor
balancing algorithm (see e.g. Sugiyama and
others 2017). To test the null hypothesis that
. Results
analogous to Propositions 1 and 2 hold in this setting. Thus, we can estimate the parameters
in the extended model much as we did in Section
2.3.1, replacing the Sinkhorn–Knopp algorithm for matrix balancing with a tensor
balancing algorithm (see e.g. Sugiyama and
others 2017). To test the null hypothesis that  are mutually
independent, we can develop a pseudo likelihood ratio test much as we did in Section 3, where instead of permuting the observations in
are mutually
independent, we can develop a pseudo likelihood ratio test much as we did in Section 3, where instead of permuting the observations in
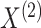 in Step 2(a) of Algorithm 2, we permute the observations in
in Step 2(a) of Algorithm 2, we permute the observations in 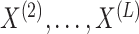 . Alternatively, one
can simply test for pairwise independence between clusterings, instead of testing for mutual
independence between clusterings on all views, as we did in Section 6.
. Alternatively, one
can simply test for pairwise independence between clusterings, instead of testing for mutual
independence between clusterings on all views, as we did in Section 6.
An R package titled  is available online at
https://github.com/lucylgao/multiviewtest and is forthcoming on CRAN. Code to
reproduce the data analysis in Section 6, and to
reproduce the simulations in Sections 4 and 5 and in Appendix C, are available online at https://github.com/lucylgao/independent-clusterings-code.
is available online at
https://github.com/lucylgao/multiviewtest and is forthcoming on CRAN. Code to
reproduce the data analysis in Section 6, and to
reproduce the simulations in Sections 4 and 5 and in Appendix C, are available online at https://github.com/lucylgao/independent-clusterings-code.
Supplementary Material
Acknowledgments
We thank Nathan Price and John Earls for responding to inquiries about the P100 data, and Will Fithian for a useful conversation. Conflict of Interest: None declared.
Funding
Natural Sciences and Engineering Research Council of Canada to L.L.G.; NIH (National Institutes of Health) (R01GM123993 to D.W. and J.B.); NSF (National Science Foundation) CAREER Award (DMS-1653017 to J.B.); NIH (DP5OD009145), NSF CAREER Award (DMS-1252624), and Simons Investigator Award No. 560585 to D.W.
References
- Agresti A. (2003). Categorical Data Analysis, Volume 482. Hoboken, New Jersey: John Wiley & Sons. [Google Scholar]
- Bickel S. and Scheffer, T. (2004). Multi-view clustering. In: Fourth IEEE International Conference on Data Mining (ICDM’04) (ICDM), Brighton, United Kingdom, Volume 4. pp. 19–26. [Google Scholar]
- Bien J. (2016). The simulator: an engine to streamline simulations. arXiv preprint arXiv:1607.00021. [Google Scholar]
- Cancer Genome Atlas Research Network. (2008). Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 455, 1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y. and Liang K.-Y. (2010). On the asymptotic behaviour of the pseudolikelihood ratio test statistic with boundary problems. Biometrika 97, 603–620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A. P., Laird N. M. and Rubin D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39, 1–38. [Google Scholar]
- Franklin J. and Lorenz J. (1989). On the scaling of multidimensional matrices. Linear Algebra and its Applications 114/115, 717–735. [Google Scholar]
- Gabasova E., Reid J. and Wernisch L. (2017). Clusternomics: integrative context-dependent clustering for heterogeneous datasets. PLoS Computational Biology 13, e1005781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong G. and Samaniego F. J. (1981). Pseudo maximum likelihood estimation: theory and applications. The Annals of Statistics 9, 861–869. [Google Scholar]
- Hastie T., Tibshirani R., Narasimhan B. and Chu G. (2017). impute: imputation for microarray data. R package version 1.50.1. [Google Scholar]
- Kirk P., Griffin J. E., Savage R. S., Ghahramani Z. and Wild D. L. (2012). Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 28, 3290–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kivinen J. and Warmuth M. K. (1997). Exponentiated gradient versus gradient descent for linear predictors. Information and Computation 132, 1–63. [Google Scholar]
- Kumar A., Rai P. and Daume H. (2011). Co-regularized multi-view spectral clustering. In: Shawe-Taylor J.and others (editors), Advances in Neural Information Processing Systems. Curran Associates, Inc., pp. 1413–1421. [Google Scholar]
- Lock E. F. and Dunson D. B. (2013). Bayesian consensus clustering. Bioinformatics 29, 2610–2616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan G. and Krishnan T. (2007). The {EM} Algorithm and Extensions, Volume 382. Hoboken, New Jersey: John Wiley & Sons. [Google Scholar]
- McLachlan G. and Peel D. (2000). Finite Mixture Models. New York: John Wiley & Sons. [Google Scholar]
- Meilă M. (2007). Comparing clusterings—an information based distance. Journal of Multivariate Analysis 98, 873–895. [Google Scholar]
- Mirkin B. (2011). Choosing the number of clusters. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 1, 252–260. [Google Scholar]
- Price N. D., Magis A. T., Earls J. C., Glusman G., Levy R., Lausted C., McDonald D. T., Kusebauch U., Moss C. L., Zhou Y., and others. (2017). A wellness study of 108 individuals using personal, dense, dynamic data clouds. Nature Biotechnology 35, 747–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid N. (1995). The roles of conditioning in inference. Statistical Science 10, 138–157. [Google Scholar]
- Rogers S., Girolami M., Kolch W., Waters K. M., Liu T., Thrall B. and Wiley H. S. (2008). Investigating the correspondence between transcriptomic and proteomic expression profiles using coupled cluster models. Bioinformatics 24, 2894–2900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scrucca L., Fop M., Murphy T. B. and Raftery A. E. (2016). mclust 5: clustering, classification and density estimation using {Gaussian} finite mixture models. The R Journal 8, 289. [PMC free article] [PubMed] [Google Scholar]
- Self S. G. and Liang K.-Y. (1987). Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. Journal of the American Statistical Association 82, 605–610. [Google Scholar]
- Shen R., Olshen A. B. and Ladanyi M. (2009). Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 25, 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugiyama M., Nakahara H. and Tsuda K. (2017). Tensor balancing on statistical manifold. In: Precup D. and Teh Y. W. (editors), Proceedings of the 34th International Conference on Machine Learning, International Convention Centre, Sydney, Australia, PMLR, pp. 3270–3279. [Google Scholar]
- Vershynin R. (2012). Introduction to the non-asymptotic analysis of random matrices. In: Eldar Y. C. and Kutyniok G. (editors), Compressed Sensing: Theory and Applications, Chapter 5. Cambridge: Cambridge University Press, pp. 210–268. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.