Abstract
The template-directed synthesis of RNA played an important role in the transition from prebiotic chemistry to the beginnings of RNA based life, but the mechanism of RNA copying chemistry is incompletely understood. We measured the kinetics of template copying with a set of primers with modified 3′-nucleotides and determined the crystal structures of these modified nucleotides in the context of a primer/template/substrate-analog complex. pH-rate profiles and solvent isotope effects show that deprotonation of the primer 3′-hydroxyl occurs prior to the rate limiting step, the attack of the alkoxide on the activated phosphate of the incoming nucleotide. The analogs with a 3E ribose conformation show the fastest formation of 3′-5′ phosphodiester bonds. Among those derivatives, the reaction rate is strongly correlated with the electronegativity of the 2′-substituent. We interpret our results in terms of differences in steric bulk and charge distribution in the ground vs. transition states.
Keywords: Prebiotic Chemistry, RNA Replication, Crystallography, Conformation, Kinetics
Graphical Abstract
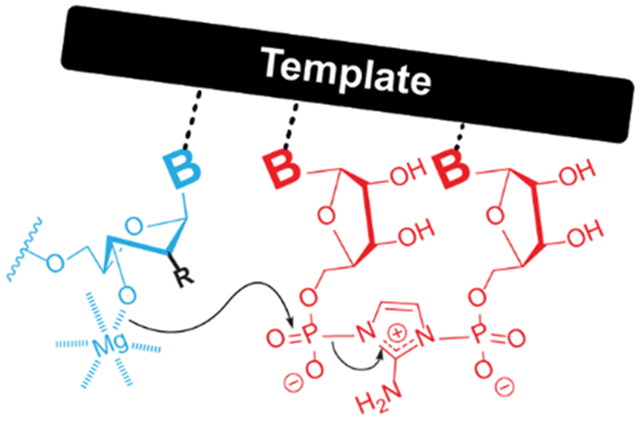
We combine X-ray crystallography and kinetic measurements of modified nucleic acid constructs to determine the requirements for efficient template copying. The 3E conformation of the furanose rings is preferred in the formation of 3′-5′ phosphodiester bonds. Our findings may explain why RNA is a privileged substrate amongst other plausible candidates.
Introduction
The catalytic synthesis of sequence defined polymers is a hallmark of biology. Organisms devote considerable resources to the template-directed synthesis of DNA, RNA, and proteins, which coordinate to carry out all cellular processes. These interrelated synthetic programs may have originated some four billion years ago shortly after life first appeared on Earth. According to the RNA World hypothesis[1], life started with genetic information stored in RNA and with the help of RNA enzymes. A possible prebiotic pathway to primordial self-replicating RNA is through the template-directed nonenzymatic synthesis of RNA. In this process, a strand of RNA directs the synthesis of its complement by bringing the necessary components together through Watson-Crick base-pairs. Considerable effort from multiple research groups has gone into understanding and optimizing this process in the past decades, but substantial problems remain unsolved[2,3]. For example, the rate and fidelity of chemical RNA replication as seen in current laboratory experiments are not high enough to sustain the reproduction and evolution of a primitive cellular organism, and the relevant reaction mechanisms are still poorly understood. A deeper understanding of the mechanism of RNA copying and the factors that contribute to fast and high-yielding reactions is necessary to evaluate the plausibility of nonenzymatic RNA replication.
We use nonenzymatic primer extension as a laboratory model for prebiotic RNA copying (Figure 1). For primer extension to occur, two RNA strands, one acting as the primer and the other as the template, anneal to form a duplex which contains a 5′-overhang. Chemically activated nucleotides bind to this overhang and the primer is extended one nucleotide at a time. Single phosphoroimidazolide mononucleotides do not participate directly in the reaction, but instead two such activated monomers react to form an imidazolium-bridged dinucleotide, which is the reactive electrophilic species[4]. The imidazolium-bridged dinucleotide, once bound to the template by two Watson-Crick base pairs, reacts with the 3′-end of the primer to generate an extension product. Understanding the structure and reactivity of the electrophile[4] has helped rationalize previously unexplained results and contributed to developing an improved RNA copying process[5]. However, the participation of the 3′-OH nucleophile and the catalytic metal ion are less well understood. Previous reports hint that the active nucleophilic species is a 3′-alkoxide, generated with the aid of a Mg2+ cation[6]. Additional studies also revealed that when the terminal primer nucleotide is in the 3E (C3′-endo) conformation primer extension proceeds more rapidly[7,8], but the reasons for this preference are not understood. Besides the conformational effects that might be at play, the acidity of the reacting hydroxyl could also affect the rate. A more acidic 3′-OH group is easier to deprotonate and thereby generate the reactive alkoxide species. However, a better understanding of both the ground and transition states of the reaction is required before the differences in rate can be adequately interpreted. For example, if 3′-OH deprotonation is the rate determining step of the reaction, then the rate will be strongly influenced by the acidity of the 3′-OH. Conversely, if the rate limiting step is the attack of the previously formed alkoxide on the adjacent phosphate of the imidazolium-bridged dinucleotide, then steric congestion surrounding the hydroxyl group will strongly affect the energy of the transition state and the rate of the reaction.
Figure 1.
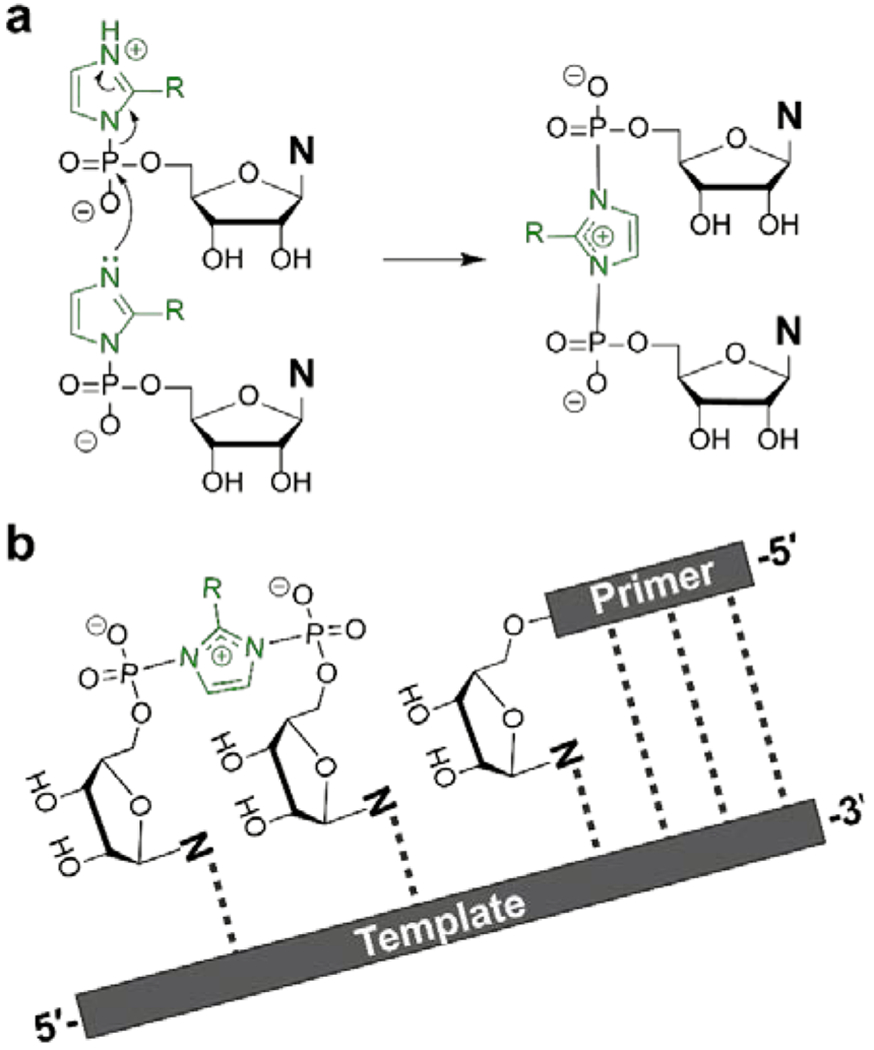
Primer extension occurs via two sequential reactions. (A) Formation of the imidazolium-bridged dinucleotide intermediate, the reactive species in nonenzymatic RNA primer extension. (B) The imidazolium-bridged intermediate anneals to the primer-template duplex and reacts with the 3′-end of the primer.
In this report we combine kinetic and structural studies of primer extension with a series of modified primers to explore mechanistic aspects of template-directed nonenzymatic primer extension. We show that the rate limiting step of the reaction is the nucleophilic attack of a Mg-alkoxide, thereby explaining the insensitivity of the reaction to differences in hydroxyl acidity. However, because the rate limiting step involves an increase in steric bulk around the nucleophilic hydroxyl group, the steric environment around the hydroxyl moiety strongly influences the reaction rate.
Results and Discussion
We set out to determine structure-activity relationships for nonenzymatic primer extension using a set of primers with modified guanosine nucleotides at their 3′-termini. The set of nucleotides includes several potentially prebiotic alternatives to ribonucleotides (threose, arabinose and deoxyribose nucleotides), as well as several synthetic modified nucleotides that serve as mechanistic probes of the reaction. We used X-ray crystallography to determine the conformation of each of these sugar-modified G nucleotides when present at the end of an oligoribonucleotide, base-paired to a template strand, and adjacent to a template bound GpppG (Figure 2a), an isosteric, unreactive analog of the imidazolium-bridged dinucleotide[9]. Although this analog has a different charge distribution and van der Waals surface than the imidazolium bridged dimer, the conformation of the last nucleotide of the primer should not be greatly perturbed by these remote differences. A similar construct was used to determine primer extension reaction rates for each modified G nucleotide. In each case the primer-template duplex was incubated with a saturating concentration[10] (20 mM) of the imidazolium-bridged dinucleotide (Figure 2b). The modified primers we studied display a wide range of primer extension reactivities, with differences of at least two orders of magnitude between the most and least reactive modifications of the 3′-terminal primer nucleotide (Figure 3).
Figure 2.
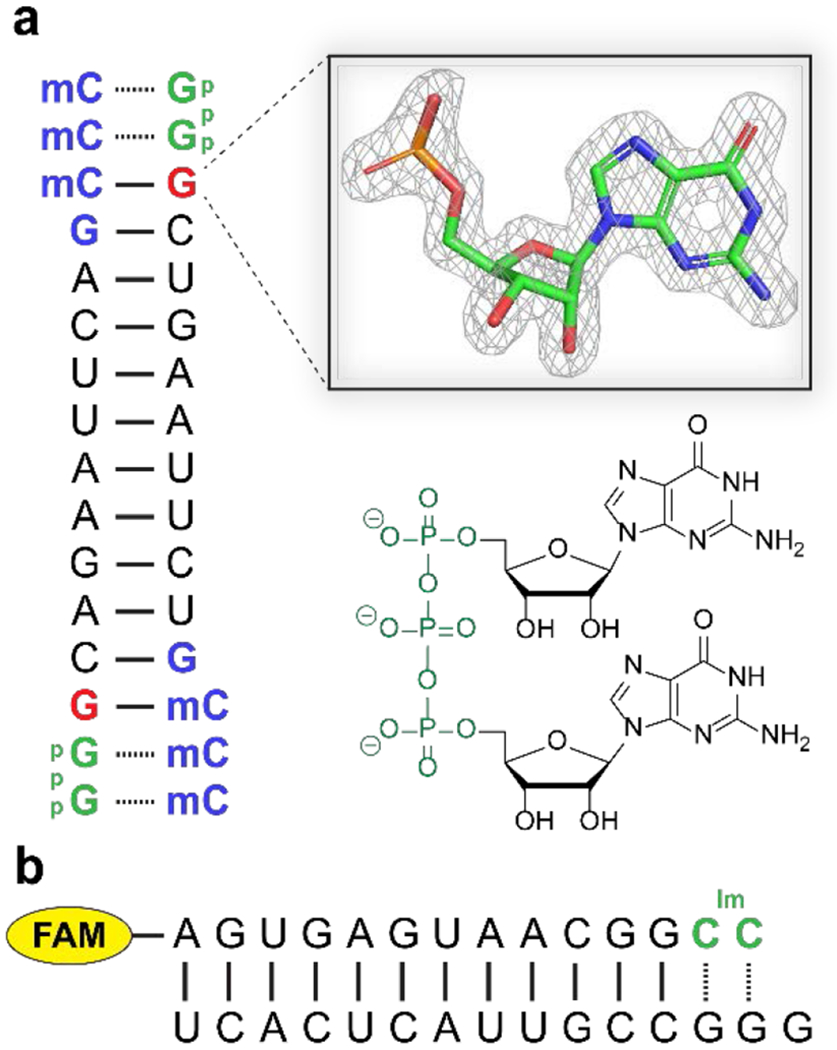
Constructs used to correlate structure and reactivity. (A) Self-annealing oligonucleotide construct used for X-ray crystallography studies. Blue: locked nucleic acid (LNA) residues; mC is 5-methyl-cytosine. Our crystallographic studies are focused on the 3′-terminal nucleotide of the primer, in red. The inset shows a 2Fo-Fc omit map contoured at 1.5 σ of the structure of this terminal nucleotide for the all-RNA primer[9]. The GpppG analog is green on the sequence diagram and its structure is shown below the inset. (B) Fluorescently labelled primer-template duplex used for kinetic measurements. The imidazolium-bridged dinucleotide is in green. FAM is 5(6)-carboxyfluorescein.
Figure 3.
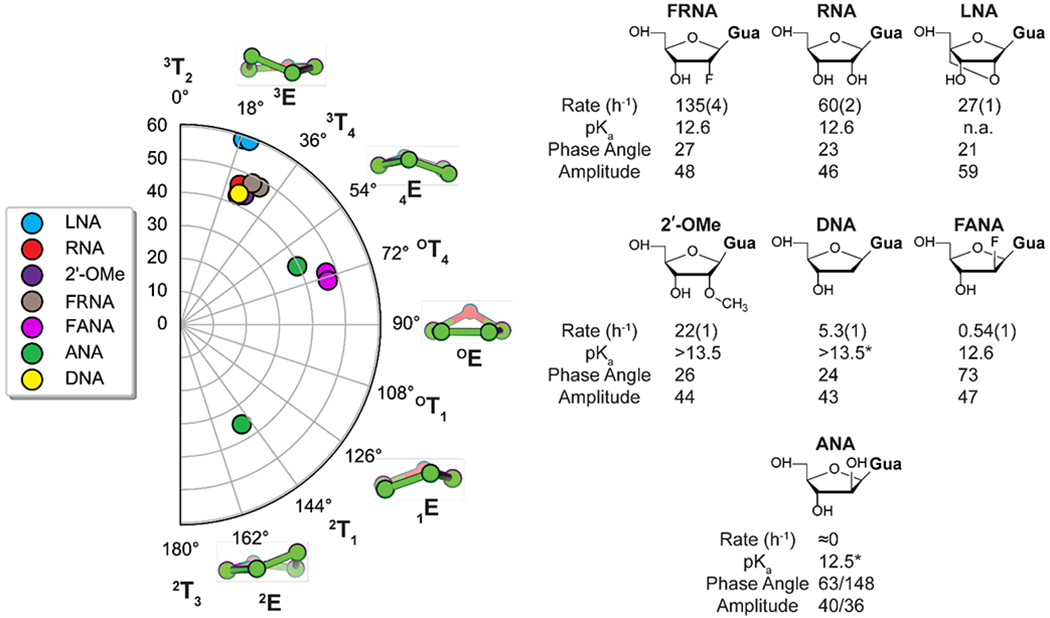
Conformational landscape of the primer 3′-terminal nucleotide modified sugars. Left side: conformation of each of the 3′-terminal sugars from crystal structures of modified primer/template/GpppG complexes. Since the crystal construct is symmetric, each modification is represented twice. Each point on the polar plot corresponds to a value of the phase angle (0°-180°) and the amplitude of the pucker (0°-60°). Five representative envelope conformations are shown, each corresponding to a 36° shift in phase angle. Right: chemical structure of each modification, its extension rate relative to that of the RNA primer, and the experimentally determined pKa value of the nucleoside. The phase angle and puckering amplitudes are listed for each nucleotide. For the modifications that crystallized symmetrically only one pair of values were shown. The complete list of structural parameters is presented in Supplementary Table S5. The reaction rates were determined in triplicate and the standard error of the mean is reported. The C*C bridged imidazolium nucleotide and 50 mM Mg2+ were used in the primer-extension reactions. *The pKa value of the arabinose nucleoside (ANA) and the deoxyribose nucleoside (DNA) are from reference 13. The crystal structures have been deposited in the Protein Data Bank (PDB), with the following depository codes: FRNA - 7KUK, DNA - 7KUL, ANA – 7LNE, FRNA – 7KUN, FANA – 7KUO, 2′-OMe – 7KUP, LNA – 7KUM.
To explain these rate differences, we first looked for correlations between rate and sugar conformation. Five membered rings avoid a strained planar conformation by puckering in two different ways: either one atom is out of the plane of the other four, resulting in an envelope conformation (E), or two atoms can be above and below the plane of the other three, resulting in a twist conformation (T). In theory, furanoses can adopt multiple twist and envelope conformations that are energetically similar[11]; in practice, decades of structure determination by crystallography and NMR have shown that 2′-deoxyribonucleotides prefer the 2E (2′-endo) conformation in which the C2′ carbon atom is above the plane of the other four atoms, whereas ribonucleotides prefer the 3E (3′-endo) conformation in which the C3′ carbon atom is above the plane of the other four atoms. All modifications we tested crystallized in the 3E conformation, except for the arabino-modifications FANA and ANA (Figure 3) which crystallized in the OT4 and 2E conformations.
Interestingly, the arabino-modifications are the slowest reacting species, especially arabino-G, for which we could not measure the rate of extension. Since the crystal construct is a symmetric self-annealing duplex, each crystal structure contains two of the 3′ modifications. The arabinose modified primer is the only one that crystallized in two different conformations. On one end, the imidazolium bridged dinucleotide analog is disordered and forms a non-canonical base-pair at the position downstream of the primer. The same structure has previously been observed in a construct with guanosine monophosphates instead of the imidazolium bridged dinucleotide[12]. The arabinose sugar is in the 2E conformation and there is a putative hydrogen bond between its 2′-OH and the N7 atom of the guanosine moiety of the imidazolium bridged dinucleotide analog (Figure S1). In this conformation no reaction is possible, since the O3′-P distance is almost 12 Å. At the other end of the duplex, the imidazolium bridged dinucleotide analog is well-ordered, forms canonical Watson-Crick base-pairs with the template, and the arabinose sugar is in the OT4 conformation. Here the O3′-P distance is 5.14 Å; while this distance is longer than for all other analogs, the difference is small and may not fully account for the extremely slow reaction rate. Additionally, previous studies revealed that the most acidic hydroxyl group in the arabino sugar is the 2′-OH. Moreover, the close packing of the palindromic RNA duplex in the crystal lattice may perturb its structure, which may therefore differ from the structure in solution.
Although the sugars that crystallize in the 3E conformation react considerably more rapidly than the ANA and FANA analogs, the reasons for this difference cannot be deduced solely from the structural parameters (Table S5). For example, the two fluoro-modifications, FRNA (3E) and FANA (OT4), have their 3′-hydroxyls at a similar distance to the adjacent phosphate (4.5Å and 4.9Å respectively), as well as similar angles between 3′-OH and the bridging P-O bond of GpppG (133° and 138°), but FRNA reacts 250 times faster. Although the 0.5Å difference could potentially explain the difference in reactivity, the 3′-OH of the LNA modification is 0.9Å closer to the adjacent phosphate when compared to FRNA, but LNA reacts 5-time more slowly than FRNA. Additionally, FRNA, RNA, DNA and 2′-OMe have very similar distances and angles of approach but the fastest (FRNA) reacts 25-times faster than the slowest (DNA).
In an effort to more fully explain the observed differences in rate we asked whether the acidity of the 3′-OH group of the primer correlates with the rate of the primer extension reaction. There are two possible ways in which the acidity of the hydroxyl group could have an impact on the rate of the reaction. First, when comparing rates at constant pH values, if the modifications lead to various extents of 3′-OH deprotonation, the differences in rate will reflect the degrees of deprotonation rather than the inherent reactivities of the alkoxides. Second, the inherent reactivities of the alkoxides should correlate with the acidity of the alcohols. An alkoxide that is more difficult to form is also more reactive. Provided all other steric and electronic factors are identical, the rate of phosphate transfer should increase as the pKa of the attacking nucleophile increases when the reaction is carried out at pH values where the alcohol is fully deprotonated. This has indeed been observed by Piccirilli for RNA analogs in trans-esterification reactions[13].
We therefore determined the 3′-OH pKa values of the modified mononucleosides by 1H NMR using the method of Chattopadhyaya[14]. Because the acidity of the 3′-OH in most nucleotides is low, only a handful of pKa values could be determined in aqueous solution. For example, only a lower bound of 13.5 could be estimated for the 3′-OH pKa of 2′-deoxy and 2′-OMe derivatives. Interestingly, the acidities of the 3′-OH in RNA, FRNA and FANA are identical within experimental error. Although FRNA and FANA lack the 2′-OH which can stabilize the anion through a hydrogen bond, the inductive effect of the fluorine atom appears to be equally well suited to stabilizing the negative charge of the O3′ alkoxide. Because the inductive effect of the fluorine atom is transmitted through bonds, the spatial orientation of the 2′-substituent is irrelevant, thus FANA and FRNA have identical acidities.
The fact that the nucleoside 3′-OH pKa values do not reflect the trends in reactivity suggested that under reaction conditions the deprotonation status of the primer 3′-OH might be quite different. Although the 3′-hydroxyl group in RNA is very weakly acidic, it is expected to be a much stronger acid when coordinated with Mg2+. Because of the inherent technical difficulties associated with determining the pKa of the 3′ -OH of the primer in a duplex and in the presence of Mg2+ by the NMR method used for the nucleosides, we used a kinetic method of determining the pKa. We determined a pH-rate profile for most of the modifications, by measuring the reaction rate at pH values ranging from 7-10. Because the reaction rates at high pH were too fast to accurately measure with the initial experimental setup, we changed the template so as to create a binding site for an imidazolium bridged di-adenosine intermediate, which reacts more slowly than its cytosine analog (Figure 4a). Despite the absolute differences in rate between the two constructs, the relative rates of the modifications follow the same trend. The rates increase linearly with pH until a plateau region is reached. The pKa values were then determined by assuming that only the Mg-alkoxide reacts (see page 17 of the SI). Considering that the nucleosides have different acidities depending on the C2′ substituent, it was somewhat surprising that for all the modifications the kinetically determined pKa values were very similar (Figure 4b). Between pH values of 7 and 8.5 the slope of the pH rate profile is close to unity, after which it begins to plateau. The kinetically determined value of the 3′-OH pKa is 9.1, suggesting that Mg2+ coordination increases the acidity of the alcohol by four orders of magnitude, as expected from the analogous increase of water acidity when coordinated to Mg[15]. Although the kinetically determined pKa values for the modified primers are identical, they need to be interpreted carefully since kinetic measurements carried out at pH values over 9 may be affected by the deprotonation of other ionizable groups. For example, the uracil and guanine moieties of U and G have a pKa of ~10. Once the nucleobases are deprotonated, they cannot engage in Watson-Crick base-pairing. However the kinetically determined pKa values are well below the pKa values of these nucleobases. Alternatively, the rate plateaus could be explained by the deprotonation of the imidazolium group of the reactive intermediate. However, NMR titration data shows that the pKa of the imidazolium group is well above the pH values used to determine rates (Figure S2).
Figure 4.
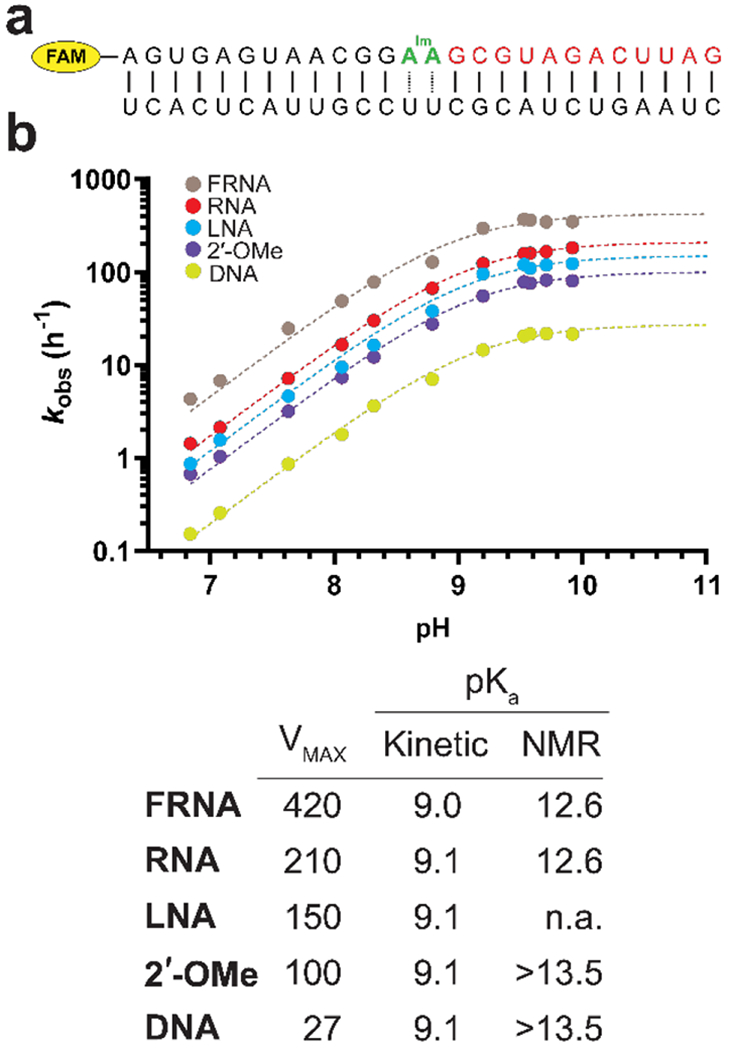
Determination of the 3′-OH pKa for five modified nucleotides. (A) The construct used for the primer extension experiments. The oligonucleotide in red is a downstream binder which pre-organizes the duplex[16] and increases the affinity of the template for the imidazolium bridged intermediate. (B) pH-rate profiles for primer extension with primers containing five distinct 3′-terminal residues. Each reaction was carried out in triplicate, and only the mean values were used to fit the data. The A*A imidazolium bridged dinucleotide and 200 mM Mg2+ were used in the primer extension reactions. The table contains the pKa and VMAX, determined from the pH-rate profiles. The right most column shows nucleoside pKa values determined by 1H NMR in the absence of Mg2+.
Additionally, the pH dependence of the reaction changes drastically when replacing Mg+2 with Ca+2, suggesting that the kinetically determined pKa values do indeed correspond to deprotonation of the 3′-OH[6]. It is worth noting that the estimated kinetically determined pKa of 9.1 for the 3′-hydroxyl of the modified nucleotides at the end of the primer is 1.4 units higher than that of a 3′-amino 2′, 3′-dideoxy nucleotide[17], a modification which is known to lead to much faster primer extension[17,18]. Considering that an alkoxide is a stronger nucleophile than an amine, what accounts for the superior reactivity of 3′-amino terminated primers? We suggest that this can be accounted for in part because at pH 8 a 3′-amine would be largely unprotonated, whereas a Mg2+ coordinated 3′-hydroxyl would be less than 10% deprotonated, and in part because a Mg2+ concentration much greater than 50-100 mM would be required to saturate the reaction center and allow maximal deprotonation of the 3′-hydroxyl. Since the kinetically determined acidity constants fail to explain the differences in reactivity between the different modifications, other factors must be at play.
Interpretations of steric and electronic effects in the primer extension reaction hinge on the identity of the rate determining step. We therefore asked whether deprotonation of the 3′-hydroxyl was rate limiting, as found for certain polymerases[19], by measuring solvent kinetic isotope effects (SKIE), which can be used to determine whether or not the breaking of an O-H bond is involved in the rate-limiting step of a reaction. In the case of primer extension, measuring the SKIE will determine whether the reaction mechanism involves the formation of a magnesium alkoxide prior to the rate-limiting step or whether the deprotonation of the 3′-OH is the rate determining step of the reaction. If the former is correct, then no SKIE is expected since the O-H bond is broken prior to the rate limiting step. If the deprotonation of the 3′-OH is the rate determining step, then a large SKIE is expected, since the zero-point energy of an O-H bond is different from that of an O-D bond. Alternatively, the deprotonation and nucleophilic attack could be concerted, in which case an intermediate SKIE is expected.
To determine where deprotonation of the 3′-OH lies on the primer extension reaction pathway, we determined the pL-rate profiles (where pL is either pH or pD) in both H2O and D2O (Figure 5). A similar pD-rate profile is observed in D2O, with a determined pKa value of 9.8 for the 3′-OD. A shift in acidity between the two solvents of this magnitude is expected because of the lower zero-point energy of the O-D bond compared to the O-H bond; this shift mirrors results reported for the hammerhead ribozyme[20]. In the linear section of the pL-rate profile the rates in H2O are roughly three times higher than the rates in D2O and converge at higher pL values as the deprotonation of the 3′-OH becomes complete. Considering that the 3′-OD is a weaker acid in heavy water than the 3′-OH in light water, the difference in rates at any given pL value can be explained by the different degrees of deprotonation of the hydroxyl group. After correcting for pKa differences, the rates in H2O and D2O are virtually identical. The absence of a SKIE suggests that there is no O-H bond breaking in the rate limiting step. This implies that the reactive species, the Mg-alkoxide, is formed before the rate limiting step and therefore, the rate limiting step of the reaction is the nucleophilic attack of the Mg-alkoxide on the adjacent phosphate of the imidazolium-bridged dinucleotide. Any stereoelectronic effects that facilitate this step will therefore lead to an acceleration in rate.
Figure 5.
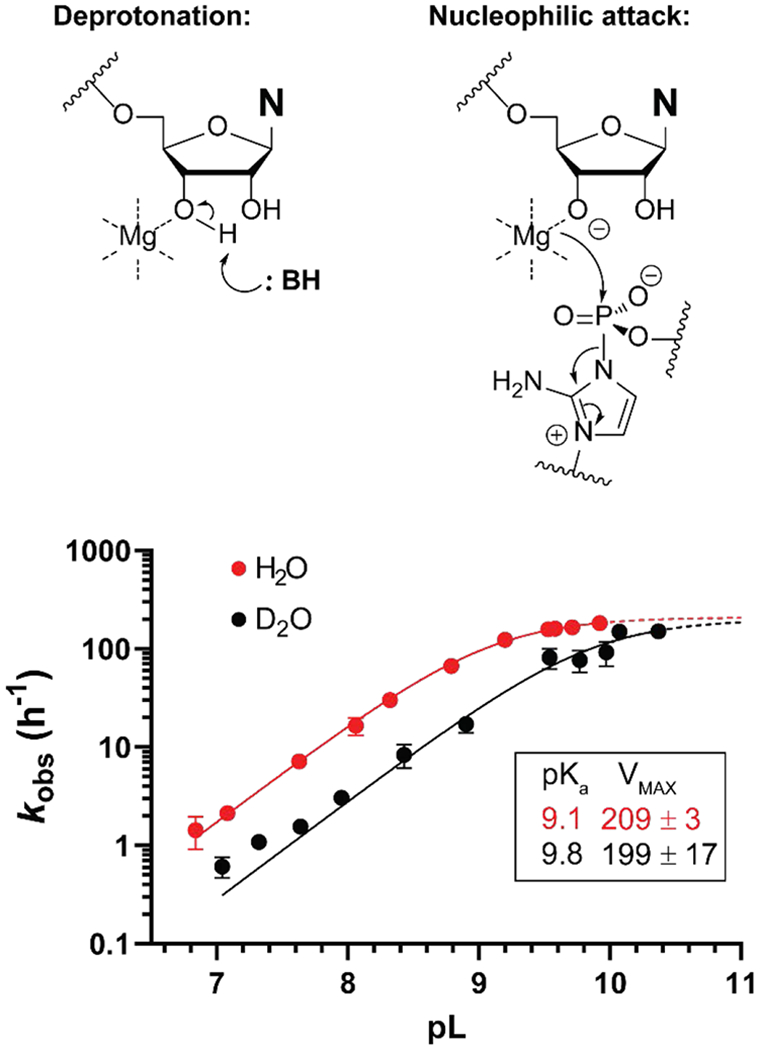
The kinetic solvent isotope effect for non-enzymatic template directed RNA primer extension. (A) Two mechanisms representing limiting cases for the rate determining step of the reaction. (B) Graph showing pL-rate profiles for primer extension in H2O and D2O. Rates were determined in triplicate. The mean value and its 95% confidence interval are shown on the graph. The A*A imidazolium bridged dinucleotide and 200 mM Mg2+ were used in the primer extension reactions.
Considering that the FANA and FRNA modifications have identical pKa values, similar distances between the 3′-OH and the adjacent phosphate group of the substrate, as well as similar O-P-N angles of attack, what is the reason for their 250-fold difference in reactivity? Possible reasons for this difference can be deduced by comparing the crystal structures of FANA and FRNA, specifically the differing environments around the 3′ -OH groups. In the 3E conformation adopted by FRNA, the reacting 3′-OH group is pseudo-equatorial, with the molecule adopting staggered conformations along the C3′-C4′ bond and the C3′-C2′ bond. On the other hand, the OT4 conformation of FANA forces an eclipsed arrangement of the substituents along the C3′-C4′ and C3′-C2′ bonds. This results in the 3′-OH, which is now pseudo-axial, being eclipsed by the H2′ and H4′ atoms, as well as a pseudo-axial 1-3 interaction with H1′ (Figure 6).
Figure 6.
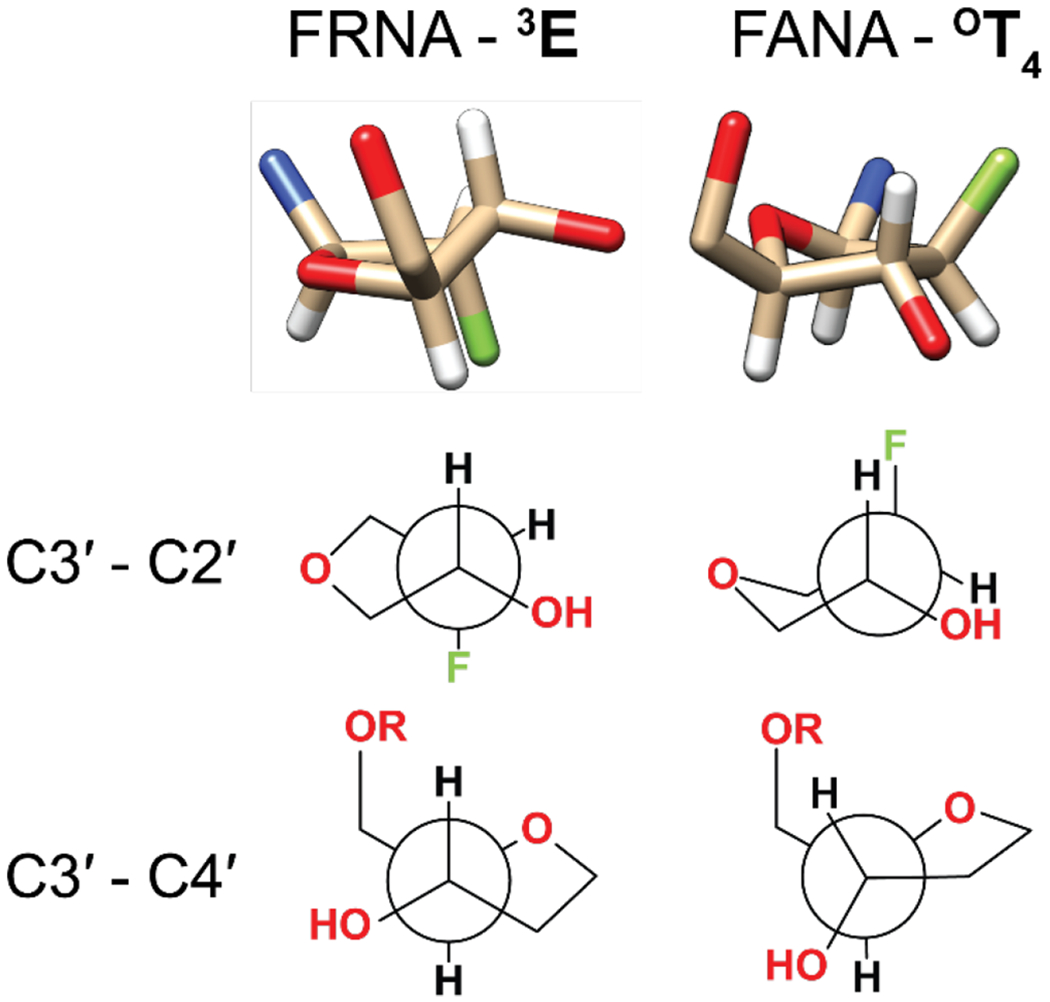
Crystal structures of the sugar moiety of 2′-fluoro guanosine and 2′-fluoroarabino guanosine. Hydrogen atoms are represented in white, oxygen in red, fluorine in green and nitrogen in blue. The bottom two rows show Newman projections across two different bonds for the two modifications.
Even for the modified nucleotides that adopt a 3E sugar conformation there is a 25-fold difference in rates, suggesting that conformation is not the sole determinant of reactivity. Considering that the kinetically determined pKa values for these five modifications are virtually identical, what is the reason for the different reactivities? Strikingly, there is a strong correlation between the rates of the reactions and the electronegativity of the 2′ substituent amongst the five modifications (Figure 7). The 3E vs. 2E conformational preference is dictated by the strength of the gauche effects in furanose rings[21], and a more electronegative substituent induces a stronger gauche effect[22]. For mononucleotides in solution, an electronegative substituent in the 2′ position biases the conformational equilibrium towards the 3E conformation[23]. Even though the five analogs are all in the 3E conformation in our crystal structures, it is possible that in solution the 3E/2E ratio shifts with the electronegativity of the 2′ substituent, and that this accounts in part for the observed changes in rate.
Figure 7.
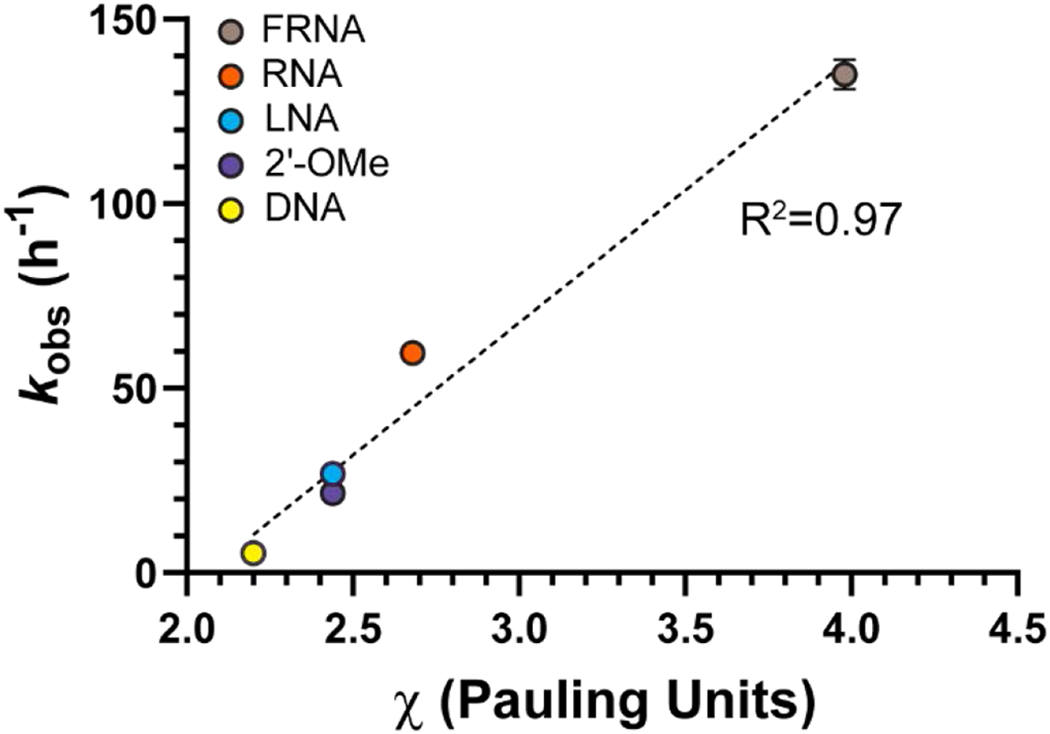
The reaction rate of the 3′-terminally modified primers correlates with the electronegativity of the 2′-substituent. We assumed that the electronegativity of the -OMe group and the OCH2R group in LNA are the same, and we used the value reported by Bratsch[24].
A more interesting potential explanation for the influence of the electronegativity of the 2′ substituent on rate in this series of modifications arises from the relationship between reaction rate and the puckering amplitude of the furanose rings. The rate of the reaction and the puckering amplitude are correlated with the electronegativity of the 2′ substituent for four of the five 3E modifications. Only the conformationally constrained LNA diverges from this correlation (Figure S3). If the conformational dynamics from the ground state to the transition state involve an increase in the puckering amplitude of the sugar in order to allow the 3′-OH to approach the phosphorous atom, then a modification that is pre-organized by a stronger puckering will require less energy to reach the transition state and therefore will react faster. In this model a more electronegative 2′ substituent pre-organizes the ground state of the reaction. The conformationally restricted LNA is limited in the ways the ring can rearrange and reacts more slowly than expected based on its puckering amplitude.
Alternatively, electrostatic repulsion between the 2′ and 3′ groups would be reduced by an increase in the amplitude of the sugar pucker, which in turn would decrease steric bulk around the negatively charged 3′-alkoxide. If an increase in sugar pucker amplitude is required for the 3′-alkoxide to approach the adjacent phosphate of the imidazolium bridged intermediate, a more electronegative substituent on C2′ could potentially increase the energy of the ground state and/or decrease the energy of the transition state, resulting in an increase in reaction rate. Ultimately, a more detailed knowledge of the structure of the transition state of the primer extension reaction is needed to decide on the merit of these alternative explanations.
Having explored the factors that govern the reactivity of the 3′-OH in the pento-furanosyl series we expanded our investigation to include sugar derivatives that cannot form a canonical 3′-5′ phosphodiester bond. Threose nucleic acid (TNA) has been proposed as a prebiotically plausible alternative to RNA by Eschenmoser and colleagues[25]. We synthesized a primer terminating in a TNA residue and measured the corresponding primer extension rate (Figure 8). Surprisingly, the TNA-terminated primer reacts only 6-times more slowly than an all RNA primer, showing that the 2′-OH of the threose moiety is a competent nucleophile in the primer extension reaction. To rationalize this result, we determined the crystal structure of the TNA terminated primer together with the analog of the imidazolium-bridged dinucleotide. The threose sugar crystallizes in a 4E (C4′-exo) conformation, in agreement with our previously determined structure[26]. The threose nucleotide is linked to the primer through a 3′-3′ phosphodiester bond which results in a rotation of the sugar so that the TNA C2′-OH is relocated to the same position as occupied by the RNA C3′-OH. In order to maintain Watson-Crick base-pairing, the threonucleotide has a chi angle of −120° (as opposed to −160 to −170° for most other modifications). This rotation brings the TNA 2′-OH close to the adjacent phosphate group of the imidazolium-bridged ribo-dinucleotide analog, resulting in a surprisingly similar reactivity to the RNA system. These results are consistent with our recent report on the reactivity of threose nucleotide systems[26]. However it is important to note that an imidazolium-bridged threo-dinucleotide is almost completely unreactive in primer extension, since the reactive phosphate is pulled away from the nucleophilic hydroxyl due to the absence of the 5′-methylene of ribose. Interestingly, a primer terminating in a 3′-deoxyguanosine residue is completely unreactive in the primer extension reaction. The crystal structure of 3′-deoxyguanosine containing complex is identical to that of the all-RNA complex, apart from the absence of the 3′-OH. As a result, the 3′-deoxyguanosine 2′-OH is far from the phosphate group and cannot react to form a 2′-5′ phosphodiester bond. Furthermore, the 3′-deoxyribose is in the 3E conformation, in which the 2′-OH fully eclipsed by its neighboring H-atoms.
Figure 8.
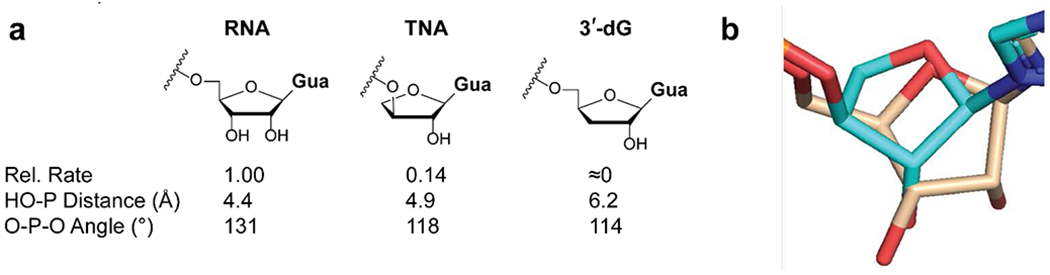
Primer extension with three different terminal nucleotides. (A) The relative rates and structural parameters for the TNA and 3’-deoxyguanosine modifications as determined from the crystal structures. Each rate has been determined in triplicate. The C*C imidazolium bridged dinucleotide was used in the primer extension reactions. (B) Top-view of the superimposed RNA (gold) and TNA (cyan) structure showing the rotation of the TNA ring. The crystal structures have been deposited in the Protein Data Bank (PDB), with the following depository codes: TNA - 7LNG, 3-dG – 7LNF.
Conclusion
Modifying the 3′-terminus of the primer has a large impact on the rate of the primer extension reaction. Of the modifications we studied, the most reactive all adopt the 3E sugar conformation in primer/template/substrate-analog crystal structures. In the presence of Mg2+ the reaction rates of all modified primers plateau at the same pH, consistent with the formation of a Mg-alkoxide nucleophile with a pKa of 9.1. The absence of a solvent kinetic imidazolium-bridged intermediate. Since approach of O3′ to the reactive phosphate necessarily involves an increase in steric crowding, the steric environment of the nucleophile strongly affects the rate of the reaction. When the terminal nucleotide of the primer is in the 3E conformation, steric congestion around the 3′-OH group is relieved and thus the reaction is faster. In addition, a higher puckering amplitude of the sugar in the 3E conformation further decreases steric crowding and results in a shorter O3′ to phosphate distance. We suggest that this effect may be favored by the presence of a more electronegative substituent at the 2′ position, since electrostatic repulsion between the 2′ substituent and the 3′ alkoxide would be relieved by an increase in sugar pucker amplitude in the 3E conformation. Taken together with previous work[12,26] these factors contribute to explaining why RNA outcompetes its alternatives (including potentially prebiotic alternatives such as ANA and TNA) in the template-directed copying of nucleic acids.
Supplementary Material
Acknowledgements
We thank Dr. Wen Zhang for insightful comments on structure refinement, Prof. Li Li and Dr. Lijun Zhou for helpful comments on the manuscript, and the Szostak group for helpful feedback. We also thank the staff at the Advanced Light Source (ALS) beamlines 501, 821 and 822, a national user facility operated by Lawrence Berkeley National Laboratory on behalf of the Department of Energy, Office of Basic Energy Sciences, through the Integrated Diffraction Analysis Technologies (IDAT) program, supported by DOE Office of Biological and Environmental Research. The Berkeley Center for Structural Biology is supported in part by the National Institutes of Health, National Institute of General Medical Sciences, and the Howard Hughes Medical Institute. GM/CA@APS has been funded by the National Cancer Institute (ACB-12002) and the National Institute of General Medical Sciences (AGM-12006, P30GM138396). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The Eiger 16M detector at GM/CA-XSD was funded by NIH grant S10 isotope for the reaction further suggests that the rate-limiting step of the reaction is not deprotonation of the 3′-hydroxyl, but rather attack of the Mg-alkoxide on the adjacent phosphate group of the OD012289. J.W.S. is an Investigator of the Howard Hughes Medical Institute. This work was supported in part by a grant from the Simons Foundation (290363) to J.W.S. and by a grant from the NSF (CHE1607034) to J.W.S.
Footnotes
Supporting information for this article is given via a link at the end of the document
REFERENCES
- [1].Gilbert W, Nature 1986, 319, 618. [Google Scholar]
- [2].Szostak JW, J. Syst. Chem 2012, 3, 2. [Google Scholar]
- [3].Sosson M, Richert C, Beilstein J. Org. Chem 2018, 14, 603–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Walton T, Szostak JW, J. Am. Chem. Soc 2016, 138, 11996–12002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Li L, Prywes N, Tam CP, O’Flaherty DK, Lelyveld VS, Izgu EC, Pal A, Szostak JW, J. Am. Chem. Soc 2017, 139, 1810–1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Giurgiu C, Wright TH, O’Flaherty DK, Szostak JW, Angew. Chem. Int. Ed 2018, 57, 9844–9848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wu T, Orgel LE, J. Am. Chem. Soc 1992, 114, 317–322. [DOI] [PubMed] [Google Scholar]
- [8].Kozlov IA, Politis PK, Van Aerschot A, Busson R, Herdewijn P, Orgel LE, J. Am. Chem. Soc 1999, 121, 2653–2656. [DOI] [PubMed] [Google Scholar]
- [9].Zhang W, Tam CP, Walton T, Fahrenbach AC, Birrane G, Szostak JW, Proc. Natl. Acad. Sci 2017, 114, 7659–7664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Walton T, Szostak JW, Biochemistry 2017, 56, 5739–5747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Li L, Szostak JW, J. Am. Chem. Soc 2014, 136, 2858–2865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kim SC, Zhou L, Zhang W, O’Flaherty DK, Rondo-Brovetto V, Szostak JW, J. Am. Chem. Soc 2020, 142, 2317–2326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ye J-D, Li N-S, Dai Q, Piccirilli JA, Angew. Chem. Int. Ed 2007, 46, 3714–3717. [DOI] [PubMed] [Google Scholar]
- [14].Velikyan I, Acharya S, Trifonova A, Földesi A, Chattopadhyaya J, J. Am. Chem. Soc 2001, 123, 2893–2894. [DOI] [PubMed] [Google Scholar]
- [15].Hawkes SJ, J. Chem. Educ 1996, 73, 516–517. [Google Scholar]
- [16].Zhang W, Tam CP, Zhou L, Oh SS, Wang J, Szostak JW, J. Am. Chem. Soc 2018, 140, 2829–2840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Kervio E, Claasen B, Steiner UE, Richert C, Nucleic Acids Res. 2014, 42, 7409–7420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhang S, Zhang N, Blain JC, Szostak JW, J. Am. Chem. Soc 2013, 135, 924–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Castro C, Smidansky E, Maksimchuk KR, Arnold JJ, Korneeva VS, Götte M, Konigsberg W, Cameron CE, Proc. Natl. Acad. Sci 2007, 104, 4267– 4272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Takagi Y, Taira K, Nucleic Acids Res. Suppl 2002, 2, 273–274. [DOI] [PubMed] [Google Scholar]
- [21].Plavec J, Tong W, Chattopadhyaya J, J. Am. Chem. Soc 1993, 115, 9734–9746. [Google Scholar]
- [22].Thibaudeau C, Plavec J, Garg N, Papchikhin A, Chattopadhyaya J, J. Am. Chem. Soc 1994, 116, 4038–4043. [Google Scholar]
- [23].Guschlbauer W, Jankowski K, Nucleic Acids Res. 1980, 8, 1421–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Bratsch SG, J. Chem. Educ 1985, 62, 101–103. [Google Scholar]
- [25].Schöning K-U, Scholz P, Guntha S, Wu X, Krishnamurthy R, Eschenmoser A, Science, 2000, 290, 1347–1351. [DOI] [PubMed] [Google Scholar]
- [26].Zhang W, Kim SC, Tam CP, Lelyveld VS, Bala S, Chaput JC, Szostak JW, Nucleic Acids Res. 2021, 49, 646–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


