Abstract
Materials with strongly correlated electrons often exhibit interesting physical properties. An example of these materials is the layered oxide perovskite Sr2RuO4, which has been intensively investigated due to its unusual properties. Whilst the debate on the symmetry of the superconducting state in Sr2RuO4 is still ongoing, a deeper understanding of the Sr2RuO4 normal state appears crucial as this is the background in which electron pairing occurs. Here, by using low-energy muon spin spectroscopy we discover the existence of surface magnetism in Sr2RuO4 in its normal state. We detect static weak dipolar fields yet manifesting at an onset temperature higher than 50 K. We ascribe this unconventional magnetism to orbital loop currents forming at the reconstructed Sr2RuO4 surface. Our observations set a reference for the discovery of the same magnetic phase in other materials and unveil an electronic ordering mechanism that can influence electron pairing with broken time reversal symmetry.
Subject terms: Electronic properties and materials, Magnetic properties and materials, Phase transitions and critical phenomena, Superconducting properties and materials
Strontium Ruthenate, Sr2RuO4, displays a remarkable number of intriguing physical phenomena, from superconductivity, to strain-induced ferromagnetism. Here, using low-energy muon spectroscopy, Fittipaldi et al. demonstrate the existence of unconventional magnetism at the surface of Sr2RuO4 in its normal state and without any applied strain.
Introduction
Electronic ordering in condensed matter systems often occurs as a result of a phase transition, meaning that it involves symmetry breaking. A classic example of the spontaneous breaking of time-reversal symmetry is ferromagnetism, which originates from the long-range ordering of electrons’ spins.
In systems of reduced dimensionality like two-dimensional (2D) materials, the increase in quantum fluctuations compared to three-dimensional (3D) systems can induce symmetry-breaking phase transitions and quantum orders that do not have a 3D equivalent1. The emergence of topological phase transitions in 2D solids and 2D superfluids in the absence of standard long-range ordering were first proposed by Kosterlitz and Thouless2, for which they were awarded the Nobel prize in 2016.
3D layered single crystals are the closest 3D analogue to 2D materials since electronic correlations in these crystals mainly develop inside the plane of each layer and the electrons’ propagation is reduced along the crystal axis perpendicular to the layers. In layered single crystal oxide perovskites, the dominance of in-plane correlations between electrons of the d orbitals often results in the emergence of exotic phases3, some of which have been discovered over the past 30 years like high-temperature superconductivity4, metal-to-insulator transitions5 and multiferroicity6.
Sr2RuO4 (SRO214) is a peculiar oxide perovskite on the verge of various electronic instabilities that can be further stabilized by the asymmetry that the SRO214 surface exhibits compared to the bulk, as a result of a structural reorganization of the surface RuO6 octahedra. Apart from intense studies7–9 aiming at determining the nature of the superconducting symmetry in SRO214, which remains under debate, evidence for spin fluctuations10 or magnetism under uniaxial pressure11 has also been reported for SRO214 single crystals in the normal state. These investigations, however, do not provide any information about the SRO214 surface selectively but rather focus on the SRO214 bulk properties.
At the surface of SRO214, it has been theoretically suggested that conventional ferromagnetic ordering can emerge possibly stabilized by the rotation of the surface RuO6 octahedra12, but definitive evidence for the existence of magnetism at the SRO214 surface has never been demonstrated, not even with scanning superconducting quantum interference device (SQUID) magnetometry13. Angle-resolved photoemission spectroscopy (ARPES) measurements on SRO214 also reveal the presence of surface states14, but the correlation between these surface states and magnetism is not conclusive15.
Here, by using the extremely high sensitivity of low-energy muon spin spectroscopy (LE-μSR) to magnetic fields and its nanometre depth resolution16,17, we find unambiguous evidence for the existence of an unconventional magnetic phase near the surface of SRO214 single crystals. The hallmark features of the magnetic phase that we unveil in SRO214 are a relatively high-temperature onset (Ton) between 50 and 75 K associated with a small amplitude of the magnetic moment (< 0.01 μB/Ru atom, with μB = 9.27 × 10-24 J T−1 being the Bohr magneton), a homogeneous distribution of the sources of magnetism within the ab-plane of the SRO214 crystals, and a decay in intensity of the magnetic signal from the SRO214 surface over a length scale of ~10–20 nm. The features of this magnetic phase suggest that it cannot be reconciled with conventional ferromagnetism. We show instead that spin-orbital entanglement of the electronic states at the Fermi level results in orbitally-frustrated loop currents within the surface RuO6 octahedra, which can generate the unconventional magnetism that we detect.
Results
We perform LE-μSR measurements on SRO214 single crystals grown by the floating zone method. The SRO214 crystals used in this experiment are highly pure and have a superconducting critical temperature of ~1.45 K and residual resistivity ratio larger than 200, as evidenced by the X-ray diffraction and electronic transport measurements in Supplementary Fig. 1.
For the LE-μSR measurements, the crystals are cleaved with a non-magnetic ZrO2 razor blade to avoid contamination from magnetic impurities and arranged to form a mosaic of size comparable to that of the muon beam (~2 cm in diameter) to maximize the amplitude of the signal (Fig. 1a). We perform most of the LE-μSR measurements with an external magnetic field (Bext) applied out-of-plane (i.e., along the c-axis of SRO214) defined as the axis z of our orthonormal reference-axes system (Fig. 1b). The LE-μSR data are collected in two different configurations, namely both with the initial muon spin polarization vector (Sμ+) oriented perpendicular to Bext, known as transverse-field (TF) configuration and with Sμ+ collinear to Bext, known as longitudinal-field (LF) configuration (Fig. 1c). We also carry out zero-field (ZF) measurements in the same setup adopted for LF but with Bext = 0, as shown in Fig. 1c.
Fig. 1. Low-energy μSR setup for measurements on SRO214 single crystals.
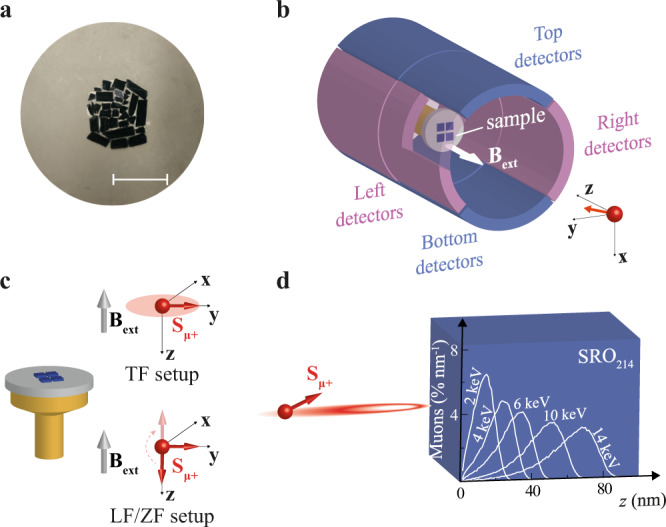
a SRO214 crystals cleaved and glued onto a Ni-coated aluminium plate to form a mosaic for the LE-μSR measurements. The scale bar corresponds to a length of 2 cm. b Experimental LE-μSR setup with applied field vector Bext perpendicular to the sample (i.e., along the c-axis of SRO214 coinciding with the axis z of our orthonormal reference-axes system) and arrays of positron detectors used to count muon decay events. The schematic cut-out allows viewing the sample inside the detectors. c LE-μSR measurement configurations for different orientations of the initial muon spin polarization vector Sμ+: Sμ+ perpendicular to the applied field vector Bext and precessing in the xy-plane of our reference-axes system as indicated by the shadowed red circle (transverse field, top) or Sμ+ collinear to Bext (longitudinal field or zero fields with Bext = 0, bottom). d Muon implantation profiles in SRO214 simulated for a few representative implantation energies.
To determine the presence of any magnetism in SRO214 and study its temperature (T) and depth dependence, we first perform LE-μSR temperature scans (T-scans) in the TF configuration as a function of energy (E). In the TF setup, the muons implanted with energy E precess about the perpendicular Bext at an average frequency ωs (E) = γμ Βloc (E) with γμ = 851.616 MHz T−1 being the muon’s gyromagnetic ratio and Bloc the amplitude of the local field experienced by muons. Each E corresponds to a different muon implantation depth profile simulated using the Monte Carlo algorithm TrimSP18 as shown in Fig. 1d.
The T-scans are carried out whilst warming up the SRO214 crystals, after zero-field cooling (ZFC) them and applying an external field with amplitude Bext = 100 G at the lowest T. For the analysis of the T-scans in TF, we model the asymmetry signal As(t) as As(t) = A0 e−λt cos [γμΒloct + φ0], where λ is the muon spin depolarization rate, which is proportional to the width of the local field distribution amplitude with average Bloc sensed by muons, A0 is the initial asymmetry which depends on the initial Sμ+, and φ0 is the initial phase depending on the initial Sμ+ and on the geometry of the detector (see Supplementary Information). We note that the finite width of the muons’ implantation profiles in LE-μSR (Fig. 1d) leads to a broadening of the field distribution experienced by the muons implanted at a given E. As a result, the asymmetry signal is better fitted assuming an exponential rather than a Gaussian relaxation rate, which is instead typically used in bulk-μSR studies where all muons implanted in a homogeneous sample experience the same field distribution. At a given E, we also perform a global fit19 including all the data points collected as a function of T and assuming A0 and φ0 as T-independent, since A0 and φ0 are both related to the initial Sμ+ which is T-independent.
The results of the analysis are shown in Fig. 2, where we plot for each E the T-dependence of the shift in λ, Δλ(Τ), from the λ value measured at the highest T (~ 270 K in Fig. 2). The analysis of Δλ allows to remove systematic effects such as variable contributions to λ due to the measurement background.
Fig. 2. Temperature dependence of magnetism in SRO214 at different implantation depths.
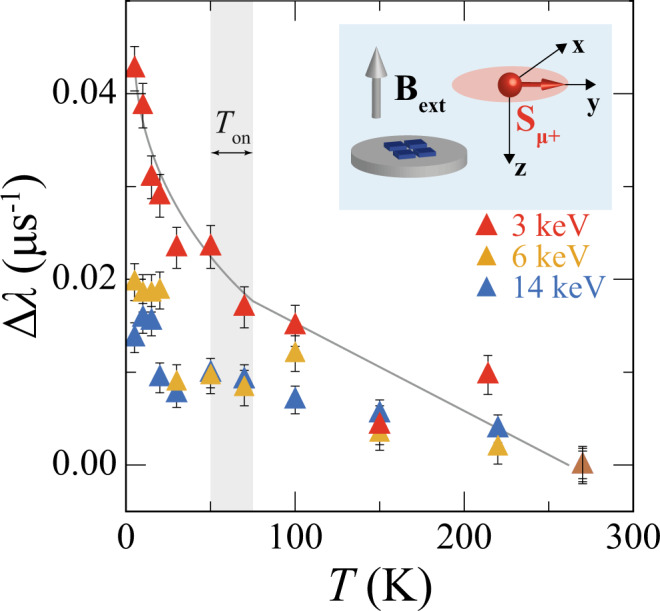
Shift in the muon depolarization rate, Δλ, from the λ value measured at T = 270 K as a function of temperature T measured in a TF setup (inset) with applied field amplitude Bext = 100 G at different implantation energy E values: E = 3 keV (red symbols with error bars), E = 6 keV (orange symbols with error bars) and E = 16 keV (blue symbols with error bars). The solid grey line serves as a guide to the eye and marks the T range (grey shaded region) where Δλ changes slope for E = 3 keV, which we identify as the onset temperature Ton of the magnetism in SRO214. The inset shows the relative orientation of the applied field Bext with respect to the muon spin polarization Sμ+ in our orthonormal reference-axes system for the TF configuration.
An increase in Δλ as T is decreased signifies a broadening in the distribution of local fields experienced by muons at their implantation sites, and therefore it is a signature of enhanced magnetism emerging in the SRO214 crystals as they are cooled down. Figure 2 shows that Δλ increases as T are lowered at all Es investigated, with a more pronounced increase in Δλ occurring closer to the SRO214 crystals’ surface at E = 3 keV corresponding to an average muon stopping depth ~ 15 nm ( values are determined from the stopping profiles in Fig. 1d). The Δλ values reported in Fig. 2, in combination with the corresponding raw asymmetry profiles and asymmetry fits reported in the Supplementary Information, show that Δλ at E = 3 keV significantly changes slope at a T between 50 and 75 K, which we identify as the Ton of the magnetism. The data sets in Fig. 2 and Supplementary Fig. 7 for E = 6 keV and E = 14 keV also demonstrate that the onset temperature Ton of the magnetism detected by muons decreases at higher implantation depths since Δλ for E keV does not change significantly until a T ~ 25 K is reached, which is lower than the estimated 50 K < Ton < 75 K. This result further confirms the surface nature of the magnetism that we measure in SRO214 because the muons implanted deeper inside SRO214 only experience an increase in their depolarization rate when the magnetism on the surface has become sufficiently strong, which occurs when T has been decreased well below the onset of the magnetic phase transition at Ton.
We note that we have verified the reproducibility of the results reported in Fig. 2 and measured the same trends for Δλ in two different batches of SRO214 crystals, which demonstrates that the observed magnetism is an intrinsic property of SRO214. The LE-μSR data on these two different batches of SRO214 crystals have been collected over three beamtime sessions with various cryostats and magnets, which also rules out other possible artefacts related to the measurement setup. We confirm the emergence of magnetism from the T-dependence of Δλ at different E values also for a different TF configuration, where Bext is applied in-plane other than out-of-plane.
To further characterize the nature of the magnetic states observed in SRO214, we study the response of these states in a higher applied Bext with amplitude Bext = 1500 G in the TF setup (Fig. 3a, b). Although we do not observe significant variations in the local field amplitude, Bloc, with T when Bext = 100 G, Fig. 3a shows that with Bext = 1500 G, Bloc increases as T is lowered for both E = 3 keV and E = 14 keV, before eventually decreasing in amplitude for T < 25 K. We also find that Bloc at E = 3 keV deviates from that measured at E = 14 keV through exhibiting a positive shift from the latter for T < 25 K (Fig. 3a).
Fig. 3. Magnetic field response and depth profile of magnetism in SRO214.
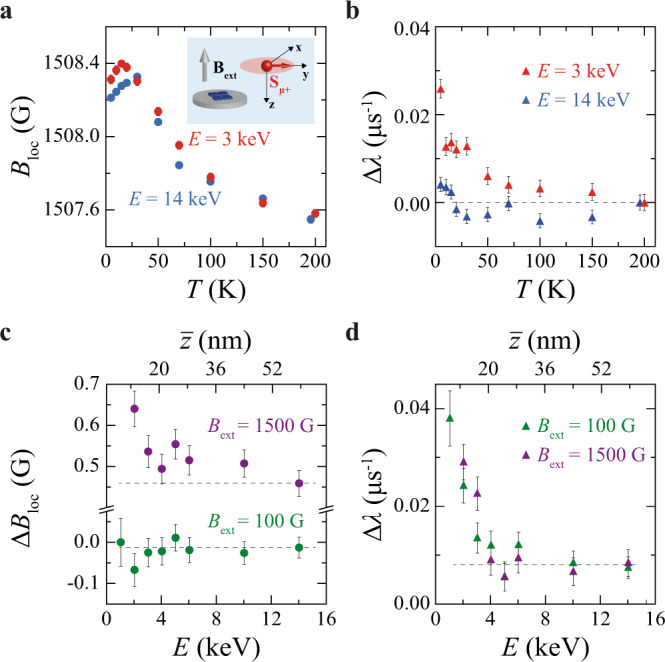
a, b, Temperature dependence of the local field amplitude Bloc (a) and of the shift in the depolarization rate, Δλ, from the λ value measured at T = 200 K (b) measured in TF with amplitude of the external field Bext = 1500 G at E = 3 keV (red symbols with error bars) and E = 14 keV (blue symbols with error bars). Error bars in (a) are within the symbols. The inset schematic in (a) shows the relative orientation of the applied field Bext with respect to the muon spin polarization Sμ+ in our orthonormal reference-axes system for the TF configuration. The Δλ values in (b) are different from those shown in Fig. 2, as they are measured at a different stage of the experiment after warming the samples to room T, degaussing the magnet and zero-field cooling the samples again before applying Bext. c, d Shift in the local field amplitude ΔBloc (c) and in Δλ (d) between T = 100 K > Ton and T = 5 K < Ton measured in TF as a function of E for Bext = 100 G (green symbols with error bars) and Bext = 1500 G (purple symbols with error bars). The top axes are the corresponding muon average stopping depth values determined from the simulated muon stopping distributions in Fig. 1d. Dashed lines in (b) to (d) are guides to the eye.
The Bloc curves in Fig. 3a are reminiscent of the Knight shift determined by nuclear magnetic resonance (NMR)10 in SRO214—which is a measure of the local susceptibility or density of states of the material near the Fermi surface. The positive shift in Bloc at E = 3 keV compared to E = 14 keV at T < 25 K (Fig. 3a) can therefore be correlated to an increase in the susceptibility based on the results in ref. 10, which is consistent with a strengthening of magnetism near the SRO214 surface. The data in Fig. 3b also indicate that Δλ in Bext = 1500 G exhibits a clear increase at E = 3 keV within the same T range reported in Fig. 2.
To determine the depth range of the magnetism whilst moving from the surface to the bulk of SRO214, we perform energy scans (E-scans) for two different Bext amplitude values (100 and 1500 G). In Fig. 3c, d we report the depth variation of the shifts in the amplitude of Bloc, ΔBloc, and in Δλ between T = 5 K and Ton measured for Bext = 100 and 1500 G. Although ΔBloc versus E is ~0 for Bext = 100 G, in a higher applied Bext = 1500 G we observe an increase in ΔBloc for E < 4 keV up to ~0.65 G (corresponding to ~0.45% of Bext). This result suggests that a ΔBloc increase can also be present for Bext = 100 G, but it may not be resolved, as it would fall within the experimental noise level of the LE-μSR technique. For both Bext values, Δλ increases for E < 4 keV (Fig. 3d), meaning that, as the samples are cooled down, the magnetic signal probed by muons becomes stronger only up to an average implantation depth of ~20 nm from the surface of the SRO214 crystals ( is determined from the simulated stopping profiles in Fig. 1d). This result also rules out magnetic impurities as the possible origin for the observed magnetic states because any magnetic impurities, if present, should not always be localized close to the surface of randomly cleaved SRO214 crystals.
We note that a paramagnetic Knight shift in the 17O NMR signal has been recently measured for SRO214 in its normal state under uniaxial strain20. The NMR Knight shift is of ~100 G in an applied field of 8 × 104 G, and it exhibits an anomalous enhancement related to spin fluctuations at the critical strain εv, defined as the strain value where the Fermi level reaches the Van Hove singularity (VHS). We note that in our experiment, the Fermi level of the SRO214 surface layers is not at the VHS and the layers underneath are just bulk-like as demonstrated by previous ARPES measurements21,22, whilst in ref. 20 the authors reach the VHS through the application of εv. Despite these dissimilarities between the two experiments, one can argue that the surface of SRO214 has a different local strain compared to the bulk, meaning that there may exist a correlation between our ΔBloc enhancement at the SRO214 surface and the Knight shift. Drawing a quantitative comparison between our ΔBloc enhancement and the Knight shift, however, is difficult for several reasons. First, as discussed in ref. 20, the Knight shift includes several contributions which cannot be fully separated and it is specifically measured for the oxygen sites, whilst the muon stopping sites do not simply coincide with the oxygen sites, meaning that the interaction of the muons with SRO214 is different. Second, our ΔBloc shift (~0.2 G in a field of 1500 G) is smaller than the Knight shift reported in ref. 20 by several orders of magnitudes, and it is measured in different experimental conditions from those of the NMR experiment, which cannot be reproduced in the LE-μSR setup where neither larger magnetic field than those used, nor strain can be applied. These factors make it difficult to determine if and to which extent the shift in ΔBloc would increase if the LE-μSR measurements could be done using similar settings to the NMR measurements. Last, even if we cannot exclude that a correlation between the NMR Knight shift and ΔBloc exists, our LE-μSR measurements suggest that the ΔBloc is characterized by different experimental signatures from those reported in ref. 20 for a paramagnetic Knight shift because ΔBloc originates from an ordered phase that breaks time-reversal symmetry and that is also static in nature, as evidenced by our ZF measurements reported below.
We also perform measurements in an LF/ZF configuration to gain further insights into the nature of the magnetism observed in SRO214 and in particular to determine whether the enhancement in close to the SRO214 surface for T < Ton (Fig. 2) is due to an increase in static magnetic fields or to a reduction in spin fluctuations as T decreases.
The measurements performed in the LF/ZF configurations demonstrate that the magnetism in SRO214 is not related to spin fluctuations, but it rather has a static nature. We fit the LF/ZF asymmetry data to an exponential/Lorentzian Kubo–Toyabe function23 (see also Supplementary Information).
Figure 4 shows that the damping in the asymmetry is decoupled as the applied field amplitude Bext is progressively increased from Bext = 0 (ZF) to Bext = 100 G (LF) for both directions of the collinear alignments of Sμ+ with Bext. The results clearly indicate that the local magnetic dipolar fields are static and of the order of ~10 G. If the asymmetry damping were instead due to magnetic fluctuations of the electronic moments, meaning due to spin-lattice relaxation, a Bext of ~10 G would not affect the spin-lattice relaxation since the exchange energy due to Zeeman splitting in a field of ~10 G is much smaller than the thermal energy at = 5 K.
Fig. 4. Static nature of magnetism in SRO214.
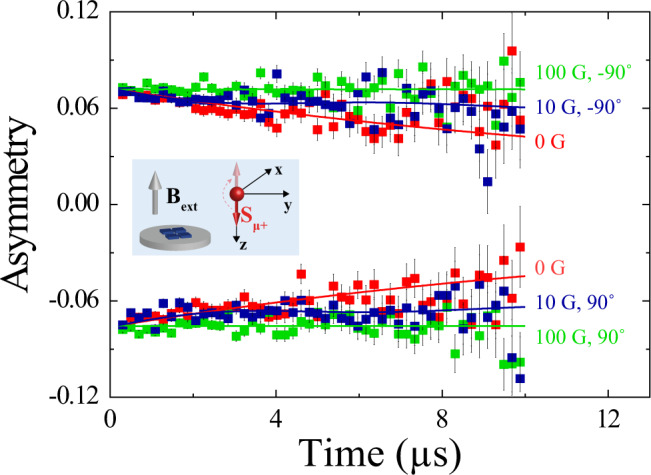
Asymmetry signal measured at = 5 K in ZF/LF for parallel (angle = 90°) and antiparallel (angle = −90°) alignments of the applied field Bext and the muon spin polarization Sμ+ with different Bext amplitude values: Bext = 0 G (red symbols with error bars), Bext = 10 G (blue symbols with error bars) and Bext = 100 G (green symbols with error bars). The inset schematic shows the relative orientation of Bext and Sμ+ in our orthonormal reference-axes system for the ZF/LF setup.
To quantify the intensity of the static magnetism that we detect, we note that spin-polarized positive muons used in this experiment are likely to implant closer to an oxygen atom with the SRO214 unit cell, due to the higher electron affinity of O compared to Ru. Since the Ru–O atomic bond length is ~2 Å in SRO214 (ref. 24), we estimate that the magnetic dipolar fields probed by muons at their implantation site (~10 G; Fig. 4) correspond to a magnetic moment much smaller than 0.01 μB/Ru atom.
Discussion
To summarize our experimental findings, we detect a magnetic phase with 50 K < Ton < 75 K (Figs. 2 and 3b) and localized within the first 10–20 nm from the SRO214 surface (Fig. 3d), which induces a positive ΔBloc shift near the surface only in higher Bext combined with a positive Δλ shift independent on Bext (Fig. 3c, d). The magnetic phase detected is not related to fluctuations, but it is static in nature, and it corresponds to an average magnetic moment experienced by muons of <0.01 μB/Ru atom at their implantation sites (Fig. 4). Based on these results, we can rule out several possibilities for the magnetic phases since they cannot account for our experimental observations.
The small magnitude of the moment in combination with the relatively high Ton suggests that the magnetic phase detected at the SRO214 surface is incompatible with conventional ferromagnetism. Ab-initio calculations indeed show that conventional ferromagnetic ordering of the Ru moments stabilized by the RuO6 octahedra rotation at the SRO214 surface would result in exchange energy due to Zeeman splitting of ~1 eV, which corresponds to a magnetic moment of ~1 μB/Ru atom12. Conventional ferromagnetism due to surface RuO6 octahedra distortion, which are present in our SRO214 crystals after cleavage as confirmed by the low-energy electron diffraction measurements (LEED) in Supplementary Fig. 2, therefore cannot account for our LE-μSR results.
Similarly, single-unit-cell thick SrRuO3 (SRO113), which is the parent ferromagnetic compound of SRO214, has a magnetic moment (~0.2 μB/Ru atom, ref. 25) that is a couple of orders of magnitudes larger than that probed by muons in our experiment and which can be detected by scanning SQUID magnetometry25. Supplementary Fig. 3 shows that scanning SQUID measurements performed by our group on the same crystals used for LE-μSR experiments cannot resolve any magnetic flux originating from SRO214, which also rules out the presence of SRO113 or other magnetic impurities in our SRO214 samples, consistently with the depth dependence of magnetism in Fig. 3c, d. We note that, in our scanning SQUID measurements, we can only detect small magnetic spots on the SRO214 crystals (Supplementary Fig. 3), most likely of extrinsic origin and possibly introduced during the cleaving process. These magnetic spots, however, only occupy a very small area of the sample surface (much smaller than 1%) and therefore they would only affect a small fraction of the implanted muons, meaning that they cannot account for the uniform increase in the depolarization rate measured in the LE-μSR signal below Ton. Our results obtained by scanning SQUID therefore further confirm that the magnetic signal which we resolve by LE-μSR in SRO214 has to be intrinsic of the material and it is associated to a magnetic moment below the typical moment values expected for conventional ferromagnetism.
Further to conventional ferromagnetism, we also rule out magnetism due to spin textures with cancelling moments26,27 or to correlations between spurious magnetic impurities as a possible explanation for our results in SRO214. This is because the appearance of such magnetic phases due to long-range correlations between magnetic spins or magnetic impurities embedded into a metallic Fermi sea at the relatively high onset temperature 50 K < Ton < 75 K we measure would require a large strength of the Ruderman–Kittel–Kasuya–Yosida interaction and/or a strong crystal field anisotropy. This, however, should result in a magnetic moment much larger than the value that we measure (much smaller than 0.01 μΒ/Ru atom).
We also exclude magnetic phases with antiferromagnetic ordering marked by a vanishing net magnetization and competing dipolar fields. This is because the SRO214 is layered and tetragonal, and therefore has inequivalent distances between the in-plane neighbouring magnetic moments and the moments in adjacent RuO2 planes. As a result, a muon implanted inside SRO214 in any energetically favourable sites, for instance close to an apical oxygen due to its electrical affinity, would very unlikely experience an almost vanishing dipolar moment. Indeed, in ruthenates with antiferromagnetic properties, the Bloc probed by muons corresponds to moments much larger than 0.01 μΒ/Ru atom28.
In addition to the above features, we also note that the time-reversal symmetry breaking (TRSB) normal (i.e., non-superconducting) phase that we detect at the SRO214 surface has to be homogenously distributed within the ab-plane of the SRO214 due to the monomodal local field distribution p (Bloc), as shown in the Supplementary Information. The magnetism sources should also correlate over a length scale comparable with the size of a single unit cell and be consistent with the SRO214 translational symmetry. This is because the signal measured at a given E is the sum of the contributions from all the muons implanted at in any position within the ab-plane of the SRO214 crystals.
Possible unconventional normal-state TRSB phases which would meet the above requirements and generate weak static magnetic dipolar fields in the absence of long-range ferromagnetic ordering include intra-unit cell spin nematicity and electronic loop currents like those reported for other materials including iron-based superconductors29,30, iridates31 and cuprates32,33. The existence of a spin-nematic phase at the SRO214 surface, however, can be excluded on the basis of symmetry considerations because a spin-nematic phase does not break inversion symmetry34, and therefore it would be energetically unfavoured by the inversion asymmetric interactions occurring at the SRO214 surface35.
Our theoretical analysis reported below shows that the origin of the normal-state TRSB phase probed on the surface of SRO214 can be ascribed to an orbital loop current with staggered magnetic flux. This orbital loop current phase is similar to that proposed to explain the intra-uni-cell antiferromagnetism in the pseudogap state of underdoped cuprates like YBa2Cu3O6+δ and HgBa2CuO4+δ (refs. 36,37). The existence of an orbital loop current phase in cuprates, however, remains still controversial not only because earlier experimental evidence supporting the existence of this phase, and mostly based on spin-polarized neutrons36,37, has not been confirmed by more recent studies, but also because alternative phases like charge density waves or spin density waves can equally account for the formation of the pseudogap in the normal state38,39. Similarly, for materials like iron-based superconductors, it is difficult to demonstrate conclusive evidence for an orbital loop current phase based on experiments demonstrating evidence for TRSB in the normal state because of the simultaneous presence of a TRSB spin density wave in the same materials40. To the best of our knowledge and as reported in ref. 41, the only two material systems for which evidence for an orbital loop current phase has been reported without effects that can be related to other coexisting TRSB phases include the Mott insulator Sr2IrO4 using non-linear optical microscopy42 and the two-leg ladder cuprate Sr14−xCaxCu24O21 using spin-polarized neutrons43. Spin-polarized neutron studies, however, have not confirmed the presence of normal-state TRSB orbital loop currents in Sr2IrO4 (ref. 42), whilst the orbital loop current phase reported for Sr14−xCaxCu24O21 cannot be directly correlated to that which we propose for SRO214, since Sr14−xCaxCu24O21 has radically different physical properties in that it is non-superconducting and behaves like a spin liquid above a certain hole doping.
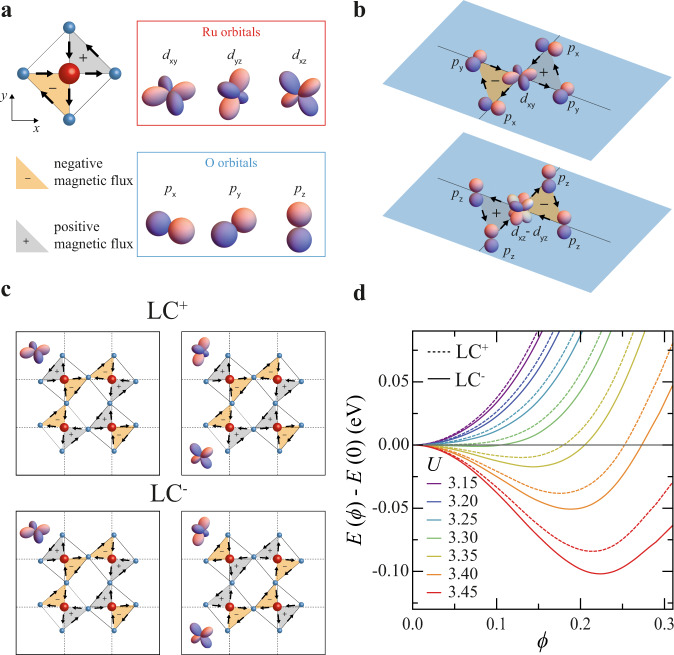
To understand the physical mechanism underlying the magnetism measured in SRO214, we consider orbital loop currents emerging as a result of electronic instabilities at the Fermi level. We use a tight-binding description of the electronic structure of SRO214 including d-orbitals at the Ru sites and p-orbitals at the planar O sites and consider d–p and p–p Coulomb interactions as responsible for the electronic instabilities yielding the orbital loop current phase (Fig. 5a).
Fig. 5. Magnetism due to orbital loop currents in SRO214.
a Illustration of the RuO4 plaquette and of the corresponding d-orbitals for the Ru atoms (red box) and p-orbitals for the O atoms (light blue box) with asymmetric loop current distributions generating magnetic flux pointing inward (yellow triangle with ‘−’ symbol) or outward (grey triangle with ‘+’ symbol) the RuO4 plane. b Possible orbital loop currents for a given RuO4 plaquette associated with the Ru–O hybridization of the dxy orbitals (top) and of the (dxz, dyz) orbitals (bottom). c Loop current states with equal (LC+ state) and opposite sign (LC− state) of the magnetic flux associated with the xy- and z-orbital sectors of the RuO plaquettes in the SRO214 supercell. d, Free energy E(ϕ)−E(0) of the LC+ (dashed lines) and LC− states (solid lines) calculated at T = 50 K for different values of the d–p Coulomb interaction ( values given in eV units are specified in the figure legend) as a function of the order parameter ϕ which sets the amplitude of the bond current.
Inversion symmetry breaking at the SRO214 surface rules out an orbital loop current phase that is spatially symmetric like that consisting of orbital currents flowing along each bond of the RuO4 plaquette (see Supplementary Information). Based on symmetry considerations, we therefore restrict our analysis to magnetic phases originating from asymmetric orbital loop currents, namely combinations of clockwise and anticlockwise orbital currents generating opposite magnetic fluxes only within two sections of the RuO4 plaquette (Fig. 5a) and determine whether this type of phase is consistent with the features of the magnetism observed in SRO214.
For a given RuO4 plaquette, there are two possible asymmetric TRSB loop current phases that differ by the way loop currents are distributed for the dxy and (dxz, dyz) orbitals sectors (Fig. 5b). Asymmetric loop current phases of several neighbouring plaquettes must combine at the SRO214 surface compatibly with the rotation of the RuO6 octahedra to yield the loop current distribution for a SRO214 supercell. The net loop current distribution in the SRO214 supercell has also resulted in staggered magnetic fluxes to prevent spontaneous current flow or charge accumulation, the existence of which is not possible in the metallic state of SRO214.
The first result which we obtain from our calculations is that the magnetic phase originating from orbital loop currents flowing inside the SRO214 supercell can indeed be the ground state of SRO214 because this magnetic phase is characterized by lower free energy compared to the non-magnetic SRO214 configuration. We also find that this unconventional orbital loop current (LC) phase can stabilize into two different energy states, the degeneracy of which is lifted by spin–orbit coupling in SRO214, depending on the distribution of the loop currents around the d-orbitals at the Ru sites. Figure 5c shows that one of these two magnetic states is generated by loop currents having the same sign for the dxy and (dxz, dyz) orbitals at the Ru sites, here denoted as LC+ state, whilst the other state is generated by loop currents for the dxy and (dxz, dyz) orbitals at the Ru sites having opposite sign (LC- state).
A calculation of the free energy for the LC− and LC+ states as a function of the Coulomb interaction U between electrons of the p- and d-orbitals of the O and Ru atoms for T below Ton shows that the LC− state is energetically favourable compared to the LC+ state (Fig. 5d and Supplementary Information). Figure 5d also shows that the free energy gain with respect to the normal state with zero flux is ~20–30 meV which is consistent with the order of magnitude of Ton. The order parameter in Fig. 5d is the expectation value of the asymmetric bonding operator in SRO214 (see Supplementary Information).
We last verify that the orbital loop currents corresponding to the most stable LC− configuration are consistent with the strength of the magnetic field probed by muons near the SRO214 surface. The magnetic field in the LC− configuration is obtained by determining the average current flowing along each bond inside the SRO214 supercell and then deriving the net total field according to the Biot–Savart law. Using experimental values for the magnetic permeability of SRO214, μm 2 × 10−2 G m−1 A−1 (ref. 10), and ab-initio values for the nearest-neighbour hopping parameters t for the d- and p-orbitals35,44, we obtain a Bloc amplitude in the range of 5–15 G which is consistent with the order of magnitude measured experimentally by LE-μSR.
In conclusion, our study demonstrates clear evidence for the existence of an unconventional magnetic phase in the surface region of SRO214. We show that loop currents with vanishing net magnetic flux due to orbital frustration can account for the hallmark signatures of the observed TRSB phase at the SRO214 surface. The orbital-dependent nature of the loop current phase suggests that mechanisms lowering the crystalline symmetry, e.g. strain, can increase the orbital imbalance and result in stronger magnetism. From this point of view, our results can be linked to the strain-induced magnetism and other magnetic phenomena already observed10,11 in the bulk of SRO214.
Another important implication of our results concerns the interplay between the normal-state TRSB phase, which we observe at the SRO214 surface, and the TRSB existing in the superconducting state of SRO214. Although the spin-triplet nature of the superconducting order parameter in SRO214 is still under debate, previous studies show that TRSB due the pairing correlations with intrinsic chirality7–9,45 (i.e., spin-singlet dxz idyz or spin-triplet px ipy) is a hallmark feature of the superconductivity in SRO214. The normal-state TRSB due to orbital loop currents does not contradict the TRSB of the superconducting state in SRO214, but it can bring further insights into the mechanism responsible for pairing formation with intrinsic chirality. This is because fluctuations of normal-state orbital loop currents, which are chiral in nature (they flow both clockwise and anticlockwise within the SRO214 supercell), may extend from the SRO214 surface, where such orbital loop currents get pinned and ordered, deeper into the bulk of SRO214 and provide an unusual electronic mechanism responsible for the formation of Cooper pairs with intrinsic chirality in SRO214.
A normal-state TRBS phase due to staggered orbital loop currents on the SRO214 surface should in principle not favour the formation of a uniform superconducting phase in SRO214 due to the incompatibility of the translation symmetry vectors of the two phases. Nevertheless, it is also possible that the superconducting order parameter in SRO214 reconstructs and follows a non-uniform profile (e.g., a pair density wave profile) to accommodate the spatial variations of the orbital loop currents phase and minimize the magnetic fields associated with them, for example by driving pairing between the dxy and (dxz, dyz) orbitals. Both scenarios, meaning the suppression or the reconstruction of the superconducting order parameter due to its competition with the normal-state TRSB loop current phase, would lead to a superconducting state at the surface different from bulk of SRO214—which can also account for some of the discrepancies between bulk-sensitive and surface-sensitive spectroscopy experiments reported to date on SRO214.
Dipolar fields generated near edge dislocations, which are particularly relevant near the SRO214 surface due to local strain inhomogeneities, can also be a source of time-reversal symmetry breaking46 and therefore further contribute to the discrepancy in the symmetry of the superconducting order parameter determined based on the bulk- and surface-sensitive spectroscopy techniques.
It is interesting to observe that, regardless of the orbital loop current mechanism that we propose to explain the magnetism on the SRO214 surface, this magnetism already represents a source of TRSB which can become more visible as superconductivity sets in, but without the TRSB being related to the superconducting order parameter per se. A normal-state TRSB phase can extend in principle to the entire sample as superconductivity sets in if an increase in the characteristic length scale of magnetism along the direction normal to the SRO214 surface takes place. For this scenario to occur, the magnetic moment at the SRO214 surface should generate dipolar fields in the superconducting state that are stronger than the critical field Hc1 of SRO214. It has been reported that Hc1 is of ~10 G at T = 0 (ref. 47), meaning that Hc1 is of the same strength as the dipolar fields probed by muons in our experiment. The dipolar fields that we detect by LE-μSR at the SRO214 surface can therefore in principle induce the formation of a vortex liquid phase like that described in ref. 47. This vortex liquid phase can give rise to a magnetic field distribution experienced by muons that is rather uniform, unlike the distribution corresponding to a vortex lattice, and possibly explain the TRSB in the superconducting state of SRO214 reported in previous experiments based on bulk μSR7,11.
Future studies will therefore have to clarify to which extent a normal-state TRSB phase at the surface can influence the superconducting state of SRO214 and determine its symmetry and possible TRSB nature since superconducting pairing must occur in the presence of a phase breaking time-reversal symmetry already in the normal state. More generally, our results set a reference for the discovery of similar electronic phases in other compounds where orbital correlations play a role and suggest a novel mechanism originating in the normal state that can result in the formation of unconventional superconducting pairing associated with time-reversal symmetry breaking.
Methods
Sample preparation
The Sr2RuO4 (SRO214) single crystals used in this experiment are grown by the floating zone method and cleaved with a non-magnetic ZrO2 to avoid contamination from magnetic impurities. The cleaved pieces are glued onto a Ni-coated aluminium plate to form a mosaic for the low-energy μSR measurements of size comparable to the muon beam (~2 cm in diameter).
Electronic transport and structural characterization
The electrical resistance of the SRO214 crystals is measured in a four-probe configuration inside a cryogen-free system (Cryogenic Ltd.) with a base temperature of ~0.3 K using a current-biased setup with a current equal to or less than 0.1 mA.
High-angle X-ray diffraction measurements on the same SRO214 samples are performed using a Panalytical X-Pert MRD PRO diffractometer. The diffractometer is equipped with a monochromatic CuKα1 radiation with wavelength λXRD = 0.154 056 nm obtained by a four-crystal Ge (220) asymmetric monochromator and a graded parabolic mirror positioned on the primary arm to the incident beam divergence to 0.12 arc sec. A triple-axis module with a triple-axis detector is used for the diffracted beam.
Low-energy electron diffraction (LEED)
LEED measurements are carried out using a LEED spectrometer (SPECS) with electron energies of 185, 199, and 251 eV after in-situ cleaving the SRO214 crystals at 10 K in an ultra-high vacuum with base pressure lower than 5 × 10−11 Torr.
Scanning SQUID
SQUID measurements are done using a custom-built piezoelectric-based scanning SQUID microscope with a 1 µm pick-up loop48 and magnetic sensitivity of 1µΦ0 (Φ0 = 2.0678 × 10−15 T m2 being the flux quantum). We use the scanning SQUID to image magnetic flux originating from the sample as a function of position. The magnetometry maps show the z-component of static magnetic flux near the surface of the sample. For the susceptometry measurements, we apply a local magnetic field of about 0.01–0.1 G using an on-chip field coil. Susceptometry is measured based on a standard lock-in technique and using the pick-up loop which resides at the centre of the field coil. An identical field coil surrounds a second pick-up loop used to correct for background magnetic fields in the magnetometry mode (gradiometric design).
Supplementary information
Acknowledgements
A.D.B. and R.H. acknowledge funding from the Humboldt Foundation in the framework of a Sofja Kovalevskaja grant endowed by the Alexander von Humboldt foundation. A.D.B. also acknowledges funding from the Zukunftskolleg at the University of Konstanz. Y.M. acknowledges support from the JSPS (Nos. JP15H05852, JP15K21717, and JP17H06136) and, along with R.F., M.T.M., S.K., Y.Y., T.M., L.A.B.O.O., C.M.P.G., V.G., W.H., J.R., M.C., A.V., from the JSPS-EPSRC-CNR-IBS Core-to-core programme Oxide Superspin (Nos. EP/P026311/1 and JPJSCCA2017002). A.B. and B.K. acknowledge the European Research Council (Grant No. ERC-2019-COG-866236), the Israeli Science Foundation (Grant No. ISF-1251/19), the QuantERA ERA-NET (Project No. 731473). W.K. and C.K. acknowledge support from the Institute for Basic Science in Korea (Grant No. IBS-R009-G2). We also acknowledge A. Fittipaldi for support during the preparation of the experiment.
Author contributions
A.D.B. conceived the idea of the project and supervised it. The experiment was designed by A.D.B., Z.S. and A.V. The samples were grown by R.F. and A.V., and characterized by R.H., R.F., S.K., Y.Y., T.M., V.G. The LEED measurements were done by W.K. and C.K., and the SQUID measurements by A.B. and B.K. The muon measurements were performed by A.D.B., Z.S., R.H. with support from W.H., S.K., L.A.B.O.O., C.M.P.G., A.S., T.P., I.K. The muons results were analysed by A.D.B., Z.S., M.C. with inputs from A.V., Y.M., E.S., J.W.A.R. and other authors. The theoretical model was developed by M.T.M. and M.C. with support from A.R. and C.N. The paper was written by A.D.B. with help from M.C. and Z.S. and inputs and comments from all the other authors.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Data availability
The datasets generated during and/or analysed during the current study have been deposited in a Zenodo repository and they are publicly available at 10.5281/zenodo.5504281.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review informationNature Communications thanks Vadim Grinenko and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: R. Fittipaldi, R. Hartmann.
Contributor Information
M. Cuoco, Email: mario.cuoco@spin.cnr.it
Z. Salman, Email: zaher.salman@psi.ch
A. Di Bernardo, Email: angelo.dibernardo@uni-konstanz.de
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-26020-5.
References
- 1.Illing B, et al. Mermin–Wagner fluctuations in 2D amorphous solids. Proc. Natl. Acad. Sci. USA. 2017;114:1856–1861. doi: 10.1073/pnas.1612964114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kosterlitz JM, Thouless DJ. Ordering, metastability and phase transitions in 2 dimensional systems. J. Phys. C. 1973;6:1181–1203. doi: 10.1088/0022-3719/6/7/010. [DOI] [PubMed] [Google Scholar]
- 3.Ji D, et al. Freestanding crystalline oxide perovskites down to the monolayer limit. Nature. 2019;570:87–90. doi: 10.1038/s41586-019-1255-7. [DOI] [PubMed] [Google Scholar]
- 4.Bednorz JG, Müller KA. Possible high Tc superconductivity in the Ba–La–Cu–O system. Z. Phys. B. 1986;64:189–193. doi: 10.1007/BF01303701. [DOI] [Google Scholar]
- 5.Imada M, Fujimori A, Tokura Y. Metal–insulator transitions. Rev. Mod. Phys. 1998;70:1039–1263. doi: 10.1103/RevModPhys.70.1039. [DOI] [Google Scholar]
- 6.Cheong SW, Mostovoy M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 2007;6:13–20. doi: 10.1038/nmat1804. [DOI] [PubMed] [Google Scholar]
- 7.Luke GM, et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature. 1998;394:558–561. doi: 10.1038/29038. [DOI] [Google Scholar]
- 8.Xia J, Maeno Y, Beyersdorf PT, Fejer MM, Kapitulnik A. High resolution polar Kerr effect measurements of Sr2RuO4: evidence for broken time-reversal symmetry in the superconducting state. Phys. Rev. Lett. 2006;97:167002. doi: 10.1103/PhysRevLett.97.167002. [DOI] [PubMed] [Google Scholar]
- 9.Pustogow A, et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature. 2019;574:72–75. doi: 10.1038/s41586-019-1596-2. [DOI] [PubMed] [Google Scholar]
- 10.Imai T, Hunt AW, Thurber KR, Chou FC. 17O NMR evidence for orbital dependent ferromagnetic correlations in Sr2RuO4. Phys. Rev. Lett. 1998;81:3006–3009. doi: 10.1103/PhysRevLett.81.3006. [DOI] [Google Scholar]
- 11.Grinenko V, et al. Split superconducting and time-reversal symmetry-breaking transitions, and magnetic order in Sr2RuO4 under uniaxial stress. Nat. Phys. 2020;16:789–794. doi: 10.1038/s41567-020-0886-9. [DOI] [Google Scholar]
- 12.Matzdorf R, et al. Ferromagnetism stabilised by lattice distortion at the surface of the p-wave superconductor Sr2RuO4. Science. 2000;289:746–748. doi: 10.1126/science.289.5480.746. [DOI] [PubMed] [Google Scholar]
- 13.Kirtley JR, et al. Upper limit on spontaneous supercurrents in Sr2RuO4. Phys. Rev. B. 2007;76:014526. doi: 10.1103/PhysRevB.76.014526. [DOI] [Google Scholar]
- 14.Damascelli A, et al. Fermi surface, surface states and surface reconstruction in Sr2RuO4. Phys. Rev. Lett. 2000;85:5194–5197. doi: 10.1103/PhysRevLett.85.5194. [DOI] [PubMed] [Google Scholar]
- 15.Shen KM, et al. Surface electronic structure of Sr2RuO4. Phys. Rev. B. 2001;64:180502 (R). doi: 10.1103/PhysRevB.64.180502. [DOI] [Google Scholar]
- 16.Di Bernardo A, et al. Intrinsic paramagnetic Meissner effect due to s-wave odd-frequency superconductivity. Phys. Rev. X. 2015;5:041021. [Google Scholar]
- 17.Krieger JA, et al. Proximity-induced odd-frequency superconductivity in a topological insulator. Phys. Rev. Lett. 2020;125:026802. doi: 10.1103/PhysRevLett.125.026802. [DOI] [PubMed] [Google Scholar]
- 18.Morenzoni E, et al. Implantation studies of keV positive muons in thin metallic layers. Nucl. Instrum. Methods Phys. Res. Sect. B. 2002;192:254–266. doi: 10.1016/S0168-583X(01)01166-1. [DOI] [Google Scholar]
- 19.Suter A, Wojek BM. Musrfit: a free platform-independent framework for μSR data analysis. Phys. Procedia. 2012;30:69–73. doi: 10.1016/j.phpro.2012.04.042. [DOI] [Google Scholar]
- 20.Luo Y, et al. Normal state 17O NMR studies of Sr2RuO4 under uniaxial stress. Phys. Rev. X. 2019;9:021044. [Google Scholar]
- 21.Veenstra CN, et al. Determining the surface-to-bulk progression in the normal-state electronic structure of Sr2RuO4 by angle-resolved photoemission and density functional theory. Phys. Rev. Lett. 2014;110:097004. doi: 10.1103/PhysRevLett.110.097004. [DOI] [PubMed] [Google Scholar]
- 22.Zabolotnyy VB, et al. Surface and bulk electronic structure of the unconventional superconductor Sr2RuO4: unusual splitting of the β band. New. J. Phys. 2012;14:063039. doi: 10.1088/1367-2630/14/6/063039. [DOI] [Google Scholar]
- 23.Uemura YJ, Yamazaki T, Harshman DR, Senba M, Ansaldo EJ. Muon-spin relaxation in AuFe and CuMn spin glasses. Phys. Rev. B. 1985;31:546. doi: 10.1103/PhysRevB.31.546. [DOI] [PubMed] [Google Scholar]
- 24.Chmaissem O, Jorgensen JD, Shaked H, Ikeda S, Maeno Y. Thermal expansion and compressibility of Sr2RuO4. Phys. Rev. B. 1998;57:5067–5070. doi: 10.1103/PhysRevB.57.5067. [DOI] [Google Scholar]
- 25.Boschker H, et al. Ferromagnetism and conductivity in atomically thin SrRuO3. Phys. Rev. X. 2019;9:011027. [Google Scholar]
- 26.Lago J, Blundell SJ, Eguia A, Jansen M, Rojo T. Three-dimensional Heisenberg spin-glass behavior in SrFe0.90Co0.10O3.0. Phys. Rev. B. 2012;86:064412. doi: 10.1103/PhysRevB.86.064412. [DOI] [Google Scholar]
- 27.Heffner RH, et al. Muon spin relaxation study of La1−xCaxMnO3. Phys. Rev. B. 2001;63:094408. doi: 10.1103/PhysRevB.63.094408. [DOI] [Google Scholar]
- 28.Carlo JP, et al. New magnetic phase diagram of (Sr,Ca)2RuO4. Nat. Mater. 2012;11:323–328. doi: 10.1038/nmat3236. [DOI] [PubMed] [Google Scholar]
- 29.Chu JH, Kuo HH, Analytis JG, Fisher IR. Divergent nematic susceptibility in an iron arsenide superconductor. Science. 2012;337:710–712. doi: 10.1126/science.1221713. [DOI] [PubMed] [Google Scholar]
- 30.Wang F, Kivelson SA, Lee DH. Nematicity and quantum paramagnetism in FeSe. Nat. Phys. 2015;11:959–963. doi: 10.1038/nphys3456. [DOI] [Google Scholar]
- 31.Zhao L, et al. Evidence of an odd-parity hidden order in a spin-orbit coupled correlated iridate. Nat. Phys. 2016;12:32–36. doi: 10.1038/nphys3517. [DOI] [Google Scholar]
- 32.Simon ME, Varma CM. Detection and implications of a time-reversal breaking state in underdoped cuprates. Phys. Rev. Lett. 2002;89:247003. doi: 10.1103/PhysRevLett.89.247003. [DOI] [PubMed] [Google Scholar]
- 33.Scagnoli V, et al. Observation of orbital currents in CuO. Science. 2011;332:696–698. doi: 10.1126/science.1201061. [DOI] [PubMed] [Google Scholar]
- 34.Fischer MH, Kim EA. Mean-field analysis of intra-unit-cell order in the Emery model of the CuO2 plane. Phys. Rev. B. 2011;84:144502. doi: 10.1103/PhysRevB.84.144502. [DOI] [Google Scholar]
- 35.Autieri C, Cuoco M, Noce C. Collective properties of eutectic ruthenates: role of nanometric inclusions. Phys. Rev. B. 2012;85:075126. doi: 10.1103/PhysRevB.85.075126. [DOI] [Google Scholar]
- 36.Mook HA, Sidis Y, Fauqué B, Balédent V, Bourges P. Observation of magnetic order in a superconducting YBa2Cu3O6.6 single crystal using spin polarized neutron scattering. Phys. Rev. B. 2008;78:020506 (R). doi: 10.1103/PhysRevB.78.020506. [DOI] [Google Scholar]
- 37.Li Y, et al. Unusual magnetic order in the pseudogap region of the superconductor HgBa2CuO4+δ. Nature. 2008;455:372. doi: 10.1038/nature07251. [DOI] [PubMed] [Google Scholar]
- 38.Fauqué B, et al. Magnetic order in the pseudogap phase of high-Tc superconductors. Phys. Rev. Lett. 2006;96:197001. doi: 10.1103/PhysRevLett.96.197001. [DOI] [PubMed] [Google Scholar]
- 39.Li ZZ, Wang WS, Wang QH. Competing orders in a three-orbital model of cuprates: is there a loop-current order? Physica C. 2014;507:103. doi: 10.1016/j.physc.2014.10.011. [DOI] [Google Scholar]
- 40.Klug M, Kang J, Fernandes RM, Schmalian J. Orbital loop currents in iron-based superconductors. Phys. Rev. B. 2018;97:155130. doi: 10.1103/PhysRevB.97.155130. [DOI] [Google Scholar]
- 41.Bourges P, Bounoua D, Sidis Y. Loop currents in quantum matter. C. R. Phys. 2021;22:1–25. doi: 10.5802/crphys.84. [DOI] [Google Scholar]
- 42.Zhao L, et al. Evidence of an odd-parity hidden order in a spin–orbit coupled correlated iridate. Nat. Phys. 2016;12:32. doi: 10.1038/nphys3517. [DOI] [Google Scholar]
- 43.Bounoua D, et al. Loop currents in two-leg ladder cuprates. Commun. Phys. 2020;3:123. doi: 10.1038/s42005-020-0388-1. [DOI] [Google Scholar]
- 44.Malvestuto M, et al. Electronic structure trends in the Srn+1RunO3n+1 family (n = 1,2,3) Phys. Rev. B. 2011;83:165121. doi: 10.1103/PhysRevB.83.165121. [DOI] [Google Scholar]
- 45.Steppke A, et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science. 2017;355:eaaf9398. doi: 10.1126/science.aaf9398. [DOI] [PubMed] [Google Scholar]
- 46.Willa R, Hecker M, Fernandes RM, Schmalian J. Inhomogeneous time-reversal symmetry breaking in Sr2RuO4. Phys. Rev. B. 2021;104:024511. doi: 10.1103/PhysRevB.104.024511. [DOI] [Google Scholar]
- 47.Shibata A, Tanaka H, Yonezawa S, Nojima T, Maeno Y. Quenched metastable vortex state in Sr2RuO4. Phys. Rev. B. 2015;91:104514. doi: 10.1103/PhysRevB.91.104514. [DOI] [Google Scholar]
- 48.Kirtley JR, et al. Scanning SQUID susceptometry of a paramagnetic superconductor. Phys. Rev. B. 2012;85:224518. doi: 10.1103/PhysRevB.85.224518. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analysed during the current study have been deposited in a Zenodo repository and they are publicly available at 10.5281/zenodo.5504281.