Agent-Based Computational Epidemiological Modeling

Abstract

The study of epidemics is useful for not only understanding outbreaks and trying to limit their adverse effects, but also because epidemics are related to social phenomena such as government instability, crime, poverty, and inequality. One approach for studying epidemics is to simulate their spread through populations. In this work, we describe an integrated multi-dimensional approach to epidemic simulation, which encompasses: (1) a theoretical framework for simulation and analysis; (2) synthetic population (digital twin) generation; (3) (social contact) network construction methods from synthetic populations, (4) stylized network construction methods; and (5) simulation of the evolution of a virus or disease through a social network. We describe these aspects and end with a short discussion on simulation results that inform public policy.

Introduction

With an increasingly connected world, the potential for large scale virus outbreaks, including epidemics and pandemics, grows. Example outbreaks include severe acute respiratory syndrome (SARS) in 2003, which claimed 800 lives47^,126; the 2015 Ebola outbreak (8833 killed to date)45; and Asian and Hong Kong influenza, each producing death tolls in the millions126, which are some of the worst outbreaks in recent history79. Over the last 40 years in the U. S., seasonal influenza has caused between 3000 and 49000 deaths annually46. Of course, the current COVID-19 pandemic is changing the world health state too rapidly to give “current” statistics.

While deaths and serious illness are immediate impacts of disease outbreaks, there are others. For example, the effects of virus outbreaks on economic costs have been studied15, illustrating that interventions can significantly reduce these costs. Secondly, shorter-term conditions can lead to longer-term trends. The so-called poverty trap is the phenomenon wherein poor economic conditions and disease prevalence can lock a society into persistent states of poor health and wealth43. A third example is the effect of disease on government instability and upheaval.93 provide a regression analysis showing that civil wars may be precipitated or exacerbated by disease outbreaks, because they decrease social health and welfare. Finally, persistent disease threat can also lead to different type of crimes120. There are several social issues coming to the fore through the 2019-initiated COVID-19 outbreak. These include closing businesses31, educational impacts117, disproportionate burden of racial minorities (e.g., in the United States) and by the poor44^,63, general heightened anxiety levels53^,125, and domestic violence80^,124. Hence, there are many reasons to study epidemics and disease outbreaks.

Epidemiologists and the health sciences community use various tools to anticipate outbreaks and help them react to those in progress, as well as perform research to understand disease dynamics and the factors that influence their spread (e.g.,16). Software simulation tools are used for these purposes and many studies have been conducted (e.g.,26^,40^,49^,57^,59^,72^,73^,114^,133).

Simulation may use ordinary differential equation (ODE) approaches that, for example, focus on groups (compartments) of people and compute the aggregated numbers of individuals that are in each state (e.g., infected, not infected) as a function of time. These equations essentially describe how many people move from one state to another based on rate equations that involve the current number of people in each compartment. They can also be used to compute characteristics of populations such as the basic reproductive number. See75 for a detailed treatment and42^,54^,57^,68^,114^,115 for particular applications and overviews.

Agent-based models (ABM)56^,65^,67^,112 represent another class of simulation wherein each human of a population is modeled as a distinct entity or agent that is attributed with traits and behaviors. These agents interact, thereby generating opportunities for contagion transmission among them. Agent interactions on a local scale produce population-level outcomes, such as numbers of cases, regions of high outbreak intensity, subpopulations with greater or lesser numbers of outbreaks, and pathways of virus transmission, among other characteristics. While ODE (aggregated) and ABM (disaggregated) methods each have their strengths, one strength of ABM is the fine-grained opportunities it offers to modify agent traits, behaviors, interactions, and disease parameters and assess their effects on outcomes15. Interventions and sensitivity analyses are two example classes of studies that make use of these refinements. Works on use of agent-based modeling for epidemic simulation include3^,59^,73^,76^,86^,89^,100^,133.

With this background, we turn to the focus of this work in the next section. This paper addresses many disciplines that comprise epidemiological study (in addition to the epidemiological modeling approaches mentioned above). All such disciplines are not covered. Those that are covered are large and wide-ranging. Several references are provided for each discipline; they should be taken as representative, not exhaustive. The topics covered are integrated to give a unified perspective.

We note that while the theme of this paper is computational epidemiology, most of the topics are applicable to other types of human behavior.

An Integrated Modeling Methodology: Scope and Motivation

Our focus is an ABM environment for computational epidemiology. Agent-based modeling of the spread of viruses or diseases is often given the most attention because it is most closely associated with the ultimate results. However, there are many technical contributions to these final results. Our goals are the construction and use of tools and methods that ultimately produce time-resolved state transitions of each agent in a population, and a quantitative understanding of the factors that produce these results. These tools and their results may then be used by policy analysts and makers41. We describe several components of this methodology: (i) theoretical foundations; (ii) population generation procedures and data; (iii) social network construction from these populations; (iv) large-scale stylized network generators; and (v) simulation software that models virus transmission.

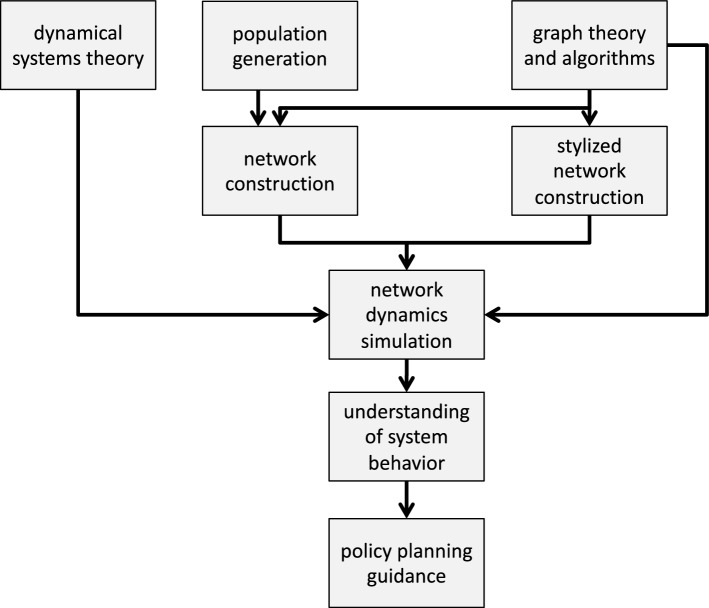
There is ample motivation for these individual components, and for their combination and integration. Figure 1 provides an overview of the components and their interactions. We use a formalism called graph dynamical systems (GDS) to study the transmission of diseases and other phenomena. This not only guides simulation software implementations, but also provides a framework to reason about such systems and applications. Examples are provided below. Diseases and other contagions propagate within populations and hence the generation of representative synthetic populations (also called digital twins), down to the individual level, is a key technology. There are many approaches for generating agent-level populations. Social contact networks, and other types of interaction networks, can be produced from these populations. Large scale stylized networks with particular properties, such as scale-free and exponential decay degree distributions, clustering coefficient distributions, assortativity, and community structure, are useful in that dynamics on them can serve as null model results. Moreover, network properties—through different network instances—can be systematically varied in stylized networks as another dimension to sensitivity and parametric studies; this is very difficult to do with synthetic populations. These results can then be compared against those from population-based networks. Disease (contagion) dynamics are computed on these networks using various simulation tools.

Figure 1:

Major components of the agent-based modeling system for computational epidemiology. These boxes are the topics in Sect. 4 below. Feedback loops are not shown. For example, based on the results of system behavior, the population construction methods may be changed, stylized networks with different properties may be generated, or parameters of the dynamics model may be changed.

The goals of these efforts are to: (i) understand baseline population behavior, (ii) quantify the effects on results of small changes in inputs (sensitivity studies) and of larger changes in inputs (parametric studies), (iii) determine the effects of different interventions, (iv) explain behaviors and establish causality, and (v) understand results in terms of policy implications.

It is useful to recall that the sizes of networks are routinely on the order of 10s or 100s of millions, or even billions, of agents (nodes) and 100s of millions or billions of edges. Hence, for many of these investigations, parallel processing is required to compute quantities efficiently.

Technical Challenges

There are many challenges in developing ABM systems. First, we seek a theoretical approach to describe disease dynamics and for this we use graph dynamical systems105. Second, to construct populations, data are required from multiple sources. These data are by their nature incomplete, often at different levels of granularity, and may be contradictory. Data fusion under these conditions is challenging. Third, big data challenges exist for generating populations that may involve 10s of millions of agents or more, and 100s of millions or billions of interactions38. In the same way, simulating dynamics on these networks requires parallel computations to drive down execution time and to enable runtime storage of large populations. Hence, efficient simulation is another challenge. A major part of a dynamics evaluation is sensitivity studies: how changes in input parameters affect the results. These require many simulation runs, increasing the need for fast simulation of large populations.

Modeling Environment

We describe four of the main elements of our modeling environment.

Graph Dynamical Systems

First we provide a theoretical overview of GDS, and then we make the ideas concrete through some examples. Then, we briefly touch on analysis problems and dynamical systems characterizations that are solved using GDS.

Theoretical Foundations

We use a discrete dynamical systems formulation known as graph dynamical systems (GDS)4^,97^,105 to model epidemiological processes. A GDS $\mathcal{S}(G(V,E),F,K,W)$ describes the system and its dynamics. Here, G is a (dependency) graph with vertex set V and edge set E. We use undirected dependency graphs in this work, but the concepts extend naturally to directed graphs. Each agent $v\in V$ is assigned a state $x_v\in K$, where K is the vertex state set. The (system) state x is given by $x=(x_1,x_2,\dots ,x_n)$ where n is the number of agents in the system; i.e., $n=|V|$. A GDS will have ${|K|}^n$ (system) states. Let n[v] be the sequence of vertex IDs for v itself and for all of its distance-1 neighbors (i.e., the vertices adjacent to v), ordered in increasing numerical order. This sequence of vertices is identified from the connectivity of G. We denote the states of v and of all of its distance-1 neighbors as x[v], such that $x[v]=(x_{n[v](1)},x_{n[v](2)},\dots ,x_{n[v](d_v+1)})$, where d(v) is the degree of v.

A vertex function $f_v$ is assigned to each agent v that describes the state transitions for it. The vertex functions for all n agents in the system comprise the sequence $F={(f_v)}_{v=1}^n$. For each $f_v$, the argument is x[v], such that the next state of v, denoted $x_v^{\prime }$, is given by $x^{\prime }=f_v(x[v])$.

Parameter W describes the order in which the vertex functions execute. We will cover two of the most common update schemes: synchronous and sequential.

A synchronous GDS map $\mathbf{F}:K^n\to K^n$ is defined by

$$\begin{array}{c}\hfill \mathbf{F}=(f_1(x[1]),f_2(x[2]),\dots ,f_n(x[n])).\end{array}$$ 1

That is, all vertex functions execute simultaneously. This is also called a parallel GDS map or a synchronous dynamical system. The system state at time $t+1$, $x(t+1)$, is given by $x(t+1)=\mathbf{F}(x(t))$.

A sequential GDS map ${\mathbf{F}}_{\pi }$ uses a permutation $\pi =({\pi }_1,{\pi }_2,\dots ,{\pi }_n)$ from the set $S_X$ of all permutations of the vertices in V, where each ${\pi }_i\in V$. We introduce the X-local function $F_v:K^n⟶K^n$, for a vertex v, given by

$$\begin{array}{c}\hfill F_v(x_1,\dots ,x_n)=(x_1,\dots ,x_{v-1},f_v(x[v]),x_{v+1},\dots ,x_n).\end{array}$$ 2

That is, only the vertex function for v is executed, with the states of all other vertices remaining unchanged. The sequential GDS map ${\mathbf{F}}_{\pi }:K^n⟶K^n$, is then the composition of the X-local functions; i.e.,

$$\begin{array}{c}\hfill {\mathbf{F}}_{\pi }=F_{{\pi }_n}\circ F_{{\pi }_{n-1}}\circ \dots \circ F_{{\pi }_2}\circ F_{{\pi }_1}.\end{array}$$ 3

This is also referred to as a sequential dynamical system. The system state at time $t+1$, $x(t+1)$, is given by $x(t+1)={\mathbf{F}}_{\pi }(x(t))$.

A forward trajectory is the sequence of (system) states $(x(0),x(1),x(2),\dots ,x(t_f))$ through which the GDS evolves from an initial state $x_0=x(0)$ to a final state $x(t_f)$, corresponding to a specified end time $t_f$. Thus, $x(1)=\mathbf{F}(x(0))$, $x(2)=\mathbf{F}(x(1))={\mathbf{F}}^2(x(0))$, and so on, until $x(t_f)=\mathbf{F}(x(t_f-1))={\mathbf{F}}^{t_f}(x(0))$ is computed. Consequently, time $t\in [0,t_f]$. A forward trajectory is sometimes referred to as a diffusion instance. If, for a deterministic system map $\mathbf{F}$—one in which there is precisely one value of $x(t+1)=\mathbf{F}(x(t))$ for each x(t)—we have that $x(t+1)=x(t)$, for some time t, then the GDS has reached a fixed point. That is, when a fixed point is reached at time $t^{\ast }$, $x(t)=x(t^{\ast })$ for all $t\ge t^{\ast }$; the system state does not change. Further, if there exists a smallest integer q such that $x(t+q)=x(t)$, and no $q^{\ast }<q$ exists such that $x(t+q^{\ast })=x(t)$ for some t, then the long-term dynamics is a repeating sequence or cycle of states $(x(t),x(t+1),\dots ,x(t+q-1))$ called a limit cycle with cycle length q. When $q=1$, the limit cycle is a fixed point.

A GDS may be deterministic or stochastic. We say that $x(t+1)$ is the successor of x(t) and that x(t) is the predecessor of $x(t+1)$. In a deterministic system, a state x may have many (or zero) predecessors, but only one successor (which may be itself). In a stochastic system, a state may have any number of predecessors and will have at least one successor, up to ${|K|}^n$ predecessors and successors. All of these states may or may not be visited in one forward trajectory of deterministic and stochastic GDSs.

Typically, for computations on large populations, the synchronous update mechanism is used to take advantage of parallel processing capabilities of simulation software that incorporates parallel execution of vertex functions.

Example: SIR Model With Explicit Dependency Graph

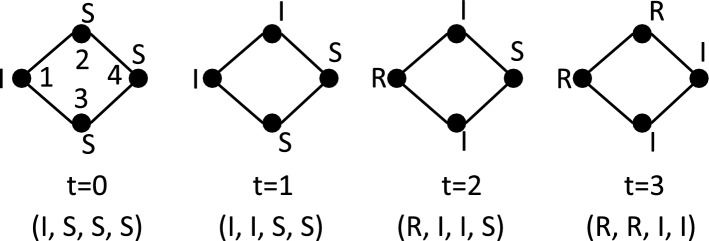
The state transition diagram for the susceptible-infectious-recovered (SIR) model is provided in Fig. 2. Vertex functions ${(f_v)}_{v=1}^n$ quantify the conditions under which the two state transitions $S⟶I$ and $I⟶R$ take place. For the sake of simplicity in this example, we let $p\in [0,1]$ be a probability of infection that holds for all agents (in many cases, p may be a function of simulation variables, such as the duration of contact between an infectious agent and a susceptible one). We let $t_{\mathit{dI}}$ be the duration (i.e., number of time steps) that a vertex spends in the infectious (I) state; again, we take this as uniform across all agents, but in practice can vary among agents. Let $t_{\mathit{iv}}$ be the time at which vertex v transitions to state I. A description of the vertex function follows, in which a vertex v transitions from $x_v$ to $x_v^{\prime }$:

Figure 2:

State transition diagrams for the susceptible-infected-recovered (SIR) model. The state set $K=\{S,I,R\}$. Vertex functions quantify the conditions under which a vertex changes state.

$\underset{\_}{\mathbf{Vertex}\mathbf{function}{\mathbf{f}}_{\mathbf{v}}\mathbf{for}\mathbf{node}\mathbf{v}}$

1. If $x_v=R$, then $x_v^{\prime }=R$, irrespective of the states of v’s neighbors.

2. If $x_v=I$ and $t_{\mathit{iv}}$ was the time at which this agent v was infected, then if the current time $t=t_{\mathit{iv}}+t_{\mathit{dI}}$, then $x_v^{\prime }=R$. Otherwise, v does not change state; i.e., $x_v^{\prime }=x_v$.

3. If $x_v=S$, then for each neighbor u of v that is in state I, v transitions to state I with probability p. If v does not change state, then $x_v^{\prime }=x_v$.

In particular for Condition 3, only one neighbor of v, in state I, is needed to cause v to change to state I. This is an example of a stochastic GDS, because, owing to the probability p, there is not a unique $x(t+1)$ given x(t).

Figure 3 provides a simple example that illustrates the dynamics of an SIR-based GDS. Each vertex is an agent, so the graph is a person-to-person contact or interaction graph. Each vertex function is the SIR function given immediately above. Let $t_{\mathit{dI}}=2$. The states at four times are shown: x(0), x(1), x(2), and x(3). Initially, only vertex 1 is infected; all other vertices are in state S. At time $t=1$, a random number $r_1<p$ is generated for vertex 2, based on its edge with vertex 1, resulting in 2 transitioning to state I. For vertex 3 and its edge to vertex 1, $r_2>p$ and hence 3 does not change state. Vertex 4 has no neighbor in state I and thus remains in state S. At time $t=2$, vertex 3 changes to state I because, based on vertex 3’s edge with vertex 1, the generated random number $r_3<p$. Vertex 4 does not change state. Vertex 1 transitions to state R at the end of time $t=2$. Other state changes occur similarly. In this example, the dependency graph is explicit. In the next example, it is implicit.

Figure 3:

Illustrative example of a 4-time step forward trajectory for a synchronous GDS where each vertex function is an SIR model. The dependency graph has 4 vertices and 4 edges. The infectious duration for each vertex (agent) is $t_{\mathit{dI}}=2$, and the probability of infection is p for each vertex. The vertices (agents) are labeled in the graph at the left, corresponding to the initial state x(0). The state corresponding to each time, displayed below the time, is given as $x(t)=(x_1,x_2,x_3,x_4)$. This particular sequence of states is dependent on the random numbers $r_i$, $1\le i\le 5$, and their relation to p.

Example: SIR Model With Implicit Dependency Graph

In the previous example, we used an explicit agent-to-agent social network for the dependency graph. In this example, we use a different type of graph, shown in Fig. 4. It is a bipartite people-locations graph (PLG), where one bipartition is the set of vertices representing people and the other bipartition is the set of vertices representing locations59. The edge labels are the times of the day at which the person is located at the specified location.

Figure 4:

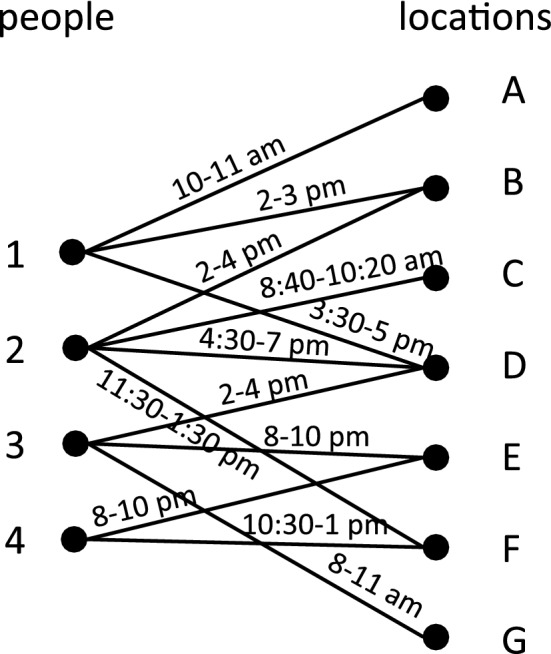
Illustrative example of a person-location bipartite graph, where people (1 through 4) are the elements of the left partite set and locations (A through G) are the elements of the right partite set. The edges are labeled with time. When two people are co-located, they form a person-person edge in a social network such as that in Fig. 3. Since these interactions give rise to the same person-person edges as in Fig. 3, and the same SIR model vertex functions are used, this network produces the same forward trajectory as that in in Fig. 3.

A person-to-person contact graph is produced in the following way: an edge between two people is generated if they appear at the same location, at the same time. We say that they are co-located. For example, consider persons 1 and 2 in Fig. 4. They are co-located at location B between 2 and 3 pm, and at location D from 4:30 to 5 pm. This results in one edge in the person-person graph in Fig. 3. Persons 1 and 3 also form an edge from the interaction at location D, because they overlap from 3:30 to 4 pm. Proceeding with this construction, we recover the dependency graph of Fig. 3.

In this example, the SIR model is the same as that in Sect. 4.1.2, and since we use the same synchronous update scheme and assume that the random numbers are the same as those in Sect. 4.1.2, we produce the same forward trajectory as above in Fig. 3.

There are variants of this approach. For example, the probability p of interaction can be a function of the contact duration between two people. In both examples, edges can be time-varying. For the first example, the edges can have labels denoting their interaction times, in a fashion similar to that in Fig. 4. In the second example, the activity pattern of an agent may change. An activity pattern is the set of locations that a person visits, along with the times of the visits.

Analysis Problems and System Characterizations

Besides providing a framework for constructing simulation software, GDS also provides a framework for investigation of analysis problems and dynamical systems characterization. Analysis problems of interest here are those regarding system dynamics of the types described in this section. The following are some examples:

1. Reachability problems. Given a state x, can the state $x^{\prime }$ be reached in one time step? More generally: given a state x, can state $x^{\prime }$ be reached in at most t time steps?

2. Predecessor existence problems. Given a state x, is there a state $x^{\prime }$ such that the system transitions from $x^{\prime }$ to x in one time step? More generally: given a state x, is there a state $x^{\prime }$ such that a GDS transitions from state $x^{\prime }$ to x in at most t time steps?

3. Fixed point existence problems. Given a GDS, does it have fixed points? A counting version is: How many fixed points does a system have?

These types of problems and their answers are important for practical reasons. For example, if a given state x of a system has been observed, one may want to know whether a particularly harmful state $x^{\prime }$ can arise; this is an example of a reachability problem. We refer the reader to numerous works on these and other related analysis problems. See17^–21^,21^,22^,24^,25^,28^,82^,116^,122.

The GDS framework also provides a foundation for characterizing dynamical systems. Useful texts include69^,105. An example of a system characterization is the following: progressive Boolean threshold systems, heavily used in the social sciences48^,71^,119 and that are similar to models popularized in78, are shown to generate only fixed points as limit cycles85. Works with other characterizations include2^,69^,83^,84^,105^,121^,127. These types of results, along with those from analysis problems, are useful not only for understanding system dynamics, but also for modeling and simulation verification and validation.

Synthetic Population Generation

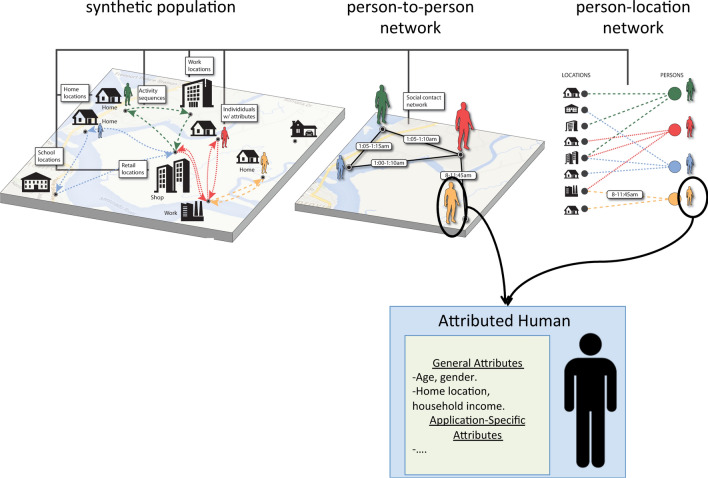
A synthetic population is a (data) representation of a group of individuals. The notion of group varies widely, from the members of a single family to all of the people of a nation. The wide range in sizes of such populations is a signal of their increasing development and use. Synthetic populations are also called “digital twins.” The individuals in a synthetic population are often endowed with (demographic) traits, such as age, gender, home location and housing. They are often given activity patterns where individuals go to particular locations and particular times of days. There is often additional data associated with synthetic individuals; particular data (assigned to synthetic individuals) depends on the requirements and use of the population. Figure 5 is a conceptual view of a synthetic population and movements of individuals as they perform daily activities; the two types of networks described above; and an attributed individual.

Figure 5:

Synthetic individuals (bottom) in a baseline synthetic population (top left) have associated demographics and are located in a specific geographic context (e.g., city, state, country). They are assigned activities to be performed at specific locations and times of day, creating a people-location network (top right). As described in Sects. 4.1.2 and 4.1.3, a person-to-person contact network (top middle) can be constructed from the people-location graph. The person-to-person network is conceptually the same as that in Fig. 3, while the people-location graph is conceptually the same as that in Fig. 4.

Typically, these populations are not one-to-one with actual populations. In other words, consider a real person who lives in a real city in the United States, on a particular street, with a family. That person is not (typically) represented in a synthetic population. Rather, distributions of characteristics of a synthetic population match those of the actual population. For example, age and gender distributions of people within a U.S. state, and distributions of household sizes are matched within a synthetic population. Because of the stochastic nature of the synthetic population construction process, one synthetic population is typically one instance or realization of a family of instances. Work has been done to assess the variability of synthetic population instances, e.g.,61.

Synthetic Populations and Their Building Blocks

The synthetic population generation process is comprised of the following steps13^,39.

$\underset{\_}{Constructingsyntheticindividualsandhouseholds.}$ Individuals and households (collections of individuals) are created. Individuals are endowed with characteristics such as age, gender, marital status. A representation of each household is created from census data by collecting individuals and assigning attributes such as household income and size.

$\underset{\_}{Determiningactivitiesofindividuals.}$ Each synthetic person in a household is assigned a set of activities to perform during a day, along with the times when the activities begin and end, as given by activity or time-use survey data.

$\underset{\_}{Determininglocationsforactivities.}$ An appropriate real location is chosen for each activity of every synthetic person based on a gravity model (i.e., locations closer to home locations are more likely to be selected, but longer distance locations are also selected, just with lesser probability) and data sources such as land use patterns, tax data, or commercial location data. Locations often have sublocations (e.g., sublocations may be rooms within a building), so that a location may be a (location, sublocation) pair.

$\underset{\_}{Generatingsocialcontactnetworks.}$ Two different representations of human interaction networks are provided. See the discussions for Figs. 3 and 4.

Below we describe each of the four steps above in more detail, for populations generated for regions of the U.S.

Constructing Synthetic Individuals and Households

A baseline population is constituted from two data sources: American Community Survey (ACS) and Public Use Microdata Sample (PUMS). The ACS data are used to create an individualized set of agents with assigned characteristics; see37 for details. The PUMS data are used to construct individuals that have, in distribution, the same traits as those of members of an actual population.

The ACS provides data for public use that are resolved to the block group level, which is a geographical region containing between 600 and 3000 people. For each block group, tables of distributions of many demographic characteristics—such as age, gender, and household size—are provided. These are marginal distributions. To create a synthetic population for the block group, a joint distribution is constructed from the given marginal distributions. This distribution is sampled the required number of times (one for each member of the target population).

The ACS also provides a 5 percent representative sample for each region, known as a PUMS, which is generated from a larger region called a Public Use Microdata Area (PUMA); the latter contains at least 100,000 people. A PUMS record is essentially a complete census record. The PUMS information is incorporated into the inference of the joint distribution from the marginal distributions using a statistical procedure called iterative proportional fitting (IPF)51^,55. IPF is an approach for combining the information from the marginal distributions and the sample data. It has been shown to preserve important properties and correlations of the data; see77^,94. The joint distribution for each block group is sampled to select households (with individuals) from the PUMS data, and these households are added to the synthetic population for that block group.

Determining Activities of Individuals

Data from the National Household Travel Survey (NHTS) are used to assign a daily activity sequence to each individual in a synthetic population. The NHTS contains detailed information on individual’s movements and activities over the course of a normative day118.

The activity patterns for different members of a household are typically dependent on each other. For instance, if there is a child under twelve years of age in the household, then an adult will likely be present in the home with the child whenever the child is at home.

NHTS surveys households, not individuals. Consequently, activity sequences are assigned by household, for each household, thereby preserving within-household activity correlations. This method is known as the Fitted-Values Method or FVM95. Essentially, a survey household is selected that is similar to the synthetic household using the asymmetric Hausdorff distance; a person within the survey household is selected that is most similar to each synthetic person; and that survey person’s activities are assigned to the synthetic individual, for each household member.

Determining Locations for Activities

Since each activity must be located, there are procedures for assigning (i) home locations and (ii) locations for other activities.

Home locations are assigned with the following procedure. U. S. Census data provide geographic boundary data (shapefiles) for each block group. The Census and ACS provide housing unit distributions (number of buildings with that contain different numbers of housing units), again for each block groups. HERE contains road networks, including geographic information. The portions of road networks that lay within the boundary of a block group are determined. Residential locations within a block group are assigned along these roadways with, e.g., single family homes more likely to be assigned to smaller (less traveled) streets. Households are assigned to these home locations.

Locations for other activities for individuals are assigned using a gravity model (see, e.g.,81^,123 for works on gravity models). The idea is that the probabilities of assigning particular locations for the next activity in a synthetic individual’s time-order list of activities are proportional to the capacities of buildings and inversely proportional to the distances from the current location to the candidate next locations. The base location is a person’s home location. From the determined current location of the most recent activity, it is more likely that a closer location of greater human capacity is chosen for the next activity’s location. For schools, National Center for Education Statistics (NCES)109^,110 information is used; for business and other activity locations, D&B data are used. See35^,59^,70 for additional information on location assignments. The above location assignments are constrained by capacities that are assigned to each building, or rooms (i.e., sublocations) within buildings. Consequently, a location may be a (location, sublocation) pair.

Generating Social Contact Networks

Each person has been assigned a (location, sublocation) pair for each activity during the day. Each activity has a start and end time. Thus, all information for the network representation in Sect. 4.1.3 is known, and a person-location graph analogous to that in Fig. 3 can be generated for a synthetic population. To generate a person-person contact social network, a graph edge is formed between two synthetic individuals (i.e., two nodes in the network) if they are located at the same (location, sublocation) with overlapping visit times during the day. Sect. 4.1.2 describes such as person-person network. Aspects of contact network evaluation can be found at59^,60^,128^,129. Illustrative examples of populations and their contact networks are provided in Table 1. It is evident that populations with billions of edges (e.g., for states and countries) are readily attainable.

Table 1:

Characteristics of selected U.S. city populations, in millions13.

City	Number of agents	Number of locations	Number of edges
Los Angeles	16.2 M	3.2M	917M
New York City	17.9 M	4.3M	961M
Seattle	3.2 M	0.78M	177M

Other Population Generation Approaches

In concluding this section, we note that there are several other approaches for generating and evaluating synthetic populations, and there are many applications. See for examples10^,30^,64^,74^,91^,96^,102^,104^,106^–108^,130^,131^,135. Reviews can be found at29^,50^,113.

Stylized Network Construction

Constructing explicit contact networks on the involved individuals allows us to study disease dynamics in more detail than possible with some other methods (e.g., compartmentalized models). A contact network is a graph $G(V,E)$, where V is the set of persons (each person is a vertex) and E is the set of contacts or edges; each edge $(u,v)\in E$ indicates the existence of the contact between two persons u and v. Use of a social contact network, in which a link represents physical contact between two people, can provide greater understanding of the disease dynamics. However, such studies require explicit networks, in which contacts (edges) exist explicitly. Although the data for these networks is difficult to get because of privacy and security concerns, conceptually these networks are well-defined. A study of epidemics (e.g., influenza, which spreads by physical contact) requires social contact networks, in which an edge represents an actual physical contact between two people at some location during the day. Procedures for generating these networks were discussed in Sect. 4.2.

In this section, we discuss several procedures for generating large stylized networks. As mentioned earlier, these networks are useful for several reasons. First, because (selected) properties of these networks can be controlled, the effects of network structure on disease dynamics (see Sect. 4.4) can be quantified. Second, even within a class of graphs, variations in parameter settings for their construction can also be evaluated to determine their effects on disease dynamics. Third, results of virus spreading on these networks can be used as null model results that can be compared with those generated with the networks of the preceding section.

Often, contact networks are approximated by various random network models such as the Erdös–Rényi model58, preferential attachment model9^,11, Chung-Lu model103, etc. The Erdös–Rényi model is the most widely-used and well-studied model due to its simplicity. Its simplicity has allowed us to perform rigorous theoretical analysis on this model over the last several decades. However, the Erdös–Rényi model generates random networks that have binomial degree distributions, which are not common in the real world. The preferential attachment model produces networks with power-law degree distributions. Many real-world networks follow power-law degree distributions, but many do not. Chung-Lu is a more general model that can produce a network from any given degree distribution. However, a degree distribution must be input to the Chung-Lu model whereas Erdös–Rényi and preferential models are controlled using just a few scalar parameters. In this section, we discuss some details of these models.

The study of complex systems has significantly increased the interest in various random graph models7^,33^,66. As some of the complex networks grow, it has become necessary to correspondingly generate massive random networks efficiently. As discussed in92, the structure of larger networks is fundamentally different from small networks, even if both are generated using the same model, and many patterns emerge only in massive graphs. Demand for large random networks necessitates the use of efficient algorithms, in terms of both running time and memory consumption, for their generation. Therefore, in addition to the description of these models, we also discuss some efficient sequential and parallel algorithms for generating random networks using the models.

Although various random graph models are being used and studied over the last several decades, even efficient sequential algorithms for generating such graphs were nonexistent until recently. Batagelj and Brandes33 justifiably said “To our surprise we have found that the algorithms used for these generators in software such as BRITE, GT-ITM, JUNG, or LEDA are rather inefficient. ...superlinear algorithms are sometimes tolerable in the analysis of networks with tens of thousands of nodes, but they are clearly unacceptable for generating large numbers of such graphs.” As a step towards meeting this goal, efficient sequential algorithms have recently been developed to generate certain classes of random graphs: Erdös–Rényi33, small world33, Preferential Attachment33^,111, and Chung-Lu103. Although these efficient sequential algorithms are able to generate networks with millions of nodes quickly, generating networks with billions of nodes can take substantially longer. Further, a large memory requirement often makes generation of such large networks using these sequential algorithms infeasible. Thus, parallel algorithms that scale to large numbers of processors and provide good speed up become a necessity.

The design of parallel distributed memory algorithms poses two main challenges in the context of generating random graphs. First, the dependencies among the edges, especially in the preferential-attachment model, impede independent operations of the processors. Second, different processors can create duplicate edges, which must be avoided. Dealing with both of these problems requires complex synchronization and communication among the processors, and thus gaining satisfactory speedup by parallelization becomes a challenging problem. Even for the Erdös–Rényi model where the existence of edges are independent of each other, parallelization of a non-naive efficient algorithm, such as the algorithm by Batagelj and Brandes33, is a non-trivial problem. A parallelization of Batagelj and Brandes’s algorithm was recently proposed in111.

Erdos–Renyi Networks

The Erdös–Rényi model58 is well-studied and one of the first random graph models. The model is as follow. We are given two parameters: an integer n and a real number p in [0, 1]. The model generates a random graph with $n=|V|$ vertices such that for every pair of vertices $u,v\in V$, edge (u, v) is included in the graph independently at random with probability p. Since there are $\left(\genfrac{}{}{0pt}{}{n}{2}\right)$ possible pairs of nodes, the expected number of edges is $\frac{1}{2}n(n-1)p$ and the expected degree of each vertex is $(n-1)p$. It is easy to see that the degree distribution is binomial.

A naive algorithm is: for each pair of vertices u and v, pick edge (u, v) independently with probability p by tossing a biased coin. Since there are $\Theta (n^2)$ pairs of vertices, this algorithm takes $\Theta (n^2)$ time. An efficient algorithm is given in33 that takes O(m) time, where m is the number of edges in the generated graph. The runtime is improved by avoiding tossing coins for the edges that are not selected. Consider a sequence of all possible edges, that is, all possible pairs of vertices as shown in Fig. 6. If we select each edge with probability p independently, a streak of edges are skipped between two selected edges (solid back circles in the figure). Instead of discarding those edges one by one, their algorithm determines the number of edges to be skipped by generating a single random number using the following geometric distribution. Let $\delta$ be a random variable denoting the number of edge to be skipped. Then $\delta$ edges are skipped and the following edge is selected to be added to the graph. This process is repeated until there is no remaining potential edges. The number edges to be skipped is called the skip length, which is computed as follows. We have

$$\begin{array}{c}\hfill Pr\{\delta =k\}={(1-p)}^{k}p\end{array}$$

i.e., $\delta$ is a geometric random variable. A geometric random number can be generated as follow.

• $r\leftarrow$ a uniform random number in [0, 1)

• $\delta \leftarrow \lfloor \frac{log(1-r)}{log(1-p)}\rfloor$

For additional details see33. Since each edge in the generated graph requires one random number and constant time, the algorithm takes O(m) time, which is optimal.

Figure 6:

A sequence of all possible potential edges. Each circle represents a potential edge. The white circles are the skipped edges, and the solid black circles are the selected edges in an Erdös–Rényi graph.

A parallelization of the above sequential algorithm is given in111. In the sequential algorithm the edges are selected one after another as the algorithm walks through the sequence of the potential edges (as shown in Fig. 6) using the skip lengths. Notice that determining a selected edge is dependent on the previous selected edges. Thus the process seems to be sequential in nature and pose a difficulty in parallelization. To deal with this difficulty, instead of generating an edge instantly after computing a skip length, all skip lengths are computed and stored by the processors, and then edges are created from these skip lengths. Another difficulty is that the algorithm does not know how many edges, and consequently how many skip lengths, need to generated in advance. The algorithm begins with an estimated number of skip lengths B. the expected number of edges $\frac{1}{2}n(n-1)p$ can serve as an estimation for B. Each of the P processors generates B/P skip lengths and stores them in an array S. Then a parallel prefix sum operation on the array S is performed by the processors to generate the actual edges. Let T be the sum of the skip lengths. If $T<\frac{1}{2}n(n-1)$ (i.e., B is an under estimation), generate some additional skip lengths. If there are some extra skip lengths, they are discard. See111 for details.

Preferential Attachment Networks

The preferential attachment model generates random evolving scale-free networks using a preferential attachment mechanism: a new node is added to the network and connected to some existing nodes that are chosen preferentially based on some properties of the nodes. In the most common applications, preference is given to nodes with larger degrees: a node is chosen with probability proportional to its degree. Below we discuss this degree-based preferential attachment (PA) model. A random network generated with a PA model has a power-law degree distribution11. In a power-law degree distribution, the probability that a node has degree d is given by $Pr\{d\}\sim d^{-\gamma }$, where $\gamma$ is a positive constant.

Let n be the number of nodes in the network we want to generate. In this model, nodes are added one by one. In phase t, $0\le t<n$, a new node t is added to the network and connected to x randomly chosen existing nodes. In this discussion, we use $x=1$. The methods described below can easily be generalized for any $x\ge 1$ (see6). Let $F_t$ be the node selected in phase t, i.e., edge $(t,F_t)$ is added to the network. Let $P_t(i)$ be the probability that node t is connected to node $i<t$; that is, $P_t(i)=Pr\{F_t=i\}=\frac{d_i}{{\sum }_j{d}_j}$, where $d_j$ represents the degree of node j. A naive implementation of this method can be inefficient. Batagelj and Brandes33 give an efficient algorithm with running time O(m). This algorithm maintains a list of nodes such that each node i appears in this list exactly $d_i$ times. The list can easily be updated dynamically by simply appending u and v to the list whenever a new edge (u, v) is added to the network. Now to find $F_t$, a node is chosen from the list uniformly at random. Since each node i occurs exactly $d_i$ times in the list, we have $Pr\{F_t=i\}=\frac{d_i}{{\sum }_j{d}_j}$.

Another algorithm, called copy model, proposed in87 also leads to preferential attachment and power law degree distribution. The algorithm works as follows. In each phase t,

• Step 1: first a random node $k\in [1,t-1]$ is chosen with uniform probability.

• Step 2: then $F_t$ is determined as follows:

  $$\begin{array}{cc}\hfill F_t=& k\text{with}\text{prob.}p\hfill \\ \hfill =& F_k\text{with}\text{prob.}(1-p)\hfill \end{array}$$

In the copy model when $p=\frac{1}{2}$, we have $Pr\{F_t=i\}=\frac{d_i}{{\sum }_j{d}_j}$6^,8. Thus, the copy model is more general. Further, it is easy to see the running time of the copy model is O(m), and it leads to more efficient parallel algorithms.

A parallel algorithm based on the copy model is given in6^,8. The dependencies among the edges pose a major challenge in parallelizing preferential attachment algorithms. Apparently any algorithm for preferential attachment seems to be highly sequential in nature: phase t cannot be executed until all previous phases are completed. However, a careful observation reveals that $F_t$ can be partially, or sometime completely, determined even before completing the previous phases. Notice that Step 1 above in the copy model can be executed for all node t simultaneously and independently. In Step 2, if $F_t=k$, we are done with the computation of $F_t$. If $F_t=F_k$, we may need to wait and coordinate with other processors as described below. Assuming there are P processors, the set of nodes V is divided into P disjoint subsets $V_1,V_2,\dots ,V_P$; that is, $V_i\subset V$, such that for any i and j, $V_i\cap V_j=\mathrm{\varnothing }$ and ${\bigcup }_i{V}_i=V$. Processor $P_i$ is responsible for computing and storing $F_t$ for all $t\in V_i$. The load balancing and performance of the algorithm crucially depend on how V is partitioned. See6 for a detailed study on load balancing and partitioning of V. Let $t\in V_i$. Now, if $F_t$ is chosen to be $F_k$, to determine $F_t$, we need to wait until $F_k$ is known. If $k\in V_j$ with $i\ne j$, processor i sends a message to processor j to find $F_k$. If $F_k$ is unknown, $P_j$ keeps this message in a queue until $F_k$ is known. Once $F_k$ is known, $P_j$ sends back a message with $F_k$ to $P_i$.

Now notice that while processor $P_i$ waits for processor $P_j$ until $F_k$ is known, it is possible that to determine $F_k$, processor $P_j$ is waiting for some other processor and so on. These events may lead to a waiting chain or dependency chain (see Fig. 7). If the lengths of the dependency chains are large, it can cause some processors wait for a long time, leading to poor performance of the parallel algorithm. Fortunately, the length of a dependency chain is small, and the performance of the algorithm is hardly affected by such waiting steps. In6^,8, it is shown that the maximum length of a dependency chain is at most $O(logn)$ with high probability. Moreover, while $O(logn)$ is the maximum length, most of the chains have much smaller length. It is easy to see that for a constant p, the average length of a dependency chain is also constant, which is at most $\frac{1}{p}$. For an arbitrary p, the average length is still bounded by $logn$. Thus, while for some nodes a processor may need to wait for $O(logn)$ steps, the processor hardly remains idle as it has other nodes on which it can work.

Figure 7:

A preferential attachment network with 5 nodes generated using the copy model. Solid lines show final decided edges, and dashed lines denote waiting of processors for node attachment to be resolved—the undecided edges. For node $t=3$, k is chosen to be 2, $F_3$ is chosen to be $k=2$, and thus edge (3, 1) is decided immediately. Similarly, edge (1, 0) is also decided immediately. For node $t=4$, k is 2 and $F_4$ is set to be $F_2$. That is, $F_4$ is dependent on $F_2$. Similarly, $F_2$ is dependent on $F_1$. Finally, we have $F_4=F_2=F_1=0$.

Chung-Lu Networks

The Chung–Lu model52 generates a random network from a given sequence of expected degrees. We are given a sequence of weights (representing expected degrees of the nodes), the model generates a random network such that the expected degree of a node is equal to the corresponding weight in the given sequence. Let the given sequence of the weights be $(W_0,W_1,\dots W_{n-1})$, where $W_v$ represents the expected degree of node v for all $v\in V=\{0,1,\dots ,n-1\}$, the set of nodes. Assuming $W_v^2<{\sum }_{k\in V}{W}_k$ for all $v\in V$, the model works as follows. For every pair of nodes $u,v\in V$, edge (u, v) is added to the network with probability

$$\begin{array}{c}\hfill p_{u,v}=\frac{W_u{W}_v}{S},\text{where}S=\sum _{k\in V}{W}_k.\end{array}$$

Now we have the expected degree for each v,

$$\begin{array}{c}\hfill E[d_v]=\sum _u{p}_{u,v}=\sum _{u\in V}\frac{W_u{W}_v}{S}=\frac{W_v}{S}\sum _{u\in V}{W}_u=W_v.\end{array}$$

Notice that above model can produce self loops. However, the self loops can easily be avoided by a simple modification of the model. One way to avoid the self loops is to simply discard any self loops created103. In such a case,

$$\begin{array}{c}\hfill E[d_v]=\sum _{u\in V,u\ne v}\frac{W_u{W}_v}{S}=W_v-\frac{W_v^2}{S}.\end{array}$$

For large graphs, where the number of nodes n is very large, the expected degree $E[d_v]$ converges to $W_v$ for each node v. It is also possible to adjust the probability $p_{u,v}$ such that even after discarding the self loops, $E[d_v]$ is exactly equal to $W_v$.

A naive algorithm for the Chung–Lu model is for each pair of nodes $u,v\in V$, create edge (u, v) with probability $p_{u,v}=\frac{W_u{W}_v}{S}$ independently (independent of the other edges). Like the Erdös–Rényi model, this naive algorithm requires $O(n^2)$ time to generate a network with n nodes since there are $\frac{1}{2}n(n-1)$ possible pairs of nodes. The difference between Erdös–Rényi model and Chung–Lu model is that in the Erdös–Rényi model all edges are created with same probability whereas in the Chung–Lu model different edges have different probabilities. An efficient $O(n+m)$ time algorithm is given in103. This algorithm is based on a technique similar to the edge skipping technique used in33 for the Erdös–Rényi model. Let the sequence of weights be sorted in non-increasing order. First consider the following algorithm. For each node u, pick each edge from the sequence of edges $(u,u+1),(u,u+2),(u,u+3),\dots$, in this order, with probability $p=p_{u,u+1}=\frac{W_u{W}_{u+1}}{S}$ until an edge (u, v) is picked. Let $q=p_{u,v}=\frac{W_u{W}_v}{S}$. Now include edge (u, v) in the generated network G with probability $\frac{q}{p}$. Then repeat the above process again beginning with edge $(u,v+1)$ and probability $p_{u,v}$. Notice that for any $u,v\in V$, edge (u, v) is included in G with probability $p·\frac{q}{p}=q=p_{u,v}.$ That is, this algorithm generates random networks following the Chung–Lu model. Since in the first step of this algorithm, the edges are picked with equal probability p, the edge skipping technique discussed in Sect. 4.3.1 can also be used for this algorithm leading to an $O(m+n)$ time algorithm, which is presented in103. A pseudocode for this algorithm using the edge skipping technique is shown in Algorithm 1.

In Algorithm 1, as we always have $u<v$ and no edge (u, v) can be selected more than once, this algorithm does not create any self-loop or parallel edges.

Based on this sequential algorithm, an efficient distributed-memory parallel algorithm is given in5 that takes $O(\frac{m+n}{P}+P)$ time with high probability, where P is the number of parallel processors. Let there be P independent processors with distributed memory system and the processors communicate with each other via exchanging messages. Computation of the probabilities $p_{u,v}$ are dependent on $W_u$ and $W_v$. Assume that every processor has a copy of the sorted (in non-increasing order) sequence of the weights in its own memory. Efficient parallelization of Algorithm 1 requires

• Computing the sum $S={\sum }_{k=0}^{n-1}{W}_k$ in parallel. Sequential computation of S takes O(n) time whereas S can be computed in parallel in $O(\frac{n}{P}+logP)$ time.

• Dividing the task of selecting and generating edges into independent subtasks.

• Balancing computation load among the processors. Load balancing is the most challenging issue in this parallel algorithm.

To compute the sum S in parallel, the weights W are divided equally among P processors such that every processor is responsible for $\frac{n}{P}$ weights. Each of the P processors adds its weights locally in $\frac{n}{P}$ time. Then these local sums from all processors can be aggregated (say, for example, using an MPI reduce function) in $O(logP)$ time. Therefore, computing sum S takes $O(n/P+logP)$ time. As the edges can be generated independently, the iterations of the for loop in Algorithm 1 can be executed by multiple processors independently and simultaneously. For the details of this algorithm along with a good and efficient load balancing method, see5.

Epidemiological Simulation

The GDS formalism of Sect. 4.1 is useful for developing simulation systems90. In this section, we look in depth at a simulation system based on the conceptual view of interactions as presented in Sect. 4.1.3. Other tools are cited in Sect. 1.

The EpiSimdemics model 26^,41^,132 is used to explore the impact of agent behavior and public policy mitigation strategies on the spread of contagion over extremely large interaction networks. The interaction network is represented by a labeled bipartite graph, where nodes consist of people and locations, referred to as a person-location graph. If a person visits a location, there is an edge between them, labeled by the type of activity and the time of the visit. The interaction graph is not static, but changes over time in response to changes in a person’s health state (e.g., stay home when sick), public policy (e.g., school closure), or behavior changes (e.g., reduce unnecessary activities during an outbreak). This new network, in turn, affects a person’s health (e.g., reducing contact with potentially infectious individuals outside the home, or increasing contact with potentially infected children inside the home). Including this co-evolution is important for correctly modeling the spread of disease27. The person-location graph is converted to a person-person graph, where nodes represent people and edges represent contact between people, labeled by the duration of contact. This graph is regenerated each timestep as the person-location graph changes.

Between-host contagion transmission and within-host contagion progression can be viewed as two connected but independently computed processes. Between-host transmission triggers the start of within-host progression by causing an uninfected individual to transition to an infected state. The disease progress of the infected individual is then fully determined by the local (vertex) function governing the within-host progression. The within-host disease progression is modeled as a Probabilistic Timed Transition Systems (PTTS), an extension of finite state machines with two additional features: the state transitions are probabilistic and timed. The system also supports multiple interacting PTTSs for modeling of multiple co-circulating diseases, enhanced sociological modeling in the agents, and the addition of more complex interventions, such as contact tracing and antiviral stockpiles.

The PTTS and the interaction network are co-evolving, as the progression of each one potentially affects the other. In simple terms, who you meet determines whether you fall sick, and the progression of a disease may change who you meet (e.g., you stay home because you are sick). The co-evolution can be much more complex, as an individual’s schedule may change depending on information exchanged with others, the health state of people they contact even if no infection takes place (e.g., more people than usual are sick at work), or even expected contacts that do not happen (e.g., coworkers who are absent from work). All of this may also be affected by an individual’s demographics (e.g., a person’s income affects their decision to stay home from work).

The Disease Model

The disease propagation (inter-host) and disease progression (intra-host) models were developed in the National Institutes of Health Models of Infectious Disease Agent Study (MIDAS) project. A disease progression model is shown in Fig. 8.

Figure 8:

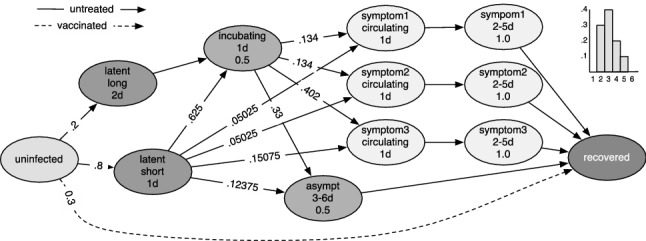
PTTS for the H5N1 disease model. Ovals represent disease states, while lines represent the transition between states, labeled with the transition probabilities. The line type represents the treatment applied to an individual. The states contain a label and the dwell time within the state, and the infectivity if different from one.

When a susceptible individual and an infectious individual are colocated, the propagation of disease from the infected individual to the susceptible individual is modeled by

$$\begin{array}{c}\hfill p_{i\to j}=1-{(1-r_i{s}_j\rho )}^{\tau }\end{array}$$ 4

where $p_{i\to j}$ is the probability of infectious individual i infecting susceptible individual j, $\tau$ is the duration of exposure, $r_i$ is the infectivity of i, $s_j$ is the susceptibility of j, and $\rho$ is the transmissibility, a disease-specific property defined as the probability of a single completely susceptible person being infected by a single completely infectious person during one minute of exposure23. Generally, $\rho$ is calibrated to produce a desired attack rate (fraction of total population infected) in the absence of any interventions. A person’s infectivity and susceptibility default to 1, but can be increased or decreased due to individual characteristics or behavioral changes. For instance, a child with less developed personal hygiene habits may be more infectious than typical (i.e., have a infectivity greater than 1), while an imuno-compromised individual may have an increased susceptibility. A person who wears a face mask in public may have reduced infectivity and/or susceptibility.

Intervention and Behavior Modification

A scenario specifies the behavior of individuals (e.g., stay home when sick), as well as public policy (e.g., school closure when a specific proportion of the students is sick). There are two fundamental changes that can be made that will affect the spread of a contagion in a social network. All behavior and public policy interventions are implemented through these changes. First, the probability of transmission of a contagion can be changed by changing the infectivity or susceptibility of one or more individuals. For example, getting vaccinated reduces an individual’s susceptibility whereas wearing a mask while sick reduces an individual’s infectivity. Taking antiviral medication, such as TamiFlu (oseltamivir), reduces the likelihood of becoming infected and reduces both the infectivity and length of the infectious period once an infection has taken place. Second, edges can be added, removed, or altered in the social network, resulting in different individuals coming into contact for different amounts of time. Individual behaviors and public policy interventions in EpiSimdemics, collectively referred to as the scenario, expose these two changes in a way that is flexible, easy to understand for the modeler, and computationally efficient.

The scenario is a series of triggers and actions written in a domain specific language. While conceptually simple, this language has proven to be quite powerful in describing a large range of interventions and public policies. A trigger is a conditional statement that is applied to each individual separately. If a trigger evaluates to true, one or more specified actions are executed. These actions can modify an individual by changing its attributes or schedule type, explicitly changing the PTTS and modifying scenario variables. Scenario variables can be written (assigned, incremented, and decremented) and read in the scenario file. The value read is always the value at the end of the previous simulation day. Any writes to a scenario variable are accumulated locally, and synchronized among processors at the end of each simulated day.

Social Network Representation

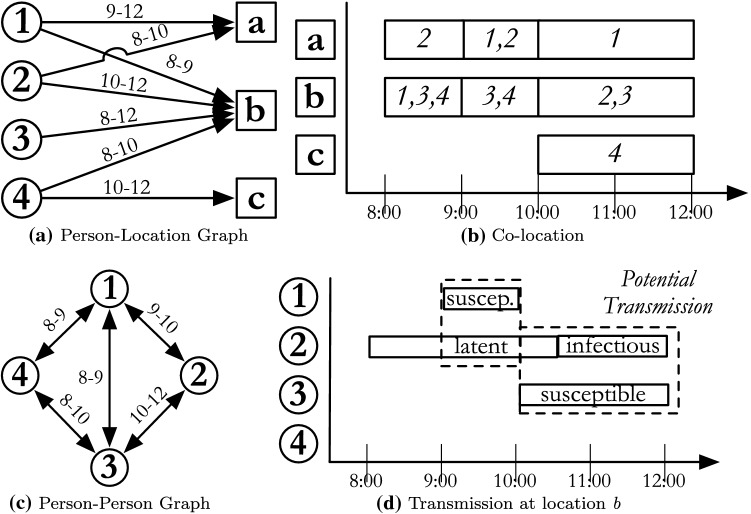
We provide four views into the simulation system, in terms of populations in Fig. 9. The two networks were addressed previously, but we now include attributes of graph elements that are particular to simulation, and how a simulation uses each type of network to compute contagion dynamics. In EpiSimdemics, the social network is represented by a labeled bipartite graph per Fig. 9a, as discussed previously. Labels attached to persons correspond to his/her demographic attributes such as age or income. The labels attached to locations specify the location’s attributes such as its geographic coordinates, the types of activity performed there, maximum capacity, etc. It is important to note that there can be multiple edges between a person and a location which record different visits. Internally, within the EpiSimdemics code, this network is converted into the equivalent person-person graph per Fig. 9c, as discussed earlier, within each (location, sublocation) pair. This form of the contact network is much more conducive for calculating interactions between people, but much less sparse, containing approximately 10 times more edges than the person-location graph. Figure 9b shows the people that are colocated in space and time. Assuming that person 2 is infected and either in the latent state (infectious, but not yet symptomatic) or infectious (contagious and symptomatic), Fig. 9d shows a potential transmission. The social contact graph is not static, but changes over time in response to changes in a person’s health state (e.g., stay home when sick), public policy (e.g., school closure), or behavior changes (e.g., reduce unnecessary activities during an outbreak). This new network, in turn, affects a person’s health (e.g., reducing contact with potentially infectious individuals outside the home, or increasing contact with potentially infected children inside the home). Including this co-evolution is important for correctly modeling the spread of disease27.

Figure 9:

An example social contact network: (a) the bipartite graph representation showing people visiting locations; (b) the temporal and spatial projection of the network; (c) the person-person graph showing interactions between temporally and spatially co-located people; (d) potential disease transmission between an infectious person 2, and susceptible people 1 and 3.

The EpiSimdemics model can be simulated with a simple discrete event simulation (DES) algorithm in which the system only changes its state upon the occurrence of an event. As shown in Fig. 9d, there are two types of events in the system: Arrive Events (person p arrives at location l at time $t_{\mathit{arrive}}$) and Depart Events (person p leaves location l at time $t_{\mathit{depart}}$).

To ensure correctness, the algorithm has to adhere to the following causality constraint: If an individual i leaves location $L_A$ at time $t_{\mathit{depart}}$ and arrives at location $L_B$ at time $t_{\mathit{arrive}}$, his/her health state when arriving at $L_B$ (denoted by $s_i(t_{\mathit{arrive}})$) has to be decided prior to calculating the states of other individuals at $L_B$ after time $t_{\mathit{arrive}}$. This causality constraint leads to temporal and spatial dependencies among nodes in the simulated system.

For simplicity of exposition, travel between locations is shown as instantaneous. In the actual system, there is a delay between leaving one location and arriving at the next location, based on an approximation of the travel time between locations. This delay can be calculated with varying degrees of accuracy12.

There are three important semantic points of the contagion diffusion problem that lead to the EpiSimdemics algorithm.

1. Individuals can only affect other individuals through interactions that occur when they are co-located in space and time.

2. An individual’s health state changes, once infected, can be precomputed.

3. There is a minimum latent period, $D_{\mathit{min}}$. This is the amount of time that must pass between a person becoming infected, and a person being able to infect others. For most infectious diseases, there is a suitable latent period that is determined by the biology of the infection. For influenza, this period is at least 24 hours.

The above observations led to a semantics-oriented problem decomposition. The existence of a latent period for newly infected individuals in the disease model provides a basis for relaxing the global clock. If the time period to be simulated is divided into n iterations, and if the length of a single simulation iteration is less than $D_{\mathit{min}}$, then all locations can be concurrently considered and interactions between individuals at these locations can be simulated in parallel.

The processing is separated into iterations that represent, for influenza, simulated days. It is important to note that state changes are not limited to time step boundaries. For example, if an individual is infected at 10:47 on day 10, and becomes infectious 36 hours later, they can start infecting others at 22:47 on day 11. Each iteration has the basic following four steps.

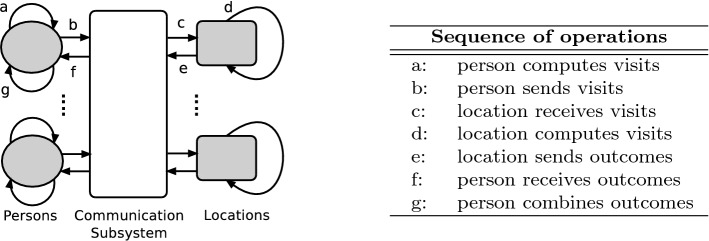
1. Each individual determines the locations that they are going to visit, based on a normative schedule, public policy, and individual behavior and health state. The person sends a message to each visited location with the details of the visit (time, duration and health state during the visit). This can be computed in parallel for each person.

2. Each location computes the pairwise interactions that occur between occupants of that location. Each interaction may or may not result in an infection, depending on a stochastic model. For the epidemiological model, disease propagation is modeled by Equation 4.

   A message is then sent to each infected person with the details of the infection (time of infection, infector and location). Again, each location can perform this computation in parallel, once it has received information for all of the individuals that will visit the location during the iteration.

3. Each person who is infected updates its health state by transitioning to an infected state. In the event that a person iis infected in multiple locations, the earliest infection is chosen.

4. Any global simulation states (i.e., total people infected) are updated.

For each iteration, there are two synchronizations required: between steps 1 and 2, and between steps 2 and 3. In addition, step 4 requires a reduction operation. These computational steps are further broken down in Fig. 10.

Figure 10:

The computational structure of the sequential EpiSimdemics algorithm.

Performance

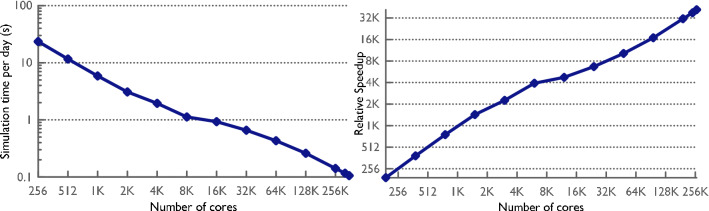
EpiSimdemics has been carefully designed to balance generality, efficiency, and scalability. It has been used to simulate the United States population (on the order of 300 million people) on both moderate sized university clusters of 1000 cores and NCSA’s BlueWaters system of 352,000 cores. The latter system was able to simulate the spread for 120 simulated days in less than 12 seconds133, as shown in Fig. 11.

Figure 11:

These plots show the performance of EpiSimdemics when run on NCSA’s Blue Waters system using up to 352,000 cores. The spread of Influenza through the population of the United States (on the order of 300 million people) is being simulated for 120 days, with no interventions, in 12 seconds.

Policy Implications

One of the most important practical results of epidemic simulations is to inform policy planning. A listing of selected studies is provide in Table 2. A few of these studies are described below. We note that simulation is not the only way to generate results to inform policy. For example, such results can be generated with compartmental models101 and game theoretic approaches34, which are not covered here.

Table 2:

Selected studies pertaining to epidemic simulations to support policy planning. The great majority of these investigate intervention strategies to reduce disease outbreaks.

Number	Type of study	Description	References
1	Epidemiological	Determine which intervention strategies are most effective in reducing outbreak size	73
2	Economic	Determine which intervention strategies are most cost-effective; i.e., the reduction in outbreak size per unit expenditure	15
3	Epidemiological	Different intervention triggers by demographic class	14
4	Epidemic tracking	Simulations run during a large outbreak by policy planners for situational awareness	36
5	Epidemiological	Demonstrates, for stylized networks, that homogeneous vaccination strategies can be counterproductive and that strategies should depend on social network local conditions	134
6	Epidemiological	Comparisons of vaccination strategies based on local versus regional conditions	98
7	Epidemiological	Evaluation of drugs and vaccines that are under development	1
8	Epidemiological	Influenza-based interventions for school-age children	32
9	Economic	Paid sick leave and its effect on outbreak size	88
10	Epidemiological	Influenza outbreak and various containment strategies	62
11	Epidemiological and social	Influenza outbreaks in (slums of) Delhi, India	100
12	Epidemiological and social	Interventions for influenza in (slums of) Delhi, India	3

Reference73 describes a multi-institutional study, exercising three different ABMs, to determine the most effective strategies for mitigating influenza spread in a 9 million agent system, similar to a population like Chicago. They found that a combination of school closures and targeted antiviral prophylaxis by individuals gave good results in decreasing the number of infected people. Additional work41 indicates that these results are robust across a different population.

In taking the73 study one step further,15 looked not only at outbreak size, but also the costs of outbreaks to determine which intervention strategies were most cost-effective. These costs include lost productivity by corporations, as well as lost income by households. So, for example, while staying at home (i.e., social distancing) may be useful in halting transmission, it also has the cost of reducing income among some socio-economic classes. Of the strategies investigated, the one that reduces the size of the outbreak and total costs is a combination of behavior modification of individuals (i.e., eliminating non-essential travel and taking antivirals) and government action (i.e., closing schools). In this case, the number of infected individuals decreases by 87% and the total cost drops by 82%. These findings indicate that the strategies that are best for decreasing outbreak size are also good for reducing their economic impact. Furthermore, it is noted in99 that paid sick leave is also cost-effective because it reduces the spread of sick workers who would otherwise come to work. Paid sick leave is also studied elsewhere (e.g.,88).

Summary

In this paper, we motivated epidemic simulation and itemized challenges in developing capabilities to perform these simulations. We focused primarily on describing fundamental elements of epidemic simulation: (i) theoretical foundations for simulation software, (ii) synthetic population (digital twin) development, (iii) social networks generated from synthetic populations, (iv) large-scale stylized network generation, and (v) simulation. We provided several examples of how epidemic simulation can support policy planning.

Biographies

Keith R. Bissett

is a Senior Software Engineer at Apple. His research interests include high performance computing, cloud services, and software systems architectures.

Jose Cadena

is a Research Staff Member in the Computational Engineering Division at Lawrence Livermore National Laboratory. His research interests include graph mining, machine learning for network data, combinatorial optimization, and approximation algorithms.

Maleq Khan

is an Assistant Professor in the Department of Electrical Engineering and Computer Science at Texas A&M University—Kingsville. His research interests include parallel and distributed algorithms, high performance computing, graphs analytics, data mining, and computational epidemiology.

Chris J. Kuhlman

is a Research Associate Professor in the Biocomplexity Institute at the University of Virginia. His research interests include modeling of human behavior, simulation, high performance and distributed computing, algorithms, and network science.