Soil textures rather than root hairs dominate water uptake and soil–plant hydraulics under drought

Abstract

Although the role of root hairs (RHs) in nutrient uptake is well documented, their role in water uptake and drought tolerance remains controversial. Maize (Zea mays) wild-type and its hair-defective mutant (Mut; roothairless 3) were grown in two contrasting soil textures (sand and loam). We used a root pressure chamber to measure the relation between transpiration rate (E) and leaf xylem water potential (ψ_{leaf_x}) during soil drying. Our hypotheses were: (1) RHs extend root–soil contact and reduce the ψ_{leaf_x} decline at high E in dry soils; (2) the impact of RHs is more pronounced in sand; and (3) Muts partly compensate for lacking RHs by producing longer and/or thicker roots. The ψ_{leaf_x}(E) relation was linear in wet conditions and became nonlinear as the soils dried. This nonlinearity occurred more abruptly and at less negative matric potentials in sand (ca. −10 kPa) than in loam (ca. −100 kPa). At more negative soil matric potentials, soil hydraulic conductance became smaller than root hydraulic conductance in both soils. Both genotypes exhibited 1.7 times longer roots in loam, but 1.6 times thicker roots in sand. No differences were observed in the ψ_{leaf_x}(E) relation and active root length between the two genotypes. In maize, RHs had a minor contribution to soil–plant hydraulics in both soils and their putative role in water uptake was smaller than that reported for barley (Hordeum vulgare). These results suggest that the role of RHs cannot be easily generalized across species and soil textures affect the response of root hydraulics to soil drying.

Root hairs of maize do not show evident contribution to root growth, water uptake, and soil–plant hydraulics, whereas soil textures affect the response of root hydraulics to soil drying.

Introduction

The role of root hairs (RHs) in nutrient acquisition, for example, phosphorus (Itoh and Barber, 1983; Gahoonia et al., 1997; Haling et al., 2013), and potassium (Drew and Nye, 1969; Klinsawang et al., 2018), has been well documented, but their contribution to water uptake remains controversial (Dodd and Diatloff, 2016; Carminati et al., 2017). Recent advances in the role of RHs on water uptake came from comparing wild-types (WTs) and their hairless mutant (Mut) counterparts. Using magnetic resonance imaging technology, Segal et al. (2008) showed that water depletion was more pronounced in the rhizosphere of WT than the hairless barley (Hordeum vulgare). Based on the images, the authors concluded that RHs increased the effective root surface area for water uptake. These results were in line with Carminati et al. (2017), who found that, in barley, RHs facilitated root water uptake by reducing the decline in matric potential at the root–soil interface (ψ_{soil_root}), especially at high transpiration rates (Es). Likewise, a study with Arabidopsis thaliana showed that water absorption by WT was 57% higher than that by its hairless Mut (Tanaka et al., 2014). Note that in the latter study, plants were grown in artificial media, such as agar and solutions. On the other hand, opposing results on the role of hairs on water uptake have also been reported. Suzuki et al. (2003) found that RHs of rice (Oryza sativa) did not contribute to water uptake under different soil moisture conditions. Similarly, Dodd and Diatloff (2016) showed that, in barley, water uptake did not differ between WT and Mut plants. They speculated that the role of RHs might have been more pronounced at high Es and enhanced root length of the Mut might have compensated for the lack of hairs. Therefore, the role of RHs in water uptake is, as yet, equivocal and hence it is still an open question to what extent and in what soil and atmospheric conditions RHs contribute to water uptake.

It is worth noting that the development of RHs (e.g. RH length and density) varied in different soils (Haling et al., 2014; Nestler et al., 2016), which, in return, may result in differences in water uptake. However, the interaction between RHs and soil textures (with different soil hydraulic properties) on water uptake remains unexplored. In wet soils, root resistance is the main constraint on water uptake (Nobel and Cui, 1992) and RHs do not substantially contribute to the resistance (Dodd and Diatloff, 2016; Carminati et al., 2017). In such conditions, water uptake is expected not to vary with soil textures and between WT and Mut (Chmielewska et al., 2014). In drying soil, however, the fast decline in soil hydraulic conductivity (k_s) at the soil–root interface became the main limiting factor on water uptake (Krounbi and Lazarovitch, 2011), with the consequence of stomatal closure (Carminati et al., 2020; Carminati and Javaux, 2020; Abdalla et al., 2021). Additionally, the decline in k_s for a given decrease in soil matric potential (ψ_Soil) varies in different soil textures. The question is to what extent would RHs cope with the fast decrease of k_s and hence attenuate the gradients at the soil–root interface for varying soil textures and atmospheric demand?

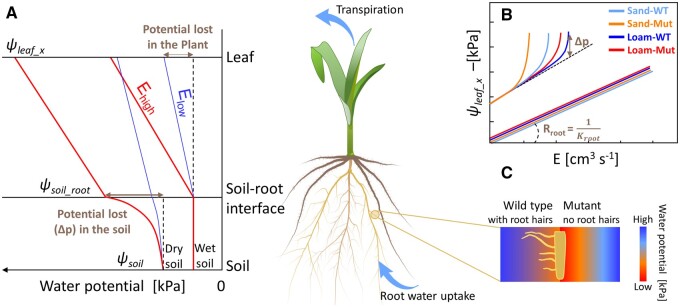
To measure the effect of hairs on root water uptake, it is not sufficient to measure transpiration during soil drying, as stomatal regulation is complex and might obscure and attenuate the role of hairs. Instead, it is essential to simultaneously measure E and the gradients in water potential across soil and plant. Figure 1 illustrates the expected gradients in water potential from the soil to the leaf xylem for different Es and ψ_Soils. In wet soils, the k_s is much higher than the flow velocity of soil water and water potential gradients in soil are negligible. Most of water potential dissipation occurs in the plants. If the conductivity of the plant tissues does not change, the water potential gradients increase linearly with the E (Figure 1A ). The relation between leaf xylem water potential (ψ_{leaf_x}) and E is linear and its slope is equal to plant hydraulic resistance (or the reciprocal of plant hydraulic conductance; Figure 1B). In dry soils, k_s decreases and substantial gradients in ψ_Soil are needed to pull water out of the soil. As k_s decreases with decreasing ψ_Soil, the gradients increase disproportionally with increasing Es. In this case, the relation between E and ψ_{leaf_x} is nonlinear (Figure 1B). Note that in dry soil conditions, nonlinearities in the plant conductivity are also expected due to xylem cavitation (Cochard, 2002) or loss of conductivities in the outer-xylem tissues (Scoffoni et al., 2017), which further increase the nonlinearity of the relation between E and ψ_{leaf_x}.

Figure 1.

Gradients in water potential in the soil–plant continuum as a function of Es and ψ_soils, including the hypothetical effect of RHs in two soil textures (sand versus loam). A, Sketch of water potential decreases from soil to leaf at low (E_low) and higher (E_high) Es in wet and dry conditions. B and C, Relation between E and ψ_leaf-x (measured with pressure apparatus, balancing pressure, P = ψ_leaf-x) and hypothetical impact of RHs and soil textures on the relation. RHs are expected to extend the root–soil contact area and hence attenuate the drop in matric potential around the roots (C).

Our hypotheses were: (1) RHs increase the maximum E that can be sustained at a given ψ_Soil and reduce the decrease in ψ_{leaf_x}, especially at high Es. The underlying mechanism is that RHs are expected to attenuate the drop in ψ_Soil around the roots, by extending the surface of the roots extracting water and thus reducing the flow velocity at the root–soil interface. This effect is expected to be particularly marked in coarse-textured soils, such as sandy soils, whose hydraulic conductivity abruptly drops with decreasing ψ_Soils; (2) the effect of RHs on the relation between E and ψ_{leaf_x} is more pronounced in sand than in loam, due to the pronounced drop in k_s of sand; (3) Mut plants develop longer and thicker roots to partly compensate for the absence of RHs. The hypotheses are also illustrated in Figure 1, B and C.

To test our hypotheses, we used two genotypes of maize (Zea mays), the Mut (roothairless 3 [rth3]), in which RH elongation is impeded, and its counterpart WT (Hochholdinger et al., 2008). The two genotypes were grown in two contrasting soil textures: sand and loam. E and ψ_{leaf_x} were measured continuously for different soil moisture conditions using the root pressure chamber method introduced by Passioura (1980) and implemented in Deery et al.(2013), Cai et al. (2020a), and Abdalla et al. (2021). The method consists of applying a hydrostatic pressure to the soil to maintain the water in the leaf xylem at atmospheric pressure. The applied pressure keeps stomata open and reduces the risk of cavitation and is therefore ideal to investigate belowground hydraulic constraints on transpiration (Abdalla et al., 2021). A simplified soil–plant hydraulic model is used to reproduce the relation between E and ψ_{leaf_x} (Carminati and Javaux, 2020). The model allows to include complementary measurements of the soil conductivity and to estimate the water potential losses in the soil and in the plant, as well as their respective hydraulic conductances. We used the model to systematically compare the two genotypes in the two soil textures and to investigate whether, thanks to RHs, the two genotypes would exhibit distinct root hydraulic properties.

Results

Variation of soil moisture and plant growth in sandy and loamy soils

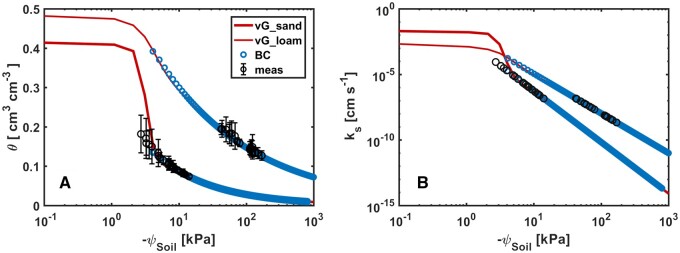
The hydraulic properties of the sandy and loamy soils are shown in Figure 2. Soil water content measured for all plants ranged from 0.18 to 0.07 (cm³· cm⁻³) and from 0.19 to 0.13 (cm³ · cm⁻³) in sand and loam, respectively. Supplemental Figure S1 shows the vertical distribution of water content in the two soils during soil drying. In loam, the water content was higher in the upper layer due to irrigation from the top. This was opposite in sand in which irrigated water moved more rapidly downwards. This was caused by the higher conductivity and the shape of the water retention curve in sand. The difference in water content between the upper and lower layers was higher in sand and this gradient in water content diminished as soil dried. We calculated the mean ψ_Soil from individual measurements of water content over depth. Both measured and estimated parameters were described in Table 1. The resulting relation between the average ψ_Soil and water content deviated slightly from the retention curve of the sandy soil (Figure 2).

Figure 2.

Soil hydraulic properties of the sandy and loamy soils. A, Soil water retention curve of the sandy (thick line) and loamy (thin line) soils fitted by the bimodal Mualem–van Genuchten (vG, red) and Brooks and Corey models (BC, blue). B, k_s as a function of ψ_Soil fitted by the vG and BC models. Bars refer to standard deviation (n = 18). The parameters of the BC model were inversely fitted using ψ_Soil data lower than −3.5 kPa from the vG model. ψ_Soil was calculated using measured soil water content (at three depths along the column) and the retention curve. Unsaturated k_s (black circle in (B)) was calculated using ψ_Soil and the corresponding hydraulic conductivity curve. Data were presented with standard deviation for the soil water content.

Table 1.

Information of key soil and plant parameters that were used in the soil–plant hydraulic model

Source	Name of Parameter	Unit	Measured	Estimated
Soil	Soil water content	cm3 cm−3	θ
	Soil matric potential	kPa	ψ Soil
	Unsaturated soil hydraulic conductivity	cm s−1	ks
	Soil conductance	cm3 s−1 kPa−1		K soil
Soil–Plant	Soil–root interface matric potential	kPa		ψ soil_root
	Root hydraulic conductance	cm3 s−1 kPa−1		K root
Plant	Root diameter	cm	r0
	Root length	cm	RL total a	RL act
	Transpiration rate	cm3 s−1	E
	Leaf xylem water potential	kPa	P (i.e. −ψleaf_x)

^a RL _total was measured after the last P(E) measurement of each plant. In earlier P(E) measurements in less dry conditions, RL_total was generated using the measured RL_total and a root growth function (Pagès et al., 2004).

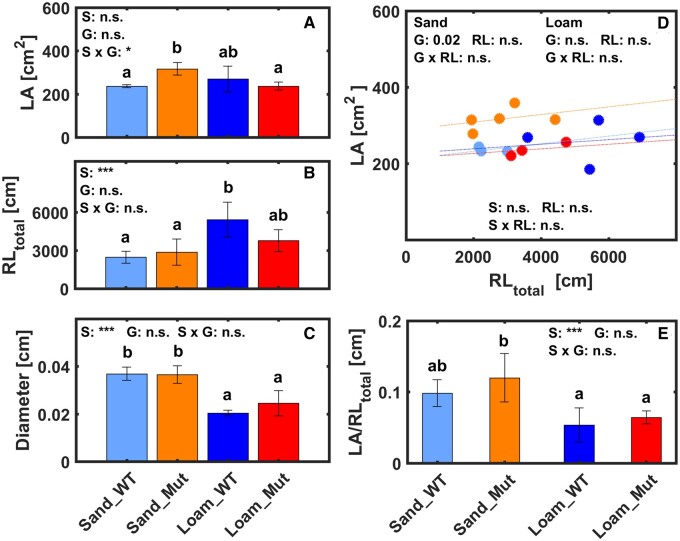
Plant growth was affected by soil characteristics (Figure 3). The Mut had a slower shoot development in sand and hence were grown 10 d longer to achieve a comparable leaf area. However, at the end of measurements, Mut in sand showed larger leaf area than WT in sand and Mut in loam (Figure 3A). Root length of WT and Mut was 2.2 and 1.3 times (1.7 times on average) longer in loam (Figure 3B), indicating a significant effect of soil type on root growth (P < 0.001). The higher root length density of both genotypes in loam was in line with Vetterlein et al. (2020), although we observed 50% lower values at a similar age. Soil type also significantly impacted root diameter with 1.6 times thicker root in sand (Figure 3C). However, genotypes showed no difference in root diameter within the same soil type. Although variations in leaf area and root length in the two soils were inconsistent, comparisons of relation between leaf area and root length revealed that Mut did not compensate for the lack of RHs by simply developing a longer root system (Figure 3, D and E).

Figure 3.

Comparison of plant parameters between WT and Mut grown in sand and loam. A, leaf area (LA). B, RL_total. C, root diameter. Relation between leaf area (D) and total root length (E) for both genotypes. Bars refer to standard deviation, n = 3, 5, 4, and 3 for WT and Mut in sand and in loam, respectively. The same number of plants was applied to the data in the figures below (Figures 4–8;  Supplemental Figure S2–S4) and Supplemental Tables S1–S3 in the supplementary materials. Two-factorial analysis of variance and multiple comparison were conducted for (A), (B), (C), and (E), and the significant difference was indicated by different letters. Regression slopes between genotypes and soil types in (D) were compared using analysis of covariance. S: soil type, G: genotype, n.s., not significant. *0.01 < P < 0.05, ***P < 0.001.

Difference in plant response to soil drying

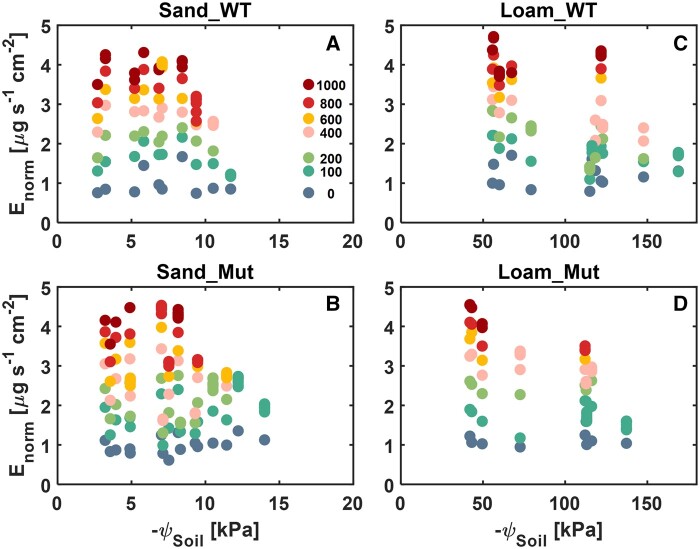
Given the slight difference in leaf area between plants (Figure 3), E was normalized by leaf area, E_norm, for both genotypes and soils during soil drying (Figure 4). Overall, before ψ_Soil dropped around −10 kPa in sand and −100 kPa in loam, both genotypes reached a similar level of E_norm (4.5 µg s⁻¹ cm⁻²) at the maximum light intensity. The maximum stable E_norm decreased as the soil dried and soil types showed a significant effect (P < 0.001) on E_norm (Supplemental Table S1), that is, E_norm decreased at less negative ψ_Soil and reduction of E_norm happened in a narrower range of ψ_Soil in sand (−6 to −15 kPa) than in loam (−60 to −180 kPa). Statistical significance was found neither in genotypes nor in the interaction between different factors for E_norm (P > 0.05; Supplemental Table S1). The impact of the individual factors and interactions between them on canopy conductance was similar to E_norm (Supplemental Figure S2; Supplemental Table S2).

Figure 4.

E _norm of WT and Mut grown in sand and loam at different light intensities (µmol m⁻² s⁻¹) during soil drying. A and B, sand and C and D, loam. The legend in (A) is for light intensity. More than two points of the same color at one ψ_Soil means that the applied pressure could not be sustained at that light intensity. The corresponding statistical analysis for the effect of different parameters on E_norm is shown in Supplemental Table S1.

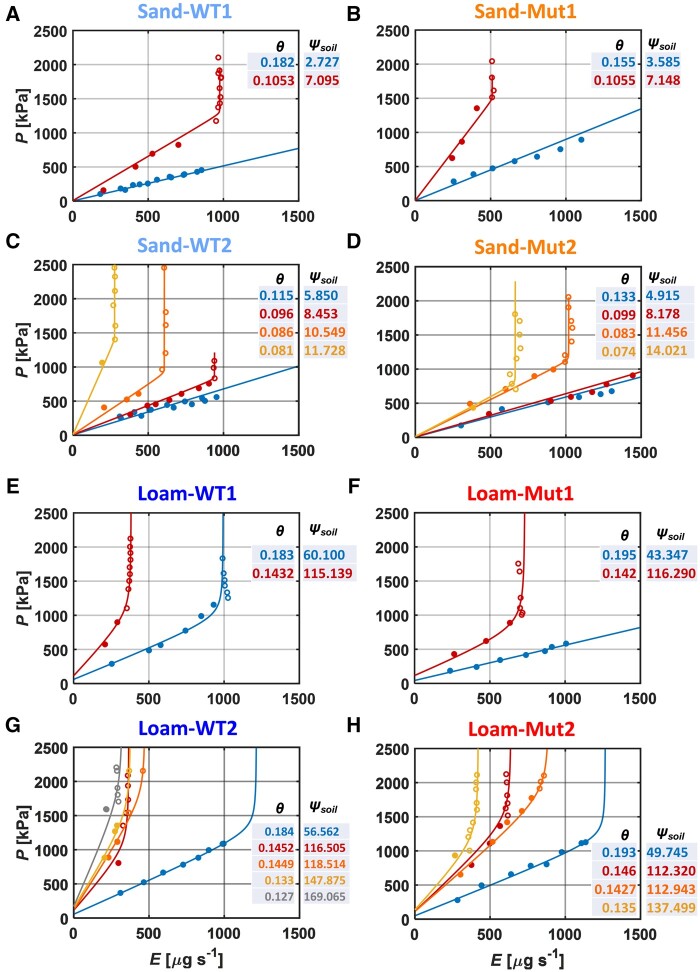
The P(E) relation of WT and Mut in sandy and loamy soils

The measured and simulated balancing pressure, P (−ψ_{leaf_x}), of WT and Mut for different E and water content is shown in Figure 5 (two replicates per genotype and soil type) and Supplemental Figure S3 (more replicates). The P(E) relations of WT and Mut in both soils were well described by the model (r² = 0.90). The slope of the P(E) relation, the reciprocal of root hydraulic conductance (K_root), increased as the soil dried in both soils (Figure 5). Detailed comparisons of K_root between genotypes and soil types were shown in the next section. In sand, P increased linearly with increasing E in both genotypes when soil water content was >0.11 cm³ cm⁻³ (ψ_Soil ≈ −10 kPa), and the P(E) relation became nonlinear with increasing E as the soil dried (Figure 5, A–D). In loam, the P(E) relation became nonlinear at soil water content around 0.18 cm³ cm⁻³ (ψ_Soil ≈ −100 kPa; Figure 5, E–H). In both soils, no differences were observed between WT and Mut in response to soil drying.

Figure 5.

Relation between balancing pressure (P, −ψ_{leaf_x}) and E in the WT and Mut plants grown in sand and loam during soil drying. A–D, sand and E–H, loam. Closed symbols are the measurements with steady-state balancing pressure, whereas open symbols are recorded pressure when no steady-state could be reached. The same color was used for the curves and corresponding soil water content (θ, cm³ cm⁻³) and ψ_Soil (kPa) (values next to the curves). The ψ_Soil was averaged from individual soil water content along the soil column. In both soils, the two genotypes were compared based on similar root length and water content. WT1 and WT2 are replicates and more replicates are shown in Supplemental Figure S3. Measurements were started in sand and P was measured more than once while keeping each level of light intensity (>0) half an hour longer for the highest soil water content, for example, blue points in (A) and (C). This was not carried out for the rest of the plants since more points at lower light intensities did not change the P(E) relation. Points distributed on the vertical part of P(E) curves were from one light intensity. Once the curve started bending, the decrease of meniscus was rapid and a fast response of “balancing pressure” was required. The time resolution of the points was 30–50 min before curve bending, whereas it was 1–5 min after bending.

Soil and root hydraulic conductance

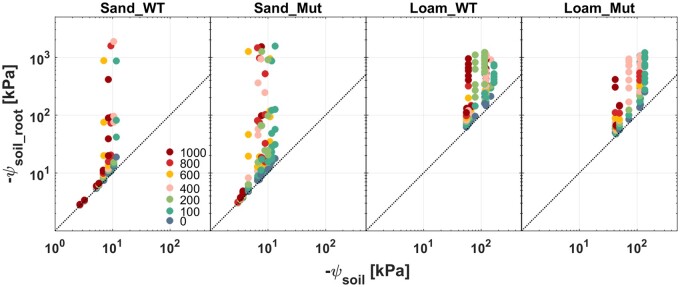
We used the soil–plant hydraulic model to reproduce the P(E) measurements and inferred the matric ψ_{soil_root} during soil drying (Figure 6). In both soils, ψ_{soil_root} was close to ψ_Soil at high matric potentials and asymptotically deviated from it at more negative matric potentials. As expected, ψ_{soil_root} deviated from ψ_Soil at higher matric potentials in sand, due to the steep slope of its hydraulic conductivity (Figure 2), which was in agreement with the findings of Dodd et al. (2010). The decline in matric ψ_{soil_root} was larger in sand (−10 to −2,000 kPa) than in loam (−200 to −1,100 kPa). No clear difference was visible between genotypes (Supplemental Figure S4).

Figure 6.

Relation between ψ_{soil_root} and ψ_Soil for the WT and Mut grown in sand and loam. ψ_{soil_root} was obtained from simulations using the soil–plant hydraulic model (Supplemental Method S1). The points correspond with the P(E) curves, which are shown in Figure 5 and Supplemental Figure S3. Matric potential with increasing E is presented by the color of light intensity steps from blue-green to red (the legend in the first subplot; unit: µmol m⁻² s⁻¹).

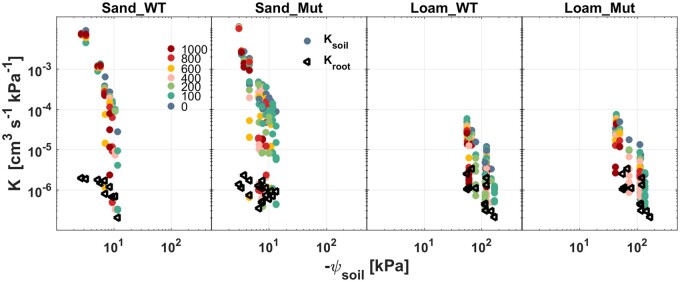
Figure 7 shows the comparison between soil conductance (K_soil) and K_root in drying soil. K_root was estimated by inverse modeling of the P(E) curve and its value was approximately equal to the P(E) slope at low Es. K_soil was calculated assuming that the hydraulic conductance of the soil–plant continuum till the leaf xylem is K_sp = (1/K_root + 1/K_soil)⁻¹, where K_sp is equal to E/(ψ_Soil – ψ_{leaf_x}) and its components were defined in Equations (5–9). In sand, K_soil was more than two orders of magnitude higher than in loam in wet conditions, but it declined more markedly than in loam during soil drying. In wet conditions, K_root was similar (around 2 × 10⁻⁶ cm³ s⁻¹ kPa⁻¹) in both genotypes and soils. K_root decreased earlier in sand (ψ_Soil ≈ −10 kPa) than in loam (ψ_Soil ≈ −100 kPa), but the decrease was not as steep as that in loam (Figure 8a). In both soils, the decline in K_soil and K_root was similar in both genotypes during soil drying (Supplemental Figure S4). Note that K_soil approached and even crossed K_root after the relation P(E) became nonlinear (Figure 5).

Figure 7.

Variation of K_soil and K_root of WT and Mut with increasing Es during soil drying. E is represented by the color of light intensity steps from blue-green to red (the legend in the first subplot; unit: µmol m⁻² s⁻¹). Note that these data were from Figures 5 and 6; Supplemental figure S3.

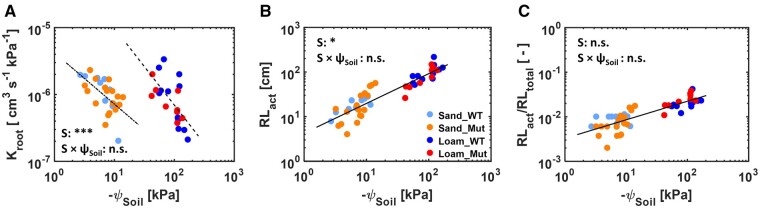
Figure 8.

Comparison of K_root, RL_act, and ratio of RL_act to RL_total between the WT and Mut for different ψ_Soils. A–C, Relation between K_root and ψ_Soil, RL_act and ψ_Soil, and RL_act/RL_total and ψ_Soil, respectively. Significant difference of the regression slopes between the genotypes and soil types was conducted using analysis of covariance and one regression slope was justified for WT and Mut or all plants in sand and loam (B and C). The detailed information of the statistical analysis is shown in Supplemental Table S3.

Parameters of the soil–plant hydraulic model

The P(E) measurements were fitted with the hydraulic model. The estimated parameters were K_root (discussed above) and active root length (RL_act; root length active in water uptake that gives the best fit of the P(E) measurements). A shorter RL_act would cause earlier and steeper nonlinearities in P(E), which was expected to be the case in the Mut. RL_act has to be interpreted as a measure of the nonlinearity in P(E). Both variables were allowed to vary as a function of ψ_Soil (Figure 8B). RL_act increased with soil drying and it was greater in loam. No significant difference in K_root and RL_act was found between WT and Mut in both soils (Supplemental Table S3). We generated the root length at the time of the P(E) measurement using the measured total root length (RL_total; Figure 3) and a root growth function (Pagès et al., 2004). The ratio of RL_act to RL_total, considering variations in root length, showed that the ratio increased during soil drying, with a larger ratio in loam (Figure 8C). Taken together, the soil hydraulic properties had a significant effect on K_root and RL_act (P < 0.001), but no difference (P > 0.05) was found between the two genotypes (Figure 8; Supplemental Table S3).

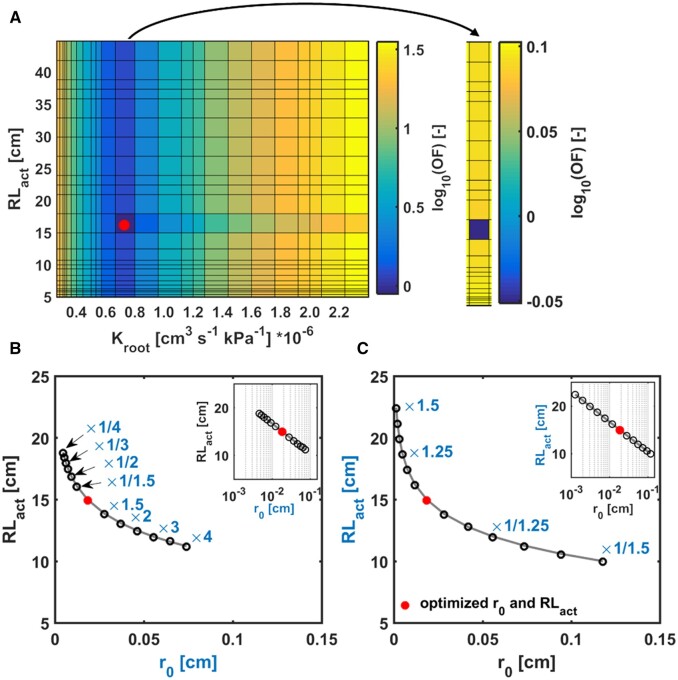
The sensitivity analysis showed that the model was sensitive to both K_root and RL_act (Figure 9A), indicating no correlation between them. The estimated global optimum indicated that these two parameters were identifiable.

Figure 9.

Parameter estimation and sensitivity analysis. A, Response surface for K_root and RL_act parameter plane of a WT grown in sand at the soil moisture of 0.105. OF, value of the objective function. Red dot, the optimum (best fit for the measurements of E and ψ_{leaf_x} relation with lowest OF) K_root and RL_act from the inverse modeling. The single plot and the adjusted color bar on the right in (A) were extracted from the main plot on the left. This is an example to show the global minimum in the defined range of K_root and RL_act. B, Sensitivity analysis for root radius (r₀) and (C) RL_act in the sandy soil. r₀ in (B) and RL_act in (C) were changed by a factor from 1/4 to 4 and 2/3 to 1.5, respectively. The insets were the same plots as (B) and (C) but with logarithm scale on the x-axis. The sensitivity analysis was performed by fixing one parameter to inversely estimate the other one during the simulation. B and C, These were conducted to illustrate the influences of the parameters on each other.

The measured root radius r₀ was larger (Figure 3) and the estimated RL_act was lower in sand (Figure 8). The sensitivity analysis showed that if r₀ decreased by two-fold, RL_act increased only by 1.1-fold (Figure 9B), which was not the case in Figure 8B. This indicated that the model was not simply compensating the smaller r₀ by increasing RL_act with a same factor. To evaluate how root surface-related parameters (r₀ and RL_act) affect each other, RL_act was changed by a factor from 2/3 to 1.5, and r₀ was inversely fitted. Figure 9C shows that if RL_act increased by 1.5-fold with a constant P(E) relation, r₀ had to be adjusted by one order of magnitude, indicating that the model was more sensitive to RL_act.

Further sensitivity analysis was performed to study how the P(E) relation was affected by RL_act with a constant K_root for different ψ_Soils in both soils. Supplemental Figure S5 shows that the P(E) relation was linear with RL_act from 5 to 20 cm in loam when ψ_Soil ranged from −3 to −6 kPa. In sand, however, the relation became nonlinear with RL_act of 9 cm at E around 3,000 µg s⁻¹ when ψ_Soil was −4 kPa. Furthermore, the drier the soil and the higher the E was, the longer the RL_act was needed in sand. This was the same in loam, but at more negative ψ_Soil and with higher RL_act.

Discussion

Difference in the P(E) relation during soil drying

The slope of the P(E) relation describes the ease of water flow in the soil–plant system. In wet conditions, when the k_s was high and the soil was expected not to limit the water flow, K_root did not differ between WT and Mut (2 × 10⁻⁶ cm³ s⁻¹ kPa⁻¹) in both soils. The lack of difference in K_root was in line with the recent study on barley (Dodd and Diatloff, 2016). The value of K_root in the two maize genotypes was approximately equal to that of pearl millet (Pennisetum glaucum;  Cai et al., 2020a), in the same order of magnitude of lupin (Lupinus albus; Hayat et al., 2019), and more than one order of magnitude larger than that of barley (Carminati et al., 2017) and wheat (Triticum aestivum; Passioura, 1980), from which plants had similar ages and no water stress.

As the soil dried, the slope of P(E) curves deviated from the linear relation. This deviation from linearity occurred at different water contents and matric potentials in the two soils (Figure 5). The P(E) curves bent at higher water content and more negative ψ_Soils in loam, which was expected based on their soil water retention curves (Figure 2). This is not surprising as the loamy soil had a higher conductivity at the same matric potential (Figure 2). However, this was not the only cause, as the nonlinearity appeared when sand was as conductive as loam (compare the points in Figure 2B). The bending at higher E was less abrupt in loam than in sand (Figure 5), which could be explained by less abrupt reduction of k_s for a given loss in matric ψ_{soil_root} (Carminati et al., 2017; Figures 2B and 6 ).

The drier the soil, the larger the deviation became in the P(E) curves (Figure 5). This could be explained by averaging the soil water content measurements over depth and, in dry soil, the variation of ψ_Soil. Water was not homogeneously distributed (Supplemental Figure S1), and averaging might have introduced errors (Figure 2). In dry soil, a slight change in water content could drive a large drop in matric potential (Figure 2), which influenced the P(E) relation in both soils. Indeed, the P(E) curves differed even when the water content was the same. The two fitting parameters K_root and RL_act were fitted independently as a function of ψ_Soil. The genotypes showed a similar trend (Figure 8). Possibly, the difference between genotypes was hidden behind the variability of the samples, but this meant that the effect of hairs was not as large as in barley (Carminati et al., 2017), where the same number of replicates was used.

The intercept of the P(E) curve, which is the suction in the xylem at null transpiration, is supposed to be equal to −ψ_Soil. The values, however, could be lower (Cai et al., 2020a) or higher (Carminati et al., 2017) than −ψ_Soil due to the difference in osmotic potential between soil and xylem (Passioura, 1980). In this study, the intercept from the linear part of the P(E) curve verged on −ψ_Soil at low matric potentials (Figures 2 and 5), indicating no apparent osmotic difference, which is in line with the study with wheat in loam (Passioura and Munns, 1984).

No significant effect of RHs on soil–plant hydraulic conductance in maize

The P(E) relation of WT and Mut in both soils did not show a significant effect of RHs on soil–plant hydraulic conductance and water uptake even at high Es and in drying soils (Figures 5–8). We could not confirm the hypotheses that RHs decrease the drop in matric potential across the root–soil interface, sustaining transpiration in dry soils. We do not exclude that variations between samples, for instance in root length, might have affected the putative role of RHs. Despite these variations, Figures 6–8 show that all plants followed the same trend with no significant differences between genotypes. This contrasted with the recent study of Carminati et al. (2017), who used the same method showing that RHs facilitate transpiration in WT of barley during soil drying. On the other hand, Dodd and Diatloff (2016) investigated the same genotypes and observed no difference in water uptake between WT and Mut. They suggested that longer roots might be a compensating strategy of Mut. This, however, was not the case in our study. The root length was even shorter in Mut in both soils when comparing plants at a similar age.

Several reasons might explain the lack of differences between WT and Mut in maize. One possibility is the shrinkage of RHs during soil drying. Keyes et al. (2017) imaged RHs of rice during soil drying using high-resolution synchrotron X-ray computed tomography. Although the authors did not quantify the shrinkage of RHs, the reduction in the diameter of RHs during soil drying was visible in their images. Zahran and Sprent (1986) showed that RHs of faba bean (Vicia faba) grown in sandy soil shrank as a consequence of salt stress. Flaccid RHs might have lower capacity to hydraulically connect the root surface to the soil. It is not clear yet at which ψ_Soil RHs started to shrink and to what extent their hydraulic function was compromised. Additionally, the lifespan of RHs could be another constraint to their role in water uptake. It was assumed that they were only active for several days (Gahoonia and Nielsen, 1998; Jungk, 2001), during which RHs might curve and twist (Li et al., 2016) and water stress shortened their lifespan (Xiao et al., 2020).

A second possibility is the length of RHs. Zhu et al. (2010) compared different maize genotypes with varying RH length in relation to the phosphorus uptake. Their results indicated that longer RHs enhanced phosphorus uptake efficiency. This was in line with a study on phosphorus uptake in barley (Gahoonia and Nielsen, 2004). Studies comparing the impact of different RH lengths in water uptake are still lacking. A recent field study with barley showed less negative minimum ψ_{leaf_x} in WT than Mut with short RHs, whose hair lengths were 0.6 and 0.1 mm, respectively (Marin et al., 2020). Note that ψ_{leaf_x} is E dependent and variations in E were not considered in the latter study. The hair length of barley in which RHs were shown to enable high transpiration was 0.6–0.8 mm (Carminati et al., 2017) and 0.75 mm (Segal et al., 2008). They were about two times longer than the RHs of the maize WT in this study (0.25 ± 0.05 mm, measured using synchrotron CT (P. Duddek, M.A. Ahmed, unpublished data); the same was also reported by Burak et al. (2021)). The length of RHs in maize was very similar to the hairs of rice WT (0.28 mm, extracted from Figure 1b in Suzuki et al. (2003)). Note that, consistent with our finding, Suzuki et al. (2003) also found that RHs did not contribute to water uptake in rice under different soil moisture conditions.

The third possibility is that the soil used by Carminati et al. (2017) and Marin et al. (2020) contained a large fraction of aggregates and macropores, referred to as soil structure. RHs might be particularly efficient in increasing the contact between roots and soil aggregates and hence soften the gradients in water potential in dry conditions. Therefore, the reasons why we did not observe differences between WT and Mut might be caused by the different soils used in this study compared to the soils used for barley (Carminati et al., 2017; Marin et al., 2020).

Changes in soil–plant hydraulic parameters as the soil dried

Soil characteristics had a strong impact on soil–plant hydraulics (Figures 6–8). E decreased at less negative ψ_Soil and the P(E) curve deviated more abruptly from the linear relation, with a minor increase in E in sand than in loam (Figure 5;  Supplemental Figure S3). The differences in the P(E) curves between soils also appeared in the fitted model parameters, K_root and RL_act. K_root started to decrease when K_soil was still relatively high in sand (Figures 7 and 8). The decrease in K_root during soil drying could be explained by shrinkage of coarse roots (Rodriguez-Dominguez and Brodribb, 2020) or dehydration of the root cortex (Cuneo et al., 2021), changes in aquaporin activity (Rodríguez-Gamir et al., 2019), root suberization (Schreiber et al., 2005), or by the loss of contact at the root–soil interface (Carminati et al., 2009). From our experiments, we cannot distinguish between such potential mechanisms of K_root reduction. K_soil dropped by several orders of magnitude as the soil dried, then reached and became even lower than K_root at matric potential of −10 kPa and −100 kPa in sand and loam, respectively. Below these ψ_Soil plants could not sustain high Es (Figures 4–7). These matric potentials were relatively high and could be fitted only by imposing a small RL_act.

In maize, it was shown that not all roots were active in water uptake (Ahmed et al., 2016, 2018). Estimations of the fraction of the root length functioning in water uptake ranged from 4% to 30% (Passioura, 1980; Carminati et al., 2017; Cai et al., 2020a). In this study, this fraction was even lower, being 1–2% (Figure 8), which was similar to Hayat et al. (2020). Note that these fractions are simulation results, and their validity depends on the model assumptions and should be taken with caution. Indeed, in the simulations, we assumed a uniform water uptake and ψ_Soil along the root. Another assumption is that the soil close to root has the same properties of the bulk soil, which might not be the case either since roots could modify the soil properties (Carminati et al., 2010). More sophisticated models, such as R-SWMS (a three-dimensional numerical water flow model in soil and roots; Javaux et al., 2008), that consider root hydraulic architecture, dynamic hydraulic properties, and nonuniform ψ_Soil may better estimate such ratios. However, those models also depend on the accuracy of root hydraulic parameters (radial and axial conductivities along the root system) that are not easily measurable, especially for roots growing in soil. Observations in maize showed that roots could be immature for 20–30 cm from the root tip and they were not active in water uptake (Wang et al., 1991; Varney and Canny, 1993). Similar findings in maize were reported using heavy water and neutron radiography (Ahmed et al., 2016). This probably explains such small ratios in maize.

The RL_act varied between the two soils (Figure 8). The small RL_act in sand might have been affected by the heterogeneous soil water distribution (Supplemental Figure S1). The soil was relatively dryer in the upper layer at the start of measurements even though the average soil moisture was around 0.18 (Supplemental Figure S1). The roots in the upper soil layers might have decreased their radial conductivity (North and Nobel, 1996; Gullo et al., 1998) and hence the capacity to extract water from the soil (Martre et al., 2001), which would appear as a reduced RL_act.

The fact that RL_act increased during soil drying could be explained using a simple architecture model (Couvreur et al., 2012). The model was composed of two soil layers and two root xylem nodes (Supplemental Figure S6). We assumed that matric ψ_{soil_root} and in the soil was uniform. We also assumed that the conductance in root xylem (K_{root_xylem}) and at the soil–root interface (K_{root_soil}) in the two layers were constant for each moisture condition. The water uptake from the two layers was: Q1 = K_{root_soil}(ψ_Soil − ψ_{soil_root}) and Q2 = (1/K_{root_xylem} + 1/K_{root_soil})⁻¹(ψ_Soil − ψ_{soil_root}). In wet conditions, root xylem was the main constraint and water uptake mainly happened in the upper layer (Q1 ≫ Q2), thus only a part of the roots was active in water uptake. In dry conditions, K_{root_soil} decreased markedly, for example, K_{root_xylem} ≫ K_{root_soil}, and Q1 ≈ Q2. Thus, roots in both layers were active in water uptake, and the total RL_act increased consequently.

Conclusions

We investigated the effect of RHs and soil characteristics on the relation between E and ψ_{leaf_x}. Contrary to previous observations with barley, we did not see a significant effect of RHs on water uptake and soil–plant hydraulic conductance in both sandy and loamy soils. The variations of soil–plant hydraulic conductance and root length indicated the response of plants to soil conditions, including the water limitation and the soil texture difference. Regulating the RL_act is one of the crucial plant adjustments, but how it changes spatiotemporally in varying water conditions needs further investigations. Our results also suggested that the role of RHs in water uptake is complex and species and soil specific. A holistic understanding of the role of RHs in water uptake would require detailed studies on RH length, density, turnover, and response to decreasing ψ_Soil, in different plant species, soil types, and climates.

Materials and methods

Plant and soil

Maize (Zea mays) seeds of the two genotypes, Mut (rth3) and its counterpart WT (Hochholdinger et al., 2008), were sterilized using 10% H₂O₂ (v/v) and saturated CaSO₄ solution. They were then sown in polyvinyl chloride columns, with a height of 22 cm and an inner diameter of 7 cm. The bottom of the column was covered with a nylon mesh (mesh size, 30 µm). The difference in RHs between the two genotypes is shown in Supplemental Figure S7. The columns were filled with 1.30 kg of sandy soil and 1.12 kg of loamy soil using a 1-mm sieve as described by Vetterlein et al. (2020). Fertilizers were mixed with soil before filling and the detailed information is listed in Supplemental Table S4. The components of sand, silt, and clay were 88.6%, 8.1%, 3.3%, and 33.2%, 47.7%, 19.1% in sandy and loamy soils, respectively (Vetterlein et al., 2020). Volumetric soil water content during growth was kept around 0.18 and 0.22 (cm³ cm⁻³) for the sandy and loamy soils, respectively. Columns were topped with aluminum disks (diameter = 21 cm, thickness = 0.8 cm), at which center a hole of 1.4 cm in diameter was located for seeding. The soil water content was measured in three holes (diameter = 0.5 mm, interval = 6 cm) distributed on the column walls using a time-domain reflectometry meter (E-Test, Lublin, Poland). The hydraulic properties of the two soils were reported by Vetterlein et al. (2020; Figure 2).

Plants were grown at day/night temperatures of 22/18°C and constant relative humidity of 65% for three weeks (adventitious roots were initiated). The photoperiod was 12 h with a light intensity of 350 µmol m⁻² s⁻¹. Plants were flushed at the seed position with low pressure (ca. 2 bar) compressed air for 10 s to dry plant collar and soil interface. Subsequently, plants were sealed with a layer of silicon-rubber glue (TACOSIL 171 with 3% (w/w) cross-linker Vernetzer 28, Thauer & Co. KG, Germany) and a layer of rigid glue (UHU plus Endfest 300, Bühl, Germany). Plants were placed in a dark place before and after measurements. Leaf area was determined before and after each measurement by multiplying the individual length and width of the leaves with a factor of 0.7 (van Oosterom et al., 2001). Root length and diameter of each plant were measured using WinRhizo Pro version 2017 (Regent Instruments Inc., Quebec, Canada) and the corresponding scanner (Epson STD 4800) after root washing.

Measurements of ψ_{leaf_x} and E

A root pressure chamber system was used to measure the E(ψ_{leaf_x}) relation (Cai et al., 2020a). Construction and calibration of the root pressure chamber system were described by Cai et al. (2020b). The measurements started with sealing the column, including the roots and soil, in the pressure chamber and placing the shoot in the cuvette. E was altered by regulating the light-emitting diode lights around the cuvette. Light intensity was stepwise increased from 0 µmol m⁻² s⁻¹ to 100, 200, 400, 600, 800, and 1,000 µmol m⁻² s⁻¹. A fan installed above the shoot was used to stir the air passing through the cuvette. The relative humidity and temperature from the inlet and outlet of the cuvette were measured every 10 s, which allows calculating the atmospheric vapor pressure deficit (VPD, kPa). VPD in the cuvette ranged from 1 to 2 kPa. E was determined ultimately by multiplying the flow rate of the ingoing air with the difference between the outgoing and ingoing humidity (Cai et al., 2020a). The canopy stomatal conductance (Gc, mol m⁻² s⁻¹) was calculated according to Jarvis and McNaughton (1986):

$$Gc=\left(E/\text{LA}\right)/\left(\text{VPD}/P_{\text{atm}}\right)$$ (1)

where LA is the leaf area (cm²) and P_atm is the atmospheric pressure (kPa).

Before turning on the light, we pressurized the soil and roots to bring a droplet on a leaf incision. The incision was subsequently connected to a meniscus system, which is made of a fine capillary tubing (diameter = 0.5 mm) and a laser. A stable reading (fluctuation ±2 mm or less) of the meniscus for at least 10 min indicated that the pressure applied to the plant xylem was equal to the tension in the xylem that had not been pressurized (Passioura, 1980). The pressure is referred to as balancing pressure, P, and is equal to the suction in leaf xylem, that is, −ψ_{leaf_x}. Note that by doing so we are neglecting the effect of osmotic potential; more precisely, we are assuming that the osmotic potential in xylem and soil is equal. A difference in osmotic potential between xylem and soil creates an offset of the P(E) curves, which are shifted along the P-axis by this offset (Munns and Passioura, 1984; Cai et al., 2020a; Abdalla et al., 2021). P was determined for each step of light intensity. Each light step lasted 30–60 min and each plant was measured for around 1 week during which the soil was let dry. The drier the soil was, the higher the pressure was needed. P could not be determined for higher light intensities in drier soils since the upper limit of the system was 2.5 MPa. Given the slight difference in soil moisture and whole duration of the measurement between all the plants, comparisons of different parameters between WT and Mut were performed by grouping plants with similar RL_total and soil moisture.

Soil–plant hydraulic model

A simplified soil–plant hydraulic model, based on the Gardner’ single root model (Gardner, 1960) and a hydraulic architecture model (Couvreur et al., 2012), was used to simulate the gradients in water potential across the soil–plant continuum. The aim was to reproduce the diurnal changes in ψ_{leaf_x} for varying Es for given soil moisture distributions considering gradients in matric potential around the roots. During the measurements (which took 5–6 h), the changes in ψ_Soil in the vertical directions were negligible compared to the radial gradients in matric potential toward the soil–root interface, which justifies using a radial model. Predicting the vertical distributions of water in the soil column during the drying periods (which took 1 – 2 weeks) would have requested a different modeling approach, which was not the objective of this study. More details of this model were described in Hayat et al. (2019), Cai et al. (2020a), Carminati and Javaux (2020), and Supplemental Method S1. We briefly describe the model: (1) all the roots of a plant are represented by a single root active in water uptake and (2) water flows in series through the soil, the root system, and the xylem vessels up to leaf xylem, according to a series of equations (shown below) equating the fluxes to water potential gradients times the hydraulic conductivity of the specific element. The water potential is calculated in the soil (ψ_Soil), at the soil–root interface (ψ_{soil_root}), and in the leaf xylem (ψ_{leaf_x}).

The radial water flux from soil toward roots is described by:

$$q=-k_s\left({\psi }_{\text{Soil}}\right)\cdot \frac{\partial {\psi }_{\text{Soil}}}{\partial r}$$ (2)

where q is the water flux (cm s⁻¹), k_s is the unsaturated soil hydraulic conductivity (cm s⁻¹), ψ_Soil is the soil matric potential (kPa, 1 kPa ≈ 10 cm), r is the radial distance (cm). k_s is parameterized according to the Brooks and Corey model:

$$k_s(\psi )=k_{\text{sat}}\cdot {\left(\frac{{\psi }_{\text{Soil}}}{{\psi }_0}\right)}^{\tau }$$ (3)

where k_sat is the saturated soil hydraulic conductivity (cm s⁻¹), ψ₀ is the air entry point (kPa), τ is a fitting parameter (−). The parameters of the Brooks and Corey model were obtained by fitting the Mualem–van Genuchten model with the ψ_Soil ranging from −3 kPa to −1,000 kPa (Figure 2). The boundary conditions are no flow at the outer radius of the soil (r_b) and a uniform flux at the soil–root interface given by:

$$q\left(r_0\right)=\frac{E}{2\pi r_{0}R{L}_{\text{act}}}$$ (4)

where r₀ is the root radius (cm) and RL_act is the root length active in water uptake (cm). r_b is given by the volume of the column (V, cm³) and RL_act, according to (V/(π RL_act))^1/2. E is given by:

$$E=K_{\text{root}}\left({\psi }_{\text{soil}\_\text{root}}–{\psi }_{\text{xylem}\_\text{root}}\right)$$ (5)

where K_root is the root hydraulic conductance (cm³ s⁻¹ kPa⁻¹). ψ_{soil_root} and ψ_{xylem_root} are the matric potentials at the soil–root interface and root collar (kPa). Water flow in aboveground xylem is defined as:

$$E=K_x\left({\psi }_{\text{xylem}\_\text{root}}–\hspace{0.17em}{\psi }_{\text{leaf}\_x}\right)$$ (6)

where K_x is the xylem conductance of the shoot (cm³ s⁻¹ kPa⁻¹). The detailed derivation of ψ_{soil_root}, ψ_{root_xylem}, ψ_{leaf_x}, and K_x is described in Supplemental Method S1.

As in our measurements, the shoot was maintained turgid throughout the measurements, we assume that no cavitation occurred and that K_x ≫ K_root (see parameterization of K_x in Supplemental Method S1). As the plant hydraulic conductance K_plant is the harmonic mean of K_x and K_root, it follows that K_plant is approximately equal to K_root. Note that this was proven for tomato (Solanum lycopersicum; Abdalla et al., 2021).

In analogy, we calculate the total soil–plant hydraulic conductance till the leaf xylem as:

$$K_{\text{sp}}=E/\left({\psi }_{\text{Soil}}–{\psi }_{\text{leaf}\_x}\right)$$ (7)

Note that based on these definitions,

$$1/K_{\text{sp}}=1/K_{\text{soil}}+1/K_{\text{root}}+1/K_x\approx 1/K_{\text{soil}}+1/K_{\text{root}}$$ (8)

Therefore, K_soil (cm³ s⁻¹ kPa⁻¹), is calculated as:

$${\mathrm{K}}_{\text{soil}}=\frac{E}{{\psi }_{\text{Soil}}-{\psi }_{\text{Soil}\_\text{root}}}$$ (9)

Comparing K_soil and K_root indicates whether water flow is limited more by soil or root as soil dries.

Applying the simplified soil–plant hydraulic model and adjusting the unknown parameters K_root and RL_act, we inversely fit the measurements. The inverse modeling was conducted by systematically minimizing the deviations between the measured and simulated ψ_{leaf_x} for each level of E. Considering the high resolution (0.1 bar, 10 kPa; Cai et al., 2020b) and upper limit (25 bar) of the pressure chamber, an objective function (OF) that is sensitive to trivial variations of applied pressure is defined below:

$$\text{OF}={\left({{\sum }_i^n\left(\frac{{({\psi }_{\text{leaf}\_x\_\text{meas}\_i}-{\psi }_{\text{leaf}\_x\_\text{sim}\_i})}^2}{{({\psi }_{\text{leaf}\_x\_\text{meas}\_i})}^2}+\frac{{({\psi }_{\text{leaf}\_x\_\text{meas}\_i}-{\psi }_{\text{leaf}\_x\_\text{sim}\_i})}^2}{{({\psi }_{\text{leaf}\_x\_\text{sim}\_i})}^2}\right)}^2\right)}^{1/2}$$ (10)

where ψ_{leaf_x_meas} and ψ_{leaf_x_sim} are the measured and simulated ψ_{leaf_x}, i and n are the ith and total number of measurements, respectively. The inverse modeling was carried out for individual measurement, that is, P(E) relation for each soil water content, thus dynamic RL_act was considered given that the measurements of each plant lasted around 1 week. The optimization was evaluated by comparing the OFs from possible combinations of the two parameters (Cai et al., 2018a, 2018b). The boundary condition of K_root was K_root__j × 0.1 and ×10, where K_root_ _j is the reciprocal of the linearly fitted P(E) slope at the highest soil water content of plant j, and of RL_act ranged from 1 cm to the measured root length (RL_{total_j}) of plant j. The initial condition of K_root and RL_act was K_root__j and RL_{total_j} × 0.1, respectively.

Sensitivity analysis of the root hydraulic resistance, RL_act, and root radius

We made a sensitivity analysis of the OF to K_root and RL_act to evaluate the uniqueness of the inverse solution. This shows the sensitivity and the correlation between the two parameters and whether they are locally or globally optimized. The product of 2πr₀ by RL_act is directly relevant to the root surface that is active in water uptake. For a constant root surface, the change of one parameter is dependent on the variation of the other. Thus, we conducted a sensitivity analysis to evaluate the effect of variation of r₀ on estimated RL_act and sensitivity of r₀ to variation of RL_act and hence illustrate their influence on each other. RL_act indicates the ability of water uptake for a root with specific hydraulic conductance. To appraise the effect of RL_act on E, a series of RL_act was used to test its sensitivity for different soil moisture conditions in the two soils.

Statistical analysis

Statistical analysis was performed using MATLAB (MathWorks Inc., Natick, MA, USA). Significance of the effect of different factors on plant growth, E, and canopy conductance was determined using analysis of variance. A mixed model was set up for the effect of all factors on E and canopy conductance. Soil texture, genotype, soil moisture, and light intensity were fixed factors while the replication of plants was a random factor. Analysis of covariance was performed to evaluate the difference in regression slopes of relation between different parameters from WT and Mut plants grown in both soils. Statistical significance was considered when the P-value was ˂0.05.

Accession numbers

Sequence data from this article can be found in the GenBank/EMBL data libraries under the accession number AY265855.

Supplemental data

The following materials are available in the online version of this article.

Supplemental Figure S1 Example of soil water content (θ) distribution at three locations along the soil column for a WT and Mut before and after the root pressure chamber measurements.

Supplemental Figure S2 Gc of WT and Mut in sand and loam at different light intensities (µmol m⁻² s⁻¹) during soil drying.

Supplemental Figure S3 Relation between balancing pressure (P, −ψ_{leaf_x}) and E in WT and Mut in sand and loam during soil drying.

Supplemental Figure S4 Comparison between matric ψ_{soil_root} and ψ_Soil and comparison between K_soil and K_root for the WT and Mut grown in sand and loam.

Supplemental Figure S5 Sensitivity analysis of RL_act on ψ_{leaf_x} for different ψ_Soil in sand and loam.

Supplemental Figure S6 Scheme of the simple root hydraulic architecture model of water uptake.

Supplemental Figure S7 Images of WT and Mut roots from plants grown in sand.

Supplemental Table S1 Analysis of variance (ANOVA) considering three-way interaction for the influence of different factors on E_norm

Supplemental Table S2 ANOVA considering three-way interaction for the influence of different factors on Gc.

Supplemental Table S3. Analysis of covariance (ANCOVA) for the regression slopes of the relation between soil (ψ_Soil) and root hydraulic (K_root and RL_act) parameters for genotypes and soil types.

Supplemental Table S4 Fertilizer applied to the sandy and loamy soils

Supplemental Method S1. Extended description of the soil–plant hydraulic model.

 

M.A.A. and A.C. acquired the funding; A.C., M.A.A., M.A., and G.C. designed the study; G.C. performed the experiments and analyzed the data; A.C. and G.C. made the simulations; G.C. wrote the text with input from A.C., M.A.A., and M.A. All authors contributed to editing and revising the manuscript.

The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (https://academic.oup.com/plphys/pages/general-instructions) is: Mutez Ali Ahmed (mutez.ahmed@uni-bayreuth.de).