CHARMM-GUI Free Energy Calculator for Practical Ligand Binding Free Energy Simulations with AMBER

Abstract

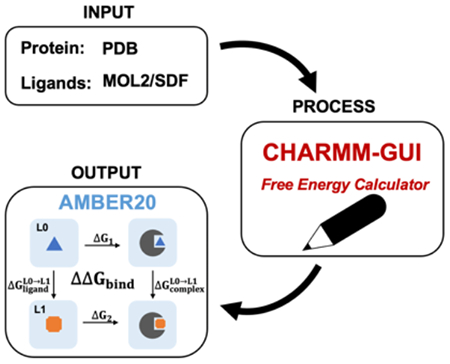
Alchemical free energy methods, such as free energy perturbation (FEP) and thermodynamic integration (TI), become increasingly popular and crucial for drug design and discovery. However, the system preparation of alchemical free energy simulation is an error-prone, time-consuming, and tedious process for a large number of ligands. To address this issue, we have recently presented CHARMM-GUI Free Energy Calculator that can provide input and post-processing scripts for NAMD and GENESIS FEP molecular dynamics systems. In this work, we extended three sub-modules of Free Energy Calculator to work with the full suite of GPU-accelerated alchemical free energy methods and tools in AMBER, including input and post-processing scripts. The BACE1 (β-secretase 1) benchmark set was used to validate the AMBER-TI simulation systems and scripts generated by Free Energy Calculator. The overall results of relatively large and diverse systems are almost equivalent with different protocols (unified and split) and with different timesteps (1 fs, 2 fs, and 4 fs), with R² > 0.9. More importantly, the average free energy differences between two protocols are small and reliable with 4 independent runs, with a mean unsigned error (MUE) below 0.4 kcal/mol. Running at least 4 independent runs for each pair with AMBER20 (and FF19SB/GAFF2.1/OPC force fields), we obtained a MUE of 0.99 kcal/mol and root-mean-square error of 1.31 kcal/mol for 58 alchemical transformations in comparison with experimental data. In addition, a set of ligands for T4-lysozyme was used to further validate our free energy calculation protocol whose results are close to experimental data (within 1 kcal/mol). In summary, Free Energy Calculator provides a user-friendly web-based tool to generate AMBER-TI system and input files for high-throughput binding free energy calculations with access to the full set of GPU-accelerated alchemical free energy, enhanced sampling, and analysis methods in AMBER.

Graphical Abstract

INTRODUCTION

Alchemical free energy calculations are widely used for computer-aided drug design and discovery.^1-8 Free energy perturbation (FEP) and thermodynamic integration (TI) are two most popular alchemical methods that show promising results with high accuracy for the absolute and relative binding free energy prediction. Both methods are implemented in various molecular dynamics (MD) simulation program packages, such as NAMD,^9-11 AMBER,^12-15 GROMACS,^{16, 17} CHARMM,¹⁸ and GENESIS.¹⁹

In particular, since the 1980s, AMBER has supported alchemical free energy simulation and has been used for drug design research for decades. AMBER supports both absolute and relative binding free energy calculations. Recently, relative binding free energy (ΔΔG_bind) calculation has drawn increasing attention, as it requires less computational resources than absolute binding free energy calculation.^{9, 20-22} These calculations have become practical with high performance implementation on graphical processing units (GPUs).^23-25 The advances in AMBER20 provide further improved reliability and simulation speed of protein-ligand ΔΔG_bind calculations.¹³

The system preparation of alchemical free energy simulation is an error-prone, time-consuming, and tedious process for a large number of ligands. Therefore, the implementation of user-friendly computational tools to automatize sophisticated system building and input generation is critical and essential for drug design and discovery research. CHARMM-GUI²⁶ (https://www.charmmgui.org) is a widely used web-based platform that provides a well-designed workflow to generate complex molecular simulation system and input scripts.^27-39 The Free Energy Calculator module includes four sub-modules (Absolute Ligand Solvator, Absolute Ligand Binder, Relative Ligand Solvator, and Relative Ligand Binder) to help researchers setup FEP/MD simulation systems and input scripts for CHARMM, NAMD, and GENESIS.^{39, 40} In this work, we present its extension to support AMBER GPU-accelerated alchemical free energy simulation system setup and input generation for Absolute Ligand Solvator, Relative Ligand Solvator, and Relative Ligand Binder. In particular, CHARMM-GUI provides various AMBER force field (FF) combinations for researchers to choose based on their preference and need. In addition, Free Energy Calculator supports hydrogen mass repartitioning (HMR) as an option to increase a timestep to 4 fs for accelerated AMBER-TI simulations.^{41, 42}

This study aims to illustrate how Free Energy Calculator can be used for practical ligand binding AMBER-TI simulations with AMBER20. For this, we performed AMBER-TI simulations for the BACE1 (β-secretase 1) benchmark set using different timesteps (1 fs, 2 fs, and 4 fs) and protocols (unified and split).^{13, 43} In the split (or stepwise or multi-step) protocol, there are “decharge-vdW-recharge” three steps in which coulombic electrostatic and van der Waals (vdW) interactions are scaled separately. For the unified (or concerted or one-step) protocol, both electrostatic and vdW interactions are scaled concurrently by the softcore potentials.⁴⁴ Our results indicate that running multiple (at least 4) independent runs is crucial and essential to get reasonable, stable, and reliable free energy results regardless of timesteps. In addition, with 4 independent runs, both unified and split protocols yield almost equivalent results. Therefore, one could obtain reliable ΔΔG_bind by performing at least 4 AMBER-TI runs using the unified protocol and 4-fs timestep with HMR.

METHODS

Amber-TI system and input generation in Free Energy Calculator

Free Energy Calculator consists of four sub-modules and designed to support various ligand solvation and binding free energy calculations: Absolute Ligand Solvator (ALS), Absolute Ligand Binder (ALB), Relative Ligand Solvator (RLS), and Relative Ligand Binder (RLB). The detailed workflow has been introduced in our recent work.³⁹ Here, we present an extension of ALS, RLS, and RLB sub-modules to support AMBER GPU-accelerated alchemical free energy simulation system and input generation. The overall workflow for AMBER system setup is the same as for NAMD and GENESIS FEP/MD setup, except for the FF selection part. Currently, AMBER-TI is only compatible with the AMBER FFs. As shown in Figure 1A, CHARMM-GUI supports various AMBER FFs: FF14SB⁴⁵ and FF19SB⁴⁶ for protein, general AMBER force field (GAFF)⁴⁷ and GAFF2.1⁴⁸ for ligand, and TIP3P,⁴⁹ TIP4PEW,⁵⁰ TIP4DP,⁵¹ and OPC⁵² for water; in this work, we do not discuss DNA, RNA, glycan, and lipid FFs, although they are supported. There are sixteen different FF combinations if we consider a protein-ligand complex system with the different water models, and researchers can choose any FF combination based on their preference and research need. Free energy Calculator checks if a given ligand set can be parameterized by GAFF or GAFF2.1 successfully, and the pair containing any ligand that is not supported by the selected ligand FF needs to be removed (Figure 1B). In addition, HMR is supported as an option to allow a simulation timestep of 4 fs (Figure 1A). We will present two systems in the main manuscript, but multiple challenging systems (Figure S1) were successfully prepared via Free Energy Calculator (see SI for more details).

Figure 1.

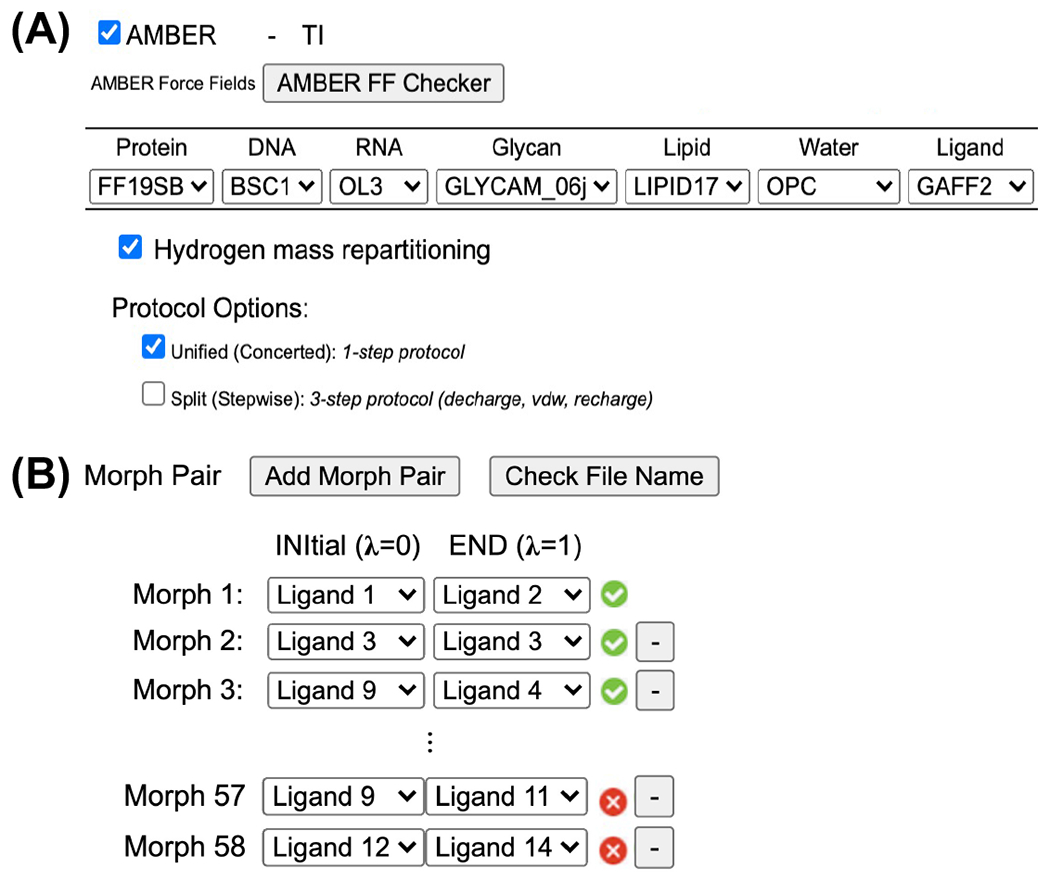
(A) AMBER FF selection in Free Energy Calculator. (B) Snapshot after clicking AMBER FF Checker and the pair containing any ligand that is not supported by the selected ligand FF is marked as an error flag in red.

System setup and protocols

BACE1 (PDB: 4DJW) was used to validate the generated AMBER-TI systems and inputs from Free Energy Calculator. As shown in Table S1, 36 ligands⁵³ were used to generate 58 pairs⁵⁴ in the BACE1 benchmark set. Based on the uploaded ligand structure files (MOL2 or SDF), Free Energy Calculator determines the common and unique atoms using a maximum common structure algorithm^{55, 56}. The common atoms of ligand 0 (L0) and ligand 1 (L1) have the same coordinates. In each alchemical transformation system, the unique atoms are in the softcore regions. The atoms in the softcore regions of L0 and L1 are defined as “scmask1” and “scmask2”, respectively. As shown in Figure S2, for example, the softcore regions of pair CAT-13a (“scmask1”) to CAT-17g (“scmask2”) are highlighted by red and blue dashed rectangles, respectively. Each pair system was generated with the unified protocol in which both electrostatic and vdW interactions are scaled concurrently by the softcore potentials. 15 pairs were randomly selected to compare the results from the unified protocol with those from the split protocol in which electrostatic and vdW interactions are scaled separately. In the split protocol, the atoms in the softcore region (i.e., the atoms that will be transformed into dummy atoms) are decharged first. Then, the decharged atoms go through the vdW transformation via the softcore potential. Finally, the atoms in the softcore region are recharged to the end state.

An accurate FF is crucial for reliable ΔΔG_bind prediction. FF19SB shows improved backbone profiles for all 20 amino acid residues and the OPC water model is recommended when it is used.⁴⁶ In this study, the protein, water, and ligands were modeled with the FF19SB, OPC, and GAFF2.1 FFs, respectively. All simulation systems were solvated in a cubic water box consisted of water molecules and neutralized by counterions (KCl).

A thermodynamic cycle for ΔΔG_bind calculation is shown in Figure S3. ΔΔG_bind between L0 and L1 ligands in the same target protein is calculated by

$$\Delta \Delta {\text{G}}_{\text{bind}}^{\text{L0}\to \text{L1}}=\Delta {\text{G}}_{\text{complex}}^{\text{L0}\to \text{L1}}-\Delta {\text{G}}_{\text{ligand}}^{\text{L0}\to \text{L1}}$$ (1)

where $\Delta {\text{G}}_{\text{complex}}^{\text{L0}\to \text{L1}}$ and $\Delta {\text{G}}_{\text{ligand}}^{\text{L0}\to \text{L1}}$ are the alchemical transformations of L0 to L1 in the complex and solution, respectively. The free energy difference between states L0 and L1 can be calculated as

$$\Delta {\text{G}}_{\text{complex/ligand}}^{\text{L0}\to \text{L1}}={{\int }_0^1\langle \frac{\partial \text{U(}\lambda \text{)}}{\partial \lambda }\rangle }_{\lambda }\text{d}\lambda$$ (2)

where U(λ) is the λ-coupled potential energy and λ is a coupling parameter varying from 0 (L0) to 1 (L1). The integration is calculated via the average of the λ derivative of the coupled potential energy at each intermediate λ state. The ΔG values are obtained by the sum of numerical integration over N (the number of λ windows) quadrature points with associated weights of ∂U/∂λ. In this work, 21 λ windows (λ value from 0 to 1 with Δλ = 0.05) were applied for each complex system and solution system. Long-range electrostatics in solution was treated with the particle mesh Ewald (PME) method and the vdW interactions were calculated with a cutoff distance of 10 Å.^{57, 58} The second-order smoothstep softcore potential, SSC(2), was applied in the simulation.¹³ The values of 0.2 and 50 Ų were used for the parameters α and β of the softcore potential, respectively. Equilibration was performed for 5 ps employing the NPT (constant particle number, pressure, and temperature) ensemble after minimization in each λ window. AMBER-TI simulations were performed in the NPT ensemble at 300 K and 1 atm (1.0135 bar) with the pmemd.cuda module of AMBER20. All 58 alchemical transformations were run with a 4-fs timestep with HMR using the unified protocol. The randomly selected 15 pairs were additionally run with a 1-fs timestep and a 2-fs timestep without HMR, and a 4-fs timestep with HMR using both the unified and split protocols. For each λ of all ΔΔG_bind calculations, 5-ns AMBER-TI simulations were performed and the last 4 ns of the simulations results were utilized for the final ΔΔG_bind values.

RESULTS AND DISCUSSION

Overall performance of three different timesteps

We randomly selected 15 pairs out of 58 pairs in the BACE1 benchmark set to run AMBER-TI simulations with both unified and split protocols and with 1-fs, 2-fs, and 4-fs timesteps. For 1-fs and 2-fs simulations, we ran 4 independent runs for each alchemical transformation. HMR was used for 4-fs timestep simulations and we ran 8 independent runs for each pair. Figure 2 shows the comparison of the ΔΔG_bind results using different timesteps within the unified and split protocols. All R² values between the systems with different timesteps are larger than 0.9, indicating consistent ΔΔG_bind prediction with different timesteps within the same protocol. Note that it is possible that one cannot perform AMBER-TI simulations with a 4-fs timestep and SHAKE. For instance, based on our experience, for the transformation having X-C-H and X-N atoms, when X-C and X-N atoms are defined as the common region and the H atom is defined as a softcore atom, a 4-fs timestep and SHAKE could be problematic. In such cases, one may need to use a 1-fs timestep without SHAKE to perform the AMBER-TI simulations.⁴³

Figure 2.

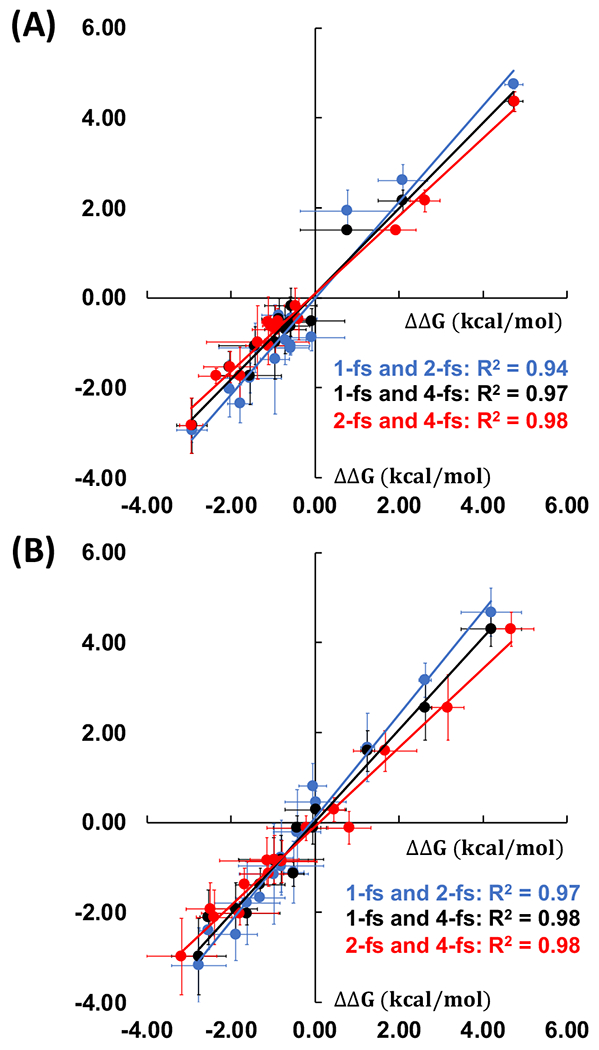
Comparison of 15 ΔΔG_bind values using different timesteps with the (A) unified and (B) split protocols. Comparisons between 1-fs and 2-fs timesteps, 1-fs and 4-fs timesteps, and 2-fs and 4-fs timesteps are shown by blue, black, and red dots with each least square fit line, respectively.

Overall performance of the unified and split protocols

To compare the results between two different protocols, for the randomly selected 15 pairs, we calculated the mean unsigned error (MUE) (|ΔΔG_unified – ΔΔG_split|) between the unified and split protocols as a function of number of independent runs. For 1-fs and 2-fs timestep simulations, 16, 36, 16, and 1 different cases need to be compared for 1, 2, 3, and 4 independent runs, respectively. Similarly, for 4-fs timestep simulations, 64, 784, 3136, 4900, 3136, 784, 64, and 1 different cases need to be compared for 1, 2, 3, 4, 5, 6, 7, and 8 independent runs, respectively. The box plots in Figures 3A-C display the distributions of data into quartiles for a given set of values and 75% of the values fall below the upper quartile. The median, middle quartile, marks the mid-point of the data and is shown by a line in the box. The middle box represents the middle 50% of the values for the group. Figures 3A and 3B show the MUE of ΔΔG_bind between the unified and split protocols for 1-fs and 2-fs simulations. Both 1-fs and 2-fs simulations show similar results and the ΔΔG_bind differences become smaller with more independent runs, with a MUE value below 0.45 kcal/mol with 4 independent runs. Figure 3C shows the comparison for the results of 4-fs simulations. The MUE between two protocols becomes converged after 4 independent runs with a MUE value below 0.40 kcal/mol. Even with more number of independent runs, the MUE value keeps almost unchanged, which is always between 0.35 and 0.40 kcal/mol after 4 independent runs. Our results indicate that multiple independent runs, at least 4, are required and necessary to get statistically consistent ΔΔG_bind from the unified and split protocols in AMBER-TI. In addition, Figure 3D shows high correlation of calculated ΔΔG_bind between the unified and split protocols for three different timesteps. The overall performance of the unified and split protocol is almost equivalent. Therefore, the unified protocol using 4-fs timestep with HMR is recommended for practical ΔΔG_bind prediction from the resource consumption perspective.

Figure 3.

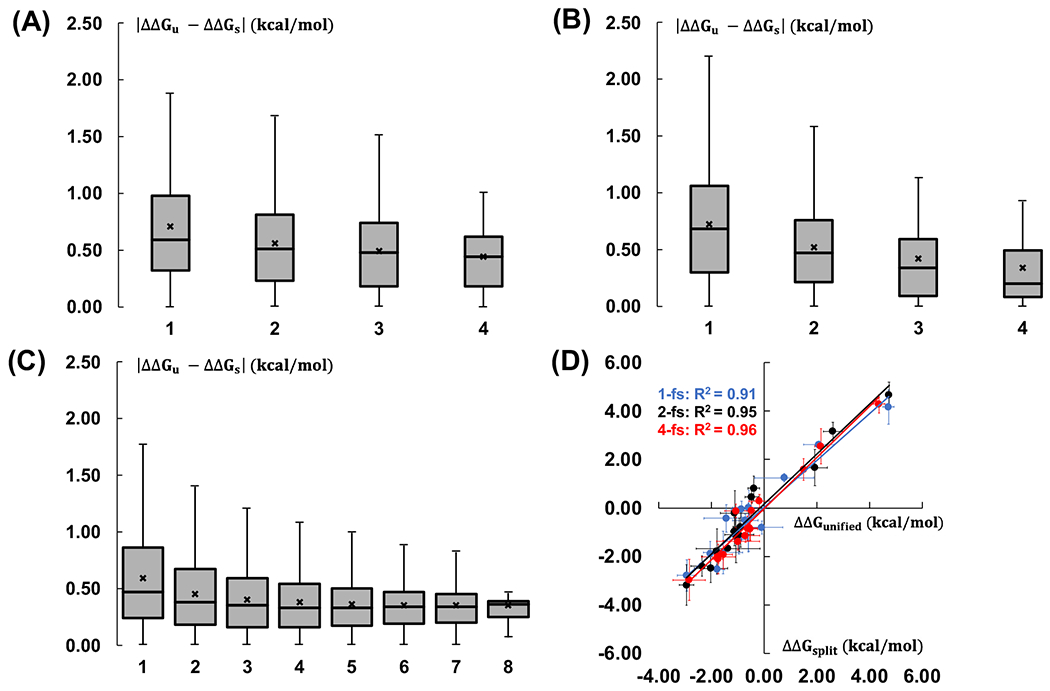
Mean unsigned energy differences between the unified and split protocols for the AMBER-TI simulations with (A) 1-fs, (B) 2-fs, and (C) 4-fs timesteps. The X-axis is the number of independent runs that are considered for the comparison. The x mark represents the average value of each comparison. All the outliers are not shown in the box and whisker plots. (D) Correlation between ΔΔG_bind from the unified and split protocols. ΔΔG_bind calculations with 1-fs, 2-fs, and 4-fs timesteps are in blue, black, and red, respectively.

Comparison between calculated and experimental ΔΔG_bind

We ran AMBER-TI simulations with 4 independent runs for the remaining 43 pairs out of 58 alchemical transformations in the BACE1 benchmark set with the unified protocol and 4-fs timestep. Figure 4A shows the comparison between experimental and our calculated ΔΔG_bind values for 58 pairs. The MUE and root-mean-square error (RMSE) of the ΔΔG_bind values compared to the experimental data are 0.99 and 1.39 kcal/mol, respectively (Table 1). We predicted the absolute binding free energy (ΔG_bind) for all 36 ligands in the BACE1 system by following the method described previously⁵⁴ and compared the results to experimental data (Figure 4B). The R² is 0.28 and three of 36 ligands deviate from their experimental free energies by more than 2 kcal/mol. The three ligands are CAT-17a, CAT-4d, and CAT-4l, and the deviations from ΔG_exp are 2.07, 2.21, and 2.44 kcal/mol, respectively. Overall, as shown in Table 1, our calculations show comparable results with a previous AMBER-TI study and both AMER-TI results are worse than the FEP+ results.

Figure 4.

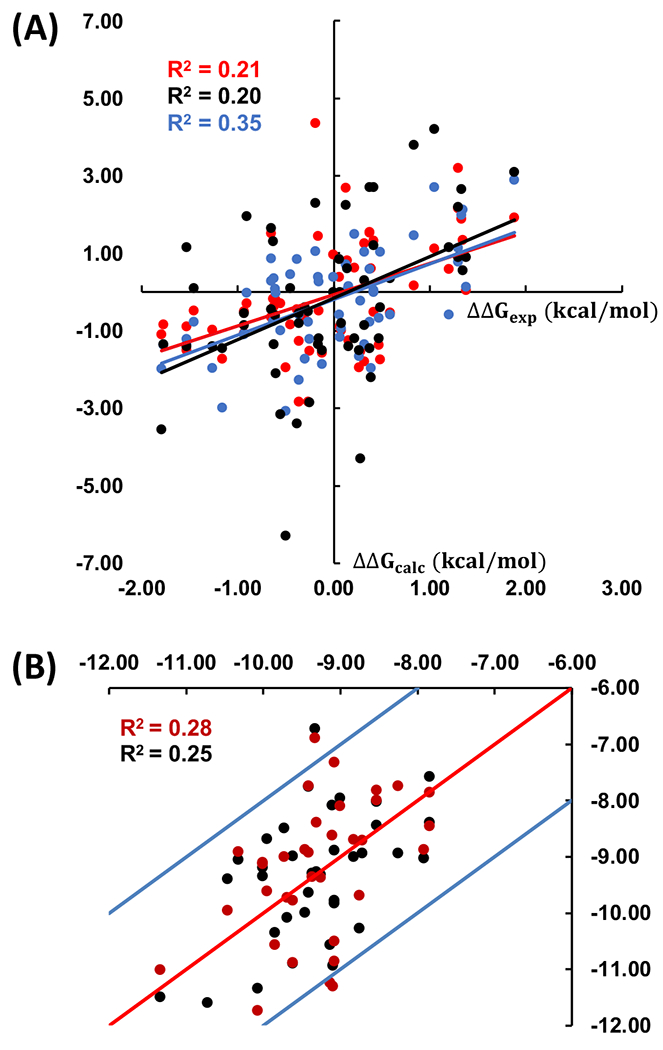
(A) Correlation between calculated ΔΔG_bind and experimental data for 58 pairs in the BACE1 benchmark set. The correlation for AMBER20, AMBER18¹⁴, and FEP+⁵⁴ are in red, black, and blue, respectively. (B) Correlation between predicated ΔG_bind and experimental results for 36 ligands in the BACE1 system for AMBER20 is in red, and the correlation between another predicated ΔG_bind (after the cycle closure convergence) and experimental results is in black. The X-axis and Y-axis are the experimental and predicated ΔG_bind (kcal/mol), respectively.

Table 1.

Statistics of ΔΔG_bind comparisons with the experimental data.

Force Field	R2	MUE (kcal/mol)	RMSE (kcal/mol)
FF-1a	0.21	0.99	1.31
FF-2b	0.20	1.33	1.79
FF-3c	0.35	0.87	1.05

^aAMBER-TI FF19SB + GAFF2.1 + OPC.

^bAMBER-TI FF14SB + GAFF1.8 + SPC/E.¹⁴

^cFEP+/OPLS 2.1 + Spc.⁵⁴

We implemented the cycle closure convergence strategy described previously⁵⁹ to get another predicated ΔΔG_bind. The R² between these predicted ΔG_bind and experimental data is not improved. However, as shown the black dots in Figure 4B, only one ligand deviates from their experimental free energies by more than 2 kcal/mol after the cycle closure convergence. The deviation from ΔG_exp of ligand CAT-17a and CAT-4d are improved to 0.88 kcal/mol and 1.84 kcal/mol, respectively, but the deviation of CAT-4l becomes 2.60 kcal/mol.

T4-lysozyme test systems

To further validate the systems generated by Relative Ligand Binder, we tested three different alchemical transformations in T4-lysozyme (Figure S4). Four AMBER-TI runs were performed for each pair and results are shown in Table 2. Calculated ΔΔG_bind of three alchemical transformations are comparable with the previous calculations based on NAMD and GENESIS, as well as the experimental data within 1 kcal/mol. The standard errors of predicated ΔΔG_bind are below 0.15 kcal/mol and are omitted in Table 2.

Table 2.

ΔΔG_bind results (kcal/mol) of three alchemical transformations in Figure S4A.

Ligand 0		Tolb
Ligand 1	Bzb	EBb	PBb
ΔΔGexp	0.33	−0.24	−1.03
ΔΔGNAMDa	−0.24	−0.66	−2.14
ΔΔGGENESISa	−0.10	−0.43	−1.57
$\Delta \Delta {\text{G}}_{\text{AMBER-TI}}^{\text{unified}}$	−0.27	−0.90	−1.68

^aΔΔG_bind results using NAMD and GENESIS are from Kim et al.³⁹

^bTol, Bz, EB, and PB are the abbreviations of toluene, benzene, ethylbenzene, and propylbenzene, respectively.

CONCLUSIONS

In this work, we have presented an extension of CHARMM-GUI Free Energy Calculator to support the full suite of GPU-accelerated alchemical free energy methods and tools in AMBER together with two benchmark testing sets. Such an extension provides a user-friendly web-based tool to generate AMBER-TI system and input files for practical throughput binding free energy calculations. The CHARMM-GUI interface allows users to select various options, including the use of HMR and the choice of protein, water, and ligand FFs.

BACE1 and T4-lysozome benchmark sets were used to validate the AMBER-TI systems and input scripts generated from Free Energy Calculator by calculating ΔΔG_bind with multiple independent runs. In particular, with randomly selected 15 pairs in the BACE1 benchmark set, our results show that the overall performance of the unified and split protocols is very similar regardless of the timesteps (1 fs, 2 fs, or 4 fs). In addition, our results indicate that multiple independent runs are required and necessary to calculate statistically reliable ΔΔG_bind using AMBER-TI. Based on our results, our recommendation is to perform at least 4 AMBER-TI runs using the unified protocol and 4-fs timestep with HMR for practical throughput ΔΔG_bind calculations. Additional independent runs might be required for more complicated protein-ligand systems. Therefore, users need to decide the number of independent runs for their own systems based on their understanding of the specific proteins.

The overall ΔΔG_bind values with FF19SB + GAFF2.1 + OPC FF combination in this study is slightly better than those with FF14SB + GAFF1.8 + SPC/E FF combination¹⁴ for the same set of ligands. This indicates that with the robust AMBER-TI calculations, better FFs would yield better predictions. In this context, our ongoing efforts are to check all AMBER FF combinations in ΔΔG_bind calculations and their dependence on the number of λ windows and simulation time.

Data and software availability

All the protein structures and molecular dynamics data are available upon request. Free Energy Calculator module can be accessed through the following link: https://www.charmmgui.org/input/fec.