ASYMPTOTIC DISTRIBUTIONS OF HIGH-DIMENSIONAL DISTANCE CORRELATION INFERENCE

Abstract

Distance correlation has become an increasingly popular tool for detecting the nonlinear dependence between a pair of potentially high-dimensional random vectors. Most existing works have explored its asymptotic distributions under the null hypothesis of independence between the two random vectors when only the sample size or the dimensionality diverges. Yet its asymptotic null distribution for the more realistic setting when both sample size and dimensionality diverge in the full range remains largely underdeveloped. In this paper, we fill such a gap and develop central limit theorems and associated rates of convergence for a rescaled test statistic based on the bias-corrected distance correlation in high dimensions under some mild regularity conditions and the null hypothesis. Our new theoretical results reveal an interesting phenomenon of blessing of dimensionality for high-dimensional distance correlation inference in the sense that the accuracy of normal approximation can increase with dimensionality. Moreover, we provide a general theory on the power analysis under the alternative hypothesis of dependence, and further justify the capability of the rescaled distance correlation in capturing the pure nonlinear dependency under moderately high dimensionality for a certain type of alternative hypothesis. The theoretical results and finite-sample performance of the rescaled statistic are illustrated with several simulation examples and a blockchain application.

1. Introduction.

In many big data applications nowadays, we are often interested in measuring the level of association between a pair of potentially high-dimensional random vectors giving rise to a pair of large random matrices. There exist a wide spectrum of both linear and nonlinear dependency measures. Examples include the Pearson correlation (Pearson, 1895), rank correlation coefficients (Kendall, 1938; Spearman, 1904), coefficients based on the cumulative distribution functions or density functions (Hoeffding, 1948; Blum, Kiefer and Rosenblatt, 1961; Rosenblatt, 1975), measures based on the characteristic functions (Feuerverger, 1993; Székely, Rizzo and Bakirov, 2007; Székely and Rizzo, 2009), the kernel-based dependence measure (Gretton et al., 2005), and sign covariances (Bergsma and Dassios, 2014; Weihs, Drton and Meinshausen, 2018). See also Shah and Peters (2020); Berrett et al. (2020) for some recent developments on determining the conditional dependency through the test of conditional independence. In particular, nonlinear dependency measures have been popularly used since independence can be fully characterized by zero measures. Indeed test of independence between two random vectors is of fundamental importance in these applications.

Among all the nonlinear dependency measures, distance correlation introduced in Székely, Rizzo and Bakirov (2007) has gained growing popularity in recent years due to several appealing features. First, zero distance correlation completely characterizes the independence between two random vectors. Second, the pair of random vectors can be of possibly different dimensions and possibly different data types such as a mix of continuous and discrete components. Third, this nonparametric approach enjoys computationally fast implementation. In particular, distance-based nonlinear dependency measures have been applied to many high-dimensional problems. Such examples include dimension reduction (Vepakomma, Tonde and Elgammal, 2018), independent component analysis (Matteson and Tsay, 2017), interaction detection (Kong et al., 2017), feature screening (Li, Zhong and Zhu, 2012; Shao and Zhang, 2014), and variable selection (Kong, Wang and Wahba, 2015; Shao and Zhang, 2014). See also the various extensions for testing the mutual independence (Yao, Zhang and Shao, 2018), testing the multivariate mutual dependence (Jin and Matteson, 2018; Chakraborty and Zhang, 2019), testing the conditional mean and quantile independence (Zhang, Yao and Shao, 2018), the partial distance correlation (Székely and Rizzo, 2014), the conditional distance correlation (Wang et al., 2015), measuring the nonlinear dependence in time series (Zhou, 2012; Davis et al., 2018), and measuring the dependency between two stochastic processes (Matsui, Mikosch and Samorodnitsky, 2017; Davis et al., 2018).

To exploit the distance correlation for nonparametric inference of test of independence between two random vectors $X\in {ℝ}^p$ and $Y\in {ℝ}^q$ with p, q ≥ 1, it is crucial to determine the significance threshold. Although the bootstrap or permutation methods can be used to obtain the empirical significance threshold, such approaches can be computationally expensive for large-scale data. Thus it is appealing to obtain its asymptotic distributions for easy practical use. There have been some recent developments along this line. For example, for the case of fixed dimensionality with independent X and Y, Székely, Rizzo and Bakirov (2007) showed that the standardized sample distance covariance by directly plugging in the empirical characteristic functions converges in distribution to a weighted sum of chi-square random variables as the sample size n tends to infinity. A bias-corrected version of the distance correlation was introduced later in Székely and Rizzo (2013, 2014) to address the bias issue in high dimensions. Huo and Székely (2016) proved that for fixed dimensionality and independent X and Y, the standardized unbiased sample distance covariance converges to a weighted sum of centralized chi-square random variables asymptotically. In contrast, Székely and Rizzo (2013) considered another scenario when the dimensionality diverges with sample size fixed and showed that for random vectors each with exchangeable components, the bias-corrected sample distance correlation converges to a suitable t-distribution. Recently Zhu et al. (2020) extended the result to more general assumptions and obtained the central limit theorem in the high-dimensional medium-sample-size setting.

Despite the aforementioned existing results, the asymptotic theory for sample distance correlation between X and Y under the null hypothesis of independence in general case of n, p and q diverging in an arbitrary fashion remains largely unexplored. As the first major contribution of the paper, we provide a more complete picture of the precise limiting distribution in such setting. In particular, under some mild regularity conditions and the independence of X and Y, we obtain central limit theorems for a rescaled test statistic based on the bias-corrected sample distance correlation in high dimensions (see Theorems 1 and 2). Moreover, we derive the explicit rates of convergence to the limiting distributions (see Theorems 3 and 4). To the best of our knowledge, the asymptotic theory built in Theorems 1–4 is new to the literature. Our theory requires no constraint on the relationship between sample size n and dimensionalities p and q. Our results show that the accuracy of normal approximation can increase with dimensionality, revealing an interesting phenomenon of blessing of dimensionality.

The second major contribution of our paper is to provide a general theory on the power analysis of the rescaled sample distance correlation. We show in Theorem 5 that as long as the population distance correlation and covariance do not decay too fast as sample size increases, the rescaled sample distance correlation diverges to infinity with asymptotic probability one, resulting in a test with asymtotic power one. We further consider in Theorem 6 a specific alternative hypothesis where X and Y have pure nonlinear dependency in the sense that their componentwise Pearson correlations are all zero, and show that the rescaled sample distance correlation achieves asymptotic power one when $p=q=o(\sqrt{n})$. This reveals an interesting message that in moderately high-dimensional setting, the rescaled sample distance correlation is capable of detecting pure nonlinear dependence with high power.

Among the existing literature, the most closely related paper to ours is the one by Zhu et al. (2020). Yet, our results are significantly different from theirs. For clarity we discuss the differences under the null and alternative hypotheses separately. Under the null hypothesis of X and Y being independent, our results differ from theirs in four important aspects: 1) Zhu et al. (2020) considered the scenario where sample size n grows at a slower rate compared to dimensionalities p and q, while our results make no assumption on the relationship between n and p, q; 2) Zhu et al. (2020) assumed that min{p, q} → ∞, whereas our theory relies on a more relaxed assumption of p + q → ∞; 3) there is no rate of convergence provided in the work of Zhu et al. (2020), while explicit rates of convergence are developed in our theory; 4) the proof in Zhu et al. (2020) is based on the componentwise analysis, whereas our technical proof is based on the joint analysis by treating the high-dimensional random vectors as a whole; See Table 1 in Section 3.4 for a summary of these key differences under the illustrative example of m-dependent components.

Table 1.

Comparison under the assumptions of Proposition 2

	Conditions for asymptotic mormality
	p → ∞, q → ∞	p → ∞, q fixed (similarly for p fixed, q → ∞)
Zhu et al. (2020)	$m_1^3/p\to 0$, $m_2^3/q\to 0$, $m_1/n^{1/4}\to 0$, $m_2/n^{1/4}\to 0$, $n\sqrt{m_1}{m}_2/\sqrt{q}\to 0,$ $n{m}_1\sqrt{m_2}/\sqrt{p}\to 0.$	No result
Our work	$m_1^3/p\to 0$, $m_2^3/q\to 0$, $m_1{m}_2/\sqrt{n}\to 0$.	$m_1^3/p\to 0$,$m_1/\sqrt{n}\to 0$.

The difference under the alternative hypothesis of dependence is even more interesting. Zhu et al. (2020) showed that under the alternative hypothesis of dependence, when both dimensionalities p and q grow much faster than sample size n, the sample distance covariance asymptotically measures the linear dependence between two random vectors satisfying certain moment conditions, and fails to capture the nonlinear dependence in high dimensions. To address this issue, a marginally aggregated distance correlation statistic was introduced therein to deal with high-dimensional independence testing. However, as discussed above, we provide a specific alternative hypothesis under which the rescaled sample distance correlation is capable of identifying the pure nonlinear relationship when $p=q=o(\sqrt{n})$. These two results complement each other and indicate that the sample distance correlation can have rich asymptotic behavior in different diverging regimes of (n, p, q). See Table 2 in Section 3.5 for a summary of the differences in power analysis. The complete spectrum of the alternative distribution as a function of (n, p, q) is still largely open and can be challenging to study. In simulation Example 6 in Section 4.3, we give an example showing that the marginally aggregated distance correlation statistic can suffer from power loss if the true dependence in data is much more than just marginal.

Table 2.

Comparison of power analysis in detecting pure nonlinear dependency

Zhu et al. (2020)	Asymptotically no power when p and q grow much faster than n (especially it requires min{p, q} ≫ n2 when X, Y consist of i.i.d. components)
Our work	Asymptotically can achieve power one when $p=q=o(\sqrt{n})$ (under the conditions of Theorem 6)

It is also worth mentioning that our Propositions A.1–A.3 (see Section A.4 of Supplementary Material), which serve as the crucial ingredient of the proofs for Theorems 2 and 4, provide some explicit bounds on certain key moments identified in our theory under fairly general conditions, which can be of independent interest.

The rest of the paper is organized as follows. Section 2 introduces the distance correlation and reviews the existing limiting distributions. We present a rescaled test statistic, its asymptotic distributions, and a power analysis for high-dimensional distance correlation inference in Section 3. Sections 4 and 5 provide several simulation examples and a blockchain application justifying our theoretical results and illustrating the finite-sample performance of the rescaled test statistic. We discuss some implications and extensions of our work in Section 6. All the proofs and technical details are provided in the Supplementary Material.

2. Distance correlation and distributional properties.

2.1. Bias-corrected distance correlation.

Let us consider a pair of random vectors $X\in {ℝ}^p$ and $Y\in {ℝ}^q$ with integers p, q ≥ 1 that are of possibly different dimensions and possibly mixed data types such as continuous or discrete components. For any vectors $t\in {ℝ}^p$ and $s\in {ℝ}^q$, denote by 〈t,X〉 and 〈s,Y 〉 the corresponding inner products. Let $f_X(t)=\mathbb{E}{e}^{i\langle t,X\rangle }$, $f_Y(s)=\mathbb{E}{e}^{i\langle s,Y\rangle }$, and $f_{X,Y}(t,s)=\mathbb{E}{e}^{i\langle t,X\rangle +i\langle s,Y\rangle }$ be the characteristic functions of X, Y, and the joint distribution (X,Y ), respectively, where i associated with the expectations represents the imaginary unit (−1)^1/2. Székely, Rizzo and Bakirov (2007) defined the squared distance covariance ${\mathcal{V}}^2(X,Y)$ as

$${\mathcal{V}}^2(X,Y)={\int }_{{ℝ}^{p+q}}\frac{{\left|f_{X,Y}(t,s)-f_X(t)f_Y(s)\right|}^2}{c_p{c}_q\Vert t{\Vert }^{p+1}\Vert s{\Vert }^{q+1}}\text{d}t\text{d}s,$$ (1)

where

$$c_p=\frac{{\pi }^{(p+1)/2}}{\mathrm{\Gamma }((p+1)/2)}$$

with Γ(·) the gamma function and ‖ · ‖ stands for the Euclidean norm of a vector. Observe that 2c_p and 2c_q are simply the volumes of p-dimensional and q-dimensional unit spheres in the Euclidean spaces, respectively. In view of the above definition, it is easy to see that X and Y are independent if and only if ${\mathcal{V}}^2(X,Y)=0$. Thus distance covariance characterizes completely the independence.

The specific weight in (1) gives us an explicit form of the squared distance covariance (see Székely, Rizzo and Bakirov (2007))

$$\begin{gathered} \begin{array}{l}{\mathcal{V}}^2(X,Y)=\mathbb{E}\left[\Vert X_1-X_2\Vert \Vert Y_1-Y_2\Vert \right]-2\mathbb{E}\left[\Vert X_1-X_2\Vert \Vert Y_1-Y_3\Vert \right] \\ +\mathbb{E}\left[\Vert X_1-X_2\Vert \right]\mathbb{E}\left[\Vert Y_1-Y_2\Vert \right],\end{array} \end{gathered}$$ (2)

where (X₁,Y₁), (X₂,Y₂), and (X₃,Y₃) are independent copies of (X,Y ). Moreover, Lyons (2013) showed that

$${\mathcal{V}}^2(X,Y)=\mathbb{E}\left[d\left(X_1,X_2\right)d\left(Y_1,Y_2\right)\right]$$ (3)

with the double-centered distance

$$d\left(X_1,X_2\right)=\Vert X_1-X_2\Vert -\mathbb{E}\left[\Vert X_1-X_2\Vert \mid X_1\right]-\mathbb{E}\left[\Vert X_1-X_2\Vert \mid X_2\right]+\mathbb{E}\left[\Vert X_1-X_2\Vert \right]$$ (4)

and d(Y₁,Y₂) defined similarly. Let ${\mathcal{V}}^2(X)={\mathcal{V}}^2(X,X)$ and ${\mathcal{V}}^2(Y)={\mathcal{V}}^2(Y,Y)$ be the squared distance variances of X and Y, respectively. Then the squared distance correlation $\mathcal{R}(X,Y)$ is defined as

$${\mathcal{R}}^2(X,Y)=\{\begin{array}{ll}\frac{{\mathcal{V}}^2(X,Y)}{\sqrt{{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}}\hfill & \text{if}{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)>0,\hfill \\ 0\hfill & \text{if}{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)=0.\hfill \end{array}$$ (5)

Now assume that we are given a sample of n independent and identically distributed (i.i.d.) observations {(X_i,Y_i),1 ≤ i ≤ n} from the joint distribution (X,Y ). In Székely, Rizzo and Bakirov (2007), the squared sample distance covariance ${\mathcal{V}}_n^2(X,Y)$ was constructed by directly plugging in the empirical characteristic functions as

$${\mathcal{V}}_n^2(X,Y)={\int }_{{ℝ}^{p+q}}\frac{{\left|f_{X,Y}^n(t,s)-f_X^n(t)f_Y^n(s)\right|}^2}{c_p{c}_q\Vert t{\Vert }^{p+1}\Vert s{\Vert }^{q+1}}\text{d}t\text{d}s,$$ (6)

where $f_Y^n(t)$, $f_Y^n(s)$, and $f_{X,Y}^n(t,s)$ are the corresponding empirical characteristic functions. Thus the squared sample distance correlation is given by

$${\mathcal{R}}_n^2(X,Y)=\{\begin{array}{ll}\frac{{\mathcal{V}}_n^2(X,Y)}{\sqrt{{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)}}\hfill & \text{if}{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)>0,\hfill \\ 0\hfill & \text{if}{\mathcal{V}}_n^2(X){\mathcal{V}}_n^2(Y)=0.\hfill \end{array}$$ (7)

Similar to (2) and (3), the squared sample distance covariance admits the following explicit form

$${\mathcal{V}}_n^2(X,Y)=\frac{1}{n^2}\sum _{k,l=1}^n{A}_{k,l}{B}_{k,l},$$ (8)

where A_k,l and B_k,l are the double-centered distances defined as

$$A_{k,l}=a_{k,l}-\frac{1}{n}\sum _{i=1}^n{a}_{i,l}-\frac{1}{n}\sum _{j=1}^n{a}_{k,j}+\frac{1}{n^2}\sum _{i,j=1}^n{a}_{i,j},$$

$$B_{k,l}=b_{k,l}-\frac{1}{n}\sum _{i=1}^n{b}_{i,l}-\frac{1}{n}\sum _{j=1}^n{b}_{k,j}+\frac{1}{n^2}\sum _{i,j=1}^n{b}_{i,j}$$

with a_k,l = ‖X_k − X_l‖ and b_k,l = ‖Y_k − Y_l‖. It is easy to see that the above estimator is an empirical version of the right hand side of (3). The double-centered population distance d(X_k,X_l) is estimated by the double-centered sample distance A_k,l and then $\mathbb{E}\left[d\left(X_1,X_2\right)\right]$ is estimated by the mean of all the pairs of double-centered sample distances.

Although it is natural to define the sample distance covariance in (6), Székely and Rizzo (2013) later demonstrated that such an estimator is biased and can lead to interpretation issues in high dimensions. They revealed that for independent random vectors $X\in {ℝ}^p$ and $Y\in {ℝ}^q$ with i.i.d. components and finite second moments, it holds that

$${\mathcal{R}}_n^2(X,Y)\underset{p,q\to \infty }{\to }1$$

when sample size n is fixed, but we naturally have ${\mathcal{R}}^2(X,Y)=0$ in this scenario. To address this issue, Székely and Rizzo (2013, 2014) introduced a modified unbiased estimator of the squared distance covariance and the bias-corrected sample distance correlation given by

$${\mathcal{V}}_n^{*}(X,Y)=\frac{1}{n(n-3)}\sum _{k\ne l}{A}_{k,l}^{*}{B}_{k,l}^{*}$$ (9)

and

$${\mathcal{R}}_n^{*}(X,Y)=\{\begin{array}{ll}\frac{{\mathcal{V}}_n^{*}(X,Y)}{\sqrt{{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)}}\hfill & \text{if}{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)>0,\hfill \\ 0\hfill & \text{if}{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)=0.\hfill \end{array}$$ (10)

respectively, where the $\mathcal{U}$-centered distances $A_{k,l}^{*}$ and $B_{k,l}^{*}$ are defined as

$$A_{k,l}^{*}=a_{k,l}-\frac{1}{n-2}\sum _{i=1}^n{a}_{i,l}-\frac{1}{n-2}\sum _{j=1}^n{a}_{k,j}+\frac{1}{(n-1)(n-2)}\sum _{i,j=1}^n{a}_{i,j},$$

$$B_{k,l}^{*}=b_{k,l}-\frac{1}{n-2}\sum _{i=1}^n{b}_{i,l}-\frac{1}{n-2}\sum _{j=1}^n{b}_{k,j}+\frac{1}{(n-1)(n-2)}\sum _{i,j=1}^n{b}_{i,j}.$$

Our work will focus on the bias-corrected distance-based statistics ${\mathcal{V}}_n^{*}(X,Y)$ and ${\mathcal{R}}_n^{*}(X,Y)$ given in (9) and (10), respectively.

2.2. Distributional properties.

In general, the exact distributions of the distance covariance and distance correlation are intractable. Thus it is essential to investigate the asymptotic surrogates in order to apply the distance-based statistics for the test of independence. With dimensionalities p, q fixed and sample size n → ∞, Huo and Székely (2016) validated that ${\mathcal{V}}_n^{*}(X,Y)$ is a U-statistic and then under the independence of X and Y, it admits the following asymptotic distribution

$$n{\mathcal{V}}_n^{*}(X,Y)\underset{n\to \infty }{\overset{\mathcal{D}}{\to }}\sum _{i=1}^{\infty }{\lambda }_i\left(Z_i^2-1\right),$$ (11)

where {Z_i, i ≥ 1} are i.i.d. standard normal random variables and {λ_i, i ≥ 1} are the eigenvalues of some operator.

On the other hand, Székely and Rizzo (2013) showed that when the dimensionalities p and q tend to infinity and sample size n ≥ 4 is fixed, if X and Y both consist of i.i.d. components, then under the independence of X and Y we have

$$T_R:=\sqrt{n(n-3)/2-1}\frac{{\mathcal{R}}_n^{*}(X,Y)}{\sqrt{1-{\left({\mathcal{R}}_n^{*}(X,Y)\right)}^2}}\underset{p,q\to \infty }{\overset{\mathcal{D}}{\to }}{t}_{n(n-3)/2-1}.$$ (12)

However, it still remains to investigate the limiting distributions of distance correlation when both sample size and dimensionality are diverging simultaneously. It is common to encounter datasets that are of both high dimensions and large sample size such as in biology, ecology, medical science, and networks. When min{p, q} → ∞ and n → ∞ at a slower rate compared to p, q, under the independence of X and Y and some conditions on the moments Zhu et al. (2020) showed that

$$T_R\stackrel{\mathcal{D}}{\to }N(0,1).$$ (13)

Their result was obtained by approximating the unbiased sample distance covariance with the aggregated marginal distance covariance, which can incur stronger assumptions including n → ∞ at a slower rate compared to p, q and min{p, q} → ∞.

The main goal of our paper is to fill such a gap and make the asymptotic theory of distance correlation more complete. Specifically, we will prove central limit theorems for ${\mathcal{R}}_n^{*}(X,Y)$ when n → ∞ and p + q → ∞. In contrast to the work of Zhu et al. (2020), we analyze the unbiased sample distance covariance directly by treating the random vectors as a whole. Our work will also complement the recent power analysis in Zhu et al. (2020), where distance correlation was shown to asymptotically measure only linear dependency in the regime of fast growing dimensionality (min{p, q}/n² → ∞) and thus the marginally aggregated distance correlation statistic was introduced. However, as shown in Example 6 in Section 4.3, the marginally aggregated statistic can be less powerful than the joint distance correlation statistic when the dependency between the two random vectors far exceeds the marginal contributions. To understand such a phenomenon, we will develop a general theory on the power analysis for the rescaled distance correlation statistic in Theorem 5 and further justify its capability of detecting nonlinear dependency in Theorem 6 for the regime of moderately high dimensionality.

3. High-dimensional distance correlation inference.

3.1. A rescaled test statistic.

To simplify the technical presentation, we assume that $\mathbb{E}[X]=0$ and $\mathbb{E}[Y]=0$ since otherwise we can first subtract the means in our technical analysis. Let $\mathbb{E}\left[X{X}^T\right]={\mathrm{\Sigma }}_x$ and $\mathbb{E}\left[Y{Y}^T\right]={\mathrm{\Sigma }}_y$ be the covariance matrices of random vectors X and Y, respectively. To test the null hypothesis that X and Y are independent, in this paper we consider a rescaled test statistic defined as a rescaled distance correlation

$$T_n:=\sqrt{\frac{n(n-1)}{2}}{\mathcal{R}}_n^{*}(X,Y)=\sqrt{\frac{n(n-1)}{2}}\frac{{\mathcal{V}}_n^{*}(X,Y)}{\sqrt{{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)}}.$$ (14)

It has been shown in Huo and Székely (2016) that ${\mathcal{V}}_n^{*}(X,Y)$ is a U-statistic. A key observation is that by the Hoeffding decomposition for U-statistics, the dominating part is a martingale array under the independence of X and Y. Then we can apply the martingale central limit theorem and calculate the specific moments involved.

More specifically, Huo and Székely (2016) showed that

$${\mathcal{V}}_n^{*}(X,Y)={\left(\begin{array}{l}n\hfill \\ 4\hfill \end{array}\right)}^{-1}\sum _{1\le i_1<i_2<i_3<i_4\le n}h\left(\left(X_{i_1},Y_{i_1}\right),\cdots ,\left(X_{i_4},Y_{i_4}\right)\right),$$ (15)

where the kernel function is given by

$$\begin{array}{l}h\left(\left(X_1,Y_1\right),\left(X_2,Y_2\right),\left(X_3,Y_3\right),\left(X_4,Y_4\right)\right)\\ =\frac{1}{4}\sum _{\begin{array}{c}1\le i,j\le 4,\\ i\ne j\end{array}}\Vert X_i-X_j\Vert \Vert Y_i-Y_j\Vert -\frac{1}{4}\sum _{i=1}^4\left(\sum _{\begin{array}{c}1\le j\le 4,\\ j\ne i\end{array}}\Vert X_i-X_j\Vert \sum _{\begin{array}{c}1\le j\le 4\\ j\ne i\end{array}}\Vert Y_i-Y_j\Vert \right)\\ +\frac{1}{24}\sum _{\begin{array}{c}1\le i,j\le 4,\\ i\ne j\end{array}}\Vert X_i-X_j\Vert \sum _{\begin{array}{c}1\le i,j\le 4,\\ i\ne j\end{array}}\Vert Y_i-Y_j\Vert .\end{array}$$ (16)

Let us define another functional

$$g\left(X_1,X_2,X_3,X_4\right):=d\left(X_1,X_2\right)d\left(X_1,X_3\right)d\left(X_2,X_4\right)d\left(X_3,X_4\right),$$ (17)

where d(·,·) is the double-centered distance defined in (4). The above technical preparation enables us to derive the main theoretical results.

3.2. Asymptotic distributions.

THEOREM 1.

Assume that $\mathbb{E}{\Vert X\Vert }^{2+2\tau }+\mathbb{E}{\Vert Y\Vert }^{2+2\tau }<\infty$ for some constant 0 < τ ≤ 1. If

$$\frac{\mathbb{E}\left({\left|d\left(X_1,X_2\right)\right|}^{2+2\tau }\right)\mathbb{E}\left({\left|d\left(Y_1,Y_2\right)\right|}^{2+2\tau }\right)}{n^{\tau }{\left[{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)\right]}^{1+\tau }}\to 0$$ (18)

and

$$\frac{\mathbb{E}\left[g\left(X_1,X_2,X_3,X_4\right)\right]\mathbb{E}\left[g\left(Y_1,Y_2,Y_3,Y_4\right)\right]}{{\left[{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)\right]}^2}\to 0$$ (19)

as n → ∞ and p+q → ∞, then under the independence of X and Y we have $T_n\stackrel{\mathcal{D}}{\to }N(0,1)$.

Theorem 1 presents a general theory and relies on the martingale central limit theorem. In fact, when X and Y are independent, via the Hoeffding decomposition we can find that the dominating part of ${\mathcal{V}}_n^{*}(X,Y)$ forms a martingale array which admits asymptotic normality under conditions (18) and (19). Moreover, it also follows from (18) that

$$\frac{{\mathcal{V}}_n^{*}(X)}{{\mathcal{V}}^2(X)}\to 1\text{and}\frac{{\mathcal{V}}_n^{*}(Y)}{{\mathcal{V}}^2(Y)}\to 1\text{in}\text{probability.}$$

Thus an application of Slutsky’s lemma results in the desired results.

Although Theorem 1 is for the general case, the calculation of the moments involved such as $\mathbb{E}\left[g\left(X_1,X_2,X_3,X_4\right)\right]$, ${\mathcal{V}}^2(X)$, and $\mathbb{E}({\left|d\left(X_1,X_2\right)\right|}^{2+2\tau })$ for the general underlying distribution can be challenging. To this end, we provide in Propositions A.1–A.3 in Section A.4 some bounds or exact orders of those moments. These results together with Theorem 1 enable us to obtain Theorem 2 on an explicit and useful central limit theorem with more specific conditions. Let us define quantities

$$B_X=\mathbb{E}[{\Vert X_1-X_2\Vert }^2]=2\mathbb{E}[\Vert X{\Vert }^2],B_Y=\mathbb{E}[{\Vert Y_1-Y_2\Vert }^2]=2\mathbb{E}[\Vert Y{\Vert }^2],$$

$$L_{x,\tau }=\mathbb{E}({|\Vert X{\Vert }^2-\mathbb{E}\Vert X{\Vert }^2|}^{2+2\tau })+\mathbb{E}({|X_1^T{X}_2|}^{2+2\tau }),$$

$$L_{y,\tau }=\mathbb{E}({|\Vert Y{\Vert }^2-\mathbb{E}\Vert Y{\Vert }^2|}^{2+2\tau })+\mathbb{E}({|Y_1^T{Y}_2|}^{2+2\tau }),$$

and

$$E_x=\frac{\mathbb{E}[{(X_1^T{\mathrm{\Sigma }}_x{X}_2)}^2]+B_X^{-2\tau }{L}_{x,\tau }^{(2+\tau )/(1+\tau )}}{{(\mathbb{E}[{(X_1^T{X}_2)}^2])}^2},$$

$$E_y=\frac{\mathbb{E}[{(Y_1^T{\mathrm{\Sigma }}_y{Y}_2)}^2]+B_Y^{-2\tau }{L}_{y,\tau }^{(2+\tau )/(1+\tau )}}{{(\mathbb{E}[{(Y_1^T{Y}_2)}^2])}^2}.$$

THEOREM 2.

Assume that $\mathbb{E}\left[\Vert X{\Vert }^{4+4\tau }\right]+\mathbb{E}\left[\Vert Y{\Vert }^{4+4\tau }\right]<\infty$ for some constant 0 < τ ≤ 1/2 and as n → ∞ and p+q → ∞,

$$\frac{n^{-\tau }{L}_{x,\tau }{L}_{y,\tau }}{{\left(\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right]\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\right)}^{1+\tau }}\to 0.$$ (20)

In addition, assume that E_x → 0 if p → ∞, and E_y → 0 if q → ∞. Then under the independence of X and Y, we have $T_n\stackrel{\mathcal{D}}{\to }N(0,1)$.

Theorem 2 provides a user-friendly central limit theorem with mild regularity conditions that are easy to verify and can be satisfied by a large class of distributions. To get some insights into the orders of the moments $B_X,L_{x,\tau },\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right]$, and $\mathbb{E}\left[{\left(X_1^T{\mathrm{\Sigma }}_x{X}_2\right)}^2\right]$, one can refer to Section 3.4 for detailed explanations by examining some specific examples. In Theorem 2, we show the results only under the scenario of 0 < τ ≤ 1/2. In fact, similar results also hold for the case of 1/2 < τ ≤ 1; see Section D of Supplementary Material for more details.

3.3. Rates of convergence.

Thanks to the martingale structure of the dominating term of ${\mathcal{V}}_n^{*}(X,Y)$ under the independence of X and Y, we can obtain explicitly the rates of convergence for the normal approximation.

THEOREM 3.

Assume that $\mathbb{E}\Vert X{\Vert }^{2+2\tau }+\mathbb{E}\Vert Y{\Vert }^{2+2\tau }<\infty$ for some constant 0 < τ ≤ 1. Then under the independence of X and Y, we have

$$\begin{gathered} \underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n\le x\right)-\mathrm{\Phi }(x)\right|\le C\{{\left(\frac{\mathbb{E}\left[g\left(X_1,X_2,X_3,X_4\right)\right]\mathbb{E}\left[g\left(Y_1,Y_2,Y_3,Y_4\right)\right]}{{\left[{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)\right]}^2}\right)}^{\frac{1+\tau }{2}} \\ {+\frac{\mathbb{E}\left[{\left|d\left(X_1,X_2\right)\right|}^{2+2\tau }\right]\mathbb{E}\left[{\left|d\left(Y_1,Y_2\right)\right|}^{2+2\tau }\right]}{n^{\tau }{\left[{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)\right]}^{1+\tau }}\}}^{\frac{1}{3+2\tau }}, \end{gathered}$$ (21)

where C is an absolute positive constant and Φ(x) is standard normal distribution function.

In view of the evaluation of the moments in Propositions A.1–A.3, we can obtain the following theorem as a consequence of Theorem 3.

THEOREM 4.

Assume that $\mathbb{E}\left[\Vert X{\Vert }^{4+4\tau }\right]+\mathbb{E}\left[\Vert Y{\Vert }^{4+4\tau }\right]<\infty$ for some constant 0 < τ ≤ 1/2,

$$B_X^{-2\tau }{L}_{x,\tau }/\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right]\le 1/18,and{B}_Y^{-2\tau }{L}_{y,\tau }/\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\le 1/18.$$ (22)

Then under the independence of X and Y, we have

$$\underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n\le x\right)-\mathrm{\Phi }(x)\right|\le C{\left\{{\left(E_x{E}_y\right)}^{\frac{1+\tau }{2}}+\frac{n^{-\tau }{L}_{x,\tau }{L}_{y,\tau }}{{\left(\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right]\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\right)}^{1+\tau }}\right\}}^{\frac{1}{3+2\tau }},$$ (23)

where C is an absolute positive constant.

The counterpart theory for the case of 1/2 < τ ≤ 1 is presented in Section D of Supplementary Material. In general, larger value of τ will lead to better convergence rates and weaker conditions, which will be elucidated by the example of m-dependent components in Proposition 2 (see Section 3.4).

Let us now consider the case when only one of p and q is diverging, say, p is fixed and q → ∞. Then by the moment assumption $\mathbb{E}\left[\Vert X{\Vert }^{4+4\tau }\right]<\infty$, all the moments related to X on the right hand side of (21) are of bounded values. Thus in light of the proof of Theorem 4, we can see that if $\mathbb{E}\left[\Vert X{\Vert }^{4+4\tau }\right]+\mathbb{E}\left[\Vert Y{\Vert }^{4+4\tau }\right]<\infty$ for some constant 0 < τ ≤ 1/2, then there exists some positive constant C_X depending on the underlying distribution of X such that under the independence of X and Y, we have

$$\underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n<x\right)-\mathrm{\Phi }(x)\right|\le C_X{\left\{{\left(E_y\wedge \frac{1}{18}\right)}^{\frac{1+\tau }{2}}+\frac{n^{-\tau }{L}_{y,\tau }}{{\left(\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\right)}^{1+\tau }}\right\}}^{\frac{1}{3+2\tau }}.$$ (24)

It is worth mentioning that the bounds obtained in (21) and (23) are nonasymptotic results that quantify the accuracy of the normal approximation and reveal how the rate of convergence depends on the sample size and dimensionalities. Since we exploit the rate of convergence in the central limit theorem for general martingales (Haeusler, 1988) under the assumption of 0 < τ ≤ 1, the result may not necessarily be optimal. It is possible that better convergence rate can be obtained for the case of τ > 1, which is beyond the scope of the current paper.

An anonymous referee asked a great question on whether similar results as in Theorems 1 and 3 apply to the studentized statistic T_R defined in (12). The answer is affirmative. Combining our Theorem 1 with Lemma 1 and (A.50), it can be shown that T_R enjoys the same asymptotic normality as T_n presented in Theorem 1. Moreover, the rates of convergence in Theorem 3 also apply to T_R. See Section F of Supplementary Material for the proof of these results for T_R. These results suggest that the studentized statistic T_R can be a good choice in both small and large samples. Yet the exact phase transition theory for the asymptotic null distribution of T_R in the full diverging spectrum of (n, p, q) remains to be developed.

3.4. Some specific examples.

To better illustrate the results obtained in the previous theorems, let us consider several concrete examples now. To simplify the technical presentation, we assume in this section that both p and q tend to infinity as n increases. Our technical analysis also applies to the case when only one of p and q diverges.

PROPOSITION 1.

Assume that $\mathbb{E}\left(\Vert X{\Vert }^{4+4\tau }\right)+\mathbb{E}\left(\Vert Y{\Vert }^{4+4\tau }\right)<\infty$ for some constant 0 < τ ≤ 1/2 and there exist some positive constants c₁,c₂ such that

$$L_{x,\tau }\le c_1{p}^{1+\tau },\mathbb{E}\left[{\left(X_1^T{\mathrm{\Sigma }}_x{X}_2\right)}^2\right]\le c_{1}p,$$ (25)

$$\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right]\ge c_{2}p,\mathbb{E}\left[\Vert X{\Vert }^2\right]\ge c_{2}p,$$ (26)

and

$$L_{y,\tau }\le c_1{q}^{1+\tau },\mathbb{E}\left[{\left(Y_1^T{\mathrm{\Sigma }}_y{Y}_2\right)}^2\right]\le c_{1}q,$$ (27)

$$\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\ge c_{2}q,\mathbb{E}\left[\Vert Y{\Vert }^2\right]\ge c_{2}q.$$ (28)

Then under the independence of X and Y, there exists some positive constant A depending upon c₁ and c₂ such that for sufficiently large p and q, we have

$$\underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n\le x\right)-\mathrm{\Phi }(x)\right|\le A{\left[{(pq)}^{-\tau (1+\tau )/2}+n^{-\tau }\right]}^{1/(3+2\tau )}.$$

Hence as n → ∞ and p, q → ∞, it holds that $T_n\stackrel{\mathcal{D}}{\to }N(0,1)$.

The first example considered in Proposition 1 is motivated by the case of independent components. Indeed, by Rosenthal’s inequality for the sum of independent random variables, (25) and (26) are automatically satisfied when X consists of independent nondegenerate components with zero mean and uniformly bounded (4+ 4τ)th moment.

We next consider the second example of m-dependent components. For an integer m ≥ 1, a sequence ${\left\{U_i\right\}}_0^{\infty }$ is m-depenendent if ${\left\{U_i\right\}}_0^n$ and ${\left\{U_i\right\}}_{n+m+1}^{\infty }$ are independent for every n ≥ 0. We now focus on a special but commonly used scenario in which X consists of m₁-dependent components and Y consists of m₂-dependent components for some integers m₁ ≥ 1 and m₂ ≥ 1. Assume that (X₁,Y₁) and (X₂,Y₂) are independent copies of (X,Y ) and denote by

$$X_1={\left(X_{1,1},X_{1,2},\cdots ,X_{1,p}\right)}^T,X_2={\left(X_{2,1},X_{2,2},\cdots ,X_{2,p}\right)}^T,$$

$$Y_1={\left(Y_{1,1},Y_{1,2},\cdots ,Y_{1,q}\right)}^T,Y_2={\left(Y_{2,1},Y_{2,2},\cdots ,Y_{2,q}\right)}^T.$$

We can develop the following proposition by resorting to Theorem 4 for the case of 0 < τ ≤ 1/2 and Theorem D.1 in Section D.1 of Supplementary Material for the case of 1/2 < τ ≤ 1.

PROPOSITION 2.

Assume that $\mathbb{E}\left({\left|X_{1,i}\right|}^{4+4\tau }\right)<\infty$ and $\mathbb{E}\left({\left|Y_{1,j}\right|}^{4+4\tau }\right)<\infty$ for any 1 ≤ i ≤ p, 1 ≤ j ≤ q with some constant 0 < τ ≤ 1, and there exist some positive constants κ₁,κ₂,κ₃,κ₄ such that

$$\max \left\{p^{-1}{\sum }_{i=1}^p\mathbb{E}\left[{\left|X_{1,i}\right|}^{4+4\tau }\right],q^{-1}{\sum }_{j=1}^q\mathbb{E}\left[{\left|Y_{1,j}\right|}^{4+4\tau }\right]\right\}\le {\kappa }_1,$$ (29)

$$\min \left\{p^{-1}\mathbb{E}\left[{\left(X_1^T{X}_2\right)}^2\right],q^{-1}\mathbb{E}\left[{\left(Y_1^T{Y}_2\right)}^2\right]\right\}\ge {\kappa }_2,$$ (30)

$$\min \left\{p^{-1}{B}_X,q^{-1}{B}_Y\right\}\ge {\kappa }_3,$$ (31)

$$\underset{1\le i\le p}{\max }\mathbb{E}\left[X_{1,i}^2\right]\le {\kappa }_4,\underset{1\le j\le q}{\max }\mathbb{E}\left[Y_{1,j}^2\right]\le {\kappa }_4.$$ (32)

In addition, assume that X consists of m₁-dependent components, Y consists of m₂-dependent components, and

$$m_1=o\left(p^{\tau /(2+\tau )}\right),m_2=o\left(q^{\tau /(2+\tau )}\right),m_1{m}_2=o\left(n^{\tau /(1+\tau )}\right).$$ (33)

Then under the independence of X and Y, there exists some positive constant A depending upon κ₁, · · · ,κ₄ such that

$$\begin{array}{l}\underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n\le x\right)-\mathrm{\Phi }(x)\right|\\ \le A{\left[{\left({\left[\left(m_1+1\right)\left(m_2+1\right)\right]}^{2+\tau }{(pq)}^{-\tau }\right)}^{\frac{1+\tau }{2}}+{\left[\left(m_1+1\right)\left(m_2+1\right)\right]}^{1+\tau }{n}^{-\tau }\right]}^{\frac{1}{3+2\tau }}.\end{array}$$ (34)

Hence under condition (33), we have $T_n\stackrel{\mathcal{D}}{\to }N(0,1)$ as n → ∞ and p, q → ∞.

Zhu et al. (2020) also established the asymptotic normality of the rescaled distance correlation. For clear comparison, we summarize in Table 1 the key differences between our results and theirs under the assumptions of Proposition 2 and the existence of the eighth moments (τ = 1).

We further consider the third example of multivariate normal random variables. For such a case, we can obtain a concise result in the following proposition.

PROPOSITION 3.

Assume that X ~ N(0,Σ_x), Y ~ N(0,Σ_y), and the eigenvalues of Σ_x and Σ_y satisfy that $a_1\le {\lambda }_1^X\le {\lambda }_2^X\le \cdots \le {\lambda }_p^X\le a_2$ and $a_1\le {\lambda }_1^Y\le {\lambda }_2^Y\le \cdots \le {\lambda }_q^Y\le a_2$ for some positive constants a₁ and a₂. Then under the independence of X and Y, there exists some positive constant C depending upon a₁, a₂ such that

$$\underset{x\in ℝ}{\sup }\left|\mathbb{P}\left(T_n\le x\right)-\mathrm{\Phi }(x)\right|\le C\left[{(pq)}^{-1/5}+n^{-1/5}\right].$$

Hence we have $T_n\stackrel{\mathcal{D}}{\to }N(0,1)$ as n → ∞ and p, q → ∞.

We would like to point out that the rate of convergence obtained in Proposition 3 can be suboptimal since the error rate n^−1/5 is slower than the classical convergence rate with order n^−1/2 of the CLT for the sum of independent random variables. Our results are derived by exploiting the convergence rate of CLT for general martingales (Haeusler, 1988). It may be possible to improve the rate of convergence if one takes into account the specific intrinsic structure of distance covariance, which is beyond the scope of the current paper.

3.5. Power analysis.

We now turn to the power analysis for the rescaled distance correlation. We start with presenting a general theory on power in Theorem 5 below. Let us define two quantities

$$L_x=\mathbb{E}\left({\left|\Vert X{\Vert }^2-\mathbb{E}\Vert X{\Vert }^2\right|}^4\right)+\mathbb{E}\left({\left|X_1^T{X}_2\right|}^4\right),L_y=\mathbb{E}\left({\left|\Vert Y{\Vert }^2-\mathbb{E}\Vert Y{\Vert }^2\right|}^4\right)+\mathbb{E}\left({\left|Y_1^T{Y}_2\right|}^4\right).$$ (35)

THEOREM 5.

Assume that $\mathbb{E}\left(\Vert X{\Vert }^8\right)+\mathbb{E}\left(\Vert Y{\Vert }^8\right)<\infty$ and (18) holds with τ = 1. If $n{\mathcal{R}}^2(X,Y)\to \infty$ and $\sqrt{n}{\mathcal{V}}^2(X,Y)/\left(B_X^{-1/2}{B}_Y^{-1/2}{L}_x^{1/4}{L}_y^{1/4}\right)\to \infty$, then for any arbitrarily large constant C > 0, $\mathbb{P}\left(T_n>C\right)\to 1$ as n → ∞. Thus, for any significance level α, $\mathbb{P}(T_n>{\mathrm{\Phi }}^{-1}(1-\alpha ))\to 1$ as n → ∞, where Φ⁻¹(1 − α) represents the (1 − α)th quantile of the standard normal distribution.

Theorem 5 provides a general result on the power of the rescaled distance correlation statistic. It reveals that as long as the signal strength, measured by ${\mathcal{R}}^2(X,Y)$ and ${\mathcal{V}}^2(X,Y)$, is not too weak, the power of testing independence with the rescaled sample distance correlation can be asymptotically one. In most cases, the population distance variances ${\mathcal{V}}^2(X)$ and ${\mathcal{V}}^2(Y)$ are of constant order by Proposition A.2. Therefore, if $B_X^{-1/2}$$B_Y^{-1/2}$$L_x^{1/4}$$L_y^{1/4}$ also of constant order, then the conditions in Theorem 5 will reduce to $\sqrt{n}{\mathcal{R}}^2(X,Y)\to \infty$, which indicates that the signal strength should not decay faster than n^−1/2. To gain some insights, assume that both $X\in {ℝ}^p$ and $Y\in {ℝ}^q$ consist of independent components with uniformly upper bounded eighth moments and uniformly lower bounded second moments. Then it holds that B_X = O(p), B_Y = O(q), L_x = O(p²), L_y = O(q²), ${\mathcal{V}}^2(X)=O(1)$, and ${\mathcal{V}}^2(Y)=O(1)$. Thus the conditions in Theorem 5 above reduce to $\mathbb{E}\left(\Vert X{\Vert }^8\right)+\mathbb{E}\left(\Vert Y{\Vert }^8\right)<\infty$ and $\sqrt{n}{\mathcal{R}}^2(X,Y)\to \infty$. In general, ${\mathcal{R}}^2(X,Y)$ and ${\mathcal{V}}^2(X,Y)$ depend on the dimensionalities and hence the conditions of Theorem 5 impose certain relationship between n and p.

Recently Zhu et al. (2020) showed that in the asymptotic sense, the distance covariance detects only componentwise linear dependence in the high-dimensional setting when both dimensionalities p and q grow much faster than sample size n (see Theorems 2.1.1 and 3.1.1 therein). In particular, when X and Y both consist of i.i.d. components with certain bounded moments, distance covariance was shown to asymptotically measure linear dependence if min{p, q}/n² → ∞. However, in view of (1) and (5), the population distance covariance and distance correlation indeed characterize completely the independence between two random vectors in arbitrary dimensions. Therefore, it is natural to ask whether the sample distance correlation can detect nonlinear dependence in some other diverging regime of (n, p, q). The answer turns out to be affirmative in the regime of moderately high dimensionality: We formally present this result in the following theorem on the asymptotic power and compare with the results in Zhu et al. (2020) in Table 2.

THEOREM 6.

Assume that we have i.i.d. observations {(X_i,Y_i),1 ≤ i ≤ n} with $X_i\in {ℝ}^p$ and $Y_i\in {ℝ}^p$, X₁ = (X_1,1, …, X_1,p) with X having a symmetric distribution, and {X_1,i, 1 ≤ i ≤ p} are m-dependent for some fixed positive integer m. Let Y₁ = (Y_1,1, …, Y_1,p) be given by Y_1,j = g_j(X_1,j) for each 1 ≤ j ≤ p, where {g_j, 1 ≤ j ≤ p} are symmetric functions satisfying g_j(x) = g_j(−x) for $x\in ℝ$ and 1 ≤ j ≤ p. Assume further that $\mathbb{E}\left(X_{1,j}^{12}\right)+\mathbb{E}\left(Y_{1,j}^{12}\right)\le c_1^{12}$, $\mathrm{var}\left(X_{1,j}\right)\ge c_2^2$, and $\mathrm{var}\left(Y_{1,j}\right)\ge c_2^2$ for some positive constants c₁, c₂. Then there exists some positive constant A depending on c₁, c₂, and m such that

$${\mathcal{V}}^2(X,Y)\ge A{p}^{-1}+O\left(p^{-3/2}\right)$$

$$and{\mathcal{R}}^2(X,Y)\ge A{p}^{-1}+O\left(p^{-3/2}\right).$$

Consequently, if $p=o(\sqrt{n})$, then for any arbitrary large constant C > 0, $\mathbb{P}\left(T_n>C\right)\to 1$ as n → ∞, and thus the test of independence between X and Y based on the rescaled sample distance correlation T_n has asymptotic power one.

Under the symmetry assumptions in Theorem 6, we can show that there is no linear dependence between X and Y by noting that cov(X_1,i,Y_1,j) = 0 for each 1 ≤ i, j ≤ p. It is worth mentioning that we have assumed the m-dependence for some fixed integer m ≥ 1 to simplify the technical analysis. In fact, m can be allowed to grow slowly with sample size n and our technical arguments are still applicable.

4. Simulation studies.

In this section, we conduct several simulation studies to verify our theoretical results on sample distance correlation and illustrate the finite-sample performance of our rescaled test statistic for the test of independence.

4.1. Normal approximation accuracy.

We generate two independent multivariate normal random vectors $X\in {ℝ}^p$ and $Y\in {ℝ}^p$ in the following simulated example and calculate the rescaled distance correlation T_n defined in (14).

EXAMPLE 1.

Let $\mathrm{\Sigma }=\left({\sigma }_{i,j}\right)\in {ℝ}^{p\times p}$ with σ_i,j = 0.7^|i−j|, and X ~ N(0, Σ) and Y ~ N(0, Σ) be independent. We consider the settings of n = 100 and p = 10, 50, 200, 500.

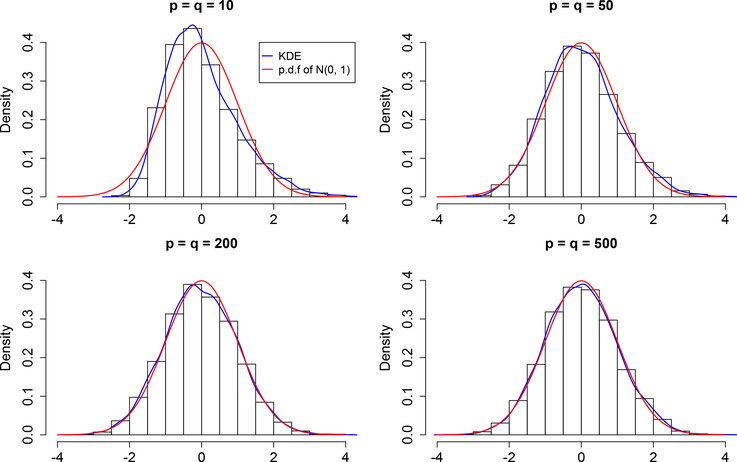
We conduct 5000 Monte Carlo simulations and generate the histograms of the rescaled test statistic T_n to investigate its empirical distribution. Histograms with a comparison of the kernel density estimate (KDE) and the standard normal density function are shown in Figure 1. From the histograms, we can see that the distribution of T_n mimics very closely the standard normal distribution under different settings of dimensionalities. Moreover, for more refined comparison, the maximum pointwise distances between the KDE and the standard normal density function under different settings are presented in Table 3. It is evident that the accuracy of the normal approximation increases with dimensionality, which is in line with our theoretical results.

Fig 1:

Histograms of the rescaled test statistic T_n in Example 1. The blue curve represents the kernel density estimate and the red curve represents the standard normal density.

Table 3.

Distances between the KDE and standard normal density function in Example 1.

n	p	Distance	n	p	Distance
100	10	0.0955	100	200	0.0288
100	50	0.0357	100	500	0.0181

4.2. Test of independence.

To test the independence of random vectors X and Y in high dimensions, based on the asymptotic normality developed for the rescaled distance correlation statistic T_n, under significance level α we can reject the null hypothesis when

$$T_n=\sqrt{\frac{n(n-1)}{2}}{\mathcal{R}}_n^{*}(X,Y)>{\mathrm{\Phi }}^{-1}(1-\alpha ),$$ (36)

since the distance correlation is positive under the alternative hypothesis. To assess the performance of our normal approximation test, we also include the gamma-based approximation test (Huang and Huo, 2017) and normal approximation for studentized sample distance correlation T_R defined in (12) (Zhu et al., 2020) in the numerical comparisons.

The gamma-based approximation test assumes that the linear combination ${\sum }_{i=1}^{\infty }{\lambda }_i{Z}_i^2$ involved in the limiting distribution of the standardized sample distance covariance $n{\mathcal{V}}_n^{*}(X,Y)$ under fixed dimensionality (see (11)) can be approximated heuristically by a gamma distribution Γ(β₁,β₂) with matched first two moments. In particular, the shape and rate parameters are determined as

$${\beta }_1=\frac{{\left({\sum }_{i=1}^{\infty }{\lambda }_i\right)}^2}{2{\sum }_{i=1}^{\infty }{\lambda }_i^2}=\frac{{\left(\mathbb{E}\Vert X-X^{\prime }\Vert \mathbb{E}\Vert Y-Y^{\prime }\Vert \right)}^2}{2{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}$$

and

$${\beta }_2=\frac{{\left({\sum }_{i=1}^{\infty }{\lambda }_i\right)}^2}{2{\sum }_{i=1}^{\infty }{\lambda }_i^2}=\frac{{\left(\mathbb{E}\Vert X-X^{\prime }\Vert \mathbb{E}\Vert Y-Y^{\prime }\Vert \right)}^2}{2{\mathcal{V}}^2(X){\mathcal{V}}^2(Y)}.$$

Thus given observations (X₁,Y₁), · · ·, (X_n,Y_n), β₁ and β₂ can be estimated by their empirical versions

$${\widehat{\beta }}_1=\frac{{\mu }^2}{2{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)}\text{and}{\widehat{\beta }}_2=\frac{\mu }{2{\mathcal{V}}_n^{*}(X){\mathcal{V}}_n^{*}(Y)}.$$

where $\mu =\frac{1}{n^2{(n-1)}^2}{\sum }_{i\ne j}\Vert X_i-X_j\Vert {\sum }_{i\ne j}\Vert Y_i-Y_j\Vert$. Then the null hypothesis is rejected at the significanve level α if $n{\mathcal{V}}_n^{*}(X,Y)>{\mathrm{\Gamma }}_{1-\alpha }\left({\widehat{\beta }}_1,{\widehat{\beta }}_2\right)-\mu$, where ${\mathrm{\Gamma }}_{1-\alpha }\left({\widehat{\beta }}_1,{\widehat{\beta }}_2\right)$ is the (1 − α)th quantile of the distribution $\mathrm{\Gamma }\left({\widehat{\beta }}_1,{\widehat{\beta }}_2\right)$. The gamma-based approximation test still lacks rigorous theoretical justification.

When the sample size and dimensionalities tend to infinity simultaneously, in view of our main result in Theorem 2 and the consistency of ${\mathcal{R}}_n^{*}(X,Y)$ (recall Lemma 1 and (A.50) in Section C.1 of Supplementary Material), one can see that under the null hypothesis, $T_R\stackrel{\mathcal{D}}{\to }N\text{(0,1)}$. Therefore, we can reject the null hypothesis at significance level α if T_R > Φ⁻¹(1− α).

We consider two simulated examples to compare the aforementioned three approaches for testing the independence between two random vectors in high dimensions. The significance level is set as α = 0.05 and 2000 Monte Carlo replicates are carried out to compute the empirical rejection rates.

EXAMPLE 2.

Let $\mathrm{\Sigma }=\left({\sigma }_{i,j}\right)\in {ℝ}^{p\times p}$ with σ_i,j = 0.5^|i−j|. Let X and Y be independent and X ~ N(0, Σ), Y ~ N(0, Σ).

EXAMPLE 3.

Let $\mathrm{\Sigma }=\left({\sigma }_{i,j}\right)\in {ℝ}^{p\times p}$ with σ_i,j = 0.5^|i−j|. Let X = (X⁽¹⁾, …, X^(p)) ~ N(0, Σ) and Y = (Y ⁽¹⁾, …, Y ^(p)) with $Y^{(i)}=0.2\left(X^{(i)}+{\left(X^{(i)}\right)}^2\right)+{\epsilon }_i$ and ${\epsilon }_i\stackrel{i.i.d.}{\sim }{t}_4$.

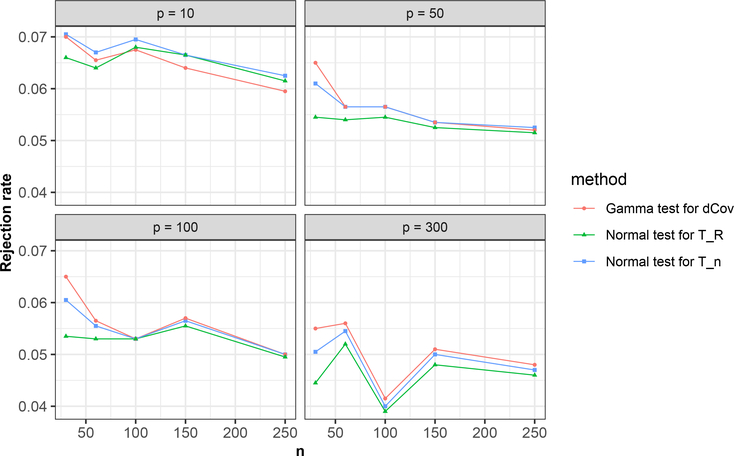
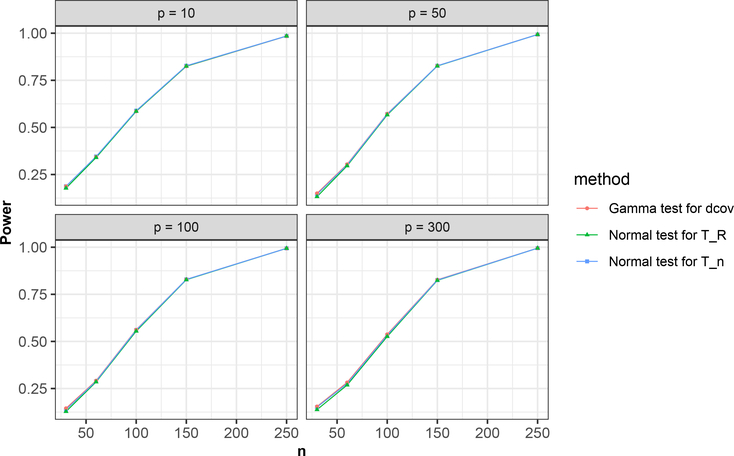
Type-I error rates in Example 2 under different settings of n and p are presented in Figure 2. From Figure 2, it is easy to see that the rejection rates of the normal approximation test for T_n tend to be closer and closer to the preselected significance level as the dimensionalities and the sample size grow. The same trend applies to the other two approches too. The empirical powers of the three tests in Example 3 are shown in Figure 3. We can observe from the simulation results in Figures 2 and 3 that these three tests perform asymptotically almost the same, which is sensible. Empirically, the gamma approximation for $n{\mathcal{V}}_n^{*}(X,Y)$ and normal approximation may be asymptotically equivalent to some extent and more details on their connections are discussed in Section E of Supplementary Material. However, the theoretical foundation of the gamma approximation for $n{\mathcal{V}}_n^{*}(X,Y)$ remains undeveloped. As for the asymptotic equivalence between T_n and the studentized sample distance correlation T_R, Lemma 1 and (A.50) imply that under the null hypothesis and some general conditions, ${\mathcal{R}}_n^{*}(X,Y)\to 0$ in probability and hence T_R can be asymptotically equivalent to T_n when n → ∞.

Fig 2:

Rejection rates of the three approaches under different settings of n and p in Example 2.

Fig 3:

Power of the three approaches under different settings of n and p in Example 3.

4.3. Detecting nonlinear dependence.

We further provide several examples to justify the power of the rescaled distance correlation statistic in detecting nonlinear dependence in the regime of moderately high dimensionality. In the following simulation examples, the significance level of test is set as 0.05 and 2000 Monte Carlo replicates are conducted to compute the rejection rates.

EXAMPLE 4.

Let X = (X⁽¹⁾, …, X^(p))^T ~ N(0, I_p) and Y = (Y ⁽¹⁾, …, Y ^(p))^T satisfying Y (i) = (X(i))².

EXAMPLE 5.

Set $\mathrm{\Sigma }=\left({\sigma }_{i,j}\right)\in {ℝ}^{p\times p}$ with σ_i,j = 0.5^|i−j|. Let X = (X⁽¹⁾, …, X^(p)) ~ N(0,Σ) and Y = (Y ⁽¹⁾, …, Y ^(p))^T with Y ⁽ⁱ⁾ = (X⁽ⁱ⁾)².

For the above two examples, it holds that cov(X⁽ⁱ⁾,Y ^(j)) = 0 for each 1 ≤ i, j ≤ p. Simulation results on the power under Examples 4 and 5 for different settings of n and p are summarized in Table 4. Guided by Theorem 6, we set $p=2[\sqrt{n}]$ with [·] denoting the integer part of a given number. From Table 4, we can see that even though there is only nonlinear dependency between X and Y, the power of rescaled distance correlation can still approach one when the dimensionality p is moderately high. One interesting phenomenon is that the power in Example 5 is higher than that in Example 4, which suggests that the dependence between components may strengthen the dependency between X and Y.

Table 4.

Power of our rescaled test statistic with $p=2[\sqrt{n}]$ in Examples 4 and 5 (with standard errors in parentheses).

Example 4			Example 5
n	p	Power	n	p	Power
10	6	0.2765 (0.0100)	10	6	0.3060 (0.0103)
40	12	0.5165 (0.0112)	40	12	0.7005 (0.0102)
70	16	0.6970 (0.0103)	70	16	0.9380 (0.0054)
100	20	0.8220 (0.0086)	100	20	0.9885 (0.0024)
130	22	0.9270 (0.0058)	130	22	0.9995 (0.0005)
160	26	0.9550 (0.0046)	160	26	0.9990 (0.0007)

Moreover, we investigate the setting when one dimensionality is fixed and the other one tends to infinity.

EXAMPLE 6.

Set $\mathrm{\Sigma }=\left({\sigma }_{i,j}\right)\in {ℝ}^{p\times p}$ with σ_i,j = 0.7^|i−j|. Let X = (X⁽¹⁾, …, X^(p)) ~ N(0,Σ) and $Y={\left({\sum }_{i=1}^p{X}^{(i)}\right)}^2/p$.

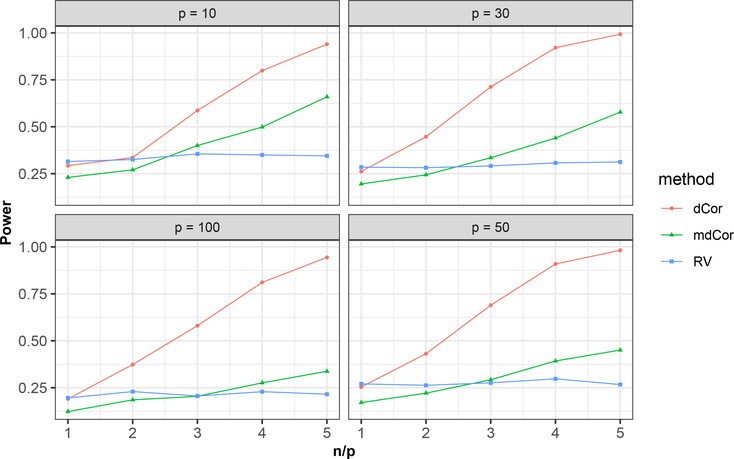
For Example 6, it holds that cov(X⁽ⁱ⁾,Y ) = 0 for each 1 ≤ i ≤ p and thus the dependency is purely nonlinear. We compare the power of our rescaled distance correlation statistic with the marginally aggregated distance correlation (mdCor) statistic (Zhu et al., 2020) and the linear measure of RV coefficient (Escoufier, 1973; Robert and Escoufier, 1976). The comparison under different settings of p and n are presented in Figure 4. We can observe from Figure 4 that under this scenario, the rescaled distance correlation statistic significantly outperforms the marginally aggregated distance correlation statistic. This is because the marginally aggregated statistic can detect only the marginal dependency between X and Y, while Y depends on the entire X jointly in this example. Since the RV coefficient measures the linear dependence, its power stays flat and low when the sample size increases.

Fig 4:

Comparison of power under different settings of n and p in Example 6.

These simulation examples demonstrate the capability of distance correlation in detecting nonlinear dependence in the regime of moderately high dimensionality, which is in line with our theoretical results on the power analysis in Theorem 6. Moreover, when X and Y depend on each other far from marginally, the marginally aggregated distance correlation statistic can indeed be less powerful than the rescaled distance correlation statistic.

5. Real data application.

We further demonstrate the practical utility of our normal approximation test for bias-corrected distance correlation on a blockchain application, which has gained increasing public attention in recent years. Specifically, we would like to understand the nonlinear dependency between the cryptocurrency market and the stock market through the test of independence. Indeed investors are interested in testing whether there is any nonlinear association between these two markets since they want to diversify their portfolios and reduce the risks. In particular, we collected the historical daily returns over recent three years from 08/01/2016 to 07/31/2019 for both stocks in the Standard & Poors 500 (S&P 500) list (from https://finance.yahoo.com) and the top 100 cryptocurrencies (from https://coinmarketcap.com). As a result, we obtained a data matrix of dimensions 755 × 505 for stock daily returns and a data matrix of dimensions 1095 × 100 for cryptocurrency daily returns, where the rows correspond to the trading dates and the columns represent the stocks or cryptocurrencies. Since stocks are traded only on Mondays through Fridays excluding holidays, we adapted the cryptocurrency data to this restriction and picked a submatrix of cryptocurrency data matrix to match the dates. Moreover, because some stocks and cryptocurrencies were launched after 08/01/2016, there are some missing values in the corresponding columns. We removed those columns containing missing values. Finally, we obtained a data matrix $X_{T\times N_1}$ for stock daily returns and a data matrix $Y_{T\times N_2}$ for cryptocurrency daily returns, where T = 755, N₁ = 496, and N₂ = 22. Although the number of cryptocurrencies drops to 22 after removing the missing values, the remaining ones are still very representative in terms of market capitalization, which include the major cryptocurrencies such as Bitcoin, Ethereum, Litecoin, Ripple, Monero, and Dash.

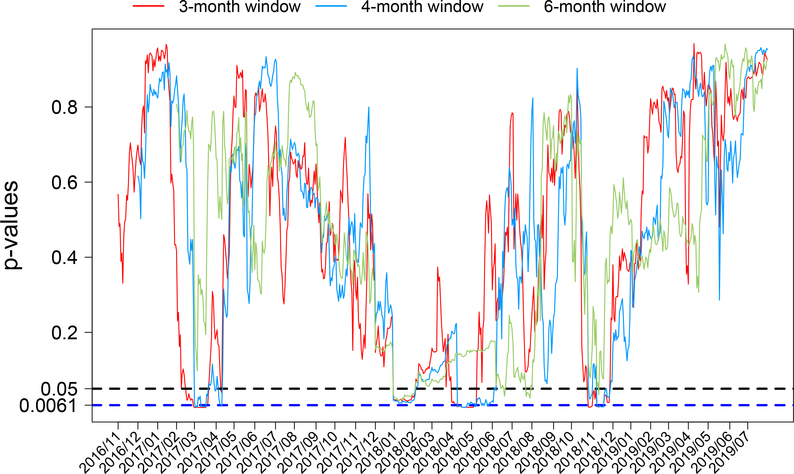
To test the independence of the cryptocurrency market and the stock market, we choose three-month rolling windows (66 days). Specifically, for each trading date t from 11/01/2016 to 07/31/2019, we set $X_{F_t\times N_1}$ as a submatrix of $X_{T\times N_1}$ that contains the most recent three months before date t, where F_t is the set of 66 rows right before date t (including date t). The data submatrix $Y_{F_t\times N_2}$ is defined similarly. Then we apply the rescaled test statistic T_n defined in (14) to $X_{F_t\times N_1}$ and $Y_{F_t\times N_2}$. Thus the sample size n = 66 and the dimensions of the two random vectors are N₁ = 496 and N₂ = 22, respectively. For each trading date, we obtain a p-value calculated by $1-\mathrm{\Phi }\left(T_n^{(t)}\right)$, where $T_n^{(t)}$ is the value of the test statistic based on $X_{F_t\times N_1}$ and $Y_{F_t\times N_2}$ and Φ(·) is the standard normal distribution function. As a result, we end up with a p-value vector consisting of $T_n^{(t)}$ for trading dates t from 11/01/2016 to 07/31/2019. In addition, we use the “fdr.control” function in R package “fdrtool,” which applies the algorithms in Benjamini and Hochberg (1995) and Storey (2002) to calculate the p-value cut-off for controlling the false discovery rate (FDR) at the 10% level. Based on the p-value vector, we obtain the p-value cut-off of 0.0061. The time series plot of the p-values is shown in Figure 5 (the red curve).

Fig 5:

Time series plots of p-values from 11/01/2016 to 07/31/2019 using three-month, four-month, and six-month rolling windows, respectively.

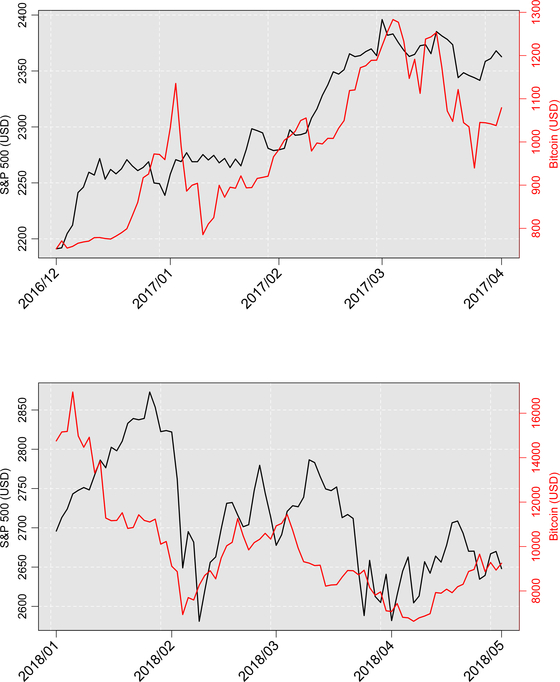
The red curve in Figure 5 indicates that most of the time the cryptocurrency market and the stock market tend to move independently. There are apparently two periods during which the p-values are below the cut-off point 0.0061, roughly March 2017 and April 2018. Since we use the three-month rolling window right before each date to calculate the p-values, the significantly low p-values in the aforementioned two periods might suggest some nonlinear association between the two markets during the time intervals 12/01/2016–03/31/2017 and 01/01/2018–04/30/2018, respectively. To verify our findings, noticing that Bitcoin is the most representative cryptocurrency and the S&P 500 Index measures the overall performance of the 500 stocks on its list, we present in the two plots in Figure 6 the trend of closing prices of Bitcoin and that of S&P 500 Index during the periods 12/01/2016–03/31/2017 and 01/01/2018–04/30/2018, respectively. The first plot in Figure 6 shows that the trends of the two prices shared striking similarity starting from the middle of January 2017 and both peaked around early March 2017. From the second plot in Figure 6, we see that both the prices of S&P 500 Index and Bitcoin dropped sharply to the bottom around early Febrary 2018 and then rose to two rekindled peaks followed by continuingly falling to another bottom. Therefore, Figure 6 indicates some strong dependency between the two markets in the aforementioned two time intervals and hence demonstrate the effective discoveries of dependence by our normal approximation test for biased-corrected distance correlation.

Fig 6:

Closing prices of Standard & Poors 500 Index and Bitcoin during the time periods 12/01/2016–03/31/2017 and 01/01/2018–04/30/2018, respectively. The black curve is for Standard & Poors 500 Index and the red one is for Bitcoin.

In addition, to show the robustness of our procedure and choose a reasonable length of rolling window, we also apply four-month and six-month rolling windows before each date t to test the independence between the cryptocurrency market and the stock market. The time series plots of the resulting p-values are presented as the blue curve and the green curve in Figure 5, respectively. From Figure 5, we see that the p-values from using the three different rolling windows (three-month, fourth-month, and six-month) move in a similar fashion. For the four-month rolling window, the p-value cut-off for FDR control at the 10% level is 0.0053. We observe that the time periods with significantly small p-values by applying four-month rolling window are almost consistent with those by applying three-month rolling window. However, when the six-month rolling window is applied, the p-value cut-off for FDR control at the 10% level is 0 and hence there is no significant evidence for dependence identified at any time point. This suggests that the long-run dependency between the cryptocurrency market and the stock market might be limited, but there could be some strong association between them in certain special periods. These results show that to test the short-term dependence, the three-month rolling window seems to be a good choice.

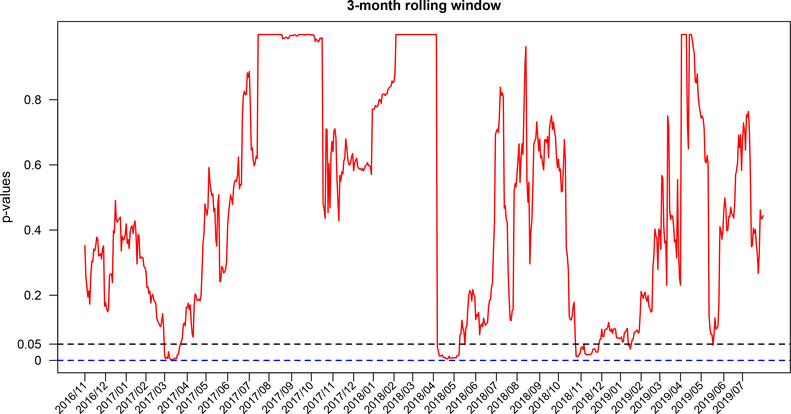
As a comparison, we conduct the analysis with the rescaled sample distance correlation statistic T_n replaced by the RV coefficient, which measures only the linear dependence between two random vectors. The three-month rolling window is utilized as before. We apply the function ‘coeffRV’ in the R package ‘FactoMineR’ to calculate the p-values of the independence test based on the RV coefficient. The time series plot of the resulting p-values is depicted in Figure 7. From Figure 7, we see that there are three periods in which the p-values are below the significance level 0.05, while there are four such periods in Figure 5 for p-values based on the rescaled sample distance correlation T_n from using three-month rolling window. Moreover, the four periods detected by T_n roughly cover the three periods detected by the RV coefficient. On the other hand, for the p-values based on the RV coefficient, the p-value cut-off for the Benjamini–Hochberg FDR control at the 10% level is 0, which implies that no significant periods can be discovered with FDR controlled at the 10% level. However, as mentioned previously, if we use T_n the corresponding p-value cut-off with the three-month rolling window is 0.0061 and two periods, roughly March 2017 and April 2018, are still significant. The effectiveness of these two periods are demonstrated in Figure 6. Therefore, compared to the linear measure of RV coeffcient, the nonlinear dependency measure of rescaled distance correlation is indeed more powerful in this real data application.

Fig 7:

Time series plot of p-values based on RV coefficient from 11/01/2016 to 07/31/2019 using three-month rolling window.

6. Discussions.

The major contributions of this paper are twofold. First, we have obtained central limit theorems for a rescaled distance correlation statistic for a pair of high-dimensional random vectors and the associated rates of convergence under the independence when both sample size and dimensionality are diverging. Second, we have also developed a general power theory for the sample distance correlation and demonstrated its ability of detecting nonlinear dependence in the regime of moderately high dimensionality. These new results shed light on the precise limiting distributions of distance correlation in high dimensions and provide a more complete picture of the asymptotic theory for distance correlation. To prove our main results, Propositions A.1–A.3 in Section A.4 of Supplementary Material have been developed to help us better understand the moments therein in the high-dimensional setting, which are of independent interest.

In particular, Theorem 6 unveils that the sample distance correlation is capable of measuring the nonlinear dependence when the dimensionalities of X and Y are diverging. It would be interesting to further investigate the scenario when only one of the dimensionalities tends to infinity and the other one is fixed. Moreover, it would also be interesting to extend our asymptotic theory to the conditional or partial distance correlation and investigate more scalable high-dimensional nonparametric inference with theoretical guarantees, for both i.i.d. and time series data settings. These problems are beyond the scope of the current paper and will be interesting topics for future research.