Deep neural network-based detection and segmentation of intracranial aneurysms on 3D rotational DSA

Abstract

Objective

Accurate diagnosis and measurement of intracranial aneurysms are challenging. This study aimed to develop a 3D convolutional neural network (CNN) model to detect and segment intracranial aneurysms (IA) on 3D rotational DSA (3D-RA) images.

Methods

3D-RA images were collected and annotated by 5 neuroradiologists. The annotated images were then divided into three datasets: training, validation, and test. A 3D Dense-UNet-like CNN (3D-Dense-UNet) segmentation algorithm was constructed and trained using the training dataset. Diagnostic performance to detect aneurysms and segmentation accuracy was assessed for the final model on the test dataset using the free-response receiver operating characteristic (FROC). Finally, the CNN-inferred maximum diameter was compared against expert measurements by Pearson’s correlation and Bland-Altman limits of agreement (LOA).

Results

A total of 451 patients with 3D-RA images were split into n = 347/41/63 training/validation/test datasets, respectively. For aneurysm detection, observed FROC analysis showed that the model managed to attain a sensitivity of 0.710 at 0.159 false positives (FP)/case, and 0.986 at 1.49 FP/case. The proposed method had good agreement with reference manual aneurysmal maximum diameter measurements (8.3 ± 4.3 mm vs. 7.8 ± 4.8 mm), with a correlation coefficient r = 0.77, small bias of 0.24 mm, and LOA of -6.2 to 5.71 mm. 37.0% and 77% of diameter measurements were within ±1 mm and ±2.5 mm of expert measurements.

Conclusions

A 3D-Dense-UNet model can detect and segment aneurysms with relatively high accuracy using 3D-RA images. The automatically measured maximum diameter has potential clinical application value.

Introduction

The worldwide prevalence of intracranial aneurysm (IA) disease is estimated to be 3.2% (95% [CI], 1.9%–5.2%).¹ Image interpretation can be time-consuming, particularly for aneurysm maximal diameter measurement,² which is an important measurement for patient risk-stratification.³ Aneurysm Size has been regarded as an important factor in the selection of the optimal management of IA.⁴ Perhaps more importantly, this measurement is subject to significant inter- and intra-observer variability,^5,6 which poses a significant challenge to reliably determining management pathways for patients. Compounding this issue is the increasing availability of imaging which has led to an increase in the number of radiological examinations that must be considered, leading to radiologists' “burn out”.⁷

Computer-assisted detection (CAD) systems have long been developed toward reducing measurement variability in this, and other pathologies for which patient care relies on manual measurements. A number of these studies have used support vector machines (SVM) or random forests (RF) for feature extraction.^8–10 However, either low sensitivity or high FPs has limited their added value for clinical use.^11–13

The development of deep convolutional neural networks (CNN) in recent years has emerged as a promising approach for aneurysm detection.^14,15 At present, most CNNs typically perform inference from 2D images as inputs, which may be sub-optimal whenever volumetric imaging information is available. More importantly, most current CAD systems for intracranial aneurysms are not designed to derive aneurysm size following detection.^16–18 Recent studies have begun to apply 3D CNNs to medical image processing with encouraging early results. A recently-developed CNN, termed the U-Net architecture, has demonstrated the ability to achieve accurate segmentation of 3D medical images from sparse annotations and for various tissues.¹⁹ However, to the best of our knowledge, this architecture has not been applied to IA detection and segmentation to date.

Most CAD studies to date have used non-invasive magnetic resonance angiography (MRA) for aneurysm evaluation.^{12,15–18,20–23} Although MRA has superior soft-tissue contrast and is used widely as a “first-line” diagnostic imaging modality, it is in part limited by low resolution and flow artifacts.²⁴ Thus to date, DSA remains the reference standard for the detection and morphological evaluation of intracranial aneurysms (IA).^24,25 A more recent DSA imaging technology, 3D-RA enables the interventionalist to view the intracranial vasculature at arbitrary angles and has now been widely implemented in clinical practice in this domain.^26,27 CAD of IA on 3D-RA images has rarely been explored to date.

The purpose of this study was to develop a 3D convolutional neural network based on the UNet architecture to detect and segment IA from reference-standard 3D-RA images. We then sought to provide a preliminary evaluation of the accuracy and clinical utility of the trained model, in terms of accuracy of maximal diameter measurements.

Materials and methods

Data acquisition

The study was approved by the ethics board of [blinded for review] Hospital. The board deemed this cross-sectional retrospective study to be minimal risk and waived the requirement for informed consent. Candidate patients were identified by a PACS system search from July 2014 to August 2018 with the following keywords: “intracranial aneurysm”, “DSA images” and “5D DSA”. We then filtered this list by review of the radiology report and images using the following criteria: (1) at least one untreated aneurysm; and, (2) the study contained a 3D-RA scan. The resulting studies were extracted and formed our final dataset.

In total, the final dataset included studies collected in three different angiographic units: a Siemens Axiom Artis (Siemens Healthcare, Erlangen, Germany); a GE Innova IGS 630 (GE Healthcare, Chicago, US); and a Phillips Allura Xper FD20 (Philips, Amsterdam, Netherlands). All angiographic studies were performed with Ultravist 300 mg I/mL (Schering AG, Berlin, Germany) as the contrast agent. Acquisition parameters were as follows: matrix size 1024 × 1024 (all systems), voxel size 0.308 × 0.308, 0.340 × 0.340, and 0.370 × 0.370 mm, for each unit respectively. The 3D-RA images are composed of 2D image projections captured at 133 angles between the right anterior oblique (RAO) and the left anterior oblique (LAO) positions.

Data labelling

DSA images were randomly and evenly divided into 5 parts and labeled by five board-certified interventional neuroradiologists, each with more than 5 years of experience in DSA interpretation. To ensure the CNN model was trained and tested with the best available data, all readers were allowed to refer to the original finalized radiology report of the study, which itself had been reported by two individual neuroradiologists, as is the current clinical practice at our institution. Finally, one of the five neuroradiologists reviewed all the labeled datasets, discrepancy was resolved by a consensus discussion. The aneurysms in those DSA images deemed positive for the presence of an IA were then segmented using ITK-SNAP’s paint tool. The contrast was first adjusted to obtain a clear view of the intracranial arteries. Then, for every aneurysm, about 10 to 15 projections were annotated at fixed intervals.

Data preprocessing

Both the DSA projection image data and, consequently, the manual expert aneurysm segmentation annotations performed, can be considered as sinograms, and as such, we were able to use them to reconstruct a 3D volumetric image and corresponding 3D segmentation annotation data set for each study, by using an inverse Radon transform (Supplemental material).

An intensity windowing image filter from ITK was first applied to the DSA images to enhance the contrast of intracranial vessels against the background. Bilinear interpolation was then applied to the annotation projections to “upsample” the sinogram. Further morphological erosion and closing were applied to the segmentation volumetric reconstruction to smooth the resulting volumetric aneurysm segmentation mask. The effect of this step is expected to be minimal; any smoothing of the segmentation mask performed by this process is unlikely to lead to an effect larger than errors involved in the manual tracing of aneurysm volumes in the images by human operators. Finally, all reconstructed 3D volumes were downsampled by a factor of 8 and cropped to 88 × 80 × 80 pixels, with isotropic spacing that was amenable for use as inputs to a 3D CNN model.

Model architecture

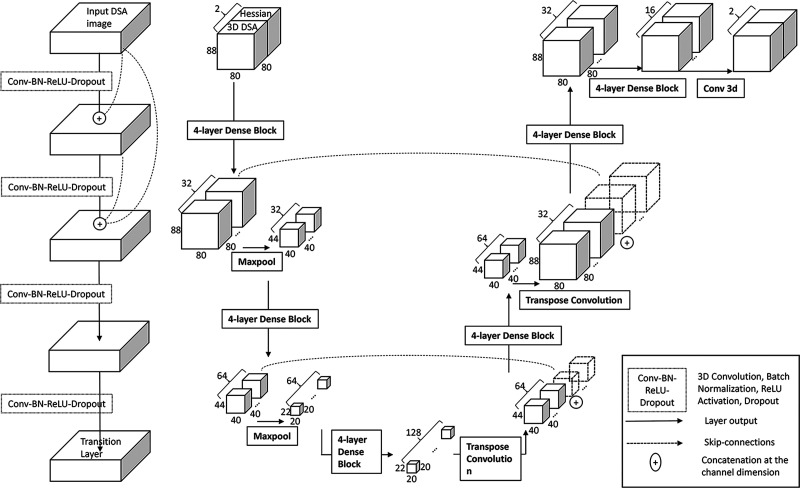
Our model is a modified U-net with dense blocks (Figure 1). Within the dense blocks, each layer is directly connected to every other layer, allowing an identity transform in between individual layers.²⁸ Furthermore, similar “skip” connections are included in the U-net across opposite layers (downsample encoding, versus upsample decoding), which help to localize a large number of features from the encoding path.²⁹ The input to the model is the fully reconstructed 3D DSA volume and its Hessian filtered 3D volume. The 3D Hessian filter produces a second-order derivative of the image.³⁰ This filter is used to make the edge of the vessel more prominent, as the gradient of the pixel intensity at the border of the vessel is much higher than its center. This filtered Hessian volume is stacked together with the original DSA volume and feed as a two-channel image into the model.³¹ To train the model, we minimized the cost function using the Adam Optimizer (Adaptive Moment Estimation).³² A combination of weighted Dice loss and weighted cross-entropy loss³³ was used for the cost function as this helps address the class imbalance of non-aneurysm background pixels in segmenting small aneurysms.³⁴ The network outputs two volumes of the same size, then the softmax function was applied to the network outputs. The output of the softmax function giving voxel-wise probabilities of background versus aneurysm was stored in a 3D matrix. Applying a threshold to this probability matrix produces a segmentation mask identical to expert annotation segmentation masks. The model’s segmentation is considered a hit if it overlaps with the human labels with DICE > 0.5 and a miss otherwise. This is then used to compute the FROC.

Figure 1.

Four-layer dense block and dense-block UNet model architecture for aneurysm detection. The left figure shows the components of the four-layer dense block, while the right figure shows the dense-block UNet model architecture for aneurysm detection.

We trained the model using batch normalization for model regularization³⁵ and a dropout rate of 0.3 to prevent overfitting.³⁶ The model was trained with an initial learning rate of 0.01 with an exponential decay rate of 0.99 for every 10,000 steps. This hyperparameter tuning was performed by testing candidate model performance on the validation dataset. Detailed parameters used in our model are shown in Supplemental Table 1 and Supplemental Text.

Maximal diameter calculation

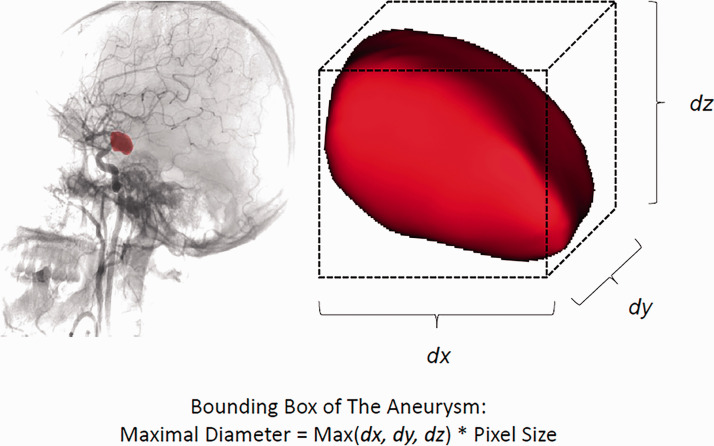
To analyze the segmentation results, the maximal diameter of the predicted aneurysm segmentation labels as well as the radiologists’ annotations of the positive cases in the test set were compared to determine their correlation. We first used a threshold to obtain the final segmentation predictions from the CNN-inferred probability maps. This threshold was selected once, a priori to final testing, as the threshold that resulted in the maximum pixelwise Dice score to expert annotations on the validation set. The maximal diameter was then calculated from the bounding box of each detected aneurysm, using the number of pixels of the longest dimension and pixel size, as shown in Figure 2.

Figure 2.

Calculating the size of an aneurysm using a bounding box. Left: angiography shows the mask (red) of an PCoA aneurysm; Right: image showing closeup of the reconstructed aneurysm; dx, dy, dz represent the number of pixels for length, width and height of the aneurysm. Aneurysm maximal diameter was defined as the maximal value of these three parameters.

Statistical analysis

All analyses were performed using MATLAB (version 2017a, MathWorks). A P value < 0.05 was considered statistically significant. Continuous data were expressed as mean ± standard deviation and categorical data were expressed as counts or percentages. The model’s diagnostic accuracy to detect aneurysms was evaluated by the sensitivity and FROC in the validation and test dataset. From the FROC, we can more intuitively see the trade-off of the increase of sensitivity over the increase of FP per case. Model segmentation results were evaluated using the clinically-relevant metric of maximal diameter using the Pearson Correlation Coefficient, Student’s t-test, Bland-Altman bias, and limits of agreement between reader annotations and prediction model-derived measurements.

Results

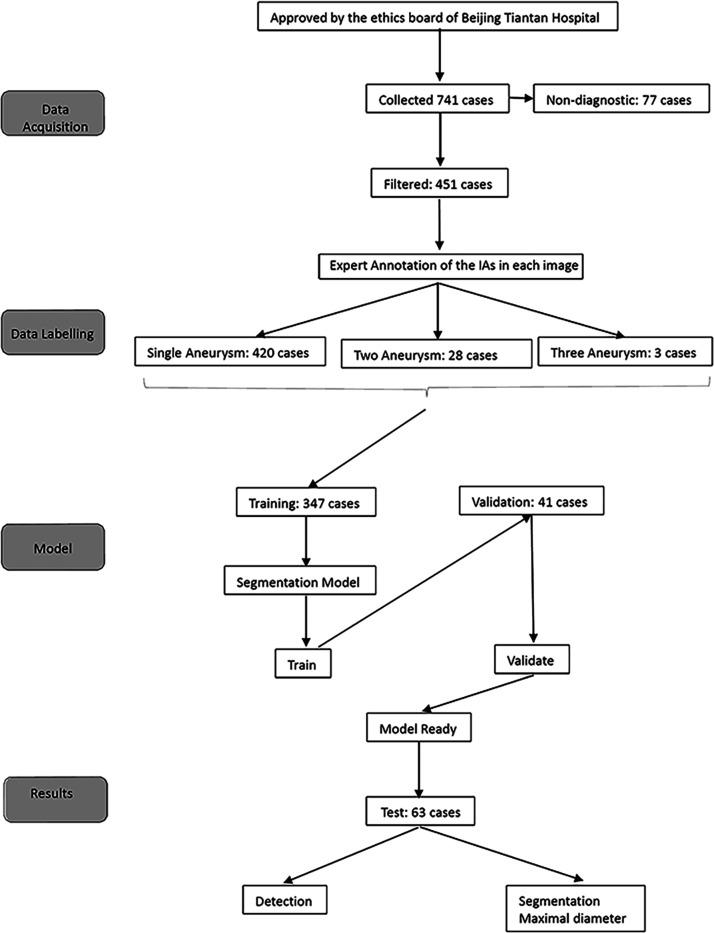
A total of 451 patients with rotational DSA images containing untreated aneurysms were extracted from 728 collected cases. We then randomly assigned them to the training (347) and validation (41) datasets in a ratio of 9:1 so as to maximize training data. A further 63 cases were used as the test dataset. A flowchart of study inclusion and data analyses is shown in Figure 3. Patient demographics and clinical characteristics are provided in Table 1.

Figure 3.

Flow chart of study.

Table 1.

The baseline of data set.

	Train	Validation	Test
No. of examinations	347	41	63
No. of aneurysms	373	43	69
No. of female patients	246 (65.8%)	26 (63.4%)	40 (60.9%)
Mean age	55 ± 11	55 ± 10	56 ± 11
No. of postoperative examinations
Location
ACA	67	4	15
MCA	21	1	15
ICA	212	30	32
PCA	9	0	4
BA	22	0	0
VA	42	8	3
Multiplicity
Single	323	39	58
Double	22	2	4
Triple	2	0	1
Size (mm)
≤5	130	16	30
5–10	156	20	28
10–15	50	4	5
15–20	19	2	6
20–25	11	1	0
≥25	7	0	0
Average (mm)	8.5	7.4	7.1
Imaging platform
Siemens	148	17	27
General Electric	77	10	14
Phillips	122	14	22

The total time for training over the 347 training samples was 55.9 hours with an average time of 9.6 min/case using a Tesla P100 GPU. Inference for the 63 test cases required a total of 83.7 s, averaging 1.3 s per sample.

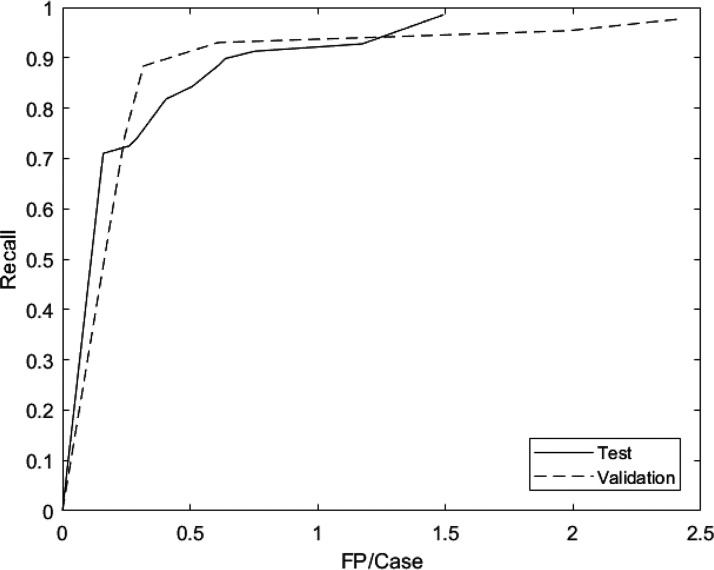
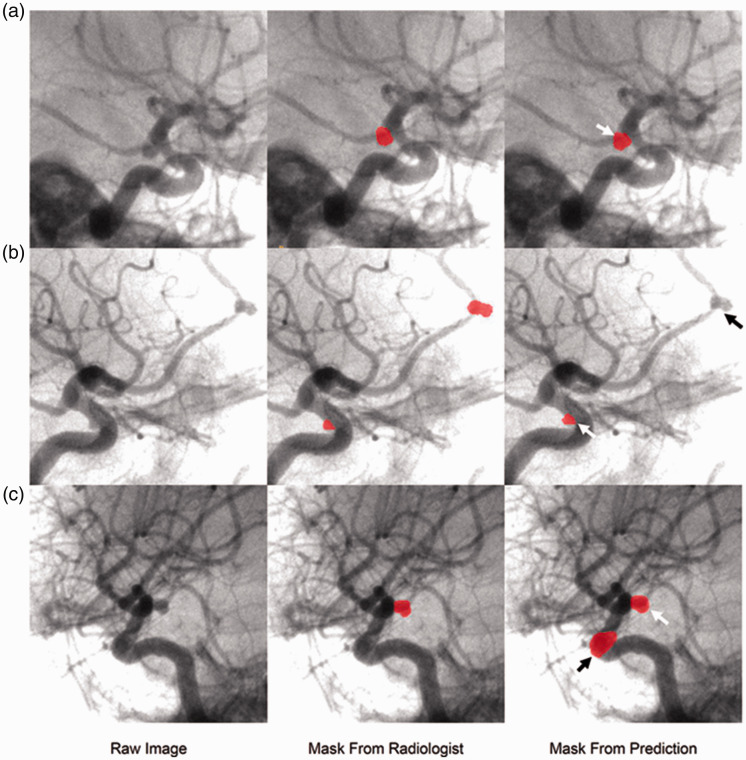
In the test set, sensitivity was 71% at 0.159 FP/case and 98.6% at 1.49 FP/case (Figure 4). At a sensitivity of 88.4% (61 of 69 aneurysms successfully detected), there was 0.61 FP/case. A subgroup analysis of the 8 missed aneurysm (false negatives) was shown in Table 2. Of the 8 missed aneurysms, all were significantly further from the circle of Willis; four were at the A2 segment of the anterior cerebral artery, two were at the middle cerebral artery bifurcation, and the remaining two were at the anterior communicating artery. Of these 8 missed aneurysms, only 1 was larger than 5 mm and 7 were smaller than or equal to 5 mm. We also observed that the model’s FPs were mainly localized around the Circle of Willis and around the carotid artery siphons. The top three locations for FPs were the praclinoid segment, the origin of the posterior communicating artery, and the anterior communicating artery. Finally, in the 5 patients with multiple aneurysms, 4 had a false negative. This could imply that the model does not perform as well in predicting the presence of multiple aneurysms, which may be a consequence of the imbalance of training cases in this category. Examples of true positive (TP), false negative (FN), and FP segmentations are shown in Figure 5.

Figure 4.

FROC curve for validation and test datasets. The model achieved 74.4% sensitivity at 0.24 FP/case and 97.7% sensitivity at 2.4 FP/case in validation data set, and 0.710 sensitivity at 0.159 FP/case and 98.6% sensitivity at 1.49 FP/case in test set.

Table 2.

Subgroup analysis of false negative base on the location and aneurysm size at a sensitivity of 88.4% with 0.61 FP/case.

	Total	TP	FN
Region
ACA	15	11	4
ICA	32	31	1
MCA	15	13	2
PCA	4	4	0
VA	3	3	0
Size (mm)
≤5	30	23	7
5–10	28	28	0
10–15	5	4	1
15–20	6	6	0

FP: false positive; TP: true positive; FN: false negative.

Figure 5.

Examples of TP, FN and FP of the test results. A: oblique angiogram of right internal carotid artery; raw image and mask from radiologist shows a PCoA aneurysm; arrow on mask from prediction indicates the TP aneurysm; B: oblique angiography of right internal carotid artery, the raw image and mask from radiologist’s interpretation indicates a paraclinoid aneurysms and an ACA (A2); white arrow and black arrow on predicted mask demarcate the TP and a FN aneurysm. C: oblique angiography of right internal carotid artery; raw image and mask from radiologist’s interpretation of a PCoA aneurysm; white arrow and black arrow on mask from prediction showed the TP and a FP aneurysm.

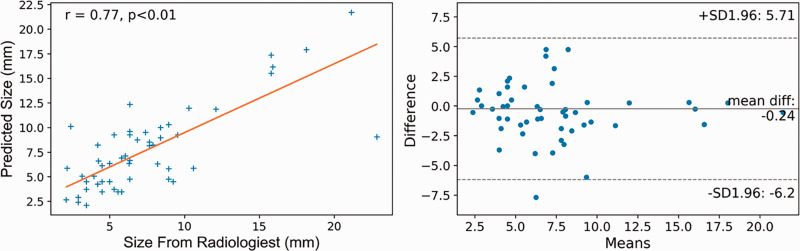
The mean maximal diameter was 7.8 ± 4.8 mm for the radiologists’ annotations, and 8.3 ± 4.3 mm for the predicted segmentation labels. The predicted mask was on average 6% larger than the radiologist’s annotations (p < 0.01). The maximal diameter of the predicted segmentation labels was strongly positively correlated with the radiologist’s measurements (Pearson correlation coefficient r = 0.77, p < 0.01), and there was a small bias (0.24 mm) of maximal diameter between radiologist measurements and predicted values and a range of the limit agreement of -6.2 to 5.7 mm. 37.0% and 77% of diameter measurements were within ±1 mm and ±2.5 mm of expert measurements. Correlation and Bland-Altman plots are illustrated in Figure 6.

Figure 6.

Maximal diameter measurement agreement plot of the test results. Left, Correlation matrix showing positive correlation between the maximal diameters of the model’s aneurysm segmentation result and radiologists’ annotation, with a Pearson correlation coefficient r = 0.77 (p < 0.01); right, Bland–Altman plot showing a small bias (0.24 mm) of maximal diameter between radiologist measurements and predicted values, and a range of the limit agreement of −6.2 to 5.7 mm. 37.0% and 77% of diameter measurements were within ±1 mm and ±2.5 mm of expert measurements.

Discussion

Although DSA is the reference standard diagnostic imaging modality for cerebral aneurysm detection, CAD using this modality remains relatively unexplored. We trained a state-of-the-art 3D-Dense-UNet using 3D-RAs to evaluate feasibility and efficacy for automated detection and volumetry of these aneurysms. The model achieved high sensitivity with relatively low FPs. Besides, the maximal diameter of TP aneurysms was derived automatically from model predictions, with the good agreement (Pearson r = 0.77) between radiologist’s measurements and the automated CNN-based measurements. This CAD system may thus aid clinical interpretation of IA.

Several CAD systems have been developed for IA detection using MRA or CTA[16,372,021,152,317,218]. Nomura et al. developed a web-based CAD platform that achieved a sensitivity of 89.5% at 3 FPs/case (median size 4-5mm).³⁷ Ueda et al. used a “ResNet-18” CNN architecture to detect IA in a large, multi-center MRA dataset, achieving a sensitivity of 91.2% at 10 FPs/case in the internal test-dataset (mean size 4.1 ± 3.2 mm). However, low sensitivity/relatively high FPs limited potential clinical application. In our study, sensitivity was 71% at 0.159 FPs/case, and sensitivity was 98.6% at 1.49 FPs/case (median size 6.2 mm). To our knowledge, our CAD system achieved the best detection results reported to date. We posit this may be due to the following reasons: 1) DSA has intrinsically higher accuracy than MRA for aneurysm detection; 2) we used a state-of-the-art 3D CNN method that has been highly successful for medical image segmentation; and, 3) the mean size of aneurysms in our study is larger than prior studies, which may suggest a limitation in that accuracy for smaller aneurysms may be lower than our findings.

Most current studies use non-invasive MRA to train CAD models. However, detection accuracy on MRA was limited, especially for smaller aneurysms.^38,39 Sichtermann at al have reported the influence of aneurysm size on detection sensitivity.¹⁸ Their study showed that sensitivity varied from 0.23–0.38 in small aneurysms (≤3mm), and from 0.91-0.96 in medium-sized aneurysms (>3 and ≤7 mm). DSA remains the reference standard imaging method for the detection and morphological evaluation of IA.^24,25 Our CAD system was evaluated on 3D-RA, with the goal of replicating clinical practice for diagnosis by radiologists, and in this sense, it is expected to reduce FPs and also to simplify the review of model inferences by the interpreting radiologist. Our CAD system achieved 76.7% sensitivity for small aneurysm (<5 mm) and 97.4% sensitivity for large aneurysm (≥5mm).

FPs and FNs for our trained CAD model varied among different IA locations. Nakao et. al. reported that most of the FPs were observed at bifurcations of small branches and at high-curvature tortuous segments of arteries.¹⁵ Similarly, in our study, the top three FPs locations were the paraclinoid segment, PCoA, and ACoA regions. We suspect this is because the ectatic meandering vessels or high concentration of branching arteries in these areas could mimic aneurysms. FNs are also known to vary among different locations. Sichtermann et al. divided aneurysms into ICA, MCA, Anterior, and Posterior groups,¹⁸ showing that sensitivity was lowest at the anterior position. In our results, the 8 missed aneurysms were away from the circle of Willis, with the A2 segment the most common location for FNs. Since the proportion of aneurysms that are away from the circle of Willis is small, it is anticipated our CNN model could become progressively more accurate as larger training datasets become available.

Maximal diameter is an important factor in aneurysm rupture risk evaluation³ and the key parameter in determining the treatment strategy for patients with IA.⁴⁰ Previously reported CAD systems have rarely been developed (or able) to derive aneurysm size from detection results. Stember et. al. used a 2D CNN to predict linear size and area of 14 basilar artery aneurysms on maximum-intensity projection (MIP) MRA images.²³ In that study, predicted linear size and area differed from expert radiologist’s measurements by 27% and 30%, respectively. Such measurement errors may reduce the clinical utility of a CAD system. In our study, we used a 3D-Dense-UNet based detection and segmentation algorithm to obtain pixel-wise measurements from a volumetric reconstruction based on a Radon transform by treating the projection DSA images as a sinogram. Our CAD system demonstrated a relatively good segmentation result, with a small difference (6%) of maximal diameter between CAD-derived measurements and expert radiologist’s annotations.

Our study has several limitations. First, deep learning was performed on only 3D-RA images. A wider range of imaging modalities should be included in a future study for comparison of the accuracy of CAD systems for different modalities. Secondly, the training dataset did not contain sufficient data for aneurysms in certain anatomic areas nor of sufficient breadth of IA sizes encountered clinically. The results of our study may thus not be generalizable to clinical practices encountering a different proportion of anatomic sites and IA sizes. Thirdly, our study excluded treated aneurysms, as there was no difference in their detectability compared with that of other aneurysms. Fourthly, Using the largest dimension from the aneurysm bounding box would lead to a systematic under-representation of the aneurysm's longest axis. Fifthly, even though we have a strict pipeline for aneurysm annotation, we didn’t report the inter-rater reliability. Sixthly, even though we used 3D-RA data, not all of these images had good subtraction quality. While the inclusion of slightly ‘noisy’ data may be regarded as a form of data augmentation that serves to increase deep learning model robustness, this may have negatively impacted our evaluation results during inference. Lastly, geometry parameters such as aneurysm size, aspect ratio, and lobulation which are regarded as important characteristics for aneurysm risk stratification, did not explore here. The measurement of all these metrics based on the precise segmentation of intracranial aneurysms. A limit agreement of −6.2 to 5.7 mm was not enough to guarantee the calculation accuracy of these geometry metrics. In the future, more advanced networks are wanted to achieve better segmentation results of intracranial aneurysms. All these limitations could generate study bias.

Conclusion

A combination of 3D-Dense-UNet model and 3D-RA images could achieve high sensitivity in IA detection with a relatively low FP rate. Meanwhile, maximal diameter derived from prediction mask showed good clinical application prospect.