Skip to main content
PMC home page
Journal of Applied Crystallography logoLink to Journal of Applied Crystallography
. 2021 Sep 4;54(Pt 5):1521–1529. doi: 10.1107/S160057672100755X

reciprocalspaceship: a Python library for crystallographic data analysis

Jack B Greisman a, Kevin M Dalton a, Doeke R Hekstra a,b,*
PMCID: PMC8493618  PMID: 34671231

reciprocalspaceship is a Python library for analyzing and manipulating reflection data from crystallography experiments. Using this library, it is possible to work interactively with crystallographic data, enabling easy integration with modern scientific computing libraries and supporting the rapid prototyping of new crystallographic methods and analyses.

Keywords: X-ray crystallography, data analysis, Python

Abstract

Crystallography uses the diffraction of X-rays, electrons or neutrons by crystals to provide invaluable data on the atomic structure of matter, from single atoms to ribosomes. Much of crystallography’s success is due to the software packages developed to enable automated processing of diffraction data. However, the analysis of unconventional diffraction experiments can still pose significant challenges – many existing programs are closed source, sparsely documented, or challenging to integrate with modern libraries for scientific computing and machine learning. Described here is reciprocalspaceship, a Python library for exploring reciprocal space. It provides a tabular representation for reflection data from diffraction experiments that extends the widely used pandas library with built-in methods for handling space groups, unit cells and symmetry-based operations. As is illustrated, this library facilitates new modes of exploratory data analysis while supporting the prototyping, development and release of new methods.

1. Introduction  

The analysis of most diffraction experiments begins with processing diffraction images and ends with refining an atomic model that is consistent with the observed data in order to answer a scientific question. Numerous software suites and command-line applications address different stages of the processing pipeline and these diverse programs are typically combined to address the challenges of a particular data set (Adams et al., 2010 ▸; Winn et al., 2011 ▸; Winter et al., 2018 ▸; Grosse-Kunstleve et al., 2002 ▸; Kabsch, 2010a ▸,b ▸; Otwinowski & Minor, 1997 ▸). However, many novel diffraction experiments do not fit easily into the processing pipelines established within existing crystallographic software. Such experiments often require custom scripts and programs to analyze the resulting data. Recent examples of such experiments include time-resolved pump–probe experiments that investigate the structural dynamics within room-temperature crystals (Hekstra et al., 2016 ▸; Dods et al., 2021 ▸; Wickstrand et al., 2020 ▸) and new approaches to phasing (Garcia-Bonete & Katona, 2019 ▸; Hatti et al., 2021 ▸). New software is needed to facilitate such custom analyses and improve the development, reproducibility and adoption of novel diffraction experiments.

A software library supporting such experiments must provide built-in methods to handle space groups, unit cells and symmetry operations. This first requirement is met by several crystallographic libraries for Python, including the Computational Crystallography Toolbox (CCTBX) (Grosse-Kunstleve et al., 2002 ▸) and GEMMI (Wojdyr, 2021 ▸). However, in our experience, exploratory analysis of reflection data and the development of new analysis methods would, in addition, greatly benefit from seamless integration with existing scientific computing software, including NumPy (Harris et al., 2020 ▸) and SciPy (Virtanen et al., 2020 ▸). This requirement is not met by the existing libraries, which use internal data structures that are not directly compatible with NumPy. As we show here, meeting this additional requirement enables crystallographers to deploy the rich arsenal of data analysis, statistics and machine-learning tools developed across other disciplines.

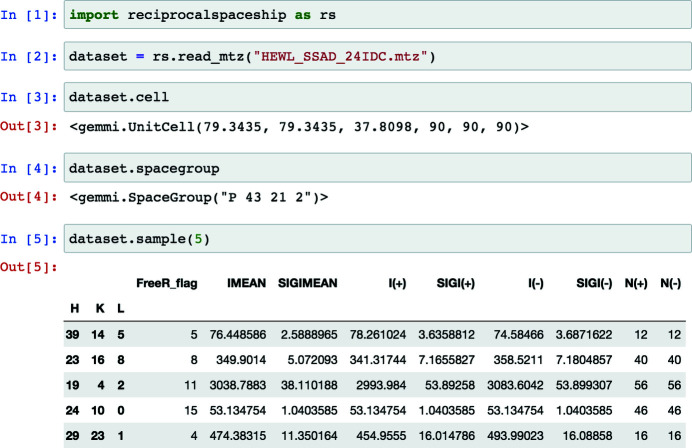
Key to such integration with scientific Python software is the observation that crystallographic data are inherently tabular due to Bragg’s law, with each observed reflection described by a Miller index. This property underlies many of the file formats for storing diffraction data: integrated intensities and any reflection-specific metadata are typically stored with the associated Miller index (see Fig. 1 ▸). For analysis in Python, tabular data are commonly represented using the pandas software library (Reback et al., 2021 ▸). pandas.Data­Frame objects provide support for the arbitrary manipulation of tabular data, storage of heterogeneous data types, and easy integration with any scientific computing or machine-learning library that supports NumPy arrays (Harris et al., 2020 ▸).

Figure 1.

Figure 1

Open in a new tab

A screenshot demonstrating the use of reciprocalspaceship in a Jupyter notebook. DataSet objects can be used to represent reflection data with associated unit-cell and space-group information.

Because of the tabular nature of crystallographic data and the widespread use of pandas in data science, we sought to develop a library that extends the DataFrame for reflection data by providing built-in support for space groups, unit cells and symmetry operations. This library, reciprocalspaceship, can be used to inspect reflection data, to develop new crystallographic methods and to release reproducible analysis pipelines for diffraction experiments. By embracing the norms for data science in Python, reciprocalspaceship will enable the development of new methods by the next generation of crystallographers.

2. reciprocalspaceship library  

2.1. Mission statement  

reciprocalspaceship is a free and open-source software library with the primary goal of simplifying the analysis of crystallographic data in Python. To achieve this goal, we sought to design a software library that is intuitive for both crystallographers and Python programmers. This requires full support for common crystallographic operations, as well as easy integration with the scientific computing and machine-learning libraries that are developed and maintained by the Python community.

2.2. Design  

The DataFrame is the core abstraction in pandas. reciprocalspaceship provides a DataSet class which extends the DataFrame, augmenting it to represent reflection data from diffraction experiments. DataSet objects store reflection data along with the associated space group and unit cell, and can be initialized from common reflection file formats such as MTZ files (Fig. 1 ▸). By extending the pandas DataFrame, it is possible to preserve its core functionality while adding built-in methods to support common crystallographic operations. These operations use the GEMMI library to represent space groups and unit cells (Wojdyr, 2021 ▸) and have been vectorized to increase performance.

This design allows reciprocalspaceship to complement the functionality of libraries such as GEMMI by providing data scientists familiar with the Python scientific computing ecosystem with an interface to reflection data that meets their expectations. In this way, reciprocalspaceship helps experts from other fields bring their perspectives and machine-learning tools to crystallography.

Furthermore, this library supports the use of MTZ files, allowing users to interface easily with existing and widely used computational crystallography infrastructure, such as CCTBX (Grosse-Kunstleve et al., 2002 ▸), CCP4 (Winn et al., 2011 ▸) and PHENIX (Adams et al., 2010 ▸). To support compatibility with MTZ files, reciprocalspaceship provides custom data types to represent different crystallographic data, such as intensities, structure factor amplitudes or phases. To ensure compatibility with other Python libraries, these data types are all represented internally using NumPy arrays of either 32-bit integer or floating-point values. Methods are also provided for inferring relevant data types based on standard MTZ column labels used to describe the data. DataSet objects can, moreover, contain any data type supported by pandas, including generic Python objects.

2.3. Features  

The primary capabilities of this library are provided through the DataSet object, which builds on the core features of the pandas DataFrame to provide crystallographic support. DataSet objects can represent both merged and unmerged reflection data and provide the attributes and methods that are summarized in Table 1 ▸.

Table 1. Core features of reciprocalspaceship.DataSet objects.

Attributes
cell Unit-cell parameters
spacegroup Space-group information
merged Identifier for merged/unmerged data
acentrics Access acentric reflections in DataSet
centrics Access centric reflections in DataSet
   
Methods
(i) Input/Output
from_gemmi() Create DataSet object from gemmi.Mtz
to_gemmi() Create gemmi.Mtz object from DataSet
write_mtz() Write DataSet to an MTZ file
   
(ii) Symmetry
apply_symop() Apply symmetry operation to reflections in DataSet
expand_anomalous() Expand data by applying Friedel operator (\overline{h},\overline{k},\overline{l})
expand_to_p1() Generate all symmetrically equivalent reflections
hkl_to_asu() Map reflections to reciprocal-space asymmetric unit
hkl_to_observed() Map reflections to observed Miller indices
   
(iii) Annotation  
compute_dHKL() Compute the real-space resolution of each reflection
compute_multiplicity() Compute the multiplicity of each reflection
label_absences() Label systematically absent reflections
label_centrics() Label centric reflections
   
(iv) Reshaping
stack_anomalous() Convert anomalous data from two- to one-column format
to_reciprocalgrid() Convert reflection data to 3D array populated at Miller indices
unstack_anomalous() Convert anomalous data from one- to two-column format
   
(v) Utilities
assign_resolution_bins() Assign reflections in DataSet to resolution bins
canonicalize_phases() Canonicalize all phase data to fall between [−180, 180) degrees
infer_mtz_dtypes() Infer MTZ dtypes from column names and underlying data
Open in a new tab

In addition to the DataSet object, reciprocalspaceship provides several algorithms that can be used for analysis. These include merge(), which implements the averaging of unmerged reflection data using maximum-likelihood weights, and scale_merged_intensities(), which implements the French–Wilson algorithm to account for negative merged intensities (French & Wilson, 1978 ▸). These implementations can serve as templates for the development of new analysis methods using reciprocalspaceship. The set of algorithms offered through this library will continue to expand as users implement new analyses intended for broader adoption.

2.4. Development and documentation  

reciprocalspaceship is maintained on GitHub under a permissive MIT license in order to foster community involvement in its development, testing and documentation. Every change to the source code is assessed using an automated testing suite in order to support continuous integration (Krekel et al., 2020 ▸). reciprocalspaceship is available through the Python Package Index (PyPI; https://pypi.org/) and can be installed on most systems using pip. Documentation is automatically generated from the reciprocalspaceship GitHub repository to ensure up-to-date information is available for users. The website includes a User Guide section describing the design and features of reciprocalspaceship and examples that use the library for crystallographic applications. The documentation also includes a guide for developers to support users who wish to contribute new features or methods to the library. By committing to an open-source development model, it will be possible to maintain this library to meet the evolving needs of crystallographers.

3. Examples  

The following examples demonstrate the use of reciprocalspaceship in the analysis of crystallographic data. These examples cover the merging of scaled observed intensities, analyzing anomalous differences from a single-wavelength anomalous dispersion (SAD) experiment and applying weights to a time-resolved difference map. These examples are intended to illustrate the breadth of crystallographic problems that can be addressed using this library, as well as its seamless integration with common scientific computing libraries. The examples are available as interactive Jupyter notebooks (Kluyver et al., 2016 ▸) in the reciprocalspaceship documentation (https://hekstra-lab.github.io/reciprocalspaceship/userguide/examples.html).

3.1. Assessing uncertainty in merging statistics  

Merging statistics are useful for assessing the internal consistency of a data set and many different metrics have been proposed over the years (Weiss, 2001 ▸; Karplus & Diederichs, 2012 ▸). Although merging statistics are commonly reported by data reduction pipelines, they are often not reported with uncertainties and do not always give access to their underlying parameters, such as the number of resolution bins or the type of correlation coefficients to report. By facilitating inspection of the underlying reflection data, reciprocalspaceship can be used to write quality control scripts to automate analysis pipelines or, as shown here, for use in the exploratory analysis of the properties of a single data set. By enabling crystallographers to try new statistical routines, reciprocalspaceship may help in the development of more robust indicators of data quality.

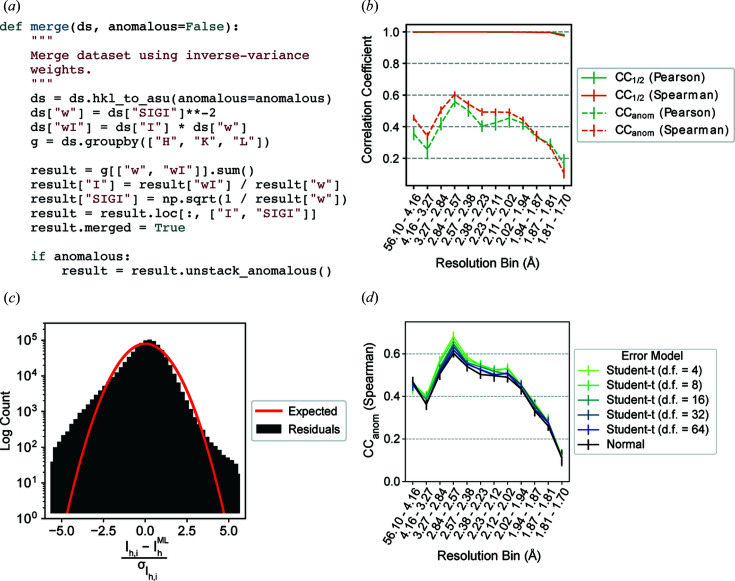
To illustrate this, we computed CC1/2 and CCanom for scaled unmerged reflection data. The data were collected at 6.5 keV on a tetragonal crystal of hen egg-white lysozyme at ambient temperature. The integrated intensities were scaled in AIMLESS and the data contain sufficient anomalous signal from the native sulfur atoms to determine experimental phases by the SAD method (Greisman et al., 2021 ▸; Adams et al., 2010 ▸; Evans & Murshudov, 2013 ▸; Terwilliger et al., 2009 ▸). Using reciprocalspaceship, it is possible to implement a function that merges redundant observations using inverse-variance weights [Fig. 2 ▸(a)]. This code takes advantage of the groupby() functionality inherited from pandas to perform calculations efficiently on a per-reflection basis (Reback et al., 2021 ▸). By partitioning the observed reflections by image, this function can be used to merge different sets of observations independently for computing CC1/2 and CCanom. Due to the modularity of this workflow, it is possible to repeat the random partitioning of observations by image to generate uncertainty estimates and to repeat these calculations using both Pearson and Spearman correlation coefficients.

Figure 2.

Figure 2

Open in a new tab

Merging statistics for a hen egg-white lysozyme sulfur SAD data set. (a) The Python function for applying inverse-variance weights to obtain maximum-likelihood merged intensity estimates using reciprocalspaceship. (b) Correlation coefficients, CC1/2 and CCanom, from repeated twofold cross validation. The Pearson CCanom is more affected by outlier measurements in low- and intermediate-resolution bins than the Spearman CCanom. (c) The distribution of residuals from observed intensities differs from the expected distribution of residuals for normally distributed observations. (d) CCanom from twofold cross validation using Student t-distributed error models with varying degrees of freedom (d.f.). Error models with heavier tails show improvements in CCanom. Error bars depict the mean ± standard deviation from 15 repeats of twofold cross validation.

As shown in Fig. 2 ▸(b), high CC1/2 values indicate that the resolution was limited by the experimental geometry rather than the crystal quality, which is common for data collected at low energy on strongly diffracting crystals. The CCanom values show that significant anomalous signal was obtained up to the highest resolution bin. Furthermore, the Spearman correlation coefficients are systematically higher and have smaller uncertainties in the low- and intermediate-resolution ranges, indicating the presence of outliers in the data.

3.2. Merging observations with a robust error model  

The difference observed for CCanom between the Pearson and Spearman correlation coefficients in Fig. 2 ▸(b) suggests the presence of outlier observations, despite the outlier rejection applied by AIMLESS (Evans & Murshudov, 2013 ▸). Since AIMLESS assumes a normally distributed error model for its observations, such outliers can have a large impact on estimates of the true merged intensity. We can evaluate whether a normally distributed error model is appropriate on the basis of the distribution of residuals between the observed intensities and the estimate of the true mean (Abrahams & Keve, 1971 ▸; Howell & Smith, 1992 ▸). This histogram can be made in just a few lines of Python by taking advantage of the pandas indexing approach [Fig. 2 ▸(c)]. Compared with the expected residuals for normally distributed observations, this data set has significantly heavier tails, with many observations several standard deviations away from the merged intensity.

The residuals in Fig. 2 ▸(c) suggest that merging may be improved by a more robust error model that can tolerate outliers. One popular choice of robust error model is the Student t distribution (Lange et al., 1989 ▸). This distribution is parameterized by a location, a scale and the number of degrees of freedom, ν, which controls the probability of large deviations from the mean. Importantly, the distribution approaches the normal distribution as ν approaches infinity. Unlike the normal distribution, though, there is no analytical expression for the maximum-likelihood estimator of the true mean given a set of observations under a Student t-distributed error model. However, we can construct an optimization problem to recover maximum-likelihood estimates of the merged intensity for each Miller index. To begin, we write the likelihood function, which is the probability of the data as a function of the mean intensity for each Miller index, h,

3.2.

This likelihood function asserts that the observed intensity I h,i, for each Miller index h and observation i, is drawn from a distribution centered at the merged intensity μh, with a scale determined by the empirical standard deviation of the observation, 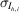Inline graphic:

3.2.

To recover maximum-likelihood estimates of the intensities 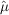Inline graphic, we need only maximize equation (1) with respect to the merged intensities. Equivalently, we may minimize the negative logarithm of the likelihood 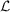Inline graphic with respect to the merged intensities as follows:

3.2.

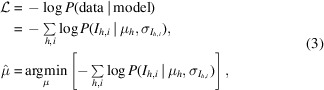which has the advantage of converting a numerically unstable product into a sum.

This optimization was implemented in PyTorch (Paszke et al., 2019 ▸) in a general form that could flexibly accept any probability distribution from the location-scale family as its error model (Paszke et al., 2019 ▸). As an example, we merged the data under a Student t-distributed error model with varying degrees of freedom. The resulting CCanom were compared with the normally distributed error model. The error models with fewer degrees of freedom outperformed the error models with more degrees of freedom, with the performance of the latter converging towards that of the normally distributed error model [Fig. 2 ▸(d)], consistent with the Student t distribution’s approach towards a normal distribution with increasing degrees of freedom.

This example demonstrates the use of reciprocalspaceship to construct a flexible merging function using a machine-learning library. This greatly reduces the overhead required to prototype a new analysis method by making it easy to use existing and well supported libraries. Furthermore, the benefit of using robust statistical estimators, as demonstrated by the improved CCanom values in Figs. 2 ▸(b) and 2 ▸(d), could readily extend to more complex procedures for scaling and merging anomalous data [e.g. as described by Terwilliger et al. (2016 ▸)] and suggests new avenues for improving the existing crystallographic analysis infrastructure. One such project, careless, combines reciprocalspaceship with TensorFlow to apply approximate Bayesian inference to new scaling and merging routines (Dalton et al., 2021 ▸; Abadi et al., 2015 ▸).

3.3. Revisiting the French–Wilson algorithm  

In the previous example, we identified anomalous differences from a room-temperature sulfur SAD experiment. Here, we will examine this anomalous signal in real space by making an anomalous difference map. Before we can make a map, we need to correct the merged intensities to account for any negative values that may result from background subtraction during integration. This is commonly handled using a Bayesian approach first proposed by French and Wilson to estimate the true intensities J h from the merged intensities I h following data reduction (French & Wilson, 1978 ▸). Briefly, this algorithm determines posterior estimates for the true intensities 〈J h〉 by solving an integral,

3.3.

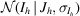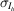where the likelihood Inline graphic is taken to be normally distributed, with the empirical error estimates for the merged intensities Inline graphic as standard deviations. The prior distribution P(J h) is the Wilson distribution (Wilson, 1949 ▸):

3.3.

which is parameterized by Σ, the mean intensity of reflections at the appropriate resolution. To estimate Σ for each reflection, the classic French–Wilson algorithm computes the mean intensity of reflections in resolution shells and interpolates the mean values from shells adjacent to the particular reflection. Since the functional form of the prior distribution has strictly positive support (Wilson, 1949 ▸), the expectations computed from equation (4) are necessarily positive. Furthermore, the posterior structure factor amplitudes can be estimated as part of the same subroutine using the following integral:

3.3.

The implementation of this method in reciprocalspaceship differs significantly from the classical one, which was limited by the computing resources and statistical tools available at the time. Notably, rather than computing mean values in shells, we use a Gaussian smoother (Murphy, 2012 ▸) to regress the mean of the intensity distributions Σ against resolution. This regression model is quite flexible and offers an anisotropic mode which estimates the mean intensity locally as a function of the Miller indices. Whereas the original paper computed the posterior by interpolating a table of cached results (French & Wilson, 1978 ▸), our implementation uses Chebyshev–Gauss quadrature to evaluate the integrals efficiently on the fly. We generate quadrature points and weights with NumPy (Harris et al., 2020 ▸) and compute the relevant log probabilities using the distribution classes implemented in SciPy (Virtanen et al., 2020 ▸). Our implementation is tested for consistency with the original paper (French & Wilson, 1978 ▸) and with CCTBX (Grosse-Kunstleve et al., 2002 ▸).

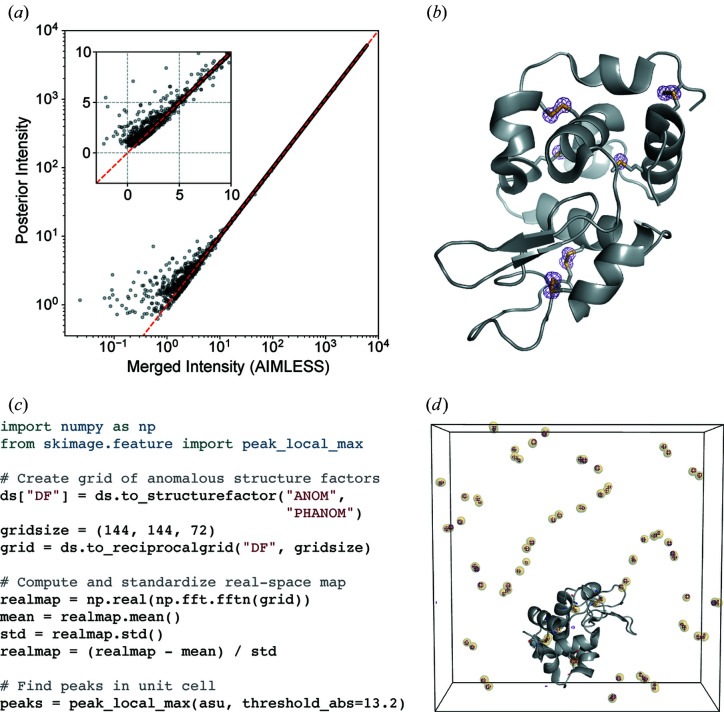
The merged intensities from the sulfur SAD experiment were rescaled using the French–Wilson algorithm and converted to structure factor amplitudes. This operation leaves large intensities relatively unchanged, while ensuring that any negative values become strictly positive [Fig. 3 ▸(a)]. Anomalous differences of the structure factor amplitudes were computed between Friedel pairs. The anomalous difference map shown in Fig. 3 ▸(b) was then constructed using phases derived from the refined model (PDB entry 7l84; J. B. Greisman, K. M. Dalton & D. R. Hekstra, to be published). The map shows significant anomalous peaks at a 5σ contour, with the density strictly localized to each of the ten sulfur atoms in the lysozyme structure.

Figure 3.

Figure 3

Open in a new tab

Analysis of anomalous differences from a sulfur SAD experiment. (a) Application of the French–Wilson algorithm to merged intensities. Large intensities are relatively unchanged, while small and negative intensities are corrected to be strictly positive. The red dashed line shows y = x and the inset highlights the small and negative merged intensities. (b) An anomalous difference map using difference structure factor amplitudes derived from the room-temperature sulfur SAD data set and phases from the refined model (PDB 7l84). The map is contoured at 5σ. (c) Example code for identifying anomalous scattering sites in an anomalous difference map. (d) The unit cell containing sulfur sites identified using the code snippet (yellow spheres), overlaid with the anomalous difference map (purple mesh, contoured at 10σ). The protein molecule from one asymmetric unit of PDB 7l84 is shown in gray. The images in (b) and (d) were rendered using PyMOL (Schrödinger, 2020 ▸).

3.4. Identifying anomalous scattering atoms in real space  

The anomalous difference map shown in Fig. 3 ▸(b) was made from the anomalous difference amplitudes and phases. It is also possible to compute a real-space map using reciprocalspaceship and NumPy, which enables one to use image processing software to automate the identification of anomalous scattering atoms. This process is illustrated in Fig. 3 ▸(c). The provided code snippet arranges the complex anomalous structure factors on a reciprocal-space grid and then computes the real-space anomalous difference map using the fast Fourier transform function (Cooley & Tukey, 1965 ▸) in NumPy. scikit-image, an image processing library (van der Walt et al., 2014 ▸), can be used to identify peaks in the map. The automatically identified sites are overlaid with the anomalous difference map in Fig. 3 ▸(d), demonstrating that this procedure successfully identifies the 80 sulfur sites in the tetragonal lysozyme unit cell (ten sulfurs per copy, eight copies)

This example illustrates the use of reciprocalspaceship to produce real-space maps from structure factors. Importantly, due to the seamless integration with NumPy, one can take advantage of Python image processing libraries to identify peaks in the real-space density. Due to the wealth of libraries and tools written by the Python community, this feature of reciprocalspaceship can provide the opportunity to develop and test new algorithms rapidly and to expand the crystallographic community by providing data science tools familiar to researchers from many other fields. In this manner, the use of reciprocalspaceship could simplify existing data processing pipelines and perhaps be useful in the development of new methods in crystallographic data analysis or structural bio­informatics.

3.5. Applying weights to a time-resolved difference map  

Time-resolved crystallography experiments make use of X-ray diffraction to monitor structural changes in a crystalline sample. Commonly, structural changes are initially evaluated on the basis of isomorphous difference maps. Such maps are computed by estimating the difference in structure factor amplitudes of the sample before and after a perturbation, such as a laser pulse. Combining these |F on| − |F off| differences with ground-state phases from a reference structure yields an estimate of the differences between the electron density of the sample before and after the perturbation. Difference maps are often noisy due to systematic errors or scaling artifacts and are frequently weighted by the magnitude of the difference signal and/or the error estimates associated with the empirical differences in structure factor amplitudes. In this example we will visualize the effects of applying weights to a time-resolved difference map of photoactive yellow protein (PYP). PYP is a model system in time-resolved crystallography based on the trans-to-cis isomerization of its 4-hydroxycinnamyl chromophore upon absorption of blue light (Genick et al., 1997 ▸). This data set was collected at the BioCARS Laue beamline APS-14-ID and comprises matched images collected in the dark and 2 ms after illumination with blue light. These data were collected and provided by Marius Schmidt and Vukica Šrajer.

Several schemes have been used to apply weights to time-resolved difference maps. 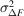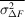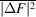Many of them take the form of equation (7), involving a term based on the squared uncertainty in the difference structure factor amplitude (Inline graphic) and its observed mean over reflections (Inline graphic) and, optionally, a scale term based on the squared magnitude of the observed difference structure factor amplitude (|ΔF|2) and its observed mean over reflections (Inline graphic):

3.5.

With α = 0, these weights take the form derived by Ursby & Bourgeois (1997 ▸). The ΔF-dependent term downweights the influence of likely outliers in the data set resulting from poorly measured differences by assigning lower weights to their map coefficients. The tolerance for large differences is controlled by the α parameter. α values of 1.0 (Šrajer et al., 2001 ▸) and 0.05 (Hekstra et al., 2016 ▸) have been reported in the literature.

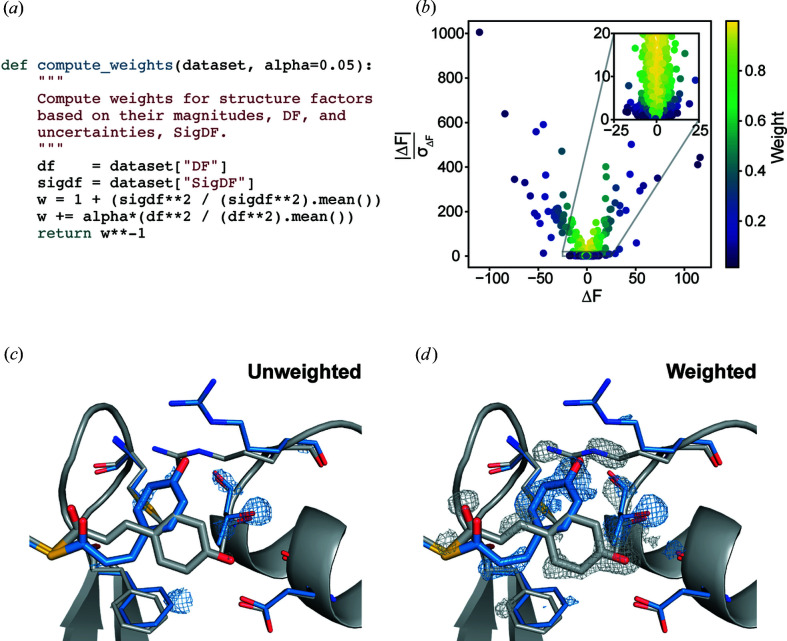
The weighting function given by equation (7) can be expressed in a few lines of Python that apply weights based on the values of |ΔF| and σΔF in an rs.DataSet object [Fig. 4 ▸(a)]. The weights computed for the PYP data set are illustrated in Fig. 4 ▸(b). Difference structure factors with low signal-to-noise ratios (large σΔF relative to |ΔF|) or large difference structure factor amplitudes are assigned lower weight. The unweighted and weighted difference maps were then made using phases derived from the ground-state model (PDB entry 2phy; Borgstahl et al., 1995 ▸). The side-by-side comparison of these difference maps shows that the weights greatly improve the interpretability of the structural changes – emphasizing the trans-to-cis isomerization of the chromophore, as well as concerted changes in the nearby Arg52 and Phe96 side chains [Figs. 4 ▸(c) and 4 ▸(d)].

Figure 4.

Figure 4

Open in a new tab

Weighting a time-resolved difference map. (a) The Python function for applying weights to arrays of difference structure factor amplitudes and uncertainties. (b) A scatter plot showing the weights assigned to each observed difference structure factor amplitude with α = 0.05. (c) An unweighted |F on| − |F off| difference map in the vicinity of the PYP chromophore. (d) A weighted |F on| − |F off| difference map with α = 0.05. The trans (ground state) PYP structure (gray) is taken from PDB entry 2phy and the cis (excited, pB state) PYP structure (blue) is taken from PDB entry 3ume (Tripathi et al., 2012 ▸). The difference maps are contoured at ±3σ and were carved within 1.2 Å of the displayed residues. These figures were rendered using PyMOL (Schrödinger, 2020 ▸).

This example illustrates the use of reciprocalspaceship to create custom maps. Importantly, it demonstrates both the exploratory analysis of different weighting schemes and the writing of MTZ files including different weight columns. These can be used to visualize the impact of the different weights in a molecular visualization suite.

4. Discussion  

reciprocalspaceship is a Python library that can form the foundation for the development of new methods in crystallographic data analysis. This library provides a DataSet object that can conveniently represent tabular reflection data while adhering to common practices in Python data analysis. This empowers crystallographers to write idiomatic Python code to analyze their experiments while having full support for the necessary features of crystallographic analysis, such as symmetry operations, unit cells and space groups. Example applications have been presented which use this library to merge scaled reflections, analyze anomalous differences from a SAD experiment and observe the impact of weights on a time-resolved difference map. These examples illustrate how reciprocalspaceship could be used in several different contexts, producing useful analyses with relatively short scripts and functions that can take full advantage of the existing Python ecosystem.

reciprocalspaceship can be used for exploratory data analysis, allowing one to inspect interesting properties of an important data set. Or it can be used to prototype, develop and ship new methods and algorithms for analyzing data sets (Dalton et al., 2021 ▸). Furthermore, this library can be useful in teaching crystallography by allowing students to familiarize themselves with reflection data, space groups and symmetry and the implementation of commonly used algorithms. By using a framework familiar to Python data scientists, this library lowers the barrier to entry for crystallographic software development.

5. Data and code availability  

reciprocalspaceship and worked-out examples are available on GitHub at https://github.com/Hekstra-Lab/reciprocalspaceship and can be installed directly from PyPI. The complete code used in these examples is available in the reciprocalspaceship documentation, and the interactive Jupyter notebooks and all supporting data can be downloaded directly from the Examples directory of the GitHub repository.

Acknowledgments

We thank the staff at the Northeastern Collaborative Access Team (NE-CAT), beamline 24-ID-C of the Advanced Photon Source, for supporting our room-temperature crystallography experiments, with special thanks to Igor Kourinov. We also thank Marius Schmidt and Vukica Šrajer for the time-resolved Laue diffraction data of photoactive yellow protein.

Funding Statement

This work was funded by Searle Scholars Program grant SSP-2018-3240 to Doeke Romke Hekstra; New York Community Trust grant 338034 to Doeke Romke Hekstra; National Science Foundation Graduate Research Fellowship grant DGE1745303 to Jack Benjamin Greisman; U.S. Department of Energy, Office of Science grant DE-AC02-06CH11357; National Institutes of Health, National Institute of General Medical Sciences grant P30 GM124165.

References

  1. Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin, M., Ghemawat, S., Goodfellow, I., Harp, A., Irving, G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur, M., Levenberg, J., Mané, D., Monga, R., Moore, S., Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke, V., Vasudevan, V., Viégas, F., Vinyals, O., Warden, P., Wattenberg, M., Wicke, M., Yu, Y. & Zheng, X. (2015). TensorFlow: Large-scale Machine Learning on Heterogeneous Systems, https://www.tensorflow.org/.
  2. Abrahams, S. C. & Keve, E. T. (1971). Acta Cryst. A27, 157–165.
  3. Adams, P. D., Afonine, P. V., Bunkóczi, G., Chen, V. B., Davis, I. W., Echols, N., Headd, J. J., Hung, L.-W., Kapral, G. J., Grosse-Kunstleve, R. W., McCoy, A. J., Moriarty, N. W., Oeffner, R., Read, R. J., Richardson, D. C., Richardson, J. S., Terwilliger, T. C. & Zwart, P. H. (2010). Acta Cryst. D66, 213–221. [DOI] [PMC free article] [PubMed]
  4. Borgstahl, G. E., Williams, D. R. & Getzoff, E. D. (1995). Biochemistry, 34, 6278–6287. [DOI] [PubMed]
  5. Cooley, J. W. & Tukey, J. W. (1965). Math. Comput. 19, 297–301.
  6. Dalton, K. M., Greisman, J. B. & Hekstra, D. R. (2021). bioRxiv, https://doi.org/10.1101/2021.01.05.425510.
  7. Dods, R., Båth, P., Morozov, D., Gagnér, V. A., Arnlund, D., Luk, H. L., Kübel, J., Maj, M., Vallejos, A., Wickstrand, C., Bosman, R., Beyerlein, K. R., Nelson, G., Liang, M., Milathianaki, D., Robinson, J., Harimoorthy, R., Berntsen, P., Malmerberg, E., Johansson, L., Andersson, R., Carbajo, S., Claesson, E., Conrad, C. E., Dahl, P., Hammarin, G., Hunter, M. S., Li, C., Lisova, S., Royant, A., Safari, C., Sharma, A., Williams, G. J., Yefanov, O., Westenhoff, S., Davidsson, J., DePonte, D. P., Boutet, S., Barty, A., Katona, G., Groenhof, G., Brändén, G. & Neutze, R. (2021). Nature, 589, 310–314.
  8. Evans, P. R. & Murshudov, G. N. (2013). Acta Cryst. D69, 1204–1214. [DOI] [PMC free article] [PubMed]
  9. French, S. & Wilson, K. (1978). Acta Cryst. A34, 517–525.
  10. Garcia-Bonete, M.-J. & Katona, G. (2019). Acta Cryst. A75, 851–860. [DOI] [PMC free article] [PubMed]
  11. Genick, U. K., Borgstahl, G. E. O., Ng, K., Ren, Z., Pradervand, C., Burke, P. M., Šrajer, V., Teng, T.-Y., Schildkamp, W., McRee, D. E., Moffat, K. & Getzoff, E. D. (1997). Science, 275, 1471–1475. [DOI] [PubMed]
  12. Greisman, J. B., Dalton, K. M. & Hekstra, D. R. (2021). Data Set for Hen Egg White Lysozyme by Native S-SAD at Room Temperature. Version 1.0.0. https://doi.org/10.5281/zenodo.4426679.
  13. Grosse-Kunstleve, R. W., Sauter, N. K., Moriarty, N. W. & Adams, P. D. (2002). J. Appl. Cryst. 35, 126–136.
  14. Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer, S., van Kerkwijk, M. H., Brett, M., Haldane, A., del Río, J. F., Wiebe, M., Peterson, P., Gérard-Marchant, P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi, H., Gohlke, C. & Oliphant, T. E. (2020). Nature, 585, 357–362. [DOI] [PMC free article] [PubMed]
  15. Hatti, K. S., McCoy, A. J. & Read, R. J. (2021). bioRxiv, https://doi.org/10.1101/2021.02.07.430107.
  16. Hekstra, D. R., White, K. I., Socolich, M. A., Henning, R. W., Šrajer, V. & Ranganathan, R. (2016). Nature, 540, 400–405. [DOI] [PMC free article] [PubMed]
  17. Howell, P. L. & Smith, G. D. (1992). J. Appl. Cryst. 25, 81–86.
  18. Kabsch, W. (2010a). Acta Cryst. D66, 133–144. [DOI] [PMC free article] [PubMed]
  19. Kabsch, W. (2010b). Acta Cryst. D66, 125–132. [DOI] [PMC free article] [PubMed]
  20. Karplus, P. A. & Diederichs, K. (2012). Science, 336, 1030–1033. [DOI] [PMC free article] [PubMed]
  21. Kluyver, T., Ragan-Kelley, B., Pérez, F., Granger, B., Bussonnier, M., Frederic, J., Kelley, K., Hamrick, J., Grout, J., Corlay, S., Ivanov, P., Avila, D., Abdalla, S., Willing, C. & Joint Development Team (2016). Positioning and Power in Academic Publishing: Players, Agents and Agendas, edited by F. Loizides & B. Scmidt, pp. 87–90. Amsterdam: IOS Press.
  22. Krekel, H., Oliveira, B., Pfannschmidt, R., Bruynooghe, F., Laugher, B. & Bruhin, F. (2020). pytest. Version 6.2.1. https://github.com/pytest-dev/pytest.
  23. Lange, K. L., Little, R. J. A. & Taylor, J. M. G. (1989). J. Am. Stat. Assoc. 84, 881–896.
  24. Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. Cambridge: MIT Press.
  25. Otwinowski, Z. & Minor, W. (1997). Methods in Enzymology, Vol. 276, Macromolecular Crystallography, Part A, edited by C. W. Carter Jr & R. M. Sweet, pp. 307–326. New York: Academic Press.
  26. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J. & Chintala, S. (2019). Advances in Neural Information Processing Systems, Vol. 32, edited by H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox & R. Garnett, pp. 8024–8035. Red Hook: Curran Associates.
  27. Reback, J., McKinney, W., Brockmendel, J., den Bossche, J. V., Augspurger, T., Cloud, P., Young, G. F., Hawkins, S., Sinhrks, Roeschke, M., Klein, A., Petersen, T., Tratner, J., She, C., Ayd, W., Naveh, S., Garcia, M., Schendel, J., Hayden, A., Saxton, D., Hoefer, P., Jancauskas, V., McMaster, A., Battiston, P., Seabold, S., Gorelli, M., Dong, K. & Hoyer, S. (2021). pandas. Version 1.2.1. https://doi.org/10.5281/zenodo.3509134.
  28. Schrödinger (2020). The pyMOL Molecular Graphics System. Version 2.4. Schrödinger LLC, New York, USA.
  29. Šrajer, V., Ren, Z., Teng, T.-Y., Schmidt, M., Ursby, T., Bourgeois, D., Pradervand, C., Schildkamp, W., Wulff, M. & Moffat, K. (2001). Biochemistry, 40, 13802–13815. [DOI] [PubMed]
  30. Terwilliger, T. C., Adams, P. D., Read, R. J., McCoy, A. J., Moriarty, N. W., Grosse-Kunstleve, R. W., Afonine, P. V., Zwart, P. H. & Hung, L.-W. (2009). Acta Cryst. D65, 582–601. [DOI] [PMC free article] [PubMed]
  31. Terwilliger, T. C., Bunkóczi, G., Hung, L.-W., Zwart, P. H., Smith, J. L., Akey, D. L. & Adams, P. D. (2016). Acta Cryst. D72, 359–374. [DOI] [PMC free article] [PubMed]
  32. Tripathi, S., Šrajer, V., Purwar, N., Henning, R. & Schmidt, M. (2012). Biophys. J. 102, 325–332. [DOI] [PMC free article] [PubMed]
  33. Ursby, T. & Bourgeois, D. (1997). Acta Cryst. A53, 564–575.
  34. Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., Vijaykumar, A., Bardelli, A. P., Rothberg, A., Hilboll, A., Kloeckner, A., Scopatz, A., Lee, A., Rokem, A., Woods, C. N., Fulton, C., Masson, C., Häggström, C., Fitzgerald, C., Nicholson, D. A., Hagen, D. R., Pasechnik, D. V., Olivetti, E., Martin, E., Wieser, E., Silva, F., Lenders, F., Wilhelm, F., Young, G., Price, G. A., Ingold, G., Allen, G. E., Lee, G. R., Audren, H., Probst, I., Dietrich, J. P., Silterra, J., Webber, J. T., Slavič, J., Nothman, J., Buchner, J., Kulick, J., Schönberger, J. L., de Miranda Cardoso, J. V., Reimer, J., Harrington, J., Rodríguez, J. L. C., Nunez-Iglesias, J., Kuczynski, J., Tritz, K., Thoma, M., Newville, M., Kümmerer, M., Bolingbroke, M., Tartre, M., Pak, M., Smith, N. J., Nowaczyk, N., Shebanov, N., Pavlyk, O., Brodtkorb, P. A., Lee, P., McGibbon, R. T., Feldbauer, R., Lewis, S., Tygier, S., Sievert, S., Vigna, S., Peterson, S., More, S., Pudlik, T., Oshima, T., Pingel, T. J., Robitaille, T. P., Spura, T., Jones, T. R., Cera, T., Leslie, T., Zito, T., Krauss, T., Upadhyay, U., Halchenko, Y. O. & Vázquez-Baeza, Y. (2020). Nat. Methods, 17, 261–272.
  35. Walt, S. van der, Schönberger, J. L., Nunez-Iglesias, J., Boulogne, F., Warner, J. D., Yager, N., Gouillart, E., Yu, T. & The scikit-image Contributors (2014). PeerJ, 2, e453. [DOI] [PMC free article] [PubMed]
  36. Weiss, M. S. (2001). J. Appl. Cryst. 34, 130–135.
  37. Wickstrand, C., Katona, G., Nakane, T., Nogly, P., Standfuss, J., Nango, E. & Neutze, R. (2020). Struct. Dyn. 7, 024701. [DOI] [PMC free article] [PubMed]
  38. Wilson, A. J. C. (1949). Acta Cryst. 2, 318–321.
  39. Winn, M. D., Ballard, C. C., Cowtan, K. D., Dodson, E. J., Emsley, P., Evans, P. R., Keegan, R. M., Krissinel, E. B., Leslie, A. G. W., McCoy, A., McNicholas, S. J., Murshudov, G. N., Pannu, N. S., Potterton, E. A., Powell, H. R., Read, R. J., Vagin, A. & Wilson, K. S. (2011). Acta Cryst. D67, 235–242. [DOI] [PMC free article] [PubMed]
  40. Winter, G., Waterman, D. G., Parkhurst, J. M., Brewster, A. S., Gildea, R. J., Gerstel, M., Fuentes-Montero, L., Vollmar, M., Michels-Clark, T., Young, I. D., Sauter, N. K. & Evans, G. (2018). Acta Cryst. D74, 85–97. [DOI] [PMC free article] [PubMed]
  41. Wojdyr, M. (2021). GEMMI – A Library for Structural Biology, https://github.com/project-gemmi/gemmi.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

reciprocalspaceship and worked-out examples are available on GitHub at https://github.com/Hekstra-Lab/reciprocalspaceship and can be installed directly from PyPI. The complete code used in these examples is available in the reciprocalspaceship documentation, and the interactive Jupyter notebooks and all supporting data can be downloaded directly from the Examples directory of the GitHub repository.

Articles from Journal of Applied Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES