Within node connectivity changes, not simply edge changes, influence graph theory measures in functional connectivity studies of the brain

Abstract

Interest in understanding the organization of the brain has led to the application of graph theory methods across a wide array of functional connectivity studies. The fundamental basis of a graph is the node. Recent work has shown that functional nodes reconfigure with brain state. To date, all graph theory studies of functional connectivity in the brain have used fixed nodes. Here, using fixed-, group-, state-specific, and individualized- parcellations for defining nodes, we demonstrate that functional connectivity changes within the nodes significantly influence the findings at the network level. In some cases, state- or group-dependent changes of the sort typically reported do not persist, while in others, changes are only observed when node reconfigurations are considered. The findings suggest that graph theory investigations into connectivity contrasts between brain states and/or groups should consider the influence of voxel-level changes that lead to node reconfigurations; the fundamental building block of a graph.

1. Introduction

With the explosion of interest in fMRI studies of functional connectivity and the application of network science to understand brain function, there have been a number of studies using graph theory measures to quantify state-based changes or group differences in brain network properties. Brain networks can be represented by graphs, describing a set of regions called “nodes” and the connections between them called “edges”. Such networks largely resemble other complex physical, biological or social networks in the sense of meaningful structure, especially small worldness. Complex network analysis, originally developed for the study of other systems, has been applied to brain networks. With approaches rooted in graph theory, it is possible to quantify and summarize complex brain networks with a minimal set of measures, that then can be meaningfully compared under different conditions. (Bassett and Sporns, 2017; Bullmore and Bassett, 2011; Rubinov and Sporns, 2010)

Brain network graphs can be constructed at different scales. When building a graph from functional MRI, voxels can be taken as nodes, but in practice, the dimensionality is reduced often by applying an atlas that serves to group tens to hundreds of voxels into nodes. (Rubinov and Sporns, 2010) A representative fMRI signal time course for each node is obtained by averaging the voxel-level time courses within the node. The Pearson correlation of the time courses for each pair of nodes, or some variant of it, then is used to represent the edge strength connecting two nodes. Meaningful node definitions are a critical component of brain network analysis.(Eickhoff et al., 2018) There is evidence that the constructed graph has a strong dependence on the node definition; that is the atlas applied (de Reus and Van den Heuvel, 2013; Wang et al., 2009). Various atlases have been used in previous studies such as the AAL-atlas (Tian et al., 2011; Tzourio-Mazoyer et al., 2002; Wang et al., 2012b), the Gordon atlas (Gordon et al., 2016; Shine et al., 2016), the Power atlas (Hearne et al., 2017; Power et al., 2011; Rudie et al., 2013), the Harvard-Oxford probabilistic atlas (Alexander-Bloch et al., 2010; Cohen and D’Esposito, 2016; Desikan et al., 2006), and the Shen atlas (Garrison et al., 2015; Pedersen et al., 2015; Shen et al., 2013). A common feature of all of the atlases used to date is that have all been fixed atlases with the underlying assumption that the node definitions are unaffected by the group or state-based connectivity edge changes of interest.

In the brain, connectivity does not only change between edges, and indeed changes at the voxel level are readily apparent. A simple test with any fixed node atlas will illustrate this point. If only changes in edges occur between brain states, then the homogeneity of voxel time-courses within a node should be constant across conditions (because the assumption is that the node isn’t changing). However, a node-homogeneity vector, reflecting the homogeneity of time-courses within each node of a fixed atlas, provides sufficient information to predict the task under which the data were collected. This suggests that functional connectivity between voxels within a fixed node varies with changes in brain state, and varies in a reproducible manner.

Recently, individualized parcellation methods have been developed to generate functional parcellations specific to each subject group, or each individual within a group (Chong et al., 2017; Kong et al., 2019; Salehi et al., 2018; Wang et al., 2015a). Such atlases can account for inter-subject variability in parcellation topography. Individualized parcellations have been shown to provide better within-parcel homogeneity of time-courses and the spatial topography of the parcels have informed predictions of features such as sex and cognitive measures (Kong et al., 2019; Salehi et al., 2018). Even more importantly for the graph theory methods considered here, is that previous work has shown that nodes, defined via parcellation of functional MRI data, reconfigure with task-induced brain states in a reliable manner (Salehi et al., 2020). It is not clear, however, to what extent and in what manner such node reconfigurations may influence graph theory measures obtained across subjects and brain states.

A large number of previously published studies using fixed atlases have shown group- or state-dependent differences in graph theory measures derived from fMRI data. In these studies, only changes in edge strength were considered. Here we show that many of these studies could come to different conclusions if they considered the changes in functional connectivity at the voxel level detectable either through fixed-node homogeneity measures, or through state- or group- dependent node reconfigurations. A sampling of several such studies covers a range of disorders including autism(Chaitra et al., 2020; Henry et al., 2018; Itahashi et al., 2014; Rudie et al., 2013), Alzheimer’s disease (Brier et al., 2014; Khazaee et al., 2015, 2016; Liu et al., 2014; Pereira et al., 2016; Sanz-Arigita et al., 2010; Supekar et al., 2008; Zhao et al., 2012), schizophrenia (Alexander-Bloch et al., 2010; Karbasforoushan and Woodward, 2012; Liu et al., 2008; Lynall et al., 2010; Su et al., 2015; van den Heuvel et al., 2013), posttraumatic stress disorder (Lei et al., 2015; Suo et al., 2015), Parkinson’s disease (Göttlich et al., 2013; Luo et al., 2015), and many other disorders (Agosta et al., 2013; Jiang et al., 2013; Lord et al., 2012; Rocca et al., 2016; Serra et al., 2020; Wang et al., 2014; Xu et al., 2013; Ye et al., 2015). Other studies that examined changes in graph measures with age (Achard and Bullmore, 2007; Chan et al., 2014; Geerligs et al., 2015; Iordan et al., 2018; Meunier et al., 2009; Onoda and Yamaguchi, 2013; Sala-Llonch et al., 2014; Stanley et al., 2015; Wu et al., 2013), sex (Satterthwaite et al., 2015; Tian et al., 2011; Wu et al., 2013; Zhang et al., 2016), cognitive states (Cohen and D’Esposito, 2016; Hearne et al., 2017; Shine et al., 2016; Wang et al., 2012b; Wen et al., 2015), and other conditions (Bruno et al., 2012; Gard et al., 2014) also did not consider connectivity changes at the node level. These studies cover a wide range of topics in psychiatry and neuroscience, and many have been high-impact, highly cited publications.

In this work, we quantify the influence of node definition and reconfiguration on a range of graph theory measures, including both node- and network-based measures. We examine fixed parcellations, individualized parcellations, state-specific group-level parcellations, and sex-specific group-level parcellations to determine the sensitivity of graph theory measures to changes in connectivity within the fundamental building block of the graph. We show that whether or not connectivity changes at the voxel level are considered can significantly influence findings. We show that when contrasting groups or conditions using graph theory measures, variance may be associated not only with changes in edges but also with changes in node configurations. Together, these results demonstrate the importance of considering not just edge-level connectivity changes but also those that influence the organization of the brain at the node level.

2. Material and methods

2.1. Data

A subset of the Human Connectome Project (HCP) S900 release was used. Only subjects who had voxel-level fMRI data for all nine functional sessions (two resting-states and seven tasks) were included. To alleviate artifacts caused by head motion, subjects with mean frame-to-frame displacement > 0.1 mm or maximum frame-to-frame displacement > 0.15 mm were excluded. The resulting dataset contains 494 subjects (266 females, age = 22–36+). The preprocessing procedures were the same as described in (Salehi et al., 2020). We applied the HCP minimal preprocessing pipeline (Glasser et al., 2013) which includes artifact removal, motion correction and registration to MNI space. All further preprocessing steps used BioimageSuite(Joshi et al., 2011), including regressing 24 motion parameters, regressing the mean time courses of the white matter and cerebrospinal fluid, and the global signal, removing the linear trend and low pass filtering. For comparison between sex groups, 16 male and 11 female subjects were excluded, in order to balance fluid intelligence and head motion, leaving 212 males and 255 females. There was no significant between-group difference in age, fluid intelligence, or head motion.

2.2. Atlases

Four types of atlases were tested in this work. A fixed atlas, applied to all subjects but derived from a group-level parcellation of an independent set of subjects, brain-state specific atlases, brain-state specific group-specific atlases, and individualized atlases customized for the individual and the task condition (state). Each is described below.

Fixed parcellation-based functional connectivity matrices were obtained based on a 268-parcel atlas determined with a spectral clustering algorithm on resting-state data of a healthy population (Shen et al., 2013). We also obtained the individualized parcellations using AALv3 (Rolls et al., 2020) as the initial atlas and report these results in the supplementary material.

We employed the exemplar-based approach previously introduced in (Salehi et al., 2020) to define an individualized parcellation for each condition for each subject. The algorithm has three steps: 1) Registration to a group-level parcellation. Here we used the Shen 268 atlas as the initial group-level parcellation. 2) Identification of an exemplar from each node by maximizing a submodular function. 3) Assignment of each voxel to the functionally closest exemplar while maintaining spatial contiguity to an exemplar. (Fig. 1)

Fig. 1. Obtaining individualized parcellation and state-specific parcellation.

For each acquisition condition (state 1 to 9), we start with the same group-level fixed parcellation (Shen 268), select one exemplar from each parcel based on the time series and assign every voxel to the functionally closest exemplar while maintaining the spatial contiguity of each parcel. This yields an individualized atlas for each state for each subject. The state-specific group parcellations are obtained by taking the majority vote across the individualized parcellations for all the subjects within a state.

State-specific parcellations were obtained by taking the majority vote over the individualized parcellations of the same acquisition condition across all the subjects. For example, in the working memory condition, a voxel is assigned to the parcellation to which the voxel is mostly frequently assigned across all 494 subject-specific working memory individualized parcellations. Similar to state-specific parcellations, sex-specific parcellations were obtained by taking the majority vote over the individualized parcellations of the same acquisition condition across all the subjects within each sex group. (Fig. 2)

Fig. 2. Obtaining state-specific and group-specific parcellation with majority vote.

After obtaining an individualized atlas for each state for each subject, the state-specific parcellations are obtained by taking the majority vote across the individualized parcellations for all the subjects within a state. The group-specific parcellations are obtained by taking the majority vote across the individualized parcellations for the subjects within each group within the same state. There are in total 9 state-specific parcellations and 18 group-specific parcellations (9 state x 2 sex-specific parcellations).

For each of these atlas types, the time course of each node was computed by averaging the voxel-level time courses within the node. The Pearson correlation coefficients of the time course of each pair of nodes were then computed and normalized using the Fisher transformation, yielding a node-by-node matrix of functional connectivity for each subject and condition.

2.3. Network construction

The 268 × 268 correlation matrices were converted into a set of binary adjacency matrices. We first excluded the negative correlations. Three levels of absolute threshold, τ_r = 0.1, 0.3, and 0.5, were applied, as well as three levels of proportional threshold, τ_p = 0.05, 0.1, and 0.3. Although negative correlations can be real, they are often ignored as they can also originate from global signal regression (Murphy and Fox, 2017). To verify that the results we obtained were not driven by elimination of negative correlations we also took the absolute values of the correlation matrices and applied the same absolute and proportional thresholds to account for potential meaningful negative connections. Some of the network measures implemented are compatible with weighted networks (Rubinov and Sporns, 2011), and thus where possible we generated weighted positive networks by keeping the positive edges of the connectivity matrices and setting all the negative edges to 0, and absolute networks by taking the absolute values of all the edges. Connection lengths are required for computation of weighted distance-based measures, so here reciprocal-based connection length matrices and negative log-based connection length matrices were obtained for both positive connectivity matrices and absolute connectivity matrices. The connection length between nodes with similar time series is shorter, and vice versa.

2.4. Network measures

A set of commonly reported network measures were calculated with MATLAB functions from the Brain Connectivity Toolbox (Rubinov and Sporns, 2010) (https://sites.google.com/site/bctnet). Network-level measures, including characteristic path length, global efficiency, transitivity, and modularity, summarize the properties of the whole network with one value. Node-level measures, including clustering coefficient, degree, betweenness centrality, local efficiency, and participation coefficient, delineate local properties for each node. Brief introductions to these measures are provided in Table 1 (details can be found in (Rubinov and Sporns, 2010)) and the features tested are presented in Table 2.

Table 1.

Network measures (Rubinov and Sporns, 2010).

Network-level Measures
Characteristic path length (CPL) is the average shortest path length between any two nodes in the network. A shorter L indicates higher edge density and more efficient information propagation. Global efficiency (Eglob) is the average inverse shortest path length in the network. Eglob is inversely related to L and a higher Eglob represents a higher functional efficiency of the brain network. Transitivity (T) is the ratio of triangles to triplets in the network. A higher T indicates stronger segregation in the network. Modularity (M) quantifies the degree to which the network can be subdivided into nonoverlapping groups with maximum number of within-group edges and minimum number of between-group edges. A higher M also indicates stronger segregation.
Node-level Measures
Clustering coefficient (C) is the fraction of triangles around a node or the fraction of the node’s neighbors that are also connected to each other. A higher C indicates clustering around that node. Local efficiency (Eloc) is the global efficiency calculated on the node’s neighbors. Eloc is related to C and is also a measure of functional segregation. Degree (d) is the number of edges connected to the node. Betweenness centrality (CB) is the fraction of all shortest paths that contain the node. A node with higher CB may connect to multiple segregated groups of nodes and play an important role in information propagation in the network. Participation coefficient (P) is a measure of the inter-modular connections of the node and also represents centrality.

Table 2.

Network construction methods (Pos = positive connectivity matrices; Abs = absolute connectivity matrices; Pro = proportional threshold; Abs = absolute threshold; H = high; M = medium; L = low).

Abbreviation	Binary	Weighted	Positive Edges	Absolute Edges	Absolute Threshold	Proportional Threshold	Additional Conversion
Pos Abs H	√		√		τr = 0.5
Pos Abs M	√		√		τr = 0.3
Pos Abs L	√		√		τr = 0.1
Pos Pro-H	√		√			τp = 0.05
Pos Pro-M	√		√			τp = 0.1
Pos Pro-L	√		√			τp = 0.3
Abs H	√			√	τr = 0.5
Abs M	√			√	τr = 0.3
Abs L	√			√	τr = 0.1
Abs Pro-H	√			√		τp = 0.05
Abs Pro-M	√			√		τp = 0.1
Abs Pro-L	√			√		τp = 0.3
Pos		√	√
Abs		√		√
Pos Inv		√	√				inv()
Pos Log		√	√				−log()
Abs Inv		√		√			inv()
Abs Log		√		√			−log()

Results based on Pos Abs L and Pos Pro-M are presented in this work for the network measures outlined in Table 1. The binary graphs are constructed by applying an absolute threshold τ_r = 0.1 or a proportional threshold τ_p = 0.1 to the functional connectivity matrix. Results based on other methods are summarized in the supplement. Results based on aggregated metrics across proportional and absolute threshold are also included in the supplementary material.

2.5. Statistical testing

The network measures listed above were obtained for fixed parcellations, state-specific parcellations, individualized parcellations, and finally sex-specific parcellations, the latter to test the impact of local connectivity changes associated with node reconfigurations on group differences in graph metrics. The corresponding network measures are referred to as “fixed network measures”, “state-specific network measures”, “individualized network measures”, and “group-specific network measures”, respectively. To evaluate the direct effect of node reconfiguration on network measures, we first performed a Wilcoxon signed rank test on fixed network measures vs. each of the other three sets of measures for each of the nine states. For node-level measures, the Wilcoxon signed rank test was performed for each node. The exemplar-based individualized parcellation method preserves the node correspondence among distinct parcellations allowing meaningful comparison of node-level network measures. (Fig. 3a)

Fig. 3. Statistical evaluation of the effect of different parcellation approaches on network measures and state-dependent changes in network measures.

(a) The direct effect that different parcellations have on network-level measures is evaluated by performing Wilcoxon signed rank test between the networks measures computed based on the two different parcellations. For node-level measures, Wilcoxon signed rank test is performed for every node. The results are summarized by the number of nodes showing a significant difference in the node-level network measures between the fixed atlas approach and the approaches that take into consideration changes in functional node organization. (b) The state contrast for each parcellation is first obtained by performing a Wilcoxon signed rank test between network measures across two different tasks. The significance level of state contrasts based on different parcellations are then presented and compared. For node-level measures, the state contrasts are computed for each node. The effect of different parcellations is quantified by counting the number of nodes that show a significant state contrast with one parcellation but not the other and the number of nodes showing reversal in the direction of the difference. The sex contrasts are computed and compared similarly except that Wilcoxon sum rank test is applied instead of Wilcoxon signed rank test because there is no correspondence between subjects in the two groups. For normally distributed network measures, the paired t-test and t-test can be applied instead of Wilcoxon signed rank test and Wilcoxon sum rank test.

To test the effect of node reconfiguration on state-dependent changes in graph metrics, Wilcoxon signed rank test was used to compare meaures for each pair of states (36 pairs in total) for each of the three cases, fixed parcellation, individualized parcellation, and state-specific parcellation. The statistical results were compared among the three cases. The results for node-level measures were summarized by the number of nodes that show significant state contrasts for one of the parcellation approaches but not the other, and the number of nodes that show reversals in the direction of significant state contrast. (Fig. 3b) To test the stability of state contrasts, we also performed a bootstrapping test by randomly subsampling 300 subjects out of 494 subjects for 100 times and repeated the analyses for each of the 300-subject subsamples. The mean and standard deviation of z scores (network-level measures) and number of nodes showing substantial changes (node-level measures) are reported.

Similar analyses were performed for comparing groups defined by sex, with two differences: 1) Wilcoxon sum rank test was used instead of Wilcoxon signed rank test because there was no direct correspondence between groups, and 2) group-specific network measures were contrasted separately for each of the state-specific measures.

Statistical analyses were performed with MATLAB. All primary findings are reported at a significance level of p<0.05. Wilcoxon signed rank test and Wilcoxon sum rank test were primarily applied because not all the network measures strictly follow normal distributions, but we also performed the same analyses with paired t-test and two-sample t-test and observed similar results.

Results with Bonferroni correction are included in supplementary material. We performed multiple comparison correction for changes in network-level measures and changes in group contrasts in network-level measures, multiple task states and multiple graph-construction methods. We also performed multiple comparison correction for changes in state contrasts in network-level measures, multiple task state pairs and multiple graph-construction methods and for node-level measures, we also took into account multiple nodes.

3. Results

In this work we computed a number of graph theory measures using HCP data. These measures were computed using a series of brain parcellation approaches to define nodes, that differed in the extent to which functional node reconfiguration was taken into account. These methods ranged from not considering functional changes at the node level (using a fixed atlas – the most common approach employed currently), to group or task specific functional node definitions, and finally individualized node definitions that were customized for each task and individual. Standard approaches to calculating graphs were used and basic node and network summary scores were compared across atlases. In addition, contrasts of these graph theory measures were generated comparing tasks or groups. The results reveal that graph theory summary scores reflecting both node and network properties changed significantly according to the extent to which regional functional changes were considered, but these changes did not occur in any particularly systematic manner.

3.1. Accounting for node reconfiguration leads to changes in graph theory measures

In the application of graph theory to fMRI connectivity matrices decisions have to be made as to whether or not nodes are connected in order to form a graph. Since both absolute threshold and proportional thresholding methods are commonly used we tested both methods and considered a range of decision thresholds in calculating graphs.

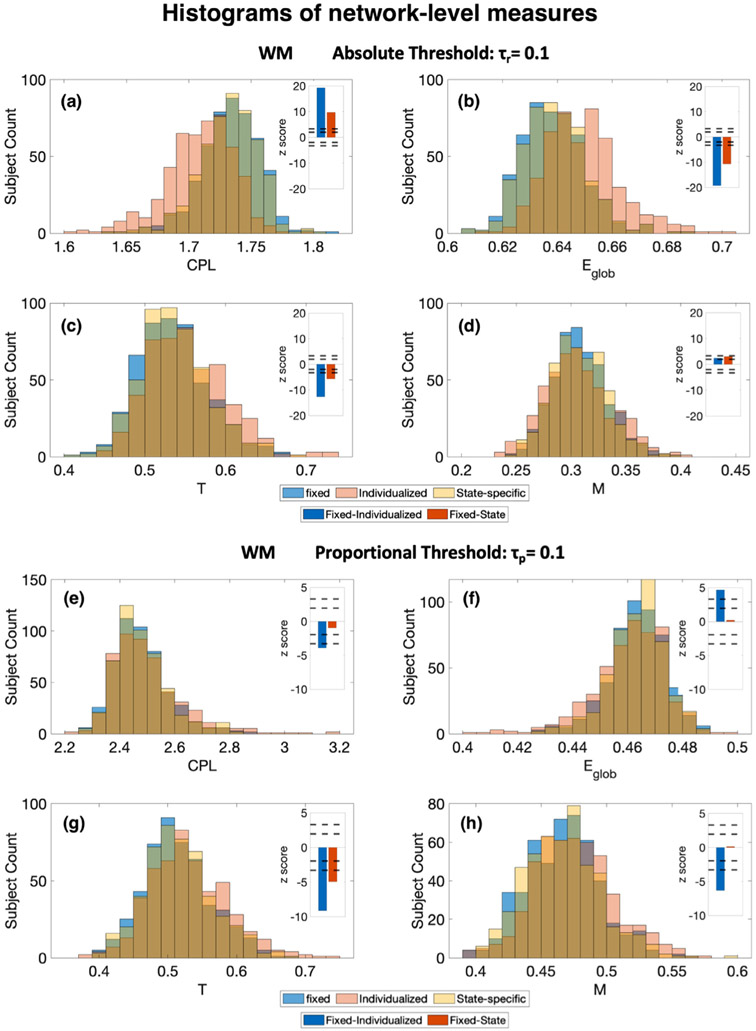
With an absolute threshold of τ_r = 0.1, all four network-level measures show significant differences between fixed parcellation and individualized parcellation, and fixed parcellation and state-specific parcellation at p = 0.05 (Fig. 4a, 4b, 4c, and 4d). The differences in characteristic path length and global efficiency are especially large (Fig. 4a and 4b). Graphs based on individualized parcellations and state-specific parcellations have shorter characteristic path length, higher global efficiency, higher transitivity, and lower modularity. The differences between fixed and individualized parcellations are more significant for most measures except for modularity (Fig. 4a, 4b, 4c, and 4d).

Fig. 4. Histograms of network-level measures, showing the distribution of scores as a function of parcellation scheme (applied to working memory task data), for absolute threshold (a-d) and proportional threshold (e-h).

The measures are characteristic path length (CPL), global efficiency (E_glob), transitivity (T), and modularity (M). The inset bar graphs on the right show the z score estimated by Wilcoxon signed rank test for fixed network measures – individualized network measures and fixed network measures – state-specific network measures. The two pairs of dotted lines indicate p = 0.05 and p = 0.001. Significant differences are observed between fixed network measures and individualized network measures at p = 0.001 for seven cases, except for (d) where the difference is significant at p = 0.05. There are significant differences between fixed network measures and state-specific network measures at p = 0.001 in cases (a), (b), (c), (g) and p = 0.05 in case (d).

With a proportional threshold of τ_p = 0.1, the differences between parcellations are less significant. There are still significant differences between fixed parcellation and individualized parcellation in all four measures at p = 0.001. (Fig. 4e, 4f, 4g, and 4h) Graphs based on individualized parcellations have longer characteristic path length, lower global efficiency, higher transitivity, and higher modularity. There are no significant differences between fixed parcellation and state-specific parcellation results except for the transitivity measure.

A large fraction of the 268 nodes show significant differences in the five node-level measures between fixed parcellation and individualized parcellation (Fig. 5a). Fewer, but still more than half of the nodes, show significant differences between fixed parcellation and state-specific parcellation (Fig. 5b). More nodes have significant changes in their graph theory measures with absolute threshold than with proportional threshold, consistent with the larger differences observed in the network-level measures with absolute threshold. With absolute threshold τ_r = 0.1, most of the nodes have higher clustering coefficients, higher local efficiency, higher degree, lower betweenness centrality, and lower participation coefficient when individualized parcellations and state-specific parcellations are applied instead of fixed parcellation. With proportional threshold τ_p = 0.1, most of the nodes have higher clustering coefficient, higher local efficiency, and lower participation coefficient. Degree and betweenness centrality show both increases and decreases among the significant changes.

Fig. 5. Node-level graph metrics show substantial differences according to the extent to which the parcellation approach considers underlying changes in the brain’s functional organization.

The number of nodes showing significant increases or decreases in node-level measures for the different atlas approaches including: fixed vs. individualized and fixed vs. state-specific with absolute threshold (a) and proportional threshold (b) during the working memory task. Measures based on fixed parcellation are used as base-lines for both comparisons. The numbers of significant increases and significant decreases are presented in the figure. The total heights of the stacked bars represent the numbers of nodes that show significant changes. (c) Maps representing the nodes showing significant increases or decreases in node-level network measures for Fixed vs. Individualized and Fixed vs. State-specific parcellations for each task state. The total numbers of significant increases and decreases for each network measure are corresponding to the numbers in (b).

After a conservative multiple comparison correction for multiple task states, multiple graph-constructing methods, and multiple nodes, the number of nodes showing significant changes in node-level measures decreases, especially for Fixed vs. State with proportional threshold. However, the principal finding still holds that the graph theory measures change when underlying connectivity changes at the node level are considered. (Figure S13, S14)

The network measures derived from data acquired during the working memory task are presented here as an example. The same analysis was performed for other task-based scans and resting-state scans (see Supplementary Table 1).

3.2. Accounting for node reconfiguration changes state contrasts in graph theory measures

Figs. 6 show how graph theory measures change between pairs of states, as a function of whether, and how, node definitions take into account the underlying reconfiguration of the brain with task-elicited brain states. Two pairs of states are contrasted: resting-state and motor; and resting-state2 and working memory. The results based on a proportional threshold τ_p = 0.1 are presented in Fig. 6 and the results based on an absolute threshold τ_r = 0.1 are reported in Figure S1.

Fig. 6. Top panel: Graph theory network-level contrasts between conditions show sensitivity to the underlying connectivity changes.

Z scores estimated by Wilcoxon signed rank test of state contrast in network-level measures for resting-state - motor (left) and resting-state2 - working memory (right) with proportional threshold τ_p = 0.1 based on three different parcellations: fixed parcellation, individualized parcellations, and state-specific parcellations. The three pairs of dotted lines indicate p = 0.05, p = 0.01, and p = 0.001, respectively. In some cases, the contrast between conditions is significant for some parcellations but not the others (e.g., b: significant REST2-WM CPL, E_glob, and T differences with fixed and individualized parcellation, but not with state-specific parcellation). In other cases, there can be reversal in direction of significant contrast (e.g. a: CPL is significantly longer during rest compared to motor with fixed parcellation but is significantly shorter during rest compared to motor with individualized parcellation). Bottom panel: The number of nodes showing changes in state contrasts in node-level measures for different parcellation approaches, including significant to non-significant changes, non-significant to significant changes, and reversal in direction of significant contrasts. Two pairs of parcellations are compared, fixed - individualized and fixed - state-specific. The bars for the two pairs are overlaid. A considerable number of nodes exhibit a change from significant to non-significant, or the reverse non-significant to significant, with different parcellation approaches. A few nodes show reversals in the direction of the significant state contrasts. In most cases, the state contrasts in node-level measures change more between fixed and individualized than between fixed and state-specific.

With a proportional threshold τ_p = 0.1, graphs based on fixed parcellation and state-specific parcellations have significantly shorter characteristic path length, higher global efficiency, higher transitivity, and higher modularity when contrasting the motor task with rest. (Fig. 6a) The contrasts are reversed with individualized parcellation. The graphs have significantly longer characteristic path length, lower global efficiency, and higher modularity. There is no significant difference in transitivity. Contrasting the rest2 and working memory conditions, significant changes are observed in characteristic path length, global efficiency and transitivity moving from fixed parcellation to the individualized parcellation approach. (Fig. 6b) The graphs have longer characteristic path length, lower global efficiency, and higher transitivity during the working memory task than rest2. There are no significant contrasts with state-specific parcellation. Modularity is significantly lower during the working memory task with all three parcellations.

For both state pairs (resting state versus the motor task, resting state2 versus the working memory task), there are nodes that show significant state contrast in the five node-level measures with fixed parcellation but have no significant state contrast with individualized or state-specific parcellation. (Fig. 6c, 3d) Similarly, some nodes have no significant state contrast in the node-level measures with fixed parcellation but show significant state contrast with the parcellation approaches that account for connectivity changes at the node level. A small number of nodes show significant contrast with both fixed and individualized parcellations but there are reversals in the direction of the differences. There are almost no sign reversals between the fixed parcellation and state-specific parcellations. In most cases, the state contrasts in node-level measures are more inconsistent comparing the fixed and individualized parcellation approaches, than when comparing the fixed and state-specific parcellation approaches.

We performed the same analysis on 100 random subsamples of 300 subjects from the full sample of 494 subjects. The significance of the state contrasts in network-level measures decreases due to the reduced sample size, but the directions of differences and relative significance levels are consistent with the results derived from the entire sample. The standard deviations of the z scores are relatively small indicating that the results are stable across these random subgroups. Compared to the results obtained for the entire sample, fewer, but still a significant number of, nodes show changes in state contrasts in the node measures when node reconfiguration is taken into consideration. The standard deviations for the number of nodes showing changes are also relatively low. (Figure S2, S3)

After multiple comparison correction, most observations hold true for network-level measures. For node-level measures, the number of nodes showing changes in state contrasts decreases, but significant changes are still present. (Figure S15)

3.3. Accounting for node reconfigurations changes group contrasts in graph theory measures

Fig. 7a shows that with a proportional threshold τ_p = 0.1, there are significant sex differences in characteristic path length, global efficiency, and transitivity during the emotion task only with sex-specific parcellation at p<0.05. The female group has longer characteristic path length, lower global efficiency, and higher transitivity during the emotion task. There is no significant group contrast in modularity with any parcellation. The differences between groups are more prominent during the working memory task. (Fig. 7b). The female group demonstrates shorter characteristic path length, higher global efficiency, and lower transitivity with all three parcellations. With individualized parcellation and sex-specific parcellation, the female group has lower modularity, but the difference is not significant with fixed parcellation.

Fig. 7. Top panel: Graph theory network level group contrasts show sensitivity to the underlying functional organization of the brain.

Z scores estimated by Wilcoxon sum rank test of sex contrast in network-level measures for emotion (left) and working memory (right) with proportional threshold τ_p = 0.1 based on three different parcellations, fixed parcellation, individualized parcellations, and sex-specific parcellations, each taking into account to a differing extent the underlying functional reconfiguration of the brain at the node level. The three pairs of dotted lines indicate p = 0.05, p = 0.01, and p = 0.001, respectively. In some cases, the significant contrast between groups can only be found when differences in functional node configuration are considered (e.g., a: significant CPL, E_glob, and T differences with sex-specific parcellation; b: significant differences in M with individualized and sex-specific parcellation). Bottom panel: Number of nodes showing changes in graph theory node-level measures contrasting groups defined by sex showing many nodal properties change dependent upon whether or not different node configurations between subject groups are accounted for. Changes include significant to non-significant, non-significant to significant, and reversal in direction of significant contrasts. Two pairs of parcellations are compared, fixed – individualized and fixed – sex-specific for two tasks, emotion (left) and working memory (right).

Consistent with less significant sex contrasts compared to the state contrasts in network-level measures, fewer nodes showed changes (significant to non-significant or non-significant to significant) in the node-level measures with the different parcellation strategies. Very few nodes showed sign reversals. (Fig. 7c and 7d). Nevertheless, the group contrasts in node-level graph theory measures are clearly sensitive to whether or not connectivity changes at the node level are considered. Results based on an absolute threshold τ_r = 0.1 are reported in Figure S4.

Most group contrasts in network-level measures don’t survive multiple comparison for any parcellation method. Very few nodes show changes in state contrasts after correction. The extremely low number of nodes with significant changes in node-level network measures group contrasts don’t indicate that the group contrasts are insensitive. They are due to the fact that group contrasts in network measures are weaker than state contrasts and few significant group contrasts survive after the multiple comparison correction for 15 network constructing methods, 9 tasks and 268 nodes. The number of nodes showing significant group contrasts is below 5 for any condition and metric (mean <1), so the numbers of nodes showing substantial changes (non-significant to significant, significant to non-significant, or sign reversal in significant contrasts) apparently cannot be higher than 5. (Figure S16)

Results based on individualized parcellations using AALv3 (Rolls et al., 2020) as the initial atlas (Figure S5, S6, S7, S8) and results based on aggregated metrics (Figure S9, S10, S11, S12) further show that the general conclusions of this work hold independent of the specific approach used. Results after Bonferroni correction (Figure S13, S14, S15, S16) show that most of the significant changes in network measures and substantial changes in contrasts of network measures are preserved even after conservative corrections.

4. Discussion

Graph theory metrics have already been widely used to examined changes in functional organization at the network level. The basic building block of a graph is the underlying node. This work demonstrates that if the functional connectivity changes that occur as a function of brain state or group are considered in the node definitions, the results of graph theory measures may change. We also demonstrate that such changes are not simply a shift up or down in terms of significance of a finding. Instead, taking into account the changes in node definitions, influences the graph theory measures in an unpredictable manner with some results unchanged, enhanced, suppressed or inverted. Previous studies have investigated differences in node-level functional connectivity between task-elicited brain states (Cole et al., 2014; Krienen et al., 2014) and groups (Satterthwaite et al., 2015; Wang et al., 2012a) . This work suggests that if one is interested in how functional connectivity changes between tasks or groups, as measured by graph metrics, then one should investigate the underlying impact of changes in connectivity at the voxel level and not assume that voxel level changes do not occur. The results of many network-level and node-level brain network measures change significantly when individualized or state-specific parcellations, approaches that take into account voxel level connectivity changes, are applied instead of a fixed parcellation. The direction of change, the significance of the change, and the effect sizes vary across brain states and graph construction methods.

Although previous studies have investigated the effects of different parcellation strategies on functional network properties (Park et al., 2013), potential node reconfiguration across states and different topography across subjects have not been considered. To date, most studies have used fixed atlases across all conditions. Fixed group atlases, derived from functional MRI data or a combination of functional and anatomical information, are commonly used to reduce the dimensionality of neuroimaging data prior to functional connectivity analyses (Arslan et al., 2018). Recent studies have shown that the spatial arrangement of cortical regions can vary across subjects (Gratton et al., 2018) and even within the same subject across different tasks or brain states (Salehi et al., 2020). A previous study showed that node reconfiguration occurs in a reliable and meaningful way such that node size can be used to predict the task condition during which the data were obtained (Salehi et al., 2020). Both node and network reconfigurations have been shown as a function of sex and behavioral phenotypes (Kong et al., 2019; Salehi et al., 2018).

Using a fixed group atlas imposes the underlying assumption that functional connectivity does not influence node definitions, and that differences in graph theory measures are all attributable to differences in edge strength. Previous work has shown that the particular spatial arrangement of cortical regions in individuals strongly influences functional connectivity. (Bijsterbosch et al., 2018) Several methods have been proposed to account for inter-subject variability and establish individualized parcellations(Chong et al., 2017; Kong et al., 2019; Salehi et al., 2018; Wang et al., 2015a). The work presented here, extends the above studies by demonstrating that not only do individual variations in node definitions influence results, but that the flexible functional organization of nodes even within an individual can influence the results. The findings here also demonstrate that group specific functional node variations may also influence our interpretation of group differences in graph theory measures of connectivity.

There are many studies in the literature reporting differences in graph properties without consideration of the possibility of voxel level connectivity differences. For example, functional brain networks were found to have reduced clustering and small-worldness, reduced probability of high-degree hubs, and increased robustness in patients with schizophrenia relative to healthy controls. (Lynall et al., 2010) Another study revealed functional brain networks in Alzheimer’s disease have a significantly lower clustering coefficient and longer characteristic path length compared to healthy controls, indicating loss of small-world properties. (Supekar et al., 2008) A recent study showed that network measures can be used as features in a machine learning framework to make diagnostic predictions of Autism Spectrum Disorder. (Chaitra et al., 2020) These studies however all used a fixed atlas approach and did not investigate the possibility that some of the differences observed in the graph theory measures were due to voxel level connectivity changes and not simply due to changes in edges.

Some network-level measures show significant contrasts across different task-elicited brain states. In general, these contrasts are stronger for absolute threshold than proportional threshold possibly because the proportional threshold removes the effect of baseline connectivity differences while maintaining the same graph sparsity for all brain networks. The strength of contrast also varies across state pairs. For example, the contrasts in CPL, E_glob, and M are stronger in the resting-state versus motor-task contrast, compared to the contrast between the resting-state2 and working memory conditions. Such contrasts can change in various ways across measures and graph construction methods when individualized parcellations are applied. Overall, there is no systematic increase of decrease in these network measures when accounting for voxel-level connectivity changes. For example, the contrast in characteristic path length between resting-state2 and working memory is significant with both fixed and individualized parcellations, but the significance level increases (Fig. 6b). In some cases, there were significant differences only with fixed parcellation but not state-specific parcellations (Fig. 6b), or only with individualized parcellations (Figure S1a). In a few cases, there were sign reversals in the direction of state contrasts (Fig. 6a). The contrasts based on state-specific parcellations are usually more similar to those based on fixed parcellation likely because there is only one uniform state-specific parcellation for all the subjects for each state and such a parcellation may be more robust to noise. However, there are cases where state-specific parcellations yield contrasts that are distinct from fixed parcellation (Fig. 6b). For most node-level measures and state pairs, a considerable number of nodes show significant state contrast with either the fixed parcellation or individualized parcellation, but the number of nodes exhibiting significant differences changed with parcellation approach. For some cases, however, such as the contrast in degree between resting-state and motor with absolute threshold (Figure S1c), the number of nodes that changed was small. Furthermore, there can even be sign reversals in the direction of contrast for a small fraction of nodes. In most cases, fewer nodes exhibit inconsistent results moving from the fixed to state-specific parcellations, compared to graph theory node measures changing between the fixed and individualized parcellations. Importantly, while the effect of applying individualized parcellations and state-specific parcellations varied across measures and state contrasts, it was stable across different subsamples, suggesting that the impact of node reconfiguration on state contrasts is reliable.

The choice of atlas can also change the results when contrasting network measures between subject groups, as shown by the case where the groups were defined by sex. The strength of the group contrast varied across brain states. For example, as shown in Fig. 7, differences between groups are more prominent for data collected during the working memory task compared to the emotion task. Consistent with a previous study, network measures are found to be unstable across different thresholding methods (Fig. 7 and S3) (Garrison et al., 2015). In addition to these factors, group contrasts in network measures are also sensitive to whether or not node reconfigurations are considered. There are significant differences in characteristic path length, global efficiency, and transitivity between groups for the emotion task with τ_p = 0.1 only based on sex-specific parcellations, but not for the other two parcellations (Fig. 7a). Likewise, the difference in modularity between groups during the working memory task is not significant with fixed parcellation, but significant when individualized or sex-specific parcellations are used (Fig. 7b). The group contrast of node-level measures is highly variable for the different atlas definitions for some nodes. The number of nodes that exhibit changes in graph theory node property measures also varies considerably for different cases. Interestingly, in most cases, group differences in node properties changed from significant to non-significant when applying individualized parcellation compared to a group-specific parcellation. Yet, more nodes changed from non-significant to significant in the group contrast when applying the group-specific parcellation compared to individualized parcellation.

Taken together these results suggest that the conclusions of brain-state or group-specific contrasts, for either node-level or network-level graph theory measures, may change if the possibility of node reconfiguration is taken into consideration. Studies in the literature that used similar task contrasts to those shown here include work by Cohen et al. (Cohen and D’Esposito, 2016), where they showed that compared to rest, modularity was lower and global efficiency was higher during an N-back task. They applied both an anatomical atlas and a functional atlas and concluded that the results are generally consistent, but differences were observed. Here, using the HCP data for the same contrasts we demonstrate that the significance level of these contrasts changes if node reconfigurations that are known to take place as a function of task (Salehi et al., 2020) are considered. The same work found that there was no significant difference in modularity and global efficiency during rest and finger tapping. However, it is possible that significant contrasts can only be observed when individualized or state-specific parcellations are used. Another study similar to the group contrast shown here, is that of Tian et al. (Tian et al., 2011). In that study they showed that there is no significant difference in characteristic path length, clustering coefficient, local efficiency and global efficiency between genders.(Tian et al., 2011) However, as we demonstrate above significant differences in some of these measures do appear if the underlying functional organization differences at the node level are considered by incorporating individualized or group-specific parcellations. The conclusions in a range of other studies of network measure changes with cognitive states (Cohen and D’Esposito, 2016; Hearne et al., 2017; Shine et al., 2016; Wang et al., 2012b; Wen et al., 2015) and groups (Satterthwaite et al., 2015; Tian et al., 2011; Wu et al., 2013; Zhang et al., 2016) could exhibit similar changes if functional connectivity changes at the voxel level are taken into consideration. This is not to say that any of those studies are wrong – but to point out that the conclusions may change if the underlying connectivity changes at the voxel level are considered. It should also be noted that there are consistencies in the parcellations across subjects and states. In each case, the 268-node atlas only varies slightly between subjects and conditions. What we show here is that if we look closely, there are meaningful but subtle changes in the local connectivity (even within a node) that influence the results of graph theory measures.

In patient studies of functional connectivity, a common overarching working hypothesis is that there will be functional connectivity differences between patients and healthy controls. Yet the majority of such studies do not investigate whether the underlying functional connectivity changes lead to node reconfigurations. While no patient group contrast was tested here, the groups defined by sex demonstrated changes in graph theory measures contrasts dependent upon whether or not voxel level changes were considered. Therefore, future graph theory investigations using functional connectivity should also include the possibility of node reconfigurations.

There are many plausible explanations for the changes in network measures and the contrasts in network measures. As revealed by previous studies, functional nodes may reconfigure across subjects, brain states, and groups. If fixed atlases are used, such differences may be misinterpreted as differences in edge connectivity driving differences in graphs of brain networks. Although the reliability of individualized parcellations has been shown in previous studies, it is possible that individualized parcellations may be more sensitive to noise in a single scan or single session, thus introducing noise into the graph theory measures. A substantial amount of data, i.e. long scans, is required to ensure the reliability of individualized parcellations. However, this is not the case for group-state specific parcellations which take the majority vote across large numbers of subjects and thus require fewer data per subject.

The changes in network measures, and contrasts in network measures, revealed here suggest that the assumptions made when applying network analysis, that the nodes are fixed and uniform, may be inappropriate. Using individualized or state-specific parcellations represents one potential approach to account for the within-node connectivity changes. Individualized parcellation methods (Chong et al., 2017; Kong et al., 2019; Salehi et al., 2018; Wang et al., 2015a) generally yield higher within-node homogeneity, and thus potentially higher stability in network analyses. Admittedly, to what extent individualized parcellations can deviate from the fixed parcellation is restricted by the exemplar-based algorithm because the number of parcels is held constant to match the fixed parcellation, the exemplar is usually near the geometric center of each node, and the voxel-to-parcel assignment has a spatial contiguity constraint. It is plausible that the individualized parcellation, state-specific parcellation, and group-specific parcellation we apply here don’t fully account for flexibility in voxel-level architecture. Methods need to be developed that co-vary for changes in node-homogeneity as a function of group or condition to account for the within-node changes in connectivity. For example, when building a predictive model based on functional connectivity relating brain to behavior, in addition to edge connectivity, metrics for within-node connectivity (such as homogeneity) could be incorporated as a predictor. Further work is warranted to explore how within-node connectivity can be incorporated into network analysis in ways other than deriving individualized parcellations. We hypothesize that with higher resolution atlases (smaller nodes) at some point the within node connectivity should stabilize such that only edge changes are apparent between states, but this is currently a subject of further investigation. Stability of within-node connectivity across tasks for example, could in fact be part of a parcellation approach potentially providing stopping criteria for determining optimal node size for each node. The extreme of this potential strategy is to analyze voxel-level rather than node-level connectivity and networks to avoid the node definition problem. In fact, voxel-based network analyses have been investigated (Hayasaka and Laurienti, 2010; Scheinost et al., 2012, 2014; Wang et al., 2015b), but the high computational cost is a major limitation.

In this study, tasks are used as a proxy for changes in brain state with the assumption of a particular node configuration across the state (task). While the methods to parcellate the brain into functional nodes are too noisy to consider dynamic changes that occur on a moment-to-moment basis, it is likely that nodes reconfigure in a much more dynamic manner. As stimuli and responses change rapidly within a fMRI experiment, different subsets of the millions of neurons within a region may be engaged leading to dynamic reconfiguration of node boundaries. It is not clear at this point how such dynamics can be incorporated into graph theory-based brain network models. However, it is clear that there are reliable average state-based node reconfigurations that are distinct and stable enough to be able to identify the task during which the data was collected simply from the parcellation (Salehi et al., 2020). Further work is needed to identify and incorporate continuous reconfigurations into brain network analyses.

5. Conclusion

In summary, we empirically demonstrate that network measures, and more importantly, contrasts in network measures between brain states and subject groups, are sensitive to functional connectivity changes at the voxel level within a node. As graph theory-based network measures are widely applied in many fMRI studies, it is worth noting that the results may change dramatically when the underlying basis for the measures, the node definitions, may be part of the functional changes that are under investigation. While there is no consensus as to which atlas to use to define nodes, all publications to date have assumed a fixed atlas across subjects, brain states and groups. There has been widespread acceptance that connectivity between regions can change under a wide array of conditions, yet little consideration has been given to the impact of local connectivity changes within the node, one manifestation of which leads to nodal reconfiguration. This work shows that when graph theory is applied in fMRI, consideration must be given to how connectivity changes at the voxel level influence the node, which is the fundamental building block of any graph.