Abstract
The COVID-19 epidemic has had a great adverse impact on the world, having taken a heavy toll, killing hundreds of thousands of people. In order to help the world better combat COVID-19 and reduce its death toll, this study focuses on the COVID-19 mortality. First, using the multiple stepwise regression analysis method, the factors from eight aspects (economy, society, climate etc.) that may affect the mortality rates of COVID-19 in various countries is examined. In addition, a two-layer nested heterogeneous ensemble learning-based prediction method that combines linear regression (LR), support vector machine (SVM), and extreme learning machine (ELM) is developed to predict the development trends of COVID-19 mortality in various countries. Based on data from 79 countries, the experiment proves that age structure (proportion of the population over 70 years old) and medical resources (number of beds) are the main factors affecting the mortality of COVID-19 in each country. In addition, it is found that the number of nucleic acid tests and climatic factors are correlated with COVID-19 mortality. At the same time, when predicting COVID-19 mortality, the proposed heterogeneous ensemble learning-based prediction method shows better prediction ability than state-of-the-art machine learning methods such as LR, SVM, ELM, random forest (RF), long short-term memory (LSTM) etc.
Keywords: COVID-19, Mortality, Stepwise multiple regression, Ensemble learning, Time series prediction, Hybrid method
1. Introduction
With an unknown type of pneumonia detected in Wuhan, now known as COVID-19, China reported the incident to the WHO Country Office in China on 31 December 2019.1 In the two months since its first detection, COVID-19 had rapidly spread in China. By the end of February 2020, the total number of confirmed cases in China was close to 80,000.2 As a result of the effective measures taken by the Chinese government and the active public support, COVID-19 was effectively curbed in China at the beginning of March, with the number of newly confirmed cases per day being controlled at about 100. But on a global scale, the battle against COVID-19 is ongoing. On 16 March, the total number of confirmed cases in the rest of the world exceeded that of China, which means that the pandemic has become a common enemy of people all over the world.
After COVID-19 broke out in China, researchers around the world scrambled to research on it, most of which concerns the diagnosis, treatment, and infection of the disease [1], [2]. For example, Abbasian et al. [3] explored the application of deep learning in computed tomography (CT) imaging, which is currently a very fast and effective method to diagnose whether patients have been infected with COVID-19. It is generally believed that artificial intelligence (AI) methods such as deep learning can effectively assist doctors in conducting CT diagnosis, reducing their work pressure. Gautret et al. [4] evaluated the role of hydroxychloroquine in lessening respiratory viral loads. In addition to these studies at the individual level of patients, there are macro-level studies. For example, Xie and Zhu [5] studied the association between ambient temperature and COVID-19 infection in 122 cities in China. Ma et al. [6] investigated the effects of temperature, diurnal temperature range, and humidity on the daily mortality of COVID-19 in the Chinese population.
To measure the impact of a pandemic disease, mortality (death rate) is a very important indicator, which is defined as
| (1) |
The level of mortality of a pandemic disease affects the attitudes of the people and government towards the disease and, to a certain extent, affects the formulation of relevant prevention measures and policies. Different virus epidemics take place throughout the world every year, but only a few escalate to the level of public concern [7]. Table 1 lists several past pandemics wreaking havoc on the world, such as the Black Death, Smallpox, and Spanish Flu. The mortality rates of these diseases varied greatly, ranging from 0.04% to 60%. Since the beginning of the 21st century, there have been many serious pandemics in the world such as severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS). So far, COVID-19 stands as the pandemic disease with the largest number of deaths in the past two decades.
Table 1.
History of pandemics (sorted by death toll).
| Name | Time | Deaths | Frequency | Mortality |
|---|---|---|---|---|
| Black Death (Bubonic Plague) | 1347–1351 | 200 M | 334 M 667 M | 30% 60% |
| Smallpox | 1520 | 56 M | 187 M | 30% |
| Spanish Flu | 1918–1919 | 50 M | 2000 M | 2.5% |
| HIV/AIDS | 1981–Present | 32 M | 1600 M | 2% |
| Asian Flu | 1957–1958 | 1.1 M | 164 M | 0.67% |
| Hong Kong Flu | 1968–1970 | 1 M | 200 M | 0.5% |
| COVID-19 | 2019–Present (2020.6.3) | 388 K | 6.6 M | 6% |
| Swine Flu | 2009–2010 | 284 K | 700 M | 0.04% |
| Yellow Fever | Late 1800s | 60 K | 170 K | 35% |
| Ebola | 2014–2016 | 11.3 K | 23 K | 50% |
| MERS | 2012–Present | 866 | 2519 | 35% |
| SARS | 2002–2003 | 774 | 8098 | 9.5% |
Center for Disease Control and Prevention (CDC), WHO, BBC, Wikipedia.
At present, there are two types of studies on COVID-19 mortality, namely individual mortality of patients and group mortality. For the first type of research, Yan et al. [8] is an example, where the researchers took a sample of 485 cases of COVID-19 infected patients in Wuhan and built an interpretable mortality prediction model based on the decision tree method. By combining the patient’s demographic data and clinical examination data, the model can accurately predict the patient’s outcome within seven days. The second type of research focuses on the prediction of COVID-19 mortality in a certain area in the future. For example, Wang et al. [7] developed the patient information based algorithm (PIBA) to predict the mortality of a new infectious disease in real time. The research in this aspect generally regards the problem of mortality prediction as a time series forecasting task and predicts the future by fitting a change curve of mortality over a period of time in the past.
Differing from the above studies, our research involves conducting an analysis of the factors of COVID-19 mortality and constructing a prediction model for COVID-19 mortality. In order to explore the impacts of various factors on the mortality rate of COVID-19, we use a stepwise multiple regression analysis method [9] to model and analyze the data on different time periods of each country. Essentially, the mortality prediction problem can be regarded as a time series prediction problem. When solving the time series prediction problem, the popular methods are mainly divided into three categories: statistical methods, machine learning methods, and deep learning methods. Statistical methods are represented by the autoregressive (AR) models and moving average (MA) models. Machine learning methods and deep learning methods are new methods that have emerged in recent years [10]. Machine learning methods slice the time series data and input them into various machine learning algorithms for training, while deep learning methods mostly use the long short-term memory (LSTM) method as the solution. Through analysis of related research [11], [12], [13], [14], we find that traditional statistical methods are often not as accurate as expected, while machine learning methods and deep learning methods achieve superior performance in many time series prediction tasks. At the same time, we notice that deep learning methods can only show unique advantages on data sets with a large number of samples [15]. Taking these two points into account, we build the COVID-19 mortality prediction model based on machine learning methods.
Among the various machine learning methods, the ensemble learning method is the most popular in recent years, which has been successfully applied in many fields such as medical diagnosis [16], risk assessment [17], and fault diagnosis [18]. The ensemble learning method generates the final prediction result by combining the outputs of multiple base learners [19]. In this way, the fault tolerance of the entire model can be effectively improved and the generalization error can be reduced. The current popular ensemble learning algorithms include Random Forest [20], XGBoost [21], and LightGBM [22], but these methods only use decision trees as the base learner, which reduces the diversity of the base learners. The better the diversity of the base learners is, the better is the overall stability of the model [23]. Based on this consideration, we design a prediction method based on heterogeneous ensemble learning, which aims to improve the prediction performance of the model by increasing the diversity of the base learners.
In summary, our findings and contributions are as follows:
-
(1)
Seeking to identify the influencing factors of mortality in various countries, we construct a comprehensive framework covering eight aspects including medical capacity, economic level, age structure etc. Then we identify an array of factors affecting COVID-19 mortality using stepwise regression analysis. Among a collection of factors, the number of hospital beds, the country’s aging degree, and nucleic acid testing capabilities will significantly affect the mortality of COVID-19 in each country. Thus, measures such as the establishment of centralized isolation points can be adopted to alleviate the shortage of medical resources and give priority care to the elderly.
-
(2)
In order to improve the performance of the ensemble learning model, we use linear regression (LR), support vector regression (SVR), and extreme learning machine (ELM) as the base learners, and linear regression as the meta-learner to construct a two-layer nested heterogeneous ensemble learning model. Experiments show that the proposed model is superior to other popular machine learning methods.
We organize the rest of the paper as follows: In Section 2 we present the framework of the factors influencing COVID-19 mortality and the related analysis methods. In Section 3 we detail the proposed prediction method based on two-layer nested heterogeneous ensemble learning. In Section 4 we analyze and discuss the experiment results. Finally, in Section 5, we conclude the paper and suggest topics for future research.
2. Stepwise multiple regression-based influencing factors analysis
2.1. Influencing factors of COVID-19 mortality
To explore the factors that affect COVID-19 mortality, we consider the relevant factors as fully as possible. As shown in Fig. 1, around the theme of COVID-19 mortality, we identify eight possible influencing factors of mortality, which are Confirmed cases, Testing, Age structure, Healthcare capacity, Economic level, Risk factors, Climate, and Disease progression.
Fig. 1.
Influencing factors of COVID-19 mortality.
In examining these eight potential factors, we have the following considerations:
Confirmed cases
From the definition of mortality in (1), we know that the number of confirmed cases should be related to mortality. However, the relationship between the two is not necessarily inversely proportional. According to Nishiura’s research [24] on the swine influenza A H1N1 (H1N1) infectious disease, the cumulative number of cases shows a positive relationship with mortality. Therefore, we include Total number of confirmed cases per million people in the study.
Testing
The disease testing strategies adopted by each country are different, and the test coverage of COVID-19 will affect the total number of confirmed cases, which may affect the COVID-19 mortality in the country [25]. Therefore, we use Number of tests per million people in the country to measure the test situation.
Age structure
With an increase in age, the probability of people suffering from serious diseases will increase accordingly [26]. The age structure of a country characterizes the aging level of the country, so we include the two variables Share who is 70 or over and Median Age in our COVID-19 mortality study.
Health care capacity
Health care capability is a key factor directly related to disease detection, prevention, and treatment [27]. We assume that a country with a strong health care capability is better able to control the overall mortality of an infectious disease. To characterize health care capability, we use two variables, namely Physicians (per 1000 people) and Hospital beds (per 100,000 people).
Economic level
Gavurová and Vagašová’s [28] found that income inequality has an impact on a disease’s mortality. At the individual level, economic conditions will directly affect the treatment options available to patients; at the national level, developed countries have better medical resources and higher medical standards. Therefore, the level of economic development of a country may also have an indirect impact on the mortality of an infectious disease [29]. So we use the following variables related to economic development: Share of the population living in extreme poverty, GDP per capita, Population, and Population density.
Risk factors
The risk factors in this study mainly refer to variables related to the general physical health of a country’s population. At the individual level, for patients suffering from some underlying diseases, the COVID-19 virus is more likely to cause death. Therefore, we assume that, at the national level, the overall national health status has an impact on COVID-19 mortality. The relevant variables for risk factors are: Diabetes prevalence (%), Deaths from cardiovascular disease (per 100,000 people), Share of people living with active tuberculosis (%), Share of the population infected with HIV (%), Share of population with cancer (%), Share of men who smoke (%), Share of women who smoke (%), Share of men who are obese (%), and Share of women who are obese (%).
Climate
Many infectious diseases such as SARS, MERS, and H1N1 can spread via air-borne droplets from a cough or sneeze, and COVID-19 is no exception. Therefore, some researchers [5], [6], [30] have studied the impacts of climatic conditions on the spread of infectious diseases. We assume that climatic conditions will affect the spread of an infectious disease, resulting in changes in the number of patients, and ultimately indirectly affecting the disease’s mortality rate. At the same time, depending on the characteristics of the disease, the climate may affect the severity of the patient’s condition. The variables we use to measure the climate in various countries include Temperature, Humidity, Wind speed, and Atmospheric pressure.
Disease progression
Disease progression is mainly used to characterize the speed of development of COVID-19 in various countries. What is behind it may be the attitudes of the governments and people of various countries towards the epidemic, which may affect the number of confirmed cases and mortality. So we use The doubling time of confirmed deaths (days) to measure this factor.
2.2. Related analysis methods
To analyze the influencing factors of COVID-19 mortality in various countries, we combine the two methods of correlation analysis and stepwise regression. First, to avoid being affected by the collinearity of the variables when using stepwise regression, we use correlation analysis to remove the highly correlated variables. After that, we use stepwise regression to find significant variables that affect mortality. At the same time, considering that with the gradual development of the pandemic, the influencing factors of mortality may change accordingly, we have intercepted data at multiple time points for analysis.
2.2.1. Correlation analysis
Correlation analysis is a statistical analysis method to study the correlation between two or more random variables of equal status. In the field of machine learning and statistical learning, correlation analysis is often used for preliminary variable selection. Pearson’s correlation coefficient [31] is the measure of correlation, which ranges (depending on the correlation) between and , where indicates the strongest positive correlation possible, while indicates the strongest negative correlation possible.
In our study we use the Pearson correlation coefficient to measure the correlation between two variables. Specifically, we define that two variables whose correlation coefficient has an absolute value greater than or equal to 0.7 as highly correlated. When two variables are highly correlated, we only retain one of the two variables. Through correlation analysis, we can effectively reduce the multicollinearity between the independent variables.
2.2.2. Stepwise multiple regression
Stepwise multiple regression analysis [32] is a better variable selection method that combines forward selection regression and backward selection regression, which belongs to the class of greedy search algorithms. The main step is to add the candidate factors into the regression equation one by one according to their ability to explain the dependent variables. After each variable is added, the significance of the whole model and each independent variable is tested. When the original factor is no longer significant due to the introduction of subsequent factors, it will be dropped from the model. This ensures that every time a new factor is introduced into the model, only significant factors are included in the model. The process is repeated until no significant variable is introduced or eliminated. In this way, the optimal regression model is obtained. The explanatory variables in the final model are all significant variables.
Following Tsai [33] and Bauweraerts [32], we use several criteria during the stepwise selection procedure. Specifically, we use the significance level of 0.05 as the cutoff line for adding variables to the model and the significance level of 0.1 as the cutoff line for removing variables from the model.
3. Two-layer nested heterogeneous ensemble learning-based prediction method
After analyzing the influencing factors of COVID-19 mortality in various countries, we examine various methods for predicting mortality. In addition, we propose a two-layer nested heterogeneous ensemble learning-based prediction method to improve the prediction accuracy of COVID-19 mortality. If we can develop a prediction model that can accurately judge the changing trend of COVID-19 mortality in the future, it will play an auxiliary decision-making role in the formulation of policies and deployment of rescue resources to combat COVID-19.
In this study we compare the performance of four types of methods, including traditional time series forecasting, single machine learning, ensemble learning, and deep learning, in predicting the mortality of COVID-19. During the experiments, we divide the time series data into two parts, namely the training set and test set. The traditional time series method can directly use the training set data for experiments, while the other three methods need to process the data before they can be used. We use the samples in the test set to feed the models to perform the prediction. After obtaining the prediction results of each method, we apply relevant performance evaluation indicators to compare the performance of different methods.
After comparing the four types of prediction methods, we select well-performing machine learning algorithms to construct the proposed two-layer nested heterogeneous ensemble learning model. By fusing the advantages of the base learners, we further improve the performance of the prediction model.
In this section we first introduce how to combine time series analysis with machine learning methods, which requires segmentation of time series data. Subsequently, we briefly discuss applying the traditional methods and deep learning methods to deal with time series problems. Third, we elaborate on the proposed two-layer nested heterogeneous ensemble learning method in detail. Finally, we discuss the related evaluation indicators.
3.1. Training and testing sets
When constructing a time series forecasting model, we divide the data set into two parts: the training set and test set. The training set is used to train the model, while the test set is used to test the performance of the model [34]. For traditional time series forecasting models, the original time series data can be used directly to construct the model. For machine learning, we need to process the data before they can be used. Simply put, we convert the original vector data into matrix data. The rows of the matrix represent the number of samples and the columns of the matrix are the days of the historical data used. For example, if we want to use the data of the last four days to predict the future, the number of columns in the matrix is five, and one of the columns contain the true value to be predicted.
As for the division of the data set, it depends on the length of the future time we want to predict. If it is one-step prediction, i.e., only predicting the state of tomorrow, the problem is much simpler. However, if multi-step prediction is required, it will involve out-of-sample prediction and in-sample prediction. In-sample prediction refers to the use of a model to predict the value within the sample, and the difference between it and the actual observed value is the error value. Out-of-sample prediction refers to the use of a model to predict out-of-sample values, reflecting the model’s ability to predict the real world. Researchers generally pay more attention to the performance of a model in making out-of-sample predictions. When making out-of-sample predictions, the prediction value of the previous day is used as the input for the prediction of the next day. Therefore, multi-step out-of-sample prediction brings great challenges to the performance of the model.
3.2. Traditional method
Traditional time series forecasting mainly includes the naïve method, average method, exponential method, and autocorrelation method as follows:
-
•
Naïve method: For naïve forecasts, all the forecasts are set to the value of the last observation, i.e., .
-
•
Average method: For the average method, the forecasts of all the future values are equal to the average of the historical data. Suppose the historical data are , then the forecast is . In addition, the moving average method is an improved method. It does not calculate the average of all the historical values, but computes the average based on the “sliding window” , so the forecast is . Furthermore, by the same token, the weighted moving average method is developed as follows: , i.e., the values of the historical data at different times are given different weights.
-
•
Exponential method: It is noted that there is a big difference between the simple average method and the weighted moving average method in the selection of time points. Therefore, a compromise method is created that assigns different weights to the data while taking all the data into consideration. For example, compared with the observations in earlier periods, this method gives greater weights to the recent observations. Known as simple exponential smoothing, it calculates the predicted value through a weighted average, in which the weight decreases exponentially with the time of the observation from the near to the distant, with the smallest weight assigned to the earliest observation.
-
•
Autocorrelation method: Exponential smoothing and autoregressive integrated moving average (ARIMA) models are the two most widely used and complementary approaches for time series forecasting [35]. While exponential smoothing models are based on a description of the trend and seasonality in the data, ARIMA models aim to describe the autocorrelations in the data. ARIMA models are generally denoted as ARIMA(, , ), where the parameters , , and are non-negative integers, denoting the order (number of time lags) of the autoregressive model, the degree of differencing (the number of times the data have had past values subtracted), and the order of the moving-average model, respectively.
3.3. Deep learning method
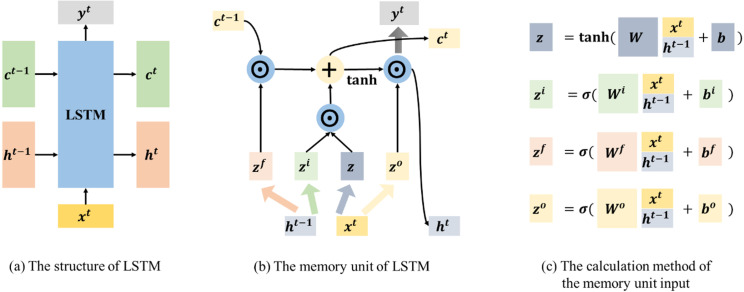
In recent years, the deep learning method has become a new research hotspot. Because of its strong fitting capability, it has been widely used in fields such as natural language processing and image processing, which however use completely different deep learning algorithms. The problems to deal with in natural language processing include the time series structure, while image processing does not have this characteristic. Since the time series prediction problem has some similarities with the natural language processing problem, their algorithms also have a certain degree of interoperability. Based on this idea, researchers have applied deep learning models in natural language processing, such as the recurrent neural network (RNN), to solve the corresponding time series forecasting problem [36]. The variant of the deep learning method we use in this paper is the long short-term memory (LSTM) model [37]. Compared with the RNN model, LSTM has a more complex internal structure. The LSTM model can solve some problems in RNN, so its performance is better than RNN. The unique gating mechanism of LSTM enables it to take into account the problems of short-term dependence and long-term dependence, so that information from a long time ago can also be retained in the model.
As shown in Fig. 2, there are three inputs to the memory unit in LSTM: (cell state), (hidden state), and (time series data). Four states (, and ) can be obtained by splicing and calculating the current input data and the passed from the previous state. In these four states, , and represent the state calculation results of the input gate, forget gate, and output gate, respectively; , and represent the weight matrix and bias unit of the corresponding gate, respectively; represents the sigmoid activation function; and represents the tanh activation function.
Fig. 2.
Long short-term memory model.
In the LSTM model, the output results and of the memory unit at time are determined by the output gate and the unit state . The calculation method is as follows:
| (2) |
| (3) |
| (4) |
where represents the unit state input at time ; and represent the state weight matrix and bias term of the input layer, respectively; and represents the Hadamard Product.
3.4. Two-layer nested heterogeneous ensemble learning method
In order to predict COVID-19 mortality more accurately, we propose a two-layer nested heterogeneous ensemble learning method. The details of the proposed method are shown in the following.
The ensemble learning method is a popular research hotspot in machine learning, which is developed based on the single machine learning method. In general, the basic learners in ensemble learning use a single machine learning algorithm. These basic learners are trained through parallel or serial training mechanisms, and finally through the combination strategies that integrate the prediction results of the base learners [38]. In many studies, ensemble learning tends to achieve better performance than the single machine learning method. For the ensemble learning method, there are two key points that have an important impact on its performance, one is the diversity of the base classifier and the other is the choice of combination strategy [39]. In this research we make improvements to both points.
From the perspective of the base classifier, ensemble learning can be divided into two categories: the homogeneous ensemble learning method and heterogeneous ensemble learning method. The homogeneous ensemble learning method uses the same learning algorithm when training the base learners, while the heterogeneous ensemble learning method uses different learning algorithms. Representative algorithms in the homogeneous ensemble learning method include random forest (RF), XGBoost, LightGBM etc. However, because the heterogeneous ensemble learning method is more flexible and changeable, there is no specific representative algorithm. Thus, compared with the homogeneous ensemble learning method, the heterogeneous ensemble learning method tends to achieve more satisfactory results. In this paper, we will construct the predictive model under the framework of heterogeneous ensemble learning.
In general, the better the diversity of the base learners in the ensemble learning method, the better is the overall performance of the method. Therefore, one important thing for ensemble is the diversity of the base learners. In this study we design two strategies to improve the diversity of the base learners (as shown in Fig. 3(a)):
Fig. 3.
The training phase of two-layer nested heterogeneous ensemble learning method.
-
(a)
Extracting data randomly from the data set by bootstrap sampling to form a data subset, so the samples learned by each base learner are all different;
-
(b)
Using different algorithms to train the base learners. Therefore, the method we propose is a two-layer nested heterogeneous ensemble learning method.
The second problem is how to aggregate the outputs of each base classifier to obtain the final output of the ensemble. When using the bagging ensemble framework, the simple average approach is usually used as a combination strategy. Based on the simple average approach, researchers have proposed the weighting approach, dynamic weighting approach, selective weighting approach etc. The above aggregation approaches can be seen as statistical aggregations, and some researchers have tried to use machine learning algorithms in aggregation because of their good non-linear approximation ability [40]. In order to obtain a better fitting effect, we use machine learning algorithms as the combiner to train the second layer model, as shown in Fig. 3(b).
Through a series of experimental comparisons, we finally select linear regression (LR), support vector regression (SVR), and extreme learning machine (ELM) as the base learners. At the same time, we use linear regression as the combiner of the second layer of the model.
Algorithm 1 details the two-layer nested heterogeneous ensemble learning method we propose, which mainly includes the training of the first-layer model, the training of the second-layer model, and the prediction of new samples. By using bootstrap to sample the original data set , we obtain data subsets with different distributions, where represents the number of samples and represents the number of base learners. Using different data subsets to train the base learners will improve the generalization ability of the model. At the same time, three different types of base learners training algorithms can also improve model stability.
In the traditional ensemble learning method, the average approach or the majority voting approach is usually used to integrate the outputs of each base learner. This traditional method is relatively simple to operate, but it depends too much on the performance of each base learner. Therefore, we propose to use a learning algorithm to integrate the outputs of each base learner instead of the averaging method. In this paper we determine the linear regression as the second-layer learning algorithm through experiments. Linear regression fits a linear model with coefficients to minimize the residual sum of squares between the true value in the dataset and the predicted value by linear approximation. Mathematically, it solves a problem of the form: . By using the linear regression algorithm to integrate the outputs of the base learners, it in fact gives different weights to the base learners. Different from the previous manual weighting method, we determine the weights by using the ordinary least square method to solve the linear regression model in this paper.
3.5. Performance evaluation
To measure the performance of a prediction model based on time series forecasting, researchers usually use the following three performance indicators:
-
•Mean Squared Error (MSE), which represents the average squared difference between the original and predicted values over the data set, is computed by
(5) -
•Root Mean Squared Error (RMSE), which is the error rate measured by the square root of MSE, is computed by
Compared with MSE, RMSE solves the problem of inconsistent dimensions.(6) -
•Mean absolute error (MAE), which represents the average absolute difference between the original and predicted values extracted over the data set, is computed by
(7)
4. Experiment results and analysis
4.1. Data preparation
For data collection, we searched all the available resources on the Internet that meet our analysis needs as far as possible, thus avoiding the impact of missing values on data analysis. The data used in this study are mainly from the Our World in Data website at https://ourworldindata.org/. Our World in Data is a project of the Global Change Data Lab at the University of Oxford. We gathered the climate data from the timeanddata website at https://www.timeanddate.com/. On the Our World in Data website, number of confirmed cases and total tests per million people in some countries are not collected, so we obtained these data from the worldometer website at https://www.worldometers.info/coronavirus/#countries. The data on GDP per capita of various countries come from the World Bank (2018) at https://data.worldbank.org/.
After data collection and processing, we obtained data on 79 countries (as shown in Table 2) with COVID-19 incidents in the world. To consider the influencing factors of COVID-19 mortality, in order to unify the standards, we used the cross-sectional values on 12 April, 29 May, and 29 June 2020 for the time-series variables of temperature, atmospheric pressure, wind speed, humidity, total confirmed cases, total tests, the doubling time of confirmed deaths, and mortality. The reason why we chose these three time points is that they corresponded to the early, middle, and late stages of the COVID-19 outbreak. Through studying these three time points, we can analyze the changes in the influencing factors of mortality in different stages of COVID-19 development. For some reasons, we could not obtain the data for all the variables in 2020, such as population density, GDP per capita, and physicians. However, the data for a single variable are all in the same year, so the data between countries are comparable.
Table 2.
List of 79 countries.
| Continent | Country |
|---|---|
| Asia (23) | Afghanistan, Armenia, Azerbaijian, China, India, Indonesia, Iran, Iraq, Japan, Kazakhstan, Kuwait, Lebanon, Malaysia, Pakistan, Philippines, Qatar, Saudi Arabia, Singapore, South Korea, Thailand, Turkey, United Arab Emirates, Uzbekistan |
| Europe (37) | Andorra, Austria, Belarus, Belgium, Bulgaria, Croatia, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Iceland, Ireland, Italy, Latvia, Lithuania, Luxembourg, Macedonia, Moldova, Netherlands, Norway, Poland, Portugal, Romania, Russia, Serbia, Slovakia, Slovenia, Spain, Sweden, Switzerland, Ukraine, United Kingdom |
| Africa (4) | Egypt, Morocco, South Africa, Tunisia |
| America (13) | Argentina, Brazil, Canada, Chile, Colombia, Costa Rica, Cuba, Dominican Republic, Ecuador, Mexico, Panama, Peru, United States |
| Australia (2) | Australia, New Zealand |
Based on the collected COVID-19 mortality data in various countries, we draw the heat map shown in Fig. 4(a)–(c). We see from Fig. 4 that the pandemic situation in Europe is particularly serious compared with the other regions in the world. Although COVID-19 first occurred in China, with effective treatment measures, China quickly controlled the spread of the outbreak and made tremendous efforts to treat the critically ill patients, thereby curtailing the rise in COVID-19 mortality. On the other hand, from the perspective of time, from 12 April to 29 June, the COVID-19 mortality of most countries increased first and then decreased, which also show that the pandemic situation in various countries experienced three stages, namely initial, middle, and late stages, of development. Of course, in some countries, such as Mexico and Peru, the pandemic situation has not been under control yet and the mortality is still rising.
Fig. 4.
Heat map of COVID-19 mortality rates by country.
4.2. Analysis of the influencing factors
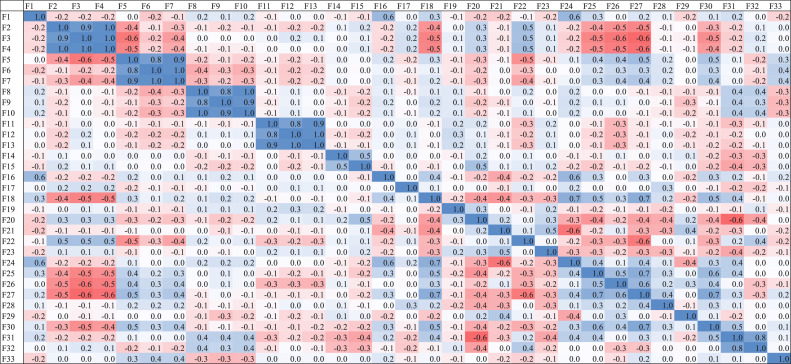
Fig. 5 reports the correlation analysis results of the data on 12 April. We see that there is a high degree of correlation between multiple independent variables, such as F18 (Share of population with cancer) and F27 (Share who is 70 or over). The high correlation between these two variables is easy to understand because the risk of cancer is closely related to age and older age groups will show a higher risk of cancer. When dealing with this pair of variables with high correlation, we consider that the risk factors contain more variables, so we keep the Share of who is 70 or over variable under the age structure. Similarly, conducting correlation analyses of the data on 29 May and 29 June, we find that the results are consistent with the variable selection results on 12 April.
Fig. 5.
Correlation coefficients between variables. F1: Total tests per million people, F2: Temperature High, F3: Temperature Low, F4: Temperature Average, F5: Atmospheric pressure High, F6: Atmospheric pressure Low, F7: Atmospheric pressure Average, F8: Wind speed High, F9: Wind speed Low, F10: Wind speed Average, F11: Humidity High, F12: Humidity Low, F13: Humidity Average, F14: The doubling time of confirmed death, F15: Population, F16: Total confirmed cases, F17: Population density, F18: Share of population with cancer, F19: Share of the population infected with HIV, F20: Share of people living with active tuberculosis, F21: Deaths from cardiovascular disease, F22: Diabetes prevalence, F23: Share of the population living in extreme poverty, F24: GDP per capita, F25: Physicians, F26: Hospital beds, F27: Share who is 70 or over, F28: Median Age, F29: Share of men who are smoking, F30: Share of women who are smoking, F31: Share of men who are obese, F32: Share of women who are obese, F33: Mortality.
After the correlation analysis, we eliminate a total of 13 variables, including Share of population with cancer, GDP per capita, Physicians, Share of women who are smoking, Share of men who are obese, Temperature High, Temperature Low, Atmospheric pressure High, Atmospheric pressure Low, Wind speed High, Wind speed Low, Humidity High, and Humidity Low.
As the pandemic progresses, the factors affecting mortality may change accordingly. Therefore, we collected data on three different time points on 12 April, 29 May, and 29 June to explore the factors that affect COVID-19 mortality. Table 3 reports the results of this experiment.
Table 3.
Analysis of the influencing factors of mortality.
| (a) Results of data on 12 April | |
|---|---|
| Mortality | |
| Atmospheric pressure average (mbar) | 1.138*** |
| (0.378) | |
| Hospital beds (per 100,000 people) | −1.598*** |
| (0.413) | |
| Share of who is 70 or over (%) | 1.178** |
| (0.448) | |
| Total tests per million people | −0.691** |
| (0.344) | |
| _cons | 3.744*** |
| (0.324) | |
| Obs. | 79 |
| R-squared | 0.289 |
| F | 7.84*** |
| Standard errors are in parentheses | |
| *** p 0.01, ** p 0.05, * p 0.1 | |
| (b) Results of data on 29 May | |
| Mortality | |
| Share of who is 70 or over (%) | 2.693*** |
| (0.488) | |
| Hospital beds (per 100,000 people) | −1.619*** |
| (0.445) | |
| Total tests per million people | −1.330*** |
| (0.388) | |
| Atmospheric pressure average (mbar) | 1.157*** |
| (0.389) | |
| Humidity average | −1.012*** |
| (0.371) | |
| _cons | 4.680*** |
| (0.358) | |
| Obs. | 79 |
| R-squared | 0.486 |
| F | 10.97*** |
| Standard errors are in parentheses | |
| *** p 0.01, ** p 0.05, * p 0.1 | |
| (c) Results of data on 29 June | |
| Mortality | |
| Hospital beds (per 100,000 people) | −0.469*** |
| (0.177) | |
| Share of who is 70 or over (%) | 0.558** |
| (0.105) | |
| _cons | 1.502** |
| (0.817) | |
| Obs. | 79 |
| R-squared | 0.272 |
| F | 14.19*** |
| Standard errors are in parentheses | |
| *** p 0.01, ** p 0.05, * p 0.1 | |
From the results in Table 3(a)–(c), we make the following observations:
-
(1)
In the early and middle stages of the spread of COVID-19, the ability to perform nucleic acid testing on the population greatly affects mortality. Because there are asymptomatic infections, large-scale testing will help find those infections, which will increase the number of confirmed cases and further reduce the mortality rate;
-
(2)
The number of hospital beds has a great impact on mortality in all stages of the development of the pandemic in various countries. Because the COVID-19 virus is very contagious, it is very easy to cause infections in a wide range of people, which imposes a heavy burden on local medical capabilities. All the infected patients must be treated promptly and effectively to avoid the rapid spread of the disease. At the same time, the number of hospital beds also characterizes the level of the corresponding medical resources. A country with ample medical resources will provide better treatment for its people, which can reduce the risk of patient death;
-
(3)
Another very important factor is the aging level of a country, measured by “share of who is 70 or over” in the table. As we all know, as people grow older, their resistance and other physical health conditions will decline, and the risk of basic diseases and malignant diseases such as cancer will increase. COVID-19 mainly infects the lungs of the human body. The clinical manifestations of severe patients are mainly respiratory diseases. The vast majority of patients die of respiratory failure. Compared with young people, the elderly has a more fragile respiratory system and are more likely to die if they are infected with COVID-19;
-
(4)
According to the experimental results in Table 3, climate factors are closely related to COVID-19 mortality in the early and middle stages of the development of the pandemic. In addition, atmospheric pressure and mortality have a positive relationship, i.e., areas with high atmospheric pressure will have relatively higher mortality. The average humidity and mortality are negatively correlated, which means that the drier the area is, the higher is the mortality.
4.3. Mortality prediction and result analysis
To ensure the rationality of subsequent prevention and control measures, we need to have an accurate assessment of the future development trend of COVID-19, for which mortality prediction is one of most important tasks.
To this end, we compare the performance of various time series prediction methods for COVID-19 mortality. To test the performance of each method, we selected 14 countries including the United Kingdom, the United States, Canada, and South Korea as the data collection objects. We set the start time of mortality data collection in various countries as two days before the occurrence of death cases, and the end time as 29 June, 2020. For countries with a small number of missing mortality values, we adopted an interpolation method to fill in the missing values. In conducting the experiment, we used the data of the last seven days as the test set, and the remaining data as the training set. For the training set used for machine learning and deep learning, we set the lag time to 5.
First, we compare the performance of various traditional time series prediction methods, and report the results in Table 4. Among the traditional methods, ARIMA and the naïve method show unique advantages. ARIMA performs well in the COVID-19 mortality prediction task in eight countries including the United States, Korea, and Mexico, while the naïve method performs well in five other countries including Australia, Chile, and Japan. When using the ARIMA(, , ) model, the three basic parameters , and , need to be determined. For the time series data of each country, first of all, we used the Augmented Dickey–Fuller (ADF) test to get the value of difference order , so as to make the time series data stable. Then, we determined the autoregressive order and moving average order by drawing autocorrelation (ACF) and partial autocorrelation (PAC) graphs. Finally, we determine that the values of the three parameters in the ARIMA model are (1, 0, 2).
Table 4.
Comparison results of traditional methods.
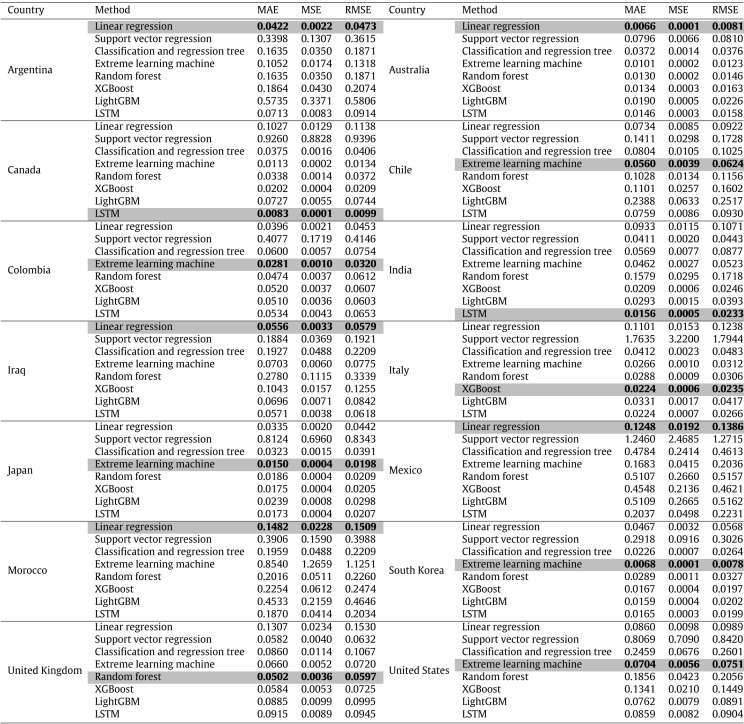
After that, we compare the performance of the machine learning method and the deep learning method, and the results are shown in Table 5. Among an array of methods, the best performing methods are linear regression (LR), extreme learning machines (ELM), and long–short term memory (LSTM) networks. At the same time, we can also note that the ensemble learning methods such as random forest (RF), XGBoost, and LightGBM do not achieve satisfactory predictive performance. It can be noted that these ensemble learning methods all use the decision tree as the base learner, and the construction mechanism of the decision tree focuses on the processing of discrete features, so facing the time series forecasting task in this paper, it does not show its advantages. However, LR, ELM and LSTM have good adaptability to continuous features, and therefore exhibit good performance.
Table 5.
Comparison results of machine learning methods and deep learning method.
Furthermore, in Table 6, we compare the performance of the proposed method with the other methods, and the experimental results show that our method has obvious advantages. On the one hand, compared with LR, SVR and ELM, the prediction performance of the model is improved through the integration of the three basic learners. On the other hand, our ensemble learning method is better than popular ensemble learning methods such as RF, XGBoost, and LightGBM. The reason is that RF, XGBoost, and LightGBM all use a single decision tree as the base learner and adopt the simple average method when integrating the outputs of the base learners. However, the proposed method adopts different types of learning algorithms when training the base learners, and uses the learning algorithm instead of the simple average method in the second-layer of integration.
Table 6.
Comparison results of the proposed method.
To further analyze the performance of the different methods, we report the development trend and degree of change in mortality in each of the 14 selected countries in Table 7. We define the degree of change in mortality as , where represents the mortality at the beginning of multi-step prediction and represents the mortality at the end of multi-step prediction. In addition, we also list the top three methods for predicting mortality in different countries in the table.
Table 7.
Trends in mortality across countries (23 June–29 June).
| Country | Trend | Change | 1st method | 2nd method | 3rd method | |
|---|---|---|---|---|---|---|
| 1 | South Korea | Falling | 1.79 | Proposed method | ELM | ARIMA |
| 2 | Japan | Falling | 1.02 | Proposed method | ELM | LSTM |
| 3 | Italy | Stabilizing | 0.43 | Proposed method | ARIMA | LSTM |
| 4 | United States | Falling | 5.22 | Proposed method | ELM | LSTM |
| 5 | United Kingdom | Stabilizing | 0.19 | Naïve method | Proposed method | RF |
| 6 | Canada | Stabilizing | 0.55 | Proposed method | LSTM | ELM |
| 7 | Morocco | Falling | 12.84 | Proposed method | LR | LSTM |
| 8 | Mexico | Stabilizing | 0.73 | Proposed method | LR | ELM |
| 9 | Australia | Stabilizing | 0.85 | Proposed method | Naïve method | LR |
| 10 | Argentina | Falling | 9.21 | LR | LSTM | Proposed method |
| 11 | Colombia | Rising | 4.30 | Proposed method | ELM | LR |
| 12 | Chile | Rising | 11.11 | Proposed method | ELM | LR |
| 13 | Iraq | Rising | 8.30 | Proposed method | ARIMA | LR |
| 14 | India | Falling | 5.60 | LSTM | XGBoost | ARIMA |
We see from Table 7 that the pandemic situations in various countries are different, which can be divided into three stages, namely rising ( and ), falling ( and ), and stabilizing (). Our proposed method is significantly better than other methods in predicting COVID-19 mortality in most countries, especially when there are large variations in mortality. When the mortality changes tend to be stable, the simpler traditional time series forecasting methods, such as the naïve method and the ARIMA method, show good performance. At the same time, it is important to note the performance of the deep learning method. Although the performance of LSTM does not exceed that of our method, when the mortality changes show a large downward trend, LSTM is better than the other popular ensemble learning methods to capture this trend, achieving good results.
To further verify the effectiveness of the proposed method, we use the Friedman test to perform hypothesis testing according to the non-parametric testing method introduced in [41]. According to the results of the Friedman test (Table 8), the corresponding p-values of MAE, MSE, and RMSE are 0.0000. Therefore, this shows that the performance of the methods is significantly different. In order to have a more accurate statistical analysis of the experimental results, we carry out post hoc statistical procedures on the proposed method. In Table 9, Table 10, Table 11 we report the results of the Holm and Hochberg post hoc tests, which show that our method is significantly superior to the other methods such as LR and SVR.
Table 8.
Friedman test ().
| Indicator | Statistic | p-value |
|---|---|---|
| MAE | 12.9244 | 0.0000 |
| MSE | 12.4618 | 0.0000 |
| RMSE | 11.2832 | 0.0000 |
Table 9.
Friedman test — Holm and Hochberg post hoc tests for MAE (using the proposed method as the control method, ).
| Method | Rank | z | Holm post hoc test |
Hochberg post hoc test |
||
|---|---|---|---|---|---|---|
| Adjusted p-value | Null hypothesis | Adjusted p-value | Null hypothesis | |||
| Naïve method | 4.7143 | 4.1116 | 0.0002 | Rejected | 0.0174 | Rejected |
| ARIMA | 4.5714 | 3.9367 | 0.0003 | Rejected | 0.0174 | Rejected |
| LR | 4.0714 | 3.3243 | 0.0027 | Rejected | 0.0174 | Rejected |
| SVR | 6.3571 | 6.1237 | 0.0000 | Rejected | 0.0174 | Rejected |
| ELM | 3.5000 | 2.6245 | 0.0174 | Rejected | 0.0174 | Rejected |
| LSTM | 3.4286 | 2.5370 | 0.0174 | Rejected | 0.0112 | Rejected |
Table 10.
Friedman test — Holm and Hochberg post hoc tests for MSE (using proposed method as the control method, ).
| Method | Rank | z | Holm post hoc test |
Hochberg post hoc test |
||
|---|---|---|---|---|---|---|
| Adjusted p-value | Null hypothesis | Adjusted p-value | Null hypothesis | |||
| Naïve method | 4.7500 | 4.1116 | 0.0002 | Rejected | 0.0197 | Rejected |
| ARIMA | 4.5000 | 3.8055 | 0.0006 | Rejected | 0.0197 | Rejected |
| LR | 4.0357 | 3.2368 | 0.0036 | Rejected | 0.0197 | Rejected |
| SVR | 6.3571 | 6.0800 | 0.0000 | Rejected | 0.0197 | Rejected |
| ELM | 3.5000 | 2.5807 | 0.0197 | Rejected | 0.0197 | Rejected |
| LSTM | 3.4643 | 2.5370 | 0.0197 | Rejected | 0.0112 | Rejected |
Table 11.
Friedman test — Holm and Hochberg post hoc tests for RMSE (using proposed method as the control method, ).
| Method | Rank | z | Holm post hoc test |
Hochberg post hoc test |
||
|---|---|---|---|---|---|---|
| Adjusted p-value | Null hypothesis | Adjusted p-value | Null hypothesis | |||
| Naïve method | 4.3571 | 3.5868 | 0.0013 | Rejected | 0.0174 | Rejected |
| ARIMA | 4.5714 | 3.8492 | 0.0006 | Rejected | 0.0174 | Rejected |
| LR | 4.1429 | 3.3243 | 0.0027 | Rejected | 0.0174 | Rejected |
| SVR | 6.3571 | 6.0362 | 0.0000 | Rejected | 0.0174 | Rejected |
| ELM | 3.5714 | 2.6245 | 0.0174 | Rejected | 0.0087 | Rejected |
| LSTM | 3.5714 | 2.6245 | 0.0174 | Rejected | 0.0174 | Rejected |
4.4. Discussion
Concerning the factors affecting COVID-19 mortality, our research results are consistent with clinical manifestations and epidemiological studies. For example, compared with other countries, countries with a high degree of aging will have a higher mortality rate, which is at the macro country level. At the individual level, it is manifested in the serious clinical symptoms and conditions of many elderly infected persons, and the risk of death is also greater [42]. This requires countries to take measures to protect and manage the health care of the elderly. For example, masks and other protective supplies should be distributed to the elderly for free, and daily necessities should be provided to the elderly to prevent them from being exposed to places with high risks of infection such as supermarkets.
In response to the shortage of medical resources in various countries, China has provided a good example for the rest of the world in terms of its deployment of “mobile cabin hospitals”. Such medical facilities can treat patients with mild illnesses in multiple places in the pandemic area, so limited medical resources can be channeled to treating the critically ill patients. At present, in addition to China, countries such as Russia, Iran, the United Kingdom, and Spain have also set up “mobile cabin hospitals” as an effective means to combat COVID-19. At the same time, countries also need to pay attention to the optimal scheduling and utilization of medical resources, such as the flow of medical staff between regions and allocation of resources to areas with severe pandemics, so as to maximize the effectiveness and efficiency of resource use.
Large-scale virus testing not only has a significant impact on mortality, but more importantly, it can detect asymptomatic infections [43]. The existence of asymptomatic infections is very dangerous because they will continue the spread of the virus, which will not be discovered until after the occurrence of large-scale transmission.
It can be seen from Table 2(a)–(b) that some climatic factors such as atmospheric pressure and air humidity are closely related to COVID-19 mortality. But such factors are constantly changing over time. At present, while there are studies showing that meteorological factors are related to the transmission and spread of COVID-19 [5], [6], [30], there are no studies that explore the relationship between meteorological factors and COVID-19 mortality. This requires more in-depth research. It should be noted that conducting research in different countries may lead to different conclusions, so a comparison of multiple countries is desired.
When using machine learning methods for COVID-19 mortality prediction, we find through experiments that the classical ensemble learning methods, such as random forest and XGBoost, do not achieve satisfactory results, while the two-layer nested heterogeneous ensemble learning method we propose achieve good results. This is because the classical ensemble learning methods are often homogeneous, i.e., the same training algorithm is used to generate multiple base learners. In the face of complex problems, such approach may lead to poor prediction results due to poor diversity of the base learners. At the same time, when the output results of the base learners are integrated, using the learning algorithm to replace the simple average method will also bring better fitting ability to the model.
5. Conclusions
In this study we explore the predictors and prediction methods for COVID-19 mortality in various countries. As an important indicator to measure the severity of an infectious disease, mortality has a very important reference value for disease prevention and policy formulation.
At present, most studies discuss the individual mortality risk of COVID-19 and there are very few studies considering the factors affecting COVID-19 mortality among different countries worldwide. To address this issue, we first construct a comprehensive model of factors affecting COVID-19 mortality. We then collect relevant data from 79 countries for experiments and analysis. The results show that the main influencing factors change with the development of COVID-19. However, at any stage of development, medical resources (number of hospital beds) and degree of aging (proportion of people over 70 years old) are always significant factors influencing the differences in COVID-19 mortality across countries.
As for the prediction of COVID-19 mortality, we design a two-layer nested heterogeneous ensemble learning method. On the one hand, different training algorithms are used to generate the base learners to improve the adaptability of the model. On the other hand, we use LR instead of the traditional simple average ensemble strategy to fuse the output results of the base learners, which improves the fitting ability of the model. At the same time, we use the bootstrap sampling method to generate different data subsets to improve the generalization ability of the model.
It is foreseeable that COVID-19 will continue to exist for some time in the future and there are risks of other pandemics. Therefore, research on COVID-19 should continue. Such studies should address the issues concerning the entire process of an infectious disease, spanning the discovery of the infected (more efficient and convenient detection methods), treatment of the infected (pathogenic mechanisms, effective drugs), and formulation and implementation of public health policies to contain and prevent the disease. As far as the prediction model is concerned, on the one hand, researchers can consider incorporating more influencing factors from different data sources into the model. On the other hand, researchers can also consider fusing a variety of different types of algorithms to improve the model’s prediction performance.
CRediT authorship contribution statement
Shaoze Cui: Conception of the study, Designed the proposed method, Analyzed the data and performed experiments, Wrote the manuscript. Yanzhang Wang: Conception of the study, Designed the proposed method, Wrote the manuscript. Dujuan Wang: Conception of the study, Designed the proposed method, Analyzed the data and performed experiments, Improve the writing of the manuscript. Qian Sai: Perform the result analysis with constructive discussions. Ziheng Huang: Analyzed the data and performed experiments. T.C.E. Cheng: Perform the result analysis with constructive discussions, Improve the writing of the manuscript.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This study was supported in part by the National Natural Science Foundation of China [Nos. 71533001, 72171161, 71971041, 71871148], the Outstanding Young Scientific and Technological Talents Foundation of Sichuan Province [No. 20JCQN0281], the Sichuan University to Building a World-class University [No. SKSYL2021-08], and the China Scholarship Council (No. 202006060162).
Footnotes
https://www.who.int/emergencies/diseases/novel-coronavirus-2019/events-as-they-happen, accessed on May 28, 2020.
https://ourworldindata.org/coronavirus-country-by-country?country=~CHN, accessed on May 28, 2020.
Appendix.
See Fig. 5.
References
- 1.Kumar A., Gupta P.K., Srivastava A. A review of modern technologies for tackling COVID-19 pandemic. Diabetes Metab. Syndr. Clin. Res. Rev. 2020;14:569–573. doi: 10.1016/j.dsx.2020.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Whittaker C., Zhu H., Berah T., Eaton J.W. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584:257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- 3.Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images : Results of 10 convolutional neural networks. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gautret P., Lagier J., Parola P., Doudier B., Courjon J., La Scola B., Rolain J., Brouqui P., Raoult D., Mailhe M., Doudier B., Courjon J. Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial. Int. J. Antimicrob. Agents. 2020 doi: 10.1016/j.ijantimicag.2020.105949. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 5.Xie J., Zhu Y. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ma Y., Zhao Y., Liu J., He X., Wang B., Fu S., Yan J., Niu J., Zhou J., Luo B. Environment effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang L., Li J., Guo S., Xie N., Yao L., Cao Y., Day S.W., Howard S.C., Graff J.C., Gu T., Ji J., Gu W., Sun D. Real-time estimation and prediction of mortality caused by COVID-19 with patient information based algorithm. Sci. Total Environ. 2020;727 doi: 10.1016/j.scitotenv.2020.138394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yan L., Zhang H.-T., Goncalves J., Xiao Y., Wang M., Guo Y., Sun C., Tang X., Jing L., Zhang M., Huang X., Xiao Y., Cao H., Chen Y., Ren T., Wang F., Xiao Y., Huang S., Tan X., Huang N., Jiao B., Cheng C., Zhang Y., Luo A., Mombaerts L., Jin J., Cao Z., Li S., Xu H., Yuan Y. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020;2 doi: 10.1038/s42256-020-0180-7. [DOI] [Google Scholar]
- 9.Yilmazer S., Kocaman S. A mass appraisal assessment study using machine learning based on multiple regression and random forest. Land Use Policy. 2020;99 doi: 10.1016/j.landusepol.2020.104889. [DOI] [Google Scholar]
- 10.Cui S., Wang D., Wang Y., Yu P.W., Jin Y. An improved support vector machine-based diabetic readmission prediction. Comput. Methods Programs Biomed. 2018;166:123–135. doi: 10.1016/j.cmpb.2018.10.012. [DOI] [PubMed] [Google Scholar]
- 11.Fong S.J., Li G., Dey N., Crespo R.G., Herrera-Viedma E. Composite Monte Carlo decision making under high uncertainty of novel coronavirus epidemic using hybridized deep learning and fuzzy rule induction. Appl. Soft Comput. J. 2020;93 doi: 10.1016/j.asoc.2020.106282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alameer Z., Elaziz M.A., Ewees A.A., Ye H., Jianhua Z. Forecasting gold price fluctuations using improved multilayer perceptron neural network and whale optimization algorithm. Resour. Policy. 2019;61:250–260. doi: 10.1016/j.resourpol.2019.02.014. [DOI] [Google Scholar]
- 13.Parmezan A.R.S., Souza V.M.A., Batista G.E.A.P.A. Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Inf. Sci. (Ny) 2019;484:302–337. doi: 10.1016/j.ins.2019.01.076. [DOI] [Google Scholar]
- 14.Fanoodi B., Malmir B., Jahantigh F.F. Reducing demand uncertainty in the platelet supply chain through artificial neural networks and ARIMA models. Comput. Biol. Med. 2019;113 doi: 10.1016/j.compbiomed.2019.103415. [DOI] [PubMed] [Google Scholar]
- 15.Kim T., Sharda S., Zhou X., Pendyala R.M. A stepwise interpretable machine learning framework using linear regression (LR) and long short-term memory (LSTM): City-wide demand-side prediction of yellow taxi and for-hire vehicle (FHV) service. Transp. Res. C. 2020;120 doi: 10.1016/j.trc.2020.102786. [DOI] [Google Scholar]
- 16.Baechle C., Huang C.D., Agarwal A., Behara R.S., Goo J. Latent topic ensemble learning for hospital readmission cost optimization. European J. Oper. Res. 2020;281:517–531. doi: 10.1016/j.ejor.2019.05.008. [DOI] [Google Scholar]
- 17.Papouskova M., Hajek P. Two-stage consumer credit risk modelling using heterogeneous ensemble learning. Decis. Support Syst. 2019;118:33–45. doi: 10.1016/j.dss.2019.01.002. [DOI] [Google Scholar]
- 18.Zhang X., Wang B., Chen X. Intelligent fault diagnosis of roller bearings with multivariable ensemble-based incremental support vector machine. Knowl.-Based Syst. 2015;89:56–85. [Google Scholar]
- 19.Cui S., Wang Y., Yin Y., Cheng T.C.E., Wang D., Zhai M. A cluster-based intelligence ensemble learning method for classification problems. Inf. Sci. (Ny) 2021;560:386–409. doi: 10.1016/j.ins.2021.01.061. [DOI] [Google Scholar]
- 20.Ranjan D., Dash R., Majhi B. Brain MR image classification using two-dimensional discrete wavelet transform and AdaBoost with random forests. Neurocomputing. 2016;177:188–197. doi: 10.1016/j.neucom.2015.11.034. [DOI] [Google Scholar]
- 21.Chang Y.-C., Chang K.-H., Wu G.-J. Application of eXtreme gradient boosting trees in the construction of credit risk assessment models for financial institutions. Appl. Soft Comput. 2018;73:914–920. doi: 10.1016/J.2018.09.029. [DOI] [Google Scholar]
- 22.Chu Z., Yu J., Hamdulla A. LPG-model: A novel model for throughput prediction in stream processing, using a light gradient boosting machine, incremental principal component analysis, and deep gated recurrent unit network. Inf. Sci. (Ny) 2020;535:107–129. doi: 10.1016/j.ins.2020.05.042. [DOI] [Google Scholar]
- 23.Malhotra R., Khanna M. Particle swarm optimization-based ensemble learning for software change prediction. Inf. Softw. Technol. 2018;102:65–84. doi: 10.1016/j.infsof.2018.05.007. [DOI] [Google Scholar]
- 24.Nishiura H. The relationship between the cumulative numbers of cases and deaths reveals the confirmed case Fatality Ratio of a Novel Influenza A (H1N1) Virus. Jpn. J. Infect. Dis. 2010;63:154–156. [PubMed] [Google Scholar]
- 25.T. Viewpoint, O.F. Rate Case-fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. J. Am. Med. Assoc. 2020;323:1775–1776. doi: 10.1001/jama.2020.4683. [DOI] [PubMed] [Google Scholar]
- 26.K.P. High Infection as a cause of age-related morbidity and mortality. Ageing Res. Rev. 2004;3:1–14. doi: 10.1016/j.arr.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 27.Miller I.F., Becker A.D., Grenfell B.T., Metcalf C.J.E. Disease and healthcare burden of COVID-19 in the United States. Nat. Med. 2020;26:1212–1217. doi: 10.1038/s41591-020-0952-y. [DOI] [PubMed] [Google Scholar]
- 28.Gavurová B., Vagašová T. Regional differences of standardised mortality rates for ischemic heart diseases in the slovak Republic for the period 1996–2013 in the context of income inequality. Health Econ. Rev. 2016;6:1–12. doi: 10.1186/s13561-016-0099-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.De Souza W.M., Buss L.F., Candido S., Carrera J., Li S., Zarebski A.E., Henrique R., Pereira M., Jr C.A.P., De Souza-santos A.A., Parag K.V., Belotti M.C.T.D, Vincenti-gonzalez M.F., Messina J., Cristina F., Andrade S., Nascimento V.H., Ghilardi F., Abade L., Gutierrez B., Kraemer M.U.G., Braga C.K.V., Aguiar R.S., Alexander N., Mayaud P., Brady O.J., Marcilio I., Gouveia N., Li G., Tami A. Epidemiological and clinical characteristics of the COVID-19 epidemic in Brazil. Nat. Hum. Behav. 2020;4:856–865. doi: 10.1038/s41562-020-0928-4. [DOI] [PubMed] [Google Scholar]
- 30.Tosepu R., Gunawan J., Effendy D.S., Ode L., Ahmad A.I., Lestari H., Bahar H., Asfian P. Correlation between Weather and Covid-19 Pandemic in Jakarta, Indonesia. Sci. Total Environ. 2020;725 doi: 10.1016/j.scitotenv.2020.138436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mu Y., Liu X., Wang L. A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf. Sci. (Ny) 2018;435:40–58. doi: 10.1016/J.INS.2017.12.059. [DOI] [Google Scholar]
- 32.Bauweraerts J. Predicting Bankruptcy in Private Firms: Towards a stepwise regression procedure. Int. J. Financ. Res. 2016;7 doi: 10.5430/ijfr.v7n2p147. [DOI] [Google Scholar]
- 33.Tsai C. Feature selection in bankruptcy prediction. Knowl.-Based Syst. 2009;22:120–127. doi: 10.1016/j.knosys.2008.08.002. [DOI] [Google Scholar]
- 34.Zhang Y., Cui S., Gao H. Adverse drug reaction detection on social media with deep linguistic features. J. Biomed. Inform. 2020;106 doi: 10.1016/j.jbi.2020.103437. [DOI] [PubMed] [Google Scholar]
- 35.Ma X., Jin Y., Dong Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Appl. Soft Comput. 2017;54:296–312. [Google Scholar]
- 36.Coulibaly P., Baldwin C.K. Nonstationary hydrological time series forecasting using nonlinear dynamic methods. J. Hydrol. 2005;307:164–174. doi: 10.1016/j.jhydrol.2004.10.008. [DOI] [Google Scholar]
- 37.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 38.Cui S., Yin Y., Wang D., Li Z., Wang Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2021;101 doi: 10.1016/j.asoc.2020.107038. [DOI] [Google Scholar]
- 39.Wang N., Zhao S., Cui S., Fan W. A hybrid ensemble learning method for the identification of gang-related arson cases. Knowl.-Based Syst. 2021;218 doi: 10.1016/j.knosys.2021.106875. [DOI] [Google Scholar]
- 40.Lin L., Wang F., Xie X., Zhong S. Random forests-based extreme learning machine ensemble for multi-regime time series prediction. Expert Syst. Appl. 2017;83:164–176. doi: 10.1016/j.eswa.2017.04.013. [DOI] [Google Scholar]
- 41.García S., Fernández A., Luengo J., Herrera F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. (Ny) 2010;180:2044–2064. doi: 10.1016/j.ins.2009.12.010. [DOI] [Google Scholar]
- 42.Davies N.G., Klepac P., Liu Y., Prem K., Jit M., C. Covid-, R.M. Eggo Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 2020;26:1205–1211. doi: 10.1038/s41591-020-0962-9. [DOI] [PubMed] [Google Scholar]
- 43.Liang L.L., Tseng C.H., Ho H.J., Wu C.Y. Covid-19 mortality is negatively associated with test number and government effectiveness. Sci. Rep. 2020;10:1–7. doi: 10.1038/s41598-020-68862-x. [DOI] [PMC free article] [PubMed] [Google Scholar]