Abstract
The major losses that limit the efficiency of a single-junction solar cell are thermalization loss and transmission loss. Thus, to efficiently utilize the full solar spectrum and to mitigate these losses, tandem solar cells (TSC) have significantly impacted the photovoltaic (PV) landscape. In this context, the research on perovskite/silicon tandems is currently dominating the research community. The stability improvements of perovskite materials and mature fabrication techniques of silicon have underpinned the rapid progress of perovskite/silicon TSC. However, the low absorption coefficient and high module cost of the silicon are the tailbacks for the mass production of perovskite/silicon TSCs. Therefore, PV technology demands to explore some new materials other than Si to be used as absorber layer in the bottom cell. Thus, here in this work, to mitigate the aforementioned losses and to reduce cost, a 23.36% efficient two-terminal perovskite-PbS CQD monolithic tandem solar cell has been designed through comprehensive device simulations. Before analyzing the performance of the proposed TSC, the performance of perovskite top cells has been optimized in terms of variation in optical properties, thickness, and interface defect density under standalone conditions. Thereafter, filtered spectrum and associated integrated filtered power by the top cell at different perovskite thickness from 50 to 500 nm is obtained to conceive the presence of the top cell above the bottom cell with different perovskite thickness. The current matching by concurrently varying the thickness of both the top and bottom subcell has also been done to obtain the maximum deliverable tandem JSC for the device under consideration. The top/bottom subcell with current matched JSC of 16.68 mA cm−2/16.62 mA cm−2 showed the conversion efficiency of 14.60%/9.07% under tandem configuration with an optimized thickness of 143 nm/470 nm, where the top cell is simulated under AM1.5G spectrum, and bottom cell is exposed to the spectrum filtered by 143 nm thick top cell. Further, the voltages at equal current points are added together to generate tandem J–V characteristics. This work concludes a 23.36% efficient perovskite-PbS CQD tandem design with 1.79 V (VOC), 16.67 mA cm−2 (JSC) and 78.3% (FF). The perovskite-PbS CQD tandem device proposed in this work may pave the way for the development of high-efficiency tandem solar cells for low-cost applications.
Subject terms: Solar cells; Electronics, photonics and device physics
Introduction
To achieve the golden triangle elements (efficiency, cost, and lifetime), the researchers are extensively working on different semiconductor materials to develop high-efficiency solar cells. However, the single-junction solar cell suffers mainly from two inherent major power loss mechanisms, viz. thermalization and transmission (transparent Eg or non-absorbed photon) losses, depicted pictorially in Fig. 1. It shows that the high-energy photons (low wavelengths), in comparison with the bandgap of the material, excites the electron residing deep inside the valence band towards deep inside the conduction band. Thereafter, the electron (hole) generated deep inside the conduction (valence) band loses their energy as heat to relax to conduction (valence) band edges1. This loss of the incoming solar energy is known as thermalization loss. While, for the low-energy photons (higher wavelength) in comparison with the bandgap of the material, the photon will not be absorbed by the material and will not participate in the generation of charge carriers. This is known as the transmission loss or non-absorbed photon loss1. Additionally, to surpass the Shockley-Queisser single-junction limits2, abundant trails were made to fabricate solar cells with multiple junctions. i.e., tandem solar cells3–9. Tandem cells tackle with both thermalizations as well as transmission photon loss, which contributes mainly in the reduction of PCE of single-junction solar cells.
Figure 1.
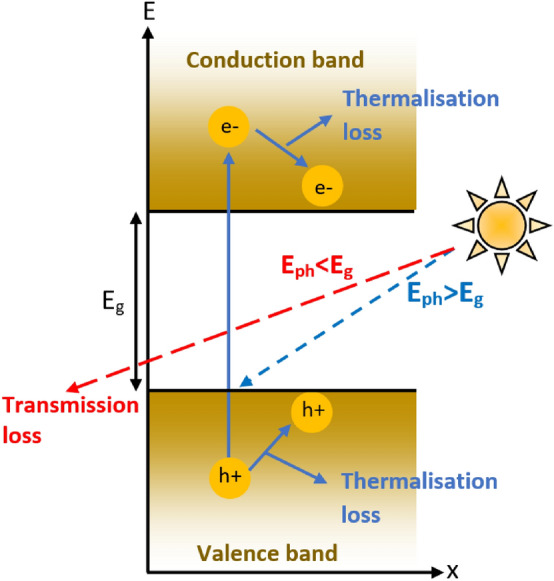
Schematic representation of power losses in single-junction solar cells viz. thermalization and transmission loss.
Tandem cells utilize the concept of dividing the power spectrum among multiple absorbers. The absorbers are selected in such a way that one of them is responsible for absorbing lower wavelength photons, while the other is assigned for photons of higher wavelength. With optimized bandgaps, a two-cell stacked tandem configuration can achieve up to 42% PCE, as stated in literature3. Further, in the year 1996, Martí et al. gave a hypothetical statement that under the standard AM1.5 illumination spectrum, an infinite stack of junctions can yield up to 65% PCE10. Typically, a two-cell stacked tandem configuration consists of a wide bandgap top cell and a narrow bandgap bottom cell to utilize high and low energy photons, respectively. Thereby the top cell reduces the transmission loss of the bottom cell while the bottom cell reduces the thermalization losses of top cell and utilizes the sun spectrum more efficiently.
For tandem cells to have better performance, researchers have used different combinations of sub-cells which include perovskite/perovskite7,11–14, perovskite/silicon8,15–18, perovskite/CIGS19,20, and all quantum dot20,21 structure and many more. All these combinations had performed well and had seen a massive rise in the performance over the decade. In most of the above-mentioned tandem configuration, perovskite, with its tunable bandgap (1.1 to 2.3 eV) and low processing cost techniques, emerged as developing material for standalone as well as tandem PV technology. The tremendous research effort of the researchers across the globe resulted in a recent record conversion efficiency of 25.6%22 followed by previous record efficiency of 25.2%23,24. The enhancement is significant compared to the initial value of conversion efficiency 3.8%, as reported in the year 2009 25. The perovskite-silicon tandem received great attention from the researchers that led to different fabrication routes for the perovskite top cell over silicon-based bottom subcells such as spin coating6, two-step hybrid method26,27, blade coating28, and slot-die coating29. Except for spin coating, the rest of the methods are investigated so as to provide a perovskite-silicon tandem design with a technique feasible at the industrial level. As of now, perovskite-silicon tandem solar cell reflected a record conversion efficiency of 29.5%30 which followed by an efficiency of 29.16%6, and the battle is still on for further improvement. However, there are some innate problems associated with perovskite-silicon tandem devices, such as low absorption coefficient and high module cost, which are the tailback for its mass production at the industrial level7,9,31–33.
Therefore, considering the detailed balance limit for the tandem solar cell, a top cell with 1.55 eV and a low-cost solution-processed bottom cell with a tunable bandgap can be well thought for the low-cost tandem design. This gives the track to the semiconductor materials that can be processed at a reduced cost to demonstrate their potential in tandem with perovskite top cells. Lead (II) sulfide colloidal quantum dots (PbS CQDs) are appropriate materials for constructing such complex multi-junction architectures because of their exceptional processibility and brilliant photoelectric properties. The conventional layer-by-layer deposition method provides them with benefits in the fabrication of tandem structures. Apart from this, tunable bandgaps can be achieved for a broad range of energies by varying the average QD size. Furthermore, in ambient conditions, CQDs offer low-cost solution processing methods and also provide additional absorption in the infrared (IR) region, which extends the absorption edge further to harvest low-energy photons in tandem configuration. These valuable properties resulted in exploring the potential of PbS CQDs-based bottom cell in the tandem configuration9,34–37.
Now, considering close to ideal properties of perovskite-based top cell and PbS CQDs-based bottom cell for tandem configuration. A perovskite-PbS CQDs-based two-terminal monolithic tandem solar cell has been designed, and detailed investigation and optimization have been performed to realize 23.36% efficient perovskite-PbS CQDs tandem solar cell. In the tandem configuration, the performance of the bottom cell highly depends on the transmitted spectrum by the top cell. Therefore, optical properties of the top cell play a vital role in determining the performance of the bottom cell and overall tandem performance. In literature, the optical properties of perovskite represented huge variations in different scholarly articles38–42, which is not in the case of any other semiconductor material. The consequences of such variations on the performance of perovskite solar cells (PSCs) have not been disclosed previously. Therefore, a detailed investigation of standalone perovskite top cell is done with different optical properties as reported in pieces of literature38–42, and the optimized top cell is sent forward for the tandem configuration with the PbS CQDs based bottom cell.
The overall manuscript is divided into four subsections. The ongoing introduction section is followed by the device structure and simulation methodology section, which provides a thorough discussion related to simulation methods, material parameters, and filtered spectrum. Thereafter, the result and discussion section are provided, which reveals the influence of the variation in the absorption coefficient of perovskite, perovskite thickness, and perovskite/ETL interface defect density followed by a design of 20.57% perovskite-PbS CQD tandem solar cell. The summary of the research work is concluded in the conclusion section, along with the future scope of the work.
Device structure and simulation methodology
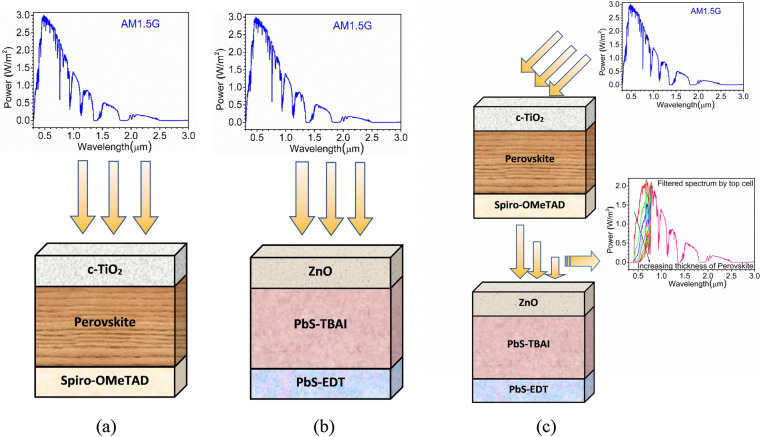
In this work, a tandem solar cell with perovskite (CH3NH3PbI3) as the top cell and PbS CQDs as the bottom cell has been designed using the SCAPS-1D simulator (a Solar Cell Capacitance Simulator). SCAPS, an open-source tool for designing solar cells, is developed at the department of electronics and information systems (ELIS), University of Ghent, Belgium43. Before simulating the proposed tandem perovskite-PbS CQDs design, both top and bottom cells are examined under standalone conditions, i.e., with AM1.5G spectrum illumination. The top cell utilized 1.55 eV perovskite (325 nm) as an absorber layer along with TiO2 (90 nm) as electron extraction layer (ETL) and Spiro-OMeTAD (460 nm) as hole extraction layer (HTL) depicted in Fig. 2(a). While the bottom cell comprises of a low bandgap absorber material, i.e., PbS- CQD layer treated tetrabutylammonium iodide (PbS-TBAI) (230 nm) with a bandgap of 1.14 eV having Mg-doped ZnO (MZO) (80 nm) as ETL and PbS CQD treated with 1, 2-ethanedithiol (PbS-EDT) (50 nm) as HTL as shown in Fig. 2(b). Both top and bottom cells are calibrated as per experimental work, and the calibration details for the top cell is provided in the results and discussion section, whereas MZO ETL based bottom cell is calibrated as per the device design published by Zhang et al.44 to have 9.43% efficient bottom cell. The results of the finding are published elsewhere45, and the same optimized device is invoked to be used as the bottom subcell.
Figure 2.
Simulated device structures along with the illuminated spectrum (a) perovskite cell under standalone condition (b) PbS-CQD cell under standalone condition (c) tandem solar cell with perovskite as the top cell (illuminated with standard AM1.5G) and PbS-CQD as the bottom cell (illuminated with the filtered spectrum of the top cell). The optical filter file for ITO has been applied to the electrode facing the illumination under both standalone and tandem configurations.
Afterward, both top and bottom subcells were stacked one over the other to form a monolithically integrated tandem device with perovskite-based wide-bandgap sub-cell as top cell and the PbS-CQDs based narrow bandgap sub-cell as bottom cell as shown in Fig. 2(c). The appropriate gap between the bandgaps of the two sub-cells makes them ideal for tandem structure. In two-terminal tandem solar cells stacking of two sub-cells results in the formation of a reverse-biased p–n junction at the interface of two subcells which eventually restricts current flow across the device46. To overcome this issue, the current matching strategy is utilized where a tunnel recombination junction (TRJ) is used, which ensures suitable equal current flow across both the devices in tandem configuration. However, owing to the limitations of SCAPS 1-D software, such TRJ is not feasible, and simulation of tandem structure is quite cumbersome. Therefore, an ideal TRJ layer is assumed without optoelectronic losses, where both top and bottom subcells are simulated independently but with different illumination spectrums. The top cell is illuminated with the standard AM1.5G spectrum while the transmitted filtered spectrum of the top cell is fed to the bottom cell so as to derive essential current matching conditions followed by construction of tandem current density–voltage (J–V) curve. This approach is widely adopted by the researchers designing tandem solar cells using SCAPS-1D7,46–49, and detailed information for calculating the absorbed and transmitted photocurrent along with filtered spectrum by the top cell at various thicknesses is provided in one of our previous publication7. The following formula is used to calculate the filtered spectrum by top cell at different absorber layer thicknesses.
Here, So(λ) is the standard AM1.5G spectrum, S(λ) is the transmitted spectrum by the top cell, α(λ) is the absorption coefficient, and d is the thickness of the respective layers. The material1, material2, and material3 represent c-TiO2, perovskite, and Spiro-OMeTAD layers, respectively. The interfacial reflection losses are ignored while computing the filtered spectrum. The extensive literature survey is done to obtain the electrical as well as optical properties for all the materials used during the simulation, and the obtained electrical parameters are reported in Table 1. The interfacial defects at the heterojunctions are also considered, and information is provided in Table 2. The optical properties of the bottom cell are obtained from44 whereas details regarding the optical properties of the top cell are provided in the results section. SCAPS-1D numerically solves coupled Poisson’s and continuity equations with dedicated boundary conditions of both holes and electrons for different interfaces and contacts. The fundamental equations for the optical model of SCAPS-1D and semiconductor equations used to simulate the optoelectronic performance are in accordance with the previously published work7, and reiteration of the same is avoided in this work. The fundamental monomolecular, bimolecular and trimolecular recombination rate in the perovskite is also considered in accordance with already published work17,50,51.
Table 1.
Electrical properties of materials used in top cell, bottom cell, and tandem solar cell8,9,17,32–34,44,45,52.
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| TiO2 | Perovskite | Spiro-OMeTAD | MgZnO (MZO) | PbS-TBAI | PbS-EDT | |
| Bandgap (eV) | 3.20 | 1.55 | 3.00 | 3.35 | 1.14 | 1.14 |
| Electron affinity (eV) | 3.9 | 3.9 | 2.45 | 4.0 | 4.0 | 3.9 |
| Dielectric Permittivity | 9 | 6.5 | 3 | 66 | 20 | 20 |
| CB effective density of states (cm−3) | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 | 1 × 1019 | 1 × 1019 | 1 × 1019 |
| VB effective density of states (cm−3) | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 | 1 × 1019 | 1 × 1019 | 1 × 1019 |
| Electron mobility (cm2V−1 s−1) | 20 | 2 | 2.0 × 10−4 | 5.0 × 10−2 | 2.0 × 10−2 | 2.0 × 10−4 |
| Hole mobility (cm2V−1 s−1) | 10 | 2 | 2.0 × 10−4 | 5.0 × 10−2 | 2.0 × 10−2 | 2.0 × 10−4 |
| Donor density ND (cm−3) | 1 × 1016 | 0 | 0 | 1 × 1017 | 1 × 1015 | 1 × 1014 |
| Acceptor density NA (cm−3) | 0 | 1 × 1014 | 1 × 1018 | 0 | 1 × 1015 | 1 × 1016 |
Table 2.
Interface defects are considered at different interfaces of the top cell, bottom cell, and tandem solar cell.
| Parameters | Interface | |||
|---|---|---|---|---|
| PbS-EDT/ PbS-TBAI interface | PbS-TBAI/ MZO interface | Spiro-OMeTAD/ Perovskite interface | Perovskite/ TiO2 interface | |
| Capture cross section electrons (cm2) | 1.2 × 10−13 | 1.0 × 10−19 | 1.0 × 10−15 | 1.0 × 10−15 |
| Capture cross section holes (cm2) | 1.2 × 10−13 | 1.0 × 10−19 | 1.0 × 10−15 | 1.0 × 10−15 |
| Energy with respect to reference (eV) | 0.50 | 0.60 | 0.75 | 0.75 |
| Total density (integrated over all energies) (cm−2) | 1 × 1016 | 2 × 1014 | 1 × 1011 | 1 × 1011 |
For all the cases, the defect type is neutral with the single energetic distribution. The reference for defect energy level (Et) is above the highest EV.
For neutral defects, carrier lifetimes are determined using and . Where are the electron capture cross-section, hole capture cross-section, thermal velocity (107 cm/s), and total defect density, respectively.
Results and discussion
Influence of variation in the absorption coefficient of perovskite
In this initial part of the result section, a perovskite-based solar cell is designed using a SCAPS-1D simulator with 460 nm thick Spiro-OMeTAD as HTL, a 325 nm absorber layer of CH3NH3PbI3 and TiO2 as ETL with the thickness of 90 nm. After that, the effect of the deviation in the absorption coefficient of the perovskite material is studied. The optical properties were taken from the previous publications, which report different values of the real and imaginary parts of the refractive index, i.e., n and k, respectively. This initiative is taken because the variations in published articles are quite significant, which is not the same for general semiconductors. There could be many reasons behind this, as different researchers choose different ways of fabricating the device. Even adopting a similar procedure and with similar chemical composition cannot ensure similar grain size distribution, and hence, the extracted properties may scatter over a wide range of values. Some minor alterations can be caused by material anisotropy and the accuracy of property extraction techniques. The consequences of these variations are not considered in any of the theoretical work related to PSC to the best of our knowledge. Since previously reported works on PSC considered a fixed wavelength-dependent absorption coefficient and did not discuss the influence of variation in optical properties, particularly absorption coefficient (α = 4πk/λ).
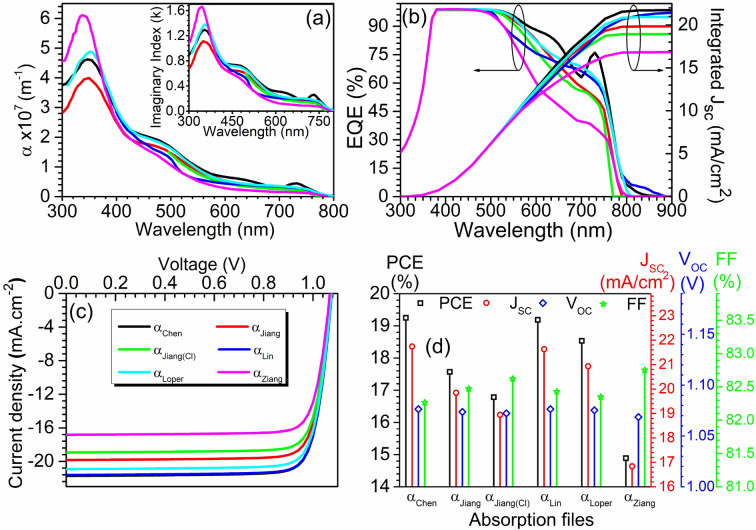
Therefore, the need to study such influence is perceived in this work. To study these variations, we calculated absorption coefficients and created absorption coefficient files (for the SCAPS-1D simulations) with the help of the imaginary parts of the refractive index (k) from five different sources such as Chen et al.38, Jiang et al.39, Lin et al.40, Löper et al.41, and Ziang et al.42. Calculated wavelength-dependent absorption coefficients from Chen et al.38, Jiang et al., Lin et al.40, Löper et al.41, and Ziang et al.42 are termed as αChen, αJiang, αJiang(Cl), αLin, αLöper, and αZiang and are shown in Fig. 3(a), the corresponding k values are also shown in the inset of the same figure. The k values corresponding to these pieces of literature are obtained from a single source, Green et al.53. All the generating absorption coefficient files are supplied to the simulator using batch setup while keeping the rest of the material parameters intact, and corresponding J–V and EQE with integrated JSC curves are obtained along with PV parameters such as JSC, VOC, FF, and PCE as reported in Fig. 3(b-d). The EQE and integrated JSC showed in Fig. 3(b) show the gradual difference in device performance, particularly in the 500–800 nm wavelength range. The integrated JSC changes to 21.7 mA cm−2 → 19.8 mA cm−2 → 18.9 mA cm−2 → 21.4 mA cm−2 → 20.9 mA cm−2 → 16.8 mA cm−2 while changing the optical data from αChen → αJiang → αJiang (Cl) → αLin → αLöper → αZiang. Result showed great variations, ranging from 16.8 mA cm−2 to 21.7 mA cm−2 for the optical data αZiang and αChen, respectively. Change in absorption coefficient reflected change in optical absorption and corresponding EQE and integrated JSC response. Figure 3(b) shows that device with superior optical response reflected highest JSC of 21.7 mA cm−2.
Figure 3.
(a) Calculated room temperature absorption coefficient data for CH3NH3PbI3 and CH3NH3PbI3(Cl). Inset shows published room temperature k values (Data sources are Chen et al.38, Jiang et al.39, Lin et al.40, Löper et al.41, and Ziang et al.42 and Green et al.53 (b) EQE and integrated JSC, (c) illuminated J–V curve and (d) PV parameters such as JSC, VOC, FF, and PCE with different optical absorption files.
Figure 3(c) and (d) are also produced to further quantify the rest of the PV parameters during the variation of the absorption file. The intersect with the current density axis and corresponding JSC data reported in Fig. 3(d) are also in accordance with the integrated JSC reported in Fig. 3(b) for the respective optical data. Results also reflected insignificant variation in VOC and FF in the range of (1.076 V – 1.075 V) and (82.26% – 82.75%) with said variation in optical data. The collective influence of JSC, VOC, and FF are reflected in the PCE as shown in Fig. 3(d), which ranges from (14.88% – 19.25%) with the highest conversion efficiency of 19.25% with αChen, followed by 19.19% with αLin.
The validity of the simulated results with experimental findings is an important part of any theoretical work. Therefore, the range of obtained efficiency is compared with the published experimental data for PSCs from the year 2013 to 2015 with device architecture TiO2 (ETL)/ perovskite (absorber layer)/ Spiro-OMeTAD (HTL). The best research cell efficiency chart published by National Renewable Energy Laboratory (NREL) showed that the conversion efficiency for the PSCs during the year 2013–2015 was ranging around (13.8% to 19.8%)54, and these values are very close to the simulated efficiency range (14.88% – 19.25%) achieved in this work. This proves the accuracy and authenticity of the simulation study carried out in this manuscript. The comparison is deliberately restricted till the year 2015 since all the absorption coefficient data used during simulations are obtained from the kinds of literature published in the single year 2015. Therefore, material and device-engineered PSCs, including the record conversion efficiency (25.2%) published after 201524,55, are ignored to have a fair comparison.
This ongoing subsection summarizes the impact of deviation in absorption coefficient on the performance of PSCs, and the next subsection discusses the influence of absorber layer thickness on the PV performance. All the analysis reported in subsequent subsections utilizes the optical file (αChen).
Impact of perovskite thickness
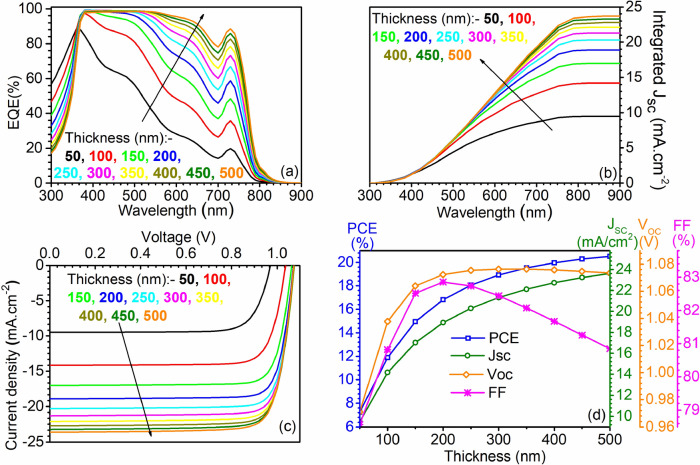
The deposition of perovskite layer in sandwiched architecture-based PSCs mostly depends on the solution process-based spin coating techniques56–58, a standard method to deposit thin films with the thickness of a few nanometers to few microns. The entire process is divided into four main steps: deposition, spin-up, spin-off, and evaporation. The thickness of the perovskite absorber layer during the fabrication process of PSCs depends on several factors such as the concentration of the material and evaporation of the solvent, which further includes ambient humidity, temperature, vapour pressure, and viscosity of the solvent. Therefore, it is crucial to estimate the device performance with different thicknesses of the absorber layer. Hence, in this subsection, the analysis of the perovskite device has been made, where the influence of CH3NH3PbI3 thickness on the PV parameters is evaluated. The variation has been performed from 0.05 µm to 0.5 µm in ten equal steps in a linear scale, keeping the remaining device parameters intact. Corresponding EQE, integrated JSC, illuminated J–V curve, and PV parameters are summarized in Fig. 4(a), (b), (c), and (d), respectively.
Figure 4.
Impact of perovskite absorber layer thickness on (a) EQE, (b) integrated JSC, (c) illuminated J–V curve, and (d) PV parameters at various thicknesses, i.e., from 50 to 500 nm. Data reported in figures are obtained from the SCAPS-1D simulator.
It is recorded that increasing the thickness of perovskite resulted in an enhancement in the optical absorption and corresponding collection efficiency, particularly at higher wavelengths, as shown in Fig. 4(a). Since most of the lower wavelength photons tend to get absorbed in a small thickness and to absorb the higher wavelength photons, a relatively higher thickness is required to prevent the transmittance losses. Therefore, an increase in thickness resulted in lower transmittance loss, enhanced absorption, and collection probability at higher wavelengths. Quantitively, while increasing the thickness from 50 nm → 100 nm → 150 nm → 200 nm → 250 nm → 300 nm → 350 nm → 400 nm → 450 nm → 500 nm resulted in enhancement in EQE from 28.23% → 48.46% → 62.96% → 73.34% → 80.57% → 86.03% → 89.77% → 92.40% → 94.24% → 95.51% at a wavelength equal to 600 nm. Although increasing the thickness increases the optical performance, absorption saturation is a common phenomenon that restricts the improvement and limits the performance at higher thickness levels. The same is being reflected in this work also where the improvement in EQE beyond 350 nm thickness is not significant, as shown in Fig. 4(a).
Enhanced optical performance anticipate the improvement in integrated JSC, i.e., increasing the thickness from 50 to 350 nm resulted in JSC improvement from 9.47 mA cm−2 to 22.10 mA cm−2 whereas further increasing the thickness beyond 350 nm to 500 nm resulted in 23.70 mA cm−2. Up to this point, only the influence on JSC being examined whereas the overall conversion efficiency is the collective outcome of all three parameters such as JSC, VOC, and FF. Therefore, illuminated J–V curve and PV parameters are also summarized in Fig. 4(c) and (d), which shows that the VOC also increases up to 250 nm and then indicates saturation. Improvement in VOC is attributed to elevated concentration of light-generated charge carriers. Obtained FF also shows improvement until 200 nm due to an increase in carrier concentration. However, it started to fall while increasing the thickness beyond 200 nm due to reduced electric field strength across the perovskite layer. In case of the thick absorber layer, the collecting ETL/perovskite and perovskite/HTL interfaces move apart, and the associated electric field strength decreases. Therefore, as reported in Fig. 4 (d), conversion efficiency reflects improvement till 350 nm, and after that, marginal improvement is noticed.
This subsection concludes a PSC with a conversion efficiency of 19.52% at the perovskite thickness of 350 nm. The same device is invoked, and the influence of perovskite/ETL defect density on PV parameters is investigated in the following subsection.
Impact of perovskite/transport layer defect density
In conventional sandwiched architecture-based PSCs, perovskite is sandwiched between ETL and HTL that consists of dissimilar semiconductor material with different electrical as well as structural properties compared to perovskite. The presence of transport layers helps in the extraction of light-generated carriers and provides higher conversion efficiencies. However, their presence also results in performance challenges in the form of interfacial recombination due to interface traps, hysteresis, and stability. The origin of interfacial traps related issues is projected in Fig. 5. The mismatch of electrical as well as structural properties between two different materials develops interfacial defects, which eventually results in elevated charge recombination at the interface, i.e., increased surface recombination velocity (SRV). Both perovskite/ETL and perovskite/HTL interface defects can significantly reduce the performance of PSCs. However, if illuminated from the ETL side, the impact of the perovskite/ETL interface defect would be large compared to the perovskite/HTL interface since most of the lower wavelength photons get absorbed in the vicinity of the perovskite/ETL interface and vice versa if illuminated from HTL side. The PSC device under consideration is illuminated from the ETL side; therefore, only the impact of perovskite/ETL interface defect density (IDD) is considered.
Figure 5.
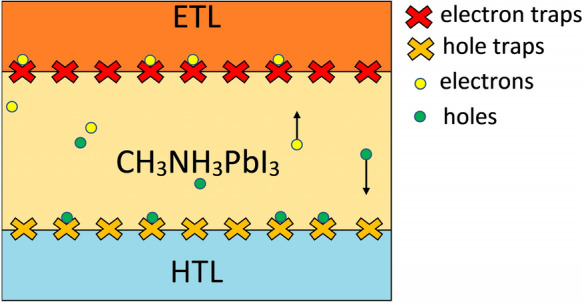
Problems associated with the interface of perovskite absorber layer/ETL and perovskite absorber layer/HTL.
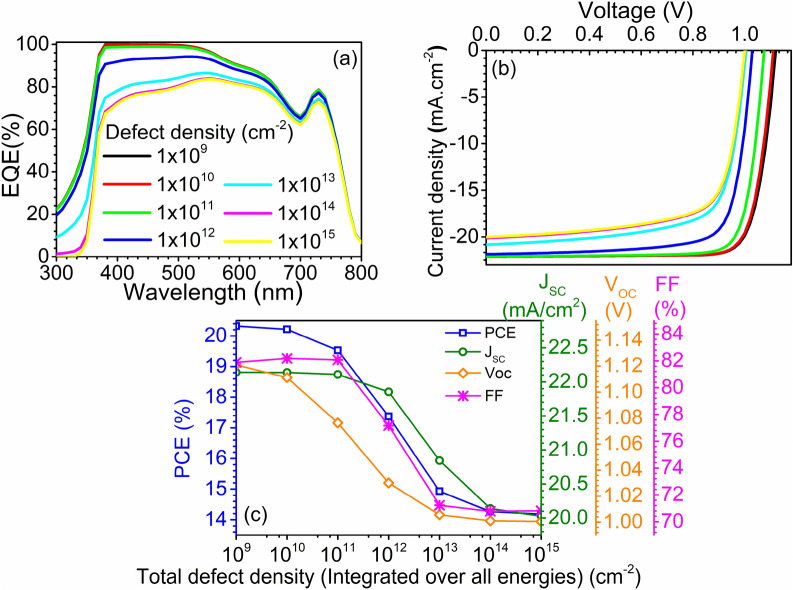
The investigation depicts that IDD at the perovskite/ETL interface has a strong effect on the performance of the device. Here the IDD (integrated over all energies) is varied from 1 × 109 cm−3 to 1 × 1015 cm−3 in seven equal steps in a logarithmic scale. The corresponding SRV for both electrons and holes is 101 cm.s−1 (at lowest IDD) and 107 cm.s−1 (at highest IDD). Figure 6(a), (b), and (c) represent the EQE, J–V curves, and PV parameters, respectively, at different IDD. Increasing the IDD from 1 × 109 cm−3 to 1 × 1015 cm−3 reduces the EQE, particularly at the lower wavelengths, as shown in Fig. 6(a). This is owing to the fact the lower wavelength photon generates the carriers in perovskite near the perovskite/ETL interface, and elevated IDD resulted in enhanced recombination and lower collection probability. Reduction is EQE leads to the drop in JSC from 22.14 mA cm−2 to 22.02 mA cm−2 (Fig. 6(b-c)). The VOC also dropped to 1.00 V from 1.12 V, and the decrease is attributed to a reduction in carrier concentration due to interfacial recombination, which rapidly neutralizes the light generated carriers. Result also reveals a drop of 11.07% in FF, which was initially 81.88%, and dropped to 70.81% as the IDD increased to 1 × 1015 cm−3 from 1 × 109 cm−3. Due to the reduction in JSC, VOC, and FF, the overall PCE of the device reduces from 20.32% to 14.18%, which unveils that IDD at the perovskite/ETL interface has a considerable effect on the device performance.
Figure 6.
Impact of perovskite/ETL interface defect density (IDD) on (a) EQE, (b) illuminated J–V curve, and (c) PV parameters. Data reported in figures are obtained from the SCAPS-1D simulator.
Design of perovskite-PbS CQD tandem solar cell
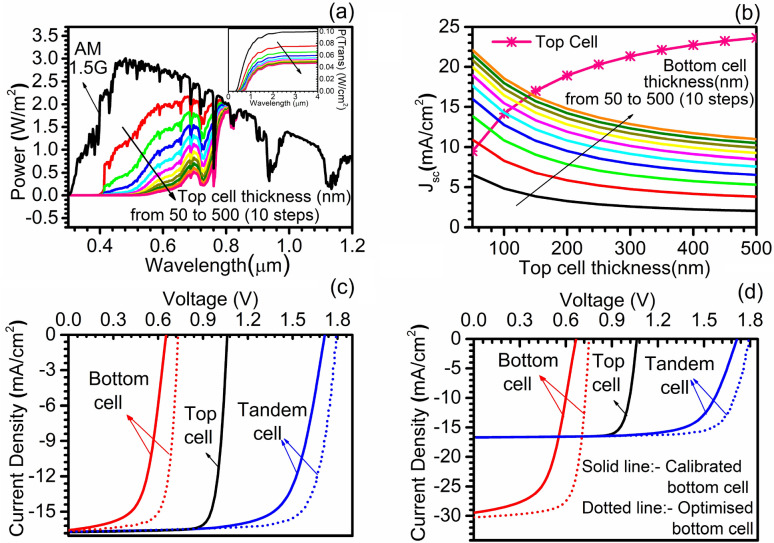
In this section, a thorough study of the tandem structure formed by combining the perovskite-based top cell and PbS CQD-based bottom cell is reported. The perovskite top cell is identical to as optimized in the previous subsection whereas the calibrated PbS CQD bottom subcell is invoked from our previous publication 45. The methodology of tandem solar cell simulation has been mentioned in simulation methodology. In brief, the top cell has been illuminated with the standard AM1.5G, whereas the bottom cell is exposed to the filtered spectrum calculated by using absorption coefficients as well as thickness of the various materials used in the top cell. In total, ten (10) filtered spectrums by the top cell are obtained by varying the thickness of the perovskite absorber layer from 50 to 500 nm in the top subcell while keeping the other parameters intact. Figure 7(a) represents the computed filtered spectrum and associated transmitted power (Ptrans) at each thickness level. The reduction in the filtered transmitted power, particularly below the 800 nm wavelength range, is observed with the increase in the thickness of the perovskite layer. This is attributed to higher absorption in the top cell with the upturn in thickness, and it is worth noting that perovskite with only 50 nm thickness reduces the power level of standard AM1.5 spectrum from 0.1 W cm−2 to 0.076 W cm−2 in term of the filtered spectrum, inset of Fig. 7(a). Trends show higher transmitted photocurrent and low absorbed current in the top cell for low values of perovskite thicknesses, i.e., 50 nm. Raising the thickness to higher values, i.e., towards 500 nm, elevates the absorbed photocurrent and simultaneously reduces the transmitted photocurrent.
Figure 7.
(a) Power transmitted by the top cell at different thickness along with standard AM1.5G spectrum, (b) current matching curve at the different top and calibrated bottom cell, (c) JV curve for standalone top cell, standalone bottom cell (calibrated and optimized), and tandem (with calibrated and optimized bottom subcell) solar cell and (d) JV curve for top cell and bottom cell (calibrated and optimized) under standalone (AM1.5G spectrum), the final tandem J–V curve with calibrated and optimized cell is also shown. Data reported in figures are obtained from the SCAPS-1D simulator.
Two terminal monolithic tandem solar cell structure resembles the architecture of back-to-back connected or series-connected diodes in which the cell with minimum current in the constituent sub-cells limits the maximum current, i.e., tandem JSC whereas the VOC is the sum of the individual VOC of the sub-cells. Mathematically, JSC (tandem) ~ min {JSC (top), JSC (bottom)} in standalone configuration and VOC (tandem) ~ VOC (top) + VOC (bottom). Hence, we have augmented the thicknesses of both the subcells so as to match maximum deliverable JSC from the tandem solar cell, which is constrained by the limiting cell, i.e., top cell. In order to obtain maximum JSC from the tandem device, the materials having different bandgaps should be adopted so that both of them can perform in their defined areas of the power spectrum. Apart from that, current matching point should be at such an appropriate thickness level that it should avoid parasitic absorption in the top cell and should not limit bottom cell performance as well. In order to achieve the same, the calculated the filtered power spectrum for ten (10) different thicknesses of the perovskite absorber (50 nm to 500 nm) is used to conceive the presence of the top cell with different perovskite thickness from 50 to 500 nm. These spectrum files are fed to the bottom sub-cell so as to measure its performance. Concurrently the thickness of PbS-TBAI of the bottom cell is also varied in 10 equal steps from 50 to 500 nm in order to calculate all the possible thickness value points where current matching could be possible. This effort resulted in the formation of current matching, i.e., JSC matching curve as shown in Fig. 7(b) at various thickness of the top and bottom subcells. The result shows that the current matching is not observed for the thickness of both cells equivalent to 50 nm and for the perovskite thickness more than 150 nm. Whereas nine (9) intersecting points are observed for the perovskite thickness range 50 nm to 150 nm and PbS-TBAI thickness range 100 nm to 500 nm. Among them, the last current matching point has opted to deliver the maximum tandem JSC of 16.62 mA cm−2 and the corresponding top and bottom subcell thickness 143 nm and 500 nm, respectively.
After identifying the corresponding top and bottom subcell thickness to get maximum JSC from the tandem device, the top cell is re-simulated with thickness 143 nm under standard AM1.5G spectrum, and another filtered spectrum is constructed with said thickness. The same filtered spectrum has been used to illuminate the bottom subcell with a thickness of 500 nm to obtain the illuminated J–V of the bottom subcell under tandem configuration. The J–V curve for both top cell (143 nm) under AM1.5G spectrum and bottom cell (500 nm) under filtered spectrum is depicted in Fig. 7(c), which validates the equal current, i.e., current matching in both top and bottom subcells. Followed by current matching, the tandem J–V curve is constructed by adding the voltage (x-axis) at equal current points (y-axis) to construct the tandem J–V curve, which is shown alongside the individual J–V curve in Fig. 7(c). The solid line tandem curve shown in Fig. 7(c-d) is constructed using calibrated PbS-CQD bottom subcell having PbS-TBAI thickness of 500 nm and showed the tandem conversion efficiency of 20.57% with VOC (1.714 V), JSC (16.62 mA cm−2), and FF (72.3%).
It should be noted that the constructed tandem device did not contain the optimized bottom subcell in terms of doping density of PbS-EDT (HTL) and MZO (ETL). Therefore, to further enhance the conversion efficiency of the tandem device, the optimized doping 5 × 1017 cm−3 is used for both HTL and ETL layers in the bottom subcell. The detailed discussion related to the optimization of the doping level in the bottom subcell is reported in our previous work published elsewhere 45. In standalone configuration the calibrated bottom cell with thickness 500 nm showed 11.24% conversion efficiency with VOC (666 mV), JSC (29.64 mA cm−2) and FF (56.9%) whereas optimized bottom cell reflected 16.88% conversion efficiency with VOC (752 mV), JSC (30.77 mA cm−2) and FF (72.9%). The significant improvement in VOC and FF anticipates the improvement in the conversion efficiency of the tandem device. However, a 1.13 mA cm−2 higher JSC value would disturb the current matching criteria that are obtained with calibrated device. Therefore, under filtered spectrum by 143 nm top cell, the thickness of PbS-TBAI in the optimized device is adjusted to 470 nm in order to have the same current matching point, i.e., similar current as of top cell. This exercise led to the formation of the J–V curve for the optimized bottom subcell (shown in the dotted line) under the filtered spectrum by the top cell. Now it can be clearly validated through Fig. 7(c) that the JSC of top cell and bottom cell for both calibrated as well as optimized device ties at the same point. This supports that another tandem curve could be constructed with an optimized bottom subcell without disturbing the current matching criteria by keeping this fact in mind that for current matching with 143 nm top subcell, the thickness of bottom subcell is 500 nm and 470 nm in for calibrated and optimized bottom subcell, respectively. The tandem device constructed with optimized bottom subcell reflected 23.36% conversion efficiency with 1.79 V (VOC), 16.67 mA cm−2 (JSC) and 78.3% (FF). The tandem device with optimized bottom subcell showed 13.6% higher conversion efficiency, and the improvement is credited to 4.4%, and 8.3% enhanced VOC and FF, respectively, compared to the tandem device having calibrated bottom subcell. Further, standalone top and bottom subcell J–V curve with optimized thickness in respect to the tandem configuration is also reported in Fig. 7(d) along with tandem J–V curve and quantitative summary of the PV parameter for all the devices considered in this subsection are provided in Table 3. This reported thorough analysis of perovskite-PbS CQD tandem solar cell concludes a 23.36% efficient tandem design.
Table 3.
Summary of the photovoltaic parameters of all the devices considered in this subsection.
| Device | Thickness (nm) | JSC (mA cm−2) | VOC (V) | FF (%) | PCE (%) | Source | |
|---|---|---|---|---|---|---|---|
| Perovskite top cell (standalone) | 143* | 16.68 | 1.061 | 82.4 | 14.60 | This work | |
| Experimental PbS-CQD bottom cell (standalone) | 230 | 24.50 | 0.620 | 62.0 | 9.41 | Zhang et al.44 | |
| Calibrated PbS-CQD bottom cell (standalone) | 230 | 24.51 | 0.633 | 60.8 | 9.43 | Pandey et al.45 | |
| Optimized PbS-CQD bottom cell (standalone) | 230 | 25.07 | 0.730 | 74.3 | 13.59 | Pandey et al.45 | |
| Calibrated PbS-CQD bottom cell | Standalone (AM1.5G) | 500* | 29.48 | 0.666 | 56.9 | 11.19 | This work |
| Under filtered spectrum | 16.57 | 0.653 | 61.5 | 6.65 | |||
| Optimized PbS-CQD bottom cell | Standalone (AM1.5G) | 500 | 30.61 | 0.752 | 72.9 | 16.80 | |
| Under filtered spectrum | 16.97 | 0.735 | 74.4 | 9.27 | |||
| Standalone (AM1.5G) | 470* | 30.24 | 0.751 | 73.2 | 16.63 | ||
| Under filtered spectrum | 16.62 | 0.733 | 74.5 | 9.07 | |||
| Perovskite/PbS-CQD tandem with calibrated bottom cell | 143 (top) /500 (bottom) | 16.62 | 1.714 | 72.3 | 20.57 | ||
| Perovskite/PbS-CQD tandem with optimized bottom cell | 143 (top) /470(bottom) | 16.67 | 1.790 | 78.3 | 23.36 | ||
*Thickness for current matching.
Conclusion
This work concludes a 23.36% efficient two-terminal monolithic perovskite-PbS CQD tandem solar cell design thorough comprehensive device simulations. Before evaluating the tandem design, a detailed standalone analysis of perovskite top cell is carried out in terms of variation in optical properties (in accordance with experimental data), absorber layer thickness, and absorber layer/transport layer interface defect density so as to optimize the standalone performance of the top cell. Further, the filtered spectrum and associated integrated power transmitted by optimized top cell at different perovskite layer thicknesses are obtained for the tandem simulation. The same filtered spectrum file is used to simulate the calibrated and optimized PbS-CQD based bottom subcell to get the current matching conditions. This has been done to get the maximum deliverable JSC of the tandem device by varying the thickness of the absorber layer in both the top and bottom subcell. Top and bottom subcell reflected 14.60% and 9.07% conversion efficiency with approximately equal current 16.68 mA cm−2 (top) and 16.62 mA cm−2 (bottom) under tandem configuration with an optimized thickness of 143 nm (top cell) and 470 nm (bottom cell), where the top cell is simulated under AM1.5G spectrum, and bottom cell is stimulated by the spectrum filtered by 143 nm thick top cell. Distinctly measured J–V curves of the top (under AM1.5G) and bottom subcell (under filtered spectrum) at equal current are summed together in series. In other words, the voltages are added at equal current to generate tandem J–V characteristics. This work concludes a tandem design which could deliver 23.36% conversion efficiency with 1.79 V (VOC), 16.67 mA cm−2 (JSC) and 78.3% (FF).
Further, in the current manuscript, a maximum JSC of 22.14 mA cm−2 and 30.61 mA cm−2 has been achieved in the standalone simulation of top and bottom subcells, respectively, which clearly shows that the perovskite top cell with JSC of 22.14 mA cm−2 needs to act as a limiting cell for the tandem JSC. Therefore, a tandem design that can deliver a JSC of 22.14 mA cm−2 would be considered as an optimum design; however, the constructed tandem device showed the tandem JSC of 16.67 mA cm−2 which is much lower compared to the limiting top cell. Therefore, the main limiting cell in the proposed design is not the top cell but the bottom cell as it is not able to maintain the JSC close to the limiting cell under tandem configuration (filtered spectrum). The same can be validated through the current matching curve provided in the manuscript. Therefore, it is required to have a PbS-CQD solar cell with a higher JSC value in standalone configuration so that the bottom cell can maintain a significant level of JSC when placed underneath the top cell, i.e., under filtered spectrum to match the JSC of standalone top cell. Therefore, there is a need to design a PbS-CQD solar cell with higher JSC values followed by the optimization of the top cell in the future to lift the conversion efficiency of the proposed design beyond the standalone perovskite solar cells. In addition, the detailed study of the tandem design reported in the current study would open the path for the development of high-efficiency, low-cost perovskite-PbS CQD tandem solar cells in the future. The influence of the physical presence of tunnel recombination junction can be done in the future.
Acknowledgements
Author Rahul Pandey is grateful to SERB, Ministry of Science and Technology, Government of India for sanctioning project grant under the Start-up Research Grant (SRG) scheme with file number: SRG/2019/000941. The administration of Chitkara University in providing all the support to carry on this research work is also acknowledged. The authors are grateful to Dr. Marc Burgelman and his staff, at the University of Gent, Belgium, for providing the open-source SCAPS-1D simulator.
Author contributions
J.M. and R.P. conceived the experiment, and J.M., K.S, and R.P. conducted the experiment, performed analysis, and generated figures. All authors reviewed the manuscript.
Data availability
The data (problem definition file of top and bottom cell, filtered spectrum, and script for tandem J–V curve) that support the findings of this study shall be made available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Karanveer Singh and Rahul Pandey.
Contributor Information
Jaya Madan, Email: jaya.madan@chitkara.edu.in.
Rahul Pandey, Email: rahul.pandey@chitkara.edu.in.
References
- 1.Green MA. Third generation photovoltaics: solar cells for 2020 and beyond. Physica E. 2002;14:65–70. doi: 10.1016/S1386-9477(02)00361-2. [DOI] [Google Scholar]
- 2.Shockley W, Queisser HJ. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961;32:510–519. doi: 10.1063/1.1736034. [DOI] [Google Scholar]
- 3.Vos AD. Detailed balance limit of the efficiency of tandem solar cells. J. Phys. D Appl. Phys. 1980;13:839–846. doi: 10.1088/0022-3727/13/5/018. [DOI] [Google Scholar]
- 4.Li W, et al. High-performance solar flow battery powered by a perovskite/silicon tandem solar cell. Nat. Mater. 2020;19:1326–1331. doi: 10.1038/s41563-020-0720-x. [DOI] [PubMed] [Google Scholar]
- 5.Xie M, et al. Two-dimensional BAs/InTe: A promising tandem solar cell with high power conversion efficiency. ACS Appl. Mater. Interfaces. 2020;12:6074–6081. doi: 10.1021/acsami.9b21102. [DOI] [PubMed] [Google Scholar]
- 6.Al-Ashouri A, et al. Monolithic perovskite/silicon tandem solar cell with >29% efficiency by enhanced hole extraction. Science. 2020;370:1300. doi: 10.1126/science.abd4016. [DOI] [PubMed] [Google Scholar]
- 7.Madan J, Shivani, Pandey R, Sharma R. Device simulation of 17.3% efficient lead-free all-perovskite tandem solar cell. Sol. Energy. 2020;197:212–221. doi: 10.1016/j.solener.2020.01.006. [DOI] [Google Scholar]
- 8.Pandey R, Singla A, Madan J, Sharma R, Chaujar R. Toward the design of monolithic 23.1% efficient hysteresis and moisture free perovskite/c-Si HJ tandem solar cell: A numerical simulation study. J. Micromech. Microeng. 2019;29:064001. doi: 10.1088/1361-6439/ab1512. [DOI] [Google Scholar]
- 9.Kashyap S, Pandey R, Madan J, Sharma R. Design and simulation of a-Si:H/PbS colloidal quantum dots monolithic tandem solar cell for 12% efficiency. Physica Status Solidi (A) 2020;217:2000252. doi: 10.1002/pssa.202000252. [DOI] [Google Scholar]
- 10.Marti A, Araújo GL. Limiting efficiencies for photovoltaic energy conversion in multigap systems. Sol. Energy Mater. Sol. Cells. 1996;43:203–222. doi: 10.1016/0927-0248(96)00015-3. [DOI] [Google Scholar]
- 11.Eperon GE, et al. Perovskite-perovskite tandem photovoltaics with optimized band gaps. Science. 2016;354:861. doi: 10.1126/science.aaf9717. [DOI] [PubMed] [Google Scholar]
- 12.Forgács D, et al. Efficient monolithic perovskite/perovskite tandem solar cells. Adv. Energy Mater. 2017;7:1602121. doi: 10.1002/aenm.201602121. [DOI] [Google Scholar]
- 13.Hossain MI, et al. Perovskite/perovskite planar tandem solar cells: A comprehensive guideline for reaching energy conversion efficiency beyond 30% Nano Energy. 2021;79:105400. doi: 10.1016/j.nanoen.2020.105400. [DOI] [Google Scholar]
- 14.Mailoa JP, et al. A 2-terminal perovskite/silicon multijunction solar cell enabled by a silicon tunnel junction. Appl. Phys. Lett. 2015;106:121105. doi: 10.1063/1.4914179. [DOI] [Google Scholar]
- 15.De Bastiani M, et al. Efficient bifacial monolithic perovskite/silicon tandem solar cells via bandgap engineering. Nat. Energy. 2021;6:167–175. doi: 10.1038/s41560-020-00756-8. [DOI] [Google Scholar]
- 16.Yang D, et al. 28.3%-efficiency perovskite/silicon tandem solar cell by optimal transparent electrode for high efficient semitransparent top cell. Nano Energy. 2021;84:105934. doi: 10.1016/j.nanoen.2021.105934. [DOI] [Google Scholar]
- 17.Pandey R, Chaujar R. Numerical simulations: Toward the design of 27.6% efficient four-terminal semi-transparent perovskite/SiC passivated rear contact silicon tandem solar cell. Superlatt. Microstruct. 2016;100:656–666. doi: 10.1016/j.spmi.2016.10.033. [DOI] [Google Scholar]
- 18.Gharibzadeh S, et al. 2D/3D heterostructure for semitransparent perovskite solar cells with engineered bandgap enables efficiencies exceeding 25% in four-terminal tandems with silicon and CIGS. Adv. Func. Mater. 2020;30:1909919. doi: 10.1002/adfm.201909919. [DOI] [Google Scholar]
- 19.Jacobsson TJ, et al. 2-Terminal CIGS-perovskite tandem cells: A layer by layer exploration. Sol. Energy. 2020;207:270–288. doi: 10.1016/j.solener.2020.06.034. [DOI] [Google Scholar]
- 20.Shivarudraiah SB, Ng M, Li CHA, Halpert JE. All-inorganic, solution-processed, inverted CsPbI3 quantum dot solar cells with a PCE of 13.1% achieved via a layer-by-layer FAI treatment. ACS Appl. Energy Mater. 2020;3:5620–5627. doi: 10.1021/acsaem.0c00584. [DOI] [Google Scholar]
- 21.Hu L, et al. Quantum-dot tandem solar cells based on a solution-processed nanoparticle intermediate layer. ACS Appl. Mater. Interfaces. 2020;12:2313–2318. doi: 10.1021/acsami.9b16164. [DOI] [PubMed] [Google Scholar]
- 22.Jeong J, et al. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature. 2021 doi: 10.1038/s41586-021-03406-5. [DOI] [PubMed] [Google Scholar]
- 23.Kim G, et al. Impact of strain relaxation on performance of α-formamidinium lead iodide perovskite solar cells. Science. 2020;370:108–112. doi: 10.1126/science.abc4417. [DOI] [PubMed] [Google Scholar]
- 24.Green M, et al. Solar cell efficiency tables (version 57) Prog. Photovoltaics Res. Appl. 2021;29:3–15. doi: 10.1002/pip.3371. [DOI] [Google Scholar]
- 25.Kojima A, Teshima K, Shirai Y, Miyasaka T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009;131:6050–6051. doi: 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
- 26.Sahli F, et al. Fully textured monolithic perovskite/silicon tandem solar cells with 252% power conversion efficiency. Nat. Mater. 2018;17:820–826. doi: 10.1038/s41563-018-0115-4. [DOI] [PubMed] [Google Scholar]
- 27.Nogay G, et al. 25.1%-Efficient monolithic perovskite/silicon tandem solar cell based on a p-type monocrystalline textured silicon wafer and high-temperature passivating contacts. ACS Energy Lett. 2019;4:844–845. doi: 10.1021/acsenergylett.9b00377. [DOI] [Google Scholar]
- 28.Chen B, et al. Blade-coated perovskites on textured silicon for 26%-efficient monolithic perovskite/silicon tandem solar cells. Joule. 2020;4:850–864. doi: 10.1016/j.joule.2020.01.008. [DOI] [Google Scholar]
- 29.Subbiah AS, et al. High-performance perovskite single-junction and textured perovskite/silicon tandem solar cells via slot-die-coating. ACS Energy Lett. 2020;5:3034–3040. doi: 10.1021/acsenergylett.0c01297. [DOI] [Google Scholar]
- 30.NREL. Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html (2021).
- 31.Lim JW, Kim G, Shin M, Yun SJ. Colored a-Si: H transparent solar cells employing ultrathin transparent multi-layered electrodes. Sol. Energy Mater. Sol. Cells. 2017;163:164–169. doi: 10.1016/j.solmat.2017.01.017. [DOI] [Google Scholar]
- 32.Pathania A, Pandey R, Madan J, Sharma R. Design and optimization of 26.3% efficient perovskite/FeSi2 monolithic tandem solar cell. J. Mater. Sci. Mater. Electron. 2020;31:15218–15224. doi: 10.1007/s10854-020-04086-z. [DOI] [Google Scholar]
- 33.Pathania A, Madan J, Pandey R, Sharma R. Effect of structural and temperature variations on perovskite/Mg2Si based monolithic tandem solar cell structure. Appl. Phys. A. 2020;126:580. doi: 10.1007/s00339-020-03758-1. [DOI] [Google Scholar]
- 34.Gao Y, et al. Enhancing PbS colloidal quantum dot tandem solar cell performance by graded band alignment. J. Phys. Chem. Lett. 2019;10:5729–5734. doi: 10.1021/acs.jpclett.9b02423. [DOI] [PubMed] [Google Scholar]
- 35.Yuan L, et al. Four-terminal tandem solar cell with dye-sensitized and PbS colloidal quantum-dot-based subcells. ACS Appl. Energy Mater. 2020;3:3157–3161. doi: 10.1021/acsaem.0c00030. [DOI] [Google Scholar]
- 36.Karani A, et al. Perovskite/colloidal quantum dot tandem solar cells: Theoretical modeling and monolithic structure. ACS Energy Lett. 2018;3:869–874. doi: 10.1021/acsenergylett.8b00207. [DOI] [Google Scholar]
- 37.Manekkathodi A, et al. Solution-processed perovskite-colloidal quantum dot tandem solar cells for photon collection beyond 1000 nm. J. Mater. Chem. A. 2019;7:26020–26028. doi: 10.1039/C9TA11462A. [DOI] [Google Scholar]
- 38.Chen C-W, et al. Optical properties of organometal halide perovskite thin films and general device structure design rules for perovskite single and tandem solar cells. J. Mater. Chem. A. 2015;3:9152–9159. doi: 10.1039/C4TA05237D. [DOI] [Google Scholar]
- 39.Jiang Y, Green MA, Sheng R, Ho-Baillie A. Room temperature optical properties of organic–inorganic lead halide perovskites. Sol. Energy Mater. Sol. Cells. 2015;137:253–257. doi: 10.1016/j.solmat.2015.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lin Q, Armin A, Nagiri RCR, Burn PL, Meredith P. Electro-optics of perovskite solar cells. Nat. Photonics. 2015;9:106–112. doi: 10.1038/nphoton.2014.284. [DOI] [Google Scholar]
- 41.Löper P, et al. Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry. J. Phys. Chem. Lett. 2015;6:66–71. doi: 10.1021/jz502471h. [DOI] [PubMed] [Google Scholar]
- 42.Ziang X, et al. Refractive index and extinction coefficient of CH3NH3PbI3 studied by spectroscopic ellipsometry. Opt. Mater. Express. 2015;5:29–43. doi: 10.1364/OME.5.000029. [DOI] [Google Scholar]
- 43.Burgelman M, Nollet P, Degrave S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films. 2000;361–362:527–532. doi: 10.1016/S0040-6090(99)00825-1. [DOI] [Google Scholar]
- 44.Zhang X, et al. Highly efficient flexible quantum dot solar cells with improved electron extraction using MgZnO nanocrystals. ACS Nano. 2017;11:8478–8487. doi: 10.1021/acsnano.7b04332. [DOI] [PubMed] [Google Scholar]
- 45.Pandey R, et al. Device simulations: Toward the design of >13% efficient PbS colloidal quantum dot solar cell. Sol. Energy. 2020;207:893–902. doi: 10.1016/j.solener.2020.06.099. [DOI] [Google Scholar]
- 46.Burdick J, Glatfelter T. Spectral response and I-V measurements of tandem amorphous-silicon alloy solar cells. Solar Cells. 1986;18:301–314. doi: 10.1016/0379-6787(86)90129-8. [DOI] [Google Scholar]
- 47.Kim K, et al. Simulations of chalcopyrite/c-Si tandem cells using SCAPS-1D. Sol. Energy. 2017;145:52–58. doi: 10.1016/j.solener.2017.01.031. [DOI] [Google Scholar]
- 48.Gupta GK, Dixit A. Theoretical studies of single and tandem Cu2ZnSn(S/Se)4 junction solar cells for enhanced efficiency. Opt. Mater. 2018;82:11–20. doi: 10.1016/j.optmat.2018.05.030. [DOI] [Google Scholar]
- 49.Islam MT, et al. Investigation of CsSn0.5Ge0.5I3-on-Si tandem solar device utilizing SCAPS simulation. IEEE Trans. Electron Devices. 2021;68:618–625. doi: 10.1109/TED.2020.3045383. [DOI] [Google Scholar]
- 50.Yang Y, et al. Comparison of recombination dynamics in CH3NH3PbBr 3 and CH3NH3PbI3 perovskite films: Influence of exciton binding energy. J. Phys. Chem. Lett. 2015;6:4688–4692. doi: 10.1021/acs.jpclett.5b02290. [DOI] [PubMed] [Google Scholar]
- 51.Wehrenfennig C, Eperon GE, Johnston MB, Snaith HJ, Herz LM. High charge carrier mobilities and lifetimes in organolead trihalide perovskites. Adv. Mater. 2014;26:1584–1589. doi: 10.1002/adma.201305172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pandey R, Saini AP, Chaujar R. Numerical simulations: Toward the design of 18.6% efficient and stable perovskite solar cell using reduced cerium oxide based ETL. Vacuum. 2019;159:173–181. doi: 10.1016/j.vacuum.2018.10.033. [DOI] [Google Scholar]
- 53.Green MA, Jiang Y, Soufiani AM, Ho-Baillie A. Optical properties of photovoltaic organic-inorganic lead halide perovskites. J. Phys. Chem. Lett. 2015;6:4774–4785. doi: 10.1021/acs.jpclett.5b01865. [DOI] [PubMed] [Google Scholar]
- 54.NREL. Best Research-Cell Efficiency Chart (1976 to the present), https://www.nrel.gov/pv/cell-efficiency.html (2020).
- 55.Jeong M, et al. Stable perovskite solar cells with efficiency exceeding 24.8% and 0.3-V voltage loss. Science. 2020;369:1615. doi: 10.1126/science.abb7167. [DOI] [PubMed] [Google Scholar]
- 56.Park N-G, Zhu K. Scalable fabrication and coating methods for perovskite solar cells and solar modules. Nat. Rev. Mater. 2020;5:333–350. doi: 10.1038/s41578-019-0176-2. [DOI] [Google Scholar]
- 57.Pandey R, Madan J, Sharma R. Enhanced charge extraction in metal–perovskite–metal back-contact solar cell structure through electrostatic doping: A numerical study. IEEE Trans. Electron Devices. 2021;68:1757–1763. doi: 10.1109/TED.2021.3057029. [DOI] [Google Scholar]
- 58.Mohammed MKA, Al-Mousoi AK, Mehde MS, Al-Gebori AM. Engineered electronic properties of the spin-coated MAPI for hole-transport-free perovskite solar cell (HT-free PSC): Spinning time and PSC performance relationship. Chem. Phys. Lett. 2020;754:137718. doi: 10.1016/j.cplett.2020.137718. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data (problem definition file of top and bottom cell, filtered spectrum, and script for tandem J–V curve) that support the findings of this study shall be made available from the corresponding author upon reasonable request.