Abstract
The degree of persistence in daily PM25 and O3 in the ten most populated US cities, namely New York, Los Angeles, Chicago, Houston, Phoenix, Philadelphia, San Antonio, San Diego, Dallas and San Jose is examined in this work. We employ a methodology based on fractional integration, using the order of integration as a measure of the degree of persistence. Using data for the time period from January 1, 2019 to December 31, 2020, our results indicate that fractional integration and long memory features are both present in all the examined cases, with the integration order of the series being constrained in the (0, 1) interval. Based on this, the estimation of the coefficients for the time trend produces results which are substantially different from those obtained under the I (0) assumption.
Keywords: Air pollutants, PM2.5, O3, Fractional integration, Long memory, Persistence
Air pollutants; PM2.5; O3; Fractional integration; Long memory; Persistence.
1. Introduction
Poor air quality can affect human health. We find suspended particles (PM2.5) and Ozone (O3) to be among the most harmful pollutants for health. The U.S. Environmental Protection Agency is increasingly concerned and is monitoring the increase of particulate matter or PM2.5 due to the confirmation of the risks they pose to health (EPA, 2002; Bell et al., 2007; Nowak et al., 2013; Feng et al., 2016; etc.). They can penetrate into the lungs, causing inflammation and a worsening of symptoms in patients with heart and lung disease. Moreover, they can carry carcinogenic compounds that could be adsorbed on the surface of the lungs. Likewise, Ozone, O3, irritates the airways of the lungs, increasing the symptoms of asthma and lung diseases. According to the U.S. Environmental Protection Agency, American Lung Association and other studies, Ozone is one of the most dangerous and least controlled pollutants in the U.S (Levy et al., 2005; Bell et al., 2015; Ito et al., 2005; Villeneuve et al., 2007; Mar and Koenig, 2009; EPA, 2013; etc.). The concern about the impact of both pollutants is confirmed by other recent studies in which they are analyzed together (Wang et al., 2019; Arter and Arunachalam, 2019). In this sense, the importance of investigating the dynamics of air pollution is clear in order to develop adequate models for prediction purposes and as a consequence to be able to design policies to manage air quality.1
Based on the above, the present work investigates the properties of the time series corresponding to daily data of PM2.5 and O3 on the ten most populated cities in the US, investigating its evolution across time. However, instead of using traditional methods which are based on a “good” I (0) behavior of the error term, we consider the possibility of long range dependence (or logn memory), which is a feature very often observed in environmental and climatological data.
The rest of the paper is organized as follows: Section 2 presents a short description of the atmospheric pollution and Section 3 features a literature review on the topic. The model and the methodology used in the paper are given in Section 4. Data and the empirical results are displayed in Section 5. Section 6 concludes the paper.
2. Atmospheric pollution
Suspended particles are a pollutant made up of liquid and solid material of very diverse composition and size, which are found in the air. Particles are a mixture of many kinds of pollutants, the product of a large number of natural and anthropogenic processes. The risk they constitute to health may be associated with their multiple physical and chemical characteristics, such as their number, size, shape, chemical composition and concentration. The origin of this pollutant includes combustion processes in vehicles, mainly those that use diesel, foundry industries, paints, ceramics and power plants. Erosion, dust pits, and forest fires are also a natural source of airborne particles (Mujica-Álvarez and Figueroa-Lar, 1996).
In recent years, greater attention has been paid to particles with a size smaller than one μm in diameter, which are known as the ultrafine fraction and to which a greater potential for damage seems to be attributed (EPA 2002; Lippmann, 1989; Rojas-Bracho and Garibay-Bravo, 2003).
Suspended particles have been associated with effects on the health of the population for more than fifty years, with the historical episodes of pollution that occurred in the Meuse Valley in Belgium, London and Donora in Pennsylvania, among others. These impacts have been corroborated with recent studies in more than 150 cities, with very diverse levels of pollution, even some below the air quality standards in force in different parts of the world. It is also known that there are population groups that can be especially sensitive to the adverse effects of particles, such as children, the elderly and people with chronic lung diseases and heart disease. The weight of scientific evidence from toxicological and epidemiological studies carried out in recent years suggests that the fine fraction, from high-temperature combustion processes, may be the most relevant in terms of adverse effects on health and possibly also ultrafine (which may contain sulfates, nitrates, strong acids, etc.), since by penetrating to the lower respiratory tract and reaching the alveoli, they can trigger inflammatory reactions.
It should be mentioned that there is also evidence on the possible effect on health of particles of geological origin and/or the coarse fraction, which could be of a similar magnitude to that reported for the fine fraction (Ostro et al., 1999; Castillejos et al., 2000). Recent studies carried out in cities in Europe, the United States and the rest of America report the possible health effects of suspended particles, such as increases in mortality rates and cytotoxic and genotoxic effects. At the same time, the World Health Organization (WHO) in its publication of the "Guide Values" for health protection, indicates the preference for the use of PM2.5 as an indicator value of air quality in large cities compared to values based on the atmospheric concentrations of PM10. The main argument in favor of the use of this new indicator is based on the fact that the current values of PM10 can be greatly influenced because in some areas there is less precipitation and ventilation than in other parts, conditioning thus the results obtained.
Another major air pollutant is ozone (O3). It is a gas molecule made up of three atoms of oxygen. Ozone pollution forms in the atmosphere when gases from exhaust pipes, smokestacks, gas, oil extraction and other sources react in the presence of sunlight. The gases that transform and form ozone are volatile organic compounds, carbon monoxide and nitrogen oxides.
Ozone levels generally rise between May and October when temperatures are higher, sunlight is greater, and static atmospheric conditions transform air pollutants into ozone. It acts as a powerful irritant of the respiratory system. Independent scientists and the United States Environmental Protection Agency (EPA) concluded that pollution caused by ozone represents a serious threat to health.
Accordingly, recent studies that have analyzed the effect of the pandemic associated with SARS-CoV-2 and the confinement adopted worldwide, on the reduction of activity in cities, have revealed positive consequences on emissions of pollutant gases and particles, atmospheric pollution, air quality and, as a consequence, an improvement in the urban health indices and in the awareness of the population in this regard (Cole et al., 2020; Brimblecombe and Lai, 2020). These papers show that the confinement of the population influenced human behavior, in terms of movements of people and goods or the use of telephones and the internet, but they also show that it cannot be said that this change in behavior has had the same positive effect on the decrease in emissions for all pollutants. The fundamental decrease has occurred in those related to emissions associated with traffic and the use of fossil fuels. However, the effects on PM10 particles were short-term and not statistically significant, as they were for SO2, closely related, in this case, to the low temperatures in the area and the dependence on coal-fired power plants. From these studies it is deduced that the specific study of the evolution of the different pollutants with negative effects on health and their possible control is relevant.
3. Literature review
Numerous institutions from different countries and innumerous works have analyzed the connection between pollution and harmful effects on health (Schwartz and Marcus, 1990; Anderson et al., 1996; Atkinson et al., 1999; Gardner and Dorling, 1999; etc.). In this sense, the importance of investigating the dynamics of air pollution in order to develop adequate models for prediction purposes and design policies to manage air quality is clear. Therefore, it is extremely important to systematically monitor fine particles and to define as soon as possible an air quality standard for their concentration in the environment in order to protect the health of the population (Anderson et al., 1996; Cohen et al., 1997; Romieu and Borja-Aburto, 1997; Atkinson et al., 1999; Gardner and Dorling, 1999; Lacasaña-Navarro et al., 1999; Borja-Aburto, 2000; Arribas-Monzón et al., 2001; Dharshana et al., 2010; Arista et al., 2012; Ikeda and Tanimoto, 2015; Shaharaiyni and Sodoudi, 2016; Khuluse, 2017; Nhung et al., 2018; Nguyen et al., 2020; Kaneyasu et al., 2020; etc.).
The present work contributes to another line of the research literature that focuses instead on the modelling of various pollutants such as ozone (O3) and particulate matter (PM2.5). Notable studies in this regard include, for example Zamri et al. (2009), which used the ARIMA approach developed in Box and Jenkins (1976) to model various pollutants in Malaysia, finding a significant upward trend in the data. Li et al. (2017) analysed the quality of air in Beijing for the time period from 2014 to 2016 using various models such as the time-delay neural network (TDNN) model, the spatio-temporal deep learning (STDL) model, the ARMA model, the support vector regression (SVR) model and the extended long-term memory neural network (LSTME) model. After careful consideration of the different models, they came to the conclusion that the LSTME model was the most appropriate one for air pollutant series characterized by long memory with optimal time lags.
Naveen and Anu (2017) examined the quality of the air in India using ARIMA, seasonal ARIMA (SARIMA) and other models. Pan and Chen (2008) is one of the few studies using ARFIMA models for air pollution data (in Taiwan). They conclude by explaining that these are more accurate than the classical ARIMA models.
Morel et al. (1999) derive an expression for the statistical distribution of the air pollutant concentrations in Santiago de Chile based on the inverse gamma distribution. According to them, it corresponds to the stationary distribution of a stochastic process, relating emission level to air pollutant concentrations. Nevertheless, Steinfeld and Pandis (1998) conclude that there is no a priori reason for the atmospheric distribution to adhere to a specific probability distribution.
We adopt in this paper a long-memory methodology that uses fractional integration. Long memory (or long range dependence) is a feature of the data that is characterized by a high level of dependence between values which are far apart in time. This property has been found to be present in many series in different disciplines such as finance and economics (Gil-Alana and Moreno, 2012; Abritti et al., 2017; Kalemkerian and Sosa, 2020; Murialdo et al., 2020; Qiu et al., 2020); climatology and meteorology (Gil-Alana, 2005; 2008; 2017; Vyushin and Kushner, 2009; Efstathiou and Varotsos, 2010, 2012; Franzke, 2012; Ludescher et al., 2016; Varotsos et al., 2016; Bunde, 2017; Yuan et al., 2019; Varotsos and Mazei, 2019; Bruneau et al., 2020; etc.), but also in environmental sciences (Barros et al., 2016; Tiwari et al., 2016; Gil-Alana and Solarin, 2018; Gil-Alana and Trani, 2019; Xayasouk et al., 2020). Recent studies using fractional integration in atmospheric pollution include among others the papers by Gil-Alana et al. (2020) and Caporale et al. (2021).
4. Persistence and fractional integration
Persistence is a common feature observed in time series data and there are many ways of modelling this behavior. A standard approach is to consider an AR (1) process and using its coefficient as a measure of persistence. In a more general context, the sum of the AR coefficients in a general AR(p) model is another approach. Nevertheless, both measures assume that the error term displays a short memory (also termed I (0)) behavior, a feature that is not always observed in environmental data. In fact, as mentioned in the above section, many series in environmental studies display a long memory pattern, which is characterized because the spectral density function explodes at the zero frequency. There are many models to explain such a feature, but one which is very popular among econometricians is that based on fractional integration or I(d) models where the parameter d indicates the order of differentiation and can be a fractional positive value.
We say that a time series follows an I(d) model if after taking its d-differences, the series becomes I (0) or short memory; that is, xt is said to be I(d) if it can be expressed as:
| (1) |
where L is the lag-operator and ut is integrated of order 0 or I (0). Then, if the differencing parameter d is positive, xt displays the property of long memory in the sense that the observations are highly dependent in time even if they are far distant, and the higher the value of d is, the higher the level of association between the observations is.
On the other hand, we are interested in the evolution of the series across time and a classical approach here is to consider a linear time trend model of the form:
| (2) |
where yt represents the observed data, and α and β are the unknown coefficients referring respectively to an intercept and a (linear) time trend. Table 1 displays the estimates of these coefficients for the two contaminants, PM2.5 and O3, under the assumption that ut in (1) is I (0) in the ten most populated US cities. We observe that for O3, (in the lower part of the table) all the slope coefficients are significantly negative, while for PM2.5 (upper part) the results are mixed: we obtain negative coefficients for three cities (New York, Chicago and San Antonio); insignificant coefficients in other two (Philadelphia and Dallas), and positive slopes for the remaining five cities.
Table 1.
Time trend coefficients imposing of I (0) errors.
| Cities | Intercept (t-value) | Time trend (t-value) |
|---|---|---|
| PM2.5 | ||
| New York | 30.9524 (32.26) | -0.0061 (-2.73) |
| Los Angeles | 37.8394 (30.37) | 0.0291 (10.03) |
| Chicago | 37.3968 (37.90) | -0.0087 (-3.81) |
| Houston | 34.1410 (34.96) | 0.0056 (2.47) |
| Phoenix | 22.4217 (26.06) | 0.0163 (8.13) |
| Philadelphia | 33.9824 (71.91) | --- |
| San Antonio | 36.4289 (32.43) | -0.0051 (-1.96) |
| San Diego | 32.4697 (27.26) | 0.0393 (10.92) |
| Dallas | 31.5704 (67.37) | --- |
| San Jose |
22.5715 (15.77) |
0.0263 (7.90) |
| O3 | ||
| New York | 25.2283 (38.45) | -0.0099 (-6.45) |
| Los Angeles | 17.8609 (33.58) | -.0.0033 (-2.68) |
| Chicago | 24.5890 (41.64) | -0.0039 (-2.84) |
| Houston | 20.2559 (37.50) | -0.0035 (-2.76) |
| Phoenix | 22.1075 (38.43) | -0.0041 (-3.04) |
| Philadelphia | 26.1255 (47.23) | -0.0074 (-5.73) |
| San Antonio | 22.1853 (40.31) | -0.0013 (-2.03) |
| San Diego | 25.5370 (36.51) | -0.0134 (-6.46) |
| Dallas | 23.5210 (45.73) | -0.0036 (-3.05) |
| San Jose | 21.8166 (50.26) | -0.0058 (-5.72) |
According to these results, it seems that the O3 emissions have been reducing across time, and the same has been happening with PM2.5 in at least three cities. The results displayed in Table 1, however, might be biased if the disturbances, xt in (2) is not an I (0) process. Thus, what we do in the following section is to estimate a more general model, combining both Eqs. (1) and (2) in a single framework, That is,
| (3) |
where ut is now I (0) and will be specified in terms of both uncorrelated (white noise) and autocorrelated errors. The estimation here is based on the Whittle function (an approximation to the likelihood function) expressed in the frequency domain (Dahlhaus, 1989) and uses a simple version of a testing procedure described in Robinson (1994) that will be very appropriate in our series since it does not discriminate between stationary (d < 0.5) and nonstationary (d ≥ 0.5) data.
Alternative methods in the analysis of long range dependence (long memory) in various pollutants (including ozono and Particular Matters) have been examined for example in Varotsos, Ondov and Efstathiou (2005) and Varotsos and Kirk-Davidoff (2006), in both cases using Detrended Fluctuation Analysis (DFA). We differ from those papers in our modelization which is based on a parametric model using fractional integration.
HEMENDIK AURRERA
5. Data and empirical results
The series correspond to the air quality (daily average) obtained from the World Air Quality Index (WAQI) at https://aqicn.org/map/world/es/. All data have been converted using the US EPA standard (United States Environmental Protection Agency). We focus on data at a daily frequency for the past 2 years (2019–2020) at https://aqicn.org/data-platform/covid19/corresponding to the 10 most populous cities in the United States: New York, Los Angeles, Chicago, Houston, Phoenix, Philadelphia, San Antonio, San Diego, Dallas and San Jose. The series are based on the measurement of PM2.5 microparticles and ozone (O3) measured in micrograms per cubic meter of air (μg/m3). The WAQI data come from the following sources: New York - New York State Department of Environmental Conservation (NYSDEC): www.dec.ny.gov/; Chicago - Illinois Environmental Protection Agency: www.epa.illinois.gov/; Philadelphia - Bureau of Air Quality, Pennsylvania's Department of Environmental Protection: www.dep.pa.gov/; Los Angeles - California Air Resources Board: www.arb.ca.gov/; Houston - Texas Commission on Environmental Quality (TCEQ): www.tceq.texas.gov/; Phoenix - Arizona Department of Environmental Quality - Air Quality Division: www.azdeq.gov/; San Antonio - Texas Commission on Environmental Quality (TCEQ): www.tceq.texas.gov/; Dallas - Texas Commission on Environmental Quality (TCEQ): www.tceq.texas.gov/; San Diego - California Air Resources Board: www.arb.ca.gov/; San Jose - California Air Resources Board: www.arb.ca.gov/.
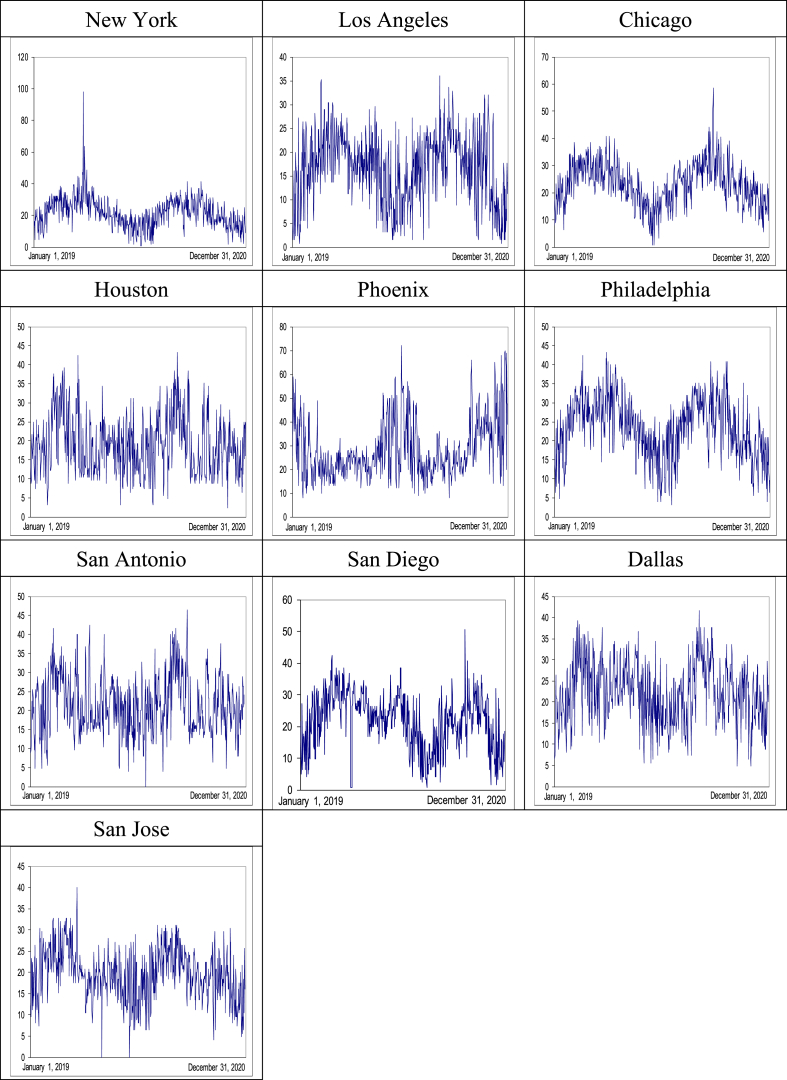
Figures 1 and 2 display respectively the time series plots of PM2.5 and O3 in the ten most populated US cities. We observe a similar pattern in all cases, with some outliers in some of the series.2
Figure 1.
Time series plots: PM2.5.
Figure 2.
Time series plots: O3.
Table 2 presents the estimated values of d (and their 95% confidence band) in a model given by Eq. (3) for the PM2.5 (upper part) and O3 (lower part), under the assumption that the error term in equation (3), i.e., ut, is a white noise process. Thus, all the time dependence in the data is described through the differentiation parameter d. In Table 3, however, we allow for autocorrelated disturbances by means of using the approach developed in Bloomfield (1973) that approximates ARMA structures with very few parameters. In both cases, we consider three potential set-ups for the deterministic terms. Thus, we report in the second column of the tables the case where α = β = 0 in (3), that is, assuming that there are no deterministic terms; the third column refers to the case of a model with a constant (i.e., imposing β = 0 in (3)), while the last column refers to the model with a constant and a linear time trend (i.e., α and β are estimated from the data along with d).
Table 2.
Estimates of differencing parameter (d): White noise disturbances.
| No regressors | A constant | A linear time trend | |
|---|---|---|---|
| PM2.5 | |||
| New York | 0.49 (0.43, 0.57) | 0.43 (0.36, 0.52) | 0.43 (0.36, 0.52) |
| Los Angeles | 0.69 (0.61, 0.79) | 0.67 (0.59, 0.77) | 0.67 (0.59, 0.77) |
| Chicago | 0.55 (0.48, 0.65) | 0.49 (0.40, 0.60) | 0.49 (0.40, 0.60) |
| Houston | 0.46 (0.40, 0.55) | 0.44 (0.36, 0.53) | 0.44 (0.36, 0.53) |
| Phoenix | 0.59 (0.52, 0.66) | 0.55 (0.48, 0.63) | 0.55 (0.48, 0.63) |
| Philadelphia | 0.51 (0.45, 0.59) | 0.45 (0.37, 0.54) | 0.45 (0.37, 0.54) |
| San Antonio | 0.47 (0.41, 0.55) | 0.45 (0.38, 0.53) | 0.45 (0.37, 0.53) |
| San Diego | 0.62 (0.53, 0.72) | 0.59 (0.50, 0.70) | 0.59 (0.50, 0.70) |
| Dallas | 0.50 (0.43, 0.57) | 0.47 (0.40, 0.55) | 0.47 (0.40, 0.55) |
| San Jose |
0.74 (0.65, 0.85) |
0.73 (0.64, 0.84) |
0.73 (0.64, 0.84) |
| O3 | |||
| New York | 0.43 (0.39, 0.48) | 0.39 (0.35, 0.44) | 0.39 (0.35, 0.44) |
| Los Angeles | 0.41 (0.37, 0.47) | 0.38 (0.34, 0.44) | 0.38 (0.34, 0.44) |
| Chicago | 0.48 (0.44, 0.53) | 0.43 (0.38, 0.48) | 0.43 (0.38, 0.48) |
| Houston | 0.54 (0.48, 0.62) | 0.50 (0.43, 0.59) | 0.50 (0.43, 0.59) |
| Phoenix | 0.55 (0.51, 0.61) | 0.53 (0.49, 0.59) | 0.54 (0.49, 0.59) |
| Philadelphia | 0.49 (0.45, 0.54) | 0.44 (0.39, 0.49) | 0.44 (0.39, 0.49) |
| San Antonio | 0.56 (0.50, 0.64) | 0.53 (0.46, 0.61) | 0.53 (0.46, 0.61) |
| San Diego | 0.47 (0.42, 0.53) | 0.43 (0.38, 0.49) | 0.43 (0.38, 0.49) |
| Dallas | 0.51 (0.46, 0.58) | 0.46 (0.40, 0.53) | 0.46 (0.40, 0.53) |
| San Jose | 0.48 (0.44, 0.54) | 0.40 (0.35, 0.47) | 0.40 (0.35, 0.47) |
In parenthesis, the 95% confidence bands of the non-rejection values of d. In bold, the selected model for each series.
Table 3.
Estimates of the differencing parameter (d): Autocorrelated disturbances.
| No regressors | A constant | A linear time trend | |
|---|---|---|---|
| PM2.5 | |||
| New York | 0.30 (0.23, 0.37) | 0.19 (0.14, 0.26) | 0.19 (0.13, 0.26) |
| Los Angeles | 0.35 (0.26, 0.44) | 0.32 (0.26, 0.41) | 0.30 (0.23, 0.39) |
| Chicago | 0.24 (0.15, 0.34) | 0.10 (0.03, 0.19) | 0.06 (-0.01, 0.17) |
| Houston | 0.20 (0.08, 0.31) | 0.16 (0.10, 0.25) | 0.16 (0.09, 0.25) |
| Phoenix | 0.41 (0.34, 0.49) | 0.35 (0.30, 0.43) | 0.35 (0.29, 0.41) |
| Philadelphia | 0.30 (0.22, 0.40) | 0.16 (0.09, 0.25) | 0.15 (0.09, 0.25) |
| San Antonio | 0.28 (0.20, 0.38) | 0.23 (0.15, 0.29) | 0.23 (0.15, 0.29) |
| San Diego | 0.30 (0.18, 0.45) | 0.31 (0.23, 0.40) | 0.23 (0.12, 0.38) |
| Dallas | 0.30 (0.20, 0.40) | 0.24 (0.16, 0.33) | 0.24 (0.16, 0.33) |
| San Jose |
0.28 (0.22, 0.37) |
0.30 (0.23, 0.38) |
0.28 (0.20, 0.37) |
| O3 | |||
| New York | 0.45 (0.41, 0.51) | 0.40 (0.35, 0.45) | 0.39 (0.35, 0.45) |
| Los Angeles | 0.37 (0.31, 0.43) | 0.32 (0.27, 0.38) | 0.32 (0.27, 0.38) |
| Chicago | 0.45 (0.39, 0.51) | 0.37 (0.33, 0.44) | 0.37 (0.33, 0.44) |
| Houston | 0.35 (0.27, 0.42) | 0.25 (0.19, 0.33) | 0.24 (0.19, 0.32) |
| Phoenix | 0.50 (0.45, 0.56) | 0.47 (0.42, 0.54) | 0.47 (0.42, 0.54) |
| Philadelphia | 0.47 (0.43, 0.53) | 0.39 (0.34, 0.45) | 0.39 (0.34, 0.45) |
| San Antonio | 0.43 (0.35, 0.51) | 0.32 (0.23, 0.41) | 0.31 (0.23, 0.42) |
| San Diego | 0.42 (0.36, 0.49) | 0.36 (0.30, 0.42) | 0.35 (0.29, 0.42) |
| Dallas | 0.42 (0.36, 0.50) | 0.31 (0.24, 0.38) | 0.31 (0.24, 0.38) |
| San Jose | 0.41 (0.35, 0.47) | 0.27 (0.23, 0.34) | 0.27 (0.22, 0.33) |
In parenthesis, the 95% confidence bands of the non-rejection values of d. In bold, the selected model for each series.
We start describing the results for the case based on white noise errors, and the first noticeable issue is that the coefficient for the time trend is not required in any single case, a constant being sufficient in all series to describe the deterministic part. Focusing on the estimated orders of integration, we observe that in all cases, the values of d are constrained between 0 and 1, supporting the hypothesis of fractional integration. Thus, for the PM2.5 data, the values of d range between 0.43 (New York) and 0.73 (San Jose). For the O3, the lowest d corresponds to Los Angeles (0.38) and the highest to Phoenix and San Jose (with an estimated d-value equal to 0.53). These results, however, do not take into account any structure on the error term. Thus, in Table 3, we permit autocorrelation for ut in (3).
We notice in Table 3 is that the time trend coefficient is found to be significant at the 5% level in a number of cases, in particular, for Los Angeles, Chicago, San Diego and San Jose with the PM2.5 data, and also for San Jose with the O3 data. In Table 4 we report the estimated coefficients for each series based on the results from Table 3. We see that the trend is positive for Los Angeles, San Diego and San Jose in the case of the PM2.5, but negative for Chicago with PM2.5 and for San Jose with O3. Focusing on d, the values are generally lower for PM2.5, ranging from 0.06 (in Chicago), 0.16 (Philadelphia and Houston) and 0.19 (New York) to 0.28 in San Jose and 0.30 in Los Angeles.3 For O3, the lowest d corresponds to Houston (0.25) and the highest one to Phoenix (0.47), and the estimates of d are significantly positive in all cases.
Table 4.
Estimated coefficients from the results in Table 3.
| No regressors | A constant | A linear time trend | |
|---|---|---|---|
| PM2.5 | |||
| New York | 0.19 (0.14, 0.26) | 29.4995 (23.47) | --- |
| Los Angeles | 0.30 (0.23, 0.39) | 40.2009 (11.37) | 0.0259 (3.20) |
| Chicago | 0.06 (-0.01, 0.17) | 37.3689 (33.94) | -0.0085 (-3.39) |
| Houston | 0.16 (0.10, 0.25) | 35.7809 (32.87) | --- |
| Phoenix | 0.35 (0.30, 0.43) | 31.90286 (13.11) | --- |
| Philadelphia | 0.16 (0.09, 0.25) | 34.2519 (34.70) | --- |
| San Antonio | 0.23 (0.15, 0.29) | 33.9031 (19.17) | --- |
| San Diego | 0.23 (0.12, 0.38) | 34.5906 (12.80) | 0.0344 (4.38) |
| Dallas | 0.24 (0.16, 0.33) | 30.9069 (18.97) | --- |
| San Jose |
0.28 (0.20, 0.37) |
24.8705 (7.22) |
0.0225 (19.17) |
| O3 | |||
| New York | 0.40 (0.35, 0.45) | 20.0441 (8.54) | --- |
| Los Angeles | 0.32 (0.27, 0.38) | 15.1218 (10.70) | --- |
| Chicago | 0.37 (0.33, 0.44) | 20.9926 (11.51) | --- |
| Houston | 0.25 (0.19, 0.33) | 18.7393 (21.27) | --- |
| Phoenix | 0.47 (0.42, 0.54) | 16.6715 (7.48) | --- |
| Philadelphia | 0.39 (0.34, 0.45) | 21.3001 (11.23) | --- |
| San Antonio | 0.32 (0.23, 0.41) | 20.8923 (15,73) | --- |
| San Diego | 0.36 (0.30, 0.42) | 20.2442 (10.67) | --- |
| Dallas | 0.31 (0.24, 0.38) | 21.0930 (16.74) | --- |
| San Jose | 0.27 (0.22, 0.33) | 21.2655 (16.47) | -0.0054 (-1.85) |
As a conclusion, we first observe that long memory or long range dependence is present in all series, with positive orders of integration in all cases examined. Thus, the hypothesis of I (0) or short memory behavior is decisively rejected in all cases. An interesting exercise is to compare the time trend coefficients under the (statistically rejected) assumption of I (0) errors (in Table 1) with those based on long memory and autocorrelated errors (in Table 4). Starting with the results for PM2.5, we observe that under I (0) errors, significant negative coefficients are found in San Antonio, New York and Chicago; insignificant coefficients for Philadelphia and Dallas, and positive ones for Houston, Phoenix, San Jose, Los Angeles and San Diego. Looking now at the results based on I(d) models, in Table 4, we observe that there is only one negative significant coefficient (Chicago); insignificant coefficients are found in six cities (New York, Houston, Phoenix, Philadelphia, San Antonio and Dallas) and three cities with positive time trends (San Jose, Los Angeles and San Diego).
The results for O3 are even more interesting. Under the (wrong) I (0) assumption, significant negative time trend coefficients are observed in all cases. However, estimating d rather than imposing it to be 0 produced insignificant coefficients in all except one city (San Jose). Thus, the conclusion that O3 emissions display a significant negative trend is seriously questioned when a long memory component is allowed in the data.
The fact that in all cases the estimates of the differencing parameter are in the interval (0, 1) implies that exogenous shocks in the series will have transitory effects, and will disappear by themselves in the long run though with long lasting effects, being longer the higher the value of d is. Thus, in the event of a positive shock, reducing the number of emissions, strong policy actions should be required to maintain the series at the new (lower) levels. On the contrary, if the shock is negative, though slowly, the series will recover by itself in the long run.
The persistence and long memory property in time series is usually associated with the aggregation of heterogeneous individual processes (see, e.g., Robinson, 1978; Granger, 1980; Parke, 1999; Souza and Smith, 2002; Souza, 2005, 2007; Hassler, 2011; Shi and Sun, 2016; etc.). However, in the case of air pollution there are additional factors such as sociological persistence (related to the COVID-19 lockdown, see, e.g., Cole et al., 2020 and Brimblecombe and Lai, 2020) and this may have an influence on the high degree of dependence observed in the data.
6. Conclusions
In this paper we have examined the degree of persistence in the daily levels of PM2.5 and O3 in the ten most populated cities in the US. For this purpose, we have employed a model that allows for time trends and where the detrended series may display a long memory pattern. Our results using fractional integration decisively reject the hypothesis of I (0) or short memory behavior, and testing simultaneously the existence of time trends and long memory produces results which substantially differ from those based on a model that imposes a degree of integration equal to 0. Thus, for example, for the case of O3, the results based on the classical I (0) assumption indicate the existence of negative time trends, which may indicate a continuous reduction in the O3 emissions across time; however, allowing for a fractional degree of integration, the I (0) hypothesis is rejected, and estimating the time trends under the I(d) specification, the coefficients are found to be statistically insignificant in nine out of the ten cities examined. Nevertheless, erroneous inference of long range dependence may also be the case due to various reasons such as incomplete data analysis, abrupt events or scaling behavior. In addition, the presence of non-linear structures or structural breaks may also produce spurious evidence of long memory. Thus, further results based on this methodology should be conducted to corroborate the present results in these and in other cities all over the world.
Declarations
Author contribution statement
Lorenzo Bermejo: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Luis A. Gil-Alana: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Marta del Rio: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
Luis A. Gil-Alana was supported by Ministerio de Economía, Industria y Competitividad (MINEIC-AEI-FEDER PID2020-113691RB-I00), Agencia Estatal de Investigación (AEI) Spain, Fondo Europeo de Desarrollo Regional (FEDER) and Projects of the Universidad Francisco de Vitoria.
Data availability statement
Data will be made available on request.
Declarations of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Footnotes
There are other pollutants which are not photochemical and that are direclty linked to primary precursors such as Carbon Monoxide or NOx. The choice of PM2.5 and O3 for this paper is based on data availability for the 10 cities examined.
Removing these outliers did not modify the main conclusions reported in this work.
For the case of Chicago, the null hypothesis of short memory (i.e., I(0)) cannot rejected at the 5% significance level.
References
- Abritti M., Gil-Alana L.A., Lovcha Y., Moreno A. Term structure persistence. J. Financ. Econom. 2017;14:331–352. [Google Scholar]
- Arista F., Saraswati R., Wibowo A. 2012. Spatial Modelling of Particular Matter 10 Distribution in Bndung City, IOP Conference Series: Earth and Environmental Science. [Google Scholar]
- Arribas-Monzón F., Rabanaque M.J., Martos M.C., Abad M.J., Alcalá-Nalvaiz T., Navarro-Elipe M. Effects of the environmental pollution on the daily mortality rate in the city of Zaragoza, Spain 1991-1995. Salud Publica Mex. 2001;43:289–297. [PubMed] [Google Scholar]
- Arter C.A., Arunachalam S. Assessing the importance of nonlinearity for aircraft emissions' impact on O3 and PM2.5. Sci. Total Environ. 2019;777:146121. [Google Scholar]
- Barros C.P., Gil-Alana L.A., Perez de Gracia F. Evidence from disaggregated data, Environmental and Resources Economics. Vol. 63. 2016. Stationarity and long range dependence of carbon dioxide emissions; pp. 45–56. 1. [Google Scholar]
- Bell M.L., Dominici F., Ebisu K., Zeger S.L., Samet J.M. Spatial and temporal variation in PM2.5 chemical composition in the United States for health effects studies. Environ. Health Perspect. 2007;115(7):989–995. doi: 10.1289/ehp.9621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell M.L., Dominici F., Samet J.M. A meta-analysis of time-series studies of ozone and mortality with comparison to the National Morbidity, Mortality, and Air Pollution Study. Epidemiology. 2015;16:436–445. doi: 10.1097/01.ede.0000165817.40152.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield P. An exponential model in the spectrum of a scalar time series. Biometrika. 1973;60:217–226. [Google Scholar]
- Borja-Aburto V.H. Vol. 42. Salud Pública de México; 2000. Ecological Studies; pp. 533–538. [PubMed] [Google Scholar]
- Box G.E.P., Jenkins G.M. Holden Day; San Francisco: 1976. Time Series Analysis: Forecasting and Control. [Google Scholar]
- Brimblecombe P., Lai Y. Effect of sub-urban scale lockdown on air pollution in Beijing. Urban Clim. 2020;34:100725. [Google Scholar]
- Bruneau N., Wang S., Toumi R. Long memory impact of ocean mesoscale temperature anomalies on tropical cyclone size. Geophys. Res. Lett. 2020;47:6. [Google Scholar]
- Bunde A. In: Chapter 11 in Nonlinear and Stochastic Climate Dynamics. Franzke Christian L.E., O’Kane Terence., editors. Cambridge University Press; 2017. Long-term memory in climate: detection, extreme events and significance of trends. [Google Scholar]
- Caporale G.M., Gil-Alana L.A., Carmona N. Particular matter PM10. Persistence and trends in eight European capitals. Air Qual. Atmos. Health. 2021;14:1097–1102. [Google Scholar]
- Castillejos N., Borja-Aburto V., Dockery D.W., Loomis D. Coarse particles and mortality in Mexico City. Inhal. Toxicol. 2000;12(Suppl. 1):61–72. [Google Scholar]
- Cohen A.J., Pope A., Speizer F.E. Ambient air pollution as a risk factor for lung cancer. Salud Publica Mex. 1997;39:346–355. doi: 10.1590/s0036-36341997000400012. [DOI] [PubMed] [Google Scholar]
- Cole M.A., Elliott R.J.R., Liu B. The impact of the Wuhan Covid-19 lockdown on air pollution and health: a machine learning and augmented synthetic control approach. Environ. Resour. Econ. 2020;76(4):553–580. doi: 10.1007/s10640-020-00483-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahlhaus R. Efficient parameter estimation for self-similar processes. Ann. Stat. 1989;17:1749–1766. [Google Scholar]
- Dharshana K.G., Kravtsov S., Kahl J.D.W. Relationship between synoptic weather disturbances and particulate matter air pollution over the United States. J. Geophys. Res. 2010;115(D24) [Google Scholar]
- Efstathiou M.N., Varotsos C. On the altitude dependence of the temperature scaling behaviour at the global troposphere. Int. J. Rem. Sens. 2010;31(2):343–349. [Google Scholar]
- Efstathiou M.N., Varotsos C. Intrinsic properties of Sahel precipitation anomalies and rainfall. Theor. Appl. Climatol. 2012;109(3):627–633. [Google Scholar]
- EPA . 2002. Third External Review Draft of Air Quality Criteria for Particulate Matter. Air Quality Criteria for Particulate Matter. Vol. I Y II. EPA/600/P-99/002aC. [Google Scholar]
- EPA 2013 . U.S. Environmental Protection Agency; Washington, DC: 2013. Integrated Science Assessment of Ozone and Related Photochemical Oxidants (Final Report) EPA/600/R-10/076F. [Google Scholar]
- Feng S., Gao D., Liao F., Zhou F., Wang X. The health effects of ambient PM2.5 and potential mechanisms. Ecotoxicol. Environ. Saf. 2016;128:67–74. doi: 10.1016/j.ecoenv.2016.01.030. [DOI] [PubMed] [Google Scholar]
- Franzke C. Nonlinear trends, long-range dependence, and climate noise properties of surface temperature. J. Clim. 2012;25(12):4172–4183. [Google Scholar]
- Gil-Alana L.A. Statistical modeling of the temperatures in the Northern hemisphere using fractional integration techniques. J. Clim. 2005;27(10):3477–3491. [Google Scholar]
- Gil-Alana L.A. Time trend estimation with breaks in temperature series. Climatic Change. 2008;89(3):325–337. [Google Scholar]
- Gil-Alana L.A. Alternative modeling approaches for the ENSO time series. Persistence and seasonality. Int. J. Climatol. 2017;37(5):2354–2363. [Google Scholar]
- Gil-Alana L.A., Moreno A. Uncovering the US term premium. An alternative route. J. Bank. Finance. 2012;36(4):1181–1193. [Google Scholar]
- Gil-Alana L.A., Solarin S.A. Have US environmental policies been effective in the reduction of US emissions? A new approach using fractional integration. Atmos. Pollut. Res. 2018;9(1):53–60. [Google Scholar]
- Gil-Alana L.A., Trani T. Time trends and persistence in the global CO2 emissions across Europe. Environ. Resour. Econ. 2019;73:213–328. [Google Scholar]
- Gil-Alana L.A., Yaya O., Awolaja O., Cristofaro L. Long memory and time trends in PM pollution in US states. J. Appl. Meteorol. Climatol. 2020;59(8):1351–1367. [Google Scholar]
- Granger C.W.J. Long memory relationships and the aggregation of dynamic models. J. Econom. 1980;14:227–238. [Google Scholar]
- Hassler U. Estimation of fractional integration under temporal aggregation. J. Econom. 2011;162:240–247. [Google Scholar]
- Ikeda K., Tanimoto H. Exceedances of air quality standard level of PM2.5 in Japan caused by Siberian wildfires. Environ. Res. Lett. 2015;10:105501. [Google Scholar]
- Ito K., De Leon S.F., Lippmann M. Associations between ozone and daily mortality: analysis and meta-analysis. Epidemiology. 2005;16:446–457. doi: 10.1097/01.ede.0000165821.90114.7f. [DOI] [PubMed] [Google Scholar]
- Kaneyasu N., Ishidoya S., Terao Y., Mizuno Y., Sugawar H. Estimation of PM2.5 emission sources in the tokyo metropolitan area by simultaneous measurements of particle elements and oxidative ratio in air. ACS Earth Space Chem. 2020;4(2):297–304. [Google Scholar]
- Kalemkerian J., Sosa A. Vol. 7. American Institute of Mathematical Sciences; 2020. Long-range Dependence in the Volatility of Returns in Uruguayan Sovereign Debt Índices; pp. 225–237. 3. [Google Scholar]
- Khuluse S.A. University of Twente; 2017. Spatial Statistical Modelling of Urban Particular Matters. Dissertation, Ph. D. Thesis. [Google Scholar]
- Lacasaña-Navarro M., Aguilar-Garduño C., Romieu I. Evolution of the air poullution and the impact on control programmes in three Latin American cities. Salud Publica Mex. 1999;41:203–215. [PubMed] [Google Scholar]
- Levy J.I., Chermerynski S.M., Sarnat J.A. Ozone exposure and mortality: an empiric Bayes metaregression análisis. Epidemiology. 2005;16:458–468. doi: 10.1097/01.ede.0000165820.08301.b3. [DOI] [PubMed] [Google Scholar]
- Li X., Peng L., Yao X., Cui S., Hi Y., Chi T. Long short-term memory neural network for air pollutant concentration predictions: method development and evaluation. Environ. Pollut. 2017;231(Part 1):997–1004. doi: 10.1016/j.envpol.2017.08.114. [DOI] [PubMed] [Google Scholar]
- Ludescher J., Bunde A., Franzke C.L., Schellnhuber H.J. Long-term persistence enhances uncertainty about anthropogenic warming of Antarctica. Clim. Dynam. 2016;46(1–2):263–271. [Google Scholar]
- Mar T.F., Koenig J.Q. Relationship between visits to emergency departments for asthma and ozone exposure in greater Seattle, Washington. Annals Allergy, Asthma Immunol. 2009;103(Issue 6):474–479. doi: 10.1016/S1081-1206(10)60263-3. [DOI] [PubMed] [Google Scholar]
- Morel B., Yeh S., Cifuentes L. Statistical distributions for air pollution applied to the study of the particulate problem in Santiago. Atmos. Environ. 1999;33(16):2575–2585. [Google Scholar]
- Mujica-Álvarez V., Figueroa-Lar J. UAM-Azcapotzalco; México: 1996. Causes and Control of Environmental Pollution. [Google Scholar]
- Murialdo P., Ponta L., Carbone A. Long-range dependence in financial markets: a moving average cluster entropy approach. Entropy. 2020;22(6):634. doi: 10.3390/e22060634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naveen V., Anu N. Time series analysis to forecast air quality indices in Thiruvananthapuram District, Kerala, India. Int. J. Eng. Res. Afr. 2017;7(6):66–84. [Google Scholar]
- Nguyen T.H., Nagashima T., Doan Q.V. Air quality modeling study on the controlling factors of fine particulate matter (PM2.5) in Hanoi: a case study in December 2010. Atmosphere. 2020;11(7):733. [Google Scholar]
- Nhung N.T.T., Schindler C., Dien T.M., Probst-Hensch, Perez N.L., Kunzli N. Acute effects of ambient air pollution on lower respiratory infections in Hanoi children: an eight year time series study. Environ. Int. 2018;110:139–148. doi: 10.1016/j.envint.2017.10.024. [DOI] [PubMed] [Google Scholar]
- Nowak D.J., Hirabayashi S., Bodine A., Hoehn R. Modeled PM2.5 removal by trees in ten U.S. cities and associated health effects. Environ. Pollut. 2013;178:395–402. doi: 10.1016/j.envpol.2013.03.050. [DOI] [PubMed] [Google Scholar]
- Ostro B.D., Hurley D., Lipsett M.J. Air pollution and daily mortality in the Coachella Valley, California: a study of PM10 dominated by coarse particles. Environ. Res. 1999;81(3):231–238. doi: 10.1006/enrs.1999.3978. [DOI] [PubMed] [Google Scholar]
- Pan J.N., Chen S.T. Monitoring long-memory air quality data using ARFIMA model. Environmetrics. 2008;19(2):209–219. [Google Scholar]
- Parke W.R. What is fractional integration? Rev. Econ. Stat. 1999;81:632–638. [Google Scholar]
- Qiu J., Wang B., Zhou C. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PloS One. 2020;15:1. doi: 10.1371/journal.pone.0227222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson P.M. Statistical inference for a random coefficient autoregressive model. Scand. J. Stat. 1978;5:163–168. [Google Scholar]
- Robinson P.M. Efficient tests of nonstationary hypotheses. J. Am. Stat. Assoc. 1994;89:1420–1437. [Google Scholar]
- Rojas-Bracho L., Garibay-Bravo V. Particular matters and health. Gac. Ecol. 2003;69:29–44. [Google Scholar]
- Shaharaiyni H.T., Sodoudi S. Statistical modeling approaches for PM10 prediction in urban areas; A review of 21st-century studies. Atmosphere. 2016;7(2):15. [Google Scholar]
- Shi W., Sun J. Aggregation and long memory: an analysis based on the discrete Fourier transform. Econ. Modell. 2016;53:470–476. [Google Scholar]
- Souza L.R. A note on Chamber’s long memory and aggregation in macroeconomic time series. Int. Econ. Rev. 2005;46(3):1059–1062. [Google Scholar]
- Souza L.R. Temporal aggregation and bandwidth selection in estimating long memory. J. Time Anal. 2007;28:701–722. [Google Scholar]
- Souza L.R., Smith J. Bias in the memory parameter for different sampling rates. Int. J. Forecast. 2002;18:489–522. [Google Scholar]
- Steinfeld J.H., Pandis S.N. Wiley; New York: 1998. Atmospheric Chemistry and Physics: from Air Pollution to Climate Change. [Google Scholar]
- Tiwari A.K., Kyophilavong P., Albulescu C.T. Testing the stationarity of CO2 emissions series in Sub-Saharan African countries by incorporating nonlinearity and smooth breaks. Res. Int. Bus. Finance. 2016;37:527–540. [Google Scholar]
- Varotsos C., Kirk-Davidoff D. Long-memory processes in ozone and temperature variations at the region 60 S-60 N. Atmos. Chem. Phys. 2006;6(12):4093–4100. [Google Scholar]
- Varotsos C., Mazei Y. Future temperature extremes will be more harmful: a new critical factor for improved forecasts. Int. J. Environ. Res. Publ. Health. 2019;16(20):4015. doi: 10.3390/ijerph16204015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varotsos C., Mazei Y., Burkovsky I., Efstathiou M.N., Tzanis C.G. Climate scaling behaviour in the dynamics of the marine interstitial ciliate community. Theor. Appl. Climatol. 2016;125(3):439–447. (2016) [Google Scholar]
- Villeneuve P.J., Chen L., Rowe B.H., Coates F. Outdoor air pollution and emergency department visits for asthma among children and adults: a case-crossover study in northern Alberta, Canada. Environ. Health. 2007;6:40. doi: 10.1186/1476-069X-6-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyushin D.I., Kushner P.J. Power-law and long-memory characteristics of the atmospheric general circulation. J. Clim. 2009;22(11):2890–2904. [Google Scholar]
- Wang P., Guo H., Hu J., Kota S.H., Ying Q., Zhang H. Responses of PM2.5 and O3 concentrations to changes of meteorology and emissions in China. Sci. Total Environ. 2019;662:297–306. doi: 10.1016/j.scitotenv.2019.01.227. [DOI] [PubMed] [Google Scholar]
- Xayasouk T., Lee H.M., Lee G. Air pollution prediction using long short-term memory (LSTM) and deep autoencoder (DAE) models. Sustainability. 2020;12:6. [Google Scholar]
- Yuan N., Huang Y., Duan J., Zhu C., Xoplaki E., Luterbacher J. On climate prediction. How much can we expect from climate memory? Clim. Dynam. 2019;52(1-2):855–864. [Google Scholar]
- Zamri I.M., Roziah Z., Marzuki I., Muhd S.L. Forecasting and time series analysis of air pollutants in several area of Malaysia. Am. J. Environ. Sci. 2009;5:625–632. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.