MR elastography: Principles, guidelines, and terminology

Abstract

Magnetic resonance elastography (MRE) is a phase contrast–based MRI technique that can measure displacement due to propagating mechanical waves, from which material properties such as shear modulus can be calculated. Magnetic resonance elastography can be thought of as quantitative, noninvasive palpation. It is increasing in clinical importance, has become widespread in the diagnosis and staging of liver fibrosis, and additional clinical applications are being explored. However, publications have reported MRE results using many different parameters, acquisition techniques, processing methods, and varied nomenclature. The diversity of terminology can lead to confusion (particularly among clinicians) about the meaning of and interpretation of MRE results.

This paper was written by the MRE Guidelines Committee, a group formalized at the first meeting of the ISMRM MRE Study Group, to clarify and move toward standardization of MRE nomenclature. The purpose of this paper is to (1) explain MRE terminology and concepts to those not familiar with them, (2) define “good practices” for practitioners of MRE, and (3) identify opportunities to standardize terminology, to avoid confusion.

1 |. INTRODUCTION

Magnetic resonance elastography (MRE) is a phase contrast–based MRI technique that images propagating mechanical waves and processes the data to generate quantitative images depicting material properties such as shear modulus.¹ It is motivated by the long-established value of palpation, which has been used for centuries as an effective clinical diagnostic technique. However, palpation is subjective and can only be used to evaluate accessible parts of the body. Magnetic resonance elastography can be thought of as quantitative, noninvasive palpation.

Magnetic resonance elastography is increasing in clinical importance; it has become widespread in the diagnosis and staging of liver fibrosis,² may soon become useful in tumor surgery planning, and many other areas are being investigated. More and more research applications are being explored, and the number of MRE and elastography papers per year is increasing rapidly (Figure 1). However, numerous types of acquisitions and processing techniques are in use, and MRE results have been expressed in many different quantities: shear modulus (possibly complex), storage modulus, magnitude of the complex shear modulus, shear stiffness (defined in different ways), wave speed, propagation, loss modulus, attenuation, loss tangent or loss factor, phase angle, damping ratio, attenuation, and penetration rate. This list is not exhaustive and does not include additional quantities related to fitting specific assumed material models or anisotropic materials. This diversity of terminology and absence of standardization can lead to confusion (particularly among clinicians) as to the meaning of certain terms, or how to interpret or compare certain types of MRE results.

FIGURE 1.

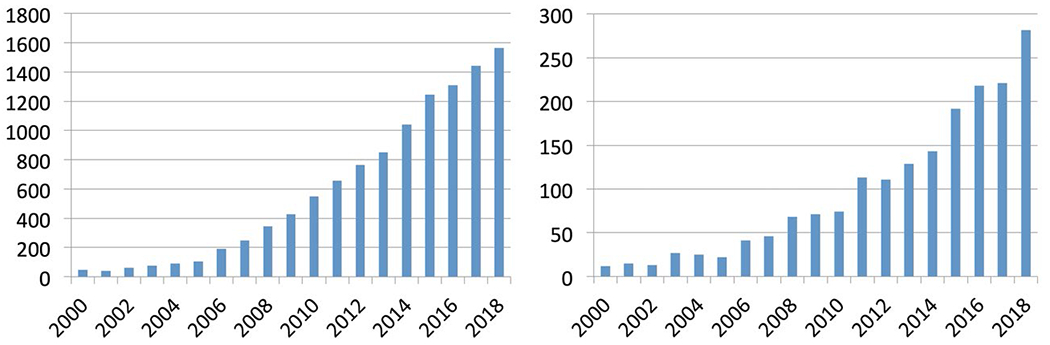
Number of publications per year returned by Web of Science searches on “elastography” (left, 13 973 total) and “magnetic resonance elastography” or “MR elastography” (right, 2157 total)

This paper is written by the MRE Guidelines Committee, a group formalized at the first meeting of the ISMRM MRE Study Group, to attempt to clarify and (to some extent) standardize MRE terminology and practice. Specifically, the purpose of this paper is to (1) explain MRE terminology to those not familiar with it, (2) define “good practices” for practitioners of MRE, and (3) discuss some practices and terms that we believe should be standardized and some that should be discouraged.

2 |. BACKGROUND

There are three main components to MRE: (1) generation of the mechanical waves and their delivery to the relevant part of the body, (2) the MR pulse sequence used for acquisition of the data, and (3) the inversion algorithm to recover mechanical parameters from the displacement data. There are many review papers (eg, Refs. 3–5) and books (eg, Refs 6 and 7) on MRE describing the state of the art, and summarizing research and clinical applications. This paper is not intended to be a comprehensive review, and this section provides only the background necessary to establish context for its recommendations. This paper will not discuss any specific applications in detail, nor summarize results.

2.1 |. Generation of mechanical waves

Several approaches have been used to generate mechanical waves for MRE. Design goals for these devices focus on achieving the desired amplitude and waveform for the applied vibration, providing appropriate mechanical coupling with the object to be imaged, and avoiding electrical and magnetic interference within the bore of the MRI system. Linear and rotary electromechanical motors and piezo-based actuators have been used successfully in MRE, particularly in preclinical (animal) research. Rotating eccentric masses have recently been successfully tested clinically and preclinically.⁸ Pneumatic MRE driver systems placed outside the MRI suite use oscillating air conducted through flexible tubing to power passive actuators located within the magnet bore. These systems are used widely in commercial versions of MRE, available from MRI manufacturers. Driver systems based on compressed air pulses have also recently been introduced.⁹

2.2 |. Magnetic resonance elastography pulse sequences and acquisition strategies

Many pulse sequences can be used for MRE applications. These include gradient-recalled echo with/without EPI,¹⁰ spin echo with/without EPI,³ balanced SSFP,¹¹ and spiral sequences.¹² Typically, gradient-recalled echo and spin echo–EPI sequences are used for most clinical applications such as liver¹³ and brain,¹⁴ with spin echo–EPI having a shorter scan time.^15–19

Most MRE in clinical scanners is performed with harmonic mechanical excitation at one frequency (typically 20-100 Hz),³ using oscillating motion-sensitizing gradients to encode displacement in the phase of the acquired data during the harmonic cycle. Preclinical MRE is based on the same principle but uses higher frequencies, typically 200-1500 Hz,^20,21 to yield shorter wavelengths within the smaller FOV. The harmonic excitation should ideally be continuous, allowing the material to reach steady state, although this may be difficult in practice in some situations. If applied for more than one cycle, motion-encoding gradients typically have the same period as the applied mechanical waves. However, motion can also be encoded with single-cycle gradient wave-forms that have a period less than that of the mechanical waves (this is termed “fractional encoding”), to minimize echo delay time.^22,23

Typically, a single acquisition encodes one component of the displacement field, in the direction of the motion-sensitizing gradient, and three acquisitions with three orthogonal motion-sensitizing directions (ie, x, y, and z) are required to capture the full 3D wave displacement field at one time point in the harmonic cycle. Often, both positive and negative motion encodings for the same displacement component are acquired to obtain the phase difference images with complex conjugate multiplication, removing static, background, and other unwanted phase. Various shapes of the motion-sensitizing gradient²⁴ are used commonly, with zeroth, first, or second-moment nulling for compensating static offset phases, flow or accelerated tissue motion, respectively. There are many variations and extensions to this basic approach to try to increase efficiency, such as multifrequency excitation,^25–27 multidirection sensitization with tetrahedral encoding,²⁸ or sample interval modulation.^29,30 There are also methods that simultaneously acquire MRE data from the phase of the MR signal and diffusion data from the magnitude of the MR signal.³¹

Acquisitions may cover 2D slices or 3D volumes. Acquisition time may become a limiting factor when considering whether to acquire full 3D spatial data or all three sensitizations of motion. Typically, 2D multislice spin-echo EPI is used to obtain 3D stiffness maps. However, 3D slab excitation with partition encoding provides higher SNR than 2D and higher spatial resolution in the slice direction.

Field strength is another factor to consider. It is known that 3 T offers substantially higher SNR and contrast-to-noise ratio than 1.5 T. However, because T₁ relaxation times are 30%-40% longer at 3 T than 1.5 T, longer repetition times are required to generate the same level of contrast-to-noise ratio.³² T₂ relaxation time is not significantly affected by field strength, but ${\mathrm{T}}_2^{*}$ increases significantly with field strength. Therefore, in liver patients with iron overload, 1.5 T is a preferred field strength compared with 3 T. However, for most MRE applications, 3 T is recommended.

A number of acquisitions are typically obtained with different phase offsets between the mechanical excitation and the motion-sensitizing gradients (typically 3-8 offsets are used, equally spaced across the harmonic cycle). Usually, the Fourier transform through time is taken, to extract the motion at the driving frequency and reduce noise. This yields a complex number at each pixel, giving the measured amplitude and phase of the harmonic motion (for one motion direction). This quantity has been called by various names, such as “first harmonic,” but we recommend calling it “motion at the driving frequency” or “motion at XXX Hz.” Approaches that generate and/or acquire multiple frequencies simultaneously can analyze material behavior at these different frequencies by taking different components of the Fourier transform.²⁷

Mechanical waves of sufficient amplitude for displacements to be measured accurately by MRE have to be excited in the tissue of interest. Displacements of tens of microns are often ideal. Larger displacements are possible in some cases, particularly at very low frequencies, but patient safety and comfort and nonlinear behavior of tissue under large deformation may become an issue. Also, because displacement detection is a phase-based technique, phase wrapping may occur if the displacement or the gradient motion-sensitization waveform amplitude is too high. The conversion of displacement to change in measured MR phase is governed by the motion-encoding sensitivity,¹ usually expressed in units of microns per radian or microns per π radians (the latter being the displacement at which phase wraps occur). Some amount of phase wrap is manageable, and may even be desirable for SNR reasons, and a wide variety of phase-unwrapping algorithms have been used successfully to unwrap MRE data. If the subsequent processing involves taking spatial derivatives before taking the Fourier transform through time (eg, when processing the curl of the data), then only local unwrapping of each derivative calculation is necessary, and this is usually very robust. However, all phase-unwrapping algorithms eventually fail if phase wraps are too strong (eg, a double phase wrap at one location, or phase wraps too close together). Large artifactual discontinuities present in the displacement measurements due to uncorrected phase wrap can lead to subsequent artifacts in the estimates of mechanical properties.

2.3 |. Inversion: Estimation of mechanical property fields from wave data

Numerous inversion algorithms have been developed to recover material properties from the acquired MRE data, based on different assumptions and approaches. The basic assumptions that are usually made are that the material is linear, and either elastic (responds to changes in force immediately; does not dissipate energy) or viscoelastic (exhibits a temporal response to changes in force; does dissipate energy).³³ The quantity of greatest interest is the shear modulus, which relates shear strain to shear stress, and is the slope of the stress/strain curve. Most soft tissues are nonlinear, and become stiffer under increased loading (Figure 2, Ref. 34). The displacements are typically very small in an MRE acquisition, so there is little movement along the stress/strain curve, and the stress/strain slope is thus well defined. However, the tissue in question is often prestressed (possibly by pressure from the mechanical driver, or for physiological reasons such as perfusion, interstitial pressure, or portal hypertension), and the modulus estimates may vary depending on where on the stress/strain curve the tissue is during the experiment (Figure 2).

FIGURE 2.

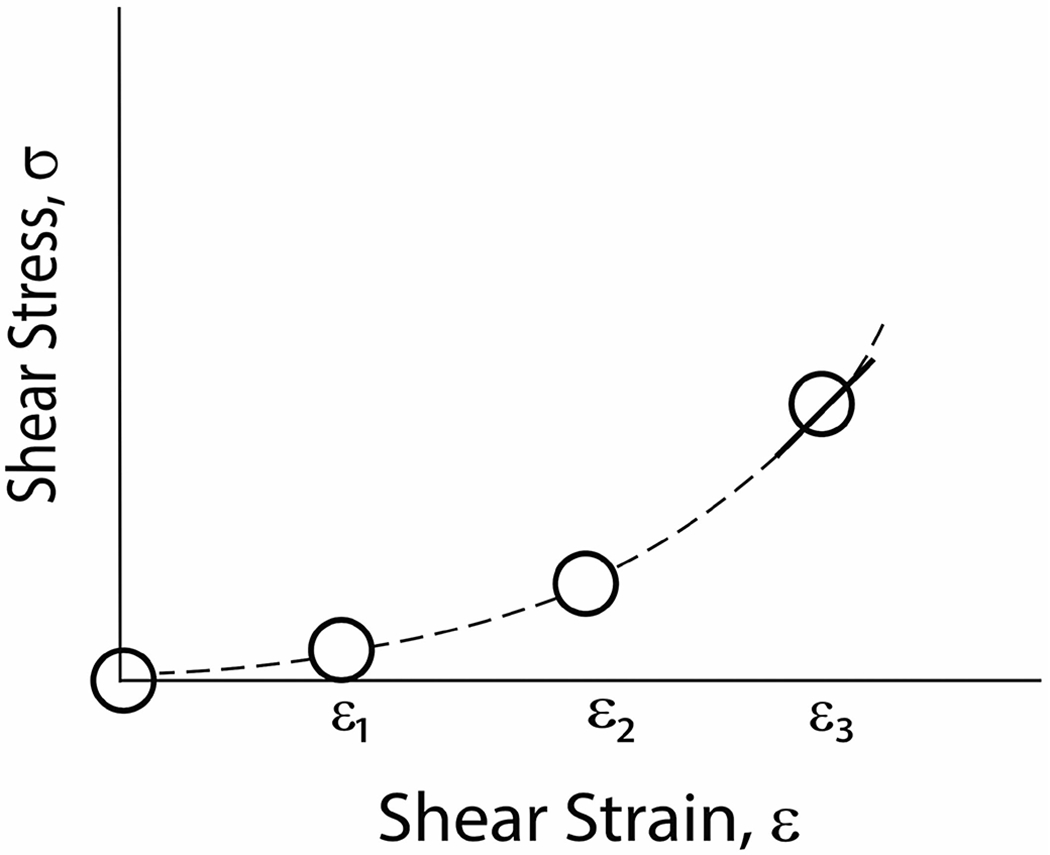
Schematic stress-strain relationship for soft tissue unloaded and at three different tissue-loading states. Magnetic resonance elastography measures the slope of this curve at a given point, as indicated by the tangent line at ε₃

The next assumption that is usually made is that the material is isotropic (has the same properties in all directions). This reduces the number of independent material parameters to two, and in MRE these are usually taken to be the Lamé constants λ and G, with G (often denoted as μ) being the shear modulus. Other parameters frequently used in the biomechanics literature to describe the elastic properties of isotropic materials (eg, Young’s modulus [ratio of compressional or tensile stress to strain], Poisson’s ratio [ratio of transverse expansion to axial contraction]) can be derived from the Lamé constants, and vice versa (see Appendix).

If the material is elastic, only two types of waves can propagate inside the material: longitudinal (compressional) waves that propagate with a speed of $c_L=\sqrt{(\lambda +2G)/\rho }$ and shear waves that propagate with a speed of $c_S=\sqrt{G/\rho }$.³⁵ Most soft tissue is viscoelastic, and wave energy is lost to the medium as the wave propagates. In such a material, the shear modulus is expressed as a complex quantity G*. The real part of the shear modulus (G′) is called the storage modulus, and the imaginary part (G″) is called the loss modulus. A loss modulus G″ > 0 implies loss of energy as the wave propagates, and an attenuation α can be defined (in units of m⁻¹) that characterizes this energy loss. Formulas relating G′ and G″ to, for example, wave speed and attenuation are found in the Appendix.

Soft tissue is almost incompressible, with Poisson’s ratio extremely close to 0.5, and λ >> G (by ~10⁶) and c_L >> c_S (by ~10³). Longitudinal waves in soft tissues propagate at very high velocities (~1540 m/s), have long wavelengths, and their speed does not vary significantly as a function of frequency or by more than about 10% in different soft tissues. Conversely, shear waves (in the MRE frequency range of interest) propagate at 1-5 m/s, and these speeds can vary significantly across tissues, making them a useful target for clinical applications. These factors make accurate estimation of λ very challenging, and longitudinal waves in general are a confounding factor in MRE. The most common techniques to remove their contribution to the data are to apply a spatial high-pass filter (to remove very long wavelengths) or to take the curl of the data.^33,36,37

Many inversion algorithms assume local homogeneity (ie, that the material is homogeneous within a small local processing window). This greatly simplifies the inversions and allows fast local computations, but leads to artifacts near tissue boundaries. If the longitudinal waves have been removed, and local homogeneity is assumed, the equation for shear modulus reduces to the Helmholtz equation: G * = −ρω²u/∇²u, where u is the complex harmonic displacement vector (or its curl), ρ is the density, ω is the angular frequency of the mechanical oscillation, and G is the shear modulus. Many MRE inversions used in practice are based on this equation (eg, direct inversion, algebraic Helmholtz inversion, or algebraic inversion of the differential equation³⁸). Such inversions are sensitive to noise, and some form of data smoothing or regularization of the inversion is usually required. Variational forms of these have been suggested,^39,40 including some that attempt to decouple shear and compressional contributions.⁴¹ Similarly, finite element–based approaches using divergence-free basis functions have been proposed.⁴²

Some alternative inversion approaches, which also assume local homogeneity, are based on estimating wavelength or (equivalently) wave speed. Local frequency estimation is based on estimating the local spatial frequency of the wave field,^33,43,44 which is then converted to wave speed or to shear stiffness (see subsequently). The phase gradient (PG) algorithm³³ simply considers the phase of the harmonic component at the driving frequency. If the motion is a simple shear wave, the gradient of this phase is the change in phase per pixel along the wave direction, convertible to wave speed and therefore to shear stiffness. The PG yields inaccurate results when the phase values do not represent a single propagating wave. Therefore, PG algorithms usually require directional filtering, which is a spatio-temporal filter that passes waves traveling in specific directions but suppresses waves traveling in other directions, before inversion, to suppress reflections and interfering waves.^45–47 This decomposes the wave field into individual propagating waves, which can then be analyzed separately.

These algorithms all assume local homogeneity, so for any results based on regions of interest (ROIs), the ROIs should be eroded in from the edges of known structures to minimize the effect of boundary artifacts, ideally by an amount equal to the half-width of the processing kernel used. This may be difficult in some situations, as it may leave very few voxels left in small ROIs, such as small tumors or tumors with small, peripheral nonnecrotic regions.⁴⁸ In addition to sharp boundaries between tissues, many tissues may well have property gradients, and results from algorithms that assume local homogeneity may be biased in such situations.

The alternative to local homogeneity is for the inversion to account for spatial variations in mechanical properties. This approach is computationally more challenging, but in principle more accurately models the physics of motion for arbitrary materials. These are typically iterative finite element–based techniques, such as nonlinear inversion, that use finite-element techniques as a forward model to calculate displacements based on assumed material parameters,^49,50 compare these to the observed wave field, and update the material parameters based on differences between the two. Direct inversions based on finite-element techniques are also possible.^51–53 In both cases, regularization plays a key role, and techniques such as sparsity-based regularization or soft prior regularization have been proposed.^50,51

In specialized situations, analytical methods are sometimes possible, such as in cylindrical test samples, in which it is possible to fit the wave equation in cylindrical coordinates using Bessel functions.^26,54,55 Specialized inversions can also be used for specific geometric shapes (thin plates, spherical shells).⁵⁶ Finally, inversions based on neural network methods have recently been explored, for both the locally homogeneous and inhomogeneous cases.^57–59

3 |. NOMENCLATURE FOR MRE

The shear modulus at a given frequency is the most commonly reported quantity. A complex shear modulus at a given frequency has a real and imaginary part, commonly denoted as G′ and G″, which represent the elastic and viscous behavior, respectively. These can also be thought of in polar coordinates as having a magnitude and a phase. The standard terms and quantities that are commonly reported, expressed in units of Pa or, more commonly, kPa; 1 Pa = 1 N m⁻² = 1 kg m⁻¹ s⁻²), are:

Storage modulus (real part, G′)—sometimes called elastic modulus or elasticity (but see subsequently).

Loss modulus (imaginary part, G″)—sometimes called viscosity (but see subsequently).

Complex shear modulus (G′ + i*G″).

Shear modulus magnitude (|G*|)—sometimes called “stiffness”² or “shear stiffness,” although these terms are used to refer to other quantities as well (see subsequently).

Alternative parameters to shear modulus are also commonly used, as follows.

3.1 |. Relative viscosity to elasticity parameters (dimensionless)

The relative importance of viscosity or energy dissipation can be summarized by any of several parameters (which are all easily converted to each other):

Loss tangent or loss factor (G″/G′)—this is a direct measure of the relative magnitude of the loss and storage moduli.

Damping ratio (G″/2G′)—this is simply half of the loss tangent, but is a standard quantity in mechanics. A damping ratio of 1 is “critical damping” for a simple harmonic oscillator (ie, the damping at which the displacement dies out as quickly as possible).

Shear modulus phase angle (arctan[(G″/G′])—this represents the phase lag between stress and strain (zero for purely elastic materials, 90° for purely viscous materials). This quantity has often been reported simply as “phase angle,” but this is potentially confusing, as phase angles are also used in MRE to measure displacement itself, and to refer to the phase of the propagating wave at a particular frequency. We therefore recommend the term “shear modulus phase angle.”

3.2 |. Wave field parameters

Fundamentally, data from MRE can be expressed from the material’s point of view (in terms of G* as before) or from the wave’s point of view (in terms of speed and attenuation). These are mathematically interchangeable but can lead to different noise sensitivities.⁵³ Methods that solve for wave speed or wavelength are solving for what the wave is physically doing, and such values that explicitly describe the wave field also form a set of potentially useful parameters:

Wave speed (m/s)—in ultrasound elastography, wave speed (equal to wavelength*mechanical frequency) is often reported as the result, as in transient experiments (commonly performed in ultrasound) it is readily measurable. Wave speed is a function of both the storage and loss modulus, so reporting it alone does not allow separation of the effects of these two quantities. Note that in MRE, the wave speed measured is a phase velocity, whereas in ultrasound transient experiments, it is a group velocity representing the combined behavior over a range of frequencies.

Shear stiffness (Pa or kPa)—this term has often been used to refer to the magnitude of the complex shear modulus. It has also been used to refer to density*wave speed squared, which is the shear modulus of a purely elastic object that exhibits the observed wave speed or wavelength at the driving frequency. This is not incorrectly assuming the object is elastic and reporting shear modulus; it is reporting a different quantity ($\rho c_S^2$), which is correct by definition, but the term “shear modulus” should not be used in this case.

Propagation (ie, spatial wave number, in m⁻¹)—the real part of the complex wave number k = β + iα (see Appendix). This carries the same information as wave speed, which is ω/β.

Attenuation (m⁻¹)—the imaginary part of the complex wave number, k = β + iα, describing the loss of amplitude of the wave with distance for a plane wave. It is important to distinguish between geometric attenuation, which does not involve loss of energy (eg, waves radiating out from a point source in an elastic medium decrease in amplitude because the wavefront is expanding, but the total energy remains constant) and true attenuation, in which wave energy is lost to a viscoelastic medium. Direct inversion and finite element–based techniques correctly distinguish true attenuation from geometric attenuation, but simpler approaches to measure attenuation based on wave amplitude may not.

Penetration rate (ω/α in m/s)—similar to propagation and attenuation, which represent a pair of complementary parameters, wave speed and penetration rate can be derived from the real and imaginary part of the complex wave number, and are simply ω/β and ω/α, respectively, both in m/s.

For single-frequency analysis, then, many different quantities are currently reported. We recommend those that are used most commonly. If a single parameter is reported, it should be |G*| or shear stiffness ($\rho c_S^2$). If two parameters are reported, to capture the full viscoelastic behavior, we recommend pairs such as storage and loss moduli; shear modulus magnitude |G*| and phase angle or damping ratio; or shear stiffness and damping ratio.

Note that all these parameters vary with frequency in soft tissue; thus, the frequency at which the value is being reported should always be made clear.

3.3 |. Notes on other terms

3.3.1 |. Stiffness

The word “stiffness” is commonly used, and makes intuitive sense to most people and to clinicians, but it is not a precise term. There are many types of stiffness (eg, longitudinal stiffness, bending stiffness, torsional stiffness; see Baumgart⁶⁰). Shear modulus is a property of the constituent material, but in many applications in biomechanics and engineering, stiffness refers to a property of a structure or component of a structure, depends on the physical dimensions that describe that component, and has different units than shear modulus.⁶¹ That said, the word “stiffness” is entrenched in the literature, and (again) makes intuitive sense. We recommend that, ideally, the term “stiffness” be restricted to qualitative statements (eg, “the spleen is stiffer than the liver”), and the correct term (and units) be used when reporting measurements (eg, “the storage modulus is 2.9 kPa”). Alternatively, if the term “stiffness” is used throughout, one should explicitly indicate the quantity that is being referred to (eg, “stiffness is defined as the magnitude of the complex shear modulus”² or “stiffness is defined as density * wave speed squared”³³).

3.3.2 |. Elasticity

Elasticity refers to the property of a body to return to its original size or shape after deforming forces have been removed. It has been used in MRE to refer to the storage modulus, to Young’s modulus, and to the wave speed. Unlike the term “stiffness,” “elasticity” is widely misunderstood. Many nontechnical readers incorrectly believe that a stiffer material can thought of as less elastic than a softer material. For this reason, we recommend against the use of this term as an informal alternative to correct terms (and units) that should be used when reporting measurements (eg, “the storage modulus is 2.9 kPa”).

3.3.3 |. Viscosity

Viscosity is the material property that relates the stresses in a material to the rate of change of deformation (ie, the strain rate), and is related to the absorption of mechanical energy. In MRE, the term viscosity has been used as a synonym for the loss modulus (G″), for the loss tangent (G″/G′), for the shear modulus phase angle (arctan [G″/G′]), as the loss modulus divided by frequency (with units of Pa*s), and as a parameter in a specific rheological model (see subsequently). In the latter two cases, viscosity is often denoted as η.

We recommend that the term “viscosity” be used to refer to the calculated parameter η and not be used as a synonym for loss modulus, loss tangent, or shear modulus phase angle. If a rheological model is used for calculating viscosity or converting G″ into η, the model used should be clearly stated (see subsequently).

3.3.4 |. Density

In all MRE inversions, the density ρ is technically another unknown, which can vary with position. Typically in MRE the assumption is made that the density of soft tissue is equal to water: 1.0 g/cm³ or 1000 kg/m³. For soft tissues, density is somewhat greater, perhaps 1.05-1.1 g/cm³, although accurate values are difficult to determine. We recommend standardizing on 1.0 g/cm³ as a community, as the error made from this assumption in most soft tissues is at most a few percent. This is likely smaller than other errors in MRE, and this assumption allows easier comparisons between studies (and with most of the past MRE literature), as well as the need to choose and justify an exact density value (which would vary across tissues, and across different papers on the same tissue). Note that the lung is the one tissue where this is not a reasonable assumption, and where density needs to be carefully considered and the treatment of density reported.

3.4 |. Magnetic resonance elastography at multiple frequencies

A purely elastic material will exhibit the same shear wave speed at different frequencies. A viscoelastic material will exhibit dispersion (ie, different wave speeds at different frequencies). In terms of shear modulus, a viscoelastic material will have frequency-dependent G′ and G″. Changes in the complex shear modulus or wave speed with frequency are increasingly being explored as additional useful biomarkers. Magnetic resonance elastography can be performed at multiple frequencies to probe this behavior: either separately with multiple acquisitions^62,63 or simultaneously.²⁷

3.4.1 |. Frequency-dependent material models

The calculation of storage and loss modulus at individual frequencies assumes no specific rheological model. However, to analyze data at multiple frequencies, different rheological models are commonly used that assume different behavior with frequency. Soft tissue has been analyzed with several such models.^55,63 There are three models that contain only two parameters: the Voigt, Maxwell, and spring-pot models. In the Voigt model, G′ is constant over frequency and G″ increases linearly with frequency. It is often used to describe solids due to its simplicity, but it does not comply with the observed increase of G′ over frequency in many biological soft tissues. The Maxwell model has G′ and G″ that vary with frequency, but G″ can decrease with frequency, and at low frequencies G′ ;becomes zero (as is typical for liquids). The spring-pot model assumes a power law increase of both G′ and G″ with frequency,^55,64 and represents soft-tissue behavior in the frequency range of MRE better than either the Voigt model or Maxwell models.⁷ Viscosity in the spring-pot model is parametrized as a dimensionless power-law coefficient. Models with three parameters have also been used (eg, Zener, standard linear solid), but the variability of resulting viscoelasticity values may increase due to introducing a third free parameter into the fitting function.⁶³ It should also be noted that most multifrequency MRE experiments span a narrow frequency range of no more than 1-2 octaves, which limits the determination of material model coefficients. Some authors thus simply report a simple linear or exponential fit across a narrow frequency range, or the ratio of results at two frequencies.⁶⁵

If a material model is used, one should always report results at individual frequencies, as well as any combined results (eg, parameters from a fit to the assumed model). This allows comparison with other work, fits with other material models to be tried, and so on. A single complex shear modulus across multiple frequencies is also sometimes reported, with approaches based on direct inversion^66,67 or PG techniques.⁴⁶

3.5 |. Waveguide or boundary effects

An infinite, isotropic, homogeneous linear elastic or viscoelastic material supports only pure longitudinal and shear waves, which propagate independently of each other at the speeds noted previously. In a finite object, there can be mode conversion near boundaries between shear and longitudinal waves, and other wave types are possible (eg, Lamb, Love, Rayleigh waves), which contain a combination of shear and longitudinal wave attributes.^68–70 In objects with at least one dimension smaller than about a wavelength (such as in the heart or within tumors), wave behavior depends on geometry as well as the inherent material properties, and such “waveguide effects” can dominate the wave propagation. Consequently, inversion approaches that do not account for this yield biased values.^37,71 This is particularly important in cardiac MRE with typical wall thicknesses around 10 mm.

Thus, results reported by MRE may or may not be significantly affected by boundaries, in part depending on the processing used. Some approaches report what the wave is doing, which includes the influence of geometric effects (ie, these report an actual wave speed or an “apparent” shear modulus). Other approaches attempt to model, understand, or remove the boundary effects, and report the true material properties (ie, the underlying, intrinsic properties of the material, such as the true shear modulus).⁵⁴

Taking the curl of the displacement wave field in a homogeneous medium removes longitudinal contributions in theory, leaving behind a wave field that propagates at the true shear wave speed, corresponding to the intrinsic shear modulus.^37,71 However, there are practical difficulties: This requires full 3D data with good resolution in z, causes noise amplification, and low resolution may mean that spatial gradient operators may cross boundaries and yield incorrect results. Alternatively, some inversion approaches (eg, nonlinear inversion) may yield more accurate results near boundaries or in waveguide situations.

4 |. GOOD PRACTICES FOR MRE PUBLICATIONS

Publications should include all details of the mechanical driving setup⁸ and the acquisition, such as number of offsets, sensitization directions, shape of motion-encoding gradient (zeroth or first moment nulled), and what components of the Fourier transform through time were kept.²⁸ The type of phase unwrapping used (if any) should be mentioned. It is acceptable if these details are given by reference to a previous publication. The strength of the motion-encoding gradient should be specified. Some measure of the tissue-displacement amplitude should be reported, such as the maximum and/or typical displacement amplitude.⁷²

Publications should also include the frequency (or frequencies) used for both the external applied motion and the motion-sensitizing gradient. These should also be mentioned when reporting results, not just elsewhere in the paper, as material properties change with frequency.³⁴

The details of inversion algorithms, including every detail of preprocessing and postprocessing, should be reported to allow anyone to fully reproduce the approach.⁵³ If bandpass or high-pass filters are used to remove longitudinal waves, the filter cutoffs should be clearly specified in physical units (m⁻¹). One should also report how the inversions from different motion sensitizations or directional filters are averaged or specify whether they are solved simultaneously.^29,62,67,73

If possible, results should always be reported in a manner that allows comparison with other results, possibly expressed in different quantities (see Appendix for conversion formulas between quantities).

The reproducibility of the results should be reported (or reference a study that does, for that experimental setup). At a minimum, this should involve repeatability analyses, taking the subjects out of the scanner between scans.^74,75

Physiological variations of the biomechanical properties should be taken into account. Several studies have reported increase of liver shear modulus after a meal. Mean shear modulus increase of about 10% has been reported in healthy volunteers and about 20% in patients with liver fibrosis.^76,77 Changes of shear modulus have also been reported in the liver, spleen, pancreas, and kidney after water intake.⁹ Therefore, patients should undergo MRE examination in a controlled fasting state.⁷⁷

4.1 |. Validation

The validity of quantitative measurements obtained with MRE techniques may be assessed in terms such as accuracy, precision, repeatability, and reproducibility. Phantom studies are often used to evaluate the accuracy and precision of measurements made with quantitative imaging techniques. Studies of the accuracy of shear modulus measurements obtained with MRE have been challenged by the lack of known methods for fabricating phantoms that have precisely pre-determined mechanical properties that are similar to tissue. Therefore, existing work has focused on comparing results with measurements of material properties obtained with dynamic mechanical analysis instruments.⁷⁸ However, measuring the shear properties of semisolid tissue-like phantom materials with dynamic mechanical analysis technology is challenging.

Therefore, most validations of quantitative biomarkers obtained with MRE have been through measurements of precision (comparing repeated measurements). In this context, the terms “repeatability” and “reproducibility” are used. Studies of the repeatability of MRE measurements assess the agreement of repeated measurements using the same system and analysis.⁷⁹ Studies of the reproducibility of MRE measurements assess the agreement of measurements of the same subject across different implementations of MRE, different systems, and different analysts.⁸⁰

4.2 |. Noise effects

Noise can affect MRE, and there is a need for reliable confidence measures for the values reported. Results (for all quantities) can be biased due to low SNR or strong regularization approaches used to combat low SNR. Other things being equal, biases due to a given noise level are usually worse in stiffer objects (because shear waves have smaller amplitudes and longer wavelengths, yielding smaller spatial derivatives, and deformation, measured by these derivatives, is the signal in MRE). Ideally, the noise level and its effects on results should be assessed, but estimating noise can be difficult in MRE.

There is no agreed upon measure for the SNR of MRE data. Measurements of phase-to-noise ratios, displacement-to-noise ratios, and octahedral shear strain SNRs (OSS-SNRs) have been proposed.^28,81 Because the MRE signal is essentially strain, OSS-SNR should give more reliable SNR estimates than displacement-to-noise ratios, especially when rigid body motion is present. For nonlinear inversion, average OSS-SNR values above 3 are claimed to indicate stable, reproducible results.⁸¹ The OSS-SNR measurement may not be suitable when the inversion algorithm takes more than one derivative of the data (eg, direct inversion, which is based on second derivatives⁸²). For local frequency estimation and PG, which are based on first derivatives, appropriate thresholds for OSS-SNR are an open question, and certainly depend on choices of the processing parameters.

4.3 |. Discretization effects

If there are not enough pixels sampled per wavelength, discretization effects when estimating derivatives can bias the results. Depending on the inversion and the derivative kernel used, this can cause about a 4% error when there are 9-10 pixels per wavelength, but the error rapidly increases with fewer pixels per wavelength.^79,83,84 Conversely, when the wavelength becomes much larger than the pixel size, the discrete derivative operations required for some inversion methods are highly affected by low SNR. It has been reported that the accuracy and precision of MRE measurements with direct inversion are optimal when six to nine voxels per wavelength are obtained and the SNR is sufficiently high⁸⁴; more recent work studies the effects of kernel width and the order of the derivative operators in the inversion.⁸⁴ Discussion of results should address this question, and whether the wavelength/pixel ratio is in an appropriate range.

4.4 |. Regions of interest

When reporting results on an ROI, one should clearly state the criteria for determining the ROI. Many MRE inversion algorithms, especially those that assume local homogeneity, give poor estimates of quantities near boundaries, so the ROI should be eroded away from tissue boundaries, and it should be stated exactly whether/how this was done. It should also be clear whether the mean or median within the ROI is being reported.

In diffuse liver disease, the use of multiple small ROIs or a large ROI has been shown to provide more reproducible results than the use of a small ROI.⁸⁵ Using large or multiple hepatic ROIs is thus recommended for follow-up studies. However, because most liver biopsies are performed in the right antero-superior segment of the right liver (segment 8), placement of only a small ROI in this segment may result in a better correlation with the results of liver biopsy.⁸⁶ Indeed, significant variation of elasticity has been reported between liver segments.⁸⁷

The SD inside an ROI is often reported, but the value of this quantity is unclear. It represents a combination of noise, real physiologic variation, and data smoothing during the processing (one can always smooth the data more and lower the SD). If the SD is used for significance testing, or for calculating confidence intervals or standard error, note that adjacent pixel results are not independent, violating the basic assumption of independent samples in such calculations. There are far fewer independent quantities in the parameter map than the number of voxels. Thus, such calculations often strongly overestimate significance or underestimate confidence intervals.

4.5 |. Resolution

Resolution in MRE refers not to the pixel size in the elastograms (ie, image resolution) but to the resolution of elastographic details (necessarily poorer than image resolution). This can be difficult to determine. Resolution phantoms are difficult to make, although some have been reported⁸⁸; analytical phantoms do not consider real-world effects, and resolution depends strongly on the details of the processing. Certainly the width of the processing kernels used sets a limit to the resolution.

4.6 |. Sources of error

Magnetic resonance elastography measurements are subject to all of the common sources of error present in MRI and, particularly, phase-contrast MRI (eg, magnetic field inhomogeneity, local background phase errors, subject motion, spatial distortion). Subject motion in general does not affect the measurement directly, as the displacements measured are harmonic displacements at a specific frequency; therefore, other nonperiodic motion is filtered out. However, subject motion can degrade the data by blurring and by making the acquired k-space inconsistent.^12,89 Uncorrected spatial distortions can change the apparent spatial behavior of the shear waves and therefore bias the results.⁸⁹ Additionally, there are a number of possible sources of error, unique to MRE, in the estimation of material parameters. Most of these relate essentially to tissue-model mismatch (ie, the assumptions of the inversion algorithm do not accurately model real tissue behavior for various reasons). Potential estimation errors include:

1. Estimation errors even if there is only a pure shear wave. These include situations in which the inversion algorithm is biased, noise corrupts the results, discretization errors bias the results, or when the inversion algorithm assumes homogeneity, leading to errors near tissue boundaries or in tissues with vascular structures of different sizes or small tumor sizes.⁹⁰

2. Estimation errors caused by several intrinsic effects including

   1. The longitudinal wave not being completely rejected, making the material appear stiffer;
   2. The existence of different shear waves (ie, fast and slow shear waves, due to anisotropy^91,92); and
   3. Effects related to prestress due to a tensile or compressive load on the tissue, making it appear stiffer due to tissue nonlinearity.³⁴ This can include effects related to a fluid phase, which imposes a pressure onto the solid phase, making it appear stiffer.⁹³

3. Estimation errors from boundary effects (waveguides or heterogeneity) biasing an algorithm that assumes there are no boundaries.⁵¹ In the waveguide case, the algorithm may be estimating the speed of the mixed wave present correctly, but it is incorrect to convert these to inherent material properties without taking into account the effects of geometry or boundaries.^37,56

4.7 |. Anisotropic materials and inversions

For some soft tissues (eg, muscle, white matter fibers, renal tissue), the assumption of an isotropic material is clearly incorrect. When analyzing anisotropic materials using an isotropic assumption, different types of excitation can give different results,^91,94 as shear waves propagate with different speeds in different directions. Several groups^92,95–97 have proposed anisotropic inversions for such materials. Most treatments to date assume transverse isotropic materials, which have a single preferred direction, and are therefore considered applicable to muscle fibers and white-matter fibers. Such materials have three independent material quantities if incompressible, and five if not.⁹² Higher-order anisotropic models of up to nine independent constants have also been reported.⁹⁸ To invert such models, generating multiple different wave fields may be required, to provide enough independent information to determine the various parameters, and to excite all of the different modes of wave propagation.⁹⁹ Several different conventions exist for reporting anisotropic material parameters, and it can be confusing to convert between these. However, we consider it premature to recommend a specific convention at this early stage.

4.8 |. Poro-elastic materials and inversions

Biological tissue is immersed by a dense network of vasculature and can therefore be drained like a sponge if compressed sufficiently slowly. Recent work suggests that at frequencies above about 50 Hz, poro-elastic effects can be disregarded (except in the lung), but such effects can play a role at frequencies below about 30 Hz, and are dominant at very low frequencies (eg, 1-2 Hz).¹⁰⁰ These effects should be considered if working at very low frequencies or in the lung. Some inversions based on poro-elastic equations have been reported.^101,102

Poro-elastic effects within the lungs are complicated and can affect a wider range of frequencies. Although compression waves travel at about 1500 m/s and 340 m/s in soft tissue and air, respectively, two compression wave speeds may exist simultaneously in a porous material, and they can travel as slowly as 20-30 m/s in lung parenchymal tissue.¹⁰³

4.9 |. Ultrasound elastography

There is a large amount of work in ultrasound elastography, including clinical applications, and increasingly results are being compared against MRE. The techniques are in some ways complementary, and a thorough discussion of the relative merits of the two is beyond the scope of this article. Here we simply note some issues that arise when comparing results. Most ultrasound work is based on transient excitation, and usually measures wave speed, but this is a group velocity rather than a phase velocity. Shear wave elastography based on acoustic radiation force impulses is comparable to time-harmonic MRE over the frequency range where the two velocities agree, approximately 120-180 Hz in liver tissue.^104–106 Young’s modulus is often the quantity reported, which is typically 3-times the shear modulus for soft tissue (see Appendix).

Time-harmonic vibrations in the same frequency range as MRE (25-60 Hz) have been exploited by ultrasound elastography¹⁰⁷ to reach deeper tissues than recommended for transient-based approaches (approximately 6-cm depth).¹⁰⁸ Ultrasound time-harmonic elastography can be directly compared with MRE, so that diagnostic thresholds can be exchanged across modalities.¹⁰⁹

APPENDIX

CONSTITUTIVE RELATIONSHIP BETWEEN STRESS AND STRAIN IN ELASTIC AND VISCOELASTIC MATERIALS

The stress tensor in an isotropic, linear elastic material is related to (small) deformations by the constitutive law

$$\mathit{\sigma }=2G\mathit{\epsilon }+\lambda \mathrm{Tr}(\mathit{\epsilon }),$$ (2)

in which G and λ are the two elastic Lamé parameters and ε is the strain tensor. The shear modulus, G, governs isochoric (volume-preserving) deformations, and the ratio between shear stress (shear force per unit area on an infinitesimal cubic element) and the change in angle between sides of that element.⁶⁸ The second Lamé parameter,λ, also known as the coefficient of volume compressibility,¹¹⁰ is important in describing the stress needed to change the volume of a material element, but not for changing its shape.

The second Lamé parameter can be expressed in terms of bulk modulus, κ, and shear modulus: λ = κ − 2G/3. Other commonly used stress-strain coefficients for isotropic, linear elastic material are the Young’s modulus (E = G(3λ + 2G) / (λ + G)) and the Poisson’s ratio (v = λ/2(λ + G)). If any two of the five coefficients (E, G, λ, κ, v) are specified, the other three can be determined through these relationships.¹¹¹

Biological soft tissue is considered nearly incompressible, because λ and κ ≫ G. If isotropy is also assumed, this leads to the approximate relationships E ≈ 3G and v ≈ 1/2.

To describe a viscoelastic material undergoing harmonic deformations (σ = σ₀ exp (iωt), ε = ε₀exp(iωt)), the real-valued elastic moduli, are replaced by complex analogs; for example, G is replaced by G* = G′ + iG″, where $i=\sqrt{-1}$.

RELATIONSHIPS BETWEEN COMMON PARAMETERS

The equation for a plane shear wave in a viscoelastic material polarized in (ie, material moving in) the x direction and propagating in the y direction is $u=\widehat{x}{e}^{-\alpha y}{e}^{i(\beta y-\omega t)}$ or, combining terms, $u=\widehat{x}{e}^{i((\beta +i\alpha )y-\omega t)}$ or $u=\widehat{x}{e}^{i(ky-\omega t)}$, where $\widehat{x}$ is a unit vector in the x direction, k = β + iα is the complex wave number, α is the attenuation, β is the spatial wave number = 2π/wavelength, and phase speed = (2π/β)*mechanical frequency = ω/β (some sources use the convention $u=\widehat{x}{e}^{i(\omega t-ky)}$, in which case k = β − iα).¹¹²

Shear wave phase speed c_s, the real part of the shear wave number β, and shear wave attenuation α can be converted to G′ and G″, and vice versa:

$$c_s^2=2{\left|G^{\ast }\right|}^2/\rho (G^{\prime }+\left|G^{\ast }\right|){\alpha }^2=\rho {\omega }^2({\left|G\right|}^{\ast }-G^{\prime })/2{\left|G^{\ast }\right|}^2$$

$$k=\omega \sqrt{(\rho /G^{\ast })}{\beta }^2=\rho {\omega }^2(G^{\prime }+|G^{\ast }|)/2{\left|G^{\ast }\right|}^2$$

$$G^{\prime }=\rho {\omega }^2\frac{({\beta }^2-{\alpha }^2)}{{({\beta }^2+{\alpha }^2)}^2}{G}^{″}=\rho {\omega }^2\frac{2\alpha \beta }{{({\beta }^2+{\alpha }^2)}^2}$$