Abstract
The effective sample size (ESS) is a metric used to summarize in a single term the amount of correlation in a sample. It is of particular interest when predicting the statistical power of genome-wide association studies (GWAS) based on linear mixed models. Here, we introduce an analytical form of the ESS for mixed-model GWAS of quantitative traits and relate it to empirical estimators recently proposed. Using our framework, we derived approximations of the ESS for analyses of related and unrelated samples and for both marginal genetic and gene-environment interaction tests. We conducted simulations to validate our approximations and to provide a quantitative perspective on the statistical power of various scenarios, including power loss due to family relatedness and power gains due to conditioning on the polygenic signal. Our analyses also demonstrate that the power of gene-environment interaction GWAS in related individuals strongly depends on the family structure and exposure distribution. Finally, we performed a series of mixed-model GWAS on data from the UK Biobank and confirmed the simulation results. We notably found that the expected power drop due to family relatedness in the UK Biobank is negligible.
Keywords: effective sample size, linear mixed models, gwas
Introduction
Genome-wide association studies (GWAS) have identified thousands of genetic variant-trait associations, improving our understanding of the genetic architecture of complex traits and diseases (Visscher et al. 2017). Most published GWAS used linear regression (LR) performed in samples of unrelated individuals due to the fast computation of statistical tests and their well-known analytical properties (Yang et al. 2011). These properties also facilitate a range of secondary analyses based on GWAS summary statistics, including meta-analyses (Sung et al. 2016), fine-mapping (Yang et al. 2012), partitioning heritability (Gazal et al. 2017; Finucane et al. 2018), and polygenic risk prediction (Vilhjálmsson et al. 2015). The increase in very large cohorts consisting of combined samples of unrelated and related individuals, such as the UK Biobank (Bycroft et al. 2018), poses new challenges to both GWAS and post-GWAS analyses. In this context, linear mixed models (LMMs) have been established as an alternative to LR that allows retaining related individuals (Loh et al. 2018), accounting for cryptic relatedness (Tucker et al. 2014), and conditioning on the polygenic signal (Yang et al. 2014). Nevertheless, works on optimizing computational algorithms and determining the analytical properties of LMMs are active areas of research (Yang et al. 2014; Joo et al. 2016; Loh et al. 2018; Pazokitoroudi et al. 2019). Among the parameters of interest, previous works briefly introduced the effective sample size (ESS), a metric quantifying the size of an equally powered GWAS performed in unrelated individuals by LR and proposed empirical solutions to estimate the ESS (Yang et al. 2012; Gazal et al. 2017; Loh et al. 2018).
In this work, we derive an analytical ESS estimator for samples with related individuals and present three applications of our estimator covering different study designs (unrelated/related individuals), association models (LR/LMM), and parameters of interest (marginal genetic/gene-environment interaction effects). First, we quantify the impact of having related rather than unrelated individuals in a sample on the statistical power (Visscher et al. 2008; Loh et al. 2018). Intuitively, having related individuals results in lowering the power, as related pairs harbor overlapping phenotypic and genetic information (Visscher et al. 2008), a situation previously discussed for sibships (Sham et al. 2000). Here, we propose a general framework applicable to any study design. Second, we revisit the impact of using LMMs in association studies of unrelated individuals, where the polygenic signal is modeled as a random effect via the genetic relationship matrix (GRM). Previous works focused on the distribution of test statistics (Yang et al. 2011, 2014) and proposed empirically estimating the ESS based on the ratio of the association chi-square statistic between LR and LMM from the top variants (Gazal et al. 2017; Loh et al. 2018). We show that this strategy should be used with caution, and we discuss more robust alternatives. Third, we tackle association studies of gene-environment interactions (Aschard 2016) and examine how family resemblance in related individuals affects the power of detecting the interaction effect using an LMM. Related works empirically evaluated different family-based designs to increase power (Gauderman 2002, 2003) but provided analytical derivations for the interaction test only for the LR model applied to unrelated individuals (Aschard 2016). Again, our analytical estimator fills this gap, covering both LR and LMMs.
For ease of interpretation, we introduce the ESS multiplier as a measure of relative power. It is defined as a ratio of the noncentrality parameters (NCPs) between an LMM and an LR model, where the LR model is applied to a sample of unrelated individuals that is the same size. The manuscript is organized as follows. We first derive approximations of the NCPs for LMM tests and use them to further derive the ESS multiplier. We then demonstrate the validity of our multiplier through extensive simulations and analysis of real data in the UK Biobank (Bycroft et al. 2018). We finally discuss the influence of multiple factors on the multiplier, including the family structure, the amount of genetic variance explained, and distribution of environmental exposure (when testing for gene-environment interactions).
Methods
Linear models
We consider an LMM and derive the Wald test statistic of association between a genetic variant and a quantitative trait. We further derive the LR statistic as a special case of LMM statistic.
Let N denotes the number of individuals, M denotes the number of genetic variants, y denote an vector of an outcome trait values, W denotes an N × M matrix of genetic variants and w denote an vector of the genetic variant tested, i.e., a column in W. We assume that the vector y and the columns in matrix W are standardized to have zero mean and unit variance, and there are no other covariates. The effect of the variants on the outcome y is then modeled using a multivariate normal distribution:
| (1) |
where β is the standardized effect size, and is the N × N covariance matrix of the trait across N individuals.
If the covariance matrix Σy is known, β can be estimated using generalized least squares (GLS) (Lynch and Walsh 1998). The Wald statistic is defined as , and it is compared to the distribution under the null hypothesis of no association: β = 0. The LMM statistic is finally expressed as (Lynch and Walsh 1998; Chen and Abecasis 2007; Joo et al. 2016):
| (2) |
| (3) |
| (4) |
The LR statistic has a simpler form. Considering that and w is standardized so that , and assuming . Since the vector y is standardized and the variance captured by the genetic variant is negligibly small, the LR statistic can be expressed as:
| (5) |
| (6) |
| (7) |
Gene-environment interaction
To study the gene-environment interaction effect on a standardized quantitative trait y, the linear model in Equation 1 is expanded by including two vectors: one vector d for environmental exposure, and another vector for the gene-environment interaction obtained by element-wise multiplication of the two vectors w and d.
| (8) |
where β, τ and δ denote the genetic variant, exposure, and interaction effect sizes, respectively. We again assume that all three vectors of covariates are standardized to have zero mean and unit variance, and there are no other covariates.
Under the assumption that two random variables of genotype and environmental exposure are generated independently, the standardized interaction effect δ can be evaluated independently from the two main effects β and τ (Aschard 2016, Appendix C]. Thus, the test statistic for the gene-environment interaction can be expressed as in Equations 2–4 by replacing w with v.
| (9) |
| (10) |
| (11) |
Estimating trait covariance
The covariance structure of y is generally unknown, but Equations 1 and 8 can be extended to further specify the covariance components. The expression for y can be written as follows:
| (12) |
where m vectors of random effects, , and residual errors, , are assumed to be mutually uncorrelated and multivariate normally distributed. The covariance of each vector of random effects is parameterized with a constant matrix Rk and scaled by the scalar parameter , referred to as variance components. Marginalizing over vectors of random effects from Equation 12 gives a multivariate normal distribution of y with the following covariance:
| (13) |
Both the fixed effect β and variance components and , are model parameters. Variance components are typically estimated by restricted maximum likelihood (REML) (Lynch and Walsh 1998), because the REML approach produces unbiased estimates by adjusting for the loss of degrees of freedom due to the fixed effect covariates. To compute the association test statistic in Equations 4 and 11, we replace the true trait covariance with its estimate:
| (14) |
Relative power and ESS
Under the alternative hypothesis, the NCP quantifies the statistical power for a given effect size β.
| (15) |
| (16) |
where α is the type I error rate and is the cumulative distribution function for the noncentral distribution with df degrees of freedom and NCP. The quantity is the inverse of F or the quantile of the noncentral distribution.
To introduce the concept of ESS, consider two association study designs: one study is based on unrelated individuals and effects are estimated using LR, and the other study is based on related individuals in families and the effect is estimated using an LMM. Both studies have the same sample size N, and we are interested in determining the power of the later design relative to the former when testing a genetic variant with effect size β. The ratio of the two corresponding NCPs offer a simple and interpretable metric that addresses this question. Plugging the variances defined in Equations 3 and 6 into the ratio and approximating with , we define the ESS multiplier as:
| (17) |
This metric quantifies the power of the LMM-based test with the sample size N relative to a standard LR-based test with the same sample size N. Conversely, the effective sample is defined as ESS . We note that the proposed ESS multiplier is similar, in principle, to the previously proposed metric of asymptotic relative efficiency (ARE) of two tests, say, one likelihood and another, for estimating a parameter θ: it is given by the ratio of the inverse asymptotic estimates for the variance of (Kraft and Thomas 2000). In this work, we aim at simplifying the numerator part of the ratio in Equation 17 using approximations described in the next section.
Alternatively, empirical estimators of the ESS can be used when the analytical form is unknown. For instance, consider two association studies in a sample of unrelated individuals, one being performed with LR and the other one with LMM. Two recent works proposed an empirical multiplier defined as the median of the ratio of statistics computed by an LMM and an LR model at Mtop top associated variants (Gazal et al. 2017; Loh et al. 2018). This approach is relevant only under the assumption that the estimates of by LR and LMM at those top variants are approximately equal and, thus, cancel each other out in the ratio of the test statistics. From Equation 17, a more obvious empirical estimator can be built by deriving, over any random set of variants, the median of the ratio of squared standard errors between the LMM and LR model. We found that this strategy has been used in at least one previous study (Yang et al. 2012). The two empirical estimators are expressed as:
| (18) |
| (19) |
Under the reasonable assumptions that the sample size is large enough and all variables are standardized in the LR model, the numerator in Equation 19 can be further simplified to , thus, allowing to derive the multiplier from the LMM using summary statistics only.
Approximations
Given the definition of an NCP in Equation 15, we compute the expected variance of the effect size estimate in Equation 3 by averaging over genetic variants w and obtain an analytical approximation for the NCP and power to detect a given effect size β. A similar computation is performed for an NCP and power to detect a gene-environment interaction effect size δ by averaging over interaction variables v. In particular, we approximate quadratic forms from LMMs, and , by their mean values, by treating w and v as vectors of random variables and as a constant matrix of linear transformation.
First, we introduce the covariance matrix of the genetic variant, , that conveys the genetic relatedness or pedigree structure of individuals. For unrelated individuals, Σw is the identity matrix. For related individuals in families, Σw is the expected kinship matrix, , and can be determined from pedigree information.
Second, we note that the covariance matrix of the gene-environment interaction variable, , can be derived from w through the vector of environmental exposure, d, given in Equation 8. Briefly, we replace the definition of v through elementwise multiplication of vectors w and d and introduce a matrix . Treating E as a constant matrix and w as a random vector, we obtain . This expression can be further simplified by defining a new matrix D and using the Hadamard product operator:
| (20) |
While the case of unrelated individuals with is trivial, we denote a special kinship matrix KD for related individuals when .
| (21) |
A numerical example of matrices E, D, K, and KD for nuclear families and binary exposure is provided in Supplementary material.
Third, we approximate the quadratic forms via their expected values. If is a vector of random variables with mean μ and (nonsingular) covariance matrix Σ, then the quadratic form is a scalar random variable with the following mean.
| (22) |
| (23) |
Because the variables w and v are standardized, we obtain the following approximations:
| (24) |
| (25) |
In this work, we consider several LMM-based scenarios with particular structures of covariance matrices Σy, Σw, and Σv (Tables 1 and 2). For each of these scenarios, we propose further approximations of Equations 24 and 25 using known relationships between the trace operator and eigenvalue decomposition (Lynch and Walsh 1998) outlined in Supplementary material.
Table 1.
Scenarios and covariance matrices for testing the marginal genetic effect
| Scenario | Model | Study design | Σy | Σw |
|---|---|---|---|---|
| Unrelated | LR | Unrelated | I | |
| Families | LMM | Related | K | |
| Unrelated+Grouping | LMM | Unrelated | I | |
| Unrelated+GRM | LMM | Unrelated | I |
The relationship matrices are as follows: K is the kinship matrix; F is the group-membership matrix; G is the GRM.
Table 2.
Scenarios and covariance matrices for testing the gene-environment interaction effect
| Scenario | Model | Study design | Σy | Σv |
|---|---|---|---|---|
| Unrelated | LR | Unrelated | diag(D) | |
| Families | LMM | Related | ||
| Unrelated+ Grouping | LMM | Unrelated | diag(D) | |
| Unrelated+ GRM | LMM | Unrelated | diag(D) |
The relationship matrices specific to testing gene-environment interactions are as follows: KI is an interaction kinship matrix (Sul et al. 2016); GI is an interaction genetic relationship (GRM) matrix defined similarly to KI.
Data Simulation
We compared relative power across four GWAS scenarios (Tables 1 and 2) with various study designs (unrelated or related individuals in families) and using LR or LMM. When analyzing unrelated individuals using an LMM and testing the marginal genetic effect, we considered a single random effect, either a grouping factor (e.g., household) or a polygenic effect with a GRM (Yang et al. 2014). In all the scenarios, the vector of trait y was standardized, so that the sum of variance components in Σy (scalars ) was equal to 1. In simulations, the parameters , and refer to the additive heritability in the family-based study, the heritability explained by genetic variants in the study of unrelated individuals [i.e., the SNP-based heritability (Yang et al. 2014)], the variance explained by a grouping factor, and the residual variance, respectively.
We conducted multiple simulations for a quantitative trait drawn from a multivariate normal distribution with the variance components specified in Tables 1 and 2. In the power analysis testing the marginal genetic effect, we simulated a single causal variant and specified its effect size β explaining 0.1% of the trait variance. In the power analysis testing the gene-environment interaction effect, we specified δ so that the (standardized) gene-environment interaction term explaining 0.1% of the trait variance (standardized main genetic and environmental effects each explains an additional 0.1% of trait variance). See Supplementary material for more details.
When simulating related individuals, we generated data for nuclear families with 2 parents and 3 offspring, if not specified otherwise. Accordingly, the kinship matrix K was added as a component of Σy for controlling the family structure in the trait covariance. A special matrix KI was also included in Σy when testing the gene-environment interaction (Sul et al. 2016). Note that matrices KD in Equation 21 and KI in ref. (Sul et al. 2016) are different, although both are derived from the kinship matrix K. In simulations of unrelated individuals with a grouping factor, each group consisted of 5 individuals. Thus, the variance-covariance matrix F is a Kronecker product of block and diagonal matrices, where each block matrix is a 5 × 5 matrix of ones.
Analysis of the UK Biobank
We first split the UK Biobank individuals into unrelated and related groups using the kinship coefficients estimated by KING (Manichaikul et al. 2010) and additionally distinguished different types of related pairs, as described in the original UK Biobank article (Bycroft et al. 2018) (Supplementary Table S2). For the analysis of unrelated individuals in the UK Biobank, we performed two LR- and LMM-based GWAS and then estimated the ESS multiplier between the two studies (rows 1 and 4 in Table 1). We followed a computationally efficient approach of low-rank LMM (Kang et al. 2010; Listgarten et al. 2011; Young et al. 2018), where the LMM has a single random genetic effect with the GRM constructed on a subset of the top 1000 SNPs, as described in another UK Biobank application (Young et al. 2018). In brief, we ranked the SNPs by their LR-based P-values, performed a clumping by PLINK 2.0 (Chang et al. 2015) with the default parameters, and selected the top 1000 SNPs to build the GRM. We also applied the standard leave-one-chromosome-out scheme (Yang et al. 2014; Young et al. 2018) and built per-chromosome GRMs when testing the SNPs. In practice, we never built the GRM and always performed linear algebra operations making use of the low-rank structure of the genotype matrix (1000 columns), applying the Woodbury formula for matrix inversion (Young et al. 2018). The analysis was restricted to 336,347 unrelated individuals of British ancestry passing principal component analysis filters and having no third-degree or closer relationships (Bycroft et al. 2018); 619,017 high-quality genotyped autosomal SNPs with missingness <10% and minor allele frequency >0.1% (Loh et al. 2018); and six anthropometric traits, including body mass index (BMI), height, hip circumference (HIP), waist circumference (waist), weight and waist-to-hip ratio (WHR). To account for population structure, 20 principal components (PCs) were included as covariates. We note that the low-rank LMM GWAS is not the most powerful strategy (Yang et al. 2014) and a standard full-genome GRM would lead to higher power. However, the latter approach is extremely computationally demanding, and the low-rank approach was sufficient to compare the relative performance of the ESS multipliers.
Efficient computation
The calculation of the parameters in Equations 24 and 25 requires inverting the trait covariance matrix Σy. This step is prohibitive in large datasets, so we have developed several solutions to mitigate the computational burden. When Σy is dense, we follow the low-rank LMM approach implemented in the custom R package biglmmz. Our package is built on the top of two R packages bigstatsr and bigsnpr with statistical methods for large genotype matrices stored on disk (Privé et al. 2018). When Σy is sparse, we apply special linear algebra methods for sparse matrices implemented in the R package Matrix; a similar approach was recently proposed for biobank-scale association studies (Jiang et al. 2019). In both analytical derivations and analysis of family-based data, we make use of the block structure of relationship matrices whenever possible.
Data availability
The individual-level genotype and phenotype data are available through formal application to the UK Biobank http://www.ukbiobank.ac.uk. The R package biglmmz, developed to perform low-rank mixed-model GWAS and calculate the effective size multiplier, is available at https://github.com/variani/biglmmz. The scripts to reproduce results of simulations and UK Biobank analyses can be found at https://github.com/variani/paper-neff.
Results
Analytical estimators for the ESS multipliers
Consider a genetic variant w with effect β on a quantitative trait y, where the covariance matrices of the trait and genetic variant are denoted by Σy and Σw, respectively. We analytically derived the ESS multiplier quantifying the relative power between the LR and LMM tests across the four scenarios described in Table 1. Using the approximation given in Equation 24 (Methods), the NCP from the LMM and the multiplier can be approximated as follows:
| (26) |
| (27) |
We next expanded Equation 27 for each scenario in Table 1, taking into account that Σy is a weighted sum of only two components: a symmetric matrix and the identity matrix (see Supplementary material). Using eigenvalue decomposition of symmetric matrices K, F, or G and denoting eigenvalues with , we obtain expressions of for each scenario in Table 1.
| (28) |
| (29) |
| (30) |
The multiplier for the Families scenario can be further simplified if, for example, the study design is based on related pairs such as full-sibling pairs. If s is the number of related pairs within each family and r is the relatedness between pairs, then is a function of s, r, and the variance components (see Supplementary material).
| (31) |
We similarly derived the NCP parameter for power to detect the gene-environment interaction effect δ (Table 2). Given that the covariance matrices of the trait and interaction variable are Σy and , respectively, and the matrix D is defined in Equation 20, we obtain the following approximation.
| (32) |
| (33) |
We validated our approximations in Equations 26 and 32 through series of simulations for six cases: the test of marginal genetic effect using LR in unrelated individuals (Supplementary Figure S1); the test of marginal genetic effect using LMM in nuclear families of two parents and three offspring (Supplementary Figure S2); the test of gene-environment interaction effect using LR in unrelated individuals (Supplementary Figure S3); and the test of gene-environment interaction effect using LMM with either two or one genetic variance components in related individuals (Supplementary Figures S4 and S5). For each case, we ran 1000 replicates with a quantitative trait simulated as a function of the variance captured by genetic variant/environmental exposure for sample size N of 100, 500, and 1000. We estimated six parameters for each model: the effect size of tested variable, its standard error, the corresponding test statistic, the residual variance, the empirical ESS multiplier based on ratios of standard errors , and the power of the test at . We confirmed that the proposed analytical ESS estimators and are valid and aligned with the estimated model parameters.
Testing the marginal genetic effect
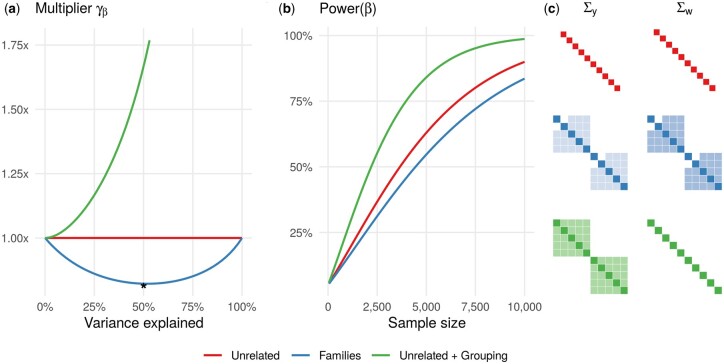
Power loss in related individuals: We first conducted a simulation study to examined the relative power for the Families scenario with (Table 1), varying the heritability parameter . For nuclear families with two parents and three offspring, the ESS multiplier is strictly less than 1 at all values of heritability and equal to 1 at extreme heritability values of 0 and 1 (blue lines in Figure 1, A and B). The amount of power loss depend directly on the structure of the matrices Σy and . For example, the kinship matrix K for nuclear families with a greater number of offspring leads to a greater loss, as K becomes denser (Supplementary Figure S6). In study designs based on related pairs, monozygotic twin pairs show a power loss of up to 50% at , as expected, while the power loss for pairs of siblings or cousins is only moderate (Supplementary Figure S7). The performance of the multiplier for the Families scenario is quantitatively described by Equation 27, in which the trace operator is applied to the product of two matrices and . The decrease in the ESS in this scenario can intuitively be associated to the smaller off-diagonal term in the covariance matrix Σy as compared to Σw (Figure 1C).
Figure 1.
The relative power of detecting marginal genetic effect β. (A) The ESS multiplier is less than one for the Families scenario and greater than one for the Unrelated+Grouping scenario compared to the baseline Unrelated scenario. The amount of variance explained by the random effect ( or ) varies from 0 to 100%. (B) The power of detecting β increases with the sample size at different rates for the Unrelated, Families, and Unrelated+Grouping scenarios. The random effect and genetic variant explain 50 and 1% of trait variance, respectively. (C) The covariance matrices of the trait and genetic variant Σy and Σw (used to compute ) are depicted when 50% of the trait variance is explained by the random effect (denoted by * on panel A).
Power gain by reducing the residual variance: We then examined the case of unrelated individuals structured into groups (the Unrelated+Grouping scenario in Table 1), varying the amount of variance explained by the grouping factor . In contrast to the power loss for the Families scenario across all values of heritability, the power gain for the Unrelated+Grouping scenario compared to the Unrelated scenario is consistent and increases as more variance is explained (Figure 1, A and B). The observed increasing trend follows from Equations 27 and 29 if one considers the trace operation and takes into account that . Thus, having individuals genetically unrelated () and explaining additional variance by a random effect is equivalent to a reduction in the residual variance by including covariates (Yang et al. 2014). We further note that two scenarios, Unrelated+Grouping and Unrelated+GRM (Table 1), are conceptually identical, because the individuals are genetically unrelated. This relationship implies that the observed trends in Figure 1 for the Unrelated+Grouping scenario are transferable to the Unrelated+GRM scenario. We confirmed this statement by simulations under the Unrelated+GRM scenario (Supplementary material).
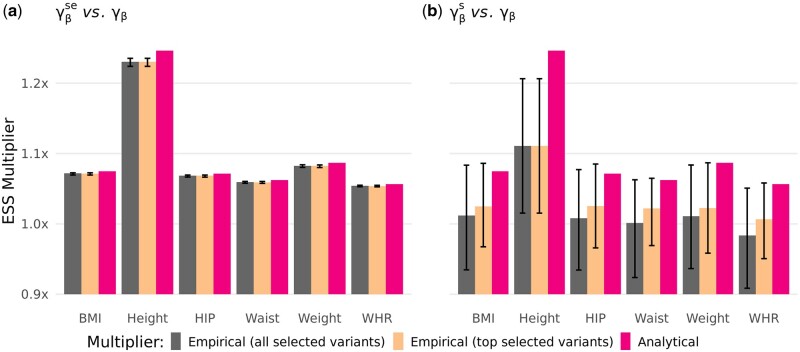
Modest power gain by a low-rank LMM in unrelated individuals in the UK Biobank: When applying a low-rank LMM to 336,348 unrelated individuals in the UK Biobank, we achieved a modest power gain, as expected, with a maximum of 1.2x for height (Figure 2). The two multipliers and produce very close estimates (Figure 2A) confirming the relevance and concordance of both estimators. Small differences in estimates are explained by applying the leave-one-chromosome-out (LOCO) scheme when producing association summary statistics for , while the results for in Figure 2 are based on the model with variants in all chromosomes. These differences are not noticeable if both multipliers and are estimated in the per-chromosome manner (Supplementary Figure S15). The other empirical multiplier , based on ratio of test statistics rather than standard errors, underestimates the value of the multiplier consistently for all traits (Figure 2B). The downward bias of is in agreement with our simulation results for the Unrelated+GRM scenario (Supplementary material), where we showed that inclusion of null variants into can bias the multiplier down to one. Even if the assumptions underlying this estimator holds (see Methods), the multiplier is expected to give much nosier estimates compared to , because the ratios of squared test statistics have a substantially wider distribution than the ratios of squared standard errors (the error bars in Figure 2).
Figure 2.
The accuracy of two empirical multipliers (A) and (B) is evaluated against the analytical multiplier (red bars). Association studies of six anthropometric traits are performed using LR and low-rank LMM in 336,347 UK Biobank unrelated individuals. The empirical multipliers are estimated from the tests statistics of the top 1000 associated variants for each trait: all 1000 variants (dark gray bars) and a subset of 1000 variants (significant in LMM, PLMM < , and nominally significant in LR, PLR < 0.05) (beige bars). The error bars show the distribution of ratios of squared standard errors () or test statistic () between the LMM and LR models, denoting first to third quartiles.
Small power loss in related individuals in the UK Biobank: We obtained estimates of the ESS multiplier for several groups of related pairs in the UK Biobank: monozygotic twins, parent-offspring, full siblings, and second-degree relatives. For 68,910 close relatives of up to the second degree, the maximum drop in the ESS of 0.94x is observed at a heritability of . We additionally derived the expected value of the multiplier stratified by groups of related pairs when varying (Supplementary Figure S8 and Table S3). Considering the impact of relatedness in the whole UK Biobank sample, the 0.94x multiplier in related individuals is scaled to 0.99x in a combined sample of unrelated and related individuals.
Testing the gene-environment interaction effect
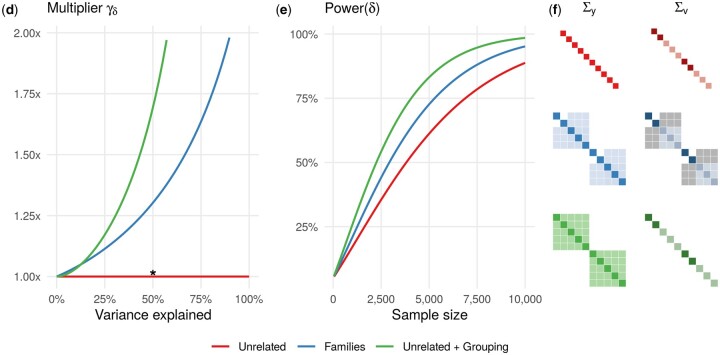
Power depends on the realized environmental exposure and variance components: We explored the power gain for the Families and Unrelated+Grouping scenarios over the baseline Unrelated scenario when testing the gene-environment interaction effect (Figure 3). The frequency of binary exposure was fixed to 0.6 for all three scenarios, but for the Families scenario, we additionally fixed the exposure status in such a way that two parents were unexposed and three offspring were exposed. Figure 3, A and B shows that the ESS multiplier for the Unrelated+Grouping and Families scenarios is always greater than 1 and increases as more variance is explained. This positive trend remains for the Unrelated+Grouping and Unrelated+GRM scenarios with other realizations of exposure, as the residual variance is simply reduced and individuals are unrelated. Contrary to the Unrelated+Grouping and Unrelated+GRM scenarios, the power gain for the Families scenario was achieved through a particular realization of exposure and covariance matrices Σy and Σv, as shown in Figure 3C.
Figure 3.
The relative power of detecting the gene-environment interaction effect δ. The frequency of binary exposure is 0.6; the exposure status is fixed for the Families scenario such that two parents are unexposed and three offspring are exposed. (A) The ESS multiplier is greater than one for both Families and Unrelated+Grouping scenarios compared to the baseline Unrelated scenario. The amount of variance explained by the random effects ( or ) varies from 0 to 100%. (B) The power of detecting δ increases with the sample size at different rates for the Unrelated, Families and Unrelated+Grouping scenarios. The random effects (jointly) and the interaction variable explain 50% and 1% of trait variance, respectively. (C) The covariance matrices of the trait and interaction variable Σy and Σv (used to compute ) are depicted when 50% of trait variance is explained by random effects (denoted by * on panel A). The colored gradients in entries of matrices denote quantitative differences for positive values, while gray-colored entries correspond to negative values. The ratio between and is fixed to 0.1; both genetic and environmental variables also explain 1% of the trait variance in addition to 1% of the interaction variable.
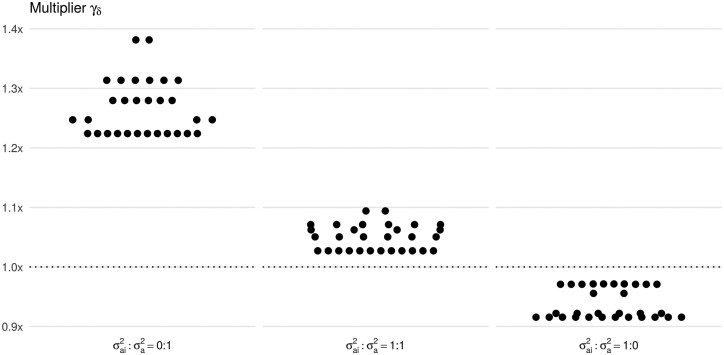
We next explored in more depth the relative power for the Families scenario as a function of the exposure realization and the interplay between covariance matrices Σy and Σv (Figure 4). In particular, we considered all possible realizations of the binary exposure variable within families and also varied the composition of variance components in while fixing the total genetic variance, . When the structure of Σy is fully defined by the kinship matrix K (, Figure 4, left panel), the multiplier is greater than 1.2 for all realizations of exposure, and the greatest power gain of 1.38 is achieved when all the offspring are either exposed or unexposed. With the increasing contribution of the environmental kinship matrix KI into the structure of Σy ( or , Figure 4, middle and right panels), the multiplier approaches 1 and remains below 1 at . This phenomenon occurs because the covariance matrices Σy and Σv become similar in their structure, leading to a power loss. This phenomenon is similar to the analysis of the Families scenario when the testing marginal genetic effect (Figure 1, Supplementary Figures S6–S8).
Figure 4.
The relative power of detecting the gene-environment interaction effect δ in nuclear families under different simulation settings. The ESS multiplier is analytically computed (i) for all possible realizations of a binary exposure within a nuclear family with 2 parents and 3 offspring (dots in each panel) and (ii) for different ratios between and (three panels). The amount of the trait variance is jointly explained by the random effects and is fixed to 50%. The largest two values of the multiplier on the left and middle panels correspond to exposure realizations: exposed offspring/unexposed parents and exposed parents/unexposed offspring.
Conclusions
LMMs are being increasingly used in GWAS. While of great benefit, the inference of mixed model parameters carries a much heavier computational burden than standard LR models and introduces substantial analytical complexities. Here, we introduced the formula for the ESS, a synthetic measure that bridges LR and LMMs. We showed how the NCP of mixed-model association tests relates to the NCP of LR conditional on the trait covariance and genetic relationship matrices. We further introduced the ESS multiplier, defined as a ratio between NCPs of the two tests, derived its expected value across various scenarios, and linked it to previously discussed empirical multiplier. Our characterization of the proposed multiplier covers common scenarios: testing the marginal genetic effect in family-based studies and in studies of unrelated individuals, as well as the extension to gene-environment interaction studies.
Conceptually, the ESS multiplier compares a given mixed-model GWAS to a virtual GWAS based on LR with a sample size that yields the same power. This definition of the ESS leads to the analytical form in Equation 17, where the ESS is a function of only the variance of the estimated effect size . There are several connections to recent developments in mixed-model methods for GWAS. First, the ESS estimator based on is expected to perform well because of the ESS definition, as shown in the previous works (Yang et al. 2012). Second, the ESS multiplier is not quite the same as the scaling constant used to approximate the test statistics by the modern mixed-model association tools (Svishcheva et al. 2012; Loh et al. 2018; Zhou et al. 2018). This scaling constant would be equal to our multiplier only in studies of unrelated individuals. Third, our approximation of the ESS in Equation 27 is derived using expectations of quadratic forms and, thus, is linked to the randomized trace estimator recently proposed for the LMM inference (Pazokitoroudi et al. 2019).
When post-GWAS methods of mixed-model GWAS summary statistics rely on the reported sample size, we recommend using the ESS multiplier to derive the ESS. Previous works have shown that ignoring the correction by the ESS can produce misleading results such as overestimation of heritability enrichment (Gazal et al. 2017) and inaccurate fine-mapping of causal variants (Yang et al. 2012). The correction is especially important when the power boost by LMM is substantial (Loh et al. 2018). For example, the linkage disequilibrium (LD) score regression (Bulik-Sullivan et al. 2015; Finucane et al. 2018) explicitly includes the sample size in its model, and the empirical multiplier in Equation (18) was proposed for correction (Gazal et al. 2017). While the assumptions underlying this approach seems reasonable, especially for large powerful GWAS including numerous genome-wide significant SNPs, our real data analysis suggests it should be used with caution. For some other methods, such as meta-analysis, correction by the ESS multiplier is required when weighting the effect estimates by the sample size. However, the inverse-variance weighted approach implicitly solves the problem, as the variance of estimates from the LMM carries on the information from the ESS multiplier.
Since most GWAS designs to-date are composed predominantly of unrelated individuals, we expect the adjustment to the ESS due to family relatedness in existing datasets to be modest. For example, we estimated that the ESS multiplier in 68,910 related individuals of British ancestry in the UK Biobank is at most 0.94x. However, the proposed ESS multiplier is likely to have a larger impact in the future for large-scale studies of founder populations (Kim et al. 2020) and healthcare studies (Staples et al. 2018). Moreover, this work is of immediate interest for all post-GWAS analyses using summary statistics from related individuals, providing guidelines and tools for accurately estimating the ESS. Our framework also provides new perspectives for improving the power of gene-environment interaction analyses through the optimization of family-based designs. For example, we showed that the power of gene-environment interaction screening can be increased substantially by using nuclear families with exposed offspring and unexposed parents. In principle, these results suggest that the power from cohorts of related individuals can be assessed before conducting actual GWAS screening of gene-environment interactions.
There are still several methodological issues arising in GWAS that are also relevant to our work. In particular, population stratification continues to be a limiting factor in GWAS and can lead to spurious associations and biased estimates of effect sizes (Jiang et al. 2019; Sohail et al. 2019). Our analytical ESS results were derived under the assumption of controlled population structure and tested only in relatively homogeneous data from UK Biobank individuals of British ancestry. As previously demonstrated (Sethuraman, 2018), the structure in admixed populations can substantially impact the estimates of genetic relatedness, and further investigation is needed to determine the impact of population structure on the analytical form of the ESS multiplier. Nevertheless, we anticipate that the empirical multiplier based on the ratios of squared standard errors remains relevant and interpretable, as long as the GWAS results are unbiased and the type I error rate is correctly controlled. Finally, we limited our analytical derivations to quantitative traits, and future work is needed to extend our results to binary traits under a liability threshold model (Lee et al. 2011).
In conclusion, the proposed analytical multiplier offers a comprehensive framework that can be used to provide insights into the statistical power of LMM as a function of the sample relatedness and the variance explained by the genetic and environmental factors. It can also be used for post-GWAS analyses explicitly requiring the ESS. Alternatively, the empirical multiplier based on the ratios of standard errors is expected to work equally well, providing a simpler and faster solution when individual-level data is not available.
Acknowledgments
This work was supported by the National Institutes of Health grants R21HG007687 (National Human Genome Research Institute) and R01CA194393 (National Cancer Institute). The research was conducted using the UK Biobank Resource under application #16549.
Conflicts of interest: None declared.
Literature cited
- Aschard H. 2016. SI: a perspective on interaction effects in genetic association studies. Genet Epidemiol. 40:678–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulik-Sullivan BK, Loh P-R, Finucane HK, Ripke S, Yang J, et al. 2015. LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat Genet. 47:291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bycroft C, Freeman C, Petkova D, Band G, Elliott LT, et al. 2018. The UK biobank resource with deep phenotyping and genomic data. Nature. 562:203–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, et al. 2015. Second-generation plink: rising to the challenge of larger and richer datasets. GigaSci. 4:s13742–015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W-M, Abecasis GR.. 2007. Family-based association tests for genomewide association scans. Am J Hum Genet. 81:913–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finucane HK, Reshef YA, Anttila V, Slowikowski K, Gusev A, et al. 2018. Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat Genet. 50:621–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman WJ. 2003. Candidate gene association analysis for a quantitative trait, using parent-offspring trios. Genet Epidemiol. 25:327–338. [DOI] [PubMed] [Google Scholar]
- Gazal S, Finucane HK, Furlotte NA, Loh PR, Palamara PF, et al. 2017. Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat Genet. 49:1421–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman WJ. 2002. Sample size requirements for matched case-control studies of gene-environment interaction. Stat Med. 21:35–50. [DOI] [PubMed] [Google Scholar]
- Jiang L, Zheng Z, Qi T, Kemper KE, Wray NR, et al. 2019. A Resource-Efficient Tool for Mixed Model Association Analysis of Large-Scale Data. Technical Report. Nature Publishing Group. [DOI] [PubMed] [Google Scholar]
- Joo JWJ, Hormozdiari F, Han B, Eskin E.. 2016. Multiple testing correction in linear mixed models. Genome Biol. 17:62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong S-y, et al. 2010. Variance component model to account for sample structure in genome-wide association studies. Nat Genet. 42:348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim HI, Ye B, Gosalia N, Köroğlu Ç, Hanson RL, et al. 2020. Characterization of exome variants and their metabolic impact in 6,716 American Indians from the southwest us. Am J Hum Genet. 107:251–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft P, Thomas DC.. 2000. Bias and efficiency in family-based gene-characterization studies: conditional, prospective, retrospective, and joint likelihoods. Am J Hum Genet. 66:1119–1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Wray NR, Goddard ME, Visscher PM.. 2011. Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet. 88:294–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J, Liu Y, Kadie CM, Davidson RI, Heckerman D, et al. 2011. Fast linear mixed models for genome-wide association studies. Nat Methods 8:833–853. [10.1038/nmeth.1681] [DOI] [PubMed] [Google Scholar]
- Loh P-R, Kichaev G, Gazal S, Schoech AP, Price AL.. 2018. Mixed-model association for biobank-scale datasets. Nat Genet. 50:906–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B.. 1998. Genetics and Analysis of Quantitative Traits. Vol. 1.Sinauer Sunderland. [Google Scholar]
- Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, et al. 2010. Robust relationship inference in genome-wide association studies. Bioinformatics. 26:2867–2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pazokitoroudi A, Wu Y, Burch KS, Hou K, Pasaniuc B, et al. 2019. Scalable multi-component linear mixed models with application to SNP heritability estimation. bioRxiv. 522003. [Google Scholar]
- Privé F, Aschard H, Ziyatdinov A, Blum MG.. 2018. Efficient analysis of large-scale genome-wide data with two r packages: bigstatsr and bigsnpr. Bioinformatics. 34:2781–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sethuraman A. 2018. Estimating genetic relatedness in admixed populations. G3 (Bethesda). 8:3203–3220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham PC, Cherny SS, Purcell S, Hewitt JK.. 2000. Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am J Hum Genet. 66:1616–1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail M, Maier RM, Ganna A, Bloemendal A, Martin AR, et al. 2019. Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. Elife. 8:e39702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staples J, Maxwell EK, Gosalia N, Gonzaga-Jauregui C, Snyder C, et al. 2018. Profiling and leveraging relatedness in a precision medicine cohort of 92,455 exomes. Am J Hum Genet. 102:874–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul JH, Bilow M, Yang W-Y, Kostem E, Furlotte N, et al. 2016. Accounting for population structure in gene-by-environment interactions in genome-wide association studies using mixed models. PLoS Genet. 12:e1005849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung YJ, Winkler TW, Manning AK, Aschard H, Gudnason V, et al. 2016. An empirical comparison of joint and stratified frameworks for studying g× e interactions: systolic blood pressure and smoking in the charge gene-lifestyle interactions working group. Genet Epidemiol. 40:404–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svishcheva GR, Axenovich TI, Belonogova NM, Van Duijn CM, Aulchenko YS.. 2012. Rapid variance components-based method for whole-genome association analysis. Nat Genet. 44:1166–1170. [DOI] [PubMed] [Google Scholar]
- Tucker G, Price AL, Berger B.. 2014. Improving the power of GWAS and avoiding confounding from population stratification with PC-select. Genetics. 197:1045–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilhjálmsson BJ, Yang J, Finucane HK, Gusev A, Lindström S, et al. 2015. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am J Hum Genet. 97:576–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Andrew T, Nyholt DR.. 2008. Genome-wide association studies of quantitative traits with related individuals: Little (power) lost but much to be gained. Eur J Hum Genet. 16:387–390. [DOI] [PubMed] [Google Scholar]
- Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, et al. 2017. 10 Years of GWAS Discovery: biology, function, and translation. Am J Hum Genet. 101:5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Ferreira T, Morris AP, Medland SE, Madden PA, et al. 2012. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat Genet. 44:369–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Weedon MN, Purcell S, Lettre G, Estrada K, et al. 2011. Genomic inflation factors under polygenic inheritance. Eur J Hum Genet. 19:807–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Zaitlen NA, Goddard ME, Visscher PM, Price AL.. 2014. Advantages and pitfalls in the application of mixed-model association methods. Nat Genet. 46:100–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young AI, Wauthier FL, Donnelly P.. 2018. Identifying loci affecting trait variability and detecting interactions in genome-wide association studies. Nat Genet. 50:1608–1614. [DOI] [PubMed] [Google Scholar]
- Zhou W, Nielsen JB, Fritsche LG, Dey R, Gabrielsen ME, et al. 2018. Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. Nat Genet. 50:1335–1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The individual-level genotype and phenotype data are available through formal application to the UK Biobank http://www.ukbiobank.ac.uk. The R package biglmmz, developed to perform low-rank mixed-model GWAS and calculate the effective size multiplier, is available at https://github.com/variani/biglmmz. The scripts to reproduce results of simulations and UK Biobank analyses can be found at https://github.com/variani/paper-neff.