Abstract
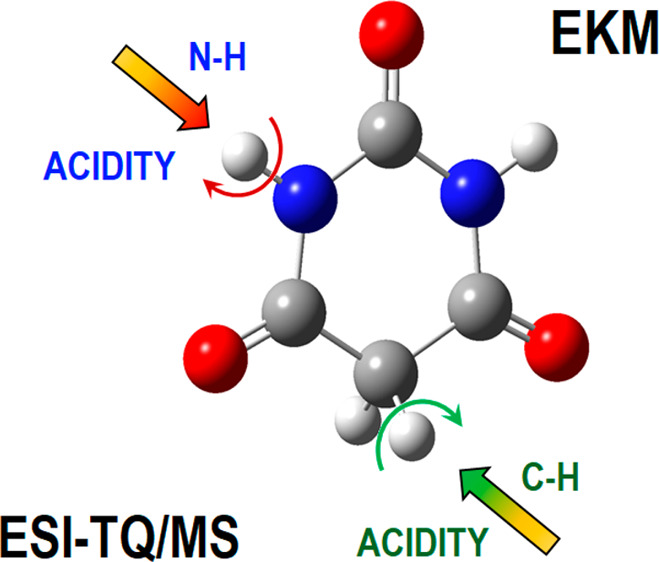
The gas phase acidities (GA) of 5,5-alkylbarbituric acids have been experimentally determined by electrospray ionization-triple quadrupole (ESI-TQ) mass spectrometry and by using the extended kinetic Cooks method (EKCM). The GAs of C–H (1330.9 ± 10.0 kJ mol–1) and N–H (1361.5 ± 10.5 kJ mol–1) deprotonated sites of bifunctional barbituric acid were determined from the selective production of their corresponding heterodimers. The GA value in the N–H site was confirmed by measuring the GAs of 5,5-dimethyl- and 5,5-diethyl barbituric acids (∼1368 kJ mol–1). The experimental results have been rationalized and discussed with the support of quantum chemical calculations with Gaussian-n (G3 and G4) composite methods, which confirmed the excellent consistency of the results.
Keywords: gas phase-acidity, alkyl-barbituric acids, extended kinetic Cooks method
Introduction
Barbituric acid (1, C4H4N2O3) is an organic compound synthesized for the first time in 1864 by Adolf von Baeyer.1 Its chemical structure is based on a pyrimidine heterocyclic skeleton and is widely used in the pharmaceutical preparation of several derivatives, e.g., the barbiturates, which are well-known for applications in medicinal chemistry due to their biological activities such as hypnotic, sedative, anticonvulsant, anesthetic, antioxidant agent, antibacterial, antifungal, antiviral, and antitumor properties.2−6
Barbituric acid, itself, is not biologically active, and the pharmacological properties of its derivatives mainly depend on the side groups attached to the C5 atom of the pyrimidine ring (Figure 1). This C5 position in the molecular structure is considered an active site because it can act either as electrophilic or nucleophilic centers. Some C5-substituted and disubstituted barbituric acids are known to exhibit pharmacological and biological activities.7
Figure 1.
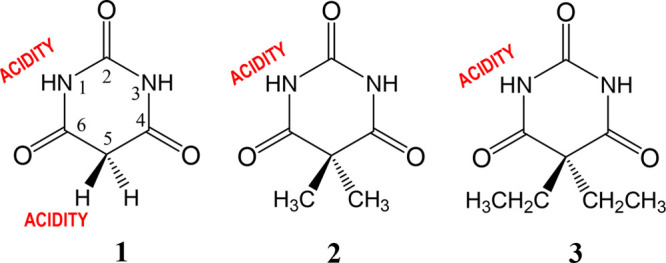
Molecular structure of 5,5-dialkylbarbituric acids, showing the acidic sites.
Another relevant structural feature of barbituric acid is that it contains five additional donor–acceptor sites (three O and two N). Its enolizable hydrogen atoms are bonded to either nitrogen, carbon, or oxygen atoms, resulting in various tautomeric forms. Theoretical and experimental studies on barbituric acid and its derivatives show that the keto-tautomer is the most stable form in the gas phase,8,9 as well as in solution,10,11 while in the solid state, Schmidt et al.12 revealed that the most thermodynamically stable form is a polymorph species formed by the enol tautomer.
The gas phase acidity (GA) of barbituric acid, structure 1 shown in Figure 1, was measured by Kebarle et al.13−15 using an equilibrium method (at 500–600 K) with a pulsed electron beam high-pressure ion source mass spectrometer. The corresponding value, GA (1) = 1369.4 ± 8.4 kJ mol–1, has been reported in the NIST database16 and the authors suggested that it is related to the deprotonation in the carbon–hydrogen (C–H) site.
Electrospray ionization sources (ESI) and mass spectrometry techniques are known as powerful tools to investigate structural, energetic, and other physical chemistry properties of thermolabile biomolecules and other species with low vaporization pressures.17 In addition, the Cooks kinetic method (CKM)18,19 has been widely employed to study the kinetics and thermodynamic properties of chemical reactions. Fenselau et al.,20,21 Wesdemiotis et al.,22,23 Armentrout et al.,24,25 among others, have improved the KM method by including entropic effects on the competitive dissociations of a mass-selected proton-bound heterodimer (cluster) ions, resulting in the so-called “extended kinetic method, EKM”.
The present work employs electrospray ionization-triple quadrupole (ESI-TQ) mass spectrometry and the extended kinetic method to investigate the deprotonation processes of the bifunctional barbituric acid, 1 (Figure 1), for which the acidic site is located either on nitrogen (N–H) or carbon atoms (C–H). In addition, with the purpose of providing reliable pathways to establish the consistency of the both acidity measurements of 1 and particularly to confirm the N–H acidity, we have selected similar structures such as those of the 5,5-dimethyl barbituric (2) and 5,5-diethyl barbituric (3, barbital) acids (Figure 1). Each of these structures features only one acidic site (N–H), because the α-carbon site is blocked by, respectively, two-methyl and two-ethyl groups. Furthermore, it is known that the methylation of some N-heterocyclic molecules, such as uracils, produces little effect on the N–H acidity.26
By using this approach, which shall be explained in detail throughout the text, we have been able to establish a consistent GA value for 1, which is discussed and compared with the previously reported value in the literature. In addition, we have determined for the first time the GA values for the structures 2 and 3.
Experimental Section
Chemicals
Barbituric acid (1, pyrimidine-2,4,6(1H,3H,5H)-trione), 5,5-diethylbarbituric acid (2, dimethylpyrimidine-2,4,6 (1H,3H,5H)-trione), and 5,5-diethylbarbituric acid (3, diethylpyrimidine-2,4,6(1H,3H,5H)-trione) samples, as well as the corresponding reference compound acids, were purchased from Merck/Sigma-Aldrich Co. and Alfa Aesar and used without further purification. The suitable reference compounds used in this work were chosen based on their known characteristic thermochemical properties and particularly for presenting similar GA (taken from NIST Database and shown in Table S1 in the Supporting Information) as compared to the target compound studied.
ESI-TQ Mass Spectrometry Measurements
The experiments were carried out on a triple-quadrupole mass spectrometer (TQ-MS) Agilent/Varian 320 equipped with an electrospray ionization (ESI) source. Approximately 5 × 10–5 M 5,5-alkylbarbituric acid and the appropriate reference acid were mixed (in a 1:1 mass ratio), and the mixture was dissolved in methanol–water solution (∼1:1, vol/vol). The solutions were directly infused into the ESI ionization source, operating in negative mode, at a flow rate of 10 μL/min. Air was used as the nebulizer gas. The drying gas temperature and the needle potential of ESI were optimized in the ranges of 100 to 280 °C and −3.5 to −6.0 kV, respectively. The adequate optimization of these parameters was a key factor to determine the acidity in the two different active sites of 1, as discussed later. The housing temperature and voltage of capillary were maintained at 50 °C and −21 V, respectively. The heterodimeric cluster anions were isolated in the first quadrupole, underwent collision induced dissociation (CID) in the second quadrupole, and finally the resulting fragments were analyzed in the third quadrupole (with the detector potential set at 2 kV). CID experiments were performed using argon as the collision gas (0.4 mTorr) in a center of mass energy (ECM) range of 0.75 to 4.0 eV. The center of mass energy was calculated as ECM = Elab[m/(M + m)] where Elab is the ion kinetic energy in the laboratory frame, m is the mass of the collision gas, and M is the mass of the heterodimeric cluster ion.
Kinetic Method (KM) and Extended Kinetic Method (EKM)
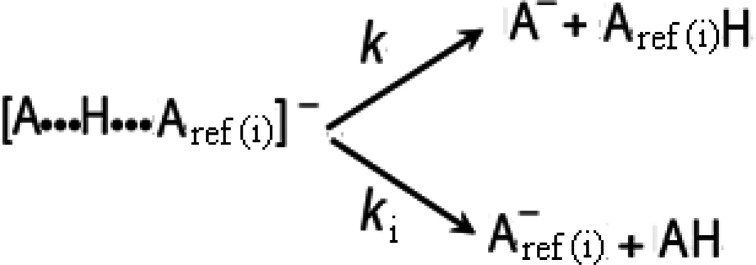
The kinetic method (EK), and its improved version (EKM), are based on the rates of competitive dissociation of mass selected cluster ions formed between a sample and a reference compound of known thermochemical properties. Therefore, to determine the gas phase acidity of a molecule AH, for instance, one must generate a proton-bound heterodimer anion [A***H***Aref(i)]−, where AH is the studied sample and Aref(i)H is a set of reference compounds with known GA experimental values.
These clusters are fragmented by collision-induced dissociation (CID) in a collision cell of the spectrometer to yield the corresponding monomeric anions of the sample A– and the reference Aref(i)–, via the two competitive dissociation channels with rate constants k and ki, respectively. If secondary fragmentation is negligible, the abundance ratio of these fragment ions, [A–]/[Aref(i)–], is equal to the ratio of the two dissociation rate constants, k/ki (Scheme 1) and the logarithm of this ratio is linearly related to the difference in the thermochemical property of interest (see eqs 2 and 3).27
Scheme 1. Collision-Induced Dissociations of [A***H***Aref(i)]−.
The gas-phase acidity (or merely acidity) of a protic acid AH, GA(AH), is defined as the Gibbs free-energy change for reaction 1:
| 1 |
The corresponding enthalpy and entropy changes for reaction 1 are referred to as gas-phase deprotonation enthalpy (ΔacidH°) and deprotonation entropy (ΔacidS°), respectively.
With the assumption that there are no reverse activation energy-barriers, the GAs of the sample AH and reference acids Aref(i)H are related by the linear eq 2, where R is the universal gas constant, and Teff is an “effective temperature” related to the excitation energy of the dissociating [A***H***Aref(i)]− heterodimers.28,29 In the third equality of the eq 2, the free energies (ΔG) are expressed in terms of enthalpies (ΔH) and entropies (ΔS).
| 2 |
In order to avoid the correlation of errors between the enthalpy and entropy differences, one must use the statistical procedure developed by Armentrout.24 Accordingly, eq 2 is converted into eq 3:
| 3 |
where ΔacidHrefavg represents the average of the deprotonation enthalpy of the acidic references. The entropic term Δ(ΔS°) is the difference of the activation entropies between the two competing dissociation channels which can be expressed as the difference in the deprotonation entropies of the AH and Aref(i)H acids, Δ(ΔS°) ≈ ΔacidS° – ΔacidSref(i)°. If the reference acids have similar deprotonation entropies, the last term can be substituted for the corresponding average entropy, ΔacidSref. One can note that eq 3 includes three unknown variables: ΔacidH°, RTeff, and ΔacidS°. These quantities can be obtained from two sets of thermokinetic plots. The first set consists of linear plots of ln([A–]/[Aref–]) vs [ΔacidHref(i)° – ΔacidHrefavg] with 1/RTeff as the slope, and the expression between brackets in eq 3 representing the negative Y-intercept values. These values (Y-intercepts and slopes) are taken and result in the second thermokinetic plot, which yields a straight line with the slope and Y-intercept given by [ΔacidH° – ΔacidHref] and −Δ(ΔS°), respectively. Thus, deprotonation enthalpy (ΔacidH°) and deprotonation entropy (ΔacidS°) can be obtained from these results. Consequently, the gas phase acidity GA value is derived from the general equation ΔG = ΔH – TΔS, where T = 298.15 K.
Computational Details
The quantum chemical calculations were carried out using the Gaussian 09 package.30 The geometry optimization and thermochemistry data calculations for the neutral 5,5-alkylbarbituric acids, as well as their corresponding deprotonated ions (see the Supporting Information), were obtained by using the Gaussian-n methods (Gn) at G3 and G4 high levels of theory.31,32 These theories have been described in detail in the literature and are well-known to provide very consistent results for a wide range of molecular systems.33,34
Results and Discussion
Proton-Bound Heterodimer Selection: Case of Barbituric Acid (1) with Two Deprotonable Sites (C–N and N–H)
In a previous work,35 we have applied the extended kinetic method (EKM) to determine the gas phase acidities (GA) of different deprotonable local groups of the same molecule (case of bifunctional hydroxycinnamic acids). The experimental-method development achieved the selective formation of specific hydrogen-bond heterodimers. Varying the drying-gas temperature in the ESI source and the solvents permitted us to generate the binding of reference acids to either local acid-groups of the hydroxycinnamic acids. Thus, the ability to select the gas-phase heterodimer was based particularly on the control of the desolvation process. However, for the barbituric acid case, we have observed that the variation of the drying gas temperature was not enough to select the specific heterodimers. It was also necessary to vary the potential needle of the ESI source. Figure 2 depicts the logarithm of the abundance ratio of ionic fragments, ln([A–]/[Aref(i)–]), in terms of two ESI-parameters: drying-gas temperature and needle-potential. Taking into account the abundance ratio of the ionic fragments, two noteworthy zones can be distinguished in this 3D-plot: (i) “high abundance ratio”, corresponding to the lowest values for both, drying-gas temperature and needle-potential (“soft conditions”), and opposite (ii) “low abundance ratio”, corresponding to the highest values for these considered ESI-parameters (“hardest conditions”).
Figure 2.
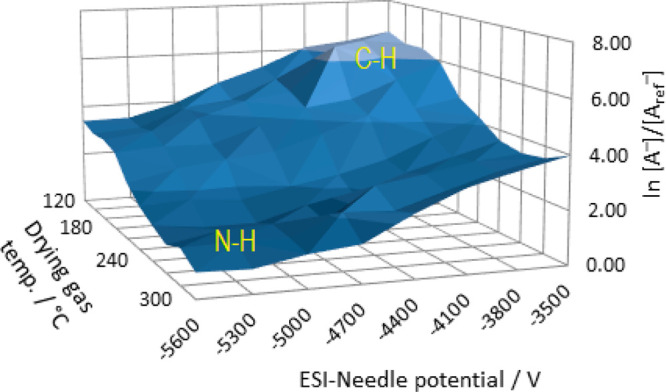
Typical 3D-plot of the natural logarithm of the abundance ratio, ln([A–]/[Aref–]), for AH = 1 and reference compound ArefH = 3-chlorobenzoic acid vs drying-gas temperature and needle-potential, both in the ESI source.
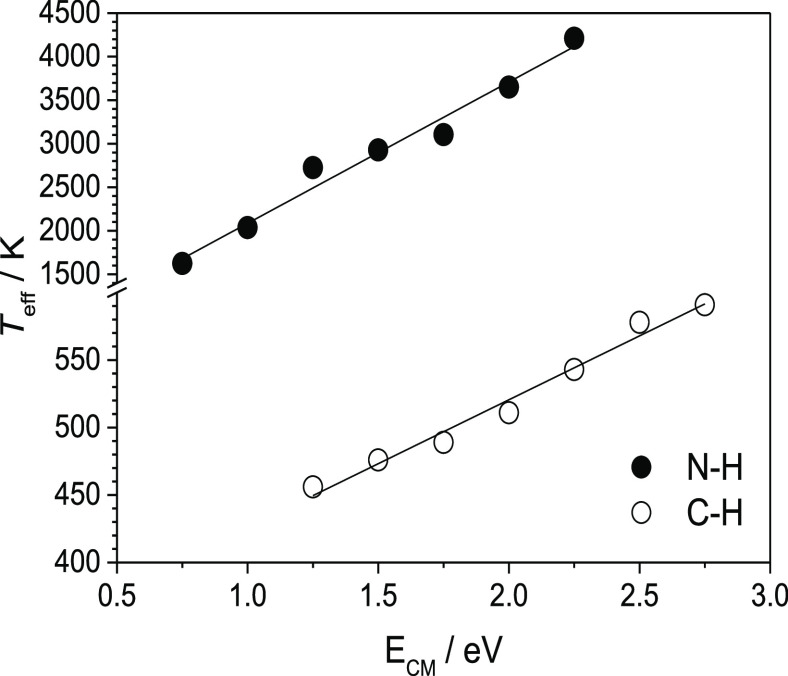
The first zone (“soft conditions”) would be related to the production of [A***H***Aref(i)]− heterodimers with weak hydrogen-bonds, which involve reference acids bonded to the more acid sites (C–H) of 1. On the contrary, the second zone (“hardest conditions”) would be related with heterodimers where the reference is bonded to the less acidic sites (N–H) of 1. In this context, and from a purely experimental point of view, we have found well-defined linear correlations between the “effective temperature” Teff (parameter associated with the excitation energy) and the center mass energy ECM of the selected dissociating heterodimers (Figure 3), where the low-values of Teff would be related to the “soft conditions” while Teff high-values would be related to the “hardest conditions”. Accordingly, we can affirm that at low temperatures only the C–H heterodimers are desolvated, and at high temperatures these heterodimers are rather selectively removed from the mixture by dissociation.
Figure 3.
Linear correlations of effective temperature (Teff) with center mass energies (ECM) for [A***H***Aref(i)]− heterodimers generated by reference acids bonded to either N–H or C–H acid sites of 1.
As mentioned above, we have established consistent experimental conditions to select heterodimers of the bifunctional barbituric acid attached to its C–H (“soft conditions”) or N–H (“hardest conditions”) groups with the purpose to determine the corresponding GA values. For the first case, we have chosen four compounds with low-GA reference acids (1328.0–1343.5 kJ mol–1): trifluoroacetic acid, salicylic acid, 4-nitrophenol, and 4-nitrobenzoic acid. Whereas for the second case, were chosen also four compounds but with high- GA reference acids (1360.6–1390.8 kJ mol–1): 3-trifluoromethyl benzoic acid, 3-chloro benzoic acid, 2-t-butyl benzoic acid, and 2-methyl benzoic acid. The corresponding thermochemical quantities for all these compounds are listed in Table S1 of the Supporting Information. The CID abundance ratios of the product ions were recorded, for both cases, at seven collision energies (ECM): from 1.25 to 2.75 eV for C–H and 0.75 to 2.25 eV for N–H sites.
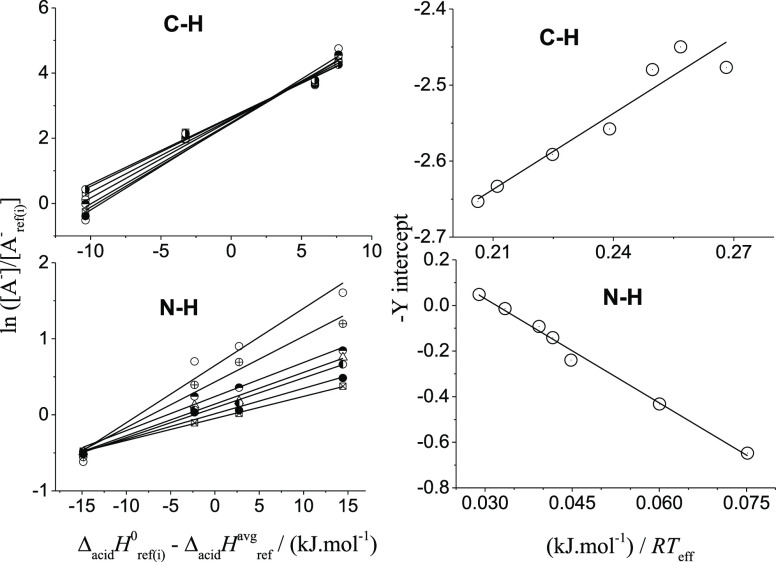
For each case, the logarithms of the abundance ratios, ln([A–]/[Aref–]), are plotted against the values of [ΔacidHref(i)° – ΔacidHrefavg] (1st thermokinetic plots, depicted in Figure 4,left). The linear regression analysis of these data yield straight lines with slopes 1/RTeff and the Y-intercepts of −[(ΔacidH0 – ΔacidHref)/RTeff – Δ(ΔS0)/R ].
Figure 4.
First (left) and second (right) sets of thermokinetic plots for the CH (up) and NH (down) groups of bifunctional barbituric acid (1), using CID data of selected [A***H***Aref(i)]− heterodimers. The symbols of left graphs correspond to seven collision energies (ECM).
These data are finally plotted (2nd thermokinetic plots, on the right of Figure 4). The deprotonation enthalpy ΔacidH° and entropy (ΔacidS°) for both the C–H and N–H sites of 1 were derived from linear-fit data of the second thermokinetic plots. As suggested by Armentrout,24 the uncertainties of the first thermo-kinetic plots were included in the second one. Our experimentally measured ΔacidH°, ΔacidS°, and ΔacidG° (= GA) were thus obtained from the ΔacidHrefavg, ΔacidSref, and their uncertainties. The corresponding results are shown in Table 1.
Table 1. Experimental Deprotonation Enthalpies (ΔacidH°), Entropies (ΔacidS°), and Gas Phase Acidities (GA) of 5,5-Alkylbarbituric Acids.
| GAtheora,d |
|||||
|---|---|---|---|---|---|
| ΔacidH0a | ΔacidS0b | GAa,c | G3 | G4 | |
| barbituric acid (C–H) | 1368.6 ± 10.0 | 125.5 ± 8.4 | 1330.9 ± 10.0 | 1332.6 | 1334.7 |
| barbituric acid (N–H) | 1389.1 ± 10.5 | 93.7 ± 8.4 | 1361.5 ± 10.5 | 1364.4 | 1369.8 |
| 5,5-dimethylbarbituric acid, 2 | 1404.2 ± 8.8 | 106.7 ± 8.4 | 1369.4 ± 8.8 | 1371.5 | 1369.0 |
| 5,5-diethylbarbituric acid, 3 | 1397.9 ± 8.8 | 98.7 ± 8.4 | 1368.2 ± 8.8 | 1367.7 | 1366.5 |
All values are given in kJ mol–1.
In J mol–1 K–1.
Derived from equation ΔG = ΔH – TΔS, with T = 298.15 K.
GA theoretical values calculated at G3 and G4 levels of theory.
The resulting slopes, Y-intercepts, effective temperatures (Teff), as well as the resulting uncertainties are summarized in Table S3 (Supporting Information). The comparison between the experimental and calculated thermochemical properties demonstrates good agreement (particularly with G3 methodology), being the deviation less than their corresponding experimental uncertainties (see Table 1).
It should be pointed out that the ancillary GA = 1369.4 ± 8.4 kJ mol–1 value reported by Cumming and Kebarle15 and currently recommended in the NIST database16 is much closer to the GA value of 1 deprotonated in N–H than in C–H site, as originally claimed. Therefore, our present results suggest that this value and assignment should be revised.
Acidity of 5,5-Dimethylbarbituric (2) and 5,5-Diethylbarbituric (3) Acids
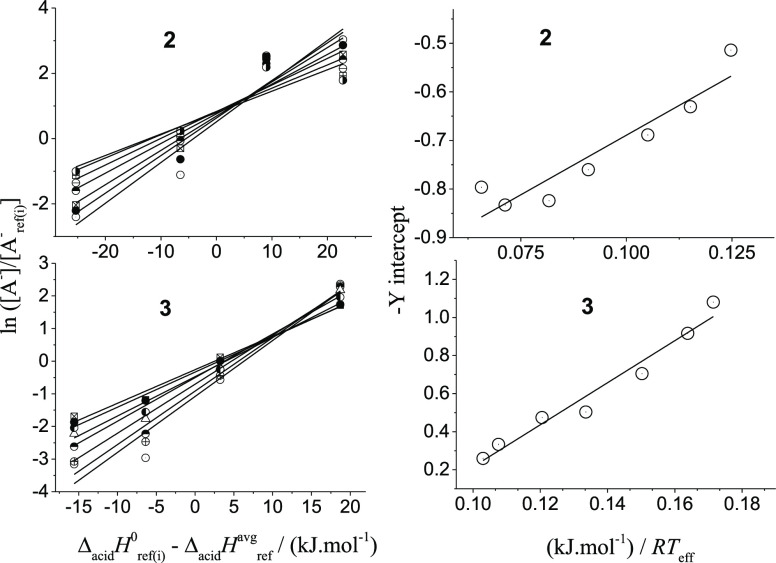
Four compounds with GAs ranging from 1343.5 to 1390.3 kJ mol–1 (listed in Table S1) were chosen as references for measuring acidity properties of both 2 (4-nitrophenol, 3-trifluorobenzoic acid, 4-hydroxybenzoic acid, 2-methyl benzoic acid) and 3 (4-nitrophenol, 4-nitro-5-methylphenol, 3-trifluoromethyl benzoic acid, 4-hydroxy benzoic acid). The CID abundance ratios of the product ions were recorded, for both compounds, at seven collision energies (ECM): from 1.0 to 4.0 eV. The EKM results were analyzed in the same manner as for 1 and are shown in Figure 5. The final derived thermochemical results are listed in Table 1. It is important to note that both, 2 and 3, are deprotonated in their N–H groups, and their corresponding thermodynamical acidity values (GA, ΔacidH° and ΔacidS°) are very close, indicating that the methylation of barbituric acid yields little effect on the N–H acidity. These results are also extended for 1, deprotonated at the same site. Finally, it is worth mentioning that a particularly good agreement has been achieved between the experimental and calculated acidity values (deviation less than 9 kJ mol–1), using the G3 and G4 composite methods.
Figure 5.
First (left) and second (right) sets of thermokinetic plots for monofunctional 5,5-dimethyl barbituric (2, upper) and 5,5-diethylbarbituric acids (3, lower), using CID data of [A***H***Aref(i)]− heterodimers. The symbols of the left graphs correspond to seven collision energies (ECM).
Conclusions
ESI-TQ mass spectrometry and the extended kinetic Cooks method (EKCM) have been employed to determine the gas phase GA, ΔacidH° and ΔacidS° for 5,5-alkylbarbituric acids: barbituric (1), 5,5-dimethyl barbituric (2), and 5,5-diethyl barbituric (3) acids. In the case of bifunctional barbituric acid, it was necessary to generate selective formation of heterodimers in the ESI source, varying both the drying gas temperature and the potential needle. These particular conditions made it possible to obtain binding of reference acids to either the C–H (“soft conditions”) or N–H (“hardest conditions”) acidic groups of 1. Thus, we have found that 1 deprotonated at C–H (1330.9 ± 10.0 kJ·mol–1) is 30.6 kJ mol–1 more acid than that deprotonated at the N–H site (1361.5 ± 10.5 kJ mol–1), and this last value is close to the GA values of 2 (1369.4 ± 8.8 kJ mol–1) and 3 (1368.2 ± 8.8 kJ mol–1), both also deprotonated at N–H groups. Overall, a very good agreement between experimental and computational (obtained at G3 and G4 levels of theory) results has been achieved in this work.
Acknowledgments
This work is dedicated to Prof. Rafael Notario (IQFR-CSIC). J.Z.D.-P. thanks the experimental technique support of Rocío Ramos and Andrés Guerrero. A.F.L. acknowledges the support from the Brazilian funding agencies CNPq, FAPESP, and CAPES. J.M.O.-E. acknowledges support from the Spanish MICINN, Grant Number CTQ2018-094644-B-C22.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jasms.1c00123.
Gas-phase thermochemical data (experimental and G-n theoretical calculations) and CID-experimental and EKM-treatment data (PDF)
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Baeyer A. Untersuchungen Über Die Harnsäuregruppe. Justus Liebigs Annalen der Chemie 1864, 131, 291–302. 10.1002/jlac.18641310306. [DOI] [Google Scholar]
- López Muñoz F.; Ucha Udabe R.; Álamo C. The History of Barbiturates a Century after Their Clinical Introduction. Neuropsychiatr. Dis. Treat. 2005, 4, 329–343. [PMC free article] [PubMed] [Google Scholar]
- Loscher W.; Rogawski M. A. How Theories Evolved Concerning the Mechanism of Action of Barbiturates. Epilepsia 2012, 53 (8), 12–25. 10.1111/epi.12025. [DOI] [PubMed] [Google Scholar]
- Smith M. C.; Riskin B. J. The Clinical Use of Barbiturates in Neurological Disorders. Drugs 1991, 42, 365–78. 10.2165/00003495-199142030-00003. [DOI] [PubMed] [Google Scholar]
- Figueiredo J.; Serrano J. L.; Cavalheiro E.; Keurulainen L.; Yli-Kauhaluoma J.; Moreira V. M.; Ferreira S.; Domingues F. C.; Silvestre S.; Almeida P. Trisubstituted barbiturates and thiobarbiturates: Synthesis and biological evaluation as xanthine oxidase inhibitors, antioxidants, antibacterial and anti-proliferative agents. Eur. J. Med. Chem. 2018, 143, 829–842. 10.1016/j.ejmech.2017.11.070. [DOI] [PubMed] [Google Scholar]
- Mohammadi Ziarani G.; Aleali F.; Lashgari N. Recent applications of barbituric acid in multicomponent reactions. RSC Adv. 2016, 6, 50895–50922. 10.1039/C6RA09874F. [DOI] [Google Scholar]
- Faidallah H. M.; Khan K. A. Synthesis and biological evaluation of new barbituric and thiobarbituric acid fluoro analogs of benzenesulfonamides as antidiabetic and antibacterial agents. J. Fluorine Chem. 2012, 142, 96–104. 10.1016/j.jfluchem.2012.06.032. [DOI] [Google Scholar]
- Zuccarello F.; Buemi G.; Gandolfo C.; Contino A. Barbituric and thiobarbituric acids: a conformational and spectroscopic study. Spectrochim. Acta, Part A 2003, 59, 139–151. 10.1016/S1386-1425(02)00146-4. [DOI] [PubMed] [Google Scholar]
- Delchev V. B. DFT ab initio study of the keto-enol tautomerism of barbituric acid. J. Struct. Chem. 2004, 45, 570–578. 10.1007/s10947-005-0031-8. [DOI] [Google Scholar]
- Senthilkumar K.; Kolandaivel P. Quantum chemical studies on tautomerism of barbituric acid in gas phase and in solution. J. Comput.-Aided Mol. Des. 2002, 16, 263–272. 10.1023/A:1020273219651. [DOI] [PubMed] [Google Scholar]
- Eigen M.; Ilgenfritz G.; Kruse W. Eine kinetische Methode zur Untersuchung schneller prototroper Tautomerisierungsreaktionen. Chem. Ber. 1965, 98, 1623–1638. 10.1002/cber.19650980539. [DOI] [Google Scholar]
- Schmidt M. U.; Bruning J.; Glinnemann J.; Hutzler M. W.; Morschel P.; Ivashevskaya S. N.; van de Streek J.; Braga D.; Maini L.; Chierotti M. R.; Gobetto R. The Thermodynamically Stable Form of Solid Barbituric Acid: The Enol Tautomer. Angew. Chem., Int. Ed. 2011, 50, 7924–7926. 10.1002/anie.201101040. [DOI] [PubMed] [Google Scholar]
- McMahon T. B.; Kebarle P. Intrinsic Acidities of Substituted Phenols and Benzoic Acids Determined by Gas phase Proton-Transfer Equilibriums. J. Am. Chem. Soc. 1977, 99 (1977), 2222–2230. 10.1021/ja00449a032. [DOI] [Google Scholar]
- Kebarle P.; Yamdagni R.; Hiraoka K.; McMahon T. B. Ion molecule reactions at high pressure. Recent proton affinities, gas phase acidities and hydrocarbon clustering results. Int. J. Mass Spectrom. Ion Phys. 1976, 19, 71–87. 10.1016/0020-7381(76)83005-7. [DOI] [Google Scholar]
- Cumming J. B.; Kebarle P. Summary of Gas Phase Acidity Measurements Involving Acids Ah. Entropy Changes in Proton Transfer Reactions Involving Negative Ions. Bond Dissociation Energies D(a-H) and Electron Affinities Ea(a). Can. J. Chem. 1978, 56, 1–9. 10.1139/v78-001. [DOI] [Google Scholar]
- Linstrom P. J.; Mallard W. G.. NIST Chemistry Webbook, NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD.
- Cooks R. G.; Wong P. S. H. Kinetic Method of Making Thermochemical Determinations: Advances and Applications. Acc. Chem. Res. 1998, 31, 379–86. 10.1021/ar960242x. [DOI] [Google Scholar]
- Cooks R. G.; Kruger T. L. Intrinsic Basicity Determination Using Metastable Ions. J. Am. Chem. Soc. 1977, 99, 1279–1281. 10.1021/ja00446a059. [DOI] [Google Scholar]
- McLuckey S. A.; Cameron D.; Cooks R. G. Proton Affinities from Dissociations of Proton-Bound Dimers. J. Am. Chem. Soc. 1981, 103, 1313–1317. 10.1021/ja00396a001. [DOI] [Google Scholar]
- Cheng X.; Wu Z.; Fenselau C. Collision Energy Dependence of Proton-Bound Dimer Dissociation: Entropy Effects, Proton Affinities, and Intramolecular Hydrogen-Bonding in Protonated Peptides. J. Am. Chem. Soc. 1993, 115, 4844–4848. 10.1021/ja00064a052. [DOI] [Google Scholar]
- Fabris D.; Kelly M.; Wu Z.; Fenselau C.; Jennings K. R. Collision Energy Effects on the Collision-Induced Dissociation of Multiply Charged Melittin. Rapid Commun. Mass Spectrom. 1994, 8, 791–795. 10.1002/rcm.1290080926. [DOI] [PubMed] [Google Scholar]
- Cerda B. A.; Hoyau S.; Ohanessian G.; Wesdemiotis Ch. Na+ Binding to Cyclic and Linear Dipeptides. Bond Energies, Entropies of Na+2 Complexation, and Attachment Sites from the Dissociation of Na+-Bound Heterodimers and Ab Initio Calculations. J. Am. Chem. Soc. 1998, 120, 2437–2448. 10.1021/ja972417j. [DOI] [Google Scholar]
- Cerda B. A.; Wesdemiotis Ch Li+, Na+, and K+2 Binding to the DNA and Rna Nucleobases. Bond Energies and Attachment Sites from the Dissociation of Metal Ion-Bound Heterodimers. J. Am. Chem. Soc. 1996, 118, 11884–11892. 10.1021/ja9613421. [DOI] [Google Scholar]
- Armentrout P. B. Entropy Measurements and the Kinetic Method: A Statistically Meaningful Approach. J. Am. Soc. Mass Spectrom. 2000, 11, 371–379. 10.1016/S1044-0305(00)00102-1. [DOI] [PubMed] [Google Scholar]
- Ervin K. M.; Armentrout P. B. Systematic and Random Errors in Ion Affinities and Activation Entropies from the Extended Kinetic Method. J. Mass Spectrom. 2004, 39, 1004–1015. 10.1002/jms.682. [DOI] [PubMed] [Google Scholar]
- Kurinovich M. A.; Lee J. K. The Acidity of Uracil and Uracil Analogs in the Gas Phase: Four Surprisingly Acidic Sites and Biological Implications. J. Am. Soc. Mass Spectrom. 2002, 13, 985–995. 10.1016/S1044-0305(02)00410-5. [DOI] [PubMed] [Google Scholar]
- Cooks R. G.; Koskinen J. T.; Thomas P. D. The Kinetic Method of Making Thermochemical Determinations. J. Mass Spectrom. 1999, 34, 85–92. . [DOI] [Google Scholar]
- Ervin K. M. Microcanonical Analysis of the Kinetic Method. Int. J. Mass Spectrom. 2000, 195, 271–284. 10.1016/S1387-3806(99)00176-1. [DOI] [PubMed] [Google Scholar]
- Ervin K. M. Microcanonical Analysis of the Kinetic Method. The Meaning of the”“” ““Apparent Entropy. J. Am. Soc. Mass Spectrom. 2002, 13, 435–452. 10.1016/S1044-0305(02)00357-4. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö, Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, 2009.
- Curtiss L. A.; Raghavachari K.; Redfern P. C.; Rassolov V.; Pople J. A. Gaussian-3 (G3) Theory for Molecules Containing First and Second-Row Atoms. J. Chem. Phys. 1998, 109, 7764–7776. 10.1063/1.477422. [DOI] [Google Scholar]
- Curtiss L. A.; Redfern P. C.; Raghavachari K. Gaussian-4 Theory. J. Chem. Phys. 2007, 126, 084108. 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
- Dávalos J. Z.; Notario R.; Cuevas C. A.; Oliva J. M.; Saiz-Lopez A. Thermochemistry of halogen-containing organic compounds with influence on atmospheric chemistry. Comput. Theor. Chem. 2017, 1099, 36–44. 10.1016/j.comptc.2016.11.009. [DOI] [Google Scholar]
- Dávalos J. Z.; Valderrama-Negrón A. C.; Barrios J. R.; Freitas V. L. S.; Ribeiro da Silva M. D. M. C. Energetic and Structural Properties of Two Phenolic Antioxidants: Tyrosol and Hydroxytyrosol. J. Phys. Chem. A 2018, 122, 4130–4137. 10.1021/acs.jpca.8b00457. [DOI] [PubMed] [Google Scholar]
- Guerrero A.; Baer T.; Chana A.; Gonzalez F. J.; Davalos J. Z. Gas Phase Acidity Measurement of Local Acidic Groups in Multifunctional Species: Controlling the Binding Sites in Hydroxycinnamic Acids’. J. Am. Chem. Soc. 2013, 135, 9681–9690. 10.1021/ja400571r. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.