Comparative phylogenetics of repetitive elements in a diverse order of flowering plants (Brassicales)

Abstract

Genome sizes of plants have long piqued the interest of researchers due to the vast differences among organisms. However, the mechanisms that drive size differences have yet to be fully understood. Two important contributing factors to genome size are expansions of repetitive elements, such as transposable elements (TEs), and whole-genome duplications (WGD). Although studies have found correlations between genome size and both TE abundance and polyploidy, these studies typically test for these patterns within a genus or species. The plant order Brassicales provides an excellent system to further test if genome size evolution patterns are consistent across larger time scales, as there are numerous WGDs. This order is also home to one of the smallest plant genomes, Arabidopsis thaliana—chosen as the model plant system for this reason—as well as to species with very large genomes. With new methods that allow for TE characterization from low-coverage genome shotgun data and 71 taxa across the Brassicales, we confirm the correlation between genome size and TE content, however, we are unable to reconstruct phylogenetic relationships and do not detect any shift in TE abundance associated with WGD.

Introduction

Genome sizes (or DNA C-value, used synonymously here) across flowering plants (angiosperms) vary from 65 Mbp/1C in Lentibulariaceae (Fleischmann et al. 2014), a family of carnivorous plants, to approximately 150 Gbp/1C in Paris japonica (Pellicer et al. 2010), making it not only the largest genome in the angiosperms but also within all Eukaryotes (Hidalgo et al. 2017). In the Brassicales, an economically important order of plants in the angiosperms, genome sizes range from 156 Mbp/1C to 4.6 Gbp/1C, with both extremes coming from the Brassicaceae family (Arabidopsis thaliana; Bennett et al. 2003 and Crambe cordifolia; Lysak et al. 2007). This incredible breadth in genome size among plant species cannot be explained solely by the number of protein-coding genes (Thomas 1971). Instead, genome size and its evolution are largely influenced by the number of noncoding sequences and repetitive elements (Elliott and Gregory 2015). There are several hypotheses trying to explain the mechanisms that drive genome size. Some suggest that lack of natural selection, possibly due to small effective population sizes, allowed accumulation of DNA material that would otherwise get purged from the genome (Lynch and Conery 2003; Doolittle 2013). Others postulate that noncoding DNA was selectively expanded to enable increase in cell size, thus lowering the metabolic rate, and permitting overall increase in body size at a lower cost (Kozlowski et al. 2003). Most recently it was suggested that climate seasonality and biotic interactions were important forces driving changes in genome size (Cacho et al. 2021). Indeed, the question of the factors driving genome size connects to deep questions regarding the structure of genomes, the interplay of natural selection and population size, and even the relationship between body size to metabolic rate.

Large portions of plant genomes are made up of transposable elements (TEs; Kubis et al. 1998). TEs are grouped into two major classes, based on their mechanism of transposition. Each of the two classes is further resolved into superfamilies, which vary in repeat domain structure. Class I TEs (or retrotransposons) move to a new genomic location via an RNA intermediate, a mechanism commonly called “copy-paste” (Wicker et al. 2007; Negi et al. 2016). This copy-paste mechanism results in an increased copy number of a retrotransposon (Wicker et al. 2007). Retrotransposons code for a reverse transcriptase, which is a defining component of their transposition mechanism. Plant genomes are often dominated by the two high-copy Class I TE superfamilies: Copia and Gypsy (Macas et al. 2015; Wicker et al. 2018).

Class II TEs (or DNA transposons) are defined by a “cut-paste” mechanism of transposition, which utilizes a DNA intermediate. The majority of Class II elements are characterized by two main features: terminal inverted repeats (TIRs) and a transposase enzyme (Wicker et al. 2007; Negi et al. 2016). One such superfamily is Mutator. In order for Mutator elements to move from one genomic location to another, a transposase needs to first recognize the TIRs and then cut both DNA strands on either end of the TE (Wicker et al. 2007). Insertion of the TE into a new location results in a small target site duplication (TSD). A TSD is a signature typical of DNA element (and some retrotransposon) transposition, as the target site will remain duplicated when the TE is excised and moves to another location in the genome (Muñoz-López and García-Pérez 2010; Lee and Kim 2014). Although they typically move in a cut-paste fashion, transposition of Class II elements can lead to an increase in their copy number when they are inserted in front of a replication fork (Wicker et al. 2007).

Selective pressure against deleterious effects of TEs and positive selection of new traits and functions that arise through TE migration, can both be drivers of evolution. TE mobilization and embedding into new genomic regions can cause a great deal of harm. Their translocation into genes can lead to gene inactivation, changes in splicing, or even gene movement once the TE is remobilized (Lisch 2013; Huang et al. 2015). Insertion into gene proximal regions can alter gene expression by modifying function of regulatory regions, or indirectly by driving changes in DNA methylation levels of nearby regions (Lisch 2013; Ong-Abdullah et al. 2015). The effects of TE movement, however, are not always damaging and have been shown to cause maize kernel variegation (McClintock 1950). TE insertions have also been found to be the source of other economically important phenotypic variation such as grape berry color, morning glory flower variegation, and parthenocarpic apple fruit (Habu et al. 1998; Clegg and Durbin 2000; Yao et al. 2001; Kobayashi et al. 2004; Bennetzen 2005; Cadle-Davidson and Owens 2008; Shimazaki et al. 2011). Some evidence suggests that TEs and TE-derived small RNAs are also involved in epigenetic reprogramming in Norway spruce pollen (Nakamura et al. 2019). All of these effects point to TEs as large contributors to genome evolution and plasticity.

The abundances of TEs in genomes, or the fraction of the genome occupied by TEs, have also been shown to be informative when inferring phylogenetic relationships among taxa, especially in groups with polyploidy, such as those in the Brassicales (Dodsworth et al. 2015; Harkess et al. 2016; Dodsworth et al. 2017; Vitales et al. 2020a). Several studies have used maximum parsimony methods to reconstruct phylogenetic trees, treating TE abundances as continuous characters (Dodsworth et al. 2015, 2017). The resulting trees are largely concordant to those produced via traditional phylogenetic methods. More recently, a study has shown the power of combining TE sequence similarity with TE abundance to understand evolutionary relationships (Vitales et al. 2020a). Generally, Copia and Gypsy are the most informative elements due to their high abundance in the genomes, whereas low-abundant TEs are insufficient to resolve the phylogenetic relations with these approaches (Dodsworth et al. 2015, 2017; Harkess et al. 2016; Vitales et al. 2020a).

Polyploidy or whole-genome duplication (WGD), is another mechanism that has been associated with changes in genome size. WGD is typically followed by extensive chromosomal rearrangements, gene loss, and epigenetic remodeling during the process of diploidization (Madlung et al. 2005; Schranz and Mitchell-Olds 2006). This genome restructuring has been correlated with both expansion and loss of TEs (Parisod et al. 2010; Ågren et al. 2016; Vicient and Casacuberta 2017). TE mobilization and proliferation following WGD have been recorded in tobacco, wheat, as well as many Brassicaceae species (Petit et al. 2010; Sarilar et al. 2011; Ben-David et al. 2013; Ågren et al. 2016; Vicient and Casacuberta 2017). TE amplification in wheat, however, seems to be family specific, as there is no evidence of massive reactivation of TEs (Wicker et al. 2018). In fact, TE abundance, landscape in gene vicinity, and the proportion of different TE families show surprising levels of similarity between the three wheat subgenomes. While there is evidence of large TE turnovers after the divergence of the A, B, and D subgenomes, these turnovers seem to have happened prior to hybridization (Wicker et al. 2018). Following polyploidization, TEs can accumulate in regions proximal to genes and gene-regulatory elements, leading to dynamic variation in gene expression (Sarilar et al. 2011; Ågren et al. 2016; Negi et al. 2016).

The Brassicales is a particularly valuable order as a model in which to elucidate the connection between WGD and repetitive element proliferation. First, there are at least four major polyploidy events in the Brassicales: “At − _ɑ” at the base of the Brassicaceae family, the tribe Brassiceae whole-genome triplication (“WGT”), “Th − _ɑ” in the Cleomaceae family (Schranz and Mitchell-Olds 2006; Barker et al. 2009; Mabry et al. 2020), and “At − _β” along the phylogenetic backbone of the order (Edger et al. 2015, 2018). Second, genomes within the Brassicales are typically small, less than 500 Mbp/1C. Several genome projects have produced highly contiguous genome assemblies with accurate gene and repeat annotations, such as A. thaliana (The Arabidopsis Genome Initiative 2000; Michael et al. 2018), several Brassica sp. genomes (Wang et al. 2011; Chalhoub et al. 2014; Liu et al. 2014; Parkin et al. 2014), and Carica papaya (Nagarajan et al. 2008).

Complex dynamics of TEs have been studied for a variety of species, but mostly focus on one or a few closely related species. More robust comparative studies are vital for understanding large-scale patterns of TE behavior in response to evolutionary pressures. Highly contiguous, whole-genome assemblies and annotations are the gold standard for repetitive element annotation and their quantification within a genome, but this is a cost-prohibitive approach as the sample number increases. Several approaches, such as RepeatExplorer (Novák et al. 2013) and Transposome (Staton and Burke 2015), have been developed to use low-cost Illumina genome shotgun data to assess repetitive element content and abundance. Here, we leverage low coverage, genome shotgun data, and 71 taxa spanning the Brassicales to test (1) if TE abundance is correlated to genome size, (2) how TE abundance relates to phylogenetic relationships, and (3) if WGD is followed by TE expansion or loss.

Materials and methods

Taxon sampling, RNA and DNA isolation, and sequencing

Sampling of 71 taxa across the Brassicales spanned seven families and 57 genera, with a focus on the Brassicaceae (47 taxa) and Cleomaceae (15 taxa; Supplementary Table S1). Leaf tissue from mature plants was collected for both RNA and DNA extraction followed by isolation and sequencing as in Mabry et al. (2020). In brief, RNA was extracted using either an Invitrogen PureLink RNA Mini Kit (Thermo Fisher Scientific, Carlsbad, CA, USA) or Qiagen RNeasy Plant Kit (Qiagen, Germantown, MD, USA) followed by Illumina sequencing on the NextSeq or HiSeq platforms for paired-end reads ranging from 75 to 250 bp. DNA was extracted using the DNeasy Plant Kit (Qiagen, Germantown, MD, USA) followed by sequencing on the Illumina NextSeq instrument for 2_×150 bp reads. All sequencing (with the exception of RNA from Cleomella serrulata) was performed at the University of Missouri DNA Core.

Estimation of genome size by flow cytometry

Single leaves from 68 taxa were cut and placed in a wet paper towel and shipped to the Benaroya Research Institute at Virginia Mason (Seattle, WA). Nuclei isolations from a single mature leaf were analyzed in four technical replicates for each sample. Analyses were carried out using the Partec PAS flow cytometer (Partec, http://www.partec.de/), equipped with a mercury lamp, following the procedure as outlined in Wang et al. (2005). Briefly, single leaves (0.1 g) were chopped in a nuclei extraction buffer (CyStain ultraviolet Precise P Nuclei Extraction Buffer; Partec, M_ünster, Germany) and filtered through a 30 mm Cell-Trics disposable filter (Partec), followed by addition of 1.2 ml of staining solution containing 4,6-diamidino-2-phenylindole. Using chicken erythrocyte nuclei (CEN) as an internal control, the relative fluorescence intensity of stained nuclei (4000 to 5000 per sample) was measured on a linear scale (Galbraith et al. 1998). The mean of the four estimates was then converted from pg/2C to Mbp/1C for downstream analyses.

Repetitive element analysis

Prior to repeat identification, DNA sequencing reads were paired to corresponding paired-end sequence files using a stand-alone Pairfq script, v 0.16.0 (https://github.com/sestaton/Pairfq) followed by removal of any reads that matched custom databases of mitochondrial and chloroplast genomes, comprised of sequences downloaded from NCBI (Supplementary Table S2). Subsequently, low quality and short reads were removed with Trimmomatic v 0.39, with MINLEN of 70 and LEADING and TRAILING thresholds set to 3 (Bolger et al. 2014). Repeats were identified using Transposome v 0.12.1 (Staton and Burke 2015), which uses graph-based clustering, with 90% identity and fraction coverage of 0.55. Transposome was chosen over other similar software due to its speed, accessibility (i.e., open source), and ability to annotate repetitive elements from sequence data without the need for an assembled genome for which accurate and complete assembly of repetitive regions is still complicated and restricted to only a small number of taxa. A database containing all repetitive elements previously annotated in the Viridiplantae was obtained from RepBase v 21.10 and used as reference for Transposome cluster annotation. Since the repeat database uses a consensus repeat model, otherwise known as an exemplar, this approach allows for a robust alignment from diverged repeat sequences. The reported genomic fraction of each TE family represents the abundance of that family that has been corrected for by the number of unclustered reads (see Specifications and example usage section; https://github.com/sestaton/Transposome/wiki/).

For all but five species, repeat identification was first performed with 500 K random paired-end reads (see Supplementary Table S3 for details). These five samples had to be further downsampled due to script limitations (see How to choose the appropriate genome coverage section; https://github.com/sestaton/Transposome/wiki/). Previous work has shown that a very low genome coverage, as low as 1–2%, is sufficient to provide reliable estimates of TE abundance genome wide. Further increase in sampling, with genome coverage going as high as 5%, was shown to improve family-level estimates of TE abundance, but had little impact on overall assessment of TE abundance. Sampling of 500 K reads therefore should be enough to explore the largest genome in our study, providing _∼2.3% genome coverage (Novák et al. 2010; Staton and Burke 2015) (see also http://repeatexplorer.org/?page_id=179). However, to further test the effect of sampling depth on the estimates of TE abundance, all species were sampled to the same genome coverage. Total reads needed to achieve 20% genome coverage was calculated using genome size estimates. This number was then divided by the read length of 150 bp and rounded to get the number of reads to randomly sample. Due to computational limitations, Transposome was only able to annotate TEs for 59 out of the 73 species when sampled to 20% genome coverage (Supplementary Tables S4 and S5).

Correlation between genome size and TE content

The issue with simple regression is that it assumes independence between data points (Felsenstein 1985). Therefore, to account for phylogenetic relationships between species, and lack of independence thus present in our data, we calculated phylogenetically independent contrasts (PICs) values for both genome sizes and TE abundances. These values were then used as input for linear regression. The pic function from R package ape was used to calculate PIC values (Paradis and Schliep 2018). The lm function from the stats package in R v 3.6.1 was then used to perform linear regression analysis using both the computed PIC values (R Core Team 2019). For some analyses, correlation between total TE abundance, Gyspy abundance, and Copia abundance and genome size was studied on a subset of data, excluding species determined to be outliers using the boxplot.stats function. These genomes were removed to avoid any bias caused by a small group of very large genomes present in Brassicaceae. Furthermore, two other species were not included in these analyses, C. serrulata due to the lack of DNA sequence and genome size data for this species, and Sisymbrium brassiformis due to lack of genome size data. Correlations were also performed without phylogenetic corrections.

Transcriptomics, phylogeny estimation, and hierarchical clustering

Transcriptome assembly and alignment follow Mabry et al. (2020), but in brief, reads were quality filtered and adapter-trimmed using Trimmomatic v 0.35 (Bolger et al. 2014), assembled using Trinity v 2.2 (Grabherr et al. 2011), and translated to protein sequences using TransDecoder v 3.0 (github.com/TransDecoder/TransDecoder). Orthology was determined using OrthoFinder v 2.2.6 (Emms and Kelly 2019) followed by filtering for taxon occupancy and alignment quality (github.com/MU-IRCF/filter_by_ortho_group, github.com/MU-IRCF/filter_by_gap_fraction). Gene trees were estimated using RAxML v 8 (Stamatakis 2014) followed by PhyloTreePruner v 1.0 (Kocot et al. 2013) to remove any potentially remaining paralogous genes. Final genes trees were produced again using RAxML v 8 (Stamatakis 2014), followed by species tree estimation in ASTRAL-III v 5.6.1 (Zhang et al. 2018).

Using both the 500 K-read and 20% coverage datasets, phylogenetic signal was tested for repetitive element abundance. Hierarchical clustering using dist and hclust functions from the stats package in R v 3.6.1 was conducted (R Core Team 2019). To construct a consensus dendrogram, hierarchical clusters produced with Copia, Gypsy, and total TE abundances were used. The consensus dendrogram was calculated using the mergeTree v 0.1.3 package in R (Hulot et al. 2019). C. serrulata was not included in these analyses, due to the lack of DNA sequencing data for this species.

Associating WGD with shifts in TE abundance

To produce an ultrametric tree necessary for comparative genomic analyses, final alignments were concatenated (those without paralogous genes) using scripts from the Washburn et al. (2017) Genome-Guided Phylo-Transcriptomic pipeline (‘concatenate_matrices.py’), followed by tree estimation in RAxML v 8 (Stamatakis 2014) with 100 bootstrap replicates and Moringa and Carica as outgroups. Branch lengths and model parameters were optimized using the ASTRAL phylogeny as a fixed input tree. Dating of the resulting tree was calculated in TreePL v 1.0 (Smith and O’Meara 2012) using two fossils. Palaeocleome lakensis was used to date the node between the Cleomaceae and Brassicaceae (minimum age = 47.8, 95% highest posterior density = 52.58; Cardinal-McTeague et al. 2016); Dressiantha bicarpellata was used to date the node between the Caricaceae and Moringaceae, and the remaining Brassicales (minimum age = 89.9, 95% highest posterior density = 98.78; Cardinal-McTeague et al. 2016).

To test for the placement and magnitude of possible adaptive shifts in the data, Bayou v 2.0 was used for both the 500 K-read and 20% coverage datasets (https://github.com/uyedaj/bayou/blob/master/tutorial.md; Uyeda and Harmon 2014). C. serrulata was again dropped from analyses due to lack of DNA sequence data for this sample. Analyses were run on total TE, Gyspy, and Copia abundances. Priors for all analyses were as follows: lognormal distributions were used for _ɑ (the strength of the pull toward trait optima) and _σ² (rate of phenotypic evolution) both with default parameters, a conditional Poisson distribution for the number of shifts using default parameters, a normal distribution for θ (the value of the optima) with mean equal to the mean of the observed data and standard deviation equal to two times the standard deviation of the data, and a uniform distribution for branch shifts with default parameters. Analyses were run for 1,000,000 generations and then checked for lack of convergence with a burn in of 0.3. Heatmaps of reconstructed values were plotted on tree branches using the plotBranchHeatMap function in Bayou. For Simmap trees, a posterior probability of 0.3 was used as a cutoff for shift identification.

To test the likelihood of WGDs being associated with identified shifts in TE abundances using both datasets of 500 K-reads and 20% genome coverage, OUwie v 2.1 was used (www.rdocumentation.org/packages/OUwie/; Beaulieu et al. 2012). Four separate selective regimes were tested: (1) At − _ɑ at the base of the Brassicaceae vs all other Brassicales, (2) the tribe Brassiceae WGT vs all other Brassicaceae, (3) Th − _ɑvs all other Cleomaceae, and (4) a reduced subset of 19 taxa for which we were confident in determining ploidy level, for which we tested diploids vs polyploids (Supplementary Tables S1 and S4; samples noted with asterisks). All seven models (single-rate Brownian motion; BM1, Brownian motion with different rate parameters for each state on a tree; BMS, Ornstein-Uhlenbeck model with a single optimum for all species; OU1, Ornstein-Uhlenbeck model with different state means and a single _ɑ and _σ² acting all selective regimes; OUM, Ornstein-Uhlenbeck model that assumes different state means as well as multiple _σ^2; OUMV, Ornstein-Uhlenbeck model that assumes different state means as well as multiple _ɑ; OUMA, Ornstein-Uhlenbeck model that assumes different state means as well as multiple _ɑ and _σ² per selective regime; OUMVA) were run for total TE, Gyspy, and Copia abundances and compared using the weighted Akaike information criterion corrected for sample-size (AICc).

Tandem repeat and gene content estimation

To further assess drivers of genome size, tandem repeats (TRs) were annotated by assembling the paired reads which had been filtered for mitochondrial and chloroplast reads into contigs using PRICE v 1.2 (Ruby et al. 2013). Along with the A. thaliana (TAIR10) cDNA as starting seed sequences, the following parameters -nc 30 -dbmax 72 -tpi 85 -tol 20 -mol 30 -mpi 85 were used. Resulting contigs were then annotated in Tandem Repeat Finder (Benson 1999) using recommended parameters. Annotated TRs were then extracted from the data file (.dat) and combined to make a fasta file, which was indexed for read mapping using BWA v 0.7.17 (Li and Durbin 2009). Mapping percent of paired reads was determined using the flagstat command in samtools v 1.9 (Li et al. 2009). Gene content was also assessed using interleaved paired reads which were blasted ( blastx using diamond and .sam format as output; Camacho et al. 2009; Buchfink et al. 2015) against the consensus ancestral sequences for each BUSCO gene from the Brassicales database (BUSCO v 5.0; Seppey et al. 2019). Mapping percent was then again determined using the flagstat command in samtools v 1.9 (Li et al. 2009).

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. Both RNA and DNA sequence data from this article can be found in the NCBI SRA data libraries under BioProject accession number PRJNA542714. Scripts are available at https://github.com/mmabry/Brassicales_RepetitiveElements. Supplementary material is available at figshare: https://doi.org/10.25387/g3.14462430.

Results and discussion

Sequence matrices and genome size patterns across the Brassicales

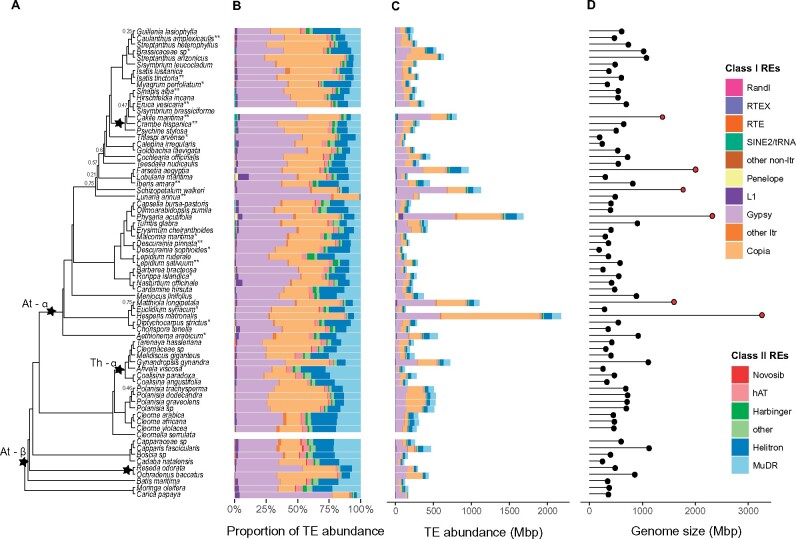
In order to investigate and interpret the evolution of genome size across the Brassicales, we first needed to construct a reliable phylogenetic framework based on our transcriptome assemblies. After determining orthology using OrthoFinder2, we recovered 35,522 orthogroups, with a final 1404 orthogroups remaining after filtering. The resulting phylogeny had all but eight nodes recovered with a local posterior probability of 0.7 or greater (Figure 1). Next, repetitive element clustering and quantification using Transposome was performed for each species, at each sampling scheme, and mapped to the species tree. After clustering using 500 K reads, less than 2.1% of reads remain unannotated for any given species (Supplementary Table S3), likely reflective of the high quality of Brassicales genome annotations in RepBase. Total repeat content of species across the Brassicales ranged from 35.5% to 72.5% (mean 52.7, SD ± 9.35; Supplementary Table S1). Overall, DNA-type “cut and paste” transposons comprise between 0.006% and 14.8% of genomes, largely dominated by MuDR and Helitron elements. When sampling to 20% genome coverage across species, up to 4% of reads are left unannotated (Supplementary Table S5), but there is little change in overall estimates, with total repeat content ranging from 34.9 to 77.2% (mean 55.6, SD ± 10.9; Supplementary Table S4). Similarly, the abundance of DNA-type elements ranges from 0.004% to 14.8%, majority being composed of MuDR and Helitron elements (Supplementary Figure S1). However, as in our analysis using 500 K reads, long terminal repeat (LTR) retrotransposons, mostly composed of Gypsy and Copia elements, tend to make up most of the total repeat content (Figure 1 and Supplementary Figure S1).

Figure 1.

Taxa sampled with corresponding transposable element (TE) abundance and genome size. (A) Phylogeny with WGDs indicated by black stars. Support values are shown for those branched with less than 0.7 local posterior probability. Asterisks (*) next to taxon indicate known samples with known ploidy levels (** = polyploid, *= diploid). (B) The proportion of transposable element abundance scaled to 100%, (C) proportion of transposable element abundance converted to base pairs (Mbp), and (D) genome size (Mbp). Red circles indicated those taxa not included in regression analyses.

Genome sizes ranged from 195.6 Mbp/1C in Descurainia sophioides to 3261.6 Mbp/1C in Hesperis matronalis. For two samples, C. serrulata and S. brassiformis, we were unable to obtain enough leaf tissue for the estimation of genome size by flow cytometry. The genome sizes recovered well represent the diversity and range of genome size that is found across the Brassicales (https://cvalues.science.kew.org/; Release 7.1, Leitch et al. 2019). The median and mean for families which were represented by more than one sample were as follows: Brassicaceae—557.5 Mbp/1C, 738.9 Mbp/1C; Capparaceae—511.0 Mbp/1C, 605.1 Mbp/1C; Cleomaceae—479.2 Mbp/1C, 549.1 Mbp/1C; and Resedaceae—684.6 Mbp/1C, 684.6 Mbp/1C (Figure 1; Supplementary Table S1). Of our 68 samples with new estimates, 23 have previously recorded genome size estimations in the Kew C-value database (Supplementary Table S6). Twelve of these estimates were similar to the published ones, while the other 11 have greater than 100 Mbp differences. Cakile maritima has the largest difference with our sample estimated at 1383.9 Mbp/1C and the Kew value recorded as 666.4 Mbp/1C (Lysak et al. 2009). A possible reason for these observed discrepancies in genome sizes is the different accessions used here and in the published estimates.

To test the accuracy in clustering of TEs using whole-genome shotgun data in Transposon, we baselined the Transposome method against several of the published genomes in the Brassicales that had corresponding samples in this study (Supplementary Table S7). Our estimates using both read sampling schemes were largely concordant with estimates published for C. papaya, differing by only 1% (Nagarajan et al. 2008) and Moringa oleifera, differing by only 3–4% (Tian et al. 2015). For our Brassicaceae representative Cardamine hirsuta, our estimate using 500 K reads was 7% less than the genome estimate (Gan et al. 2016), while our TE estimate was 12% higher using 20% genome coverage for read sampling. Therefore, while not exact estimates, we argue these three test species indicate that one can reasonably estimate TE content using low coverage sequencing data.

Repetitive elements positively relate to genome size

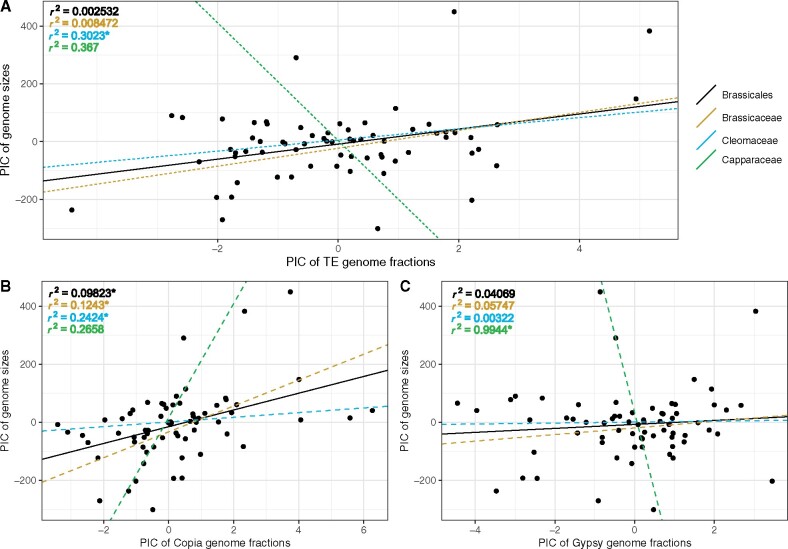
To test for a relationship between TE abundance and genome size, we used the 500 K reads and 20% genome coverage datasets, with or without phylogenetic correction, both with and without outliers using linear regression analyses. In general, the analyses resulted in a mixture of patterns for significance, but we found that using the 20% genome coverage dataset resulted in more significant tests and higher fits to the model (r²; Supplementary Table S8). We note several relationships that are recovered as significant regardless of what analyses we ran. One example of this is of total TE content in the Cleomaceae, where total TE is consistently recovered as significantly related to genome size and explains up to 63% of the observed variation (Figure 2A, Supplementary Figures S2–S6; Supplementary Table S8). The Brassicales, Brassicaceae, and Cleomaceae all indicate that there is a significant relationship between Copia elements and genome size with Copia elements explaining up to 28% of the variation in genome size in the Brassicales, 37% in the Brassicaceae, and 49% in the Cleomaceae (Figure 2B, Supplementary Figures S2–S6; Supplementary Table S8). Analyses of Gypsy elements in the Capparaceae are also consistently recovered as significant, yet we caution these findings as they only include four samples. Total TE content is also recovered as significantly related to genome size in four of our six analyses for the Brassicales and Brassicaceae and explains about half of the observed variation (50% and 48% respectively; Supplementary Figures S3–S6; Supplementary Table S8). Gypsy elements in the Cleomaceae are also recovered as significantly related to genome size in four of our six analyses, explaining around 60% of the variation in genome size (Supplementary Figures S3–S6; Supplementary Table S8). Interestingly for two analyses, Gypsy elements in the Brassicace and Copia elements in the Capparaceae, we do not recover any significant relationship between abundance and genome size (Figure 2, Supplementary Figures S2–S6; Supplementary Table S8).

Figure 2.

Phylogenetic corrected linear regression analysis of the relationship between (A) total TE, (B) Copia, (C) Gypsy element abundance and genome size. PIC, phylogenetically independent contrasts. Asterisks (*) next to r² values denotes significant P-values at the ɑ = 0.1 level.

While we are certainly not the first to report that repetitive elements positively correlate to genome size (Lee and Kim 2014; Harkess et al. 2016; Vitales et al. 2020b; Wang et al. 2021), we highlight that we do not always find support for these conclusions, especially when analyses are further broken down and compared across families vs orders and TE type. Lysak et al. (2009) have previously hinted at the lack of interdependence between TE abundance and genome size in Brassicaceae species. They found that, while there are exceptions, most Brassicaceae species have relatively small genomes, despite having undergone multiple polyploidization events and TE proliferation, both of which are expected to lead to an increase in genome size (Johnston et al. 2005; Lysak et al. 2009). Another reason we may not always find correlation between TE and genome size and analyses with poor fit to our data is perhaps due to small sampling sizes only capturing a snippet of the diversity in Brassicales. Despite this, we show that even if not exhaustive, uniform sampling across the species is better suited when studying relationships between genome size and the abundance of repetitive elements in genomes of vastly different sizes. We further show that repeat content is an important contributor to genome size in flowering plants, albeit likely one of many.

Other known drivers of genome size, gene content and TRs, ranged from 1.06 to 12.56% with a median of 6.03% and a mean of 6.25%, and from 0.07 to 3.98% with a median of 0.34% and a mean of 0.47%, respectively (Supplementary Figure S7). In all analyses of the Brassicales, Brassicaceae, and Cleomaceae, we recover a positive correlation between gene content and genome size (Supplementary Figures S8 and S9; Supplementary Table S9). However, for these analyses, we recover large ranges in the observed variation in genome size for the Brassicales and Brassicaceae (12–42% and 18–49%, respectively). Percent TRs are only recovered as significant in analyses of the Cleomaceae, explaining between 38 and 63% of variation in genome size (Supplementary Figures S8 and S9; Supplementary Table S9). While these results are interesting we again caution any significant interpretation as input data for these analyses (short reads) are limited in their ability to thoroughly annotate complete genes and TRs. However, these results, especially that of correlation between TRs and genome size in the Cleomaceae should be further investigated as previous work has indicated that no relationship exists (Zhao et al. 2014; Wang et al. 2021).

TE content does not reflect phylogenetic relationships

To test the congruence of the ASTRAL species tree with a repeat clustering-based tree, we performed hierarchical clustering of TE abundances for Copia and Gypsy elements, as well as total TE content. We specifically highlight these superfamilies since previous studies which have used TE abundances to reconstruct phylogenetic trees found that Copia and Gypsy elements bear the strongest signal (Dodsworth et al. 2015, 2017; Harkess et al. 2016; Vitales et al. 2020a). However, we were unable to reproduce the species tree using our TE abundance data (Supplementary Figure S10). While a few relationships were established correctly, none of the resulting dendrograms mirrored the tree obtained through ASTRAL using transcriptome data. At the family level, similar to previous publications, we did observe mirroring relationships within some clades (Supplementary Figure S12), while the overall dendrogram was still in conflict with the species phylogeny (Dodsworth et al. 2015; Vitales et al. 2020a). Overall, we observed more agreement within genera, with the level of conflict increasing in higher taxonomic ranks, resulting in a poorly resolved tree across the Brassicales. Our data indicate that this approach does not have enough resolution to elucidate the complex evolutionary history of the Brassicales order. Furthermore, these observations remain unchanged when all species are sampled to 20% genome coverage (Supplementary Figures S11 and S13).

While some of the disagreement between the species phylogeny and TE abundance analyses could come from the different methods used, we speculate that, on a large scale, other factors driving genome evolution in the Brassicales such as polyploidy or environmental stress may dilute the phylogenetic signal coming from TE abundances. One possibility is related to certain technical compromises that were necessary in order to run such a large number of species in Transposome. We did not attempt to pool all 71 species into a single clustering analysis, such as performed in smaller species groups like eight species of Asparagus (Harkess et al. 2016), six Nicotiana species (Dodsworth et al. 2015, 2017; Vitales et al. 2020a), and nine Fabeae species (Dodsworth et al. 2015; Vitales et al. 2020a). Similarly, while we did not adjust for genome size in our 500 K analysis due to the large number of sampled species and drastic genome size differences across the samples, our analyses of 20% genome coverage for each species resulted in the same patterns. Other studies which have identified phylogenetic signals in their TE content have used much smaller sample sizes and have a much narrower phylogenetic focus on taxa of study (Dodsworth et al. 2015, 2017; Harkess et al. 2016; Vitales et al. 2020a). Interestingly, Vitales et al. (2020b) were also able to reconstruct phylogenetic relationships in their Anacyclus study when using repeat sequence similarities, but not when using repeat abundances. They attribute this to repeat abundance not evolving due to genetic drift as sequence data does.

Polyploidy is not correlated to shifts in TE abundance

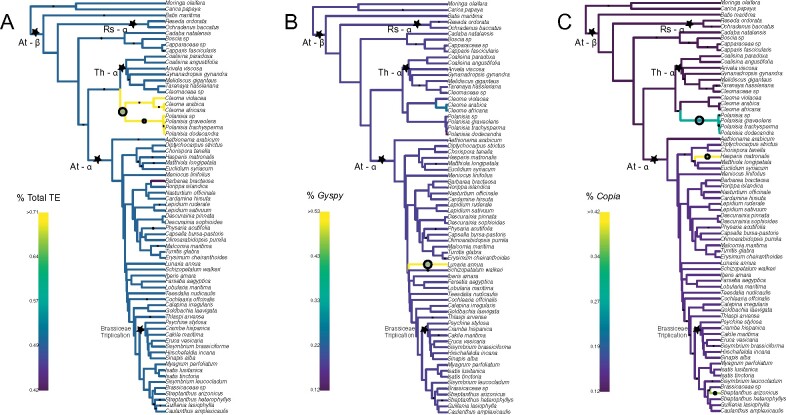
Previous work, restricted to neopolyploids, has indicated that WGD and TE abundance, both expansion and loss, are correlated (Parisod et al. 2010; Ågren et al. 2016; Vicient and Casacuberta 2017). Here, we did not recover any evidence to support such a correlation using both our 500 K and 20% genome coverage read sampling schemes across the Brassicales, a much older timescale than has been tested before (Figure 3 and Supplementary Figure S14). In both analyses, for total TE abundance, we identified a shift in phenotypic evolution toward a higher abundance in a clade of the Cleomaceae comprising the genus Polanisia and three species of Cleome. Surprisingly, this group is sister to the clade recently characterized by the Cleomaceae specific WGD, Th - _ɑ (Mabry et al. 2020). For Gypsy elements alone, we identified a single shift in Lunaria annua; this was unsurprising, as in Figure 1, clear differences in the proportion of these elements can be seen. When sampling at 20% genome coverage the largest shift in phenotypic evolution we detect is for C. maritima, which belongs to the Brassiceae. Two shifts were identified for Copia abundance, one for H. matronalis, which has a very large genome, and one for the Polanisia clade. In the Polanisia clade, Copia elements comprised, on average, 31.5% of the genome, which can be compared to its sister clade, in which Copia elements make up on average 8.5% of the genome. This shift is also recovered when using our 20% genome coverage dataset. For all three TE categories, using both datasets, we did not recover any shifts that overlap with known polyploidy events in the Brassicales (Figure 3 and Supplementary Figure S14).

Figure 3.

Bayou analysis for detecting shifts of phenotypic evolution for transposable element abundance. (A) Heatmap of total TE, (B) Gyspy, and (C) Copia abundance with identified shifts plotted. Only shifts with a posterior probability of 0.3 are plotted. Circle size corresponds to the posterior probability of having a shift. WGDs are denoted by black stars with named events indicated.

To further test the hypothesis that WGD and TE abundances are correlated, we constrained our analyses to implicitly test for shifts at known WGD events using OUwie. All analyses indicated that there is no correlation between TE proliferation and WGD (Supplementary Tables S10 and S11). Specifically, when testing for correlations between At − _ɑ at the base of the Brassicaceae vs all Brassicales for total TE abundance using our 500 K read dataset, the BMS model (Brownian motion, with different rate parameters for each state on a tree) was assigned the most weight compared to the other models tested. The BMS model suggests that there is no optimum the taxa are moving toward, but there are different rates across the tested clades (_σ² = 0.0001378363 for no WGD and 0.0003516384 with the WGD). Using our 20% genome coverage data, the OUMVA model is assigned the most weight, suggesting that the Brassicaceae are moving toward different optima with different rates compared to the rest of the Brassicales, however, this model did return with the error “You might not have enough data to fit this model well.” So conclusions should be further tested. For both read sampling datasets, the OU1 model (Ornstein-Uhlenbeck model with a single optimum for all species) was weighted highest for both Gyspy and Copia elements when constraining the selection regium at At − _ɑ, suggesting that there is a single optimum that the plants are moving toward, regardless if they have experienced the At − _ɑ event or not. For the tribe Brassiceae WGT when compared to Brassicaceae, the OU1 model was again weighted highest when compared to the others, meaning that for this event, taxa with or without the WGT are moving toward a single optimum in TE abundance (total TE, Gyspy, and Copia). Results did not change when using the 20% genome coverage dataset.

Testing correlation of TE abundance to the Th − _ɑ event of the Cleomaceae resulted in the BM1 model given the most weight and Gyspy and Copia analyses weighing the OU1 model highest, meaning that for total TE there are no general optima, but that taxa with or without the WGD are moving toward an optima for Gyspy and Copia elements. When testing these same hypotheses using the 20% genome coverage dataset, the BMS model was given the most weight for total TE, while BM1 was selected for Gyspy and Copia. Indicating that while these clades have different rate parameters for total TE, there are no optima that all taxa are moving toward. Specifically for Cleomaceae our two different sampling schemes are telling two different stories regarding phenotypic evolution of TEs. This was somewhat surprising, as phylogenetic comparative analyses recovered a shift for one clade of Cleomaceae when testing total TEs, and then a shift was observed for just the Polanisa clade for Copia abundance alone. In general, it seems the genus Polanisa is driving much of the observed TE patterns and further warrants additional study.

Because previous studies which have shown a correlation between WGD and TE abundance have typically used neopolyploid species, we further subsetted our dataset to include only taxa for which we had recently sequenced the genome (unpublished data) and therefore could confidently identify ploidy, allowing us to test neopolyploids vs known diploids. These analyses still found no correlation between TE abundance and WGD (Supplementary Tables S10 and S11). The BM1 model was most highly weighted for total TE and Gyspy while the OU1 model was most highly rated for Copia. Analyses on our 20% genome coverage dataset found similar patterns, but with total TE and Gyspy being best described by the OU1 model and Copia unchanged. This result suggests that perhaps that all three traits are moving toward some sort of optimum, but that neopolyploids are no different than diploids.

Although it has been hypothesized that WGD may be correlated with genome size (Ågren et al. 2016; Vicient and Casacuberta 2017), we did not recover support for this correlation within the Brassicales, a group characterized by multiple WGD events, variation in chromosome numbers, and more than an order of magnitude difference in genome sizes. One hypothesis for these patterns is that the genomes that share the three events tested here (At − _ɑ, Th − _ɑ, and the tribe Brassiceae WGT) have already diploidized. However, we were especially surprised to find no correlation between TE and WGD when testing neopolyploidy events using the reduced subset of data for which we knew ploidy levels. Many of the studies which have found evidence for this correlation have typically tested a single species with a recent WGD, for example, Petit et al. (2010) found TE proliferation after polyploidization in tobacco, Madlung et al. (2005) show increased activity of several transposons in newly formed allopolyploid Arabidopsis, as did Kashkush et al. (2003) and Lopes et al. (2013) in wheat and coffee respectively, with many more additional examples of polyploidy correlated with TEs composed by Vicient and Casacuberta (2017). Yet, Ågren et al. (2016) suggest that for Capsella bursa-pastoris, TE abundance increased due to relaxed selection, while Hu et al. (2010) and Charles et al. (2008) found no evidence of proliferation of TEs after WGD in cotton and wheat, respectively. Looking more broadly for support for this WGD—TE abundance correlation, Staton and Burke (2015) assessed 15 taxa across the Asteraceae. Although they place WGD events on their phylogeny, they note that further work is needed to test if this is a true correlation. It seems that although there still exists this predominant theory that WGD and TE abundance are correlated, researchers have begun to appreciate that the story is much more complex with mechanisms that take place after WGD, such as diploidization, playing important roles in genome size evolution (Parisod et al. 2010; Sarilar et al. 2013).

In the absence of a technical explanation, another possibility relates to the genome dynamics of species in the Brassicales following polyploidy and subsequent diploidization. That is, there could exist a mechanism(s) to suppress repetitive element proliferation and diversification enabling the tape of evolution to be “replayed” (Bird et al. 2020). For example, when testing resynthesized polyploid Brassica napus lines, Bird et al. (2020), found that the same parental subgenome was consistently more dominantly expressed in all lines and generations. The subgenomes of wheat were also found to be surprisingly stable after hybridization (Wicker et al. 2018) as were the genomes of Anacyclus species (Vitales et al. 2020b). Overall, results here and from others cited within provide support for a type of punctuated equilibria, where evolutionary development is marked by isolated episodes of rapid change as noted in many crop polyploid species, between long periods of little or no change, as a way to explain the patterns we see here (Zeh et al. 2009).

While we do find support for a relationship between genome size and TE abundance in the Brassicales, many times the data did not fit the model well. In addition, we are unable to reconstruct the known phylogenetic relationships, or make correlations between phenotypic shifts of TEs and WGD. This study is the first to assess TE abundance across an entire plant order with this many samples. We suggest that although TE abundance may follow phylogenetic signals at shallow phylogenetic levels, it should be used with caution for determining relationships at deeper nodes of a phylogeny. We also suggest that, although TE abundance may be driven by WGD at short time scales, TE expansion does not leave an overall lasting imprint on a genome and that TE purging mechanisms, such as intrastrand homologous recombination and illegitimate recombination, work efficiently to bring genomes to stability (Hawkins et al. 2009). As the cost of genomes continues to decrease, the opportunities to test these patterns by annotating TEs in multiple assembled genomes per family will be possible, although hinging on computational limitations. These analyses paired with others that test for patterns of TE evolution in other groups of organisms will hopefully provide insight to further understand the evolution of genome size across the tree of life.

A.B., M.E.M., A.E.H., J.B., P.P.E., M.E.S., G.C.C., B.C.M., and J.C.P. designed the study. M.E.M. and J.B. grew, sampled, and collected RNA/DNA from plants. A.B. conducted TE annotation, regression analyses, and phylogenetic comparisons of TE-derived phylogeny to species tree. M.E.M. performed species tree inference and comparative genomic analyses. A.E.H., M.E.S., and G.C.C. helped with analyses. A.B. and M.E.M. wrote the manuscript. All authors provided feedback and helped shape the final manuscript.

Funding

This work was supported by the Department of Energy Defense Threat Reduction Agency (HDTRA 1-16-1-0048) and the National Science Foundation (IOS 1339156).

Conflict of interest

The authors declare that they have no conflict of interest.