Eagle for better genome-wide association mapping

Abstract

Eagle is an R package for multi-locus association mapping on a genome-wide scale. It is unlike other multi-locus packages in that it is easy to use for R users and non-users alike. It has two modes of use, command line and graphical user interface. Eagle is fully documented and has its own supporting website, http://eagle.r-forge.r-project.org/index.html. Eagle is a significant improvement over the method-of-choice, single-locus association mapping. It has greater power to detect SNP-trait associations. It is based on model selection, linear mixed models, and a clever idea on how random effects can be used to identify SNP-trait associations. Through an example with real mouse data, we demonstrate Eagle’s ability to bring clarity and increased insight to single-locus findings. Initially, we see Eagle complementing single-locus analyses. However, over time, we hope the community will make, increasingly, multi-locus association mapping their method-of-choice for the analysis of genome-wide association study data.

The Eagle package was developed to meet a shared need in animal, plant, and human genetics. It was built to make multi-locus association mapping easy. Multi-locus association mapping is more powerful, statistically, than single-locus association mapping (Wang et al. 2016; Zhang et al. 2019). By being able to model the association between multiple single-nucleotide polymorphisms (SNPs) and a trait simultaneously, multi-locus association mapping better captures the hidden reality of heritable traits with complex genetic architectures. Yet, multi-locus association mapping is rarely used in practice. Many of the current multi-locus software implementations are driven by high-level statistical theory making their inner statistical workings difficult to follow for non-statisticians. Eagle does not suffer from this limitation.

We created the Eagle package to be as fast as single-locus association mapping, to be easy to use even for non-R users, and to give easily interpretable results. It implements the Eagle method for association mapping (George et al. 2020). It is based on linear mixed models (LMMs) and model selection. Methodologically, it is only a little more complicated than single-locus methods. The “best” LMM is built iteratively. At each iteration, the SNP in strongest association with a trait is identified from the random effects part of the model and moved to the fixed effects part of the model. This process is simple yet ingenious. It simultaneously identifies those regions of the genome that house genes influencing a trait while also accounting for all other SNP-trait associations.

R, by default, comes with single-threaded math libraries. By replacing these libraries with their multi-threaded counterparts, certain linear algebra operations become parallelized, implicitly. The Eagle package has been structured, purposely, to make extensive use of these implicitly parallelized operations. In the parts of Eagle where this has not been possible, we have instead written C++ routines and parallelized the code explicitly through openMP (Dagum and Menon 1998). Eagle differs most from competing packages in its ease-of-use for non-R users. Considerable effort has been invested into making Eagle equally usable to R and non-R users. Eagle is available on CRAN (https://cran.r-project.org/). The package comes with a browser-based graphical user interface (GUI). A user need only issue a single R command, OpenGUI(), to harness the full functionality of Eagle. Eagle has its own website (http://eagle.r-forge.r-project.org/index.html) with instructions on how to install a multi-threaded version of R, quick start guide, tutorials, videos, and answers to frequently asked questions. Users can experiment with Eagle, prior to installing the package, by analyzing a test data set on our public server (http://eagle.r-forge.r-project.org/demo.html).

Methods

Notation

Suppose genotypes are collected on L loci from n_g individuals/lines/strains. The genotypes are coded as −1, 0, and 1 corresponding to SNP genotypes AA, AB, and BB, respectively. Ideally, missing genotypes are imputed prior to analysis. If not, missing genotypes are set to 0 by Eagle. Let ${\mathit{M}}^{(n_g\times L)}=[{\mathit{m}}_1{\mathit{m}}_2\dots {\mathit{m}}_L]$ be the matrix of SNP genotype data where the vector ${\mathit{m}}_j^{(n_g\times 1)}$ contains the genotypes −1, 0, and 1 for the jth SNP. Furthermore, let ${\mathit{y}}^{(n\times 1)}$ contain the quantitative trait data. Examples of the quantitative trait data include flowering time and grain yield in plants, weight gain and feed efficiency in animals, and blood pressure and cholesterol levels in humans. Here, n can be larger than n_g if multiple measurements, as is common in plant studies, are recorded on the same line/strain.

The model is built iteratively. At each iteration, an SNP is selected and moved from the random effects to the fixed effects part of the LMM. Suppose s iterations of the model building process have been performed. Let $S=\{S_1,S_2,\dots ,S_s\}$ be a set of ordinal numbers. The number S_k corresponds to the S_kth SNP in the marker map that was selected in the kth iteration of the model building process. For example, if $S=\{101,12,1143\}$, then the 101th, 12th, and 1143th SNPs in the marker map were selected in the first, second, and third model selection iterations, respectively.

Multi-locus model

The standard LMM for association mapping is

$$\mathit{y}=\mathit{X}\mathit{\tau }+\mathit{Z}{\mathit{u}}_g+\mathit{e}$$ (1)

where ${\mathit{X}}^{(n\times p)}$ and ${\mathit{Z}}^{(n\times n_g)}$ are known design matrices, n is the number of observations, n_g is the number of individuals/lines/strains/with $n_g\le n$, ${\mathit{\tau }}^{(p\times 1)}$ is a vector with p fixed effects parameters including the intercept, and ${\mathit{u}}_g^{(n_g\times 1)}$ is a vector containing the genetic effects. The residuals, ${\mathit{e}}^{(n\times 1)}$, are assumed to follow a normal distribution with mean 0 and covariance matrix ${\sigma }_e^2{\mathit{I}}^{(n\times n)}$ where ${\sigma }_e^2$ is an unknown residual variance.

In the standard LMM, the genetic effects, ${\mathit{u}}_g^{(n_g\times 1)}$, are a random polygenic term that accounts for the genetic background (Yu et al. 2006; Zhao et al. 2007). It is assumed to follow a $N(\mathbf{0},{\sigma }_g^2{\mathit{G}}^{(n\times n)})$ where G is a relationship matrix and ${\sigma }_g^2$ is the unknown genetic variance. The relationship matrix is calculated from pedigree records or from SNP data. However, Eagle models ${\mathit{u}}_g$ differently and this is where the innovation lies. Instead of relying on the relatedness between individuals to model the genetic background, Eagle accounts for genetic background by modeling the association between all the SNPs and trait simultaneously. A similar idea exists in genomic selection (Goddard 2009).

For a detailed explanation of how ${\mathit{u}}_g$ is formed and its statistical justification, the interested reader is referred to Verbyla et al. (2007, 2012). Briefly, the genetic effects are modeled as

$${\mathit{u}}_g=\sum _{k=1}^s{\mathit{m}}_{S_k}{a}_{S_k}+{\mathit{M}}_{-S}{\mathit{a}}_{-S}$$ (2)

where ${\mathit{m}}_{S_k}^{(n_g\times 1)}$ is the vector of genotypes for the kth selected SNP, $a_{S_k}$ is the additive effect of the kth selected SNP, ${\mathit{M}}_{-S}^{(n_g\times L-s)}$ is the matrix of SNP genotypes with the data for the SNPs in S removed, and ${\mathit{a}}_{-S}^{(L-s\times 1)}$ is a random effect whose distribution is ${\mathit{a}}_{-S}\sim N(\mathbf{0},{\sigma }_a^2{\mathit{I}}^{(L-s\times L-s)})$. The first term on the left-hand side is the fixed effects. The second term is the random effects. The fixed effects measure the additive effect of the S already-selected SNPs on the trait. The random effects measure the association between all other L–s SNPs and trait, simultaneously. Here, SNPs are assumed to be uncorrelated to reduce model complexity, making the analysis more manageable. Also, for a working model, it is not uncommon to assume SNP effects are pairwise uncorrelated. Such an assumption has long been made for marker-assisted selection with ridge regression (Whittaker et al. 2000).

There will be situations where the standard LMM is not appropriate such as when additional random effects are needed or, as occurs in multi-environment trials in plants, the assumption of uncorrelated errors is violated. A partial solution is a stage analysis (George et al. 2020) but Eagle’s reliance on uncorrelated errors is a limitation. Any analysis by Eagle where the residuals are in fact correlated would be approximate. Further testing is needed to measure the impact of such a violation.

Dimension reduction

In modern genome-wide association studies, the number of loci, L, can be very large, sometimes in the tens of millions. This creates a problem, computationally, when fitting (2) as the vector ${\mathit{a}}_{-S}$ contains a large number of elements. Fortunately, the dimensionality of (2) can be reduced by orders of magnitude.

The goal is to form an equivalent model for (2) of lower dimension but where the equivalent model has the same variance. The variance structure of ${\mathit{u}}_g^{(n_g\times 1)}$ is the $n_g\times n_g$ matrix ${\sigma }_a^2{\mathit{M}}_{-S}{\mathit{M}}_{-S}^T$. Here, the only unknown is the variance ${\sigma }_a^2$. By taking the matrix square root,

$${\mathit{Z}}_e={({\mathit{M}}_{-S}{\mathit{M}}_{-S}^T)}^{1/2}$$

an equivalent, dimension-reduced, model for ${\mathit{u}}_g$ is

$${\mathit{u}}_g=\sum _{k=1}^s{\mathit{m}}_{S_k}{a}_{S_k}+{\mathit{Z}}_e{\mathit{a}}^{*}$$ (3)

where ${\mathit{a}}^{*}$ is a random effect with only n_g elements and distributed as $N(\mathbf{0},{\sigma }_a^2{\mathit{I}}^{(n_g\times n_g)})$.

The Eagle algorithm requires estimates of ${\mathit{a}}_{-S}$ and its variance to identify the SNP in strongest association with the trait. These can be recovered from the fitting of the dimension-reduced model (Verbyla et al. 2012, 2014) since

$$\tilde{\mathit{a}}=\left[{\mathit{M}}_{-S}^T{({\mathit{M}}_{-S}{\mathit{M}}_{-S}^T)}^{-1/2}\right]{\tilde{\mathit{a}}}^{*}$$ (4)

and its variance matrix is

$$\text{var}(\tilde{\mathit{a}})={\mathit{M}}_{-S}^T{({\mathit{M}}_{-S}{\mathit{M}}_{-S}^T)}^{-1/2}\text{var}({\tilde{\mathit{a}}}^{*}){({\mathit{M}}_{-S}{\mathit{M}}_{-S}^T)}^{-1/2}{\mathit{M}}_{-S}$$ (5)

Only the diagonal elements of the variance matrix are needed which simplifies its calculation.

The Eagle algorithm

Eagle treats association mapping as a model selection problem. The model is built iteratively, via forward selection. At each iteration, from the current model, a new model is formed. This is done by selecting an SNP from the random effects and moving it to the fixed effects. The SNP is selected based on a score statistic. The reasoning behind moving effects from random to fixed is if there are major SNP-trait associations, then at first, they are contained in the genetic background of the model. This gives opportunity for the genetic background, which is being modeled by the random term in (2), to act as an SNP selection mechanism. Major SNP–trait associations are identifiable as outliers (or unusually large random effects in (2)) when compared to background effects (or the other random effects in (2)).

Suppose s iterations of the model building process have been performed. The current model is of the forms (1) and (3). The vector of genetic effects ${\mathit{u}}_g$ has s fixed effects for the s discovered SNP–trait associations. The model has been fitted and parameter estimates obtained via maximum likelihood (ML). The vector of random effects ${\tilde{\mathit{a}}}^{*}$ and its variance $\mathit{var}({\tilde{\mathit{a}}}^{*})$ are then computed.

The following steps are performed for the $(s+1)$th iteration of the model building process.

Step 1: SNP selection. An SNP is selected from the random effects based on the maximum score statistic

$$t_j^2=\frac{{\tilde{a}}_j^2}{\text{var}({\tilde{a}}_j)}$$

where j refers to the jth SNP in the marker map, the j index is over all SNPs except the s SNPs already selected, ${\tilde{a}}_j^2$ is a scalar value formed from the square of the best linear unbiased predictor of the jth SNP’s random effect, and $\text{var}({\tilde{a}}_j)$ is its variance. These values are recovered from ${\tilde{a}}^{*}$ and $\text{var}({\tilde{a}}^{*})$, which were obtained from the fitting of the current model and (4) and (5). By choosing the SNP with the maximum score statistic, we are selecting the SNP, which is in strongest association with the trait, from amongst those SNPs whose association is being modeled by the random effects.

Step 2: model building and fitting. A new dimension-reduced model is built, according to (1) and (3), from the trait data y, and known matrices X, Z, and ${\mathit{M}}_{-S}$. Here, S is the set of indexes of the s previously selected SNP and the additional SNP found in the previous step. The model is fitted to the data and parameters estimated via maximum likelihood.

Step 3: model selection. The importance of the $(s+1)$th selected SNP is determined via the extended Bayes information criteria (extBIC, Chen and Chen 2008). The extBIC is a model selection measure that takes into account the number of parameters and the complexity of the model space. If the extBIC increases, then the new model is accepted and the iterative model building process continues.

Upon completion, S is the set of indexes of the SNP in strongest and measurable association with the trait. Each SNP identifies a different part of the genome housing genes that are influencing the trait.

Basing the above algorithm on ML is a departure from what was first proposed in George et al. (2020), which was residual maximum likelihood (REML). REML’s advantage over ML is that it yields unbiased estimates of the variance components. However, it is not appropriate, statistically, to then use its maximized log-likelihood value in a model selection statistic such as the extBIC. This necessitated an extra ML calculation for every iteration of the model building process. By replacing REML with ML, we reduced the amount of computation needed per iteration, improving the speed of the algorithm considerably. Also, in the context of genome-wide association studies, the sample size is much larger than the number of fixed effects. This results in minimal bias when using ML. For the data sets we have analyzed, we have found no discernible difference between the variance component estimates under ML and REML.

The Eagle package

Overview

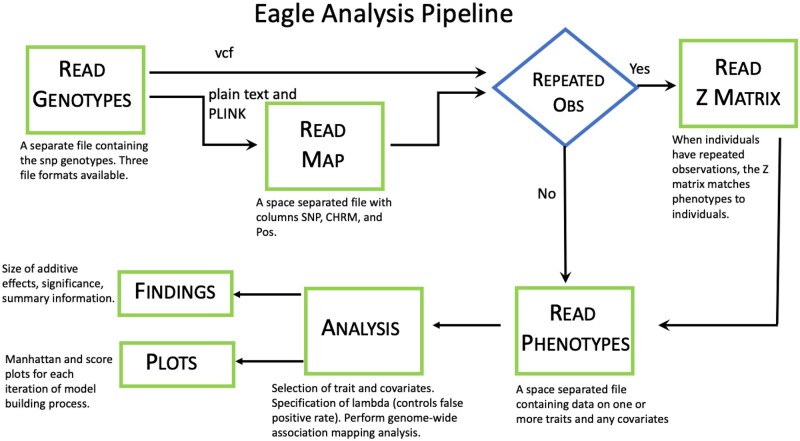
Eagle is an R package for the genome-wide analysis of association data. It can handle data collected from inbred or outbred study populations. The populations can be of arbitrary and unknown complexity. The data can be larger than the memory capacity of the computer. Since Eagle is framed within a LMM paradigm, it is best suited to the analysis of data on continuous normally distributed traits. However, LMMs can also tolerate non-normal data (Schielzeth et al. 2020). A flow chart of the analysis pipeline for Eagle is shown in Figure 1. The package contains functions for opening the GUI, inputting the data, performing genome-wide analyses, and for summarizing and visualizing the results. Non-R users need only be familiar with a single function OpenGUI that opens the GUI.

Figure 1.

A flow chart of the analysis pipeline for Eagle. Each green box corresponds to a separate page of the GUI.

Installation

Eagle is available on CRAN. As such, it can be installed in the usual way. However, Eagle has been designed to make extensive use of implicit parallelization. Many of the vector, matrix, and linear algebra operations in R link directly to the API’s of BLAS (Basic Linear Algebra Subroutines, see Blackford et al. 2002) and LAPACK (Linear Algebra Package, see Anderson et al. 1999). R, by default, comes with single-threaded versions of these libraries. If these libraries are replaced by their multi-threaded counterparts, such as MKL and openBLAS, parts of R become multi-threaded, implicitly. Detailed instructions for converting R to multi-threaded computation are available on the Eagle website (http://eagle.r-forge.r-project.org/instruction.html).

We have also developed an alternate approach for running Eagle. Docker is an open platform that packages an application and its dependencies inside virtual containers. Here, we have created two Eagle containers, a container for running the GUI (geo047/eagle: 2.4.5_app) and a different container for running RStudio with Eagle pre-installed (geo047/eagle: 2.4.5_rstudio). Both containers come with multi-threaded R. For a user, once Docker is installed on their system, a container can be run with the “docker run” command. This then allows the user to access either the GUI or RStudio via their web-browser. Instructions for running the Eagle containers are available at https://hub.docker.com/r/geo047/eagle.

Data input

There are, potentially, four different types of data required by Eagle for input. These are the phenotypic data, the genotypic data, the marker map, and the Z matrix. Whether all four are needed is dependent upon the study design and format of the genotypic data. Each input data type is discussed below.

The phenotypic data consist of observations on one or more traits and any explanatory variables. A trait may have a single observation per individual/line/strain or, as is common in plant studies, may have repeat observations. The data are arranged into columns. The first row contains the column headings. The observations can be space or comma separated. Missing trait and/or explanatory variable values are allowed. The data are read into Eagle with the function ReadPheno.

The genotypic data are the genotypes observed on the individuals/lines/strains from the SNPs. Since association studies can collect genotypes on thousands of individuals across millions of SNPS, these data can be extremely large. Fortunately, Eagle can handle data beyond a computer’s memory capacity. Eagle will accept genotypic data that are in variant call format, space delimited ASCII format (the default), or PLINK ped format. The data are read with the function ReadMarker. The argument type, which has the value “vcf”, “text”, or “PLINK”, specifies the type of data being read. The argument availmemGb tells Eagle how much memory, in gigabytes, is available. The order of the SNPs in the input file must correspond to their map order. Ideally, missing genotypes are imputed prior to input but some missing genotypic data can be tolerated.

The marker map consists of the names and locations of the SNPs. The map is specified via three columns of data. The first column contains the SNP labels. The second has the names of the chromosomes upon which the SNPs residue. The third column has their chromosomal positions. The data are space separated with the first row being the column names. The SNPs are in map order. Missing values are not allowed. The data are read with the function ReadMap. If the genotypic data are in variant call format, a separate marker map file is not needed. A variant call format file contains not only the SNP genotypes but also marker map information.

The Z matrix is needed only if a trait has repeat observations. It is an incidence matrix. As such, it contains zeroes and ones only. The number of rows in the matrix equals the number of rows of phenotypic data. The number of columns equals the number of rows of genotypic data. The data are space separated. The function ReadZmat reads the data.

Controlling the type 1 error rate

All association mapping methods commit type 1 errors. For some, the type 1 error rate is controlled explicitly. For others, it is implicit to the internal workings of the methodology. In Eagle, the conservativeness of the model building process is managed explicitly via the parameter λ. The parameter λ is part of the extBIC. It ranges from zero to one. The conservativeness of the extBIC increases with increasing λ. Although it is possible to set λ analytically, the desired type 1 error rate is not part of the calculation. Instead, an empirical approach is adopted in Eagle.

A permutation approach is implemented in the function FPR4AM. It finds the type 1 error rate for discrete values of λ. Suppose the number of permutations performed is n_perm and their are $n_{\lambda }$ discrete values of λ being considered, potentially this means $n_{\mathit{perm}}\times n_{\lambda }$ genome-wide analyses are required. For large data sets, this quickly becomes computationally intractable. Fortunately, even though the trait data y change across replicates, the SNP and explanatory variable data remain the same. This means, for a permutation, only those parts of the Eagle algorithm impacted by a change in y need recalculation. Also, through vectorization, the type 1 error rates corresponding to all $n_{\lambda }$ discrete values of λ can be calculated simultaneously, for each permutation.

In the example below, the run time for FPR4AM was 1.36 min and for the analysis it was 53 s but the run times are situation specific. Having to run FPR4AM can more than double the computational cost of an analysis but being able to control the type 1 error more than compensates for this cost.

Association mapping analysis

One of the most important functions in the package, from a user’s perspective, is AM. This function implements the methodology presented above. It is the function that performs association mapping. The function has 12 arguments. The important arguments are as follows. The trait and fixed effects are specified via the arguments trait and fformula, respectively. The data are passed to AM through the arguments pheno, geno, map, and if required, Zmat. The number of threads, for parallel computation, is set with ncpu. The type 1 error rate is controlled with lambda. Its value is found by running FPR4AM.

As an example, suppose the phenotypic data, SNP data, and marker map have been read with the functions described above and stored in data objects phenoObj, genoObj, and mapObj, respectively. The trait name is “y”. The explanatory variables of interest are “cov1” and “cov2”. These explanatory variables can be continuous such as weight and height, ordinal such as day and education level, or categorical such as race and sex. The fixed effects part of (1) has the form cov1 + cov2 + cov1*cov2 where cov1*cov2 is an interaction term. Let the λ value that gives a type 1 error rate of 0.05 be 0.78 and it was found with FPR4AM. Then, the function call that performs the analysis is

R> AM(trait=“y”,fformula=“cov1+cov2+cov1*cov2”,

+ geno=genoObj, pheno=phenoObj, map=mapObj,

+ ncpu = 8, lambda = 0.78)

The number of threads for parallel computation has been set to 8. After running the function, the SNPs closest to the genes underlying “y” are reported. Each SNP identifies a different region of interest on the genome.

Results

Additional analysis information is obtained with the function SummaryAM. Three tables are generated. They are a table of summary information, a findings table, and an effects table. The summary table contains information on items such as the number of cpu that were available, number of samples, the fixed effects formula, number of significant SNP–trait associations, and the λ value at which the analysis was performed. The findings table lists the names, chromosomes, and positions of those SNPs that were found to be in association with the trait. The effects table has the effect sizes, degrees of freedom, Wald statistic values, and P-values of the fixed effects in the model, including the SNPs that were identified as being in association with the trait.

Visualization

PlotAM is an interactive function for viewing the strength of association along a chromosome or genome. This is done on an iteration-by-iteration basis. It is useful for better understanding how a model is built, how SNP–trait association varies within a region, and how the strength of association for SNPs changes over the model building process.

The function has the form

PlotAM(AMobj=NULL, itnum = 1, chr=“All”,type=“Manhattan”).

An example of its use is given in the Example section.

Browser-based GUI

To release users from the requirement of having to know R, a GUI was built. Here, a user only needs to know how to load the package with library(Eagle) and start the GUI with OpenGUI(). After running OpenGUI(), a browser automatically opens to the GUI’s home page. By clicking on the tabs in the navigation bar at the top of a page, a user can access pages for reading the input data, for performing analyses, and for summarizing/visualizing results.

Help

Detailed help files are available for each of the functions in the package. These help files include many worked examples. Help on a function is accessed in the usual way, with the library function. With the GUI, every page contains a help banner that gives a summary of the functionality contained within the page. Single sentence help descriptions also appear as the mouse cursor hovers over different parts of a page. External to the package, an email address eaglehelp@csiro.au has been set up to answer any queries. Also, help is available via the website http://eagle.r-forge.r-project.org/index.html.

Improvements to Eagle

The Eagle package has undergone continued development since it was first introduced in George et al. (2020). There have been significant improvements to its performance and utility. Eagle can analyze marker data larger than a computer’s memory capacity. Previously, it was doing this by converting the raw SNP data into a packed binary file and storing it on disk. The packed file would then be unpacked and read into memory when needed. However, this unpacking process, when repeated many times, incurs a significant computational cost. Unpacking can be avoided by instead converting the raw marker data into a simple ASCII file containing the snp genotypes 0, 1, and 2. We have been able to reduce the run time of AM by 50% and FPR4AM by an order of magnitude. The latest version of Eagle can handle vcf data and comes with an interactive plotting facility (see Results). Also, the internal handling of missing data has been improved, the reporting of final results has been refined, and the type of errors that can be caught by Eagle has been broadened. Users of the old version of Eagle are encouraged to update to the latest version (Version 2.4.4 at the time of submission).

Results

Here, the steps for performing association mapping with Eagle are presented. Both modes of use are given. That is, via function statements issued at the R command line and via the GUI. For each function statement, a screenshot of its matching GUI page is shown where applicable. The example is for the analysis of a mouse data set. As stated previously, the goal of association mapping is to find the SNPs in strongest association with the genes underlying a heritable trait. The data are real. They were collected from a large GWAS in outbred mice (Nicod et al. 2016). Many different traits were measured but our focus is on high-density lipoprotein (Bioch.HDL). We chose this trait because from previous analyses, a number of genomic regions of interest across multiple chromosomes have been reported. In the original study (Nicod et al. 2016), this trait was found to be influenced by the explanatory variables for sex (Sex), batch number (Batch), and average weight (Weight.Average). These same variables are treated as explanatory variables in our analysis. Even though large data sets are not a problem for Eagle, we wanted the example data to be easily accessible to R. A way of doing this is to host the data on GitHub (https://github.com/geo047/Example_Data). GitHub has a file size limit of 10 megabytes, which made it necessary to base the example on a subset of the original data.

Creating the input files

Three input files were created. These are the files phenoex.dat with the phenotypic data, genoex.dat with the genotypic data, and mapex.dat with the maker map. In the original study, data were collected from 1887 outbred mice on a large number of traits and SNPs. As such, this data set was too large to house on GitHub. So the study size was reduced to 800 randomly selected mice. Our focus was restricted to the analysis of a single trait, Bioch.HDL. The genotypic data were reduced to the genotypes from 70,484 SNPs. The SNPs were selected from every 5th locus of the original set where loci with a minor allele frequency of less than 1% have been removed along with loci on the sex chromosome.

The phenotypic data in phenoex.dat are space separated and arranged into 801 rows and four columns. The rows correspond to data on different mice. The columns contain data on Bioch.HDL and the explanatory variables Sex, Batch, and Weight.Average. The first row has the column names.

The genotypic data in genoex.dat has 800 rows and 70,484 columns. The data are space separated. The columns are not named, nor are there missing values. Each row contains the genome-wide data for a mouse. Each column contains the genotypes for an SNP. Rows in the two files are assumed to be ordered such that the same row in each file corresponds to data collected on the same mouse. The columns are in marker map order. A numeric coding of 0, 1, and 2 was used for the SNP genotypes, AA, AB, and BB, respectively.

The marker map in mapex.dat is space separated and has 70,485 rows and three columns. The first row is the column names. The rows contain map information on the SNPs. The rows are ordered according to the SNPs map order. The first column has the names of the SNPs. The second column contains the chromosome names upon which the SNPs reside. The third column has the chromosome positions of the SNPs. It is assumed that the row order of the SNPs in this file matches the column order in genoex.dat.

The input files are downloaded and uncompressed from GitHub with the R commands

R> DIR <- “https://raw.githubusercontent.com/

+ geo047/Example_Data/master/”

R> download.file(paste0(DIR, “mapex.dat”))

R> download.file(paste0(DIR, “phenoex.dat”))

R> download.file(paste0(DIR, “genoex.dat.zip”))

R> unzip(“genoex.dat.zip”)

Single-locus association mapping

We begin by analyzing these data in the “usual” way, with single-locus association mapping. As stated previously, for a single-locus analysis, a separate LMM is fitted to the data for each SNP. The statistical significance of an SNP, when treated as a fixed effect, is a measure of the strength of association between the SNP and trait. The data were analyzed with the R package gaston (Wang and Zhang 2018). The process was to read in the phenotypic and genotypic information with fread from the R package data.table. Scale the marker data. Convert the explanatory variables into a usable form with covObj¡-model.matrix(Sex+Batch+Weight.Average, phenoObj). Calculate the genetic relationship matrix with the gaston function GRM and its eigenvalues/eigenvectors with the base function eigen. Perform the analysis with the gaston function association.test with the arguments method=“lmm” and test=“wald” along with arguments for the trait data, the eigenvalues/eigenvectors of the scaled marker data, and covariate matrix. The R script for performing the analysis is available upon request.

The single-locus analysis results are shown in the Manhattan plot in Figure 2. The positions of the SNPs on the genome are on the x-axis and the significance scores $(-{\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}(p-\text{value}))$ of the SNPs are on the y-axis. We would conclude from this analysis that there is a single region of interest on chromosome 5. In fact, from our Eagle analysis (see below), we know that there are five regions of interest for this trait. These are on chromosomes 1, 5, 6, and 10. The region on chromosome 5 is obvious. The regions on 1 and 6 we might have suspected but lacked the power under a single-locus analysis to confirm. However, the region on chromosome 10 is only revealed after the effects of the other regions have been accounted for. Also, it is not at all obvious from a single-locus analysis that we are dealing with two closely linked regions on chromosome 5.

Figure 2.

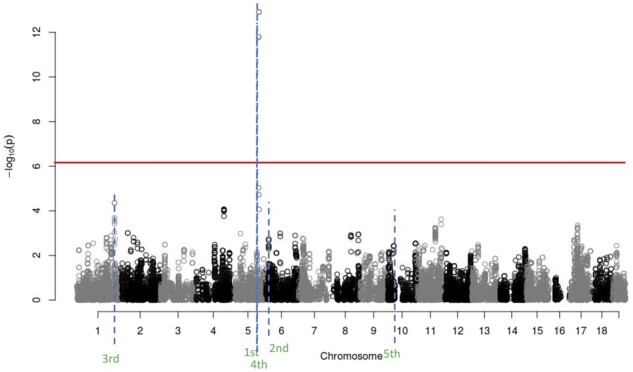
Manhattan plot for the single-locus analysis of the example data. Each point is the strength of association between an SNP and trait. Results are shown for the entire genome. The red horizontal line is the 5% genome-wide significance threshold, calculated via a Bonferroni correction. The blue dashed horizontal lines are the locations of the findings from Eagle. The order in which Eagle found these findings is given below the blue line. Where single-locus association mapping found only a single region of interest, because of Eagle’s increased statistical power, Eagle found five regions of interest.

Reading the data into Eagle

The function statements for reading the phenotype and map input files are simple. Only the file names need specifying. This is also true if using the GUI. By default, the two input files are assumed space separated. If comma or tab separated, an additional argument is needed in the function statement. For comma separated files, sep=“,”. For tab separated files, sep=“\t”. The GUI has a checkbox for choosing if the file is space or comma separated. A tab separated option is not yet available.

The function statements for reading the two input files are

R> phenoObj <- ReadPheno(“phenoex.dat”)

R> mapObj <- ReadMap(“mapex.dat”)

Both the phenoObj and mapObj are data frame objects.

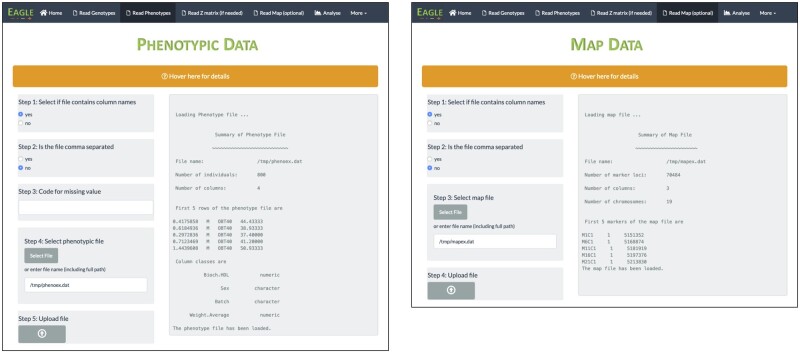
Screenshots of the corresponding GUI pages are shown in Figure 3. They were taken after the relevant information had been entered via the selections made in the left-half of the GUI page and the files uploaded. The output from uploading a file is printed in the right-half of the page. These are the same outputs that appear when running the function statements from the command line.

Figure 3.

Screenshots of the GUI pages after the phenotypic data (left) and marker map (right) have been uploaded. Any output from the underlying functions is shown in the right-half of a page.

The function statement for reading the SNP data differs from the two previous input statements. Besides the file name, additional arguments are required. The file type needs specifying. Here, since the marker data are in a space delimited text file, the type=“text” argument is included in the function statement. Other allowable formats are variant call format (type=“vcf”) and PLINK ped (type=“PLINK”). Text files give the user the freedom to select their own coding scheme but how these codes map to the SNP genotypes need specifying. In this example, the file contains codes 0, 1, and 2 for SNP genotypes AA, AB, and BB, respectively. This means that the function statement includes the arguments AA = 0, AB = 1, and BB = 2. Also, it is good practice to set the amount of available memory, in gigabytes, with the availmemGb argument. The default is to assume 16 GB of memory.

The ReadMarker function statement for this example is

R> genoObj<- ReadMarker(“genoex.dat”,type=“text”,

+ AA = 0, AB = 1, BB = 2, availmemGb = 8)

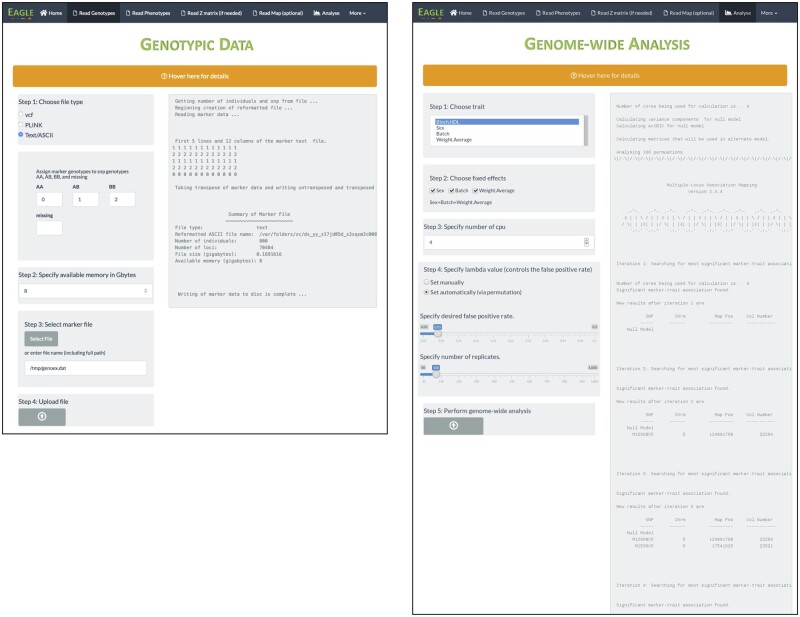
A screenshot of the corresponding GUI page after uploading the file is shown in Figure 4. The output from running the statement is the same as the output shown in the right-half of the GUI page. Unlike the other input functions, ReadMarker does not read the data into memory. Instead, the marker data, and its transpose, are stored on disk in a binary form. By not holding the genotype data in memory, it gives Eagle the ability to analyze marker data larger than the memory capacity of a computer. The object returned by ReadMarker is a list object that holds elements containing information on the dimensions of the marker data, the name and location of the reformatted marker data, and the number of phenotypic samples.

Figure 4.

Screenshots of the GUI pages after the genotypic data (left) have been uploaded and the multi-locus association mapping analysis (right) performed. Output is shown in the right-half of the page.

Controlling the type 1 error and performing the Eagle analysis

To find the value of lambda that will give a 5% type 1 error rate for the analysis, we ran the function FPR4AM. For its arguments, we specified the desired type 1 error rate (falseposrate = 0.05), the number of permutations (numreps = 100), the trait name (trait=“Bioch.HDL”), the fixed effects part of the model (fformula=“Sex+Batch+Weight.Average”), the phenotypic data (pheno=phenoObj), the genotypic data (geno=genoObj), the marker map (map=mapObj), and the number of processes (ncpu = 8).

The function statement is

R> fdr <- FPR4AM(falseposrate = 0.05,

+  numreps = 100, trait=“Bioch.HDL”,

+  fformula=“Sex+Batch+Weight.Average”,

+ pheno=phenoObj, geno=genoObj, map=mapObj, ncpu = 8)

Once run, a lambda value of 0.53 (rounded to two significant digits) is reported. This value is used in AM to set the type 1 error rate to 5%.

To perform multi-locus association mapping of the example data, the function statement is

R> res <- AM(trait= “Bioch.HDL”,

+     fformula=“Sex+Batch+Weight.Average”,

+     pheno=phenoObj, geno=genoObj, map=mapObj,

+     ncpu = 8, lambda = 0.53)

As the function is run, a user can see how the model is being built. For each iteration, the selected SNPs, their chromosome, their map position, the column number of the SNP locus in the marker data file, and the extBIC value are printed. The final results are shown below (Table 1).

Table 1.

Final results

SNP	Chrm	Map Pos	Col Num	extBIC
Null model				1700.22
M12008C5	5	124,991,768	22,264	1659.56
M1530C6	6	17,541,026	23,521	1652.16
M26336C1	1	171,730,395	5254	1644.45
M12020C5	5	125,044,979	22,267	1643.63
M11706C10	10	125,357,987	41,402	1643.24

Gamma value for model selection was set to 0.53.

In Figure 4, a screenshot of the Analysis page is shown of how the same analysis can be performed via the GUI. Here, a user chooses a trait for analysis, selects any fixed effects, lets Eagle find lambda by selecting the Set automatically option or specifies their own lambda value by selecting Set manually, and performs the analysis. The same output from the above two functions is printed in the right-half of the Analysis page.

Summarizing the results

A summary of the results is produced with

R> SummaryAM(AMobj=res)

where res is the list object obtained from AM. Three tables are printed (Table 2–4). These same three tables are available within the GUI by going to the Summary page (page not shown). The first table (Table 2) contains summary information such as the number of cpu, trait name, and number of significant snp-trait associations found. The second table (Table 3) gives the names and locations of the SNPs. The third table (Table 4) contains the effect sizes and statistical significances of the explanatory variables and the selected SNPs.

Table 2.

Summary information

Number cpu	8
Max memory (Gb)	8
Number of samples	800
Number of snp	70,484
Trait name	Bioch.HDL
Fixed model	Sex + Batch + Weight.Average
Number samples missing obs	0
Number significant snp-trait assocs	5
Lambda value for extBIC	0.53

Table 4.

Size and significance of effects in final model

	Effect size	Df	Wald statistic	Pr(Chisq)
(Intercept)	−2.31	1	35.98	1.995E−09
SexM	1.13	1	507.16	0.000E+00
BatchOBT02	0.00	1	0.00	9.869E−01
BatchOBT03	−0.28	1	1.29	2.561E−01
BatchOBT63	−0.16	1	0.43	5.117E−01
BatchOBT64	−0.11	1	0.21	6.448E−01
BatchOBT65	−0.12	1	0.21	6.491E−01
BatchOBT66	−0.20	1	0.85	3.570E−01
Weight.Average	0.05	1	148.30	0.000E+00
M12008C5	0.35	1	23.30	1.387E−06
M1530C6	0.15	1	29.76	4.878E−08
M26336C1	0.15	1	26.03	3.363E−07
M12020C5	−0.20	1	18.98	1.324E−05
M11706C10	−0.23	1	17.89	2.346E−05

Table 3.

Findings

SNP	Chrm	Position	Col Num
M12008C5	5	124,991,768	22,264
M1530C6	6	17,541,026	23,521
M26336C1	1	171,730,395	5254
M12020C5	5	125,044,979	22,267
M11706C10	10	125,357,987	41,402

Visualizing the findings

Suppose we are interested in viewing how the pattern of significance varies throughout the model building process. Here, we focus on chromosome 5. This chromosome is interesting because it has two closely linked regions housing genes underlying the trait.

Using the function statement

R> PlotAM(AMobj=res, itnum = 1, chr = “5”,

+    type = “Manhattan”)

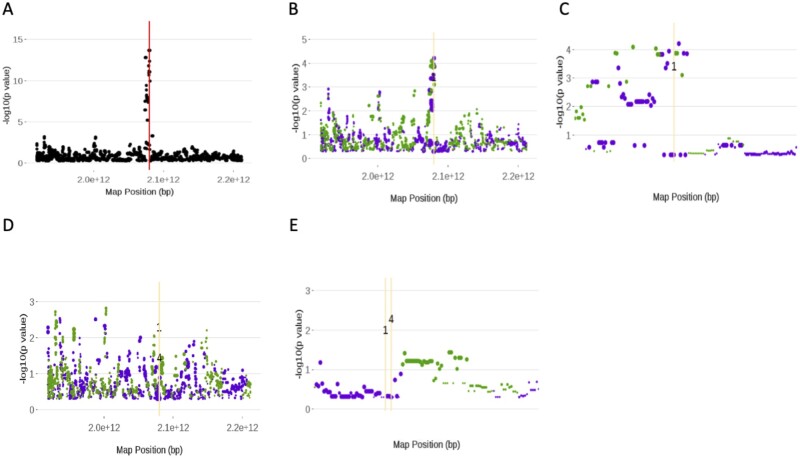
the resulting plot, for chromosome 5 and iteration 1, is shown in Figure 5A. Each point is a measure of the strength of association between a SNP and trait. The measure is calculated as the $-lo{g}_{10}$ of the p-value of the score statistic (see The Eagle Algorithm) for the SNP, since type=“Manhattan”. There is a clear spike toward the middle of the chromosome. In fact, the SNP in strongest association across the entire genome, at iteration 1, was on chromosome 5. Its position is given by the red vertical line.

Figure 5.

Screenshots of the plots from running the Eagle function PlotAM. All plots are Manhattan plots and are of chromosome 5. These plots show how the significance of the SNPs changes throughout the model building process. The red vertical line is the position of the SNP that has the largest score statistic and strongest association with the trait at that iteration. The orange vertical lines are the positions of SNPs found in previous iterations to be in strongest association with the trait. Green (purple) points denote SNPs that have increased (decreased) in significance from the previous iteration. The size of the point is proportional to the size of the change in significance. Images (A), (B), and (D) are plots of the first, second, and fifth iterations, respectively, of the model building process. Images (C) and (E) were created from (B) and (D), respectively, by using PlotAM’s interactive zoom feature.

By the end of the second iteration of the model building process, the SNP, which was identified in the first iteration, has been found to be significant. Its effect has been moved from the random to the fixed effects part of the model. This change impacts the significance of the other SNPs. By using the above command but with itnum set to 2, the plot in Figure 5B is generated. Here, the SNPs that have increased (decreased) in significance are denoted by green (purple) points. The size of the point is proportional to the size of the change in significance from the previous iteration. Unsurprisingly, the largest changes have occurred around the SNP whose effect is now being treated as a fixed effect. We can see this more clearly by using the zoom feature in PlotAM to focus on the region around the SNP of interest (Figure 5C).

What is interesting about Figure 5C is that there are still several SNPs in strong association with the trait. This suggests that there may be other statistically significant SNP–trait associations here. This is in fact the case, because by the fifth iteration, a second SNP has been found and fitted as a fixed effect. The pattern of association is shown in Figure 5D with the same zoomed region as before shown in Figure 5E. The drop in significance between fitting a single SNP in this region as a fixed effect to fitting two closely linked SNPs as fixed effects is apparent when you compare Figure 5C and E, noting the change in scales of the y-axes.

Multi-locus analysis via Blink

We thought that it would be informative to compare the performance of Eagle to another state-of-the-art multi-locus association mapping package. We chose Blink (Huang et al. 2019) as implemented in the R package GAPIT3 (Wang and Zhang 2020). Blink improves on the multi-locus method FarmCPU (Liu et al. 2016). It is faster and more powerful (Huang et al. 2019). An analysis was performed by reading in the phenotypic, genotypic, and map data into R. A covariate matrix was formed with covObj¡-model.matrix(Sex+Batch+Weight.Average, phenoObj). An analysis was then performed with the GAPIT3 function GAPIT with the argument model set to “Blink”. Blink found four of the five SNPs found by Eagle. It found one of the two SNPs on chromosome 5 and the same SNPs as Eagle on chromosomes 1, 6, and 10. Further testing would be needed to discover if, in general, Eagle has greater power than Blink for uncovering association between tightly linked SNP.

Computing speed

In terms of run times for the single-locus and multiple-locus analyses, gaston took 1.67 min, Eagle took 2.25 min, and Blink took 2.16 min. There is a C-based version of Blink that is an order of magnitude faster than the version tested here. However, due to R’s ever expanding ecosystem, our preference is for the R version of Blink.

Discussion

The Eagle package has been created to make genome-wide multi-locus association mapping easy. The package accepts marker data in different formats, has easy-to-use functions, comes with a user-friendly GUI, and has an interactive plotting function for visualizing the model building process. We welcome feedback via eaglehelp@csiro.au from users on how the functionality and usability of the package could be even further improved. As we saw in the example, Eagle brings clarity to situations where there are tightly linked SNPs in association with a trait. It can also uncover significant SNP–trait associations that are otherwise hidden to single-locus association mapping. At the very least, Eagle complements single-locus association mapping. However, ultimately, with the aid of Eagle, our hope is that the genetics community will shift to multi-locus association mapping as the method-of-choice for the genome-wide analysis of association data.

Data availability

The Eagle package is implemented in R and is freely available from https://CRAN.R-project.org/package=Eagle. An R script for performing the analyses presented in Results is available upon request. The input files used in the analysis are available from https://github.com/geo047/Example_Data.

Conflicts of interest

None declared.