Abstract
Characterizing epistatic gene interactions is fundamental for understanding the genetic architecture of complex traits. However, due to the large number of potential gene combinations, detecting epistatic gene interactions is computationally demanding. A simple, easy-to-perform method for sensitive detection of epistasis is required. Due to their homozygous nature, use of recombinant inbred lines excludes the dominance effect of alleles and interactions involving heterozygous genotypes, thereby allowing detection of epistasis in a simple and interpretable model. Here, we present an approach called RIL-StEp (recombinant inbred lines stepwise epistasis detection) to detect epistasis using single-nucleotide polymorphisms in the genome. We applied the method to reveal epistasis affecting rice (Oryza sativa) seed hull color and leaf chlorophyll content and successfully identified pairs of genomic regions that presumably control these phenotypes. This method has the potential to improve our understanding of the genetic architecture of various traits of crops and other organisms.
Keywords: epistasis, RILs, GWAS, rice, modeling
Introduction
Understanding the links between the genes and phenotypes of organisms is a key objective in biology. Nonadditive gene interaction is called epistasis (Fisher 1919; Phillips 2008) and is important for crop improvement through cross-breeding (Cordell 2002; Carlborg and Haley 2004; Xu and Crouch 2008; Heffner et al. 2009; Wang et al. 2012).
Genome-wide association studies (GWAS) are widely employed to elucidate genetic variations that affect complex phenotypic traits, allowing the identification of candidate loci controlling crop phenotypes (Huang et al. 2012; Sukumaran et al. 2015; Zhou et al. 2015). An organism’s phenotype is affected by biological pathways that involve interactions of multiple genes (Mackay 2014). GWAS have conventionally been used to identify major quantitative trait loci (QTLs) associated with a phenotype of interest. In most cases, these QTLs were considered to contribute additive effects to the trait values, independent of the effects of other loci. If there are strong phenotypic effects of gene–gene interactions, however, GWAS potentially miss important loci that control the trait in combination with other loci. In such cases, additive QTLs may not explain all the phenotypic variation (Carlborg and Haley 2004; Mackay and Moore 2014). Epistasis should be taken into account to better understand the genetic factors controlling phenotypic variations.
Identifying epistatic gene pairs is challenging, because the large number of combinations of genotypes incurs a heavy computational load and low statistical power due to multiple test correction. Despite these difficulties, numerous methods have been developed to identify epistatic gene pairs, including exhaustive statistical, regularization, Bayesian, and machine learning methods [for reviews, see Wei et al. (2014) and Niel et al. (2015)].
The exhaustive statistical approach is designed to test all combinations of genetic variants, most commonly single-nucleotide polymorphisms (SNPs) (Wan et al. 2010; Hemani et al. 2011; Li 2017). This method has a lower risk of failure in detecting epistasis but requires greater computational input and has lower statistical power due to multiple tests resulting from studying a large number of combinations of genetic variations (Wei et al. 2014). Reduction of the search space is needed to mitigate the computational burden. Multifactor dimensionality reduction (MDR) is commonly used for this purpose, and improvement of MDR has been reported, including quantitative MDR (QMDR), unified model based MDR (UM-MDR), and classification based MDR (CMDR) (Ritchie et al. 2001; Yu et al. 2015, 2016; Yang et al. 2017). Another way of reducing the search space is by incorporating additional information on the candidate genes involved in the phenotypes based on metabolic pathways, gene ontology, and protein–protein interactions (Ritchie 2011; Sun et al. 2014). However, the candidate gene approach is prone to ignoring unknown, but important, genes affecting the phenotype. Regularization methods such as logistic regression and group lasso algorithm use penalized regression models that perform variable selection by shrinking the number of coefficients (Park and Hastie 2008; Stanislas et al. 2017). Results of these methods are easy to interpret; however, regression models tend to have the overfitting problem. Bayesian methods represented by bayesian epistasis association mapping (BEAM) and its improved versions, BEAM3 and joint bayesian analysis of subphenotypes and epistasis (JBASE), are also used to detect epistasis (Zhang and Liu 2007; Zhang 2012; Colak et al. 2016). However, these methods focus only on qualitative traits and tend to lead to complex models. Machine learning algorithms such as support vector machine, ant colony algorithm, and random forest attempt to make nonparametric models to detect epistasis (Chen et al. 2008; Li et al. 2016; Yuan et al. 2017; Niel et al. 2018). Machine learning approaches are useful in detecting higher-order epistatic relationships thanks to their low computational costs. However, these approaches tend to generate highly complex models and sometimes suffer from a local optimality problem (Wei et al. 2014; Tuo 2018). Especially in analyses with small sample sizes, complexity of the models easily becomes too large compared to the sample size, leading to overfitting of the model to the data (Niel et al. 2015). Therefore, a nonexhaustive approach is not useful in samples with small sizes.
Recombinant inbred lines (RILs) are generated by performing an intercross of genetically distinct inbred parents to obtain F1 progeny. F1 plants are self-pollinated to obtain F2 plants, and each of the F2 progeny is self-pollinated several times by single seed descent (SSD) method to obtain further generations (Bailey 1971). Each self-pollination reduces heterozygosity by half, so that after substantial number of generations (e.g., >F6), genotypes of the RILs become random mosaics of parental genotypes with the majority of genomic regions being homozygous. Using RILs enables us to remove the effects of heterozygous genotypes, which contributes to reducing the complexity of models used in the detection of epistasis. Since the genotypes of RILs are random mosaics of parental genotypes, there are combinations of genes that did not exist in the parental lines, which may reveal gene–gene interactions that have not been previously identified. In addition, RILs allow phenotyping of multiple individuals from the same genotype, increasing the reliability of phenotype measurements.
In this study, we report a new approach, named RIL-StEp (recombinant inbred line stepwise epistasis detection), to detect epistasis in a pair of genetic variations of RILs based on the comparison of simple linear models. This model considers the additive effects of significant QTLs as well as epistatic effects between two selected SNPs. Therefore, the model is simple and easy to interpret. We applied the method to study epistatic relationships of loci that affect seed hull color and leaf chlorophyll content of rice (Oryza sativa) and successfully identified genomic regions that are epistatically interacting. Thus, RIL-StEp will be a valuable tool to gain insight into the genetic architecture of phenotypes in important crops and other organisms.
Materials and methods
Materials
The japonica rice (O. sativa) cultivar Hitomebore and the aus rice cultivar Kaluheenati from the National Agriculture and Food Research Organization World Rice Core Collection (Kojima et al. 2005) were crossed, and RILs of F9 generations consisting of 235 lines were generated by the SSD method.
Methods
Genotyping of RILs by whole-genome resequencing
To obtain the genotypes of all RILs, we performed whole-genome resequencing of the parents and 235 RILs using the Illumina platform. We filtered and trimmed these sequences using prinseq (Schmieder and Edwards 2011) and FaQCs (Lo and Chain 2014). Then, the quality-trimmed short reads were aligned against the reference genome using burrows-wheeler alignment tool (BWA) (Li and Durbin 2009). We used the genome sequence of Os-Nipponbare-Reference-IRGSP-1.0 as the reference (Kawahara et al. 2013). After mapping, we sorted and prepared index files from BAM files using samtools (Li et al. 2009). These BAM files were subjected to variant calling with bcftools (Narasimhan et al. 2016). Finally, we imputed the variants based on Hitomebore and Kaluheenati genotypes using LB-impute (Fragoso et al. 2016). For biallelic SNPs in our RILs, there are three genotypic classes: Hitomebore–Hitomebore, Hitomebore–Kaluheenati, and Kaluheenati–Kaluheenati. These genotype classes were parameterized to {0, 1, 2}. We identified a total of 1,046,779 SNPs between the two rice parents. We assessed the linkage disequilibrium (LD) statistics based on the LD decay plot as generated by PopLDdecay (Zhang et al. 2019). The LD decay plot showed that the average LD between SNPs located 5 kb apart is sufficiently high (r2 = 0.997) (Supplementary Figure S1). SNPs located within 5-kb distance mostly showed the identical genotypes in our RIL population. Therefore, we used only one SNP per 5-kb interval to reduce the calculation cost. We analyzed a total of 59,287 SNPs.
Phenotyping and quantification
We addressed two phenotypes: seed hull color and leaf chlorophyll content. Images of seeds of each line were scanned and saved for phenotyping of seed hull color. The numerical soil and plant analyzer development (SPAD) values (Uddling et al. 2007) were measured using an SPAD-502 chlorophyll meter (Konica Minolta, Tokyo, Japan) for phenotyping the relative chlorophyll content in the sample leaf. Five plants were measured in each RIL, and three SPAD readings per leaf were averaged as the mean SPAD reading of the leaf.
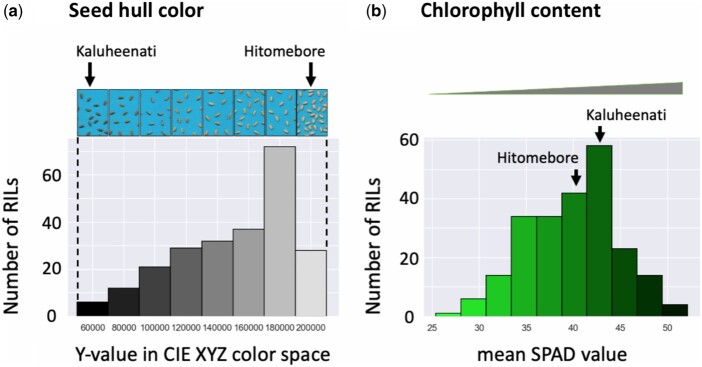
In the RILs, seed hull color showed gradation between beige and black (Figure 1A). Quantification of phenotypes tends to improve statistical power and interpretability of relationships between genetic variants and phenotypes (Bush and Moore 2012). Therefore, to convert seed hull color to quantitative values, we measured the brightness of the seed hull color. First, we extracted the seed image from the original scanned image and constructed a matrix of RGB values of the image. Then, we applied principal component analysis to extract the RGB values to detect representative color of all seeds in the image (Supplementary Figure S2). We applied this process to each RIL and obtained the representative RGB value of seed hull color for each line. Then, we converted these representative RGB values to CIE XYZ color space. The y-axis value showed the brightness in CIE XYZ color space, which was used as quantitative phenotypes. Larger y-axis values indicate brighter colors, whereas smaller y-axis values correspond to darker colors (Figure 1A). Finally, we applied inverse normal transformation to reach normally distributed phenotypic values (Supplementary Table S1).
Figure 1.
Variation in seed hull color and chlorophyll content among the RILs and the distribution of phenotypic values. (A) Seed hull color: in the histogram, the x-axis shows the range of phenotypic values (y-values in CIE XYZ color space). The top panel shows representative images of seeds in each range of the phenotypic values. (B) Leaf chlorophyll content: in the histogram, the x-axis shows the range of phenotypic values (mean SPAD values). In (A) and (B), the y-axis shows the number of RILs with phenotypic values in each range.
To quantify chlorophyll content, we used an SPAD meter (Uddling et al. 2007). Larger SPAD values indicate a higher chlorophyll content in the leaf (Figure 1B, Supplementary Table S1).
Recombinant inbred lines stepwise epistasis detection
To detect genomic regions of RILs that interact epistatically, we developed a simple method named RIL-StEp. In RIL-StEp, we generate linear models incorporating major QTLs as well as two SNPs at a time that are sampled from the entire genome. Two models, one with epistasis between the two SNPs and the other without epistasis, are compared using the Bayes factor. Specifically, we consider the following two linear models:
| (1) |
| (2) |
y is an n-vector of phenotypic values for n samples; is an intercept term; is the additive effect of each SNP detected by QTL analysis; is the number of QTLs; is the effect of the first SNP and is the effect of the second SNP. are the interaction effects of the alleles from the two SNPs: , P1 (Parent 1) allele and P2 (Parent 2) allele; , P2 allele and P1 allele, , P2 allele and P2 allele, for the first and second SNPs, respectively. One combination of alleles (P1–P1) is not included to escape multicollinearity (Supplementary Table S2a). are the n-dimensional genotype vectors of 1 and 0 s for each QTL and the two selected SNPs. are n-dimensional vectors with 1 s for samples with the specific combination of alleles of selected SNPs and 0 s for the rest. is an n-vector of residual error and is residual error variance.
only includes QTLs and two selected SNPs as the variables. In , we also incorporated the variables of epistasis effects between the two selected SNPs. We compared and based on the Bayes factor. The Bayes factor is a ratio of the marginal likelihoods of the two models of hypotheses. To measure the better fit of as compared to , we use the Bayes factor given by:
| (3) |
is the probability that phenotypic data are produced under the assumption of the Model. Bayes factor means (the model with epistasis) is more strongly supported by the phenotype dataset than is . We considered values of >100 as evidence of epistasis, following the interpretation table (Jarosz and Wiley 2014).
We used the R package “BayesFactor” (Morey et al. 2018) to compute Bayes factors by integrating the likelihood with respect to the priors on parameters. We estimated Bayes factors based on Monte Carlo sampling for the integration of parameters. Equations can be expressed as:
| (4) |
is a design matrix of genotypes for QTL or epistasis variables. is a vector of QTL and epistasis effects. is the sum of the number of QTLs and epistasis variables used in the model. In Monte Carlo sampling, we specified the prior distribution of following default settings of “BayesFactor” package and Liang et al. (2008) as given by:
| (5) |
The number of iterations to estimate the Bayes factor was 10,000. We applied these processes to a total of 17,573,556 combinations of SNPs.
In our RIL population with 235 lines, the average frequency of heterozygous genotypes at SNPs was around 4.6%. Therefore, the number of RILs with combinations of SNPs with heterozygous genotypes is very small, which makes it impractical to address the importance of epistasis involving heterozygous SNPs. Therefore, we focused on identifying interactions of homozygous genotypes and did not consider RILs with heterozygous genotypes at the selected SNPs.
However, the omission of samples with heterozygous genotypes may limit the application of the method to only highly inbred RILs. In addition, heterozygous genotypes could cause heterosis of certain traits. To account for these considerations, we developed a more generalized method of epistasis detection that can be applicable to heterozygous genotypes as well, which is given in Supplementary information.
To identify the SNPs corresponding to major QTLs and include them in our linear models, we used a GWAS approach based on the mixed linear model (Yu et al. 2006). We used the R package “GWASpoly” (Rosyara et al. 2016) to identify genomic regions that show a significant association with the phenotypic effect. Then, we selected an SNP with the largest values of –log10 (p) as the representative SNP for the QTL. These selected SNPs were included in and as the major QTLs.
We developed a program called “RIL-StEp” that performs the GWAS process and calculates Bayes factors for SNP combinations. The source code and detailed usage instructions of RIL-StEp are freely available from GitHub (https://github.com/slt666666/RILStEp) under MIT license.
Data availability
The genotype dataset, seed images of RILs, and supporting information (Supplementary Figures, Tables, Information) were deposited in Zenodo (10.5281/zenodo.4686057). All other relevant data are within the paper and the Supplementary files. RIL-StEp package source codes and a user manual are freely available through GitHub (https://github.com/slt666666/RILStEp) under MIT license. The scripts used in the phenotyping process are also deposited in GitHub (https://github.com/slt666666/Phenotyping_RILStEp).
Results
Rice seed hull color is not controlled by a single gene
To quantify rice seed hull color, we converted the color to numeric values based on the CIE XYZ color space. We then measured color values of the F9 generation seeds of 235 RILs derived from a cross between the rice cultivar Hitomebore (japonica type) and Kaluheenati (aus type). Seed hull color of RILs showed a gradation and was not categorized into the two discrete parental phenotypes, beige and black for Hitomebore and Kaluheenati, respectively (Figure 1, Supplementary Table S1). Frequency distribution of seed hull color values of the 235 RILs was skewed toward the higher phenotypic value (Figure 1); approximately one-third of RILs had whitish brown seeds (the higher phenotypic values) whereas the rest had darker brown seeds (the lower phenotypic values). From these data, we conclude that seed hull color is not controlled by a single gene. However, the phenotype was skewed toward higher values, and we hypothesized that significant nonadditive gene effects such as epistasis may be involved.
QTL analysis of seed hull color
We first carried out conventional QTL analysis to identify SNPs to be included in the RIL-StEp models. Between the genomes of the two parents Hitomebore and Kaluheenati, we identified a total of 1,046,779 SNPs. We selected one SNP per 5-kb interval and used 59,287 SNPs for subsequent QTL analysis and RIL-StEp. QTL analysis was carried out using 235 RILs by an R package “GWASpoly” (Rosyara et al. 2016) to detect SNPs associated with seed hull color. We found three genomic regions showing statistical significance, i.e., > 3 as well as FDR (false discovery rate) <0.05, on chromosomes 4 and 9 (Figure 2, Supplementary Table S3). Then, we selected three SNPs showing the highest values in each region. These SNPs were located on chr04:23121877, chr04:33353823, and chr09:6953870. We incorporated these three SNP values into the RIL-StEp models as the QTL variables.
Figure 2.
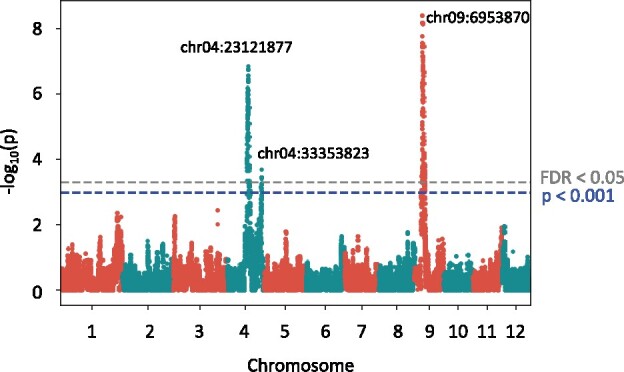
Quantitative trait locus analysis of rice seed hull color. Manhattan plot showing the significant association of SNPs with seed hull color phenotype as calculated by GWASpoly (Rosyara et al. 2016). The y-axis shows the –log10 (p) value of each SNP. The x-axis shows the genomic position. The blue dashed line indicates the significance, i.e., –log10 (p) > 3. The value corresponding to FDR <0.05 is given in gray dashed line. Only SNPs located near chr04:23121877, chr04:33353823, and chr09:6953870 exceeded the threshold P < 0.001 and FDR <0.05.
To study the effect of these three loci, we examined the effects of their genotype on the phenotype. When the SNP located on chr04:23121877 had the Kaluheenati genotype, phenotype values tended to be lower (Supplementary Figure S3A). The SNPs located on chr04:33353823 and chr09:6953870 showed a similar tendency (Supplementary Figure S3, B and C). Thus, Kaluheenati alleles of the genes located in the three QTLs result in darker seed hull color.
Application of RIL-StEp to rice seed hull color
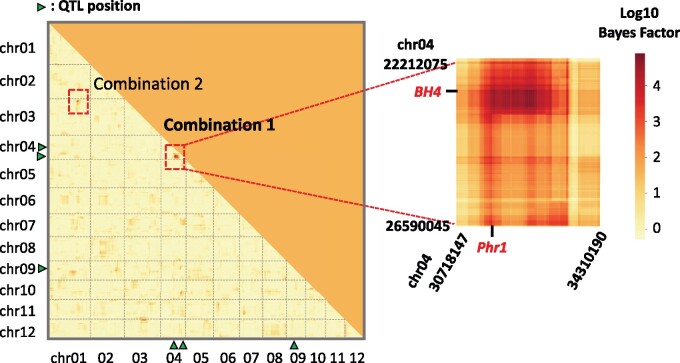
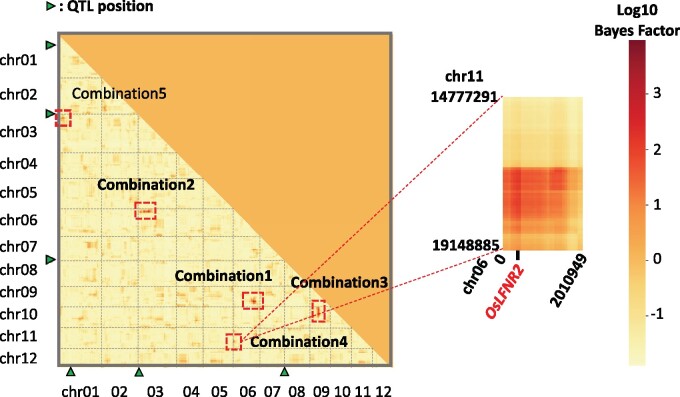
We used RIL-StEp to detect SNP pairs showing significant genetic interactions in rice seed hull color. In this analysis, we incorporated the three major QTLs on chromosomes 4 and 9 (Figure 2). To detect epistatic loci, we first selected 1 of every 10 SNPs out of 59,287 SNPs across the genome, resulting in 5929 SNPs. We applied RIL-StEp to all pairs of the 5929 SNPs. After calculating the Bayes factors for SNP pairs (Supplementary Table S4), we focused on the genomic regions with SNP combinations showing Bayes factor values >100. After establishing approximate positions of the loci showing possible epistasis, we applied RIL-StEp again to all combinations of SNPs in the two regions (Figure 3, Supplementary Table S5). We identified two combinations of two genomic regions, Combination 1 and Combination 2, as the candidate regions showing epistatic interactions (Figure 3). Two genomic regions of Combination 1 matched the positions of the SNPs detected by QTL analysis (chr04:23121877 and chr04:33353823) (Figure 2). SNP pairs between these regions showed large Bayes factor values. The highest Bayes factor value () was 77652 for Combination 1 and 281 for Combination 2 (Figure 3, Supplementary Table S5).
Figure 3.
Heatmap showing Bayes factors for combinations of SNPs as revealed by RIL-StEp for rice hull color. The left heatmap shows the Bayes factors of SNP combinations over the whole genome. In Combination 1 (chr04:22212075–26590045 × chr04:30718147–34310190) and Combination 2 (chr01:30334348–31519089 × chr03:2401129–3212328), Bayes factors of combinations of SNPs located between two regions were >100. Positions of major QTLs are indicated by green triangles. The right heatmap magnifies genomic regions that potentially include epistatic genes. Names of candidate genes possibly involved in the epistasis are indicated by red color.
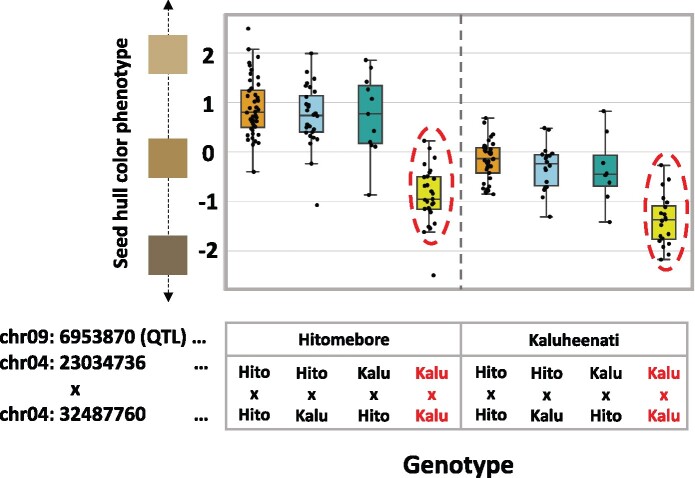
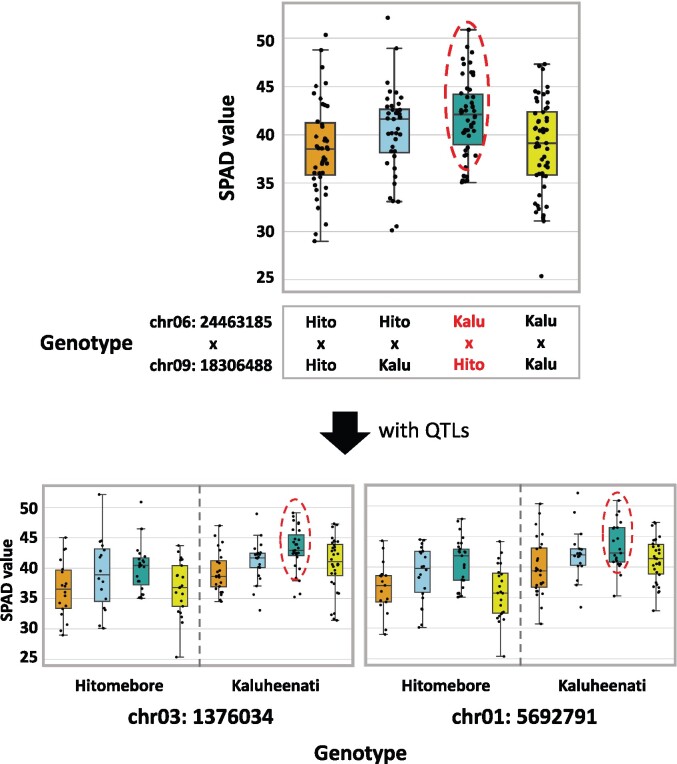
We hypothesized that the genes located in these two regions are interacting with each other. To test this hypothesis, we selected SNP pairs with the highest Bayes factors and plotted the phenotype values for the combination of genotypes for the SNP pair considering the genotypes at the significant QTL located on chr09:6953870 as detected by QTL analysis. Combination 1 showed a clear epistasis effect (Figure 4). When the genotypes at SNPs located on chr04:23034736 and chr04:32487760 are both Kaluheenati types, the phenotype values tend to be low. On the other hand, if the genotypes are in other combinations, the color values were higher and similar to each other (Figure 4). This result suggested that both these regions would need to be Kaluheenati types to make seed hull color black. We assumed that two genes located close to these SNPs function together to determine the seed hull color. In Combination 2, when the genotype combinations of chr01:30449415 and chr03:2749620 are Kaluheenati–Hitomebore or Hitomebore–Kaluheenati types, the phenotypic values tend to be higher than the parental combinations (Supplementary Figure S4). However, the epistatic relationship was not clear because the number of RILs showing the Kaluheenati type at SNPs on chr01:30449415 was small. Therefore, we focused on Combination 1 for further analysis.
Figure 4.
Relationships between rice seed hull color phenotypes and genotypes of the three loci. A boxplot showing the phenotypic values of RILs with different combinations of genotypes at SNPs on chr04:23034736, chr04:32487760, and chr09:6953870. The horizontal line inside each box represents median value. Box range is the first and third quantile. The whisker extends to last datum less than the third quantile + 1.5*interquartile range (IQR) and the first datum greater than the first quantile—1.5*IQR. The x-axis shows the combinations of genotypes. The y-axis shows phenotypic values. When SNPs on chr04:23034736 and chr04:32487760 both have Kaluheenati genotypes, phenotypic values tended to be low (indicated by red circles and red characters), whereas in other combinations, the values were higher and similar.
Identifying candidate genes involved in seed hull color epistasis
We surveyed genes located in the two regions as detected by RIL-StEp and tried to identify genes that may affect seed hull color. The region chr04:22212075–26590045 contained Black Hull 4 (BH4: chr04:22969845–22971859). In the region chr04:30718147–34310190, we identified Phenol reaction 1 (Phr1: chr04:31749141–31751604). Loss of function of Bh4 changed the black hull phenotype of wild rice species to white hull of cultivated rice (Zhu et al. 2011). Phr1 is associated with the phenol reaction (Yu et al. 2008). Brown hull color of indica rice is caused by the presence of Phr1 (Yu et al. 2008). RIL-StEp identified a pair of SNPs with a high Bayes factor (Figure 3), and two genes located close to the SNPs control seed hull color. Therefore, we hypothesized that these genes are the major factors epistatically affecting seed hull color in our RILs.
We compared the nucleotide sequences of BH4 and Phr1 from the parental cultivars Hitomebore and Kaluheenati used for generating the RILs. Kaluheenati had intact BH4 and Phr1 genes, whereas Hitomebore had a 22-bp deletion in BH4 and an 18-bp deletion in Phr1 (Supplementary Figure S5). These deletions are identical to those reported in other japonica-type cultivars (Fukuda et al. 2012) and were reported to cause loss of function in the respective genes (Yu et al. 2008; Zhu et al. 2011). Thus, we conclude that BH4 and Phr1 function is maintained in Kaluheenati but lost in Hitomebore.
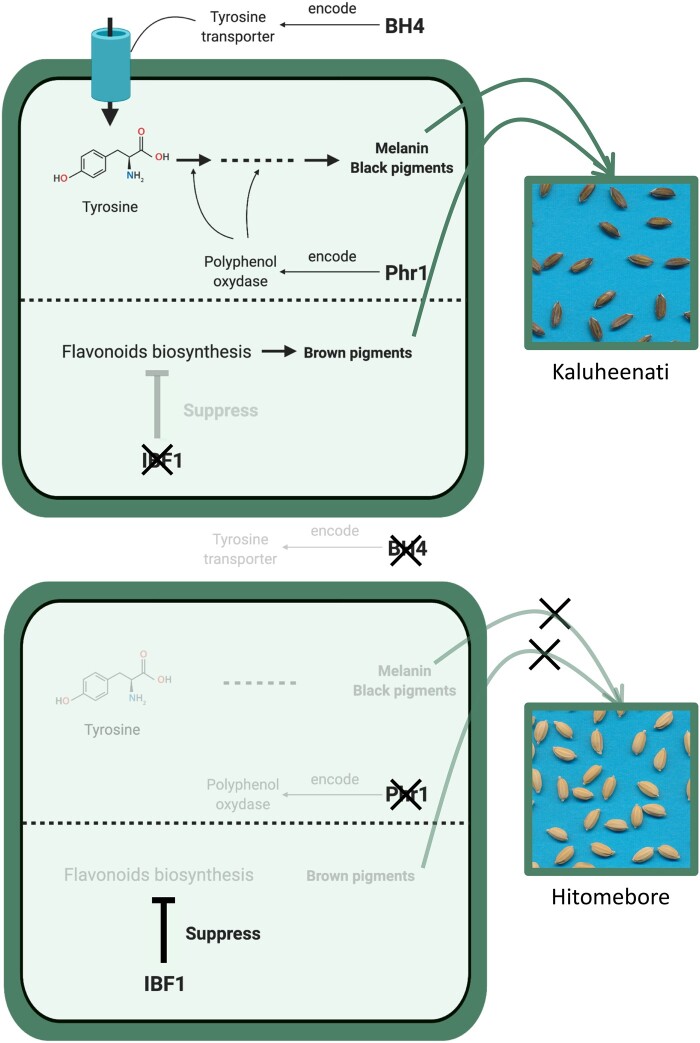
Using a line crossed between the indica-type cultivar Habataki and the japonica-type cultivar Arroz da Terra, Fukuda et al. (2012) reported that both BH4 and Phr1 are necessary for maintaining black hull phenotype. BH4 encodes a tyrosine transporter and Phr1 encodes a polyphenol oxidase of the tyrosinase family (Yu et al. 2008; Zhu et al. 2011). Tyrosine is converted by the tyrosinase to melanin, the main black pigment (Riley 1997). We assumed that BH4 is required for transportation of tyrosine and Phr1 for melanin biosynthesis (Figure 5) and that the melanin biosynthesis pathway does not operate if either of these genes does not function. This line of thinking is consistent with the result that seed hull color tends to be lighter when one of the two SNPs has the Hitomebore genotype (Figure 4).
Figure 5.
Simplified scheme of the pathways related to rice seed hull color as hypothesized in the present study. This figure summarizes the biological functions of BH4, Phr1, and IBF1 in rice seed hull color. BH4 encodes a tyrosine transporter (Zhu et al. 2011) and Phr1 encodes a polyphenol oxidase (Yu et al. 2008). These genes are related to melanin biosynthesis pathway. IBF1 inhibits flavonoid biosynthesis as a suppressor (Shao et al. 2012). Thick black arrows indicate biosynthesis pathways of pigments and thin black arrows indicate genes and proteins involved in their synthesis.
In addition, we surveyed genes located near the SNP chr09:6953870 as identified by the QTL analysis to address its contribution to seed hull color in combination with BH4 and Phr1. We identified Inhibitor for brown furrows1 (IBF1) on chr09:6873236–6874612. A previous study showed that ibf1 mutants of japonica- and indica-type cultivars accumulate brown pigments during seed maturation. Thus, IBF1 is a suppressor of brown pigment deposition in rice hull furrows (Shao et al. 2012). We compared the sequences of IBF1 in the two parental cultivars. Kaluheenati had a 19-bp deletion in IBF1, whereas Hitomebore had an intact protein-coding region (Supplementary Figure S5). This result suggests that the 19-bp deletion in Kaluheenati caused loss of function of IBF1, preventing it from suppressing the accumulation of brown pigmentation in rice hull furrows. This is in line with the lower phenotypic value (brown color) of RILs with Kaluheenati-type genotype around the IBF1 gene (Figure 4). IBF1 is involved in flavonoid biosynthesis (Shao et al. 2012).
The relationship between seed hull color and genotypes of the three SNPs located near BH4, Phr1, and IBF1 showed that the effect of IBF1 is independent of that of BH4 and Phr1 (Figure 4). Thus, the pathway involving BH4 and Phr1 and that of IBF1 probably function independently (Figure 5).
Phenotype variation of chlorophyll content in rice RILs
We used the mean SPAD values to quantify leaf chlorophyll content. The phenotype values are distributed normally (Figure 1B). Therefore, the chlorophyll content is likely controlled by multiple genes.
QTL analysis of chlorophyll content
We carried out QTL analysis to identify SNPs to include in the models of RIL-StEp and identified three genomic regions on chromosomes 1, 3, and 7 that showed statistical significance, i.e., –log10(p) >3 (Figure 6, Supplementary Table S6). Among them, only the genomic region on chromosome 3 showed FDR <0.05. However, in order to include all potential QTLs in consideration, we selected the three SNPs showing the highest values in each region. These SNPs were located on chr01:5692791, chr03:1376034, and chr07:25128206. We incorporated these three SNP values into RIL-StEp models as the QTL variables. To study the effect of these three loci, we examined the effects of their genotype on the phenotype. When the SNP located on chr01:5692791 has the Kaluheenati genotype, phenotype values tended to be higher (Supplementary Figure S6A). The SNP located on chr03:1376034 showed a similar tendency (Supplementary Figure S6B), whereas the SNP located on chr07:25128206 showed an opposite tendency (Supplementary Figure S6C).
Figure 6.
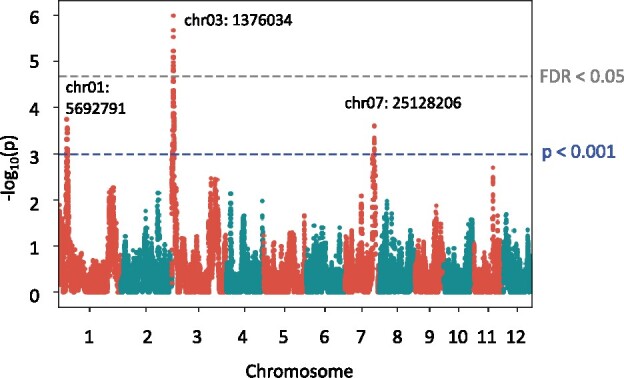
Quantitative trait locus analysis of leaf chlorophyll content. A Manhattan plot showing the significant association of SNPs with leaf chlorophyll content as calculated by GWASpoly (Rosyara et al. 2016). The y-axis shows the –log10(p) value of each SNP. The x-axis shows the genomic position. Blue dashed line indicates the significance, i.e., –log10(p) >3. The value corresponding to FDR <0.05 is given in gray dashed line. SNPs located near chr01:5692791, chr03:1376034, and chr07:25128206 exceeded the threshold (P < 0.001) and only SNPs close to chr03:1376034 exceeded FDR <0.05.
Application of RIL-StEp to chlorophyll content trait
We used RIL-StEp to detect SNP pairs showing significant genetic interactions in leaf chlorophyll content. We incorporated three potential QTLs on chromosomes 1, 3, and 7 (Figure 6). As with the grain color, we first identified combinations of genomic regions showing Bayes factor values >100 after considering 1 SNP every 10 SNPs (Supplementary Table S7). Subsequently, we applied RIL-StEp again to the combinations of all SNPs in the identified regions (Figure 7, Supplementary Table S5). We identified five combinations of genomic regions as candidate epistatic interactions (Figure 7, Supplementary Table S5). The highest Bayes factor () value was 9226 for Combination 1, followed by 857 for Combination 2, 299 for Combination 3, 190 for Combination 4, and 186 for Combination 5 (Figure 7, Supplementary Table S5). One of the genomic regions of Combination 5 matched the position of the SNP detected by QTL analysis (chr01:5692791) (Figure 7). The other regions detected by RIL-StEp did not correspond to the major QTLs. Thus, we hypothesized that genes located in the respective regions interact with each other. To test this hypothesis, we selected SNP pairs with the highest Bayes factors and plotted the phenotype values for the combination of genotypes for the SNP pair taking QTL genotypes in consideration. All combinations showed clear epistasis effect (Figure 8, Supplementary Figure S7).
Figure 7.
Heatmap showing Bayes factors for combinations of SNPs as revealed by RIL-StEp for mean SPAD value. The left heatmap shows the Bayes factors of SNP combinations over the whole genome. In Combination 1 (chr06:24053623–26700388 × chr09:16870158–20228711), Combination 2 (chr03:6283299–10572916 × chr06:2563469–3937767), Combination 3 (chr09:10799441–12292861 × chr10:2896894–10329230), Combination 4 (chr06:400132–495498 × chr11:16691276–17670071), and Combination 5 (chr01:5005036–5346178 × chr03:3956604–4008211), Bayes factors of combinations of SNPs located between two regions were >100 (indicated by red squares). Positions of major QTLs are indicated by green triangles. The right heatmap magnifies genomic regions with a candidate gene OsLFNR2 potentially involved in the epistasis of Combination 4.
Figure 8.
Relationships between leaf chlorophyll content phenotypes and genotypes of the epistatic loci of Combination 1. Top boxplot shows the phenotypic values of RILs with different combinations of genotypes at SNPs on chr06:24463185 and chr09:18306488. The horizontal line inside each box represents median value. Box range is the first and third quantile. The whisker extends to last datum less than the third quantile + 1.5*interquartile range (IQR) and the first datum greater than the first quantile—1.5*IQR. The x-axis shows the combinations of genotypes. The y-axis shows phenotypic values. Bottom boxplots show the phenotypic values of RILs with different combinations of genotypes of epistatic loci and QTLs. When the genotype at the SNPs on chr06:24463185 is Kaluheenati and on chr09:18306488 is Hitomebore, phenotypic values tended to be high (indicated by red circles and red characters).
When the genotype at SNPs located on chr06:24463185 is Kaluheenati type and that of chr09:18306488 is Hitomebore type (Combination 1), the phenotype values tend to be high (Figure 8). This tendency is pronounced when the genotypes of the QTLs (on chromosomes 1 and 3) are Kaluheenati type (Figure 8, Supplementary Figure S7A). This result suggested that the combination of Kaluheenati (chr06)-Hitomebore (chr09) genotypes of the two epistatic regions (Combination 1) with Kaluheenati-type alleles of the two QTLs on chromosomes 1 and 3 produces greater leaf chlorophyll content. The phenotypes of other combinations (Combinations 2–5) are summarized in Supplementary Figure S7 and Table S8A. We hypothesize that the genes located close to the SNP pair of each combination may function together to influence leaf chlorophyll content.
We surveyed genes located in the five combinations of genomic regions showing epistasis as detected by RIL-StEp and tried to identify candidate genes that may affect leaf chlorophyll content. Results are summarized in Supplementary Figure S8 and Table S8B. In most cases, the candidate genes differed between the parents Hitomebore and Kaluheenati by indels in the 3ʹ or 5ʹ untranslated region or by base substitutions in the coding regions, so that their effects were not obvious. In Combination 4, we found a gene encoding leaf-type FNRs (OsLFNR2: chr06:479261–481572) in the region chr06:400132–495498 (Supplementary Figure S8E). Overexpression of OsLFNR2 in Arabidopsis led to low chlorophyll content caused by impairment of photosynthetic electron transport around photosystem I (Higuchi-Takeuchi et al. 2011). Sequence comparison of OsLFNR2 genes showed Hitomebore had an intact OsLFNR2, whereas Kaluheenati had a 10-bp deletion in the exon region (Supplementary Figure S8E), which may lead to loss of function. We hypothesize that there is a previously unreported gene located on chr11:16691276–17670071 that interacts with OsLFNR2 to control chlorophyll content. Future study will reveal the genes involved in the observed epistasis.
Discussion
In this study, we describe a new approach called RIL-StEp for detecting epistatic relationships of genes. This approach is specialized to RIL populations and based on Bayes factors for comparison of simple linear models. Using RIL-StEp, we successfully detected pairs of genomic regions showing epistasis that affect seed hull color and leaf chlorophyll content.
We identified a combination of genomic regions that showed an epistatic effect on seed hull color and a QTL region that showed an independent effect. The difference in seed hull color between the two parental lines is most likely controlled by the genes linked to the three identified regions. Among the three regions, two seem to interact with each other as revealed by RIL-StEp. Seed hull color exhibited a gradual change and the distribution of color values was skewed to the higher end depending on the genotypes of these genes (Figures 1A and 4). This result suggested that RIL-StEp succeeded in identifying epistatic gene loci. However, these three loci were detected by GWAS even without considering epistasis (Figure 2). Therefore, when addressing traits that are controlled by a small number of loci (e.g., two or three loci), it may be sufficient to evaluate the presence of epistasis only among the QTLs identified by GWAS (Laurie et al. 2014).
As another example, RIL-StEp identified five combinations of genomic regions that showed epistasis on the chlorophyll content. These regions did not overlap the QTL as detected by GWAS, except for in one region. This result suggests RIL-StEp has the potential to identify genomic regions involved in epistasis that were not detected by GWAS. SPAD values reflecting chlorophyll content were distributed normally (Figure 1B), indicating that the trait is controlled by multiple genes. Thus, RIL-StEp has the potential to elucidate the epistatic genetic architecture of traits that are controlled by multiple genes.
An advantage of RIL-StEp is its high interpretability as compared to other approaches that consider many variables at once. Our model includes as variables only significant QTLs and the effects of two SNPs and their epistasis at a time. Thus, the results of our model can be easily validated by plotting a graph of effects of epistasis of two SNPs, taking into account the major QTL effect (Figures 4 and 8, Supplementary Figure S7). In addition, our model has low complexity, circumventing problems of overfitting that are inherent in the complex model. Thus, our model avoids the failure in detecting epistasis due to the local optimality problem. Therefore, RIL-StEp is a suitable option for detecting epistasis in any traits when RILs are used. Our approach adopted Bayes factors, which can incorporate prior assumption on the effect of each genetic variant (Wakefield 2009; Runcie and Crawford 2019). Although we specified prior distribution according to a previous report (Liang et al. 2008), our approach is capable of incorporating any prior assumptions such as spike and slab prior and MIXTURE model (Ishwaran and Rao 2005; Luan et al. 2009).
A disadvantage of our approach is the difficulty in detecting higher-order (e.g., more than three loci) epistatic relationships. Detecting high-order relationships using our exhaustive approach increases computational cost explosively and decreases the interpretability of the models (Taylor and Ehrenreich 2015). Therefore, the nonexhaustive approach may be more appropriate to identify high-order epistasis. Our approach attempted to identify interacting SNP pairs based on the comparison of two models with and without an epistasis effect, and it may reveal false positives, but we prioritized avoiding false negatives caused by local optimality. In addition, the simplicity of our model possibly leads to an underfitting problem such that the model is not able to fully explain the relationship between phenotype and genotype. Therefore, our model is not appropriate for the purpose of precise genomic prediction. For genomic prediction, more complex models or nonexhaustive approaches that consider whole genotypic information would be better options (Azodi et al. 2019).
We succeeded in identifying genomic regions that show epistasis. We used K > 100 as the threshold of candidate epistatic regions, following the interpretation table (Jarosz and Wiley 2014). In our study, we identified seven combinations of genomic regions that had high Bayes factor values (K = 186–77652). Six of them showed epistasis effects (Figures 4 and 8, Supplementary Figure S7). It was difficult to interpret the epistatic relationship in one combination (Combination 2 of seed hull color trait: K = 281) due to the biased distribution of genotypes of this combination (Supplementary Figure S4). Therefore, we believe the threshold of K > 100 may be appropriate to detect candidate epistatic genomic regions in most cases. However, spurious epistasis may be possibly identified due to the bias of genotypes in a population, and careful validation is needed to conclude the epistatic effect of candidate loci. The identified regions may contain multiple genes, and we could not specify the responsible genes by genetic analysis alone. A challenge of GWAS is to bridge the gap between the identification of the genomic regions and of the causative genes responsible for the phenotype (Gallagher and Chen-Plotkin 2018). Using more RILs and applying a stricter threshold in the epistasis analysis should make it possible to pin down a much smaller genomic region. However, applying a stricter threshold has a risk of missing true positives. Indeed, the genomic regions of the interacting gene pair BH4 and Phr1 were not in the regions that showed the highest Bayes factor values (Figure 3). It is challenging to strike the appropriate balance between controlling for type I and type II errors (Todorov and Rao 1997). Identifying genes using only statistical significance thresholds is usually not possible and not appropriate.
Here, we successfully specified strong candidate genes presumably controlling the seed hull phenotype using knowledge about the candidate genes and the sequence analysis. However, this approach may not be applicable in every case. There may be several approaches to validate the epistatic relationship between the genes, such as co-expression analysis to explore genes in the same biological processes (Aoki et al. 2007; Mao and Chen 2012; van Dam et al. 2018) or eQTL analysis to identify genetic variants regulated by specific genes (Gilad et al. 2008; Feltus 2014). Combining information from other sources of evidence with RIL-StEp results may enhance our capability to identify interacting genes.
To summarize, we propose a novel approach based on simple linear models to detect epistatic interactions underlying quantitative traits in the RIL population. By applying RIL-StEp, we succeeded in identifying genomic regions related to rice seed hull color and chlorophyll content. Incorporating additional information allowed us to identify candidate genes involved in seed hull color. Thus, our approach has the potential to identify epistasis in various biological traits.
R.T. and T.S. conceptualized the study. T.S., A.A., and M.S. performed the research. The original draft was written by T.S. and reviewed by R.T., A.A., and M.S. All authors read and approved the final manuscript.
Acknowledgments
We thank the National Agriculture and Food Research Organization (NARO) gene bank, Japan for providing the World Rice Core Collection seed. We thank Sophien Kamoun for valuable comments and Shigeru Kuroda for continuous support of the project.
Funding
This study was supported by grants from the Project of the NARO Bio-oriented Technology Research Advancement Institution (research program on development of innovative technology) and by grants JSPS KAKENHI 15H05779 and 20H00421 to R.T., 17H03752 and 20H02962 to A.A.
Conflicts of interest
None declared.
Literature cited
- Aoki K, Ogata Y, Shibata D.. 2007. Approaches for extracting practical information from gene co-expression networks in plant biology. Plant Cell Physiol. 48:381–390. [DOI] [PubMed] [Google Scholar]
- Azodi CB, Bolger E, McCarren A, Roantree M, de los Campos G, et al. 2019. Benchmarking parametric and machine learning models for genomic prediction of complex traits. G3 (Bethesda). 9:3691–3702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey DW. 1971. Recombinant-inbred strains: an aid to finding identity, linkage, and function op histocompatibility and other genes. Transplantation. 11:325–327. [DOI] [PubMed] [Google Scholar]
- Bush WS, Moore JH.. 2012. Chapter 11: genome-wide association studies. PLoS Comput Biol. 8: e1002822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlborg Ö, Haley CS.. 2004. Epistasis: too often neglected in complex trait studies? Nat Rev Genet. 5:618–625. [DOI] [PubMed] [Google Scholar]
- Chen SH, Sun J, Dimitrov L, Turner AR, Adams TS, et al. 2008. A support vector machine approach for detecting gene-gene interaction. Genet Epidemiol. 32:152–167. [DOI] [PubMed] [Google Scholar]
- Colak R, Kim T, Kazan H, Oh Y, Cruz M, et al. 2016. JBASE: joint Bayesian analysis of subphenotypes and epistasis. Bioinformatics. 32:203–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell HJ. 2002. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum Mol Genet. 11:2463–2468. [DOI] [PubMed] [Google Scholar]
- Feltus FA. 2014. Systems genetics: a paradigm to improve discovery of candidate genes and mechanisms underlying complex traits. Plant Sci. 223:45–48. [DOI] [PubMed] [Google Scholar]
- Fisher RA. 1919. XV.—the correlation between relatives on the supposition of Mendelian inheritance. Trans R Soc Edinb. 52:399–433. [Google Scholar]
- Fragoso CA, Heffelfinger C, Zhao H, Dellaporta SL.. 2016. Imputing genotypes in biallelic populations from low-coverage sequence data. Genetics. 202:487–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda A, Shimizu H, Shiratsuchi H, Yamaguchi H, Ohdaira Y, et al. 2012. Complementary genes that cause black ripening hulls in f 1 plants of crosses between Indica and Japonica rice cultivars. Plant Prod. Sci. 15:270–273. [Google Scholar]
- Gallagher MD, Chen-Plotkin AS.. 2018. The post-GWAS era: from association to function. Am J Hum Genet. 102:717–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilad Y, Rifkin SA, Pritchard JK.. 2008. Revealing the architecture of gene regulation: the promise of eQTL studies. Trends Genet. 24:408–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffner EL, Sorrells ME, Jannink JL.. 2009. Genomic selection for crop improvement. Crop Sci. 49:1–12. [Google Scholar]
- Hemani G, Theocharidis A, Wei W, Haley C.. 2011. EpiGPU: exhaustive pairwise epistasis scans parallelized on consumer level graphics cards. Bioinformatics. 27:1462–1465. [DOI] [PubMed] [Google Scholar]
- Higuchi-Takeuchi M, Ichikawa T, Kondou Y, Matsui K, Hasegawa Y, et al. 2011. Functional analysis of two isoforms of leaf-type ferredoxin-NADP +-oxidoreductase in rice using the heterologous expression system of Arabidopsis. Plant Physiol. 157:96–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, Zhao Y, Wei X, Li C, Wang A, et al. 2012. Genome-wide association study of flowering time and grain yield traits in a worldwide collection of rice germplasm. Nat Genet. 44:32–39. [DOI] [PubMed] [Google Scholar]
- Ishwaran H, Rao JS.. 2005. Spike and slab variable selection: Frequentist and Bayesian strategies. Ann Stat. 33:730–773. [Google Scholar]
- Jarosz AF, Wiley J.. 2014. What are the odds? A practical guide to computing and reporting Bayes factors. J Probl Solving. 7:2–9. [Google Scholar]
- Kawahara Y, de la Bastide M, Hamilton JP, Kanamori H, McCombie WR, et al. 2013. Improvement of the Oryza sativa Nipponbare reference genome using next generation sequence and optical map data. Rice (N Y). 6:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima Y, Ebana K, Fukuoka S, Nagamine T, Kawase M.. 2005. Development of an RFLP-based rice diversity research set of germplasm. Breed Sci. 55:431–440. [Google Scholar]
- Laurie C, Wang S, Carlini-Garcia LA, Zeng ZB.. 2014. Mapping epistatic quantitative trait loci. BMC Genet. 15: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R.. 2009. Fast and accurate short read alignment with Burrows–Wheeler transform. Bioinformatics. 25:1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, et al. ; 1000 Genome Project Data Processing Subgroup. 2009. The sequence alignment/map format and SAMtools. Bioinformatics. 25:2078–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Malley JD, Andrew AS, Karagas MR, Moore JH.. 2016. Detecting gene-gene interactions using a permutation-based random forest method. BioData Min. 9:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X. 2017. A fast and exhaustive method for heterogeneity and epistasis analysis based on multi-objective optimization. Bioinformatics. 33:2829–2836. [DOI] [PubMed] [Google Scholar]
- Liang F, Paulo R, Molina G, Clyde MA, Berger JO.. 2008. Mixtures of g priors for Bayesian variable selection. J Am Stat Assoc. 103:410–423. [Google Scholar]
- Lo CC, Chain PSG.. 2014. Rapid evaluation and quality control of next generation sequencing data with FaQCs. BMC Bioinformatics. 15:366–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luan T, Woolliams JA, Lien S, Kent M, Svendsen M, et al. 2009. The accuracy of genomic selection in Norwegian red cattle assessed by cross-validation. Genetics. 183:1119–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay TFC. 2014. Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nat Rev Genet. 15:22–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay TFC, Moore JH.. 2014. Why epistasis is important for tackling complex human disease genetics. Genome Med. 6:125–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mao D, Chen C.. 2012. Colinearity and similar expression pattern of rice DREB1s reveal their functional conservation in the cold-responsive pathway. PLoS One. 7:e47275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morey RD, Rouder JN, Jamil T, Urbanek S, Forner K, et al. 2018. Package ‘BayesFactor’.https://cran.r-project.org/web/packages/BayesFactor/BayesFactor.pdf (26 April 2021, date last accessed).
- Narasimhan V, Danecek P, Scally A, Xue Y, Tyler-Smith C, et al. 2016. BCFtools/RoH: a hidden Markov model approach for detecting autozygosity from next-generation sequencing data. Bioinformatics. 32:1749–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niel C, Sinoquet C, Dina C, Rocheleau G.. 2015. A survey about methods dedicated to epistasis detection. Front Genet. 6: [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niel C, Sinoquet C, Dina C, Rocheleau G.. 2018. SMMB: a stochastic Markov blanket framework strategy for epistasis detection in GWAS. Bioinformatics. 34:2773–2780. [DOI] [PubMed] [Google Scholar]
- Park MY, Hastie T.. 2008. Penalized logistic regression for detecting gene interactions. Biostatistics. 9:30–50. [DOI] [PubMed] [Google Scholar]
- Phillips PC. 2008. Epistasis—the essential role of gene interactions in the structure and evolution of genetic systems. Nat Rev Genet. 9:855–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley PA. 1997. Melanin. Int J Biochem Cell Biol. 29:1235–1239. [DOI] [PubMed] [Google Scholar]
- Ritchie MD. 2011. Using biological knowledge to uncover the mystery in the search for epistasis in genome-wide association studies. Ann Hum Genet. 75:172–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, et al. 2001. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet. 69:138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosyara UR, de Jong WS, Douches DS, Endelman JB.. 2016. Software for genome-wide association studies in autopolyploids and its application to potato. Plant Genome. 9:1–10. [DOI] [PubMed] [Google Scholar]
- Runcie DE, Crawford L.. 2019. Fast and flexible linear mixed models for genome-wide genetics. PLoS Genet. 15:e1007978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmieder R, Edwards R.. 2011. Quality control and preprocessing of metagenomic datasets. Bioinformatics. 27:863–864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao T, Qian Q, Tang D, Chen J, Li M, et al. 2012. A novel gene IBF1 is required for the inhibition of brown pigment deposition in rice hull furrows. Theor Appl Genet. 125:381–390. [DOI] [PubMed] [Google Scholar]
- Stanislas V, Dalmasso C, Ambroise C.. 2017. Eigen-Epistasis for detecting gene-gene interactions. BMC Bioinformatics. 18:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukumaran S, Dreisigacker S, Lopes M, Chavez P, Reynolds MP.. 2015. Genome-wide association study for grain yield and related traits in an elite spring wheat population grown in temperate irrigated environments. Theor Appl Genet. 128:353–363. [DOI] [PubMed] [Google Scholar]
- Sun X, Lu Q, Mukheerjee S, Crane PK, Elston R, et al. 2014. Analysis pipeline for the epistasis search - statistical versus biological filtering. Front Genet. 5:106–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor MB, Ehrenreich IM.. 2015. Higher-order genetic interactions and their contribution to complex traits. Trends Genet. 31:34–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov AA, Rao DC.. 1997. Trade-off between false positives and false negatives in the linkage analysis of complex traits. Genet Epidemiol. 14:453–464. [DOI] [PubMed] [Google Scholar]
- Tuo S. 2018. FDHE-IW: a fast approach for detecting high-order epistasis in genome-wide case-control studies. Genes (Basel). 9:435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddling J, Gelang-Alfredsson J, Piikki K, Pleijel H.. 2007. Evaluating the relationship between leaf chlorophyll concentration and SPAD-502 chlorophyll meter readings. Photosynth Res. 91:37–46. [DOI] [PubMed] [Google Scholar]
- van Dam S, Võsa U, van der Graaf A, Franke L, de Magalhães JP.. 2018. Gene co-expression analysis for functional classification and gene-disease predictions. Brief Bioinform. 19:575–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakefield J. 2009. Bayes factors for Genome-wide association studies: comparison with P-values. Genet Epidemiol. 33:79–86. [DOI] [PubMed] [Google Scholar]
- Wan X, Yang C, Yang Q, Xue H, Fan X, et al. 2010. BOOST: a fast approach to detecting gene-gene interactions in genome-wide case-control studies. Am J Hum Genet. 87:325–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D, Salah El-Basyoni I, Baenziger PS, Crossa J, Eskridge KM, et al. 2012. Prediction of genetic values of quantitative traits with epistatic effects in plant breeding populations. Heredity (Edinb). 109:313–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei WH, Hemani G, Haley CS.. 2014. Detecting epistasis in human complex traits. Nat Rev Genet. 15:722–733. [DOI] [PubMed] [Google Scholar]
- Xu Y, Crouch JH.. 2008. Marker-assisted selection in plant breeding: from publications to practice. Crop Sci. 48:391–407. [Google Scholar]
- Yang CH, Chuang LY, Da Lin Y.. 2017. CMDR based differential evolution identifies the epistatic interaction in genome-wide association studies. Bioinformatics. 33:2354–2362. [DOI] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Bi IV, Yamasaki M, et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 38:203–208. [DOI] [PubMed] [Google Scholar]
- Yu W, Kwon MS, Park T.. 2015. Multivariate quantitative multifactor dimensionality reduction for detecting gene-gene interactions. Hum Hered. 79:168–181. [DOI] [PubMed] [Google Scholar]
- Yu W, Lee S, Park T.. 2016. A unified model based multifactor dimensionality reduction framework for detecting gene-gene interactions. Bioinformatics. 32:i605–i610. [DOI] [PubMed] [Google Scholar]
- Yu Y, Tang T, Qian Q, Wang Y, Yan M, et al. 2008. Independent losses of function in a polyphenol oxidase in rice: differentiation in grain discoloration between subspecies and the role of positive selection under domestication. Plant Cell. 20:2946–2959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan L, Yuan CA, Huang DS.. 2017. FAACOSE: a fast adaptive ant colony optimization algorithm for detecting SNP epistasis. Complexity. 2017:1. [Google Scholar]
- Zhang C, Dong SS, Xu JY, He WM, Yang TL.. 2019. PopLDdecay: a fast and effective tool for linkage disequilibrium decay analysis based on variant call format files. Bioinformatics. 35:1786–1788. [DOI] [PubMed] [Google Scholar]
- Zhang Y. 2012. A novel Bayesian graphical model for genome-wide multi-SNP association mapping. Genet Epidemiol. 36:36–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Liu JS.. 2007. Bayesian inference of epistatic interactions in case-control studies. Nat Genet. 39:1167–1173. [DOI] [PubMed] [Google Scholar]
- Zhou Z, Jiang Y, Wang Z, Gou Z, Lyu J, et al. 2015. Resequencing 302 wild and cultivated accessions identifies genes related to domestication and improvement in soybean. Nat Biotechnol. 33:408–414. [DOI] [PubMed] [Google Scholar]
- Zhu BF, Si L, Wang Z, Zhou Y, Zhu J, et al. 2011. Genetic control of a transition from black to straw-white seed hull in rice domestication. Plant Physiol. 155:1301–1311. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The genotype dataset, seed images of RILs, and supporting information (Supplementary Figures, Tables, Information) were deposited in Zenodo (10.5281/zenodo.4686057). All other relevant data are within the paper and the Supplementary files. RIL-StEp package source codes and a user manual are freely available through GitHub (https://github.com/slt666666/RILStEp) under MIT license. The scripts used in the phenotyping process are also deposited in GitHub (https://github.com/slt666666/Phenotyping_RILStEp).