Abstract
Root system architecture (RSA) is a crucial factor in resource acquisition and plant productivity. Roots are difficult to phenotype in the field, thus new tools for predicting phenotype from genotype are particularly valuable for plant breeders aiming to improve RSA. This study identifies quantitative trait loci (QTLs) for RSA and agronomic traits in a rice (Oryza sativa) recombinant inbred line (RIL) population derived from parents with contrasting RSA traits (PI312777 × Katy). The lines were phenotyped for agronomic traits in the field, and separately grown as seedlings on agar plates which were imaged to extract RSA trait measurements. QTLs were discovered from conventional linkage analysis and from a machine learning approach using a Bayesian network (BN) consisting of genome-wide SNP data and phenotypic data. The genomic prediction abilities (GPAs) of multi-QTL models and the BN analysis were compared with the several standard genomic prediction (GP) methods. We found GPAs were improved using multitrait (BN) compared to single trait GP in traits with low to moderate heritability. Two groups of individuals were selected based on GPs and a modified rank sum index (GSRI) indicating their divergence across multiple RSA traits. Selections made on GPs did result in differences between the group means for numerous RSA. The ranking accuracy across RSA traits among the individual selected RILs ranged from 0.14 for root volume to 0.59 for lateral root tips. We conclude that the multitrait GP model using BN can in some cases improve the GPA of RSA and agronomic traits, and the GSRI approach is useful to simultaneously select for a desired set of RSA traits in a segregating population.
Keywords: genomic selection, selection index, machine learning, Bayesian network, QTL mapping, root structure, root architecture, Genomic Prediction, GenPred, Shared Data Resource
Introduction
Root system architecture (RSA) is the spatial arrangement of roots in soil or rooting medium. RSA that is optimized for the soil environment will promote efficient uptake of water and nutrients (Lynch 1995; Jung and McCouch 2013) and RSA has a role in abiotic stress tolerance and environmental plasticity (Lynch 1995; Jung and McCouch 2013; Koevoets et al. 2016). Above-ground agronomic and developmental traits including growth rate and grain yield (GY) are influenced by RSA (Lynch 1995; Jung and McCouch 2013). RSA is also an important factor in weed competition (Wedger et al. 2019). Evaluating RSA requires invasive and labor-intensive methods (e.g., Shovelomics) for field studies (Trachsel et al. 2011) or, alternatively, can be accomplished using artificial media (e.g., agar) under controlled conditions (Iyer-Pascuzzi et al. 2010; Clark et al. 2013; Xu et al. 2013). Selection for ideal RSA is not practical in plant breeding programs because of the difficulty and expense of phenotyping root traits on large numbers of plants. Thus, new tools for predicting RSA phenotypes from genotype will be particularly valuable for plant breeders aiming to create new varieties with improved RSA characteristics.
The components of RSA have been described at the levels of geometry, topology, and the root segments (Lynch 1995; Lobet et al. 2015). Root geometry represents the physical positions of roots in space and time. The geometry is critical when soil resources are unevenly distributed. Root geometry is difficult to phenotype accurately in field-grown plants because excavation disturbs much of the three-dimensional information and is difficult to accomplish in unfavorable environments (Tuberosa 2012; Sharma and Carena 2016). Ground-penetrating radar can visualize belowground root structures, but this method has low resolution especially for plants with fine roots, and is ineffective in saturated soils (Delgado 2017). Root topology describes the pattern of root elongation and branching and can be represented by a network. The root topology is a factor in soil exploration and influences the transport of water and solutes. Topology is preserved in carefully excavated roots and can be measured in two dimensions; however, excavation may damage fine topology details. The root segments are the individual root axes and have measurable properties such as diameter, color, and presence or absence of hairs (Godin and Sinoquet 2005). Root segment properties may be difficult to recover from excavated samples because of damage caused when separating roots from the soil.
One nonfield-based method commonly used to investigate RSA involves growing plants on agar plates for 2-D root imaging (Atkinson et al. 2019). The system has gained more importance with the development of fast and accurate software solutions for high-throughput image analysis of root systems in these plates (Arsenault et al. 1995; Lobet et al. 2011; Galkovskyi et al. 2012; Pound et al. 2013). However, the current inability for these image analysis systems to decipher complex RSA in mature plants with tangled and overlapping roots, and eliminate noisy background continues to limit accurate root image analyses to species or plant stages with smaller, less tangled root systems (Atkinson et al. 2019).
Molecular marker information is used by plant breeders and geneticists to predict phenotype from genotype (Eathington et al. 2007). Conventionally, marker-assisted selection (MAS) has focused on genetic markers associated with QTLs that have large effects on a trait. However, this has left much of the genetic variation out of consideration in quantitative traits controlled by many small-effect QTL. A new method of MAS, genomic prediction (GP), which uses markers saturating the whole genome, has been proven to be an important tool for improving efficiency of selection and prediction in animal and plant breeding (Meuwissen et al. 2001; Wong and Bernardo 2008; García-Ruiz et al. 2016; Crossa et al. 2017). It eliminates the requirement of progeny testing, reduces generation intervals, and leads to efficient utilization of genetic resources by genome-enabled parent selection (Meuwissen et al. 2016; Crossa et al. 2017; Cobb et al. 2019; Allier et al. 2020). GP could be especially useful for selection of RSA traits. In previous studies, a moderate prediction accuracy (PA) of 0.55 was found for root length in maize seedlings grown in water (Pace et al. 2015).
The advent of cheap and effective genotyping has greatly increased the number of markers available in many crops (García-Ruiz et al. 2016; Crossa et al. 2017). However, the estimation of marker effect of a large number of predictor markers (p) using the phenotypes of a small number of available individuals (n) (i.e., p ≫ n) has been a challenge for GP (Cobb et al. 2019; Allier et al. 2020). Statistical models for GP have been used to either uniformly [e.g., Bayesian ridge regression (BRR)] or differentially shrink marker effects (e.g., Bayes A, Bayes B) to improve GP (Meuwissen et al. 2001; Pérez and de los Campos 2014). GP methods, including genomic best linear unbiased prediction (GBLUP), do not require pedigree information as the traditional BLUP method does, with kinship instead calculated from SNPs (Meuwissen et al. 2016). Bayesian GP methods such as Bayes A and B utilize prior distribution of marker variance in their model while computing GP. The Bayes B method has been found to be more accurate than other GP methods with few genes and dense SNPs (Habier et al. 2007; Meuwissen et al. 2016). However, with many genes or lower SNP density, GBLUP has been found to perform better (Meuwissen et al. 2016). Apart from these additive models nonlinear approaches have been applied to GP including reproducing kernel Hilbert space regression (De los Campos et al. 2009) and random forest (González-Recio and Forni 2011). A multivariate modeling approach of the Bayesian network (BN) learning-based algorithm “Bnlearn” has been used for GP to include both additive and gene–gene (epistasis) interactions in networks of traits and SNPs (Scutari 2010; Scutari et al. 2013, 2014).
The missing heritability problem, i.e., genetic variation not explained by QTLs or variants identified by genome-wide association, is commonly encountered when predicting phenotype from genotype. This has been explained in part due to epistasis or gene-gene interactions (Zuk et al. 2012), which would be overlooked by prediction methods commonly used in plant breeding which model only additive genetic variance (Hill et al. 2008; Hallauer et al. 2010). Pathway analysis using the BN learning method has been used to improve GP using multiple traits, SNPs and their interactions (Scutari et al. 2014; Zeng et al. 2016). GP accuracy of quantitative traits has been reported to be higher with BN learning than with single trait GBLUP or elastic net, and BN was found to have PA similar to multivariate GBLUP (Scutari et al. 2014). BN has also been used for discovering association between a trait and SNPs for feature selection (informative markers) in the BN model by finding the Markov blanket (Malovini et al. 2009; Scutari et al. 2013). The Markov blanket in BN is the subset of SNPs and traits that contain all useful information for predicting a trait. Use of a Markov blanket has made the learning of an optimal network architecture efficient for high-dimensional data including multiple traits, and SNPs. In conventional BN without use of a Markov blanket, the number of possible networks scales super-exponentially with the increase in number of features making computational demand NP-hard (Scutari et al. 2013; Wang et al. 2019). BN can be important for an annually grown crop like rice because BN is acyclic, which allows for the direction of causal effects to be ordered by developmental stage and time, such that, for example, tiller number may influence GY, but GY may not influence tiller number (Scutari et al. 2014).
In this study, we evaluate the utility of GP of RSA traits in rice using BNs constructed from SNP genotypes, above-ground agronomic traits and RSA traits. The GP from multitrait BN was compared to single trait GP models of Bayes B and BRR. Also, we have used the rank-sum index of Mulamba and Mock (1978) to create a genomic rank-sum index (GSRI) to improve ranking accuracy among unphenotyped progenies predicted by GP to be phenotypically divergent, and thus increase breeder ability to identify and select or continue to breed with progenies containing more numerous desirable RSA alleles. The overall goal of this research was to develop tools to accurately predict RSA by using more easily obtainable data on genotype and nonRSA phenotypes. The specific objectives were: (i) to discover and confirm QTLs and key genetic markers controlling the RSA and above-ground traits using both BN and inclusive composite interval mapping (ICIM); (ii) to compare the accuracy of MAS, single trait GP and multitrait GP models; and (iii) to validate the ranking accuracy by phenotyping RSA in a set of divergent lines selected using our newly created GSRI.
Materials and methods
Population
The genetic material used in this study consisted of a RIL population of 329 F8 to F9 individuals developed using single seed descent from a cross of “PI312777” (weed suppressive, allelopathic, larger root system, high tillering, indica) × “Katy”(nonweed-suppressive, smaller root system, low tillering, tropical japonica [TRJ]) (Gealy et al. 2014; Gealy and Rohila 2018) for phenotypic study. Among them, 272 F8 RILs were genotyped and they were used for the genomic study. The methods of phenotyping, genotyping, and analysis of this population are described below.
Above-ground agronomic trait phenotyping
The RIL population was phenotyped under field conditions using a randomized complete block design (RCBD) with three replications per year in 2015 (F8) and 2016 (F9) at the Dale Bumpers National Rice Research Center (DBNRRC) located near Stuttgart, AR (34.49°N, 91.55°W). The soil at this location is DeWitt silt loam (fine smectitic, thermic, typic albaqualfs) with 1.2% organic matter and a pH of 5.8 (Gealy and Fischer 2010). Agronomic and irrigation practices followed those used in Arkansas, USA for conventional management of drill-seeded rice under a full-season, continuous flood (University of Arkansas 2013). Fertilizer was applied pre-flood as urea at 112 kg N ha−1. The seeding rate was ∼320–330 seeds/plot in 2.13 m long plots consisting of two rows 30.5 cm apart. Fields were flooded approximately 5–7 weeks after plant emergence, which allowed time to complete extensive collection of data pre-flood, and were kept flooded until the later-maturing RILs had accomplished seed set.
The plant height (PHT) was measured from the base of the plant to the tip of the longest leaf during the vegetative stage (at active tillering and panicle initiation), and to the tip of the tallest panicle at plant maturity. Growth rates in cm day−1 were calculated based on changes in average plant height (cm) between various growth stages and averaged per year. These were emergence to active tillering (GREV), active tillering to panicle initiation (GRVR), emergence to panicle initiation (GRER), and panicle initiation to maturity (GRRT). The average leaf number per plant (LFNV), leaf length (cm; LFLV), and leaf width at the midpoint (mm; LFWDV) were recorded pre-flood at the active tillering stage. We also used these traits to estimate the leaf area per plant (TLFAV; =LFNV × LFLV × LFWDV) at active tillering, and the rate of increase in leaf number per plant from emergence to active tillering (GRLFNV). Tiller angle was estimated at panicle initiation (TAR) and at maturity (TAT) using the International Rice Research Institute Standard Evaluation System for rice ranging from 1 (erect) to 9 (procumbent) (IBPGR-IRRI 1980). Tiller number was estimated at panicle initiation (TNR) and again at maturity (TNT) based on a scale ranging from 1 for Katy with few tillers to 5 indicating approximately as many tillers as seen on that date on the high-tillering parent PI312777. The heading date (HDT) was measured as a number of days from emergence to 50% of panicles with visible anthers. Leaf area index (LAIR) of the canopy was estimated indirectly based on penetration of light (sun flecks) through the canopy using an Accupar LP80 Ceptometer. LAIR readings were recorded at 2 months after emergence, which was after panicle initiation and approximately three weeks prior to heading. Leaf chlorophyll content (CHLF) in healthy, fully expanded leaves was estimated using an atLEAF handheld chlorophyll meter. Chlorophyll measurements are time intensive, requiring many days to accomplish on this large population. In 2015, they were collected during 15–17 weeks after emergence, by which time the parents and most RILs were at or near grain maturity. In 2016, they were collected at 13–15 weeks after emergence, which was prior to the grain fill period in the RILs and at the time that parental plots were approaching or at heading. Grain was harvested from all plants in each plot, threshed, and weighed. Weights were adjusted to a 12% grain moisture basis to determine GY per plot. To prevent confounding of the GY data with poor germination, GY from plots noted for poor plant stands were omitted from further analyses. This was based on pre-flood visual estimates showing a plot to have 40% or less of the plant densities observed in the parental check plots.
Above-ground agronomic traits analysis
The individual RIL genotypes were considered as random effects and each year was considered a different environment, represented by three replications per year. Each trait was analyzed separately for significant differences across genotypes. For each trait, significant differences among genotypes were declared with P ≤ 0.05 by F-test for experiment and Student’s t-test for parents. The normality analysis of data was performed with Kolmogorov–Smirnov and Shapiro–Wilk tests for each trait each year. Traits were analyzed using standard RCBD analysis considering both genotypes and environment as random with MIXED model using package “lme4” in R program (R Development Core Team 2020). Restricted maximum likelihood (REML) procedure was used to parse the variance into genetic and environmental components. The broad-sense heritability was calculated for each trait on a line mean basis as described by Hallauer et al. (2010) as:
| (1) |
where, = Genetic variance, = Genotype by environment variance, = Error variance, r is number of replicates and E is number of environments. Heritability for data without environments was calculated as Equation (2) with complete replications. The standard error of heritability was calculated as described by Sing et al. (1993). The exact confidence interval of heritability was calculated according to Knapp et al. (1985). Best linear unbiased predictor values (BLUP) computed from R package “lme4” was used for further analysis (Bates et al. 2011).
Data for LAIR were collected in 2015 from replicated blocks of 197 RILs with five check varieties, including the two parents, planted repeatedly three times in each block. Data were analyzed considering each block with replicated checks as random blocks in Augmented design (Federer 1961).
RSA phenotyping in agar plates
A subset of 71 F8 RILs was used to assess RSA traits in agar at the seedling stage at DBNRRC, Stuttgart, AR in 2016, 2017, and 2018 using six sets (averaging 30 RILs per set) to obtain replicated RSA data. Out of these, 68 genotyped RILs were used for genomic study of RSA. In addition to the RILs, each set contained as checks five replications of each of the two parents. Seeds were surface sterilized with 8.25% sodium hypochlorite and 0.1% Tween 20 for 4 minutes and rinsed with autoclaved-sterilized deionized water. Seeds were incubated for 2 consecutive days in the dark in a growth chamber (Conviron, PGR15) at 25°C and 90% relative humidity (RH) in 10 cm by 10 cm Petri plates with germination paper and 6 ml of autoclave-sterilized deionized water. On Day 3, two pregerminated seeds selected for having a healthy visible radicle (∼5–10 mm) were transplanted into each 10 cm by 10 cm Petri plate containing autoclave-sterilized agar (0.075%). The plates were pre-cut with a narrow opening on the “top” edge to accommodate the plant stem, pre-sealed with clear silicon sealant to prevent leakage of the liquid agar, and filled to ∼95% maximum volume capacity (∼5 mm head space) to encourage greater oxygen diffusion into the agar. Roots were submerged into the agar with the seed positioned horizontally just below the surface of the agar as it began to solidity. The plates were encased in aluminum-coated paper bags to exclude light from the roots and placed on wooden racks at a ∼30° angle slant, which forced roots to grow in direct contact with the plate wall. From Day 3 to 13, plants were maintained in the growth chamber at a constant 25°C and 90% RH, and a 13-hour photoperiod at minimal light intensity (a single metal halide bulb) that facilitated adequate greening and growth of the leaves and kept the heat load low, which helped maintain hydration of the agar. On Day 7, the seedlings were thinned to a final density of one per plate retaining only the plant with the largest/healthiest-appearing root system. On Day 13, plates were scanned with an EPSON Expression 11000XL flatbed scanner at 600 dpi resolution. The images were then analyzed with the WinRHIZO Reg program.
WinRHIZO Reg classified root components based on diameter class and pixel distances (Arsenault et al. 1995). We set the diameter classes at 0.15 mm intervals. In our rice seedling roots, the smallest diameter class of 0–0.15 mm was composed of fine lateral roots emanating from primary and crown roots (Figure 1). Seedling root classes with diameters greater than 0.15 mm (0.15–0.30, 0.30–0.45, and 0.45–0.60 mm, and so on.) did not distinguish root types, but contained various root types (e.g., primary and crown roots) that were combined as totals over the three aforementioned larger diameter classes. Collectively, these were classified as coarse roots (Figure 1). With WinRHIZO Reg the following traits were obtained for the fine or lateral root, coarse root, and total root (coarse and fine combined) classes from each image: root length, surface area (cm2), volume (cm3) combined across all segments of that size classification, number of crossings, and tip count. The number of tips in the fine root class indicated the number of lateral roots in the image, and was used to compute lateral root length(LRL)/total root length (%), lateral root surface area (LRSA)/total area (%), and average LRL. The lateral root density (LRD) and total root surface density (TRD) in each image were calculated as:
Figure 1.
An image of 13-day-old rice seedlings grown in agar plates in a Conviron growth chamber, (A) image of parent “PI312777” showing different components of seedling root architecture (RSA), (B) the image of parent “PI312777” showing analyzed region in green color loop and bar chart of different color pixels extracted from RSA components based on 0.15 mm diameter class intervals shown on top, (C) an image of parent “Katy” seedling showing analyzed region in green color loop and bar chart of different color pixels extracted from RSA components based on 0.15 mm diameter class intervals shown on top of image. To improve visual clarity in photographs, images shown above were obtained after seedlings had been removed from the agar and rescanned in water.
LRD (Tips/cm) = Number of lateral root tips/coarse root length (cm)
TRD (Tips/cm2) = Number of all root tips (lateral + coarse)/total root surface area (cm2)
RSA traits analysis
Significant differences in phenotypic data between parents were declared with P ≤ 0.05 using Student’s t-test in JMP SAS (2020). The RSA traits were analyzed as an augmented design with each set including lines with replicated checks as parents considered as a block. In total 71, F8 RIL seedlings and parents were imaged in six blocks containing partial replications. The significance was tested considering RIL and blocks as fixed and random effects, respectively. The experiment was analyzed using mixed models in R with the “lme4” package. REML procedure was used to calculate the component of genetic and environmental variance after the significance test. The heritability was calculated in line mean basis as described by Hallauer et al. (2010).
| (2) |
where, = Genetic variance, = Error variance, and r is number of random incomplete blocks. Best linear unbiased prediction (BLUP) computed from R package “lme4” was used for further analysis (Bates et al. 2011).
Genotyping and genomic similarity measures
The 272 F8 RILs were genotyped using the Illumina Infinium SNP array containing 7000 SNP markers (C7AIR) (Thomson et al. 2017). In total, 1578 SNPs were found polymorphic. SNP marker order was determined based on physical position in the rice IRGSP 1.0 genome assembly. The linkage map and recombination rates between markers were obtained using the Kosambi mapping function in IciMapping (Meng et al. 2015). Imputation of 0.8% missing SNP alleles was performed using the expectation maximization (EM) algorithm implemented in the R package “rrBLUP” (Endelman 2011). The marker density was visualized with r package “CMplot” (Yin et al. 2020). Segregation distortion was tested by χ2 conformity test against the Mendelian segregation ratio of 1:1. The distorted and redundant SNPs identified with P ≤ 0.05 of either allele for parents “PI312777” or “Katy” were discarded using the QTL IciMapping program to reduce multicollinearity. With this method, a total of 597 redundant SNPs were filtered reducing polymorphic SNPs from 1578 to 981 for learning BN.
Genome-wide linkage analysis
QTL mapping was performed with ICIM method using the “QTL IciMapping” program (Meng et al. 2015). The Log-of-odds (LODs) threshold to declare a QTL was calculated to ensure genome-wide Type-1 error rate to be ≤0.05 and calculated by 1000 permutation test. The scanning step was set to 0.2 cM. The largest probability for entering variables in stepwise regression of residuals on marker variables, PIN, was set to 0.001. The QTLs were named according to the nomenclature proposed by McCouch et al. (1997). The genetic map was drawn using the MapChart program (Voorrips 2002). The proportion of total phenotypic variance explained (PVE) by each and by multiple QTLs was calculated as R2 value. QTL additive mapping was used to calculate total phenotypic variation explained by all additive QTLs for a trait as a final regression model (Meng et al. 2015). The adjusted linear model for muti-QTL (Li et al. 2007) was used:
| (3) |
where is the phenotypic value of individual i, is the overall mean, m + 1 is ordered markers, is the dummy variable for the genotype of the ith individual at jth marker locus. is the regression coefficient of the phenotype on the jth marker conditional all other markers. residual error considered to be normally distributed. ICIM has found to increase detection power, reduce false detection rate and reduce biased estimates of QTL effects by adjusting the above equation (Li et al. 2007).
Bioinformatic tools SNP seek database (https://snp-seek.irri.org/), Oryzabase (https://shigen.nig.ac.jp/rice/oryzabase/) and the rice annotation project (RAP) database (https://rapdb.dna.affrc.go.jp/) were searched to confirm relative position of QTLs to functional genes.
Genomic prediction model
GP was computed using an additive genetic model between markers and genotypes as described by Meuwissen et al. (2001):
| (4) |
where is the phenotypic value of individual i, is the vector of fixed effect or overall mean, N is the number of marker loci, is the marker genotype of individual i at locus j. The marker genotypes were coded -1 (homozygous PI312777 allele) and 1 (homozygous Katy allele). is the allele substitution effect of marker j or marker effect which were considered random, is indicator variable of 0/1. The value is 1 for rrBLUP, GBLUP and 0 or 1 in Bayes B, and is the vector of random residual effects assumed to be normally distributed. The model computes genomic estimated breeding value (GEBV) as a cumulative effect of marker loci.
Genomic best linear unbiased prediction
GBLUP computes GEBV from mmer function in R package “Sommer (Covarrubias-Pazaran 2016)” which solves the mixed model equations (Covarrubias-Pazaran 2016). The additive relationship matrix was computed using the A. mat function (Endelman 2011). The statistical model in GBLUP is:
| (5) |
where 1n is the vector with all ones, y is vector of phenotypic values, µ is overall mean, Z is incidence matrix of g, g is the vector of genetic effects with covariance matrix, , K is the genomic relationship matrix, is the additive genetic variance, is error term, and is the residual variance. The kinship matrix, K, was calculated according to VanRaden (2008) using SNP alleles as,
| (6) |
where Z is genotype matrix. The elements in column i of Z are (0-2pi), (1-2pi), and (2-2pi) representing genotypes AA, AB, BB, respectively where pi is the allele frequency of BB genotype calculated from observed markers.
Bayes B
For phenotypes with relatively few QTLs there will be many markers without effect. To account for this, Bayes B utilizes two component mixture priors including mixture of point of mass as zero and a univariate t-scaled distribution (Meuwissen et al. 2001; Perez and de los Campos 2016). The t is considered univariate normal with unknown locus specific variance. It utilizes a nonzero parameter π. For locus j, a Bernoulli variable is 0 with probability π and 1 with proabability (1- π). The additive effect has a scaled inverse chi square prior with scale parameter S2 and degrees of freedom υ which was kept default 5 in our computation
Bayesian ridge regression
The method is similar to rrBLUP (Meuwissen et al. 2001). As rrBLUP, the genetic variance is considered the same for all markers, g ∼N(0, ). Here, the Gaussian prior is used to shrink marker estimates toward zero and to make shrinkage homogeneous across effects (Pérez and de los Campos 2014). The additive effect has a scaled inverse chi square prior with scale parameter S2 and degrees of freedom υ which was kept default 5 in our computation
Bayes B and BRR were conducted in “BGLR” R computing package (Pérez and de los Campos 2014). Analysis was conducted with Monte Carlo Markov Chain (MCMC) run of 45,000 iterations as samples runs drawn from resulting posterior distribution, the initial 5000 iterations were discarded as burn-in and thinning interval was maintained at 10.
Genomic prediction accuracy of the models
The genomic predictive ability (GPA) was computed from the Pearson correlation, r), between the predicted and the realized observations in the validation set (VS). The GP accuracy (PA), r), was calculated as Legarra et al. (2008),
| (7) |
where H2 is broad sense heritability computed from Equations 1 (for above-ground traits) and 2 (for RSA traits)(7).
Validation of the GP models
Ten-fold cross validation was used for validation of the GP models. The data were split into a training set (TS) (containing 90% of RILs) and a VS (containing 10% of RILs). Marker effects estimated from the TS were used to predict the phenotypes of the VS. A random sample of RILs [TS = (9/10) × N] was used the TS, with N being the total number of RILs used per trait. The remaining RILs (VS = N-TS) were used as the VS. The process was repeated 10 times, each time with different randomly selected RILs in the VS to ensure phenotypes were predicted for all of the RILs (Legarra et al. 2008).
Bayesian network analysis
For RSA traits GBLUPs for 204 RILs with genotype data were computed using 68 RILs as the TS with both phenotype and genotype data. These analyses used the 981 SNPs remaining after filtering for distorted segregation and redundancy. The computed BLUPs were used in learning the BN. The BN analysis and ridge regression were implemented in R computing packages “bnlearn” and “penalized.”
BN is a probabilistic model (Pearl 1988). In BN, a directed acyclic graph (DAG) is used to define the computed random dependencies which are quantified by a probability distribution. A DAG consists of nodes and arches. We have associated 981 polymorphic SNPs and 31 traits (Supplementary Table S2) including 18 agronomic and 13 RSA traits, as nodes. The model stated as each variable X={Xi} for network learning included T traits, Xt1, …….,XtT, and S SNPs Xs1,………,Xss. Each of these traits and SNPs are associated with a node in the DAG.
The arcs between nodes in a network reveal the computed random dependencies between nodes (Pearl 1988). These determine how a global distribution of X decomposes into a set of local distributions, one for each variable Xi, depending only on its parents .
| (8) |
The assumptions of BN learning in the R package “bnlearn” are based on an additive genetic model (Meuwissen et al. 2001) for quantitative traits (Scutari et al. 2014). The basic assumption of this learning process are: each variable Xi is normally distributed, and X is multivariate normal; computed random dependencies are assumed to be linear; traits can depend on SNPs but not vice versa, but they can depend on each other; SNPs can depend on other SNPs
The “bnlearn” package also assumes the dependencies between traits follow a temporal order in which traits are measured. In this study, we have grouped successive traits in tiers, with the first tier of traits including seedling RSA which appeared first in temporal order of RIL population study. These have been included in the R scripts. The tiers of traits are shown in Supplementary Table S2.
Based on these assumptions. The local distribution ) for X variables with t traits and s SNPs is computed using Gaussian BN as nodes (Scutari et al. 2014),
| (9) |
where I is an identity matrix.
Because we used a biparental RIL population we coded allele counts as 0 and 2, referring to parents with AA and BB genotype. Here, the local distribution of each SNP is,
| (10) |
where I is an identity matrix.
Each parent of the nodes added one parameter to the local distribution. Because we have dense nodes, we used a penalized estimator, a ridge regression (Hoerl and Kennard 1970), to validate the BN. The complete BN can be explained by a global distribution denoted as P(X) in equation 8. Where X has a multivariate normal distribution, say X ∼N(). Similarly, conditional independence of the corresponding variable given the rest is represented by graphical separation of two nodes Xi and Xj in the DAG.
The “bnlearn” R package utilizes the formula where BNs are equivalent to multivariate GBLUP models (Henderson and Quaas 1976). Hence, for example, if we model two traits and with the common set of SNP genotypes Xs, then the multivariate GBLUP model would take the form (Scutari et al. 2014);
| (11) |
where and are the random effects for the two traits example BLUPs,
Zs is the design matrix of genotypes Xs;
are the population means;
are the error terms;
and are independent of each other and distributed as multivariate normal with zero mean and covariance matrix as;
and
The covariance matrix , models the pleiotropic effects of the SNPs on traits, potentially increasing the accuracy of multivariate GBLUP compared to a single trait model (Scutari et al. 2014).
Because of the stochastic assumptions of linear dependencies, each trait , i = 1, 2 has a population mean and an error term that is normally distributed and independent of the SNP effects. The residual variance is also specific to each trait. The two traits depend directly on each other because of the covariances , , and depend indirectly through the covariance structure of the SNP effects . If we denote COV ) as G and COV ) as R, covariance matrix of the global distribution will be as (Scutari et al. 2014),
| (12) |
BN computes the precision matrix Ω using the SNP genotype covariance matrix which is a submatrix (the global covariance matrix) and this determines the arcs present in the DAG between the SNPs. One advantage of using “bnlearn” is that the submatrix also includes linkage disequilibrium (LD) patterns between the SNPs as measured by the squared allelic correlation r. Such patterns are reflected in the BN as the precision matrix Ω, thus provides intuitive representation of LD as well as of genetic effects on phenotypes as a single, coherent whole (Scutari et al. 2014).
The “bnlearn” package learns by iteratively selecting and estimating the model. The process is, (1) feature selection to find parents and children of traits in the Markov blanket by Semi-Interleaved HITON PC algorithm, which is very similar to single SNP analysis. In our model, the dependence was analyzed using Student’s t-test for Pearson’s correlations with alpha at 0.1 to obtain the Markov blanket to capture polygenic effects. The large values of alpha were used because it allows Markov blankets to initially involve SNPs that are weakly associated with the trait, to the point that they would be individually discarded. In addition, among them there may be sets of SNPs that are jointly significant due to epistasis, and such sets are retained in the Markov blanket (Scutari et al. 2014); and (2) structure learning which finds the DAG, computing the conditional independence present in data. It was carried out by score-based algorithm using a heuristic optimization technique. Each candidate DAG is assigned a network score reflecting its goodness of fit, which the algorithm then attempts to maximize. The optimal structure is declared that maximizes the Bayesian Information Criterion (Schwarz 1978); and (3) second step called parameter learning was used to estimate the parameters of local distributions, with ridge regression using α = 0.001.
Comparison of genomic prediction models
Across each above-ground and RSA trait, the GPAs of the prediction models BayesB, BRR, and BN were compared using analysis of variance (ANOVA) and Tukey’s honestly significant difference test of multiple comparison (Tukey 1949). The significance was declared at P < 0.05.
Validation of genomic predictions of multiple RSA traits
A subset of 36 RILs not previously phenotyped for RSA traits was selected and phenotyped to validate selections based on a genomic selection rank sum index (GSRI) calculated across the 13 RSA traits. This population size represents approximately a 7% selection intensity in each direction of the selection of RILs with divergent phenotype. To create the GSRI, we first calculated marker-predicted BLUPs, hereafter called GEBVs. The GEBVs were computed for each RSA trait using the “Sommer” (Covarrubias-Pazaran 2016) R Package. The models were trained with 68 previously phenotyped RILs and 1578 SNPs, then used to predict the GEBV for remaining set of 204 RILs out of 272 genotyped RILs. For each trait, the 204 RILs were ranked from 1 to 204 based on their GEBVs. The sum of these ranking numbers per RIL across the 13 RSA traits created a new multitrait GSRI for each RIL. The GSRI was used to rank the original RIL population minus the TS from 1 to 204, then approximately 7% of the RILs with high GSRI and low GSRI were selected. We selected RILs from the top and bottom of the GEBVs-GSRI ranking, then verified that they also had extreme rankings based on GEBVs. Thus, selection of RILs for the VS was based on nonlinear or nonparametric rank sum index of GEBVs. We have, for the first time, modified and used the rank sum index (RSI) of Mulamba and Mock (1978) to include individual GEBV to create a GSRI. Because we computed population mean and heritability of the jth trait from a TS, those were kept constant. Based on Equation 4 (Handerson and Quaas 1976; Walsh and Lynch 2018) the GSRI was computed as:
| (13) |
| (14) |
where is the marker computed BLUPs or GEBV of ith line and jth trait and is the heritability of jth trait.
Based on the RIL ranking per GSRI, 15 RILs with the highest RSA values and 21 RILs with the lowest RSA values were identified (close ties in ranking caused the selection of more RILs having low GSRI than with high GSRI). The 36 validation RILs thus selected were evaluated for RSA traits using the same growing conditions and RSA phenotyping method as described before.
Validation experiments were carried out in six sets, each with 18 random RILs plus two replications of each parent. This completely randomized validation experiment had three replicates, each made up of an agar plate containing one seedling. The parental checks in each experiment were used to calculate an adjusted mean of each RSA trait using a linear model as described by Federer (1961):
| (15) |
where is the RSA trait in ith block with jth checks, is population mean, is the ith random blocks, is the jth checks, is the kth entries within ith block, and residual is a random effect. The R package augmentedRCBD (Aravind et al. 2020) was used to compute analysis of variance of augmented randomized block design and adjusted means of the RILs that account for variation among the six sets as detected by the parental checks. To determine if the two groups of RILs selected from the top versus the bottom of the GSRI differed for predicted (GBEV) or observed traits, population trait means were tested for significant difference using Least square means Student’s t-test with P < 0.05 in JMP SAS (2020). Spearman’s rank correlation was used to compare the predicted (GEBV) and observed RSA trait rankings of the validation RILs (now numbered 1–36) to further evaluate the ranking accuracy of the GEBVs. The graphs were generated using R package ggplot2 (Wickham 2009).
Data availability
Genotype and phenotype data used for QTL mapping and genomic selection are available through the figshare portal. QTL positions for RSA and agronomic traits are in Supplementary Table S1. Scripts are available at https://github.com/jeremyde/rice_roots_bayesian_networks.
Supplementary material is available at G3 online.
Results
Phenotypic and genotypic variation in agronomic and RSA traits
The RILs and parents were observed in field trials across 2 years to assess variance components and heritability of each measured agronomic trait (Table 1). The parents differed significantly (P < 0.05) for all measured agronomic traits except leaf area index (LAIR), and genetic variance was observed among the RIL progeny (Table 1). The broad sense heritability of the traits ranged from a low of 13% for leaf width (LFWDV) followed by 22% heritability for leaf area index (LAIR) to the high heritabilities of 97% for heading date (HDT) and 93% for plant height (PHT) (Table 1).
Table 1.
Genetic Variance (), residual variance , and broad sense heritability (H2) estimates of 18 above-ground and 12 root system architecture traits measured in PI312777 x Katy RILs
| Variance estimates of phenotypes |
||||||
|---|---|---|---|---|---|---|
| Trait Name | (H 2 ) | 95% CI | Parentsa | |||
| Above-ground traits in flooded field | ||||||
| CHLF, % | 6.59 | 5.19 | 24.47 | 0.50 ± 0.025 | [0.47, 0.53] | *** |
| GREV, cm/day | 0.011 | —b | 0.015 | 0.61 ± 0.021 | [0.58, 0.64] | *** |
| GRER, cm/day | 0.01 | — | 0.01 | 0.77 ± 0.014 | [0.75, 0.79] | *** |
| GRVR, cm/day | 0.0302 | — | 0.026 | 0.70 ± 0.018 | [0.68, 0.72] | ** |
| GRRT, cm/day | 979 | — | 921 | 0.68 ± 0.019 | [0.66, 0.70] | *** |
| GRLFNV, Leaf/day | 0.00372 | — | 0.00429 | 0.63 ± 0.021 | [0.61, 0.66] | *** |
| GY, Kgha-1 | 24084 | 25147 | 19761 | 0.60 ± 0.022 | [0.58, 0.63] | *** |
| HDT, Days | 223.96 | 7.85 | 18.93 | 0.97 ± 0.002 | [0.97, 0.97] | *** |
| LAIR | 0.331 | — | 2.39 | 0.22 ± 0.07 | [0.06, 0.37] | |
| LFNV, No. | 1.63 | 0 | 6.66 | 0.59 ± 0.022 | [0.57, 0.62] | *** |
| LFLV, cm | 1.82 | 0 | 15.08 | 0.42 ± 0.026 | [0.39, 0.45] | *** |
| LFWDV, mm | 0.03 | 0 | 1.31 | 0.13 ± 0.027 | [0.10, 0.16] | ** |
| PHT, cm | 309.8 | 24.5 | 58.1 | 0.93 ± 0.005 | [0.93, 0.94] | *** |
| TAR, IRRI Scale | 0.8 | 0.21 | 0.88 | 0.76 ± 0.015 | [0.74, 0.78] | *** |
| TAT, IRRI Scale | 0.8 | 0.02 | 0.67 | 0.87 ± 0.009 | [0.86, 0.88] | *** |
| TLFAV, cm2/plant | 6.79 | — | 5.41 | 0.72 ± 0.017 | [0.69, 0.74] | *** |
| TNR, (scale 1–5) | 0.23 | 0.17 | 0.78 | 0.52 ± 0.024 | [0.49, 0.55] | *** |
| TNT, (scale 1–5) | 0.34 | 0.11 | 0.94 | 0.61 ± 0.021 | [0.59, 0.64] | *** |
| Seedling root architecture traits in agar plates | ||||||
| CRSA, cm2 | 0.1961 | — | 0.5261 | 0.69 ± 0.04 | [0.59, 0.79] | *** |
| CRL, cm | 20.04 | — | 42.5 | 0.74 ± 0.04 | [0.65, 0.82] | ** |
| LRD, Tips/cm | 8.371 | — | 21.714 | 0.70 ± 0.04 | [0.60, 0.79] | * |
| LRL, cm | 75.9 | — | 235 | 0.66 ± 0.04 | [0.56, 0.76] | ** |
| LRAL, cm | 0.0252 | — | 0.3439 | 0.31 ± 0.05 | [0.18, 0.43] | ** |
| LRPL , % | 58 | — | 178.8 | 0.66 ± 0.04 | [0.56, 0.76] | *** |
| LRSA, cm2 | 0.0427 | — | 0.1476 | 0.63 ± 0.05 | [0.53, 0.74] | ** |
| LRSAP, % | 23.78 | — | 68.48 | 0.68 ± 0.04 | [0.57, 0.78] | ** |
| LRT, No. | 4112 | — | 13543 | 0.65 ± 0.05 | [0.54, 0.75] | ** |
| RV, cm3 | 0.00002 | — | 0.0001 | 0.47 ± 0.05 | [0.34, 0.60] | * |
| TRD, Tips/cm2 | 0.59 | — | 2.79 | 0.56 ± 0.05 | [0.43, 0.67] | ** |
| TSA, cm2 | 0.358 | — | 1.318 | 0.62 ± 0.05 | [0.51, 0.73] | *** |
The plants were grown in 2 years × 3 replicates in flooded, direct seeded field plots and Conviron growth chamber respectively in Stuttgart, AR, USA.
a Significance codes, P <0.0001 “***” 0.001 “**” 0.01 “*” 0.05.
b Growth rate traits (GREV, GRER, GRVR, and GRRT), total leaf area (TLFAV), and leaf area index (LAIR) were calculated on data averaged across the replications per environment, giving just one value per environment: not enough for providing estimates of GxE.
Seedlings of RILs and parents were grown in agar in a controlled environment chamber to assess the variance components and heritability of the RSA traits (Table 1). The parents were significantly different (P < 0.05) for all RSA traits (Table 1) showing the potential for segregation in the derived RIL population (Figure 1). The analysis of variance showed the RILs differed significantly across the traits except for root volume (RV) and lateral root average length (LRAL) (Table 1). The broad sense heritabilities for RSA traits were all >60% except for LRAL (31%) and RV (47%). Coarse root length (CRL) had the highest heritability at 74%.
Genome-wide linkage analysis
A total of 1578 SNPs were distributed across the 12 chromosomes. The linkage map has a total length of 1476.8 cM, and 369.1 Mb, for an average of 3.95 cM/Mb (Supplementary Table S3). The SNP markers were fairly distributed across chromosomes with an average marker interval of 0.94 cM, or 0.23 Mb and an average of 4.2 SNPs per Mb. The number of SNPs mapped per linkage groups ranged from maximum 244 (chromosome 1) to minimum 60 (chromosome 12) (Supplementary Table S3). The distribution of markers across chromosomes were less uniform on chromosomes 4, 9, and 12. The chromosome had gaps in SNP coverage in centromeric regions (Supplementary Figure S2).
Analyses using QTL IciMapping (ICIM) identified a total of 102 QTLs associated with four RSA and 18 agronomic traits (Table 2). QTLs were identified with significant LOD scores (Type-1 error ≤0.05) determined through permutation and were spread over the 12 rice linkage groups. Chromosomes 1 and 3 harbored the highest (20) number of QTLs followed by chromosome 4 (19). Chromosomes 11 and 12 harbored the fewest QTLs (3 and 2, respectively).
Table 2.
Summary of QTLs detected using IciMapping with LOD threshold = 3.0 in the PI31277 × Katy RIL population
| Trait names | No of QTLsa | MultiQTL R2 × 100b | Linkage group |
|---|---|---|---|
| Above-ground agronomic traits | |||
| CHLF, % | 9 | 54.1 | 1,2,3,4,4,5,6,7,7 |
| GREV, cm/day | 10 | 42.11 | 1,4,4,5,6,7,7,8,10,11 |
| GRER, cm/day | 9 | 51.93 | 1,1,2,3,4,4,5,6,9 |
| GRLFNV, cm/day | 5 | 34.61 | 1,3,3,5,10 |
| GRVR, cm/day | 5 | 32.44 | 1,2,3,4,6 |
| GRRT, cm/day | 2 | 22.14 | 1,4 |
| GY, Kgha-1 | 3 | 25.54 | 3,3,8 |
| HDT, Days | 3 | 71.56 | 3,7,8 |
| LAIR | 1 | 14.01 | 6 |
| LFLV, cm | 11 | 51.31 | 1,1,2,3,3,4,4,5,6,6,10 |
| LFNV, cm | 5 | 28.75 | 1,3,3,4,5 |
| LFWDV, cm | 7 | 39.66 | 1,1,1,2,4,5,12 |
| PHT, cm | 6 | 75.62 | 1,2,3,4,8,12 |
| TAR, IRRI Scale | 5 | 62.87 | 1,3,8,8,9 |
| TAT, IRRI Scale | 3 | 62.14 | 1,8,9 |
| TLFAV, cm2/plant | 1 | 7.95 | 11 |
| TNR (scale 1-5) | 7 | 48.28 | 3,3,3,4,4,4,9 |
| TNT (scale 1-5) | 5 | 43.45 | 1,3,3,4,9 |
| Seedling root system architecture traits | |||
| LRD, Tips/cm | 1 | 21.8 | 11 |
| LRPL , % | 1 | 34.53 | 5 |
| LRSAP, % | 2 | 34.1 | 5,11 |
| TRD, Tips/cm2 | 1 | 28.3 | 3 |
Number of QTLs with LOD = 3.0.
Multi QTL from adjusted additive model.
The maximum LOD score for the RSA QTLs ranged from 3.3 to 3.9 and explained from 16.7 to 23.3% of total PVE (Supplementary Table S1). A total of five QTLs were detected affecting four RSA traits. Two QTLs were identified for LRSA over total area (LRSAP) on chromosome 5 (at 25.7 Mb) and 11 (23.4 Mb). These LRSAP QTLs had LOD scores of 3.33 and 3.55, and PVE of 17 and 19%, respectively. A QTL for LRL over total length (LRPL) had the same peak SNP on chromosome 5 (25.7 Mb), and a QTL for LRD was located nearby on chromosome 11 (25.0 Mb) as well. The QTL affecting LRD had LOD score of 3.9 and PVE of 23% PVE, the LRPL QTL had a peak LOD score 3.9 and explained 21.6% of PVE. A QTL for total root density (TRD) was identified on chromosome 3 with a LOD score of 3.3 and PVE of 17%. (Supplementary Table S1).
The maximum LOD scores of QTLs for above-ground phenotypes ranged from 3.2 to 71.6 and explained from 2 to 54.2% of PVE (Supplementary Table S1). The largest PVE was by a QTL affecting tiller angle at harvest (TAT) on chromosome 9 (20.5 Mb) with LOD score of 57 and PVE of 54.2%, followed by a QTL affecting plant height at harvest (PHT) on chromosome 1 (38.4 Mb) with LOD score of 71.6 and PVE of 50.6%. The smallest PVE of a QTL meeting the LOD threshold of 3.0 was by a PHT QTL located on chromosome 12 with LOD score of 5.2 and PVE of 2%, followed by a QTL for early growth rate (GREV) with LOD score of 3.2 and PVE of 2.0%.
For RSA traits, the PVE (model R2) by the multi-QTL models ranged from 21.8 to 34.5% (Table 2), while the PVEs ranged from 7.95 to 75.62% for above-ground phenotypes, with this high PVE coming from plant height (PHT) for which one QTL explained more than 50% PVE by itself. The number of QTLs per trait ranged from maximum of 11 QTLs for leaf length at active tillering (LFLV) followed by early growth rate (GREV) with 10 QTLs (Table 2). The one above-ground trait for which the parents did not differ, LAIR, had a single QTL, as did three of the four RSA traits for which QTLs were identified, specifically LRL over total (LRPL), LRD, and TRD. QTLs affecting early growth rates (GREV) were located on eight chromosomes followed by leaf length at tillering (LFLV) and chlorophyll content (CHLF) in seven chromosomes.
Bayesian-network analysis
Use of bnlearn with 10-fold cross validation and α = 0.001 identified a causal phenotype and genotype network (Supplementary Figure S1). The network was based on 31 traits including 13 seedling RSA traits plus 18 above-ground phenotypes, and 981 nonredundant SNPs as nodes leading to observed GY at harvest. The resulting DAG identified 17 QTLs significantly affecting each other and multiple traits each (Table 3). Four QTLs affected only above-ground phenotypes, and two influenced only RSA traits, while the majority of QTLs (11 of 17) affected both above-ground and RSA traits. The DAG clustered the RSA and the above-ground traits into two separate networks, with only one RSA trait (LRAL) being directly connected with three of the 18 traits in the above-ground network (Supplementary Figure S1). The agronomic traits plant height (PHT), tiller number at panicle initiation (TNR) [but notably not at maturity (TNT)], and early growth rate (GREV) were strongly and directly connected to GY (Supplementary Figure S1). Further evidence of these relationships is provided by the colocation of QTLs governing these traits as identified by IciMapping (Figure 2, Supplementary Figure S3). The RSA and above-ground traits DAG networks were connected through the LRAL which was also connected with GY, heading date (HDT) and leaf chlorophyll content (CHLF) (Supplementary Figure S1). With so few direct relationships in the DAG, it is noteworthy that a majority (65%, 11 of 17) of the QTLs detected by BN affected both above-ground and RSA phenotypes (Table 3, Supplementary Figure S1). Fourteen out of 17 QTLs detected by BN were confirmed by similarly located ICIM QTLs for the same traits (Supplementary Table S4).
Table 3.
QTLs identified with 10-fold cross validation and P = 0.001 in a DAG of Bayesian network including 31 traits [18 above-ground agronomic (AGR), 13 root system architecture (RSA)] and 981 non redundant SNPs in population of 272 PI31277 × Katy RILs
| Chr | QTL name | Trait and QTLs effectedb | Peak position (Mb) | Trait type |
|---|---|---|---|---|
| 1 | qKTPI1.1 | CHLF, GY, GREV, qKTPI8 | 0.192836 | AGR |
| 1 | qKTPI1.2 | LFWDV and LRD | 22.353686 | AGR and RSA |
| 1 | qKTPI1.3 | LRPL AND LRSA | 27.471641 | RSA |
| 1 | qKTPI1.4 | LFWDV and GREV | 35.847644 | AGR |
| 1 | qKTPI1.5 | CHLF, PHT, GRRT, LRD, TSA | 36.480265 | AGR and RSA |
| 2 | qKTPI2.2 | LFWDV, LFLV, LRSAP, LRSA | 35.229992 | AGR and RSA |
| 3 | qKTPI3.1 | HDT, TNR, LRL | 2.594469 | AGR and RSA |
| 3 | qKTPI3.2 | LRAL, TAT, TNR, GRLFNV, LRL, LRPL | 31.893660 | AGR and RSA |
| 4 | qKTPI4 | LFWDV, GRLFEV, HDT, GREV, CHLF, CRL, LRSA | 31.350359 | AGR and RSA |
| 5 | qKTPI5 | LFWDV, RV | 7.999631 | AGR and RSA |
| 6 | qKTPI6 | LAIR, GRLFEV | 1.501961 | AGR |
| 7 | qKTPI7.1 | LRPL, LRL, CHLF | 2.637123 | AGR and RSA |
| 7 | qKTPI7.2 | TAR, HDT | 19.147047 | AGR |
| 8 | qKTPI8 | LFLV, HDT, GREV, TAR, LRSA, LRD | 4.306618 | AGR and RSA |
| 9 | qKTPI9.1 | TAR, LRSAP, qKTPI9.2 | 20.482091 | AGR and RSA |
| 9 | qKTPI9.2 | HDT, TAT, TAR, LRL | 20.834777 | AGR and RSA |
| 11 | qKTPI11 | LRL, CRL, LRSAP | 1.378959 | RSA |
a Megabase.
b Traits, GY, grain yield; HDT, heading date; PHT, plant height; TAT, tiller angle at maturity; TAR, tiller angle at panicle initiation; TNT, tiller number at maturity; TNR, tiller number at panicle initiation; LFWDV, leaf width at active tillering; LFLV, leaf width at active tillering; LFNV, leaf number at active tillering; GRLFNV, growth rate based on leaf number at active tillering; GREV, growth rate based on height from emergence to active tillering; GRVR, growth rate based on height from active tillering to panicle initiation; GRRT, growth rate based plant height from panicle initiation to maturity; CHLF, chlorophyll content; LAIR, leaf area index; LRSAP, lateral root surface area over total area; LRPL, lateral root length over total; CR, number of crossings; LRD, lateral root length density; CORSA, coarse root surface area; LRL, lateral root length; LRT, lateral root tips; CRL, coarse root length; LRAL, lateral root average length; LRSA, lateral root surface area.
Figure 2.
Genetic map of rice chromosome 3, 4–7, 9–11 on the PI312777 × Katy RIL population along with the previously identified QTLs and major genes identified from SNP Seek database (https://snp-seek.irri.org/), Oryzabase (https://shigen.nig.ac.jp/rice/oryzabase/) and the rice annotation project (RAP) database (https://rapdb.dna.affrc.go.jp/). The identified QTL are positioned in floating vertical color bar graph whereas the known priori major gene, QTL and QTL detected by BN is shown as loci with the lead SNP reported in previous studies. The abbreviation in parenthesis represent effect on traits in this and prior studies. The length of chromosome is shown in mega base (Mb) scale.
The direct and indirect effects revealed by the BN DAG suggest that part of the detected QTL effects could be due to interaction between traits (Supplementary Figure S1). For example, pKTPI7.2 on chromosome 7 affects TAR and HDT, which are themselves connected (Table 3, Supplementary Figure S1). The directional arrows in Supplementary Figure S1 indicate that TAR is a “parent node” of HDT, which suggests that the effect of pKTPI7.2 on HDT might be indirect and coming through a direct effect of pKTPI7.2 on TAR. The qKTPI4 on chromosome 4 and qKTPI8 on chromosome 8 (Supplementary Figure S1) were connected with the highest number of nodes, seven and six nodes respectively, with each QTL affecting both above-ground and RSA traits. Additional detail on trait relationships associated with these two QTLs is shown in Figure 5. The qKTPI4 allele from parent “Katy” reduced CHLF, CRL, and LRSA but increased leaf width (LFWDV) (Figure 5A). ICIM also identified similarly located QTLs for CHLF and LFWDV but did not detect association with any RSA traits in this QTL region (Figures 2 and 5) which is within 0.2 Mb of NAL1 (Cho et al. 2014), a major gene previously reported to affect leaf width, chlorophyll content and RSA (Cho et al. 2014; Wang et al. 2015). The effect of qKTPI4 on heading date (HDT), and early growth rate (GRLFNV) was likely indirect and through a direct effect of pKTPI4 on GREV (Figure 5A). Another QTL affecting both above-ground and RSA traits, qKTPI8, is located near the major heading date gene Ghd8 (Zhang et al. 2015) (Figure 2). The allelic effect determined for qKTPI8 indicates that the allele from “Katy” was associated with a large 18-day delay in heading date. However, the DAG (Figure 5B) indicates that the effect of qKTPI8 on heading date is indirect and coming through interaction between heading date (HDT) and tiller angle at panicle initiation (TAR). The qKTPI8 QTL also has a positive direct effect on LRSA, however, its negative effect on LRD may be indirect and due to effects of LRSA on LRD. qKTPI8 also increases both early leaf length (LFLV) and early growth rates (GREV) (Figure 5B). The qKTPI9.2 QTL had a strong direct effect on LRL. However, its effect on TAR, TAT, and HDT appeared to be indirect even though strong because of their trait interactions as indicated in the DAG (Table 3, Supplementary Figure S1). Effects of qKTPI9.2 are strong enough and direct enough, however, that ICIM also identified co-located QTLs for TAR and TAT, with and the ICIM and BN DAG QTLs being within 0.5 Mb of the Tiller Angle Control 1 (TAC1) gene (Yu et al. 2007). DAG showed a QTL on chromosome 3 (at 31.9 Mb), qKTPI3.2, that had direct effect on tiller number (TNR), tiller angle at harvest (TAT), early growth rate (GRLFNV), and lateral root traits (LRAL, LRL, and LRPL) (Supplementary Figure S1). Validation by ICIM was again seen, with similarly located QTLs for TNR, TAR, and GRLVNV, plus a QTL for a different root trait (TRD) located 4.6 Mb proximal to qKTPI3.2, which, with a mapping population of 71 RILs, can be considered close.
Figure 5.
Subnetwork of learned BN with P = 0.001 in 31 traits (18 above ground agronomic and 13 RSA traits). Arrows shows unidirectional relationship among variables and the value above arrows shows direct and indirect allelic effect of, (A) QTL qKTPI4 affecting early growth rates (GREV), leaf length (LFLV), flowering (HDT), tiller angle (TAR), and lateral root traits (LRSA and LRD), (B) QTL qKTPI8 affecting early growth rates (GREV and GRLFEV), flowering (HDT), leaf chlorophyll content (CHLF), leaf width (LFWDV), lateral root (LRSA), and coarse roots (CRL), and (C) showing direct effect of above-ground traits early growth rates (GREV), tiller number (TNR), and plant height (PHT) and lateral roots (LRAL) leading to grain yield in PI312777 × Katy RIL population. Nodes with solid edges represent above-ground traits and with dashed edges are root traits. Note: The BN was learned using 18 above-ground agronomic, 13 root system architecture traits (RSA), 981 nonredundant SNPs using 10 runs of 10-fold CV with P = 0.001.
Genomic prediction
To compare the accuracy of various GP models across traits, we used two single trait GP models (Bayes B, and BRR) and one multitrait GP model (BN) computed for 18 above-ground agronomic traits and 10 of the RSA traits. Cross validated means of genomic predictive abilities (GPA) were used to compare models using ANOVA and multiple comparisons using Tukey’s honestly significant difference test.
Across 18 above-ground agronomic traits, differences (P < 0.05) were found between the GPAs, r(y, ŷ), computed from the GP models for all traits except LAIR, GRRT, LFLV, and TNR (Table 4). These differences in GPA among the models also varied by trait. For example, BN had significantly higher GPA than all the other GP methods for GRER, GRVR, GY, LAIR, LFNV, TLFAV, TNT, coarse root trait (CRSA), lateral root traits (LRD, LRAL, LRPL, LRSA, LRSAP, and LRT), RV and TRD. It was tied for the “most accurate” method for GRRT, LFLV, TAR, PHT, and TAT, TNR but had significantly lower accuracy than all other methods for CHLF, GREV, GRLFNV, HDT, LFWDV, and LRL. Bayes B had significantly higher GPA for HDT (Table 4).
Table 4.
Validated GPA ± their standard error (SE), across single trait (BB and BRR) and multitrait GP model (BN) for 18 above-ground agronomic and 10 RSA traits in PI31277 × Katy RIL population
| Genomic predictive ability, r(y, ŷ) |
|||
|---|---|---|---|
| Trait name | BBa | BRRb | BNc |
| Above-ground traits in flooded field | |||
| CHLF, % | 0.69 ± 0.03 ad | 0.69 ± 0.03 a | 0.57 ± 0.03 b |
| GREV, cm/day | 0.55 ± 0.04 a | 0.55 ± 0.04 a | 0.47 ± 0.04 b |
| GRER, cm/day | 0.58 ± 0.04 b | 0.52 ± 0.04 b | 0.74 ± 0.04 a |
| GRVR, cm/day | 0.45 ± 0.06 b | 0.43 ± 0.06 b | 0.97 ± 0.06 a |
| GRRT, cm/day | 0.45 ± 0.04 a | 0.43 ± 0.04 a | 0.49 ± 0.04 a |
| GRLFNV, Leaf/day | 0.50 ± 0.02 a | 0.50 ± 0.02 a | 0.43 ± 0.02 b |
| GY, Kgha-1 | 0.46 ± 0.02 b | 0.46 ± 0.02 b | 0.54 ± 0.02 a |
| HDT, Days | 0.85 ± 0.01 a | 0.75 ± 0.01 b | 0.75 ± 0.01 b |
| LAIR | 0.23 ± 0.06 c | 0.26 ± 0.06 b | 0.28 ± 0.06 a |
| LFNV, No. | 0.43 ± 0.04 b | 0.43 ± 0.04 b | 0.93 ± 0.04 a |
| LFLV, cm | 0.59 ± 0.04 a | 0.55 ± 0.04 a | 0.64 ± 0.04 a |
| LFWDV, mm | 0.50 ± 0.02 a | 0.50 ± 0.02 a | 0.41 ± 0.02 b |
| PHT, cm | 0.87 ± 0.03 a | 0.52 ± 0.03 b | 0.84 ± 0.03 a |
| TAR, IRRI Scale | 0.80 ± 0.02 a | 0.72 ± 0.02 b | 0.76 ± 0.02 a |
| TAT, IRRI Scale | 0.75 ± 0.02 a | 0.66 ± 0.02 b | 0.79 ± 0.02 a |
| TLFAV, cm2/plant | 0.15 ± 0.05 b | 0.16 ± 0.05 b | 0.50 ± 0.05 a |
| TNR, (scale 1-5) | 0.67 ± 0.02 a | 0.66 ± 0.02 a | 0.61 ± 0.02 a |
| TNT, (scale 1-5) | 0.61 ± 0.02 b | 0.60 ± 0.02 b | 0.72 ± 0.02 a |
| Seedling root architecture traits in agar plates | |||
| CRSA, cm2 | 0.20 ± 0.10 b | 0.19 ± 0.10 b | 0.92 ± 0.10 a |
| LRD, Tips/cm | 0.38 ± 0.10 b | 0.38 ± 0.10 b | 0.93 ± 0.10 a |
| LRL, cm | 0.25 ± 0.10 a | 0.26 ± 0.10 a | −0.20 ± 0.10 b |
| LRAL, cm | 0.34 ± 0.08 b | 0.38 ± 0.08 b | 0.84 ± 0.08 a |
| LRPL , % | 0.43 ± 0.09 b | 0.43 ± 0.09 b | 0.86 ± 0.09 a |
| LRSA, cm2 | 0.25 ± 0.10 b | 0.26 ± 0.10 b | 0.99 ± 0.10 a |
| LRSAP, % | 0.49 ± 0.08 b | 0.49 ± 0.08 b | 0.98 ± 0.08 a |
| LRT, No. | 0.21 ± 0.09 b | 0.21 ± 0.09 b | 0.82 ± 0.09 a |
| RV, cm3 | 0.29 ± 0.10 b | 0.29 ± 0.10 b | 0.95 ± 0.10 a |
| TRD, Tips/cm2 | 0.20 ± 0.10 b | 0.20 ± 0.10 b | 0.95 ± 0.10 a |
a Bayesian B.
b Bayesian ridge regression.
c Bayesian network learning, Bnlearn, Network was learned with 18 agronomic and 13 RSA traits that also included total root surface areas (TSA), coarse root length (CRL), and number of root crossings (CR).
d Multiple comparison was computed using Tukey’s honestly significant difference test. For each trait same letter represents not significantly different at <0.05 significance level between the prediction model.
In general, there was minimal improvement in GPA, r), of BN over other methods for traits where the multi-QTL model accounted for high PVE (>50%), but in many of the traits with variance less well accounted (<50%) for by the multi-QTL model, the BN method outperformed other prediction methods by a large margin (Tables 2 and 4). Among the single trait models, the Bayes B model had higher GPA than BRR for the traits for which the multi-QTL model had high PVE (>63%) (HDT, PHT, and TNR) (Tables 2 and 4, Figure 3). The reduced GPA of the multi-QTL model compared to the GP models was greatest for ordinal traits (TNR, TNT, and TAR), later stage traits (GY, GRRT, and GRVR), RSA traits (LRD, LRPL, and LRSAP), and LFNV (Tables 2 and 4, Figure 3).
Figure 3.
Bar chart displaying GPA of cross validated Bayes B (BB), BRR, BN for seven important above-ground and five RSA traits. Error bars represent SEM.
The genetic variance explained r), or PA in comparison to phenotypic heritability, were also followed similar relationships. The PA with BN was improved in low heritable traits (<50%) (LFWDV, LFLV, LAIR, LRAL, and RV) and moderate heritable traits (50%–<70%) (GY, LFNV, TNT, LRPL, GRRT, CR, LRSA, LRSAP, CRSA, GRVR, LRD RV, LRT, and TRD) (Supplementary Table S5). The PA was decreased in BN for traits with high heritability (>70%) (PHT, HDT, and TAR) and moderate heritability (CHLF, TNR, GREV, GRLFNV, and LRL) (Supplementary Table S5).
Validation of genomic predictive ability by GSRI
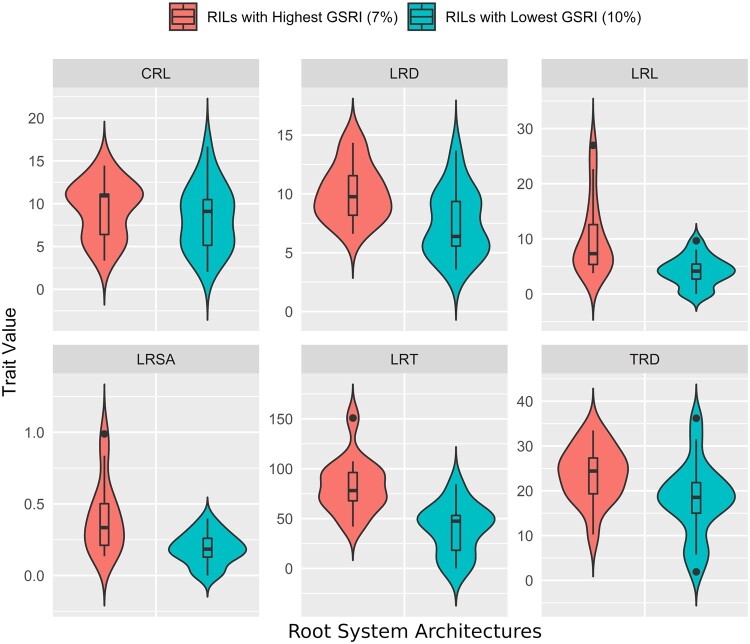
To test the ability to make valid selections in the absence of phenotypic data on many individuals using a GP, we calculated GEBVs for each RIL for each RSA trait, merged the many GEBV trait rankings into a single multitrait ranking using a GSRI, selected a subset of RILs extreme high and low GSRI, then phenotyped the selected RILs to see if the divergent GSRI selection based on trait predictions caused actual differences in any of the RSA traits. Data showed that means of the divergently selected RIL groups did indeed differ (P < 0.05) in the expected directions for seven of 13 RSA traits (Table 5, Figure 4). For LRL, the mean of the RILs selected for high GSRI was nearly twofold greater than that of RILs selected for low GSRI (10.2 mm vs 5.3, respectively). A twofold difference was also seen between the divergently selected groups for LRSA, with the upper and lower GSRI groups having means of 0.23 cm2 and 0.46 cm2, respectively. While the differences in group means after divergent selection for other RSA traits were less dramatic, they were significant for five additional RSA traits, including LRD, LRPL, LRSAP, LRT, and TRD (Table 5).
Table 5.
Progeny mean variation and genomic ranking ability (GRA) in 36 progenies (∼7%) divergently selected groups (low and high) for predicted divergence in RSA based on a GSRI, then characterized for 13 seedling RSA traits to evaluate phenotypic shifts caused by GSRI-based divergent selection
| Trait names | Progeny mean and SEa |
Range |
p(2-tailed) (Low vs. High) | GRAc, ρ(y, ŷ) | ||
|---|---|---|---|---|---|---|
| RILsb with low GSRI | RILs with high GSRI | RILs with low GSRI | RILs with high GSRI | |||
| CR, No. | 13.27 ± 3.53 | 10.53 ± 3.63 | 0–55.88 | 0–41.97 | ns | 0.07 |
| CRL, cm | 8.34 ± 0.83 | 9.32 ± 0.85 | 2.04–16.69 | 3.35–14.46 | ns | 0.48** |
| CRSA, cm2 | 1.65 ± 0.15 | 1.85 ± 0.17 | 0.58–3.04 | 0.74–3.25 | ns | 0.52** |
| LRAL, cm | 0.1 ± 0.01 | 0.12 ± 0.01 | 0.05–0.22 | 0.04–0.26 | ns | 0.027 |
| LRD, Tips/cm | 9.27 ± 1.39 | 10.96 ± 1.03 | 3.57–29.47 | 6.61–22.85 | ** d | 0.26 |
| LRL, cm | 5.27 ± 0.96 | 10.19 ± 1.82 | 0–16.68 | 3.78–26.97 | ** | 0.33* |
| LRPL, % | 30.19 ± 1.96 | 39.46 ± 3.19 | 16.21–51.1 | 23.8–63.98 | * | 0.23 |
| LRSA, cm2 | 0.23 ± 0.04 | 0.46 ± 0.08 | 0–0.66 | 0.14–1.16 | ** | 0.23* |
| LRSAP, % | 10.87 ± 0.99 | 16.13 ± 1.93 | 4.85–22.82 | 5.79–30.94 | * | 0.23 |
| LRT, No. | 52.26 ± 10.25 | 86.98 ± 8.14 | 0–138.255 | 41.92–150.87 | *** | 0.59** |
| RV, cm3 | 0.07 ± 0.01 | 0.06 ± 0.01 | 0–0.15 | 0–0.12 | ns | 0.14 |
| TRD, Tips/cm2 | 18.11 ± 1.86 | 23.78 ± 1.58 | 1.92–36.21 | 10.24–33.48 | * | 0.44** |
| TSA, cm2 | 3.25 ± 0.33 | 3.52 ± 0.43 | 0.31–5.7 | 1.19–6.68 | ns | 0.40* |
a Standard error.
b Recombinant inbred lines.
c Genomic ranking accuracy.
d Significance codes: <0.0001 “***” 0.001 “**” 0.01 “*” 0.05.
Figure 4.
Violin and box plot of the distribution of means in 36 divergent progeny seedlings for RSA traits selected based on GSRI using 68 RILs TS and 1578 polymorphic SNPs in PI312777 × Katy RIL population.
When the individual trait GEBVs for the 36 RILs were analyzed per the high vs low GSRI grouping, the same traits that showed differences for group trait means again showed differences for the means of their predicted GEBVs (Table 5). The lateral root traits were more likely to show actual and GEBV mean differences than were the coarse root (CRL and CRSA) and total root (RV, TRD, and TSA) traits, suggesting that the divergent selection was more successful for traits related to lateral roots than for traits characterizing other types of roots.
To expand this evaluation of selection effect to individuals, as opposed to the divergent RIL groups, we evaluated genomic versus actual trait rankings among the 36 individual RILs. The GEBVs calculated per RIL per trait for the calculation of GSRI were used to rank the 36 RILs for each trait, then these marker-predicted ranks were correlated with trait-determined ranks to measure the genomic ranking accuracy (GRA) for each RSA trait post-selection as spearman rank correlation (ρ). The GRA ranged from a minimum of ρ = 0.07 for root crossings (CR), followed by ρ = 0.14 in RV, to a maximum of ρ = 0.59, for lateral root tips (LRT) followed by 0.52 in coarse root surface area (CRSA) (Table 5). Spearman’s correlations were significant (P < 0.05) and positive for 7 of the 13 RSA traits, including CRL and surface area (CRSA), and lateral toot length (LRL), tips (LRT), surface area (LRSA), and TRD (Table 5). The significant differences among the RSA traits showed that progenies divergently selected based on GRSI differed in both their genomic ranks and their group means for both coarse and lateral root traits.
Discussion
QTLs for root and above-ground traits identified using ICIM and BN
Components of RSA are highly affected by selection of above-ground agronomic traits, and root components affect above-ground health and vigor by capturing necessary resources and serving as a sink for carbohydrates and other reserves (Lynch 1995; Jung and McCouch 2013). Thus, we anticipated finding colocation among QTLs affecting root and above-ground traits in the PI312777 × Katy RIL population. Using ICIM, five QTLs affecting four RSA traits were identified. Overlap among these QTLs pointed to just three chromosomal locations affecting RSA, one each on chromosomes 3, 5, and 11, and contrary to our expectations, there were not similarly located QTLs for agronomic traits. While QTLs among agronomic traits often peaked at the same or close (<0.5 Mb distant) SNPs (e.g., the long bar of similarly located traits from 38 to 39 Mb on chromosome 1) (Figure 2), there was no colocation among root and agronomic QTLs identified by ICIM. In contrast, analysis of the same trait and marker datasets using BN, revealed 13 RSA QTLs, 11 of which were also associated with one or more above-ground traits. This could be because the BN not only includes the relationship between phenotype and SNPs, but also includes conditional independence between the variables in model (Malovini et al. 2009). Just one RSA QTL was identified using both ICIM and BN, on chromosome 11, and interestingly, these ICIM RSA QTL were not associated with any above-ground traits using either ICIM or BN. BN has been useful for elucidating causal structure in data, however, when structure is solely based on observed data, as in other statistical methods, caution should be practiced on possible violation of assumptions on BN as described in Equation 8 (Pearl 1988; Scutari et al. 2013, 2014). In addition to direct observations, latent variables derived from Bayesian confirmatory factor analysis have been useful in exploring potential causal relationships in rice phenotypes using BN (Yu et al. 2019).
While BN identified fourfold more (13) RSA QTLs than ICIM (3), the opposite was true for above-ground traits. ICIM identified 97 QTLs for individual agronomic traits (Supplementary Table S1), 28 of which (29%) could be considered single-trait QTLs on the basis of LOD peaks being 1 Mb or more from other QTLs. In contrast, BN identified 34 total QTLs, four, or 12% of which were associated with just one above-ground trait, but all BN QTLs were associated with at least one trait when both RSA and agronomic traits were considered, which merges the 34 BN agronomic trait QTLs into just 17 multitrait QTLs (Table 3, Figure 2), 11 of which affected both RSA and agronomic traits. The directional trait-to-trait interactions determined by BN (Supplementary Figure S1) indicated separate RSA and agronomic trait clusters with only one RSA trait, average length of lateral roots (LRAL), interacting directly with any of the above-ground traits. It appears that a large portion of the connectivity between root and agronomic traits is at the shared-gene level as opposed to direct trait-to-trait impacts. Plant hormone contents and ratios between them (e.g., auxin contents and auxin/cytokinin ratios) are known to regulate tiller number, plant height, and root growth in the presence and absence of external stresses, possibly through their impact on source-sink relations (Albacete et al. 2014).
QTLs identified in ICIM and BN mapping spanned regions containing candidate genes that potentially explain the QTL molecular mechanisms (Figure 2, Supplementary Figure S3). The ICIM identified plant height QTL qPHT1 at 38.4 ± 0.02 Mb encompasses the semi dwarf (sd-1) gene also at 38.38 Mb (Spielmeyer et al. 2002). Katy is known to contain the Sd-1 allele for wild type tall height, while PI312777 is a semi dwarf containing the mutant sd-1allele, which is known to impact seedling growth rates as well as mature plant height. Thus, identification of QTL for PHT and several growth rate traits at the sd-1 locus was expected. BN analysis placed the plant height and growth rate QTLs at 36.5 Mb, approximately 2 Mb from the known sd-1 location, but still “close” for a QTL mapped based on genetic recombination in a biparental mapping population. What was not predictable due to few prior reports and little knowledge on root trait QTLs was association of qKTPI1.5 and sd-1 with root traits, specifically total surface area (TSA) and LRD along the LRD. However, there is an auxin transporter gene (OsAUX1) at 37.0 Mb that could be affecting root traits (Alarcón et al. 2019) in lieu of, or in addition to sd-1.
Another well-known gene with major effect on plant architecture is the Tiller Angle Control 1 (TAC1) gene (Yu et al. 2007) near the bottom of chromosome 9 at 20.7 Mb. Tiller angle is a plant architecture trait historically important for breeder and natural selection because wider space between tillers from a wider tiller angle decreases shading, increases photosynthetic efficiency, and creates an environment that is less favorable for pathogen development. We rated tiller angle visually on a 1–5 scale at heading (TAR) and again at maturity (TAT). ICIM and BN both identified QTLs for tiller angle at one or both plant stages near TAC1, with ICIM identifying a peak SNP at 20.4 Mb, while BN identified two close, but flanking SNPs (at 20.5 and 20.8 Mb) associated with tiller angle. ICIM but not BN also detected a colocated QTL for tiller number, while only BN detected association also with root traits, specifically LRSAP and LRL. This newly detected association between TAC1 and desirable increases in LRL and percentage of surface area, add new perspective and increase interest in what has been a well-known plant architecture gene. TAC1 is a member of the IGT gene family and is similar to the DEEP ROOTING1 (DRO1) gene (Uga et al. 2013). The gene has been found to be highly conserved during domestication of rice, with the relatively low levels of sequence variation in OsTAC1 aligning with the ancestral divide into the japonica and indica rice subspecies (Jiang et al. 2012). A mutation in the 3’-splicing site of the fourth intron in the japonica allele was found to suppress TAC1 expression, resulting in the compact architecture exhibited by our japonica parent “Katy,” compared to the higher expression and larger tiller angle characteristic of our parent “PI312777” and indica rice in general (Yu et al. 2007; Jiang et al. 2012). The BN network DAG (Supplementary Figure S1) indicates that longer average length of lateral roots (LRAL) relates directly to GY. The two RSA traits with QTLs near TAC1 are parental nodes, or contributors to LRAL.
Another QTL cluster identified among the PI312777 × Katy RILs by both ICIM and BN affected nearly the same regime of traits associated with the TAC1-linked QTLs. QTLs for tiller angle, tiller number, growth rate, and four RSA traits impacted by lateral root number and individual length (LRL, LRPL, LRAL, and TRD) were identified between 27.3 and 31.9 Mb on chromosome 3, with the allele from PI312777 increasing both lateral root growth and tiller number as well as angle. Within this span, at 30.5 Mb, is OsIAA13, an auxin responsive gene that has shown to be involved in auxin signaling which in turn controls the expression of genes that are required for lateral root initiation in rice (Kitomi et al. 2012).
The two QTL clusters just discussed near the long arm telomeres of chromosomes 9 and 3 affected RSA traits and tiller number, a plant architecture trait that contributes directly to GY not just in rice, but in all small grain crops. Several studies have documented that the number of tillers a grass plant produces is affected by interaction between nitrogen and gibberellin, and positively affects GY (Wu et al. 2020). The qKTPI3.1 QTL region on chromosome 3 at 2.6 Mb, was associated with RSA traits, tiller number, and heading date by ICIM and BN analyses, and further associated with early growth rate and GY by ICIM. This gene is close to the Dwarf 14 (D14) gene physically located at 5.4 Mb on chromosome 3 which was first recognized to affect plant height and tiller number, and later show to also affect heading date (HDT), and LRL. D14 is now known to be involved in the strigolactone signaling pathway which inhibits tillering, shoot branching, and initiation of symbiosis by rice roots (Gutjahr 2015; Hu et al. 2017). Lateral roots are below-ground branches, and tillers are above-ground branches. Branching in plant tissues starts with initiation of an axillary meristem that is either be kept dormant, often through hormonal repression, or allowed to extend into a branch. Of the 13 QTL regions identified from ICIM or BN as affecting RSA, four also affected tiller number (chromosomes 3, 3, 4, and 9), and another (chromosome 8) affected tiller angle but not number. It appears that a portion of the yield contribution from LRAL seen in the DAG is due to positive correlations between lateral root number, length, or both, and tiller number.
Two instances of RSA and agronomic QTLs locating near auxin genes have already been discussed, with QTLs near the OsAux1 efflux gene (chromosome 1 37.0 Mb) which is a member of the AUX/LAX gene family, and the OsIAA13 (chromosomes 3 30.5 Mb) gene involved with auxin signaling. This study also identified qKTPI4 affecting leaf width (LFWDV), growth rates (GRLFNV and GREV), chlorophyll content (CHLF), and coarse as well as LRSA (CRSA and LRSA) (Table 3, Figure 5A) to be within 0.15 Mb of the NARROW LEAF1 (NAL1) gene on chromosome 4 (Figure 2). NAL1 is a positive regulator of adventitious roots, and effects lateral and longitudinal growth of leaves and stem by regulating two unlinked genes, CROWN ROOTLESS1 (CRL1) and the PIN-FORMED (PIN) auxin efflux carrier (Cho et al. 2014). NAL1 has also been reported as a major gene for natural variation of chlorophyll content (Wang et al. 2015). The present QTLs and NAL1 match for both proximity and traits affected.
The length of maturity, or number of days between emergence and heading, is an attribute that regulates ecogeographical adaptation and yield potential (Zhang et al. 2015). Among the traits studied in the PI312777 × Katy RIL population, we found heading date (HDT) to have the most (9) direct connections with other DAG nodes, and was connected with eight agronomic traits (LFNV, GRRT, GRLFEV, TAR, GRER, PHT, TAT, and CHLF) plus one lateral root trait (LRAL) (Supplementary Figure S1). Four QTLs connected with HDT in DAG affected both root and agronomic traits (qKTPI3.1, qKTPI4, qKTPI8, and qKTPI9.2), and one affected only agronomic traits (qKTPI7.2). While HDT was not directly connected to GY, it connected indirectly through plant height (PHT). The heading date QTL qKTPI8 (chromosome 8 4.31 Mb), which was close and proximal to the Ghd8/DTH8 gene (chromosome 8 4.22 Mb) on chromosome 8, affected heading date (HDT), tiller angle (TAR), leaf width (LFWDV) and length (LFLV), and early growth rate (GREV) as well as LRD and surface area (LRSA). ICIM confirmed association between the chromosomal region containing Ghd8 with heading date (HDT), tiller angle (TAR and TAT), and early growth rate (GREV), and detected association with plant height (PHT) and GY. Ghd8 is reported to have pleiotropic effects in rice for flowering time suppression, stem growth and development, and GY (Zhang et al. 2015). Ghd8 delays flowering time by down-regulating expression of Ehd1 and Hd3a in long-day conditions (Wei et al. 2010). The many pleiotropic effects of this gene were found to be due to HAP2 and HAP5 subunit orthologs with conserved domain that is responsible for DNA binding or protein–protein interaction (Wei et al. 2010). We identified a QTL with major effect on heading date (HDT) that, like the closely mapped Ghd8 gene, showed pleiotropic effects on stem growth and development as well as yield, but was also determined to affect lateral root traits (LRD and LRSA).
For rice producers, it is important for modern rice varieties to provide both high yield and desired eating and processing qualities. The DAG indicated GY to be directly influenced by early growth rates (GREV), plant height (PHT) and LRAL, showing the importance of early growth of both roots and shoots to yield (Figure 5C). This study of PI312777 × Katy RILs found evidence that genes regulating the development of coarse and lateral roots at the seedling stage also have epistatic effects on adult plant flowering time, auxin transport, and tiller number and angle. Further study of the molecular pathways underlying the QTLs affecting root and agronomic traits could clarify how the root factors contribute to those agronomically important traits. In a recent study, transcript and sequence data from maize seedlings (V1 stage) were found useful for predicting the genetic variation in several mature plant agronomic traits, including flowering time, height, and GY (Azodi et al. 2020). The present DAG suggests that epistatic genes causing roots differences in rice seedlings as young as 13 days could be similarly used to predict adult plant traits.
Interaction among SNPs and traits affects genomic predictive ability in genomic selection
In the RIL population we found that, for most traits, the GP models had a higher GPA than the multi-QTL model (Tables 2 and 4). We also found that the GPA advantage of GP models over the multi-QTL model was smaller for traits with fewer large effect (>54%) QTLs, e.g., CHLF, PHT, HDT, and TNR. This suggests that for less genetically complex traits (controlled by fewer loci with large additive effect), a multi-QTL model may be sufficient, but for traits controlled by many QTLs with small individual effect, a GP model may improve the accuracy of predictions.
The GPAs from multitrait GP models of BN and from the differential marker shrinkage model of Bayes B were significantly different (P < 0.05) than single trait models (Table 4). We found a higher GPA (>70%) of Bayes B when traits (PHT, HDT, TAR, and TAT) were controlled by few large QTL (Supplementary Table S1). Whereas BRR predicted consistently regardless of number of QTL. Similar results were also reported in simulation studies (Hayes et al. 2009; Daetwyler et al. 2010). Higher GPAs of Bayesian model of multitrait BN for some traits (Table 4) may be due to accounting of polygenic effects by relationship matrix in multitrait Bayesian model. Similar results were also reported in other studies (Hayashi and Iwata 2013). Bayes B could have computed higher GPA due to LD by decreasing the probability of nonzero variance (Habier et al. 2013). Whereas for models that use infinitesimal additive models like BRR, GPA could have been low because of gene-by-gene interaction (Habier et al. 2007). The computational demand in terms of time for BN and Bayes B models, however, was higher compared to BRR model in our analysis.
The observed improvement of GPA with BN vs other methods for low and moderately heritable traits is consistent with previous studies where genetic correlations with highly heritable traits in multitrait GP were compared to single trait GP (Jia and Jannink 2012; Hayashi and Iwata 2013). In traits where BN had lower GPA than other methods, this could be due to low genetic correlation for these traits with other traits having higher heritability. This effect of genetic correlation to GPA can be important for breeders since many of the traits plant breeders include in their breeding program have low heritability and they are correlated (Hallauer et al. 2010). Understanding trait relationships and their genetic underpinnings could provide key insight to breeders working to improve a desired trait that is in a cause-effect relationship with an undesirable trait (Chen and Lubberstedt 2010; Jia and Jannink 2012).
GSRI as a tool to select multiple RSA traits in breeding
GEBVs have been commonly used for selections aimed at single traits (Meuwissen et al. 2001; Lorenz et al. 2012; Ceron-Rojas et al. 2015). In crop improvement, however, breeder selections more often aim at improving multiple desired traits per round of selection (Hallauer et al. 2010). As early as the 1940’s, plant and animal breeders began using various mathematical equations to combine data on multiple traits into a single value, or selection index, to better identify breeding progeny containing improvements in multiple traits. One method for creating a multitrait selection index to rank the population for each individual trait, then summing the rankings across the traits, resulting in what is known as a rank sum index (Mulamba and Mock 1978). Combining the idea of selection indices with genomic selection, Ceron-Rojas et al. (2015) used a linear combination of GEBVs from different traits to create a genomic selection index (GSI) to support simultaneous and efficient improvement of traits. More recently, multiobjective optimized genomic breeding strategies (Akdemir et al. 2019) and modified look ahead selection (LAS) algorithms (Moeinizade et al. 2020) have been used to optimize alleles for multiple traits in breeding and selection. Application of these methods is currently limited, however, by their significant computational complexity.
We applied the rank sum index of Mulamba and Mock (1978) to multiple trait GEBVs to create, for the first time, a GSRI for use as a selection tool. In this manner, we combined the power of GP to capture the breeding value of epistatic genes with a selection index to identify by GP the best performing individuals to advance to the next generation, or use as parents for the next round of crossing. The rank sum index by Mulamba and Mock (1978) used because it is a simple, parameter (or weight) free index that does not require computationally complex estimation of population parameters including variance and covariances.
We then selected for high versus low GSRI calculated on RSA traits among the PI312777 × Katy RILs, and evaluated the impact of the GSRI-based selections in terms of effect on each of the RSA traits. We determined that the divergent GSRI selections did result in significant differences between the upper and lower GSRI population means in the expected (upper or lower) directions for several of the lateral root related traits (LRD, LRL, LRPL, LRSA, LRSAP, and LRT) and one of the total root traits (TRD), which, by definition, comprises lateral, and coarse root attributes. However, the GSRI selections did not significantly alter either of the two coarse roots traits (CRL and CRSA), nor two of the three total root traits (RV and TSA). RIL population means also did not differ for the derived trait of average LRL (Table 5). The nonsignificance impact of selection seen for total or coarse root traits (CRL, CRSA, RV, and TSA) and derived root traits (LRAL and RV) could be due to their complex compositions or derivations. Our data on coarse roots included both primary and crown roots (Figure 1). An RSA having more crown roots and a short primary root, and one having a long primary root and few crown roots could have similar values for these coarse root traits. Distinguishing all functional root types using diameter classifications is a significant challenge (Rose 2017). It must also be recognized that two of the RSA traits used in the calculation of GSRI were for coarse roots alone (CRL and CRSA) while 7 RSA traits were focused on lateral roots, and that though total root traits contain both coarse and lateral roots, they are often heavily weighted toward lateral root contributions (e.g., 100- to 200-fold more LRT than other root tips in the calculation of TRD, Figure 1). Thus, this apparent larger impact of GSRI selection on lateral roots than coarse roots might be due to a greater overall proportion and importance of lateral roots, or it might be due to a bias in the GSRI as calculated in this study.
When breeding for a particular idiotype, such as an RSA that is well suited for a target environment, many traits need to be simultaneously selected. Those traits may be correlated or anti-correlated. Use of a BN model for selection could help to ensure that gains in one trait are not detrimental for other relevant traits. The use of a GSRI could be an effective method for breeders to simultaneously select many traits in a breeding population.
Although the acquisition of root trait data from images is somewhat automated with software, there are manual steps required and each agar plate must be placed on the scanner and processed individually. In addition, the method of growing plants in agar plates is time consuming, particularly at the stage of pouring agar plates and placing the germinated seeds, all of which must be done under sterile conditions to prevent contamination. For these reasons, and because of time and resource limitations the sample size for GP of RSA traits was less than optimal. The use of a divergently selected validation population somewhat alleviated sample size concerns. The GSRI provided a method to select a validation population that was more efficient than a population that would have been selected randomly. In future studies, the GP models could be refined based on the validation data, and a new divergently selected validation population could be selected using a GSRI on the refined models, and this process could be iterated until satisfactory accuracies are achieved. Such a strategy could be applied to a breeding program over multiple rounds of crossing and selection to simultaneously improve RSA and above-ground traits (Figure 6).
Figure 6.

Proposed genomic selection strategy to incorporate GSRI in breeding of crops. Genomic breeding values (GEBVs) calculated from genotype and phenotype information from multiple traits of the parent TS facilitate calculation of GSRI which can be used for both parent selection and selection of segregating progenies through index selection.
Conclusions
In this study, we identified QTLs for above-ground and RSA traits and presented a novel way to improve GP and selection of RSA traits in rice using multitrait BN and GSRI. Multi-QTL models that assess the combined effects of alleles at multiple loci were moderately successful in predicting several traits. An advantage of multi-QTL models over GP models is that only a small number of markers linked to the QTL need to be genotyped vs the genome-wide marker requirements for GP. Many of the QTLs were found collocated or associated with multiple traits suggesting pleiotropic effects. The BN analysis also detected several of the QTLs identified by ICIM, and the BN helped to clarify how QTL pleiotropic effects arise in causal relationships between traits. Candidate gene analysis suggested potential molecular mechanisms for the QTLs and their networks of trait and epistatic interactions. We compared the GPA of single-trait GP methods with multitrait BN and found that inclusion of correlated traits with high heritability in the BN improved GPA of low to moderately heritable traits. To achieve selection across multiple RSA traits we used a new method of GSRI and validated the GSRI predictions in two divergently selected groups. The results of this study offer several opportunities for breeders aiming to improve RSA through QTLs for use in MAS, improved GP methods, and GSRI to guide selection decisions in segregating progeny.
Supplementary Material
Acknowledgments
This research used facilities and assistance provided by USDA Agricultural Research Service Dale Bumpers National Rice Research Center. Dr. Santosh Sharma was supported by USDA-ARS headquarters-funded postdoc award. Mention of a trademark or proprietary product does not constitute a guarantee or warranty of the product by the USDA and does not imply its approval to the exclusion of other products that also can be suitable. The USDA is an equal opportunity provider and employer. All experiments complied with the current laws of the United States, the country in which they were performed.
Conflicts of interest
None declared.
Literature cited
- Akdemir D, Beavis W, Fritsche-Neto R, Singh AK, Isidro-Sánchez J.. 2019. Multi-objective optimized genomic breeding strategies for sustainable food improvement. Heredity (Edinb). 122:672–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alarcón MV, Salguero J, Lloret PG.. 2019. Auxin modulated initiation of lateral roots is linked to pericycle cell length in maize. Front Plant Sci. 10:11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albacete AA, Martínez‐Andújar C, Pérez‐Alfocea F.. 2014. Hormonal and metabolic regulation of source‐sink relations under salinity and drought: from plant survival to crop yield stability. Biotechnol Adv. 32:12–30. [DOI] [PubMed] [Google Scholar]
- Allier A, Teyssèdre S, Lehermeier C, Charcosset A, Moreau L.. 2020. Genomic prediction with a maize collaborative panel: identification of genetic resources to enrich elite breeding programs. Theor Appl Genet. 133:201–255. [DOI] [PubMed] [Google Scholar]
- Aravind J, Mukesh Sankar S, Wankhede DP, Kaur V.. 2020. augmentedRCBD: analysis of Augmented randomized complete block design. R package Version:0.1.3. ICAR-NBPGR. 10.5281/zenodo.1310011. [DOI]
- Arsenault J, Poulcur S, Messier C, Guay R.. 1995. WinrhizoTM: a root measuring system with a unique overlap correction method. HortScience. 30:906D–906. [Google Scholar]
- Atkinson JA, Pound MP, Bennett MJ, Wells DM.. 2019. Uncovering the hidden half of plants using new advances in root phenotyping. Curr Opin Biotechnol. 55:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azodi CB, Pardo J, VanBuren R, de los Campos G, Shiu SH.. 2020. Transcriptome-based prediction of complex traits in maize. Plant Cell. 32:139–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, Maechler M, Bolker B.. 2011. Lme4: Linear mixed effects models using s4 classes. http://cran.rproject.org/web/packages/lme4/index.html.
- Ceron-Rojas JJ, Crossa J, Arief VN, Basford K, Rutkoski J, et al. 2015. A genomic selection index applied to simulated and real data. G3 (Bethesda). 5:2155–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Lubberstedt T.. 2010. Molecular basis of trait correlations. Trends Plant Sci. 15:454–461. [DOI] [PubMed] [Google Scholar]
- Cho S, Yoo S, Zhang H, Lim J, Paek N.. 2014. Rice NARROW LEAF1 regulates leaf and adventitious root development. Plant Mol Biol Rep. 32:270–281. [Google Scholar]
- Clark RT, Famoso AN, Zhao K, Shaff JE, Craft EJ, et al. 2013. High-throughput two-dimensional root system phenotyping platform facilitates genetic analysis of root growth and development. Plant Cell Environ. 36:454–466. [DOI] [PubMed] [Google Scholar]
- Cobb JN, Juma RU, Biswas PS, Arbelaez JD, Rutkoski J, et al. 2019. Enhancing the rate of genetic gain in public-sector plant breeding programs: lessons from the breeder’s equation. Theor Appl Genet. 132:627–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covarrubias-Pazaran G. 2016. Genome assisted prediction of quantitative traits using the R package sommer. PLoS One. 11:e0156744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J, Pérez-Rodriguez P, Cuevas J, Montesinos-López O, Jarquín D, et al. 2017. Genomic selection in plant breeding: methods, models, and perspectives. Trends Plant Sci. 22:961–975. [DOI] [PubMed] [Google Scholar]
- Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA.. 2010. The impact of genetic architecture on genome-wide evaluation methods. Genetics. 185:1021–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Gianola D, Rosa GJ.. 2009. Reproducing kernel Hilbert spaces regression: a general framework for genetic evaluation. J Anim Sci. 87:1883–1887. [DOI] [PubMed] [Google Scholar]
- Delgado A, Hays DB, Bruton RK, Ceballos H, Novo A, et al. 2017. Ground penetrating radar: a case study for estimating root bulking rate in cassava (Manihot esculenta Crantz). Plant Methods. 13:65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eathington SR, Crosbie TM, Edwards MD, Reiter RS, Bull JK.. 2007. Molecular markers in a commercial breeding program. Crop Sci. 47:S154–S163. [Google Scholar]
- Endelman JB. 2011. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome. 4:250–255. [Google Scholar]
- Federer WT. 1961. Augmented designs with one-way elimination of heterogeneity. Biometrics. 17:447–473. 10.2307/2527837. [DOI] [Google Scholar]
- Galkovskyi T, Mileyko Y, Bucksch A, Moore B, Symonova O, et al. 2012. GiA Roots: software for the high throughput analysis of plant root system architecture. BMC Plant Biol. 12:116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Ruiz A, Cole JB, VanRaden PM, Wiggans GR, Ruiz-Lopez FJ, et al. 2016. Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc Natl Acad Sci USA. 113:E3995–E4004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gealy DR, Fischer AJ.. 2010. 13C discrimination: a stable isotope method to quantify root interactions between C3 rice (Oryza sativa) and C4 barnyardgrass (Echinochloa crus-galli) in flooded fields. Weed Sci. 58:359–368. [Google Scholar]
- Gealy DR, Rohila JS.. 2018. Field performance of an Indica x tropical Japonica rice mapping population under AWD stress. In: Thirty-Seventh Rice Technical Working Group Meeting Proceedings. Long Beach, CA. p. 19–22. [Google Scholar]
- Gealy DR, Jia Y, Pinson SR.. 2014. Exploring optimization of weed suppression, yield, and biotic stress tolerance in an allelopathic X non-allelopathic rice mapping population. In: Proceedings of the 7th World Congress on Allelopathy. Vigo, Spain. International Allelopathy Society. International Allelopathy Congress. p. 224.
- Godin C, Sinoquet H.. 2005. Functional–structural plant modelling. New Phytol. 166:705–708. doi:10.1111/j.1469-8137.2005.01445.x. [DOI] [PubMed] [Google Scholar]
- González-Recio O, Forni S.. 2011. Genome-wide prediction of discrete traits using bayesian regressions and machine learning. Genet Sel Evol. 43:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutjahr C, Gobbato E, Choi J, Riemann M, Johnston MG, et al. 2015. Rice perception of symbiotic arbuscular mycorrhizal fungi requires the karrikin receptor complex. Science. 350:1521–1524. [DOI] [PubMed] [Google Scholar]
- Habier D, Fernando RL, Garrick DJ.. 2013. Genomic BLUP decoded: a look into the black box of genomic prediction. Genetics. 194:597–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D, Fernando RL, Dekkers JCM.. 2007. The impact of genomic relationship information on genome-assisted breeding value. Genetics. 177:2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallauer AR, Carena MJ, Miranda Fo JB.. 2010. Quantitative Genetics in Maize Breeding. 3rd ed.New York, NY: Springer. [Google Scholar]
- Hayes BJ, Bowman PJ, Chamberlain AJ, Goddard ME.. 2009. Invited review: genomic selection in dairy cattle: progress and challenges. J Dairy Sci. 92:433–443. [DOI] [PubMed] [Google Scholar]
- Hayashi T, Iwata H.. 2013. A Bayesian method and its variational approximation for prediction of genomic breeding values in multiple traits. BMC Bioinformatics. 14:34–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson CR, Quaas RL.. 1976. Multiple trait evaluation using relatives' records. J Anim Sci. 43:1188–1197. [Google Scholar]
- Hill WG, Goddard ME, Visscher PM.. 2008. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 4:e1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoerl AE, Kennard RW.. 1970. Ridge regression: biased estimation for nonorthogonal problems. Technometrics. 12:55–67. [Google Scholar]
- Hu Q, He Y, Wang L, Liu S, Meng X, et al. 2017. DWARF14, a receptor covalently linked with the active form of strigolactones, undergoes strigolactone-dependent degradation in rice. Front Plant Sci. 8:1935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- IBPGR-IRRI Rice Advisory Committee (International Rice Research Institute and International Board for Plant Genetic Resources), 1980. Descriptors for rice Oryza sativa L. The International Rice Research Institute, Manila, Philippines.
- Iyer-Pascuzzi A, Symonova O, Mileyko Y, Hao Y, Belcher H, et al. 2010. Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiol. 152:1148–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia Y, Jannink JL.. 2012. Multiple-trait genomic selection methods increase genetic value prediction accuracy. Genetics. 192:1513–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J, Tan L, Zhu Z, Fu Y, Liu F, et al. 2012. Molecular evolution of the TAC1 gene from rice (Oryza sativa L.). J Genet Genomics. 39:551–560. [DOI] [PubMed] [Google Scholar]
- JMP® 14. SAS Institute Inc., Cary, NC, 1989-2020.
- Jung JK, McCouch S.. 2013. Getting to the roots of it: genetic and hormonal control of root architecture. Front Plant Sci. 4:e186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitomi Y, Inahashi H, Takehisa H, Sato Y, Inukai Y.. 2012. OsIAA13-mediated auxin signaling is involved in lateral root initiation in rice. Plant Sci. 190:116–122. [DOI] [PubMed] [Google Scholar]
- Knapp SJ, Stroup WW, Ross WM.. 1985. Exact confidence intervals for heritability on a progeny mean basis. Crop Sci. 25:192–194. [Google Scholar]
- Koevoets IT, Venema JH, Elzenga JT, Testerink C.. 2016. Roots withstanding their environment: exploiting root system architecture responses to abiotic stress to improve crop tolerance. Front Plant Sci. 7:1335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legarra A, Robert-Granie C, Manfredi E, Elsen JM.. 2008. Performance of genomic selection in mice. Genetics. 180:611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Ye G, Wang J.. 2007. A modified algorithm for the improvement of composite interval mapping. Genetics. 175:361–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobet G, Pages L, Draye X.. 2011. A novel image-analysis toolbox enabling quantitative analysis of root system architecture. Plant Physiol. 157:29–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobet G, Pound MP, Diener J, Pradal C, Draye X, et al. 2015. Root System Markup Language: toward a unified root architecture description language. Plant Physiol. 167:617–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz AJ, Smith KP, Jannink J-L.. 2012. Potential and optimization of genomic selection for Fusarium head blight resistance in six-row barley. Crop Sci. 52:1609–1621. [Google Scholar]
- Lynch J. 1995. Root architecture and plant productivity. Plant Physiol. 109:7–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malovini A, Nuzzo A, Ferrazzi F, Puca AA, Bellazzi R.. 2009. Phenotype forecasting with SNPs data through gene-based Bayesian networks. BMC Bioinformatics. 10:S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mccouch S, Cho Y, Yano M.. 1997. Report on QTL nomenclature. Rice Genet. Newsl. 14:11–13. [Google Scholar]
- Meng L, Li H, Zhang L, Wang J.. 2015. QTL IciMapping: integrated software for genetic linkage map construction and quantitative trait locus mapping in biparental populations. Crop J. 3:269–283. [Google Scholar]
- Meuwissen T, Hayes B, Goddard M.. 2016. Genomic selection: a paradigm shift in animal breeding. Anim Front. 6:6–14. [Google Scholar]
- Meuwissen THE, Hayes BJ, Goddard ME.. 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 157:1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeinizade S, Kusmec A, Hu G, Wang L, Schnable PS.. 2020. Multi-trait genomic selection methods for crop improvement. Genetics. 215:931–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulamba NN, Mock JJ.. 1978. Improvement of yield potential of the Eto Blanco maize (Zea mays L.) population by breeding for plant traits. Egyptian J Genet Cytol. 7:40–51. [Google Scholar]
- Pace J, Yu X, Lübberstedt T.. 2015. Genomic prediction of seedling root length in maize (Zea mays L.). Plant J. 83:903–912. [DOI] [PubMed] [Google Scholar]
- Pearl J. 1988. Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufman, San Francisco.
- Pérez P, de los Campos G.. 2014. Genome-wide regression and prediction with the BGLR statistical package. Genetics. 198:483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pound MP, French AP, Atkinson JA, Wells DM, Bennett MJ, et al. 2013. RootNav: navigating images of complex root architectures. Plant Physiol. 162:1802–1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. 2020. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Rose L. 2017. Pitfalls in root trait calculations: how ignoring diameter heterogeneity can lead to overestimation of functional traits. Front Plant Sci. 8:898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz GE. 1978. Estimating the dimension of a model. Ann Stat. 6:461–464. [Google Scholar]
- Scutari M, Mackay I, Balding DJ.. 2013. Improving the efficiency of genomic selection. Stat Appl Genet Mol Biol. 12:517–527. [DOI] [PubMed] [Google Scholar]
- Scutari M. 2010. Learning Bayesian networks with the bnlearn R Package. J Stat Soft. 35:1–22. [Google Scholar]
- Scutari M, Howell P, Balding DJ, Mackay I.. 2014. Multiple quantitative trait analysis using Bayesian networks. Genetics. 198:129–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma S, Carena MJ.. 2016. BRACE: a method for high throughput maize phenotyping of root traits for short-season drought tolerance. Crop Sci. 56:2996–3004. [Google Scholar]
- Singh M, Ceccarelli S, Hamblin J.. 1993. Estimation of heritability from varietal trials data. Theor Appl Genet. 86:437–441. [DOI] [PubMed] [Google Scholar]
- Spielmeyer W, Ellis MH, Chandler PM.. 2002. Semidwarf (sd-1), “green revolution” rice, contains a defective gibberellin 20-oxidase gene. Proc Natl Acad Sci USA. 99:9043–9048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson MJ, Singh N, Dwiyanti MS, Wang DR, Wright MH, et al. 2017. Large-scale deployment of a rice 6 K SNP array for genetics and breeding applications. Rice (NY). 10:40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trachsel S, Kaeppler SM, Brown KM, Lynch JP.. 2011. Shovelomics: high throughput phenotyping of maize (Zea mays L.) root architecture in the field. Plant Soil. 341:75–87. [Google Scholar]
- Tuberosa R. 2012. Phenotyping for drought tolerance of crops in the genomics era. Front Physiol. 3:1–26. [10.3389/fphys.2012.00347]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tukey JW. 1949. Comparing individual means in the analysis of variance. Biometrics. 5:99–114. [PubMed] [Google Scholar]
- Uga Y, Sugimoto K, Ogawa S, Rane J, Ishitani M, et al. 2013. Control of root system architecture by DEEPER ROOTING 1 increases rice yield under drought conditions. Nat Genet. 45:1097–1102. [DOI] [PubMed] [Google Scholar]
- University of Arkansas, 2013. MP192-Rice production handbook (MP192-2M-11-13RV). In: Hardke JT, editor. University of Arkansas Division of Agriculture Cooperative Extension Service. Little Rock. [Google Scholar]
- VanRaden PM. 2008. Efficient methods to compute genomic predictions. J Dairy Sci. 91:4414–4423. [DOI] [PubMed] [Google Scholar]
- Voorrips RE. 2002. MapChart: software for the graphical presentation of linkage maps and QTLs. J Hered. 93:77–78. [DOI] [PubMed] [Google Scholar]
- Walsh B, Lynch M.. 2018. Evolution and Selection of Quantitative Traits. Oxford: Oxford University Press. [Google Scholar]
- Wang L, Audenaert P, Michoel T.. 2019. High dimensional Bayesian network inference from systems genetics data using genetic node ordering. Front Genet. 10:1196. [10.3389/fgene.2019.01196]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Xie W, Xing H, Yan J, Meng X, et al. 2015. Genetic architecture of natural variation in rice chlorophyll content revealed by a genome-wide association study. Mol Plant. 8:946–957. [DOI] [PubMed] [Google Scholar]
- Wedger MJ, Topp CN, Olsen KM.. 2019. Convergent evolution of root system architecture in two independently evolved lineages of weedy rice. New Phytol. 223:1031–1042. [DOI] [PubMed] [Google Scholar]
- Wei X, Xu J, Guo H, Jiang L, Chen S, et al. 2010. DTH8 suppresses flowering in rice, influencing plant height and yield potential simultaneously. Plant Physiol. 153:1747–1758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickham H. 2009. ggplot2. New York, NY: Springer New York. [Google Scholar]
- Wong CK, Bernardo R.. 2008. Genomewide selection in oil palm: increasing selection gain per unit time and cost with small populations. Theor Appl Genet. 116:815–824. [DOI] [PubMed] [Google Scholar]
- Wu K, Wang S, Song W, Zhang J, Wang Y, et al. 2020. Enhanced sustainable green revolution yield via nitrogen-responsive chromatin modulation in rice. Science. 367:eaaz2046. [DOI] [PubMed] [Google Scholar]
- Xu W, Ding G, Yokawa K, Baluska F, Li Q, et al. 2013. An improved agar‐plate method for studying root growth and response of Arabidopsis thaliana. Sci. Rep. 3:1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin L, Zhang H, Tang Z, Xu J, Yin D, et al. 2020. rMVP: a memory-efficient, visualization-enhanced, and parallel-accelerated tool for genome-wide association study. bioRxiv. 2020. 08.20.258491. 10.1101/2020.08.20.25849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu B, Lin Z, Li H, Li X, Li J, et al. 2007. TAC1, a major quantitative trait locus controlling tiller angle in rice. Plant J. 52:891–898. [DOI] [PubMed] [Google Scholar]
- Yu H, Campbell MT, Zhang Q, Walia H, Morota G.. 2019. Genomic Bayesian confirmatory factor analysis and bayesian network to characterize a wide spectrum of rice phenotypes. G3 (Bethesda). 9:1975–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Z, Jiang X, Neapolitan R.. 2016. Discovering causal interactions using Bayesian network scoring and information gain. BMC Bioinformatics. 17:221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Zhou X, Yan W, Zhang Z, Lu L, et al. 2015. Combinations of the Ghd7, Ghd8 and Hd1 genes largely define the ecogeographical adaptation and yield potential of cultivated rice. New Phytol. 208:1056–1066. [DOI] [PubMed] [Google Scholar]
- Zuk O, Hechter E, Sunyaev SR, Lander ES.. 2012. The mystery of missing heritability: genetic interactions create phantom heritability. Proc Natl Acad Sci USA. 109:1193–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Genotype and phenotype data used for QTL mapping and genomic selection are available through the figshare portal. QTL positions for RSA and agronomic traits are in Supplementary Table S1. Scripts are available at https://github.com/jeremyde/rice_roots_bayesian_networks.
Supplementary material is available at G3 online.