Abstract
Growth in working memory capacity, the number of items kept active in mind, is thought to be an important aspect of childhood cognitive development. Here, we focused on participants’ awareness of the contents of their working memory, or meta-working-memory, which seems important because people can put cognitive abilities to best use only if they are aware of their limitations. In two experiments on the development of meta-working-memory in children between 6 and 13 years old and adults, participants were to remember arrays of colored squares and to indicate if a probe item was in the array. On many trials, before the probe recognition test, they reported a meta-judgment, how many items they thought they remembered. We compared meta-working-memory judgments to actual performance and looked for associations between these measures on individual and trial-by-trial levels. Despite much lower working memory capacity in younger children there was little change in meta-working-memory judgments across age groups. Consequently, younger participants were much less realistic in their meta-judgments concerning their working memory capability. Higher cognitive capacity was associated with more accurate meta-working-memory judgments within an age group. Trial-by-trial tuning of meta-judgments was evident only in young adults, and then only for small array set sizes. In sum, meta-working-memory ability is a sophisticated skill that develops with age and may be an integral aspect of the development of working memory across the school years.
Keywords: Working Memory, Metacognition, Cognitive Development, Meta-Memory, Working Memory Capacity
Working memory (WM) holds mental representations for use in ongoing cognitive activities (e.g., Logie & Cowan, 2015). WM capacity is considered key to cognitive development (Bayliss et al., 2003; Cowan, 2016; Holmes et al., 2010) and individual differences in aptitude (Conway et al., 2003; Cowan et al., 2005; Jarrold & Towse, 2006). Performance on tasks thought to measure WM typically improves during childhood (e.g., Brockmole & Logie, 2013; Cowan et al., 2006a, 2006b, 2010; Gathercole et al., 2004; Isbell et al., 2015; Riggs et al., 2006; 2011). The well-established link between WM and educational difficulties (Adams & Gathercole, 2000; Alloway et al., 2009; Cowan, 2014; Gathercole & Pickering, 2000; Holmes & Adams, 2006; McCormack et al., 2013) has spawned research intended to train WM (e.g., Melby-Lervåg et al., 2016; Holmes & Gathercole, 2014) and to match educational materials to WM levels (Cowan, 2014; Jaroslawska et al., 2016; Sweller et al., 1998).
In this study, we focus on a less-explored but potentially important aspect of WM development: awareness of the contents of one's WM (meta-memory for WM, or meta-WM). Meta-WM may affect performance. For example, when task instructions overwhelm children's WM (Jaroslawska et al., 2016), awareness of forgetting would, at least, allow a child to ask for repeated instructions instead of proceeding using partial or misremembered instructions. It might also lead to the intention to try harder in the future. Understanding the development of meta-WM may, therefore, be critical to understanding the development of WM and its role in education (cf. Gathercole et al., 2019). More accurate meta-memory insight has been associated with better learning (Balcomb & Gerken, 2008; Garner, 1987; Schneider & Pressley, 1989), including better mnemonic strategies, allocation of attention, and awareness of the limits of comprehension (Schraw, 2001).
While meta-WM in adults has received some attention recently (Adam & Vogel, 2017; Cowan et al., 2016; Rademaker et al., 2012), developmental meta-memory research seems largely restricted to the long-term memory domain. This is the case despite ample research highlighting the central role of WM capacity in childhood cognitive development (e.g., Cowan, 2016), and the importance of meta-memory in long-term memory development (e.g., Brown et al., 1983; Flavell, et al., 1993; Schneider & Pressley, 2013). We briefly review literature on visual WM development, WM meta-memory in adults, and the development of long-term meta-memory, leading up to the gap in the literature that we sought to address in this paper, which is the development of meta-WM in childhood during the school years.
WM Capacity and Its Development
Cognitive psychologists have long investigated limits of human information processing. Miller (1956) proposed a well-known ‘magical’ limit of seven (plus or minus two) items. Cowan (2001) proposed a limit of about four items in short-term (or working) memory, supported by a wide variety of studies in which participants presumably could not use strategies such as grouping and chunking. Others have suggested that WM is not limited to a specific number of items, but depends on the allocation of a general resource, resulting in less precision per item when more items are represented (Bays et al., 2009). Despite disagreement on the nature of WM limits, it is generally agreed that WM storage is essential for ‘doing the work of cognition’ such as language use, problem-solving, and planning (see Logie & Cowan, 2015). Hence, WM is seen as essential for navigating our daily lives.
Adults can keep between 3 – 4 separate visual items in mind (e.g., Cowan, 2001; Luck & Vogel, 1997). This memory capacity (k), however, increases from lower levels in childhood and varies between individuals within an age group (Adam et al., 2017, Cowan et al., 2005; Conway et al., 2003; Jarrold & Towse, 2006). Preschoolers and early school-aged children seem able to retain only about 2 to 2.5 items according to models based on recognition of a probe of an item from a briefly-presented spatial or temporal array (e.g., Cowan et al., 2005; Cowan et al., 1999; 2010, 2011; Riggs et al., 2006; Simmering, 2012). WM capacity limits might impose a bottle-neck on various cognitive processes.
Meta-memory and Its Development
The term metacognition is attributed to Flavell (1971), who defined it as thinking about one's thinking. ‘Meta-memory’ includes one’s potentially verbalizable knowledge of aspects of information storage and retrieval. Flavell suggested awareness of one’s memory processes might promote the use memory-boosting strategies (cf. Sternberg, 1997). Metacognitive ability appears to be positively related to memory performance (e.g., Schneider & Pressley, 2013; Renner & Renner, 2001; Dunlosky et al., 2005).
Evidence from various tasks suggests that adults have access to some information about their WM contents (e.g., Amichetti et al., 2013; Bunnell et al., 1999; Levin et al., 2000; Bona & Silvanto, 2014; Mutluturk & Boduroglu, 2014; Vandenbroucke et al., 2014; Suchow et al., 2017; Rademaker et al., 2012). Typically, WM meta-memory is measured by asking healthy young adult participants to rate their level of confidence in their WM representation. More confident ratings tend to correspond to trials with more accurate memory, suggesting subjective insight into the strength of WM representations. Moreover, individual differences in metacognitive monitoring accuracy predict overall WM performance, sparking suggestions that such monitoring may be crucial for WM success (Adam & Vogel, 2017).
Rather than measuring participants’ confidence, Cowan et al (2016) explored their insight into the number of items from an array of colors held in WM (i.e., their WM capacity; k). Their young-adult participants estimated the overall number of items retained on a given trial, before seeing or responding to the memory probe in which some items had changed. Typically, participants overestimated the number of items in mind, compared to actual performance. These meta-memory storage judgments predicted trial-to-trial fluctuations in memory performance. Moreover, overestimation of items in WM caused participants to be too confident that if a change was not noticed, the change must not have occurred. Here, we used a similar meta-WM question within the simpler paradigm in which only one item per array is probed, to explore children’s ability to introspect on the number of items in WM.
The literature on children’s WM meta-memory is sparse. There is evidence on the development of meta-memory in the long-term domain. The 1970s saw a surge of research on the development of children's awareness of their memory (for reviews, see Brown et al., 1983; Flavell, et al., 1993; Schneider & Pressley, 2013), with the suggestion that such awareness may be required for the development of strategies to improve one’s memory (see Brown, 1978). Typically, younger children appear more prone to overestimating their memory abilities (e.g., Kreutzer et al., 1975; Myers & Paris, 1978; Weinert & Schneider, 1999; Koriat & Helstrup, 2007; Maki, 1999) and the accuracy of metacognitive monitoring is related to academic achievement (Freeman et al., 2017, see also Krebs & Roebers, 2010). Children under 12 years often appear unaware of what they fail to understand within text passages (Markman, 1979). Younger children overestimate how well they will perform on a test after studying materials, both prior to testing and after (Pressley et al., 1987). While children 8 to 10 year olds describe learning as a process (e.g., “when you practice again and again until you know it”), younger children typically do not, with a less- developed theory of mind (Sobel & Letourneau, 2015).
The developmental trajectory of meta-knowledge of information held in WM has, however, received little attention. Recently, Applin and Kibbe (2020) explored meta-WM in 5- to 6-year old children by hiding 2 to 5 objects in separate locations. They probed children's memory for the items and then asked them to bet between 0 and 3 tokens (e.g., candies or stickers) depending on their confidence in their memory response. Higher bets were associated with better memory accuracy, suggesting that pre-school children accurately monitored their memory representations. Such self-insight might inspire a child to try alternative approaches to cognitive tasks, as in the long-term memory literature (e.g., Schneider & Pressley, 2013; Renner & Renner, 2001; Dunlosky et al., 2005).
The Present Study
We explored how meta-WM develops with age. We related judgments of items in WM to WM capacity (k): a model-based estimate of how many items one can hold in WM, a key index of cognitive development (Cowan et al., 2005; Cowan, 2014). We report two experiments investigating the development of meta-memory ability in participants between 6 years and adulthood. Meta-memory investigation in WM affords a procedure that is not possible in research on long-term memory. In the latter case, a participant cannot have a feeling of knowing or not knowing a specific item until that item is presented to be judged. Therefore, what participants need in order to carry out a meta-memory judgment is awareness of the retrieval process. In WM, in contrast, we were able to present a visual array, remove the array, and sometimes ask participants how many array items they thought they still had in mind, before testing the accuracy of their meta-memory by presenting a specific probe for actual recognition. Across trials, therefore, we were able to place a numerical estimate on participants’ knowledge of their WM contents without the bias of knowing how easy or hard the memory question would seem on that trial. The comparison between WM and meta-WM can be fully quantitative, revealing just how inaccurate meta-WM is in each age group.
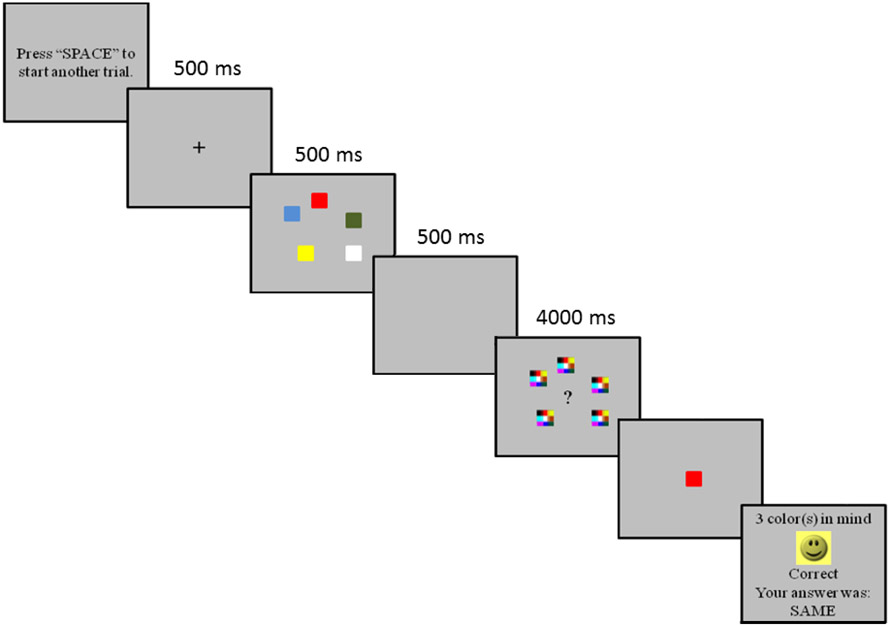
Our participants saw a set of colored squares (500 ms) and reported how many of the items they believed they remembered (see Figure 1). After providing that estimate, participants responded to the change detection probe, which across trials allowed estimation of their mean k score (an estimate of the number of items in WM) in addition to their ‘meta-WM’ (i.e., each participant’s subjective estimation of their average k). Importantly, on some trials the meta-judgment was omitted in order to assess its potentially disruptive effect on items in WM. If participants’ meta-WM ratings correspond to their actual performance, it would indicate that some of the ‘mental workspace’ used to remember colored arrays is open to conscious introspection, matching suggestions that WM involves attention (e.g., Barrouillet et al., 2011; Cowan, 2001).
Figure 1.
Outline of a typical trial in Experiment 1.
The developmental trend of meta-WM inaccuracy theoretically could go either way. Cowan (2001) proposed that the capacity limits of WM come from a limit in the focus of attention to 3–5 separate units. Then, if awareness of the information in the focus of attention (i.e., WM meta-memory) requires attention, younger children might have less attention to spare for that purpose, resulting in failure to notice some items in the focus of attention, so meta-WM would underestimate capacity. Showing that meta-memory can be resource-demanding, Stine-Morrow et al. (2006) found that older adults’ memory for sentences was comparatively more impaired than that of younger adults when participants had to monitor their meta-memory. With less attention or fewer resources in younger children, they might tend to rely on a bias toward overestimation of their ability.
It is also possible that younger participants are aware of the items in the focus of attention but unaware of processing factors that reduce their ability to demonstrate memory for those items. For instance, they may fail to understand that some knowledge of an object does not imply complete knowledge, or fail to consider the role of decay and interference in retaining the memory trace. On the basis of such factors, younger participants might be expected to overestimate their capacity more than older participants. Thus, we have suggested reasons why younger children might either underestimate their WM capacity more or overestimate it more than older children and young adults. We also have suggested that, in any case, younger children should be less accurate in their meta-memory for WM than older children and adults.
In addition to developmental changes, we are interested in whether meta-memory accuracy is associated with higher WM capacity or general cognitive ability, and whether participants are aware of trial-to-trial fluctuations in the number of items in WM. Previous research has indicated that adults are aware of trial-to-trial variations in the extent to which they pay attention to the array (see Adam et al., 2015; Cowan et al., 2016; Rouder et al., 2008; van den Berg et al., 2014) and we are interested in whether children would exhibit similar trial-to-trial level insight. To answer questions related to individual differences, we examine auxiliary measures of WM capacity and intelligence in relation to meta-memory scores.
Experiment 1
Methods
Participants
Age groups were based on extensive experience about the ages at which children can do our WM tasks, and approximately equally-spaced groups according to WM development. The sample size was based on group sizes in previous, related, published work in this laboratory. We retrospectively used Bayes Factors design analysis to show that our sample size was adequate for our purposes (see online supplement for details).
We recruited participants from five different age groups (1st - 2nd graders: N = 30, mean age 7.2, SD = 0.8 years, 10 male; 3rd - 4th graders: N = 31, mean age 9.1, SD = 0.7 years, 16 male; 5th - 7th graders: N = 30, mean age = 11.3, SD = 0.8 years, 14 male; college students: N = 30, mean age 20.2 years SD = 2.3, 19 male; and parents or guardians of the child participants: N = 30, mean age 40.6, SD = 6.8 years, 7 male). One child was excluded due to a computer crash, and one opted to quit. Out of the 151 participants, 6.6% identified as having More Than One Race, 1.3% as Asian, 5.3% as Black or African American, and 86.8% as White. Also, 1.3% identified as Hispanic or Latino, and 4.6% did not report it. Payment for families was $5 per 30 min per participant and a book for children, or partial course credit for college students. The study was approved by the local IRB at the University of Missouri, IRB Project Number 99-04-095, study title: The Development of Short-Term Memory for Speech Attributes.
Apparatus, Stimuli, and Procedure
All tasks were presented on a computer screen and completed in a sound-attenuated booth, except Raven’s progressive matrices which used physical stimuli and took place in a different quiet room. The task order was: Raven’s Matrices, the visual memory task, the Running Span task, and the Letter Span task.
Visual memory task.
We used a visual change detection memory task popularized by Luck and Vogel (1997), in which participants study a briefly-presented array of colored squares on each trial and, after a brief retention interval, were asked to judge whether a single probe item was part of the original array or not. In our procedure, however, participants sometimes saw a question mark in a period before the probe appeared, which signified that they were to assess how many of the array items were in their WM (the meta-memory judgment), before the probe appeared. This question mark or a sign indicating no such meta-memory judgment was surrounded by a masking field that was imposed in order to ensure that the procedure could not be completed using sensory memory (see Cowan et al., 2014).
Each array to be remembered included 5 colored squares. For the arrays, each color was selected without replacement from ten common, easily discriminable colors (black, white, red, blue, green, yellow, brown, cyan, purple, and dark-blue-green). Each colored square was 6 × 6 mm and presented at least 17.5 mm from the center of the screen, and at least 17.5 mm away from the center of any subsequently presented colored square. The squares were presented on a grey background, within an area measuring 74 mm wide × 56 mm high. The probe item was different for 50% of the trials, and the same for the other 50%.
Participants completed 4 practice trials and 128 experimental trials divided into four blocks to encourage breaks. Participants initiated each trial by pressing the SPACE key. A central fixation cross then appeared for 1000 ms, followed by an array of 5 colored squares for 500 ms. A blank screen appeared for 500 ms, followed by a visual mask screen for 4000 ms, consisting of squares at the same locations as in the to-be-remembered array. Each square in the masking array was multicolored, comprising 9 colors from the 10 possible, including the probe color. Visual masks were identical on a given trial but differed between trials.
During the mask screen, a large ‘?’ or an ‘X’ in the center of the screen told participants whether a storage judgment was required or not; it was required only with the question mark, which occurred on half of the trials. On trials in which a storage judgment was required, participants told the experimenter the number of colored squares for which they believed they remembered the colors. This verbal response had to be given during the 4000-ms mask screen interval, and if participants failed to respond within this timeframe, their response was recorded as 'absent'. Next, the memory probe item appeared in the center of the screen, until participants responded ‘same’ (present in the previous array) or ‘different’ (not in the array) using a button box with these two options.
Feedback was provided after each memory response, comprising information on the correct response (same or different), whether the answer was correct (conveyed with a line-drawn happy or sad face) and, for trials that included a meta-WM judgment, what that judgment had been, i.e., how many items were claimed to be remembered.
Auxiliary tasks.
The main task was supplemented by Ravens Progressive Matrices as a measure of intelligence and two working memory tasks known to correlate well with cognitive aptitudes (Cowan et al., 2005; Lépine et al., 2005). The Ravens task (Raven & Raven, 1998) is considered a measure of fluid reasoning or intelligence. Participants saw a pattern of images in which one section was missing. They chose a section that would complete the pattern from six or eight options. Parents or guardians did not complete this task because of logistic issues. Running span was adapted from Cowan et al. (2005). On every trial, participants heard a sequence of between 12 - 20 digitally compressed digits presented at a fast rate of 4/s. When the sequence ended participants were asked to repeat back as many numbers from the end of the list as possible, in the same order as they were presented. Since list length varied, participants could not predict when the list would end, preventing rehearsal. The response was right-justified so that the last digit entered by the participant was considered to be the recall of the final list item. These data were scored as mean items per list correct by serial position, for the last 7 positions. A letter span task was adapted from Lépine et al. (2005). Participants were presented with four letters (at a 1/s rate) followed by a digit. They were asked to say both letters and digits out loud but only needed to retain the digit for future recall. At the end of the list, participants had to repeat each of the digits in the presented order. Participants completed three trials at each list length (starting with 2 digits) and had to get at least one trial correct to advance to the next level or the task was discontinued. The score was the proportion of trials within a list length that yielded perfect accuracy on both tasks, added across list lengths.
Data Analysis
Estimations of working memory capacity (k).
Estimates of WM capacity, or k, are often obtained using a change-detection paradigm, in which participants are asked to study an array of items and then judge if a single probe item belongs to the original array or not. In a scenario with N to-be-remembered items followed by a single probe item, a participant would correctly discern that the probe item is not new if it matches an item held in WM. However, if a match is not detected, the participant must guess whether this is because the probe item is new or because it corresponds to a presented item that they failed to retain in WM. WM capacity (k) can be derived from rates of false alarms (incorrectly guessing ‘change’) and hits (correctly indicating ‘change’). See the online supplement for model details. We compared k values to meta-WM estimates from participants’ judgments of how many items they knew.
Inferential statistical approaches.
We analyzed the data using Bayesian model comparison, which involves comparison of the likelihood of specified models given the data. This approach yields an odds ratio, termed the Bayes Factor (BF10), which quantifies the evidence for supporting the specified model including a factor against the comparable model without that factor, the null model. Evidence for the null model over the stated model can be obtained by computing 1/BF10 (BF01) (Rouder et al., 2012). BF greater than 3 is considered ‘substantial’, between 10 and 30 ‘strong’, 30 – 100 ‘very strong’, and over 100 ‘decisive’ evidence (Wetzels & Wagenmakers, 2012). For further details see the online supplement. For descriptive purposes, we also present traditional statistics.
Results
Average k and Meta-WM
In this section, we examine the effects of injecting meta-WM judgments into the change-detection procedure. Then we examine the development of WM and meta-WM, and put them together to examine meta-WM accuracy.
Effects of the meta-judgment requirement.
First, we tested whether memory performance differed when a meta-judgment was or was not required (Age Group × Storage Judgement ANOVA). 329 trials were excluded due to participants’ failure to provide a storage estimate when prompted to do so (3.4 % of meta-judgment trials). There seemed to be more missing trials in younger children, and average WM performance on these trials appeared lower than those for which meta-memory judgments were accurately given (1st – 2nd Graders: 26 participants had 154 missing values, M = 0.48; 3rd – 4th graders: 21 participants had 76 missing values, M = 0.58; 5th – 7th graders: 15 participants had 65 missing values, M = 0.52; College Students: 12 participants had 21 missing values, M = 0.57; Parents or guardians: 8 participants had 13 missing values, M = 0.38).
While there was strong evidence for an age effect (BF10 = 5.25 × 1065, F(4,146) = 33.60, ηp2 = .48) on memory performance, there was evidence against the hypothesis that providing a storage judgment influenced memory performance (BF01 = 27.07, F(1,146) = 1.62, ηp2 = .011), and there was strong evidence against an interaction of these factors (BF01 = 2.16 × 104, F(4,146) = 0.40, ηp2 = .011), indicating that memory performance in all age groups was equally unaffected by providing the storage judgment (No Storage/Storage; 1st – 2nd Graders: M = 0.56, SD = 0.08 / M = 0.57, SD = 0.09; 3rd – 4th graders: M = 0.62, SD = 0.08 / M = 0.60, SD = 0.09; 5th – 7th graders: M = 0.66, SD = 0.08 / M = 0.64, SD = 0.06; College Students: M = 0.73, SD = 0.08 / 0.72, SD = 0.09; Parents or guardians: M = 0.73, SD = 0.08 / M = 0.72, SD = 0.08). Therefore, k-values for the capacity analyses below were obtained from all memory trials (i.e., with and without a storage judgment).
Age differences in WM (k) and meta-WM.
Testing the effect of Age Group on memory capacity (k), we observed strong evidence that k increased across age groups, BF10 = 9.12 × 1019, F(4,146) = 41.24, ηp2 = .53, similar to previous studies (see Table 1 for mean values). Next, we found no evidence that participants in different age groups differed in their meta-WM estimates, BF01 = 16.55, F(4, 146) = 0.69, ηp2 = .019. This is our key result in its simplest form; despite striking differences in capacity, meta-memory judgments tended to be overestimations and were unexpectedly comparable across age groups (see Figure 2).
Table 1.
Descriptive statistics of Working Memory capacity (k), Meta-memory k, and Meta-Memory Accuracy by Age Group
| Age Group | k | Meta-WM | Meta inaccuracy (absolute) |
Hit Rate | False Alarms | |
|---|---|---|---|---|---|---|
| Exp. 1 | 1st- 2nd Grade | 0.98 (0.8) | 3.1 (1.0) | 2.1 (1.3) | 0.63 (0.14) | 0.50 (0.11) |
| 3rd – 4th Grade | 1.6 (0.81) | 3.4 (1.2) | 1.9 (1.2) | 0.70 (0.14) | 0.47 (0.14) | |
| 5th – 7th Grade | 2.1 (0.71) | 3.2 (0.71) | 1.1 (0.86) | 0.70 (0.09) | 0.40 (0.10) | |
| College Students | 3.0 (0.68) | 3.3 (0.63) | 0.60 (0.55) | 0.73 (0.13) | 0.28 (0.083) | |
| Parents or guardians | 2.9 (0.67) | 3.3 (0.77) | 0.72 (0.64) | 0.76 (0.13) | 0.32 (0.099) | |
| Exp. 2 | 1st- 2nd Grade | 1.5 (1.03) | 4.4 (2.09) | 3.0 (2.45) | 0.71 (0.18) | 0.47 (0.16) |
| 3rd – 4th Grade | 2.2 (1.35) | 4.5 (2.15) | 2.4 (2.26) | 0.74 (0.16) | 0.38 (0.19) | |
| 5th – 7th Grade | 2.5 (1.17) | 3.8 (1.42) | 1.5 (1.76) | 0.75 (0.20) | 0.34 (0.20) | |
| College Students | 3.3 (1.34) | 4.2 (1.62) | 1.2 (1.41) | 0.83 (0.15) | 0.28 (0.20) |
Note. Values represent mean values and in parenthesis, standard deviations. Values from experiment 2 are averaged across set sizes 3, 6, and 9. Hit Rate = the proportion of correctly identified change trials. False Alarms = the proportion of no-change trials incorrectly identified as change trials.
Figure 2.
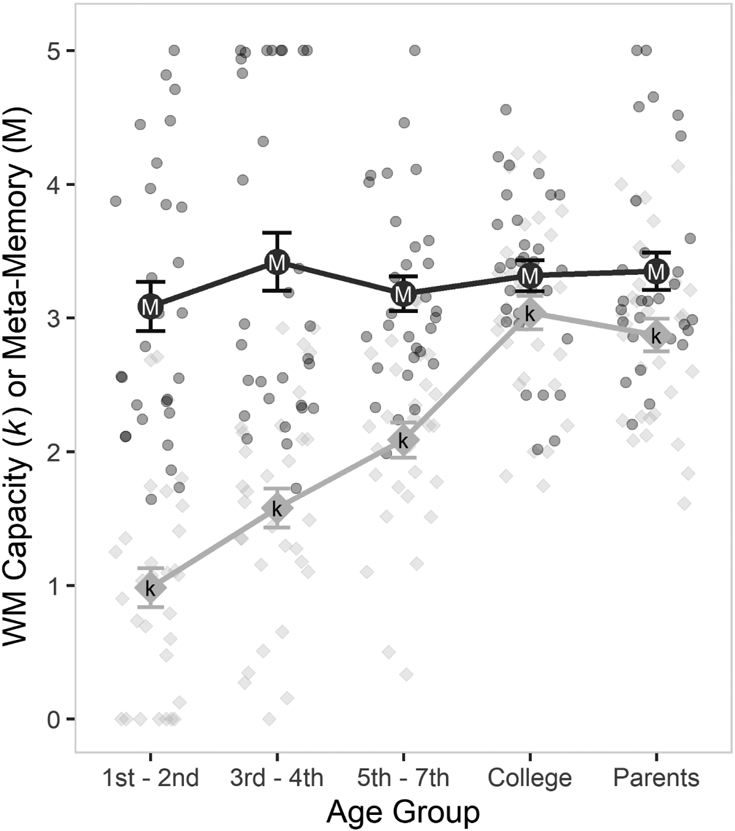
Experiment 1: Working Memory Capacity (k; represented by the diamonds) and meta-memory judgements (M; black circles), by Age Group. Lighter and smaller circles and triangles represent individual participants, and these values are jittered slightly to avoid overlap. Error bars represent the standard error of the mean.
We analyzed the proportions of hits and false alarms in the age groups to examine biases, and found that younger participants appeared to make more false alarm errors than adults (BF10 = 4.85 × 1011, F(4,146) = 22.65, ηp2 = .38), and fewer hits (BF10 = 22.65, F(4,146) = 4.75, ηp2 = .115, see Table 1). We also compared the error rates from same vs. different trials. Overall, there was an age effect (BF10 = 3.58 × 1013, F(4,146) = 34.54, ηp2 = .486), and condition effect (BF10 = 1.49 × 109, F(1,146) = 37.30, ηp2 = .203), and evidence for an interaction (BF10 = 5.85, F(4,146) = 2.71, ηp2 = .069), indicating that younger children were more prone to making false alarm errors (incorrectly saying there was a change) than failing to make a hit (i.e., failing to identify a change; see Figure 3).
Figure 3.
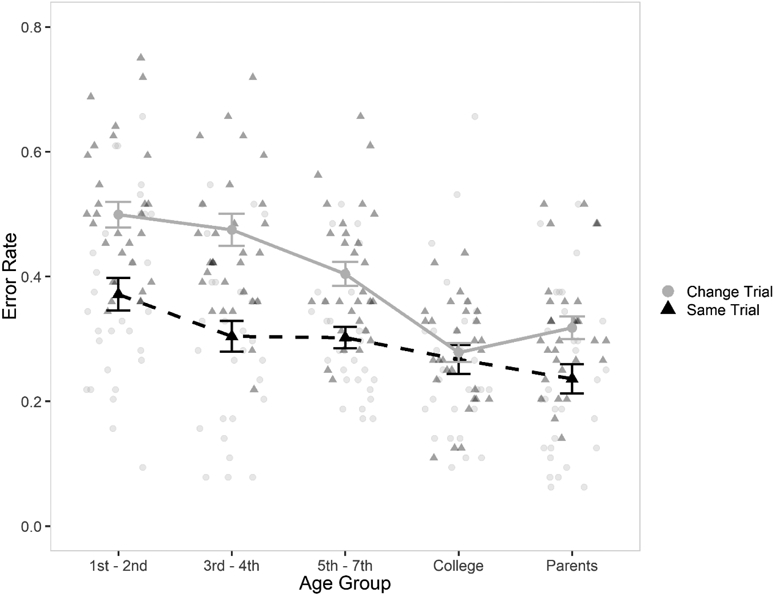
Experiment 1: Error Rate for Change Trials (False Alarm Rates, represented by the grey circles) and Same Trials (1 – Hit Rate, black triangles), by Age Group. Lighter and smaller circles and triangles represent individual participants, and these values are jittered slightly to avoid overlap. Error bars represent the standard error of the mean.
Development of Meta-WM accuracy.
Next, we focused on the differences between actual k and meta-WM estimates, i.e. meta-WM inaccuracy. We found strong evidence that the accuracy of meta-WM estimates (i.e., the absolute difference between an individual’s average k and their average meta-memory estimate) differed by age group, BF10 = 2.31 × 108, F(4,146) = 16.39, ηp2 = .310. As Figure 2 shows, younger children’s meta-memory estimates appeared less accurate, as these children seemed more prone to overestimate their memory capacity compared to older participants.
Meta-WM accuracy can also be conceptualized in proportional terms, as the absolute meta-WM inaccuracy divided by memory k. This measure is important because a developmental change in the absolute discrepancy (meta-WM - k) could occur even if k is always overestimated by a constant proportion. However, the proportional measure of meta-memory accuracy also differed by age group, BF10 = 8.94 × 102, F(4,138) = 7.32, ηp2 = .175, with more accurate meta-memory in older age groups1.
The Relationship Between Cognitive Ability and Meta-WM Accuracy
WM Capacity (k) and Meta-WM.
The relationship between meta-WM accuracy and k can be seen in Figure 4. We tested whether higher-capacity participants’ meta-WM judgments tended to be more accurate, and whether that effect differed between age groups, using a general linear model (generalTestBF), with age group and standardized k-values as predictors. We found strong evidence that age-standardized k-scores predicted age-standardized meta-memory accuracy (BF10 = 1.28 × 108) , but no evidence that this effect differed between age groups (age group × k interaction; BF01 = 78.51), indicating that being relatively high-k within ones age group was associated with better meta-memory accuracy, to similar extents across age. Similar results were found when using age-standardized raw difference scores (i.e., signed measure including whether inaccuracy came from under- or overestimating one’s memory), effect of k on meta-WM accuracy; BF10 = 1.29 × 1010, evidence against an interaction, BF01 = 366.26). We report frequentist correlations coefficients (Pearson’s r) between age-standardized k for the absolute and signed measures, respectively, in Table 4.
Figure 4.
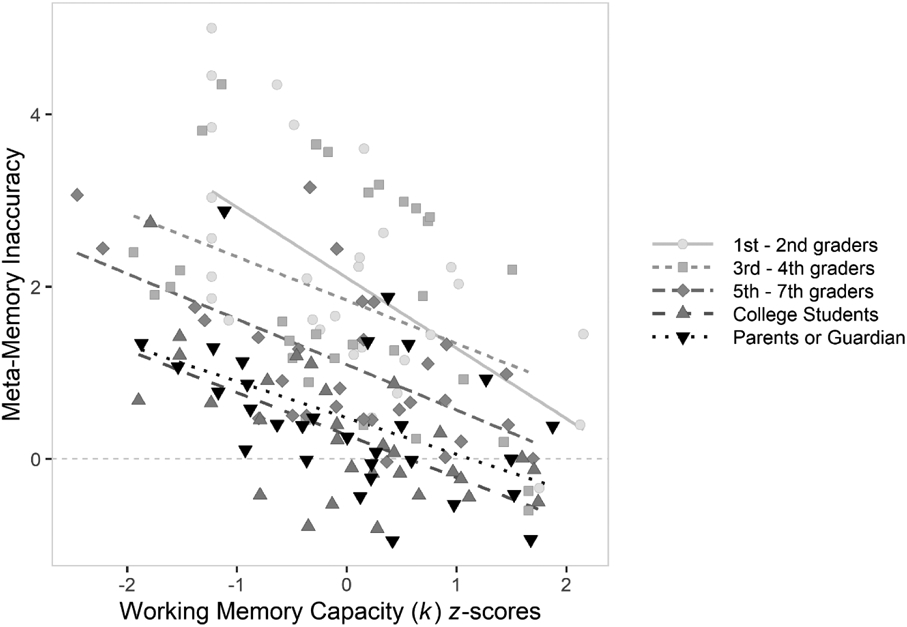
Experiment 1: Correlations between k (standardized within each age group) and meta-WM inaccuracy across age groups. The lines represent frequentist linear regression lines.
Table 4.
Correlations of age-standardized scores: Working Memory capacity (k), Meta-Memory Inaccuracy by Age Group, and Auxiliary Measures
| Running Span |
Letter Span | Raven’s | k | Meta inaccuracy (absolute) |
|
|---|---|---|---|---|---|
| Experiment 1 | |||||
| Running Span | – | ||||
| Letter Span | .14 | – | |||
| Raven’s | .26** | .27** | – | ||
| k | .26** | .37*** | .18 | – | |
| Meta inaccuracy (absolute) | −.16 | −.19* | −.20* | −.51*** | – |
| Meta inaccuracy (raw) | −.14 | −.20* | −.19* | −.56*** | .91*** |
| Experiment 2 | |||||
| Running Span | – | ||||
| Letter Span | .26* | – | |||
| Raven’s | .44*** | .41*** | – | ||
| k | .33** | .37*** | .27* | – | |
| Meta inaccuracy (absolute) | −.19 | −.21* | −.19 | −.69*** | – |
| Meta inaccuracy (raw) | −.22* | −.21* | −.19 | −.72*** | .98*** |
Note. Correlations (Pearson’s r) between age-standardized Working Memory capacity (k), meta-memory inaccuracy, and auxiliary scores.
p < 0.05
p < 0.01
p < 0.001. Meta inaccuracy (absolute) measures the absolute distance between each participant’s meta-WM rating and their actual k, regardless of whether inaccuracy was driven by under- or overestimating one’s memory. Meta inaccuracy (raw) accounts for the direction of the inaccuracy, i.e., whether inaccuracy was driven by under- or overestimation).
Auxiliary measures of cognitive ability and meta-WM.
Table 2 shows mean values and standard deviations for all auxiliary measures (Letter Memory Span, Running Memory Span, and Raven’s Matrices). We observed strong evidence that performance on all auxiliary tasks varied by age groups (Letter Span, BF10 = 9.32 × 1015, F(4,146) = 31.69, ηp2 = .465; Running Span, BF10 = 1.55 × 106; F(4,146) = 12.58, ηp2 = .256; Ravens Matrices, BF10 = 2.39 × 1014, F(3,109) = 30.99, ηp2 = .46, completed by all participants except the parents or guardians).
Table 2.
Descriptive statistics of Auxiliary tasks by Age Group
| Age Group | Ravens Matrices | Running Span | Letter Span | |
|---|---|---|---|---|
| Experiment 1 | 1st – 2nd Grade | 26.7 (9.48) | 1.91 (0.73) | 0.60 (0.60) |
| 3rd – 4th Grade | 32.6 (10.1) | 2.22 (0.81) | 1.17 (0.58) | |
| 5th – 7th Grade | 39.5 (7.38) | 2.66 (0.95) | 1.86 (1.04) | |
| College Students | 49.1 (6.41) | 3.13 (0.71) | 2.61 (0.94) | |
| Parents or guardians | - | 2.90 (0.62) | 2.40 (0.85) | |
| Experiment 2 | 1st – 2nd Grade | 36.4 (6.22) | 1.76 (0.82) | 0.85 (0.66) |
| 3rd – 4th Grade | 40.5 (6.86) | 2.23 (0.79) | 1.67 (0.87) | |
| 5th – 7th Grade | 41.8 (7.80) | 2.20 (0.92) | 1.96 (0.85) | |
| College Students | 53.0 (4.15) | 3.21 (0.59) | 3.37 (0.83) |
Note. Values represent mean values and in parenthesis, standard deviations.
To account for age differences, we standardized performance on the auxiliary tasks within each age group. Standardized letter span performance predicted meta-memory accuracy (BF10 = 3.42), but there was no evidence for an interaction with age group (BF01 = 100.61). We observed inconclusive evidence that standardized running span performance predicted meta-memory accuracy (BF10 = 1.90), and against it differing between the age groups (age group × running span interaction; BF01 = 2.43). Finally, we observed weak evidence that standardized Raven’s Matrices performance predicted meta-WM accuracy (BF10 = 2.81), and no evidence for an age group × Raven’s score interaction; BF01 = 20.26).
Do Meta-WM Ratings Predict Trial-level Memory Accuracy?
Last, we tested whether participants’ meta-memory judgments predicted memory performance on a given trial in the different age groups. See Figure 5 for memory performance by meta-memory rating, in each age group. We explored the relationship between age group, meta-memory ratings, and trial accuracy. We found no clear evidence for a main effect of meta-memory (BF01 = 6.82) or age group (BF01 = 11.74) on accuracy, but evidence for their interaction (BF10 = 5.08).
Figure 5.

Experiment 1: The proportion of responses for each meta-memory rating (grey histogram), and proportion correct accuracy for each meta-memory rating (black triangles), for each age group. Error bars represent the standard error of the mean.
In the three groups of child participants, meta-memory judgments did not appear to predict memory performance (1st – 2nd graders: BF01 = 18.60, 3rd – 4th graders: BF01 = 18.64, 5th – 7th graders: BF01 = 6.27). In the young adults however, we observed some evidence for an effect (BF10 = 13.25), as higher meta-memory judgments appeared associated with more accurate responses, as can be observed in Figure 5, which shows the mean performance for every value of meta-memory judgment. For the parents or guardians, the evidence for such an effect was inconclusive (BF01 = 1.01).
Discussion
Experiment 1 indicated that younger children have trouble accurately estimating their WM capacity. All participants’ estimated meta-WM was in line with the theoretical limit of adult WM (about three items; Cowan, 2001; our observed mean meta WM scores were between 3.1 and 3.4, see Table 1). Due to capacity differences, this was closer to actual capacity in adults than in children. Additional results indicated some increased ability of more capable participants to discern their own ability levels. Within individuals, only young adults appeared capable of having insight into their performance on a trial-by-trial basis.
The reason why meta-WM judgments are comparable across age groups is unclear. It could be that, as explained in the introduction, younger participants are more affected by factors of which they are unaware. According to that hypothesis, meta-WM reflects an actual capacity as it exists in a hypothetical state before some detrimental factors that are inaccessible to awareness interfere with performance. As one such example, children could be more susceptible to memory decay during the retention interval (e.g., Towse et al., 1998) after the meta-WM judgment, which might exacerbate their meta-memory discrepancies. To explore this, in Experiment 2, participants had 2000 ms to provide their meta-memory response in half of the trials, compared to trials with an additional 2000 ms delay.
Participants at some or all ages might have been biased towards using the middle option, suggesting an error of central tendency (Hollingworth, 1910). This phenomenon has been observed for responses to Likert scale questionnaires (Klopfer & Madden, 1980, see also Cowan & Morse, 1986; Hellström, 1985). Using the middle option or using all response options equally, could have produced an average meta-WM of about 3.
To assess the contrasting explanations, in Experiment 2 we replicated this study, including a wider range of array set sizes (3, 6, and 9 items). If meta-WM judgments reflect a stable judgment not dependent on the exact experimental context then, once again, we should find meta-WM values fixed at around 3 in all age groups. However, if participants in an age group provide meta-WM judgments at the center of the response range or distributed throughout the range, then these judgments should increase as a function of set size.
Experiment 2
Methods
Participants
The sample size was limited by practical constraints; see the online supplement for indications that it was sufficient for the present purposes. Age groups and grade levels were similar to Experiment 1. Six participants in the youngest group were excluded for failing to give storage responses (between 0 and 39 valid storage trials). Five participants in the youngest group and 1 in the second youngest did not complete the meta-WM task due to stated boredom or fatigue. The final sample included: 1st- 2nd Graders; (N = 20, mean age = 6.9, years, 8 female), 3rd - 4th graders; (N = 19, mean age = 8.8 years, 11 female), 5th-7th graders (N = 16, mean age = 11.3 years, 5 female), and College Students (N = 30, mean age = 23.5 years, 24 female), however no parents or guardians were included because of practical constraints. In all, 12.9% of participants identified as having More Than One Race, 11.8% as Asian, 1.1% as Black or African American, 1.1% as Other, and 72.9% as White or European; 8.2% identified as Hispanic or Latino and this was unknown for another 9.4%. The study was approved by the university’s IRB ([blinded]).
Apparatus, Stimuli, and Procedure
Equipment and task order were the same as in Experiment 1. So were other methodological details, except where differences are noted. Unlike Experiment 1, which always had 5 items and an interval of 4000 ms after the masking screen, we manipulated the array set size (3, 6, or 9 items), and the time between the memory array and the response (participants always had 2000 ms to make the meta-judgment, sometimes followed by an additional 2000 ms delay), resulting in 6 different experimental blocks. Each block contained 2 practice and 24 experimental trials. The block order was randomized with the constraint that the two blocks of a specific set size were adjacent, and half of the participants always started with no additional delay (2000 ms meta-judgement), the other half with the delay (2000 ms meta-judgement + 2000 ms delay). Also, unlike Experiment 1, in which half of the trials required no meta-storage judgment, in this experiment all trials required a meta-storage judgment, so as to yield enough data for three array sizes and two interval durations. The Letter and Running span tasks were as in Experiment 1 but a computerized version of Raven’s Progressive Matrices was used.
Results
New topics compared to Experiment 1 include effects of the retention interval and the possibility of central tendency responding. After that, as in Experiment 1, we examine age differences in WM (k) and meta-WM, meta-WM accuracy, its relation to k and auxiliary cognitive tasks, and trial-by-trial tuning of meta-WM.
The Effect of Retention Interval
First, we tested the effect of retention interval (2000 vs. 4000 ms) on memory accuracy in the different age groups in a Bayesian ANOVA with Age Groups (4 levels) between participants and two within-participant factors: Retention Intervals (2 levels) and Set Sizes (3 levels). We found no clear evidence that the retention interval manipulation influenced memory accuracy (BF01 = 4.05) and, importantly, no evidence that it influenced participants in different age groups differently (BF01 = 344.95), in any of the three Set Sizes. Moreover, there was no evidence that the retention interval influenced meta-memory judgments (BF01 = 11.30), nor that it influenced meta-memory judgements differently in the different age groups BF01 = 1.35 × 103. Therefore, for k estimates, we combined data across retention intervals.
Central Tendency Responding?
We explored whether the results of Experiment 1 might be driven by a bias towards selecting the middle value, or simply selecting equally across all options. As Figure 6 shows, meta-WM ratings did not cluster around these central values (indicated by dashed line). Moreover, the distributions of meta-storage ratings did not indicate that results were driven by a preference for the middle option or for a flat response distribution (see Figure 9).
Figure 6.
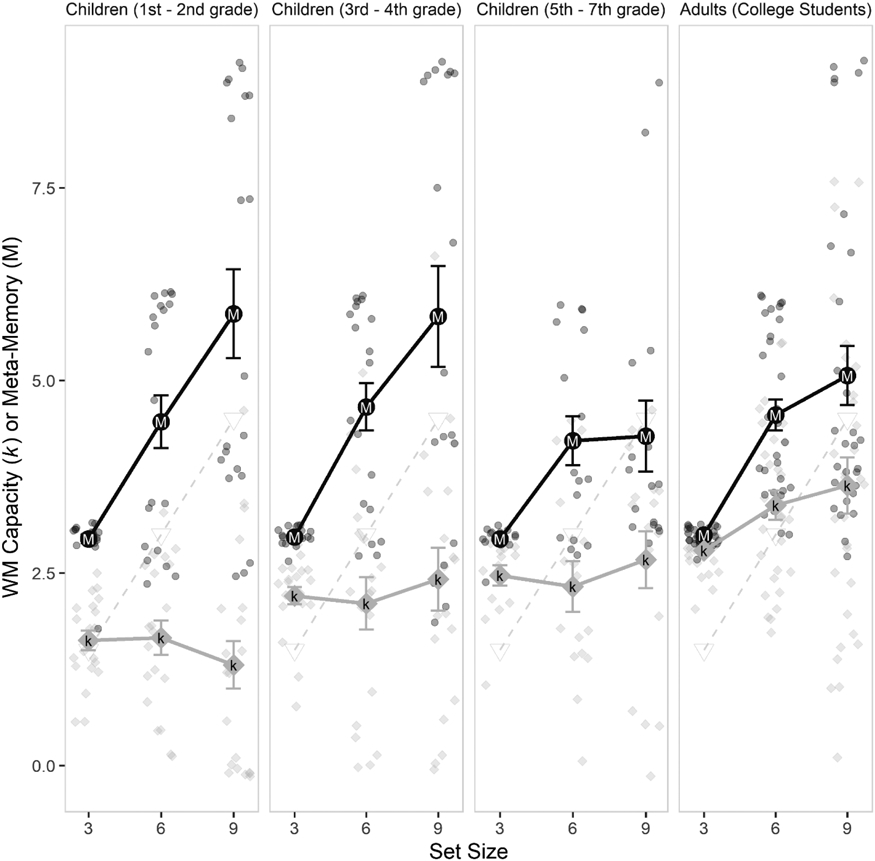
Experiment 2: Meta-WM judgements (M; black circles) and k (k; grey diamonds) across the set-sizes for each age group. Lighter and smaller circles and triangles represent individual participants, and these values are jittered slightly to avoid overlap. The white triangles and dashed line illustrate hypothetical middle-group responding. Error bars represent the standard error of the mean.
Figure 9.
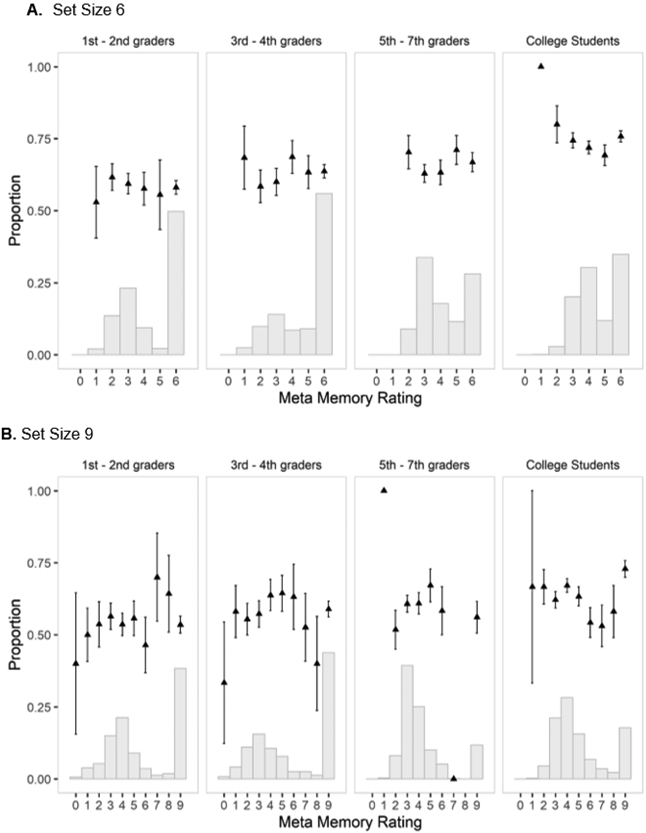
Experiment 2: The proportion of responses for each meta-memory rating (grey histogram), and proportion correct accuracy for each meta-memory rating (black triangles), for each age group. Error bars represent the standard error of the mean. Panel A shows these distributions across Set Size 6 trials, Panel B across Set Size 9 trials. Set Size 3 is not visualized here because the majority of meta-ratings was 3 items.
Age Differences in k and Meta-WM
For these analyses, one k and one meta-WM value was calculated for each participant, for each of the set sizes (3, 6, or 9 items). For the following analyses, we also tested the effect of set size (3, 6, or 9 items) on k and meta-WM estimates, and whether any age group effects interacted with set size. See Figure 6 and Table 3 for k estimates for each individual, by age group and set size. We found strong evidence of age effects on mean k estimates, BF10 = 3.03 × 1011, F(3, 81) = 16.23, ηp2 = .375, but no evidence for an effect of set size, BF01 = 10.52, F(1.65, 133.85) = 1.00, ηp2 = .012, and no evidence for an interaction of age group and set size, BF01 = 7.73, F(4.96, 133.85) = 1.55, ηp2 = .054.
Table 3.
Experiment 2. Descriptive statistics of Meta-Memory Accuracy by Age Group and Set Size
| Age Group | Set Size | k | Meta-WM | Meta accuracy (absolute) |
Hit Rate | False Alarms |
|---|---|---|---|---|---|---|
| 1st – 2nd Grade | 3 | 1.6 (0.57) | 2.9 (0.24) | 1.3 (0.59) | .85 (0.11) | .38 (0.14) |
| 6 | 1.7 (1.0) | 4.5 (1.50) | 2.8 (1.9) | .65 (0.14) | .48 (0.15) | |
| 9 | 1.3 (1.4) | 5.9 (2.58) | 4.7 (2.96) | .61 (0.17) | .54 (0.16) | |
| 3rd – 4th Grade | 3 | 2.2 (0.48) | 3.0 (0.096) | 0.76 (0.50) | .88 (0.083) | .23 (0.14) |
| 6 | 2.1 (1.5) | 4.7 (1.34) | 2.6 (1.66) | .71 (0.14) | .47 (0.18) | |
| 9 | 2.4 (1.8) | 5.8 (2.86) | 3.8 (2.82) | .62 (0.14) | .45 (0.15) | |
| 5th – 7th Grade | 3 | 2.5 (0.53) | 2.9 (0.19) | 0.47 (0.38) | .87 (0.14) | .14 (0.12) |
| 6 | 2.3 (1.3) | 4.2 (1.27) | 2.2 (1.56) | .73 (0.19) | .43 (0.16) | |
| 9 | 2.7 (1.5) | 4.3 (1.84) | 1.9 (2.31) | .65 (0.23) | .45 (0.14) | |
| College Students | 3 | 2.8 (0.22) | 3.0 (0.039) | 0.20 (0.22) | .96 (0.051) | .065 (0.064) |
| 6 | 3.4 (1.1) | 4.6 (1.10) | 1.5 (1.24) | .82 (0.12) | .35 (0.14) | |
| 9 | 3.6 (2.0) | 5.1 (2.10) | 2.01 (1.65) | .72 (0.14) | .43 (0.17) |
Note. Values represent mean values and in parenthesis, standard deviations.
Next, we explored age group differences in meta-WM and observed evidence against age differences, BF01 = 4.47, F(3, 81) = 1.27, ηp2 = .055, a strong effect of set size, BF10 = 1.38 × 1015, F(1.26, 101.69) = 71.27, ηp2 = .468, and evidence against an interaction, BF01 = 8.79, F(3.77, 101.69) = 1.90, ηp2 = .066, indicating that that meta-WM ratings increased with set-size to similar extents across age groups (see Figure 6).
The rate of false alarm errors differed between age groups, BF10 = 4.03 × 109, F(3, 81) = 11.19, ηp2 = .293, and set size, BF10 = 9.67 × 1024, F(1.89, 152.76) = 145.90, ηp2 = .643, but evidence against an interaction, BF01 = 5.91, F(5.66, 152.76) = 5.59, ηp2 = .171. Similarly, the hit rate also differed by age group, BF10 = 1.75 × 105, F(3, 81) = 7.01, ηp2 = .206, and set size BF10 = 1.73 × 1021, F(1.99, 161.32) = 106.69, ηp2 = .568, but there was no interaction, BF01 = 41.31, F(5.97, 161.32) = 0.53, ηp2 = .019. We also compared the error rates from same vs. different trials. Overall, there was an age effect (BF10 = 3.50 × 1016, F(3,81) = 28.48, ηp2 = .513), and trial type effect (BF10 = 1.12 × 1018, F(1,81) = 37.40, ηp2 = .316), with inconclusive evidence for a three-way interaction between age group, trial type, and set size (BF10 = 1.27, F(5.85,157.83) = 3.19, ηp2 = .106, p = .006; see Figure 7).
Figure 7.
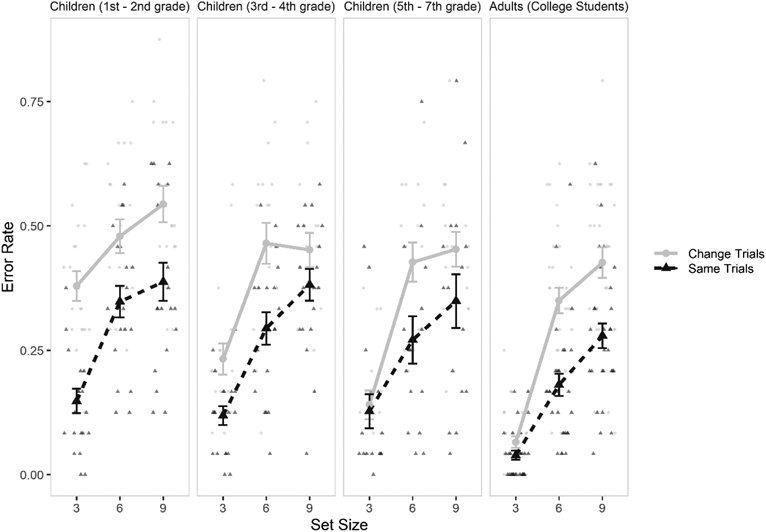
Experiment 2: Error Rate for Change Trials (False Alarm Rates, represented by the grey circles) and Same Trials (1 – Hit Rate, black triangles), by Age Group and Set Size. Lighter and smaller circles and triangles represent individual participants, and these values are jittered slightly to avoid overlap. Error bars represent the standard error of the mean.
Development of Meta-k Accuracy
As in Experiment 1, we found strong evidence that the absolute inaccuracy of meta-WM estimates (i.e., the absolute difference between an individual’s average k and their average meta-memory estimate) differed by age group, BF10 = 3.10 × 106, F(3, 81) = 9.23, ηp2 = .255. There was strong evidence of a set size effect on meta-inaccuracy, BF10 = 1.22 × 1014, F(1.60, 129.94) = 63.01, ηp2 = .438, and weak evidence against an interaction, BF01 = 2.04, F(4.81, 129.94) = 2.39, ηp2 = .097. See Figure 6 for k and meta-WM plotted across set sizes.
Finally, we used a proportional measure of meta-memory accuracy2, which also differed by age group, BF10 = 38.89, F(3, 65) = 3.48, ηp2 = .138, and by set size, BF10 = 49.05, F(1.65, 107.21) = 6.84, ηp2 = .095, but without an interaction (BF01 = 22.69, F(4.95, 107.21) = 0.90, ηp2 = .040). Like in the first experiment, younger children’s meta-memory estimates appeared less accurate, as they appeared to overestimate their memory capacity more.
The Relationship Between Cognitive Ability and Meta-WM
Working memory capacity (k) and meta-WM.
The relationship between meta-WM accuracy and k can be seen in Figure 8. We tested whether higher-capacity participants’ meta-WM judgments tended to be more accurate, and whether that effect differed between age groups, using a general linear model (generalTestBF), with age group and standardized k-values as predictors. We found strong evidence age-standardized k-scores predicted age-standardized meta-memory accuracy (BF10 = 1.28 × 108), but no evidence that this effect differed between age groups (BF01 = 78.51), indicating that being relatively high-k within one’s age group was associated with better meta-memory accuracy, across age. Similar results were found when using age-standardized raw difference scores (i.e., signed measure including whether inaccuracy came from under- or overestimating one's memory), effect of k on meta-WM accuracy; BF10 = 1.29 × 1010, evidence against an interaction, BF01 = 366.26). We report frequentist correlations coefficients (Pearson’s r) between age-standardized k for the absolute and signed measures, respectively, in Table 4.
Figure 8.
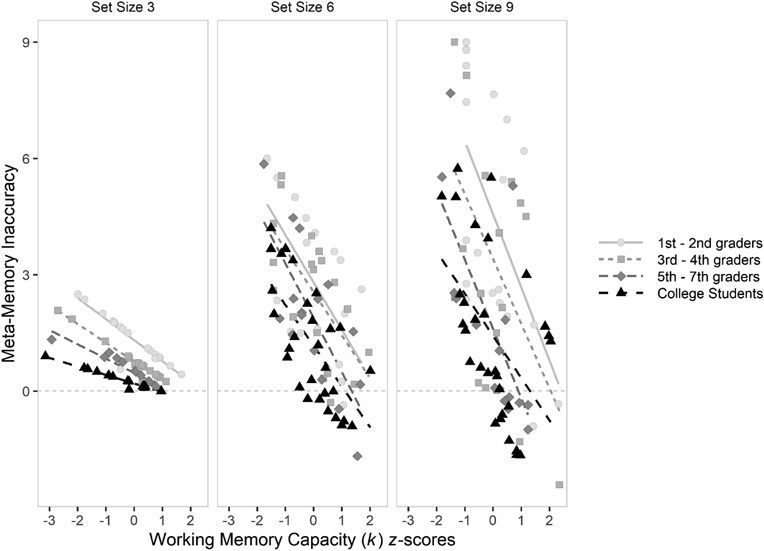
Experiment 2: Correlations between k (standardized within each age group) and meta-WM inaccuracy across age groups and set sizes. The lines represent frequentist linear regression lines.
Auxiliary measures of cognitive ability and meta-WM.
We observed strong evidence that letter span varied by age group (BF10 = 6933 × 1013, F(3, 81) = 42.90, ηp2 = .614), as well as running span (BF10 = 9.63 × 105, F(3, 81) = 16.52, ηp2 = .380), and Ravens Matrices (BF10 = 7.00 × 1011, F(3, 81) = 35.02, ηp2 = .565). See Table 2 for mean values and standard deviations for all auxiliary measures. Each participant had three meta-WM inaccuracy scores (one for each set size), and participant ID was included as a random effect in the model. Standardized letter span performance seemed to predict standardized meta-WM inaccuracy (BF10 = 7.39), but there was no evidence for an interaction with age group (BF01 = 62.70), indicating that this effect was similar across developmental stages. Similarly, standardized running span performance predicted meta-memory accuracy (BF10 = 5.00), to similar extents across age groups (age group × running span interaction; BF01 = 14.40). Finally, we observed evidence that standardized Raven’s Matrices performance predicted meta-WM accuracy (BF10 = 4.43), and evidence against an age group × Raven’s score interaction; BF01 = 12.54). See Table 4 for frequentist correlations coefficients (Pearson’s r) between these age-standardized measures and meta-memory inaccuracy.
Do Meta-WM Ratings Predict Trial-level Memory Accuracy?
We used a similar Bayesian approach as in Experiment 1, to explore whether meta-WM judgments predicted performance within individual trials. There is insufficient variation in the data at set size 3 for the analysis be meaningful (Table 3). We excluded data from 7.6% of trials in which participants failed to judge meta-WM within the timeframe, and one trial with a meta-WM judgment that exceeded the presented items (6). There seemed to be more missing trials in younger children, and average WM performance on these trials appeared lower than those for which meta-memory judgments were accurately given (1st – 2nd Graders: 20 participants had 364 missing values, M = .58; 3rd – 4th graders: 18 participants had 332 missing values, M = .57; 5th – 7th graders: 16 participants had 130 missing values, M = .60; College Students: 20 participants had 102 missing values, M = .64).
The distribution of responses and the average accuracy as a function of meta-WM judgments for larger set sizes are presented in Figure 9. We found no clear evidence for a main effect of meta-WM (BF01 = 17.12) but some evidence of an age group effect (BF10 = 3.41), and very strong evidence for a Set Size effect (BF10 = 1.21 × 106). In contrast to Experiment 1, we observed evidence against an age group × meta-memory judgment interaction (BF01 = 13.59). To follow up on this discrepancy, we explored the relationship between meta-memory ratings and accuracy at Set Size 6, for the young adults – the condition that was most similar to Experiment 1 – but again, we observed evidence against a meta-memory effect (BF01 = 16.08; see Figure 9).
Discussion
As in Experiment 1, the accuracy of meta-WM differed between age groups; in general, older participants were more accurate. As illustrated in Figure 6, while meta-WM estimates did increase at higher set sizes, there was no clear evidence for middle-ground responding. The most common response was often the highest estimate (see Figure 9). Moreover, there was no effect of retention interval (2000 vs 4000 ms) on memory accuracy in any age group.
Participants with higher WM (k) values tended to have better meta-WM accuracy, in all age groups. Those with better aptitudes as measured by auxiliary cognitive tasks also seemed to have better meta-WM accuracy. Finally, participants’ meta-judgments in this study did not seem to predict memory on a trial-to-trial basis – not even in young adults, for whom moderate evidence for such an effect was observed in Experiment 1.
General Discussion
Meta-WM ability appears linked to how children remember and perform long-term memory tasks (e.g., Brown, 1978; Schneider & Pressley, 2013). Here, we explored the development of WM meta-memory ability, which could be a crucial factor mediating the impact of WM capacity limitations in real-world settings, if awareness of one’s memory limitations promotes deliberate improvement of encoding, maintenance, or retrieval strategies. Average meta-WM ratings were similar across age groups (generally around 3 – 4 items), despite poorer actual capacity in younger children. Hence, younger children overestimated their WM capacity more than older children and adults. Moreover, children’s greater inaccuracy did not seem driven by greater difficulty generating a meta-memory judgment, or the relatively long retention interval. These results did not appear to be an artifact of 'middle-ground responding' in which the meta-WM judgment would be made in the middle of the response range. We used a range of set sizes in Experiment 2 and observed a similar age effect on meta-WM accuracy as in Experiment 1, without indications of middle-ground responding. Accurate meta-WM also appeared associated with high cognitive ability, to similar extents in all age groups. Finally, we found some evidence that meta-WM ratings predicted trial-level memory performance in young adults, in Experiment 1 only.
We discuss the theoretical implications of these results in two main parts. First, we examine the development of meta-WM accuracy and its relation to cognitive ability and, second, we contemplate why we found only limited trial-by-trial tuning of meta-WM.
Theoretical Implications of the Development of Meta-WM Accuracy
It seems likely that developmental processes and individual differences in meta-WM in both children and adults have much in common. The kinds of differences between individuals that can be attributed to developmental growth are similar to the kinds of differences that can be attributed to individual differences in cognitive aptitudes. Thus, children’s meta-WM accuracy appears to improve across development but never reaches a point of complete realism in most individuals; mean meta-WM still exceeded mean WM capacity (k) in adults.
Individual differences in maturation and in its endpoint both relate to our detailed findings. As hypothesized, meta-WM inaccuracy, the difference between actual and perceived memory capacity, was higher in younger children. This result extends previous evidence that meta-memory abilities improve substantially during middle childhood (DeMarie & Ferron, 2003; Kreutzer et al., 1975). Also as hypothesized, meta-WM accuracy correlated with performance on other measures of cognitive ability (memory capacity (k), WM Running and Letter Span, and Raven’s Matrices). This development may occur for several different reasons, which we now discuss.
Limits in a Resource Common to WM and meta-WM?
Limits in a common resource used in both WM and meta-WM task performance could lead to inaccuracy of meta-WM in either direction, as discussed in the introduction. The finding that younger children overestimated capacity more rules out the possibility that more items in WM go unnoticed in younger children. Instead, the resources needed to hold items in WM theoretically could also be needed to judge one's performance and hold in check a natural tendency to overestimate one's own abilities. Young children presumably would have fewer of these resources. However, in Experiment 1, some trials had no meta-WM judgment task and performing meta-WM judgments did not appear to tax WM. Therefore, the k – meta-WM correlation cannot easily be attributed to a resource shared by memory and meta-WM.
Limits in Knowledge About Memory Processes?
As documented in the introduction, the developmental literature on meta-memory suggests that children do not understand their own long-term memory and tend to think they will not forget (e.g., Kreutzer et al., 1975; Koriat & Helstrup, 2007). It seems likely that similar processes apply to WM and could account for the greater discrepancy between WM and meta-WM in younger children. It could also account for the relation between k and our auxiliary tasks as well as meta-WM.
The conceptual difficulty in children may be an extreme version of what persists in many adults, an overestimation of abilities sometimes known as the Dunning-Kruger effect (Kruger & Dunning, 1999; Ehrlinger et al., 2008). In that effect, participants in a task who have inadequate knowledge to do well at the task also have inadequate knowledge to realize that they are not doing well, which tends to occur when it is the same kind of knowledge. According to one interpretation of that effect consistent with our data, it could occur through a combination of the imprecision in meta-judgments combined with people generally overestimating their ability; this combination of tendencies leads to more overestimation in less-capable (including younger) participants (Gignac & Zajenkowski, 2020). Participants yielding lower ratings (more common in younger children) will also have the smallest discrepancy between k and meta-WM, but it might not reflect poor meta-WM per se.
Further thought could be given to what kinds of knowledge younger children especially lack that would be needed for good performance in WM and meta-WM tasks. Wellman and Johnson (1979) found that children’s ability to correctly use mental verbs such as ‘remembering’ and ‘forgetting’ was very limited (see also Johnson & Wellman, 1980; Lockl & Schneider, 2006, cf. Astington & Olson, 1990; Schwanenflugel et al., 1994). Interestingly, though, recent long-term memory research indicates that implicit metacognitive memory processes operate in children even younger than those in our sample. For instance, 3.5-year-old children more often declined to respond to items for which they displayed worse memory performance in a subsequent test (Balcomb & Gerken, 2008), and exhibited pupil dilation when viewing correctly remembered as opposed to forgotten items (Paulus et al., 2013), suggesting that implicit metacognitive abilities might precede the development of explicit metacognitive knowledge.
Similarly, participants may differ in their interpretation of the instruction to report how many items they thought they remembered. The instruction could be interpreted either as ‘how many items do you think you will remember sufficiently well to perform the memory task’, or ‘how many items did you initially encode’. Perhaps some young children and participants who vastly overestimated capacity applied the latter interpretation. Indeed, some children always judged that they remembered a number of items equal to the set size, whereas most (not all) adults provided more moderate estimates at higher set sizes (Supplement, Figure S1). It is difficult to determine whether such participants overestimated memory capacity or misunderstood the task. The ability to introspect on the contents of WM and the ability to understand the instruction to introspect may be closely linked.
The number of seen versus successfully remembered items may correspond to the number of items held in visual sensory memory (Sligte et al., 2008), as opposed to in visual WM. Visual sensory memory is thought to be a high-capacity memory store in which items are overwritten by a new display of similar items (Makovski et al., 2008; Pinto et al., 2013), distinguishing it from WM, which is comparatively low-capacity, but not easily overwritten (Baddeley & Hitch, 1974; Durstewitz et al., 2000; Pinto et al., 2013). Some studies suggest that adults could subjectively evaluate their access to items in both visual sensory memory and WM (Vandenbroucke et al., 2014) but young children might more often count sensory storage images in their meta-WM judgments even if these will be unavailable at test time.
A final instance of poor knowledge use is an inability to implement task feedback appropriately. Levin et al. (1977) found that 6-year-olds failed to use feedback regarding their long-term memory performance to adjust their exaggerated estimates of how many items they would remember in a future, similar task. In our design, the correct interpretation of feedback required understanding that around half of the trials would be correct due to random guessing. A better understanding of how the performance feedback related to memory capacity in older participants likely would boost their meta-WM accuracy.
Inability to Use Some Representations Initially in WM?
Despite children’s comparatively poor WM performance, their meta-WM ratings were indistinguishable from those of adult participants. Curiously, the meta-WM ratings were often similar to the typical adult 3 – 4 item WM capacity limit (Adam et al., 2017; Cowan, 2001; Luck & Vogel, 1997). Perhaps this common, age-independent intuition of remembering 3 – 4 items reflects a general limit of the human information processing system. If so, the discrepancy between this estimate and children’s performance might be caused by children’s inability to use this information appropriately during the memory task. Some research suggests that even 18-month old infants may remember around 3 objects when tested using simple, infant-appropriate WM tasks (e.g., Ross-Sheehy et al., 2003; Zosh & Feigenson, 2015). Children might initially remember items but forget them during the course of the trial, because of interference from the visual masks or the memory probe item (cf. Woodman & Luck, 2003). Their meta-ratings may not take into account that forgetting. Alternatively, children may think they know an item because they know something about it, even if they have not encoded the critical, color information needed to carry out the memory test.
Compliance to Task demands?
Child participants’ inflated meta-memory ratings might be influenced by demand characteristics, if they believe that good memory stems from trying hard (see Kurtz & Weinert, 1989). Then, a wish to appear compliant or impress the experimenter may inflate ratings. Younger participants may also fail to differentiate between their wishes and their expectations for their task performance (see Schneider, 1998). Similarly, their ratings may reflect general (over)confidence in their abilities – potentially varying across developmental stages, but disconnected from actual capacity as measured in our task.
Potential Mechanisms of meta-WM Inaccuracy: Summary Remarks.
We have suggested a number of potential reasons for developmental and individual differences in meta-WM accuracy. These influences are by no means mutually exclusive. We expect that all of them are worthwhile bases for future investigations. Interestingly, even though adults' meta-WM was less inflated than that of young children, adults still, on average, tended to overestimate their capacity. This is aligned with research suggesting that adults have a positive illusory bias in their perception of themselves in various domains (e.g., Robins & Beer, 2001). Understanding the reasons behind adults' overestimation tendencies may provide insight into why meta-WM increases across childhood.
Why Are Meta-WM Ratings Not More Consistently Tuned to Trial-level WM?
Finally, we investigated trial-to-trial variation in meta-memory ratings in relation to trial-level performance. Our hypothesis was that if participants’ meta-memory estimates were accurate, their memory performance should be better on trials in which they estimated remembering more, rather than fewer, items. We were also interested in whether the potential predictiveness of meta-judgments increased with age. We observed some evidence that college-age participants’ meta-memory ratings predicted performance in Experiment 1, in which the set size was always 5 items. These results are similar to those of Cowan et al. (2016). They also fit with suggestions that the mental workspace used to remember arrays is open to some degree of conscious introspection, and that the attention system is used for retention of information (e.g., Barrouillet et al., 2011; Cowan, 1995, 2001; Cowan et al., 2014; Oberauer, 2013). However, the evidence was rather weak, not observed in other age groups, and absent in Experiment 2. There are several possible explanations for the difference between experiments in this regard. First, it may be more difficult to introspect when the number of items in the memory array far exceeds WM capacity. This could explain why no effect was found at set size 9. Also, perhaps reducing the response interval in Experiment 2 to 2000 ms (versus 4000 ms in Experiment 1 and in Cowan et al., 2016) did not leave sufficient time for high-precision or careful introspection on each trial.
Differences in the distributions of meta-ratings between the two experiments also might reflect different maintenance strategies between participants, age groups, and even trials (see Portrat et al., 2009; Barrouillet & Camos, 2015; Camos & Barrouillet, 2011). For instance, the larger set sizes and shorter retention intervals in Experiment 2 might have encouraged a switch from verbal rehearsal to the quicker process of attentional refreshing (i.e., rapid rotation of attention among WM representations: Barrouillet & Camos, 2015). Refreshing might lead to higher storage judgements than verbally rehearsing the items, if it draws attention to the items, thus making the participants aware that items are being retained, in a way that rehearsal does not do because it is not attention-based.
Different Meta-WM Paradigms
Our meta-WM measure differs from others in the literature in three main ways. (1) Our participants estimated the number of items they thought they remembered, not their confidence in a particular response. (2) Our participants rated their memory prior to the memory test. In contrast, confidence ratings are given after the memory response. (3) Because we used this paradigm, time to respond was limited as we needed to ensure that the time between memory encoding and memory response was always similar. We used this method pioneered by Cowan et al. (2016), because we were interested in participants' explicit insight into their working memory capacity. However, our measure is likely less sensitive on a trial-by-trial basis because at the time of the meta-WM judgment, participants do not know which item they will be probed on. While research using other measures suggest that children as young as 3 years have accurate insight into the accuracy of their responses after they have been given (e.g., Applin & Kibbe, 2020), we found no evidence that children’s meta-WM ratings predicted their trial-level memory performance. Differences in paradigms may explain these discrepancies as predictions are typically worse than 'post-dictions' on various memory tasks (e.g., in younger and older adults: Devolder et al., 1990).
Being aware of the contents of one's memory before giving a response appears to have crucial implications for many tasks. For instance, if a child realized that they do not remember the complete set of task-instructions, they can ask their teacher to repeat the instructions. Accurate estimation of whether a memory response one has just given is correct or not is also important, but arguably is a different skill. Our results show that while children may be able to do the latter (e.g., Applin & Kibbe, 2020), their insight into their memory capacity prior to responding is inflated cannot accurately predict trial-by-trial performance. There may be a distinction between metacognitive sensitivity versus metacognitive bias, such as overconfidence (e.g., see Mamassian, 2020; Maniscalco & Lau, 2012). Our trial-level analyses probe sensitivity, whilst the meta-k accuracy estimates may tend to reflect metacognitive bias. Except college students in Experiment 1, the trial-level ratings did not predict task performance. Children’s greater tendency to overestimate capacity fits with a general bias in children to be overconfident regarding various abilities (e.g., physical abilities, Plumert, 1995; how things work, Mills & Keil, 2004; social standing, Pickert & Wall, 1981).
Missing Meta-WM responses
We excluded trials in which participants failed to provide a meta-WM rating within the required timeframe. Younger children appeared more prone to such failures. Interestingly, not providing a meta-WM judgment could be seen as an indicator of meta-knowledge, reflecting meta-memory uncertainty. For instance, Balcomb and Gerken (2008) found that 3-year-old children opted not to respond to items they did not remember. In our task, failure to provide a meta-WM rating might reflect uncertain meta-memory knowledge. Participants may fail to give a response because they (1) were not paying attention, (2) remember very few items but do not want to admit that, (3) may still be considering what judgment to give and run out of time, or (4) deliberately ignore the memory judgment to focus entirely on remembering the items. Note that (1) and (2) would likely be associated with poor performance and (4) with good performance. It is difficult to disentangle which of these processes a missing meta-response reflects. Moreover, the contribution of these different factors may differ between age groups. Future work could consider this.
In real-life settings, introspection regarding what has been forgotten may be more or less beneficial, depending on circumstances. For instance, actively assessing how many facts you have forgotten from the beginning of the lecture might reduce your ability to pay attention to the end of the lecture. Choosing when to introspect could be an important metacognitive skill.
It is possible that our participants, especially children, chose not to pay attention to the meta-WM rating. Children might have found it difficult to introspect or felt that deep reflection interfered with their ability to focus on the memory test. Perhaps allowing more time for the rating, or a reward for meta-WM accuracy could improve this performance.
Possible Effects of Meta-WM on Response Biases and their Development
Inappropriately inflated meta-WM in younger children may affect response biases – and consequently performance levels – in the WM task. Children seem more susceptible to ‘false alarm’ errors in which a familiar item is judged to be new (cf. Ruffman et al., 2001). Indeed, in younger children we observed higher false alarm rates. This occurred at set sizes 3 (Experiment 2; see Figure 7) and 5 (Experiment 1; see Figure 3), which seems to reflect an assumption in younger children that a probe not matching an item in memory must be novel (see Cowan et al., 2016). In contrast, younger children appeared comparatively less over-prone to incorrectly guessing ‘same’ when the probe did not match an item in memory (for old-item, same trials). These differences illustrate that children's overestimation of their meta-WM knowledge correspond to – and possibly even influence – how they approach the memory task. A comparable developmental shift in response bias was found to take a monotonic course over the life span (Cowan et al., 2006b), suggesting that it may shift because of increasing knowledge of having had memory failures, not yet as well known to young children.
Conclusion
Our results suggest that both WM and meta-memory ability improve with age. While there is a long research tradition on the development of long-term memory meta-memory, this study provides evidence for a similar development in WM capacity meta-memory. Improved meta-WM accuracy in older participants may be driven by numerous processes, including increased resources and knowledge needed for meta-judgments and failure of younger children to take into account forgetting processes that will occur after the meta-judgment. Younger children also may be less adept at interpreting performance feedback or they may understand the meta-memory judgment prompt or task compliance differently.
We also observed some evidence that higher cognitive capacity was associated with better meta-memory accuracy. Finally, we found some evidence that young adults were accurate in noticing trial-by-trial variation when the set sizes were not too large. However, children appeared less adept at predicting trial-by-trial performance. Failure to appreciate the limits of one’s own WM may lead to the impression that a seemingly unfamiliar object must be novel, rather than forgotten. At lower set-sizes, younger participants appeared especially prone to such false alarms. In sum, meta-memory ability seems to develop with age and may contribute to – and support – the development of WM performance across childhood.
Supplementary Material
Acknowledgments
We thank Bret Glass for assistance with data collection. All analyses and data are available via the OSF [ https://osf.io/82634/?view_only=0371237a29b941a5b8fb9225bfb750c8 ]. We gratefully acknowledge NIH Grant R01 HD021338 to Cowan.
Footnotes
All analyses and data are available via the anonymized OSF page [ https://osf.io/82634/?view_only=0371237a29b941a5b8fb9225bfb750c8 ].
For this analysis, we excluded eight participants with k values of 0 (7 in the youngest age group, 1 in the second-youngest age group), to avoid division by 0.
We excluded values of k = 0 from these analyses, to avoid division by 0. Specifically, for four children, two observations were excluded (set size 6 and 9; two in youngest age group 1, one each for the second and third youngest). 15 other individual observations were removed (1 at set size 3, 5 at set size 6, 9 at set size 9).
References
- Adam KC, & Vogel EK (2017). Confident failures: Lapses of working memory reveal a metacognitive blind spot. Attention, Perception, & Psychophysics, 79(5), 1506–1523. 10.3758/s13414-017-1331-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adam KC, Vogel EK, & Awh E (2017). Clear evidence for item limits in visual working memory. Cognitive Psychology, 97, 79–97. 10.1016/j.cogpsych.2017.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams AM, & Gathercole SE (2000). Limitations in working memory: Implications for language development. International Journal of Language & Communication Disorders, 35(1), 95–116. [DOI] [PubMed] [Google Scholar]
- Alloway TP, Gathercole SE, Kirkwood H, & Elliott J (2009). The cognitive and behavioral characteristics of children with low working memory. Child Development, 80(2), 606–621. 10.1111/j.1467-8624.2009.01282.x [DOI] [PubMed] [Google Scholar]
- Amichetti NM, Stanley RS, White AG, & Wingfield A (2013). Monitoring the capacity of working memory: Executive control and effects of listening effort. Memory & Cognition, 41(6), 839–849. 10.3758/s13421-013-0302-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Applin JB, & Kibbe MM (2020). Young children monitor the fidelity of visual working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 10.1037/xlm0000971 [DOI] [PubMed] [Google Scholar]
- Astington JW, & Olson DR (1990). Metacognitive and metalinguistic language: Learning to talk about thought. Applied Psychology, 39(1), 77–87. 10.1111/j.1464-0597.1990.tb01038.x [DOI] [Google Scholar]
- Baddeley AD, & Hitch G (1974). Working memory. In Psychology of learning and motivation (Vol. 8, pp. 47–89). Academic press. [Google Scholar]
- Balcomb FK, & Gerken L (2008). Three-year-old children can access their own memory to guide responses on a visual matching task. Developmental science, 11(5), 750–760. 10.1111/j.1467-7687.2008.00725.x [DOI] [PubMed] [Google Scholar]
- Barrouillet P & Camos V (2015). Working memory: Loss and reconstruction. Hove: Psychology Press. [Google Scholar]
- Barrouillet P, Portrat S, & Camos V (2011). On the law relating processing to storage in working memory. Psychological Review, 118(2), 175. 10.1037/a0022324 [DOI] [PubMed] [Google Scholar]
- Bayliss DM, Jarrold C, Gunn DM, & Baddeley AD (2003). The complexities of complex span: Explaining individual differences in working memory in children and adults. Journal of Experimental Psychology: General, 132(1), 71. 10.1037/0096-3445.132.1.71 [DOI] [PubMed] [Google Scholar]
- Bays PM, Catalao RF, & Husain M (2009). The precision of visual working memory is set by allocation of a shared resource. Journal of Vision, 9(10), 7–7. 10.1167/9.10.7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bona S, & Silvanto J (2014). Accuracy and confidence of visual short-term memory do not go hand-in-hand: behavioral and neural dissociations. PLoS One, 9(3), e90808. 10.1371/journal.pone.0090808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockmole JR, & Logie RH (2013). Age-related change in visual working memory: a study of 55,753 participants aged 8–75. Frontiers in Psychology, 4, 12. 10.3389/fpsyg.2013.00012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown AL (1978). Knowing when, where, and how to remember; a problem of metacognition. Advances in Instructional Psychology, 1. [Google Scholar]
- Brown AL, Bransford JD, Ferrara RA & Campione JC (1983). Learning, remembering, and understanding. Handbook of Child Psychology, 3, 77–166. [Google Scholar]
- Bunnell JK, Baken DM, & Richards-Ward LA (1999). The effect of age on metamemory for working memory. New Zealand Journal of Psychology, 28(1), 23. [Google Scholar]
- Camos V, & Barrouillet P 2011. Factors of working memory development: The Time-Based Resource-Sharing Approach. In Cognitive development and working memory: From neopiagetian to cognitive approaches. Barrouillet P & Gaillard V, Eds.: 151–176. Hove: Psychology Press. [Google Scholar]
- Conway AR, Kane MJ, & Engle RW (2003). Working memory capacity and its relation to general intelligence. Trends in Cognitive Sciences, 7(12), 547–552. 10.1016/j.tics.2003.10.005 [DOI] [PubMed] [Google Scholar]
- Cowan N (1995). Attention and memory: An integrated framework. Oxford University Press. [Google Scholar]
- Cowan N (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24(1), 87–114. 10.1017/S0140525X01003922 [DOI] [PubMed] [Google Scholar]
- Cowan N (2014). Working memory underpins cognitive development, learning, and education. Educational Psychology Review, 26(2), 197–223. 10.1007/s10648-013-9246-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2019) Short-term memory based on activated long-term memory: A review in response to Norris (2017). Psychological Bulletin, 145(8), 822–847. 10.1037/bul0000199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, & Morse PA (1986). The use of auditory and phonetic memory in vowel discrimination. The Journal of the Acoustical Society of America, 79(2), 500–507. 10.1121/1.393537 [DOI] [PubMed] [Google Scholar]
- Cowan N, AuBuchon AM, Gilchrist AL, Ricker TJ, & Saults JS (2011). Age differences in visual working memory capacity: Not based on encoding limitations. Developmental Science, 14(5), 1066–1074. 10.1111/j.1467-7687.2011.01060.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Blume CL, & Saults JS (2013). Attention to attributes and objects in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(3), 731. 10.1037/a0029687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Elliott EM, Saults JS, Morey CC, Mattox S, Hismjatullina A, & Conway AR (2005). On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cognitive Psychology, 51(1), 42–100. 10.1016/j.cogpsych.2004.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Fristoe NM, Elliott EM, Brunner RP, & Saults JS (2006a). Scope of attention, control of attention, and intelligence in children and adults. Memory & Cognition, 34(8), 1754–1768. 10.3758/BF03195936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Hardman K, Saults JS, Blume CL, Clark KM, & Sunday MA (2016). Detection of the number of changes in a display in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 42(2), 169. 10.1037/xlm0000163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Morey CC, AuBuchon AM, Zwilling CE, & Gilchrist AL (2010). Seven-year-olds allocate attention like adults unless working memory is overloaded. Developmental Science, 13(1), 120–133. 10.1111/j.1467-7687.2009.00864.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Naveh-Benjamin M, Kilb A, & Saults JS (2006b). Life-span development of visual working memory: When is feature binding difficult?. Developmental Psychology, 42(6), 1089. 10.1037/0012-1649.42.6.1089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Nugent LD, Elliott EM, Ponomarev I, & Saults JS (1999). The role of attention in the development of short-term memory: Age differences in the verbal span of apprehension. Child Development, 70(5), 1082–1097. 10.1111/1467-8624.00080 [DOI] [PubMed] [Google Scholar]
- Cowan N, Saults JS, & Blume CL (2014). Central and peripheral components of working memory storage. Journal of Experimental Psychology: General, 143(5), 1806. 10.1037/a0036814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMarie D, & Ferron J (2003). Capacity, strategies, and metamemory: Tests of a three-factor model of memory development. Journal of Experimental Child Psychology, 84(3), 167–193. 10.1016/S0022-0965(03)00004-3 [DOI] [PubMed] [Google Scholar]
- Destan N, Hembacher E, Ghetti S, & Roebers CM (2014). Early metacognitive abilities: The interplay of monitoring and control processes in 5-to 7-year-old children. Journal of Experimental Child Psychology, 126, 213–228. 10.1016/j.jecp.2014.04.001 [DOI] [PubMed] [Google Scholar]
- Devolder PA, Brigham MC, & Pressley M (1990). Memory performance awareness in younger and older adults. Psychology and Aging, 5(2), 291. 10.1037/0882-7974.5.2.291 [DOI] [PubMed] [Google Scholar]
- Dunlosky J, Rawson KA, & Middleton EL (2005). What constrains the accuracy of metacomprehension judgments? Testing the transfer-appropriate-monitoring and accessibility hypotheses. Journal of Memory and Language, 52(4), 551–565. 10.1016/j.jml.2005.01.011 [DOI] [Google Scholar]
- Durstewitz D, Seamans JK, & Sejnowski TJ (2000). Neurocomputational models of working memory. Nature neuroscience, 3(11), 1184–1191. 10.1038/81460 [DOI] [PubMed] [Google Scholar]
- Ehrlinger J, Johnson K, Banner M, Dunning D, & Kruger J (2008). Why the unskilled are unaware: Further explorations of (absent) self-insight among the incompetent. Organizational behavior and human decision processes, 105(1), 98–121. 10.1016/j.obhdp.2007.05.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flavell JH (1971). Stage-related properties of cognitive development. Cognitive Psychology, 2(4), 421–453. 10.1016/0010-0285(71)90025-9 [DOI] [Google Scholar]
- Flavell JH, Miller P, & Miller S (1993). Cognitive development. Engelwood Cliffs. [Google Scholar]
- Freeman EE, Karayanidis F, & Chalmers KA (2017). Metacognitive monitoring of working memory performance and its relationship to academic achievement in Grade 4 children. Learning and Individual Differences, 57, 58–64. 10.1016/j.lindif.2017.06.003 [DOI] [Google Scholar]
- Garner R (1987). Metacognition and reading comprehension. Ablex Publishing. [Google Scholar]
- Gathercole SE, & Pickering SJ (2000). Working memory deficits in children with low achievements in the national curriculum at 7 years of age. British Journal of Educational Psychology, 70(2), 177–194. 10.1348/000709900158047 [DOI] [PubMed] [Google Scholar]
- Gathercole SE, Dunning DL, Holmes J, & Norris D (2019). Working memory training involves learning new skills. Journal of Memory and Language, 105, 19–42. 10.1016/j.jml.2018.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gathercole SE, Pickering SJ, Ambridge B, & Wearing H (2004). The structure of working memory from 4 to 15 years of age. Developmental Psychology, 40(2), 177. 10.1037/0012-1649.40.2.177 [DOI] [PubMed] [Google Scholar]
- Gignac GE, & Zajenkowski M (2020). The Dunning-Kruger effect is (mostly) a statistical artefact: Valid approaches to testing the hypothesis with individual differences data. Intelligence, 80, 101449. 10.1016/j.intell.2020.101449 [DOI] [Google Scholar]
- Forsberg A (2020, September 18). The Development of Metacognitive Accuracy in Working Memory Across Childhood. Open Science Framework. Retrieved from osf.io/82634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellström Å (1985). The time-order error and its relatives: Mirrors of cognitive processes in comparing. Psychological Bulletin, 97(1), 35. 10.1037/0033-2909.97.1.35 [DOI] [Google Scholar]
- Henry LA (1996). The relationships between memory performance, use of simple memory strategies and metamemory in young children. International Journal of Behavioral Development, 19(1), 177–200. 10.1080/016502596386018 [DOI] [Google Scholar]
- Holmes J, & Adams JW (2006). Working memory and children’s mathematical skills: Implications for mathematical development and mathematics curricula. Educational Psychology, 26(3), 339–366. 10.1080/01443410500341056 [DOI] [Google Scholar]
- Holmes J, & Gathercole SE (2014). Taking working memory training from the laboratory into schools. Educational Psychology, 34(4), 440–450. 10.1080/01443410.2013.797338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes J, Gathercole SE, & Dunning DL (2010). Poor working memory: impact and, interventions. In Advances in Child Development and Behavior (Vol. 39, pp. 1–43). JAI. 10.1016/B978-0-12-374748-8.00001-9 [DOI] [PubMed] [Google Scholar]
- Isbell E, Fukuda K, Neville HJ, & Vogel EK (2015). Visual working memory continues to develop through adolescence. Frontiers in Psychology, 6, 696. 10.3389/fpsyg.2015.00696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaroslawska AJ, Gathercole SE, Logie MR, & Holmes J (2016). Following instructions in a virtual school: Does working memory play a role?. Memory & Cognition, 44(4), 580–589. 10.3758/s13421-015-0579-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarrold C, & Towse JN (2006). Individual differences in working memory. Neuroscience, 139(1), 39–50. 10.1016/j.neuroscience.2005.07.002 [DOI] [PubMed] [Google Scholar]
- Jeffreys H (1961). Theory of Probability. Oxford: UK Oxford University Press. [Google Scholar]
- Johnson CN, & Wellman HM (1980). Children's developing understanding of mental verbs: Remember, know, and guess. Child Development, 1095–1102. 10.2307/1129549 [DOI] [Google Scholar]
- Klopfer FJ, & Madden TM (1980). The middlemost choice on attitude items: Ambivalence, neutrality, or uncertainty?. Personality and Social Psychology Bulletin, 6(1), 97–101. 10.1177/014616728061014 [DOI] [Google Scholar]
- Koriat A, & Helstrup T (2007). Metacognitive aspects of memory. In Everyday Memory (pp. 263–286). Psychology Press. [Google Scholar]
- Krebs SS, & Roebers CM (2010). Children's strategic regulation, metacognitive monitoring, and control processes during test taking. British Journal of Educational Psychology, 80(3), 325–340. 10.1348/000709910X485719 [DOI] [PubMed] [Google Scholar]
- Kreutzer MA, Leonard C, Flavell JH, & Hagen JW (1975). An interview study of children's knowledge about memory. Monographs of the Society for Research in Child Development, 1–60. 10.2307/11659551102959 [DOI] [Google Scholar]
- Kruger J, & Dunning D (1999). Unskilled and unaware of it: how difficulties in recognizing one's own incompetence lead to inflated self-assessments. Journal of Personality and Social Psychology, 77(6), 1121. 10.1037/0022-3514.77.6.1121 [DOI] [PubMed] [Google Scholar]
- Kurtz BE, & Weinert FE (1989). Metamemory, memory performance, and causal attributions in gifted and average children. Journal of Experimental Child Psychology, 48(1), 45–61. 10.1016/0022-0965(89)90040-4 [DOI] [PubMed] [Google Scholar]
- Lépine R, Parrouillet P, & Camos V (2005). What makes working memory spans so predictive of high-level cognition?. Psychonomic Bulletin & Review, 12(1), 165–170. 10.3758/BF03196363 [DOI] [PubMed] [Google Scholar]
- Levin DT, Momen N, Drivdahl IV SB, & Simons DJ (2000). Change blindness blindness: The metacognitive error of overestimating change-detection ability. Visual Cognition, 7(1-3), 397–412. 10.1080/135062800394865 [DOI] [Google Scholar]
- Levin JR, Yussen SR, Pressley M, & de Rose TM (1977). Developmental changes in assessing recall and recognition memory capacity. Developmental Psychology, 13(6), 608. 10.1037/0012-1649.13.6.608 [DOI] [Google Scholar]
- Lockl K, & Schneider W (2006). Precursors of metamemory in young children: The role of theory of mind and metacognitive vocabulary. Metacognition and Learning, 1(1), 15–31. 10.1007/s11409-006-6585-9 [DOI] [Google Scholar]
- Logie RH, & Cowan N (2015). Perspectives on working memory: introduction to the special issue. Memory & Cognition, 43(3), 315–324. 10.3758/s13421-015-0510-x [DOI] [PubMed] [Google Scholar]
- Luck SJ, & Vogel EK (1997). The capacity of visual working memory for features and conjunctions. Nature, 390(6657), 279–281. 10.1038/36846 [DOI] [PubMed] [Google Scholar]
- Maki RH (1999). The roles of competition, target accessibility, and cue familiarity in metamemory for word pairs. Journal of Experimental Psychology: Learning, Memory, and Cognition, 25(4), 1011. / 10.1037/0278-7393.25.4.1011 [DOI] [Google Scholar]
- Makovski T, Sussman R, & Jiang YV (2008). Orienting attention in visual working memory reduces interference from memory probes. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(2), 369. 10.1037/0278-7393.34.2.369 [DOI] [PubMed] [Google Scholar]
- Mamassian P (2020). Confidence forced-choice and other metaperceptual tasks. Perception, 49(6), 616–635. 10.1177/0301006620928010 [DOI] [PubMed] [Google Scholar]
- Maniscalco B, & Lau H (2012). A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Consciousness and Cognition, 21(1), 422–430. 10.1016/j.concog.2011.09.021 [DOI] [PubMed] [Google Scholar]
- Markman EM (1979). Realizing that you don't understand: Elementary school children's awareness of inconsistencies. Child Development, 643–655. 10.2307/1128929 [DOI] [PubMed] [Google Scholar]
- McCormack T, Simms V, McGourty J, & Beckers T (2013). Blocking in children’s causal learning depends on working memory and reasoning abilities. Journal of Experimental Child Psychology, 115(3), 562–569. / 10.1016/j.jecp.2012.11.016 [DOI] [PubMed] [Google Scholar]
- Melby-Lervåg M, Redick TS, & Hulme C (2016). Working memory training does not improve performance on measures of intelligence or other measures of “far transfer” evidence from a meta-analytic review. Perspectives on Psychological Science, 11(4), 512–534. 10.1177/1745691616635612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller GA (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81. 10.1037/h0043158 [DOI] [PubMed] [Google Scholar]
- Mills CM, & Keil FC (2004). Knowing the limits of one's understanding: The development of an awareness of an illusion of explanatory depth. Journal of Experimental Child Psychology, 87(1), 1–32. 10.1016/j.jecp.2003.09.003 [DOI] [PubMed] [Google Scholar]
- Mutluturk A, & Boduroglu A (2014). Effects of spatial configurations on the resolution of spatial working memory. Attention, Perception, & Psychophysics, 76(8), 2276–2285. 10.3758/s13414-014-0713-4 [DOI] [PubMed] [Google Scholar]
- Myers M, & Paris SG (1978). Children's metacognitive knowledge about reading. Journal of Educational Psychology, 70(5), 680. 10.1037/0022-0663.70.5.680 [DOI] [Google Scholar]
- Pashler H (1988). Familiarity and visual change detection. Perception & Psychophysics, 44(4), 369–378. 10.3758/BF03210419 [DOI] [PubMed] [Google Scholar]
- Paulus M, Proust J, & Sodian B (2013). Examining implicit metacognition in 3.5-year-old children: An eye-tracking and pupillometric study. Frontiers in Psychology, 4, 145. 10.3389/fpsyg.2013.00145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickert SM, & Wall SM (1981). An investigation of children's perceptions of dominance relations. Perceptual and Motor Skills, 52(1), 75–81. 10.2466/pms.1981.52.1.75 [DOI] [Google Scholar]
- Pinto Y, Sligte IG, Shapiro KL, & Lamme VA (2013). Fragile visual short-term memory is an object-based and location-specific store. Psychonomic Bulletin & Review, 20(4), 732–739. 10.3758/s13423-013-0393-4 [DOI] [PubMed] [Google Scholar]
- Plumert JM (1995). Relations between children's overestimation of their physical abilities and accident proneness. Developmental Psychology, 31(5), 866. 10.1037/0012-1649.31.5.866 [DOI] [Google Scholar]
- Portrat S, Camos V, & Barrouillet P (2009). Working memory in children: A time-constrained functioning similar to adults. Journal of Experimental Child Psychology, 102(3), 368–374. 10.1016/j.jecp.2008.05.005 [DOI] [PubMed] [Google Scholar]
- Pressley M, Levin JR, Ghatala ES, & Ahmad M (1987). Test monitoring in young grade school children. Journal of Experimental Child Psychology, 43(1), 96–111. 10.1016/0022-0965(87)90053-1 [DOI] [Google Scholar]
- Rademaker RL, Tredway CH, & Tong F (2012). Introspective judgments predict the precision and likelihood of successful maintenance of visual working memory. Journal of Vision, 12(13), 21–21. 10.1167/12.13.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raven J, & Raven JC (1998). Court JH (1998). Manual for Raven’s Progressive Matrices and Vocabulary Scales. [Google Scholar]
- Renner CH, & Renner MJ (2001). But I thought I knew that: Using confidence estimation as a debiasing technique to improve classroom performance. Applied Cognitive Psychology: The Official Journal of the Society for Applied Research in Memory and Cognition, 15(1), 23–32. 10.1002/1099-0720 [DOI] [Google Scholar]
- Riggs KJ, McTaggart J, Simpson A, & Freeman RP (2006). Changes in the capacity of visual working memory in 5-to 10-year-olds. Journal of Experimental Child Psychology, 95(1), 18–26. 10.1016/j.jecp.2006.03.009 [DOI] [PubMed] [Google Scholar]
- Riggs KJ, Simpson A, & Potts T (2011). The development of visual short-term memory for multifeature items during middle childhood. Journal of Experimental Child Psychology, 108(4), 802–809. 10.1016/j.jecp.2010.11.006 [DOI] [PubMed] [Google Scholar]
- Robins RW, & Beer JS (2001). Positive illusions about the self: short-term benefits and long-term costs. Journal of Personality and Social Psychology, 80(2), 340. 10.1037/0022-3514.80.2.340 [DOI] [PubMed] [Google Scholar]
- Roebers CM, Cimeli P, Röthlisberger M, & Neuenschwander R (2012). Executive functioning, metacognition, and self-perceived competence in elementary school children: An explorative study on their interrelations and their role for school achievement. Metacognition and Learning, 7(3), 151–173. 10.1007/s11409-012-9089-9 [DOI] [Google Scholar]
- Ross-Sheehy S, Oakes LM, & Luck SJ (2003). The development of visual short-term memory capacity in infants. Child development, 74(6), 1807–1822. 10.1046/j.1467-8624.2003.00639.x [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, & Pratte MS (2008). An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences, 105(16), 5975–5979. 10.1073/pnas.0711295105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Speckman PL, & Province JM (2012). Default Bayes factors for ANOVA designs. Journal of Mathematical Psychology, 56(5), 356–374. / 10.1016/j.jmp.2012.08.001 [DOI] [Google Scholar]
- Ruffman T, Rustin C, Garnham W, & Parkin AJ (2001). Source monitoring and false memories in children: Relation to certainty and executive functioning. Journal of Experimental Child Psychology, 80(2), 95–111. 10.1006/jecp.2001.2632 [DOI] [PubMed] [Google Scholar]
- Schneider W (1998). Performance prediction in young children: Effects of skill, metacognition and wishful thinking. Developmental Science, 1(2), 291–297. 10.1111/1467-7687.00044 [DOI] [Google Scholar]
- Schneider W, & Pressley M (2013). Memory development between two and twenty. Psychology Press. [Google Scholar]
- Schraw G (2001). Promoting general metacognitive awareness. In Metacognition in learning and instruction (pp. 3–16). Springer, Dordrecht. 10.1007/978-94-017-2243-8_1 [DOI] [Google Scholar]
- Schwanenflugel PJ, Fabricius WV, & Alexander J (1994). Developing theories of mind: Understanding concepts and relations between mental activities. Child Development, 65(6), 1546–1563. 10.1111/j.1467-8624.1994.tb00835.x [DOI] [PubMed] [Google Scholar]
- Simmering VR (2012). The development of visual working memory capacity during early childhood. Journal of Experimental Child Psychology, 111(4), 695–707. 10.1016/j.jecp.2011.10.007 [DOI] [PubMed] [Google Scholar]
- Sligte IG, Scholte HS, & Lamme VA (2008). Are there multiple visual short-term memory stores?. PLOS one, 3(2), e1699. 10.1371/journal.pone.0001699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobel DM, & Letourneau SM (2015). Children's developing understanding of what and how they learn. Journal of Experimental Child Psychology, 132, 221–229. 10.1016/j.jecp.2015.01.004 [DOI] [PubMed] [Google Scholar]
- Soto D, & Silvanto J (2014). Reappraising the relationship between working memory and conscious awareness. Trends in Cognitive Sciences, 18(10), 520–525. 10.1016/j.tics.2014.06.005 [DOI] [PubMed] [Google Scholar]
- Stefan AM, Gronau QF, Schönbrodt FD, & Wagenmakers EJ (2019). A tutorial on Bayes Factor Design Analysis using an informed prior. Behavior Research Methods, 51(3), 1042–1058. 10.3758/s13428-018-01189-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternberg RJ (1997). The concept of intelligence and its role in lifelong learning and success. American Psychologist, 52(10), 1030. 10.1037/0003-066X.52.10.1030 [DOI] [PubMed] [Google Scholar]
- Stine-Morrow EA, Shake MC, Miles JR, & Noh SR (2006). Adult age differences in the effects of goals on self-regulated sentence processing. Psychology and Aging, 21(4), 790. 10.1037/0882-7974.21.4.790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suchow JW, Fougnie D, & Alvarez GA (2017). Looking inward and back: Real-time monitoring of visual working memories. Journal of Experimental Psychology: Learning, Memory, and Cognition, 43(4), 660. 10.1037/xlm0000320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas AK, Bonura BM, Taylor HA, & Brunyé TT (2012). Metacognitive monitoring in visuospatial working memory. Psychology and Aging, 27(4), 1099. 10.1037/a0028556 [DOI] [PubMed] [Google Scholar]
- Towse JN, Hitch GJ, & Hutton U (1998). A reevaluation of working memory capacity in children. Journal of Memory and Language, 39(2), 195–217. 10.1006/jmla.1998.2574 [DOI] [Google Scholar]
- Van den Berg R, Awh E, & Ma WJ (2014). Factorial comparison of working memory models. Psychological Review, 121(1), 124. 10.1037/a0035234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenbroucke AR, Sligte IG, Barrett AB, Seth AK, Fahrenfort JJ, & Lamme VA (2014). Accurate metacognition for visual sensory memory representations. Psychological Science, 25(4), 861–873. 10.1177/0956797613516146 [DOI] [PubMed] [Google Scholar]
- Weinert FE, & Schneider W (Eds.). (1999). Individual development from 3 to 12: Findings from the Munich Longitudinal Study. Cambridge University Press. [Google Scholar]
- Wellman HM, & Johnson CN (1979). Understanding of mental processes: a developmental study of" remember" and" forget". Child Development, 79–88. 10.2307/1129044 [DOI] [Google Scholar]
- Wetzels R, & Wagenmakers EJ (2012). A default Bayesian hypothesis test for correlations and partial correlations. Psychonomic Bulletin & Review, 19(6), 1057–1064. 10.3758/s13423-012-0295-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodman GF, & Luck SJ (2003). Dissociations among attention, perception, and awareness during object-substitution masking. Psychological Science, 14(6), 605–611. 10.1046/j.0956-7976.2003.psci_1472.x [DOI] [PubMed] [Google Scholar]
- Zosh JM, & Feigenson L (2015). Array heterogeneity prevents catastrophic forgetting in infants. Cognition, 136, 365–380. 10.1016/j.cognition.2014.11.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.