Abstract
Objective
The objective of this study was to compare the biomechanical differences of different rod configurations following anterior column realignment (ACR) and pedicle subtraction osteotomy (PSO) for an optimal correction technique and rod configuration that would minimize the risk of rod failure.
Methods
A validated spinopelvic (L1-pelvis) finite element model was used to simulate ACR at the L3–4 level. The ACR procedure was followed by dual-rod fixation, and for 4-rod constructs, either medial/lateral accessory rods (connected to primary rods) or satellite rods (directly connected to ACR level screws). The range of motion (ROM), maximum von Mises stress on the rods, and factor of safety (FOS) were calculated for the ACR models and compared to the existing literature of different PSO rod configurations.
Results
All of the 4-rod ACR constructs showed a reduction in ROM and maximum von Mises stress compared to the dual-rod ACR construct. Additionally, all of the 4-rod ACR constructs showed greater percentage reduction in ROM and maximum von Mises stress compared to the PSO 4-rod configurations. The ACR satellite rod construct had the maximum stress reduction i.e., 47.3% compared to dual-rod construct and showed the highest FOS (4.76). These findings are consistent with existing literature that supports the use of satellite rods to reduce the occurrence of rod fracture.
Conclusion
Our findings suggest that the ACR satellite rod construct may be the most beneficial in reducing the risk of rod failure compared to all other PSO and ACR constructs.
Keywords: Adult spinal deformity, Anterior column realignment, Multirod constructs, Finite element analysis, Rod fracture, Pedicle subtraction osteotomy
INTRODUCTION
Adult spinal deformity (ASD) is prevalent in up to 68% of the population and is associated with poor health-related quality of life [1]. There is an estimated 27.5 million people with ASD in the United States alone, and as life expectancy continues to increase, the number of people with ASD will also see a spike [2,3]. For ASD patients, pedicle subtraction osteotomy (PSO) is a common surgical procedure that shortens the spine posteriorly and uses 2 or more rods and pedicle screws to restore spinal alignment. However, there are serious complications associated with PSO including excessive bleeding and implant failure [4]. Some studies estimate a 61% complication rate with the most common being rod fracture, with an occurrence of 22% [5-8]. The spinal segment is further stiffened with additional rods to reduce rate of implant failure, but the risk associated with excessive bleeding still remains [9].
To address this concern, anterior column realignment (ACR) has become a trusted, minimally invasive alternative to PSO. In an ACR procedure, an interbody cage is used to replace an intervertebral disc and the anterior longitudinal ligament (ALL) is released. ACR has shown similar radiographic correction as PSO, with lesser complications [10,11]. Additionally, classifications of different ACR procedures make it a useful surgery in a variety of clinical situations [12]. However, similar to PSO, rod constructs are used in ACR, meaning there are similar risks of implant failure. An in vitro study done by La Barbera et al. [13] concluded that bilateral posterior rod fixation following ACR surgery may not be enough to stabilize the operated region. Thus, the use of 4-rod constructs is recommended, just as in PSO [14]. Literature suggests an optimal 4-rod construct configuration following PSO to reduce rate of rod fractures, but similar literature on optimal 4-rod configurations following ACR is sparse [13,15].
Thus, the objective of this study was to use finite element analysis (FEA) to suggest the most optimal procedure and rod configuration for ASD correction. For this purpose, 4 different rod configurations were investigated following ACR: dual-rod configuration, additional medial accessory rods (ACR-MED), additional lateral accessory rods (ACR-LAT), and additional short satellite rods (ACR-SAT). These rod combinations were chosen being among the common configurations seen in clinical practice. Also, these rods configurations have been investigated following PSO in our previous study [15]. Thus this study simulated the same rod configurations following ACR to draw comparison among different rod configurations in PSO versus ACR.
MATERIALS AND METHODS
A previously validated osteo-ligamentous spinopelvic model (L1-pelvis) was used to simulate ACR at the L3–4 level in this study [15-18]. The geometry of the initial model was based on computed tomography (CT) scans of a healthy 55-year-old adult male. The CT data were used to reconstruct the 3-dimentional (3D) geometry of the model in MIMICS (Materialize Inc., Leuven, Belgium). The 3D geometry of the model was meshed in IAFE-MESH (University of Iowa, Iowa) and HyperMesh (Altair Engineering, Michigan, USA) software. The meshed parts were assembled and assigned material properties for computational analysis in Abaqus (Dassault Systemes, Simulia Inc., Providence, RI, USA). The cancellous bone in the pelvis and vertebrae was surrounded by an outer layer of cortical bone with a thickness of 1 mm and 0.5 mm, respectively [19-23]. The intervertebral disc consisted of nucleus and annulus ground substances with fibers embedded in it. The ligaments in the model were represented using truss elements. The material properties for all the components were acquired from literature (Table 1) [20,23,24].
Table 1.
| Component | Element type | Young modulus (MPa) | Poisson ratio |
|---|---|---|---|
| Bone | |||
| Cortical bone | C3D8 | 12,000 | 0.3 |
| Cancellous bone | C3D8 | 100 | 0.2 |
| Pelvic cortical bone | C3D8 | 17,000 | 0.3 |
| Pelvic cancellous bone | C3D8 | 10 | 0.2 |
| Intervertebral disc | |||
| Nucleus | C3D8H | C1 = 0.12, C2 = 0.003, D1 = 0.0005 | 0.49 |
| Annulus ground substance | C3D8 | Hyperelastic (C10, 0.348; D1, 0.3) | |
| Annulus fibers | Rebar | 357–550 | |
| Ligaments | T3D2 | Non-Linear | |
| Apophyseal joints | Nonlinear, soft contact, GAPUNI elements | ||
| Sacroiliac joints | Nonlinear, soft contact | ||
| Implants | |||
| ACR cage (PEEK) | C3D8 | 3,600 | 0.25 |
| Screw head (CoCr) | C3D4 | 241,000 | 0.3 |
| Primary/supplementary rods (CoCr) | C3D8 | 241,000 | 0.3 |
| Ti6Al4V pedicle screw shaft | C3D4 | 11,500 | 0.3 |
ACR, anterior column realignment; PEEK, polyether ether ketone; CoCr, cobalt-chromium.
1. FE Model of ACR Procedure
To simulate the ACR surgery at the L3–4 level, the intervertebral disc at the index segment was completely removed along with the ALL. Additionally, resection of the posterior elements (facets, lamina) was performed at L3–4 level [25]. Next, a 30° hyperlordotic cage was inserted at the index segment and secured to L3 and L4 level by short titanium alloy (Ti6Al4V) screws, followed by L1–S1 bilateral pedicle screw posterior fixation using 5.5-mm pedicle screws with a length of 45 mm and cobaltchromium (CoCr) rods with a diameter of 5.5 mm. The pedicle screw shaft was assigned a material property of Ti6Al4V whereas the screw head was assigned the property of CoCr [14]. Additionally, the supplementary rods (accessory/satellite) were assigned the property of CoCr. The interaction between the screw shaft and bone was simulated by the “TIE” contact formulation to simulate the complete osteointegration of screw shaft with the bone. The rods were also constrained using the TIE formulation to the screw head. The interaction between cage-bone interface was simulated with a coefficient of friction of 0.2 using the surface-to-surface contact formulation. The same interactions were used in our previously study, simulating different rod configurations following PSO [15].
Overall, the ACR surgery was simulated with 4 different rod configurations (Figs. 1 and 2):
Fig. 1.
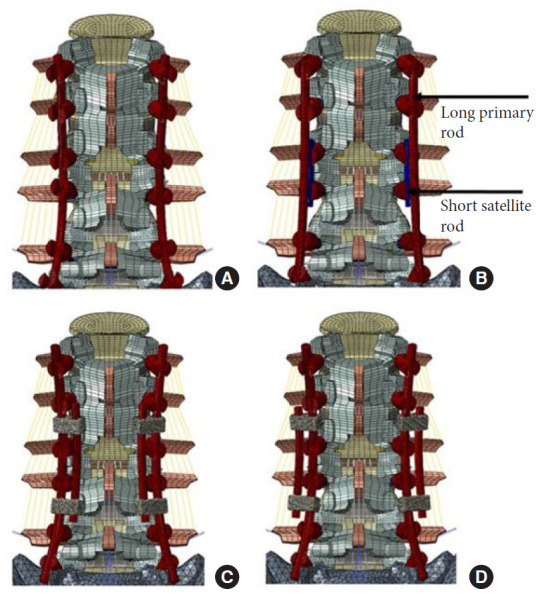
Posterior view of the different anterior column realignment (ACR) rod configurations. (A) Bilaterally fixated ACR model (ACR). (B) Four-rod instrumented ACR model with short satellite rods at L3–4 (ACR-SAT). (C) Four-rod instrumented ACR model with medially affixed accessory rods (ACR-MED). (D) Four-rod instrumented ACR model with laterally affixed accessory rods (ACR-LAT).
Fig. 2.
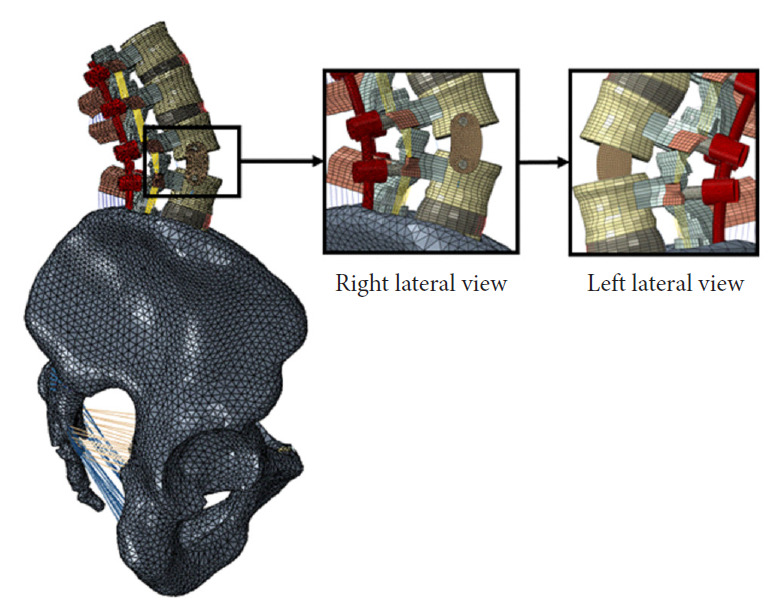
Two lateral views of the anterior column realignment (ACR) model. The magnified views show the 30° hyper lordotic cage at L–4.
• A 30° hyperlordotic cage at L3–4 level and bilateral rod fixation from L1–S1. (ACR)
• A 30° hyperlordotic cage at L3–4 level and bilateral rod fixation from L1–S1 + short satellite rods at L3–4. In this configuration, primary rods are not connected to the L3–4 pedicle screws. (ACR-SAT)
• A 30° hyperlordotic cage at L3–4 level and bilateral rod fixation from L1–S1 + medially affixed accessory rods connected to the primary rods via connectors at L2–3 and L4–5 regions. (ACR-MED)
• A 30° hyperlordotic cage at L3–4 level and bilateral rod fixation from L1–S1 + laterally affixed accessory rods connected to the primary rods via connectors at L2–3 and L4–5 regions. (ACR-LAT)
2. Boundary Conditions and Loading
The pelvis was constrained in all of the models. All of the models were subjected to a 400 N physiological compression load followed by a 7.5 Nm pure moment applied to the L1-superior endplate to simulate flexion/extension, lateral bending, and axial rotation [26].
3. Data Analysis
The global ROM (L1–S1) for all of the models was analyzed. Also, the maximum von Mises stress in the rod for all of the rod configurations was used to calculate the factor of safety (FOS). FOS was determined by dividing the yield stress of CoCr by the maximum von Mises recorded for a given rod configuration. The higher the FOS lesser are the chances of rod fracture. The data for ACR rod configurations were also compared to the same rod configurations following PSO. The percentage change for ACR 4-rod constructs was calculated with respect to the dualrod ACR construct while percentage change for PSO 4-rod constructs was calculated with respect to the dual-rod PSO construct.
where, CoCr yield stress= 989 MPa.
RESULTS
1. Range of Motion
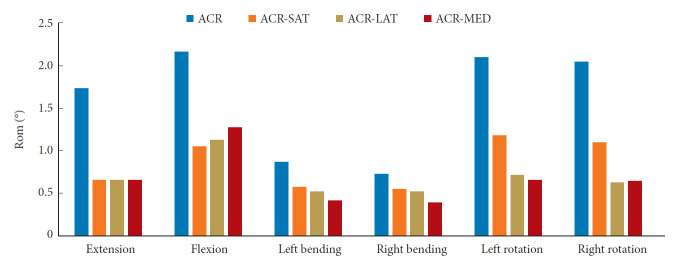
The predicted global ROM showed that the use of more rods correlated to the lower ROM as higher ROM was observed in the dual-rod ACR model when compared to the 4-rod constructs (Fig. 3). Under extension loading, the ACR-SAT, ACR-LAT, and ACR-MED showed similar changes in ROM with a 62% decrease for all models. Under flexion loading (clinically most crucial motion), the ACR-SAT model showed the greatest reduction in ROM with a 51% decrease compared to the ACR model. The ACR-LAT and ACR-MED models demonstrated a 48% and 41% decrease in ROM, respectively, when compared to the ACR model. Under all other loadings, the ACR-SAT generally showed the lowest percentage decrease in ROM compared to ACR-LAT and ACR-MED. The ACR-SAT, ACR-LAT, and ACR-MED models showed that ROM decreased by 34%, 40%, 51% under left bending and 25%, 29%, and 47% under right bending, respectively. The greatest changes in ROM were found under axial rotation conditions for both the ACR-LAT and ACR-MED models where there was a 66% and 68% decrease in left rotation and 70% and 69% decrease in right rotation, respectively. Meanwhile, the ACR-SAT model only showed a 44% and 46% decrease in left and right rotation, respectively.
Fig. 3.
Comparison of the instrumented L1–S1 global range of motion (ROM) for different loading directions and configurations. ACR, anterior column realignment; ACR-SAT, ACR-short satellite rods; ACR-LAT, ACR-lateral accessory rods; ACR-MED, ACR-medial accessory rods.
2. Maximum Rod Stress
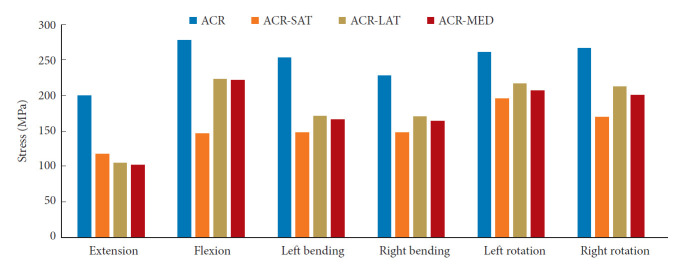
The maximum von Mises stress in rods was computed under all loading conditions (Fig. 4). The dual-rod ACR construct was associated with the highest maximum von Mises stress on the rods. All models except the ACR-SAT model showed the highest rod stresses under flexion loading. The ACR-SAT model, however, showed the highest rod stresses under left rotation. Extension loading consistently showed the lowest rod stresses for all models.
Fig. 4.
Comparison of the maximum von Mises stress (MPa) found for the primary rods in the ACR, ACR-SAT, ACR-LAT, and ACR-MED models under all loading conditions. ACR, anterior column realignment; ACR-SAT, ACR-short satellite rods; ACR-LAT, ACR-lateral accessory rods; ACR-MED, ACR-medial accessory rods.
The location of the maximum rod stress and percentage differences of rod stress when compared to the ACR model are summarized in Table 2. In the ACR model, it was found that the maximum von Mises stress occurred at the index segment. For the ACR-SAT model, the maximum stress was found at L5–S1 under flexion, right bending, and left bending and found at L1–2 under extension, right rotation, and left rotation. Additionally, the ACR-SAT model showed the highest reduction of rod stresses under all loadings except extension. A 42% decrease in rod stress was observed for extension for the ACR-SAT model compared to a 48% and 49% decrease for the ACR-LAT and ACR-MED models, respectively. Both the ACR-LAT and ACR-MED model demonstrated a 20% reduction under flexion loading while the ACR-SAT showed a 47% decrease when compared to the ACR model. The ACR-LAT model showed the lowest reduction in rod stresses under lateral bending and axial rotations with only a 32%, 25%, 17%, and 20% decrease found for left bending, right bending, left rotation, and right rotation, respectively. However, all 4-rod models showed a decrease in maximum rod stresses compared to the ACR model, and all maximum rod stresses were located on the primary rods.
Table 2.
Values and locations of the maximum von Mises stress recorded on the rods for the 4-rod configurations tested
| Motion | ACR | ACR-SAT | ACR-LAT | ACR-MED |
|---|---|---|---|---|
| Flexion | 277.3 | -47.35% | -19.73% | -20.34% |
| ACR Index | L5–S1 | Adjacent to domino | Adjacent to domino | |
| Extension | 200 | -41.50% | -47.80% | -49.10% |
| ACR Index | L1–2 | Adjacent to domino | Adjacent to domino | |
| Right bending | 228 | -35.53% | -25.44% | -28.07% |
| ACR Index | L5–S1 | Adjacent to domino | Adjacent to domino | |
| Left bending | 253 | -41.50% | -32.41% | -34.51% |
| ACR Index | L5–S1 | Adjacent to domino | Adjacent to domino | |
| Right rotation | 267 | -36.33% | -20.30% | -24.72% |
| ACR Index | L1–2 | Adjacent to domino | Adjacent to domino | |
| Left rotation | 260 | -25.00% | -16.54% | -20.85% |
| ACR Index | L1–2 | Adjacent to domino | Adjacent to domino | |
| Factor of safety | 3.35 | 4.76 | 4.17 | 4.20 |
Maximum values are reported for the ACR model, but percent difference with respect to the ACR model is reported for the ACR-SAT, ACR-LAT, and ACR-MED models. The factor of safety for each rod is also recorded.
ACR, anterior column realignment; ACR-SAT, ACR-short satellite rods; ACR-LAT, ACR-lateral accessory rods; ACR-MED, ACR-medial accessory rods.
The FOS was 3.35 in the ACR model. All 4-rod constructs saw this number increase with the ACR-SAT model showing the greatest FOS at 4.76. The ACR-LAT and ACR-MED showed a FOS of 4.17 and 4.20, respectively.
3. Comparison of ACR and PSO Rod Configuration Results
The previous study done by Vosoughi et al. [15] also recorded the percent change in both ROM and maximum von Mises rod stress between dual-rod and 4-rod constructs after PSO implementation (Tables 3 and 4). The global ROM decreased by 12%, 11%, 1%, 1%, and 7% for their lateral accessory rod construct and 16%, 15%, 8%, 8%, 8%, and 8% for their medial lateral rod construct under extension, flexion, left bending, right bending, left rotation, and right rotation, respectively. Additionally, their satellite rod construct showed a 4%, 11%, 54%, 61% decrease in global ROM while a 31% increase in global ROM during axial rotation loading. Overall, the PSO models demonstrated an average 6% and 11% decrease in ROM for the lateral and medial accessory rod configurations, respectively, but the ACR models showed a 52% and 56% average decrease in ROM. The PSO satellite rod model showed an average ROM decrease of 11% while the ACR satellite rod model showed an average ROM decrease of 44%.
Table 3.
Values for the percentage change of global ROM of the 4-rod construct when compared to its respective ACR or PSO dual-rod model under all loading types
| Variable | Satellite rods |
Lateral accessory rods |
Medial accessory rods |
|||
|---|---|---|---|---|---|---|
| ACR model | PSO model | ACR model | PSO model | ACR model | PSO model | |
| Extension | -62% | -4% | -62% | -12% | -62% | -16% |
| Flexion | -51% | -11% | -48% | -11% | -41% | -15% |
| Left bending | -34% | -54% | -40% | -1% | -51% | -8% |
| Right bending | -25% | -61% | -29% | -1% | -47% | -8% |
| Left rotation | -44% | 31% | -66% | -7% | -69% | -8% |
| Right rotation | -47% | 31% | -70% | -7% | -69% | -8% |
| Average | -44% | -11% | -52% | -6% | -56% | -11% |
The average percent difference is also reported.
ROM, range of motion; ACR, anterior column realignment; PSO, pedicle subtraction osteotomy.
Table 4.
Values for the percentage change of maximum rod stress of the 4-rod construct when compared to its respective ACR or PSO dual-rod model under all loading types
| Variable | Satellite rods |
Lateral accessory rods |
Medial accessory rods |
|||
|---|---|---|---|---|---|---|
| ACR model | PSO model | ACR model | PSO model | ACR model | PSO model | |
| Extension | -42% | -10% | -48% | 5% | -49% | -2% |
| Flexion | -47% | -34% | -20% | -4% | -20% | -8% |
| Left bending | -42% | -12% | -32% | 0% | -35% | -3% |
| Right bending | -36% | -14% | -25% | +3% | -28% | -3% |
| Left rotation | -25% | -11% | -17% | +11% | -21% | -2% |
| Right rotation | -36% | -12% | -20% | +8% | -25% | 0% |
| Average | -38% | -16% | -27% | +4% | -30% | -2% |
The average percent difference is also reported.
ACR, anterior column realignment; PSO, pedicle subtraction osteotomy.
The PSO models done by Vosoughi et al. [15] additionally explored the change in maximum rod stress when compared to the 2-rod PSO construct (Table 4). However, their PSO constructs that utilized lateral accessory rod construct only showed a 4% decrease in flexion loading while showing a 5%, 0%, 3%, 11%, and 8% increase in maximum rod stress in extension, left bending, right bending, left rotation, and right rotation, respectively. Similar results were shown by the medial accessory rod constructs as the maximum rod stress decreased by 2%, 8%, 3%, and 3% in extension, flexion, left bending, and right bending but increased by 2% and 0% in left and right rotation, respectively. These are in contrast to much higher stress reductions predicted in the ACR models. The average stress reductions for all loadings in the ACR-LAT, ACR-MED, and ACR-SAT models were 27%, 30%, and 38%, respectively, while its PSO counterparts demonstrated a 4% increase and 2% and 16% decrease in maximum rod stress, respectively.
DISCUSSION
1. Comparison of Rod Configurations in PSO Versus ACR
Since PSO and ACR are among the most used procedures in correcting ASD, the dual and 4-rod configurations in either PSO or ACR were compared. Data from a previous study for dual and 4-rod constructs following PSO was used for comparison. Vosoughi et al. [15] observed a decrease in global ROM after the inclusion of accessory and satellite rods to the dual-rod construct. Following PSO, they observed a reduction in global ROM of 11%, 6%, and 11% for satellite rod, lateral accessory rod, and medial accessory rod constructs, respectively. Comparatively, in our ACR model, a reduction in global ROM of 44%, 52%, and 56% was observed for satellite rod, lateral accessory rod and medial accessory rod constructs, respectively. The possible reason for less mobility in the ACR constructs could be the presence of a 30° hyperlordotic cage at L3–4 level which is secured to the L3 and L4 vertebrae via titanium alloy (Ti6Al4V) screws, providing additional stability to the ACR constructs.
Moreover, the study by Vosoughi et al. [15] found that the use of satellite rods decreased the maximum rod stress by 16% while the use of lateral and medial accessory rods increased rod stress by 4% and decreased rod stress by 2%, respectively. In comparison, the addition of satellite rods to our ACR model decreased the maximum rod stress by 38% while the addition of lateral and accessory rods decreased the maximum rod stress by 27% and 30%, respectively.
A possible explanation for why the use of additional rods in ACR leads to higher reduction of rod stresses is the use of an interbody cage at the index segment, which has been shown to reduce rod stresses in PSO models as well [27]. These comparisons suggest that the ACR constructs are generally better at reducing maximum rod stresses when compared to PSO. This conclusion is backed by a study done by Januszewski et al. [27] which compared PSO to ACR and came to a similar conclusion. Additionally, the results from the study of Vosoughi et al. [15] and present study point to satellite rod configurations as the recommended 4-rod construct in reducing the occurrence of rod fracture following PSO and ACR, respectively [22]. However, in vitro and clinical studies would be required to support this recommendation. Moreover, comparisons among the ACR models of this study and PSO models of Vosoughi et al. [15] must be interpreted considering that factors such as the length of the constructs and material for the screw-heads were not identical to our model. Although these factors may influence the results marginally, the conclusions should remain the same.
2. Comparison of Dual Versus 4-Rod Constructs Following ACR
The results of our numerical analyses demonstrate a decreased global L1–S1 ROM in all 4-rod constructs compared to the 2-rod construct, suggesting that the use of additional rods leads to a reduction in motion. Our results also indicated that the maximum von Mises stresses on the primary rods were considerably lower in all of the 4-rod constructs compared to the 2-rod construct. Our findings are consistent with the study of Januszewski et al. [27] in which they observed the addition of rods led to a decrease in stresses on the primary rods. However, the comparison of rod configurations done in that study were different from the present study.
Godzik et al. [1] conducted a multicenter retrospective study on rod fractures after ACR surgery and found that the rod fractures occurred adjacent to the ACR site. Our dual-rod ACR construct model also predicted higher stresses on the rods at the ACR site. Thus, a possible explanation for rod fracture at the ACR site could be the fact that the stress concentration occurs in this region.
However, with the addition of accessory rods, the high-stress regions on the primary rods migrated away from the ACR site to adjacent to the domino. Shen et al. [28] also observed rod fractures adjacent to the domino after the addition of accessory rods. Although the incidence of rod fracture decreases with the addition of accessory rods, drawbacks such as the addition of more metal mass and hindrance in wound closure can become problematic, especially in the case of lateral accessory rods. In contrast, the satellite rod construct does not have such drawbacks but demonstrates a lower value of stresses and thus a higher FOS (4.76). The superiority of the satellite rod constructs over accessory rods in PSO and ACR could be possibly explained by the fact that the satellite rod construct eliminates the need for domino requirement for connecting additional rods to the primary rods. Thus, the notch effect is absent in satellite rod construct that tends to affect the stress on the primary rods. Additionally, satellite rods reduce the need for severe rod contouring of the primary rods. However, the primary rods in accessory rod construct require severe rod contouring that enhances the risk for rod failure [29].
In summary, our FEA assessed the global (L1–S1) ROM and maximum von Mises stress for a dual-rod construct and 3 different 4-rod constructs. The addition of accessory/satellite rods models resulted in higher reduction of maximum von Mises stress on the primary rods when used in the ACR models as compared to the PSO models. The ACR-SAT rod construct showed the highest FOS compared to all other ACR and PSO constructs. The findings of this study are consistent with the literature. Studies done by La Barbera et al. [13] and Godzik et al. [14] have observed that four-rod constructs successfully decrease rod fracture in ACR. Additionally, biomechanical study by Godzik et al. [14] comparing dual versus satellite rod construct following ACR concluded satellite rod construct to be superior to dual-rod construct in terms of reduction of ROM and rod strain. However, the stresses on the rods were not evaluated neither a comparison for other rod configurations following ACR or PSO was not done in that study. Additionally, La Barbera et al. [13] found that simple, 2-rod constructs suffered from much lower stability and higher rod fracture as compared to 4-rod constructs. The results of our computational study also predicted that 4-rod constructs experience lower maximum rod stresses when compared to the dual-rod model following both ACR and PSO. Thus, we highly recommend the use of supplementary rods to reduce the risk for implant failure in ACR and PSO. Due to relatively high failure rate of bilateral rods in PSO, supplementary rods are often used in PSO. On contrary, ACR is relatively a new technique, limited data are able available to compare it with the failure rates of rods in PSO. In a recent study, failure rate of 4.4% was reported for rods following ACR [1]. However, the study did not state that if the ACR constructs had supplementary rods or not. Thus, we believe more clinical data are required that compares failure in bilateral ACR construct vs bilateral rods plus supplementary rods.
3. Limitations
As with any computational study, our FEA also had certain limitations. This study did not consider the adverse effects of notches that are created on rods during manual rod contouring in a surgical environment. This study also did not simulate cyclic loading and thus how soon the rod construct will fail cannot be predicted. Another limitation of our study was that the model did not include paraspinal muscles. However, this limitation was addressed by the addition of follower loads that mitigate the muscle contractions and the bodyweight as proposed by Patwardhan et al. [30]. Other limitations of this FEA include the simplification of material properties and interactions between the different components of the model. Additionally, the use of rods with different materials that can influence the stress values of the rod constructs was not studied. However, this aspect should be explored and may prove to be beneficial in understanding the failure mechanism in rod constructs of different materials.
CONCLUSION
In conclusion, the 4-rod constructs consistently demonstrated lower maximum rod stresses when compared to the dualrod model following both ACR and PSO. The results of our study suggest that the 4-rod constructs proved to be more effective in ACR models rather than PSO models. These findings were consistent with existing literature that suggested the occurrence of rod fracture decreased when 4-rod constructs were implemented. Additionally, the ACR-SAT model is associated with the highest FOS and lowest maximum rod stress when compared to all other models. ACR reduces the risk for complication compared to PSO, but the use of 4-rod constructs may also be more beneficial in ACR compared to PSO. However, additional in vitro and clinical studies are required to confirm that this type of construct is superior to other constructs tested in this study.
Acknowledgments
The work was supported in part by NSF Industry/University Cooperative Research Center at The University of California at San Francisco, San Francisco, CA, The University of Toledo, Toledo, Ohio, The Ohio State University, Columbus, Ohio and Northeastern University, Boston, Massachusetts (www.nsfcdmi.org), and by an allocation from the Ohio Supercomputer Center.
Footnotes
The authors have nothing to disclose.
REFERENCES
- 1.Godzik J, Haglin JM, Alan N, et al. Retrospective multicenter assessment of rod fracture after anterior column realignment in minimally invasive adult spinal deformity correction. World Neurosurg. 2019;130:e400–5. doi: 10.1016/j.wneu.2019.06.096. [DOI] [PubMed] [Google Scholar]
- 2.Safaee MM, Ames CP, Smith JS. Epidemiology and socioeconomic trends in adult spinal deformity care. Neurosurgery. 2020;87:25–32. doi: 10.1093/neuros/nyz454. [DOI] [PubMed] [Google Scholar]
- 3.Kanter AS, Shaffrey CL, Mummaneni P, et al. Introduction: adult spinal deformity: pathophysiology and corrective measures. Neurosurg Focus. 2014;36 doi: 10.3171/2014.3.FOCUS14112. Introduction. [DOI] [PubMed] [Google Scholar]
- 4.Gupta MC, Gupta S, Kelly MP, et al. Pedicle subtraction osteotomy. JBJS Essent Surg Tech. 2020;10:e0028.1–11. doi: 10.2106/JBJS.ST.19.00028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hyun SJ, Rhim SC. Clinical outcomes and complications after pedicle subtraction osteotomy for fixed sagittal imbalance patients: a long-term follow-up data. J Korean Neurosurg Soc. 2010;47:95–101. doi: 10.3340/jkns.2010.47.2.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith JS, Shaffrey E, Klineberg E, et al. Prospective multicenter assessment of risk factors for rod fracture following surgery for adult spinal deformity. J Neurosurg Spine. 2014;21:994–1003. doi: 10.3171/2014.9.SPINE131176. [DOI] [PubMed] [Google Scholar]
- 7.Guevara-Villazón F, Boissiere L, Hayashi K, et al. Multiplerod constructs in adult spinal deformity surgery for pelvic-fixated long instrumentations: an integral matched cohort analysis. Eur Spine J. 2020;29:886–95. doi: 10.1007/s00586-020-06311-z. [DOI] [PubMed] [Google Scholar]
- 8.Banno T, Hasegawa T, Yamato Y, et al. Multi-rod constructs can increase the incidence of iliac screw loosening after surgery for adult spinal deformity. Asian Spine J. 2019;13:500–10. doi: 10.31616/asj.2018.0209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Benoit D, Wang X, Crandall DG, et al. Biomechanical analysis of sagittal correction parameters for surgical instrumentation with pedicle subtraction osteotomy in adult spinal deformity. Clin Biomech (Bristol, Avon) 2020;71:45–52. doi: 10.1016/j.clinbiomech.2019.10.014. [DOI] [PubMed] [Google Scholar]
- 10.Mundis GM, Turner JD, Kabirian N, et al. Anterior column realignment has similar results to pedicle subtraction osteotomy in treating adults with sagittal plane deformity. World Neurosurg. 2017;105:249–56. doi: 10.1016/j.wneu.2017.05.122. [DOI] [PubMed] [Google Scholar]
- 11.Massie LW, Macki M, Zakaria HM, et al. Anterior column reconstruction vs pedicle subtraction osteotomy for severe sagittal plane deformity: early clinical and radiographic outcomes using a hyperlordotic expandable lateral interbody device [abstract #603] Neurosurgery. 2019;66(Supplement 1):123. [Google Scholar]
- 12.Uribe JS, Schwab F, Mundis GM, et al. The comprehensive anatomical spinal osteotomy and anterior column realignment classification. J Neurosurg Spine. 2018;29:565–75. doi: 10.3171/2018.4.SPINE171206. [DOI] [PubMed] [Google Scholar]
- 13.La Barbera L, Wilke HJ, Liebsch C, et al. Biomechanical in vitro comparison between anterior column realignment and pedicle subtraction osteotomy for severe sagittal imbalance correction. Eur Spine J. 2020;29:36–44. doi: 10.1007/s00586-019-06087-x. [DOI] [PubMed] [Google Scholar]
- 14.Godzik J, Pereira BdA, Newcomb AGUS, et al. Optimizing biomechanics of anterior column realignment for minimally invasive deformity correction. Spine J. 2020;20:465–74. doi: 10.1016/j.spinee.2019.09.004. [DOI] [PubMed] [Google Scholar]
- 15.Vosoughi AS, Joukar A, Kiapour A, et al. Optimal accessory rod constructs to mitigate rod failure following pedicle subtraction osteotomy (PSO): a finite element study. Spine J. 2019;19:931–41. doi: 10.1016/j.spinee.2018.11.003. [DOI] [PubMed] [Google Scholar]
- 16.Goel VK, Grauer JN, Patel T, et al. Effects of charité artificial disc on the implanted and adjacent spinal segments mechanics using a hybrid testing protocol. Spine (Phila Pa 1976) 2005;30:2755–64. doi: 10.1097/01.brs.0000195897.17277.67. [DOI] [PubMed] [Google Scholar]
- 17.Goel VK, Mehta A, Jangra J, et al. Anatomic Facet Replacement System (AFRS) restoration of lumbar segment mechanics to intact: a finite element study and in vitro cadaver investigation. SAS J. 2007;1:46–54. doi: 10.1016/SASJ-2006-0010-RR. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Palepu V. Biomechanical effects of initial occupant seated posture during rear end impact injury [dissertation] Toledo (OH): University of Toledo; 2013. [Google Scholar]
- 19.Edwards WT, Zheng Y, Ferrara LA, et al. Structural features and thickness of the vertebral cortex in the thoracolumbar spine. Spine (Phila Pa 1976) 2001;26:218–25. doi: 10.1097/00007632-200101150-00019. [DOI] [PubMed] [Google Scholar]
- 20.Joukar A, Shah A, Kiapour A, et al. Sex specific sacroiliac joint biomechanics during standing upright: a finite element study. Spine (Phila Pa 1976) 2018;43:E1053–60. doi: 10.1097/BRS.0000000000002623. [DOI] [PubMed] [Google Scholar]
- 21.Bruna-Rosso C, Arnoux PJ, Bianco RJ, et al. Finite element analysis of sacroiliac joint fixation under compression loads. Int J Spine Surg. 2016;10:16. doi: 10.14444/3016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kiapour A. Investigation into lumbar spine biomechanics of 360 motion preservation systems [dissertation] Toledo (OH): University of Toledo; 2009. [Google Scholar]
- 23.Ivanov AA, Kiapour A, Ebraheim NA, et al. Lumbar fusion leads to increases in angular motion and stress across sacroiliac joint: a finite element study. Spine (Phila Pa 1976) 2009;34:E162–9. doi: 10.1097/BRS.0b013e3181978ea3. [DOI] [PubMed] [Google Scholar]
- 24.Lindsey DP, Kiapour A, Yerby SA, et al. Sacroiliac joint fusion minimally affects adjacent lumbar segment motion: a finite element study. Int J Spine Surg. 2015;9:64. doi: 10.14444/2064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Uribe JS, Harris JE, Beckman JM, et al. Finite element analysis of lordosis restoration with anterior longitudinal ligament release and lateral hyperlordotic cage placement. Eur Spine J. 2015;24 Suppl 3:420–6. doi: 10.1007/s00586-015-3872-7. [DOI] [PubMed] [Google Scholar]
- 26.Shim CS, Park SW, Lee SH, et al. Biomechanical evaluation of an interspinous stabilizing device, Locker. Spine (Phila Pa 1976) 2008;33:E820–7. doi: 10.1097/BRS.0b013e3181894fb1. [DOI] [PubMed] [Google Scholar]
- 27.Januszewski J, Beckman JM, Harris JE, et al. Biomechanical study of rod stress after pedicle subtraction osteotomy versus anterior column reconstruction: a finite element study. Surg Neurol Int. 2017;8:207. doi: 10.4103/sni.sni_44_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shen FH, Qureshi R, Tyger R, et al. Use of the “dual construct” for the management of complex spinal reconstructions. Spine J. 2018;18:482–90. doi: 10.1016/j.spinee.2017.08.235. [DOI] [PubMed] [Google Scholar]
- 29.Tang JA, Leasure JM, Smith JS, et al. Effect of severity of rod contour on posterior rod failure in the setting of lumbar pedicle subtraction osteotomy (PSO) a biomechanical study. Neurosurgery. 2013;72:276–83. doi: 10.1227/NEU.0b013e31827ba066. [DOI] [PubMed] [Google Scholar]
- 30.Patwardhan AG, Havey RM, Carandang G, et al. Effect of compressive follower preload on the flexion-extension response of the human lumbar spine. J Orthop Res. 2003;21:540–6. doi: 10.1016/S0736-0266(02)00202-4. [DOI] [PubMed] [Google Scholar]