Sample size calculation for two-arm trials with time-to-event endpoint for non-proportional hazards using the concept of Relative Time when inference is built on comparing Weibull distributions.

Abstract

Sample size calculations for two-arm clinical trials with a time-to-event endpoint have traditionally used the assumption of proportional hazards (PH) or the assumption of exponentially distributed survival times. Available software provides methods for sample size calculation using a nonparametric logrank test, Schoenfeld’s formula for Cox PH model, or parametric calculations specific to the exponential distribution. In cases where the PH assumption is not valid, the first-choice method is to compute sample size assuming a piecewise linear survival curve (Lakatos approach) for both the control and treatment arms with judiciously chosen cut-points. Recent advances in literature have used the assumption of Weibull distributed times for single-arm trials, and, newer methods have emerged that allow sample size calculations for two-arm trials using the assumption of proportional times (PT) while considering non-proportional hazards. These methods, however, always assume an instantaneous effect of treatment relative to control requiring that the effect size be defined by a single number whose magnitude is preserved throughout the trial duration. Here, we consider the scenarios where the hypothesized benefit of treatment relative to control may not be constant giving rise to the notion of Relative Time (RT). By assuming that survival times for control and treatment arm come from two different Weibull distributions with different location and shape parameters, we develop the methodology for sample size calculation for specific cases of both non-PH and non-PT. Simulations are conducted to assess the operation characteristics of the proposed method and a practical example is discussed.

1. Introduction

Two-arm randomized control trials (RCTs) are considered the gold standard in phase II and phase III clinical trials as they allow biomedical researchers to measure and assess the benefit of a new experimental treatment relative to a standard control. When the primary endpoint in such RCTs constitutes time-to-event data, existing methods for sample size calculation are traditionally done assuming either proportional hazards (PH) or by assuming that the survival time follows an exponential distribution. Standard statistical software can be used to perform the sample size calculations using the non-parametric logrank test of Freedman (1982) or Lachin and Foulkes (1986). Other popular options include the Schoenfeld (1981, 1983) sample size formula for semi-parametric PH model of Cox (1972), or the Bernstein and Lagakos (1978) sample size formula using the F-test for exponentially distributed survival times. Typically, a statistician consults his/her research collaborators about the design inputs such as one-sided or two-sided hypotheses, type I error, power, accrual time, follow-up time, effect size, and the proportion of dropouts expected during the trial. Once this is done, sample size calculation often proceeds by first calculating the number of events required to be observed in the trial, followed by calculations that account for potential administrative censoring and random loss to follow-up or drop-outs in order to get the number of subjects that need to be enrolled in the study.

When the underlying assumptions do not hold, the above-mentioned traditional methods may not be preferred and there is a need to develop a method that is derived under more realistic assumptions, provides high power while controlling for the type I error, and one which provides related estimates that are easy to understand. Often the indication of the inappropriateness of the underlying assumptions is available through published results of previously conducted similar studies and through subject matter discussions with biomedical collaborators. For example, when designing a two-arm phase III RCT, such indications about the non-constancy of the hazard ratio (HR) may be available through results of a phase II study by means of observed-vs-expected plot and the log-log survival plot thus making it less appropriate to still assume PH for the current phase III study. Likewise, the Kaplan Meier (KM) plot together with a log-survival (LS) plot may bring into question the assumption of exponentially distributed survival times. Thus, other methods are needed to perform the sample size calculations in these situations.

Recent advances in literature in the last ten years have proposed alternate methods of sample size calculation for certain special scenarios when the above-mentioned assumptions are not valid. For example, finding the PH assumption to be quite restrictive, Royston and Parmar (2013) have proposed sample size calculation on the basis of restricted mean survival time (RMST) whereas Zhao et al. (2016) has proposed a calculation on the basis of event rates. In cases where the lack of PH assumption is due to there being a ‘cured’ fraction in both the study arms, Xiong and Wu (2017) have developed sample size calculations for the ‘cure-rate’ model by improving on the calculations proposed by Wang et al. (2012). Likewise, Gigliarano et al. (2017) have discussed comparison of two survival curves for the log-scale-location family of survival time models, and, Phadnis et al. (2017) have developed sample size calculations when survival times follow a three-parameter generalized gamma distribution using the concept of Proportional Time (PT). Recent developments in the last two years include contributions by Magirr and Burman (2019) who have shown that their modestly weighted logrank tests provides high power under a delayed-onset treatment effect scenario, and, Jimenez et al. (2019) who have studied the properties of the weighted log-rank test in designing studies with delayed effects. As all these methods are yet to find wide-spread acceptance (perhaps, due to the lack of free and commercial software), another approach to calculate sample sizes is by using simulations by assuming piecewise constant hazards in each of the two arms. This approach requires the statistician to judiciously choose time intervals such that in each interval of time the hazard in each of the two study arms is a constant though this hazard may change from one interval to another. Then assuming a constant hazard ratio, one can find the sample size that yields an acceptable value of power corresponding to pre-determined effects size by using simulations. Thus, though different hazard shapes emerging from distributions other than the exponential distribution can be approximated, the effect size is still defined by means of a constant HR thereby restricting its use when such a restriction is not appropriate (we discuss this more in Results section). In recent literature, Mok et al. (2019) have used the piecewise HRs to account for the possibility of non-PH in an oncology trial. Also, Gregson et al. (2019) provide a good overview of different methods of accounting for non-PH for time-to-event outcomes in clinical trials in cardiology.

The default (or ‘go-to’) method for sample size calculation in the non-PH case, is thus the method proposed by Lakatos (1988) that uses Markov state transition probabilities to perform the sample size calculations. This requires the user to have a good idea of how the survival curves in the two arms look under the alternate hypothesis. Then the statistician constructs time intervals such that the true shape of the two survival curves is well approximated by piece-wise linear functions. This method offers flexibility in terms of incorporating loss to follow-up, non-compliance, and administrative censoring while being able to calculate sample sizes for the two arms by considering any general shape of the two survival curves. The limitations are that some trial and error is required to determine the number of piece-wise intervals in addition to making many critical assumptions about the transition probabilities. It is important to note that this method allows effect sizes to vary over the course of the trial (small effect at the beginning and large effect at the end, or vice-versa). Due to its generalizability, this method is available in popular software like SAS, R, nQuery, and PASS. The advantages and disadvantages of the methods using the logrank statistic for sample size calculation under the exponential distribution, PH and non-PH scenarios has been studied by Lakatos and Lan (1992).

In this paper, we discuss a new parametric approach to calculate sample sizes for a two-arm RCT allowing for non-PH as well as for non-PT (this concept is explained in the Methods section) using Weibull distributions with different parameters for the two arms. That is, we propose a method of sample size calculation that can be used for both of the following scenarios: {i} new treatment shows a small improvement in longevity compared to a standard control during the early period of the trial and the magnitude of this improvement increases as the trial progresses, and, {ii} new treatment shows a large improvement in longevity compared to a standard control during the early period of the trial and the magnitude of this improvement decreases as the trial progresses. We do not allow arbitrary crossing of two survival curves in our proposed method, but allow it at reasonably small or large values of the survival percentiles.

Our method is motivated by a combination of the previous works done by us and by other authors and we have structured in the following way. Section 2 discusses two motivating examples highlighting the need for adopting our proposed method for sample size calculations. The main methodology is explained in Section 3 wherein the test statistic development is followed by calculation of sample size accounting for administrative censoring, and, this is further followed by justification for inflation to the sample size due to dropouts. We also discuss an alternate model formulation and offer two ways to analyze the data after the trial is concluded. Analytical and simulation-based results are discussed in Section 4 to provide insights into the operation characteristics of the proposed method. In Section 5, we summarize and discuss the advantages and limitations of our method and suggest recommendations for future research in this area. We have used SAS software (2017) for creating macros that implement our proposed method. Some details related to mathematical derivations and ancillary topics are mentioned in the Appendix.

2. Motivating Examples

We discuss two examples representing the two main scenarios that highlight the application of our proposed method. Additional variations of these two main scenarios are discussed in the Results section to allow the reader to assess how the sample size calculations vary as a function of the varying design inputs.

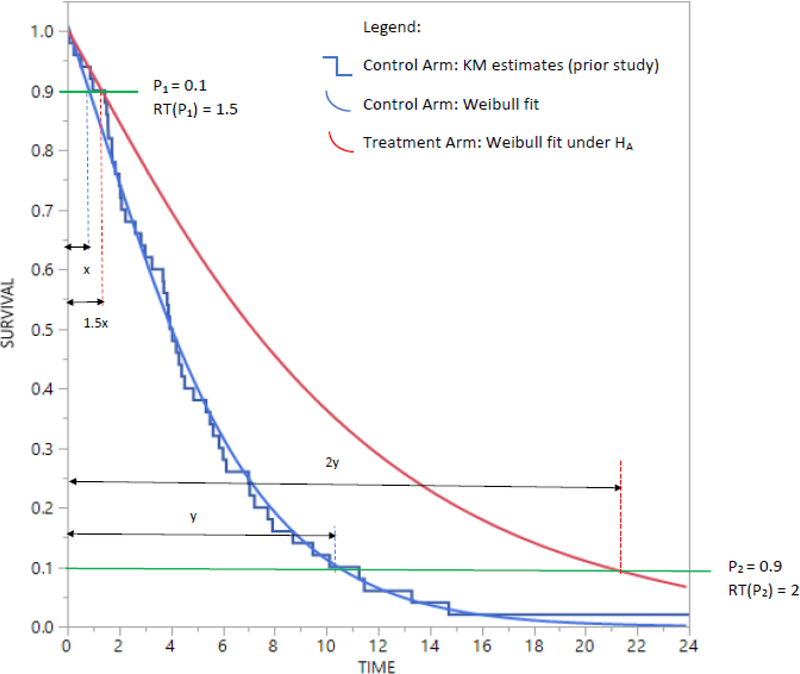
The first example concerns the design of a two-arm phase III RCT for treating patients suffering from chemotherapy refractory advanced metastatic biliary cholangiocarcinoma, a “rare” but aggressive neoplasm. Such patients undergo an initial treatment followed by a second-line treatment. Researchers are interested in comparing a new experimental (E) second-line treatment to a standard control (C) second-line treatment with progression-free survival (PFS) as the time-to-event endpoint (hereafter the letters E and C are used for recurring references to experimental treatment and standard control respectively). The PFS for the C arm has been studied in a prior single-arm phase II study with results being reported using a KM curve in addition to reporting the median of 4 months and interquartile range (IQR) of 2–7 months. The researchers hypothesize that in the two-arm trial under consideration the E arm will show a clinically meaningful improvement in the median PFS. However, they are also of the opinion that this improvement in longevity measured in the metric of time will be gradual. That is, the improvement for 10^th percentile of PFS will be by a factor of 1.5 and as the effect of treatment improves with passage of time, the improvement for 90^th percentile of PFS will be by a factor of 2. That is, the effect size of interest is improvement in the median PFS but that this improvement is not instantaneous upon delivery of treatment, rather, it increases gradually over time. In other words, the new treatment confers an improvement in longevity for a range of survival quantiles (though the median is of specific interest to the researchers). Accrual and follow-up times are both 12 months, type I error is taken at 5% for a one-sided test (which is acceptable for rare cancers) with a target power of 80%. Thus, contrary to the assumption of PH or of exponentially distributed times, the effect size is not defined through a single constant number such as a hazard ratio or constant ratio of medians (note using the exponential distribution assumptions, the ratio of medians is the same as ratio of means or the ratio of any two quantiles of time). This example thus represents frequently real-life scenarios in cancer trials where researchers expect long-term survivors to benefit maximum from a new treatment but expect only small realistic improvements for the short-term survivors. This scenario is represented in Figure 1 (some notations are explained later in the Methods section). Due to varying magnitudes of the expected improvement during the trial, the research hypothesis intends to find a clinically meaningful improvement in median PFS.

Figure 1.

Scenario #1 with effect size defined as RT(0.1) = 1.5 and RT(0.9) = 2.

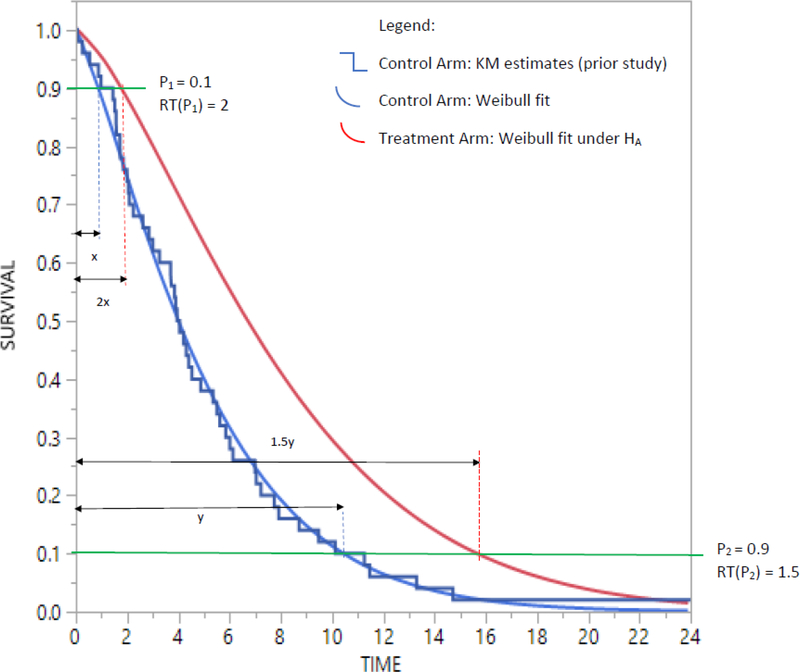
The second example (See Figure 2) is representative of a real-life scenario pertaining to surgery as an experimental treatment whose performance is compared to a non-surgical standard-of-care control. Researchers hypothesize that patients randomized to receiving surgery, will, following surgery, experience an immediate benefit in terms of improved longevity which is considerably large in magnitude, but that this improvement will wane as time progresses. That is, the improvement for 10^th percentile of Overall Survival (OS) will be by a factor of 2 and as the effect of treatment improves over time, the improvement for 90^th percentile of OS will be by a factor of 1.5. Again, the effect size used to do the sample size calculations will be based on a clinically meaningful improvement of median OS, with all other design parameters the same as in the first example.

Figure 2.

Scenario #1 with effect size defined as RT(0.1) = 2 and RT(0.9) = 1.5.

In both the above-mentioned examples, researchers would like to perform a sensitivity analyses by varying some of the design parameters. For example, if the calculated sample size is very large, researchers would like to consider larger values of accrual and follow-up time and re-do the sample size calculations. Likewise, they also want to assess how sample size calculations change when the improvement factors of 1.5 and 2 are defined at the 25^th and 75^th percentile of survival time in place of the 10^th and 90^th percentiles of survival time. In the next section, we develop the methodology for performing the calculations by imposing some restrictions on the crossing of the survival curves of the two arms.

3. Methods

As both scenarios discussed in Section 2 are concerned with improvement in longevity as a measure of assessing the E vs C benefit, we develop a modeling framework in which the main calculations are performed in the metric of time. This is also inspired by the fact that in our collaborations with biomedical researchers, we found that they were more comfortable in defining E vs C benefit in terms of median survival time rather than a hazard ratio. Here it should also be noted that when the survival times in the two arms follow an exponential distribution then an effect size definition in terms of ratio of medians can, by taking the reciprocal, be expressed as a hazard ratio. But when the assumption of exponential distribution is suspect, a closed form conversion formula may not always be available. For example, an oncologist may hypothesize that new treatment increases the median survival time in control group of 6 months to 9 months. This implies the effect size defined as ratio of medians is 1.5 but without the assumption of exponential distribution, one cannot say the study should be powered to detect a HR of 6/9 = 0.667.

3.1. Modeling framework and concept of Relative Time

Recent papers for sample size calculation for single arm trials such as Wu (2015) and Phadnis (2019) have used the assumption of Weibull distributed time for the standard control arm. The Weibull distribution is a two-parameter distribution whose probability density function is:

$$\begin{array}{c}f\left(t\right)=\frac{\beta }{{\theta }^{\beta }}{t}^{\beta -1}\text{exp}\left\{-{\left(t/\theta \right)}^{\beta }\right\}\theta ,\beta >0,t>0\end{array}$$ (1)

Here, θ is a scale parameter and β is a shape parameter that determines the shape of the hazard function (β>1 gives hazard that increases over time, β<1 gives hazard that decreases over time, and β=1 represents the special case of exponential distribution with constant hazard). Both Wu (2015) and Phadnis (2019) have used a point estimate of β in their sample size calculation and have recommended that users obtain an estimate of β from prior historical studies. Through simulation studies, Phadnis et al. (2020) have investigated how accurate the estimate of β is when it is estimated from the x-y coordinates (x = time, y = survival probability) of a KM plot published using prior study data. Their simulations suggest that for prior studies with moderate right-censoring of up to 40%, a sample size of 50 keeps the average relative bias (ARB) consistently below 10% even when only 3 x-y coordinate pairs are used to estimate β and the accuracy increases (ARB decreases) as information from more x-y coordinates is used. Additionally, the scaled root mean square error (SRMSE) and coefficient of variation (CV) are maintained below 20% and 12% respectively. Encouraged by these results, in our current proposal also, we assume that β for the standard control arm is either known or can be estimated with reasonably accuracy from prior study data or published KM plots. We call this β₀ with the subscript 0 indicating the control arm.

Next, we briefly discuss the concept of Relative Time although an excellent description of the same can be found in Cox et al. (2007). Relative time can be defined as the ratio of times at which exactly 100*p % of the individuals in one study arm experience an event of interest. Due to the dependence on p, it is denoted as RT(p). Thus, the interpretation of RT(p) is that the time required for 100*p % of the individuals in one study arm to experience an event is RT(p)-fold times the time required for 100*p % of the individuals in other study arm. That is,

$$RT\left(p\right)=\frac{t_1\left(p\right)}{t_0\left(p\right)}$$ (2)

Here, ${{t_i\left(p\right)=S}_i}^{-1}\left(1-p\right)$ is the inverse survival function for study arm i (i = 0, 1). Let θ_i and β_i (for i = 0, 1) represent the scale and shape parameters of two different Weibull distributions for C and E. From (2) we also have 1−p=S_i{t_i(p)} and from (1) we know that S_i{t_i(p)}=exp[−{t_i(p)/θ_i}^β_i] leading to

$$t_i\left(p\right)={\theta }_i{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p}\right)\right\}}^{1/{\beta }_i}$$ (3)

Thus RT(p) can be expressed as

$$RT\left(p\right)=\frac{t_1\left(p\right)}{t_0\left(p\right)}=\frac{{\theta }_1}{{\theta }_0}{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p}\right)\right\}}^{\frac{1}{{\beta }_1}-\frac{1}{{\beta }_0}}$$ (4)

On the logarithm scale, equation (4) becomes

$$\text{log}\left\{RT\left(p\right)\right\}=\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left({\theta }_1\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left({\theta }_0\right)\right\}+\left(\frac{1}{{\beta }_1}-\frac{1}{{\beta }_0}\right)\cdot \text{log}\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p}\right)\right\}$$ (5)

From equations (4) and (5) we see that when β₁=β₀, the dependency on p disappears and in that case RT(p) is a constant and can be called ‘Proportional Time (PT)’ which reduces, in our case to a standard accelerated failure time (AFT) model using the assumption of Weibull distributed survival times. In case of the Weibull, this also simultaneously results in the PH assumption being true, but this is not true for other distributions. See Cox et al. (2007) for more details on this topic where the Weibull is a special case of the generalized gamma distribution and how the PT assumption reduces to a standard AFT model.

3.2. Setting up the hypotheses

As an example in a practical RCT setting, we consider the scenario that researchers consult a statistician to design a trial such that an improvement in median survival time in C (say, 4 months) to E is detectable with 80% power using a one-sided (or two-sided) hypotheses after incorporating the information that at p₁=0.10, RT(p₁)=1.5 and p₂=0.90, RT(p₂)=2. Since the median survival time in C is known, we have θ₀=t₀(0.5)/{ln (2)}^1/β₀. Taking logarithm on both sides of (4) and writing it as two separate equations, first with p₁=0.10, RT(p₁)=1.5, and, second with p₂=0.90, RT(p₂)=2, we have two equations with two unknowns and we can calculate θ₁ and β₁ thereby determining the survival curves for C and E. Given these values, we can calculate the desired effect size at p_mid=(p₁+p₂)/2 as

$$RT\left(p_{mid}\right)=\frac{t_1\left(p_{mid}\right)}{t_0\left(p_{mid}\right)}=\frac{{\theta }_1}{{\theta }_0}{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)\right\}}^{\frac{1}{{\beta }_1}-\frac{1}{{\beta }_0}}$$ (6)

We can now write down our hypotheses in the following way:

$$\begin{gathered} {\mathrm{H}}_0:RT\left(p_{mid}\right)\le 1 \\ {\mathrm{H}}_1:RT\left(p_{mid}\right)>1 \end{gathered}$$ (7)

Noting that for p₁=0.10 and p₂=0.90, we have p_mid=0.5 with t₀(0.5) and t₁(0.5) representing the median survival time in the C and E respectively, our hypotheses will be

$$\begin{gathered} {\mathrm{H}}_0:RT\left(0.5\right)\le 1 \\ {\mathrm{H}}_1:RT\left(0.5\right)>1 \end{gathered}$$ (8)

That is, if the researchers desire to draw inference on the improvement in median survival time for E vs C, the statistician can ask them to provide information of p₁ and p₂ such that p_mid=(p₁+p₂)/2 is ensured. Alternatively, in our SAS code, we have also allowed the user to choose a p_user≠p_mid and define the hypotheses at this p_user value. It should be noted that although the examples considered by us use a one-sided type I error of 5% (owing to the specific disease under consideration), a type I error of 2.5% (or any other reasonable value) can also be dealt by our proposed method.

An important feature of our proposed method are the user-defined inputs at p₁, p₂, RT(p₁) and RT(p₁). These inputs determine the value of RT(p_mid) through equation (6). That is, information about p_j and RT(p_j) for j=2 are enough to perform the sample size calculations due to the fact that (5) can be seen as a straight-line equation of the type $y=b_0+b_{1}x$ in which $b_0=\mathrm{l}\mathrm{o}\mathrm{g}\left({\theta }_1\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left({\theta }_0\right)$ plays the role of an intercept and $b_1=\frac{1}{{\beta }_1}-\frac{1}{{\beta }_0}$ plays the role of the slope with this straight line passing through the [x, y] coordinate pairs $\left[\mathrm{l}\mathrm{o}\mathrm{g}\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_j}\right)\right\},\mathrm{l}\mathrm{o}\mathrm{g}\left\{RT\left(p_j\right)\right\}\right]$. If instead, user-inputs are defined with j>2, then sample size calculations can still be performed at $p_{mid}=\frac{1}{j}{\sum }_j{p}_j$ but the straight-line is no longer guaranteed to pass through the [x, y] coordinate pairs $\left[\mathrm{l}\mathrm{o}\mathrm{g}\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_j}\right)\right\},\mathrm{l}\mathrm{o}\mathrm{g}\left\{RT\left(p_j\right)\right\}\right]$. Instead, it will be the “line of best fit” passing through the mean $\left[\mathrm{l}\mathrm{o}\mathrm{g}\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)\right\},\mathrm{l}\mathrm{o}\mathrm{g}\left\{RT\left(p_{mid}\right)\right\}\right]$. For example, the user inputs β₀=0.5, median survival in C arm = 4 months, p₁=0.1, p₂=0.9, RT(p₁)=1.5, and RT(p₂)=2 will yield RT(p_mid)=RT(0.5)=1.788 (see also Section 3.6). Instead if the user inputs are p₁=0.1, p₂=0.25, p₃=0.75, p₄=0.9, RT(p₁)=1.5, RT(p₂)=1.667, RT(p₃)=1.833, and RT(p₄)=2 then the value of p_mid is still 0.5, but RT(p_mid)=RT(0.5) will be 1.773 instead of 1.788 resulting in a slightly increased sample size. Thus, although in principle p_j and RT(p_j) with j>2 can be used to perform the calculations, researchers may find it practically friendly to inform the statistician about the hypothesized RT(p)-fold improvement at only two percentiles of survival data.

3.3. Development of a new test statistic

Let ${\widehat{\theta }}_i$ for i = 0, 1 be the maximum likelihood estimate of θ_i in the C and E arms respectively. Then we know that for the Weibull distribution with all observations as events (no censoring) with d_i events in the i^th arm

$$\begin{array}{c}{\widehat{\theta }}_i={\left(\frac{\sum _{j=1}^{d_i}{t}_{ij}^{{\beta }_i}}{d_i}\right)}^{1/{\beta }_i}\end{array}$$ (9)

Since each t_ij~weibull(θ_i,β_i), it can be shown that (see Appendix A.1) ${\widehat{\theta }}_i~\mathrm{G}\mathrm{G}\left(d_i,{\theta }_i/{d_i}^{1/{\beta }_i},{\beta }_i\right)$ where the letters GG stand for a 3-parameter generalized gamma distribution.

From this we get

$$\begin{array}{c}{\widehat{\theta }}_i{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)\right\}}^{\frac{1}{{\beta }_i}}~GG\left[d_i,{\theta }_i{\left\{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)}{d_i}\right\}}^{\frac{1}{{\beta }_i}},{\beta }_i\right]\end{array}$$ (10)

Using a reparameterization by taking ${\lambda }_i=1/\sqrt{d_i},{\sigma }_i=1/\left({\beta }_i\sqrt{d_i}\right)$ and ${\mu }_i=\mathrm{l}\mathrm{o}\mathrm{g}\left[{\theta }_i{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)\right\}}^{\frac{1}{{\beta }_i}}\right]$ we can say that ${\widehat{\theta }}_i{\left[\mathrm{l}\mathrm{o}\mathrm{g}\left\{1/\left(1-p_{mid}\right)\right\}\right]}^{1/{\beta }_i}~\mathrm{G}\mathrm{G}\left({\lambda }_i,{\mu }_i,{\sigma }_i\right)$. The advantage of this reparameterization is that we can see that as the number of events d_i increases, λ_i decreases towards 0. Even for d_i=25, we get λ_i=0.2. A well-known property of the GG distribution is that as λ_i→0, the distribution converges to a lognormal distribution. That is, denoting $Q_i={\widehat{\theta }}_i{\left[\mathrm{l}\mathrm{o}\mathrm{g}\left\{1/\left(1-p_{mid}\right)\right\}\right]}^{1/{\beta }_i}$, we get $Q_i\mathrm{ }\dot{~}\mathrm{ }\mathrm{L}\mathrm{o}\mathrm{g}\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}({\mu }_i,{\sigma }_i)$. See Stacy and Mihram (1965) and Cox et al. (2007) for more properties of the GG distribution along with a brief discussion in the Appendix A.2 mentioning how some popular distributions such as Weibull, lognormal, gamma, ammag, inverse Weibull, inverse gamma, and exponential are special cases. Appendix A.3 further elaborates the Relative Time framework using a Venn diagram and briefly explains where the proposed method fits in this framework. Some additional discussion is provided describing the motivation to choose the proposed method (two different Weibull distributions) based on practical considerations.

Klein and Moeschberger (2003) discuss that the three-parameter GG distribution is infrequently used to model time-to-event data for reporting analysis results. Instead, after fitting a GG distribution to a dataset, Klein and Moeschberger (2003) mention that based on estimate of λ, statisticians often choose a two (or single) parameter distribution. In practice, an estimate of 0.2 or lower for λ will be a comfortable justification for using a lognormal distribution. In the context of our topic, d_i=25 should be considered large enough for us to claim $Q_i\dot{~}\mathrm{L}\mathrm{N}({\mu }_i,{\sigma }_i)$. Then using the relationship between a lognormal and Gaussian distributions, we can also say that $\ln \left(Q_i\right)\dot{~}\mathrm{N}({\mu }_i,{\sigma }_i)$. In this notation, note that the ${\sigma }_i$ is standard deviation and not variance.

That is, we now develop a new test statistic on asymptotic normality in the following way.

$$\begin{array}{c}{Q}^{\mathrm{\text{'}}}=\text{log}\left(Q_1\right)-\text{log}\left(Q_0\right)\dot{~}N\left({\mu }_d,{\sigma }_d\right)\end{array}$$ (11)

where ${\mu }_d={\mu }_1-{\mu }_0=\mathrm{l}\mathrm{o}\mathrm{g}\left[\frac{{\theta }_1}{{\theta }_0}{\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1}{1-p_{mid}}\right)\right\}}^{\frac{1}{{\beta }_1}-\frac{1}{{\beta }_0}}\right]$ and ${\sigma }_d=\sqrt{{\sigma }_1^2+{\sigma }_0^2}=\sqrt{\frac{1}{d_1{\beta }_1^2}+\frac{1}{{d_0\beta }_0^2}}$

If we define an allocation ratio as r = d₁/d₀, then we have

$$\begin{array}{c}{\sigma }_d=\sqrt{\frac{1}{d_0}\left(\frac{1}{r{\beta }_1^2}+\frac{1}{{\beta }_0^2}\right)}=\left(\sqrt{\frac{1}{r{\beta }_1^2}+\frac{1}{{\beta }_0^2}}\right)/\sqrt{d_0}\end{array}$$ (12)

Thus, our newly proposed test statistic is defined as

$$\begin{array}{c}Z=\frac{Q^{\mathrm{\text{'}}}-{\mu }_d}{{\sigma }_d}\end{array}$$ (13)

Thus, under the null H₀ we have Z~N(0,1), and under the alternate H₁ we have Z~N(μ_d/σ_d, 1). Then, for a one-sided test with a given allocation ratio r, the number of events in the two study arms can be calculated as

$$\begin{gathered} d_0={\left[\frac{\left(Z_{\omega }+Z_{1-\alpha }\right)}{\mathrm{l}\mathrm{o}\mathrm{g}\left\{RT\left(p_{mid}\right)\right\}}\right]}^2\left(\frac{1}{r{\beta }_1^2}+\frac{1}{{\beta }_0^2}\right) \\ {d}_1=r{d}_0 \end{gathered}$$ (14)

where α is the type I error for the one-sided test and ω is the target power of the test. For a two-sided test, we can use α/2 in place of α.

Thus, knowledge of β₀ through the historical study and the calculation of β₁ through the effect size pre-specification allows us to perform the sample size calculations.

The interesting feature of the formula in (14) is that when β₁=β₀=β, that is, for the special case of proportional time (PT), it reduces to

$$\begin{array}{c}{d}_0={\left\{\frac{\left(Z_{\omega }+Z_{1-\alpha }\right)}{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{{\theta }_1}{{\theta }_0}\right)}\right\}}^2\left(\frac{1+r}{r{\beta }^2}\right)\end{array}$$ (15)

Then letting q=d₀/(d₀+d₁) and 1−q=d₁/(d₀+d₁) as the proportional of events in the C and E arms respectively, we can re-express the formula in (13) as

$$d_0={\left[\frac{\left(Z_{\omega }+Z_{1-\alpha }\right)}{\mathrm{\beta }\left\{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{{\theta }_1}{{\theta }_0}\right)\right\}}\right]}^2\frac{1}{q\left(1-q\right)}$$ (16)

which further simplifies to

$$\begin{array}{c}{d}_0=\frac{{\left(Z_{\omega }+Z_{1-\alpha }\right)}^2}{q\left(1-q\right){\mathrm{l}\mathrm{o}\mathrm{g}}^2\left({\mathrm{\Delta }}_{\mathrm{H}\mathrm{R}}\right)}\end{array}$$ (17)

which is the exact same sample size formula obtained by Schoenfeld (1981) for the Cox PH model. That is, we can interpret our new sample size formula in (14) as an extra adjustment to Schoenfeld formula when accounting for the two different shape parameters of two different Weibull distributions. Alternatively, the Schoenfeld formula can be thought of as a special case of our newly developed sample size formula.

3.4. Calculation of sample size accounting for administrative censoring

Assuming a uniform accrual, the censoring distribution function G(t) is given by

$$\begin{array}{c}G\left(t\right)=\left\{\begin{array}{c}1\\ \frac{a+f-t}{a}\\ 0\end{array}\begin{array}{c}\mathrm{i}\mathrm{f}t\le f\\ \mathrm{i}\mathrm{f}f\le t\le a+f\\ \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right\}\end{array}$$ (18)

where a and f are the accrual and follow-up time respectively. Then the probability that a subject experiences an event during the trial in arm i (i = 0, 1) is

$$\begin{array}{c}{v}_i=\underset{0}{\overset{\mathrm{\infty }}{\int }}G\left(t\right).f_i\left(t\right)dt\end{array}$$ (19)

where f_i(t) is f(t) with θ=θ_i and β=β_i. Dividing the number of events obtained through the sample size formula in (14) by v=(v₀+v₁)/2 gives the sample size adjusted for administrative censoring. Alternatively, v_i can be calculated using Simpson’s rule by

$$\begin{array}{c}{v}_i=1-\frac{1}{6}\left\{S_i\left(f\right)+4S_i\left(f+0.5a\right)+S_i\left(f+a\right)\right\}\end{array}$$ (20)

where S_i(t) is the survival function of the Weibull with θ=θ_i and β=β_i.

3.5. Reformulation as an Extended Cox model and accounting for dropouts

Thus far, we have accounted for administrative censoring in the sample size calculation. Before proceeding to the discussion about adjusting for random loss to follow-up, we briefly discuss the topic of reformulation using an Extended PH model. It should be noted that the method of analysis consistent with the sample size calculation should be pre-specified in the study protocol (although one may use another simpler sample-size method to get an approximation, or alternatively, even change the chosen method of analysis later in the Statistical Analysis Plan). As the proposed method involves two different Weibull distributions, the most direct way to analyze the data after study completion is to fit the data from each study arm using two separate Weibull fits. See Section 3.7 for more details on this process.

As many researchers are accustomed to a hazard ratio interpretation when summarizing RCT data, they would like to know how the HR changes over time given that the PH assumption is not true. In this context, we can see that the ratio of hazards for the two study arms at time t is

$$\begin{array}{c}\frac{h_1\left(t\right)}{h_0\left(t\right)}=\frac{{\beta }_1}{{\beta }_0}\frac{{{\theta }_0}^{{\beta }_0}}{{{\theta }_1}^{{\beta }_1}}{t}^{{\beta }_1-{\beta }_0}\end{array}$$ (21)

The above equation can be reformulated as

$$\begin{array}{c}{h}_1\left(t\right)=h_0\left(t\right).\exp \left\{{\gamma }_0\mathrm{X}+{\gamma }_1\mathrm{X}\cdot \log \left(\mathrm{t}\right)\right\}\end{array}$$ (22)

where X is the indicator variable with X=0 indicating C arm and X=1 indicating the E arm, h₀(t) is the hazard of the C arm at time t, ${\gamma }_0=\mathrm{l}\mathrm{o}\mathrm{g}\left\{\left({\beta }_1/{\beta }_0\right)\left({{\theta }_0}^{{\beta }_0}/{{\theta }_1}^{{\beta }_1}\right)\right\}$ is the time-independent change is hazard for E vs C, and can be interpreted as the hazard at t = 1. Similarly, γ₁=β₁−β₀ is the regression coefficient for the interaction between the study arm and logarithm of time. Due to the additional interaction term, Equation (22) can thus be considered as an Extended Cox model. That is, two different Weibull distributions corresponding to two study arms can be fit using a single semi-parametric extended Cox model. The converse, however, is not necessarily true.

The advantage of this reformulation is that the parameters of a semi-parametric model are obtained through maximization of the partial likelihood. Since the partial likelihood is only evaluated at the event times and not at the time of right censoring, we can argue that to account for loss due to drop-outs (right-censored observations), we can inflate the sample size calculated after using (14) and (19) by simply dividing by 1 minus the drop-out rate. Thus, for a drop-out rate ρ, the final sample size in the two study arms can be calculated as

$$\begin{gathered} n_0=\frac{d_0}{\left(1-\rho \right)v} \\ {n}_1=r{n}_0 \end{gathered}$$ (23)

3.6. Disallowing arbitrary crossing of survival curves from the two arms

The main research question in RCTs with time-to-event endpoint often pertains finding statistical evidence to show that a new experimental treatment outperforms a standard control. To be consistent with this overall goal, we do not allow any arbitrary crossing of two survival curves from the C and E arms. For example, it is possible that the 10^th and 90^th percentile of PFS is higher in E compared to C, but for a different early (or late) percentile t(p), say 5^h (or 95^th) percentile, S{(t_p)} is higher for C compared to E. Suppose this early inversion at 5^th percentile (due to crossing of the two survival curves) is not consistent with the real-life application under consideration for biological/clinical reasons, then in that case we have added an error check in our SAS code informing the statistician that the current set of inputs entered are inappropriate and need to be reconsidered. For example, consider the following user inputs for our proposed method in the case of the first cholangiocarcinoma example:

User Inputs:

One-sided test, α=0.05, ω=0.8, β₀=0.5, median survival in C arm = 4 months, p₁=0.1, p₂=0.9, RT(p₁)=1.5, RT(p₂)=2, r=1, a=12, f=12, ρ=0.2, q_min=0.001, q_max=0.999

Here, q_min represents the smallest value for p at which the crossing of two curves is permitted as considered plausible based on biological/clinical considerations. Thus 0<q_min<p₁ is the range for q_min and plays a role in the sample size calculation when RT(p₁)<RT(p₂). Analogously, q_max represents the largest value for p at which the crossing of two curves is permitted. Thus p₂<q_max<1 is the range for q_max and plays a role in the sample size calculation when RT(p₁)<RT(p₂).

The above input parameters are obtained from the information provided by the research collaborators, but that RT(p₁)=1.5<RT(p₂)=2 results in crossing of the two survival curves at p=0.00135. At p=0.001 this combination results in RT(0.001)=0.972 which is less than 1 implying that at very early in the observation window, survival in arm C is better than that in arm E. If this inversion of survival benefit is biologically/clinically impossible (as in the case of this cholangiocarcinoma trial, the SAS output generates an error message and recommends the user to take one of the following actions:

1. Decrease the user-input value of p₁ OR

2. Increase the user-input value of RT(p₁) OR

3. Increase the user-input value of p₂ OR

4. Decrease the user-input value of RT(p₂) OR

5. Choose a larger value for q_min (that is, relax the percentile at which the two curves can cross)

Alternatively, keeping p₁ and p₂ same as earlier, we make a recommendation to the user for inputting values for RT(p₁) and RT(p₂) such that RT(0.001)≥1 is always maintained. For the choice of initial user inputs discussed in this example, we recommend using RT(p₁)=1.52 and RT(p₂)=1.98. This results in a sample size of 270 in each arm such that we have 80% power to detect RT(0.5) of 1.788 as greater than 1 with a type I error of 5% using a one-sided test. These values of RT(p₁)=1.52 and RT(p₂)=1.98 are used by us in the Results section related to this example. In other real-life applications where q_min or q_max are not as extreme, a statistician can simply execute our code without expecting an error message. For example, the combination of p₁=0.1, p₂=0.9, RT(p₁)=1.5, RT(p₁)=2 and q_min=0.01 will not produce an error message. Sample size in this case will still be 270 in each arm.

As a second example (for some other trial), if a researcher selects p₁=0.1, p₂=0.9, RT(p₁)=1.25RT(p₂)=3 (with all other user inputs same as in the above example), then the two survival curves will cross at p=0.0469 indicating probable early toxicity. Thus, in this case, setting q_min=0.05 will yield a sample size of 180 in each arm without displaying an error message. But if we choose q_min=0.03, then an error message with a recommendation (similar to the first example) will be displayed. If none of the recommendations are acceptable, the user will be prompted to consider RT(p₁)=1.37, RT(p₂)=2.92 while retaining p₁=0.1, p₂=0.9, q_min=0.03. This yields a sample size of 168 in each arm.

3.7. Data Analysis after completion of trial

For data analysis to be consistent with the proposed method of sample size calculation, PROC LIFEREG in SAS can be used to fit data separately from both study arms by holding the shape parameters β₀ and β₁ constant. PROC LIFEREG will give estimates of ${\widehat{\theta }}_0$ and ${\widehat{\theta }}_1$ along with their corresponding standard errors. Then equation (5) can be used to obtain $\widehat{RT}\left(p_{mid}\right)$ as a point estimate of RT(p_mid). The delta method can be used to utilize the standard errors of ${\widehat{\theta }}_0$ and ${\widehat{\theta }}_1$ to obtain the standard error of $\widehat{RT}\left(p_{mid}\right)$ and results can be reported with a 100(1−α)% confidence interval.

For analyzing data with the semi-parametric extended Cox model, PROC PHREG in SAS can be used to obtain ${\widehat{\gamma }}_0$ and ${\widehat{\gamma }}_1$ along with the corresponding standard errors. At any time t* of interest, the HR can be calculated as $HR\left(t^{*}\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left\{{\widehat{\gamma }}_0+{\widehat{\gamma }}_1.\mathrm{l}\mathrm{n}\left(t^{*}\right)\right\}$ with the corresponding 100(1−α)% confidence interval given by $\mathrm{e}\mathrm{x}\mathrm{p}\left[\left\{{\widehat{\gamma }}_0+{\widehat{\gamma }}_1\mathrm{l}\mathrm{o}\mathrm{g}\left(t\right)\right\}\pm 1.645\cdot SE\left\{{\widehat{\gamma }}_0+{\widehat{\gamma }}_1\mathrm{l}\mathrm{o}\mathrm{g}\left(t\right)\right\}\right]$. See Section 4.3 for simulation results justifying data analysis using this Extended Cox model.

3.8. Sample size adjustments for extra covariates in the model

The sample size formula given in (23) assumes that the randomization process in an RCT balances out the effect of any additional covariates that could be associated with the time-to-event endpoint. In case such extra covariates exist, extra adjustments to the sample size can be made using a variance inflation factor (VIF) adjustment proposed by Hsieh and Lavori (2000) in the context of a Cox model. Briefly, if the main covariate of interest (the study arm: standard control or new treatment) is denoted by X₁ with X₂,X₃,…,X_k being the extra covariates and γ₂,γ₃,…,γ_k their corresponding regression coefficients in the Extended Cox model h₁(t)=h₀(t). exp{γ₀X₁+γ₁X₁.log (t)+γ₂X₂+γ₃X₃+…+γ_kX_k, then if ${\rho }_{cov}^2$ is the proportion of variance explained by the regression of X₁ on X₂,X₃,…,X_k then the conditional variance of X₁|X₂,X₃,…,X_k is smaller than the marginal variance of X₁ by a factor of ${\left({1-\rho }_{cov}^2\right)}^{-1}$. Thus, to preserve power, we can use this VIF to calculate the adjusted sample size using the formula ${\mathrm{N}}_{adjusted}={\mathrm{N}}_{total}/\left({1-\rho }_{cov}^2\right)$. Thus, in the presence of extra covariates, the Extended Cox model can be used to analyze data from such a clinical trial.

4. Results

We now discuss the results emanating from the analytical calculations discussed in the previous section as well as from evaluating the performance of the proposed method using simulations.

4.1. Sample size comparison: Proposed method vs Lakatos method

Table 1 displays the sample size calculation comparing the proposed method to the popularly used Lakatos (piecewise linear survival) method for different settings. For all scenarios presented in this table, we have a one-sided test with α=0.05, target power ω=0.8, median survival in C arm = 4 months, r=1, a=12, f=12, ρ=0. The left panel in this table refers to the user-input of p₁=0.1 and p₂=0.9, the percentiles of survival time at which the longevity improvement factors RT(p₁) and RT(p₂) are defined. Likewise, the right panel in this table refers to the user-input of p₁=0.25 and p₂=0.75. Within the first panel, there are two sub-panels representing two different scenarios: {i} RT(p₁)=1.52, RT(p₁)=1.98 implying gradual improvement in longevity over time in the E vs C arm. {ii} RT(p₁)=2, RT(p₂)=1.5 implying gradual decline in longevity over time (from 100% to 50%) in the E vs C arm. Within the second panel, there are two sub-panels representing two different scenarios: {i} RT(p₁)=1.5, RT(p₁)=1.667 implying gradual improvement in longevity over time in the E vs C arm. {ii}RT(p₁)=1.667, RT(p₂)=1.5 implying gradual decline in longevity over time (from 100% to 50%) in the E vs C arm. The left-most column has the user-input β₀ values that are common to both panels (and sub-panels). The rows in this left-most column represent different scenarios from β₀=0.25 (Weibull hazard decreasing over time in the C arm) to β₀=2 (Weibull hazard increasing over time in the C arm). The middle value of β₀=1 refers to the exponential distribution with constant hazard. For each sub-panel mentioned above we have four columns.

Table 1.

Event size/Sample size (given by d/n) for Proposed method (equal allocation ratio) with α=0.05, one-sided test, 80% power, accrual time 12 months, follow-up time 12 months - for varying combinations of Control-Arm shape parameter β₀ and effect size definitions (RT[p₁] and RT[p₂]) with p₁=0.10, p₂=0.90 and p₁=0.25, p₂=0.75 compared to Event Size/Sample size from Piece-wise Linear (Lakatos) method for varying number ‘m’ of equally spaced intervals

Control arm Shape β0	Time Quantiles at which the effect size is defined
	p1=0.10, p2=0.90												p1=0.25, p2=0.75
	RT(p1)=1.52, RT(p2)=1.98						RT(p1)=2.00, RT(p2)=1.50						RT(p1)=1.500, RT(p2)=1.667						RT(p1)=1.667, RT(p2)=1.500
	Proposed Method			Piecewise Linear (Lakatos) method			Proposed Method			Piecewise Linear (Lakatos) method			Proposed Method			Piecewise Linear (Lakatos) method			Proposed Method			Piecewise Linear (Lakatos) method
	β 1	d/n		#m	d/n		β 1	d/n		#m	d/n		β 1	d/n		#m	d/n		β 1	d/n		#m	d/n
β0 =0.25	β1 =0.2448	601/991		m=2 m=3 m=4 m=6 m=12	629/1044 618/1021 612/1010 607/1001 603/994		β1 =0.2560	722/1182		m=2 m=3 m=4 m=6 m=12	904/1488 871/1428 852/1396 832/1361 809/1323		β1 =0.2459	933/1525		m=2 m=3 m=4 m=6 m=12	978/1608 959/1572 949/1554 941/1539 935/1528		β1 =0.2543	953/1552		m=2 m=3 m=4 m=6 m=12	1176/1926 1134/1853 1111/1812 1086/1764 1058/1723
β0 =0.50	β1 =0.4795	154/216		m=2 m=3 m=4 m=6 m=12	160/228 152/214 148/209 146/205 144/202		β1 =0.5247	177/244		m=2 m=3 m=4 m=6 m=12	262/366 237/329 226/312 216/298 207/285		β1 =0.4838	238/329		m=2 m=3 m=4 m=6 m=12	249/348 235/327 229/318 224/311 222/307		β1 =0.5174	235/321		m=2 m=3 m=4 m=6 m=12	339/470 307/424 293/403 280/384 269/369
β0 =0.75	β1 =0.7047	70/87		m=2 m=3 m=4 m=6 m=12	77/97 69/86 66/82 64/79 63/78		β1 =0.8064	77/93		m=2 m=3 m=4 m=6 m=12	142/175 117/142 107/130 100/121 95/115		β1 =0.7141	108/131		m=2 m=3 m=4 m=6 m=12	120/148 106/130 102/124 98/119 96/117		β1 =0.7898	103/123		m=2 m=3 m=4 m=6 m=12	183/223 150/182 138/167 129/156 123/148
β0 =1.00	β1 =0.9211	41/46		m=2 m=3 m=4 m=6 m=12	50/58 41/48 38/44 37/42 36/41		β1 =1.1029	43/47		m=2 m=3 m=4 m=6 m=12	104/118 74/83 65/72 59/65 55/61		β1 =0.9371	62/69		m=2 m=3 m=4 m=6 m=12	79/90 63/72 59/66 56/63 54/61		β1 =1.0720	57/63		m=2 m=3 m=4 m=6 m=12	134/151 96/106 84/92 76/84 72/79
β0 =1.25	β1 =1.1290	27/29		m=2 m=3 m=4 m=6 m=12	40/44 30/33 27/29 25/27 24/26		β1 =1.4150	27/27		m=2 m=3 m=4 m=6 m=12	95/102 55/59 45/48 40/42 37/38		β1 =1.1532	40/43		m=2 m=3 m=4 m=6 m=12	64/70 46/50 40/44 38/40 36/38		β1 =1.3645	36/38		m=2 m=3 m=4 m=6 m=12	123/132 71/75 58/61 51/54 47/49
β0 =1.50	β1 =1.3291	19/20		m=2 m=3 m=4 m=6 m=12	36/39 24/26 21/23 19/20 18/19		β1 =1.7440	18/19		m=2 m=3 m=4 m=6 m=12	106/111 45/47 35/36 29/30 26/27		β1 =1.3628	29/30		m=2 m=3 m=4 m=6 m=12	61/65 38/40 32/33 29/30 27/28		β1 =1.6680	25/25		m=2 m=3 m=4 m=6 m=12	140/145 59/61 45/46 38/39 34/34
β0 =2.00	β1 =1.7073	11/12		m=2 m=3 m=4 m=6 m=12	45/47 19/19 16/17 14/14 12/13		β1 =2.4586	10/10		m=2 m=3 m=4 m=6 m=12	325/330 33/34 25/25 19/19 15/15		β1 =1.7633	17/17		m=2 m=3 m=4 m=6 m=12	91/94 29/30 24/25 20/21 17/18		β1 =2.3102	14/14		m=2 m=3 m=4 m=6 m=12	227/229 45/46 33/33 25/25 20/20

The first two of these four columns represent:

1. Proposed Method – Calculated value of β₁ given all other user-input values

2. Proposed Method – Number of events / Sample size adjusted for administrative censoring

The last two of these four columns represent:

1. Lakatos Method – Number of intervals m used to define the piece-wise linear cut-points

2. Lakatos Method – Number of events / Sample size adjusted for administrative censoring

From observing the results in the first main panel, we see that in the first sub-panel when RT(p₁)=1.52 and RT(p₂)=1.98, the sample sizes obtained by the two methods for the varying values of β₀ are comparable. For the more extreme values of β₀=0.25 and β₀=2, the Lakatos method requires 12 intervals to get the same sample size as our proposed method. For all other values of β₀ ranging from 0.5 to 1.5, the proposed method sample size is similar to that of the Lakatos method with 3 or 4 intervals. In the second sub-panel of the first main panel when RT(p₁)=2 and RT(p₁)=1.5, however, the proposed method yields a much smaller sample size than that obtained by the Lakatos method even with 12 intervals. This difference in sample size for the two-scenarios (see third row of first panel with β₀=0.75) – {i}RT(p₁)=1.52; RT(p₁)=1.98 vs {ii} RT(p₁)=2; RT(p₂)=1.5 can be explained by recalling that although the Lakatos method can be used in the case of non-PH, it is based on using the logrank test statistic whose performance is optimal when the two survival curves have the relationship S₁(t)=S₀(t)^Δ_HR where Δ_HR is the hazard ratio from a proportional hazards model. As noted by Lakatos and Lan (1992) the performance would vary based on the extent to which hazards between the two survival curves were non-proportional. If we discretize the time axis with total study time of 24 months into small intervals of length dt (dt could be taken as small as 0.1), then in the first case, we get an average HR of 0.642 whereas in the second case we get an average HR of 0.723. The difference in these values is the reason why we get drastically different sample sizes when using the Lakatos method. In fact, even using the more popular Schoenfeld formula we get total number of events 127 (approximately 64 in each arm) in the first scenario and total number of events as 234 (117 in each arm) in the second scenario. This matches the Lakatos answer (see Table 1) for m=6 intervals in the first scenario and m=3 intervals in the second scenario and hence should not be surprising. This reinforces the fact that sample size calculations are quite sensitive to the user inputted values and in the example explained above, a HR difference of 0.723 – 0.624 = 0.081 has almost doubled the number of events. On the other hand, the proposed method is based on RT(p) and uses knowledge of the estimated Weibull parameters to take into account the possibility of non-proportionality of hazards while calculate the number of events and sample size. In the case of PH assumption being true, the proposed method, Schoenfeld formula, and Lakatos method provide very similar answers.

A similar trend is observed in the second main panel, where in the first sub-panel with RT(p₁)=1.5, RT(p₂)=1.667, the two methods yield similar sample sizes when m = 3, 4, or 6. However, in the second sub-panel when considering RT(p₁)=1.667, RT(p₂)=1.5, the proposed method yields smaller sample sizes than Lakatos method highlighting its potential for use in real-world applications.

4.2. Simulation results for empirical vs nominal error and power

Table 2 displays the results pertaining to assessment of operation characteristics (empirical type I error, empirical power, average relative bias, mean square error, and coverage) from 10,000 simulations for the user-inputs discussed in first paragraph of Section 4.1 with RT(p₁)=1.52, RT(p₁)=1.98 in the case of 1:1 randomization for the two study arms. Two other scenarios for allocation ratio (r=0.5, 2) are considered in the Supplementary material (Table 6 and 7). The first through fourth columns are similar to Table 1. The fifth and sixth column contain the values of empirical type I error and empirical power respectively. For all values of r, empirical power is close to the nominal value of 80% and never falls below 78% even for small sample sizes. Likewise, the empirical type I error is close to the nominal value of 5% when r=0.5 and r=1. When r=2, we see slightly elevated empirical type I error in case of sample sizes smaller than 20. However, this is not a cause of concern as most two-arm RCTs will have sample sizes >= 20 (see comment in section 3.3 mentioning the need for approximately 25 events to justify asymptotic normality of the test statistic).

Table 2.

Empirical type I error and Empirical Power for different settings of the Proposed method compared to Nominal type I error of 5% and Nominal Power of 80% for one-sided test with a = 12, f = 12, p₁=0.10, p₂=0.90 from 10,000 simulations for 1:1 randomization in the two study arms

Control arm Shape parameter β0	Effect Size definitions for survival curves	Treatment arm shape β1 calculated via defined effect size	Event size/Sample Size (Each arm)	Empirical Type I error rate %	Empirical Power %	Average Relative Bias (ARB) % Under HA	Mean Square Error (MSE) Under HA	Coverage% Under HA using 90% confidence interval
β0=0.25	RT(p1)=1.52 RT(p2)=1.98	β1=0.2448	601/991	4.43%	80.77%	2.826%	0.1899	90.39%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.2560	722/1182	4.87%	79.28%	2.391%	0.1314	89.82%
β0=0.50	RT(p1)=1.52 RT(p2)=1.98	β1=0.4795	154/216	4.26%	81.47%	3.222%	0.1983	89.60%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.5247	177/244	5.14%	79.25%	2.587%	0.1353	90.15%
β0=0.75	RT(p1)=1.52 RT(p2)=1.98	β1=0.7047	70/87	3.61%	81.48%	2.745%	0.1960	89.69%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.8064	77/93	5.47%	78.26%	2.390%	0.1356	89.92%
β0=1.00	RT(p1)=1.52 RT(p2)=1.98	β1=0.9211	41/46	3.67%	81.90%	3.442%	0.2017	89.19%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.1029	43/47	5.24%	79.06%	2.384%	0.1326	90.36%
β0=1.25	RT(p1)=1.52 RT(p2)=1.98	β1=1.1290	27/29	3.49%	82.28%	3.240%	0.1965	89.97%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.4150	27/27	5.64%	79.10%	2.223%	0.1326	90.06%
β0=1.50	RT(p1)=1.52 RT(p2)=1.98	β1=1.3291	19/20	3.78%	81.77%	3.711%	0.2088	89.33%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.7440	18/19	6.09%	80.67%	2.767%	0.1313	90.48%
β0=2.00	RT(p1)=1.52 RT(p2)=1.98	β1=1.7073	11/12	3.26%	80.94%	2.818%	0.1893	89.89%
	RT(p1)=2.00 RT(p2)=1.50	β1=2.4586	10/10	6.40%	80.21%	2.707%	0.1369	89.85%

The seventh column displays the values of average relative bias (average of the simulations for the difference between the observed and actual value of the parameter of interest) calculated as

$$\begin{array}{c}ARB=\frac{1}{10000}\sum _{j=1}^{10000}\left\{{\widehat{RT}}_j\left(0.5\right)-RT\left(0.5\right)\right\}/RT\left(0.5\right)\end{array}$$ (24)

where ${\widehat{RT}}_j\left(0.5\right)$ is the estimate from the j^th simulation under the alternate hypothesis. We see that for most scenarios the ARB is quite small and always below 5% (with a maximum of 4.53%).

The second from last column displays the values of mean square error (MSE) – the average of the squared errors (difference between ${\widehat{RT}}_j\left(0.5\right)$ and RT(0.5)). For all scenarios in Table 2, the MSE is somewhat high. When the true value of RT(0.5) is 1.786, the MSE is approximately in the range of 0.19 – 0.20 and when the true value of RT(0.5) is 1.677, the MSE is approximately in the range of 0.13 – 0.136. One reason for these somewhat high MSEs is that to estimate RT(0.5), we need to fit two separate Weibull models with each of them contributing to the variability in the measurement thereby increasing the overall variability. Finally, the last column displays the percent coverage, that is, 100 times the proportion of 10,000 simulations whose 90% confidence interval around ${\widehat{RT}}_j\left(0.5\right)$ included the true value of RT(0.5)). In all scenarios of Table 2, we observe that the coverage is adequate with small fluctuations around the expected value of 90% (due to one-sided type I error of 5%).

4.3. Relationship between Proposed method and the Extended Cox model

The relationship between our proposed method (left panel) and the extended Cox model (right panel) can be best understood by studying the results displayed in Table 3. The first four columns in the left panel are the same as in Table 2. The fifth column in this panel displays the hazard ratio as a function of time and is evaluated at $t_{avg}=\left(t_{med,C}+t_{med,E}\right)/2$, the average of the median survival time in the C and E arms. This average is calculated to allow us making comparisons with the extended Cox model on a common scale (in the metric of hazard instead of time).

Table 3.

Empirical type I, Empirical Power, Coverage for different settings of Extended Cox model compared to Nominal type I error of 5%, Nominal Power of 80% for one-sided test, a =12, f = 12, r = 1, using 10,000 simulations

Relative Time Method (Design parameters and Quantities of Interest)					Extended Cox Model: ${\mathit{h}}_1\left(\mathit{t}\right)={\mathit{h}}_0\left(\mathit{t}\right).\mathit{e}\mathit{x}\mathit{p}\left\{{\mathit{\gamma }}_0+{\mathit{\gamma }}_1\mathbf{l}\mathbf{o}\mathbf{g}\left(\mathit{t}\right)\right\}$
Control arm Shape parameter β0	Effect Size definitions for survival curves	Treatment arm Shape β1 calculated via defined effect size	Event Size/ Sample Size (Each arm)	True HR calculated at ${\mathit{t}}_{\mathit{a}\mathit{v}\mathit{g}}=\frac{{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}+{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{E}}}{2}$ $\mathbf{H}\mathbf{R}=\frac{{\mathit{\beta }}_1{{\mathit{\theta }}_0}^{{\mathit{\beta }}_0}}{{\mathit{\beta }}_0{{\mathit{\theta }}_1}^{{\mathit{\beta }}_1}}{{\mathit{t}}_{\mathit{a}\mathit{v}\mathit{g}}}^{{\mathit{\beta }}_1-{\mathit{\beta }}_0}$	Coverage % for HR at ${\mathit{t}}_{\mathit{a}\mathit{v}\mathit{g}}=\frac{{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}+{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{E}}}{2}$ using 90% CI: exp $\left\{\left[{\widehat{\mathit{\gamma }}}_0+{\widehat{\mathit{\gamma }}}_1\mathbf{log}\left(\mathit{t}\right)\right]\pm 1.645\cdot \mathit{S}\mathit{E}\left[{\widehat{\mathit{\gamma }}}_0+{\widehat{\mathit{\gamma }}}_1\mathbf{l}\mathbf{o}\mathbf{g}\left(\mathit{t}\right)\right]\right\}$	Coverage % for: Line 1: log(HR) at t=1 using ${\widehat{\mathit{\gamma }}}_0\pm 1.645.\mathit{S}\mathit{E}\left({\widehat{\mathit{\gamma }}}_0\right)$ Line 2: ${\mathit{\beta }}_1-{\mathit{\beta }}_0$ using ${\widehat{\mathit{\gamma }}}_1\pm 1.645.\mathit{S}\mathit{E}\left({\widehat{\mathit{\gamma }}}_1\right)$	Approximation for $\widehat{\mathbf{R}\mathbf{T}}\left(\mathit{p}\right)$ calculated at ${\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}$ using ${\widehat{\mathbf{R}\mathbf{T}}}_{\mathit{a}\mathit{p}\mathit{p}\mathit{r}\mathit{o}\mathit{x}}\left(\mathit{p}\right)={\left\{\frac{\left({\mathit{\beta }}_0+{\widehat{\mathit{\gamma }}}_1\right)\mathbf{e}\mathbf{x}\mathbf{p}\left(-{\widehat{\mathit{\gamma }}}_0\right)}{{\mathit{\beta }}_0{\left({\widehat{\mathit{t}}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}\right)}^{{\widehat{\mathit{\gamma }}}_0}}\right\}}^{1/\left({\mathit{\beta }}_0+{\widehat{\mathit{\gamma }}}_1\right)}$
							Empirical Type I error %	Empirical Power %
β0=0.25	RT(p1)=1.52 RT(p2)=1.98	β1=0.2448	601/991	0.8479	90.28%	90.49% 90.27%	4.56%	79.58%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.2560	722/1182	0.8984	90.01%	89.86% 89.68%	4.65%	80.16%
β0=0.50	RT(p1)=1.52 RT(p2)=1.98	β1=0.4795	154/216	0.7211	90.05%	89.80% 90.14%	5.18%	78.45%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.5247	177/244	0.8054	89.91%	89.83% 90.19%	5.56%	79.88%
β0=0.75	RT(p1)=1.52 RT(p2)=1.98	β1=0.7047	70/87	0.6150	90.27%	90.32% 90.87%	5.49%	76.87%
	RT(p1)=2.00 RT(p2)=1.50	β1=0.8064	77/93	0.7202	89.75%	90.00% 90.52%	6.25%	77.41%
β0=1.00	RT(p1)=1.52 RT(p2)=1.98	β1=0.9211	41/46	0.5258	89.58%	90.50% 90.62%	7.00%	77.00%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.1029	43/47	0.6423	90.04%	90.57% 90.11%	7.35%	77.75%
β0=1.25	RT(p1)=1.52 RT(p2)=1.98	β1=1.1290	27/29	0.4507	90.00%	90.95% 90.82%	7.31%	75.32%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.4150	27/27	0.5712	89.55%	90.79% 90.23%	7.26%	76.11%
β0=1.50	RT(p1)=1.52 RT(p2)=1.98	β1=1.3291	19/20	0.3872	89.52%	92.47% 91.48%	7.89%	74.41%
	RT(p1)=2.00 RT(p2)=1.50	β1=1.7440	18/19	0.5064	89.64%	92.58% 90.95%	7.60%	77.09%
β0=2.00	RT(p1)=1.52 RT(p2)=1.98	β1=1.7073	11/12	0.2877	91.41%	94.35% 93.44%	6.65%	70.72%
	RT(p1)=2.00 RT(p2)=1.50	β1=2.4586	10/10	0.3938	91.14%	93.37% 92.44%	8.49%	75.58%

The first column in the second panel displays the percent coverage when the HR is evaluated using (20) for the Extended Cox model along with its corresponding 90% confidence interval at t_avg. We observe that for all scenarios the percent coverage is close to 90% and hence considered adequate. The second column in this panel consists of two lines of results. The first line displays the percent coverage for the logarithm of the hazard ratio at t = 1 and can be calculated as 100 times the proportion of 10,000 simulations for which the confidence interval given by ${\widehat{\gamma }}_0\pm 1.645.SE\left({\widehat{\gamma }}_0\right)$ contains the true value of the HR at t = 1. Likewise, the second line displays the percent coverage for difference in the values of the shape parameters of the two study arms. This can be calculated as 100 times the proportion of 10,000 simulations for which the confidence interval given by ${\widehat{\gamma }}_1\pm 1.645.SE\left({\widehat{\gamma }}_1\right)$ contains the true value of β₁−β₀. We observe that in both cases, adequate coverage of around 90% is obtained. These results lead further credence to the justification that to account for random loss to follow-up or dropouts, we can simply inflate the sample size by the event rate. The advantage of this is that the relationship between the two methods will be preserved and it will be possible to analyze the RCT data in two different but equivalent ways. The proposed method will help a statistician draw inferences on the ‘RT(p) fold improvement in longevity in the E vs C arm’, and, the Extended Cox model will allow inference on the ‘HR (E vs C) as a function of time’. Together these two approaches will provide a comprehensive summary of the results and even provide guidance on meaningful effect size definition to other future or concurrent phase IV trials.

The last column contains the values of empirical type I error and empirical power when the Extended Cox model is used along with some of the user-input values to draw approximate inferences on RT(p). Though the inference on RT(p) is easily obtainable by using our proposed method and this step is not necessary, many researchers are accustomed to interpretation from a Cox model. We therefore wish to investigate if after fitting an Extended Cox model, reliable inferences can be drawn about RT(p) without fitting two different Weibull models to the two study arms. To do so we first obtain ${\widehat{\gamma }}_0$ and ${\widehat{\gamma }}_1$ from fitting the Extended Cox model for each of the 10,000 simulated datasets. These estimates can be combined with the user-input values of β₀ and the median survival time in C arm to obtain an approximate estimate of RT(p) using

$$\begin{array}{c}{\widehat{\mathrm{R}\mathrm{T}}}_{approx}\left(p\right)={\left\{\frac{\left({\beta }_0+{\widehat{\gamma }}_1\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\widehat{\gamma }}_0\right)}{{\beta }_0{\left({\widehat{t}}_{med,C}\right)}^{{\widehat{\gamma }}_0}}\right\}}^{1/\left({\beta }_0+{\widehat{\gamma }}_1\right)}\end{array}$$ (25)

From the values shown in this column we can see that the empirical type I error is somewhat inflated compared to the nominal value of 5% with highest inflations observed for scenarios with small sample sizes. Similarly, the empirical power is somewhat below 80% in most cases with small sample sizes resulting in most loss of power. Thus, these results indicate the need to analyze the data using the proposed method when drawing inferences on RT(p) and use the Extended Cox model only when drawing inferences on the HR as a function of time. Together, both approaches may provide a complete picture when analyzing data from such RCTs.

4.4. Assessing the robustness of the proposed method

To further assess the performance of our proposed method, we conducted additional simulations to:

{i} Evaluate differences in sample size when PH assumption is not valid but is incorrectly assumed to be true, and {ii} Evaluate the robustness of the proposed method when a study is designed using a piecewise exponential model.

The simulation results of the first assessment scenario are displayed in Table 4. The first three columns of this table display the design features of the proposed method - control arm shape parameter, effect size user input, and true HR calculated at the midpoint of the median time in the two arms. The third column allows us an important reference point t_avg at which we can compare the calculations to methods that assume a constant HR. The fourth column displays the number of events and sample size obtained by using the proposed method when the PH assumption is not valid (as represented by the user entry of effect size in the third column). The fifth column displays the number of events and sample size if the Schoenfeld formula (Cox PH model) is used to do the calculations keeping the HR at as a constant (PH assumption). That is, if we assume that a researcher has a clear idea of how the treatment survival curve will look like compared to the control curve should the treatment be beneficial, then if the researcher were to assume the PH assumption to be valid, he/she would use the entries in column 3 as the effect size for planning a trial using the Schoenfeld formula. The results displayed in the fifth column clearly suggest that incorrectly using the Schoenfeld formula would either result in an underpowered (small sample sizes) or overpowered (unnecessarily large sample sizes) trial. As an example, in the first scenario when β₀=0.25, the HR at t_avg=5.573 is 0.8479 when RT(p₁)=1.52 and RT(p₂)=1.98 resulting in a sample size of 751 with 455 events in each arm. Conversely, when RT(p₁)=2 and RT(p₂)=1.5 is used, then the HR at t_avg=5.356 is 0.8984 resulting in a sample size of 1766 with 1079 events in each arm. These calculations demonstrate how the sensitivity of the sample size calculations when we use the constant HR as a measure of the effect size when it would be inappropriate to do so. The last two columns in Table 4 show the empirical power under the alternate hypothesis for the proposed method compared to the Cox model when the interaction term from equation (22) is incorrectly ignored. While the empirical power is close to 80% for the proposed method in all scenarios, same cannot be said to be true for the Cox Model which expectedly yields empirical power that either exceeds the target power of 80%, or, falls short of the target power depending on the values of RT(p₁) and RT(p₂).

Table 4.

Sample sizes using the Schoenfeld formula when the effect size is defined using ‘Hazard Ratio at t_avg (average of median survival times in the two study arms) vs Proposed Method (when the assumption of ‘Relative Time’ is valid) for various scenarios with type I error rate of 5% and Nominal Power of 80% for one-sided test with accrual time = 12 months, follow-up time = 12 months, and r=1.

Design features of the proposed method			# Events/ Sample Size: Proposed method vs Schoenfeld formula		Empirical Power of two methods when data is simulated under proposed method
Control arm Shape parameter β0	Effect Size User Input	True HR calculated at ${\mathit{t}}_{\mathit{a}\mathit{v}\mathit{g}}=\frac{{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}+{\mathit{t}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{E}}}{2}$ $\mathbf{H}\mathbf{R}=\frac{{\mathit{\beta }}_1{{\mathit{\theta }}_0}^{{\mathit{\beta }}_0}}{{\mathit{\beta }}_0{{\mathit{\theta }}_1}^{{\mathit{\beta }}_1}}{{\mathit{t}}_{\mathit{a}\mathit{v}\mathit{g}}}^{{\mathit{\beta }}_1-{\mathit{\beta }}_0}$	Proposed Method	Schoenfeld using HR at tavg as effect size	Proposed Method	Cox model (without an interaction term)
β0=0.25	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.8479	601/991	455/751	80.77%	80.46%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.8984	722/1182	1079/1766	79.28%	79.41%
β0=0.50	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.7211	154/216	116/164	81.47%	82.49%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.8054	177/244	265/366	79.25%	76.90%
β0=0.75	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.6150	70/87	53/67	81.48%	83.36%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.7202	77/93	115/140	78.26%	73.26%
β0=1.00	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.5258	41/46	30/35	81.90%	84.37%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.6423	43/47	64/71	79.06%	71.31%
β0=1.25	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.4507	27/29	20/22	82.28%	84.80%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.5712	27/27	40/42	79.10%	69.81%
β0=1.50	p1=0.10; p2=0.90; RT[p1]=1.52; RT[p2]=1.98	HR = 0.3872	19/20	14/15	81.77%	83.60%
	p1=0.10; p2=0.90; RT[p1]=2.00; RT[p2]=1.50	HR = 0.5064	18/19	27/28	80.67%	70.66%
β0=0.25	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.8764	933/1525	711/1163	80.58%	80.49%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.9076	953/1552	1317/2146	79.69%	79.59%
β0=0.50	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.7696	238/329	181/251	81.08%	82.62%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.8225	235/321	325/446	78.99%	76.60%
β0=0.75	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.6770	108/131	82/101	81.22%	83.98%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.7443	103/123	142/171	78.75%	74.53%
β0=1.00	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.5966	62/69	47/53	81.40%	84.80%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.6724	57/63	79/87	79.54%	73.52%
β0=1.25	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.5266	40/43	31/34	81.01%	85.05%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.6063	36/38	50/53	79.67%	71.90%
β0=1.50	p1=0.25; p2=0.75; RT[p1]=1.50; RT[p2]=1.667	HR = 0.4656	29/30	21/22	80.93%	84.96%
	p1=0.25; p2=0.75; RT[p1]=1.667; RT[p2]=1.50	HR = 0.5458	25/25	34/35	79.15%	70.35%

The simulation results displayed in Table 5 pertain to studying the robustness of the proposed method. To do so, we considered the situation where a statistician plans to design a two-arm trial using the piecewise exponential model. After consulting with his/her collaborators, the statistician decides to divide the time axis into 3 intervals and has information about the hazard in each arm (constant within an interval but changing across intervals). The hazard ratio under the alternate hypothesis is assumed to be 0.75, target power is 80%, and type I error is 5%. The first column in Table 5 represents the different situations in which the control arm hazard is decreasing over time, increasing over time, constant over time, bathtub shaped, or arc-shaped. The intervals are fixed at 2 months, 4 month and 24 months (see second column). The third and fourth column give the values of the hazard in each interval h(t), and the cumulative hazard H(t) in each interval respectively. The fifth column displays the values of the point estimate of the HR and the empirical power using 10,000 simulations from the piecewise exponential model with number of events set at 150 in each arm. Based on these values, the piecewise exponential model seems to be a good choice for designing the trial.

Table 5.

Performance of Proposed Method when a two-arm trial is designed using a Piecewise Exponential Model with various hazard shapes and constant HR of 0.75

Scenario	Piecewise Exponential Model				Proposed Method (Parameter estimates based on plotting H(t) vs log(t) for Control arm)							Proposed Method (10000 Simulations)
	Interval	Hazard in each interval	Cumulative hazard at interval midpoint	$\widehat{\mathbf{H}\mathbf{R}}$ and Empirical power when using 150 events in each arm (10000 simulations)	Shape ${\widehat{\mathit{\beta }}}_0={\widehat{\mathit{\beta }}}_1$ (due to PH)	Control Arm scale ${\widehat{\mathit{\theta }}}_0$	Control arm median ${\widehat{\mathit{t}}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}$	Treatment Arm scale ${\widehat{\mathit{\theta }}}_1$	Treatment arm median ${\widehat{\mathit{t}}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{E}}$	$\widehat{\mathbf{R}\mathbf{T}}\left(\mathit{p}\right)=\mathbf{P}\mathbf{T}=\frac{{\widehat{\mathit{t}}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{E}}}{{\widehat{\mathit{t}}}_{\mathit{m}\mathit{e}\mathit{d},\mathit{C}}}$	Number of Events*	$\widehat{\mathbf{R}\mathbf{T}}\left(\mathit{p}\right)$ and Empirical power (when using 150 events in each arm – data from PE model)
Decreasing hazard	0 – 2	0.70	0.70	0.7549; 77.23%	0.2982	1.9328	0.5655	5.0720	1.4839	2.6242	150	2.1416; 82.56%
	2 – 4	0.10	1.50
	4 – 24	0.001	1.61
Decreasing hazard	0 – 2	0.90	0.90	0.7535; 81.38%	0.4913	0.9839	0.4666	1.7670	0.8380	1.7959	150	1.7049; 87.17%
	2 – 4	0.30	2.10
	4 – 24	0.10	3.40
Decreasing hazard	0 – 2	0.30	0.30	0.7536; 79.89%	0.7486	4.6197	2.8313	6.7845	4.1580	1.4686	150	1.4952; 81.84%
	2 – 4	0.20	0.80
	4 – 24	0.12	2.20
Constant hazard	0 – 2	0.20	0.20	0.7535; 80.10%	1.000	5.000	3.4656	6.6665	4.6209	1.3333	150	1.3441; 80.55%
	2 – 4	0.20	0.60
	4 – 24	0.20	2.80
Increasing hazard	0 – 2	0.50	0.50	0.7548; 79.68%	1.2487	1.8528	1.3816	2.3329	1.7395	1.2591	150	1.2625; 74.58%
	2 – 4	0.60	1.60
	4 – 24	1.10	13.2
Increasing hazard	0 – 2	0.20	0.20	0.7548; 79.68%	1.5133	2.8068	2.2031	3.3945	2.6644	1.2094	150	1.1882; 77.98%
	2 – 4	0.80	1.20
	4 – 24	0.90	11.0
Increasing hazard	0 – 2	0.10	0.10	0.7548; 79.68%	1.7500	3.9817	3.2293	4.6929	3.8062	1.1787	150	1.1454; 75.78%
	2 – 4	0.30	0.50
	4 – 24	0.90	9.80
Hazard decreases constant	0 – 2	0.80	0.80	0.7538; 80.05%	0.5407	1.3285	0.6745	2.2618	1.1483	1.7024	150	1.6546; 85.10%
	2 – 4	0.15	1.75
	4 – 24	0.15	3.40
Bathtub shaped hazard	0 – 2	0.80	0.80	0.7528; 80.15%	0.7536	1.3943	0.8573	2.0425	1.2559	1.4648	150	1.4827; 82.86%
	2 – 4	0.10	1.70
	4 – 24	0.40	5.80
Arc shaped hazard	0 – 2	0.10	0.10	0.7540; 79.62%	1.2730	5.4465	4.0839	6.8276	5.1195	1.2536	150	1.3135; 83.54%
	2 – 4	0.40	0.60
	4 – 24	0.20	3.00
Arc shaped hazard	0 – 2	0.10	0.10	0.7528; 80.22%	1.4379	4.1210	3.1938	5.0335	3.9009	1.2215	150	1.2871; 86.51%
	2 – 4	0.80	1.00
	4 – 24	0.30	4.80

^*Sample size for proposed method is exactly same as that obtained by Schoenfeld formula with HR = 0.75 as in each scenario the Weibull property of ${\widehat{\gamma }}_{PH}=-{\widehat{\gamma }}_{AFT}$. β is satisfied where ${\widehat{\gamma }}_{PH}$ is the log-hazard ratio, ${\widehat{\gamma }}_{AFT}\mathrm{ }$ is the time ratio and β is the shape parameter corresponding to a Weibull model. Target power for all scenarios in the table is 80%. Type I error is 5% for one-sided test.

The sixth through tenth columns in Table 5 are useful for assessing how the proposed method works when we try to design a trial with the same information as mentioned in the above paragraph. To do so, we can plot H(t) from the fourth column versus log(time) to estimate the parameters of the Weibull using the well-known relationship specific to the Weibull: log{H(t)=−βlog (θ)+βlog (t)}. Thus, the control arm shape parameter β₀ and scale parameter θ₀ can be estimated and these estimates can be used to estimate the control arm median survival time ${\widehat{t}}_{med,C}$. Using the hazard ratio of 0.75, we can similarly obtain ${\widehat{\beta }}_1={\widehat{\beta }}_0,{\widehat{\theta }}_1$ and ${\widehat{t}}_{med,E}$. These in turn can be used to calculate RT(p₁) which will be a constant (owing to the fact that we assumed a constant HR and a Weibull distribution) and hence can be calculated as ${\widehat{t}}_{med,E}/{\widehat{t}}_{med,C}$. With these inputs, the proposed method can be used to calculate the number of events which turn out to be exactly 150 in all scenarios. These results indicate that when the HR assumption is true, then even if the individual median times in the two study arms are inaccurately estimated, the “relative time” ratio is consistent with the hazard ratio. That is the Weibull property ${\widehat{\gamma }}_{PH}=-{\widehat{\gamma }}_{AFT}.\beta$ where ${\widehat{\gamma }}_{PH}$ is the log-hazard ratio, ${\widehat{\gamma }}_{AFT}$ is the time ratio and β is the shape parameter comes into play. That is, the information contained in RT(p₁)=2.6242 and ${\widehat{\beta }}_1={\widehat{\beta }}_0=0.2982$ is consistent with the information contained in HR of 0.75. However, this does not imply that the proposed method should be indiscriminately used when the underlying assumptions supporting it are not valid. This aspect can be understood by studying the last column of Table 5. Suppose we assume that the piecewise exponential model is the true model and simulate time-to-event data using the design features represented in the first four columns of Table 5. Then the last column of Table 5 displays the average (of 10000 simulations) of the observed values of RT(0.5) and the corresponding empirical power. It can be seen that in some cases the empirical power falls short of the target power of 80% and in some other cases it exceeds it. To understand why this happens, we need to recall that the Weibull distribution can model hazards that increase over time from 0 to infinity or decrease over time from infinity to 0. If these aspects of the hazard shapes are not represented in the data, then the performance of methods based on the Weibull are likely to flounder. That is, while designing the trial even if the number of events were correctly calculated as 150, since the Weibull is not a good fit for the data, it should not be used to analyze the data. A simple Cox model will be a better choice to design the trial and analyze the data emerging from it.

5. Discussion

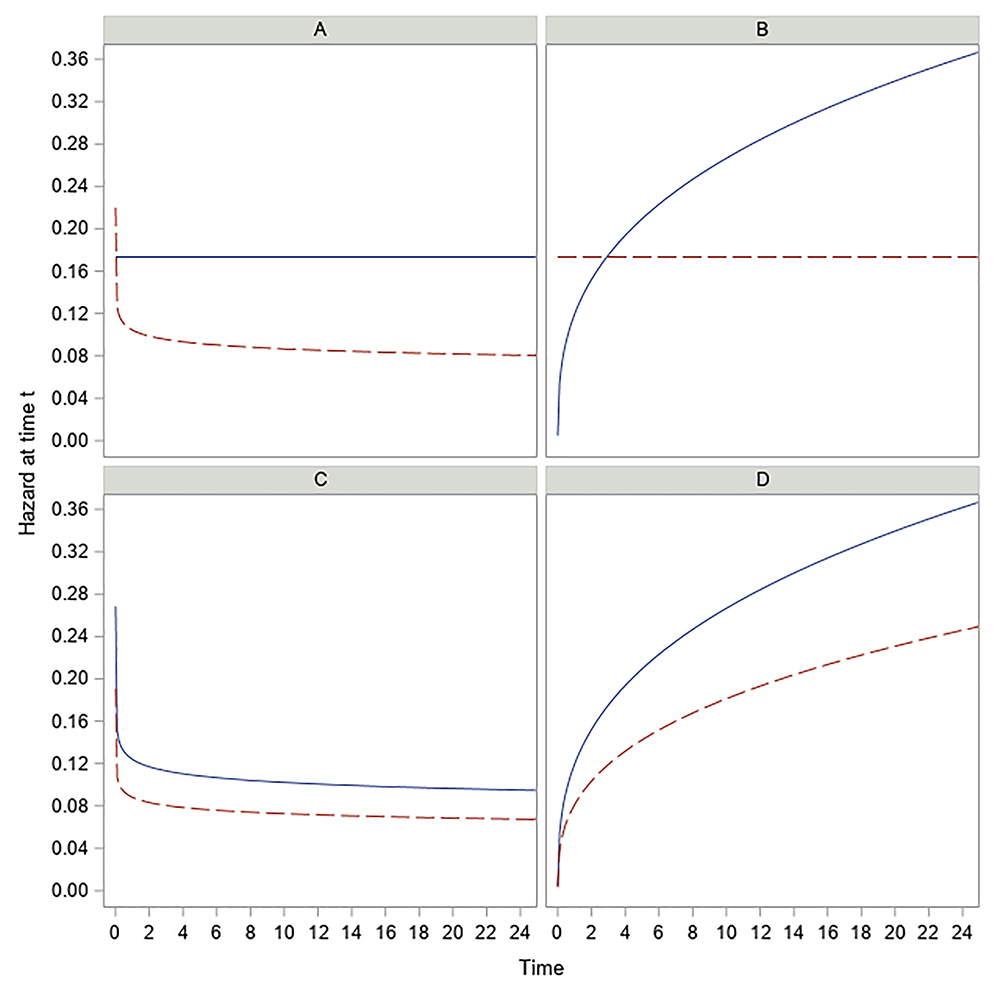
In our work we have proposed a new method of sample size calculation allowing for non-proportional hazards as well as non-proportional time for phase II and III RCTs. This is achieved by allowing the two study arms to be modeled by two separate Weibull distributions. That is, the main advantage of our method is that we are willing to consider the possibility that a newly proposed experimental treatment has the potential to not only change the location effect of a standard control but to also alter the shape of the hazard. Conceptually, this allows the flexibility to model many different real-life scenarios. This is because for a Weibull distribution, the parameter β controls the shape of the hazard function with β<1, β=1, β>1 implying hazard that is decreasing over time, constant, and increasing over time respectively. Thus, it is possible that a well-established standard control has a hazard that is constant over time, but a new treatment (such as surgery) increases the median survival by increasing θ and decreasing β below 1. This scenario is reflected in Figure 3a where the Weibull hazard of E arm starts with a theoretical infinity at time 0 and decreases over time. This situation is realistic because it is plausible that a new surgical intervention has a very high risk immediately after surgery but as the patients stabilize, the effect of surgery is to reduce the hazard over time thereby benefitting the patients. Likewise, Figure 3b represents a scenario in which a standard control used for treating cancer patients offers only limited benefits in that with the progression of time, the cancer worsens leading to hazard that increases over time. A new breakthrough treatment may offer substantial benefit to the patients in that the hazard, though still high, may now become constant over time. Other possible scenarios are represented in Figure 3c and Figure 3d wherein the general shape of the hazard remains the same following a new treatment regimen compared to the standard control, but the change in slope is large enough for the treatment to be considered effective. Figures like these provide an opportunity to better understand how the hazard of the experimental treatment changes over time relative to the standard control and should be used while analyzing data from RCTs with a time-to-event endpoint. The proposed method offers an RCT design taking into account the possibility of non-proportional hazards while analyzing the final data. Here it is important to note the distinction between crossing of hazard curves and crossing of survival curves. While our method allows crossing of hazards as shown in Figure 3, we do not allow any arbitrary crossing of survival curves. Our proposed method is motivated by effect size definitions of RT(p₁)>1 and RT(p₂)>1 provided by researchers who hypothesize improved benefit for E vs C at both p₁ and p₂. These four inputs p₁,p₂,RT(p₁) and RT(p₂) impose natural restrictions on where the two survival curves will cross as discussed in Section 3.6.

Figure 3.

Hazard vs time for Control arm (solid) and Treatment arm (dashed) – four different cases.

Another important advantage of our method is that it is based on a realistic and practical interpretation of effect size defined in the metric of time. For biomedical researchers investigating new treatments, the end goal is to demonstrate higher survival compared to that offered by existing treatments. Published results of RCTs through KM plots mention the median and IQR of time-to-event endpoints. Thus, when researchers hypothesize the new treatment to confer a survival benefit, the very first inclination is to state “by how many time units does the median survival change?”. While increase in median PFS works through reduction in hazard, from a practical standpoint it is easier to quantify improvement in longevity in the metric of time. This is especially true in the case of RCTs in oncology where patients with a not-so-good quality of life may be encouraged to participate in a trial if researchers can quantify and convey the hypothesized benefit in terms of how much longer they can survive. That is, telling potential participants that “median PFS is hypothesized to improve from 4 months to 6 months” is more understandable for patients than saying “hazard will be reduced by 33%”.

An interesting feature of our method is that it is not restricted to user entry for high values of p₂. Thus, even in cases where making assumptions for ‘later’ time points is unrealistic, the method can be implemented. For example, in clinical trials where the median is not determinable as would be the case in rare diseases or trials with limited follow-up time, the proposed method can be used to provide convenient user inputs such as (say, for example), p₁=0.05, p₂=0.4 and in this case the sample size calculations can be conducted using p_mid=(0.05+0.4)/2=0.225. In general, a statistician designing the trial can elicit information about p₁ and p₂ from their collaborator by asking the right questions about the hypothesized benefit of the treatment compared to the control. When using methods that define the effect size using a single measure such as a constant HR, or improvement in median, the implicit assumption is that this effect stays the same for the duration of the trial. In real-life situations, a collaborator may have an idea of how the treatment benefit changes over time but may not mention this to the statistician unless the statistician asks for it. That is, our method encourages the statistician to ask an important question to their collaborator before designing a trial – “Is the improvement in longevity (say median of 6 vs 4 months) consistent at all survival quantiles” – rather than assuming that “effect size defined at the median” is sufficient to design the trial. In this context, our method allows the statistician to take responsibility to ensure that the trial design better captures the hypothesized benefit of the treatment. Before finalizing the sample size calculations, a statistician can also check with their collaborator if the value of RT(p_mid) calculated at p_mid is a good representation of the treatment benefit at the midpoint of p₁ and p₂.

One limitation of our method is that it is dependent on the Weibull assumption. While being more flexible than the exponential distribution in terms of modeling the hazard shape, it has the limitation that at time 0, hazard starts from 0 or from ∞ and this may always not be true. More research is needed in this direction to accommodate other distributions to allow for even more flexibility in the hazard shapes. On the other hand, the Lakatos method is more generalizable and is based on state transition probabilities using a Markov assumption and can incorporate different weights as well as account for non-compliance in a RCT. Still, when reliable information is available about the Weibull shape parameter of the standard control arm from prior studies, in some cases, our proposed method yields smaller sample sizes than the Lakatos method. Additionally, the Schoenfeld formula can be considered as only a special case of our method and this insight should be taken into consideration by practicing statisticians while designing a RCT. A second minor limitation of our method is its reliance on asymptotic normality of the test statistic. However, given that most two-arm phase II and phase III RCTs are at least moderate sized, this is not a serious limitation. Another minor limitation is that estimate of β₀ may be mis-specified when it is estimated from a previous study (see Section 3.1). However, as described in Section 3.1, if the previous study had 50 subjects with up to 40% censoring, then even if this estimate is obtained from three survival quantiles (say 25^th, 50^th, 75^th percentile), the estimate will be within 10% of the true beta. Since for a Weibull distribution (see Table 1) sample size increases as β₀ decreases, a statistician who wishes to err on the side of being conservative to prevent a somewhat underpowered study can simply multiply this estimate by 0.9 when using our method to perform the sample size calculations. Overall, we recommend that input for β₀ should be obtained from historical sources and if such historical information is not available, a last choice would be to assume β₀=1 indicating that survival times in the C arm come from the exponential distribution.

Our proposed method of sample size calculation offers additional insights to statisticians analyzing time-to-event outcomes in RCTs in that the recommended method of analysis using two separate Weibull fits is consistent with analyzing the data as an extended Cox model (with interaction between study arm and logarithm of time). Thus, the final data can be analyzed using a non-constant time ratio as well as a non-constant hazard ratio. Our proposed method should be seen as complementing the existing methods of sample size calculation. When the Weibull assumption is correct it offers a practical easy-to-implement method for sample size calculation. We hope that statisticians will find it a useful addition to their arsenal when designing RCTs with time-to-event endpoints. A direct future extension to this area of research will be the construction of more complex sequential and adaptive designs with its operation characteristics validated comprehensively with simulations.

Appendix

A.1. Derivation of test statistic

Let t_j for j=1,2,3,…d be i.i.d random variables that follow Weilbull distribution with scale parameter θ and shape parameter β. That is t_j~ Weibullθ,β with θ,β>0

Then t_j^β~Exponentialθ(^β) leads to $\frac{1}{d}{\sum }_{j=1}^d{t_j}^{\beta }~\mathrm{G}\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{a}\left(d,\frac{{\theta }^{\beta }}{d}\right)$.

Therefore, $\widehat{\theta }={\left(\frac{1}{d}{\sum }_{j=1}^d{t_j}^{\beta }\right)}^{1/\beta }~\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}\mathrm{G}\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{a}\left(d,\frac{\theta }{d^{1/\beta }},\beta \right)$

A.2. Basics of the generalized gamma distribution

The generalized gamma (GG) distribution (see Stacy and Mihram (1965)) is a three-parameter family of distributions with a probability density function:

$$\begin{array}{c}f\left(t\right)=\frac{\beta }{\mathrm{\Gamma }\left(\mathrm{k}\right).\mathrm{\theta }}{\left(\frac{t}{\mathrm{\theta }}\right)}^{k\beta -1}exp\left\{-{\left(t/\theta \right)}^{\beta }\right\}\end{array}$$ (26)

where β>0 and k> are the shape parameters, θ>0 is the scale parameter and Γ(k) is the gamma function defined as $\mathrm{\Gamma }\left(\mathrm{k}\right)=\underset{0}{\overset{\infty }{\int }}{x}^{k-1}{e}^{-x}dx$.

For model fitting purposes a re-parametrization GG(μ,σ,λ) is used to avoid convergence problems using location parameter μ, scale parameter σ and shape parameter λ that generalizes the two-parameter gamma distribution. The density function is given by:

$$\begin{array}{c}{f}_{GG}\left(t\right)=\frac{\left|\lambda \right|}{\sigma t\mathrm{\Gamma }\left({\lambda }^{-2}\right)}{\left[{\lambda }^{-2}{\left\{\exp \left(-\mu \right)t\right\}}^{\lambda /\sigma }\right]}^{{\lambda }^{-2}}exp\left[-{\lambda }^{-2}{\left\{\exp \left(-\mu \right)t\right\}}^{\lambda /\sigma }\right]\end{array}$$ (27)

where σ>0, μ∈(−∞,∞), λ∈(−∞,∞), $\mathrm{\Gamma }\left(\mathrm{x}\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{m}^{x-1}{e}^{-m}dm$ is gamma function of x.

The parameters of (24) and (25) are related in the following way:

$$\begin{gathered} \mu =\mathrm{l}\mathrm{n}\left(\mathrm{\theta }\right)+\frac{1}{\beta }\mathrm{l}\mathrm{n}\left({\lambda }^{-2}\right) \\ \sigma =\frac{1}{\beta \sqrt{k}} \\ \lambda =\frac{1}{\sqrt{k}}=\beta \sigma \end{gathered}$$ (28)

A complete taxonomy of the various hazard functions for the GG family is explained in Cox et al. (2007). Briefly, the GG family allows the flexibility of modeling different hazard shapes such as increasing from 0 to ∞ or from a constant to ∞, decreasing from ∞ to 0, or from ∞ to a constant, arc shaped hazards, and bathtub shaped hazards. Special cases of the GG family are {i} two parameter gamma: λ=σ {ii} standard gamma (μ=0;σ=1) for fixed values of λ {iii} Weibull: λ=1 {iv} exponential: λ=σ=1 {v} lognormal: λ=0 {vi} inverse Weibull: λ=−1 {vii} inverse gamma: λ=−σ {viii} ammag: λ=1/σ {ix} inverse ammag: λ=−1/σ and {x} lognormal distribution with σ’=1.82σ approximates the loglogistic distribution.

A.3. The Relative Time RT(p) framework and reasons motivating the proposed method

The 3-parameter GG distribution can be used to analyze large observational study datasets as shown in Cox et al. (2007). The most general case is when survival times in both study arms are assumed to follow two separate GG(μ,σ,λ) distributions. As discussed in Cox et al. (2007), this requires very large datasets for conducting the statistical analysis. Many special cases such as same λ but different μ,σ for the two study arms run into similar issues.

Our proposed method based on fixing λ=1 allows the survival times in the two study arms to follow two different Weibull distributions. It allows us to design a two-arm clinical trial achieving the following objectives:

1. Both non-PH and non-PT assumptions are simultaneously true.

2. Trial should not yield extremely large sample sizes making it unrealistic to adopt in practice.

3. Knowledge of extra parameters required for sample size calculation for the Phase III trial should be achievable through practical means such as looking into previously conducted phase II trials. There should be some mechanism through which these extra parameters (β₀ and β₁) can be estimated with some acceptable level of accuracy. See Phadnis et al. (2020) that discuss this issue.

4. The special cases on the method based on RT(p) such as {i} PH but not PT {ii} PT but not PH {iii} Both PH and PT – should yield sample sizes that are similar to those yielded by already known methods such as Schoenfeld formula for Cox Model and Logrank methods that assume exponential distribution, They should also be comparable to the piecewise linear Lakatos method and the piecewise exponential model.

Following Venn diagram illustrates where the proposed method fits in the RT(p) framework.

Note: The area of rectangles in the diagram do not mean anything, it is just a representation of partitions shown in the Venn diagram.

A + C + D + E + F + G + H = The most general Relative Time RT(p) scenario.

B + C + E = Proportional Hazards models

D + C + E = Accelerated Failure Time (AFT) models also called Proportional Time models by Cox et al. (2007) from the Generalized Gamma distribution (with both study arms having the same shape parameters)

F = Accelerated Failure Time (AFT) models also called Proportional Time models from distributions other than Generalized Gamma.

C + E = Weibull model with common shape parameter for both study arms. This property of satisfying both PH and AFT assumption is specific to the Weibull.

E = Exponential model (special case of Weibull with shape parameter beta fixed at 1)

B = PH models in which baseline hazard does not come from the Weibull distribution.

D = Accelerated Failure Time (AFT) models also called Proportional Time models by Cox et al. (2007) from the Generalized Gamma distribution with both study arms having the same shape parameters) but not including the Weibull.

G + H = non-PH, non-PT models from the Generalized Gamma distribution when shape parameters are different for the two study arms.

G = non-PH, non-PT models from the Weibull when shape parameters are different for the two study arms. Thus, G is a subset of G + H.

In this framework, our proposed method for sample size calculation is for the C + E + G section of the diagram. Thus, it covers the following situations:

1. G = Non-PH, non-AFT based on Relative Time with two separate Weibull distributions for the two study arms.

2. C + E = When the shape parameters of the two Weibull distributions are same, we get a model that satisfies both PH and PT property.

3. E = Special case of {ii} above with shape parameter fixed at 1 i.e. the exponential distribution.

In writing this manuscript, we hope that statisticians designing a trial will have an extra option to handle the $\overline{\mathrm{B}}$ (not-B) scenario when they are comfortable with assumptions that fall under the partition represented by G.