Predicting the effective reproduction number of COVID-19: inference using human mobility, temperature, and risk awareness

Abstract

Objectives

The effective reproduction number ($R_t$) has been critical for assessing the effectiveness of countermeasures during the coronavirus disease 2019 (COVID-19) pandemic. Conventional methods using reported incidences are unable to provide timely $R_t$ data due to the delay from infection to reporting. Our study aimed to develop a framework for predicting $R_t$ in real time, using timely accessible data — i.e. human mobility, temperature, and risk awareness.

Methods

A linear regression model to predict $R_t$ was designed and embedded in the renewal process. Four prefectures of Japan with high incidences in the first wave were selected for model fitting and validation. Predictive performance was assessed by comparing the observed and predicted incidences using cross-validation, and by testing on a separate dataset in two other prefectures with distinct geographical settings from the four studied prefectures.

Results

The predicted mean values of $R_t$ and 95% uncertainty intervals followed the overall trends for incidence, while predictive performance was diminished when $R_t$ changed abruptly, potentially due to superspreading events or when stringent countermeasures were implemented.

Conclusions

The described model can potentially be used for monitoring the transmission dynamics of COVID-19 ahead of the formal estimates, subject to delay, providing essential information for timely planning and assessment of countermeasures.

1. Introduction

The first confirmed case of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection was reported in Japan on January 15, 2020; since then, the transmission of coronavirus disease 2019 (COVID-19) has continuously affected the entire country. As the incidence of COVID-19 began to surge, a state of emergency was declared by the national government on April 16, requesting the voluntary reduction of physical contact, which likely helped to suppress the epidemic (Jung et al., 2021). However, resuming socioeconomic activities in late May led to a resurgence of cases. Although a temporal decline in incidence was observed, the country experienced the third wave from late October 2020. In response, prefectural governments with a large number of cases requested bars and restaurants to curtail their operational hours from late November (Ministry of Health, Labour and Welfare, 2020a). Despite these measures, the spread of disease continued, leading the national government to declare a second state of emergency on January 7, 2021, asking citizens to refrain from non-essential outings (Cabinet Relations Office, 2021).

As part of evaluation of countermeasures, the effective reproduction number ($R_t$), defined as the expected number of secondary cases arising from a single primary case at calendar time $t$, is widely used for monitoring trends in community transmission (Nishiura et al., 2009). However, timely and accurate estimation of $R_t$ using incidence data remains challenging. First, to precisely link the timing of a control measure and resulting changes in the transmission trend, it is vital to estimate $R_t$ as a function of the infection time (Gostic et al., 2020). Since infection times are rarely observed in practice, they need to be estimated while accounting for empirical delay distributions. Moreover, the estimation of $R_t$ is further complicated because of right truncation with respect to the time interval from infection to reporting. In real-time practice, the number of recent infections is underestimated due to cases that are already infected but not yet reported. Considering the empirically observed time delay of around 9 days from infection to reporting in Japan, the estimated $R_t$ from reported incidences is likely to be biased, at least within 9 days from the latest reporting date.

Considering that SARS-CoV-2 transmission is facilitated by human-to-human contact, digital proxies of human mobility patterns can provide an important route to inferring the directly unobservable transmission patterns as a function of time. Indeed, various datasets of mobility patterns have started to become widely available during the ongoing COVID-19 pandemic, and have been used to monitor the time-dependent patterns of physical distancing (Buckee et al., 2020; Kishore et al., 2020; Leung et al., 2021; Nouvellet et al., 2021; Xiong et al., 2020). Moreover, published studies have reported that temperature is inversely associated with COVID-19 transmission (Li et al., 2020; Pequeno et al., 2020; Qi et al., 2020; Smith et al., 2021; Ujiie et al., 2020; Wang et al., 2021). These data are often more readily accessible than case counts (which are typically subject to delays of ∼ 9 days), and thus may enable near real-time assessment of interventions if they can be used to predict $R_t$. Furthermore, quantified risk awareness can also help to predict more accurate $R_t$ values, because induced adherence to personal protective behaviors (e.g. wearing a mask or washing hands) can reduce virus transmissions (West et al., 2020).

Accumulated evidence suggests that integrating human mobility with temperature and risk awareness reflects contact patterns as a function of time. Thus, the integrative model could provide an opportunity for the timely prediction of $R_t$ during the ongoing COVID-19 pandemic. Our study aimed to develop a simple statistical framework to predict values of $R_t$, using key driving factors of COVID-19 transmission that can be used before a formal estimate relying on reported case counts is available.

2. Methods

2.1. Empirical datasets in Japan

2.1.1. Epidemiological data

The information on confirmed cases of COVID-19 in six prefectures in Japan — Tokyo, Osaka, Aichi, Hokkaido, Fukuoka, and Okinawa — was retrieved from a publicly available data source, from January 16, 2020 through February 15, 2021 (Ministry of Health, Labour and Welfare, 2020b). The data for the six prefectures were categorized into two types: ‘training data’ and ‘test data’. The training data were used for the model training and cross-validation, while the test data were from regions not included in the training data, and were used to evaluate the predictive performance of the trained model in different geographical settings. To ensure that a sufficient number of cases was included in the training data, four prefectures (Tokyo, Osaka, Aichi, and Hokkaido), accounting for more than 200 cases before the first state of emergency, were selected for the training data. The test data comprised those for the other two prefectures (Fukuoka and Okinawa), which are geographically distinct from those in the training data. According to the history of travelling abroad within 7 days prior to the illness onset, all cases were classified as either imported or domestic. In total, 217 258 confirmed COVID-19 cases, including 166 imported cases, were included in the study. Within the training data, 32 130 and 150 706 cases were assigned to the period for model training (‘training period’) and cross-validation (‘validation period’), respectively, while 22 379 cases were included in the test data.

2.1.2. Reconstruction of COVID-19 incidence according to infection time

Of the 217 258 total cases, were 114 277 (53%) were confirmed COVID-19 cases with unknown illness onset dates. Thus, to estimate $R_t$ as a function of infection time, a back-projection was conducted in two steps. First, the missing illness onset dates for these cases were back-projected from the date of laboratory confirmation, with a right-truncated time interval distribution from illness onset to laboratory confirmation, in each prefecture (Jung et al., 2021). Second, infection times were back-projected for all reported COVID-19 cases, from either the observed or back-projected illness onset date, using the incubation period distribution (Linton et al., 2021). The R package ‘Surveillance’ (Höhle, 2007) was used for nonparametric back-projection.

2.1.3. Explanatory variable data

Human mobility patterns and temperatures were hypothesized as driving factors for COVID-19 transmission, and so those datasets for the abovementioned time period were collected. Google community mobility reports (hereafter Google mobility) were used to capture the human mobility patterns (Google, 2021). Google mobility data provide six different categories (‘retail and recreation’, ‘grocery and pharmacy’, ‘parks’, ‘transit stations’, ‘workplaces’, and ‘residential’) of changes in human mobility, relative to the average for each category on the same day of the week in the pre-pandemic period (i.e. January 3 to February 6, 2020). Mobility patterns relating to ‘retail and recreation’ were used in our analyses, based on our domain knowledge that this category likely represents mobility in the close-contact settings associated with COVID-19 transmission (Cazelles et al., 2021). Daily temperature data were retrieved from the Japan Meteorological Agency (Japan Meteorological Agency, 2021) by selecting one representative observatory close to the location of the government office for each prefecture. To extract the overall trend for these time-series, without being influenced by daily noise, both datasets were smoothed by taking a 7-day moving average.

2.2. Model and statistical analysis

A prediction model for $R_t$, integrating human mobility, temperature, and risk awareness, was designed and evaluated using the following steps. First, three candidate regression models were fitted to the reconstructed COVID-19 incidences during the training period via the renewal process. The performances of these candidate models were then compared by cross-validation against the estimated $R_t$ from data in the validation period, and the best model was selected. Last, the predictive performance of the best-ranked model was evaluated using the separate test data, by comparing estimated $R_t$ values with the predicted values produced by the trained model to determine the applicability of the model to other geographic settings.

2.2.1. Model for predicting the effective reproduction number

Three simple regression models that incorporated different combinations of explanatory factors for COVID-19 transmission were proposed: only Google mobility (Model 1), Google mobility and temperature (Model 2), and Google mobility, temperature, and risk awareness over COVID-19 (Model 3). In each model, corresponding variables were included in a log-linear regression form. The $R_t$ in the model with all three factors (Model 3) was formulated as follows:

$$R_{t,i}=R_{0,i}\text{exp}\left(a{m}_i\left(t\right)+b{k}_i\left(t\right)+c\text{min}(w_{limit,i},w_i\left(t\right))\right),$$ (1)

where $R_{0,i}$ is the baseline effective reproduction number in prefecture $i$. $R_{0,i}$ was assumed to be similar for all four prefectures of the training data group, following a gamma distribution with a mean $\overline{R}$ and fixed coefficient of variation (CV) of 0.5 (Park et al., 2020). The value of CV was fixed due to the small number of prefectures, but a varied CV in the range 0.25–1 produced similar results. Covariates $m_i\left(t\right)$ and $k_i\left(t\right)$ are smoothed values of Google mobility and temperature at calendar time $t$ and in prefecture $i$, respectively. $w_i\left(t\right)$ is the degree of risk awareness at calendar time $t$ and in prefecture $i$; this was graded by assuming that it was linearly associated with the smoothed number of newly reported COVID-19 cases, following a positive association between confirmed cases and risk perception found in a UK study, using longitudinal data (Schneider et al., 2021). The effect of this variable $w_i\left(t\right)$ was capped at a predefined upper limit ($w_{limit,i}$), corresponding to the government definition of ‘highest alert level’ incidence in Japan (i.e. 25 confirmed cases per 100 000 population in a week) (Cabinet Relations Office, 2020). According to the definition, a daily number of cases giving an upper limit for each prefecture $i$ ($w_{limit,i}$) was specified as 497 in Tokyo, 315 in Osaka, 270 in Aichi, 188 in Hokkaido, 182 in Fukuoka, and 52 in Okinawa. The $R_t$ values in Models 1 and 2 were specified for models whose coefficients for non-included variables in Equation (1) were fixed at 0.

A likelihood function was constructed for the proposed regression models of $R_t$ (Models 1–3), based on the renewal process, and the corresponding parameters of each regression model were estimated by fitting them to the COVID-19 incidence during the training period. The expected number of daily reported domestic cases $c_{domestic,i}\left(t\right)$ at calendar time $t$ in a given prefecture $i$ was calculated using the equation:

$$\mathrm{E}\left(c_{domestic,i}\left(t\right)\right)=R_{t,i}\sum _{\tau =1}^{t-1}{c}_{total,i}\left(t-\tau \right)g\left(\tau \right)\frac{F_i\left(T-t\right)}{F_i\left(T-t+\tau \right)},$$ (2)

where $c_{total,i}\left(t\right)$ denotes the total (imported + domestic) daily number of COVID-19 cases at time $t$ reported in prefecture $i$. $g(·)$ is the probability mass function (PMF) of generation time (Nishiura et al., 2020). To account for the right truncation, the cumulative mass function, $F_i(·)$, for the time delay from infection to report was calculated by convoluting the PMF of the incubation period and of the time interval from illness onset to reporting in prefecture $i$ (see Section 2 - 1, 2). The training period used covered the first pandemic wave in Japan (March 15 to May 1, 2020) and part of the second wave (July 15 to August 31, 2020). The intra-wave period from May 1 to 15 July 15, 2020 was excluded because of the low count numbers observed during that period. For parameter estimation, a Poisson likelihood was used:

$$\begin{array}{ccc}& & \mathrm{L}\left(\theta ;c_{domestic,i}\left(t\right)\right)\hfill \\ & & =\prod _{t=1}^T\frac{\exp \left(-E\left(c_{domestic,i}\left(t\right)\right)\right){\left(E\left(c_{domestic,i}\left(t\right)\right)\right)}^{c_{domestic,i}\left(t\right)}}{c_{domestic,i}\left(t\right)!},\hfill \end{array}$$ (3)

where the set $\theta$ includes all or some of the parameters (i.e., $R_{0,i}$, $\overline{R}$, $a$, $b$, and $c$) specific for each of the three proposed models. The maximum likelihood method was employed, with 95% confidence intervals (CIs) for each parameter derived from 10 000 samples from a Laplace approximation normal distribution.

2.2.2. Model selection through cross-validation

To select the best model among those proposed, a cross-validation was conducted by comparing the predicted and estimated ‘ground-truth’ $R_t$ during the validation period (from September 1, 2020 to January 31, 2021) in the four prefectures. Each regression model produced predictive $R_t$ values for the validation period using the explanatory variables based on the estimated parameters in Method 2-2-1. The $R_t$ values estimated from incidence data via the renewal process (Equation (2)) were used as the ground-truth. $R_t$ was estimated as a free time-dependent parameter from the COVID-19 incidences during the validation period using the following likelihood function:

$$\begin{array}{ccc}& & \mathrm{L}\left(R_{t,i};c_{domestic,i}\left(t\right)\right)\hfill \\ & & =\prod _{t=1}^T\frac{\exp \left(-E\left(c_{domestic,i}\left(t\right)\right)\right){\left(E\left(c_{domestic,i}\left(t\right)\right)\right)}^{c_{domestic,i}\left(t\right)}}{c_{domestic,i}\left(t\right)!}.\hfill \end{array}$$ (4)

The 95% CIs were derived using the profile likelihood method. Considering the right-truncation in the recent reported incidences, the estimated $R_t$ for the latest 15 days (February 1–15, 2020) were excluded from the cross-validation. Furthermore, to smooth out abrupt fluctuations (e.g. superspreading events) in the estimated $R_t$ values, a 7-day moving average was taken. Next, a predictive performance of each model (i.e. a comparison between the predicted and estimated $R_t$ during the validation period) was quantitatively assessed using four different measurements: bias, root-mean-square error (RMSE), ranked probability score, and Dawid-Sebastiani score (Funk et al., 2019), and the best model was selected. In addition, the number of predicted infections using the conditional forecasting method (i.e. forecasting a future incidence based on the predicted $R_t$ and empirically reported incidences in the past) was also compared against the back-projected incidence by infection dates.

2.2.3. Evaluation of the predictive performance using the test data

Lastly, a predictive performance of the finally selected model was evaluated using the test data, indicating a potential applicability of the proposed model to other geographical settings. Accordingly, the $R_t$ values in two test data prefectures (Fukuoka and Okinawa) were predicted from July 15, 2020 through January 31, 2021, relying only on the trained model, and were compared against the estimated $R_t$ from the renewal process. In addition, the predicted number of infections using the conditional forecasting method were compared with the empirical data in each of the two prefectures.

3. Results

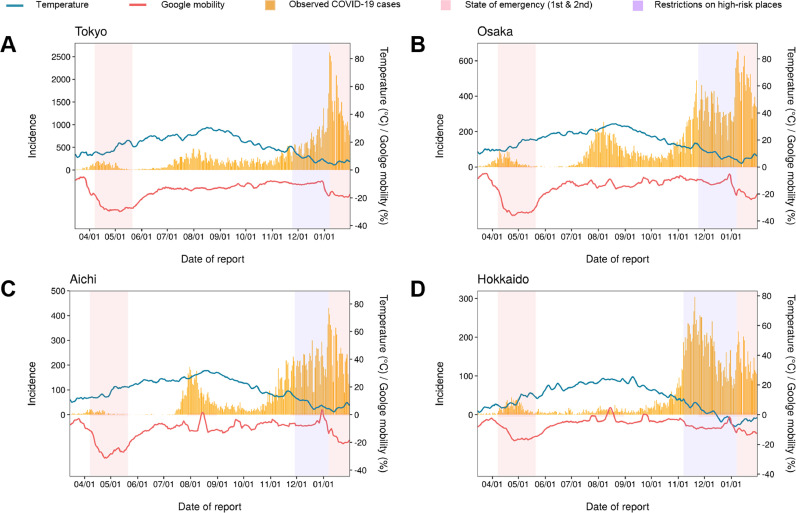
Figure 1 shows the epidemic curve of COVID-19 by reporting date in the four selected training data prefectures, along with the time trend of Google mobility and temperature. Substantial reductions in Google-based mobility were observed in all regions during the first and second state of emergency, consistent with only small numbers of reported cases by the end of the declaration. The human mobility patterns tended to show abrupt increases on consecutive national holidays and, accordingly, the number of reported cases increased slightly after roughly 9 days, consistent with the empirical time delay from infection to reporting in Japan.

Figure 1.

Epidemiological curves for COVID-19 by date of report, along with trends of Google mobility and temperature in Tokyo, Osaka, Aichi, and Hokkaido, Japan.

The number of COVID-19 cases by date of report (yellow bars) from March 15, 2020 to January 12, 2021 in the four training data prefectures of Japan: (A) Tokyo, (B) Osaka, (C) Aichi, and (D) Hokkaido. Red lines indicate trends of changes in human mobility patterns (the ‘retail and recreation’ category in Google community mobility reports) compared with those in the pre-pandemic period (January 3 to February 6, 2020). Blue lines show trends for the daily temperature in each region; both mobility and temperature were smoothed using 7-day moving averages. In each figure, two red-shaded areas indicate the time periods for the first and second nationwide states of emergency, respectively, while purple-shaded areas show the time periods when stringent restrictions on bars and restaurants were implemented by each prefectural government right before the second state of emergency.

Table 1 shows the estimated parameters from the data in the training period and summarizes the predictive performance of proposed models during the validation period. Among the three models, the model that incorporated Google mobility, temperature, and risk awareness (Model 3) was selected as the best model, based on the Dawid-Sebastiani score, while the model that accounted for only Google mobility (Model 1) showed the best performance with regard to RMSE, bias, and ranked probability score. The predicted time trend of $R_t$ using Model 1 (an almost linear trend close to the value of 1; Figure S1) was less informative compared with Model 3, indicating that Model 1 would be not suitable for time trend analysis. Thus, Model 3 was selected as the best model. Using Model 3, the baseline value $R_{0,i}$ was estimated at 4.40 (95% CI 4.07–4.73) for Tokyo, 2.85 (95% CI 2.62–3.07) for Osaka, 2.20 (95% CI 2.02–2.38) for Aichi, and 1.99 (95% CI: 1.84–2.15) for Hokkaido. The regression coefficient accounting for Google mobility was estimated to be 0.03 per percentage point (95% CI 0.03–0.03), while temperature and risk awareness were negatively associated with estimated coefficients of −0.02 per degree Celsius (95% CI −0.02 to −0.01) and −0.12 per 100 reported cases (95% CI −0.15 to −0.10), respectively. All coefficients were statistically significant.

Table 1.

Summary of the estimated parameters and predictive performances of the proposed models

Model	Parameter	Value	Bias	RMSE	Ranked probability score	Dawid-Sebastiani score
Model 1	$R_0$ (Tokyo)	1.74 (1.66–1.82)	0.28	1.65	168.94	479 953
	$R_0$ (Osaka)	1.37 (1.32–1.41)
	$R_0$ (Aichi)	1.15 (1.11–1.19)
	$R_0$ (Hokkaido)	1.33 (1.25–1.41)
	Google mobility	0.02 (0.01–0.02)
Model 2	$R_0$ (Tokyo)	4.39 (4.05–4.72)	-1.06	2.29	264.41	328 849
	$R_0$ (Osaka)	3.23 (3.02–3.44)
	$R_0$ (Aichi)	2.59 (2.43–2.75)
	$R_0$ (Hokkaido)	2.09 (1.95–2.23)
	Google mobility	0.03 (0.03–0.03)
	Temperature	−0.03 (−0.03 to −0.03)
Model 3	$R_0$ (Tokyo)	4.40 (4.07–4.73)	0.55	1.77	171.60	147 027
	$R_0$ (Osaka)	2.85 (2.62–3.08)
	$R_0$ (Aichi)	2.20 (2.02–2.38)
	$R_0$ (Hokkaido)	1.99 (1.84–2.15)
	Google mobility	0.03 (0.03–0.03)
	Temperature	−0.02 (−0.02 to −0.01)
	Risk awareness	−0.12 (−0.15 to −0.10)

Model 1: Google mobility; Model 2: Google mobility and temperature; Model 3: Google mobility, temperature, and risk awareness; RMSE: root-mean-square error

Each value describes the estimated parameters of three different models and their 95% confidence intervals derived by maximum likelihood estimation and Laplace approximation normal distribution. Predictive performances of each model were compared using three measures (root-mean-square error, ranked probability score, and Dawid-Sebastiani score) and by summing estimates of four regions in Japan (prefectures for the training data — Osaka, Tokyo, Aichi, and Hokkaido).

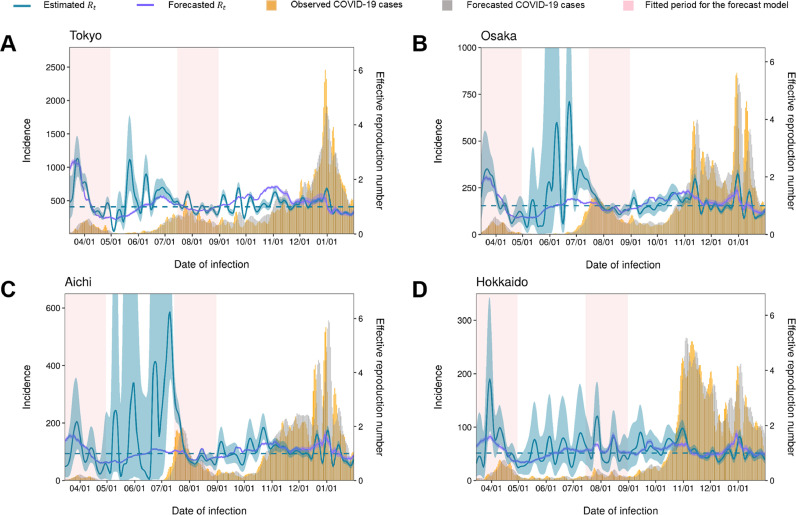
Figure 2 shows the comparison of estimated and predicted $R_t$ for the four training data prefectures, using the best-ranked Model 3. Although the model was fitted to cases over a relatively short period of time, the predicted values and 95% CIs captured the temporal patterns of the estimated $R_t$ in all the prefectures well, showing clear signs of $R_t$ rising above 1 at the beginning of the second and third waves of the epidemic. However, with the implementation of stringent countermeasures (e.g. requesting reduced opening hours for night-life spots) from November 2020, the predicted $R_t$ showed larger deviations from the estimated values, suggesting a diminished predictive performance. The predicted $R_t$ values using Model 1 (Figure S1) and Model 2 (Figure S2) were less consistent with the estimated $R_t$.

Figure 2.

Comparison of estimated and predicted effective reproduction numbers for COVID-19, using the model accounting for Google mobility, temperature, and risk awareness.

Comparison between the estimated and predicted effective reproduction numbers ($R_t$) for COVID-19. The model (Model 3; considering Google mobility, temperature, and risk awareness of COVID-19) was applied to the four training data prefectures of Japan: (A) Tokyo, (B) Osaka, (C) Aichi, and (D) Hokkaido. Yellow bars represent reconstructed numbers of COVID-19 cases by infection time; grey bars show the number of predicted incidences using the conditional forecasting method. Blue lines and shaded areas indicate the estimated $R_t$ values and their 95% confidence intervals using the renewal process and profile likelihood, while purple lines and shaded areas indicate the predicted $R_t$ values and their 95% confidence intervals derived from the Laplace approximation normal distribution. Red shaded areas indicate the training period (i.e. March 15 to May 1, 2020 and July 15 to August 31, 2020) used for estimating the parameters of the model.

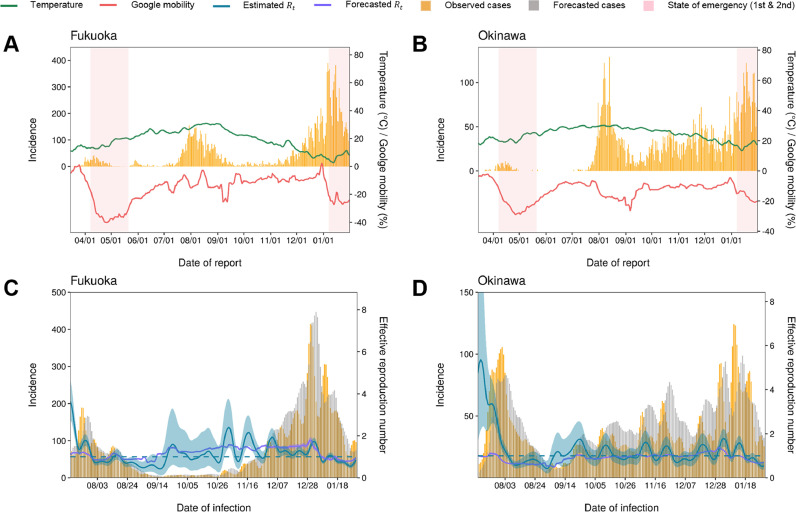
Figure 3 shows the test performance of the best model (Model 3), by comparing the estimated and predicted $R_t$ in Fukuoka and Okinawa (test data). With the default value of $R_{0,i}$ offset to 2.50, the inferred values of $R_t$ were consistent with the overall trend of the ground-truth $R_t$ values, indicating the applicability of the proposed model to other geographical settings.

Figure 3.

Comparison of estimated and predicted effective reproduction numbers for COVID-19, using the best model and two other geographic settings (test data) in Japan

(A–B) The number of COVID-19 cases by date of report (yellow bars) from March 15, 2020 to January 12, 2021 in two of the test data prefectures: (A) Fukuoka and (B) Okinawa. Red lines indicate trends of changes in human mobility patterns (the ‘retail and recreation’ category in Google community mobility reports) and the green lines show trends in daily temperatures for each region. Both mobility and temperature were smoothed using 7-day moving averages. (C–D) Comparison between the estimated and predicted effective reproduction number ($R_t$) for COVID-19, using the best model (Model 3; considering Google mobility, temperature, and risk awareness) and the test data: (C) Fukuoka and (D) Okinawa. Yellow bars represent reconstructed numbers of COVID-19 cases by infection time; grey bars show the number of predicted incidences using the conditional forecasting method. Blue lines and shaded areas indicate the estimated $R_t$ values and their 95% confidence intervals, using the renewal process and profile likelihood, while purple lines and shaded areas are the predicted $R_t$ values and their 95% confidence intervals from the best model and its estimated parameters.

4. Discussion

Our study proposed a simple regression model for predicting the real-time $R_t$ of COVID-19, accounting for human mobility, temperature, and risk awareness. Our analysis suggested that the human mobility pattern was positively associated with COVID-19 transmission, while temperature and risk awareness were negatively associated.

These findings indicate that the reduction in socioeconomic activities and increased level of risk awareness may be linked to a reduction in transmission, highlighting the potential of social distancing interventions and risk communication for controlling the COVID-19 epidemic (Anderson et al., 2020; Heydari et al., 2021). The inverse association between temperature and COVID-19 transmission was also in line with other published papers (Li et al., 2020; Ma et al., 2021; Smith et al., 2021). This finding could be explained by two possible mechanisms. First, cold temperature induces behavioral changes and increases indoor contact, which is associated with the transmission risk of SARS-CoV-2 (McClymont and Hu, 2021). Second, the virus enjoys greater survivability in cold environments (Riddell et al., 2020), as has been the case for other human coronaviruses (Chan et al., 2011; van Doremalen et al., 2013). Although the cumulative number of reported cases during the summer season was higher than that of the winter season in 2020 (Figure 1), this observation should be approached with a caution, considering the mixture of multiple factors, including the increase in physical contact after the lifting of the initial population-wide restrictions). Indeed, the majority of infections in the summer season were reported to be associated with night/town activities (Ministry of Health, Labour and Welfare, 2020c).

Values of $R_t$ predicted by the simple linear regression model fitted to the very limited data points aligned well with the estimates empirically obtained from the time series of COVID-19 incidence, showing a clear emerging signal ($R_t$> 1) for the second and third waves in Japan. This performance of the proposed model suggests that our framework can provide a plausible proxy of the latest $R_t$ for COVID-19, using readily accessible data, which conventional methods relying on reported incidences are not able to generate in a timely manner, due to the inherent delays. Timely assessment of $R_t$ is essential to inform public health policies, for example those aiming to bring the epidemic under control before the hospital and intensive care unit occupancies reach full capacity. Although abrupt changes in $R_t$ values — presumably induced by temporary local surges of cases (e.g. clusters in hospitals and nursing homes) — could not be fully captured by the proposed model, it was still able to provide a timely signal of changes in $R_t$ before the formal estimates become available.

Despite the overall good performance of the proposed model, our framework over- or underestimated $R_t$ when stringent interventions (e.g. reduced opening hours for restaurants and bars from November 2020) were in place. Although the inclusion of mobility patterns associated with retail and recreation, to represent the physical mixing in high-risk settings, was considered a reasonable choice, such data — with limited temporal and spatial resolution — may not fully reflect the detailed social contact patterns.

It has been suggested that the transmission of COVID-19 involves substantial individual variations, characterized by a highly dispersed offspring distribution (Endo et al., 2020). Thus, stringent control measures were imposed, primarily on settings regarded as high risk (e.g. nightclubs, bars, and restaurants). The resulting changes in detailed contact patterns in those places may not have been fully reflected by the simple summary data for human mobility. Moreover, the digital proxies for human mobility patterns were suggested to be not very informative regarding changes in densities of individuals within high-risk places; this metric may play a crucial role in SARS-CoV-2 transmission (Chang et al., 2021). These limitations of the mobility data may account for the temporary deviations in the prediction.

Our study had some additional limitations. First, the relationship between the number of COVID-19 cases and the degree of risk awareness may change in the long run. Indeed, a decrease in adherence to non-pharmaceutical interventions was reported in the USA from April to November, 2020 (Crane et al., 2021), in spite of the continuously increasing number of reported COVID-19 cases. Second, the upper limit for the effect of risk awareness was rather arbitrarily chosen, and not necessarily theoretically justified. It was assumed that risk awareness affects the transmission risk via personal behavioral changes that are not reflected in the changes in mobility (e.g. wearing a mask or avoiding crowded places during outside visits). It is likely that there is a certain limit to the risk reduction achieved by such behavioral changes, which we incorporated in our model as a prespecified cap. Third, with the roll-out of COVID-19 vaccines, the proposed model might become insufficient for predicting $R_t$, due to the herd immunity effect conferred by vaccination. Lastly, more accurate prediction may require an extended model that accounts for age-stratified transmission dynamics (e.g. age-specific susceptibility), along with age-specific mobility patterns.

5. Conclusion

Our study suggests that human mobility, temperature, and risk awareness can be integrated into the renewal process to provide timely predictions of the effective reproduction number during the ongoing COVID-19 transmission — i.e. ahead of the formal empirical estimates, which are subject to delays. This would generate essential information for timely planning and assessment of epidemic control measures.

Funding

This research was mainly supported by the Environment Research and Technology Development Fund (JPMEERF20S11804) of the Environmental Restoration and Conservation Agency of Japan. S-m.J received funding from the Japan Society for the Promotion of Science (JSPS) KAKENHI (20J2135800). A.E. is financially supported by the Nakajima Foundation. H.N. received funding from Health and Labor Sciences Research Grants (19HA1003, 20CA2024, and 20HA2007); the Japan Agency for Medical Research and Development (AMED; JP19fk0108104, JP20fk0108140 and JP20fk0108535s0101); JSPS KAKENHI (17H04701 and 21H03198); the GAP fund program of Kyoto University; the Japan Science and Technology Agency (JST) CREST program (JPMJCR1413); and the SICORP program (JPMJSC20U3 and JPMJSC2105). This study was also supported by German Federal Ministry of Health (BMG) COVID-19 research and development funding to the World Health Organization. The funders were not involved in the collection, analysis, or interpretation of the data, the writing of the manuscript, or the decision to submit the work for publication.

Ethical approval and consent to participate

Our study analyzed publicly available data (Ministry of Health, Labour and Welfare, 2021). As such, the datasets used in our study were de-identified and fully anonymized in advance, and the analysis of publicly available data without identity information did not require ethical approval.

Availability of data and materials

The time-series data on COVID-19 were publicly available on the websites of the Ministry of Health, Labour and Welfare (Ministry of Health, Labour and Welfare, 2021). The relevant code for this research work is stored in the GitHub: https://github.com/SungmokJung/Prediction_Rt_COIVD19.

Consent for publication

Not applicable

Conflicts of interest

A.E. received research funding from Taisho Pharmaceutical Co., Ltd.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.