Joint Estimation of Generation Time and Incubation Period for Coronavirus Disease 2019

A statistical framework was developed to jointly estimate the distribution of generation time and incubation period from human-to-human transmission pairs of COVID-19, accounting for sampling biases due to exponential growth of the epidemic during the data collection period.

Abstract

Background

Coronavirus disease 2019 (COVID-19) has caused a heavy disease burden globally. The impact of process and timing of data collection on the accuracy of estimation of key epidemiological distributions are unclear. Because infection times are typically unobserved, there are relatively few estimates of generation time distribution.

Methods

We developed a statistical framework to jointly estimate generation time and incubation period from human-to-human transmission pairs, accounting for sampling biases. We applied the framework on 80 laboratory-confirmed human-to-human transmission pairs in China. We further inferred the infectiousness profile, serial interval distribution, proportions of presymptomatic transmission, and basic reproduction number ($R_0$) for COVID-19.

Results

The estimated mean incubation period was 4.8 days (95% confidence interval [CI], 4.1–5.6), and mean generation time was 5.7 days (95% CI, 4.8–6.5). The estimated $R_0$ based on the estimated generation time was 2.2 (95% CI, 1.9–2.4). A simulation study suggested that our approach could provide unbiased estimates, insensitive to the width of exposure windows.

Conclusions

Properly accounting for the timing and process of data collection is critical to have correct estimates of generation time and incubation period. $R_0$ can be biased when it is derived based on serial interval as the proxy of generation time.

On 11 March 2020, the World Health Organization declared coronavirus disease 2019 (COVID-19) a pandemic [1], and by 30 April 2021 it has caused over 150 million cases and 3.2 million deaths [2]. Transmission dynamics are determined by a number of key epidemiological parameters, such as the incubation period, generation time, and basic or effective reproduction numbers [3]. The incubation period is defined as the time period between infection and symptom onset. The generation time is defined as the time interval between the infections of the infector and infectee in a transmission chain [4]. Similarly, the serial interval describes the time interval between the symptom onsets of the infector and infectee in the transmission chain [5]. While a number of early studies estimated the incubation period and serial interval distributions from readily available official or public data [6–11], estimates of the generation time distribution have rarely been reported [12, 13], because it is usually difficult to determine when a person was infected.

The generation time distribution is a particularly important epidemiologic distribution because it can be used to estimate the basic or effective reproduction number from the epidemic growth rate [14, 15]. While the serial interval distribution is used to approximate the generation time distribution for this estimation [12, 16, 17], it is only valid for diseases in which infectiousness starts after symptom onset [18]. However, presymptomatic transmission of COVID-19 has been estimated to account for up to 40% or more of transmission events [19–21], and negative serial intervals have been reported [12]. Furthermore, even though the generation time distribution and serial interval distribution can share the same mean, they have different variances [4], potentially affecting the validity of approximating the generation time distribution with the serial interval distribution.

On the other hand, estimates of the incubation period distribution or generation time distribution could be biased if the impact of sampling during epidemic growth is not accounted for [22]. While the exact infection time cannot be observed, an exposure window can be defined by the possible contact time between the infector and infectee with detailed contact tracing. In the early phase of the first COVID-19 epidemic wave in China, transmission chains can be more clearly determined based on travel history to Wuhan, which was the epicenter of the outbreak. Hence, based on published data from the early phase of the outbreak in China [23], we jointly estimated the incubation period and generation time of COVID-19, informed by symptom onset time and exposure windows. We also determined the potential impact of using the serial interval distribution rather than the generation time distribution to estimate the basic reproduction number of COVID-19.

METHODS

Data Sources

We reanalyzed published data from a study on presymptomatic transmission of COVID-19 in mainland China [23]. The information published in that report was derived from epidemiological reports in the Chinese Public Health Event Surveillance System. This system recorded epidemiological information on clusters of suspected cases in each county, which were required to be investigated and reported. There were 449 COVID-19 confirmed cases detected outside Hubei province with illness onset between 1 and 29 January 2020. All cases were laboratory-confirmed following the case definition of the Novel Coronavirus Pneumonia Prevention and Control Protocol published by the National Health Commission [16, 24]. The data included the information on human-to-human transmission pairs with onset and possible exposure dates that can be used to infer the distribution of the incubation period and generation time distributions. The infectees were identified as those who did not have recent travel to Wuhan but had close contact with another confirmed case with recent travel to Wuhan, providing clarity on the directionality of transmission even for negative serial intervals, because at this time the epidemic outside Hubei was still mainly driven by cases linked to Wuhan [25].

Model Specification

We used the onset dates of the infector and infectee of each transmission pair to estimate several distributions of epidemiological importance (Figure 1). While times of symptom onset can be observed, infection times are generally not observable but bounded within a window of time when exposure occurred, which allows us to infer the incubation period and generation time of COVID-19. Therefore, we developed a statistical framework to jointly estimate the incubation period and generation time distributions, accounting for the possible sampling biases due to the exponential growth of the epidemic (Supplementary Material). In general, we could estimate the incubation period and generation time by constructing the likelihood of observing the onset times of the transmission pair as follows:

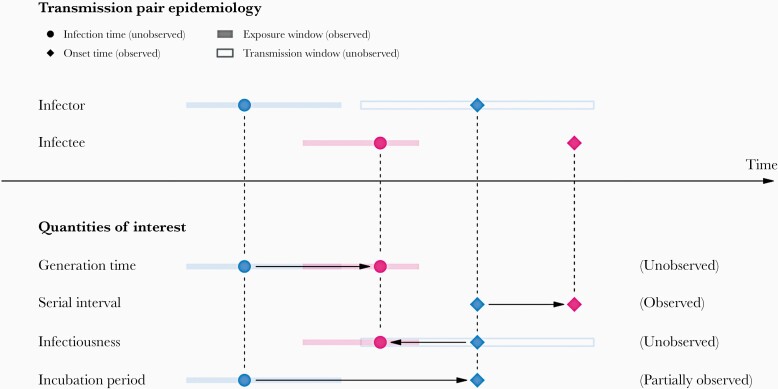
Figure 1.

A schematic of the relationship of different time periods of transmission between an infector and an infectee in a transmission pair. Exposure window is defined as the time interval having viral exposure, and transmission window is defined as the time interval for onward transmission with respect to the infection time. Incubation period is defined as the period between infection and symptom onset; generation time is defined as the duration between the infection times of an infector and an infectee; infectiousness profile is defined as the time interval for the transmission to an infectee with respect to the onset time of the infector; serial interval is defined as the duration between onset times of the infectors and infectees.

$$\begin{array}{l}likelihood=P(O_s,O_i)\end{array}$$

$$\begin{array}{l}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}P(O_s,O_i,I_s,I_i)d{I}_{s}d{I}_i\end{array}$$

$$\begin{array}{l}={\stackrel{}{\int }}_{L_i}^{U_i}{\stackrel{}{\int }}_{max(I_i,L_s)}^{U_s}P\left(O_s|I_s\right)P\left(I_s|I_i\right)P\left(O_i|I_i\right)P\left(I_i\right)d{I}_{s}d{I}_i\end{array}$$

$$\begin{array}{l}={\stackrel{}{\int }}_{L_i}^{U_i}P\left(O_i|I_i\right)P\left(I_i\right)\left({\stackrel{}{\int }}_{max(I_i,L_s)}^{U_s}P\left(O_s|I_s\right)P\left(I_s|I_i\right)d{I}_s\right)d{I}_i\end{array}$$

where $O$ is the onset time, $I$ is the infection time, $L$ and $U$ are the lower bound and upper bound of the exposure window, respectively. The subscripts $i$ and $s$ denote infector and infectee, respectively. $P\left(O_i|I_i\right)$ and $P\left(O_s|I_s\right)$ are the probability density functions of incubation period for infectors and infectees respectively, while $P\left(I_s|I_i\right)$ is the probability density function of generation time for infectors. We assumed that the incubation period of an infectee is independent of the epidemiological characteristics of the infector after conditioning on infection time of the infectee, and the symptom onset of the infector is independent of infectiousness conditioning on the infection time of infector.

However, the data were collected under the backward approach because we first identified the cohort of infectees and then determined their infectors, during the early phase of the epidemic in China. Hence, in estimation we followed backward in time from the symptom onset to infection for the incubation period, and from infectee to infector for the generation time. Therefore the sampling distribution could be biased towards shorter incubation periods and shorter generation times and adjusted by a previous approach [17, 26]. We assumed the exponential growth rate (denoted by $r$) to be 0.14 according to a previous study [23]. The sampling bias can be adjusted for by the following equation,

$$\begin{array}{l}{h}_b\left(t\right)=\frac{h_f\left(t\right)\exp (-rt)}{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{h}_f\left(t\right)\exp (-rt)dt}\end{array}$$

where $h_f\left(t\right)$ and $h_b\left(t\right)$ are the distributions of interest under the forward approach (ie, identifying the cohort of infector first and then determining the respective infectee) and the backward approach respectively, where $h_f\left(t\right)$ provides a good approximation of the intrinsic distribution (true distribution) during the exponential growth of epidemics [17]. On the other hand, these intervals for infector might be less subject to the sampling bias for the given infectee cohort because we found estimation bias in the intervals for infectors when applying the same adjustment to both infectors and infectees (Supplementary Material). We thus introduced a proportionality constant, $p$, for the partial adjustment in infector (ie, adjusted by $\exp (-prt)$ instead) (Supplementary Material). Model parameters were estimated by maximum likelihood method. The 95% confidence interval (CI) was constructed by the percentile bootstrap method with 1000 bootstrapped samples. Statistical analyses were conducted using R version 4.0.3 (R Foundation for Statistical Computing).

Serial Interval, Infectiousness Profile, and Basic Reproduction Number

To account for the possibility of presymptomatic transmission, we used Monte Carlo method to estimate the infectiousness profile, defined as the time interval for the transmission to infectee with respect to the onset time of the infector ($I_s-O_i$), by generating 1 000 000 samples from the fitted generation time ($I_s-I_i$) and fitted incubation period of the infector ($O_i-I_i$) and their difference. Similarly, we estimated the distribution of serial interval, defined as the duration between onset times of the infector and infectee ($O_s-O_i$), by summing the incubation period of the infectee ($O_s-I_s$) and the generation time ($I_s-I_i$), and then subtracting the incubation period of the infector ($O_i-I_i$).

We further used the fitted generation time to calculate the basic reproduction number, $R_0$, defined as the number of secondary infections (infectees) caused by a typical primary case (infector) in an entirely susceptible population. Hence, the basic reproduction number can be derived by the following Lotka-Euler equation (Supplementary Material).

Model Variations

Sensitivity analysis on different exponential growth rates was conducted. We also tested alternative choices of distribution (eg, Weibull, log normal) for the incubation period and generation time.

Model Validation

Simulations were conducted to assess if the proposed estimation method could recover the incubation period and generation time distributions. We simulated the infection times of infectee within the exposure window based on the infection times of the infector and an assumed generation time distribution. The symptom onset times for both infector and infectee were simulated similarly and independently (Supplementary Material). To account for exponential growth of the epidemic, infection times of infectors were simulated with weighting proportional to $\exp \left(rt\right)$ (Supplementary Material). To account for the backward-looking nature of the observed data, we randomly selected those transmission pairs with symptom onset time of the infectee falling into predefined intervals (Supplementary Material). In the simulations, we tested the assumption on the distribution of the exposure window and the situation with missing exposure windows for infector and assessed how these assumptions may influence the estimation accuracy. We also simulated the onset times of infector and infectee to assess the model fitness by comparing the observed and simulated onset times of infector and infectee by using the Monte Carlo method (Supplementary Material).

RESULTS

Incubation Period and Generation Time

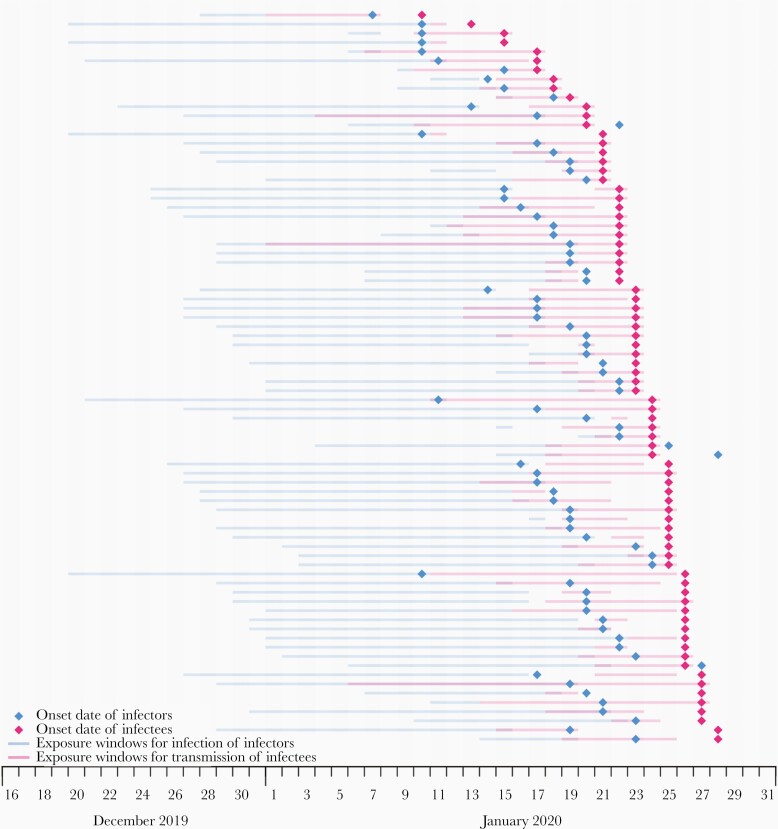
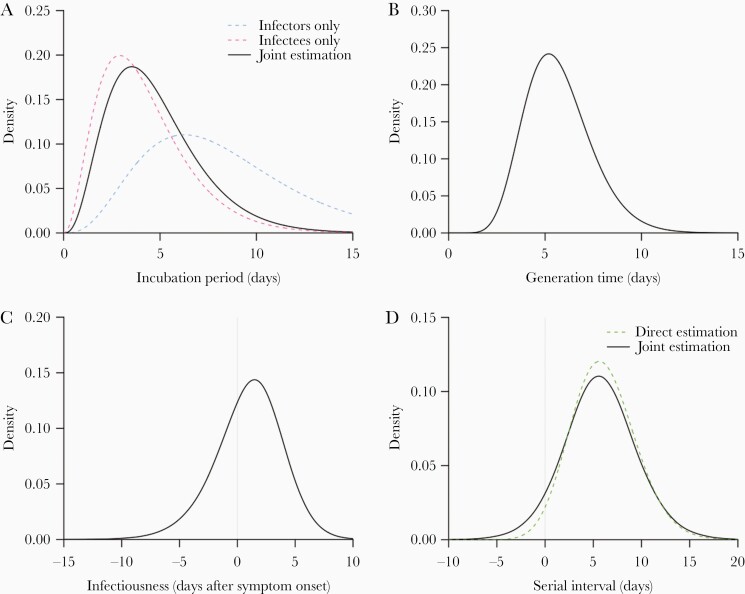
We extracted information on exposure windows and onset dates in 80 human-to-human transmission pairs of COVID-19 in mainland China (Figure 2) [23]. All reported estimates have been adjusted for sampling bias. If infectors and infectees were all considered separately, the estimated mean incubation periods were 8.3 (95% CI, 6.1–10.2) and 4.2 (95% CI, 3.3–5.1) days, respectively (Supplementary Table 1), which were significantly different (Figure 3A). When the infectors and infectees were assumed to have a shared distribution of incubation period in our joint estimation model (Supplementary Table 1), the estimated incubation period has a mean of 4.8 days (95% CI, 4.1–5.6) and a 95th percentile of 9.3 days (95% CI, 7.8–11.3), while the estimated generation time distribution has a mean of 5.7 days (95% CI, 4.8–6.5) and standard deviation of 1.7 days (95% CI, .7–2.5) (Figure 3B). Without the adjustment for sampling bias, the mean incubation period in infectees would be underestimated by 15% (4.1 days), and the mean generation time would be underestimated by 6.8% (5.3 days).

Figure 2.

Data on 80 human-to-human transmission pairs analyzed in the current study, extracted from a published study [23]. Diamonds indicate the dates of onset of infectors and infectees. The shaded area in blue in each row indicates the period of exposure for the infector and that in red indicates the period of exposure of the infectee to the infector.

Figure 3.

Epidemiological distributions of COVID-19: (A) incubation period; (B) generation time; (C) infectiousness; and (D) serial interval. The black lines indicate the fitted/derived distributions from joint estimation. A, The dashed blue line and the dashed pink line indicate the incubation periods for infectors and infectees, respectively, which were calculated based on the interval censored likelihood of γ distribution according to their exposure windows. D, The green dashed line indicates the estimated serial interval based on the difference of onset times in the transmission pairs assuming it is γ-distributed with an extra parameter allowing horizontal shift in the distribution for negative serial intervals.

Serial Interval, Infectiousness Profile, and Basic Reproduction Number

Based on the joint estimation (Supplementary Table 2), the serial interval distribution was estimated to have a mean of 5.7 days (95% CI, 4.8–6.5) and standard deviation of 3.8 (95% CI, 3.1–4.7). Based on the estimated generation time distribution and exponential growth rate of 0.14, the basic reproduction number was estimated to be 2.2 (95% CI, 1.9–2.4). If the serial interval distribution were used as a proxy for the generation time, the estimated $R_0$ would be underestimated by about 5%–20% depending on the true growth rate (Table 1), because the variance of the serial interval distribution was much larger than that of the generation time distribution (Supplementary Tables 1 and 2). Besides, the 2.5th percentile of the onset of infectiousness was 5.5 days (95% CI, 4.0–8.0) before symptom onset and the 97.5th percentile was 6.3 days (95% CI, 3.9–8.5) days after symptom onset (Supplementary Table 2). The estimated proportion of transmission before symptom onset was 34% (95% CI, 26%–51%). The infectiousness profile and serial interval distribution are also illustrated in Figure 3C and 3D, respectively.

Table 1.

Basic Reproduction Number $\left(R_0\right)$ Estimates Under Different Assumed Growth Rates

	Growth Rate
	0.10	0.14	0.18
Based on generation time	1.71 (1.59–1.83)	2.16 (1.92–2.38)	2.75 (2.30–3.19)
Based on serial interval	1.61 (1.49–1.72)	1.93 (1.65–2.10)	2.25 (1.69–2.58)

Data are estimated R₀ (95% confidence interval).

Note that $R_0=1$ when the growth rate $r=0$.

Model Adequacy

We simulated the data based on the fitted distributions and found that the confidence intervals of onset time for 96% of individuals could cover the observed one, suggesting good fit of the model (Supplementary Figure 1).

Model Variations

We tested the choice of distributions by using Weibull or lognormal distribution for the intervals for comparison (Supplementary Table 3), and the Akaike information criterion (AIC) among them were similar (difference < 5). We also compared the estimates under alternative growth rate and they were not particularly sensitive to this assumption (Supplementary Table 4).

Model Validation

We performed another simulation study to assess the performance of the proposed estimation method. Simulation results suggested that the partial adjustment, $p$, could avoid the estimates of incubation period for infectors being overadjusted for the sampling bias compared to the simulation values, and give unbiased estimates (Supplementary Tables 5 and 6). Considering the practical situation where the majority of infectors had missing exposure windows as in the observed data, we also defined the exposure windows to start as early as 21 days before illness onset for a certain proportion of the infectors in the simulation (Supplementary Tables 7–9), and our model was able to recover the simulation values. Correspondingly, 76% to 98% (depending on the parameter) of 95% CIs covered the simulation value in the simulation with a 30-day study period (out of 50 simulated data sets), suggesting that the algorithm could estimate the model parameter adequately. We also conducted simulations to assess the impact of exposure window on estimation accuracy, suggesting that our model was not sensitive to the width of exposure windows (Supplementary Tables 5–9).

Discussion

Unlike the incubation period, which is partially observed (Figure 1) and can be estimated easily, generation time cannot be unobserved directly and must be inferred based on other information. In this study, we developed a statistical framework to use exposure windows and onset times of the transmission pairs, which are accessible, to jointly estimate the incubation period and generation time distributions, accounting for the fact that data were collected during the exponential phase of the initial spread of COVID-19, and using a backward approach, that is identifying infectees first and subsequently determining their infectors. Based on the likelihood we developed, our estimated generation time had a mean of 5.7 days (95% CI, 4.8–6.5), which was in line with previous estimated means of 5.2 days by Ganyani et al [12] using data from Singapore, 5.0 days by Ferretti et al [20], and 5.7 days by Hu et al [27]. As discussed by Nishiura et al [14] and Park et al [17], the estimated generation time distribution can be different depending on using a forward-looking (identifying infector first) or a backward-looking (identifying infectee first) approach. During the early epidemic growth, when the data were collected under the backward-looking approach, the observed epidemiological distributions were subjected to sampling bias as we were more likely to observe shorter intervals given the increasing number of infections. Our estimates have been adjusted for such bias. Besides, we estimated that the mean serial interval is 5.7 days, which was comparable with reported estimates despite some of those estimates not accounting for the possibly of negative serial intervals or the growth rate of the outbreak [7, 13].

Based on the estimated generation time distribution, we estimated the basic reproduction number of 2.2 (95% CI, 1.9–2.4). Depending on the type of models and the period of study (timing of the data collected), the estimates of basic reproduction number for COVID-19 ranged from 1.2 to 6.5 [28]. Some high estimates of $R_0$ could be due to overestimation of the serial interval distribution that did not account for the possible negative serial intervals due to presymptomatic transmission [16, 17]. It is not uncommon to use the serial interval as a proxy for the generation time, which is strictly positive, to estimate $R_0$, because the serial interval is more easily accessible [17]. However, the $R_0$ estimate based on the serial interval is likely to be biased because the serial interval distribution usually has a larger variance than the generation time distribution [16]. There could be more severe underestimation especially when the correlation between incubation period and generation time is neglected inside the serial interval [17].

Under the separate estimation, the longer estimated incubation periods for the infector could be attributed to the wide exposure windows (Supplementary Table 1). In the data, there were 16 (20%) infectors with missing exposure windows, and 38 (48%) infectors with unknown start dates of exposure. The start dates of exposure for the infectors who were residents of Wuhan were more difficult to obtain [13]. For those cases, the start dates of exposure were set as 21 days before the symptom onset dates when missing, given that the infection time was very unlikely to be 3 weeks before the time of symptom onset, while the end dates of exposure were set as the symptom onset dates when missing. Therefore, the majority of infectors had systematically wide exposure windows, as shown in Figure 2, and such loose information on the exposure for the infectors resulted in much longer estimated incubation period. Another possible reason would be that the infectors with short incubation period had already had symptoms and were isolated in Wuhan, whereas those who had a long incubation period were able to leave Wuhan before symptom onset and formed the transmission chains outside Wuhan. On the other hand, the joint estimated incubation period had a mean of 4.8 days (95% CI, 4.1–5.6) and the 95th percentile of 9.3 days (95% CI, 7.8–11.3), which was comparable with the previous results estimating a mean of approximately 5 days [16, 29–32]. Regarding the infectiousness profile, our estimated proportion of presymptomatic transmission was 34% (26%–51%), which was consistent with the result from Wu et al of 38% [33]. However, it was slightly lower than other studies. He et al reported that 44% (95% CI, 30%–57%) of transmission occurred before symptom onset [19], and Ganyani et al suggested 48%–77% based on the Singapore and Tianjin dataset [12], while Ferretti et al had a pooled estimate of 56% (95% CI, 35%–78%) [20], and Hu et al suggested an estimate of 59% [27]. One possible reason is that potential infectors who developed symptoms early were more likely to be isolated in Wuhan and less likely to travel. Thus, those infectors who were able to travel to other provinces probably had longer incubation periods and had already spent some of time being presymptomatic in Wuhan, hence reducing presymptomatic transmission elsewhere. This is consistent with a longer incubation period in infectors and a lower proportion of presymptomatic transmission in our study.

We conducted extensive simulation studies to determine when the generation time and incubation period could be recovered. Simulation results suggested that our model was insensitive to the width of exposure windows and the presence of missing exposure windows in infectors. Such strength was also demonstrated in the main analysis despite the wide exposure windows for infectors in the data. We also modified our framework allowing for the partial adjustment for infectors, because the incubation period for infectors may be less affected by the sampling bias compared with the secondary cases.

Our framework has important implications for advancement of methods when encountering new emerging pathogens in the future. When a novel pathogen first emerges, like severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in 2019, early estimates of key epidemiological parameters like the incubation period distribution or reproduction numbers are essential to understanding the severity and transmissibility of the pathogen to inform appropriate and timely disease control polices. Thus, information on the infected cases is usually collected during the exponential phase of the epidemic, and estimation is often carried out under the backward-looking approach. However, the resulting sampling bias would lead to the underestimation of duration of these intervals and may affect the impact of public health responses. Our framework can account for potential sampling bias and provide more accurate early estimates, which is crucial for early response to novel pathogens.

Our study has some limitations. First, our estimate of the generation time distribution was based on data with only symptomatic cases and may not be generalizable to transmission pairs that involve asymptomatic cases. Second, the data might suffer from the recall biases because the time of symptom onset was self-reported. Third, several control measures, such as isolation or quarantine, had been implemented throughout China since 23 January [34, 35]. Those measures might shorten the effective infectious period of infectors. Therefore, human-to-human transmissions were only allowed to occur within a short period before the infectors’ symptom onset, and might underestimate the generation time and serial interval [36]. Fourth, the incubation period and generation time were assumed to be independent in the likelihood, which may not be realistic biologically as patients were likely most infectious around symptom onset [19, 37]. However, presymptomatic transmission is observed for COVID-19, and up to now the literature does not clearly indicate a strong correlation between infectiousness and incubation period for COVID-19 [38].

In conclusion, our analytical framework allows joint estimation of the incubation period and generation time distributions. Our framework adjusted for the sampling bias due to the data collected under the backward-looking approach during the exponential phase of epidemics, and provided improved estimates, which were robust to various uncertainties in the exposure windows. Using our approach, we estimated that an infected individual with COVID-19 would have symptom onset with a mean of 4.8 days after infection, and would transmit the virus to an infectee on average 5.7 days after infection. In practice, accounting for the timing and process of data collection is important to allow more accurate estimates of the generation time and incubation period distributions and to design public health and social measures more efficiently.

Supplementary Data

Supplementary materials are available at The Journal of Infectious Diseases online. Supplementary materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supplementary data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.

Notes

Financial support. This work was supported by the Health and Medical Research Fund, Food and Health Bureau, Government of the Hong Kong Special (SAR) Administrative Region (grant number COVID190118); and the Collaborative Research Fund, the Research Grants Council of the Hong Kong SAR Government (grant number C7123-20G). B. J. C. is supported by the AIR@innoHK program of the Innovation and Technology Commission of the Hong Kong SAR Government.

Potential conflicts of interests. B. J. C. reports honoraria from GSK, Sanofi Pasteur, AstraZeneca, Roche, and Moderna. All other authors report no other potential conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.