Unmasking the mask studies: why the effectiveness of surgical masks in preventing respiratory infections has been underestimated

Abstract

Background: Pre-pandemic empirical studies have produced mixed statistical results on the effectiveness of masks against respiratory viruses, leading to confusion that may have contributed to organizations such as the WHO and CDC initially not recommending that the general public wear masks during the coronavirus disease 2019 pandemic.

Methods: A threshold-based dose–response curve framework is used to analyse the effects of interventions on infection probabilities for both single and repeated exposure events. Empirical studies on mask effectiveness are evaluated with a statistical power analysis that includes the effect of adherence to mask usage protocols.

Results: When the adherence to mask usage guidelines is taken into account, the empirical evidence indicates that masks prevent disease transmission: all studies we analysed that did not find surgical masks to be effective were under-powered to such an extent that even if masks were 100% effective, the studies in question would still have been unlikely to find a statistically significant effect. We also provide a framework for understanding the effect of masks on the probability of infection for single and repeated exposures. The framework demonstrates that masks can have a disproportionately large protective effect and that more frequently wearing a mask provides super-linearly compounding protection.

Conclusions: This work shows (1) that both theoretical and empirical evidence is consistent with masks protecting against respiratory infections and (2) that non-linear effects and statistical considerations regarding the percentage of exposures for which masks are worn must be taken into account when designing empirical studies and interpreting their results.

Introduction

In 1910, one of the first western-trained Chinese physicians adapted surgical masks for use against a respiratory plague that killed >60 000 people in 4 months.¹ The logic behind their function is apparent: a mask can block some viral or bacterial particles from entering and/or dispersing from the wearer’s respiratory tract. Face masks, among other measures such as isolation, quarantine, lockdowns, social distancing and vaccination, have been used for prevention in a wide range of disease outbreaks and medical settings, and there is currently a general consensus that surgical and cloth masks help prevent infected individuals from spreading coronavirus disease 2019 (COVID-19).^2,3 Surprisingly, given the logic of their utility, there is less of a consensus that surgical/cloth masks also protect the wearer and many government health organizations did not initially recommend wearing them during the early months of the COVID-19 pandemic.^4,5

It is well established that face masks block some fraction of virus-containing particles of various sizes.^6–15 (The fraction blocked can depend on the size of the virus-carrying particles, with different types of masks providing differing levels of protection against droplets of various sizes. For instance, surgical masks have been shown to be less effective against aerosol transmission compared with respiratory droplets, whereas properly used N95 masks and powered air-purifying respirators are effective against both types of transmission.^8,9,12) The amount of virus transmitted between an infected and a susceptible individual is therefore expected to be reduced if either is wearing a mask, with both wearing masks giving the best protection. However, this straightforward inference has been difficult to establish in experimental studies.

Here we analyse why some experimental studies find masks to be effective, whereas others do not. Typically, studies have a control group in which participants do not wear masks, and an intervention group in which participants are asked to wear face masks. If the difference in the risk of infection between the two groups is statistically significant (usually P < 0.05), then the null hypothesis that masks are not effective is rejected. The statistical power—i.e. the probability of detecting a difference of risk when a difference of risk actually exists—depends on the sample size of the study, the risk of infection in the control group and the effect size (the difference in risk between the control and intervention groups). Although many studies conducted power analyses to determine the minimum sample size required for 80% power, they did so under the assumption that using face masks will lead to a 50% decrease in the risk of infection. However, even if masks were 100% effective, a 50% decrease in risk is unrealistic if masks are worn for a very small percentage of exposures. Given that a very commonly noted limitation of these studies was low compliance to mask usage, we calculate statistical power for studies taken from a recent meta-analysis by taking into account the relationship between the effect size and adherence (i.e. the fraction of exposure events for which masks are used).

We also provide a framework for understanding the non-linear effects of mask-wearing on the probability of infection. Experiments that do not take such factors into account provide misleading results, unless interpreted carefully. Although the precautionary principle^16,17 would recommend the use of masks during the COVID-19 pandemic in any case (due to the asymmetric risks of using vs not using masks), the analyses we provide gives consistency to theoretical analyses, experimental studies and epidemiological recommendations.

Methods

Statistical power

Here we calculate statistical power while taking into account the effect of adherence. In order to do so, we make two conservative assumptions that will result in our overestimating the studies’ statistical powers. First, we assume that the degree to which a mask reduces the probability of infection is proportional to the fraction of exposures for which it is worn (e.g. we assume wearing a mask half as often provides half as much protection); in fact, wearing a mask half as often will reduce the probability of infection by less than half as much (Figure 2), meaning that we overestimate the statistical power of these studies. Second, the numbers we calculate represent the power the studies would have had were masks 100% effective (i.e. were it impossible to become infected while wearing a mask). To the extent that masks are <100% effective, even larger sample sizes would be needed.

Figure 2.

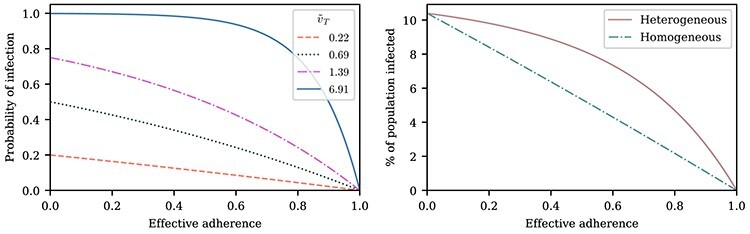
Mask usage frequency and its non-linear effects on infection probability. Left: A susceptible individual’s probability of infection as a function of effective adherence 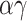(mask effectiveness 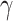multiplied by the fraction of exposures for which the mask is worn 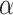) for various values of that individual’s total effective exposure 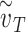(the total effective exposure is proportional to the number of exposure events). For high values of 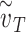, the infection probability is non-linear in the adherence, whereas for low values of 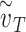, the infection probability decreases approximately linearly with adherence. Right: For a group of individuals (e.g. in an arm of a study), the total effective exposure will in general vary from individual to individual such that even if on average the total effective exposure is relatively low, it may be high for the individuals who make up the bulk of those being infected. The dashed curve depicts the expected percentage of infected individuals for the homogeneous case in which everyone experiences the same total effective exposure, whereas the solid curve depicts a case in which the exposure is heterogeneous; in both cases, the percentages of individuals that would be infected without masks (e.g. in a control group) are identical (~10%).

We consider a sample of studies taken from a recent systematic review¹⁸ (Supplementary Table S3 of Supplementary Data and Methods for a list of studies that were excluded and why) and conduct a statistical power analysis that takes into account the mask usage frequency of study participants. The systematic review searched the SCOPUS, EMBASE and Medline databases for original research that was published after January 1980, studied the effect of masks on prevention of disease and symptoms among non-clinically trained individuals and included a control or comparator group. These studies span a variety of settings and locations—university residence halls, Hajj pilgrimage, households and hospitals, and consequently have different risks of infection in their control groups. Most of the studies we examine measure whether surgical masks protect the wearer; the exceptions are studies nos. 8, 12 and 15, which measure whether masks prevent the wearer from infecting others, and studies nos. 1, 7, 13, and 18, in which both the susceptible and infected individuals sometimes wore masks (Supplementary Table S2). See Supplementary Data and Methods for the details of the statistical power analysis and how the mask usage frequency for each study was estimated.

Non-linear effects

In this section, we develop a framework with which to understand the effect of masks. Although there is insufficient data to precisely describe the probability of infection as a function of the viral dose inhaled in a single exposure event, we can nonetheless derive some constraints on its shape. For a susceptible individual, the probability of infection (or any other outcome such as hospitalization or death) 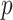is a function of the viral dose 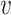, i.e. the quantity of virus to which the individual is exposed. (This function 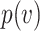will vary from individual to individual based on biological factors and vaccination status, but should retain the general properties described below.) The viral dose 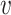can depend on multiple factors such as non-pharmaceutical interventions or the cultural and social setting of transmission events. For small 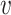, the probability of a susceptible individual becoming infected will approach zero, because there is a threshold for the viral dose (the amount of the virus inhaled) below which the probability of infection is very small due to the innate immune system.^19,20 For large 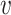, this probability will approach one, p(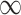) = 1. Thus, the probability of infection as a function of viral dose 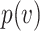is described by a sigmoid function or S-curve (Figure 3). Concave curves have also been used to model dose response curves, but such an approach ignores threshold effects.^21,22 Since receiving two viral doses at once should not result in a lower probability of infection than the hypothetical in which the exposure to each viral dose could be modelled as an independent event, we have that

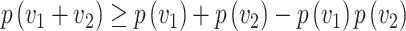(1)

Figure 3.

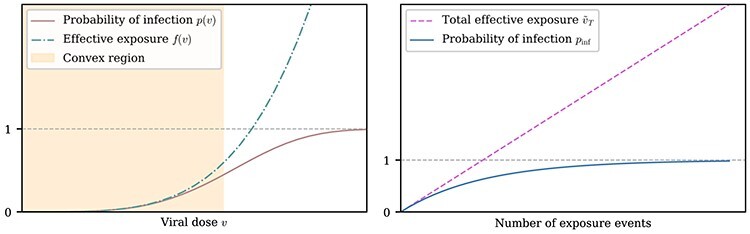
Non-linearities in the dose response curve and probability of infection. Left: A representative function for a susceptible individual’s probability of infection p as a function of viral dose v for a single exposure event, together with the effective exposure 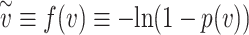, where f(v) is convex for all v, whereas p(v) is convex for sufficiently small v. The convexity of f(v) (which is demonstrated in Methods) yields an S-curve for p(v). Note that for any particular viral dose v, the effective exposure 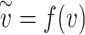can vary from individual to individual. Right: A depiction of how the total effective exposure 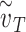and the probability of eventually becoming infected scale with the number of exposure events. The total effective exposure is the sum of the effective exposures from each exposure event; see Methods for details.

Equality will hold only in the absence of threshold effects; given that such effects are well established, we expect the inequality to be strict for small 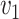and 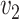. In order to characterize the set of functions satisfying Equation (1), we transform 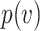using 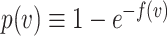, or equivalently, 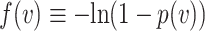. Equation (1) is then equivalent to

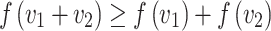Thus, Equation (1) is equivalent to 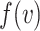being convex. Choosing a convex 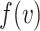and then transforming back to 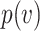yields an S-curve (Figure 3), also known as a sigmoid function or sigmoid curve.

When 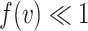, it can be shown by Taylor expansion that 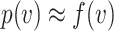. Thus, for small viral doses, 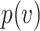will be convex as well. If a mask reduces the viral dose 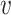by a factor 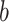,^6,7 then the mask will reduce the probability of infection (or of some other outcome denoted by 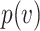such as the probability of severe infection or death) by a factor of 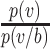, which depends on 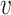. The parameter 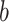depends on the filtration capacity of the mask material, the quality of fit of the mask and sizes of the virus-carrying particles. When 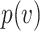is convex, the factor by which the mask reduces the probability of infection will be greater than 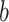(since convexity implies that 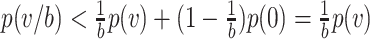). Thus, for small exposures, masks can result in a surprisingly large reduction in the probability of infection (see Supplementary Data and Methods for further details).

The S-curve describes the probability of infection for a single exposure event. For 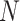independent exposure events, the probability of getting infected is 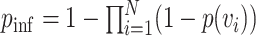. Using 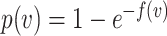as discussed above,

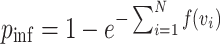Defining the ‘effective exposure’

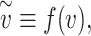and defining

 

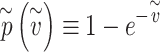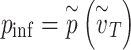where 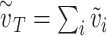is the total effective exposure. Considering the effective exposure 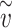rather than the actual dose 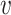is convenient since the effective exposure for repeated independent exposures is simply the sum of the individual effective exposures. Note that for small effective exposures, the probability of being infected is approximately equal to the effective exposure, i.e. 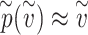for .

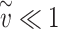The probability of infection as a function of effective adherence 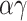(mask effectiveness 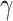multiplied by the fraction of exposures for which the mask is worn 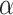) is then given by

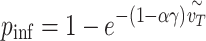(see Supplementary Data and Methods for further details).

Results

Statistical power

Some empirical studies find masks to be effective in preventing disease transmission, whereas others do not.^16,18–26 We determined that the studies that did not find masks to be effective were under-powered to such an extent that even if masks were 100% effective, they still would have been unlikely to find a statistically significant result. None of the studies we analyse that did not find masks to be effective had sufficient statistical power. Our results concerning the statistical power of mask studies are summarized in Figure 1, which shows that all studies that had a large enough sample size and/or adherence for 80% power (above and to the right of the grey lines) show a statistically significant reduction in infections among mask-wearers. As would be expected, most studies with less statistical power (towards the lower left) did not find a statistically significant effect.

Figure 1.

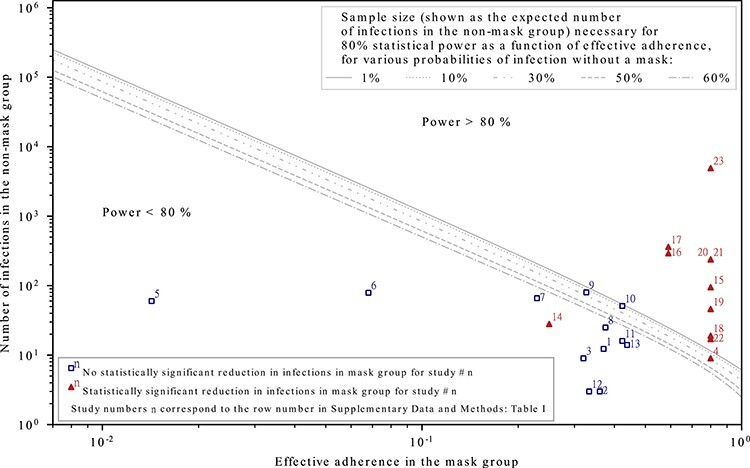
The effective adherence and sample sizes of studies that found masks to be effective (triangles) and those that did not (squares). Empirical studies with higher levels of statistical power consistently show that masks protect the wearer; studies with lower statistical power are mixed, as would be expected. The statistical power depends on the sample size, the effective adherence (i.e. mask effectiveness multiplied by the fraction of exposures for which masks are on average worn in the mask group) and probability of being infected without a mask in the setting of the study. Each curve depicts the required sample size (expressed as the expected number of infections in the non-mask group) as a function of effective adherence in order for the study to have a power of 80%. The scattered data points depict the size and effective adherence of studies taken from a recent systematic review¹⁸; the numbers on the data points correspond to row numbers of the studies in Supplementary Data and Methods: Supplementary Table S1. (Note that they do NOT correspond to the numbers in References.) The effective adherence for the studies are overestimated by assuming that masks are 100% effective; even with this assumption, the studies numbered 1 through 14 were found to have <80% statistical power. See Supplementary Data and Methods for data and mathematical details.

For example, a randomized control trial (RCT) at the Hajj pilgrimage²⁴ assumed a reduction in infection probability from 12 to 6% in order to determine the sample size necessary for a statistical power of 80%. After taking into account that the randomization was done by cluster (i.e. tent) rather than individual, the required sample size was ~6000. However, the study reports that individuals in the intervention group on average wore masks for far less than half the time. Under these conditions, even with perfectly effective masks, a 50% reduction in infection probability from 12 to 6% is impossible. The data reported in the study indicate an adherence in the mask group of 3.2%, which could cause at most a 3.2% reduction in the probability of infection. However, the adherence in the control group was 1.8%, meaning that the maximum possible expected reduction in infection between the two groups would be (0.032 – 0.018)/(1 – 0.018) = 0.014 [Supplementary Data and Methods: Equation (6)]. Thus, the effective adherence value used for this study is 0.014. In addition, the probability of infection without masks is reported to be quite low (2%). Under these conditions, the required sample size to achieve the desired statistical power of 80% would be about 7.8 million (with individual randomization; with cluster randomization an even larger number of participants is needed).

Non-linear effects

The framework developed in the Methods section shows that the probability of infection is a concave function of the total effective exposure (Figure 3). Thus, the protection afforded by a mask is super-linear in the percentage of exposures for which it is worn (e.g. wearing a mask twice as often is more than twice as effective; Figure 2). These non-linear effects can be substantial for high cumulative exposures. Under such conditions, a mask may need to be worn for most or nearly all of the exposure events in order to provide significant protection; otherwise, the individual is likely to be infected during the exposures for which the mask is not worn. In the limit of an extremely high total exposure, a mask will of course not have an effect on the probability of infection since a susceptible individual will be infected with nearly 100% probability, regardless of whether or not the mask is worn.

On the other hand, for low total exposures, the protection masks provide will be approximately proportional to the fraction of exposures for which they are worn. It should be noted that the total exposure of individuals can vary within any given study, such that even if the overall probability of infection is low, most of those who were infected may have been subjected to high cumulative exposures. Studies with low overall probabilities of infection also have an additional difficulty, which is that large sample sizes will be necessary in order that there may be enough infections in the non-mask group to produce a statistically meaningful comparison. In other words, for sufficiently low total exposure, the probability of infection will be quite low even without a mask, and so further reductions to this probability, even if proportionally large, will be small in absolute terms.

We also use this framework to analyse certain compound effects that are not considered in most empirical studies. For instance, masks worn on both the infected and susceptible individuals may prevent a transmission event even if neither mask individually would have. Furthermore, this compound effect may be super-linear: if the effect of only an infected individual wearing a mask is to reduce the infection probability by a factor of p₁ and the effect of only a susceptible individual wearing a mask is to reduce the infection probability by a factor of p₂, both individuals wearing a mask could reduce the infection probability by far greater than a factor of p₁p₂, especially for large total effective exposures. In the example shown in Figure 4, the probability of transmission is reduced by only a factor of 1.08 (a 7% reduction) due to one or the other individuals wearing a mask, whereas if both wear a mask, the probability of transmission will be reduced by a factor of 2.17 (a 54% reduction).

Figure 4.

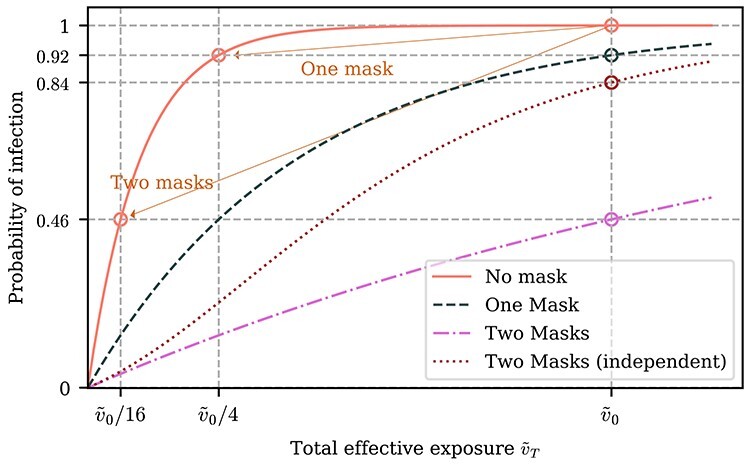
Effect of one vs both individuals wearing a mask. The effect of both the susceptible and infected individual wearing a mask can be much larger than the effect of only one of them wearing a mask. In the depicted example, the total effective exposure 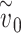if neither the infected nor susceptible individual are wearing masks is such that the probability of infection 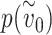is very close to one. If each mask reduces the effective exposure by a factor of four, then the probability of infection if only one of the two individuals is wearing a mask is 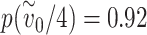, i.e. a reduction in risk by a factor of 1.08. If both individuals are wearing a mask, however, the probability of infection is 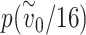= 0.46, corresponding to a reduction in risk by a factor of 2.17, which is greater than the product of the effects of each mask individually (shown by the red dotted curve). For illustrative purposes, we have assumed that the infectious individual wearing a mask has the same effect as the susceptible individual wearing a mask, but relaxing this assumption will not qualitatively change the results; see Supplementary Data and Methods for details.

We also find that the proportional risk reduction from masks is expected to be large because—due to the convexity of the S-curve (Figure 3) when exposure is low (as is likely for many exposure events)—the probability of the mask-wearer being infected is decreased by a greater factor than the decrease in the viral dose. For these low exposure events, although the probability of infection may be small for any given potential transmission event, given multiple events, the large factors by which the probabilities of infection decrease due to this convexity can significantly reduce both the spread of the virus and the probability that the wearer eventually is infected. In other words, wearing a mask may not only prevent the wearer from spreading viruses to others but may also have a surprisingly large protective effect for the mask-wearer. Indeed, studies that analyse population-level data show that masks significantly reduce transmission.^17,27–30

In addition to the probability of infection, the implications of a non-linear dose–response curve apply to several other outcomes as well. In all of the above analyses, the probability of infection can be replaced with the probability of death or the probability of a particular degree of severity of symptoms, each of which can have a unique S-curve (that can also vary from individual to individual). Thus, even when a mask does not prevent infection, it may reduce the severity of symptoms and the chance of long-term health damage or death. It has been observed for the influenza virus that increasing the viral dose may lead to more adverse symptoms,^31–33 an effect that may also apply to SARS-CoV-2.^33–37

Discussion

Original research and reviews have commonly acknowledged that RCTs and surveys of mask effectiveness suffer from poor adherence, thus reducing the quality of empirical evidence.^18,20,21,26 A recent COCHRANE review³⁸ found that surgical mask usage had very little or no effect on the risk of infection, with low (for respiratory illness) or moderate certainty (for laboratory confirmed infection). It noted that low compliance with guidelines prevented drawing a robust conclusion from the empirical evidence. The review also noted that no study had investigated the relationship between adherence to protocols and effect size. Our work investigates this relationship by using dose–response curves, providing an explanation to the puzzle as to why many studies did not find masks to be effective.

Although we focus on face masks, the non-linear dose response framework developed in this study can be applied to any kind intervention that reduces the exposure to viral dose. For instance, just as there can be a super-linear compound effect from both individuals wearing masks, there can also be super-linear compound effects when mask-wearing is combined with other behaviours that reduce exposure, such as social distancing. Non-linear effects continue to accumulate when multiple individuals perform multiple behavioural changes that reduce exposure. Recognizing these non-linear effects is a key to appreciating the effectiveness of transmission prevention policies. The potential for non-linear effects such as those described above should be considered when interpreting evidence on both pharmaceutical and non-pharmaceutical impacts (e.g. vaccines and non-pharmaceutical interventions could non-linearly compound, a possibility that does not seem to have been considered by many studies or discussions).

Any interpretation of empirical data requires a model for inferring generalizations, which will necessarily have assumptions and limitations.³⁹ In this case, the conventional statistical analysis adopted by meta-analyses assumed that aggregated data from studies with various levels of adherence would give a meaningful assessment of overall mask effectiveness. Our results demonstrate the importance of clearly recognizing the implicit assumptions in analyses of empirical data and of addressing their limitations using models that have explicit and clear assumptions.

A significant limitation of our analysis is the difficulty in estimating adherence, since many studies report adherence in either qualitative or a mixture of qualitative and quantitative manner. To overcome this limitation, we have consistently overestimated the statistical power by overestimating the adherence. In addition, we checked the robustness of our results to changes in the estimation of the probability of infection in the control group. Further detail can be found in Supplementary Data and Methods.

Other factors such as false positives may also limit statistical power. For instance, a recent study⁴⁰ conducted in Denmark reported that a mask recommendation did not have a statistically significant effect: in the study’s primary composite outcome, 42 vs. 53 people tested positive in the intervention and control groups, respectively. However, the vast majority of these positive results were from antibody tests, and given the antibody tests’ comparable incidence and false positive rates (~2 and 0.8%, respectively), a substantial fraction of the positive antibody tests in both the control and intervention groups are likely to be false positives, which would affect both the study’s power and its statistical analyses.⁴¹ Further false positives could arise from individuals who were infected before the study, but for whom seroconversion did not occur until partway through the study. These effects were not accounted for in the study’s statistical analysis, undermining the validity of the study’s conclusions. If only the more reliable polymerase chain reaction tests from this study are considered, then the reduction in infection due to masks (zero vs five infections) is statistically significant (P < 0.05).

In summary, masks block some fraction of viral particles from dispersing from those who are infected and from infecting those who are susceptible and are understood to prevent disease transmission through this mechanism. However, this simple understanding has been questioned based upon what has appeared to be mixed empirical evidence. However, studies that did not find masks to be effective had limited statistical power and therefore do not imply that masks are ineffective. Furthermore, for many exposure events, masks will reduce the probability of infection by a greater factor than the factor by which they filter viral particles, an effect that can non-linearly compound when both infected and susceptible individuals wear masks. When interpreted in light of these considerations, the evidence indicates that, in addition to preventing the wearer from spreading respiratory infections, masks also protect the wearer from contracting them. The studies that did not find statistically significant effects prove only that masks cannot offer protection if they are not worn.

Authors’ Contribution

All authors contributed to the conceptual framework. A.F.S. developed the mathematical formalisms. P.K.K. conducted the literature review. P.K.K., A.F.S. and N.N.T. performed the statistical analyses. All authors contributed to writing the manuscript.

Funding

This work was supported by the National Science Foundation Graduate Research Fellowship Program (Grant No. 1122374) and by the Hertz Foundation.

Conflict of Interest

None declared.