Towards scaling elementary flux mode computation

Abstract

While elementary flux mode (EFM) analysis is now recognized as a cornerstone computational technique for cellular pathway analysis and engineering, EFM application to genome-scale models remains computationally prohibitive. This article provides a review of aspects of EFM computation that elucidates bottlenecks in scaling EFM computation. First, algorithms for computing EFMs are reviewed. Next, the impact of redundant constraints, sensitivity to constraint ordering and network compression are evaluated. Then, the advantages and limitations of recent parallelization and GPU-based efforts are highlighted. The article then reviews alternative pathway analysis approaches that aim to reduce the EFM solution space. Despite advances in EFM computation, our review concludes that continued scaling of EFM computation is necessary to apply EFM to genome-scale models. Further, our review concludes that pathway analysis methods that target specific pathway properties can provide powerful alternatives to EFM analysis.

Introduction

Advances in understanding and engineering of living cells have shown promise in the production of commercially useful biomolecules, including polyesters [1], building blocks for industrial polymers [2], biofuels [3] and therapeutic natural products derived from isoprenoids [4–7], polyketides [8, 9] and non-ribosomal peptides [7]. Advancing the design and engineering of biological systems will lead to reduced development cost, time and effort, which in turn will enable new discoveries that have a positive impact on human health and the environment. Computational tools can play a critical role in expediting the design process by exploring design options and validating design choices before performing lab experiments [3, 4, 10].

One powerful and important computational approach is elementary flux mode (EFM) analysis. EFM analysis decomposes a metabolic network into pathways that have three properties: thermodynamic feasibility, quasi steady-state operation and independence of other pathways [11]. Thermodynamic feasibility imposes that each irreversible reaction proceeds to have a non-negative flux rate. Quasi steady-state operation ensures that metabolites internal to the network are neither accumulated nor depleted. Mutual independence of other pathways, together with the other two properties, guarantees that the EFM decomposition is unique. Several applications have benefitted from EFM analysis. Example applications include validation of metabolic model construction [12], analyzing and understanding metabolic network including robustness and cellular regulation [13–17], analyzing competitive microbial strategies [18], increasing product yield [19, 20] and assessing plant fitness and agricultural productivity [21].

The biggest challenge in EFM analysis is its scalability to allow for the analysis of genome-scale models. From a computational complexity perspective, the lack of scaling is understandable. A problem is considered scalable if it has a runtime that scales linearly (or sublinearly), or even polynomially, with the size of the input problem (e.g. number of reactions or number of metabolites when analyzing metabolic networks) in the worst case scenario. The problem of computing EFMs does not exhibit such behavior. Enumerating EFMs is equivalent to edge or vertex enumeration for a pointed-bounded-polytope. The complexity of enumerating vertices of polytopes is a famous and long-standing open question [22]. Acuna et al. showed that vertex enumeration of any (possibly unbounded) polyhedron cannot be achieved in polynomial total time unless P = NP [23]. This article provides a detailed review on computing and scaling EFM computation.

EFMs and pointed polyhedra

A flux mode is a steady-state flux pattern in which flux proportions are fixed while their absolute magnitudes are indeterminate [24]. Given an 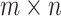stoichiometric matrix, 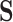, representing 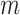metabolites and 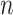reactions, and an 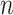-vector 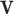of reaction fluxes, three conditions must be met to label 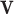as an ‘elementary flux mode’ or ‘elementary pathway’:

EFM Condition 1: The network reactions proceed in a direction dictated by thermodynamic feasibility. The flux in a reaction is greater than or equal to zero if the reaction is irreversible. This condition can be expressed as 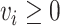for all irreversible reactions.

EFM Condition 2: The network is in quasi steady-state condition with no accumulation or depletion of internal metabolites in the network. Mathematically, this condition can be expressed as 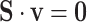, where the rows of 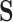include only metabolites internal to the network.

EFM Condition 3: Each elementary mode 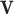must be independent from other elementary modes in the network. In other words, there is no other vector y ( 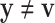and 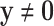and y fulfills C1 and C2) such that the set of reactions participating in is strictly a proper subset of the reactions in y.

Each EFM is minimal. That is, the removal of any reaction from any of the EFMs will cause it to violate one of the conditions above. Extreme pathways (EPs) are a subset of the EFMS, but are more restrictive [25–27]. An EP cannot be expressed as a convex combination of any other pathway fulfilling the above conditions [26]. Importantly, every steady-state flux distribution in the network can be represented as a linear (convex) combination of EFMs or EPs.

Gagneur and Klamt [28] suggested that by splitting the reversible reactions into irreversible reaction pairs, the feasible steady-state flux space is defined by a pointed convex cone (Figure 1) that has extreme rays passing through origin and the cone lies in the positive quadrants. The feasible steady-state flux space is bounded by hyper-planes defined by steady-state constraints. The irreversibility of reactions enforces the flux cone to be in the positive quadrant. Further, genetic independence condition makes extreme rays of the cone equivalent to EFMs. Therefore, algorithms from computational geometry (based on double-description method) have been used to compute EFMs. Additionally, pivotal algorithms such as reverse search algorithm can be used to enumerate extreme rays of the convex polyhedral. Without loss of generality, we assume in the rest of this review that reversible reactions are split into irreversible reaction pairs, and that the updated networks have only irreversible reactions.

Figure 1 .

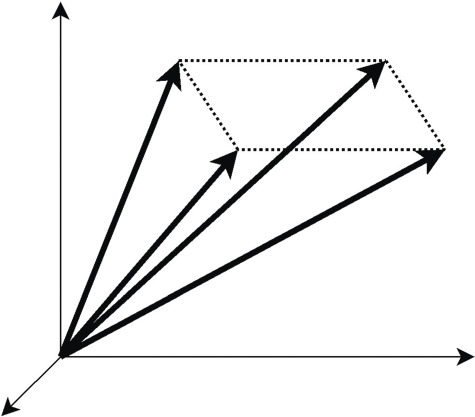
A graphical representation of pathways in 3-dimensional ux space. Each axis corresponds to a reaction ux. A pathway is geometrically represented as a ray. The dark lines are the extreme rays (correspond to EFMs) of a convex cone.

Algorithms for computing EFMs

The double-description method

The double-description method has been rediscovered under different names such as Motzkin elimination [29], Chernokova’s algorithm [30] and beneath-and-beyond methods [31]. Mathematically, the feasible steady-state flux space of a network with 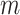internal metabolites and 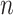reactions can be represented as

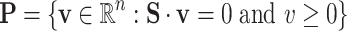where 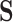is the stoichiometric matrix of the network and 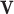represents a steady-state flux. The double-description method provides an alternative representation of the flux space by transforming the representative matrix of the network A to an equivalent representative matrix 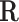. Given a representative matrix 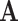of the network, the steady-state flux space can be described as

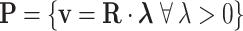where 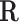represents set of EFMs. Based on the choice of the initial representative matrix 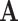, there are two approaches used for computing EFMs, the canonical basis approach and the null-space approach.

The two approaches are summarized in Table 1. The first step of both approaches is network reconfiguration, in which reversible reactions are split into irreversible reaction pairs. The second step is the initialization of the A and R matrices. The next step consists of iterative constraint processing. For the double-description method, each row of matrix A represents a constraint. In each iteration, rays (intermediate EFMs, each vector representing a ray of the convex cone) are divided into three groups J⁺, J^- and J⁰, based on the current constraint. The constraint is satisfied by combining rays from J⁺ and J^-. Only extreme rays (independent vectors) are generated by performing adjacency test on the rays to be combined. Two adjacency tests (algebraic and combinatorial) are well-known tests [32]. If the rays are adjacent, a new ray is generated using Gaussian Combination by satisfying the current constraint. After processing the current constraint, matrix R is updated. After all constraints are processed, a post-processing step removes futile two-cycles that result from reconfiguration of the network. A two-cycle is a cycle consisting of a reversible reaction broken into forward and reverse irreversible reaction pair. In the last step, the network configuration is restored resulting in EFMs in R.

Table 1.

Comparison of the canonical basis and the null-space approaches (adapted from [26])

The canonical basis approach

In the canonical basis approach, the stoichiometric matrix is used as the network representative matrix 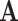. Each row in 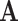corresponds to an internal metabolite and the corresponding constraint needed to balance the metabolite. The equivalent representation matrix 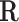is initialized with the identity matrix of size equal to the number of reactions, where each flux vector r in 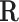corresponds to a reaction in the network. The net production or consumption of the 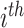metabolite in 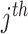flux vector 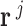is represented by 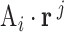. A positive value indicates net production. A negative value represents a net consumption. A zero value represents a balance in production, with no net consumption or production of the metabolite. A metabolite with balanced production is referred to as a balanced metabolite. In each iteration of the algorithm, flux vectors are grouped into three groups: J⁺ (flux vectors producing the metabolite), J^- (flux vectors consuming the metabolite) and J⁰ (flux vectors for which the metabolite is balanced). The internal metabolite is balanced by combining flux vectors 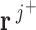and 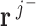(Gaussian combination) to generate flux vectors containing the balanced metabolite. The Gaussian combination ensures that no reaction operates in the reverse direction thus resulting in thermodynamically feasible flux vectors except futile two-cycles (eliminated in a post processing step). Only adjacent flux vectors are combined to generate independent flux vectors.

Schuster and Hilgetag [11] introduced the double-description method to compute EFMs. The algorithm, originally referred to as Schuster’s Algorithm, was adapted from the Mavrovouniotis’ approach for synthesis of balanced pathways in biochemical networks [33]. Later, Schuster’s algorithm was called the Canonical basis approach [26]. Schuster’s algorithm was a matrix-based implementation. Schuster et al. claimed that graph based approaches are not viable for computation of EFMs. However, Ullah et al. [34, 35] recently showed that graph based approach can be a viable alternative for computing EFMs. A distinct and important advantage of graph-based approaches is using knowledge about the network topology to minimize the intermediate number of flux vector combinations generated in each step of the iterative algorithm. As discussed later, constraint ordering directly impacts algorithm performance.

The null-space approach

The null-space approach was proposed by Wagner [36] as an alternative to the Canonical basis approach. In this approach, the double-description method uses the null space of 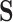as the initial representative matrix 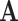, and also as the initial value for 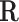. The null space is defined as

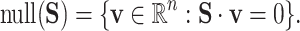Each row in null(S) corresponds to a reaction and each column represents a balanced flux vector. Each row entry specifies how the corresponding reaction should proceed within each flux vector under steady-state constraints. The relative activity of 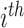reaction in 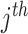flux vector is represented by 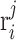. A positive value indicates the reaction operating in the forward direction, a negative value indicates the reaction operating in the reverse direction and zero value represents the reaction is not active, indicating that the reaction is not present in the pathway represented by the flux vector. In each iteration of the algorithm, the flux vectors are grouped into three groups: J⁺ (flux vectors with the thermodynamic feasible reaction), J^- (flux vectors with the thermodynamic infeasible reaction) and J⁰ (flux vectors for which the reaction is not active). The thermodynamic feasibility of the reaction is satisfied by combining flux vectors 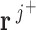and 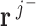(Gaussian combination). The Gaussian combination step combines two balanced flux vectors resulting in balanced flux vectors. Only adjacent flux vectors are combined to generate independent flux vectors.

Comparison of the canonical basis and the null-space approach

There are several differences between the canonical basis approach and the null-space approach.

1. The canonical basis approach uses the 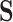matrix for constraint processing and the null-space uses null space of the 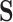matrix.

2. The equivalent representative matrix 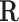is initialized with identity matrix in the canonical basis approach and to the null space of 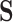in the null-space approach.

3. Each constraint in the canonical basis approach corresponds to a mass balance constraint for an internal metabolite whereas each constraint in the null-space approach corresponds to the thermodynamic feasibility constraint of reactions.

4. The number of constraints in the canonical basis approach is equal to the number of internal metabolites whereas it is equal to the number of reactions in the null-space approach. If 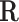is represented in reduced row echelon form, the first 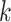constraints are automatically satisfied where 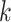is the rank of .

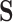5. In the canonical basis approach, flux vectors J⁰ are passed to the next iteration without processing. In the null-space approach, flux vectors J⁰ and J⁺ are passed to the next iteration without processing.

Klamt and Stelling [26] suggested that runtime of the Null-Space approach is less than that of the canonical basis approach due to lesser number of constraints processed in the null-space approach. In both approaches, the runtime is dependent on the number of combinations generated, which is highly dependent on network topology and the order in which constraints are processed. We explore the runtimes further when comparing various implementations in the Performance Evaluation section.

Pivotal methods

Another class of algorithms used for the enumeration of extreme rays or vertices is based on pivotal methods, similar to the simplex algorithm [37]. The simplex algorithm finds the optimal solution in a convex polyhedral by traversing through vertices of the convex polyhedral defined by the constraints. For a bounded convex polyhedral, the optimum solution is always guaranteed to lie on one of the vertices. The simplex algorithm starts with an initial solution (a vertex of the convex polyhedral) and traverses through vertices that have lower value of a cost function defining the objective of optimization. All the possible paths taken by the simplex algorithm can be represented by a directed graph that leads to the vertex corresponding to the optimal solution. Avis and Fukuda [38] proposed a reverse search algorithm for vertex enumeration. The reverse search algorithm is pivotal, running the simplex algorithm in the opposite direction. The reverse search algorithm starts with the optimal solution vertex and explores the whole graph enumerating all the vertices visited.

Reverse search algorithms pose two problems: the non-uniqueness of the starting optimal solution vertex, and degeneracy. The degeneracy problem occurs if same vertex is visited through different traversal paths, as the same vertex may be defined by different sets of constraints. These problems are addressed by lexicographic reverse search algorithm (lrs) proposed by Avis [39], where the cost function is defined such that the optimal solution is unique; therefore, the reverse search graph can be represented by a tree with a single starting point for the search. Degeneracy is addressed by using a lexicographic pivot selection rule.

Pivotal methods such as lrs are known to have slower performance when compared to other methods for the enumeration of extreme rays. However, pivotal methods are parallelizable and claimed to be useful when solving extremely large problems [40].

Computational complexity

Identifying EFMs is a computationally challenging problem. Computing EFMs is equivalent to vertex/ray enumeration of convex polyhedral. The complexity of vertex/ray enumeration is a long-standing open problem [22, 41]. Runtime complexity of vertex/ray enumeration problem cannot be expressed in terms of the problem size such as number of constraints (metabolites in metabolic network) and dimensionality of space (number of reactions in the network) due to the combinatorial nature of the problem. No algorithm is shown to have a scaling in proportion to the number of rays or vertices [42, 43]. All algorithms exhibit in the worst-case super-linear behavior in the size of the rays/vertices [41]. For the lrs algorithm, the runtime for computing a single vertex/ray is O(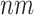); therefore, the runtime for enumeration is dependent on the total number of vertices/rays. Avis et al. showed that the runtime and space requirements to solve the non-homogeneous version of the ray enumeration problem are proportional to the number of extreme rays [44]. The complexity of EFM computation is dependent on the number of EFMs in the network. Acuna et al. proved that computation of EFMs is not possible in polynomial runtime unless P = NP [23]. From these complexity results, it should be clear that any implementation has limited scalability when running on a single, unthreaded compute node, and will run indefinitely with suitably large test cases. However, improving the runtime of the various algorithms through innovative techniques such as constraint reordering, compression and redundancy removal may lead to substantial speedups.

Performance evaluation and enhancement

In this section, we focus on several practical issues for speeding EFM compuation. We review how the number of generated candidate EFMs differs between the null-space and the canonical approaches, and how constraint-ordering heuristics can play a critical role in performance improvement for the canonical basis approach. Further, we evaluate the use of redundancy removal and network compression to expedite computing EFMs.

We compare four state-of-the-art tools: MetaTool [45], a MATLAB implementation of the matrix-based canonical basis approach; gEFM, which implements in C++ the canonical basis approach using a graph based approach [35]; EFMTool, implemented in Java for the null-space approach [46]; a C++ implementation of lrs algorithm [47].

We use three different variations of the Escherichia coli model derived from the central carbon metabolism [20]. The first test case, E. coli is the original central carbon metabolism model. The second test case, E. coli (irrev), restricts the directionality of all reactions to the directionality specified by the default reaction listing, thus allowing us to assess the impact of reaction reversibility. The third test case, E. coli (gluc), is restricted to only use glucose as the carbon source. The statistics of the test cases are listed in Table 2.

Table 2.

Model statistics, without and with compression

	Uncompressed		Compressed
Model	Reactions	Metabolites	Reactions	Metabolites	EFMs
	(Reversible)	(Internal)	(Reversible)	(Internal)
E. coli	70 (19)	68 (52)	44 (12)	26 (26)	429,276
E. coli (irrev)	70 (0)	68 (52)	26 (0)	12 (12)	840
E. coli (gluc)	60 (19)	63 (47)	39 (12)	26 (26)	33,220

Compression techniques are common for reducing the size of biochemical networks [28, 45, 48]. We use compression methods provided by EFMTool [46]. The dead-end metabolite removal method eliminates internal metabolites that are either only produced or only consumed. Reactions associated with such metabolites are also eliminated. The coupled-zero compression method removes all reactions that always carry zero flux at steady state. The coupled-contradicting compression method removes negatively coupled reactions. The unique-flows compression method removes metabolites that are produced by only one reaction and consumed by only one other reaction by combining the producing and consuming reactions. The coupled-combine compression method removes all flux-coupled reactions, ones for which their relative flux is always constant, except one representative reaction. The flux values for the removed reactions can be computed based on the retained reaction for all the compression techniques. Table 2 lists all the statistics for the compressed models obtained by applying all the techniques in the order described above.

While these examples do not capture the complexity of a genome-scale model, they provide a comparative point for evaluating the issues discussed in this section. We have benchmarked the tools disabling multi-threading. All experiments were performed on a 2.83 GHz Intel Xeon E5440 CPU with 6 MB cache running Red Hat Linux.

Cumulative and total number of candidate rays

In the null-space approach, the number of iterations corresponds to the number of constraints on the steady-state operation derived after computing the null-space kernel, and is equal to [48], where 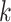is the size of the null-space kernel matrix and is bounded by 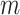. For the canonical basis approach, the number of iterations corresponds to the number of mass balance constraints, or the number of internal metabolites 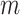. The difference in the number of processed constraints and the ordering of constraint processing affects the cumulative number of candidates generated and the cumulative number of comparisons.

We illustrate this issue for compressed E. coli (gluc) model in Figure 2. The x-axis corresponds to the iteration number. We show the cumulative number of combinations generated and cumulative number of comparisons performed in each iteration. Combinations correspond to rays generated by combining existing rays (positive J⁺ and negative J^- rays) after satisfying a constraint. The number of combinations 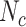is equal to .

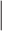Figure 2 .

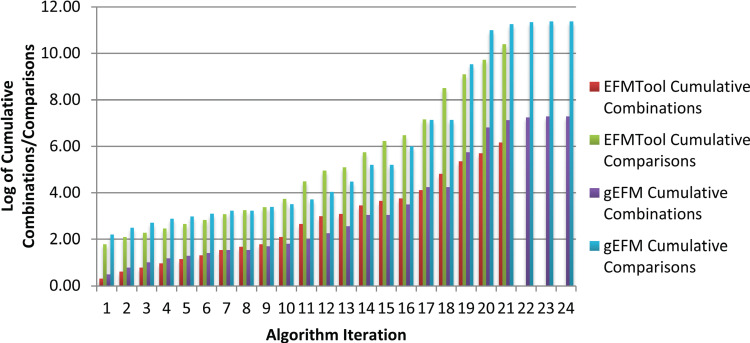
Cumulative combinations and comparisons performed in different algorithmic iterations of EFM-Tool and gEFM. Each iteration corresponds to a constraint. Cumulative combinations and comparisons for EFMTool are less than that of gEFM.

In each iteration of the EFMTool, combinations are generated by satisfying thermodynamic constraints and combinations are compared to the existing rays (positive J⁺, negative J^- and zero rays J⁰). The number of comparisons performed 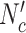is equal to N_c × (|J⁺| + |J^-| + |J⁰|).

Similarly, in each iteration of gEFM, combinations are generated by satisfying mass balance constraint and combinations are compared to the existing rays resulting in the number of comparisons equal to .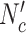

The results indicate that for a model with 26 metabolites and 39 reactions the total number of combinations generated is of the order of millions and the number of comparisons performed is of the order of billions. For the given test case, the number of iterations for the null-space approach is less than that of the canonical basis approach. Moreover, the total number of combinations generated and the total number of comparisons performed is greater for the canonical basis approach when compared to the null-space approach. These results confirm the efficiency of the null-space approach over the canonical basis approach [48].

Sensitivity to constraint ordering

A challenging issue when implementing the double-description method is its sensitivity to constraint ordering. Several researchers who utilized the null-space approach noted this limitation, and the issue was addressed by sorting the constraints using different heuristics [28, 46, 49]. To illustrate the severity of this issue, we ran MetaTool [28, 50] using 10 random orderings of constraints, and recorded the cumulative number of candidate EFMs. The minimum number of cumulative number of elementary modes provides 24,083,196 fewer (20%) candidates over the current implementation with a total of 120,242,940 candidates. We performed the same experiment for gEFM. None of the 10 runs that randomly processed metabolites finished within a 15-min period, while the original ordering finished in 2.57 s. This observation is critical, indicating that exploiting knowledge about network topology is central to addressing the development of EFM computing techniques.

Impact of removing redundant constraints

We evaluate the impact of removing redundant constraints on the performance of all tools. Constraints covered by other constraints are redundant. Redundant constraints can be removed by solving a linear program, as recommended for lrs [47]. The results are reported in Table 3. Constraint redundancy removal consistently benefits lrs because it removes degeneracy. Overwhelmingly, the other three tools suffer. In methods other than lrs, redundant constraints play a significant role in eliminating candidate solutions and therefore these methods underperform after redundancy removal. This type of redundancy removal has not been evaluated in the context of EFM computation before, and settles in the negative the unanswered question posed by Gagneur and Klamt of whether using linear algebraic redundancy will benefit current implementations [28].

Table 3.

Runtime (in seconds) for tools on the uncompressed models, with and without redundancy removal

		Original			Redundancy removed
Model		Meta Tool	EFMTool	gEFM	lrs		Meta Tool	EFMTool	gEFM	lrs
E. coli		<0.01	13,129.94	1464.60	26,400.50		<0.01	20,149.87	10,315.00	87,906.96
E. coli (irrev)		0.84	0.57	<0.01	177.22		1.80	1.16	<0.01	4.95
E. coli (gluc)		976.03	38.74	2.52	14,364.22		<0.01	122.64	14.75	5230.30

Impact of compression

We apply the four algorithms to the models compressed using all established compression techniques, and the models compressed using each compression technique independently. In dead-end compression, all dead-end metabolites are removed along with reactions connected to the dead-end metabolites. In coupled-zero compression, all the reaction carrying zero flux are removed. The reactions are identified by computing the null space of the network and reactions corresponding to the rows containing all zeros are coupled zero reactions. In coupled contradicting compression, reverse coupled reactions (reaction group that always operate in the opposite direction with respect to a reference reaction with a fixed flux ratio) are identified and only the reference reactions are kept in the network. Fluxes of the removed reactions are computed by scaling the flux of reference reactions. In coupled combine compression, forward coupled reactions (reaction group that always operate in the same direction with respect to a reference reaction with a fixed flux ratio) are identified and only reference reactions are kept in the network. Fluxes of the removed reactions are computed by scaling the flux of reference reactions. In unique flows compression, reactions carrying a unique flow are collapsed to a single reaction. Unique flows compression reduces the number of reactions and metabolites the most. A speedup is expected by each compression technique (if it reduces the network size) but in some cases the compression may increase the runtime. A possible cause can be the change in ordering of reactions and metabolites that can lead to a different order of constraint processing if the tool does not order the constraints as a preprocessing step such as lrs.

The results are shown in Table 4. The first column lists the model name. The second column lists the tool used. The third column reports the runtime in seconds for each model using each tool. The fourth column, labeled ‘all’, reports the speed up of the tool on the model compressed using all possible techniques in reference to the runtime of the uncompressed model. The rest of the columns report the speedups relative to the uncompressed model for each of compression techniques. An entry with a value less than one indicates a slowdown whereas an entry greater than one indicates a speed up. Using all compression techniques together consistently speeds all cases. lrs is greatly improved using all network compression, an approach that has not been previously evaluated as a pre-processing step to lrs. The three other tools also benefit from all compression; however, EFMTool benefits more so than MetaTool and gEFM.

Table 4.

Speedup for different compression techniques. Only the runtime (seconds) for no compression is reported

Model	Tools	No compression	All	Dead-end	Coupled	Coupled	Coupled	Unique
					zero	contradicting	combine	flows
	MetaTool	<0.01	-	-	-	-	-	-
E. coli	EFMTool	13,129.94	249.88	1.51	1.52	1.57	116.36	313.79
	gEFM	1464.60	1.27	1.32	1.33	1.33	1.62	1.62
	lrs	26,400.50	23.62	0.83	0.83	0.82	8.92	13.63
	MetaTool	0.84	0.99	0.06	0.15	0.07	0.18	1.12
E. coli	EFMTool	0.57	3.45	1.80	1.23	1.22	2.89	3.47
(irrev)	gEFM	-	-	-	-	-	-	-
	lrs	177.22	904.17	7.60	5.27	7.60	2.15	496.41
	MetaTool	976.03	1.52	0.51	0.53	0.53	3.80	1.26
E. coli	EFMTool	38.74	21.32	1.94	1.91	1.97	12.56	21.05
(gluc)	gEFM	2.52	1.16	0.94	0.94	0.94	1.14	1.16
	lrs	14,364.22	19.14	1.22	1.20	1.22	15.34	19.08

Overcoming scalability challenges using more powerful computation

Since 1965, integrated circuit complexity has doubled approximately every 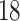months in accordance to Moore’s law [51], allowing for faster computers with more memory. In particular, the availability of specialized hardware enabling multi-threading, parallel computing and graphics-processing units (GPUs) has enabled the scalability of many algorithms. As described earlier, generating candidate rays and testing them for dependency is the major bottleneck in the double-description method. We explore in this section how these hardware advances have improved the computation FEMs using double-description algorithms.

Earlier parallelization efforts for EFM computation are based on the canonical approach [52, 53]. Samatova et al. claimed to be the first out-of-core implementation of the algorithm for computation of EPs. The authors divided the generation of new candidate rays and dependency testing into small jobs that can be distributed to different processors or different computers. The algorithm was implemented on 20 SUN SPARC workstations. Lee et al. implemented the same algorithm using message passing interface. The algorithm was implemented on a Linux cluster of 2.4 GHz Intel Pentium-4 CPUs using Myrinet interconnection among the dual-CPU nodes. The two approaches showed for a metabolic subsystem of E. coli (66 metabolites and 118 reactions) super-linear speedups with the number of processors used.

Klamt et al. [54] proposed a divide-and-conquer approach for splitting EFMs into disjoint subsets across a subset of reactions. Conceptually, the computation can be divided by selecting a particular reaction, and allowing two computations to proceed based on presence or absence of the reaction. Each computation is further divided based on assuming that another reaction is present or absent. Load balancing is required to ensure similar runtimes across the compute-nodes as there is no a priori way of guaranteeing equal division of labor. Communication among the nodes was necessary to merge the EFMs and eliminate duplicated elementary modes computed locally on each compute node. The authors computed the sub-tasks on a 2.4 GHz Pentium 4 processor for E. coli central metabolism and the results indicated that the runtime did not scale well with the number of processors. It was observed that there was an optimal number of processors for the two test cases used to evaluate the performance.

Terzer [50] presented a multithreaded implementation of the null-space approach (EFMTool) using bit pattern trees for dependency testing. A bit pattern tree is created for the set of positive, negative and non-participating sets rays. For creation of new candidate rays, the positive and negative bit pattern trees are recursively combined. For the parallel implementation, the trees are traversed up to a certain level (level 6 is used in their implementation) and a job is created to traverse the rest of the levels in the trees. Threads equal to the number of cores/processors are used for the parallel computation. Each thread removes a job from the job queue and creates new rays and checks the dependency. After completing a job, threads keep on dequeuing jobs till all the jobs are processed. Semaphores are used for handling concurrency of the threads. This is a more fine-grained partitioning of the computation compared to the divide-and-conquer approach presented by Klamt [54]. Multithreading has a significant impact on the performance improvement, up to five times for eight parallel threads as shown in Table 5. The performance is evaluated on 2.83 GHz Intel Xeon E5440 CPU running Red Hat Linux.

Table 5.

Impact of multithreading for EFMtool

Model	Runtime (s)		Speedup
	1 thread	8 threads
E. coli	13,129.94	3709.69	3.5
E. coli (irrev)	0.57	0.16	3.6
E. coli (gluc)	38.74	10.91	5.1

Jevremovic et al. [55] developed a distributed memory parallel implementation of the null-space algorithm to enable handling the computational aspect of genome-scale metabolic networks. The algorithm assumes a parallel environment consisting of a set number of compute-nodes, each with their own memory. The compute-nodes communicate via messages. The authors tested their algorithm on the Blue Gene/P and Intel Xeon (Clovertown) parallel platform, attaining the computation of more than 13 million EFMs for the Saccharomyces cerevisiae strain, which contains 62 metabolites and 80 reactions, of which 31 reactions are reversible.

GPUs are specialized processors that were used for efficient graphics processing. GPUs were designed to support thousands of parallel threads that perform the same operation on different data. GPUs have shown significant improvements in various scientific applications. The primary advantage of using GPUs for a critical part of the computation is to parallelize the computation to achieve performance improvement. Khalid et al. [56] exploited the power of concurrent threads in GPUs by using a hybrid approach of using CPUs and GPUs. Khalid et al. generated new candidate rays using GCC 4.4.3 and CUDA 5.0 on Ubuntu SMP 12.04 for Tesla 2050 GPU (Fermi architecture). The implementation is 6x faster than the serial implementation and 1.8x faster than the multithreaded implementation for their five test cases on Intel Xeon E5620 CPU.

Although all scaling approaches have shown performance improvement, each has some disadvantages. Out-of-core computation requires load balancing, where partitioned computation must be distributed over available cores / processors. Synchronization of completed jobs is also required. Moreover, this approach is limited by the number of available cores / processors. Parallel computing suffers the same issues as that of out-of-core computation along with communication overheads. The communication overheads in distributed computing can be reduced by assigning big balanced jobs to the computing nodes. Although GPUs offer a huge number of concurrent threads, double-description implementations are difficult to speedup due to high thread divergence and synchronization overheads. Moreover, implementation of advanced data structure is a challenge for GPU implementation. The advantages and disadvantages of different parallel approaches are summarized in Table 6.

Table 6.

Summary of scaling techniques

Scaling approach	Pros	Cons
Out-of-Core	• Concurrent computations	• Load balancing
Computation	• In-memory calculations	• Synchronization overhead
		• Limited by number of processor cores
Parallel	• Concurrent computations	• Inefficient for longer iteration steps
Computing	• Unlimited nodes	• Out-of-memory computation
		• Load balancing
		• Synchronization overhead
		• Communication overhead
Graphical	• Huge number of concurrent threads	• High thread divergence
Processing	• In-memory (GPU memory) calculations	• Data structures cannot be used
Units (GPUs)	• Low data transfer overhead compared to distributed computing	• Synchronization overhead

Alternative pathway analysis approaches

EFM analysis utilizes only structural information (stoichiometry) of the network, which results in many identified EFMs that are infeasible, as they do not consider factors such as thermodynamic considerations, regulatory mechanisms and physiological concentrations of metabolites. Gerstl et al. [57] proposed thermodynamic elementary flux mode analysis (tEFMA) that verifies thermodynamic feasibility of EFMs. In tEFMA, intermediate EFMs are checked for thermodynamic feasibility using network embedded thermodynamic (NET) analysis [58]. NET analysis is formulated as a linear optimization problem that checks for the thermodynamic feasibility of all the reactions in an EFM (or intermediate EFM) in the context of whole EFM (or intermediate EFM). The optimization problem is not computationally expensive as it deals with the number of reactions equal to the length of EFM. All infeasible EFMs are immediately discarded thus reducing the number of combinations in each iteration of the algorithm. Gerstl et al. used this approach on an E. coli network (76 metabolites and 163 reactions). On glucose minimal medium, only 19% EFMs were feasible. Iterative application of thermodynamic constraints reduced the runtime and memory requirement by half.

Jungreuthmayer et al. [59] used transcriptional regulatory rules to discard infeasible EFMs. Transcriptional regulatory networks are often modeled as Boolean rule set. Boolean rules encode genes that represent activation or repression of a reaction. Expression of a gene ensures that only those EFMs are feasible in which activated reactions are present and repressed reactions are absent. The regulatory rules are applied as additional constraints in each iteration of EFM computation and infeasible intermediate EFMs are discarded. Jungreuthmayer et al. used this approach on an E. coli network (218 metabolites and 230 reactions). The actual number of EFMs for the network was 92.4 million with a computation time of 54.5 h. For four regulatory rules used by Jungreuthmayer, the number of EFMs was reduced to 0.45 million. Iterative application of the rules reduced the runtime by a factor of 132 and memory requirement by a factor of 146.

In an effort to avoid enumeration of all the EFMs, Kaleta et al. [60] proposed a method to identify balanced pathways in sub-networks in the context of the entire network. Kaleta et al. introduced the concept of flux patterns that define balanced pathways in a sub-network of a bigger network operating at steady-state. The flux values of the reactions in the sub-network are considered to be non-negative while considering the flux values of rest of the reactions in the network to be zero. Specifically, a flux pattern s in a sub-network of reactions 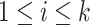satisfies the following conditions:

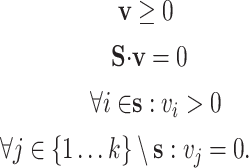Elementary flux patterns (EFP) can be identified by removing the flux pattern that can be expressed as combination of other flux patterns. Kaleta et al. showed that each EFP can correspond to at least one EFM in the complete network. EFPs can be used to determine the composition of minimal media required for the production of a compound of interest, determine the robustness of metabolic networks and analyze host–pathogen interactions. Flux patterns were used to specify minimum cut sets (MCS), irreducible sets of reactions whose removal hinders the activity of a target flux pattern [61]. Importantly, computing MCS in a primal network is equivalent to computing EFMs in the dual network [62 ]. Thus, techniques for computing EFMs can be used to compute MCS, e.g. [63, 64].

EFPs are identified by iteratively solving a mixed-integer linear program (MILP). Constraints of the MILP are updated in each iteration such that no flux pattern is identified that is a combination of already found flux pattern. The computational complexity of the algorithm is polynomial in the size of the entire system and exponential in the size of the sub-network. Although identification of EFPs is not computationally expensive compared to computation of EFMs, Marashi et al. identified three shortcomings of EFPs [65].

1. Flux values are ignored in EFPs; therefore, they cannot replace applications of EFMs where exact flux values are required.

2. Different EFMs can be represented using the same EFP due to absence of flux values.

3. Although each EFP can be mapped to at least one EFM, EFPs do not necessarily cover all EFMs.

Marashi et al. addressed the shortcomings by introducing the concept of Projected Cone Elementary Modes (ProCEMs). ProCEMs are projections of EFMs onto a lower dimensional subspace defined by the reactions of the sub-network. ProCEMs are computed by projecting the flux cone using the block elimination method [66] and then using the double-description method on the projected cone to compute extreme rays. The extreme rays of the projected cone represent ProCEMs.

Larhlimi and Bockmayr [67] represented metabolic networks in terms of minimal metabolic behaviors (MMB). MMBs have properties similar to EFMs and EPs such as set minimality and uniqueness. MMB representation uses an outer description of the flux cone based on sets of non-negativity constraints. MMBs represent faces of the flux cone encapsulated by EFMs. A single MMB can involve more than one EFM. Thus, the number of MMBs in a network is less than the number of EMFs in the network. Rezola et al. [68] proposed an optimization-based method for computing a convex basis of EFMs based on MMBs.

Barrett et al. [69] used Monte Carlo sampling and principal component analysis to obtain reactions that account for all range of flux states in the metabolic network. The sampling algorithm generates physiologically unrealistic inefficient flux distributions corresponding to high substrate uptake rates and very low growth rates. To overcome this problem, biasing in the sampling was introduced to generate flux distributions with growth rates of at least 90% of the maximum achievable growth rate. The analysis was applied to a reconstructed integrated transcriptional regulatory and metabolic network of E. coli [70], revealing that the top seven principle components are representative of the regulation of gene product activity by post-translational mechanisms [69].

Croes et al. [71] used shortest path algorithm to identify metabolic routes in biochemical networks. Blum et al. [72] developed MetaRoute, a search algorithm that identifies all the pathways between a given substrate and product. Ullah et al. [73] used graph traversal to identify flux limiting reactions in biochemical networks.

Further, Gerstl et al. [74] introduced the concept of flux tope (FT). FT is a pointed subcone of the flux cone generated by fixing the directions of all reversible reactions. Since FT is a full-dimensional cone, every FT contains a full pathway. FT analysis enables the determination of feasibility for combinations of reaction directions. FT enumeration is performed efficiently using reverse search [38] and EFMs can be computed for each FT without increasing the dimensions of the flux space.

Enumeration of all the EFMs makes EFM analysis a powerful tool; however, not all pathways are of interest. Limiting the EFM search to those EFMs or pathways with desirable properties is a promising alternate approach to identify all EFMs. Kaleta et al. [75] coupled optimization framework with a genetic algorithm (EFMEvolver) to explore the solution space and determine specific EFMs of interest. de Figueiredo [76] developed an integer linear programming framework to efficiently determine the k-shortest EFMs in large-scale metabolic networks. Pey et al. [77] used linear programming-based tree search method (TreeEFM) to enumerate a subset of EFMs. Pey and Planes [78] incorporated linear constraints in a linear programming framework to enumerate EFMs of interest. Arabzadeh et al. [79] selected reactions based on connectivity to metabolites/reactions of interest to compute a subset of EFMs. The integration of ‘omics’ data with EFM computing is another promising direction for focusing EFM analysis on flux modes of interest [80]. In general, limiting the EFM solution space has the advantage of significantly speeding the identification of the relevant EFMs.

Conclusion

EFM analysis is a powerful technique for a number of applications in the fields of metabolic engineering and systems biology. We reviewed two approaches based on the double-description method, namely the canonical and null-space approaches, and the pivotal method. Algorithms used for EFM computation have polynomial runtime in terms of the number of EFMs but the runtime complexity of the algorithms in terms of the network size is still an open problem. In general, the null-space approach outperforms the canonical approach as the former generates a smaller number of flux vector combinations and requires fewer comparison operations than the latter. Pivotal methods such as lrs underperformed those based on the double-description method. We reviewed several performance enhancement methods. Network compression consistently benefits all methods, including the lrs method where compression benefits were not previously evaluated. All double-description method algorithms are sensitive to constraint ordering. Importantly, knowledge about the network structure allows for a more robust ordering heuristic, as demonstrated for graph-based implementation. Removal of redundant constraints was beneficial to lrs. However, the removal of redundant constraints did not benefit any of the double-description algorithms.

Despite advances, identifying EFMs for genome scale models remains a computational challenge when using single-core computing. Threading improves performance but synchronization between threads is necessary and may limit expected linear scalability. Out-of-core computation and distributed computing have been proven to scale super-linearly with the number of processors used. An attempt has been made to use GPUs for generating combinations but so far GPUs have not been used for dependency testing, the most computationally intensive step in EFM computation. Despite out-of-core computation, distributed computing and GPUs have improved performance of EFM computation, scaling of EFM computation for genome-scale models and making it accessible to researchers remains an open challenge. Further, more targeted pathway analysis methods can provide powerful alternatives to EFM computing. Despite advance basic algorithms and computational scaling using GPUs, threading and distributed computing, identifying EFMs for genome scale models and making it accessible to researchers remains an open challenge.

Key Points

• Algorithms for computing EFMs are based on either the double-description method or pivotal methods.

• Constraint ordering and network compression can be utilized as preprocessing steps to improve EFM computing.

• Removal of redundant constraints does not seem to benefit double-description based methods.

• Parallel computing techniques promise to speed computing EFMs.

• Instead of the costly enumeration of all EFMs, there are many alternative pathway analysis approaches that aim to identify EFMs or pathways having specific properties.

 

Ehsan Ullah received her PhD degree in Computer Science from Tufts University and is currently working at Qatar Computing Research Institute.

Mona Yousofshahi received her PhD degree in Computer Science from Tufts University and is currently working in the medical device industry.

Soha Hassoun is Professor and past Chair of the Department of Computer Science at Tufts University.