Dependence of Tendon Multiscale Mechanics on Sample Gauge Length is Consistent with Discontinuous Collagen Fibrils

Abstract

While collagen fibrils are understood to be the primary load-bearing elements in tendon, controversy still exists on how fibrils functionally transmit load from muscle to bone. Specifically, it’s unclear whether fibrils are structurally continuous along the tendon length and bear load independently, or if they are discontinuous and transfer load through interfibrillar shear forces. To address this question, we investigated whether the multiscale mechanics of rat tail tendon fascicles is dependent on sample gauge length. We hypothesized that as the grip-to-grip length is reduced and approaches the length of the collagen fibrils, tendon fascicles will adopt a multiscale mechanical response consistent with structurally continuous fibrils. Our findings show that, for gauge lengths of 20 mm or greater, the local fibril strains are less than the bulk tissue strains, which can be explained by relative sliding between discontinuous collagen fibrils. In contrast, at a 5 mm gauge length, the fibril strains are equivalent to the applied tissue strains, suggesting that the collagen fibrils are structurally continuous between the grips. Additionally, the macroscale tissue modulus is increased at gauge lengths of 5 and 10 mm. Together, these data support the hypothesis that collagen fibrils in rat tail tendon fascicles are discontinuous and also suggest that their length is between 5 and 10 mm. This fundamental information regarding tendon structure-function relationships underscores the importance of the tissue components that transmit load between fibrils and is critical for understanding tendon pathology as well as establishing structural benchmarks for suitable tissue engineered replacements.

Introduction

Tendons transmit load from muscle to bone and are critical for musculoskeletal function. The high load bearing capabilities of tendon are due to its unique hierarchical structure [1]. In general, collagen molecules (predominantly type I) are densely organized into aligned fibrils that are further grouped into bundles (i.e., fibers) [2]. The fibers are themselves subunits of fascicles, which are the largest tendon subunit and are separated by loose connective tissue carrying blood vessels and nerves [3]. Despite this detailed understanding of tendon structure, it is still unclear whether collagen fibrils are structurally continuous and extend across the entire length of the tissue. This information has important implications regarding the how load is functionally transmitted from muscle to bone. For example, if collagen fibrils in tendon are not continuous, then the intervening structures that transmit load between the fibrils are also critically important for tendon function [4,5]. Therefore, conclusively answering the question of collagen fibril continuity is essential to understanding proper tendon function and the structural deficiencies responsible for tendon degradation, injury, and aging.

An obvious approach for investigating whether collagen fibrils in tendon are continuous is to directly measure their lengths. Intact fibrils have been successfully extracted from embryonic tendons, demonstrating that collagen fibrils are indeed discontinuous during tenogenesis [6]. This is consistent with more recent studies that tracked collagen fibrils within intact embryonic tendons using serial block-face scanning electron microscopy (SBF-SEM) and measured lengths between 100 and 600 μm [7]. However, fibrils cannot be extracted from mature tendon [6], and they are too long to successfully track across their entire length using SBF-SEM. Most recently, Svensson et al. tracked more than 2,500 fibrils over 25 μm in human patellar and hamstring tendons and found only one that ended within the imaging window [8]. Using probabilistic analysis, they estimated that the fibrils were at least 14 mm long, which the authors suggested is long enough that, even if collagen fibrils in tendon are not structurally continuous, they functionally behave as such (i.e., tendon failure results from fibril rupture rather than excessive fibril sliding). These conclusions are supported by additional studies that found no fibril ends in mature rat ligaments or tail tendon fascicles and reported similar estimates of fibril lengths ranging from 0.86 mm to 12.7 mm depending on maturity [9,10]. The interpretation that fibrils behave as functionally continuous structures is also consistent with mechanical data demonstrating that creep failure of bovine tail tendons under static load is the result of fibril denaturation and rupture rather than interfibrillar slippage [11]. Altogether, these findings suggest that collagen fibrils are structurally continuous and bear load independently.

On the other hand, there is a significant body of data suggesting that collagen fibrils in tendon are discontinuous and transfer load through viscous interfibrillar shear forces. Measurement of fibril strains using X-ray diffraction, confocal microscopy, and atomic force microscopy has shown that the fibril strains in rat tail fascicles and mouse Achilles tendons during uniaxial testing are significantly less than the bulk tissue strains [12–15]. In these papers, the strain discrepancy between length scales is explained by relative sliding between discontinuous fibrils. Consistent with this hypothesis, additional studies using x-ray diffraction during tendon creep testing showed that the fibril strains remained constant while the tissue elongated [16]. Similarly, data from multiscale stress relaxation experiments demonstrate that fibril strains in tendon are time dependent and follow the viscoelastic response of the macroscale tissue stress but not the bulk tissue strain [12,17,18]. Furthermore, following short periods of creep loading, the fibrils fully recover their original length, suggesting that non-recoverable interfibrillar sliding is responsible for tendon creep [19]. This is also consistent with work demonstrating that tendon multiscale mechanics can be uniquely explained by shear lag models incorporating plastic (i.e., non-recoverable) interfibrillar sliding and shear load transfer [20]. Similar sliding behavior is observed in tendon at smaller (i.e., collagen molecules) [21] and larger (e.g., fascicles) [22] length scales. Therefore, sliding between tendon subcomponents may be a hierarchically conserved phenomenon that sacrifices tissue stiffness for toughness [23–25]. Together, these data suggest that fibrils in tendon are discontinuous, and this discontinuous structure has an important impact on tendon mechanics and function.

To address this controversy, the objective of this study was to assess the functional length of collagen fibrils in tendon by investigating the dependence of tendon multiscale mechanics on sample gauge length. While the macroscale mechanical properties of tendon are known to be sensitive to sample gauge length [26], the microscale mechanisms mediating this effect are unclear. We hypothesized that, as the grip-to-grip length approaches the average length of the collagen fibrils, the tendon multiscale mechanical response will shift from a discontinuous to continuous fibril loading behavior, which will provide an estimate of the functional fibril length in tendon. Multiscale experimental testing was performed on rat tail tendon fascicles to examine differences in fibril strains compared to the bulk tissue strains at different gauge lengths. Our results demonstrate that the fibril strains were equivalent to the applied tissue strains at shorter gauge lengths, which also exhibited a significant increase in the macroscale tissue modulus. Together, these data suggest that the collagen fibrils in rat tail tendon fascicles are discontinuous and have an average length between 5 and 10 mm. Furthermore, this suggests that the structures linking the discontinuous fibrils and transmitting loads between them are as important in tendon structure-function relationships as the fibrils themselves. This fundamental information regarding tendon structure-function relationships is critical for understanding tendon pathology as well as establishing structural benchmarks for suitable tissue engineered replacements.

2. MATERIALS & METHODS

2.1. Sample Preparation

Twenty-two tail tendon fascicles were harvested from six one-year old Long Evan rats received from a separate IACUC-approved study. Upon harvesting, each sample was dragged through wet filter paper with light pressure to remove the paratenon and then stained with dichlorotriazinylaminofluorescein (5-DTAF, Invitrogen). Specifically, samples were incubated on a rotating mixer at room temperature for twenty minutes in 1.5 ml of a 5 μg/ml solution of 5-DTAF and 0.1 M sodium bicarbonate buffer (pH 9.0) [27]. After incubation, samples were washed with phosphate-buffered saline (PBS) for ten minutes to remove unbound stain.

2.2. Mechanical Testing

After staining, the sample ends were potted with cyanoacrylate [Loctite 454] in custom machined grips that incorporated a sinusoidal gripping surface (Fig. 1A–B). Tissue samples were mounted into grips and secured using a compression plate with the screws tightened to 5 in-lb of torque. Samples were randomly assigned to four different gauge lengths (GLs) of 30 mm (n = 6), 20 mm (n = 6), 10 mm (n = 5), and 5 mm (n = 5) while maintaining tissue hydration with PBS. All tests were conducted utilizing a 10 lb load cell (Model 31, Honeywell Inc.) with an accuracy and sampling frequency of ± 0.067 N and 100 Hz, respectively. In order to measure the fascicle dimensions, each sample was twisted and placed in a custom uniaxial tensile-testing device mounted atop an inverted confocal microscope (Nikon A1R HD) (Fig. 1C) with a PBS bath to ensure adequate hydration during testing. The twisted samples were loaded to 1 mN, and a stitched z-stack image (2.175 μm z-step, 0.83 um/px resolution) was captured spanning ~3.5 mm of the tissue centered at the sample’s midpoint. From the helical profile of the twisted sample, measurements of the major and minor diameters were made and used to calculate the cross-sectional area assuming an elliptical cross-section. The samples were then untwisted and preloaded to 1 mN to establish their initial reference lengths 30.53 ± 0.07 mm, 20.13 ± 0.17 mm, 10.64 ± 0.57 mm, 5.35 ± 0.06 mm). Finally, the samples were preconditioned at 1% grip-to-grip strain for 5 cycles at 0.03 Hz.

Figure 1:

Experimental setup for multiscale mechanical testing. (A) Custom grips with a sinusoidal mounting face for compressing the tendon sample. B) Uniaxial tensile testing device mounted atop a confocal microscope. C) Representative image of a 30 mm gauge length sample with photobleached line (PBL) sets at the sample center and ± 1.25 mm, ± 5 mm, and ± 10 mm locations.

Following preconditioning, sets of photobleached lines (PBL) (4 lines, 100 μm apart, 5 μm wide) were bleached at the sample center and at ± 1.25 mm, ± 5 mm, and ± 10 mm from the center (as permitted by the sample gauge length) (Fig. 1D). Samples were then stretched in 2% grip-to-grip strain increments at 10%/min followed by a 15 min stress relaxation. At the end of each relaxation period, z-stack images (2.175 μm z-step, 0.83 um/px resolution) were acquired at all PBL locations, and the microscope stage positions were recorded. Testing was stopped once there was a decrease in the equilibrium stress at the end of the relaxation period between strain increments. These incremental strain ramps and relaxation periods ensured that the applied stress values were stable while imaging the PBL sets, which were used to measure the fibril and macroscale tissue strains [12].

2.3. Image Processing and Data Analysis

Custom image processing code (MATLAB, MathWorks) was developed for determining the fibril strains from the PBL z-stack images as previously reported [12,23]. In short, a two-dimensional projection of the curved tendon surface was generated using Sobel edge detection [23]. At every position across the tissue width, the pixel locations of each PBL were determined by the pixel with the lowest local intensity value. For each grip-to-grip strain increment, the microscale fibril strains were measured as the change in the distance between the photobleached lines within the PBL sites at the sample center and at the ± 1.25 mm locations. The fibril strains were then averaged across the three PBL sites to provide a single value for each grip-to-grip strain increment. The macroscale tissue strains were calculated optically as the change in distance between the centroid position of the ± 1.25 mm PBL sets as measured from the recorded microscope stage positions. To determine whether the collagen fibrils are functionally continuous, the fibril:tissue strain ratio was calculated at each grip-to-grip strain increment by dividing the fibril strain by the macroscale tissue strain. As previously shown [20], this ratio is equal to one in the case of continuous collagen fibrils and is below one for discontinuous fibrils.

The equilibrium modulus, ultimate tensile strength (UTS), and percent stress relaxation were calculated to determine the tendon macroscale response as a function of sample length. A moving average (step size = 30 data points) was used to smooth the values from the load cell. The equilibrium stress value for each grip-to-grip strain increment was calculated by averaging the last 30 seconds of data within the 15 min relaxation period and plotted versus the optically measured tissue strain. The equilibrium modulus for each sample was then calculated by fitting a line through the initial portion of this stress-strain curve (i.e., data points between 0 and 1.5% strain). Note that, for these initial strain increments, the stress relaxation curves had reached equilibrium for all sample gauge lengths (Suppl. Fig. 1). The UTS was defined as the peak stress value over the course of the test, and the percent stress relaxation was calculated as the relative decrease in stress during each relaxation period.

2.4. Grip Effects and Strain Heterogeneity

To ensure that the results for the smaller gauge length samples were not confounded by strain concentrations resulting from gripping, we evaluated the strain heterogeneity along the sample lengths at the highest grip-to-grip strain prior to the onset of failure (i.e., decrease in equilibrium stress). Specifically, the regional macroscale tissue strain was measured as the change in distance between each neighboring set of photobleached lines (i.e., strain between the grip interface and the 10 mm PBL set, 10 and 5 mm PBL sets, 5 and 1.25 mm PBL sets, 1.25 mm and center PBL sets). Given the symmetric placement of the PBL sets along the sample length, the regional strain values from each side of the sample were averaged together and plotted as a function of the distance between the grip and the sample center.

We also investigated whether potential strain heterogeneity across the sample length affected the measurement of the fibril:tissue strain ratio described above (section 2.3). To ensure consistency with previous work [12], the 30 mm gauge length samples were used for this evaluation. Specifically, the fibril strains were calculated by averaging the values at the ± 1.25 mm PBL locations, and the fibril:tissue strain ratio was calculated by dividing this value by the macroscale tissue strain measured between these two locations. This was repeated to calculate the fibril:tissue strain ratio using the ± 5 mm and ± 10 mm PBL sites. For each calculation of the fibril:tissue strain ratio, the change with increasing tissue strain was determined. By comparing the behavior of the fibril:tissue strain ratios calculated using the different PBL sites, we can determine whether our measurements (and importantly our interpretation regarding fibril continuity) are influenced by the PBL locations.

2.5. Statistical Methods

Based on our previous data [12], we expect that the fibril:tissue strain ratio will start at one and decrease with increasing applied tissue strains, which is consistent with discontinuous collagen fibrils and plastic interfibrillar shear load transfer [20]. Therefore, to evaluate whether the multiscale mechanical response at different gauge lengths is consistent with discontinuous fibrils, linear regressions were conducted to test whether the fibril:tissue strain ratio was negatively correlated with the applied tissue strain, and an ANCOVA was used to test for differences in the slope for each gauge length. Additionally, Student’s t-tests were used to determine if the fibril:tissue strain ratio was different from one at the largest strain increment. However, given that the last strain increment exhibited a drop in the equilibrium stress, which may indicate fibril rupture, we also analyzed the data excluding the last strain increment and any data points where there was a reduction in sample number due to sample rupture. A one-way ANOVA was conducted to test whether the UTS and macroscale equilibrium modulus were affected by the sample gauge length. Post-hoc Dunnett’s tests corrected for multiple comparisons were then conducted to evaluate the UTS and modulus differences compared to the 30 mm gauge length samples. An ANCOVA was utilized to test whether the percent stress relaxation (controlling for the applied tissue strain) was dependent on the sample gauge length with Bonferroni post-hoc tests. Finally, an ANCOVA was conducted to test whether the slope between the fibril:tissue strain ratio and the applied tissue strain was dependent on the location of the PBL sets for the 30 mm samples. All data sets were confirmed to be normally distributed with a Kolmogorov-Smirnov test prior to statistical assessment. Statistical tests were conducted utilizing GraphPad Prism (Version 8.3.0) and R (Version 3.6.6), statistical significance was set to p < 0.05, and all data are presented as the mean ± the standard deviation.

3. RESULTS

3.1. Accounting for Strain Heterogeneity Along Sample Length

Using the multiple sets of lines photobleached onto each sample, the macroscale tissue strains were calculated at various points along the sample length to assess the strain heterogeneity and possible grip effects for each gauge length. At 6% grip-to-grip strain, a clear strain gradient was observed with large strains near the grip interface and low strains near the center of the sample (Fig. 2). Importantly, we did not find large macroscale tissue strains at the sample center for the short gauge length samples. This suggests that, even for the 5 mm gauge length samples, the macroscale strain measurements calculated using the ± 1.25 mm PBL sites did not include the strain concentrations at the grips. Additionally, we confirmed that this strain heterogeneity was also observed with different types of sample grips to ensure that it is not an artifact unique to our setup (Suppl. Fig. 2).

Figure 2:

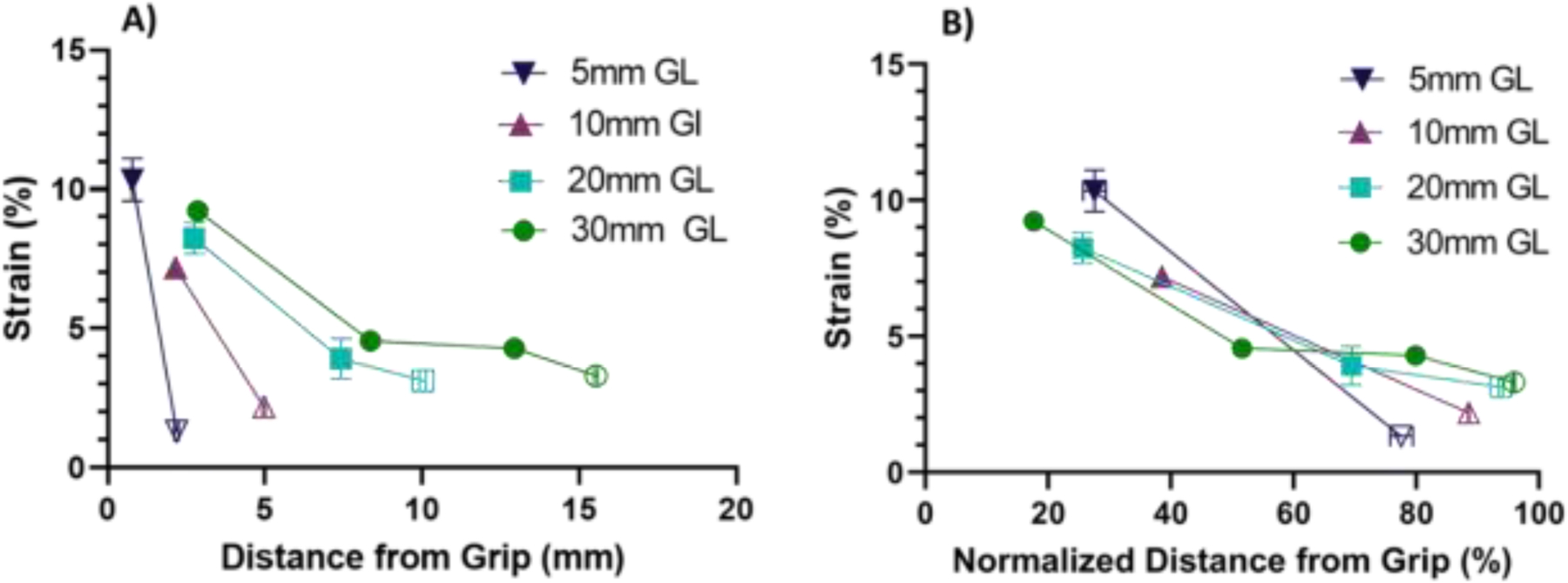
Strain heterogeneity along tissue length at 6% grip-to-grip strain for each sample gauge length. A) All sample lengths exhibited significant strain gradients, which increased with decreasing sample length. B) Normalizing the distance from the grip by the length between the grip and the sample center shows that the macroscale tissue strains nearest the sample center calculated using the ± 1.25 mm PBL sets (unfilled data points) are comparable for all groups.

The large macroscale tissue strain gradients observed in Fig. 2 suggest that the measurement of the fibril:tissue strain ratio may be dependent on the location of the photobleached lines. In addition, as the distance separating the PBL sets is reduced, the strain between the PBL sets (i.e., macroscale tissue strain) will approach the strain between the individual photobleached lines (i.e., fibril strain). Therefore, we investigated whether the negative correlation between the fibril:tissue strain ratio and the applied tissue strain observed previously using PBL sites at ± 5 mm [12] is still measurable when using the ± 1.25 mm PBL sites. Tests conducted on 30 mm gauge length samples indicate that, while the absolute value of the fibril:tissue strain ratio depends on the location of the PBL sites used to calculate the macroscale strains, the dependence on the applied tissue strain remains consistent (Fig. 3). Specifically, the fibril:tissue strain ratio at the last strain increment was significantly less than one (p < 0.001) for all PBL site locations. Additionally, linear regressions showed a significant negative slope (p < 0.001) with increasing applied tissue strain regardless of which PBL sites were utilized. Furthermore, the slopes themselves were not statistically different from one another (p = 0.72). Altogether, these findings demonstrate that the data obtained using the ± 1.25 mm PBL sites is consistent with previous studies showing discontinuous collagen fibril behavior for 30 mm tendon fascicles and can be used to compare results from samples with smaller gauge lengths without influence from gripping artifacts.

Figure 3:

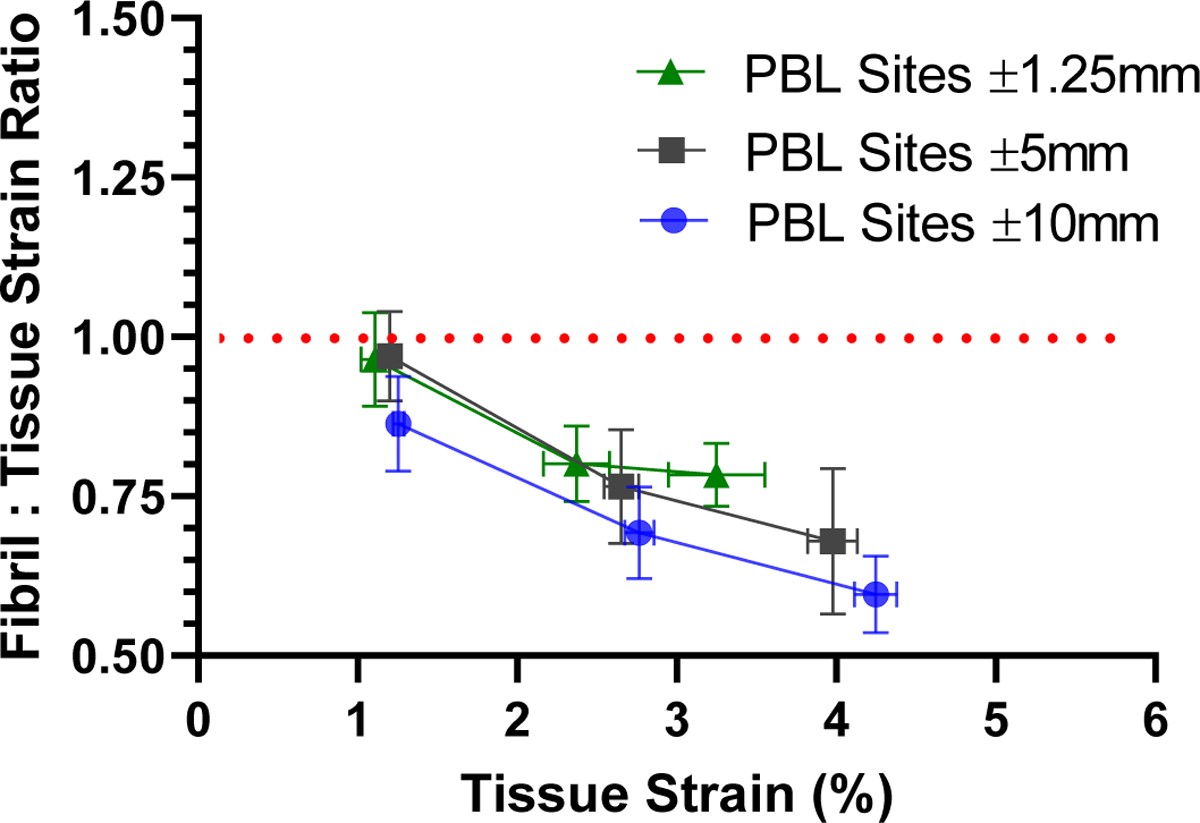
Fibril:tissue strain ratio in 30 mm long samples calculated using PBL sets at different positions along sample length. Regardless of the PBL sets used to measure the multiscale tendon strains, the fibril:tissue strain ratio showed the same negative correlation with the applied tissue strain (p = 0.72). This demonstrates that the ±1.25 mm PBL sets can be used to measure a valid fibril:tissue strain ratio.

3.2. Dependence of Tendon Multiscale Mechanics on Sample Gauge Length

After validating that the ± 1.25 mm PBL sets can be used to provide accurate measurements of the fibril:tissue strain ratio and macroscale tissue strains, we used these PBL sets to investigate whether tendon multiscale mechanics is affected by the sample length. At the macroscale level, we found a clear difference between the shorter (≤ 10 mm) and longer (≥ 20 mm) samples (Fig. 4). Specifically, the 5 mm and 10 mm samples had a significantly greater equilibrium modulus compared to the 30 mm samples (p < 0.001). Note that only the data points between 0 and 1.5% tissue strain were used to calculate the equilibrium modulus. The stress relaxation following each strain increment increased with the applied tissue strain (p < 0.001) and was dependent on the sample gauge length (p < 0.001) (Fig. 4C). Post-hoc comparisons with the 30 mm samples demonstrated that the stress relaxation was not different for the 20 mm samples (p = 0.8) but was increased for the 5 and 10 mm samples (p < 0.01 and p < 0.05, respectively). Finally, no difference was observed with sample length for the UTS (p = 0.41) (Fig. 4D).

Figure 4:

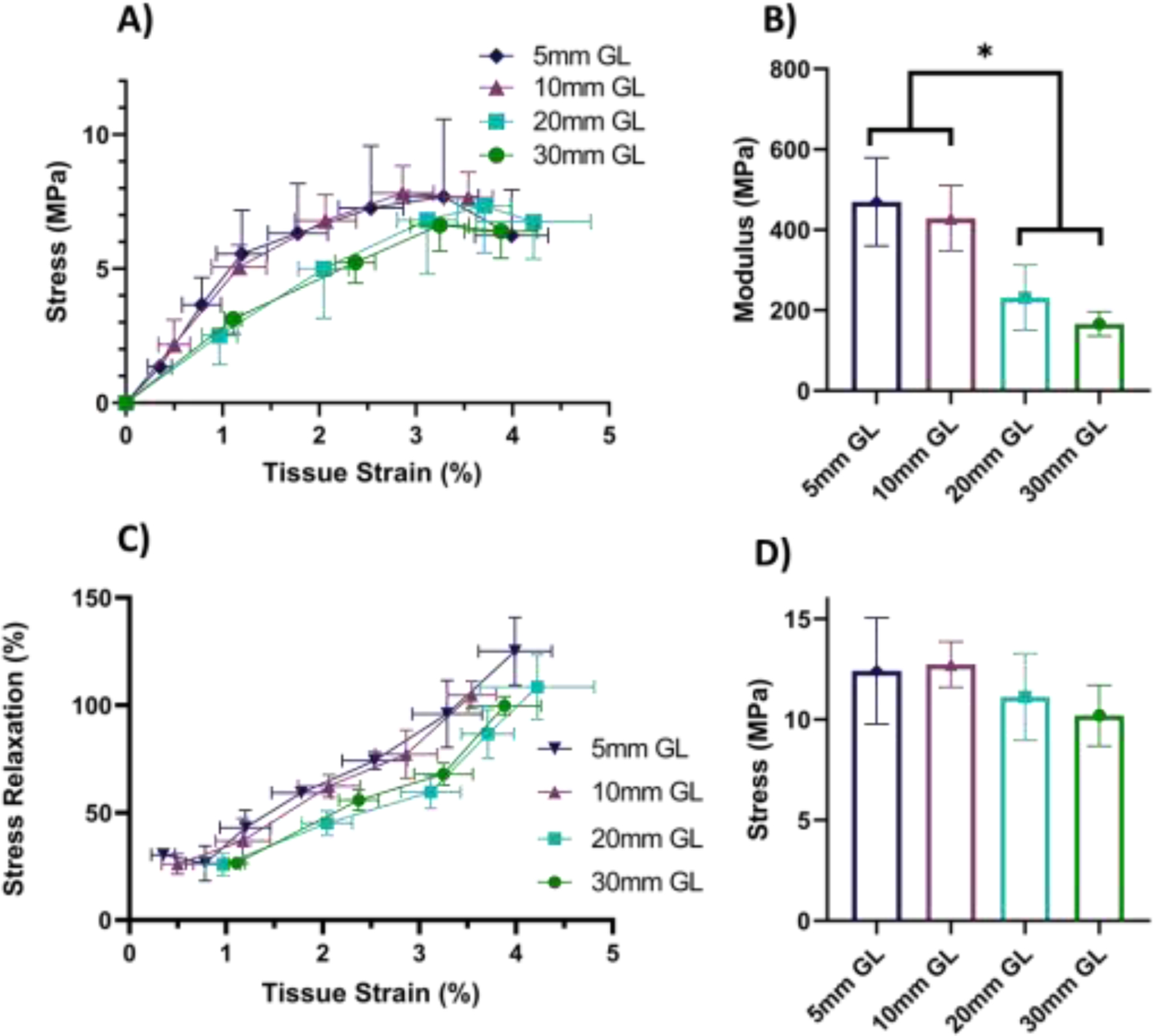
Tendon macroscale mechanical response at various gauge lengths. A) Equilibrium stress vs strain response for 30 mm (n=6), 20 mm (n=6), 10 mm (n =5) and 5 mm (n =5) gauge lengths. Note that, while one-sided error bars were used for clarity, the error is still symmetric about the mean. B) The macroscale tissue equilibrium modulus of the 5 mm and 10 mm samples was significantly greater than the 30 mm gauge length samples (* p < 0.001). C) The stress relaxation was also significantly greater in the 5 mm and 10 mm samples compared to the 30 mm samples (p < 0.001). D) While the ultimate tensile stress exhibited an increasing trend with decreasing gauge length, the difference was not statistically significant (p = 0.41).

Using the entire dataset for the analysis of the fibril strains, we found that the fibril:tissue strain ratio ultimately dropped below one for all sample lengths (30 mm: p < 0.0001, 20 mm: p < 0.05, 10 mm: p < 0.005, 5 mm: p < 0.05) (Fig. 5A). Additionally, there was a negative correlation between the fibril:tissue strain ratio and the applied tissue strain for all samples (30mm: p < 0.0001, 20mm: p < 0.05, 10 mm: p < 0.01, 5mm: p < 0.001) and the slopes were not significantly different between groups (p = 0.50). Given that sample failure may be due to fibril rupture [11,28], which would decrease the fibril lengths and reduce the fibril:tissue strain ratio, we also analyzed the results excluding the data points suggestive of sample failure (i.e., the final strain increment that exhibited a drop in the equilibrium stress and any data points where there was a reduction in sample number due to sample rupture). With these adjustments, we found that the fibril:tissue strain ratio still dropped below one for the 30 mm and 20 mm gauge lengths (p < 0.0001 and p < 0.05, respectively) (Fig. 5A). However, prior to the onset of sample failure, the fibril:tissue strain ratio for the 5 mm and 10 mm samples was not statistically different from one (p = 0.77 and p = 0.15, respectively). Additionally, linear regressions of the fibril:tissue strain ratio with the applied tissue strain through only the pre-failure increments (filled data points) demonstrated a negative correlation for the 30 mm and 10 mm samples (p < 0.0001 and p < 0.05, respectively), while the 20 mm and 5 mm samples did not (p = 0.09 and p = 0.27, respectively). Therefore, the 5 mm gauge length samples were the only group that exhibited both a fibril:tissue strain ratio that was equivalent to one and was independent of the applied tissue strain prior to the onset of sample failure.

Figure 5:

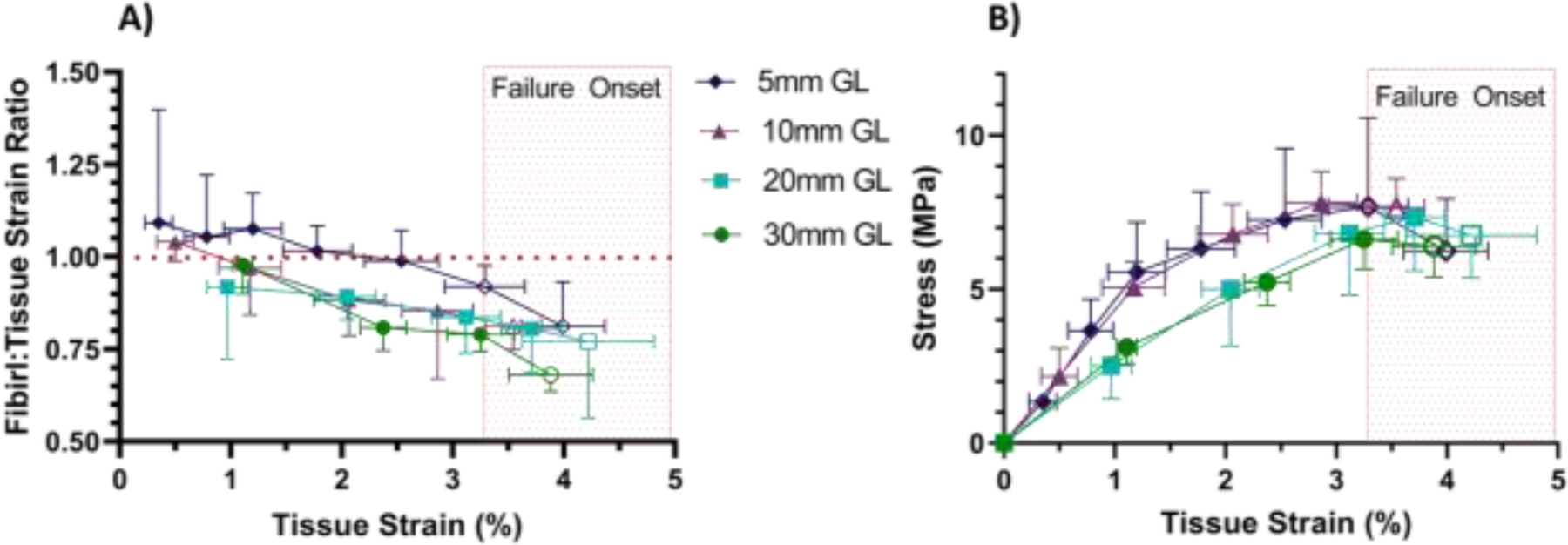
Multiscale mechanical response as a function of applied tissue strain for all sample gauge lengths (GL). A) Analysis of the full dataset demonstrated that ultimately the fibril:tissue strain ratio dropped below one for all samples (30 mm: p < 0.0001, 20 mm: p < 0.05, 10 mm: p < 0.005, 5 mm: p < 0.05) and was negatively correlated with applied tissue strain (30 mm: p < 0.0001, 20 mm: p < 0.05, 10 mm: p < 0.01, 5 mm: p < 0.001). Exclusion of data points suggestive of sample failure (unfilled markers) shows that the fibril:tissue strain ratio prior to failure still dropped below one for the 30 and 20 mm GL samples (p < 0.0001 and p < .05, respectively) and was negatively correlated with tissue strain for the 30 mm and 10 mm GL samples (p < 0.001 and p < 0.05 respectively). However, prior to failure, the fibril:tissue strain ratio for the 5 mm samples did not drop below one and was independent of applied tissue strain. B) Equilibrium stress vs. tissue strain for all samples. Unfilled data points indicate the strain increments where there was a drop in the equilibrium stress or there was a reduction in sample size due to sample rupture. The light red box is intended to highlight that the onset of sample failure (i.e., unfilled markers) is generally consistent for all sample lengths. While one-sided error bars were used for clarity, the error is symmetric about the mean.

4. DISCUSSION

This study demonstrated that sample gauge length has a significant effect on the multiscale mechanical properties of tendon fascicles. More specifically, prior to the onset of failure, rat tail tendon fascicles with gauge lengths greater or equal to 20 mm exhibited a fibril:tissue strain ratio that is less than one and that decreases with increasing applied tissue strain. Previous studies have suggested that this behavior is indicative of discontinuous fibrils that transfer loads via plastic interfibrillar sliding [12,20]. In contrast, rat tail tendon fascicles with a 5 mm gauge length exhibited a pre-failure fibril:tissue strain ratio equivalent to one that is independent of the bulk macroscale tissue strain, suggesting that, prior to the onset of failure, the collagen fibrils were continuous between the grips at this gauge length [20]. This interpretation is further supported by an increase in the macroscale equilibrium tissue modulus in the 5 mm gauge length samples. Interestingly, the 10 mm gauge length samples exhibited a mixture of discontinuous and continuous fibril behavior. That is, while the 10 mm samples had a macroscale equilibrium modulus that was identical to the 5 mm samples, they exhibited a decrease in the fibril:tissue strain ratio with increasing applied tissue strain prior to the onset of failure, which is similar to the 30 mm samples and consistent with plastic sliding between discontinuous fibrils [12,20]. We hypothesize that the 10 mm gauge length represents a transition between discontinuous and continuous fibril behavior in which a mixed population of continuous/discontinuous fibrils exists between the grips. This interpretation is consistent with previous estimates of fibril lengths of 0.86 – 12.7 mm in mature rat tail tendons [9,10,29]. Furthermore, for a fibril length of 5–10 mm, shear lag modeling suggests that an interfibrillar shear stress of approximately 1 kPa is necessary to produce the multiscale mechanical behavior of tendon fascicles [12], which is within the 32 ± 33 kPa estimate obtained from previous experiments [23]. Together, these data support the hypothesis that collagen fibrils in rat tail tendon fascicles are discontinuous and have a length on the order of 5 to 10 mm.

After the onset of failure (i.e., a drop in the equilibrium stress), all samples, regardless of gauge length, exhibited a mechanical behavior consistent with discontinuous fibrils (i.e., a fibril:tissue strain ratio that was less than one and negatively correlated with the applied tissue strain) (Fig. 5). It is possible that the rapid reduction in the fibril:tissue strain ratio after the onset of failure for the 5 mm samples is due to rupture of a substantial proportion of the collagen fibrils. Further inspection of the multiscale mechanics of the 5 mm samples suggests that some fibril rupture may occur even in the pre-failure region of the stress-strain curve. Specifically, at approximately 1% tissue strain, there is a clear decrease in the slope of the stress-strain curve for the 5 mm samples (Fig. 5B). Interestingly, there also appears to be a decrease in slope for the fibril:tissue strain ratio (Fig. 5A) and an increase in the stress relaxation (Fig. 4C) for the 5 mm samples at this same data point. While speculative, we hypothesize that, prior to 1% applied tissue strain, the 5 mm samples have structurally continuous fibrils between the grips, agreeing with the constant fibril:tissue strain ratio of one, increased macroscale equilibrium modulus, and stable stress relaxation. Beyond 1% tissue strain, some of the fibrils rupture, initiating a partially discontinuous fibril response with a reduced macroscale tissue modulus and a decrease in the fibril:tissue strain ratio with increasing applied tissue strain. Additionally, the stress relaxation begins to increase with tissue strains above 1%. At the onset of macroscale sample failure (red region in Fig. 5), the fibril:tissue strain ratio drops more rapidly due to pervasive fibril rupture, which then leads to rupture of the whole sample.

Our interpretation that the 5 mm samples undergo progressive fibril rupture during testing is consistent with studies suggesting that collagen fibrils are at least functionally (if not structurally) continuous and that the primary failure mechanism within tendon is fibril rupture rather than excessive interfibrillar sliding [8,11]. That is, even if the fibrils are discontinuous, they are long enough such that the axial stress that accumulates in the fibrils due to interfibrillar load transfer exceeds the fibril ultimate tensile strength [8]. This would suggest that regardless of fibril continuity, tendon failure is due to fibril failure. This is supported by a recent study by Hijazi et al. showing that tendon creep failure under static loading is the result of fibril denaturation and rupture rather than uncontrolled interfibrillar sliding [11]. Our current data also support this idea; even though the 5 mm samples initially behave as though the fibrils are continuous between the grips, they have a similar ultimate tensile strength as the 30 mm samples (Fig. 4D), which exhibit a discontinuous fibril behavior throughout testing. Furthermore, the greater stress relaxation in the 5 mm and 10 mm samples above 1% tissue strain (Fig. 4C) suggests that interfibrillar sliding [15,18,24] and fibril failure/denaturation [11,30] contribute additively to tendon viscoelastic behavior. This is further supported by the rapid increase in stress relaxation after the onset of failure (> 3.25% tissue strain) for all sample gauge lengths.

Based on our current findings and existing literature, we propose that collagen fibrils are discontinuous with a length of 5–10 mm and that tendon damage is a combination of non-recoverable interfibrillar sliding and fibril rupture. With initial loading, there is little damage to the collagen fibrils, which is supported by creep testing showing that, prior to tertiary creep, the collagen fibrils are undamaged and exhibit full elastic recovery with unloading [11,19]. At this point, permanent tendon elongation is due to non-recoverable interfibrillar sliding potentially resulting from damage to sacrificial small diameter fibrils that transmit load between the larger diameter axial load-bearing collagen fibrils [4,31,32]. Nevertheless, the shear stress generated via interfibrillar sliding is sufficient to rupture these large diameter fibrils leading to macroscale tissue failure [11]. This is consistent with plastic shear lag modeling, which suggests that the interfibrillar shear stress would be about 1 kPa for collagen fibrils that, based on our current data, are approximately 10 mm long [12]. Assuming that the interfibrillar overlap between fibrils is on average half of the fibril length, the maximum axial stress within the fibrils can be calculated as τL/r [8], where τ is the interfibrillar stress, L is the average fibril length, and r is the average fibril radius (i.e., 70 nm [33]). This would produce a maximum fibril stress of about 140 MPa, which is within the range of the UTS estimated from mechanical testing of individual collagen fibrils [34,35].

A significant issue with comparing mechanical data for soft tissue samples with varying gauge lengths is accounting for gripping artifacts. Indeed, using optical strain measurements, we found that there were large strain gradients along the sample lengths. Because these gradients were greatest for the samples with the smallest gauge lengths, the strains near the center of the samples (i.e., within the ± 1.25 mm PBL sites) were similar across groups and not affected by the large strain concentrations at the grips (Fig. 3). Therefore, the optical measurements of the macroscale tissue strain in this central region enabled accurate evaluation of the effects of sample gauge length on the multiscale mechanics of tendon fascicles. Highlighting this point, a previous study that used grip-to-grip measurement of the tissue strains found that the modulus of tendon fascicles decreases with smaller sample gauge lengths [26], which is the exact opposite of our data. Since their calculations includes the strain concentrations at the grips, it is likely that the difference in methodology accounts for these incongruent findings.

A limitation to this study is that confocal microscopy does not have sufficient resolution to image collagen fibrils directly. Indeed, the resolution of our images was 0.83 μm/pixel, which is approximately 6 times the average fibril diameter [33]. However, this is significantly less than the 10–50 μm diameter of fibril bundles (i.e., fibers) [2]. Given that the photobleached lines remained continuous throughout testing down to the individual pixel (Suppl. Fig. 3 & 4), this suggests that our microscale measurements represent a local average of the individual fibril strains rather than the strains of fibril bundles. This is further supported by the fact that studies using X-ray diffraction to directly measure fibril strains in tendon also found that the fibril strains are substantially less than the applied tissue strains [15,16]. An additional limitation is that rat tail tendon fascicles may not be representative of clinically relevant human tendons. While they share the same general hierarchical collagenous structure as other tendons [2], rat tail tendon fascicles also have certain unique structural features (e.g., acid-labile crosslinks) [28]. Nevertheless, previous studies estimated comparable fibril lengths in human patellar and hamstring tendons (> 14 mm) and rat tail tendon fascicles (~ 13 mm), suggesting that our findings may indeed apply to human tissue. Finally, it is possible that fibril lengths vary with age. Indeed, fibril lengths are known to change rapidly during embryonic and neonatal stages of development [33,36,37]. Future work will investigate whether these structural changes are responsible for the functional changes in tendon mechanics observed during the same time period [38].

4.1. Conclusion

This study demonstrates that sample gauge length has a significant effect on the multiscale mechanical properties of tendon fascicles. Specifically, as the gauge length is reduced, the fibril strains become equal to the macroscale tissue strains and the tissue equilibrium modulus increases. Together, this supports our hypothesis that collagen fibrils in tendon are discontinuous and suggests that they are approximately 5–10 mm long in rat tail tendon fascicles. While not structurally continuous, this length suggests that the fibrils are still functionally continuous such that that ultimate tendon failure is likely due to fibril rupture rather than excessive interfibrillar sliding. Nevertheless, establishing that the load-bearing fibrils are discontinuous highlights the importance of the intervening structures that transmit interfibrillar loads (e.g., small diameter sacrificial collagen fibrils) [31,32]. This information is essential to understanding how structural changes lead to tendon pathology and what structures are important for tissue engineering biomaterials that replicate tendon function.